Производные от: производный от | Перевод производный от?

Производные от войны – Газета Коммерсантъ № 81 (6561) от 15.05.2019

В мае вновь вырос пессимизм международных инвесторов в отношении торгового противостояния между США и Китаем. Росту негативных настроений способствуют взаимные обвинения сторон в срыве переговоров и обещания повысить ввозные пошлины. Впрочем, инвесторы не спешат сокращать вложения в акции, предпочитая захеджировать свои позиции производными инструментами.

Фото: China Stringer / Reuters

В ежемесячном международном опросе управляющих Bank of America Merrill Lynch приняли участие 250 респондентов, под управлением которых находятся активы общей стоимостью $687 млрд. Исследование показало, что в мае вновь выросли опасения инвесторов относительно торгового противостояния между США и Китаем. По данным опроса, 37% управляющих назвали торговую войну ключевым риском с непредсказуемым последствием для мировой экономики. В предыдущий раз инвесторы выражали столь серьезные опасения в конце прошлого года.

Вместе с тем в начале года опасения инвесторов относительно начала торговой войны преимущественно снижались. Этому способствовали стартовавшие в середине января переговоры между представителями обеих стран. Хотя за четыре месяца стороны так и не подписали торговый договор, но заявления официальных политиков и чиновников свидетельствовали о том, что они близки к его заключению. Ситуация изменилась на прошлой неделе, когда президент США Дональд Трамп в Twitter написал, что с 9 мая поднимет пошлины с 10% до 25% на китайский импорт на сумму около $200 млрд. В ответ Китай пообещал ответные шаги. «Рынки оценивали торговую сделку между США и Китаем как почти свершившийся факт. Однако сделка сорвалась по неизвестным причинам»,— отмечает заместитель директора инвестиционного департамента UFG Wealth Management Евгений Пундровский.

Дональд Трамп, президент США, на странице в Twitter, 5 мая 2019 года
В течение десяти месяцев Китай платил пошлины США в 25% на высокотехнологичную продукцию стоимостью $50 млрд и 10% на $200 млрд других товаров. Эти платежи частично сыграли роль в выдающихся результатах нашей экономики. А в пятницу 10% вырастут до 25%

В таких условиях аппетит к риску у инвесторов заметно снизился. По данным опроса BofA, число управляющих, уровень вложений в акции которых превышает индикативный, на 11% превысило число тех, кто их сокращал. Месяцем ранее оптимистов было на 17% больше. Наиболее сильно снизились позиции инвесторов в акциях американских и азиатских компаний. Число управляющих, у которых вес таких акций в портфелях превысил индикативный уровень, сравнялся с числом тех, у кого он был ниже. При этом инвесторы продолжают держать большие позиции в акциях компаний развивающихся стран. «От значительной распродажи управляющих удерживает вера в принципы челночной дипломатии, заложенной еще Генри Киссинджером, которые позволят найти баланс интересов. Инвесторы верят, что большая война не выгодна никому, а маленькая нужна, чтобы выпустить пар»,— считает гендиректор по фондовым операциям УК ТФГ Равиль Юсипов.

Смягчающим фактором в этой истории является ожидание смягчения монетарной политики американского регулятора. «Сейчас вероятность одного снижения ставки ФРС уже превысила 40%, и такие ожидания вызывают спрос на US Treasuries»,— отмечает господин Юсипов.

Вместе с тем более трети опрошенных инвесторов приняли меры защиты от резкого падения фондовых рынков в течение следующих трех месяцев, что является самым высоким уровнем в истории опроса. «Инвесторы хорошо хеджированы, но не расположены к срыву торговых переговоров»,— заявил главный инвестиционный стратег BofA Merrill Lynch Майкл Хартнетт. По словам Евгения Пундровского, после твитов господина Трампа о повышении тарифов большинство инвесторов увеличили долю наличных денежных средств в портфеле, многие из них захеджировали длинные позиции в акциях с помощью деривативов. «Ряд технических показателей по американскому фондовому рынку (S&P 500) в последнее время указывают на его перекупленность. Это и индекс RSI (индикатор, определяющий силу тренда и вероятность его смены), показатель волатильности VIX, индикатор Bull Bear.

К тому же мультипликатор p/e вернулся к отметке 16,8, что выше среднего значения за десять лет (14,7). Кроме того, рынок недавно вновь достиг абсолютного максимума, а сезонность выступает в поддержку коррекции»,— отмечает аналитик General Invest Татьяна Симонова.

Виталий Гайдаев

Местоимения some, any, no, every и производные от них

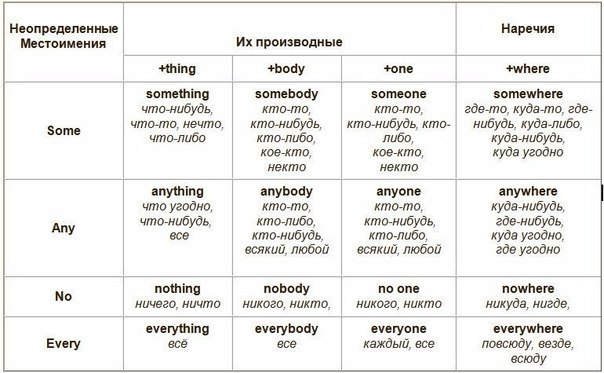
МЕСТОИМЕНИЯ И НАРЕЧИЯ, ПРОИЗВОДНЫЕ ОТ SOME, ANY, NO, EVERY
ОСНОВНЫЕ МЕСТОИМЕНИЯ	ПРОИЗВОДНЫЕ МЕСТОИМЕНИЯ			ПРОИЗВОДНЫЕ НАРЕЧИЯ
	+thing	+body	+one	+where
Some	something что-то, что-нибудь, что-либо, нечто	somebody кто-то, кто-нибудь, кто-либо, кое-кто, некто	someone кто-то, кто-нибудь, кто-либо, кое-кто, некто	somewhere где-то, где-нибудь, куда-то, куда-нибудь, куда-либо, куда угодно
Any	anything что-нибудь,  все, что угодно	anybody кто-то, кто-либо, кто-нибудь, всякий, любой	anyone кто-то, кто-либо, кто-нибудь, всякий, любой	anywhere где-нибудь, куда-нибудь, где угодно, куда угодно
No	nothing ничто, ничего	nobody никто, никого	no one никто, никого	nowhere нигде, никуда
Every	everything всё	everybody все	everyone все, каждый	everywhere везде, повсюду, всюду

производных.

С нуля | Каспер Мюллер

С нуля

Изображение автора

Мир меняется. Если мы хотим понять природу и законы, которым она должна следовать, нам нужны язык и инструмент, хорошо подходящие для этого. Исчисление является таким инструментом, и первый действительно полезный инструмент, который вы изучаете в исчислении, — это дифференцирование и производные.

В этой статье мы рассмотрим следующее:

· Моя первая встреча с деривативами
· Склон 9a
∘ Обозначение
∘ Линейность
· Правила дифференцирования
∘ Правило произведения
∘ Правило частных
∘ Цепное правило
· Правило Лопиталя
· Серия Тейлора
∘ Применение серии Тейлора

5 опыт работы с деривативами. Я учился в гимназии (средней школе). Было лето и выходные (наконец-то!).

Мне нужно было сделать кое-какую надоедливую домашнюю работу, поэтому я заварил чашку кофе и устроился под яблоней в саду моих родителей (хотя ни одно яблоко не упало мне на голову, что дало мне отличные идеи).

В то время я вообще не любил математику. Я думал, что это было скучно и пыльно. Очевидно, я понятия не имел, что это было на самом деле.

Вернувшись в сад, я читал об этой концепции поиска наклонов графиков функций и о том, как ее можно использовать для решения задач оптимизации.

Теорию я понял не сразу, но у меня был (в то время) навороченный калькулятор, который почти все расчеты делал за меня.

Мой папа сел рядом со мной и мельком увидел особенно раздражающую проблему, с которой я боролся, и через несколько секунд он сказал мне, каково окончательное решение.

Я ему не поверил, потому что не думал, что можно так быстро решить проблему в уме. Я программировал свой технический математический инструмент и тратил на это очень много времени, чтобы решить его, а он только один раз взглянул на задачу и тут же дал мне ответ!

Когда я, наконец, пришел к решению, разумеется, он был прав. Я был удивлен! Тоже немного в шоке. Как это было возможно?

С этого момента я решил, что стану хорош в математике, и начал читать все книги по математике, которые попадались мне в руки. Даже книги, которые были слишком продвинуты для меня в то время. Но я начал с изучения производных и исчисления в целом и за год или около того стал в этом довольно приличным.

Я говорю вам это потому, что даже если вам не хватает некоторых фундаментальных областей математики, на самом деле можно начать здесь с этого предмета, а затем прочитать основы на стороне.

Напомним, что для линейного многочлена, то есть линии, наклон постоянен, что означает, что он не зависит от входной переменной. Фактически, это свойство является определяющей чертой линии.

Отправной точкой исчисления является обобщение понятия наклона на нелинейные функции.

Допустим, у нас есть функция

f(x) = x³ – x² + x.

Проведем прямую через график, пересекающую его (как минимум) в двух точках. Такая линия называется секущей.

Напомним, что формула для расчета наклона этой линии — Δf/Δx.

Допустим, мы хотим вычислить наклон секущей через точки (x, f(x)) и (x + Δx, f(x + Δx)) . Тогда наклон определяется как:

Это, конечно, просто расчет наклона для линии.

Идея состоит в том, что если мы позволим второй точке пересечения приблизиться к первой точке, приравняв Δx к 0, то если мы увеличим масштаб первой точки пересечения на графике f так, чтобы мы смотрели на маленькую окрестности вокруг этой точки , , затем график f будет выглядеть как секущая в этой окрестности.

В самом деле, если мы возьмем предел как Δ x → 0, то секущая будет приближаться к линии, касающейся графика f , не просматривая график f в этой точке. Эта ограничительная линия показана на следующем изображении:

Такая линия называется касательной f в точке (x, f(x)) . Если мы будем приближать точку, то чем больше мы будем приближать, тем больше касательные будут похожи на график f , и в пределе они станут неразличимы.

Следовательно, мы можем определить наклон f в этой точке пределом наклона секущей, когда Δx стремится к 0, который затем становится наклоном касательной.

Так мы определяем наклон для нелинейных функций. По пределу. Мы называем это «производной f », а действие по вычислению производной называется дифференцированием.

На самом деле это из математики. Когда вы находитесь рядом с точкой, вы приближаетесь к графику, но по мере продвижения по касательной вы все дальше и дальше от него удаляетесь.

Обратите внимание, что, в отличие от линейной функции, производная нелинейной функции непостоянна. То есть это сама непостоянная функция. Обозначим производную от 9a

Рассмотрим приведенную выше функцию. Как бы мы вычислили производную этого, используя только определение?

Начнем с простого случая f (x) = x² .

Итак, мы доказали, что производная от x² равна 2x . На самом деле, умело используя биномиальную теорему и определение, мы можем доказать, что для любого действительного числа a ∈ ℝ, мы имеем

Обозначение

Это хорошее место, чтобы ввести еще одно обозначение, видите ли, исчисление был изобретен независимо Ньютон и Лейбниц . Они использовали совершенно разные обозначения, и в целом обозначения Лейбница — это те, которые мы используем, хотя Ньютон изначально получил большую часть заслуг в открытии. Этот спор — длинная и довольно интересная история сама по себе, но мы должны вернуться в нужное русло.

Другим способом написания оператора со стрелкой импликации в приведенном выше примере является следующий

Однако иногда мы опускаем круглые скобки . Идея в том, что это 9Символ 0057 d/dx — это оператор в функциональном пространстве, который отображает функции в другие функции (производные).

Обратите внимание, что у нас будут следующие обозначения:

То есть df/dx является производной. Функция.

Обратите внимание, что символ df/dx выглядит как дробь чисел. Это не случайно. Если вспомнить определение производной, мы определяли ее как предел Δf/Δx при Δx → 0. То есть, хотя и выглядит как df и dx — бесконечно малые величины (Лейбниц называл эти величины бесконечно малых ), их отношение — это просто наклон прямой (касательной) в данной точке.

Представьте, что у нас есть некоторые вычисления, связанные с этим символом df/dx . В некоторых ситуациях мы могли бы представить, что вернемся назад и заменим его определением предела, чтобы манипулировать Δf и Δx как реальными величинами, которые они представляют, только для того, чтобы позже принять предел.

Это имеет для нас огромные полезные последствия, потому что внезапно мы можем (в некоторых ситуациях) лечить df/dx как дробь действительных чисел со всеми нашими правилами дробей в нашем распоряжении. Однако важно знать, что это скорее наше мнемоническое правило, чем реальная действительная математика, но мы вернемся к этому чуть позже.

Линейность

В этом разделе мы докажем очень важное свойство дифференциального оператора. А именно, что он линейный.

То есть

и

Таким образом, производная суммы — это сумма производных, а производная скаляра — это скаляр, умноженный на производную.

Доказательство этого — простое упражнение, но, поскольку концепция линейности важна, я приведу доказательство для полноты.

Если положить h(x) = f(x) + g(x) , то

и тем самым, если h(x) = c f(x) , то

В этом разделе , мы собираемся доказать некоторые полезные правила, которые нужно знать наизусть и никогда не забывать.

Они используются постоянно.

Правило продукта

При дифференциации продукта применяется особое правило. А именно

Доказательство.

Пусть h(x) = f(x)g(x) , тогда

Правило частных

Таким же образом можно доказать еще одно не менее важное свойство.

Факторное правило следующее.

Доказательство.

Во-первых, обратите внимание, что

Теперь мы можем просто использовать правило произведения.

Цепное правило

Это удивительное правило, которое вместе с двумя приведенными выше правилами дает нам возможность дифференцировать любую дифференцируемую функцию. Это на самом деле более удивительно, чем вы думаете, потому что, как мы узнаем в следующих статьях, это неверно для обратной операции.

Цепное правило гласит:

Я дам вам набросок доказательства, используя бесконечно малые числа в качестве чисел. Это не совсем строго, но его можно сделать строгим с помощью правильных аргументов. Причина, по которой я показываю вам это, состоит в том, что это отличное мнемоническое правило. То есть не забудешь.

Обратите внимание, что в выражении f(g(x)) мы можем рассматривать f как функцию g .

Тогда мы имеем,

Очень важный и мощный результат в исчислении, называемый правилом Лопиталя в честь французского математика Guillaume de l’Hôpital можно использовать во многих ситуациях, чтобы найти пределы.

Прежде чем сформулировать и доказать это, заметим, что определение производной можно записать как

, что эквивалентно нашему определению заменой a = x + Δx и b = x.

Утверждение в общих чертах формулируется следующим образом: Предположим, что пределы, когда x приближается к некоторому числу c , отношений f(x)/g(x) и g´(x)/f´(x ) существует, тогда

Доказательство.

Ниже мы докажем частный, но полезный случай теоремы.

Предположим, что f и g непрерывно дифференцируемы при вещественном числе c, что f(c) = g(c) = 0 и что g´(c) ≠ 0. Тогда

Обратите внимание, что последнее равенство выполняется, поскольку определение этого частного равно f´(c)/g´(c) .

В прошлой статье об исчислении мы наткнулись на неприятный предел. Напомним, что мы хотели найти

Теперь у нас есть инструменты для этого. Давай сделаем это.

Воспользуемся правилом Лопиталя.

Если вы не знаете, что такое серия, я расскажу об этом в другой статье. На данный момент вам разрешено просто сидеть сложа руки и наслаждаться поездкой, и если это не имеет для вас смысла, это вполне понятно, и мы вернемся к этому в будущем.

Одним из самых мощных инструментов реального и комплексного анализа является тот факт, что аналитические функции имеют разложение в степенной ряд.

То есть, если f бесконечно дифференцируемо и локально задано сходящимся степенным рядом в точке 9(n) означает f , дифференцированное n раз.

Я не буду приводить здесь доказательство этого факта, но читатель может убедиться в этом факте, продифференцировав пару раз обе части и подставив x=a или , написав f в виде суммы и остаточного члена вместо a. ряд и рассмотрим предел, поскольку сумма получает все больше и больше членов, а оставшийся член обращается в нуль.

Однако доказательство этого требует учета некоторых условий ограниченности производных, сходимости ряда и т.д.

Применение ряда Тейлора

Это один из наиболее часто используемых инструментов в исчислении. Оказывается, это еще более фундаментально, чем ожидалось вначале, потому что в комплексном анализе (комплексная) функция либо не дифференцируема, либо дифференцируема бесконечно много раз и аналитична, что дает ей степенной ряд. Таким образом, все комплексные дифференцируемые (или голоморфные) функции имеют ряд Тейлора.

Используем их для доказательства тождества дифференциального оператора.

Сначала рассмотрим 9x , синус, и косинус, мы получаем

Теперь нужно только подключить и переставить, чтобы получить тождество Эйлера

, которое все время используется для переключения между полярными координатами и декартовыми координатами.

Это третий рассказ из серии рассказов об исчислении. Предыдущие истории можно найти здесь:

Функции и непрерывность

Предпосылки для исчисления

www.cantorsparadise.com

Пределы

Начало исчисления

www.cantorsparadise.com

Мезенхимальные производные нервного гребня

Обзор

. 1982 г., май; 45 (2): 127–38.

doi: 10.1679/aohc.45.127.

Х Накамура

• PMID: 6751280
• DOI: 10.1679/aohc.45.127

Обзор

H Накамура. Arch Histol Jpn. 1982 май.

. 1982 г., май; 45 (2): 127–38.

doi: 10.1679/aohc.45.127.

Автор

Х Накамура

• PMID:
  6751280
• DOI: 10.1679/aohc.45.127

Абстрактный

1. Клетки перепелов и клетки кур можно различить с помощью световой и электронной микроскопии. В этой статье обсуждается происхождение мезенхимальных тканей из нервного гребня, основанное главным образом на методе химеры перепелов и цыплят с использованием перепелиных клеток в качестве биологических клеточных маркеров. 2. Клетки нервного гребня до уровня 4-го сомита способны становиться мезэктодермой при нормальном развитии птиц.

Месектодермальные клетки дифференцируются в кости и хрящи висцерального скелета, дерму лица и вентральной части шеи, соединительную ткань слюнных желез и производные глотки, такие как щитовидная железа, паращитовидная железа и тимус. Стромальные и эндотелиальные клетки роговицы, одонтобласты и гладкомышечные клетки артерий жаберных дуг также являются производными мезэктодермы. 3. Хотя судьба клеток нервного гребня при нормальном развитии точно зависит от их исходного положения на нервной оси, сигналы окружающей среды также очень важны для определения их судьбы.

Похожие статьи

• Мезенхимальные производные нервного гребня: анализ химерных перепелиных и куриных эмбрионов.

  Le Lièvre CS, Le Douarin NM. Le Lièvre CS и др. J Embryol Exp Morphol. 1975 г., август; 34 (1): 125–54. J Embryol Exp Morphol. 1975 год. PMID: 1185098

• Месектодермальные возможности туловищного нервного гребня птиц.

  Накамура Х., Айер-ле Ливр CS. Накамура Х. и др. J Embryol Exp Morphol. 1982 авг.; 70:1-18. J Embryol Exp Morphol. 1982. PMID: 7142892

• Участие клеток нервного гребня в генезисе черепа у птиц.

  Ле Льевр CS. Ле Льевр CS. J Embryol Exp Morphol. 1978 окт; 47:17-37. J Embryol Exp Morphol. 1978 год. PMID: 722230

  903:50

• Нервный гребень и миоидные клетки тимуса.

  Накамура Х., Айер-Ле Льевр К. Накамура Х. и др. Curr Top Dev Biol. 1986; 20:111-5. doi: 10.1016/s0070-2153(08)60658-4. Curr Top Dev Biol. 1986 год. PMID: 3514131 Обзор. Аннотация недоступна.

• Паттерн производных нервного гребня у птичьего эмбриона: исследования in vivo и in vitro.

  Ле Дуарен Н.М., Циллер С., Кули Г.Ф. Ле Дуарен Н.М. и соавт. Дев биол. 1993 г., сен; 159 (1): 24–49. doi: 10.1006/dbio.1993.1219. Дев биол. 1993. PMID: 8365563 Обзор.

Посмотреть все похожие статьи

Цитируется

• Анализ миграции и дифференцировки нервного гребня при межвидовой трансплантации.

  Griswold SL, Lwigale PY. Грисволд С.Л. и соавт. J Vis Exp. 2012 7 февраля; (60): 3622. дои: 10.3791/3622. J Vis Exp. 2012. PMID: 22349214 Бесплатная статья ЧВК.

• Дифференциальная экспрессия раневых фиброзных факторов между дермальными фибробластами лица и туловища.

  Курита М., Окадзаки М., Каминиши-Таникава А., Ниикура М. , Такусима А., Харии К. Курита М. и др. Подключить тканевый рез. 2012;53(5):349-54. дои: 10.3109/03008207.2012.657309. Epub 2012 24 июля. Подключить тканевый рез. 2012. PMID: 22260504 Бесплатная статья ЧВК.

• Специфическая для клеток нервного гребня делеция Rac1 приводит к дефектным взаимодействиям клетки с матриксом и тяжелым черепно-лицевым и сердечно-сосудистым порокам развития.

  Томас П.С., Ким Дж., Нуньес С., Глогауэр М., Картинен В. Томас П.С. и др. Дев биол. 2010 15 апреля; 340 (2): 613-25. doi: 10.1016/j.ydbio.2010.02.021. Epub 2010 23 февраля. Дев биол. 2010. PMID: 20184871 Бесплатная статья ЧВК.

  903:50

• Мультипотентные предшественники кожного происхождения: предшественники нервного гребня взрослых с терапевтическим потенциалом.