Производные с дробями: Производная дроби, формула и примеры

SavePearlHarbor

Во вторник — 25 октября 2022 — состоится частное солнечное затмение — явление, при котором для некоторых людей на планете Земля Луна закроет собой на некоторое время некоторую часть Солнца. Затмение будет видимо не на всей Земле, а на меньшей её части. На ночной стороне земного шара, где во время затмения будет ночь, разумеется, никакого затмения не увидеть. Но и на дневном полушарии Земли затмение будет наблюдаться далеко не везде, а лишь там, куда упадет лунная полутень.

Полного затмения (явления, при котором Луна полностью закроет собой Солнце, небо потемнеет и на нем появятся несколько ярких звезд и планет) нигде на Земле наблюдаться в этот раз не будет. Лунная тень пройдет мимо Земли — выше северного полюса, но лунная полутень накроет собой значительную часть Евразии и даже зацепит северо-восток Африканского континента. Читать далее →

Рубрика: Без рубрики | Добавить комментарий

Опубликовано 22. 10.2022 автором admin

Аннотация

Метод Р. Калмана используется для сглаживания рядов, которые используются повсеместно, так как любую функцию можно представить в виде ряда.Поэтому он получил большое распространение в области обработки научной информации, в анализе информации получаемой с датчиков. В этой статье мы реализуем алгоритм Калмана на языке Python и наглядно увидим его работу.

Введение

Рудольф Эмиль Калман Венгерский инженер разработал данный алгоритм, а позже алгоритм назвали в честь Р. Калмана. Основная цель алгоритма предложенного Калманом это борьба с погрешностями измерений, шумами при обработке информации, что позволяет повысить эффективность ее обработки, очевидно, что это это имеет большое значение науке и технике. Основная информация о самом алгоритме и используемых переменных представлена в работе [1]. Поэтому мы опустим описание и перейдем к реализации.

Программная реализация алгоритма

Для реализации алгоритма нам потребуются библиотеки:

Читать далее →

Рубрика: Без рубрики | Добавить комментарий

Опубликовано 22. 10.2022 автором admin

Данная вступительная статья рассчитана на самый начальный уровень, “продвинутых” в области электроники читателей сможет заинтересовать следующая, где я доберусь до анализа схемотехники

реальных машин
Давно позади стены альма матер, но мир сегодня меняется так быстро, что надо всегда бежать, даже если всего лишь хочешь стоять на месте. В области разработки электронной техники эта бессмертная фраза Алисы имеет наверное самую большую актуальность. В последние годы у меня появилось новое хобби — ремонт бытовой электронной техники. Ремонтирую не ради денег, чисто для себя и родственников, то что ранее выкидывал не задумываясь и заменял на новое.
Электронная начинка современных бытовых приборов, особенно если речь идёт не о наколенной сборке в мастерской дядюшки Ли, а известных брендах, представляет собой чудеса оптимизации. Занимаясь ремонтом, я попутно подсматриваю достойные внимания технические решения, улыбаюсь замечая промахи проектировщиков. Временами их бывает крайне сложно объяснить чем то иным, кроме как требованиями маркетологов вносить в конструкцию элементы “планового устаревания”.
Погода на дворе не очень, очередной прототип отправляется на опытную эксплуатацию, почему бы не рассказать о чём то интересном? Давно я не писал на Хабр!
Почему двигатель, почему стиральные машины?
Читать далее →

Рубрика: Без рубрики | Добавить комментарий

Опубликовано 22.10.2022 автором admin

Аннотация

В статье дано подробное описание приложения, позволяющего обмениваться текстовыми сообщениями между Android-устройствами с помощью встроенных динамика и микрофона. Дана ссылка на полный исходный код, а для ключевых моментов приведены поясняющие блок-схемы. Приложение представляет практический интерес и готово к применению, работает достаточно стабильно и имеет большой потенциал для дальнейших экспериментов и улучшений. В ходе работы затронуты вопросы формирования звука, фильтрации, реализации скользящей средней, сохранения и оцифровки аналогового сигнала. Материал может быть рекомендован в первую очередь начинающим разработчикам для повторения и закрепления указанных тем.

Введение. Проблема. Цель

Во-первых, большое количество людей регулярно используют рации, потому что это, с одной стороны, удобно, а с другой – иногда и вовсе не имеет альтернатив.

Читать далее →

Рубрика: Без рубрики | Добавить комментарий

Опубликовано 22.10.2022 автором admin

Системный аналитик превращает хаос в красивые решения и наводит порядок. Эта роль ‒связующее звено между заказчиком и программистом, аналитик переводит с бизнесового на технический язык. Профессия сложная, но интересная и перспективная, поэтому если хочешь перейти в ИТ, обратите внимание на эту профессию.

В школе оценивают ваши знания с помощью ЕГЭ или экзаменов для поступления в ВУЗ на конкретную специальность. Предлагаю проверить знания по системному анализу в тесте «Готов ли я стать системным аналитиком». После прохождения вы узнаете насколько велики ваши шансы стать системным аналитиком или нужно уделить внимание подготовке. Если тест покажет, что необходимо еще набраться знаний, то приходите на курс

«Системный аналитик с нуля», чтобы сэкономить время на поиске материала в интернете  (прим. информация в статье и тестирование ‒ это мое личное мнение, которое может не совпадать с мнением читателя).

С помощью теста вы пройдете самопроверку перед собеседованием.

Тест

Читать далее →

Рубрика: Без рубрики | Добавить комментарий

Сайт работает на WordPress

Разложение рациональных дробей на простейшие.

Покажем, что всякую правильную рациональную дробь можно разложить на сумму простейших дробей.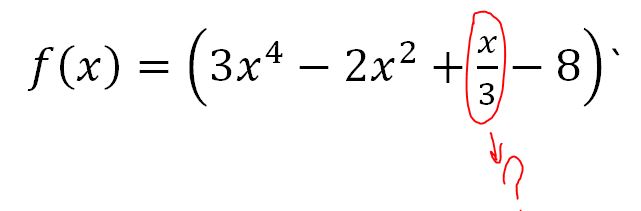

Пусть дана правильная рациональная дробь  .

Причём последовательное применение данной теоремы ко второму слагаемому данной теоремы приводит:

                (2-134)

   

Где  многочлен, степень которого ниже степени знаменателя. И аналогично формуле (2-134) можно получить:

.     (2-136)

63. Интегрирование элементарных дробей.

k

64. Интегрирование рациональных функций

 

Определение. Функция называется рациональной, если ее можно представить в виде дроби

, где P(x)  и  Q(x) – многочлены.

 

Из класса всех дробей выделяют основные простые дроби:

где a, p , q, M, N ÎR , kΠN.

Интегралы от первых двух типов простых дробей находятся с помощью подстановки t = x-a:

,

= .

Интеграл от третьего типа простых дробей рассмотрим в предположении, что знаменатель не имеет корней, т.е.

q – p² >0. Выделим полный квадрат в знаменателе

,

где a² = q – p² >0.

=

Если степень числителя выше степени знаменателя, то дробь называется неправильной; в таком случае выполнив деление, получим

65. Интегрирование иррациональных функций.

Интеграл вида R , где R – рациональная функция, с помощью подстановки =t приводиться к интегралу от рациональной функции от t и, следовательно, является берущимся.

Интеграл R(x, )dx сводиться к интегралу от рациональной функции с помощью одной из следующих подстановок:

1. Если a0, то = t

2. Если c0, то = tx

3. Если ax²+bx+c = a(x – x₁)·(x – x₂), то = (x – x₁)t.

Здесь t – новая переменная

66. Интегрирование тригонометрических функций

1°. Интегралы вида

находятся с помощью тригонометрических формул

2°. Интегралы вида

где m и n – четные числа находятся с помощью формул понижения степени

Если хотя бы одно из чисел m или n – нечетное, то полагают (пусть m = 2k + 1)

3°. Если m = -m, n = -l – целые отрицательные числа одинаковой четности, то

В частности, к этому случаю сводятся интегралы

4°. Интегралы вида

где R – рациональная функция от sinx и cosx, приводятся к интегралам от рациональных функций новой переменной с помощью подстановки при этом Если R{-sin x, cosx) = R(sinx, cosx), то целесообразно применить подстановку tgx = t. при этом

67. Задачи, приводящие к понятию определенного интеграла

Из геометрического смысла первообразной следует, что производная функции даёт угловой коэффициент касательной к соответствующему графику . Поэтому задача отыскания первообразной для заданной функции равносильна задаче нахождения кривой, для которой закон изменения углового коэффициента известен . Поскольку кривые отличаются друг от друга на постоянную интегрирования, то для того, чтобы из этого множества кривых выбрать одну кривую, достаточно задать точку , через которую кривая должна проходить, т.

Е. определить постоянную интегрирования.

Из механического истолкования неопределённого интеграла если задан закон изменения скорости от времени , то зависимость пути S от времени определяется интегралом , т. к. скорость движения точки – это производная . Постоянная интегрирования находится из заданного начального условия, иначе получим бесчисленное множество решений.

Исчисление

– Как найти производную дроби?

Спросил 8 лет, 3 месяца назад

Изменено 8 лет, 3 месяца назад

Просмотрено 111 тысяч раз

$\begingroup$

Итак, у меня есть интересная задача, над которой я работал два дня:

Мне нужно найти две вещи:

1) $f'(t)$
2) $f'(2)$

Я попытался включить его в определение производной, но не знаю, как решить из-за его сложности. 97$ найти $f'(t)$, чем найти $f'(2)$.

Как преобразовать эту задачу в более читаемый формат? (без дробей и деления), иначе, как мне составить его с дробями?

Спасибо

• исчисление
• пределы
• производные

$\endgroup$

$\begingroup$

Я вижу, что были представлены некоторые методы перезаписи, и в данном случае это самый простой и быстрый метод. Но его также можно решить как дробь, используя правило частных, поэтому для справки здесь приведен действительный метод решения его как дроби. 9{-7-1})$$

Сможете ли вы выполнить это?

$\endgroup$

5

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. Исчисление

– Когда мы не можем рассматривать дифференциалы как дроби? А когда все нормально?

Несмотря на то, что это уже закрыто, я лично не доволен ни одним из этих ответов, и я думаю, что все еще могу сказать что-то полезное.

Прежде всего: когда мы пишем что-то вроде $$\frac{\text{d}y}{\text{d}x},$$ символы $\text{d}y$ и $\text{d}x$ НЕ представляют собой дифференциальные формы. Дифференциальная форма — это линейная антисимметричная $n$-форма: линейный оператор, который принимает $n$ векторов и выдает число. Эти символы не обязательно должны представлять это, они могут представлять настоящие действительные числа. Давайте сделаем это официально.

Представьте, что у нас есть реальная функция $f\space\colon\space\mathcal{D}\subseteq\mathbb{R} \longrightarrow \mathbb{R}$, которая дифференцируема ($\iff$ выводима) в $\mathcal {D}$. Если у нас есть $y=f(x)$, и мы делаем изменение $\Delta x$ в независимой переменной, зависимая переменная изменится на $\Delta y$, поэтому $$y+\Delta y=f(x+\Delta x) \ подразумевает \Delta y=f(x+\Delta x)-y=f(x+\Delta x)-f(x)$$ Определим функцию $\eta(\Delta x)$ только потому, что: $$\eta(\Delta x) \equiv \frac{f(x+\Delta x)-f(x)}{\Delta x}-f'(x)$$ Здесь $f'(x)$ обозначает производную функцию $f$, существование которой мы знаем, поскольку $f$ дифференцируема. Эта функция $\eta(\Delta x)$ обладает следующим свойством:

$$\lim_{\Delta x \to 0}{\eta(\Delta x)}=f'(x)-f'(x)=0$$

Это пригодится через секунду. Найдем $\Delta y$ в определении функции $\eta(\Delta x)$:

$$\Delta y = f'(x)\Delta x + \eta(\Delta x)\Delta x$$

Если мы доведем $\Delta x$ до $0$, мы обнаружим, что первый член стремится к $0$ линейно (с той же скоростью, что и сам $\Delta x$), а второй член, как следствие того, что предел $\eta(\Delta x)$ равен $0$, достигает $0$ быстрее, чем $\Delta x$. Это означает, что первый член ($f'(x)\Delta x$) является линейной частью $\Delta y$. Вы можете узнать это как первый член разложения Тейлора $f$ вокруг точки $x$. 9k$ для некоторого $k \neq 1$). И вы можете видеть из этого определения, что имеет смысл говорить, что $\text{d}x=\Delta x$, потому что $\Delta x$ очевидно изменяется так же, как и $\Delta x$.

Итак, имеем:

$$\text{d}y = f'(x) \text{d}x \ подразумевает \frac{\text{d}y}{\text{d}x} = f'(x)$$

Обратите внимание, что мы всегда брали $x$ в качестве фиксированной точки, в которой $f(x)$ дифференцируема, а это означает, что мы действительно должны писать:

$$\left(\frac {\ text {d} y} {\ text {d} x} \ right) _ {x = a} = f ‘(a) $ $

Зная это, совсем не удивительно, что при заданных $u=\varphi(x)$, $w=\phi(x)$ и $y=f(x)$, дифференцируемых в интересующих нас точках , мы можем доказать. ..

$$\left(\frac{\text{d}y}{\text{d}u}\right)_{u=\varphi(a)}\left(\frac {\ text {d} u} {\ text {d} x} \ right) _ {x = a} = \ left (\ frac {\ text {d} y} {\ text {d} x} \ right) _{x=a}$$

… что мы называем цепным правилом; и, соответственно…

$$\left(\frac{\text{d}y}{\text{d}u}\right)_{u=\varphi(a)}\left(\frac {\ text {d} w} {\ text {d} x} \ right) _ {x = a} = \ left (\ frac {\ text {d} y} {\ text {d} x} \ right) _{x=a}\left(\frac{\text{d}w}{\text{d}u}\right)_{u=\varphi(a)}$$

… и его многочисленные последствия (обратная производная является производной обратной функции, если она вообще существует и т. д.)

Обратите внимание, что эти манипуляции ВСЕГДА ИСТИННЫ, ПРИ УСЛОВИИ, ЧТО производная существует в первую очередь. По сути, это говорит о том, что «манипулирование дифференциалами совершенно нормально, но вы предполагаете, что эти вещи дифференцируемы, вместо того, чтобы доказывать это». Если вы делаете доказательство, вы обычно не будете делать такого рода манипуляции, но совершенно нормально отменять, перемещать и делать что-либо с полными дифференциалами первого порядка при решении дифференциальных уравнений или решении любой физической задачи.

Впрочем, это не ново. Рассматривать деривативы как дроби так же опасно, как обращаться со старыми добрыми дробями как с дробями. Как и в случае с дифференциалами, выполнение манипуляций типа $$\frac{x}{y}\frac{y}{z}=\frac{x}{z}$$ подразумевает, что вы знаете, что все эти дроби существуют (т. е. вы знаете, что $y,z\neq0$, особенно $y$, поскольку именно его вы «отменяете» здесь).

Таким образом, регулярное сокращение дробей может привести к проблемам. Например, если вам дано уравнение… 92+5x=0 \подразумевает x(x+5)=0$$

… и вас просят найти $x$, вы можете подумать, что можете разделить обе части на $x+5$ и получить $x=0$ как единственное решение, но сокращение $x+5$ в числителе на $x+5$ в знаменателе подразумевало заранее знание того, что $x+5\neq0$, поэтому этот метод не работал. t дать вам также решение $x=-5$.

Надеюсь, это помогло, спасибо за чтение. И, о, в качестве последнего комментария, определение символа $\text{d}y$ как дифференциальной формы связано с тем, которое я дал здесь, следующим уравнением (данное $y = f(x^1,.