Расчет пути и времени движения | 7 класс
Содержание
На прошлых уроках мы познакомились с определением механического движения, узнали, каким бывает движение, изучили его свойства и характеристики. Теперь нам известны формулы для расчета скорости при равномерном движении ($\upsilon = \frac{S}{t}$) и средней скорости при неравномерном ($\upsilon_{ср} = \frac{S}{t}$).
На данном уроке мы посмотрим на эти формулы с другой стороны — научимся использовать их для расчета пути и времени движения, а также рассмотрим графики скорости и пути для равномерного движения.
Формулы для расчета пути и времени движения при равномерном движении тела
Скорость тела при равномерном движении вычисляется по формуле $\upsilon = \frac{S}{t}$. Отсюда, если мы знаем скорость и время, то можем найти пройденный путь:
$S = \upsilon t$.
Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время его движения.
Выразим время:
$t = \frac{S}{\upsilon}$.
Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.
{"questions":[{"content":"Если тело двигалось равномерно, то, чтобы рассчитать пройденный им путь нужно[[choice-33]]","widgets":{"choice-33":{"type":"choice","options":["скорость умножить на время движения","скорость разделить на время движения","среднюю скорость умножить на время движения"],"answer":[0]}}}]}Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле:
$\upsilon_{ср} = \frac{S}{t}$.
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$\large S = \upsilon_{ср} t$.
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$t = \frac{s}{\upsilon_{ср}}$.
{"questions":[{"content":"Чтобы найти время неравномерного движения необходимо[[choice-38]]","widgets":{"choice-38":{"type":"choice","options":["путь разделить на среднюю скорость","путь разделить на скорость","среднюю скорость разделить на путь"],"answer":[0]}}}]}График скорости равномерного движения
Так как скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.
Рисунок 1. Положительная и отрицательная скоростиЕсли динозавр начнет двигаться к дому, то его скорость будет положительной, так как направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, так как направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.
Рисунок 2. График скорости равномерного движенияИз графика видно, что скорости с течением времени не изменяется – они постоянны в любой выбранный момент времени. Если мы посмотрим на график положительной скорости, то увидим, что $\upsilon = 6 \frac{м}{с}$, на график отрицательной — $\upsilon = -4 \frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени.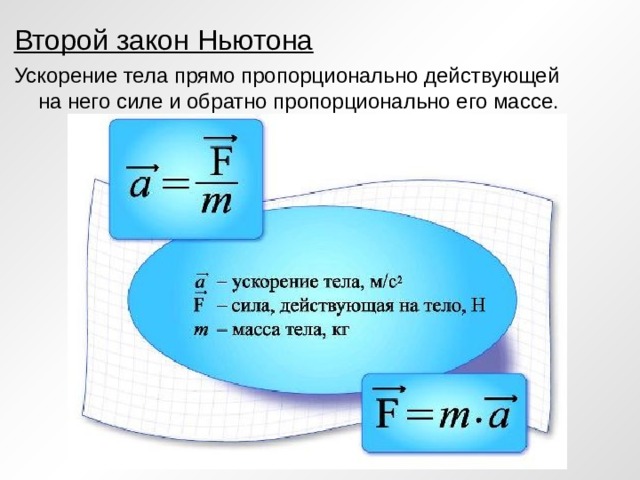 Рассчитаем какой путь пройдет тело с положительной скоростью за $4 \space с$.
Рассчитаем какой путь пройдет тело с положительной скоростью за $4 \space с$.
$S = \upsilon t = 6 \frac{м}{с} \cdot \space 4 c = 24 \space м$.
{"questions":[{"content":"График зависимости скорости равномерного движения от времени имеет вид[[choice-41]]","widgets":{"choice-41":{"type":"choice","options":["прямой, параллельной оси времени","прямой, параллельной оси скоростей","прямой пропорциональности","обратной пропорциональности"],"answer":[0]}}}]}График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Рисунок 3. График пути равномерного движенияЗдесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 \space с$, $S = 2 \space м$. Тогда,
Тогда,
$\upsilon = \frac{S}{t} = \frac{2 \space м}{1 \space с} = 2 \frac{м}{с}$.
Задачи
Задача №1
Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 \frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 \frac{км}{ч} = 120 \cdot \frac{1000 \space м}{3600 \space с} \approx 33 \frac{м}{с}$.
Дано:
$\upsilon = 120 \frac{км}{ч}$
$t = 3 \space c$
СИ:
$\upsilon = 33 \frac{м}{с}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = \upsilon t$,
$S = 33 \frac{м}{с} \cdot 3 с \approx 100 \space м$
Ответ: $S = 100 \space м$.
Задача №2
Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 \frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 \frac{км}{ч} = 40 \cdot \frac{1000 м}{3600 с} \approx 11 \frac{м}{с}$,
$900 \space км = 900 \space 000 м$.
Дано:
$\upsilon_{ср} = 40 \frac{км}{ч}$
$S = 900 \space км$
CИ:
$\upsilon_{ср} = 11 \frac{м}{с}$
$S = 900 \space 000 \space м$
$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = \frac{s}{\upsilon_{ср}}$,
$t = \frac{900 \space 000 \space м}{11 \frac{м}{с}} \approx 82 \space 000 \space с$.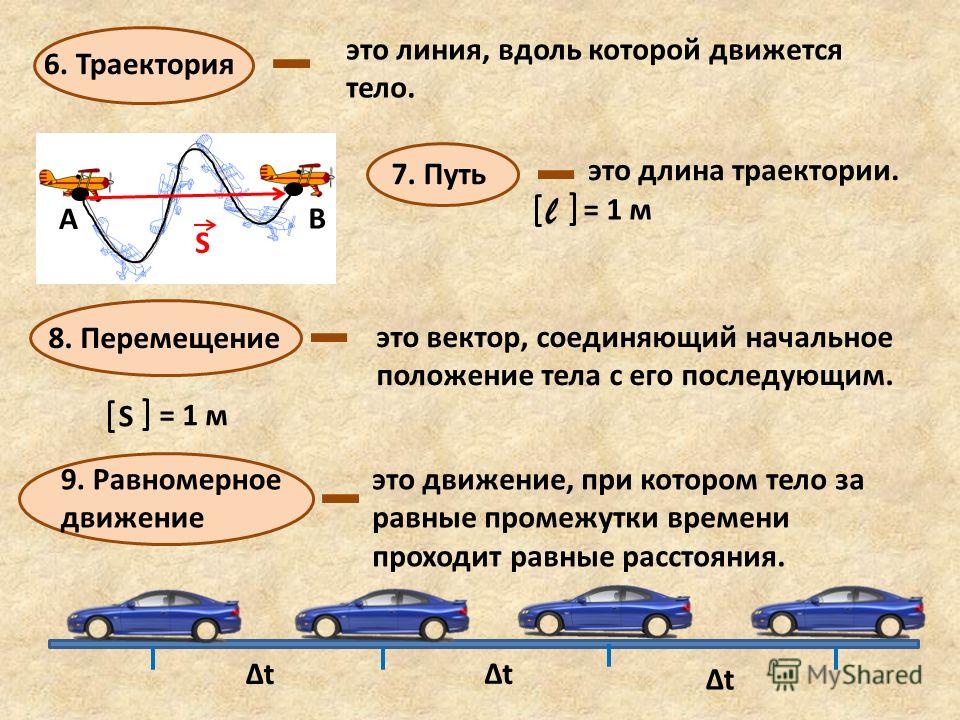
Переведем время в часы:
$1 \space ч = 60 \space мин = 60 \cdot 60 \space c = 3600 \space c$.
Тогда:
$t = \frac{82 \space 000 \space c}{3600 \space c} \approx 23 \space ч$.
Ответ: $t = 23 \space ч$.
Больше задач на расчет пути и времени движения с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Пользуясь таблицей 1 из прошлого урока, найдите скорости страуса, автомобиля, искусственного спутника Земли. Определите пути, пройденные ими за $5 \space с$.
Дано:
$\upsilon_1 = 22 \frac{м}{с}$
$\upsilon_2 = 20 \frac{м}{с}$
$\upsilon_3 = 8000 \frac{м}{с}$
$t = 5 \space с$
$S_1 — ?$
$S_2 — ?$
$S_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь, пройденный страусом:
$S_1 = \upsilon_1 t$,
$S_1 = 22 \frac{м}{с} \cdot 5 \space с = 110 \space м$.
Путь, пройденный автомобилем:
$S_2 = \upsilon_2 t$,
$S_2 = 20 \frac{м}{с} \cdot 5 \space с = 100 \space м$.
Путь, пройденный искусственным спутником Земли:
$S_3 = \upsilon_3 t$,
$S_3 = 8000 \frac{м}{с} \cdot 5 \space с = 40 \space 000 \space м = 40 \space км$.
Ответ: $S_1 = 110 \space м$, $S_2 = 100 \space м$, $S_3 = 40 \space км$.
Упражнение №2
На велосипеде можно без особого напряжения ехать со скоростью $3 \frac{м}{с}$. На какое расстояние можно уехать за $1.5 \space ч$?
Дано:
$t = 1.5 \space ч$
$\upsilon = 3 \frac{м}{с}$
СИ:
$t = 5400 \space с$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем путь, который можно проехать на велосипеде с указанной скоростью:
$S = \upsilon t$,
$S = 3 \frac{м}{с} \cdot 5400 \space с = 16 \space 200 \space м = 16.2 \space км$.
Ответ: $S = 16.2 \space км$.
Упражнение №3
На рисунке 4 показан график зависимости пути равномерного движения тела от времени ($S$ — ось пройденного пути, $t$ — ось времени).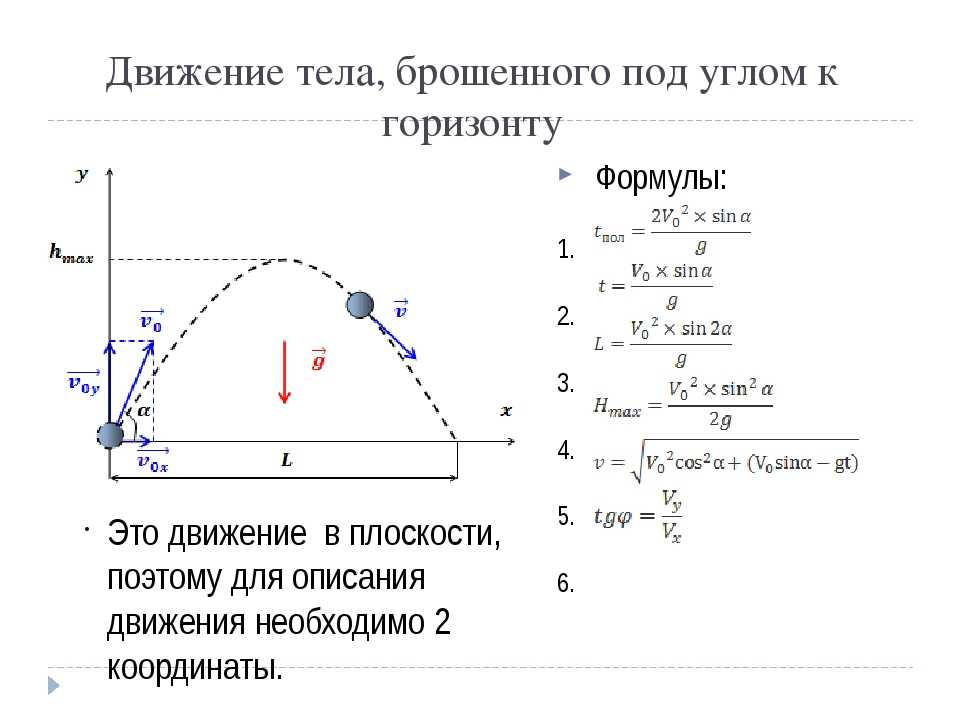 По этому графику найдите, чему равен путь, пройденный телом за $2 \space ч$. Затем рассчитайте скорость тела.
По этому графику найдите, чему равен путь, пройденный телом за $2 \space ч$. Затем рассчитайте скорость тела.
Определим из графика путь, пройденный телом за $2 \space ч$. Этому времени на графике соответствует значение пути, равное $200 \space км$. Запишем условие задачи и решим ее.
Дано:
$S = 200 \space км$
$t = 2 \space ч$
$\upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитываем по формуле:
$\upsilon = \frac{S}{t}$.
$\upsilon = \frac{200 \space км}{2 \space ч} = 100 \frac{км}{ч}$.
Ответ: $\upsilon = 100 \frac{км}{ч}$.
Упражнение №4
График зависимости скорости равномерного движения тела от времени представлен на рисунке 5. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за $2 \space ч$, $4 \space ч$.
Рисунок 5.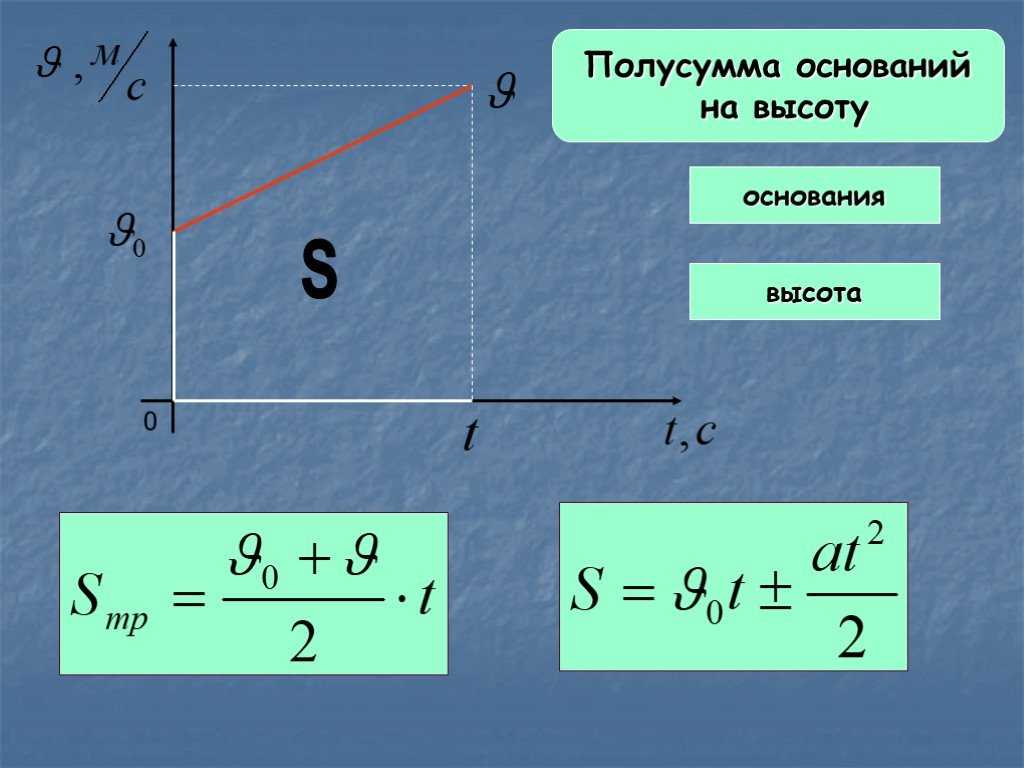 График зависимости скорости равномерного движения от времени
График зависимости скорости равномерного движения от времениИз графика видно, что скорость тела равна $8 \frac{м}{с}$. Этот график представляет собой прямую, параллельную оси времени, потому что движение равномерное, и скорость тела не изменяется с течением времени. Запишем условие задачи и решим ее.
Дано:
$t_1 = 2 \space ч$
$t_2 = 4 \space ч$
$\upsilon = 8 \frac{м}{с}$
СИ:
$t_1 = 7200 \space с$
$t_2 = 14 \space 400 \space с$
$S_1 — ?$
$S_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь рассчитаем по формуле: $S = \upsilon t$.
За $2 \space ч$ тело пройдет путь:
$S_1 = \upsilon t_1$,
$S_1 = 8 \frac{м}{с} \cdot 7200 \space с = 57 \space 600 \space м = 57.6 \space км$.
За $4 \space ч$ тело пройдет путь:
$S_2 = \upsilon t_2$,
$S_2 = 8 \frac{м}{с} \cdot 14 \space 400 \space с = 115 \space 200 \space м = 115.2 \space км$.
Ответ: $S_1 = 57. 6 \space км$, $S_2 = 115.2 \space км$.
6 \space км$, $S_2 = 115.2 \space км$.
Упражнения №5
По графикам зависимости путей от времени (рисунок 6) двух тел, движущихся равномерно, определите скорости этих тел. Скорость какого тела больше?
Рисунок 6. Графики зависимости путей от времени равномерного движения двух телДля того, чтобы рассчитать скорость тела, нам нужно знать путь и время, за которое этот путь был пройден. Возьмем эти значения для двух тел из их графиков. Первое тело (I) проходит путь, равный $4 \space м$, за $2 \space с$. Второе тело (II) проходит путь, равный $4 \space м$, за $4 \space с$. Запишем условие задачи и решим ее.
Дано:
$S = 4 \space м$
$t_1 = 2 \space с$
$t_2 = 4 \space с$
$\upsilon_1 — ?$
$\upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем скорость первого тела:
$\upsilon_1 = \frac{S}{t_1}$,
$\upsilon_1 = \frac{4 \space м}{2 \space с} = 2 \frac{м}{с}$.
Рассчитаем скорость второго тела:
$\upsilon_2 = \frac{S}{t_2}$,
$\upsilon_2 = \frac{4 \space м}{4 \space с} = 1 \frac{м}{с}$.
Получается, что скорость первого тела больше скорости второго.
Ответ: $\upsilon_1 = 2 \frac{м}{с}$, $\upsilon_2 = 1 \frac{м}{с}$, $\upsilon_1 > \upsilon_2$.
Пройденный путь Калькулятор | Вычислить Пройденный путь
✖Начальная скорость — это скорость, с которой начинается движение.ⓘ Начальная скорость [u] | Сантиметр / часСантиметр / минутуСантиметр / секКосмическая скорость – ПервыйКосмическая скорость – ВторойКосмическая скорость – ТретьяСкорость ЗемлиЛапка / часЛапка / минутуНога / секКилометры / часКилометры / минутуКилометры / секМорской узелУзел (Великобритания)маакМаха (стандарт СИ)Метр / часМетр / минутуМетр / секмили / часмили / минутумили / секМиллиметр / часМиллиметр / минутуМиллиметр / секМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20 ° C и 10 метров глубиной)Двор / часДвор / минутуДвор / сек | +10% -10% | |
✖Время, затраченное на путешествие – это общее время, затраченное объектом на то, чтобы добраться до пункта назначения. | АттосекундаМиллиард летсантисекундаВекаЦикл переменного тока 60 ГцЦикл переменного токаДеньДесятилетиеДекасекундаДецисекундаExasecondФемтосекундаГигасекундагектосекундаЧаскилосекундаМегасекундамикросекундаМиллениумМиллион летМиллисекундаминутМесяцНаносекундаПетасекундаПикосекундавторойСведбергТерасекундаТысяча летНеделюГодYoctosecondЙоттасекундаЗептосекундаЗеттасекунда | +10% -10% | |
✖Ускорение – это скорость изменения скорости к изменению во времени.ⓘ ускорение [a] | Ускорение свободного падения на ХаумеаУскорение свободного падения на ЮпитерУскорение свободного падения на МарсеУскорение свободного падения на МеркурииУскорение свободного падения на НептунеУскорение свободного падения на ПлутонеУскорение свободного падения на СатурнеУскорение свободного падения на ЛунеУскорение свободного падения на СолнцеУскорение свободного падения на УранеУскорение свободного падения на ВенереУскорение свободного паденияСантиметр / Площадь ВторойДекаметровое / Площадь ВторойДециметровая / Площадь ВторойЛапка / Площадь ВторойгалГалилеоГектометровом / Площадь ВторойДюймы / Площадь ВторойКилометр / час секундаКилометры / Площадь ВторойМетр / квадратный часМетр на квадратную миллисекундуМетр / квадратная минутаметр / Квадрат ВторойМикрометр / Площадь Второймили / Площадь ВторойМиллиметр / квадратная секундаНанометра / Площадь ВторойСекунды от 0 до 100 км/чСекунды от 0 до 100 миль в часСекунды от 0 до 200 км/чСекунды от 0 до 200 миль в часСекунды от 0 до 60 миль в часДвор / Площадь Второй | +10% -10% |
|
✖Пройденное расстояние – это общая длина пути, пройденного между двумя позициями. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Пройденный путь Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.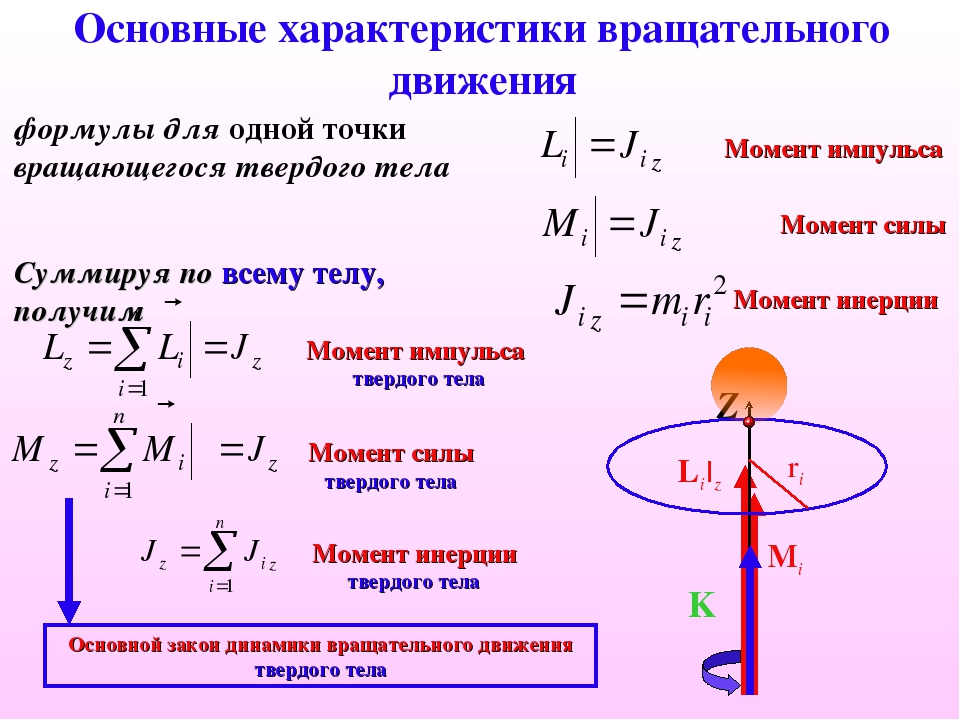 2
2
Определить начальную скорость?
Скорость – это скорость изменения положения объекта относительно времени. Силы, действующие на объект, вызывают его ускорение. Это ускорение изменяет скорость. Начальная скорость vi – это скорость объекта до того, как ускорение вызовет изменение.
Share
Copied!
виды и формулы, примеры механического перемещения тел, решение задачи
Физика
12.11.21
13 мин.
Движение различных объектов окружает человека с самого рождения. Перемещение автомобиля по асфальтированной дороге, полет самолета, бег атлета на спортивных соревнованиях, вращение планеты Земля вокруг своей звезды — это лишь малая доля примеров изменения пространственного положения объектов. Для решения задач по физике нужно знать, что такое равномерное движение.
Оглавление:
- Пространственная система координат
- Понятие механического движения
- Физические величины
- Виды перемещения в пространстве
- Равномерное изменение положения
- Пример решения задачи
Пространственная система координат
Состояние Вселенной в общем случае можно представить в виде функции, зависящей от четырех координат. Три координаты описывают положение тела в пространстве, четвертая — это время, которое характеризует последовательность событий. Пространственные координаты в большинстве задач по физике и геометрии удобно представлять в виде прямоугольной декартовой системы. Эта система является совокупностью трех пересекающихся под углом 90 градусов осей, на каждой из которых выбран единичный вектор.
Три координаты описывают положение тела в пространстве, четвертая — это время, которое характеризует последовательность событий. Пространственные координаты в большинстве задач по физике и геометрии удобно представлять в виде прямоугольной декартовой системы. Эта система является совокупностью трех пересекающихся под углом 90 градусов осей, на каждой из которых выбран единичный вектор.
Положение любой точки в декартовой системе координат можно математически представить в виде суммы целых длин единичных векторов для каждой из трех осей. Благодаря этой системе можно легко описывать изменение положения тел в пространстве.
Понятие механического движения
Любое изменение пространственных координат тела во времени принято называть механическим движением. Школьников слово «механический» может вводить в заблуждение, поскольку оно связано с каким-либо механизмом. Для некоторых из них перемещение автомобиля или мотоциклиста — это движение механическое, а бег животного или полет птицы уже не вписывается в эту категорию.
При рассмотрении типа изменения пространственных координат физика сосредотачивает свое внимание на законах этого изменения, а также на силах, которые его вызвали. При этом она не исследует природу объекта, поэтому любое движение считается механическим.
Физические величины
Путь, время, скорость и ускорение — это 4 главные величины, которые характеризуют пространственное изменение координат объектов. Каждая из них относится к одной из двух групп:
- векторная;
- скалярная.
Путь и время — это скаляры, для их определения достаточно знать начальное и конечное состояние тела. Например, объект, перед тем как начать движение, имел координату x0, в момент завершения своего перемещения его координата стала равной x1. Численное значение пройденного пути S в этом случае определяется просто:
S = x1 — x0.
Скорость и ускорение — характеристики векторные.
Это означает, что для их полного определения недостаточно знать только начальное и конечное положение тела. Обе величины определяют характер самого движения.
По определению, скорость v — это быстрота изменения координат объекта в пространстве, ускорение a — это быстрота изменения самой скорости. Величина v для всякого типа перемещения тел направлена всегда вдоль траектории (воображаемая линия, вдоль которой объект движется). Ускорение a совершенно не связано ни с величиной v, ни с траекторией. Направление вектора a однозначно определяется результирующей суммой сил, действующих на изучаемое тело в движении.
Виды перемещения в пространстве
Примеры механического движения можно встретить в живом и неживом мире, в технике, в микромасштабе и в масштабах галактики. Несмотря на огромное разнообразие, физика выделяет всего 2 группы видов перемещения тел:
- равномерное;
- неравномерное.
В первую группу входят все явления, перемещение тел для которых происходит без изменения абсолютного значения скорости на протяжении всего пути.
Соответственно, вторая группа описывает виды движения, в процессе которых скорость, так или иначе изменяется по модулю.
Во время равномерного перемещения объектов в пространстве ускорение не всегда равно нулю. В процессе неравномерного движения величина a всегда отлична от нуля. Примером, относящимся к первой группе, является перемещение автомобиля с заданной скоростью по дороге. Падение камня с некоторой высоты на поверхность земли — это пример неравномерного движения с ускорением свободного падения.
Равномерное изменение положения
Этот тип перемещения в пространстве рассматривают в начальных классах школ, поскольку он наиболее простой в изучении и понимании смысла физических формул. Тем не менее часто школьники отождествляют равномерное и прямолинейное перемещение, что неправильно.
По прямой линии
Самолет, летящий в облаках с постоянной скоростью по воображаемой прямой линии, в первом приближении можно полагать хорошим примером равномерного прямолинейного движения. Для физического описания подобных перемещений используют 2 скалярные величины — пройденный путь S и время t, и одну векторную характеристику — скорость v. Формула равномерного движения по прямой имеет следующий вид:
Для физического описания подобных перемещений используют 2 скалярные величины — пройденный путь S и время t, и одну векторную характеристику — скорость v. Формула равномерного движения по прямой имеет следующий вид:
S = v*t.
Левая и правая часть выражения имеет размерность длины, которая в международной системе СИ выражается в метрах (м). Часто S также выражают в миллиметрах, сантиметрах или километрах. Поскольку t имеется размерность времени (секунды, минуты, часы), величина v выражается в единицах длины по отношению к единицам времени, то есть в метрах в секунду (м/с), километрах в час (км/ч) и т. д.
Формулу пути S можно легко переписать, чтобы определить скорость равномерного движения v или время t:
v = S/t; t = S/v.
Кривая траектория
Планета Земля вращается вокруг Солнца в космическом пространстве. Является ли ее движение равномерным? Да. Является ли оно прямолинейным? Нет. Если бы наблюдатель мог со стороны посмотреть на движение Земли, то увидел бы, что она перемещается по окружности с огромной скоростью (приблизительно 30 км/с). В каждый момент времени вектор скорости планеты изменяется за счет действия гравитационного притяжения Солнца, однако абсолютная величина скорости не испытывает каких-либо изменений. По этой причине продолжительность года на Земле является постоянной величиной.
В каждый момент времени вектор скорости планеты изменяется за счет действия гравитационного притяжения Солнца, однако абсолютная величина скорости не испытывает каких-либо изменений. По этой причине продолжительность года на Земле является постоянной величиной.
Движение тел по кривым траекториям, в процессе которого ускорение изменяет только направление скорости, а не ее величину, в физике принято называть равномерным криволинейным перемещением. Чаще всего рассматривают круговое движение, для которого вводят важную характеристику — центростремительное ускорение ac. Эта величина всегда направлена к центру окружности, а ее модуль вычисляется по следующей формуле:
ac = v 2 /r.
Здесь r — радиус круговой траектории, v 2 — квадрат скорости.
Угловые характеристики и период
Равномерное движение по окружности удобно описывать не линейными, а угловыми физическими величинами, то есть угловой скоростью w и углом перемещения Q. Величина w измеряется в радианах в секунду (рад/с), Q — в радианах. Поскольку полная окружность представляет собой 2*pi радиан (pi = 3,14 — число пи), угловые характеристики через их линейные аналоги можно рассчитать по следующим формулам:
Величина w измеряется в радианах в секунду (рад/с), Q — в радианах. Поскольку полная окружность представляет собой 2*pi радиан (pi = 3,14 — число пи), угловые характеристики через их линейные аналоги можно рассчитать по следующим формулам:
w = v/r; Q = S/r.
Еще одна важная величина, которую необходимо знать для полного описания равномерного движения по окружности — период T. Он представляет собой время, которое затрачивает тело для совершения полного оборота по замкнутой траектории. Вычисляется период следующим образом:
T = 2*pi/w.
Период обращения Земли вокруг своей звезды равен продолжительности года, то есть 365 дней и 6 часов. Для удобства времяисчисления каждый четвертый год на планете на 1 день длиннее предыдущих трех.
Пример решения задачи
Мотоциклисту необходимо попасть из пункта A в пункт C, совершая при этом остановку в пункте B на 1 час. Известно, что между пунктами A и B мотоциклист двигался с некоторой постоянной средней скоростью v1. Между пунктами B и C его движение также было равномерным, но уже со скоростью v2, которая на 20% была больше, чем v1. Какое расстояние преодолел мотоциклист, если известно, что затраченное на переезд время составило 5 часов, скорость v1 была равна 50 км/ч, и расстояние между B и С он преодолел в 1,5 раза быстрее, чем путь между A и B.
Между пунктами B и C его движение также было равномерным, но уже со скоростью v2, которая на 20% была больше, чем v1. Какое расстояние преодолел мотоциклист, если известно, что затраченное на переезд время составило 5 часов, скорость v1 была равна 50 км/ч, и расстояние между B и С он преодолел в 1,5 раза быстрее, чем путь между A и B.
Пусть на переезды между пунктами A-B и B-C мотоциклист затратил время t1 и t2, соответственно. Справедливо следующее выражение:
t1 + 1 + t2 = 5.
Здесь 1 час в левой части равенства отражает время отдыха в пункте B. Чтобы найти t1 и t2, следует обратиться к условию задачи. Известно, что величина t2 в 1,5 раза меньше, чем t1:
t1 = 1,5*t2.
Из двух записанных выражений следует, что t1 = 2,4 часа, t2 = 1,6 часа.
Прохождение пути определяется как сумма дистанций между AB и BC. Длина траектории S, то есть расстояние между A и C, рассчитывается по формуле для равномерного движения:
S = v1*t1 + v2*t2.
Согласно условию v1 = 50 км/ч, и v2 = 1,2*v1, значит, v2 = 60 км/ч. Все определенные величины, подставленные в формулу для S, приводят к следующему результату:
S = 50*2,4 + 60*1,6 = 216 км.
Траектория движения мотоциклиста между пунктами A и C необязательно должна быть прямолинейной. Для нахождения пройденного расстояния S важно, чтобы на каждом отрезке пути он двигался с некоторой постоянной по модулю скоростью.
AC Определение пройденного пути по скорости
Мотивирующие вопросы
Если мы знаем скорость движущегося тела в каждой точке данного интервала, можем ли мы определить расстояние, пройденное объектом за этот интервал времени?
Как задача нахождения пройденного пути связана с нахождением площади под некоторой кривой?
Что значит антидифференцировать функцию и почему этот процесс важен для нахождения пройденного расстояния? 92\text{.
 }\) Мы исследовали среднюю скорость мяча на интервале \([a,b]\text{,}\), вычисленную по разностному фактору \(\frac{s(b)-s( a)}{b-a}\text{.}\) Мы обнаружили, что можем определить мгновенную скорость мяча в момент времени \(t\), взяв производную функции положения,
}\) Мы исследовали среднюю скорость мяча на интервале \([a,b]\text{,}\), вычисленную по разностному фактору \(\frac{s(b)-s( a)}{b-a}\text{.}\) Мы обнаружили, что можем определить мгновенную скорость мяча в момент времени \(t\), взяв производную функции положения,\begin{уравнение*} s'(t) = \lim_{h \to 0} \frac{s(t+h)-s(t)}{h}\text{.} \end{уравнение*}
Таким образом, если его функция положения дифференцируема, мы можем найти скорость движущегося объекта в любой момент времени.
Благодаря этому изучению положения и скорости мы многому научились. Мы можем использовать производную, чтобы найти мгновенную скорость изменения функции в любой точке области, чтобы найти, где функция увеличивается или уменьшается, где она вогнута вверх или вогнута вниз, и найти относительные экстремумы. Подавляющее большинство задач и приложений, которые мы рассмотрели, связаны с ситуацией, когда конкретная функция известна, и мы ищем информацию, основанную на знании мгновенной скорости изменения функции.
 Во всех этих задачах мы переходим от функции \(f\) к ее производной \(f’\text{,}\) и используем значение производной, чтобы помочь нам ответить на важные вопросы.
Во всех этих задачах мы переходим от функции \(f\) к ее производной \(f’\text{,}\) и используем значение производной, чтобы помочь нам ответить на важные вопросы.Мы также столкнулись с обратной ситуацией, когда мы знаем производную функции \(f’\text{,}\) и пытаемся вывести информацию о \(f\text{.}\). Мы сосредоточим наше внимание в главе 4 по этой проблеме: если мы знаем мгновенную скорость изменения функции, можем ли мы найти саму функцию? Начнем с более конкретного вопроса: если мы знаем мгновенную скорость объекта, движущегося по прямолинейному пути, можем ли мы найти соответствующую ему функцию положения?
Предварительный просмотр 4.1.1.
Предположим, что человек идет по длинному прямому пути с постоянной скоростью 3 мили в час.
На левых осях, представленных на рисунке 4.1.1, нарисуйте помеченный график функции скорости \(v(t) = 3\text{.}\)
Рисунок 4.1.1. Слева оси для построения \(y = v(t)\text{;}\), справа для построения \(y = s(t)\text{. }\)
}\)Обратите внимание, что хотя шкала на двух наборы осей одинаковы, единицы измерения на правой оси отличаются от единиц на левой. Правые оси будут использоваться в вопросе (d).
Какое расстояние проехал человек за два часа? Как это расстояние связано с площадью некоторой области под графиком \(y = v(t)\text{?}\)
Найдите алгебраическую формулу \(s(t)\text{,}\) для положения человека в момент времени \(t\text{,}\), предполагая, что \(s(0) = 0\text {.}\) Объясните свою мысль.
На правых осях, представленных на рисунке 4.1.1, нарисуйте размеченный график функции положения \(y = s(t)\text{.}\)
При каких значениях \(t\) функция положения \(s\) возрастает? Объясните, почему это так, используя соответствующую информацию о функции скорости \(v\text{.}\)
Подраздел 4.1.1 Площадь под графиком функции скорости
В предварительном упражнении 4.1.1 мы узнали, что когда скорость движущегося объекта постоянна (и положительна), площадь под кривой скорости за интервал времени говорит нам о пройденном объектом расстоянии.
Рисунок 4.1.2. Слева функция постоянной скорости; справа непостоянная функция скорости.
На левом графике рисунка 4.1.2 показана скорость объекта, движущегося со скоростью 2 мили в час за интервал времени \([1,1.5]\text{.}\) Площадь \(A_1\) заштрихованная область под \(y = v(t)\) на \([1,1.5]\) равна
\begin{уравнение*} A_1= 2 \, \frac{\text{мили}} }{\text{час} } \cdot \frac{1}{2} \, \text{часы} = 1 \, \text{миля}\text{ .} \end{уравнение*}
Этот результат — просто тот факт, что расстояние равно скорости, умноженной на время, при условии, что скорость постоянна. Таким образом, если \(v(t)\) постоянна на интервале \([a,b]\text{,}\), то пройденное расстояние на \([a,b]\) равно площади \( А\) дано
\begin{уравнение*} A = v(a) (b-a) = v(a) \Delta t\text{,} \end{уравнение*}
, где \(\Delta t\) — изменение \(t\) за интервал. (Поскольку скорость постоянна, мы можем использовать любое значение \(v(t)\) на интервале \([a,b]\text{,}\) мы просто выбрали \(v(a)\text{ ,}\) значение в левой конечной точке интервала.
 ) Несколько примеров, когда функция скорости является кусочно-постоянной, см. в этом апплете 1 .
) Несколько примеров, когда функция скорости является кусочно-постоянной, см. в этом апплете 1 .Ситуация усложняется, когда функция скорости непостоянна. Но на относительно небольших интервалах, где \(v(t)\) сильно не меняется, мы можем использовать принцип площадей для оценки пройденного расстояния. График справа на рисунке 4.1.2 показывает непостоянную функцию скорости. На интервале \([1,1.5]\text{,}\) скорость изменяется от \(v(1) = 2,5\) до \(v(1,5) \приблизительно 2,1\text{.}\) оценка пройденного пути равна площади изображенного прямоугольника,
\begin{уравнение*} A_2 = v(1) \Delta t = 2,5 \, \frac{\text{мили} }{\text{час} } \cdot \frac{1}{2} \, \text{часы} = 1,25 \, \text{мили}\text{.} \end{уравнение*}
Обратите внимание, что поскольку \(v\) убывает на \([1,1.5]\text{,}\) \(A_2 = 1.25\), это завышенная оценка фактического пройденного расстояния.
Чтобы оценить площадь под этой непостоянной функцией скорости на более широком интервале, скажем, \([0,3]\text{,}\) один прямоугольник не даст хорошего приближения.
Рисунок 4.1.3. Использование шести прямоугольников для оценки площади под \(y = v(t)\) на \([0,3]\text{.}\) Вместо этого мы могли бы использовать шесть прямоугольников, изображенных на рис. 4.1.3, найти площадь каждого прямоугольника и сложить общую сумму. Очевидно, есть выбор, который нужно сделать, и вопросы, которые нужно понять: сколько прямоугольников мы должны использовать? Где мы должны вычислить функцию, чтобы определить высоту прямоугольника? Что произойдет, если скорость иногда будет отрицательной? Можем ли мы найти точную площадь под любой непостоянной кривой?
Вместо этого мы могли бы использовать шесть прямоугольников, изображенных на рис. 4.1.3, найти площадь каждого прямоугольника и сложить общую сумму. Очевидно, есть выбор, который нужно сделать, и вопросы, которые нужно понять: сколько прямоугольников мы должны использовать? Где мы должны вычислить функцию, чтобы определить высоту прямоугольника? Что произойдет, если скорость иногда будет отрицательной? Можем ли мы найти точную площадь под любой непостоянной кривой?Мы изучим эти и другие вопросы в дальнейшем; сейчас достаточно заметить, что простое представление о площади прямоугольника дает нам мощный инструмент для оценки пройденного расстояния по функции скорости, а также для оценки площади под произвольной кривой. Чтобы изучить использование нескольких прямоугольников для аппроксимации площади при непостоянной функции скорости, см. этот апплет 9.0073 2 .
Мероприятие 4.
 1.2.
1.2.Предположим, что человек идет таким образом, что его скорость незначительно меняется в соответствии с информацией, приведенной в таблице 4.1.4, и графиком, приведенным на рисунке 4.1.5.
Таблица 4.1.4. Данные о скорости идущего человека.
Рисунок 4.1.5. График \(y = v(t)\text{.}\)\(т\) \(в(т)\) \(0,00\) \(1.500\) \(0,25\) \(1,789\) \(0,50\) \(1,938\) \(0,75\) \(1,992\) \(1.00\) \(2.000\) \(1,25\) \(2.008\) \(1,50\) \(2.063\) \(1,75\) \(2.211\) \(2.00\) \(2.500\) Используя сетку, график и полученные данные, оцените расстояние, пройденное пешеходом за двухчасовой интервал от \(t = 0\) до \(t = 2\text{.
 }\) Вы должны использовать временные интервалы шириной \(\Delta t = 0,5\text{,}\) выбирая способ последовательного использования функции для определения высоты каждого прямоугольника, чтобы приблизить пройденное расстояние. 92+1.5t+1.5\text{.}\) Помните, что \(v\) является производной функции положения ходячего, \(s\text{.}\) Найдите формулу для \(s\) так, чтобы \(s’ = v\text{.}\)
}\) Вы должны использовать временные интервалы шириной \(\Delta t = 0,5\text{,}\) выбирая способ последовательного использования функции для определения высоты каждого прямоугольника, чтобы приблизить пройденное расстояние. 92+1.5t+1.5\text{.}\) Помните, что \(v\) является производной функции положения ходячего, \(s\text{.}\) Найдите формулу для \(s\) так, чтобы \(s’ = v\text{.}\)Основываясь на вашей работе в (c), каково значение \(s(2) – s(0)\text{?}\) Каково значение этой величины?
Подраздел 4.1.2 Два подхода: площадной и антидифференцировочный
Когда скорость движущегося объекта положительна, положение объекта всегда увеличивается. (Вскоре мы рассмотрим ситуации, когда скорость отрицательна, а сейчас сосредоточимся на ситуации, когда скорость всегда положительна.) Мы установили, что всякий раз, когда \(v\) постоянна на интервале, точное пройденное расстояние равно площади под кривая скорости. Когда \(v\) непостоянна, мы можем оценить общее пройденное расстояние, найдя площади прямоугольников, которые аппроксимируют площадь под кривой скорости.

Таким образом, мы видим, что нахождение площади между кривой и горизонтальной осью является важным упражнением: помимо интересного геометрического вопроса, если кривая дает скорость движущегося объекта, площадь под кривой говорит нам точное пройденное расстояние. на интервале. Мы можем оценить эту площадь, если у нас есть график или таблица значений функции скорости.
В задании 4.1.2 мы столкнулись с альтернативным подходом к определению пройденного расстояния. Если \(y = v(t)\) – формула для мгновенной скорости движущегося объекта, то \(v\) должна быть производной функции положения объекта, \(s\text{.}\) Если мы можем найти формулу для \(s(t)\) из формулы для \(v(t)\text{,}\) мы будем знать положение объекта в момент времени \(t\text{,}\ ), а изменение положения за определенный интервал времени говорит нам о пройденном расстоянии за этот интервал.
В качестве простого примера рассмотрим ситуацию из предварительного задания 4.1.1, где человек идет по прямой с функцией скорости \(v(t) = 3\) миль в час.
Рисунок 4.1.6. Функция скорости \(v(t) = 3\) и соответствующая функция положения \(s(t) = 3t\text{.}\)
На левом графике функции скорости на рисунке 4.1.6 мы см. связь между площадью и пройденным расстоянием,
\begin{уравнение*} A = 3 \, \frac{\text{мили}} {\text{час}} \cdot 1,25 \, \text{часы} = 3,75 \, \text{мили}\text{.} \end{уравнение*}
Кроме того, мы наблюдаем 3 , что если \(s(t) = 3t\text{,}\), то \(s'(t) = 3\text{,}\), поэтому \(s(t) = 3t\) — функция положения, производная которой — заданная функция скорости, \(v(t) = 3\text{.}\) Соответствующие местоположения человека в моменты времени \(t = 0,25\) и \(t = 1,5\) равны \(s(1,5) = 4,5\) и \(s(0,25) = 0,75\text{,}\) и, следовательно,
\begin{уравнение*} s(1,5) – s(0,25) = 4,5 – 0,75 = 3,75 \ \text{мили}\text{.} \end{уравнение*}
Это изменение положения человека на \([0.25,1.5]\text{,}\), что точно соответствует пройденному расстоянию. В этом примере есть глубокие идеи и связи, которые мы будем изучать в главе 4.
 2 + 5\) также является функцией, производная которой равна \(g\text{,}\) и, следовательно, \( H\) — еще одна первообразная от \(g\text{.}\)
2 + 5\) также является функцией, производная которой равна \(g\text{,}\) и, следовательно, \( H\) — еще одна первообразная от \(g\text{.}\)Мероприятие 4.1.3.
Мяч брошен вертикально таким образом, что функция его скорости определяется выражением \(v(t) = 32 – 32t\text{,}\), где \(t\) измеряется в секундах, а \(v\) в футах в секунду. Предположим, что эта функция действительна для \(0 \le t \le 2\text{.}\)
При каких значениях \(t\) скорость мяча положительна? Что это говорит вам о движении мяча на этом интервале значений времени?
Найдите первообразную \(s\text{,}\) от \(v\), которая удовлетворяет \(s(0) = 0\text{.}\)
Вычислите значение \(s(1) – s(\frac{1}{2})\text{.}\) В чем смысл найденного вами значения?
Используя график \(y = v(t)\), представленный на рисунке 4.1.8, найдите точную площадь области между кривой скорости и осью \(t\) между \(t = \frac{ 1}{2}\) и \(t = 1\text{.}\) В чем смысл найденного вами значения?
Рисунок 4. 1.8. График \(y = v(t)\text{.}\)
1.8. График \(y = v(t)\text{.}\)Ответьте на те же вопросы, что и в (c) и (d), но вместо этого используйте интервал \([0,1]\text{.}\)
Каково значение \(s(2) – s(0)\text{?}\) Что этот результат говорит вам о полете мяча? Как это значение связано с предоставленным графиком \(y = v(t)\text{?}\) Объясните.
Подраздел 4.1.3 Когда скорость отрицательна
Предположение, что скорость положительна на данном интервале, гарантирует, что движение объекта всегда происходит в одном направлении, и, следовательно, гарантирует, что изменение его положения будет таким же, как расстояние, которое он проходит. Как мы видели в Упражнении 4.1.3, существуют естественные условия, в которых скорость объекта отрицательна, и мы хотели бы понять и этот сценарий.
Рассмотрим простой пример, когда женщина идет на прогулку по пляжу вдоль участка очень прямой береговой линии, идущей с востока на запад. Мы предполагаем, что ее начальное положение равно \(s(0) = 0\text{,}\) и что функция ее положения увеличивается по мере того, как она движется на восток от своего начального местоположения.
 Например, \(s = 1\) миля представляет собой одну милю к востоку от начального местоположения, а \(s = -1\) говорит нам, что она находится в одной миле к западу от того места, где она начала идти по пляжу.
Например, \(s = 1\) миля представляет собой одну милю к востоку от начального местоположения, а \(s = -1\) говорит нам, что она находится в одной миле к западу от того места, где она начала идти по пляжу.Теперь предположим, что она ходит следующим образом. С самого начала в \(t = 0\text{,}\) она идет прямо на восток с постоянной скоростью \(3\) миль в час в течение 1,5 часов. Через 1,5 часа она резко останавливается и начинает идти на запад с постоянной скоростью \(4\) миль в час и делает это в течение 0,5 часов. Затем, после еще одной резкой остановки и начала движения, она продолжает идти с постоянной скоростью \(3) мили в час на восток еще один час. Какое общее расстояние она прошла за время от \(t = 0\) до \(t = 3\text{?}\) Каково общее изменение ее положения за это время?
На эти вопросы можно ответить без вычислений, потому что скорость постоянна на каждом интервале. От \(t = 0\) до \(t = 1,5\text{,}\) она проехала
\begin{уравнение*} D_{[0,1.5]} = 3 \ \text{мили в час} \cdot 1.
 5 \ \text{часы} = 4.5 \ \text{мили}\text{.}
\end{уравнение*}
5 \ \text{часы} = 4.5 \ \text{мили}\text{.}
\end{уравнение*}От \(t = 1,5\) до \(t = 2\text{,}\) пройденное расстояние равно
\begin{уравнение*} D_{[1.5,2]} = 4 \ \text{мили в час} \cdot 0.5 \ \text{часы} = 2 \ \text{мили}\text{.} \end{уравнение*}
Наконец, в последний час она шла
\begin{уравнение*} D_{[2,3]} = 3 \ \text{мили в час} \cdot 1 \ \text{час} = 3 \ \text{мили}\text{,} \end{уравнение*}
, поэтому общее расстояние, которое она преодолела, равно
.\begin{уравнение*} D = D_{[0,1.5]} + D_{[1.5,2]} + D_{[2,3]} = 4,5 + 2 + 3 = 9,5 \ \text{мили}\text{.} \end{уравнение*}
Поскольку скорость для \(1,5 \lt t \lt 2\) равна \(v = -4\text{,}\), что указывает на движение в западном направлении, женщина сначала прошла 4,5 мили на восток, затем 2 мили на запад, затем еще 3 мили на восток. Таким образом, общее изменение ее положения равно
\begin{уравнение*} \text{изменение позиции} = 4,5 – 2 + 3 = 5,5 \ \text{мили}\text{.
 }
\end{уравнение*}
}
\end{уравнение*}Нам удалось довольно легко ответить на эти вопросы, и если мы подумаем о задаче графически, мы сможем обобщить наше решение для более сложной ситуации, когда скорость непостоянна и, возможно, отрицательна.
Рисунок 4.1.9. Слева функция скорости идущего человека; справа соответствующая функция положения.На рисунке 4.1.9 мы видим, как рассчитанные нами расстояния можно рассматривать как площади: \(A_1 = 4,5\) получается путем умножения скорости на время (\(3 \cdot 1,5\)), как и \(A_2\). ) и \(A_3\text{.}\) Но в то время как \(A_2\) является площадью (и, следовательно, положительна), поскольку функция скорости отрицательна для \(1,5 \lt t \lt 2\text{,} \) с этой областью связан отрицательный знак. Отрицательная область различает пройденное расстояние и изменение положения.
Пройденное расстояние равно сумме площадей,
\begin{уравнение*} D = A_1 + A_2 + A_3 = 4,5 + 2 + 3 = 9,5 \ \text{мили}\text{.} \end{уравнение*}
Но изменение положения должно учитывать движение в отрицательном направлении.
 Площадь над осью \(t\) считается положительной, поскольку она представляет расстояние, пройденное в положительном направлении, а площадь под осью \(t\) считается отрицательной, поскольку она представляет собой перемещение в отрицательном направлении. Таким образом, изменение положения женщины составляет
Площадь над осью \(t\) считается положительной, поскольку она представляет расстояние, пройденное в положительном направлении, а площадь под осью \(t\) считается отрицательной, поскольку она представляет собой перемещение в отрицательном направлении. Таким образом, изменение положения женщины составляет\begin{уравнение*} s(3) – s(0) = (+4,5) + (-2) + (+3) = 5,5 \ \text{мили}\text{.} \end{уравнение*}
Другими словами, женщина проходит 4,5 мили в положительном направлении, затем две мили в отрицательном направлении, а затем еще 3 мили в положительном направлении.
Отрицательная скорость также видна на графике функции положения \(y=s(t)\text{.}\). Его наклон отрицателен (в частности, \(-4\)) на интервале \(1,5\lt t\lt 2\), потому что скорость на этом интервале равна \(-4\). Отрицательный наклон показывает, что функция положения уменьшается, потому что женщина идет на восток, а не на запад.
Подводя итог, мы видим, что если скорость иногда отрицательна, изменение положения движущегося объекта отличается от пройденного им расстояния.
 Если мы вычислим отдельно пройденное расстояние на каждом интервале, где скорость положительна или отрицательна, мы сможем вычислить либо общее пройденное расстояние, либо общее изменение положения. Мы присваиваем отрицательное значение расстояниям, пройденным в отрицательном направлении, когда вычисляем изменение положения, и положительное значение, когда вычисляем общее пройденное расстояние.
Если мы вычислим отдельно пройденное расстояние на каждом интервале, где скорость положительна или отрицательна, мы сможем вычислить либо общее пройденное расстояние, либо общее изменение положения. Мы присваиваем отрицательное значение расстояниям, пройденным в отрицательном направлении, когда вычисляем изменение положения, и положительное значение, когда вычисляем общее пройденное расстояние.Мероприятие 4.1.4.
Предположим, что объект, движущийся по прямолинейному пути, имеет скорость \(v\) (в метрах в секунду) в момент времени \(t\) (в секундах), заданную кусочно-линейной функцией, график которой изображен слева на рис. 4.1.10. Мы рассматриваем движение вправо как движение в положительном направлении (с положительной скоростью), а движение влево — в отрицательном направлении.
Рисунок 4.1.10. Функция скорости движущегося объекта.Предположим далее, что начальное положение объекта в момент времени \(t = 0\) равно \(s(0) = 1\text{.}\)
Определить общее пройденное расстояние и полное изменение положения на интервале времени \(0 \le t \le 2\text{.
 }\) Каково положение объекта в \(t = 2\text{?} \)
}\) Каково положение объекта в \(t = 2\text{?} \)Через какие промежутки времени функция положения движущегося объекта возрастает? Почему? Через какие промежутки положение объекта уменьшается? Почему?
Какова позиция объекта в \(t = 8\text{?}\) Сколько всего метров он прошел, чтобы добраться до этой точки (включая расстояние в обоих направлениях)? Отличается ли это от полного изменения положения объекта на \(t = 0\) до \(t = 8\text{?}\)
Найдите точное положение объекта в точке \(t = 1, 2, 3, \ldots, 8\) и используйте эти данные для построения точного графика \(y = s(t)\) на предоставленных осях справа на рисунке 4.1.10. Как вы можете использовать предоставленную информацию о \(y = v(t)\) для определения вогнутости \(s\) на каждом соответствующем интервале?
Подраздел 4.1.4 Резюме
Если мы знаем скорость движущегося тела в каждой точке заданного интервала и скорость везде положительна, мы можем оценить пройденное телом расстояние и в некоторых случаях точно определить это значение.

В частности, когда скорость положительна на интервале, мы можем найти общее пройденное расстояние, найдя площадь под кривой скорости и над осью \(t\) на данном интервале времени. Мы можем только оценить эту площадь в зависимости от формы кривой скорости.
Первообразная функции \(f\) — это новая функция \(F\), производная которой равна \(f\text{.}\). То есть \(F\) является первообразной функции \(f\ ) при условии, что \(F’ = f\text{.}\) В контексте скорости и положения, если мы знаем функцию скорости \(v\text{,}\), первообразная \(v\) является функция положения \(s\), которая удовлетворяет \(s’ = v\text{.}\) Если \(v\) положительна на заданном интервале, скажем, \([a,b]\text{,}\) тогда изменение положения \(s(b) – s(a)\text{,}\) измеряет расстояние, которое прошел движущийся объект \([a,b]\text{.}\)
Если его скорость иногда отрицательна, движущийся объект иногда движется в противоположном направлении или возвращается назад. Чтобы определить пройденное расстояние, мы должны вычислить расстояние отдельно для интервалов, где скорость положительна или отрицательна, и учесть изменение положения на каждом таком интервале.

Упражнения 4.1.5 Упражнения
1. Оценка пройденного расстояния по данным скорости.
Автомобиль останавливается через шесть секунд после того, как водитель затормозил. При включенных тормозах регистрируются следующие скорости:
Время после торможения (сек) 0 2 4 6 Скорость (фут/с) 90 46 17 0 Дайте нижнюю и верхнюю оценки (используя все доступные данные) расстояния, пройденного автомобилем после торможения.
нижняя:
верхняя:
(для каждого, включая единицы 4 )
На графике зависимости скорости от времени покажите нижнюю и верхнюю оценки, которые вы нашли выше. .
2. Расстояние от линейной функции скорости.
Скорость автомобиля равна \(f(t) = 11 t\) метров в секунду. Используйте график \(f(t)\), чтобы найти точное расстояние, пройденное автомобилем, в метрах, от \(t=0\) до \(t=10\) секунд.

расстояние = (включая единицы 5 )
3. Изменение положения от линейной функции скорости.
Скорость частицы, движущейся вдоль оси \(x\), определяется выражением \(f(t) = 12 – 4 т\) см/сек. Используйте график \(f(t)\), чтобы найти точное изменение положения частицы от времени \(t=0\) до \(t=4\) секунд.
изменение позиции = (включая единицы 6 )
4. Сравнение пройденного расстояния с графиками скоростей.
Два автомобиля стартовали одновременно и движутся в одном направлении по прямой дороге. На рисунке ниже показана скорость \(v\) (в км/час) каждого автомобиля как функция времени (в часах).
Скорость автомобиля A показана сплошной синей кривой, а скорость автомобиля B – пунктирной красной кривой.
(a)
Какой автомобиль развивает большую максимальную скорость?
А
Б
(b)
Что останавливается первым?
А
Б
(c)
Что едет дальше?
А
Б
5.
 Нахождение среднего ускорения по данным скорости.
Нахождение среднего ускорения по данным скорости.Предположим, что разгоняющийся автомобиль разгоняется с 0 до 68,2 миль в час за пять секунд. Его скорость указана в следующей таблице в пересчете из миль в час в футы в секунду, так что все измерения времени даны в секундах. (Примечание: 1 миля в час равна 22/15 футов в секунду = 22/15 футов в секунду.) Найдите среднее ускорение автомобиля в течение первых двух секунд.
\(т\) 0 1 2 3 4 5 \(в(т)\) 0,00 34.09 59,09 77,27 90,91 100,00 среднее ускорение за первую секунду = (включая единицы 7 )
среднее ускорение за вторую секунду = (включая единицы 8 )
6. Изменение положения от квадратичной функции скорости. 92 — 3 t + 2\) для частицы, движущейся вдоль линии. Найти смещение (чистое пройденное расстояние) частицы за интервал времени \([-2,5]\text{.
 }\)
}\)смещение =
7.
Вдоль восточного берега озера Мичиган от озера Макатава (недалеко от Голландии) до Гранд-Хейвена проходит велосипедная дорожка, которая идет почти прямо с севера на юг. Для целей этой задачи предположим, что дорога совершенно прямая и что функция \(s(t)\) отслеживает положение велосипедиста на этом пути в милях к северу от озера Пиджен, которое находится примерно на полпути между концами велосипедная дорожка.
Предположим, что функция скорости байкера задана графиком на рис. 4.1.11 на интервале времени \(0 \le t \le 4\) (где \(t\) измеряется в часах), и что \(s (0) = 1\текст{.}\)
Рисунок 4.1.11. График скорости байкера \(y = v(t)\text{,}\) слева. Справа оси для приблизительного наброска \(y = s(t)\text{.}\)Насколько примерно к северу от Пиджен-Лейк находилась велосипедистка, когда она находилась на наибольшем расстоянии от Пиджен-Лейк? В какое время это произошло?
Каково общее изменение положения велосипедиста на интервале времени \(0 \le t \le 2\text{?}\) В \(t = 2\text{,}\) он был севернее или южнее Голубя Озеро?
Какое общее расстояние проехала велосипедистка \(0 \le t \le 4\text{?}\) Насколько близко она была в конце поездки к точке, с которой начала?
Нарисуйте приблизительный график \(y = s(t)\text{,}\) функции положения велосипедиста на интервале \(0 \le t \le 4\text{.
 }\) не менее четырех важных точек на графике \(s\text{.}\)
}\) не менее четырех важных точек на графике \(s\text{.}\)
8.
Игрушечная ракета запускается вертикально с земли в безветренный день. Вертикальная скорость ракеты в момент времени \(t\) (в секундах) равна \(v(t)= 500-32t\) футов/сек.
Через какое время после запуска ракеты скорость ракеты равна нулю? Назовите это значение времени \(a\text{.}\) Что происходит с ракетой в точке \(t = a\text{?}\)
Найдите значение общей площади, ограниченной \(y = v(t)\) и \(t\)-осью на интервале \(0 \let t \le a\text{.}\) Что представляет ли эта область с точки зрения физической постановки задачи?
Найти первообразную \(s\) функции \(v\text{.}\) То есть найти такую функцию \(s\), что \(s'(t) = v(t)\text {.}\)
Вычислите значение \(s(a) – s(0)\text{.}\) Что представляет это число с точки зрения физической постановки задачи?
Вычислить \(s(5) – s(1)\text{.}\) Что это число говорит вам о полете ракеты?
9.

Мгновенная скорость объекта, движущегося вдоль горизонтальной оси, в момент времени \(t\) в секундах определяется функцией \(v\), изображенной на рисунке 4.1.12, где \(v\) измеряется в футах/сек. Предположим, что кривые, составляющие части графика \(y=v(t)\), являются либо участками прямых, либо участками окружностей.
Рисунок 4.1.12. График \(y = v(t)\text{,}\) функции скорости движущегося объекта.Определить точное общее расстояние, пройденное объектом \(0 \le t \le 2\text{.}\)
Каково значение и значение \(s(5) – s(2)\text{,}\), где \(y = s(t)\) — функция положения движущегося объекта?
За какой промежуток времени объект прошел наибольшее расстояние: \([0,2]\text{,}\) \([2,4]\text{,}\) или \([5,7] \текст{?}\)
На каком интервале времени функция положения \(s\) возрастает? В какой точке (точках) \(s\) достигает относительного максимума?
10.
Фильтры на очистных сооружениях со временем загрязняются и, следовательно, становятся менее эффективными; они заменяются каждые 30 дней.
Таблица 4.1.13. Данные о загрязнении фильтров для воды. В течение одного 30-дневного периода скорость, с которой загрязнение проходит через фильтры в близлежащее озеро (в единицах твердых частиц в день), измеряется каждые 6 дней и приводится в следующей таблице. Время \(t\) измеряется в днях с момента замены фильтров.
В течение одного 30-дневного периода скорость, с которой загрязнение проходит через фильтры в близлежащее озеро (в единицах твердых частиц в день), измеряется каждые 6 дней и приводится в следующей таблице. Время \(t\) измеряется в днях с момента замены фильтров.День, \(т\) \(0\) \(6\) \(12\) \(18\) \(24\) \(30\) Уровень загрязнения в ед./сут, \(p(t)\) \(7\) \(8\) \(10\) \(13\) \(18\) \(35\) Отобразите полученные данные на наборе осей со временем по горизонтальной оси и уровнем загрязнения по вертикальной оси.
Объясните, почему объем загрязнения, попавшего в озеро за этот 30-дневный период, точно определяется площадью, ограниченной \(y = p(t)\) и осью \(t\) на интервале времени \([0,30]\текст{.
 }\)
}\)Оцените общее количество загрязнений, попадающих в озеро за этот 30-дневный период. Внимательно объясните, как вы определили свою оценку.
gvsu.edu/s/9Tgvsu.edu/s/9UЗдесь мы делаем неявное предположение, что \(s(0) = 0\text{;}\) мы обсудим различные возможности значений \(s(0)\) в последующем исследовании.
/webwork2_files/helpFiles/Units.html/webwork2_files/helpFiles/Units.html/webwork2_files/helpFiles/Units.html/webwork2_files/helpFiles/Units.html/webwork2_files/helpFiles/Units.htmlСмещение: определение, формула и примеры
Смещение: определение, формула и примеры | StudySmarterВыберите язык
Предлагаемые языки для вас:
Европа
английский (DE) английский (Великобритания)
StudySmarter — универсальное учебное приложение.

4.8 • Рейтинг +11k
Более 3 миллионов загрузок
Бесплатно
Сохранять
Распечатать
Редактировать
смещение
СОДЕРЖАНИЕ :
ОГЛАВЛЕНИЕ
Вы когда-нибудь гуляли буквально где-нибудь? Тогда угадайте, что вы используете измерение, которое мы знаем как смещение. Смещение используется повсеместно в области физики: если что-то движется, нужно найти его смещение, чтобы знать об этом все остальное. Это переменная, без которой мы просто не можем жить! Но что такое смещение и как его решить? Давай выясним.

Определение смещения
Предположим, объект меняет положение: он перемещается из положения \(A\) в положение \(B\).
Смещение объекта — это вектор, указывающий из положения \(A\) в положение \(B\): это разница между этими положениями.
Если что-то начиналось в начальном положении, двигалось в любом направлении, в течение любого промежутка времени и различными способами и заканчивалось в конечном положении, можно провести линию от начального до конечного положения. Если мы превратим эту линию в стрелку, указывающую на конечное положение, мы получим графическое представление вектора смещения.
Перемещение является векторной величиной. Как вектор, смещение имеет как величину, так и направление. Из определения, являющегося разницей в позициях, мы видим, что перемещение измеряется метрами.
Величина смещения
Смещение, как мы знаем, является вектором. Это означает, что у нас есть и величина, и направление. Если мы уберем смещение и оставим только величину, вместо этого мы получим расстояние от одной точки до другой, превратив наше векторное смещение в скалярное расстояние.

Расстояние между положениями \(A\) и положением \(B\) является величиной смещения между этими двумя положениями.
Расстояние против смещения
Как вы знаете, прямая линия от начального положения до конечного положения — не единственный способ измерения длины. Что, если человек, путешествующий между этими точками, выбрал менее прямой путь? Если вы измеряете весь путь от точки \(A\) до точки \(B\), игнорируя направление, вместо этого вы будете измерять пройденное расстояние. Расстояние — это скаляр, который, в отличие от вектора, не учитывает направление, то есть не может быть отрицательным. Например, если кто-то путешествовал налево на \(9\,\mathrm{ft}\), их смещение будет \(-9\,\mathrm{ft}\), если мы выберем левое отрицательное направление. Однако расстояние этого человека до начальной точки будет равно \(9\,\mathrm{ft}\), так как направление, в котором он двигался, совершенно не имеет значения для расстояния. Простой способ понять это так: если вы возьмете свое перемещение и отбросите информацию о направлении, у вас останется только информация о расстоянии.

Перемещение населения: в данном контексте важно, в каком направление движения человек, а не только то, как далеко они уходят от своей отправной точки, Wikimedia Commons Public Domain
Что такое формула смещения?
Как указывалось ранее, смещение — это вектор, идущий от начальной позиции \(x_\text{i}\) к конечной позиции \(x_\text{f}\). Следовательно, уравнение для расчета смещения \(\Delta x\) выглядит так:
\[\Delta\vec{x}=\vec{x}_\text{f}-\vec{x}_\ text{i}.\]
Важно знать, что когда речь идет о смещении, значение может быть отрицательным в зависимости от направления смещения. Если мы выберем положительное значение вверх, то смещение парашютиста между прыжком и приземлением будет отрицательным. Однако, если мы выберем отрицательное значение вверх, то их смещение будет положительным! При этом расстояние между их прыжком и приземлением в обоих случаях будет положительным.
Примеры смещения
Вот несколько примеров, которые мы можем использовать, чтобы попрактиковаться в том, как можно использовать смещение для решения проблем.

Джеймс движется \(26\,\mathrm{ft}\) на восток через футбольный стадион, прежде чем двигаться \(7\,\mathrm{ft}\) на запад. Затем он перемещается еще на \(6\,\mathrm{ft}\) на запад, а затем возвращается на \(15\,\mathrm{ft}\) на восток. Каково перемещение Джеймса после того, как он проделает описанное путешествие? Каково расстояние до его начального положения?
Во-первых, мы решили для себя сделать восток положительным направлением. Джеймс смещается на \(26\,\mathrm{ft}\) на восток, поэтому после этого шага смещение Джеймса составляет \(26\,\mathrm{ft}\) на восток. Затем он перемещается на \(7\,\mathrm{ft}\) на запад, что равно \(-7\,\mathrm{ft}\) на восток. Это означает, что мы вычитаем \(7\) из \(26\), что дает нам общее смещение \(19\,\mathrm{ft}\) теперь на восток. Затем Джеймс перемещается еще на \(6\,\mathrm{ft}\) на запад, что дает нам смещение \(19\,\mathrm{ft}-6\,\mathrm{ft}=13\,\mathrm{ футов}\) на восток. Наконец, Джеймс перемещается на \(15\,\mathrm{ft}\) на восток, совершая окончательное полное перемещение \(28\,\mathrm{ft}\) на восток.

Расстояние между его конечной и начальной позицией равно \(28\,\mathrm{ft}\).
София идет на север вверх по улице на \(50\,\mathrm{ft}\). Затем она путешествует \(20\,\mathrm{ft}\) на запад через улицу, затем еще \(25\,\mathrm{ft}\) на север. Каким будет ее двухмерное перемещение, когда она прибудет в пункт назначения?
Поскольку это расчет двумерного смещения, мы выбираем направления на восток и север как положительные. Мы считаем, что София начинается со смещения \((0,0)\,\mathrm{ft}\) на восток и север соответственно. Во-первых, она перемещается на север за \(50\,\mathrm{ft}\), и, поскольку смещение с севера на юг идет последним в наших координатах, мы называем ее смещением после этого перемещения \((0,50)\,\mathrm{ футов}\). Далее, \(20\,\mathrm{ft}\) west дает нам отрицательное значение смещения с востока на запад, делая общее смещение равным \((-20,50)\,\mathrm{ft}\) . Наконец, она перемещается на \(25\,\mathrm{ft}\) на север.
 Добавление этого к нашему смещению с севера на юг дает нам окончательное смещение \((-20,75)\,\mathrm{ft}\) в наших координатах. Чтобы ответить на вопрос, вернем наши координаты обратно в реальность и придем к выводу, что София смещается на \(75\,\mathrm{ft}\) на север и на \(20\,\mathrm{ft}\) на запад.
Добавление этого к нашему смещению с севера на юг дает нам окончательное смещение \((-20,75)\,\mathrm{ft}\) в наших координатах. Чтобы ответить на вопрос, вернем наши координаты обратно в реальность и придем к выводу, что София смещается на \(75\,\mathrm{ft}\) на север и на \(20\,\mathrm{ft}\) на запад.Расстояние от начальной точки до конечной можно рассчитать с помощью теоремы Пифагора.
Пример того, как перемещение может выглядеть в реальной жизни. В городском квартале есть четкие и конкретные пути для передвижения, а это означает, что расстояние, которое вы путешествуете, может включать в себя извилистые улицы. Однако смещение между двумя точками всегда будет прямой линией, направленной из одной точки в другую, Wikimedia Commons CC BY-SA 4.0
Вектор смещения
Мы рассмотрели смещение и знаем, что это вектор, а это означает, что смещение имеет как величину, так и направление, когда мы его описываем. Вектор, который мы называем смещением, может быть задан в одном, двух или трех измерениях.
 Мы уже рассмотрели смещение в двух измерениях, но что, если мы добавим третье? Мы живем в трехмерном пространстве, поэтому важно знать, как используется смещение в трех измерениях.
Мы уже рассмотрели смещение в двух измерениях, но что, если мы добавим третье? Мы живем в трехмерном пространстве, поэтому важно знать, как используется смещение в трех измерениях.В трех измерениях вектор изображается в виде матрицы: \(\begin{pmatrix}i\\ j\\ k\end{pmatrix}\). Здесь \(i\) представляет смещение в направлении \(x\), \(j\) представляет смещение в направлении \(y\), а \(k\) представляет смещение в \( г\) направление.
С точки зрения сложения и вычитания в векторах это довольно просто. Все, что вам нужно сделать, это взять значения \(i\), \(j\) и \(k\) одного вектора и добавить или вычесть их из соответствующих значений другого вектора. Это полезно при смещении, поскольку смещение между двумя позициями равно разнице между позициями.
Вам явно нужно смещение с вертикальным компонентом, чтобы достичь вершины этой горы, Wikimedia Commons Public Domain
Предположим, вы поднялись на самую высокую точку США, Денали, и хотите узнать свое перемещение между началом восхождения (в координатах \((62.
 966284,\,-151.156684)\,\text{градус}\) и высота \(7500\,\mathrm{ft}\)) и вершина (в координатах \((63.069042,\,-151.006347)\,\text{град}\) и высота \(20310\,\mathrm{ фт}\)). Что вы делаете, так это вычисляете разницу между этими двумя векторами, чтобы получить вектор смещения \(\Delta\vec{x}\):
966284,\,-151.156684)\,\text{градус}\) и высота \(7500\,\mathrm{ft}\)) и вершина (в координатах \((63.069042,\,-151.006347)\,\text{град}\) и высота \(20310\,\mathrm{ фт}\)). Что вы делаете, так это вычисляете разницу между этими двумя векторами, чтобы получить вектор смещения \(\Delta\vec{x}\):\[\Delta\vec{x}=\begin{pmatrix}63,069042\,\mathrm{град} – 62.966284\,\mathrm{град} \\ -151.006347\,\mathrm{град}+151.156684\,\mathrm{град} \\ 20310\,\mathrm{ft}-7500\ ,\mathrm{ft}\end{pmatrix} =\begin{pmatrix}0.102758\,\mathrm{deg} \\ 0.150337\,\mathrm{deg} \\ 12810\,\mathrm{ft} \end{pmatrix} .\]
Конечно, это удобно перевести в метры, и мы получим
\[\Delta\vec{x}=\begin{pmatrix} 11,5 \\ 7,6 \\ 3,9 \end{pmatrix}\ ,\mathrm{km}.\]
Теперь у нас есть смещение в виде вектора, поэтому мы можем разобрать его и сделать вывод, что ваше смещение было \(11,5\,\mathrm{км}\) на север, \( 7,6\,\mathrm{км}\) на восток и \(3,92}=14.3\,\mathrm{км}.\]
Смещение – основные выводы
Смещение – это вектор, описывающий разницу между начальным и конечным положениями.

Формула смещения: \(\Delta\vec{x}=\vec{x}_\text{f}-\vec{x}_\text{i}\).
Расстояние — это длина или величина вектора смещения.
Перемещение и расстояние различаются тем, что они являются вектором и скаляром соответственно.
Расстояние не может быть отрицательным.
Часто задаваемые вопросы о смещении
Смещение — это измерение величины и направления от начальной начальной точки до конечной точки.
Формула смещения представляет собой начальное положение, вычтенное из конечного положения.
Всякий раз, когда вы перемещаетесь из одного места в другое, вы «перемещаете» себя, то есть вы создаете смещение между тем, с чего вы начали, и тем, где вы оказались.
 Это смещение зависит от того, в каком направлении вы пошли и как далеко вы пошли.
Это смещение зависит от того, в каком направлении вы пошли и как далеко вы пошли.Первая производная смещения по времени — это скорость, а вторая производная смещения по времени — ускорение.
Уравнение для расчета смещения объекта состоит в том, чтобы умножить его скорость на время, затраченное на перемещение с этой скоростью.
Заключительный тест по смещению
Вопрос
Является ли смещение векторной или скалярной величиной?
Показать ответ
Ответ
вектор.
Показать вопрос
Вопрос
Кратко опишите, что такое смещение.
Показать ответ
Ответ
Смещение — это разница между двумя местоположениями в пространстве, принимая во внимание как величину, так и направление разницы/изменения местоположения.

Показать вопрос
Вопрос
Что такое скалярный эквивалент перемещения?
Показать ответ
Ответ
Расстояние.
Показать вопрос
Вопрос
В чем разница между смещением и расстоянием?
Показать ответ
Ответ
Перемещение — это вектор, а расстояние — это скаляр. Расстояние — это длина вектора смещения.
Показать вопрос
Вопрос
Какое уравнение используется для расчета смещения?
Показать ответ
Ответ
Показать вопрос
Вопрос
Если мы знаем смещение, мы всегда знаем расстояние.

Показать ответ
Ответ
Показать вопрос
Вопрос
В какой ситуации это верное предложение?
“Мое перемещение было 5 метров.”Показать ответ
Ответ
Во всех ситуациях.
Показать вопрос
Вопрос
Автомобиль стартует в 5 футах справа от вас и проезжает 7 футов вправо от вас. Каков его водоизмещение по сравнению с вами?
Показать ответ
Ответ
12 футов справа от вас.
Показать вопрос
Вопрос
Автобус стартует в 3 футах слева от вас и проезжает 10 футов вправо. Каков его водоизмещение по сравнению с вами?
Показать ответ
Ответ
7 футов вправо от вас.

Показать вопрос
Вопрос
Поезд имеет смещение относительно вас -12 футов после движения -6 футов. Какова была его исходная позиция по сравнению с вами?
Показать ответ
Ответ
-6 футов.
Показать вопрос
Вопрос
Смещение имеет максимальное число измерений, в которых оно может произойти.
Показать ответ
Ответ
Неверно.
Показать вопрос
Вопрос
Может ли составляющая вектора смещения быть меньше величины смещения?
Показать ответ
Ответ
Показать вопрос
Вопрос
Если вы куда-то едете, является ли расстояние между начальной и конечной точкой таким же, как расстояние, которое проехала ваша машина?
Показать ответ
Ответ
Показать вопрос
Вопрос
Если вы занимаетесь подводным плаванием, что вы можете сказать о смещении по вертикали между вашим положением на пляже и вашим положением под водой?
Показать ответ
Ответ
Это вниз.

Показать вопрос
Вопрос
Как складывать и вычитать векторы?
Показать ответ
Ответ
Возьмите каждый соответствующий компонент и сложите или вычтите их друг из друга, чтобы сформировать компоненты нового вектора, который является ответом на сложение или вычитание.
Показать вопрос
Подробнее о смещении
Откройте для себя подходящий контент для ваших тем
Не нужно обманывать, если у вас есть все необходимое для успеха! Упаковано в одно приложение!
Учебный план
Будьте идеально подготовлены вовремя с индивидуальным планом.

Тесты
Проверьте свои знания с помощью игровых тестов.
Карточки
Создавайте и находите карточки в рекордно короткие сроки.
Заметки
Создавайте красивые заметки быстрее, чем когда-либо прежде.
Учебные наборы
Все учебные материалы в одном месте.
Документы
Загружайте неограниченное количество документов и сохраняйте их в Интернете.
Study Analytics
Определите сильные и слабые стороны вашего исследования.
Еженедельные цели
Ставьте индивидуальные учебные цели и зарабатывайте баллы за их достижение.
Умные напоминания
Хватит откладывать на потом наши напоминания об учебе.
Награды
Зарабатывайте очки, открывайте значки и повышайте уровень во время учебы.
Волшебный маркер
Создавайте карточки в заметках полностью автоматически.
Умное форматирование
Создавайте самые красивые учебные материалы, используя наши шаблоны.

Как найти общее расстояние / полное перемещение
Посмотрите видео с двумя примерами того, как найти общее пройденное расстояние в исчислении — на интервале [0, 5] — или прочитайте ниже:
Как найти общее расстояние на интервал [0. 5]
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Содержание (Нажмите, чтобы перейти к этому разделу):
- Как найти общее расстояние
- С деривативами
- С интегралами
- Расстояние от точки до линии
- Общее расстояние и общее перемещение
- Как найти полный водоизмещение
Большинство проблем расстояния в исчислении дают вам функцию скорости , которая является производной функции положения. Формула скорости обычно представлена в виде квадратного уравнения.
Полное расстояние можно найти двумя способами: с помощью производных или путем интегрирования функции скорости по заданному интервалу.

Пример задачи : Найдите общее расстояние, пройденное частицей, движущейся в горизонтальном направлении от t = 0 до t = 5 секунд в соответствии с функцией положения:
s(t) = 8t 2 – 4t.Шаг 1: Найдите функцию скорости. Функция скорости является производной функции положения. Итак, чтобы найти функцию скорости, вам нужно продифференцировать s(t) = 4t 2 – 2t, используя степенное правило и производную постоянного правила:
v(t) = 16t – 4Шаг 2: Установите функцию скорости на ноль, затем решите, чтобы найти, где функция скорости меняет направление:
- v(t) = 16t – 4 = 0
- 16 т – 4 (+ 4) = 0 (+ 4)
- 16t(/16) = 4 (/16)
- т = 4/16 = 1/4
Примечание : В качестве альтернативы вы можете построить график функции скорости и отметить, где области графика находятся выше или ниже оси x. Здесь скорость как вектор изменила направление.

Шаг 3: Решите функцию положения для значений начального и конечного интервалов (которые равны 0 и 5, согласно вопросу) и любых значений t, которые вы нашли на шаге 2:
- s(0) = 8(0) 2 – 4(0) = 0,
- с(1/4) = 8(¼) 2 – 4(1/4) = -½
- с(5) = 8(5) 2 – 4(5) = 180.
Это дает вам положение объекта в каждый временной интервал.
Шаг 4: Найдите расстояние, пройденное между каждой точкой. Это векторы, поэтому мы должны использовать абсолютные значения, чтобы найти расстояние:
- Между 0 и -½, расстояние = |-½ – 0| = ½
- Между -½ и 180, расстояние = |180 – (-½)| = 180½
Шаг 5: Сложите значения из шага 4, чтобы найти общее пройденное расстояние.
½ + 180 ½ = 181Пример вопроса : Частица движется в соответствии со следующей функцией скорости:
v(t) = 3t 2 – 12.
Каково общее расстояние, пройденное от t = 1 до t = 3?Шаг 1: Установите скорость равной нулю, чтобы найти, где функция меняет направление:
- v(t) = 3t 2 – 12 = 0
- 3(t 2 – 4) = 0 (разложение).

- 3(т – 2)(т + 2) = 0
- т = -2, +2
Мы работаем с закрытым интервалом [1, 3] (из вопроса), поэтому интересующая нас точка (та, которая попадает в интервал) равна t = 2.
Шаг 2: Интегрируем функция скорости для каждого интервала. Для решения нужны два отдельных определенных интеграла:
- От начальной точки (t = 1) до нуля (t = 2),
- От нуля (t = 2) до конечной точки (t = 3).
Шаг 3: Добавьте абсолютные значения сумм, рассчитанных на шаге 2:
5 + 7 = 12.
Общее пройденное расстояние равно 12 единицам.Расстояние от точки до прямой — это длина кратчайшего пути между этой точкой и ближайшим к ней местом на прямой. Этот путь всегда представляет собой линию, перпендикулярную (под прямым углом) исходной линии.
1. Если вы знаете координаты
Если вы знаете декартовы координаты вашей точки и у вас есть уравнение для вашей линии, вы можете рассчитать расстояние между точкой и линией по формуле:
Где :
- x 0 , y 0 координаты точки,
- a, b и c — коэффициенты (и константы) для линии a x + b y + c = 0.

Пример
Предположим, ваша линия задается как 4 x + y = 0, а ваша точка равна (2, 2).
Поскольку у вас есть координаты, вы можете использовать первое уравнение, приведенное выше.
Расстояние от точки до прямой будет:
|4 · 2 + 1 · 2 | / √(4+4).
Это эквивалентно |10|/(2 √2) или приблизительно 3,54.2. Если у вас нет координат
Иногда у вас нет уравнения для прямой. Если все, что вы знаете о своей линии, это две точки, которые она пересекает, вы можете использовать другую формулу для расчета расстояния между точкой и линией. Давайте сделаем нашу точку x 0 , y 0 снова и определить точку как точку, которая проходит через x 1 , y 1 и x 2 , y 2 . Тогда расстояние равно
.
Эти формулы можно доказать с помощью алгебры, геометрии и векторного анализа.
Определенный интеграл функции скорости объекта дает вам общее смещение — насколько далеко объект находится от исходной точки.
 Однако это отличается от пройденного расстояния. Допустим, вы идете на местный рынок, который находится примерно в 1,6 км от вашего дома. Полное перемещение, когда вы достигнете пункта назначения, составляет 1 милю. Когда вы вернетесь домой, ваше полное перемещение будет равно нулю (вы вернетесь в исходную точку). Но пройденное расстояние равно 2 милям: одна миля до рынка и одна миля обратно. Перемещение не отражает пройденное расстояние.
Однако это отличается от пройденного расстояния. Допустим, вы идете на местный рынок, который находится примерно в 1,6 км от вашего дома. Полное перемещение, когда вы достигнете пункта назначения, составляет 1 милю. Когда вы вернетесь домой, ваше полное перемещение будет равно нулю (вы вернетесь в исходную точку). Но пройденное расстояние равно 2 милям: одна миля до рынка и одна миля обратно. Перемещение не отражает пройденное расстояние. Если объект движется в одном направлении (например, вдоль оси x), не реверсируя и не меняя курса, то общее расстояние равно полному перемещению.
Формула для полного водоизмещения :
Где:
- Σ = обозначение суммирования (суммировать все)
- Δx i — индивидуальные смещения.
Пример вопроса: Автомобиль проехал 2 мили на восток, а затем 4 мили на запад. Каково полное перемещение?
Решение:
На этом этапе может помочь начертить график задачи.
 Вот что мы пытаемся найти в этом вопросе:
Вот что мы пытаемся найти в этом вопросе:
На рисунке видно, что автомобиль находится в -2 милях от своего начального положения. Мы можем доказать это математически с помощью формулы.Шаг 1: Рассчитайте отдельные перемещения (Δx i ), используя формулу перемещения:
Δx = x f – x 0
Где:- x f = конечная позиция,
- x 0 = начальная позиция.
Для этого вопроса у нас есть два индивидуальных перемещения: 2 мили на восток и 4 мили на запад. = 2
- 2 мили S: Мы начали с «2» и закончили с -2, поэтому:
Δx = -2 – (2) = -4
Шаг 2: Сложите индивидуальные смещения, рассчитанные на шаге 1:
2 + (-4) = -2.
Вот и все!
Ссылки
Гор, Бхалчандра. О нахождении кратчайшего расстояния от точки до прямой. Получено с
https://www.ias.ac.in/article/fulltext/reso/022/07/0705-0714 15 декабря 2018 г.

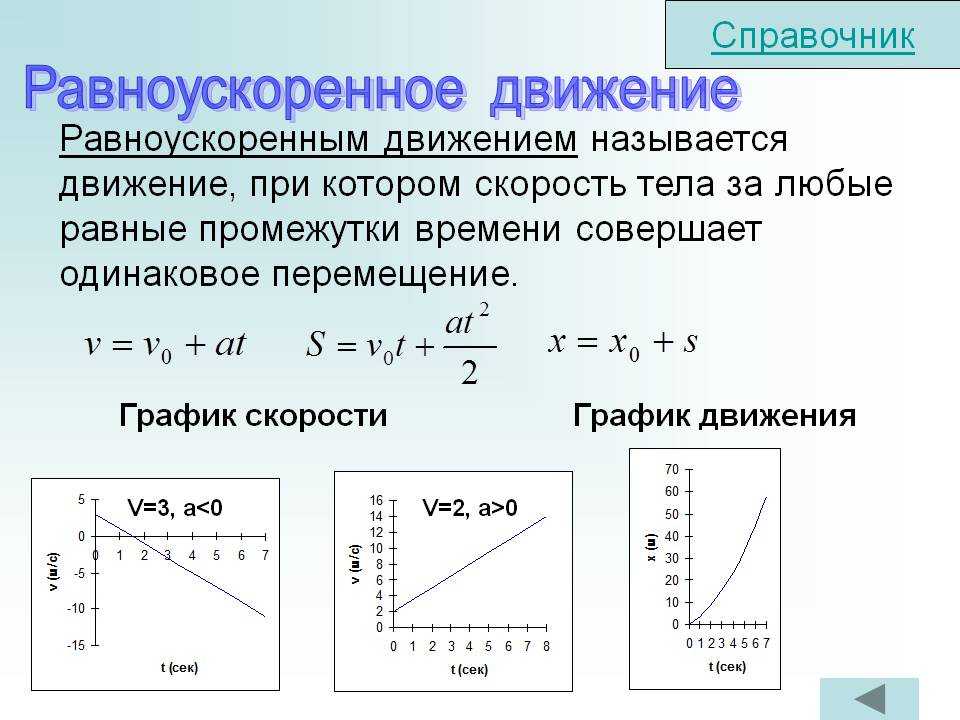
 ⓘ Пройденный путь [s]
ⓘ Пройденный путь [s]
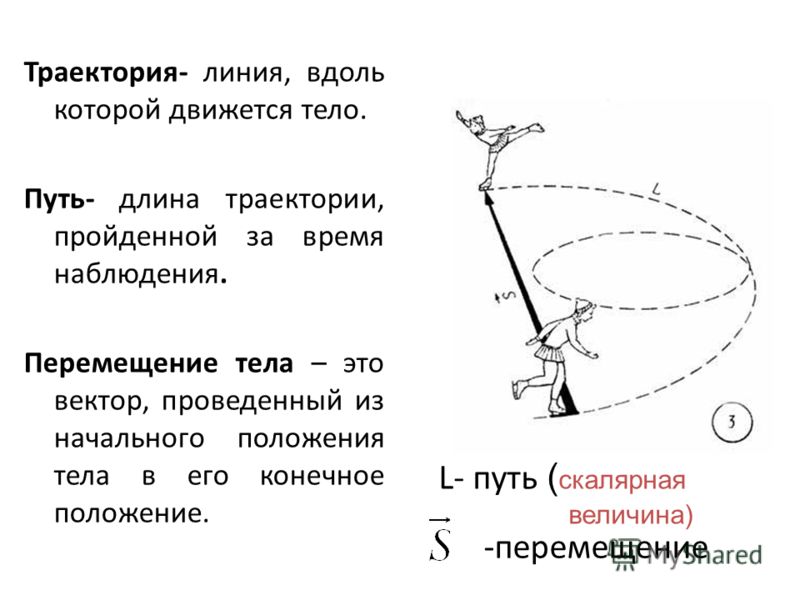 Это означает, что для их полного определения недостаточно знать только начальное и конечное положение тела. Обе величины определяют характер самого движения.
Это означает, что для их полного определения недостаточно знать только начальное и конечное положение тела. Обе величины определяют характер самого движения.
 }\) Мы исследовали среднюю скорость мяча на интервале \([a,b]\text{,}\), вычисленную по разностному фактору \(\frac{s(b)-s( a)}{b-a}\text{.}\) Мы обнаружили, что можем определить мгновенную скорость мяча в момент времени \(t\), взяв производную функции положения,
}\) Мы исследовали среднюю скорость мяча на интервале \([a,b]\text{,}\), вычисленную по разностному фактору \(\frac{s(b)-s( a)}{b-a}\text{.}\) Мы обнаружили, что можем определить мгновенную скорость мяча в момент времени \(t\), взяв производную функции положения, Во всех этих задачах мы переходим от функции \(f\) к ее производной \(f’\text{,}\) и используем значение производной, чтобы помочь нам ответить на важные вопросы.
Во всех этих задачах мы переходим от функции \(f\) к ее производной \(f’\text{,}\) и используем значение производной, чтобы помочь нам ответить на важные вопросы. }\)
}\)
 ) Несколько примеров, когда функция скорости является кусочно-постоянной, см. в этом апплете 1 .
) Несколько примеров, когда функция скорости является кусочно-постоянной, см. в этом апплете 1 . Вместо этого мы могли бы использовать шесть прямоугольников, изображенных на рис. 4.1.3, найти площадь каждого прямоугольника и сложить общую сумму. Очевидно, есть выбор, который нужно сделать, и вопросы, которые нужно понять: сколько прямоугольников мы должны использовать? Где мы должны вычислить функцию, чтобы определить высоту прямоугольника? Что произойдет, если скорость иногда будет отрицательной? Можем ли мы найти точную площадь под любой непостоянной кривой?
Вместо этого мы могли бы использовать шесть прямоугольников, изображенных на рис. 4.1.3, найти площадь каждого прямоугольника и сложить общую сумму. Очевидно, есть выбор, который нужно сделать, и вопросы, которые нужно понять: сколько прямоугольников мы должны использовать? Где мы должны вычислить функцию, чтобы определить высоту прямоугольника? Что произойдет, если скорость иногда будет отрицательной? Можем ли мы найти точную площадь под любой непостоянной кривой? 1.2.
1.2. }\) Вы должны использовать временные интервалы шириной \(\Delta t = 0,5\text{,}\) выбирая способ последовательного использования функции для определения высоты каждого прямоугольника, чтобы приблизить пройденное расстояние. 92+1.5t+1.5\text{.}\) Помните, что \(v\) является производной функции положения ходячего, \(s\text{.}\) Найдите формулу для \(s\) так, чтобы \(s’ = v\text{.}\)
}\) Вы должны использовать временные интервалы шириной \(\Delta t = 0,5\text{,}\) выбирая способ последовательного использования функции для определения высоты каждого прямоугольника, чтобы приблизить пройденное расстояние. 92+1.5t+1.5\text{.}\) Помните, что \(v\) является производной функции положения ходячего, \(s\text{.}\) Найдите формулу для \(s\) так, чтобы \(s’ = v\text{.}\)

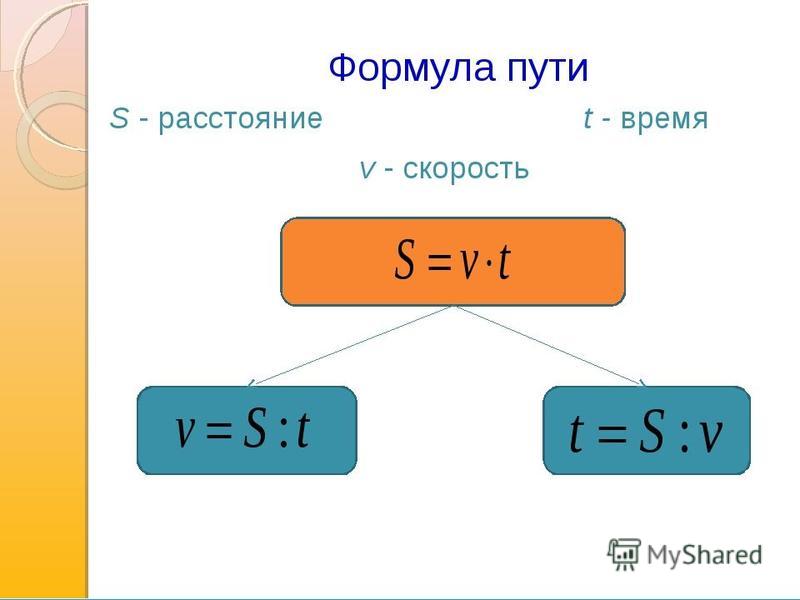 2 + 5\) также является функцией, производная которой равна \(g\text{,}\) и, следовательно, \( H\) — еще одна первообразная от \(g\text{.}\)
2 + 5\) также является функцией, производная которой равна \(g\text{,}\) и, следовательно, \( H\) — еще одна первообразная от \(g\text{.}\) 1.8. График \(y = v(t)\text{.}\)
1.8. График \(y = v(t)\text{.}\) Например, \(s = 1\) миля представляет собой одну милю к востоку от начального местоположения, а \(s = -1\) говорит нам, что она находится в одной миле к западу от того места, где она начала идти по пляжу.
Например, \(s = 1\) миля представляет собой одну милю к востоку от начального местоположения, а \(s = -1\) говорит нам, что она находится в одной миле к западу от того места, где она начала идти по пляжу. 5 \ \text{часы} = 4.5 \ \text{мили}\text{.}
\end{уравнение*}
5 \ \text{часы} = 4.5 \ \text{мили}\text{.}
\end{уравнение*} }
\end{уравнение*}
}
\end{уравнение*} Площадь над осью \(t\) считается положительной, поскольку она представляет расстояние, пройденное в положительном направлении, а площадь под осью \(t\) считается отрицательной, поскольку она представляет собой перемещение в отрицательном направлении. Таким образом, изменение положения женщины составляет
Площадь над осью \(t\) считается положительной, поскольку она представляет расстояние, пройденное в положительном направлении, а площадь под осью \(t\) считается отрицательной, поскольку она представляет собой перемещение в отрицательном направлении. Таким образом, изменение положения женщины составляет Если мы вычислим отдельно пройденное расстояние на каждом интервале, где скорость положительна или отрицательна, мы сможем вычислить либо общее пройденное расстояние, либо общее изменение положения. Мы присваиваем отрицательное значение расстояниям, пройденным в отрицательном направлении, когда вычисляем изменение положения, и положительное значение, когда вычисляем общее пройденное расстояние.
Если мы вычислим отдельно пройденное расстояние на каждом интервале, где скорость положительна или отрицательна, мы сможем вычислить либо общее пройденное расстояние, либо общее изменение положения. Мы присваиваем отрицательное значение расстояниям, пройденным в отрицательном направлении, когда вычисляем изменение положения, и положительное значение, когда вычисляем общее пройденное расстояние. }\) Каково положение объекта в \(t = 2\text{?} \)
}\) Каково положение объекта в \(t = 2\text{?} \)


 Нахождение среднего ускорения по данным скорости.
Нахождение среднего ускорения по данным скорости. }\)
}\) }\) не менее четырех важных точек на графике \(s\text{.}\)
}\) не менее четырех важных точек на графике \(s\text{.}\)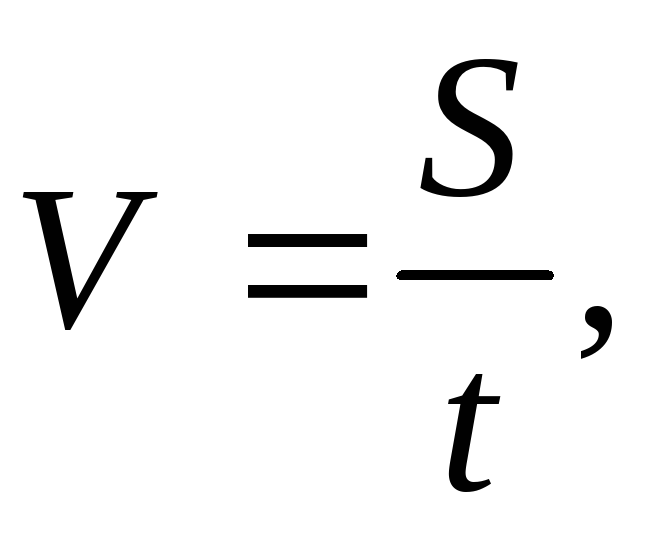
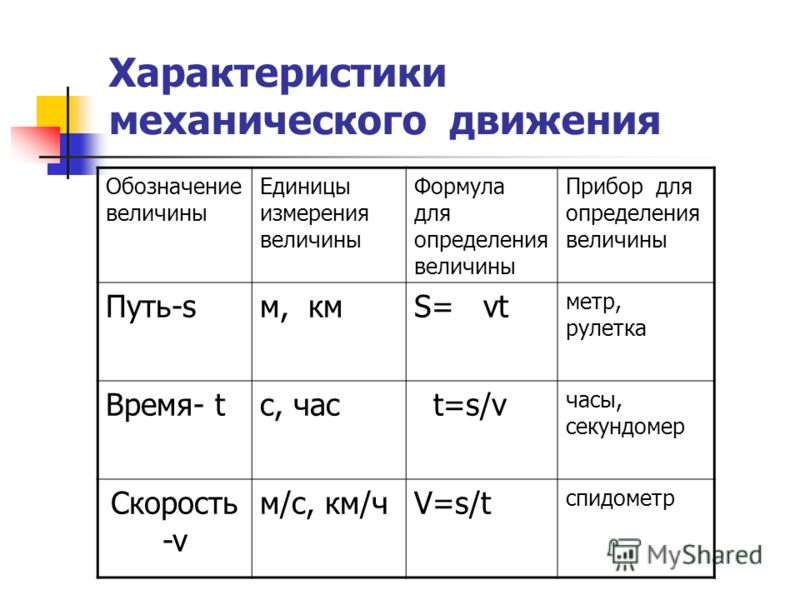 В течение одного 30-дневного периода скорость, с которой загрязнение проходит через фильтры в близлежащее озеро (в единицах твердых частиц в день), измеряется каждые 6 дней и приводится в следующей таблице. Время \(t\) измеряется в днях с момента замены фильтров.
В течение одного 30-дневного периода скорость, с которой загрязнение проходит через фильтры в близлежащее озеро (в единицах твердых частиц в день), измеряется каждые 6 дней и приводится в следующей таблице. Время \(t\) измеряется в днях с момента замены фильтров. }\)
}\)





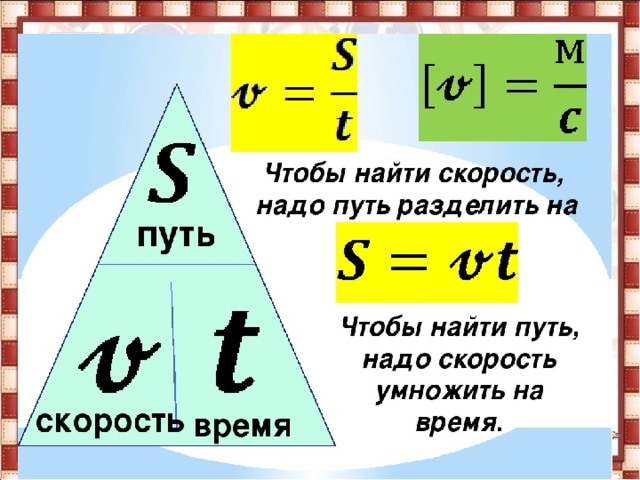 Добавление этого к нашему смещению с севера на юг дает нам окончательное смещение \((-20,75)\,\mathrm{ft}\) в наших координатах. Чтобы ответить на вопрос, вернем наши координаты обратно в реальность и придем к выводу, что София смещается на \(75\,\mathrm{ft}\) на север и на \(20\,\mathrm{ft}\) на запад.
Добавление этого к нашему смещению с севера на юг дает нам окончательное смещение \((-20,75)\,\mathrm{ft}\) в наших координатах. Чтобы ответить на вопрос, вернем наши координаты обратно в реальность и придем к выводу, что София смещается на \(75\,\mathrm{ft}\) на север и на \(20\,\mathrm{ft}\) на запад. Мы уже рассмотрели смещение в двух измерениях, но что, если мы добавим третье? Мы живем в трехмерном пространстве, поэтому важно знать, как используется смещение в трех измерениях.
Мы уже рассмотрели смещение в двух измерениях, но что, если мы добавим третье? Мы живем в трехмерном пространстве, поэтому важно знать, как используется смещение в трех измерениях. 966284,\,-151.156684)\,\text{градус}\) и высота \(7500\,\mathrm{ft}\)) и вершина (в координатах \((63.069042,\,-151.006347)\,\text{град}\) и высота \(20310\,\mathrm{ фт}\)). Что вы делаете, так это вычисляете разницу между этими двумя векторами, чтобы получить вектор смещения \(\Delta\vec{x}\):
966284,\,-151.156684)\,\text{градус}\) и высота \(7500\,\mathrm{ft}\)) и вершина (в координатах \((63.069042,\,-151.006347)\,\text{град}\) и высота \(20310\,\mathrm{ фт}\)). Что вы делаете, так это вычисляете разницу между этими двумя векторами, чтобы получить вектор смещения \(\Delta\vec{x}\):
 Это смещение зависит от того, в каком направлении вы пошли и как далеко вы пошли.
Это смещение зависит от того, в каком направлении вы пошли и как далеко вы пошли.



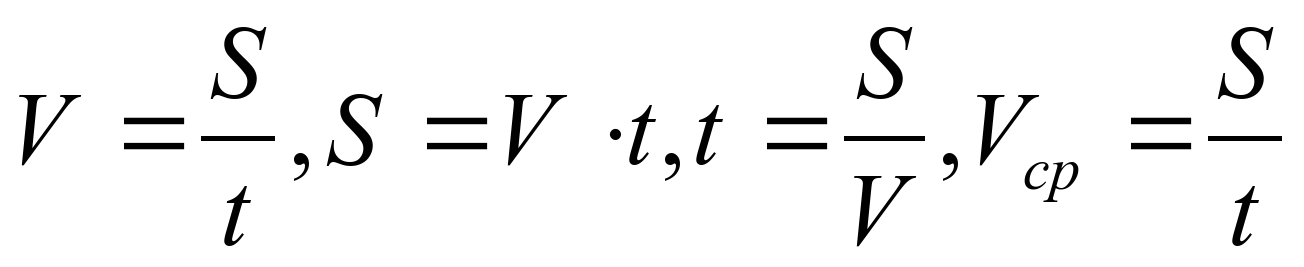





 Однако это отличается от пройденного расстояния. Допустим, вы идете на местный рынок, который находится примерно в 1,6 км от вашего дома. Полное перемещение, когда вы достигнете пункта назначения, составляет 1 милю. Когда вы вернетесь домой, ваше полное перемещение будет равно нулю (вы вернетесь в исходную точку). Но пройденное расстояние равно 2 милям: одна миля до рынка и одна миля обратно. Перемещение не отражает пройденное расстояние.
Однако это отличается от пройденного расстояния. Допустим, вы идете на местный рынок, который находится примерно в 1,6 км от вашего дома. Полное перемещение, когда вы достигнете пункта назначения, составляет 1 милю. Когда вы вернетесь домой, ваше полное перемещение будет равно нулю (вы вернетесь в исходную точку). Но пройденное расстояние равно 2 милям: одна миля до рынка и одна миля обратно. Перемещение не отражает пройденное расстояние. 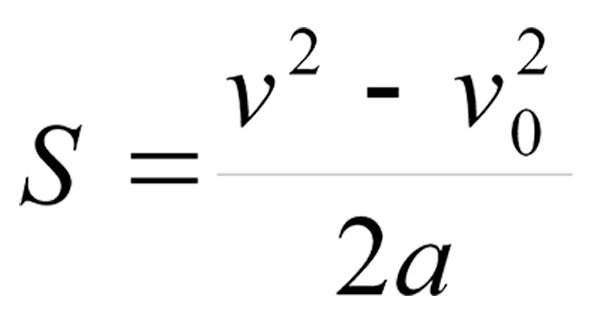 Вот что мы пытаемся найти в этом вопросе:
Вот что мы пытаемся найти в этом вопросе: