Проверка метода гаусса: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

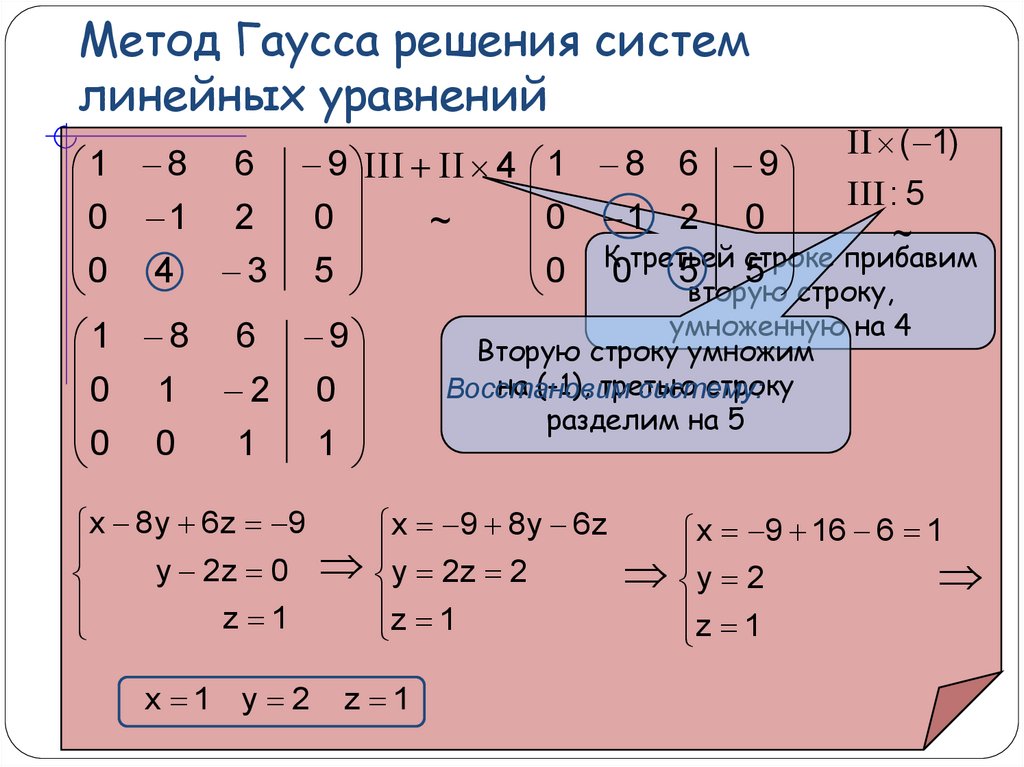
Лабораторная работа 2 Решение систем линейных алгебраических уравнений методом Гаусса

Работа выполняется с использованием палитры программирования системы автоматизации математических вычислений Mathcad

Задание на работу:

1. Разработать программу для решения системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента по столбцам.

2. Решить систему уравнений, определенную вариантом задания.

3. Произвести проверку решения.

4. Изменить матрицу коэффициентов А, сделав систему уравнений линейно зависимой, и проверить работоспособность программы в этом случае.

Варианты заданий .

( Система уравнений в матричной записи имеет вид Ax = b)

1. A= , b=2. A= , b=

3. A= , b=

4. A= , b=

5. A= , b=6. A= , b=

7. A= , b=8. A= , b=

9. A= , b=10. A= , b=

11. A= , b=12. A= , b=

13. A= , b = 14. A= , b=

15. A= , b = 16. A= , b=

17. A= , b = 18. A= , b=

19. A= , b = 20. A= , b=

21. A= , b =

Требования к оформлению отчета

Отчет должен содержать:

• Название и цель работы

• Задание на работу

• Текст программы на Mathcadе

• Результаты работы программы

• Проверку решения

Пример разработки программы для решения системы линейных агебраических уравнений в системе Mathcad

Этап 1. Объявление переменных

Определим переменные и зададим матрицу системы линейных уравнений:

С оздадим новый лист в MathCAD и для начала напишем оператор ORIGIN := 1 – это для того чтобы MathCAD начинал нумерацию в матрицах с 1, а не с нуля.

Теперь определим матрицу А.

Обратите внимание, что в MathCAD строчные и прописные буквы различны, следите за регистром переменных.

Наберите A:= нажмите меню Insert  Matrix задайте размерность матрицы 3 на 3 и нажмите OK. Заполните матрицу как показано на рисунке. Тем же способом задайте матрицу-столбец B.

Объединим все в одну расширенную матрицу matr с помощью оператора augment.

Присвоим переменной n значение 3, она будет определять количество корней системы.

Чтобы посмотреть значение любой переменной, достаточно написать ее имя и поставить знак равенства. Выведем значение переменной matr.

Еще одной важной особенностью MathCAD является последовательность операторов, например, если мы попробуем написать выражение matr:=augment(A,B) перед определением матриц A и B, то MathCAD выдаст ошибку.

Переменные определены, теперь перейдем к написанию функции проверки матрицы на линейно-зависимые строки.

Этап 2. Проверка на линейно-зависимые строки

На языке Pascal эта процедура будет выглядеть так:

Function Proverka(): boolean;

var d1: single;

da: word;

lin: boolean;

begin

d1:=0;

da:=0;

lin:=False;

For i:=0 to n-2 do

For j:=i+1 to n-1 do

Begin

For k:=0 to n-1 do

If matr[j,k]<>0 then d1:=d1+matr[i,k]/matr[j,k];

d1:=d1/n;

For k:=0 to n-1 do

If matr[j,k]<>0 then If d1=matr[i,k]/matr[j,k] then da:=da+1;

If da=n then lin:=True;

d1:=0;

da:=0;

end;

If lin then Proverka:=True Else Proverka:=False;

e nd;

Проверка на линейно-зависимые строки в Mathcadе

О

Рис 2.

3

Рис 2.4

ткройте панель, изображенную на рисунке 2.3. С помощью меню view  Math Palette. Щелкните на третьей строке во втором столбике иконки и перед вами откроется еще одна панель инструментов (рис. 2.4), отвечающая за встроенный язык программирования.

Так же в процессе решения нам понадобятся еще некоторые панели инструментов рис.2.5 и рис.2.6.

Найдите их на панели Math Palette (рис.2.3).

О

Рис 2.6

ператор Add Line обозначает в MathCAD программный модуль – вертикальную черту, справа от которой последовательно записываются операторы.

О ператор  означает присваивание: F  2+B

Otherwise – это оператор аналогичный Else в Pascal. С остальными операторами, думаю, вы знакомы.

Н

Рис 2.5

Рис 2.7

апишем имя функции, оператор присваивания и вставим программный модуль, несколько раз нажав кнопку

Add Line на панели программирования, вот что должно получиться (рис. 2.7).

Определим локальные переменные:

Еще одной особенностью языка MathCAD является то, что он сам определяет тип переменных.

d1 – будет хранить результат деления строк матрицы.

da – будет хранить количество совпавших элементов деления.

s1 – для хранения сообщения и результата проверки. (в Pascal эта переменная lin)

Теперь нам нужно разделить все строки между собой друг на друга и определить общее частное. Легче всего это сделать, разделив поочередно сначала первую строчку на все другие, затем вторую на оставшиеся и т.

д.

Запишем это так:

i будет обозначать делимое, а j делитель.

Совет. Чтобы вставить последовательность 1..n-1 нажмите на панели инструментов.

Внимание! Не вводите с клавиатуры имена программных операторов. Для их вставки с клавиатуры можно применять лишь сочетания клавиш, которые приведены в тексте всплывающей подсказки.

Рис 3.

В тело цикла вставьте Add Line и вставим еще один цикл для того, чтобы найти сумму всех частных. Следует учитывать ситуацию деления на ноль, поэтому ограничим действия с помощью условного оператора if.

Обратите внимание! Что в MathCAD оператор if записывается, наоборот, в отличие от записи в Pascal. Т.е. сначала действие, которое произойдет, если выполниться условие.

Следующим шагом найдем среднее от частного, разделив на число слагаемых n и присвоив это значение d1.

Т еперь проверим, сколько слагаемых равны d1. Переменную da будем увеличивать на единицу, если условие верно. Так же как и в предыдущем случае не стоит допускать деления на ноль, поэтому здесь используется вложенный оператор if.

После выполнения цикла, проверим, равно ли da = n, если так, то эти строки линейно зависимые.

Пример:

Допустим, матрица выглядит так: .

d1 будет равно = 1/2+2/4+3/6= 1.5

d

1 = 1.5 / n = 1.5 / 3 = 0.5

d1 = 1/2 = 2 /4 = 3/6 = 0.5 , то da = 3 и равно n, значит строки линейно-зависимые.

Далее установим значение переменных da и dl на ноль. Чтобы гарантировать нормальную работу алгоритма при следующих итерациях.

Возвратим результат функции. Если значение строковой переменной s1 так и не изменилось, то возвратим матрицу matr, в противном случае выведем сообщение наличии линейной зависимости.

Этап 3. Нахождение максимального элемента в столбце

Для реализации модифицированного метода Гаусса нам понадобиться функция нахождения максимального элемента в столбце и возвращение номера строки этого элемента.

Алгоритм этой функции достаточно прост и не требует подробных объяснений.

Этап 4. Перестановка строк в матрице

После того как найдена строка с максимальным элементом в столбце, возможно, нам понадобиться поменять эти строки местами. Для этого создадим функцию:

Определим переменные: i1 будет использоваться в цикле, а temp для временного хранения элементов матрицы. Далее цикл и стандартный алгоритм замены переменных.

Возвратим матрицу matr.

Этап 5. Прямой ход

Все дополнительные функции определены, теперь можно перейти непосредственно к поиску решения. Выполним прямой ход в методе Гаусса:

Определим некоторые переменные: i1 будет использоваться в цикле, а s1 для хранения сообщения о том, что система не имеет единственного решения. Создадим главный цикл.

Первым делом найдем строку с максимальным элементом через ранее объявленную функцию maxcol и присвоим это значение переменной max. Чтобы застраховать себя от частного случая, проверим, не является ли максимальный элемент равным нулю, если это так, то система не имеет единственного решения, и выйдем из цикла, используя команду break. В Pascal сразу произведем замену Zamena (i1,MaxCol(i1)) и реализуем алгоритм проверки в теле функции maxcol:

В MathCAD :

Если все в порядке, то поменяем строки местами.

Получим разрешающее уравнение, разделив каждый элемент на первый в строке i1

Получим:

П рисвоим единицу коэффициенту при x_i1

Умножим разрешающее уравнение i1 на первый коэффициент уравнения j и вычтем полученное из уравнения j.

Присвоим ноль коэффициенту при х_j,i1

После выполнения всех итераций матрица примет треугольный вид, теперь не сложно найти корни системы.

Н о не забудьте возвратить преобразованную матрицу или, в случае, если система не имеет единственного решения, соответствующее сообщение.

Этап 6. Обратный ход

Теперь не составит труда найти корни уравнения, выполнив обратный ход. Напишем еще одну функцию oh:

Выполним обратный цикл, задав диапазон значений от n до 2, где n >= 2.

Тем самым пройдем по строкам в обратном порядке.

Далее, еще один цикл, чтобы пройти по всем элементам строки, от последнего до первого. Последовательно исключив неизвестные переменные, получим в последнем столбце матрицы корни уравнения.

Задача решена, осталось только вывести результаты.

Этап 7. Вывод ответа

С оздадим матрицу-столбец a из последнего столбца матрицы matr и возвратим ее.

Соберем все воедино в функции otvet:

1. Выполним проверку на линейную зависимость.

2. Выполним прямой ход, если значение matr удовлетворяет условию.

3. Затем обратный ход с аналогичной проверкой.

4. И присвоим matr полученный результат.

5. Вернем значение функции (им может быть или матрица-столбец с корнями системы или одно из двух сообщений)

В заключении выведем ответ, набрав otvet =. Ответ может быть трех типов:

Решение систем линейных алгебраических уравнений в пакете MATLAB

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Решение систем линейных алгебраических уравнений

в пакете MATLAB

2. Ранее

» Возможности MATLAB
‣ левостороннее деление
› x = A\b
‣ обратная матрица
› x = inv(A)*b
21.04.2022
2

3.

Небольшие системы уравнений» Небольшая система содержит, как привило, не
более трех уравнений
» Решение, чаще всего, может не требовать
компьютера
» Методы
‣ графический
‣ Крамера
‣ исключения неизвестных
21.04.2022
3

4. Графический метод

21.04.2022
4

5. Сложные случаи решений

» Три случая
1. Параллельные линии
› нет решения
2. Совпадающие линии
› множество решений
3. Близкие линии
› трудно определить точку пересечения
» Системы в 1 и 2 случае
называются – вырожденными
(особыми, сингулярными)
» Случай 3 соответствует плохо
обусловленной системе
‣ существуют сложности при численном
решении
21.04.2022
5

6. Метод Крамера

21.04.2022
6

7. Метод Крамера

21.04.2022
7

8. Исключение неизвестных

21.04.2022
8

9. Исключение неизвестных

21.04.2022
9

10. Метод Гаусса

21.04.2022
10

11. Метод Гаусса – Прямой ход

21. 04.2022
11

12. Метод Гаусса – Прямой ход

21.04.2022
12

13. Метод Гаусса – Прямой ход

21.04.2022
13

14. Метод Гаусса – Прямой ход

21.04.2022
14

15. Метод Гаусса – Обратный ход

21.04.2022
15

16. Пример

21.04.2022
16

17. Метод Гаусса с обратной подстановкой

» В рассмотренном варианте метода Гаусса могут
возникнуть ситуации когда решение не может быть
найдено или иметь существенную погрешность
‣ например, в случае если главный элемент равен 0, при
нормализации возникает деление на 0
‣ также существенно меньшее значение главного элемента
по сравнению с остальными может привести к
увеличению погрешности вычислений
» Решение – выбор главного элемента
‣ частный
› выбор максимального значения главного элемента с
последующей перестановкой строк
‣ полный (применяется редко)
› выбор максимального значения главного элемента с
последующей перестановкой строк и столбцов
21. 04.2022
17

18. Пример – Частный выбор главного элемента

21.04.2022
18

19. Пример – Частный выбор главного элемента

Разряды
х2
х1
Ошибка х1, %
3
0,667
-3,33
1099
4
0,6667
0,0000
100
5
0,66667
0,30000
10
6
0,666667
0,330000
1
7
0,6666667
0,3330000
0,1
Разряды
х2
х1
Ошибка х1, %
3
0,667
0,333
0,1
4
0,6667
0,3333
0,01
5
0,66667
0,33333
0,001
6
0,666667
0,333333
0,0001
7
0,6666667
0,3333333
0,0000
21.04.2022
19

20. Пример – MATLAB

21.04.2022
20

21. Расчет определителя матрицы

21.04.2022
21

22. Факторизация матриц

» В математике факторизация или факторинг – это
декомпозиция объекта (например, числа, полинома
или матрицы) в произведение других объектов или
факторов, которые, будучи перемноженными, дают
исходный объект
» Целью факторизации является приведение объекта
к «основным строительным блокам»
‣ Матрица может также быть факторизована на
произведение матриц специального вида для
приложений, в которых эта форма удобна
» Виды факторизации матриц
‣ LU
‣ Холецкого
‣ QR
21. 04.2022
22

23. LU факторизация

21.04.2022
23

24. LU факторизация

21.04.2022
24

25. LU факторизация

‣ факторизация
› выполняется декомпозиция
матрицы А на верхнюю U и
нижнюю L треугольные
матрицы
‣ подстановка
› прямая подстановка
определяет промежуточный
вектор d
› обратная подстановка
определяет вектор
неизвестных x
21.04.2022
прямая
подстановка
» Два основных шага
решения системы
факторизация
LU факторизация
обратная
25

26. Метод Гаусса как LU факторизация

21.04.2022
26

27. Метод Гаусса как LU факторизация

21.04.2022
27

28. Метод Гаусса как LU факторизация

21.04.2022
28

29. Метод Гаусса как LU факторизация

21.04.2022
29

30. Пример – Проверка

21.04.2022
30

31. Пример – Проверка

21.04.2022
31

32. Метод Гаусса как LU факторизация

21.04.2022
32

33.

Пример21.04.2022
33

34. Пример

21.04.2022
34

35. LU факторизация с выбором главного элемента

» Аналогично методу Гаусса для обеспечения
надежности решения при использовании LU
факторизации необходимо применять частный
выбор главного элемента
‣ одним из способов является использование матрицы
перестановки
› единичная матрица для взаимной замены строк и столбцов
21.04.2022
35

36. LU факторизация с выбором главного элемента

21.04.2022
36

37. Пример

21.04.2022
37

38. Пример

21.04.2022
38

39. LU факторизация – MATLAB функции

» lu
‣ [L,U] = lu(A) – возвращает верхнюю треугольную
матрицу U и психологическую нижнюю матрицу L
(то есть произведение нижней треугольной матрицы
и матрицы перестановок), так что A=L*U
‣ [L,U,P] = lu(A) – возвращает верхнюю
треугольную матрицу U, нижнюю треугольную
матрицу L и сопряженную (эрмитову) матрицу
матрицы перестановок P, так что L*U =P*A
21. 04.2022
39

40. Пример

21.04.2022
40

41. Факторизация Холецкого

21.04.2022
41

42. Пример

21.04.2022
42

43. Пример

21.04.2022
43

44. Факторизация Холецкого

21.04.2022
44

45. Факторизация Холецкого – MATLAB функции

» chol
‣ U = chol(A) – для квадратной матрицы A
возвращает верхнюю треугольную матрицу U, так
что U’*U=A
› Разложение Холецкого возможно для действительных и
комплексных эрмитовых матриц
21.04.2022
45

46. Пример

21.04.2022
46

47. Левостороннее деление MATLAB

» При использовании левостороннего деления
«\» MATLAB выполняет оценку матрицы
коэффициентов и применяет оптимальный
метод для решения
‣ MATLAB проверяет вид матрицы коэффициентов
при неизвестных для возможности нахождения
решения без применения полного метода Гаусса
› разреженная
› треугольная
› симметричная
‣ В противном случае применяется для квадратной
матрицы применяется метод Гаусса с частным
выбором главного элемента
21. 04.2022
47

48. QR факторизация

21.04.2022
48

49. QR факторизация – MATLAB функции

» qr
‣ [Q,R] = qr(A) – вычисляет верхнюю треугольную
матрицу R того же размера, как и у A, и унитарную
матрицу Q, так что X=Q*R
‣ [Q,R,P] = qr(A) – вычисляет матрицу перестановок P,
верхнюю треугольную матрицу R с убывающими по
модулю диагональными элементами и унитарную
матрицу Q, так что A*P=Q*R
› Матрица перестановок P выбрана так, что abs(diag(R))
уменьшается
‣ [Q,R] = qr(A,0) и [Q,R,P] = qr(A,0) – вычисляют
экономное разложение, в котором P – вектор
перестановок, так что Q*R=A(:,P)
› Матрица P выбрана так, что abs(diag(R)) уменьшается
21.04.2022
49

50. Пример

21.04.2022
50

51. Итерационные методы

» Итерационные или аппроксимационные методы
являются альтернативой ранее рассмотренным
методам решения СЛАУ, основанным на
исключении неизвестных
» Можно выделить два основных этапа
‣ выбор начального приближения
‣ последующее систематическое уточнение
» Методы
‣
‣
‣
‣
‣
Гаусса-Зейделя
Якоби
релаксации
бисопряженных градиентов
и др.
21.04.2022
51

52. Метод Гаусса-Зейделя

21.04.2022
52

53. Метод Гаусса-Зейделя

21.04.2022
53

54. Пример

21.04.2022
54

55. Пример

21.04.2022
55

56. Пример

21.04.2022
56

57. Метод Якоби

» Метод Гаусса-Зейделя
использует
найденное значение
х сразу же для
нахождения
следующего х из
другого уравнения
» Несколько
альтернативный
подход, называемый
методом Якоби,
заключается в
расчете всех х на
основании
предыдущей
итерации
21.04.2022
57

58. Сходимость и диагональное преобладание

21.04.2022
58

59. Пример

21.04.2022
59

60. Метод релаксации

21.04.2022
60

61. Метод релаксации

21.04.2022
61

62. Пример

21.04.2022
62

63. Пример

21.04.2022
63

64. Пример

21.04.2022
64

English     Русский Правила

линейная алгебра – Доказательство того, что исключение Гаусса-Жордана работает

Задавать вопрос

спросил 10 лет, 9 месяцев назад

Изменено 4 года, 11 месяцев назад

Просмотрено 4к раз

$\begingroup$

Исключение Гаусса-Жордана — это метод, который можно использовать для вычисления обратных матриц (если они обратимы). Его также можно использовать для решения одновременных линейных уравнений.

Однако после нескольких поисков в Google мне не удалось найти доказательство того, что этот алгоритм работает для всех $n \times n$, обратимых матриц. Как бы вы доказали, что метод использования исключения Гаусса-Жордана для вычисления матриц будет работать для всех обратимых матриц конечных размеров (мы допускаем перестановку двух строк)?

Возможна идея индукции по $n$: базовый случай очень ясен, но как доказать шаг индукции?

Мы , а не , пытаемся показать, что ответ, сгенерированный с использованием Гаусса-Жордана, будет правильным. Мы пытаемся показать, что принцип Гаусса-Жордана применим ко всем обратимым матрицам.

Примечание. Я понимаю, что здесь есть аналогичный вопрос, но этот вопрос отличается тем, что требует доказательства для обратимых матриц.

• линейная алгебра
• матрицы
• обратные
• исключение Гаусса

$\endgroup$

1

$\begingroup$

Это один из типичных случаев, когда самая очевидная причина того, что что-то верно, заключается в том, что соответствующий алгоритм не может дать сбой.

Грубо говоря, единственный способ, которым Гаусс-Жордан может застрять, это если (в любой промежуточной точке) есть столбец, содержащий слишком много нулей, поэтому нет строки, которую можно было бы поменять местами, чтобы получить ненулевую запись в ожидаемое место. Однако если это все-таки происходит, то легко видеть, что матрица необратима, а поскольку операции над строками не вызвали этого, то виновата должна быть исходная матрица.

$\endgroup$

2

$\begingroup$

Допущение: квадратная обратимая матрица.

Метод Гаусса-Жордана обычно преподается после метода исключения Гаусса для решения системы линейных уравнений. Итак, я предполагаю, что вы знаете о исключении Гаусса.

Рассмотрим систему линейных уравнений $Ax=b$.

$Ax=b$………………………………..(1) 9{-1}b$…………. {-1}$.

$\endgroup$

Гауссовский вариант алгоритма Фрейвалдса для эффективной и надежной проверки матричного произведения

Ключевые слова: Отказоустойчивость; алгоритмическая устойчивость; гауссовский вариант алгоритма Фрейвалдса; умножение матриц; Гауссовский случайный вектор; вероятность отказа

Благодарности

Мы хотели бы поблагодарить доктора Стефана Олариу за его ценные предложения по рукописи.

Каталожные номера

[1] Н. Алон, О. Голдрайх, Й. Хостад и Р. Перальта, Простые конструкции почти 𝑘-мудрых независимых случайных величин, 31-й ежегодный симпозиум по основам компьютерных наук, Vol. I, II (Сент-Луис, 1990 г.), IEEE Press, Лос Аламитос (1990), 544–553. 10.1109/FSCS.1990.89575Поиск в Google Scholar

[2] П. Банерджи и Дж. А. Абрахам, Границы отказоустойчивости на основе алгоритмов в многопроцессорных системах, IEEE транс. вычисл. 100 (1986), вып. 4, 296–306. 10.1109/TC.1986.1676762Поиск в Google Scholar

[3] П. Банерджи, Дж. Т. Рахмех, К. Станкель, В. С. Наир, К. Рой, В. Баласубраманян и Дж. А. Абрахам, Отказоустойчивость на основе алгоритма на многопроцессорном гиперкубе, IEEE транс. вычисл. 39 (1990), вып. 9, 1132–1145. 10.1109/12.57055Поиск в Google Scholar

[4] С. Больдо и Ж.-М. Мюллер, Точная и приближенная погрешность FMA, IEEE транс. вычисл. 60 (2011), вып. 2, 157–164. 10.1109/TC.2010.139Поиск в Google Scholar

[5] Г. Босилка, Р. Дельмас, Х. Донгарра и Ж. Лангу, Отказоустойчивость на основе алгоритма, применяемая к высокопроизводительным вычислениям, J. Параллельное распределение. вычисл. 69(2009), нет. 4, 410–416. 10.1016/j.jpdc.2008.12.002Поиск в Google Scholar

[6] К. Л. Ченг, Ч. В. Ван и Дж. Н. Ли, Fame: система анализа отказов памяти на основе шаблонов ошибок, Международная конференция по автоматизированному проектированию, IEEE Press, Пискатауэй (2003), 595–598. Поиск в Google Scholar

[7] Д. Д. Чинн и Р. К. Синха, Границы размера выборочного пространства для проверки матричного произведения, Поставить в известность. Процесс. лат. 48 (1993), вып. 2, 87–91. 10.1016/0020-0190(93)90183-AПоиск в Google Scholar

[8] Д. Копперсмит и С. Виноград, Умножение матриц через арифметические прогрессии, Материалы 19-го ежегодного симпозиума ACM по теории вычислений, ACM, Нью-Йорк (1987), 1–6. 10.1145/28395.28396Поиск в Google Scholar

[9] Дж. В. Деммель и Н. Дж. Хайэм, Стабильность блочных алгоритмов с быстрым бласом уровня 3, АКМ транс. Мат. ПО 18 (1992), вып. 3, 274–291. 10.1145/131766.131769Поиск в Google Scholar

[10] Дж. Дж. Донгарра, Дж. Дю Кро, С. Хаммарлинг и И. Дафф, Алгоритм 679: набор базовых подпрограмм линейной алгебры уровня 3: реализация модели и программы тестирования, АКМ транс. Мат. ПО 16 (1990), вып. 1, 18–28. 10.1145/77626.77627Поиск в Google Scholar

[11] П. Дринеас, Р. Каннан и М. В. Махони, Быстрые алгоритмы Монте-Карло для матриц. I. Аппроксимирующее матричное умножение, СИАМ Дж. Вычисл. 36 (2006), вып. 1, 132–157. 10.1137/S0097539704442684Поиск в Google Scholar

[12] П. Дринеас, Р. Каннан и М. В. Махони, Быстрые алгоритмы Монте-Карло для матриц. II. Вычисление приближения низкого ранга к матрице, СИАМ Дж. Вычисл. 36 (2006), вып. 1, 158–183. 10.1137/S0097539704442696Поиск в Google Scholar

[13] П. Дринеас, Р. Каннан и М. В. Махони, Быстрые алгоритмы Монте-Карло для матриц. III. Вычисление сжатого приближенного матричного разложения, СИАМ Дж. Вычисл. 36 (2006), вып. 1, 184–206. 10.1137/S0097539704442702Поиск в Google Scholar

[14] Э. Н. Эльнозахи, Л. Алвиси, Ю. М. Ван и Д. Б. Джонсон, Обзор протоколов отката-восстановления в системах передачи сообщений, АКМ вычисл. Surv. 34 (2002), вып. 3, 375–408. 10.1145/568522.568525Поиск в Google Scholar

[15] С. Эрикссон-Бике, М. Солбриг, М. Стефанелли, С. Варкентин, Р. Эбби и И. К. Ф. Ипсен, Выборка важности для алгоритма умножения матриц Монте-Карло с применением к поиску информации, SIAM J. Sci. вычисл. 33 (2011), вып. 4, 1689–1706 гг. 10.1137/10080659XПоиск в Google Scholar

[16] Р. Фрейвалдс, Вероятностные машины могут использовать меньше времени работы, Обработка информации 77, Северная Голландия, Амстердам (1977), 839–842. Поиск в Google Scholar

[17] К. Галливан, В. Джалби и У. Мейер, Использование blas3 в линейной алгебре на параллельном процессоре с иерархической памятью, SIAM J. Sci. Стат. Комп. 8 (1987), нет. 6, 1079–1084. 10.1137/0908086Поиск в Google Scholar

[18] Л. Гасенец, К. Левкопулос и А. Лингас, Эффективно исправлять матричные продукты, Алгоритмы и вычисления, Примечания к лекциям по вычислительной технике. науч. 8889, Спрингер, Чам (2014), 53–64. 10.1007/978-3-319-13075-0_5Поиск в Google Scholar

[19] Дж. Н. Глосли, Д. Ф. Ричардс, К. Дж. Касперсен, Р. Э. Радд, Дж. А. Ганнелс и Ф. Х. Штрейц, Расширение стабильности за пределы процессорного тысячелетия: атомистическое моделирование нестабильности Кельвина-Гельмгольца в микронном масштабе, Материалы конференции ACM/IEEE 2007 г. по суперкомпьютерам, ACM, Нью-Йорк (2007), 1–11. 10.1145/1362622.1362700Поиск в Google Scholar

[20] Дж. А. Ганнелс, Д. С. Кац, Э. С. Кинтана-Орти и Р. А. Ван де Геджин, Отказоустойчивое высокопроизводительное умножение матриц: теория и практика, Материалы Международной конференции по надежным системам и сетям, IEEE Press, Пискатауэй (2001), 47–56. 10.1109/DSN.2001.941390Поиск в Google Scholar

[21] Н. Халко, П. Г. Мартинссон и Дж. А. Тропп, Нахождение структуры со случайностью: вероятностные алгоритмы построения приближенных матричных разложений, SIAM Rev. 53 (2011), вып. 2, 217–288. 10.1137/090771806Поиск в Google Scholar

[22] Э. Хокенек, Р. К. Монтойе и П. В. Кук, Риск второго поколения с плавающей запятой IEEE J. Твердотельные схемы 25 (1990), нет. 5, 1207–1213. 10.1109/4.62143Поиск в Google Scholar

[23] К. Х. Хуанг и Дж. А. Абрахам, Алгоритмическая отказоустойчивость матричных операций, IEEE транс. вычисл. 100 (1984), вып. 6, 518–528. 10.1109/TC.1984. 1676475Поиск в Google Scholar

[24] И. Корец и Дж. Видерманн, Детерминированная проверка целочисленного матричного умножения за квадратичное время, SOFSEM 2014: Теория и практика компьютерных наук, Примечания к лекциям по вычислительной технике. науч. 8327, Спрингер, Чам (2014), 375–382. 10.1007/978-3-319-04298-5_33Поиск в Google Scholar

[25] А. Кумар и Дж. Л. Роч, Безопасный и отказоустойчивый аутсорсинг матричных вычислений на основе алгоритмов, препринт (2013 г.), https://hal.archives-ouvertes.fr/hal-00876156/file/JC2S.pdf. Поиск в Google Scholar

[26] С. Лей, С. Ляо, Т. Хуан и Х. Ли, Служба облачных вычислений: случай вычисления детерминанта большой матрицы, IEEE транс. Серв. вычисл. 8 (2015), вып. 5, 688–700. 10.1109/TSC.2014.2331694Поиск в Google Scholar

[27] Дж. Л. Лева, Быстрый нормальный генератор случайных чисел, АКМ транс. Мат. ПО 18 (1992), вып. 4, 449–453. 10.1145/138351.138364Поиск в Google Scholar

[28] Ю. Ли и М. Масканьи, Приложение Монте-Карло на основе сетки, Материалы третьего международного семинара/конференции по грид-вычислениям — GRID02, Спрингер, Берлин (2002), 13–25. 10.1007/3-540-36133-2_2Поиск в Google Scholar

[29] Ю. Ли и М. Масканьи, Повышение производительности за счет репликации вычислений в крупномасштабной вычислительной сетке, Материалы Третьего международного симпозиума IEEE/ACM по кластерным вычислениям и грид-системам, IEEE Press, Пискатауэй (2003), 442–448. Поиск в Google Академии

[30] Ю. Ли и М. Масканьи, Анализ крупномасштабных приложений Монте-Карло на основе сетки, Междунар. J. Высокая производительность. вычисл. заявл. 17 (2003), 369–382. 10.1177/10943420030174003Поиск в Google Scholar

[31] Дж. В. Линдеберг, Eine neue Herleitung des Exponentialgesetzes in der Wahrscheinlichkeitsrechnung, Мат. З. 15 (1922), вып. 1, 211–225. 10.1007/BF01494395Поиск в Google Scholar

[32] К. Лисбоа, М. Эригсон и Л. Карро, Недорогая программа проверки умножения матриц, Латиноамериканский тестовый семинар IEEE, 2007 г. Поиск в Google Академии

[33] Ф. Т. Лук и Х. Парк, Анализ основанных на алгоритмах методов отказоустойчивости, J. Параллельное распределение. вычисл. 5 (1988), вып. 2, 172–184. 10.1117/12.936896Поиск в Google Scholar

[34] Э. Лукач и Э. П. Кинг, Свойство нормального распределения, Анна. Мат. Статистика 25 (1954), 389–394. 10.1214/aoms/1177728796Поиск в Google Scholar

[35] С. Э. Михалак, К. В. Харрис, Н. В. Хенгартнер, Б. Э. Такала и С. А. Вендер, Прогнозирование количества фатальных программных ошибок в суперкомпьютере asc q Лос-Аламосской национальной лаборатории, IEEE Trans Device Mater. отн. 5 (2005), вып. 3, 329–335. 10.1109/TDMR.2005.855685Поиск в Google Scholar

[36] Р. Дж. Мюрхед, Аспекты многомерной статистической теории, Джон Уайли и сыновья, Нью-Йорк, 1982 г., 10.1002/9780470316559Поиск в Google Scholar

[37] Дж. Наор и М. Наор, Вероятностные пространства с малым смещением: эффективные конструкции и приложения, СИАМ Дж. Вычисл. 22 (1993), вып. 4, 838–856. 10.1145/100216.100244Поиск в Google Scholar

[38] Б. Шредер, Э. Пинейро и В. Д. Вебер, Ошибки драм в дикой природе: крупномасштабное полевое исследование, коммун. ACM 54 (2011), вып. 2, 100–107. 10.1145/1555349.1555372Поиск в Google Scholar

[39] П. Шивакумар, М. Кистлер, С. В. Кеклер, Д. Бургер и Л. Алвизи, Моделирование влияния технологических тенденций на частоту мягких ошибок комбинационной логики, Материалы Международной конференции по надежным системам и сетям, IEEE Press, Пискатауэй (2002), 389–398. 10.1109/DSN.2002.1028924Поиск в Google Scholar

[40] Эй Джей Ван де Гур, Тестирование полупроводниковой памяти: теория и практика, Джон Вили и сыновья, Нью-Йорк, 1991. Поиск в Google Академии

[41] В. В. Уильямс, Умножение матриц быстрее, чем у Копперсмита – Винограда, Материалы симпозиума ACM по теории вычислений 2012 г. — STOC’12, ACM, Нью-Йорк (2012), 887–898. 10.1145/2213977.2214056Поиск в Google Scholar

[42] В. Ю, Ю. Гу и Ю. Ли, Эффективные рандомизированные алгоритмы для аппроксимации матриц низкого ранга с фиксированной точностью, СИАМ Дж. Матричный анал. заявл. 39 (2018), вып. 3, 1339–1359. 10.1137/17M1141977Поиск в Google Scholar

[43] Б.