Прямолинейное равноускоренное движение материальной точки задано уравнением: Прямолинейное движение точки задано уравнением x=-2+3t-0,5t^2 (м). Найти

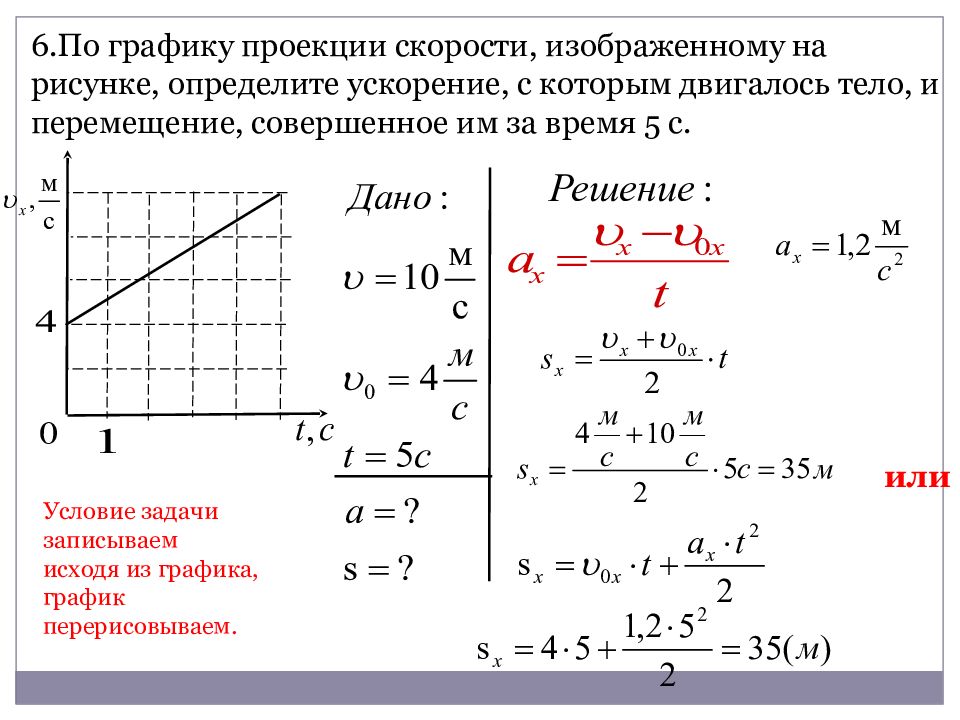
texvx = 2 + 5t/tex. какое перемещение совершит эта точка за 4 с? какова ее скорость в момент text = 4/texс?​ — Школьные Знания.net

• Все предметы

• Математика

• Литература

• Алгебра

• Русский язык

• Геометрия

• Английский язык

• Физика

• Биология

• Другие предметы

• История

• Обществознание

• Окружающий мир

• География

• Українська мова

• Информатика

• Українська література

• Қазақ тiлi

• Экономика

• Музыка

• Беларуская мова

• Французский язык

• Немецкий язык

• Психология

• Оʻzbek tili

• Кыргыз тили

• Астрономия

• Физкультура и спорт

Ответ дан

PandaVeka

Дано:

Vₓ = 2+5t

Решение:

Vₓ = V₀+aₓt ⇒ V₀ = 2 м/с; aₓ = 5 м/с²

Перемещение:

x = x₀+Vₓ₀+ aₓt²/2

x₀ = 0 м

x = 2+5*4²/2

x = 42 м

ΙSΙ = x₁ – x₀ = 42-0 = 42м

Скорость через 4 с:

Vₓ = 2+5*4 = 22 м/с

Ответ: ΙSΙ = 42м, Vₓ = 22 м/с

Кинематические характеристики движения точки – презентация онлайн

КИНЕМАТИКА
Тема 1. 3. Кинематические характеристики
движения точки
Тема 1.4. Частные случаи движения точки

2. 1.3. Кинематические характеристики точки

При векторном способе
задания движения
При координатном
способе задания
движения
Вектор скорости точки
Вектор ускорения точки
Скорость точки
Ускорение точки
Оси естественного
трехгранника
При естественном
способе задания
движения
Алгебраическое значение
скорости
Полное, касательное и
нормальное ускорения
точки
Кинематические характеристики точки при ее
векторном способе задания движения
z
V ср
Вектор скорости точки
M1
r
r1
V
Средняя скорость точки
Пусть положение точки в момент
времени t определяется
радиусом –
вектором r .
r
О
у
В момент времени
t1 – радиусом –
вектором r1 .
х
За t = t1 – t радиус – вектор
точки получат приращение
M
r r1 r .
Опр. Средней скоростью точки называется отношение V
СР
r
t .
Опр. Мгновенной скоростью точки называется вектор
V
lim
t 0
r
t
d
r
dt
.
Вывод. Вектор скорости точки в момент времени t равен
первой производной по времени от радиуса вектора точки
V
dr .
dt
(*)
Вектор мгновенной скорости точки направлен по
касательной к ее траектории.
Вектор ускорения точки
Опр. Ускорением точки называется векторная величина,
характеризующая изменение с течением времени модуля и
направления скорости точки.
V,
Пусть при t точка занимает положение
М и имеет скорость
а в момент времени t1 – скорость V1 . За промежуток времени
t = t1 – t скорость точки получит приращение V V1 V .
Вектор V всегда направлен в сторону
М
V
вогнутости траектории.
М1
V
Опр. Средним ускорением точки
а
V1
называется вектор, который
аср
определяется по формуле аср V t .
V1
Опр. Ускорением точки в данный
момент времени
называется вектор а lim V t .
t
или с учетом того, что V
0
dr
dt
,
переходя к приделу, получим
2
а dV dt d r / dt 2 .
(**)
Вывод. Вектор ускорения точки определяется по формуле (**),
направлен в сторону вогнутости траектории и лежит в
соприкасающейся плоскости.
Задание 1.
Движение материальной точки
М задано
уравнением
r 5t i cost j 11 k .
Вектор скорости точки направлен …
Варианты ответа
1) параллельно плоскости xOz
(не параллельно осям)
2) перпендикулярно плоскости xOy
3) параллельно оси Оz
4) перпендикулярно оси Оz
dr d(5t i cost j 11 k ) d(5t i ) d(cost j ) d(11 k )
V
dt
dt
dt
dt
dt
d(5t) d(cost) d(11)
i
j
k 5 i sint j .
dt
dt
dt
Задание 2.
Движение материальной точки М задано уравнением
r 4 i sint j 3t k .
Вектор ускорения точки направлен …
Варианты ответа
1) перпендикулярно оси Oу
2) параллельно плоскости xOz
3) параллельно оси Оу
4) перпендикулярно плоскости уОz
(непараллельно осям)
2
2
2
2
2
d r d (4 i sint j 3t k ) d (4 i ) d (sint j ) d (3t k )
а 2
2
2
2
2
dt
dt
dt
dt
dt
sint j .
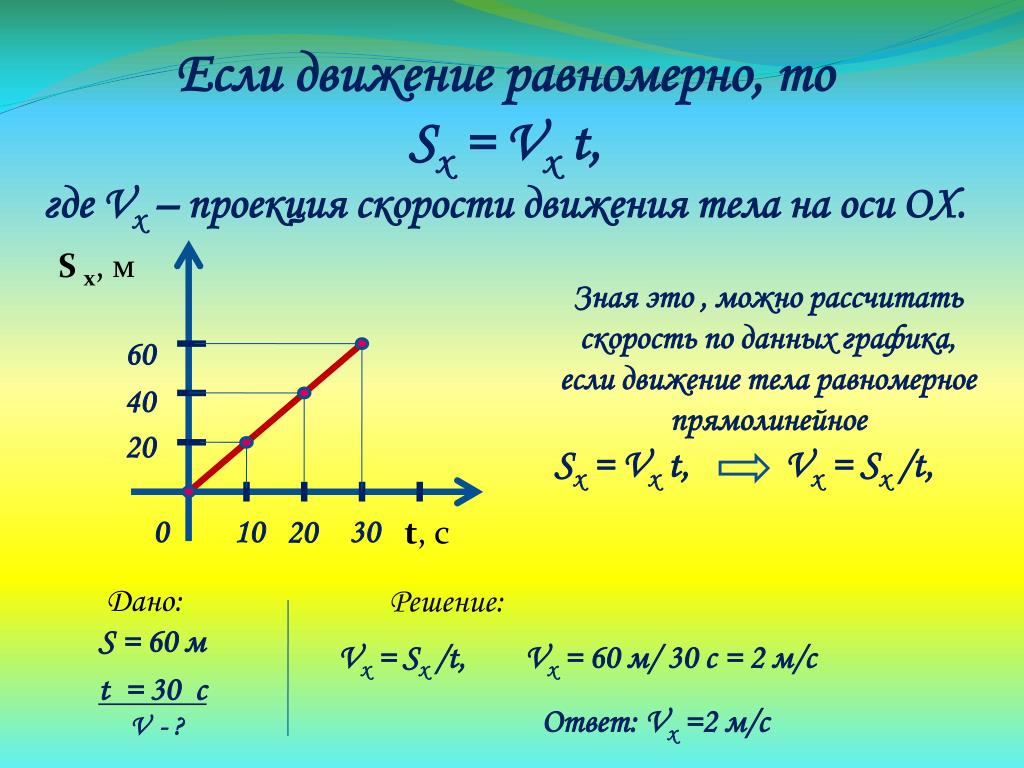
Кинематические характеристики точки при ее координатном
способе задания движения
Теорема. Проекция производной от вектора на ось,
неподвижную в данной системе отчета, равна производной
от проекции дифференцируемого вектора на ту же ось, т. е:
d
p
d pх
d pz
d pу
,
.
q ,
, qz
если
то q х
qу
(1)
dt
dt
d
t
dt
Определение скорости точки
Вектор скорости точки V
d r
d t
z
.
Отсюда, учитывая, что
rх = х , rу = у, rz = z , найдем
Vх
d х
d у
d z
х, V у
у, V z
z .
d t
d t
d t
M
k
О
i
(2)
j
r
rу = у
х
rz = z
rx = х у
Вывод. Проекции скорости точек на координатные оси
равны первым производным от соответствующих
координат точки по времени.
Модуль и направление скорости точки определяются по
формулам:
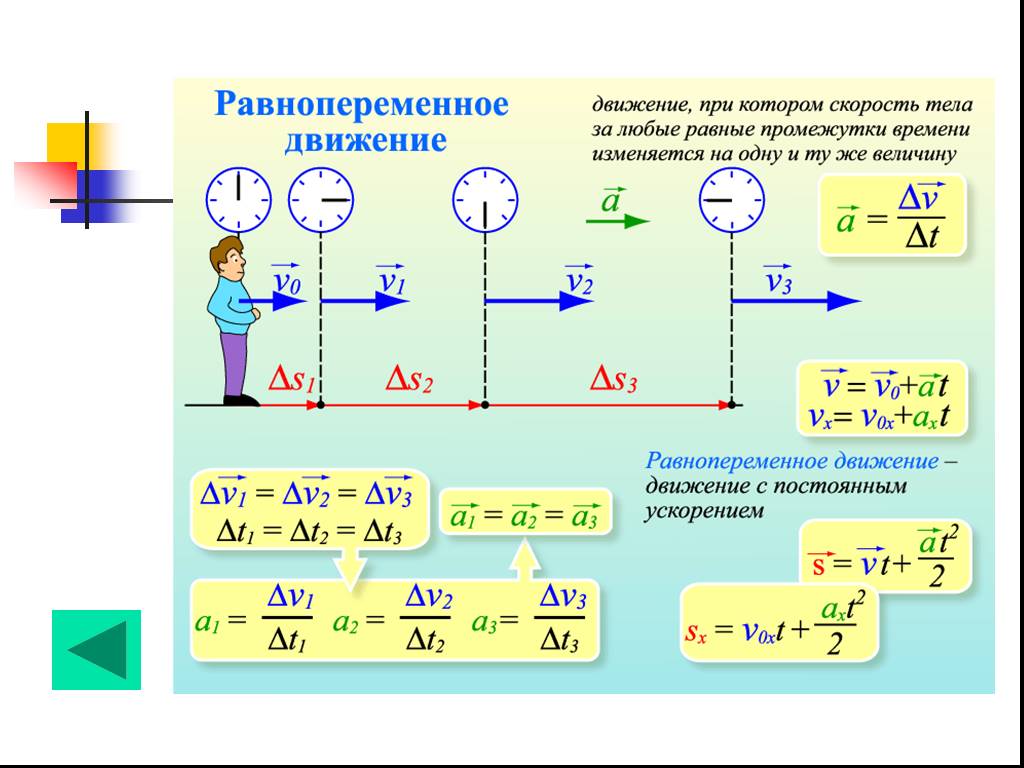
z
А) пространственный случай:
соs Vx / | V |,
| V | V x 2 V 2у V z 2 , сos V у / | V |, (3)
cos Vz / | V | .
Vz
х
Vу
у
у
В) плоский случай:
| V | V x 2 V 2у ,
Vx
А
V
соs Vx / | V | . (4)
Vу
О
V
Vх
х
Определение ускорения точки
Вектор ускорения точки а dV dt .
Тогда на основании формулы (1) получаем:
d Vx
ах d t
d Vу
ау d t
dVz
аz d t
d x
d t
2
2
d 2у
d t2
d 2z
d t2
V x
x
,
V у
у
,
V z
z .
(5)
Вывод. Проекции ускорения точек на координатные оси
равны первым производным от проекций скорости или
вторым производным от соответствующих координат точки
по времени.
Модуль и направление ускорения точки найдутся из формул:
| а | а x 2 а 2у а z 2 ,
(6)
соs 1 а x / | а |, сos 1 а у / | а |, cos 1 а z / | а |,
где 1, 1, 1 – углы, образуемые вектором ускорения с
координатными осями.
Вывод. Если движение точки задано координатным способом,
т. е. заданы уравнения движения: х = f 1 (t), у = f 2 (t), z = f 3 (t),
то скорость точки определяется по формулам (3) и (4), а
ускорение – по формулам (5) и (6).
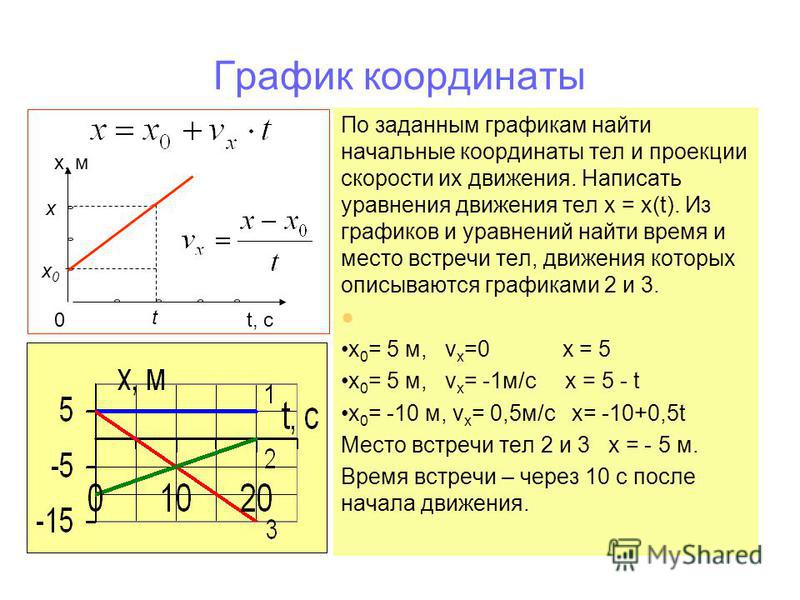
При прямолинейном движении
dх
Vх d t
х
,
d Vx
ах d t
d x
d t
2
2
V x
x .
Кинематические характеристики точки при ее
естественном способе задания движения
Оси естественного трехгранника
V
n
Скорости и ускорения точки при ее
естественном способе задания
движения определяются с помощью
подвижных осей М nb.
–О +
Эти оси называются осями
естественного трехгранника .
х
z
s
/
М
b
О
у
Ось М – направлена по касательной к траектории в сторону
положительного отсчета координаты s;
Ось Мn – (главная нормаль) – направлена по нормали к
траектории, лежащей в соприкасающейся плоскости.
Ось Мb (бинормаль) – направлена перпендикулярно к
первым двум осям.
Определение скорости точки
Вектор скорости точки всегда
направлен по касательной к ее
траектории, поэтому проектируется
только на ось М , то есть | V | = |V |.
z
V
s
М
–О +
/
О
у
х
Алгебраическое значение скорости точки (проекция скорости
точки на касательную М : V = V ) в данный момент времени
равно первой производной от координаты s этой точки по
времени, т. е.
ds
V
s .
dt
(1)
Вывод. Вектор скорости точки в данный момент времени
направлен по касательной к траектории точки, а
алгебраическое значение скорости точки при ее естественном
способе задания определяется по формуле (1).
Если V 0, то скорость направлена
в сторону возрастания дуговой
координаты s, если V 0, то в
сторону убывания.
z
–О +
/
О
х
s
V<0
V>0
М
у
Определение ускорения точки
Ускорение точки при естественном способе
задания ее движения равно геометрической
сумме двух векторов а аn а τ .
(2)
n
а
аn
М
Вектор аn направлен по главной нормали и называется
аτ
нормальным ускорением.
Вектор а τ направлен по касательной и называется
касательным ускорением.
Модуль нормального ускорения определяется по формуле
а n = V 2/ ,
(3)
где – радиус кривизны траектории в точке М.
Алгебраическое значение касательного ускорения находится
по формуле
2
dV
d
s V s .
аτ
dt
dt 2
(4)
Если а 0, то оно направлено в сторону
возрастания дуговой координаты s,
если а < 0, то – в сторону убывания s.
Модуль полного ускорения определиться
в виде
2
2
| а | а n а τ ,
а
аn
s
а > 0
М
– О /+ а
< 0
(5)
а направление – по формуле
tg | a | / аn .
(6)
Вывод. Если движение точки задано естественным способом,
то, зная траекторию и закон движения, т. е. зависимость
s = s (t), можно по формулам (1) – (6) определить модуль и
направление векторов скорости и ускорения точки в любой
момент времени.
1.4. Некоторые частные случаи движения точки
Гармонические
колебания
Равнопеременное
криволинейное
движение
Ускоренное и
замедленное
движения
Равномерное
криволинейное
движение
Прямолинейное
движение
Равноускоренное и
равнозамедленное
движения
Равномерное
прямолинейное
движение
Прямолинейное движение точки
Опр. Движение точки называется прямолинейным, если ее
траекторией является прямая линия.
При прямолинейном движении = и аn= V 2/ = 0, то есть
ускорение точки равно только одному касательному
dV .
ускорению: а = а = dt
Вывод. Физический смысл нормального ускорения
заключается в том, что оно характеризует изменение
скорости точки по направлению.
Равномерное криволинейное движение точки
Опр. Равномерным называется такое криволинейное
движение точки, в котором числовое значение скорости все
время остается постоянным: V = const.
При равномерном криволинейном движение а = dV 0,
dt
то есть ускорение точки равно только одному нормальному
ускорению: а = аn .
Закон равномерного движения точки имеет вид: s = sО + V . t.
Вывод. Физический смысл касательного ускорения
заключается в том, что оно характеризует изменение
числового значения (величины) скорости.
Равномерное прямолинейное движение точки
Опр. Движение точки называется равномерным
прямолинейным, если ее траекторией является прямая
линия, и в котором числовое значение скорости все время
остается постоянным: V = const.
Так как движение прямолинейное, то = и аn= V 2/ = 0, и
так как движение равномерное, то а =
полное ускорение точки а = 0.
dV 0 ,
dt
то есть
Вывод. Равномерное прямолинейное движение точки – это
единственный вид движения, в котором полное ускорение
точки все время равно нулю.
Равнопеременное криволинейное движение точки
Опр. Равнопеременным называется такое криволинейное
движение точки, в котором касательное ускорение всё время
остается постоянным: а = const.
Вывод. При равнопеременном криволинейном движении
точки ее скорость изменяется по закону: V = VО + а · t, а
закон движения точки имеет вид:
s = s 0 + V0 · t + а ·
t2
.
2
Ускоренное и замедленное движение точки
Опр. Движение точки называется ускоренным, если модуль
скорости возрастает, и замедленным, если убывает.
Вывод. Движение будет ускоренным,
если знаки V и а совпадают (Рис.а)),
и замедленным, если знаки
противоположные (Рис. б) и в)).
V
Рис б)
s
– О / +
аτ
М
а < 0
V>0
Рис а)
s
– О /+
М
а < 0
V<0
аτ
Рис в)
s
– О /+
а > 0
V>0
М
а > 0
V<0
V
Равноускоренное и равнозамедленное движение точки
Опр. Равноускоренным движением точки называется ее
ускоренное равнопеременное движение, а равнозамедленным
– замедленное равнопеременное движение.
Гармонические колебания точки
А1
Опр. Движения точки, происходящие по закону: x=А· cos (kt),
называются гармоническими
колебаниями.
М0
Т
М2
А
0
1
М1
М
-1
-А
Опр. Величина А, равная наибольшему отклонению точки от
центра колебаний О, называется амплитудой колебаний.
Опр. Промежуток Т = 2 / k, в течение которого точка совершает одно полное колебание, называется периодом колебаний.
Вывод. Скорость и ускорение точки при гармонических
колебаниях изменяются по гармоническим законам:
V = Vx= – А · k · sin (kt),
a = ах = – А · k2 · cos (kt).
Аналогичные колебания происходят и при законе x = А· sin(kt),
только движение в этом случае начинается из точки О.
Пример выполнения задачи К1
По заданным уравнениям движения точки М
х = 4 t см;
у
= 16 t 2 – 1 см; установить вид ее траектории и для момента
времени t1 = ½ с найти положение точки на траектории, ее
скорость, полное, касательное и нормальное ускорения, а
также радиус кривизны траектории в соответствующей точке.
Решение.
1. Определим траекторию точки
Исключим время t из уравнений движения, тогда: у = х 2 – 1.
Это выражение есть уравнение параболы.
2. Определим скорость точки
Найдем проекции скорости на оси координат:
Vx x 4 см / с; V у у 32 t см / с.
Модуль скорости точки
При t1 = 1/2с
| V | V 2х V 2у 4 2 1024 t 2 .
V1 = V |t = 0,5 = 16, 5см/c .
3. Определим ускорение точки
Найдем проекции ускорения на оси координат:
а х х 0;
а у у 32 см / с 2 .
Модуль ускорения точки
| а | a x2 a у2 32 см / с 2 .
4. Определим касательное ускорение точки
dV |
посредством дифференцирования скорости a |
dt
2 V x V x 2 V у V у V x а x V у а у
dV
.
dt
V
2 V 2x V 2у
При t1 = 1/2с
dV
dt
4 0 16 32
16,5
= 31 см/с2.
Следовательно, модуль касательного ускорения а = 31 см/с2.
Знак «+» при а показывает, что движение точки ускоренное
и, следовательно, направления а и V совпадают.
5. Определим нормальное ускорение точки и радиус
кривизны траектории при t1 = 1/2 с .
Из формулы для полного ускорения | а | а
аn =
2
а а = 7,94 см/с2 и
2
2
n
а
2
τ
получим:
= V 2/ а n= 16,5 2 / 7,94 = 34,3 см.
Полученные данные представим в виде таблицы
Координаты,
см
Скорость,
см/с
х
у
Vx Vу
2
3
4
V
16 16,5
Ускорение,
см/с2
ах ау
0
а
a
Радиус
кривизны, см
an
32 32 31 7,94
34,3
4. Построим траекторию точки и изобразим векторы скоростей
и ускорений
Траекторией точки является параболы
у
6,0
у = х2 – 1, вершина которой имеет
5,0
V
координаты (0; -1). Так как х = 4 t > 0,
а
а
у
Vу
то траекторией точки является только
4,0
аτ
правая ветвь параболы.
аn
3,0
Vх
М1(2; 3)
Точка начинает движение из вершины
2,0
параболы так как х0 = 4 · 0 = 0,
1,0
у0 = 16 · 0 2 – 1 = – 1 и при t = ½ с
0,0
имеет координаты х 1 = 2, у1 = 3.
0
1
2 х
-1,0
Вектор скорости строим по
М0
-2,0
составляющим векторам Vх и Vу .
При этом вектор скорости должен быть направлен по
касательной к траектории точки.
Он должен
Вектор ускорения строим по векторам а τ и а
n.
быть направлен вертикально, так как а х 0 и а а у .

Прямолинейное движение частиц. Определение, вывод формул и примеры

Если положение объекта изменяется относительно времени и его окружения, говорят, что тело находится в движении. Математически движение можно описать смещением, скоростью и ускорением в определенной системе отсчета. Движение частицы можно классифицировать на основе ее траектории, самой простой из которых является движение по прямой линии, а именно прямолинейное движение. Векторы смещения, скорости и ускорения ограничены одним измерением. Прямолинейное движение бывает трех видов: равномерное движение (нулевое ускорение), равноускоренное движение (ненулевое постоянное ускорение) и движение с неравномерным ускорением. Примерами прямолинейного движения являются свободное падение под действием силы тяжести и простое гармоническое движение массы, прикрепленной к пружине.

Определение прямолинейного движения

Если частица ограничена в движении по прямой линии, ее движение называется прямолинейным (или линейным) движением. Такое движение можно описать, используя только одну координату. Смещение частицы и его производные, то есть скорость и ускорение, все являются одномерными векторами. Свободное падение в гравитационном поле Земли автомобиля, движущегося по прямой траектории, можно аппроксимировать прямолинейными движениями.

(Изображение скоро будет загружено)

Математическая форма движения

Для качественного изучения прямолинейного движения рассматривается одномерная система отсчета, состоящая из оси (оси X) и начала координат в точке O (x = 0).

Положение, расстояние и смещение: Положение частицы представляет собой векторную величину, которая указывает от начала координат до частицы. Его величина определяется расстоянием между ними. Когда частица приводится в движение, она следует по траектории, так что ее положение меняется со временем. Смещение — это разность векторов положения через интервал времени, и оно указывает от начального положения до конечного положения. Расстояние – это полный путь, пройденный по траектории, а перемещение – это кратчайший путь. Если положение частицы меняется с xi на xf за время Δt, смещение определяется выражением

x = xf – xi 

Скорость и скорость: Скорость изменения расстояния называется скоростью, а скорость изменения смещения во времени называется скоростью. Скорость — это скаляр, но скорость — это вектор, направление которого совпадает с направлением перемещения. Мгновенная скорость в момент времени t определяется как

\[v = \frac{d}{dt} x\]

Ускорение: Если скорость изменяется со временем, скорость изменения во времени определяется как ускорение. 2}\]

Поскольку все векторы ограничены одним измерением, достаточно рассмотреть только величины.

Графическое представление

Если положение отображается как функция времени, на графике отображается траектория движения частицы. Скорость в любой момент определяется наклоном этого графика, поскольку скорость является производной по времени от положения. Ускорение является производной скорости по времени, поэтому оно определяется наклоном графика зависимости скорости от времени.

Вывод формул прямолинейного движения

Учитывая различные значения ускорения, прямолинейное движение можно разделить на три типа: равномерное прямолинейное движение, равноускоренное движение и движение с неравномерным ускорением.

Равномерное прямолинейное движение Определение: описывает движение по прямой с нулевым ускорением. Скорость частицы не меняется со временем, так что

\[\frac{d\upsilon}{dt}  = 0\] 

\[\upsilon = \upsilon_0\]

\[\upsilon_0\] есть постоянная скорость. Из приведенного выше уравнения  9t dt\]

\[x(t) = x_0 + \upsilon_0 t\]

\[x(t) = x_0 + \upsilon_0 t\]

Здесь x₀ – начальное положение частицы, т.е. x (t=0) = x0

Ясно, что траектория частицы представляет собой прямую линию с постоянным наклоном v₀ и точкой пересечения y с x₀. Графики положение-время и скорость-время показаны ниже.

Равномерно ускоренное прямолинейное движение Определение: если ускорение постоянно при значении a0, т. е. a=a0 

\[\frac{d\upsilon}{dt} = a_0\] 92 + 2a_0 (x – x_0) \]

Это уравнение связывает положение и скорость в любой произвольный момент времени. Поскольку ускорение постоянно во времени, его можно представить в виде прямой линии, параллельной оси времени. Скорость также линейна, но меняется со временем, поэтому представляет собой прямую линию с ненулевым наклоном. Перемещение квадратично по времени, а траектория параболична.

Движение с неравномерным ускорением: Ускорение изменяется со временем и положением в этих движениях. Простое гармоническое движение является примером, когда величина ускорения пропорциональна положению. Траектория СГМ синусоидальная.

Пример

Свободное падение под действием силы тяжести: Если ускорение свободного падения объекта из-за гравитационного притяжения Земли считается постоянным на интересующем расстоянии, свободное падение объекта в гравитационном поле Земли можно аппроксимировать как прямолинейное движение с постоянным ускорением. Любые неконсервативные силы, такие как сопротивление воздуха, вязкость, в задаче считаются отсутствующими.

Если объект свободно падает с высоты h над землей под действием силы тяжести, его начальная высота d(t = 0) равна h, а начальная скорость v(t = 0) равна нулю. Постоянное ускорение g = 90,8 м/с2. Используя выражения положения и скорости,

Скорость в любой момент времени t is, 

v(t)=gt

Перемещение в любой момент времени t is,

d(t)=12gt2

Это перемещение от начальной высоты направлен вниз так, что высота объекта со временем уменьшается.

Знаете ли вы?

Движение двух частиц под действием центральной силы (например, электростатической силы) можно аппроксимировать прямолинейным движением.

Свободное падение под гравитационным полем Земли на самом деле не является прямолинейным движением из-за вращения Земли. Сила Кориолиса из-за вращения заставляет траекторию свободного падения искривляться.

Линейное движение и вращение (на плоскости) вокруг оси имеют сходную динамику.

В таких местах, как музеи, розничные магазины и даже здания, требуется линейное управление движением.

Равномерно ускоренное движение – GeeksforGeeks

Когда тело движется по плоскости или по прямой линии, для описания его движения используются три параметра: расстояние, скорость и ускорение. Расстояние или смещение говорят сами за себя. Скорость представляет собой скорость изменения положения, а ускорение представляет собой скорость изменения скорости. Все три величины являются векторными величинами. Ускорение может быть равномерным и неравномерным. Равномерное ускорение имеет постоянную величину и направление. Необходимо знать уравнение движения, описывающее движение тела при равномерном ускорении. Давайте рассмотрим их подробно.

Ускорение

Ускорение определяется как скорость изменения вектора скорости. Ускорение может быть постоянным или переменным. В случае постоянного ускорения его значение определяется отношением чистого изменения скорости к общему затраченному времени. Его также называют средним ускорением. В случаях, когда ускорение меняется со временем, вычисляют мгновенное ускорение.

Среднее ускорение: 

Мгновенное ускорение: 

Равномерное ускорение

Равномерное ускорение — это ускорение, которое не меняется со временем. В таких случаях скорость изменения скорости остается постоянной. Поскольку ускорение является векторной величиной, даже направление движения остается неизменным при постоянном ускорении. Поскольку тело движется в одном направлении с постоянной величиной ускорения, векторные обозначения можно опустить.

Некоторые примеры постоянного ускорения включают

1. Свободно падающий объект.
2. Мяч катится по склону без трения.
3. Велосипед со включенными тормозами.

Уравнения равномерно ускоренного движения

В этом случае значение ускорения остается постоянным. Уравнения движения могут быть описаны. Допустим, начальная скорость объекта была «u», теперь приложена постоянная сила, которая заставляет тело двигаться с постоянным ускорением «a», и тело достигает скорости за время «t», преодолевая расстояние «s».

Первое уравнение движения

В случае постоянного ускорения его значение определяется формулой

Второе уравнение движения

Это уравнение можно переписать – расположены в следующем виде,

ds = vdt  

Подставляя значение скорости из предыдущего уравнения,

ds = (u + at)dt

Интегрируя обе части,

Третье уравнение движения

Мгновенное ускорение и мгновенная скорость определяются по формуле 03

Перемножение обоих этих уравнений, 

v ² = u ² + 2as

Примеры задач

Вопрос 1. Если тело движется с ускорением 2 м/с

2 . Какой будет скорость через 5 секунд, если начальная скорость 15 м/с?

Ответ: 

Пусть u обозначает начальную скорость, а v обозначает конечную скорость.

Дано: u = 15 м/с, a = 2 м/с ² и t = 5 

Для определения значения «v» можно использовать первое уравнение движения.

v = u + at 

Подставляя значения в это уравнение, 

v = u + at 

⇒ v = 15 + (2)(5) 

⇒ v = 15 + 10 

9 0126 ⇒ v = 25 м/с 

Вопрос 2. Если тело движется с ускорением -5 м/с ² . Какой путь он пройдет за 5 секунд, если начальная скорость была 30 м/с?

Ответ: 

Пусть u обозначает начальную скорость, а v обозначает конечную скорость.

Дано: u = 40 м/с, a = -5 м/с ² и t = 5 

Для определения значения «v» можно использовать первое уравнение движения.

v = u + at 

Подставляя значения в это уравнение, 

v = u + at 

⇒ v = 30 – (5)(5) 

⇒ v = 30 – 25

⇒ v = 5 м/с

Вопрос 3. Если тело движется с ускорением -5 м/с ² . Какой будет скорость через 5 секунд, если начальная скорость 40 м/с?

Ответ:

Обозначим начальную скорость через

. Дано: u = 40 м/с, a = -5 м/с 6 Для выяснения значения «s », можно использовать первое уравнение движения.

Подставив значения в это уравнение, 

Вопрос 4. Если тело движется с ускорением 10 м/с ² . Какой будет скорость через 2 секунды, если начальная скорость 20 м/с?

Ответ:

Обозначим начальную скорость через

. Дано: u = 20 м/с, a = 10 м/с 26 Для выяснения значения «s» , можно использовать первое уравнение движения.

Подставив значения в это уравнение, 

Вопрос 5. Гоночный автомобиль разгоняется до скорости 20 м/с за 2 секунды. Найдите расстояние, пройденное автомобилем при этом.

Ответ: 

Пусть u обозначает начальную скорость, а v обозначает конечную скорость.

Дано: u = 0 м/с, v = 20 м/с и t = 2.

Для определения значения «а» можно использовать первое уравнение движения.

v = u + at 

Подставляя значения в это уравнение,

v = u + at

⇒ 20 = 0 + (a)(2)

⇒ 20 = 2a

⇒ a = 10 м/с ²

 Для для определения расстояния будет использовано третье уравнение движения.

v ² = u ² + 2as

⇒ 20 ² = 0 + 2(10)s

⇒ 400 = 20s 900 03

⇒ 20м = с

Вопрос 6: Ракета ловит скорость 50 м/с за 5 секунд. Найдите расстояние, пройденное ракетой при этом.

Ответ: 

Пусть u обозначает начальную скорость, а v обозначает конечную скорость.