Путь скорость ускорение: Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.

Материальная точка. Поступательное движение твердого тела. Системы отчета. Перемещение, путь, скорость, ускорение.

Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени. В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда. Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Материальна точка – тело, размерами и формой, которого в данной ситуации можно пренебречь. Так можно поступать, например, при изучении движения планет вокруг Солнца. Если все части тела движутся одинаково, то такое движение называется

поступательным. Поступательно движутся, например, кабины в аттракционе «Гигантское колесо», автомобиль на прямолинейном участке пути и т.д. При поступательном движении тела его также можно рассматривать как материальную точку. Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой. Понятие материальной точки играет важную роль в механике. Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют

траекторией движения тела. По форме траектории механическое движение может быть прямолинейным и криволинейным. Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x(t), y = y(t), z = z(t) (координатный способ), либо при помощи зависимости от времени радиус-вектора  (векторный способ), проведенного из начала координат до данной точки.

Определение положения точки с помощью координат x = x(t), y = y(t) и z = z(t) и радиус–вектора . – радиус–вектор положения точки в начальный момент времени.

Перемещением тела  называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.

Для характеристики движения вводится понятие средней скорости. Средней скоростью называется физическая величина, равная отношению вектора перемещения точки к промежутку времени, за который это произошло это перемещение:
 

  В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
 

Ускорение – величина, характеризующая быстроту изменения скорости.

Средним ускорением называют отношение изменения скорости к промежутку времени, за который это изменение произошло.

Мгновенным ускорением (или просто ускорением) тела называют предел отношения малого изменения скорости к малому промежутку времени Δt, в течение которого происходило изменение скорости:
 

Простейшим видом механического движения является движение тела вдоль прямой линии с постоянной по модулю и направлению скоростью. Такое движение называется равномерным

. При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX. Поэтому перемещение и скорость при прямолинейном движении можно спроектировать на ось OX и рассматривать их проекции как алгебраические величины.

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Расчет стоимостиГарантииОтзывы

Если в некоторый момент времени t1 тело находилось в точке с координатой x1, а в более поздний момент t2 – в точке с координатой x2, то проекция перемещения Δs на ось OX за время Δt = t2 – t1 равна

Δs = x2 – x1.

 

Эта величина может быть и положительной, и отрицательной в зависимости от направления, в котором двигалось тело.

При равномерном движении вдоль прямой модуль перемещения совпадает с пройденным путем. Скоростью равномерного прямолинейного движения называют отношение

 

Если υ > 0, то тело движется в сторону положительного направления оси OX; при υ < 0 тело движется в противоположном направлении.

Зависимость координаты x от времени t (закон движения) выражается при равномерном прямолинейном движении линейным математическим уравнением

:

x(t) = x0 + υt.

 

В этом уравнении υ = const – скорость движения тела, x0 – координата точки, в которой тело находилось в момент времени t = 0.

В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха).

При равноускоренном прямолинейном движении скорость тела определяется формулой

υ = υ0 + at.

В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение.

Поможем написать любую работу на аналогичную тему

• Реферат

  Материальная точка. Поступательное движение твердого тела. Системы отчета. Перемещение, путь, скорость, ускорение.

  От 250 руб

• Контрольная работа

  Материальная точка. Поступательное движение твердого тела. Системы отчета. Перемещение, путь, скорость, ускорение.

  От 250 руб

• Курсовая работа

  Материальная точка. Поступательное движение твердого тела. Системы отчета. Перемещение, путь, скорость, ускорение.

  От 700 руб

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Механические явления (коды ОГЭ 1.1 – 1.5)

Справочник по физики для ОГЭ. Версия для ознакомления перед покупкой.
Механические явления (коды ОГЭ 1.1 — 1.5).

Вы смотрели Справочник по физики «Механические явления (коды ОГЭ 1.1 — 1.5)». Выберите дальнейшее действие:

OSR-текст раздела (только текст)

Механические явления (коды ОГЭ 1.1 — 1.5) 1.1. Механическое движение. Относительность движения. Траектория. Путь. Перемещение. Скорость. Ускорение. Равномерное и неравномерное движение. Средняя скорость. Формула для вычисления средней скорости Механическим движением называется изменение положения тела в пространстве относительно других тел с течением времени.

Материальной точкой считается тело, размеры которого малы по сравнению с другими характерными размерами, встречающимися при решении поставленной задачи. Траектория – воображаемая линия, вдоль которой движется тело. Относительность механического движения: 1. Механическое движение можно наблюдать только относительно других тел. Тело, относительно которого рассматривается механическое движение, называется телом отсчёта. 2. В различных системах отсчёта скорость и перемещение, характеризующие движение одного и того же тела, могут иметь разные модули и направления. 3. Координаты тела, траектория движения, путь зависят от выбора системы отсчёта, то есть для одного и того же тела могут быть разными. Основные физические величины, характеризующие механическое движение 1. Путь – длина траектории. Внимание! Путь не может быть отрицательным! 2. Перемещение – направленный отрезок прямой (вектор), соединяющий начальное положение тела с его последующим положением. Проекция вектора перемещения на координатную ось sХ = x – x0 , где х0 – начальная координата тела, х – конечная координата тела. Модуль вектора перемещения может не совпадать по числовому значению с длиной пути. Его можно рассчитать с помощью проекций вектора перемещения на координатные оси 3. Средняя путевая скорость равна отношению всего пути, пройденного телом, к промежутку времени, в течение которого этот путь пройден: ʋср = l/t. Внимание! Не является векторной величиной! 4. Вектор средней скорости равен отношению вектора перемещения к промежутку времени, в течение которого это перемещение произошло: . В проекциях на координатную ось 0х . Внимание! Вектор средней скорости сонаправлен с вектором перемещения. 5. Мгновенная скорость – скорость тела в данной точке пространства в данный момент времени. Внимание! 1). Вектор мгновенной скорости направлен по касательной к траектории движения в каждой её точке. 2). Проекция перемещения на соответствующую координатную ось численно равна площади под графиком зависимости проекции скорости на эту ось от времени. 6. Ускорение – векторная физическая величина, характеризующая изменение скорости с течением времени. Для равноускоренного движения вектор ускорения равен отношению вектора изменения скорости к тому промежутку времени, в течение которого это изменение произошло: . В проекциях на координатную ось . Физический смысл: численно равно изменению скорости за 1 с. 1.2. Равномерное прямолинейное движение. Зависимость координаты тела от времени в случае равномерного прямолинейного движения. Графики зависимости от времени для проекции скорости, проекции перемещения, пути, координаты при равномерном прямолинейном движении Равномерное прямолинейное движение – прямолинейное движение, при котором скорость тела не меняется. Внимание! Для описания любого прямолинейного движения достаточно одной координатной оси. Уравнение движения – уравнение, выражающее зависимость координат от времени, например: x = x(t). Характер изменения основных величин, характеризующих движение 1. Ускорение. Равно нулю: а̅ = 0 . 2. Скорость. Не равна нулю, постоянна по величине и направлению: ʋ̅ = const. Для равномерного движения проекция вектора скорости равна отношению изменения координаты (проекции вектора перемещения) к тому промежутку времени, в течение которого это изменение произошло Физический смысл: численно равна изменению координаты (проекции вектора перемещения) за 1 с. 3. Перемещение. Вектор перемещения при равномерном прямолинейном движении прямо пропорционален времени: s = ʋt. В проекциях на координатную ось: sx = ʋxt. Внимание! Здесь и применительно к описанию зависимости других величин от времени под t понимается промежуток времени от начала движения (t0 = 0) ! В первом и во втором случае тело движется в направлении координатной оси Ох. Во втором случае тело движется в направлении, противоположном направлению оси Ох. По модулю ʋ1 > ʋ2 > ʋ3 (сравниваем модули перемещения за одинаковые промежутки времени). Для расчёта проекции вектора перемещения удобно пользоваться графиком зависимости проекции скорости от времени: величина проекции вектора перемещения численно равна площади под графиком зависимости проекции скорости от времени. 4. Координата. Поскольку х = x0 + sx , зависимость координаты от времени описывается линейной функцией: х = x0 +vxt. На графике изображены следующие случаи движения. 1. Движение в направлении оси Ох, начальная координата отрицательна. 2. 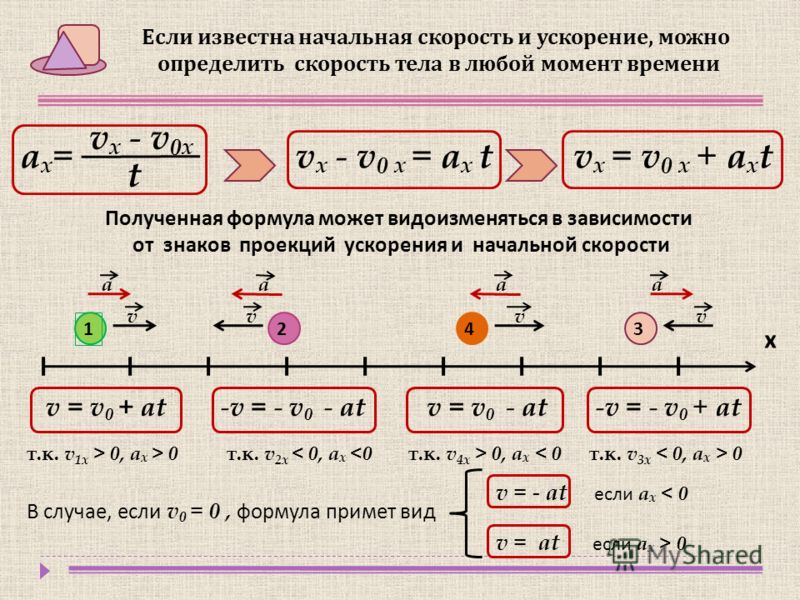Движение в направлении оси Ох, начальная координата положительна. 3. Движение в направлении, противоположном направлению оси Ох, начальная координата равна нулю. 4. Движение в направлении оси Ох, начальная координата отрицательна. 5. Движение в направлении, противоположном направлению оси Ох, начальная координата положительна. 5. Путь. При равномерном прямолинейном движении в одном направлении равен модулю вектора перемещения: l = s. Внимание! Путь не может быть отрицательным! График зависимости проекции ускорения от времени График зависимости проекции вектора скорости на координатную ось от времени График зависимости проекции вектора перемещения на координатную ось от времени График зависимости координаты от времени 1.3. Прямолинейное равноускоренное движение. Зависимость координаты тела от времени в случае равноускоренного прямолинейного движения. Формулы для проекции перемещения, проекции скорости и проекции ускорения при равноускоренном прямолинейном движении. Графики зависимости от времени для проекции ускорения, проекции скорости, проекции перемещения, координаты при равноускоренном прямолинейном движении Прямолинейное равноускоренное движение – прямолинейное движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени. Основные величины, характеризующие движение. 1. Ускорение. Не меняется, то есть постоянно по величине и направлению: . Физический смысл: ускорение численно равно изменению скорости за 1 с. Например, ускорение равно 5 м/с2 – это значит, что скорость тела изменяется на 5 м/с за каждую секунду своего движения. 2. Мгновенная скорость. Меняется равномерно, увеличиваясь или уменьшаясь одинаково за равные промежутки времени. Уравнение, описывающее изменение скорости с течением времени: , в проекциях ʋx = ʋ0x + axt. На графике изображены следующие случаи движения. 1. Проекция начальной скорости больше нуля. то есть тело движется в направлении координатной оси с увеличивающейся по модулю скоростью. 2. Проекция начальной скорости равна нулю. то есть тело движется в направлении координатной оси с увеличивающейся по модулю скоростью. 3. Проекция начальной скорости больше нуля, то есть тело движется в направлении координатной оси с уменьшающейся по модулю скоростью. 4. Проекция начальной скорости меньше нуля.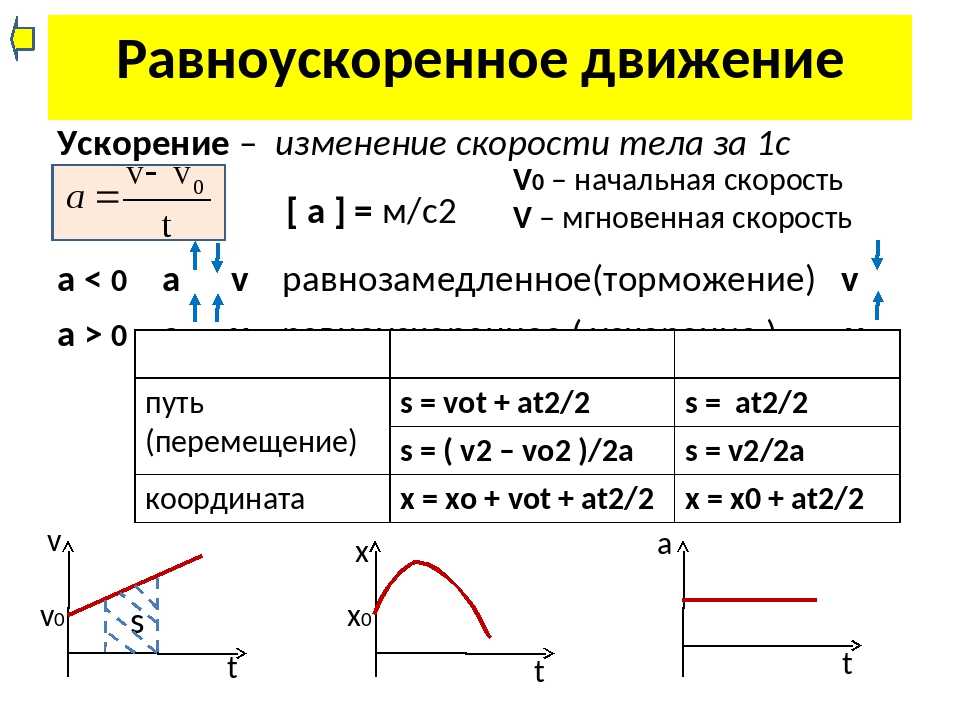 то есть тело движется в направлении, противоположном направлению координатной оси, с уменьшающейся по модулю скоростью. 5. Проекция начальной скорости равна нулю. График зависимости проекции скорости на координатную ось от времени то есть тело движется в направлении, противоположном направлению координатной оси, с увеличивающейся по модулю скоростью. 6. Проекция начальной скорости отрицательна. то есть тело движется в направлении, противоположном направлению координатной оси, с увеличивающейся по модулю скоростью. 3. Перемещение. Зависимость перемещения от времени описывается квадратичной функцией: . В проекциях на координатную ось: . Иногда удобно пользоваться другими формулами для расчёта перемещения, которые получаются из исходной и уравнения зависимости проекции скорости от времени: Для расчёта проекции вектора перемещения удобно пользоваться графиком зависимости проекции скорости от времени. В случае, изображённом на рисунке: sx =S1 – S2, где S1, и S2 – числовые значения площадей треугольников. 4. Координата. Поскольку х = х0 + sx, зависимость координаты от времени тоже описывается квадратичной функцией: Если использовать другие варианты расчёта ускорения при равноускоренном движении, получаем: . 5. Путь. Если направление движения не меняется, то l = s. Если направление движения меняется, то l = s1 +s2, где s1 – модуль вектора перемещения до остановки, s2 – модуль вектора перемещения при движении в обратном направлении. Внимание! Путь не может быть отрицательным! 1.4. Свободное падение. Формулы, описывающие свободное падение тела по вертикали (движение тела вниз или вверх относительно поверхности Земли). Графики зависимости от времени для проекции ускорения, проекции скорости и координаты при свободном падении тела по вертикали Свободное падение – движение под действием одной силы тяжести, частный случай равноускоренного движения. Ускорение свободного падения обозначается особой буквой: . Оно одинаково для всех тел в данной точке планеты, направлено к центру планеты и равно g ~ 10 м/с2 (см. раздел 1.13). В зависимости от направления начальной скорости тела может реализовываться один из представленных ниже вариантов движения. Независимо от направления движения тела (вверх или вниз) для свободного падения справедливы формулы для расчёта основных кинематических величин при равноускоренном движении с учётом того, что ускорение заранее известно и равно g = const. Проекция вектора перемещения: Координата в любой момент времени: или 1.5. Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления центростремительного ускорения. Формула, связывающая период и частоту обращения Равномерное вращение – движение точки с постоянной по модулю скоростью (ʋ = const) по траектории, представляющей собой окружность. Равномерное движение точки по окружности – это движение, при котором точка за любые равные промежутки времени проходит равные пути. Но так как скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Значит, равномерное движение по окружности – это ускоренное движение! Величины, характеризующие равномерное вращение 1. Линейная скорость равномерного вращения . По величине ʋ = l / t, где l – путь, пройденный по дуге окружности за промежуток времени t. Вектор линейной скорости в каждой точке направлен по касательной к дуге окружности в данной точке. 2. Период обращения . Время одного полного оборота: Т = t / N, где N – число полных оборотов за промежуток времени t. 3. Частота обращения . Число оборотов в единицу времени: v = N / t. Связана с периодом обращения соотношением v = 1 / T. Внимание! Полезно установить связь между линейной скоростью с другими параметрами обращения! За один полный оборот . 4. Центростремительное ускорение : где ʋ – модуль линейной скорости в данной точке окружности. Вектор центростремительного ускорения перпендикулярен вектору скорости и направлен по радиусу к центру окружности.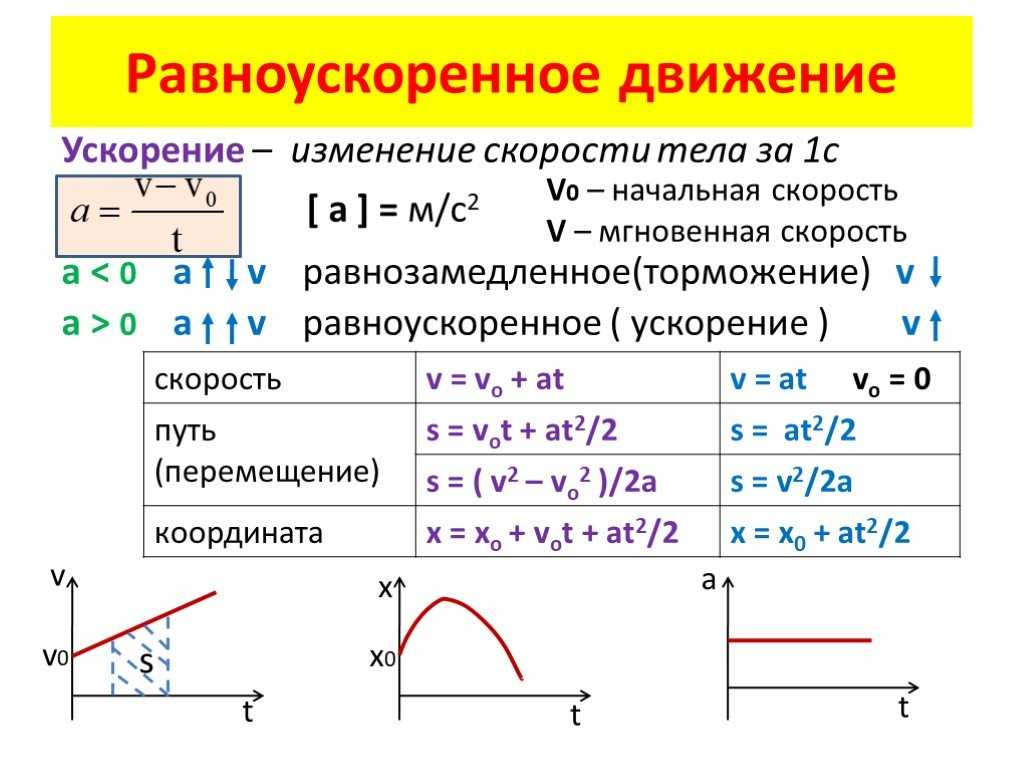 Центростремительное ускорение меняет скорость по направлению, но не меняет по величине. При равномерном вращении центростремительное ускорение постоянно по величине и связано с периодом и частотой вращения соотношениями:

1.1. Механическое движение. Относительность движения. Траектория. Путь. Перемещение. Скорость. Ускорение. Равномерное и неравномерное движение. Средняя скорость. Формула для вычисления средней скорости.
1.2. Равномерное прямолинейное движение. Зависимость координаты тела от времени в случае равномерного прямолинейного движения. Графики зависимости от времени для проекции скорости, проекции перемещения, пути, координаты при равномерном прямолинейном движении.
1.3. Прямолинейное равноускоренное движение. Зависимость координаты тела от времени в случае равноускоренного прямолинейного движения. Формулы для проекции перемещения, проекции скорости и проекции ускорения при равноускоренном прямолинейном движении. Графики зависимости от времени для проекции ускорения, проекции скорости, проекции перемещения, координаты при равноускоренном прямолинейном движении.
1.4. Свободное падение. Формулы, описывающие свободное падение тела по вертикали (движение тела вниз или вверх относительно поверхности Земли). Графики зависимости от времени для проекции ускорения, проекции скорости и координаты при свободном падении тела по вертикали.
1.5. Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления центростремительного ускорения. Формула, связывающая период и частоту обращения.

18A: Круговое движение — центростремительное ускорение

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

3328

• Джеффри В. Шник
• Колледж Святого Ансельма

Существует тенденция полагать, что если объект движется с постоянной скоростью, то он не имеет ускорения. Это действительно верно в случае объекта, движущегося по прямолинейному пути. С другой стороны, частица, движущаяся по криволинейной траектории, ускоряется независимо от того, меняется ее скорость или нет. Скорость имеет как величину, так и направление. В случае частицы, движущейся по криволинейной траектории, направление скорости постоянно меняется, и, таким образом, частица имеет ускорение.

Обратимся теперь к случаю, когда объект движется по кругу. Мы начнем с простейшего случая кругового движения, случая, когда скорость объекта постоянна, случая, называемого равномерным круговым движением. На данный момент позвольте вам быть объектом. Представьте, что вы находитесь в автомобиле, который едет против часовой стрелки, скажем, со скоростью 40 миль в час, если смотреть сверху, по довольно небольшой круговой дорожке. Вы путешествуете по кругу. Ваша скорость непостоянна. Величина вашей скорости не меняется (постоянная скорость), но направление вашей скорости постоянно меняется, вы продолжаете поворачивать налево! Теперь, если вы постоянно поворачиваете налево, вы должны постоянно приобретать некоторую скорость движения влево. На самом деле, ваше ускорение должно быть точно влево, под прямым углом к ​​вашей скорости, потому что, если ваша скорость не меняется, но ваша скорость постоянно меняется, это означает, что у вас есть некоторое ускорение \(\vec{a}=\dfrac{d \vec{v}}{dt}\), то для каждого бесконечно малого изменения показаний часов \(dt\) изменение скорости \(d\vec{v}\), которое происходит в течение этого бесконечно малого интервала времени, должно быть перпендикулярно к самой скорости. (Если бы он не был перпендикулярен, то скорость увеличивалась бы или уменьшалась.) Таким образом, независимо от того, где вы находитесь в круге (вокруг которого вы движетесь против часовой стрелки, если смотреть сверху), у вас есть ускорение, направленное точно влево, перпендикулярно направление вашей скорости. Теперь, что всегда находится прямо слева от вас, если вы движетесь против часовой стрелки по кругу? Именно так! Центр круга всегда находится прямо слева от вас. Таким образом, ваше ускорение всегда направлено по центру. Мы называем направленное к центру ускорение, связанное с круговым движением, центростремительным ускорением, потому что слово «центростремительный» означает «направленный к центру». Обратите внимание, что если вы движетесь по кругу по часовой стрелке, если смотреть сверху, вы постоянно поворачиваете направо, и ваше ускорение направлено вправо, прямо к центру круга. Эти соображения применимы к любому объекту — объект, движущийся по кругу, имеет центростремительное (направленное к центру) ускорение.

У нас есть несколько способов описать движение частицы, движущейся по окружности. Во-первых, мы характеризуем его с точки зрения того, как далеко частица прошла по окружности. Если нам нужна переменная положения, мы устанавливаем начальную точку на окружности и положительное направление. Например, для окружности с центром в начале координат плоскости x-y мы можем определить точку, в которой окружность пересекает положительную ось x, как начальную точку, а направление, в котором должна двигаться частица, чтобы двигаться против часовой стрелки вокруг окружности, как начальную точку. положительное направление. Имя, данное этой переменной позиции, — s. Позиция s — это общее расстояние, измеренное по окружности, которое прошла частица. Тогда скорость частицы равна скорости изменения s, \(\dfrac{ds}{dt}\), а направление скорости является касательной к окружности. Сама окружность определяется своим радиусом. Второй способ описания движения частицы состоит в том, чтобы описать его в терминах воображаемого отрезка, идущего от центра окружности к частице. Чтобы использовать этот метод, также необходимо определить отрезок опорной линии — положительная ось x является обычным выбором для случая окружности с центром в начале системы координат x-y. Затем, если вы знаете радиус r окружности, угол \(тета\), который линия к частице образует с опорной линией, полностью определяет местоположение частицы.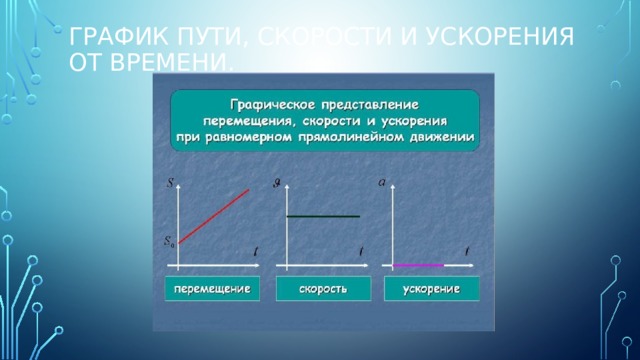

В геометрии переменная положения s определяет длину дуги на окружности. Напомним, что по определению угол \(\theta\) в радианах представляет собой отношение длины дуги к радиусу:

\[\тета=\dfrac{s}{r} \]

Решение для s мы имеем:

\[s=r\тета \метка{18-1}\]

, в котором мы интерпретируем s как положение частицы на окружности, а \(\theta\) как угол, который составляет воображаемый отрезок от центра окружности к частице с опорный сегмент линии, такой как положительная ось x. Ясно, что чем быстрее движется частица, тем быстрее изменяется угол тета, и действительно, мы можем получить связь между скоростью частицы и скоростью изменения \(\тета\), просто взяв производную по времени от обоих стороны уравнения \(\ref{18-1}\). Давайте сделаем это.

Начнем с производной обеих частей уравнения \(\ref{18-1}\) по времени:

\[\dfrac{ds}{dt}=r\dfrac{d\theta}{dt} \]

, а затем перепишите результат как:

.

\[\dot{s} =r\dot{\theta}\]

просто для того, чтобы читатель привык к идее, что мы представляем производную по времени переменной, то есть скорость изменения этой переменной, записывая символ переменной с точкой над ним.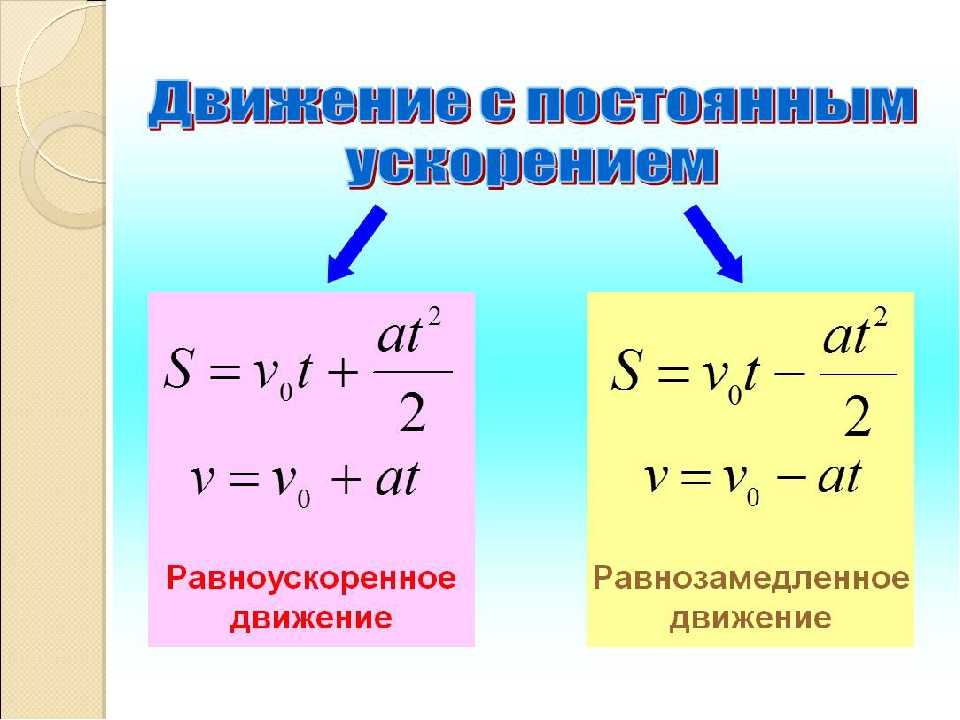 Затем мы перепишем результат как

\[v=r \точка{\theta}\метка{18-2}\]

, чтобы подчеркнуть тот факт, что скорость изменения положения на окружности есть скорость частицы (величина скорости частицы). Наконец, мы определяем переменную \(\omega\) (“omega”) как скорость изменения угла, что означает, что \(\omega\) равно \(\dfrac{d\theta}{dt}\) и \(\omega\) равно \(\dot{\theta}\). Должно быть ясно, что \(\omega\) — это скорость вращения воображаемой линии от центра круга к частице. Мы называем эту скорость вращения величиной угловой скорости сегмента линии. (Выражение «угловая скорость» \(\omega\) чаще используется для характеристики того, насколько быстро и в какую сторону вращается твердое тело, а не воображаемая линия.) Переписав \(v=r\dot{\theta} \) с заменой \(\dot{\theta}\) на \(\omega\) дает:

\[v=r\omega \метка{18-3}\]

Теперь мы можем вывести выражение для направленного к центру (центростремительного) ускорения, о котором мы говорили в начале этой главы. Рассмотрим короткий интервал времени \(\Delta t\). (Мы возьмем предел, когда \(\Delta t\) стремится к нулю до конца этой главы.) В течение этого короткого промежутка времени частица проходит расстояние \(\Delta s\) по окружности и угол, который линия, идущая от центра круга к частице, изменяется с опорной линией на величину \(\Delta \theta\).

Кроме того, за это время \(\Delta t\) скорость частицы изменяется от \(\vec{v}\) до \(\vec{v}’\), изменение \(\ Дельта \vec{v}\), определяемая \(vec{v}’=\vec{v}+\Delta\vec{v}\), изображенная на следующей векторной диаграмме (на которой стрелки представляют векторы \(\ vec{v}\) и \(\vec{v}’\) были скопированы сверху без изменения ориентации или длины). Обратите внимание, что малый угол \(\Delta \theta\), появляющийся на диаграмме сложения векторов, совпадает с тем \(\Delta \theta\), который появляется на диаграмме выше.

Хотя \(\vec{v}’\) — новый вектор, отличный от \(\vec{v}\), мы установили, что скорость частицы является постоянной, поэтому вектор \( \vec{v}’\) имеет ту же величину, что и вектор \(\vec{v}\). То есть \(\vec{v}’=\vec{v}\). Мы перерисовываем диаграмму сложения векторов, помечая оба вектора скорости одним и тем же символом v.

Величина центростремительного ускорения по определению может быть выражена как } \dfrac{\Delta V}{\Delta t}\] 9\круг\). Таким образом, в пределе, когда \(\Delta t\) приближается к 0, треугольник является прямоугольным, и в этом пределе мы можем написать:

\[\dfrac{\Delta v}{v}=tan(\Delta \theta )\]

\[\Delta v=v \tan(\Delta \theta)\]

Подставив это в наше выражение для \(a_c\), мы получим:

\[a_c=\underset{\Delta t \rightarrow 0}{lim} \dfrac{vtan(\Delta\theta)}{\Delta t} \label{18-4}\]

Теперь мы используем приближение малого угла из математики плоской геометрии, приближение которое становится реальным уравнением в пределе, когда \(\Delta\theta\) приближается к нулю.

Приближение малого угла

Для любого угла, который очень мал по сравнению с \(\pi\) радианами (чем меньше угол, тем лучше приближение), тангенс угла приблизительно равен самому углу, выраженному в радианы; а синус угла примерно равен самому углу, выраженному в радианах. Фактически,

\[tan(\Delta \theta) \underset{\Delta \theta \rightarrow 0}{\rightarrow} \Delta\theta\]

и

\[sin(\Delta \theta) \ подмножество{\Delta\theta\rightarrow 0}{\rightarrow} \Delta\theta\]

где \(\Delta\theta\) в радианах.

Приближение малых углов позволяет нам записать

\[a_c=\underset{\Delta t\rightarrow 0}{lim} \dfrac{v \Delta \theta}{\Delta t}\]

[где мы заменили \(tan(\Delta\theta)\) в уравнении \(\ref{18-4}\) выше на \(\Delta \theta\) ].

Константу v можно вывести за пределы, что даст \(a_c=\underset{\Delta t\rightarrow 0}{lim} \dfrac{\Delta \theta}{\Delta t}\). Но \(\underset{\Delta t\rightarrow 0}{lim} \dfrac{\Delta\theta}{\Delta t}\) – это скорость изменения угла \(\theta\), то есть по определению угловая скорость \(\omega\). Таким образом 92\label{18-6}\]

Следует отметить, что, несмотря на то, что мы сосредоточили наше внимание на случае, когда частица, движущаяся по окружности, движется с постоянной скоростью, частица имеет центростремительную ускорение независимо от того, меняется скорость или нет.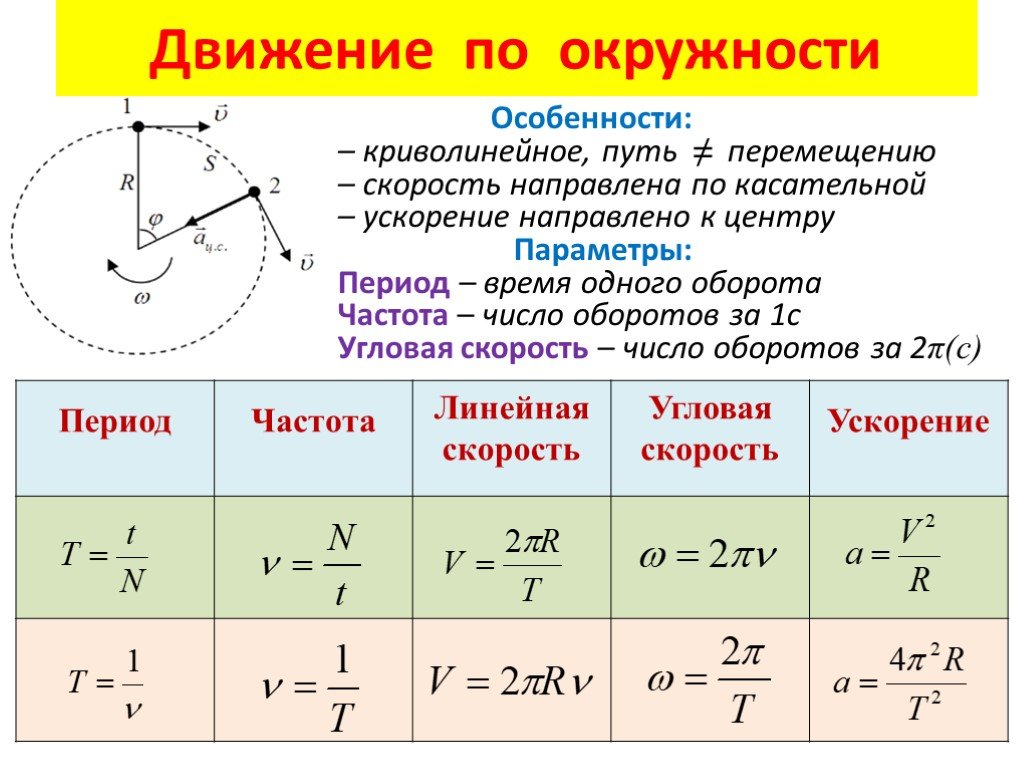 Если скорость частицы изменяется, центростремительное ускорение в любой момент (по-прежнему) определяется уравнением \(\ref{18-5}\), где \(v\) является скоростью частицы в этот момент ( и в дополнение к центростремительному ускорению частица также имеет некоторое ускорение вдоль окружности, известное как тангенциальное ускорение). Случай, который мы исследовали, является, однако, замечательным случаем. Даже если скорость частицы постоянна, частица имеет некоторое ускорение только потому, что направление ее скорости постоянно меняется. Более того, центростремительное ускорение не является постоянным ускорением, потому что его направление постоянно меняется. Визуализируйте это. Если вы едете против часовой стрелки (если смотреть сверху) по круговой трассе, направление, в котором вы видите центр круга, постоянно меняется (и это направление является направлением центростремительного ускорения). Когда вы находитесь в самой восточной точке круга, центр находится к западу от вас. Когда вы находитесь в самой северной точке круга, центр находится к югу от вас. Когда вы находитесь в самой западной точке круга, центр находится к востоку от вас. А когда вы находитесь в самой южной точке круга, центр находится к северу от вас.

---

Эта страница под названием 18A: Круговое движение – Центростремительное ускорение распространяется под лицензией CC BY-SA 2.5 и была создана, изменена и/или курирована Джеффри В. Шником посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джеффри В. Шник

   Лицензия

   CC BY-SA

   Версия лицензии

   2,5

   Показать оглавление

   нет

2. Теги

   1. центростремительное ускорение
   2. Круговое движение
   3. источник@http://www.cbphysics.org

Алгоритм

– Самый быстрый путь с ускорением в точках

Задавать вопрос

спросил 6 лет, 5 месяцев назад

Изменено 6 лет, 4 месяца назад

Просмотрено 939 раз

Это просто то, что я придумал сам, но это кажется забавной задачей, и это ставит меня в тупик.

У вас есть набор точек в двухмерном пространстве, одна из которых обозначена как «Начало», а другая — «Конец». Каждая точка имеет координаты (в метрах от начала координат), а также «число ускорения» (в метрах/секундах дельта-V). Достигнув точки (включая старт), вы можете ускориться до значения ускорения этой точки в любом направлении. Стоимость Edge зависит от вашей текущей скорости, но вы также должны двигаться в правильном направлении.

Существует ли эффективный алгоритм поиска кратчайшего пути к конечной точке? Я не придумал ничего лучше, чем “Попробовать каждый путь и проверить результаты”. Алгоритмы Джикстры и другие простые алгоритмы не работают, потому что вы не можете легко сказать, что один путь к промежуточной точке лучше или хуже другого, если вы прибываете с разными начальными скоростями.

Если это слишком просто, что, если добавить требование остановки в конечной точке? (т. е. у вас должно быть меньше значения ускорения, когда вы дойдете до конца.)

РЕДАКТИРОВАТЬ: Чтобы было ясно, направление имеет значение.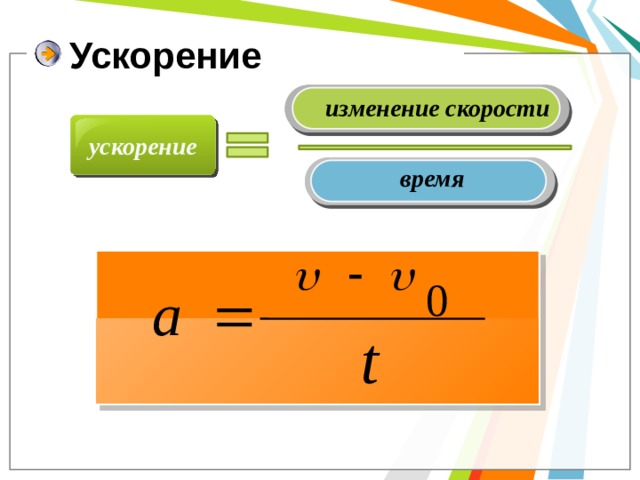 Вы сохраняете вектор скорости по мере прохождения графика, а ускорение означает добавление к нему вектора, величина которого ограничена числом ускорения этой точки. Это означает, что бывают ситуации, когда наращивание огромной скорости вредно, так как вы будете двигаться слишком быстро, чтобы «направиться» к другим ценным точкам/пункту назначения.

• алгоритм
• математика
• теория графов
• кратчайший путь

8

Я думаю, что требование использовать ускорение из каждой точки только один раз делает эту задачу NP полной в общем случае. Рассмотрим ввод, который выглядит следующим образом:

Если «огромное расстояние» между конечной точкой и остальными точками достаточно велико, чтобы доминировать в стоимости окончательного решения, поиск оптимального решения сводится к нахождению способ получить как можно больше ускорений с самого начала графика. Если вы разрешаете проходить каждую точку только один раз, это будет эквивалентно задаче о гамильтоновом пути, которая является NP-полной.

Тем не менее, в вашей задаче есть дополнительные правила (расстояния евклидовы, граф всегда полный), которые могут упростить задачу.

3

Вы можете попробовать решить эту проблему в обратном порядке, рекурсивно проследив пути от конца к другому узлу, а затем назначив максимальную скорость вдоль линии, чтобы иметь возможность повернуть от этого узла к любому другому. Правило отбраковки будет состоять в том, что если существует путь от текущего к следующему узлу с меньшей скоростью и меньшим временем, затрачиваемым от конца, это будет означать, что другой путь по умолчанию более оптимален, поскольку он может достигать большего количества узлов и занимает меньше времени. Как только путь достигает начального узла, он должен быть пересчитан на основе максимальной скорости, достижимой в начале, и сохранен. Затем вы собираете путь с меньшими затратами времени.

Вы должны искать любой доступный путь здесь, потому что доступные пути на вашем графике зависят от прошлого состояния с косвенной механикой, использование меньшей скорости дает больше возможностей для выбора.