Главная
Q физика: что означает буква Q в физике — Спрашивалка

Q физика: что означает буква Q в физике — Спрашивалка

Содержание

активную, реактивную, полную[br] (P, Q, S), а также коэффициент мощности (PF)

Из письма клиента:
Подскажите, ради Бога, почему мощность ИБП указывается в Вольт-Амперах, а не в привычных для всех киловаттах. Это сильно напрягает. Ведь все уже давно привыкли к киловаттам. Да и мощность всех приборов в основном указана в кВт.
Алексей. 21 июнь 2007

 

 

В технических характеристиках любого ИБП указаны полная мощность [кВА] и активная мощность [кВт] – они характеризуют нагрузочную способность ИБП. Пример, см. фотографии ниже:

 

 

Мощность не всех приборов указана в Вт, например:

  • Мощность трансформаторов указывается в ВА:
    http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП: см приложение)
    http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ: см приложение)
  • Мощность конденсаторов указывается в Варах:
    http://www.
    elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39: см приложение)
    http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК: см приложение)
  • Примеры других нагрузок – см. приложения ниже.

 

Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.

Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность и реактивная мощность точно характеризуют нагрузку.

Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т. д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).

Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).

Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности. Все эти 4 параметра:

  1. Активная мощность: обозначение P, единица измерения: Ватт
  2. Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
  3. Полная мощность: обозначение S, единица измерения: ВА (Вольт Ампер)
  4. Коэффициент мощности: обозначение k или cosФ, единица измерения: безразмерная величина

Эти параметры связаны соотношениями:  S*S=P*P+Q*Q,   cosФ=k=P/S

Также cosФ называется коэффициентом мощности (Power Factor – PF)

Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.

Например, электромоторы, лампы (разрядные) – в тех. данных указаны P[кВт] и cosФ:
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР: см. приложение)
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ: см. приложение)
(примеры технических данных разных нагрузок см. приложение ниже)

То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.

Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др.

– при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.

 

См. учебники по электротехнике, например:

1. Евдокимов Ф. Е. Теоретические основы электротехники. – М.: Издательский центр “Академия”, 2004.

2. Немцов М. В. Электротехника и электроника. – М.: Издательский центр “Академия”, 2007.

3. Частоедов Л. А. Электротехника. – М.: Высшая школа, 1989.

Так же см. AC power, Power factor, Electrical resistance, Reactance http://en.wikipedia.org
(перевод: http://electron287.narod.ru/pages/page1.html)

 

Приложение

 

Пример 1: мощность трансформаторов и автотрансформаторов указывается в ВА (Вольт·Амперах)

Трансформаторы питания номинальной выходной мощностью 25-60 ВА
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП)

 

http://metz. by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)

 

АОСН-2-220-82
Латр 1.25 АОСН-4-220-82
Латр 2.5 АОСН-8-220-82





АОСН-20-220



АОМН-40-220




http://www.gstransformers.com/products/voltage-regulators.html (ЛАТР / лабораторные автотрансформаторы TDGC2)

 

 

Пример 2: мощность конденсаторов указывается в Варах (Вольт·Амперах реактивных)

http://www.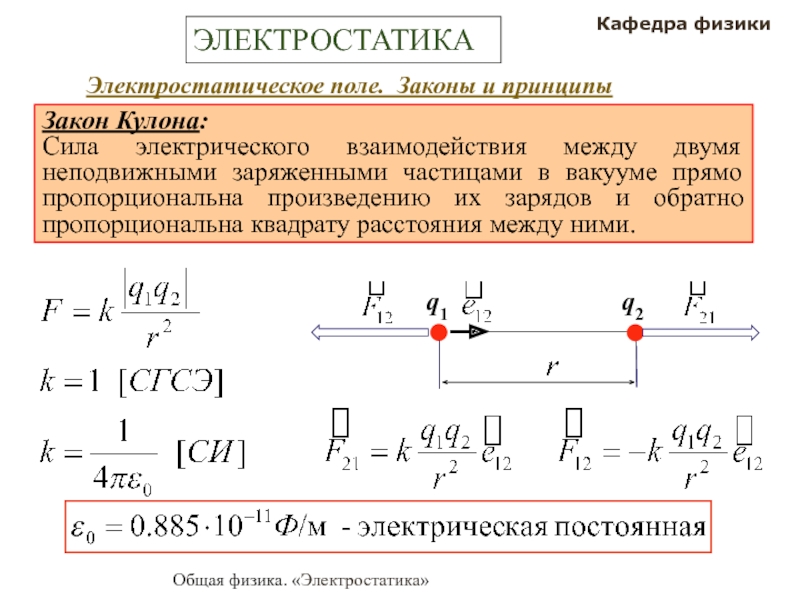 elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)

 

http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК)

 

 

Пример 3: технические данные электромоторов содержат активную мощность (кВт) и cosФ

Для таких нагрузок как электромоторы, лампы (разрядные), компьютерные блоки питания, комбинированные нагрузки и др. – в технических данных указаны P [кВт] и cosФ (активная мощность и коэффициент мощности) или S [кВА] и cosФ (полная мощность и коэффициент мощности).

http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР)

 

http://www.weiku.com/products/10359463/Stainless_Steel_cutting_machine.html
(комбинированная нагрузка – станок плазменной резки стали / Inverter Plasma cutter LGK160 (IGBT)

 

Технические данные разрядных ламп содержат активную мощность (кВт) и cosФ
http://www. mscom.ru/katalog.php?num=38 (лампы ДРЛ)

 

http://www.silverstonetek.com.tw/product.php?pid=365&area=en (блок питания ПК)

 

 

Дополнение 1

Если нагрузка имеет высокий коэффициент мощности (0.8 … 1.0), то её свойства приближаются к активной нагрузке. Такая нагрузка является идеальной как для сетевой линии, так и для источников электроэнергии, т.к. не порождает реактивных токов и мощностей в системе.

Если нагрузка имеет низкий коэффициент мощности (менее 0.8 … 1.0), то в линии питания циркулируют большие реактивные токи (и мощности). Это паразитное явление приводит к повышению потерь в проводах линии (нагрев и др.), нарушению режима работы источников (генераторов) и трансформаторов сети, а также др. проблемам.

Поэтому во многих странах приняты стандарты нормирующие коэффициент мощности оборудования.

 

Дополнение 2

Оборудование однонагрузочное (например, БП ПК) и многосоставное комбинированное (например, фрезерный промышленный станок, имеющий в составе несколько моторов, ПК, освещение и др. ) имеют низкие коэффициенты мощности (менее 0.8) внутренних агрегатов (например, выпрямитель БП ПК или электромотор имеют коэффициент мощности 0.6 .. 0.8). Поэтому в настоящее время большинство оборудования имеет входной блок корректора коэффициента мощности. В этом случае входной коэффициент мощности равен 0.9 … 1.0, что соответствует нормативным стандартам.

 

Дополнение 3. Важное замечание относительно коэффициента мощности ИБП и стабилизаторов напряжения

Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8.

В стабилизаторах напряжения дело обстоит иначе. Для стабилизатора коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.

 

Дополнение 4

Наглядные примеры чистой активной и чистой реактивных нагрузок:

  • К сети переменного тока 220 VAC подключена лампа накаливания 100 Вт – везде в цепи есть ток проводимости (через проводники проводов и вольфрамовый волосок лампы). Характеристики нагрузки (лампы): мощность S=P~=100 ВА=100 Вт, PF=1 => вся электрическая мощность активная, а значит она целиком поглащается в лампе и превращается в мощность тепла и света.
  • К сети переменного тока 220 VAC подключен неполярный конденсатор 7 мкФ – в цепи проводов есть ток проводимости, внутри конденсатора идёт ток смещения (через диэлектрик). Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.

 

Дополнение 5

Для обозначения преобладающего реактивного сопротивления (индуктивного либо ёмкостного) коэффициенту мощности приписывается знак:

+ (плюс) – если суммарное реактивное сопротивление является индуктивным (пример: PF=+0.5). Фаза тока отстаёт от фазы напряжения на угол Ф.

– (минус) – если суммарное реактивное сопротивление является ёмкостным (пример: PF=-0,5). Фаза тока опережает фазу напряжения на угол Ф.

 

Дополнение 6

В различных областях техники мощность может быть либо полезной, либо паразитной НЕЗАВИСИМО от того активная она или реактивная. Например, необходимо различать активную полезную мощность рассеиваемую на рабочей нагрузке и активную паразитную мощность рассеиваемую в линии электропередачи. Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.

 

 

Дополнительные вопросы

 

Вопрос 1:
Почему во всех учебниках электротехники при расчете цепей переменного тока используют мнимые числа / величины (например, реактивная мощность, реактивное сопротивление и др.), которые не существуют в реальности?

Ответ:
Да, все отдельные величины в окружающем мире – действительные. В том числе температура, реактивное сопротивление, и т. д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].

Замечание:
Раньше в физике использовались только одиночные величины и при расчете все математические величины соответствовали реальным величинам окружающего мира. Например, расстояние равно скорость умножить на время (S=v*t). Затем с развитием физики, то есть по мере изучения более сложных объектов (свет, волны, переменный электрический ток, атом, космос и др.) появилось такое большое количество физических величин, что рассчитывать каждую в отдельности стало невозможно. Это проблема не только ручного вычисления, но и проблема составления программ для ЭВМ. Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:

  1. Полное сопротивление (импеданс) Z=R+iX
  2. Полная мощность S=P+iQ
  3. Диэлектрическая проницаемость e=e’+ie”
  4. Магнитная проницаемость m=m’+im”
  5. и др.

 

 

Вопрос 2:

На странице http://en.wikipedia.org/wiki/Ac_power показаны S P Q Ф на комплексной, то есть мнимой / несуществующей плоскости. Какое отношение это все имеет к реальности?

 

 

Ответ:
Проводить расчеты с реальными синусоидами сложно, поэтому для упрощения вычислений используют векторное (комплексное) представление как на рис. выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.

 

 

 

Вопрос 3:
Обычными токовыми клещами и мультиметром измерен ток нагрузки 10 A, и напряжение на нагрузке 225 В. Перемножаем и получаем мощность нагрузки в Вт: 10 A · 225В = 2250 Вт.

Ответ:
Вы получили (рассчитали) полную мощность нагрузки 2250 ВА. Поэтому ваш ответ будет справедлив только, если ваша нагрузка чисто активная, тогда действительно Вольт·Ампер равен Ватту. Для всех других типов нагрузок (например электромотор) – нет. Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:

 

 

 

См. дополнительную литературу, например:

 

[1]. Евдокимов Ф. Е. Теоретические основы электротехники. – М.: Издательский центр “Академия”, 2004.

[2]. Немцов М. В. Электротехника и электроника. – М.: Издательский центр “Академия”, 2007.

[3]. Частоедов Л. А. Электротехника. – М.: Высшая школа, 1989.

[4]. AC power, Power factor, Electrical resistance, Reactance
http://en.wikipedia.org (перевод: http://electron287.narod.ru/pages/page1.html)

[5]. Теория и расчёт трансформаторов малой мощности Ю.Н.Стародубцев / РадиоСофт Москва 2005 г. / rev d25d5r4feb2013

[6]. Международная система единиц, СИ, см напр. ГОСТ 8.417-2002. ЕДИНИЦЫ ВЕЛИЧИН

Ключевые моменты при решении задач повышенного уровня по теме «Конденсаторы и их соединения»

Ключевые слова: ЕГЭ, ЕГЭ по физике, конденсаторы

При подготовке к ЕГЭ по физике и решении задач повышенной сложности очень часто обучающиеся сталкиваются с трудностями анализа физических процессов в конденсаторах. Целью данной работы является некоторая систематизация и выделение ключевых позиций при решении задач повышенной сложности по теме «Конденсаторы и их соединение». Реализовывая системно-деятельностный подход к изучению физики, возможно рассмотрение следующих ситуаций анализа решаемых задач, а также вариативных вопросов к ним.

I. Рассмотрим известную задачу, которая раскрывает взаимосвязь физических характеристик конденсатора и последовательность их изменений [2]:

Плоский конденсатор, между пластинами которого находится воздух, заряжен от источника питания. Как меняются заряд конденсатора, напряженность электрического поля, разность потенциалов между пластинами, энергия и плотность энергии электрического поля, если увеличить в n раз расстояние между пластинами в ситуациях, если а) конденсатор отключить от источника питания и б) с включенным источником питания.

Рассмотрим первую ситуацию: изменяем расстояние между пластинами при отключенном источнике.

В ключевых позициях устанавливаем два опорных положения, которые позволяют анализировать изменения физических характеристик

– Что остается неизменным в данном процессе. (q = const, заряд на пластинах конденсатора при отключении источника тока)

– Что происходит с емкостью конденсатора (Конденсатор плоский: d увеличивается, C уменьшается)

Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:

1) Напряженность электрического поля конденсатора E = ϭ/(2ε0) (не изменяется)

2) Разность потенциалов между пластинами C = q/U (С уменьшается, U увеличивается в n раз)

3) Энергия электрического поля W = qU/2 (U увеличивается в n раз, W увеличивается в n раз)

4) Плотность энергии ω = ε0E2/2 (не изменяется)

Рассмотрим вторую ситуацию: изменяем расстояние между пластинами при включенном источнике питания.

В ключевых позициях устанавливаем два опорных положения, которые позволяют анализировать изменения физических характеристик

– Что остается неизменным в данном процессе. (U = const, напряжение на пластинах конденсатора при включении источнике тока)

– Что происходит с емкостью конденсатора (Конденсатор плоский: d увеличивается, C уменьшается)

Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:

1) При неизменном напряжении и уменьшении емкости, заряд конденсатора должен уменьшиться в n раз (анализ C = q/U)

2) Напряженность электрического поля конденсатора E = ϭ/(2ε0) (E уменьшается в n раз при уменьшении заряда в n раз)

3) Энергия электрического поля W = qU/2 (q уменьшается в n раз, W уменьшается в n раз)

4) Плотность энергии ω = ε0E2/2 уменьшается в n2 раз (при уменьшении напряженности)

Особое внимание следует обратить на энергетические превращения в конденсаторе. При увеличении расстояния между пластинами совершается положительная механическая работа, но энергия конденсатора уменьшается. Согласно закону сохранения энергии источник должен забирать энергию, равную убыли энергии конденсатора и механической работы внешних сил. Иначе, если источник является аккумулятором, то он будет заряжаться от конденсатора. Если источником является гальванический элемент, то на нем будет выделяться тепло.

Поставленную задачу можно не ограничивать данными изменениями, а можно выполнить анализ при изменении площади пластин конденсатора или замене диэлектрика между пластинами. В результате поможет сформировать у обучающихся целостное и устойчивое представление физических процессов и их характеристик в конденсаторе, варьируя ситуации.

II. Рассмотрим две возможные ситуации при параллельном подключении одного конденсатора к другому, если обкладки конденсаторов соединены одноименными зарядами и разноименными зарядами [2]:

Конденсатор емкостью C1 заряжен до разности потенциалов U1. Какой заряд и каково напряжение будет на обкладках конденсатора, если к нему подключить параллельно другой конденсатор емкостью C2, заряженный до разности потенциалов U2.

Если обкладки конденсаторов соединены одноименными зарядами, то решение задачи сводится к составлению уравнения закона сохранения заряда до соединения и после соединения конденсаторов. Закон сохранения заряда будет ключевым моментом анализа задачи. Второй момент – равенство напряжений на конденсаторах при параллельном подключении, дает возможность упростить и решить данную задачу.

Иначе дело обстоит, если обкладки конденсаторов соединены разноименными зарядами. При соединении двух конденсаторов возникает ситуация, когда при распределении зарядов после подключения происходит перезарядка одного из конденсаторов и смена знаков зарядов на его обкладках. В этом случае при составлении уравнения закона сохранения заряда как ключевого момента следует не забыть изменить знак заряда на противоположный. Положим, в данном примере U2 > U1, то при соединении конденсаторов, первый конденсатор перезарядится, и знаки зарядов на его пластинах сменятся. Поэтому удобно при составлении закона сохранения заряда, принять заряд первого конденсатора, до соединения к нему второго, за отрицательный заряд.

Закон сохранения заряда для данного примера будет выглядеть: -q1+ q2 = q1‘+ q2‘.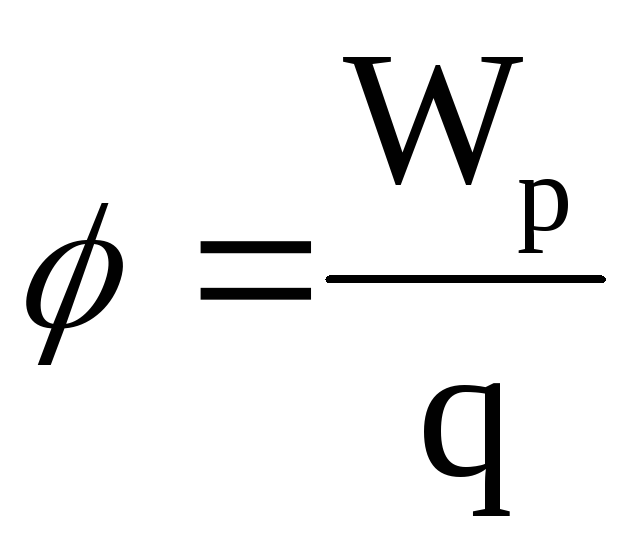 Последующее равенство напряжений на конденсаторах при параллельном подключении дает возможность упростить и решить данную задачу.

III. Рассмотрим анализ схемы соединения конденсаторов, где их соединения не сводятся к совокупности параллельных и последовательных соединений.

Например, в разветвленной схеме требуется найти напряжения на конденсаторах. Данный пример подробно описан [1]. Из данного примера выделим следующие ключевые моменты:

1) Составляем независимые уравнения, связывающие напряжения на конденсаторах с электродвижущими силами, выбрав точки разности потенциалов.

А) Между точками F и D: Ɛ1+ Ɛ2= U1+ U2

Б) Между точками F и A: Ɛ1= U1+ U3

2) Составляем уравнение алгебраической суммы зарядов в узле точки B:

q1– q2 – q3= 0 или C1U1– C2U2 – C3U3= 0

Система трех независимых уравнений с тремя неизвестными дает их решение. Если схема симметрична (Ɛ1 = Ɛ2, C1 = C2), то U3(Напряжение между точками A и B) равно нулю, а напряжение U1= U2.

В связи с данным примером, возникает упрощенный анализ схем при переключении в цепи с конденсаторами, например [1]:

Для положения ключа в состоянии A и B между точками F и D выражение Ɛ1 + Ɛ2 = U1 + U2справедливо в обоих случаях. Следовательно, U2не изменяется при переключении.

Для узла N сумма зарядов в узле равна нулю: q1– q2 ± q3= 0. Следовательно, не изменится заряд третьего конденсатора, а вместе с ним и не изменится напряжение U3.

После переключения U2= U3, конденсаторы соединены параллельно.

В данном примере интересен вывод: точки A и B имеют одинаковый потенциал, следовательно Ɛ2= 0.

IV. Рассмотрим некоторые варианты изменения энергии конденсатора с точки зрения закона сохранения энергии, подробные объяснения которых обсуждаются в источнике [3].

Изменение энергии конденсатора можно произвести от источника питания или путем совершения механической работы внешними силами.

Увеличение энергии конденсатора при зарядке конденсатора в общем виде можно определить из уравнения закона сохранения:

Aист. = ΔWк + A + Q,

где Aист. – работа источника при зарядке конденсатора, ΔWк – изменение энергии конденсатора, A – механическая работа сил электрического поля, Q – выделяющееся тепло. В идеальном случае, при отсутствии потерь энергии от источника: Aист. = ΔWк

Однако наиболее часто встречаются задания, где изменение энергии заряженного конденсатора происходит путем совершения работы внешней силы в ситуациях с отключенным и подключенным источником тока.

Рассмотрим первую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при отключенном источнике питания.

– обращаем внимание на то, что в данной ситуации остается неизменным заряд q конденсатора.

– обращаем внимание на то, что емкость при выемке диэлектрика или раздвижении пластин уменьшается емкость конденсатора (C = εε0S/d)

Формируем вывод исходя из формулы энергии при неизменном заряде: W = q2/2C – энергия конденсатора увеличивается. Увеличение энергии произошло за счет работы внешней силы. ΔWк = Aвнеш.

Рассмотрим вторую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при включенном источнике питания.

– обращаем внимание на то, что в данной ситуации остается неизменным напряжение U на обкладках конденсатора.

– обращаем внимание на то, что емкость при выемке диэлектрика или раздвижении пластин уменьшается емкость конденсатора (C = εε0S/d)

Формируем вывод исходя из формулы энергии при неизменном напряжении: W = CU2/2 – энергия конденсатора уменьшается. Уменьшение энергии произошло за счет того, что источник совершает отрицательную работу, забирая часть заряда с обкладок конденсатора при положительной работе внешних сил:. ΔWк = Aист. + Aвнеш.

Возможны и другие очевидные вариации изменения энергии конденсатора с помощью работы внешних сил.

В данной работе рассмотрена лишь небольшая часть анализа ключевых ситуаций по данной теме. Но все рассмотренные ситуации являются опорными для формирования разбора задач и их решения.

Литература

1. Е.И.Бутиков, А.А.Быков, А.С.Кондратьев. Физика в примерах и задачах, МЦНМО, Пероглиф, 2019, стр. 297-301.

2. А.С.Кондратьев, В.М.Уздин. Физика. Сборник задач, М., ФИЗМАТЛИТ, 2020, стр. 67-69.

3. А.С.Кондратьев, Л.А.Ларченкова, В.А.Ляпцев. Методы решения задач по физике. М., ФИЗМАТЛИТ, 2019, стр.149-154.

Закон Кулона: расчет электростатической силы

Закон Кулона: расчет электростатической силы

Узнайте о законе Кулона и электростатической или электрической силе. Притяжение или отталкивание, вызванное двумя зарядами, находящимися на расстоянии друг от друга.

Закон Кулона Учебные мишени
  • Я могу связать третий закон движения Ньютона с зарядами
  • Я понимаю закон Кулона и взаимосвязь между электростатической силой, зарядом и расстоянием
  • Я могу найти электростатическую силу, заряд и расстояние, используя закон Кулона с двумя зарядами

Посмотрите видео-урок о законе Кулона и электростатической силе или перейдите ниже, прочитайте и проработайте примеры в своем собственном темпе, как в учебнике.

Переменные закона Кулона
Имя Переменная Блок МКС Сокращение единиц измерения
Сила Ф Ньютон Н
Константа закона Кулона к Ньютон-метр в квадрате разделить на Кулон в квадрате Н·м 2 /C 2
Плата(ы) q, q 1 или q 2 Кулон С
Расстояние д метров м
Радиус р Счетчик м

Электростатический заряд (q)

Стандартной физической единицей MKS для заряда (переменная q или Q) является кулон (C). Примечание. В зависимости от таблицы уравнений вы можете использовать переменную q или Q. Мы будем использовать q для представления заряда в этой единице.

Один кулон равен заряду 6,25 x 10 18 электронов . Это выходит за рамки того, с чем вы обычно сталкиваетесь, если только не вычисляете заряд, переносимый ударом молнии. Поскольку кулон является таким большим зарядом, для описания заряда часто используется префикс микро (µ) или 1×10 -6 . Если вы видите единицу µC, просто добавьте (x10 -6 ) к вашему числу, чтобы при решении уравнений оно стало кулоном. Таким образом, 5 мкКл будут равны 5×10 -6 C.

Какие три фактора влияют на электростатическую силу?

На электростатическую силу влияют три фактора: заряд , расстояние между объектами и изолирующий материал между объектами. Все задачи из этого раздела будут иметь заряды, разделенные воздухом в качестве изолятора. Все три вышеуказанных фактора можно увидеть в уравнении электростатической силы, формально называемом законом Кулона.

Закон Кулона и электростатическая сила

В уравнении закона Кулона q 1 и q 2 — два платежа. Создаваемая сила ( F ) зависит от расстояния между объектом ( d ) и постоянной закона Кулона ( k ) для изолирующего материала, разделяющего эти заряды. Постоянная закона Кулона для воздуха равна 9,0×10 9 (Nm 2 /C 2 ) . Не пугайтесь блока (Nm 2 /C 2 ), так как всего 9,0×10 9 будет использоваться в расчетах.

Сила притяжения возникает, когда заряды имеют противоположные знаки: положительный (+) и отрицательный (-).

Сила отталкивания будет возникать, когда заряды имеют один и тот же знак положительный (+) и положительный (+) или отрицательный (-) и отрицательный (-).

В любом случае сила создается попарно на каждый объект, и эта сила равна и противоположна. Чтобы узнать больше о третьем законе Ньютона и парах действия-реакции, вернитесь к этому уроку здесь.

Электростатическая сила и заряд прямо пропорциональны

Электростатическая сила (F) и заряд (либо q) прямо пропорциональны. Чтобы проанализировать это, увеличьте то, что вы анализируете, на один заряд (q 1 ) и посмотрите, что происходит с силой, когда все, включая один заряд, равно 1. Затем сделайте этот заряд равным 2 и посмотрите, как сила (F) увеличивается с той же скоростью и становится 2.

Электростатическая сила пропорциональна обратному квадрату расстояния

Электростатическая сила (F) обратно пропорциональна квадрату расстояния. По мере увеличения расстояния с использованием того же метода, что и раньше, сила уменьшается пропорционально обратному квадрату. Если расстояние изменяется от 1 до 2, сила увеличивается от 1 до 1/4. Расстояние оказывает гораздо большее влияние на силу, чем такое же увеличение или уменьшение заряда.

Правило единиц и закон Кулона

Чтобы найти точное изменение одной переменной на другую, вы можете использовать правило единиц. Вернитесь к этому уроку, нажав на ссылку, если вы знакомы с этим методом.

Стандартный тип задачи на закон Кулона

Большинство задач на закон Кулона связаны с зарядами, расстояниями и возникающими силами. Проблема даст вам достаточно информации, и вам придется решать неизвестное. При использовании закона Кулона для решения задач принято оставлять знак заряда снятым. Если у вас есть два одинаковых заряда, произойдет отталкивание. Если заряды противоположны положительным (+) и отрицательным (-), будет притяжение.

Когда два заряда по закону Кулона одинаковы, формулу можно упростить. Поскольку заряды одинаковые, замените q на оба q 1 и q 2 . Затем упростите, как показано ниже:

Уравнение закона Кулона и наиболее распространенные ошибки в расчетах

Вы можете увидеть конечный результат преобразования уравнения закона Кулона для расстояния или заряда.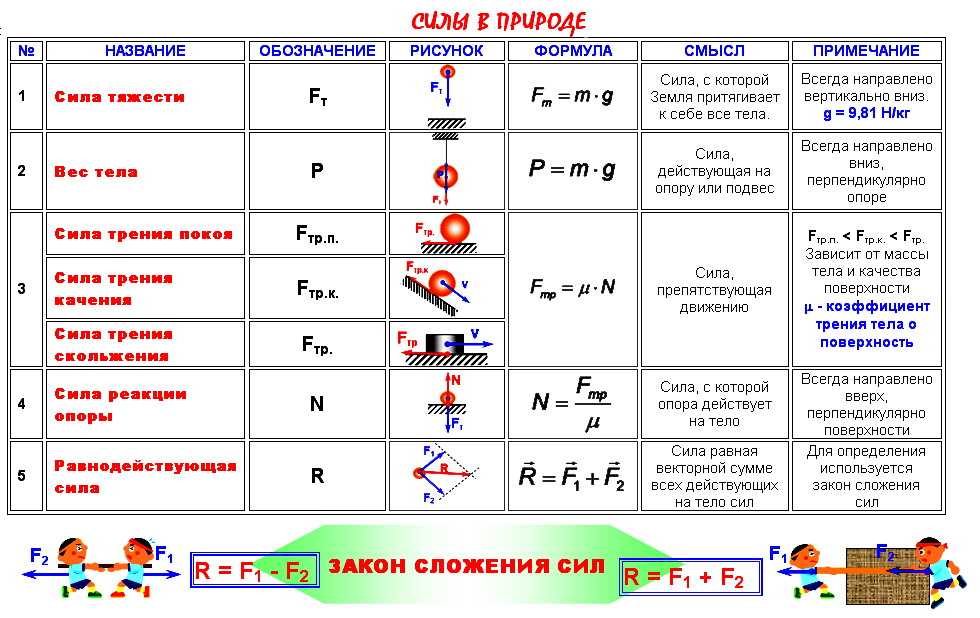 Я добавил дополнительные скобки, чтобы помочь вам избежать распространенных ошибок.

Самая распространенная ошибка № 1 Ошибка закона Кулона: решение для квадрата расстояния (d 2 ), а не для расстояния (d)

0007  извлеките квадратный корень из d 2 и другой части уравнения . Если нет, то вы будете находить d 2 случайно, когда уравнение запрашивает d. После извлечения квадратного корня из обеих сторон d 2 станет d. Вы также получите квадратный корень из всей другой части уравнения (kq 1 q 2 /F). При расчетах ставьте дополнительные скобки вокруг всего, что следует за квадратным корнем. При этом √(kq 1 q 2 /F) , позволит избежать случайного извлечения квадратного корня только из части стороны.

Самая распространенная ошибка в законе Кулона № 2: k и
q 2 не включены вместе в знаменатель

Если в вопросе вам предлагается решить для любого заряда, переставленное уравнение включает одну и ту же алгебру.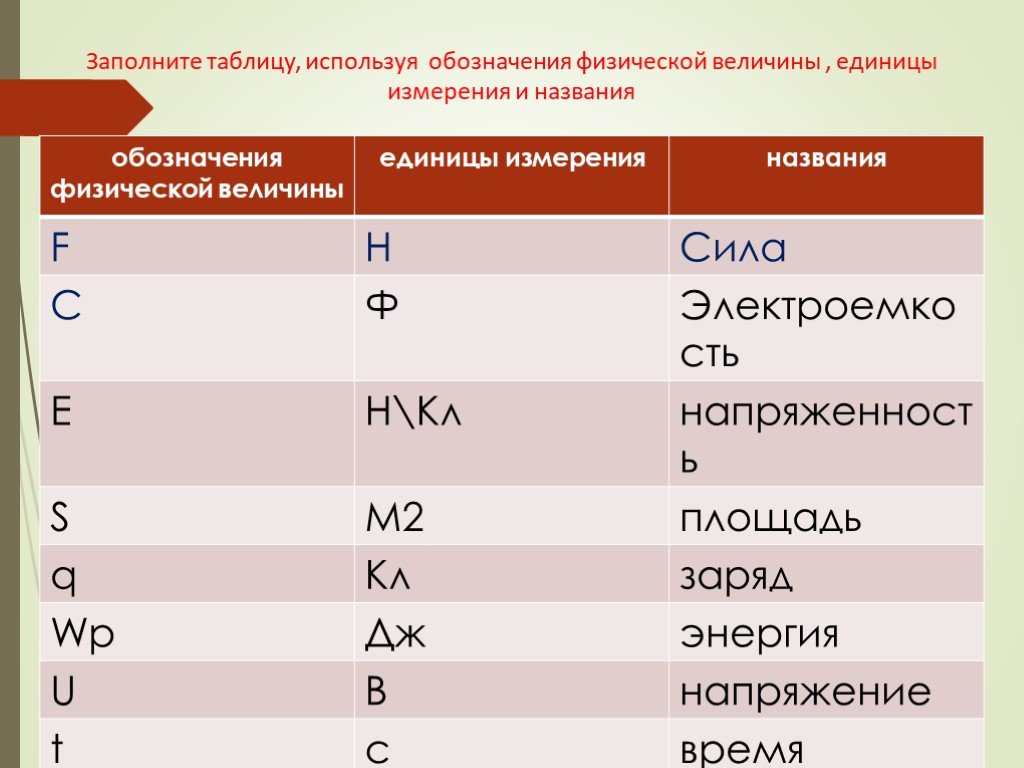 Убедитесь, что включает дополнительные скобки вокруг знаменателя , нижней части уравнения, как показано в перестроенном уравнении. Это заставляет калькулятор умножать постоянную закона Кулона (k) и другой заряд (q 2 ) вместе в знаменателе, прежде чем делать что-либо еще.

Примеры задач

1. Если заряд каждого объекта удвоить, а расстояние между ними увеличить в четыре раза, как изменится сила?

(Нажмите на картинку, чтобы увидеть работу в большем размере)

2. Как пропорциональны заряд и электрическая сила?

Непосредственно : Если заряд увеличивается, изменяется от 1 до 2, сила увеличивается пропорционально, также увеличивается от 1 до 2.

3. Как электрическая сила пропорциональна расстоянию?

Пропорционально обратному квадрату расстояния:  Когда расстояние увеличивается, изменяется от 1 до 2, сила не просто уменьшается, но пропорциональна обратному квадрату расстояния.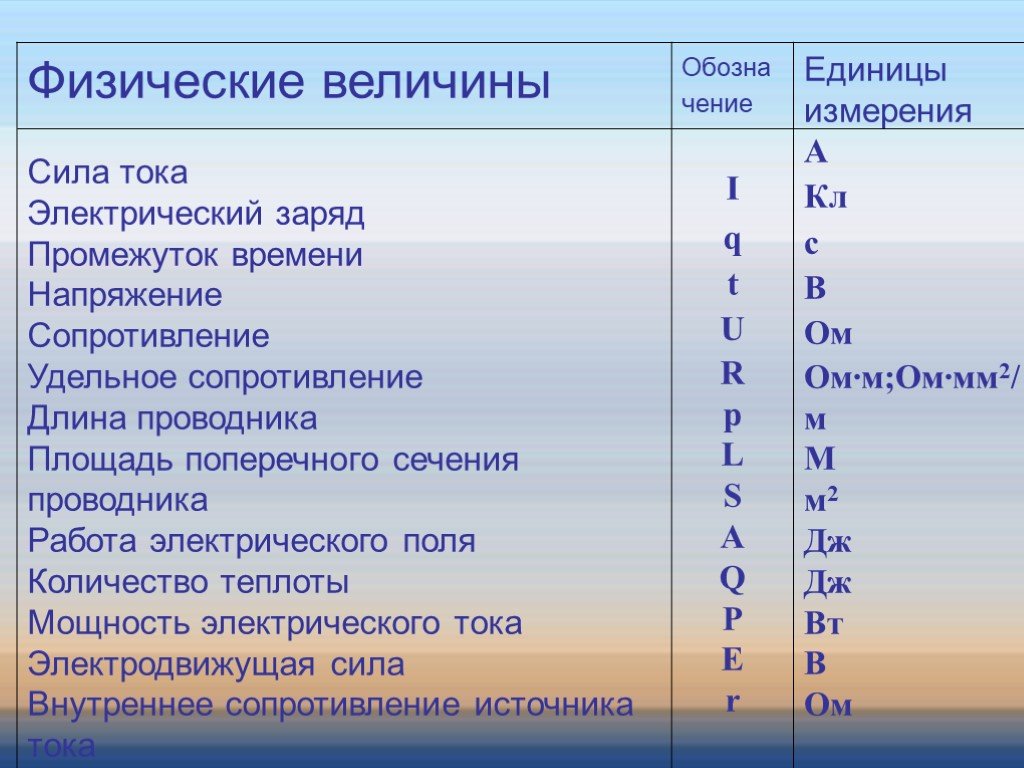 Сила идет на 1/4. Расстояние больше влияет на силу, чем заряд.

4. Чем лучше изолятор между объектами, тем ______ значение «k».

Ниже, Если бы у вас был лучший изолятор, сила, ощущаемая между двумя зарядами, была бы меньше. Таким образом, чем ниже k, тем лучше изолятор. Еще раз, мы делаем математику только с воздухом в качестве изолятора и k со значением 9,0 x 10 9 Нм 2 /C 2 , но это число будет меньше с лучшим изолятором, чем воздух.

5. Если заряд каждого объекта удвоить, а расстояние между ними увеличить в четыре раза, как изменится сила?

6. Какова электростатическая сила между двумя объектами, +13 мкКл и -22 мкКл, которые находятся на расстоянии 0,055 м друг от друга (мкКл = 1 x 10 -6 Кл), и является ли это притяжением или отталкиванием?

(Нажмите на картинку, чтобы увеличить работу)

7.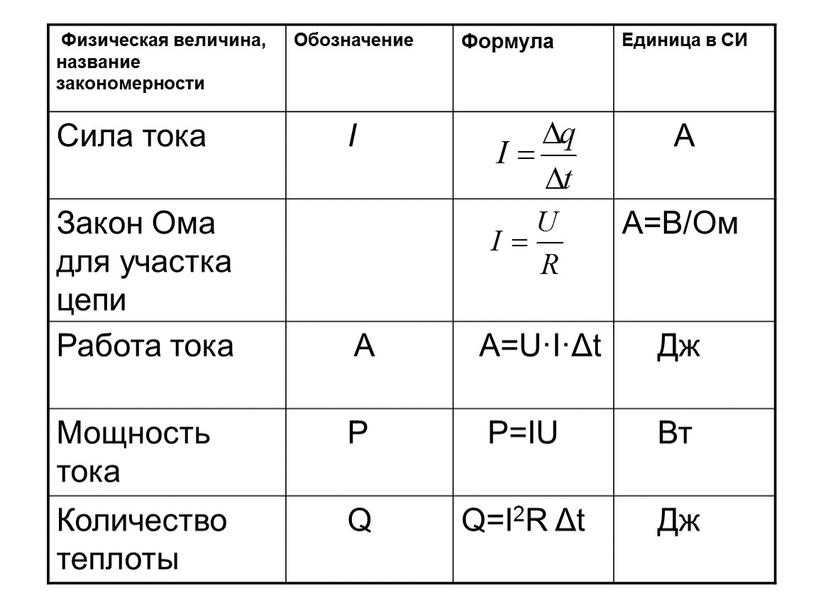 Какова электростатическая сила между двумя объектами -14 x 10 -6 C и -22 x 10 -6 C, которые находятся на расстоянии 0,86 м друг от друга?

(Нажмите на картинку, чтобы увидеть работу в большем размере)

8. Электростатическая сила между двумя объектами составляет 6,4 Н, когда заряды составляют -4,5 x 10 -6 Кл и -8,8 x 10 -6 Кл.  На каком расстоянии друг от друга находятся объекты?

(Нажмите на картинку, чтобы увеличить изображение)

9. Сила притяжения 1,1 Н действует между двумя заряженными объектами, когда они находятся на расстоянии 0,43 м друг от друга. Заряд одного объекта составляет -5,7 x 10 -6 Кл. Каков заряд другого объекта?

(Нажмите на картинку, чтобы увеличить работу)

 

Закон Кулона Викторина

Электростатика Викторина 2: Закон Кулона

1 / 11

частицы, когда она вытирает через стол. -8 м

0,0027 м

0,046 м

2,53 м

2 / 11

Если труба из ПВХ стала отрицательно заряженной, как это произошло?

он потерял протоны

он приобрел протоны

он потерял электроны

он приобрел электроны

3 / 11

Если шерстяная ткань стала положительно заряженной, как она это сделала?

потерял электроны

приобрел протоны

приобрел электроны

потерял протоны

4 / 11

Заряд -60 C и заряд +20 C находятся на расстоянии 2 метров друг от друга. Будут ли они притягиваться или отталкиваться?

отталкивают

притягивают

5 / 11

Электростатическая сила между двумя зарядами, находящимися на расстоянии 2 м друг от друга, равна 15 Н. Какова будет сила между этими зарядами, когда они находятся на расстоянии 1 м друг от друга?

10 N

20 N

60 N

30 N

6 / 11

Две заряженные частицы находятся на неизвестном расстоянии друг от друга. Если расстояние между ними уменьшилось вдвое, а заряды обеих частиц удвоились, во сколько раз отличается новая сила по сравнению с первоначальной?

4 раза

1/4 раза

2 раза

16 раз

7 / 11

Две заряженные частицы находятся на неизвестном расстоянии друг от друга. Если расстояние между частицами увеличить вдвое, во сколько раз новая сила будет отличаться от первоначальной?

2 раза

4 раза

16 раз

1/4 раза

8 / 11

Две заряженные частицы находятся на неизвестном расстоянии друг от друга. Если заряд обеих частиц удвоится, во сколько раз будет отличаться новая сила по сравнению с первоначальной?

16 раз

1/4 раза

4 раза

2 раза

9 / 11

Две заряженные частицы находятся на неизвестном расстоянии друг от друга. Если заряд одной из частиц увеличить вдвое, во сколько раз будет отличаться новая сила по сравнению с первоначальной?

16 раз

4 раза

2 раза

1/4 раза