Q физика формулы: А для чего формулы? Q=c*m*t , t=Q/cm и зачем в кДж переводить??

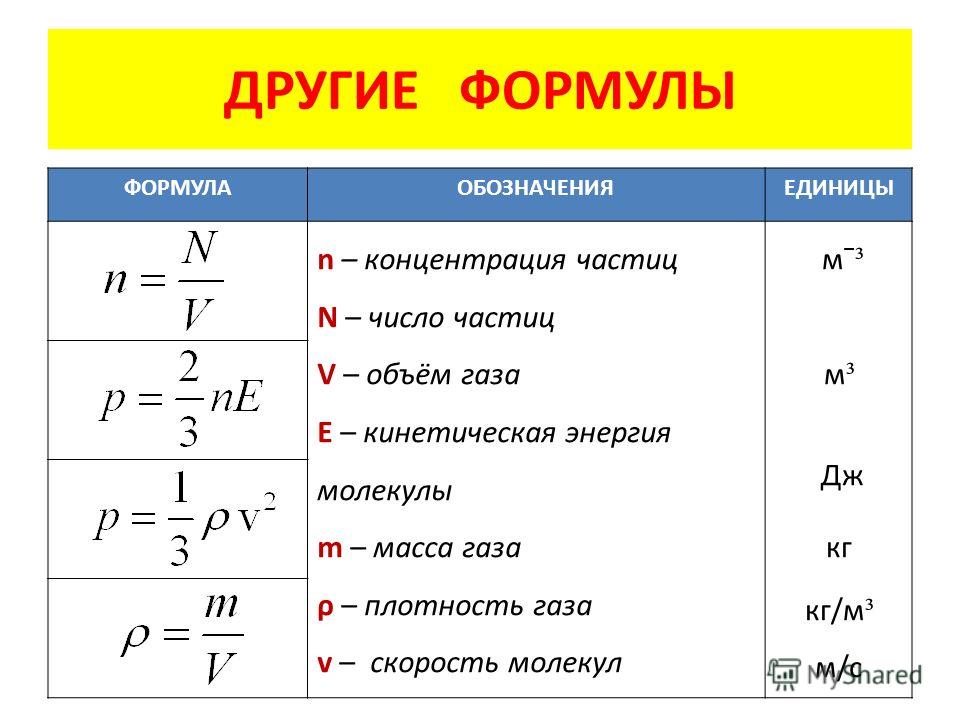
Электростатика – формулы, закон Кулона

Оглавление

Время чтения::  6 минут

495

Электростатикой называют раздел физики, в котором изучают неподвижные, покоящиеся электрические заряды и поля. В статье мы рассмотрим самые важные законы электростатики, определения и формулы этой важнейшей области науки о свойствах и формах окружающей нас материи.

Понятие электрического заряда и его важнейшие законы электростатики

Определения 1 — 2

Электрическим зарядом именуют физическую величину, характеризующую способность тел вступать между собой в электромагнитное взаимодействие. Обозначается электрический заряд обычно буквами q или Q. В системе он измеряется в Кулонах.

Один Кулон равняется заряду, проходимому через проводник (его поперечное сечение) за 1 секунду с силой тока в 1 Ампер.

---

 

Элементарный электрический заряд – минимальный электрический заряд, существование которого допускается природой. {*} \mathrm{e}\]

Существуют два типа зарядов – положительные (они обозначаются знаком +) и отрицательные (они обозначаются знаком — ). Между одноимёнными электрическими зарядами всегда происходит отталкивание, разноимёнными — притяжение.

Закон сохранения электрического заряда

Закон 1 + формула

Это важнейший закон не только электростатики, но и всей физики. Суть его состоит в том, что сумма зарядов любой системы, которая электрически изолирована, не может измениться ни при каких обстоятельствах. На языке математики — это можно записать так:

\[\mathrm{q}_{1}+\mathrm{q}_{2}+\mathrm{q}_{3}+\ldots+\mathrm{q}_{\mathrm{n}}=\text { const }\]

Процессы появления/исчезновения зарядов наукой зафиксированы, но тот и другой процесс предполагает их парное (положительный и отрицательный) появление или уничтожение. Причём возникающие и исчезающие заряды должны быть не только противоположны между собой по знаку, но и равны по абсолютной величине.

Определение 3

Электризацией называют явление перераспределения электрического заряда между физическими телами.

Основными способами электризации являются трение, касание и влияние. Тела, ставшие в силу тех или иных процессов электрически заряженными, называют электризованными.

Если мы имеем два тела одинакового размера и формы, заряжённые один q₁, второй q₂, то из выше приведённого закона сохранения явным образом следует, что если привести их в соприкосновение друг с другом, а затем развести, величина заряда каждого из них станет равной

q^, = (q₁ + q₂)/2.

Величина заряда никак не зависит от его движения и скорости. Это означает, что если заряжённое тело начнёт двигаться, то от это никак не повлияет на величину его заряда, не уменьшит и не увеличит её.

Электростатика закон кулона

Определение 4

Точечными электрическими зарядами именуются такие электрически заряженные физические тела, формой и размерами которых при рассмотрении процесса их взаимодействия можно пренебречь.

Одни и те же тела в одних условиях можно считать точечными, а в других нет. {2}\]

k – коэффициент пропорциональности, зависящий от выбранной системы измерений. В СИ он равен k = 9*10⁹ (Н*м²)/Кл².

Если заряженные тела находятся в каком-либо веществе, в указанном законе появляется ещё один коэффициент, называемый диэлектрической проницаемостью.

Определение 5

Диэлектрическая проницаемость – величина, обозначающая, во сколько раз сила (F) взаимодействия зарядов, находящихся в веществе, меньше их силы взаимодействия в вакууме (F₀). Обозначается диэлектрическая проницаемость чаще всего, буквой ε.

Из определения можно сделать вывод, что диэлектрическая проницаемость вакуума равняется единице (ε =1). Диэлектрическую проницаемость воздуха при рассмотрении очень многих явлений можно тоже считать равной 1.

Проводниками называют вещества, в которых присутствуют свободные носители заряда. Диэлектриками – вещества, в которых их нет.

Самый яркий и хорошо известный пример проводника – металлы. Носителями заряда в них являются свободные электроны. Также проводниками являются недистиллированная вода, влажный грунт, растворы солей и т. д.

У диэлектриков свободные заряды почти полностью отсутствуют. К подобным веществам относятся воздух, стекло, фарфор, сухое дерево, резина, пластмассы и т. д.

Закон Кулона хотя и описывает взаимодействие электрических зарядов, совершенно ничего не говорит о его природе. Многочисленные эксперименты подтвердили, что заряжённые тела действуют друг на друга не непосредственно, а с помощью электростатического поля. О его важнейших характеристиках поговорим далее.

Напряжённость

Закон 3 + формула

Векторная величина, равная силе, которой поле оказывает действие на помещённый в него единичный положительный заряд.

\[\mathrm{E}=\mathrm{F} / \mathrm{q}\]

Единицей измерения напряжённости служат Н/Кл или В/м.

Для описания электрического поля часто используют так называемые силовые линии.

Особо следует подчеркнуть, что силовые линии в природе не существуют. Они являются плодом человеческого воображения, помогающим лучше и нагляднее описать электрическое поле и более ничем.

Основными свойствами силовых линий считаются:

• Совпадение с направлением вектора напряжённости;
• Незамкнутость. Принято считать, что линии идут положительных зарядов к отрицательным;
• Стабильность во времени. Напомним, речь здесь идёт об электростатических электрических полях. В электродинамике, где поля не постоянны, всё несколько иначе;
• Непересекаемость между собой. Линии никогда не находят одна на другую, какое бы явление мы ни рассматривали;
• Перпендикулярность плоскости поверхности основного проводника. Последний можно представить в виде совокупности множества точечных зарядов из которых силовые линии исходят или, наоборот, входят в них.

Электростатический потенциал

Определение 6 + формула

Электростатический потенциал — это скалярная величина, равная потенциальной энергии находящегося в нём единичного положительного заряда. Вычисляется она по формуле

\[\varphi=\mathrm{W}_{\text {потенциал }} / \mathrm{q}\]

Часто под потенциалом электростатического поля понимают работу, которую нужно затратить, чтобы переместить единичный положительный заряд из точки, где он находится, на бесконечность.

Работа по перемещению заряда в электростатическом поле определяется лишь его начальным и конечным положениями, но не путём перемещения. Такое поле называют потенциальным.

Конкретная величина потенциала почти никакой информации о поле не даёт. Значение имеет разность потенциалов.

Определения 7 — 9

Напряжением в электростатике называют разность потенциалов между двумя точками поля \[\mathrm{U}=\varphi_{2}-\varphi_{1}\].

Единицей измерения потенциала является Вольт. Он равен 1 В = 1 Дж/Кл

---

 

Электроёмкостью называют физическую величину, характеризующую способность проводников (в том числе систем проводников) накапливать электрический заряд. Чаще всего её обозначают буквой C. Измеряется в Фарадах. Один Фарад равен ёмкости, которую имеет конденсатор с зарядом каждой из пластин в 1 Кулон и напряжением между ними в 1 Вольт.

---

 

Конденсаторами именуют устройство накопления электрического заряда, состоящее из проводящих пластин, разделённых между собой диэлектриком. Форма пластин может быть абсолютно любой. Чаще всего встречаются плоские, цилиндрические и сферические. Диэлектрик тоже бывает разным: слюда, керамика, бумага и пр.

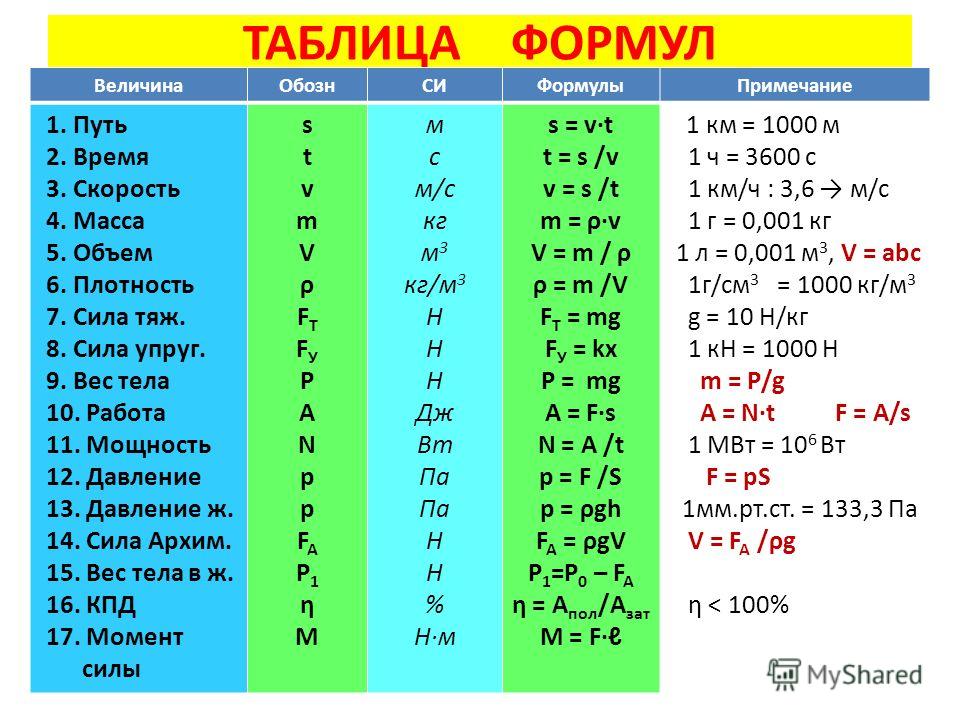
Приведём в таблице основные формулы электростатики:

Электродинамика: формулы (тест начального уровня)

(Если вы просматриваете сайт как турбо-страницу Яндекса, то для решения тестов перейдите на полную (мобильную) версию сайта по кнопке снизу. Турбо-страницы не содержат всех необходимых скриптов)

1. По какой из приведенных ниже формул можно рассчитать в СИ модуль напряженности электростатического поля точечного заряда q, находящегося в однородном изотропном диэлектрике?
E = Fq
E = kq/r
E = q/(4πεε_or)
E = q/(εε_oS)
затрудняюсь ответить

2.

По какой из приведенных ниже формул можно рассчитать в СИ потенциал электростатического поля точечного заряда q, находящегося в однородном изотропном диэлектрике?
Φ = q/(4πε_or)
Φ = kq/r²
Φ = q/(4πεε_or)
Φ = E(d₁ − d₂)
затрудняюсь ответить

3. Емкость батареи, состоящей из двух конденсаторов, соединенных параллельно, определяется по формуле:
C = C₁ + C₂
C = C₁ − C₂
C = C₁C₂/(C₁ + C₂)
C = (C₁ + C₂)/2
затрудняюсь ответить

4. Емкость плоского конденсатора, пространство между обкладками которого заполнено диэлектриком с диэлектрической проницаемостью ε, в СИ определяется по формуле:
C = 2q/U
C = εε_oS/d
C = εS/d
C = εS/2d
затрудняюсь ответить

5. По какой из приведенных ниже формул можно рассчитать плотность энергии электростатического поля w заряженного конденсатора?
w = q²/(2εε_oS²)
w = 2qE/S
w = εε_oE²/2
w = E²/(2εε_o)
затрудняюсь ответить

6. По какой из приведенных ниже формул можно рассчитать удельное сопротивление металлического проводника ρ при температуре t, если его сопротивление при температуре 0 °С равно ρ_о?
ρ = ρ_о(1 − αt)
ρ = ρ_о(1 + αt)
ρ = ρ_о/(1 + αt)
ρ = ρ_о/(1 + αt²)
затрудняюсь ответить

7. Какая из приведенных ниже формул является математическим выражением закона Ома для однородного участка цепи?
I = U/R
I = Ε/(R + r)
I = (ΔΦ + Ε)/(R + r)
I = Ε/r
затрудняюсь ответить

8. По какой из приведенных ниже формул можно рассчитать тепловую мощность тока P на внешнем участке цепи?

P = A/Δt
P = UI
P = I²R
P = IΕ − I²R
затрудняюсь ответить

9. По какой из приведенных ниже формул можно рассчитать модуль силы Ампера F?
F = qE
F = qνBsin α
F = IBlsin α
F = kq₁q₂/r²
затрудняюсь ответить

10. По какой из приведенных ниже формул можно рассчитать модуль индукции магнитного поля B длинного прямолинейного проводника с током I, который находится в вакууме?

B = μμ_oI/r
B = μμ_oI/(2πr)
B = μ_oI/(2πr)
B =μ_oI/(πr)
затрудняюсь ответить

Следующий тест: Электродинамика: определения

Формула электрического заряда – GeeksforGeeks

Когда материя находится в электрическом или магнитном поле, она развивает электрический заряд, который заставляет ее испытывать силу. Текущий электрический заряд создает магнитное поле, которое связано с электрическим полем. Электромагнитное поле состоит из комбинации электрического и магнитного полей. Электромагнитная сила, являющаяся основой физики, создается при взаимодействии зарядов. Давайте подробнее рассмотрим концепцию электрического заряда,

Электрический заряд

Свойство субатомных частиц, которое позволяет им испытывать силу при помещении в электрическое или магнитное поле, известно как Электрический заряд.

Скалярная величина, электрический заряд. Величина, называемая вектором, должна удовлетворять законам сложения векторов, таким как закон сложения векторов треугольника и закон сложения векторов параллелограмма, в дополнение к величине и направлению; только тогда сумма называется векторной величиной. В случае электрического тока результирующий ток представляет собой алгебраическую сумму, а не векторную сумму, когда два тока встречаются на стыке. В результате электрический ток, хотя и имеет величину и направление, является скалярной величиной. Электрический заряд обозначается Q.

Единица электрического заряда в системе СИ: Кулон и Другие единицы измерения: Фарадей, Ампер-час.

Положительные и отрицательные электрические заряды переносятся протонами и электронами соответственно. Субатомные частицы и частицы материи являются примерами различных форм зарядов:

• Положительно заряженные протоны
• Отрицательно заряженные электроны
• Нейтрон имеет нулевой заряд

Формула электрического заряда

Формула электрического заряда

Q = I × t

Где,

• Q = электрический заряд,
• I = электрический ток,
• t = время.

Примеры вопросов

Вопрос 1. По какой причине электрический заряд является скалярной величиной?

Ответ :

Результирующий ток двух токов, встречающихся на стыке, представляет собой алгебраическую сумму, а не векторную сумму. Таким образом, скалярная величина представляет собой электрический ток. Это свойство электрического заряда известно как KCL, также известное как закон тока Кирхгофа.

Вопрос 2: Когда возникает отрицательный и положительный электрический заряд?

Ответ :

Считается, что вещество имеет отрицательный заряд, если в веществе больше электронов, чем протонов, и считается, что оно имеет положительный заряд, если в веществе больше протонов, чем электронов.

Вопрос 3: Цепь с током 150 мА работает в течение 2 минут. рассчитать количество заряда, протекающего по цепи.

Решение:

Дано: I = 150 мА = 150 × 10 ^-3 A, T = 2 мин = 2 × 60 = 120S

С тех пор

Q = I × T

∴. Q = 150 × 10 ^-3 × 120

∴ Q = 18 C

Вопрос 4. Если проводник с током подключен к внешнему источнику питания на 20 секунд, всего 6 × 10 ⁴⁶ электронов течет через него. Определить значение тока в проводнике.

Решение:

Дано: n = 6 × 10 ⁴⁶ Электроны, T = 20S, E = 1,6 × 10 ^-19 C

С,

Q = I × T

∴ ∴

Q = I × T

∴

I = Q/T

по токовой формуле,

Q = NE

∴ I = NE/T

∴ I = 6 × 10 ⁴⁶ × 1,6 × 10 ^-19 /20

∴ I = 4,8 × 10 ²⁶ А

Вопрос 5: По проводнику течет ток силой 0,6 А. Вычислите количество заряда, которое пройдет через поперечное сечение проводника за 37 секунд.

Решение:

Дано: I = 0,6 a, T = 37 S

,

Q = I × T

∴ Q = 0,6 × 37

∴ Q = 22,2 C

Q = 22,2 C

Q = 22,2 C

Q = 22,2 C

Q = 22,2 C

Q = 22,2 C

Вопрос 6: Если сила электрического тока равна 200 А, а время равно 3 мин, то найдите электрический заряд.

Решение:

Дано: I = 200 А, t = 3 мин = 3 × 60 = 180 с0003

∴ Q = 36000 C

Физическая формула для класса 12, глава — Емкость

Физическая формула

1. с = кв.

где c = емкость конденсатора (фарад)

Емкость специального проводника C = 4πε ₀ R

q-заряд (кулон), V-потенциал (вольт)

2. С = ε0 – A/d

Где c ₀ = емкость плоского конденсатора (воздух является средой)

A = π r ² для круглых пластин

d = расстояние между плитами (м)

ε 0 = Диэлектрическая проницаемость свободного пространства (ф/м)

3. Если между пластинами поместить среду с диэлектрической проницаемостью k, то ее емкость составит

C = K ε 0 A/K(d – t) + t

4. Последовательная комбинация из трех конденсаторов,

(a) Q одинакова для всех конденсаторов

т. е. Q = Q ₁ = Q ₂ = Q ₃

Соотношение зарядов 1 : 1 : 1

(б) Суммарный потенциал, v = v ₁ + v ₂ + v ₃

Отношение потенциалов v ₁ :v ₂ :v ₃

=

V = Q/C ₁ + Q/C ₂ + Q/C ₃

V/Q ₌ 1/C ₁ + 1/C ₂ + 1/C ₃

1/С = 1/С ₁ + 1/С ₂

V ₁ = C ₂ /C ₁ + C ₂ ; V ₂ = (C ₁ /C ₁ + C ₂ )V

1/К = 1/К ₁ + 1/К ₂ + 1/К ₃ + 1/К ₄ +………

(c) Эффективная емкость

С/Н

Для двух конденсаторов

1/К = 1/К ₁ + 1/К ₂

Примечание:- Если все одинаковые конденсаторы, то

С/Н

Параллельная комбинация «3» конденсаторов.

(a) «v» одинаково для всех конденсаторов

т. е. v = v ₁ = v ₂ = v ₃

Соотношение потенциалов 1 : 1 : 1

(b) Общий заряд, Q = Q ₁ + Q ₂ + Q ₃ = C ₁ : C ₂ : C ₃

(c) эффективная мощность, C _P = C ₁ +C ₂ +C ₃

Примечание. Если все конденсаторы идентичны,

Тогда С

1 = С ₂ = С ₃ = С и

C _P 3C, C _P nC [для конденсатора n]

5. Энергия, запасенная в конденсаторе

U = 1/2 CV ² = 1/2 QV = 1/2 Q ² /С

Где C – емкость конденсатора

V – потенциал, Q – заряд, U – запасенная энергия в Дж

6. Если диэлектрик «k» толщиной «t» поместить между пластинами плоского конденсатора, то его емкость составит

C = [ε0 A/(d – t) {1 + 1/t}]

Концептуальные точки:

• Емкость проводника – это отношение заряда (q) на нем к его потенциалу (В). с = д/об
• Единицей емкости является кулон/вольт или фарад.
• Емкость проводника равна одной фараде, если к проводнику добавить заряд в 1 кулон, чтобы повысить его потенциал на 1 вольт.

Следуйте NCERT Solutions для класса 12 Physics , подготовленным экспертным факультетом физики Wallah. Студенты также могут получить важные вопросы для 12 класса CBSE по физике .

Часто задаваемые вопросы (FAQ)

Q1. Какая емкость для 12 класса?

Ответ. Емкость (C) конденсатора определяется как отношение заряда (Q) к разности потенциалов (V), приложенной ко всем проводникам, т. е. C = Q / V. Единицей измерения емкости в системе СИ является фарад (Ф).

Q2. Что такое единица измерения емкости в СИ?

Ответ. Единицей измерения емкости в системе СИ является фарад.

Q3. Какова формула конденсатора?

Ответ. Основное уравнение для расчета конденсатора: C = εA/d. В этом уравнении C — емкость; ε – диэлектрическая проницаемость, показатель того, насколько хорошо диэлектрический материал удерживает электрическое поле; A — площадь параллельной пластины, d — расстояние между двумя проводящими пластинами.

Q4. Какие два типа конденсаторов существуют?

Ответ . Конденсаторы делятся на две механические группы: постоянные конденсаторы с постоянными и переменные конденсаторы с переменными (подстроечными) или регулируемыми (перестраиваемыми) значениями емкости. Наиболее важной группой является фиксированный конденсатор.

В5. Где используются конденсаторы?

Ответ. Конденсаторы очень популярны во многих системах, таких как силовые цепи, электронные схемы и блоки питания. Конденсатор называют Большой тройкой пассивных компонентов, а резисторы катушек — основы электрических цепей.

Q6.