Формула нахождения q в физике. Основные законы и формулы
ОПРЕДЕЛЕНИЕ
Электрический заряд – это первичное понятие, что означает, его нельзя определить при помощи других еще более простых понятий, можно только описать его свойства. Электрический заряд определяет способность тел к электрическому взаимодействию.
Фундаментальным свойством электрического заряда является существование двух видов зарядов: положительных и отрицательных. Заряды, имеющие один знак, отталкиваются. Взаимодействие зарядов разного знака определяют как притяжение. Телу можно сообщить заряд любого знака. В макроскопическом теле заряды разных знаков могут взаимно компенсировать друг друга.
Электрический заряд является релятивистски инвариантной величиной. Это значит, что величина заряда не зависит от системы отсчета, не важно, движется заряд (заряженное тело) или покоится.
Электрический заряд тела находят как суммарный заряд его частей.
Разделения электрических зарядов разных знаков можно добиться путем электризации посредством непосредственного контакта тел (например, трением) или без контакта, например посредством электрической индукции.
При соединении заряженного проводника с незаряженным, заряд перераспределяется между обоими телами. Допустим, что одно тело несет отрицательный заряд, его соединяют с незаряженным телом. Электроны заряженного тела под воздействием сил взаимного отталкивания переходят на незаряженное тело. При этом заряд первого тела уменьшается, заряд второго увеличивается, до тех пор, пока не наступит равновесие.
Элементарный заряд
Немецкий физик и физиолог Г. Гельмгольц обратил внимание на то, что заряды, которые переносят ионы при явлении электролиза, являются целыми, кратными некоторой величине, равной Кл. Каждый одновалентный ион переносит такой заряд. Любой двухвалентный ион несет заряд, равный Кл, и так далее. Гельмгольц сделал вывод о том, что заряд Кл является минимальным количеством электричества, которое существует в природе. Данный заряд получил название элементарного заряда.
Каждый одновалентный ион переносит такой заряд. Любой двухвалентный ион несет заряд, равный Кл, и так далее. Гельмгольц сделал вывод о том, что заряд Кл является минимальным количеством электричества, которое существует в природе. Данный заряд получил название элементарного заряда.
Закон сохранения заряда
Закон сохранения заряда является фундаментальным законом природы. Он был установлен на основании обобщения экспериментальных данных. Подтвержден в 1843 г. английским физиком М. Фарадеем.
Формулировка закона: В любой замкнутой системе алгебраическая сумма зарядов – это неизменная величина, и не важно, какие процессы происходят в этой системе:
где N – количество зарядов.
Закон Кулона
На вопрос: С какими силами взаимодействуют неподвижные точечные заряды? Отвечает закон Кулона, который можно записать в виде формулы как:
где – сила, с которой заряд действует на заряд ; – радиус вектор, который проведен от второго заряда к первому; – электрическая постоянная; – диэлектрическая проницаемость вещества в котором находятся заряды. В соответствии с третьим законом Ньютона первый заряд действует на второй с силой равной по модулю и противоположной по направлению силе Обратите внимание, что заряды в формуле (2) точечные.
В соответствии с третьим законом Ньютона первый заряд действует на второй с силой равной по модулю и противоположной по направлению силе Обратите внимание, что заряды в формуле (2) точечные.
Примеры решения задач по теме «Электрический заряд»
ПРИМЕР 1
| Задание | Два одинаковых проводящих шарика находятся на расстоянии, которое много больше, чем размеры самих шариков. Шарики несут заряды разного знака, причем заряд одного из них по модулю в два раза больше, чем другого. Шарики соединили и снова разнесли на прежнее расстояние. Найдите отношение () силы взаимодействия шариков до соединения () к силе их взаимодействия поле соединения (). |
| Решение | До соединения система из двух шариков имела заряд: После соединения каждый шарик имеет заряд равный: После соединения каждый шарик имеет заряд равный:В первом случае сила Кулона по модулю будет равна: Во втором случае имеем: Найдем отношение : |
| Ответ |
ПРИМЕР 2
| Задание |
Тема 1.1 ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ.
Раздел 1 ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
1. Электризация тел. Понятие о величине заряда.
Закон сохранения заряда.
2. Силы взаимодействия между зарядами.
Закон Кулона.
3. Диэлектрическая проницаемость среды.
4. Международная система единиц в электричестве.
1. Электризация тел. Понятие о величине заряда.
Закон сохранения заряда.
Если две поверхности привести в плотное соприкосновение, то возможен переход электронов с одной поверхности на другую, при этом на этих поверхностях появляются электрические заряды.
Это явление называется ЭЛЕКТРИЗАЦИЕЙ. При трении площадь плотного соприкосновения поверхностей увеличивается, увеличивается и величина заряда на поверхности – такое явление называют ЭЛЕКТРИЗАЦИЕЙ ТРЕНИЕМ.
В процессе электризации происходит перераспределение зарядов, в результате которого обе поверхности заряжаются равными по величине, противоположными по знаку зарядами.
Т.к. все электроны имеют одинаковые заряды (отриц.) е = 1,6 10Кл, то для того, чтобы определить величину заряда на поверхности (q), необходимо знать, сколько электронов в избытке или недостатке на поверхности (N) и заряд одного электрона.
В процессе электризации новые заряды не появляются и не исчезают, а только происходит их перераспределение между телами или частями тела, поэтому суммарный заряд замкнутой системы тел остается постоянным, в этом и заключается смысл ЗАКОНА СОХРАНЕНИЯ ЗАРЯДА.
2. Силы взаимодействия между зарядами.
Закон Кулона.
Электрические заряды взаимодействуют между собой, находясь на расстоянии, при этом одноименные заряды отталкиваются, а разноименные – притягиваются.
Впервые выяснил опытным путем отчего зависит сила взаимодействия между зарядами французский ученый Кулон и вывел закон, названный законом КУЛОНА. Закон фундаментальный т.е. основан на опытах. При выводе этого закона Кулон использовал крутильные весы.
3) k – коэффициент, выражающий зависимость от окружающей среды.
Формула закона Кулона.
Сила взаимодействия между двумя неподвижными точечными зарядами прямо пропорциональны произведению величин этих зарядов и обратно пропорциональна квадрату расстояний между ними, и зависит от среды, в которой находятся эти заряды, и направлена вдоль прямой, соединяющей центры этих зарядов.
3. Диэлектрическая проницаемость среды.
Е – диэлектрическая проницаемость среды, зависит от окружающей заряды среды.
Е = 8,85*10 – физическая постоянная, диэлектрическая проницаемость вакуума.
Е – относительная диэлектрическая проницаемость среды, показывает во сколько раз сила взаимодействия между точечными зарядами в вакууме больше чем в данной среде. В вакууме самое сильное взаимодействие между зарядами.
В вакууме самое сильное взаимодействие между зарядами.
4. Международная система единиц в электричестве.
Основной единицей для электричества в системе «СИ» является сила тока в 1А, все остальные единицы измерения являются производными от 1Ампера.
1Кл – количество электрического заряда, переносимого заряженными частицами через поперечное сечение проводника при силе тока в 1А за 1с.
q=N;
Тема 1.2 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
1. Электрическое поле – как особый вид материи.
6. Связь разности потенциалов с напряженностью электрического поля.
1. Электрическое поле – как особый вид материи.
В природе как вид материи существует электромагнитное поле. В разных случаях электромагнитное поле проявляет себя по – разному, так например около неподвижных зарядов проявляет себя только электрическое поле, которое называют электростатическим. Около подвижных зарядов можно обнаружить как электрическое, так и магнитное поля, которые в совокупности представляют ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ.
Рассмотрим свойства электростатических полей:
1) Электростатическое поле создается неподвижными зарядами, обнаружить такие поля можно
с помощью пробных зарядов (небольшой по величине положительный заряд), т.к. только на них электрическое поле оказывает силовое действие, которое подчиняется закону Кулона.
2. Напряженность электрического поля.
Эл.поле как вид материи обладает энергией, массой, распространяется в пространстве с конечной скоростью и теоретических границ не имеет.
Практически считается, что поля нет если оно не оказывает заметного действия на пробные заряды.
Так как обнаружить поле можно с помощью силового действия на пробные заряды, то основной характеристикой электрического поля является напряженность.
Если в одну и ту же точку электрического поля вносить разные по величине пробные заряды, то между действующей силой и величиной пробного заряда прямая пропорциональная зависимость.
Коэффициентом пропорциональности между действующей силой и величиной заряда является напряженность Е.
Е = -формула расчета напряженности электрического поля, если q = 1 Кл, то | E | = | F |
Напряженность является силовой характеристикой точек электрического поля, т.к. она численно равна силе, действующей на заряд в 1 Кл в данной точке электрического поля.
Напряженность – величина векторная, вектор напряженности по направлению совпадает с вектором силы, действующей на положительный заряд в данной точке электрического поля.
3. Линии напряженности электрического поля. Однородное электрическое поле.
Для того, чтобы наглядно можно было изображать электрическое поле, т.е. графически, используют линии напряженности электрического поля. Это такие линии, иначе называемые силовыми линиями, касательные к которым по направлению совпадают с векторами напряженности в точках электрического поля через которые эти линии проходят,
Линии напряженности обладают следующими свойствами:
1) Начинаются на полож. зарядах, заканчиваются – на отрицательных, или начинаются на положител. зарядах и уходят в бесконечность, или приходят из бесконечности и заканчиваются на положительных зарядах..
зарядах и уходят в бесконечность, или приходят из бесконечности и заканчиваются на положительных зарядах..
2) Эти линии непрерывны и нигде не пересекаются.
3) Густота линий (кол-во линий на единицу площади поверхности) и напряженность электрического поля находятся в прямой и пропорциональной зависимости.
В однородном электрическом поле напряженность во всех точках поля одинакова, графически такие поля изображаются параллельными линиями на равном расстоянии друг от друга. Такое поле можно получить между двумя параллельными плоскими заряженными пластинами на маленьком расстоянии друг от друга.
4. Работа по перемещению заряда в электрическом поле.
Поместим в однородное электрическое поле электрический заряд. Со стороны поля на заряд будут действовать силы. Если заряд перемещать, то может совершаться работа.
Совершенная работа на участках:
А = q E d – формула расчета работы по перемещению заряда в электрическом поле.
Вывод: Работа по перемещению заряда в электрическом поле от формы траектории не зависит, а она зависит от величины перемещаемого заряда (q) , напряженности поля (Е), а также от выбора начальной и конечной точек перемещения (d).
Если заряд в электрическом поле перемещать по замкнутому контуру, то совершаемая работа будет равна 0. Такие поля называются потенциальными полями. Тела в таких полях обладают потенциальной энергией, т.о. электрический заряд в любой точке электрического поля обладает энергией и совершаемая работа в электрическом поле равна разности потенциальных энергий заряда в начальной и конечной точках перемещения.
5. Потенциал. Разность потенциалов. Напряжение.
Если в данную точку электрического поля помещать разные по величине заряды, то потенциальная энергия заряда и его величина находятся в прямой пропорциональной зависимости.
-(фи) потенциал точки электрического поля
примем
Потенциал является энергетической характеристикой точек электрического поля, т.к. он численно равен потенциальной энергии заряда в 1 Кл в данной точке электрического поля.
На равных расстояниях от точечного заряда потенциалы точек поля одинаковы. Эти точки образуют поверхность равного потенциала, и такие поверхности называются эквипотенциальными поверхностями. На плоскости это окружности, в пространстве – это сферы.
На плоскости это окружности, в пространстве – это сферы.
Напряжение
Формулы расчета работы по перемещению заряда в электрическом поле.
1В – напряжение между точками электрического поля при перемещении в которых заряда в 1Кл совершается работа в 1 Дж.
– формула, устанавливающая связь между напряженностью электрического поля, напряжением и разностью потенциалов.
Напряженность численно равна напряжению или разности потенциалов между двумя точками поля взятыми вдоль одной силовой линии на расстоянии 1м. Знак (-) означает, что вектор напряженности всегда направлен в сторону точек поля с уменьшающимся потенциалом.
Закон Кулона:
где F – сила взаимодействия двух точечных зарядов q 1 и q 2 ; r – расстояние между зарядами; – диэлектрическая проницаемость среды; 0 – электрическая постоянная
.
Закон сохранения заряда:
,
где
– алгебраическая сумма зарядов, входящих
в изолированную систему;n
– число зарядов.
Напряженность и потенциал электростатического поля:
;
, или
,
где – сила, действующая на точечный положительный зарядq 0 , помещенный в данную точку поля; П – потенциальная энергия заряда; А ∞ – работа, затраченная на перемещение заряда q 0 из данной точки поля в бесконечность.
Поток вектора напряженности электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле:
,
или
,
где – угол между вектором напряженности и нормальюк элементу поверхности;dS – площадь элемента поверхности; E n – проекция вектора напряженности на нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
.
Поток вектора напряженности через замкнутую поверхность –
(интегрирование ведется по всей поверхности).
Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –
,
где – алгебраическая
сумма зарядов, заключенных внутри
замкнутой поверхности; n
– число зарядов.
Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –
.
Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:
внутри сферы (r R) Е=0;
на поверхности сферы (r=R)
;
вне сферы (r R)
.
Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой
В случае двух электрических полей с напряженностями иабсолютное значение вектора напряженности составляет
где – угол между векторами и.
Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –
,
где – линейная плотность заряда.
Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):
.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –
,
где – поверхностная плотность заряда.
Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:
.
Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –
.
Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.
Электрическое смещение связано с напряженностьюэлектрического поля соотношением
,
которое справедливо только для изотропных диэлектриков.
Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:
.
Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:
.
Потенциал электрического поля в бесконечности условно принят равным нулю.
Потенциал электрического поля, создаваемый точечным зарядом q на
расстоянии r от заряда, –
.
Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков:
внутри сферы (r R)
;
на поверхности сферы (r = R)
;
вне сферы (r R)
.
Во всех формулах, приведенных для потенциала заряженной сферы, есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
Потенциал электрического поля, образуемого системой n точечных зарядов в данной точке в соответствии с принципом суперпозиции электрических полей, равен алгебраической сумме потенциалов
, создаваемых отдельными точечными зарядами
:
.
Энергия W взаимодействия системы точечных зарядов
определяется работой, которую эта система может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой
,
где – потенциал поля, создаваемый всеми (n-1) зарядами (за исключением i-го) в точке, где находится заряд .
Потенциал связан с напряженностью электрического поля соотношением
.
В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой
,
или в скалярной форме
.
В случае однородного поля, т.е. поля, напряженность которого в каждой его точке одинакова как по абсолютному значению, так и по направлению, –
,
где 1 и 2 – потенциалы точек двух эквипотенциальных поверхностей; d – расстояние между этими поверхностями вдоль электрической силовой линии.
Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал 1 , в другую, имеющую потенциал 2 , равна
,
или
,
где E – проекция вектора на направление перемещения;
– перемещение.
В случае однородного поля последняя формула принимает вид
,
где – перемещение; – угол между направлениями вектора и перемеще-ния.
Диполь есть система двух точечных (равных по абсолютному значению и противоположных по знаку) зарядов, находящихся на некотором расстоянии друг от друга.
Электрический момент диполя есть вектор, направленный от отрицательного заряда к положительному, равный произведению зарядана вектор, проведенный от отрицательного заряда к положительному, и называемый плечом диполя, т.е.
.
Диполь называется точечным, если его плечо намного меньше расстоянияr от центра диполя до точки, в которой нас интересует действие диполя ( r), см. рис. 1.
Напряженность поля точечного диполя:
,
где р – электрический момент диполя; r – абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; – угол между радиус-вектором и плечомдиполя.
Напряженность поля точечного диполя в точке, лежащей на оси диполя
(=0), находится по формуле
;
в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины
, – по формуле
.
Потенциал поля точечного диполя в точке, лежащей на оси диполя (=0), составляет
,
а в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины
, –
Напряженность и потенциал неточечного диполя определяются так же как и для системы зарядов.
Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е, –
,
или
,
где – угол между направлениями векторов и.
Электроемкость уединенного проводника или конденсатора –
,
где q – заряд, сообщенный проводнику; - изменение потенциала, вызванное этим зарядом.
Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью , –
.
Если сфера полая и заполнена диэлектриком, то ее электроемкость при этом не изменяется.
Электроемкость плоского конденсатора:
,
где
S
– площадь каждой пластины конденсатора;
d
– расстояние между пластинами;
– диэлектрическая проницаемость
диэлектрика, заполняющего пространство
между пластинами.
Электроемкость плоского конденсатора, заполненного n слоями диэлектрика толщиной d i и диэлектрической проницаемостью i каждый (слоистый конденсатор), составляет
.
Электроемкость сферического конденсатора (две концентрические сферы радиусом R 1 и R 2 , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ) находится так:
.
Электроемкость последовательно соединенных конденсаторов составляет:
в общем случае –
,
где n – число конденсаторов;
в случае двух конденсаторов –
;
.
Электроемкость параллельно соединенных конденсаторов определяется следующим образом:
в общем случае –
С=С 1 +С 2 +…+С n ;
в случае двух конденсаторов –
С= С 1 +С 2 ;
в случае n одинаковых конденсаторов с электроемкостью С 1 каждый –
Энергия заряженного проводника выражается через заряд q, потенциал и электроемкость С проводника следующим образом:
.
Энергия заряженного конденсатора –
,
где q – заряд конденсатора; С – электроемкость конденсатора; U – разность потенциалов на его пластинах.
основные понятия по теме в физике, формулы с пояснениями, законы
Содержание:
-
Электростатика как раздел электродинамики
- Основные понятия по теме в физике
- Закон Кулона
- Электрический заряд и его свойства
- Формулы с пояснениями, вывод
Содержание
-
Электростатика как раздел электродинамики
- Основные понятия по теме в физике
- Закон Кулона
- Электрический заряд и его свойства
- Формулы с пояснениями, вывод
Электростатика как раздел электродинамики
ОпределениеЭлектростатика является разделом учения об электричестве, задачей которого является исследование неподвижных электрических зарядов.
С давних времен известно, что определенные материалы – такие, как янтарь, – могут притягивать легкие предметы (к примеру, пух, пыль, кусочки бумаги). Возникновение электростатических явлений, главным образом, обусловлено взаимодействием электрических зарядов друг с другом. Сила такого взаимодействия описана законом Кулона.
Несмотря на то, что электростатические силы кажутся слабыми, в некоторых случаях они превосходят силу гравитации. Например, протон и электрон в атоме водорода взаимодействуют с силой, которая на 36 порядков больше действующей между ними гравитационной силы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Существует масса примеров электростатических явлений, включая простое притяжение воздушного шарика к шерстяному свитеру, притяжение бумаги и тонера в лазерных принтерах, спонтанное воспламенение зернохранилища как результат электризации зерна. {,}=const\)
{,}=const\)
Закон Кулона
Закон Кулона позволяет количественно описать процесс, при котором взаимодействуют заряженные тела. Это фундаментальный закон – утверждение было доказано экспериментальным путем, а не является следствием природных закономерностей.
Закон Кулона справедлив в том случае, когда точечные заряды неподвижны и находятся в вакууме. Понятие точечного заряда является условным, так как подобные частицы отсутствуют в действительности. Однако точечными можно считать такие заряды, размеры которых существенно меньше, чем расстояние между ними.
Сила, с которой взаимодействуют заряды в воздухе, практически не отличается от силы их взаимодействия в вакууме. В первом случае сила слабее менее, чем на одну тысячную. Электрический заряд является физической величиной и характеризует способность частиц и тел вступать в электромагнитные силовые взаимодействия.
ПримечаниеПервым закон взаимодействия зарядов, находящихся в состоянии покоя, открыл французский физик Ш.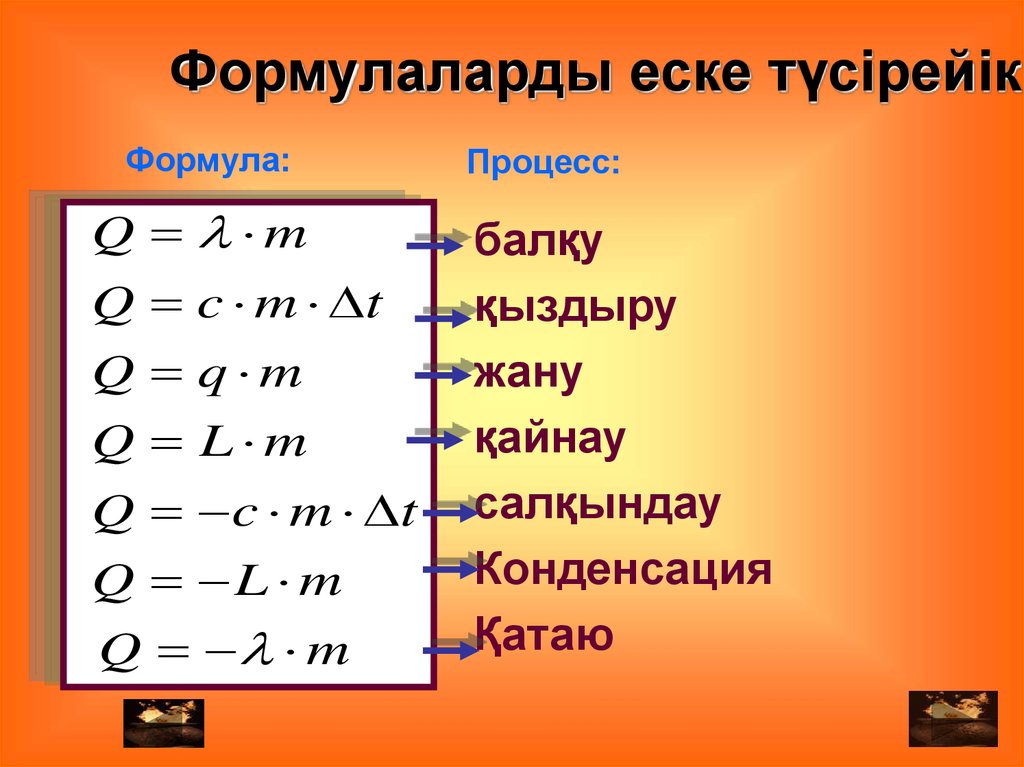 9\) — коэффициент пропорциональности в законе Кулона.
9\) — коэффициент пропорциональности в законе Кулона.
Согласно третьему закона Ньютона:
\(\vec{F}_{12}=\vec{F}_{21}\)
Данные силы взаимодействия представляют собой силы отталкивания в том случае, когда заряды имеют одинаковые знаки, и являются силами притяжения при разных знаках зарядов. Для обозначения электрического заряда, как правило, используют буквы q или Q.
Исходя из совокупности данных, полученных экспериментальным путем, можно сделать следующие выводы:
- Электрические заряды бывают двух типов, которые условно называют отрицательными и положительными.
- Заряды обладают способностью передаваться (к примеру, в процессе непосредственного контакта) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемым параметром данного тела. Одно и то же тело при разных условиях может обладать неодинаковым зарядом.
- Заряды с одинаковым знаком отталкиваются, а с разными – притягиваются. Таким образом проявляется принципиальная разница между электромагнитными и гравитационными силами.
 Гравитацией всегда является сила притяжения.
Гравитацией всегда является сила притяжения.
Взаимодействие неподвижных электрических зарядов является электростатическим или кулоновским взаимодействием. Электростатика является отдельным разделом электродинамики, задача которого заключается в изучении кулоновского взаимодействия.
Закон Кулона применим в случае точечных заряженных тел. На практике закономерность выполняется в том случае, когда размеры заряженных тел много меньше, чем расстояние между ними. Условия выполнения закона Кулона:
- точечность зарядов;
- неподвижность зарядов;
- взаимодействие зарядов в вакууме.
В международной системе СИ заряд измеряют в Кулонах (Кл).
ОпределениеКулон – заряд, который проходит за 1 секунду через поперечное сечение проводника при силе тока 1 А.
Единица силы тока (Ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.
Электрический заряд и его свойства
Электрическим зарядом называют физическую величину, которая характеризует свойство частиц или тел вступать в электромагнитные взаимодействия. Заряд обозначают, как q или Q, и измеряют в Кл. Свободный заряд в 1 Кл представляет собой гигантскую величину заряда, которую практически невозможно встретить в природе. Обычно, в процессе изучения, можно встретить заряды, исчисляемые в микрокулонах, нанокулонах, пикокулонах. Свойства электрического заряда:
Заряд обозначают, как q или Q, и измеряют в Кл. Свободный заряд в 1 Кл представляет собой гигантскую величину заряда, которую практически невозможно встретить в природе. Обычно, в процессе изучения, можно встретить заряды, исчисляемые в микрокулонах, нанокулонах, пикокулонах. Свойства электрического заряда:
- электрический заряд является видом материи;
- на электрический заряд не влияет движение частицы и ее скорость;
- заряды обладают способностью перемещаться (например, в процессе непосредственного контакта) от одного тела к другому, не являются неотъемлемой характеристикой тела;
- электрические заряды бывают отрицательными и положительными, что соответствует их условным типам;
- заряды взаимодействуют друг с другом, при этом одноименные заряды притягиваются, а разноименные – отталкиваются;
- силы взаимодействия зарядов представляют собой центральные силы, то есть лежат на одной прямой, которая соединяет центры этих зарядов;
- минимально возможный по модулю заряд называют элементарным, \(e= 1,6*10^{-19}.
 {,}=\frac{q_{1}+q_{2}}{2}\)
{,}=\frac{q_{1}+q_{2}}{2}\)Современная наука полагает, что носителями зарядов являются элементарные частицы. Известно, что все тела состоят из атомов, которые включают в себя протоны с положительным зарядом, электроны с отрицательным зарядом и нейтральный частицы, называемые нейтронами. Из протонов и нейтронов состоят атомные ядра. Электронная оболочка атомов образована электронами.
Протон и электрон обладают одинаковыми по модулю электрическими зарядами, которые равны элементарному заряду е. Если атом нейтральный, то количество протонов в ядре соответствует числу электронов в оболочке. Данное число называют атомным номером.
Атом рассматриваемого вещества может лишиться одного или нескольких электронов либо приобрести лишний электрон. В этом случае нейтральный атом трансформируется в положительно или отрицательно заряженный ион.
Следует отметить, что ядро атома состоит из положительных протонов, в связи с этим их количество может увеличиться или уменьшиться только в процессе ядерной реакции.
 Известно, что электризация тел не сопровождается ядерными реакциями. Таким образом, при любых электрических явлениях количество протонов остается стабильным, может измениться лишь число электронов.
Известно, что электризация тел не сопровождается ядерными реакциями. Таким образом, при любых электрических явлениях количество протонов остается стабильным, может измениться лишь число электронов.Можно сообщить телу отрицательный заряд, то есть передать ему лишние электроны. Сообщение телу положительного заряда подразумевает отнимание электронов, а не добавление протонов. Передача заряда от одного тела к другому осуществляется порциями, которые включают в себя целое число электронов.
В определенных случаях при решении задач можно встретить примеры распределения электрического заряда по какому-либо телу. Описать такое распределение можно с помощью специальных величин.
Линейная плотность заряда необходима, чтобы описать, каким образом заряд распределен по нити. Величина измеряется в Кл/м. Формула линейной плотности заряда:
\(\lambda =\frac{q}{L}\)
где L – является длиной нити.
Поверхностная плотность заряда позволяет определить, как заряд распределен по поверхности тела.
 Величина измеряется в кулонах на квадратный метр. Формула поверхностной плотности заряда:
Величина измеряется в кулонах на квадратный метр. Формула поверхностной плотности заряда:\(\sigma =\frac{q}{S}\)
где S – площадь поверхности тела.
Объемную плотность заряда целесообразно применять для описания распределения заряда по объему тела. Величина измеряется в кулонах на м³. Формула объемной плотности заряда:
\(\rho =\frac{q}{V}\)
где V – это объем тела.
Формулы с пояснениями, вывод
В случае электрических зарядов действует принцип суперпозиции: результирующая сила, действующая на определенный заряд \(q_{1}\) со стороны нескольких зарядов \(q_{2}… q_{n},\) равна геометрической сумме, то есть векторной сумме сил \(F_{12}+….F_{1n}\), которые действуют на данный заряд со стороны каждого из зарядов:
\(\vec{R}=\vec{F_{12}}+…+\vec{F_{1n}}\)
Заряженные частицы взаимодействуют друг с другом с конечной скоростью с помощью электрического поля. Данное утверждение является теорией близкодействия электрических зарядов.
 {2}}\)
{2}}\)Принцип суперпозиции электрических полей состоит в том, что при создании заряженными частицами в определенной точке пространства электрических полей с напряженностями \(E_{1}, E_{2},…, E_{n}\), результирующая напряженность электрического поля в данной точке равна векторной сумме отдельных напряженностей:
\(\vec{E}=\vec{E_{1}}+…+\vec{E_{n}}\)
Заряд q в однородном электрическом поле напряженности Е обладает потенциальной энергией:
\(\vec{E}:W=qEd\)
где d является расстоянием до плоскости с нулевой потенциальной энергией.
ОпределениеПотенциал электростатического поля в точке является отношением потенциальной энергии заряда в поле, к этому заряду, учитывая знак заряда.
Формула для расчета потенциала электростатического поля:
\(\varphi =\frac{W}{q}=Ed\)
Потенциалом электростатического поля также называют работу, которая выполняется в процессе перемещения единичного положительного заряда из рассматриваемой точки в бесконечность.

Напряжение соответствует разности потенциалов между точками и определяется, как отношение работы поля при перемещении заряда из начального положения в конечное, к данному заряду, учитывая знак заряда:
\(U=\varphi _{1}-\varphi _{2}=\frac{A}{q}\)
В числовом выражении, но не по размерности, данная величина представляет собой работу, которую выполняет поле, перемещая единичный положительный заряд из одной точки в другую.
Однородное поле характеризуется наличием связи между разностью потенциалов и напряженностью:
\(E=\frac{U}{\Delta d}\)
где U является разностью потенциалов между точками, которые связывает вектор перемещения \(\Delta d\), совпадающий по направлению с вектором Е.
Электроемкостью пары проводников называют отношение заряда Q, который соответствует одному из проводников, к разности потенциалов U между этим проводником и соседним:
\(C=\frac{Q}{U}\)
ОпределениеКонденсатор – система из пары проводников, называемых обкладками конденсатора, которые разделены диэлектрическим слоем с толщиной меньшей, чем размеры обкладок.
 {2}}{2}\)
{2}}{2}\)В современной технике практикуется использование электростатических эффектов. Например, чтобы качественно очистить воздух от частиц гари и пыли с помощью специальных электрических фильтров, равномерно распределять красящие составы благодаря краскопультам, распечатывать материалы в офисных установках (таких, как «Ксерокс»), производить наждачную бумагу.
Электростатическую защиту оснащают при помощи экранирующих проводников, что позволяет оградить от электрических полей электроизмерительные чувствительные устройства.
Конструкции в виде металлических сеток защищают любые огнеопасные объекты, включая склады с порохом, от внезапного удара молнии. Характеристика избыточных электрических зарядов определяется на поверхности проводников, а затем широко используется в приборе генератора Ван-дер-Граафа, который представляет собой устройство для получения сверхсильных электрических и магнитных полей.
Электростатика, как научная область, мало изучена. Ученые длительное время избегали данной темы из-за ее ограниченного применения в технике.
 Активное использование полимеров в промышленных масштабах послужило причиной поиска новых решений, позволяющих нейтрализовать постоянные и статические заряды.
Активное использование полимеров в промышленных масштабах послужило причиной поиска новых решений, позволяющих нейтрализовать постоянные и статические заряды.Сегодня электростатика отличается многогранными и многочисленными сферами применения. Электростатические явления используют в технике и медицине, что делает направление перспективным для дальнейшего развития.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Общая физика II
Помните, В ОТЛИЧИИ заряды притягиваются,
или
и ПОДОБНЫЕ заряды отталкивают,
или
Что определяет величину этой электрической силы F?
Сила F прямо пропорциональна зарядам Q и д,
Ф Вопрос Сила F обратно пропорциональна квадрат расстояние р между зарядами,
Ф 1/р 2
Ф 1/р 2
Ф 1/р 2
Мы можем объединить их как
Ф Q к/р 2 Пока пропорциональности ар хорош для качественных дискуссий и сравнений, уравнения много легче использовать для расчетов.
 Мы можем изменить это на уравнение с константа
пропорциональность , к.
Мы можем изменить это на уравнение с константа
пропорциональность , к. F = kQq/r 2 Эта константа пропорциональности k зависит от единиц мы используем. Если мы измеряем силу F в ньютонах (Н), расстояние r в метрах (м), а заряжает Q и q в кулонах (Кл), то k имеет значение из
к = 9 х 10 9 Н м 2 /С 2 Теперь мы должны спросить, что такое кулон заряда, в любом случае?
Электрический заряд электрона или протона обозначен e и равен . . .
Закон Кулона описывает силу F между двумя электрическими заряды, Q и q, расстояние r друг от друга,
Какова сила между двумя положительными зарядами, 1 С и 2 С, когда их разделяет расстояние 1 м?
Помните, сила – это вектор .
 Закон Кулона позволяет нам
рассчитать величину электрической силы, но мы должны
еще имейте ввиду что сила это вектор!
Закон Кулона позволяет нам
рассчитать величину электрической силы, но мы должны
еще имейте ввиду что сила это вектор! Пример Кулона Закон Мы также когда-нибудь запишем эту «постоянную Кулона» как
, где “эпсилон-ноль”
и известен как «диэлектрическая проницаемость свободного пространства». Что имя звучит более зловеще, чем нужно. Это просто еще одна форма «постоянной Кулона» — и ничего больше! Там основные ситуации или основные уравнения, в которых мы получаем фактор
, что тогда удобнее записать как
Возможно, вы смотрели на Cavendish Balance, когда Вы говорили о гравитации. Кавендиш использовал очень деликатный весы для измерения невероятно малых сил. Кулон при измерении электрические силы, имели большие силы для работы.
 Вот
эскиз весов, которые он использовал для измерения электрических сил и
определить один над r-квадрат характеристикой электрического
сила:
Вот
эскиз весов, которые он использовал для измерения электрических сил и
определить один над r-квадрат характеристикой электрического
сила:
(с) Дуг Дэвис, 2002 г.; все права защищеныИзоляторы и дирижеры
Электрическое поле
Вернуться к главе 33 ТОС Общая физика II
Закон Кулона говорит нам о силе между двумя точками обвинения. Наш вариант сообщает нам Электрическое поле из-за одноточечный заряд .
 Что нам делать, если у нас есть непрерывных
распределение заряда? Мы можем суммировать электрическое поле
вызвано каждой крошечной, бесконечно малой частью заряда
распределение. Это означает интеграл по распределению заряда:
Что нам делать, если у нас есть непрерывных
распределение заряда? Мы можем суммировать электрическое поле
вызвано каждой крошечной, бесконечно малой частью заряда
распределение. Это означает интеграл по распределению заряда:Для одноточечного заряда Q мы имели
, где r — расстояние от заряда Q. Помните, что E — это всего лишь величина электрического поля; мы должны позаботиться о его вектор природа отдельно! Это важно! Теперь у нас есть распределение заряда, и мы должны заменить Q на dQ и E на dE — и позаботьтесь о направлении E .
р, расстояние от крошечного, элементарного, бесконечно малого заряда dQ к рассматриваемому вопросу, является функцией того, где этот заряд dQ является. И что значит «интегрировать по заряду dQ»? Мы знать, как интегрировать по переменной, такой как dx, или по плоскости, такой как dA = dx dy или dA = 2 r dr или dA = r d dr или объем вида dV = dx dy dz.
 Так что нам нужно будет изменить с этого символического заряда dQ на плотность заряда
умноженный на некоторый пространственный дифференциал,
Так что нам нужно будет изменить с этого символического заряда dQ на плотность заряда
умноженный на некоторый пространственный дифференциал,dQ = дх дQ = дА
dQ = дВ
См. пример 23.7 в учебнике Серуэя и Бейхнера (стр. 724): Стержень длиной имеет равномерный заряд на единицу длины и полный заряд Q. Вычислить электрическое поле в точке P вдоль оси стержня на расстоянии d от одного конца.
Чему равно электрическое поле в точке P из-за маленького кусочка бесплатно Q находится в позиции x, как показано на рисунке?
Э = к Q / х 2 Проведем интегрирование от x = d до x = d + так нам нужно изменить это небольшое количество заряда Q на малую длину x,
Q = х Е = к (х) / х 2
где
= Q / dE = k ( dx) / x 2
dE = k (dx / х 2 )
Как насчет других геометрий?
Посмотрите на Пример 23.
 8 на странице 724 текста Серуэя и Бейхнера.
Найти электрическое поле, создаваемое кольцом с зарядом : Кольцо радиусом a
имеет однородную плотность заряда с полным зарядом Q. Рассчитайте электрическую
поле по оси кольца в точке P, на расстоянии x от
центр кольца.
8 на странице 724 текста Серуэя и Бейхнера.
Найти электрическое поле, создаваемое кольцом с зарядом : Кольцо радиусом a
имеет однородную плотность заряда с полным зарядом Q. Рассчитайте электрическую
поле по оси кольца в точке P, на расстоянии x от
центр кольца.Плотность заряда
= Q / (2 а) Помните, наше уравнение для электрического поля относится к величина электрического поля. Рассмотрим небольшой кусочек зарядить dq, как показано на схеме. Поскольку этот заряд dq равен там в точке P существует электрическое поле dE в направлении показано. компонента dEx этого электрического поля вдоль направление оси перпендикулярно плоскости кольца
dE x = dE cos dE x = dE (x/r)
dE x = [k dq/r 2 ] (x/r)
dE х = [k dq/r 3 ] х
dE x = [k x dq/r 3 ]
dE x = [k x/r 3 ] dq
Обратите внимание, что в этой геометрии после указания радиуса кольца a и позицию x, полностью определяющую r.
 r и x делают не изменяют как
интегрируем по dq.
r и x делают не изменяют как
интегрируем по dq.
[[ Помните, что SQRT() означает «квадратный корень из ()», потому что это проще чтобы я печатал. ]]r = SQRT(a 2 + x 2 ) r 3 = (a 2 + x 2 ) 3/2
1/r 3 = 1/(a 2 9006 0 + х 2 ) 3/2
Помните, что x и a являются , а не переменными.
Как насчет компонента E, который перпендикулярен к это направление? По симметрии этот компонент равен нулю . Из диаграммы видно, что для каждого элемента заряда dq, есть еще один элемент заряда dq на напротив сторона кольца, создающая электрическое поле, которое просто отменяет первый – то есть их компоненты перпендикулярно оси симметрии как раз отменяет .
 Обратите внимание, что их компоненты по оси не отменяют
ибо они лежат в одном и том же направлении. Диаграммы очень
важный. Не начинайте писать уравнения, пока не сделаете
хорошие, четкие, полные схемы!
Обратите внимание, что их компоненты по оси не отменяют
ибо они лежат в одном и том же направлении. Диаграммы очень
важный. Не начинайте писать уравнения, пока не сделаете
хорошие, четкие, полные схемы!Теперь, когда мы рассмотрели электрическое поле из-за кольцо г заряда, мы можем опираться на него, расширять наши идеи и смотреть на электрические поле из-за диска заряда. См. пример 23.9 на стр. 725 учебника Серуэя и Бейхнера.
Диск радиусом R имеет равномерный заряд на единицу площади. Вычислите электрическое поле в точке P, лежащей вдоль центральной оси диска и на расстоянии x от его центра.
Рассмотрим кольцо заряда, как показано здесь. Кольцо имеет радиусом r и толщиной dr и несет заряд dq. Но этот заряд dq как раз пропорционален площади,
дк = дА дкв = [С др]
дк = [ (2 г) др ]
дкв = 2 р др
Вспомните, что мы только что сделали в предыдущем примере.


 Гравитацией всегда является сила притяжения.
Гравитацией всегда является сила притяжения. {,}=\frac{q_{1}+q_{2}}{2}\)
{,}=\frac{q_{1}+q_{2}}{2}\) Известно, что электризация тел не сопровождается ядерными реакциями. Таким образом, при любых электрических явлениях количество протонов остается стабильным, может измениться лишь число электронов.
Известно, что электризация тел не сопровождается ядерными реакциями. Таким образом, при любых электрических явлениях количество протонов остается стабильным, может измениться лишь число электронов. Величина измеряется в кулонах на квадратный метр. Формула поверхностной плотности заряда:
Величина измеряется в кулонах на квадратный метр. Формула поверхностной плотности заряда: {2}}\)
{2}}\)
 {2}}{2}\)
{2}}{2}\) Активное использование полимеров в промышленных масштабах послужило причиной поиска новых решений, позволяющих нейтрализовать постоянные и статические заряды.
Активное использование полимеров в промышленных масштабах послужило причиной поиска новых решений, позволяющих нейтрализовать постоянные и статические заряды.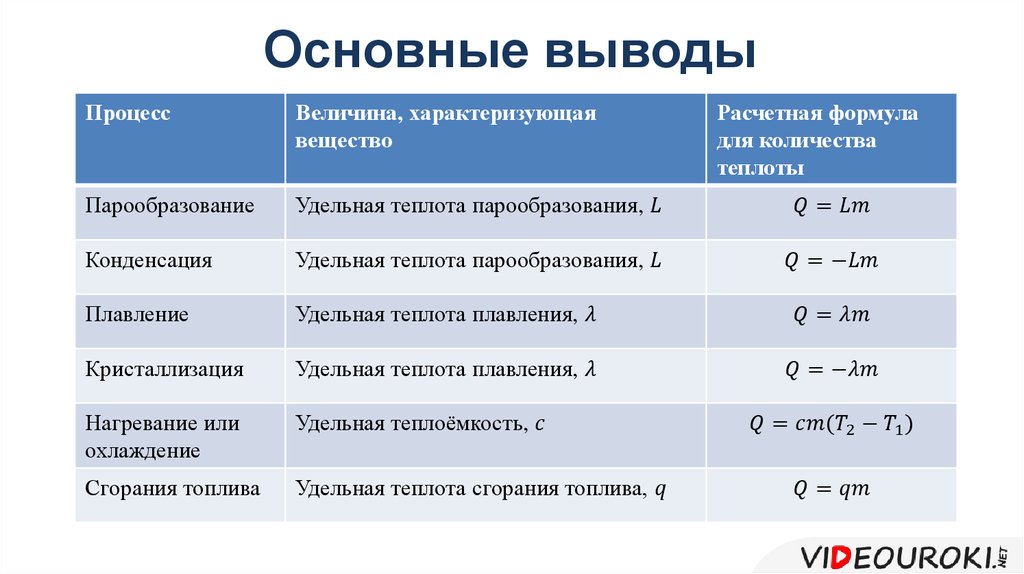 Мы можем изменить это на уравнение с константа
пропорциональность , к.
Мы можем изменить это на уравнение с константа
пропорциональность , к.  Закон Кулона позволяет нам
рассчитать величину электрической силы, но мы должны
еще имейте ввиду что сила это вектор!
Закон Кулона позволяет нам
рассчитать величину электрической силы, но мы должны
еще имейте ввиду что сила это вектор!  Вот
эскиз весов, которые он использовал для измерения электрических сил и
определить один над r-квадрат характеристикой электрического
сила:
Вот
эскиз весов, которые он использовал для измерения электрических сил и
определить один над r-квадрат характеристикой электрического
сила: Что нам делать, если у нас есть непрерывных
распределение заряда? Мы можем суммировать электрическое поле
вызвано каждой крошечной, бесконечно малой частью заряда
распределение. Это означает интеграл по распределению заряда:
Что нам делать, если у нас есть непрерывных
распределение заряда? Мы можем суммировать электрическое поле
вызвано каждой крошечной, бесконечно малой частью заряда
распределение. Это означает интеграл по распределению заряда: Так что нам нужно будет изменить с этого символического заряда dQ на плотность заряда
умноженный на некоторый пространственный дифференциал,
Так что нам нужно будет изменить с этого символического заряда dQ на плотность заряда
умноженный на некоторый пространственный дифференциал, 8 на странице 724 текста Серуэя и Бейхнера.
Найти электрическое поле, создаваемое кольцом с зарядом : Кольцо радиусом a
имеет однородную плотность заряда с полным зарядом Q. Рассчитайте электрическую
поле по оси кольца в точке P, на расстоянии x от
центр кольца.
8 на странице 724 текста Серуэя и Бейхнера.
Найти электрическое поле, создаваемое кольцом с зарядом : Кольцо радиусом a
имеет однородную плотность заряда с полным зарядом Q. Рассчитайте электрическую
поле по оси кольца в точке P, на расстоянии x от
центр кольца. r и x делают не изменяют как
интегрируем по dq.
r и x делают не изменяют как
интегрируем по dq.  Обратите внимание, что их компоненты по оси не отменяют
ибо они лежат в одном и том же направлении. Диаграммы очень
важный. Не начинайте писать уравнения, пока не сделаете
хорошие, четкие, полные схемы!
Обратите внимание, что их компоненты по оси не отменяют
ибо они лежат в одном и том же направлении. Диаграммы очень
важный. Не начинайте писать уравнения, пока не сделаете
хорошие, четкие, полные схемы!