Решение задач по физике №11. Физические основы механики. Кинематика.
1.51. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением аr = 5 см/с2. Через какое время t после начала движения нормальное ускорение аn точки будет: а) равно тангенциальному; б) вдвое больше тангенциального? Решение:
1.52. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аr. Найти тангенциалъное ускорение аr точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки V = 79,2 см/с.
Решение:
1.53. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аr . Найти нормальное ускорение аn точки через время t = 20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 10 см/с.
Решение:
1.55. Колесо радиусом R = 10 см вращается с угловым ускорением E – 3,14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения:
а) угловую скорость w ;
б) линейную скорость v;
в) тангенциальное ускорение аt;
г) нормальное ускорение an;
д) полное ускорение а;
е) угол а, составляемый вектором полного ускорения с радиусом колеса.
Решение:
| Гость
спасибо большущее))))))))**********
| Гость
помогли)
| Гость
Спасибочки за решения…
| Гость
Спасибо!!!!
| Гость
Спасибо
| Гость
| Гость
ай саул эээ
| Гость
большое спасибо))))))
| Гость
Выручили, спасибо!!!
| Гость
спасибо
| Гость
Спасибо большое)
| Гость
спасибо
| Гость
ссылки битые, поправьте
Физика – 10
Численное значение линейной скорости при равномерном движении по окружности равно отношению пройденного пути ко времени, затраченному на его прохождение:
v = l
t .
Материальная точка, двигаясь равномерно по окружности, за время, равное периоду обращения (
v = 2π
TR = ωR.
Центростремительное ускорение. Быстрота изменения направления линейной скорости при равномерном движении по окружности характеризуется физической величиной называемой центростремительным, или нормальным, ускорением. Вектор центростремительного, или нормального, ускорения в любой точке траектории направлен по радиусу к центру окружности
a = v2
R.
Докажите, что:
- линейная скорость при равномерном движении по окружности связана с частотой обращения формулой:
v = 2πvR.
- центростремительное ускорение при равномерном движении по окружности связано с перидом и частотой обращения и числом оборотов по формулам:
a = 4π2R
T 2; a = 4π 2v 2R, a = 4π2N2
t 2R . - центростремительное ускорение при равномерном движении по окружности связано с угловой и линейной скоростью формулой:
a = ωv .

- Постройте графики зависимости линейной скорости материальной точки, равномерно движущейся по окружности, от радиуса окружности, периода и частоты обращения.
- Постройте графики зависимости центростремительного ускорения материальной точки, равномерно движущейся по окружности, от радиуса окружности, периода и частоты обращения.
- Длина секундной стрелки наручных часов 2 см, а длина минутной стрелки 1,5 см. Конец какой из стрелок движется с большим центростремительным ускорением и на сколько?
- Где в повседневной жизни можно встретить равномерное движение по окружности? Что можно сказать о периоде и частоте их обращения?
- Какие понятия повторили на уроке? Что из этого вы хорошо поняли, а что осталось вам не ясным?
Вращательное движение вокруг неподвижной оси – еще один частный случай движения твердого тела.Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения (рис.2.4). В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов. Угловая скорость. Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время разные пути. Так, , поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время на один и тот же угол . Угол – угол между осью ОХ и радиус-вектором , определяющим положение точки А (см.  рис.2.5). рис.2.5).Пусть тело вращается равномерно, т. е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол , а другое – на угол , то мы говорим, что первое тело вращается быстрее второго в 2 раза. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени , за который этот поворот произошел. Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению Угловая скорость выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска – около 140 рад/с1. Угловую скорость можно выразить через частоту вращения, т.  е. число полных оборотов за 1с. Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде: е. число полных оборотов за 1с. Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде:Полному обороту тела соответствует угол . Поэтому согласно формуле (2.1) Если при равномерном вращении угловая скорость известна и в начальный момент времени угол поворота , то угол поворота тела за время t согласно уравнению (2.1) равен: Если , то , или . Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательные, когда он уменьшается. Тем самым мы можем описать положение точек вращающегося тела в любой момент времени. Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости.  Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова. Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так: Так как , то Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора , а для точек на широте Санкт-Петербурга . На полюсах Земли . Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности: Следовательно, Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет. Итак, мы научились полностью описывать движение абсолютно твердого тела, вращающегося равномерно вокруг неподвижной оси, так как, пользуясь формулами , можем находить положение, модули скорости и ускорения любой точки тела в произвольный момент времени.  Знаем мы и направления и , a также форму траекторий точек. Знаем мы и направления и , a также форму траекторий точек. |
Равномерное круговое движение
Равномерное круговое движениеРавномерное круговое движение
Обзор:
Объект, движущийся по окружности радиусом r
с постоянной скоростью v ускоряется. То
направление вектора его скорости все время меняется, но величина
вектор скорости остается постоянным. Вектор ускорения не может иметь
компонента в направлении вектора скорости, так как такая компонента
вызвать изменение скорости.Поэтому вектор ускорения должен быть
перпендикулярно вектору скорости в любой точке окружности. Этот
ускорение называется радиальным ускорением
или центростремительное ускорение, и оно указывает
к центру круга. Величина центростремительной
вектор ускорения равен a
Какова сила при различных обстоятельствах?
Решим несколько задач, исследуя этот вопрос.
Проблема:
Груз массой 3 кг, прикрепленный к легкой нити, вращается по горизонтальной поверхности без трения. Таблица. Радиус окружности равен 0,8 м, а струна может выдержать массу
25 кг до разрыва. Какой диапазон скоростей может иметь масса перед струной
перерывы?
Таблица. Радиус окружности равен 0,8 м, а струна может выдержать массу
25 кг до разрыва. Какой диапазон скоростей может иметь масса перед струной
перерывы?
Решение:
- Обоснование:
Масса, прикрепленная к нити, вращается по горизонтали, стол без трения.
Предположим, что масса вращается с постоянной скоростью. это ускорение. Направление ускорения в сторону центр круга, а его величина v 2 /r. В струне есть напряжение. Нить натягивает массу с силой F, направленной к центру окружности. Этот сила F отвечает за центростремительное ускорение, F = mv 2 /r.
Струна может выдержать массу 25 кг до разрыва, т.е.е. мы может позволить массе до 25 кг висеть на веревке рядом с поверхность земли. Максимальное натяжение струны поэтому F max = mg = (25 кг)(9,8 м/с
Учитывая F max = 245 Н и F = mv 2 /r, мы можем найти v max .
- Детали расчета:
v макс. 2 = F макс. об/мин = (250 Н)(0,8 м)/(3кг). v max = 8,1 м/с.
Проблема:
Монета, помещенная на расстоянии 30 см от центра вращающегося горизонтального поворотного стола
когда его скорость 50 см/с.
а) Какая сила обеспечивает центростремительное ускорение, когда монета неподвижна?
относительно поворотного стола?
б) Каков коэффициент статического трения между монетой и поворотным столом?
Решение:
- Обоснование:
Когда монета покоится относительно вращающегося поворотного стола, сила статическое трение между монетой и поворотным столом обеспечивает центростремительное ускорение.
Сила трения покоя имеет максимальное значение f с = μ с Н = μ с мг.
Настройка μ с мг = mv 2 /r, мы можем решить для μ s . - Детали расчета:
(a) Сила трения покоя между монетой и поворотным столом обеспечивает центростремительное ускорение.
(b) Величина максимального сила трения покоя равна f с = μ с Н.Этот максимальная сила трения покоя равна mv 2 /r при v = 0,5 м/с. Имеем µ с N = µ с mg = mv 2 /r,
или мк с = v 2 /(rg) = (0,5 м/с) 2 /(0,3 м 9,8 м/с 2 ) = 0,085.
Проблема:
Рассмотрим конический маятник с грузом массой 80 кг на проволоке длиной 10 м, образующей угол.
θ = 5 o с вертикалью. Определить
(а) горизонтальная и вертикальная составляющая силы, действующей со стороны проволоки на
маятник и
(b) центростремительное ускорение боба.
Решение:
- Обоснование:
Диаграмма свободного тела боба показана справа.
Боб не меняет своего вертикального положения, y = константа, v y = a y = 0. Вертикальный компонент T должен иметь величина мг.
Горизонтальная составляющая Т обеспечивает центростремительное (радиальное) ускорение а р . - Детали расчета:
(a) Вертикальный компонент T должен иметь величина мг.
Tcos(5 o ) = мг, T = (80 кг 9,8 м/с 2 )/cos(5 o ) = 787 N
Величина горизонтальной составляющей T равна Tsin(5 o ) = 68,6 Н. Горизонтальная составляющая силы направлена к центру круг.(b) Tsin(5 o ) = ma r , a r = (68,6 Н)/(80 кг) = 0,857 м/с 2 .
Скорость боба находится из a r = v 2 /r, v = (a r r) ½ .
Поскольку r = (10 м)*sin(5 o ), мы имеем v = 0,86 м/с.
Проблема:
Автомобиль массой 1800 кг преодолевает неровность на дороге, идущей по дуге окружности.
радиусом 42 м.
а) С какой силой дорога действует на автомобиль при прохождении автомобиля?
наивысшая точка горки, если автомобиль движется со скоростью 16 м/с?
б) С какой максимальной скоростью может двигаться автомобиль, проезжая через этот горб?
потеря связи с дорогой?
Решение:
- Обоснование:
Показана схема свободного кузова автомобиля.
Единственными силами, действующими на автомобиль, движущийся с постоянной скоростью, являются сила тяжести и нормальная сила, действующая на дорогу. Если эти силы равны по величине, автомобиль не разгоняется. Если автомобиль движется по дуга окружности, то она ускоряется. Ускорение равно r = v 2 /р. Следовательно, гравитационная сила должна иметь большую величины, чем нормальная сила.
- Детали расчета:
Нам нужно
мг – n = mv 2 /r, или n = m(g – v 2 /r).
n = (1800 кг)(9,8 м/с 2 – (16 м/с) 2 /(42 m)) = 6669 N(b) Автомобиль теряет контакт с дорогой, когда n становится равным нулю. Тогда дорога больше не поддерживает машину. Это происходит, когда g – v 2 /r = 0, или v 2 = gr = 411,6 м 2 /с 2 , v = 20,3 РС.
Модуль 5: Вопрос 1
Чувствуете ли вы, что вас бросает в обе стороны, когда вы преодолеваете кривую, которая идеально накрен для скорости вашего автомобиля? Как направлена сила, приложенная на вас возле автокресла?
Обсудите это со своими однокурсниками на форуме!
Гравитация
Массивные объекты обладают инерцией. Требуется сила, чтобы изменить их состояние
движение. Все массивные объекты взаимодействуют через силу гравитации . Частица массой m 1 действует с силой
F 12 на частицу массой m 2 . Закон тяготения Ньютона дает эту силу как
Требуется сила, чтобы изменить их состояние
движение. Все массивные объекты взаимодействуют через силу гравитации . Частица массой m 1 действует с силой
F 12 на частицу массой m 2 . Закон тяготения Ньютона дает эту силу как
F 12 = (-G м 1 м 2 /r 12 2 )
( р 12 / р 12 ).
Здесь r 12 — расстояние между частицами 1
и 2, и ( r 12 / r 12 )
Единичный вектор , указывающий от частицы 1 к частице
2.
G — гравитационная постоянная, G = 6,67*10 -11 Нм 2 /кг 2 .
Сила F 21 , действующая на частицу массой m 2 действует на частицу массой m 1 , равно – F 12 ,
по третьему закону Ньютона. Сила тяжести всегда
привлекательный.
Точка в объекте, от которой расстояние r 12 равно измеряется его центр масс.Масса m 1 тянет массу m 2 , и масса m 2 тянет на массу m 1 . Центр масса каждого тела притягивается к центру масс другого объект.
Взвешивание земли
Радиус Земли R = 6368 км. Если вы подниметесь на гору высотой 1000 м,
ваше расстояние от центра земли изменится на (1/6368) * 100 % = 0,016 %
а величина гравитационной силы, действующей на вас, изменится на (1/6368) 2 *100
% = 2.4*10 -6 %. Для всех объектов вблизи поверхности земли
расстояние от центра почти постоянно, а величина
Поэтому вектор гравитационной силы приблизительно постоянен. За малым
расстояния, когда кривизной земной поверхности можно пренебречь,
направление вектора гравитационной силы также почти постоянно. Это указывает
прямо вниз к центру земли.
Сила тяжести, действующая на тело массой m на поверхности земли, равна
величина F = мг.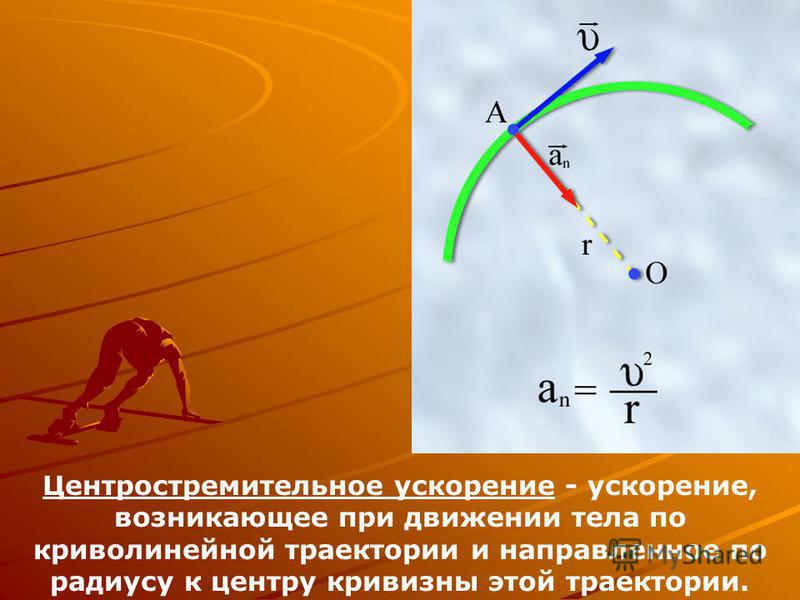 Используя закон всемирного тяготения Ньютона, мы пишем GMm/R 2 =
мг, где М — масса Земли. Таким образом, мы имеем M = gR 2 /G.
Используя закон всемирного тяготения Ньютона, мы пишем GMm/R 2 =
мг, где М — масса Земли. Таким образом, мы имеем M = gR 2 /G.
Используя R = 6,4*10 6 м, находим M = (9,8 м/с 2 )(6,4*10 6 м) 2 /(6,67*10 -11 Н·м 2 /кг 2 ) =
6*10 24 кг.
Орбитальный
Гравитационное притяжение между объектом и землей притягивает объект к центру земли.Когда объект вращается вокруг Земли, направление силы тяжести на объекте постоянно меняется. То радиус Земли настолько велик, что Земля кажется в некоторых местах плоской наблюдатель, стоящий на поверхности. Когда проблема касается только расстояний, которые намного меньше радиуса Земли, мы часто пренебрегаем кривизной земной поверхности и предположим, что сила гравитации направлена в одну и ту же направление вниз везде.
Ссылка: Спутник как снаряд
Предположим, что вблизи поверхности земли в
x-направление, как показано на рисунке выше. Первоначально он ускоряется только в
Y-направление. Но по мере движения объекта направление ускорения
изменения. Если начальная скорость объектов достаточно высока, мы должны принять
изменение направления силы учитывать при расчете объектов
траектория. Объект на круговой орбите вокруг Земли находится
постоянно падает к центру земли. Это постоянно
ускорение. Но пока он движется по криволинейной траектории, поверхность
Земля изгибается в сторону от объекта так, что расстояние между Землей и
объект остается постоянным.
Первоначально он ускоряется только в
Y-направление. Но по мере движения объекта направление ускорения
изменения. Если начальная скорость объектов достаточно высока, мы должны принять
изменение направления силы учитывать при расчете объектов
траектория. Объект на круговой орбите вокруг Земли находится
постоянно падает к центру земли. Это постоянно
ускорение. Но пока он движется по криволинейной траектории, поверхность
Земля изгибается в сторону от объекта так, что расстояние между Землей и
объект остается постоянным.
Сила тяжести всегда направлена к центру объекта. круговой орбите и отвечает за центростремительное ускорение объект.
F = mv 2 /r
Для объекта вблизи поверхности земли F = mg и r = 6,4*10 6 м. Скорость орбитального объекта находится из mg = mv 2 /r, v 2 = gr = (9,8 м/с 2 )(6,4*10 6 м).Имеем v = 7919 м/с,
или примерно 8000 м/с. Требуется объект t = 2πr/v = (6,28*6,4*10 6 м)/(7919 м/с) = 5075 с = 84 мин, чтобы совершить полный оборот по орбите.
Если тот же объект двигался по круговой орбите с большим радиусом, сила силы тяжести на объекте будет меньше. Поскольку мы удваиваем расстояние от центра земли сила тяжести уменьшается в 1/4 раза. То центростремительное ускорение v 2 /r уменьшается в 1/4 раза.Этот означает, что v 2 должно уменьшиться в 1/2 раза. Имеем v = 5600 м/с а для совершения оборота по орбите требуется 14355 с = 240 мин.
Объектов на геосинхронных орбитах совершить полный оборот за 24 часа или 86400 с. Следовательно, их скорость равна v =
2πr/(86400 с). Запись GMm/r 2 = mv 2 /r = m(2πr/(86400 с)) 2 /r,
или r 3 = GM(86400s) 2 /(4π). мы можем решить это
уравнение для радиуса геосинхронной орбиты.С М = 6*10 24 кг имеем r=42260 км. Геосинхронный спутник вращается вокруг 42260
км – 6400 км = 35860 км над поверхностью земли. Радиус его орбиты
в 6,6 раза больше радиуса Земли.
Луна совершает один оборот вокруг Земли за 27,3 дня. Мы можем найти расстояние до Луну таким же образом мы нашли расстояние до геосинхронного спутника. Расстояние от Земли до Луны 384400 км.
Проблема:
Когда падающий метеор находится на расстоянии над земной поверхностью в 3 раза больше Радиус Земли, каково ускорение ее свободного падения под действием силы тяжести приложенная к нему сила?
Решение:
- Обоснование:
Сила, действующая на метеор, равна F = ma = GMm/r 2 .Следовательно, a = GM/r 2 . - Детали расчета:
a = GM/r 2 , a = (6,67*10 -11 Нм 2 /кг 2 )*(6*10 24 кг)/(4*6,4*10 6 м) 2 = 0,61 м/с 2 .
(Метеор находится на 3 земных радиуса над земной поверхностью, значит, это 4 земных радиуса от его центра.)
Для получения дополнительной информации о равномерном круговом движении изучите это
материал из “Кабинета физики”.
Ссылка: Движение Характеристики кругового движения
- Скорость и скорость
- Ускорение
- Требование к центростремительной силе
- Запретное F-слово
- Математика кругового движения
Ссылка: Применение кругового движения
- Второй закон Ньютона – Новый взгляд на
- Парк развлечений Физика
- Легкая атлетика
Равномерное круговое движение
Равномерное круговое движение: движение по круговой траектории с постоянной скоростью.
Здесь задействовано ускорение?
- Да
- Нет
Да – скорость меняется, потому что меняется ее направление.
Мяч вращается по кругу. Если отпустить нить, когда мяч находится в показанном положении, по какой траектории пойдет мяч?
Если отпустить струну, нет силы, которая могла бы отклонить траекторию мяча, поэтому он будет двигаться по прямой, следуя траектории 2.
Основные определения
r = радиус кругового пути
T = период, время одного обхода
v = 2πr/T
Как и при прямолинейном движении, соотношение между a и v такое же, как между v и r:
а = 2πv/T
Объединение этих двух уравнений дает нам:
центростремительное ускорение: a c = v 2 /r
Угловые переменные
Для движения по круговым траекториям может быть полезно описать движение с использованием угловых переменных.Вместо того, чтобы спрашивать, какое расстояние было пройдено, мы иногда спрашиваем, на какой угол что-то повернулось. Есть эквивалентные вопросы для скорости и ускорения.
Расстояние: s = rθ
Скорость: v = rω
Ускорение: a t = rα
Это ускорение включает ускорение или замедление объекта при его движении по круговой траектории и равно нулю при равномерном круговом движении. А направлена по касательной к окружности, значит, это тангенциальное ускорение. Это сильно отличается от центростремительного ускорения, которое действует в радиальном направлении.
Это сильно отличается от центростремительного ускорения, которое действует в радиальном направлении.
Диаграммы свободного тела
Принимая во внимание, что диаграмма свободного тела показывает все силы, действующие на объект, и что эти силы возникают в результате взаимодействия между этим объектом и другими объектами, как выглядит диаграмма свободного тела для Земли на ее примерно круговой орбите вокруг Солнца?
Единственное взаимодействие, о котором нам нужно беспокоиться, это сила гравитации.Солнце оказывает на Землю гравитационную силу, направленную в сторону Солнца.
Зная расстояние до Солнца и время, за которое Земля совершает оборот вокруг Солнца, мы можем рассчитать ускорение, которое испытывает Земля.
r = 150 млн км = 1,5 х 10 11 м
Т = 1 год = π х 10 7 с
v = 2π r / t = 3 x 10 4 м/с = 30000 м/с = 30 км/с.
а с = v 2 /r = 9 х 10 8 / 1. 5 x 10 11 = 6 x 10 -3 м/с 2
5 x 10 11 = 6 x 10 -3 м/с 2
Довольно маленький, но в самый раз, чтобы держать нас на орбите.
Центростремительное ускорение
Центростремительное ускорение — это особая форма ускорения, когда объект совершает равномерное круговое движение. Это:
а с = v 2 / р
и направлен к центру круга.
Второй закон Ньютона можно записать так:
Σ F = ma = mv 2 /r
Я предпочитаю НЕ использовать фразу «центростремительная сила», потому что она заставляет вас думать, что существует магическая сила, которая возникает, когда объект совершает равномерное круговое движение.Такого нет, и, на мой взгляд, никогда не следует помещать центростремительную силу на диаграмму свободного тела.
Когда объект совершает равномерное круговое движение, определенно существует результирующая сила, направленная к центру круга, но эта сила исходит от одной или нескольких стандартных сил, которые мы уже обсуждали. В зависимости от ситуации это может быть сила тяжести, нормальная сила, натяжение, трение, некоторая их комбинация или даже комбинация этих компонентов.
В зависимости от ситуации это может быть сила тяжести, нормальная сила, натяжение, трение, некоторая их комбинация или даже комбинация этих компонентов.
Центростремительное ускорение
Центростремительное ускорение
Рассчитать Прозрачный
⚠️ Сообщить о проблеме
Слово «центростремительный» подразумевает все, что направлено к центру. Очевидно, этот термин применим к любому объекту, который находится в круговом движении.
Что такое центростремительное ускорение?
Рассмотрим камень, привязанный к веревке и удерживаемый вашей рукой. Если вращать, крепко удерживая его рукой, камень движется по круговой траектории с радиусом, равным длине струны.Нить, крепко удерживаемая вашей рукой, воздействует на камень с силой, называемой центростремительной силой.
Согласно второму закону Ньютона, каждый объект испытывает ускорение, направленное в направлении силы, действующей на него. Здесь сила направлена к центру.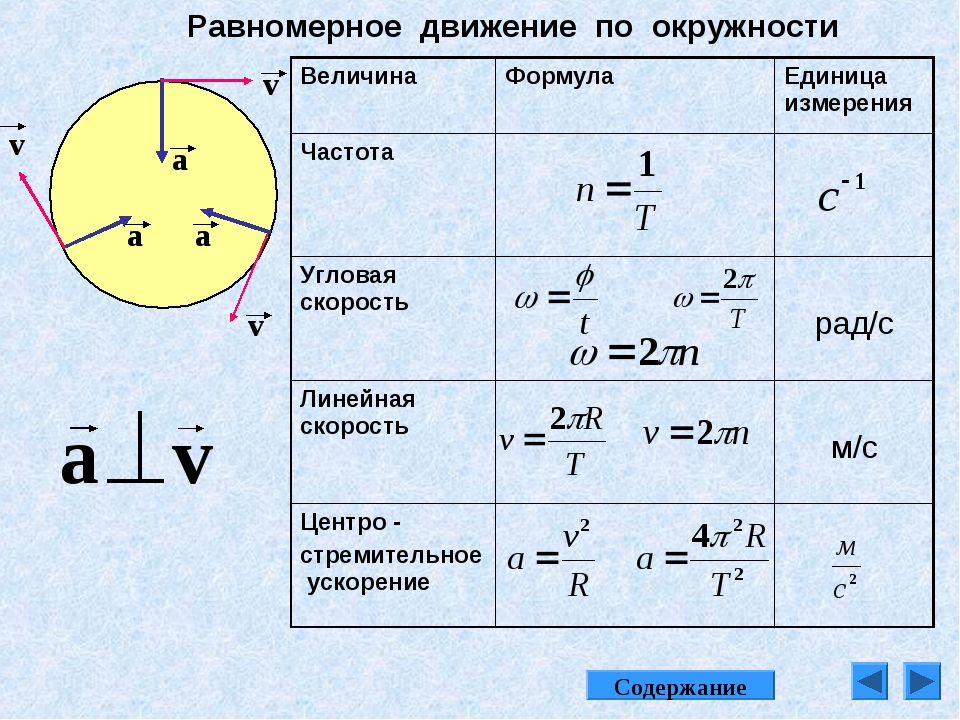 Следовательно, камень испытывает ускорение, называемое центростремительным ускорением, направленное к центру, то есть к вашей руке.
Следовательно, камень испытывает ускорение, называемое центростремительным ускорением, направленное к центру, то есть к вашей руке.
Центростремительное ускорение – это ускорение, которое тело, движущееся по окружности, испытывает под действием центростремительной силы.
Если вы внезапно покинете камень, когда он движется по круговой траектории, он будет двигаться по прямой линии, касательной к этой точке в этот момент. Скорость, с которой он покидает круговой путь, называется тангенциальной скоростью «v».
Какие виды ускорения испытывает тело при движении по окружности?
Объект, движущийся по круговой траектории, испытывает три типа ускорений:
- Угловое ускорение: α = Δω Δt
- Тангенциальное ускорение: at = rα в м с 2
- Центростремительное ускорение: ac = vt 2 r = rω 2 .
В то время как угловое ускорение является угловой величиной, остальные две величины являются линейными величинами.
Какова формула центростремительного ускорения?
Для тела массой m, движущегося по окружности радиусом r с тангенциальной скоростью v, центростремительное ускорение определяется выражением: ac = v 2 / r
В терминах линейной скорости вы можете рассчитать центростремительное ускорение как ac= ω 2 r, так как мы знаем, что v=rω
Центростремительное ускорение также определяется как скорость изменения тангенциальной скорости: ac= Lim(Δv→0)[(Δvt/Δt)]
Замечания о центростремительном ускорении
- Центростремительное ускорение всегда направлено радиально внутрь к центру окружности, по которой он движется.
- Тело, движущееся по окружности, испытывает как центростремительное ускорение, так и угловое ускорение. Таким образом, чистое ускорение, которое испытывает тело, определяется как корень суммы квадратов обоих ускорений.
- Луна, которая движется вокруг Земли, является лучшим примером объекта, движущегося по круговой траектории.
 Гравитация Земли вызывает на Луне центростремительное ускорение, которое всегда направлено к Земле.
Гравитация Земли вызывает на Луне центростремительное ускорение, которое всегда направлено к Земле. - Если угловую скорость оставить постоянной, а радиус изменить, центростремительное ускорение изменится; если радиус уменьшается, центростремительное ускорение увеличивается и наоборот.
- Центростремительное ускорение может измениться двумя способами: либо из-за огромного изменения центростремительной скорости за заданное время, либо из-за внезапного изменения центростремительной скорости за короткий промежуток времени.
- Центростремительное ускорение и тангенциальное ускорение всегда перпендикулярны друг другу; потому что в то время как центростремительное ускорение направлено к радиусу, тангенциальное ускорение направлено к мгновенной касательной. Мы знаем, что радиус и касательная всегда перпендикулярны в данной точке окружности.
Примечание. Объект, движущийся по круговой траектории, может иметь нулевое тангенциальное ускорение, но не нулевое центростремительное ускорение. Если тангенциальное ускорение тела равно нулю, значит, оно движется с постоянной угловой скоростью и угловое ускорение также равно нулю.
Если тангенциальное ускорение тела равно нулю, значит, оно движется с постоянной угловой скоростью и угловое ускорение также равно нулю.
Но если тело, движущееся по круговой траектории, имеет нулевое центростремительное ускорение, это означает, что его тангенциальная скорость не меняется, что означает, что оно вообще не движется по окружности.
Луна притягивается к Земле и под действием силы тяжести постоянно отклоняется от прямолинейного движения и удерживается на своей орбите.
– Исаак Ньютон
Применение центростремительного ускорения в повседневной жизни
Устройство под названием Центрифуга работает по принципу центростремительного ускорения. Центрифуга — это устройство, которое используется в лабораториях и на производстве для отделения частиц различной плотности, в основном из жидкостей.
Центрифуга контейнер, содержащий жидкость, вращается с высокой скоростью и прикладывает перпендикулярную силу к оси вращения. В результате более плотные частицы движутся наружу, а более легкие – к центру.
Этот принцип центрифуги обычно используется в следующих отраслях промышленности:
- Сепаратор сливок на молочных заводах
- Установки для переработки отходов для отделения взвешенных веществ и жидкостей различной плотности.
- Для имитации атмосферы высокой гравитации для обучения пилотов и военнослужащих.
- Стиральные машины также работают по принципу центрифуги.
Вы знаете?
Для проверки уровней толерантности космонавтов человеческие центрифуги проектируются с чрезвычайно большими значениями ускорений, которые часто во много раз превышают гравитацию Земли.
Человеческие центрифуги, чрезвычайно большие центрифуги, использовались для проверки устойчивости астронавтов к воздействию ускорений, превышающих гравитацию Земли.
Как вам поможет калькулятор центростремительного ускорения CalculatorHut?
Используя бесплатный онлайн-калькулятор центростремительного ускорения CalculatorHut, вы можете рассчитать любой параметр, связанный с центростремительным ускорением – радиус, скорость и центростремительное ускорение. Это очень удобный инструмент для студентов, чтобы проверить правильность своих расчетов.
Это очень удобный инструмент для студентов, чтобы проверить правильность своих расчетов.
CalculatorHut — это универсальный онлайн-калькулятор для научных и ненаучных целей, который бесплатно удовлетворит все ваши потребности в онлайн-калькуляторе. Все калькуляторы удобны в использовании и дают результаты с точностью до многих знаков после запятой.
CalculatorHut также предлагает широкий выбор из более чем 100 калькуляторов на различные темы — калькуляторы здоровья, калькуляторы финансов, калькуляторы транспортных средств, калькуляторы физики, калькуляторы химии, математические калькуляторы и многие другие онлайн-калькуляторы для научных исследований бесплатно.
Если вы хотите получить любой из наших онлайн-калькуляторов бесплатно в виде бесплатного виджета для встраивания в виде виджетов на их веб-сайты, свяжитесь с нами по адресу [email protected].
Мы пропустили какой-нибудь бесплатный онлайн-калькулятор? Пожалуйста, дайте нам знать. Мы были бы более чем счастливы всегда бесплатно обслуживать ваши потребности в онлайн-калькуляторе!
Вы знаете? Вы также можете бесплатно носить с собой наш широкий выбор онлайн-калькуляторов. Да! Приложение CalculatorHut бесплатное и станет вашим другом, который сделает любой расчет проще и легче! Удачных расчетов!
Да! Приложение CalculatorHut бесплатное и станет вашим другом, который сделает любой расчет проще и легче! Удачных расчетов!
4.4 Равномерное круговое движение – University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Найдите центростремительное ускорение объекта, движущегося по круговой траектории.
- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
- Объясните разницу между центростремительным ускорением и тангенциальным ускорением в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорения при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение — это особый тип движения, при котором объект движется по окружности с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна.Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна.Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости меняется, или [latex]d\mathbf{\overset{\to }{v}}\text{/}dt\ne 0.[/latex] Это показано на рисунке.Когда частица движется против часовой стрелки во времени [латекс]\Delta t[/латекс] по круговой траектории, ее вектор положения перемещается из [латекс]\mathbf{\overset{\to }{r}}(t)[/латекс] to [latex]\mathbf{\overset{\to }{r}}(t+\Delta t).[/latex] Вектор скорости имеет постоянную величину и касается пути при изменении от [latex]\mathbf{ \overset{\to }{v}}(t)[/latex] to [latex]\mathbf{\overset{\to }{v}}(t+\Delta t),[/latex] меняет только свое направление. Поскольку вектор скорости [латекс]\mathbf{\overset{\to }{v}}(t)[/latex] перпендикулярен вектору положения [латекс]\mathbf{\overset{\to }{r}}( t), [/latex] треугольники, образованные векторами положения и [latex]\Delta \mathbf{\overset{\to }{r}},[/latex] и векторами скорости и [latex]\Delta \mathbf {\overset{\to}}{v}}[/latex] похожи.Кроме того, поскольку [латекс]|\mathbf{\overset{\to }{r}}(t)|=|\mathbf{\overset{\to }{r}}(t+\Delta t)|[/latex] и [латекс]|\mathbf{\overset{\to }{v}}(t)|=|\mathbf{\overset{\to }{v}}(t+\Delta t)|,[/latex] два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
Поскольку вектор скорости [латекс]\mathbf{\overset{\to }{v}}(t)[/latex] перпендикулярен вектору положения [латекс]\mathbf{\overset{\to }{r}}( t), [/latex] треугольники, образованные векторами положения и [latex]\Delta \mathbf{\overset{\to }{r}},[/latex] и векторами скорости и [latex]\Delta \mathbf {\overset{\to}}{v}}[/latex] похожи.Кроме того, поскольку [латекс]|\mathbf{\overset{\to }{r}}(t)|=|\mathbf{\overset{\to }{r}}(t+\Delta t)|[/latex] и [латекс]|\mathbf{\overset{\to }{v}}(t)|=|\mathbf{\overset{\to }{v}}(t+\Delta t)|,[/latex] два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
[латекс]\frac{\Delta v}{v}=\frac{\Delta r}{r}[/latex] или [латекс]\Delta v=\frac{v}{r}\Delta r.[ /латекс]
Рисунок 4.18 (a) Частица движется по окружности с постоянной скоростью, с векторами положения и скорости в моменты времени [latex]t[/latex] и [latex]t+\Delta t.{2}}{r}.[/латекс] Направление ускорения также можно найти, заметив, что по мере того, как [латекс]\Delta t[/латекс] и, следовательно, [латекс]\Дельта \тета[/латекс] приближаются к нулю, вектор [латекс]\Дельта \mathbf{ \overset{\to }{v}}[/latex] приближается к направлению, перпендикулярному [латексу]\mathbf{\overset{\to }{v}}. [/latex] В пределе [латекс]\Delta t\ до 0,[/латекс] [латекс]\Delta \mathbf{\overset{\to} {v}}[/latex] перпендикулярно [латексу]\mathbf{\overset{\to} {v}}.[ /latex] Поскольку [latex]\mathbf{\overset{\to }{v}}[/latex] касается окружности, ускорение [latex]d\mathbf{\overset{\to }{v}}\ text{/}dt[/latex] указывает на центр круга.{2}}{r}.[/латекс]
[/latex] В пределе [латекс]\Delta t\ до 0,[/латекс] [латекс]\Delta \mathbf{\overset{\to} {v}}[/latex] перпендикулярно [латексу]\mathbf{\overset{\to} {v}}.[ /latex] Поскольку [latex]\mathbf{\overset{\to }{v}}[/latex] касается окружности, ускорение [latex]d\mathbf{\overset{\to }{v}}\ text{/}dt[/latex] указывает на центр круга.{2}}{r}.[/латекс]
Вектор ускорения направлен к центру окружности (рисунок). Это радиальное ускорение называется центростремительным ускорением , поэтому мы даем ему нижний индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать) и, таким образом, принимает значение «искание центра».
Рисунок 4.19 Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении.Вектор скорости также показан и касается окружности. Давайте рассмотрим несколько примеров, иллюстрирующих относительные величины скорости, радиуса и центростремительного ускорения.
Пример
Создание ускорения 1
gРеактивный самолет летит со скоростью 134,1 м/с по прямой линии и делает разворот по круговой траектории на уровне земли. Каким должен быть радиус окружности, чтобы пилот и реактивный самолет получили центростремительное ускорение 1 g по направлению к центру круговой траектории?
Стратегия
Зная скорость струи, мы можем найти радиус окружности в выражении для центростремительного ускорения.{2}}=1835\,\text{м}=1,835\,\text{км}\text{.}[/latex]
Значение
Чтобы создать у пилота большее ускорение, чем g , реактивный самолет должен либо уменьшить радиус своей круговой траектории, либо увеличить скорость на существующей траектории, либо и то, и другое.
Проверьте свое понимание
Маховик имеет радиус 20,0 см. Какова скорость точки на краю маховика, если она испытывает центростремительное ускорение [латекс]900.{2}?[/латекс]
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны кругового пути. Типичные центростремительные ускорения приведены в следующей таблице.
Типичные центростремительные ускорения приведены в следующей таблице.
| Объект | Центростремительное ускорение (м/с 2 или коэффициенты g ) |
|---|---|
| Земля вокруг Солнца | [латекс]5,93\раз {10}^{-3}[/латекс] |
| Луна вокруг Земли | [латекс]2. {22}[/латекс] {22}[/латекс] |
Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана вектором ее положения [латекс]\mathbf{\overset{\to }{r}}(t).[/latex] На рисунке показана частица, совершающая круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [latex]\mathbf{\overset{\to }{r}}(t)[/latex], образующий угол [latex]\theta[/latex] с осью x-, показан со своими компонентами вдоль x – и y – оси.Величина вектора положения равна [латекс] A = |\ mathbf {\ overset {\ to }{r}} (t) | [/ латекс], а также радиусу окружности, так что с точки зрения его компонентов ,
[латекс]\mathbf{\overset{\to}}{r}}(t)=A\,\text{cos}\,\omega t\mathbf{\hat{i}}+A\,\text{ sin}\,\omega t\mathbf{\hat{j}}.[/latex]
Здесь [латекс]\омега[/латекс] — константа, называемая угловой частотой частицы. Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду.Угол [латекс]\тета[/латекс], который имеет вектор положения в любой конкретный момент времени, равен [латекс]\омега t[/латекс].
Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду.Угол [латекс]\тета[/латекс], который имеет вектор положения в любой конкретный момент времени, равен [латекс]\омега t[/латекс].
Если T – это период движения или время, необходимое для совершения одного оборота ([латекс]2\пи[/латекс] рад), то
[латекс]\omega =\frac{2\pi }{T}.[/latex]
Рисунок 4.20 Вектор положения частицы в круговом движении с его компонентами вдоль осей x и y. Частица движется против часовой стрелки. Угол [латекс]\тета[/латекс] — это угловая частота [латекс]\омега[/латекс] в радианах в секунду, умноженная на t.Скорость и ускорение можно получить из функции положения дифференцированием:
[латекс] \ mathbf {\ overset {\ to {v}} (t) = \ frac {d \ mathbf {\ overset {\ to {r}} (t)} {dt} = \ text {− } A \ omega \, \ text {sin} \, \ omega t \ mathbf {\ hat {i}} + A \ omega \, \ text {cos} \, \ omega t \ mathbf {\ hat {j}} . {2} \, \ text {sin} \, \ омега т \ mathbf {\ шляпа {j}}.{-7}\text{s}=200\,\text{ns}\text{.}[/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
{2} \, \ text {sin} \, \ омега т \ mathbf {\ шляпа {j}}.{-7}\text{s}=200\,\text{ns}\text{.}[/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
Значение
Мы выбрали начальное положение частицы на оси x-. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас была бы другая конечная позиция при t = 200 нс.
Неравномерное круговое движение
Круговое движение не обязательно должно быть с постоянной скоростью.Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а окружность имеет фиксированный радиус. Если меняется и скорость частицы, то вводим дополнительное ускорение в направлении, касательном к окружности. Такие ускорения возникают в точке на волчке, меняющем скорость вращения, или на каком-либо ускоряющемся роторе. В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени.Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени.Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
[латекс] {a} _ {\ text {T}} = \ frac {d | \ mathbf {\ overset {\ to {v}} |} {dt}. [/latex]
Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения направлено радиально внутрь к центру окружности. Таким образом, частица, движущаяся по окружности с тангенциальным ускорением, имеет полное ускорение , которое представляет собой векторную сумму центростремительного и тангенциального ускорений:
[латекс] \ mathbf {\ overset {\ to {a}} = {\ mathbf {\ overset {\ to {a}}} _ {\ text {C}} + {\ mathbf {\ overset {\ на {a}}}_{\text{T}}.[/латекс]
Векторы ускорения показаны на рисунке. Обратите внимание, что два вектора ускорения {a}}}_{\text{T}}[/latex] перпендикулярны друг другу, при этом [latex]{\mathbf{\overset{\to}}{a}}}_{\text{C}} [/latex] в радиальном направлении и [latex]{\mathbf{\overset{\to }{a}}}_{\text{T}}[/latex] в тангенциальном направлении.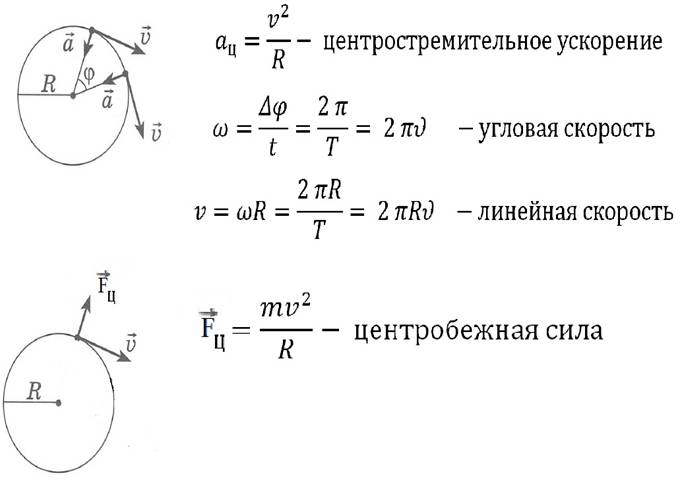 Полное ускорение [латекс]\mathbf{\overset{\to }{a}}[/latex] указывает на угол между [латекс]{\mathbf{\overset{\to }{a}}}_{\text {C}}[/латекс] и [латекс]{\mathbf{\overset{\to}}{a}}}_{\text{T}}.[/латекс]
Полное ускорение [латекс]\mathbf{\overset{\to }{a}}[/latex] указывает на угол между [латекс]{\mathbf{\overset{\to }{a}}}_{\text {C}}[/латекс] и [латекс]{\mathbf{\overset{\to}}{a}}}_{\text{T}}.[/латекс]
Пример
Общее ускорение во время кругового движения
Частица движется по окружности радиусом r = 2,0 м. На интервале времени от до = 1.{2}},\enspace{c}_{1}=4.0\,\text{m}\text{/}\text{s,}\enspace{c}_{2}=6.0\,\text{ m}\cdot\text{s}\text{.}[/latex]
Чему равно полное ускорение частицы при т = 2,0 с?
Стратегия
Нам известны скорость частицы и радиус окружности, поэтому мы можем легко рассчитать центростремительное ускорение. Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекс]|v(t)|[/латекс] с помощью рисунка и оценив ее при t = 2.\circ[/latex] от касательной к окружности. См. рисунок.
Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекс]|v(t)|[/латекс] с помощью рисунка и оценив ее при t = 2.\circ[/latex] от касательной к окружности. См. рисунок.
Значение
Направления центростремительного и тангенциального ускорений удобнее описывать в полярной системе координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, используемая для движения по криволинейным траекториям, подробно обсуждается далее в книге.{2}\text{/}р.[/латекс]
 Это ускорение называется тангенциальным ускорением [latex]{\mathbf{\overset{\to }{a}}}_{\text{T}}.[/latex] величина скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности.Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
Это ускорение называется тангенциальным ускорением [latex]{\mathbf{\overset{\to }{a}}}_{\text{T}}.[/latex] величина скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности.Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.Концептуальные вопросы
Может ли центростремительное ускорение изменить скорость частицы, совершающей круговое движение?
Может ли тангенциальное ускорение изменить скорость частицы, совершающей круговое движение?
Проблемы
Маховик вращается со скоростью 30 об/с. {2} = r \ enspace {a} _ { \текст{С}}=78.4,\enspace v=8.85\,\text{m}\text{/}\text{s}[/latex]
{2} = r \ enspace {a} _ { \текст{С}}=78.4,\enspace v=8.85\,\text{m}\text{/}\text{s}[/latex]
[латекс]T=5,68\,\text{s,}[/latex], что составляет [латекс]0,176\,\text{rev}\text{/}\text{s}=10,6\,\text{rev }\текст{/}\текст{мин}[/латекс]
Бегун, участвующий в забеге на 200 м, должен обежать конец дорожки, имеющей дугу окружности с радиусом кривизны 30,0 м. Бегун начинает гонку с постоянной скоростью. Если она пробежит 200 м за 23,2 с и будет бежать с постоянной скоростью на протяжении всей гонки, каково будет ее центростремительное ускорение, когда она пробегает кривую часть трассы?
Каково ускорение Венеры по отношению к Солнцу, если предположить, что она движется по круговой орбите?
Показать решениеВенере 108 лет.{2}[/латекс]
Экспериментальная реактивная ракета летит вокруг Земли по экватору прямо над ее поверхностью. С какой скоростью должна двигаться струя, если модуль ее ускорения равен g ?
Вентилятор вращается с постоянной скоростью 360,0 об/мин. Чему равно ускорение точки одной из его лопастей на расстоянии 10,0 см от оси вращения?
Чему равно ускорение точки одной из его лопастей на расстоянии 10,0 см от оси вращения?
[latex]360\,\text{rev}\text{/}\text{min}=6\,\text{rev}\text{/}\text{s}[/latex]
[латекс]v=3.{2}.[/latex] Как далеко точка от оси вращения секундной стрелки?
Глоссарий
- угловая частота
- [латекс]\омега,[/латекс] скорость изменения угла, с которым объект движется по круговой траектории
- центростремительное ускорение
- составляющая ускорения объекта, движущегося по окружности, направленная радиально внутрь к центру окружности
- тангенциальное ускорение
- величина которого есть скорость изменения скорости во времени.2)/р
Силы и движение
Доказательство F = mv²/R
Учебное руководство за 14-16
Метод А
Это следует непосредственно из эксперимента
Зарисовка орбиты спутника и предсказание ее периода
Математика непосредственно следует из наброска, полученного в ходе этого эксперимента и воспроизведенного ниже.
 Это метод Ньютона.
Это метод Ньютона.Он в значительной степени опирается на теорему о скрещенных хордах для окружности, которую следует дать.
Окружность представляет собой орбиту спутника радиусом R , движущегося со скоростью v . Спутник перемещается из точки А в точку В за время t . Без силы спутник двигался бы к K с постоянной скоростью.
Теперь «включите» гравитацию, и спутник упадет на расстояние ч за то же время от касательной из точки А в точку В.Неважно, позволите ли вы ему сначала упасть из точки А, а затем продолжите движение в тангенциальном направлении или наоборот. Всем, кто возражает, что падение от К до В происходит не по радиусу, следует еще раз взглянуть на их масштабную диаграмму: почти невозможно увидеть разницу между h и радиальным падением. [Возможно, вам придется говорить о
в пределе
.]Из свойства скрещенных хорд h (2R- h ) = x 2
Но 2 R >> H Поэтому 2v = x 2 и так H = x x 2 2 R (уравнение 1)
теперь x = AK, что почти равно arcAB = v t (уравнение 2)
Объединение 1 и 2, h = ( v t ) 2 2 R (уравнение 3)
h — вертикальное падение, поэтому используя s = ½ a t 2 = h (уравнение 4)
Затем из (уравнение 3) и (уравнение 4)
½ a t 2 = ( v t ) 2 2 R
ведет к a = v 2 R
Использование F = м a затем F = м v 2 R
То же верно для движения во всех местах по кругу.
 Под вертикалью всегда понимают направление от спутника к центру притягивающего тела.
Под вертикалью всегда понимают направление от спутника к центру притягивающего тела.Метод Б
Этот метод основан на понимании векторов.
Окружность представляет собой орбиту спутника радиусом R , движущегося со скоростью v . Спутник перемещается из точки А в точку В за время t .
Нарисуйте вектор AP для представления начальной скорости спутника в точке A, которая проходит по касательной в точке A.Нарисуйте второй вектор той же длины, BQ, чтобы представить более позднюю скорость в B.
Перерисовать начальный и последующие векторы, начиная с одной и той же точки D. Оба имеют модуль, равный v . FG, представляющий изменение скорости, должен быть добавлен к старой скорости, чтобы получить новую скорость.
AOB и FDG — подобные треугольники.
изменение скорости v = AB R
ускорение = изменение скорости от A до B = AB x v R x время от A до B = v 2 R
Использование F = м a затем F = м v 2 R
Уравнение F = m v 2 R иллюстрирует эти соотношения:
- чем выше скорость v , тем больше сила, необходимая для удержания объектов на орбите, а значит, тем больше центральное ускорение
- для той же скорости, чем меньше радиус или чем круче кривая, тем больше сила и, следовательно, тем больше должно быть ускорение.

Ускорение увеличивается с увеличением орбитальной скорости, v , но уменьшается при увеличении радиуса, R .
Объяснение урока: Орбитальная скорость | Nagwa
В этом объяснителе мы научимся вычислять орбитальную скорость объекта, движущегося по круговой орбите, с учетом его орбитальной радиус и массу объекта, вокруг которого он вращается.
Для начала вспомним некоторые ключевые свойства кругового орбитального движения.
Помните, что для круговых орбит любое тело на орбите имеет скорость с постоянной величиной, но с постоянно меняющимся направлением. На приведенной ниже диаграмме показан спутник Юпитера Европа, вращающаяся вокруг Юпитера. Направление скорости Луны всегда указывает вдоль касательной к его орбитальному пути, обозначенному синей стрелкой. Гравитация Юпитера действует как центростремительная сила, которую мы know должен всегда указывать радиально внутрь, как показано красной стрелкой.

Это соотношение помогает объяснить, почему орбитальная скорость Луны постоянна: гравитационная сила не имеет компонента в в том же направлении, что и скорость Луны.Таким образом, величина скорости изменяется не за счет силы тяжести, а направление постоянно изменяется, потому что гравитационная сила постоянно перенаправляет его по круговой траектории. В любой точке орбиты направления двух величин всегда указывают под прямым углом, или 90∘, друг другу.
Как показано выше, гравитационная сила массивного объекта всегда направлена внутрь, к его собственному центру масс. Помните что ускорение свободного падения 𝑎 в точке вблизи массивного объекта, такого как планета, определяется выражением 𝑎=𝐺𝑀𝑟, где 𝐺 — универсальная гравитационная постоянная, 𝑀 — масса планеты, а 𝑟 — расстояние между точкой и планетой.
В этом случае гравитационное ускорение, которое всегда направлено внутрь и удерживает Луну на круговой орбите, действует как центростремительное ускорение.
 Таким образом, для объекта, такого как луна, находящегося на круговой орбите, центростремительное ускорение объекта
дан кем-то
𝑎=𝑣𝑟,
где 𝑣 — линейная скорость Луны, а 𝑟 — радиус орбиты.
Таким образом, для объекта, такого как луна, находящегося на круговой орбите, центростремительное ускорение объекта
дан кем-то
𝑎=𝑣𝑟,
где 𝑣 — линейная скорость Луны, а 𝑟 — радиус орбиты.Поскольку гравитация обеспечивает центростремительное ускорение, мы можем приравнять значения 𝑎 и 𝑎: 𝑣𝑟=𝐺𝑀𝑟.
В обеих частях уравнения в знаменателе стоит 𝑟, поэтому мы можем упростить уравнение, умножив обе стороны на 𝑟: 𝑟⋅𝑣𝑟=𝑟⋅𝐺𝑀𝑟𝑣=𝐺𝑀𝑟.
Мы можем взять квадратный корень из обеих частей, чтобы сделать 𝑣 предметом уравнения: 𝑣=𝐺𝑀𝑟.
Теперь у нас есть уравнение для орбитальной скорости объекта, движущегося по круговой орбите, для заданного радиуса орбиты и массы объекта, вокруг которого он вращается.
Обратите внимание, что уравнение не зависит от 𝑚, массы объекта на орбите.Это означает, что все объекты, независимо от их массы, движущиеся по круговым орбитам с одинаковым радиусом орбиты, вокруг планет с та же масса, будет иметь ту же орбитальную скорость.
 Помните, что это соотношение применяется только в случае круговых орбит,
где орбитальная скорость постоянна; некруговые орбиты не подчиняются этому уравнению.
Помните, что это соотношение применяется только в случае круговых орбит,
где орбитальная скорость постоянна; некруговые орбиты не подчиняются этому уравнению.Прежде чем приступить к некоторым вычислениям, следует отметить, что универсальная гравитационная постоянная обычно встречается повсюду. астрономии и других областях физики и имеет неизменное значение 𝐺=6.67×10/⋅мкг.
Определение: уравнение орбитальной скорости — круговая орбита
В частном случае круговой орбиты орбитальная скорость объекта 𝑣 определяется уравнением 𝑣=𝐺𝑀𝑟, где 𝐺 — универсальная гравитационная постоянная, 𝑀 — масса большого объекта в центр орбиты, а 𝑟 — радиус орбиты.
Теперь, когда у нас есть уравнение для орбитальной скорости, давайте применим его в некоторых примерах.
Пример 1: Расчет орбитальной скорости
Для того, чтобы спутник двигался по круговой орбите вокруг Земли в радиусе 10 000 км, какая у него должна быть орбитальная скорость? Используйте значение 5.
 97×10 кг для массы Земли
и 6,67×10 м 3 /кг⋅с 2 для значения всемирного тяготения
постоянный. Дайте ответ с точностью до метра в секунду.
97×10 кг для массы Земли
и 6,67×10 м 3 /кг⋅с 2 для значения всемирного тяготения
постоянный. Дайте ответ с точностью до метра в секунду.Ответ
Здесь нам даны значения для 𝑀, 𝑟 и 𝐺. Обратите внимание, что 𝑟 дается в километрах, поэтому мы должны преобразовать в метров, прежде чем мы сможем использовать его в уравнении: 𝑟=10000=1,0×10 км
Теперь мы готовы подставить все наши значения в уравнение орбитальной скорости: 𝑣=𝐺𝑀𝑟=(6.67×10/⋅)(5,97×10)1,0×10=6310,3/.mkgskgmms
Округлив до ближайшего метра в секунду, мы нашли, что спутник должен вращаться со скоростью 6 310 м/с.
Обратите внимание, что нам не нужно знать массу спутника, чтобы найти ответ. Это потому, что уравнение орбитальной скорости делает не зависит от массы объекта на орбите 𝑚.
Иногда нам будет предоставлена информация об орбитальной системе, отличной от просто 𝑀 и 𝑟.
 В зависимости от того, какая информация предоставлена, мы можем изменить уравнение орбитальной скорости, чтобы решить другую величину, помимо
𝑣.Например, в следующем примере мы вычислим радиус орбиты для системы.
В зависимости от того, какая информация предоставлена, мы можем изменить уравнение орбитальной скорости, чтобы решить другую величину, помимо
𝑣.Например, в следующем примере мы вычислим радиус орбиты для системы.Пример 2: Расчет орбитального радиуса
Планета движется по круговой орбите вокруг звезды. Он вращается вокруг звезды со скоростью 17,9 км/с, а масса звезды 2,18×10 кг. Каков радиус орбиты планеты? Используйте значение 6,67×10 м 3 /кг⋅с 2 для универсальной гравитационной постоянной и 1.5×10 м на длину 1 АЕ. Дайте ответ ближайшему астрономическая единица.
Ответ
Здесь нам даны значения для 𝑣, 𝑀 и 𝐺, и мы должны решить для 𝑟. Для этого мы можем изменить уравнение орбитальной скорости так, чтобы 𝑣=𝐺𝑀𝑟 становится 𝑟=𝐺𝑀𝑣.
Прежде чем мы сможем вычислить, мы должны преобразовать значение для 𝑣 в единицы метров в секунду: 𝑣=17.
 9/=17900/.kmsms
9/=17900/.kmsmsТеперь, подставив наши значения, мы имеем 𝑟=6.67×10/⋅2,18×10(17900/)=4,54×10.mkgskgmsm
Однако это не окончательный ответ, так как 𝑟 в настоящее время выражается в метров, и нам нужно преобразовать его в астрономические единицы: 𝑟=4,54×10×11,5×10=3,03.mAUmAU
Округляя до ближайшей астрономической единицы, мы находим, что планета имеет орбитальный радиус 3 а.е.
Давайте теперь сместим наше внимание с этих вычислительных примеров на пару примеров, которые являются более концептуальными.
Пример 3: переменная зависимость в уравнении орбитальной скорости
Какая линия на графике показывает зависимость между орбитальной скоростью и радиусом орбиты для объектов, движущихся по круговым орбитам из-за гравитации?
Ответ
Начнем с уравнения орбитальной скорости, которое связывает орбитальную скорость 𝑣 и радиус орбиты, 𝑟: 𝑣=𝐺𝑀𝑟.

Исходя из этого, мы составим пропорцию, которая поможет нам описать взаимосвязь между орбитальной скоростью и радиусом. С 𝐺 и 𝑀 являются константами в этом контексте, они не появятся в нашей пропорции. Используя 1 в качестве заполнителя в числителе, мы имеем 𝑣∝1√𝑟.
Таким образом, можно сказать, что 𝑣 и 𝑟 обратно пропорциональны друг другу, так как увеличение одной величины указывает на уменьшение другой. Из этой обратной зависимости мы знаем, что 𝑣 должно уменьшаться по мере увеличения 𝑟, поэтому зеленая линия неверна.
Далее, поскольку независимая переменная 𝑟 стоит в знаменателе, мы знаем, что соотношение между 𝑣 и 𝑟 не может быть линейным. Следовательно, красная линия также неверна.
Синие и оранжевые линии имеют одинаковую форму, но сильно различаются по оси 𝑦. Оранжевый кривая пересекает ось, где синяя кривая имеет вертикальную асимптоту. Чтобы определить, как здесь должен выглядеть график, давайте подумаем, как ведет себя уравнение орбитальной скорости вблизи 𝑟=0.

Как упоминалось ранее, 𝑟 появляется в знаменателе, и мы знаем, что мы не можем осмысленно делить на ноль. Таким образом, когда 𝑟 стремится к нулю, функция стремится к бесконечности и не определена на оси 𝑦.
Таким образом, синяя линия правильно показывает соотношение между орбитальной скоростью и радиусом орбиты для объектов в круговом орбита.
Пример 4: Переменная зависимость в уравнении орбитальной скорости
Спутник следует по круговой орбите вокруг Земли на радиальном расстоянии 𝑅 и с орбитальной скоростью 𝑣.Если бы спутник приблизили к Земле так, чтобы он двигался по круговой орбите радиусом 𝑅9, с какой скоростью в пересчете на 𝑣 он должен двигаться, чтобы поддерживать его орбита?
Ответ
В этом примере мы рассмотрим, как соотносятся орбитальная скорость и радиус, составив пропорцию. Сначала мы необходимо определить уравнение, которое включает обе эти величины, поэтому мы будем использовать уравнение орбитальной скорости: 𝑣=𝐺𝑀𝑟.

Затем мы идентифицируем постоянные значения в уравнении, чтобы мы могли удалить их, чтобы сформировать нашу пропорцию, поскольку пропорции исследовать, как переменные изменяются по отношению друг к другу. Мы знаем, что 𝐺 представляет собой константу, поэтому не появляются в пропорции. И хотя 𝑀 фигурирует как переменная в уравнении орбитальной скорости, в В контексте этой проблемы 𝑀 представляет массу Земли, которая практически постоянна.
Теперь мы можем написать пропорцию, чтобы показать, как 𝑣 и 𝑟 зависят друг от друга, используя символ для пропорциональности, ∝.Мы больше не можем использовать знак равенства, чтобы связать 𝑣 и 𝑟, так как истинное равенство их значений зависит от некоторых постоянных величин, не относящихся к наша пропорция. Число 1 будет выступать в качестве заполнителя в числителе, где постоянные значения были в исходном уравнении: 𝑣∝1√𝑟.
Таким образом, можно утверждать, что 𝑣 обратно пропорционально квадратному корню из 𝑟.
 То
зависимость описывается как обратная, потому что увеличение одной величины вызывает уменьшение другой — помните, что
увеличение знаменателя соответствует уменьшению общего значения, а уменьшение знаменателя соответствует увеличению
в общей стоимости.Если спутник приблизить к Земле, мы знаем, что радиус орбиты уменьшится, поэтому мы можем
предсказывают, что орбитальная скорость увеличится.
То
зависимость описывается как обратная, потому что увеличение одной величины вызывает уменьшение другой — помните, что
увеличение знаменателя соответствует уменьшению общего значения, а уменьшение знаменателя соответствует увеличению
в общей стоимости.Если спутник приблизить к Земле, мы знаем, что радиус орбиты уменьшится, поэтому мы можем
предсказывают, что орбитальная скорость увеличится.Мы можем найти точный множитель, описывающий изменение 𝑣, подставив множитель, описывающий изменение 𝑟 – в этом отношении пропорция ведет себя аналогично уравнению. Мы хотим изменить радиус орбиты спутника от 𝑅 до 𝑅9, поэтому 𝑅 в настоящее время умножаем на коэффициент 19, который подставляем в пропорцию: 𝑣∝1.
Упрощая математику, 1=1=3.
Следовательно, умножение 𝑅 на коэффициент 19 означает, что 𝑣 должно быть умножается на коэффициент 3.
Таким образом, перемещение спутника на новый орбитальный радиус 𝑅9 заставит спутник двигаться со скоростью новая орбитальная скорость 3𝑣.

В предыдущем примере мы использовали уравнение орбитальной скорости без каких-либо реальных, точных значений для подстановки, однако мы по-прежнему смогли найти значимый результат, изучив взаимосвязь между соответствующими переменными.
Как показано в следующем примере, мы не ограничиваемся использованием в наших расчетах только уравнения орбитальной скорости. Нам может быть предоставлена другая информация о системе, например, период обращения, 𝑇. Помните, что орбитальная уравнение периода 𝑇=2𝜋𝑟𝑣.
Нам может понадобиться использовать это в сочетании с уравнением орбитальной скорости, чтобы узнать о системе.
Пример 5: Расчет массы тела на орбите
Ио — один из четырех галилеевых спутников Юпитера.Ио делает один полный оборот вокруг Юпитера каждые 1,77 дня. Предполагая, что орбита Ио круговая с радиус 422 000 км, рассчитайте массу Юпитера. Используйте значение 6,67×10 м 3 /кг⋅с 2 для универсальной гравитационной постоянной.
 Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.
Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.Ответ
Мы хотим найти массу, которая фигурирует в нашем уравнении для орбитальной скорости, 𝑣=𝐺𝑀𝑟.
Теперь решим уравнение орбитальной скорости для 𝑀. Мы начинаем с возведения в квадрат обеих сторон, чтобы отменить радикальное на правой стороне: 𝑣=𝐺𝑀𝑟.
Теперь умножим обе части уравнения на 𝑟𝐺: 𝑟𝐺⋅𝑣=𝑟𝐺⋅𝐺𝑀𝑟𝑀=𝑟𝑣𝐺.
Теперь у нас есть уравнение, которое мы можем использовать для решения массы Юпитера, но обратите внимание, что у нас еще нет значения для каждого из переменные — мы знаем значения 𝑟 и 𝐺, но не знаем орбитальную скорость Ио, поэтому нам нужен способ вычислить 𝑣.Нам дан период обращения Ио, 𝑇=1,77 дня, и мы знаем уравнение, связывающее орбитальный период и орбитальная скорость: 𝑇=2𝜋𝑟𝑣.
Мы можем переписать уравнение для решения для 𝑣: 𝑣=2𝜋𝑟𝑇.
Мы знаем 𝑟 и 𝑇, но заметим, что нам дано значение для 𝑇, выраженное в днях, что не является единицей СИ, поэтому мы должны преобразовать в секунды, единица СИ для времени.
 Преобразование выглядит следующим образом:
241×601×601=86400.часыденьминутычасысекундыминутысекундыдень
Преобразование выглядит следующим образом:
241×601×601=86400.часыденьминутычасысекундыминутысекундыденьПрименив это к нашему значению 𝑇, 𝑇=1.77×86400=152928.dayssecondsdayseconds
Мы подставим это значение 𝑇 в уравнение орбитального периода, чтобы найти 𝑣. Но сначала, поскольку нам дано значение 𝑟, выраженное в километрах, нам нужно преобразовать 𝑟 в метры. Напомним, что 1=1000км, поэтому 𝑟=422000000м, но это значение лучше выразить в научных обозначение как 𝑟=4,22×10м. Давайте теперь заменим эти значения в уравнение орбитального периода для решения для 𝑣: 𝑣=2𝜋𝑟𝑇=2𝜋4,22×10152928=17338/.msms
Теперь, когда у нас есть значения для 𝑣, 𝑟 и 𝐺, мы можем подставить их в переставил уравнение орбитальной скорости для расчета 𝑀, массы Юпитера: 𝑀=𝑟𝑣𝐺=4,22×10(17338/)6,67×10/⋅=1,90×10,mmsmkgskg
Таким образом, мы нашли массу Юпитера равной 1 01,90 кг.
Давайте закончим резюмированием нескольких важных понятий.

Ключевые точки
- Для движения объекта по круговой орбите вокруг большого объекта массы 𝑀 на радиальном расстоянии 𝑟, он должен иметь орбитальную скорость 𝑣, определяемую выражением 𝑣=𝐺𝑀𝑟.
- Орбитальная скорость не зависит от массы объекта на орбите.
- Мы можем использовать 𝑣=𝐺𝑀𝑟, чтобы найти 𝑀 или 𝑟∶𝑀=𝑟𝑣𝐺, и 𝑟=𝐺𝑀𝑣.
Формула линейной скорости Физика | Решенные и практические вопросы
Линейная скорость — это тема, в которой большое значение придается формулам. Вам нужно запомнить несколько формул именно в этой субъединице. Если вы не можете вспомнить формулы, не волнуйтесь, мы здесь, чтобы помочь! Линейная скорость – это расстояние, пройденное движущимся объектом.Скорость, с которой объект движется по линейной траектории, называется линейной скоростью. Простыми словами, мы можем понять, что линейная скорость – это расстояние, пройденное телом за данный интервал времени. Давайте лучше поймем, что такое линейная скорость, а также решим несколько задач!
Определение линейной скорости
Изменение расстояния во времени называется линейной скоростью.
 Это изменение может быть мгновенным или может происходить в течение определенного периода времени. Когда линейная скорость измеряется в течение очень короткого интервала, она называется мгновенной линейной скоростью, а когда она измеряется в течение заданного периода времени, она называется средней линейной скоростью.Однако, когда линейная скорость измеряется в течение короткого интервала времени, она является более точной.
Это изменение может быть мгновенным или может происходить в течение определенного периода времени. Когда линейная скорость измеряется в течение очень короткого интервала, она называется мгновенной линейной скоростью, а когда она измеряется в течение заданного периода времени, она называется средней линейной скоростью.Однако, когда линейная скорость измеряется в течение короткого интервала времени, она является более точной.Формула линейной скорости
V(линейная скорость) = ∆S/∆T
Выше приведена формула средней линейной скорости. Это мера изменения линейной скорости по отношению ко времени в течение заданного периода времени.
∆S представляет собой изменение расстояния
И ∆T представляет собой время, за которое тело проходит заданное расстояние.
V(линейная скорость) = dS/dT
Выше приведена формула мгновенного измерения линейной скорости.Это измеряет изменение расстояния в течение доли секунды движения.

Здесь dS представляет мгновенное изменение расстояния, а dT представляет долю секунды, затраченную на изменение. Мгновенная скорость является более точной, так как период, учитываемый при нахождении мгновенной линейной скорости, намного меньше.
Формула линейной скорости при круговом движении
Когда тело совершает круговое движение, оно имеет два разных вида скоростей.
Угловая скорость
Линейная скорость
Линейная скорость и угловая скорость вместе составляют скорость тела при круговом движении. Линейная скорость при круговом движении толкает тело двигаться вперед, тогда как угловая скорость возникает из-за центростремительной силы, которая заставляет тело продолжать движение по круговой траектории. Центростремительная сила создает внутреннюю тягу и, следовательно, ограничивает движение по круговой траектории.
 Линейная скорость отвечает за движение тела. Без наличия линейной скорости круговое движение прекратится. Без наличия угловой скорости круговое движение было бы нарушено и движение продолжилось бы в тангенциальном направлении. Следовательно, оба компонента одинаково важны для ограничения движения тела по круговой траектории.
Линейная скорость отвечает за движение тела. Без наличия линейной скорости круговое движение прекратится. Без наличия угловой скорости круговое движение было бы нарушено и движение продолжилось бы в тангенциальном направлении. Следовательно, оба компонента одинаково важны для ограничения движения тела по круговой траектории.Угловая линейная скорость
Как мы видели ранее, вращательное движение имеет два вида скоростей.Угловая скорость тела при вращательном движении обусловлена ускорением, которое толкает тело вперед и заставляет его двигаться по круговой траектории. Формула для угловой линейной скорости приведена ниже
V=rw
Где v — линейная скорость тела, r — радиус окружности, а w — омега, угловая скорость тела, которое движется по круговой траектории.
Решенные вопросы
1. Тело выходит из состояния покоя и движется с ускорением 10 рад с⁻² по окружности радиусом 5 м.
 Найдите линейную скорость тела через 6 с.
Найдите линейную скорость тела через 6 с.Ans:
Ускорение a = 10 рад с⁻²
Радиус r = 5 м
Время t = 6 с
6)
= 60 рад⁻¹
Линейная скорость определяется как
v = r ω
= 5 м × 60 рад с⁻¹
v= 300 м/с.
Следовательно, линейная скорость данного тела равна 300 м/с. Это означает, что если центростремительная сила, действующая на тело, будет устранена, тело продолжит двигаться по касательной.
2. Найдите линейную скорость тела, движущегося со скоростью 30 об/мин по окружности радиусом 5 м?
ANS:
ANS:
Указанные
Угловая скорость = 30 об / мин
= 30 π / 30
= 1 RAD / S
RADIUS R = 2 M
Линейная скорость задается
V = R Ω
v = 2 м × 1 рад/с
v = 2 м/с
3.
 Мальчик вращает йо-йо в радиусе 5 м. Если линейная или тангенциальная скорость йо-йо равна 6 м/с, найдите угловую скорость йо-йо.
Мальчик вращает йо-йо в радиусе 5 м. Если линейная или тангенциальная скорость йо-йо равна 6 м/с, найдите угловую скорость йо-йо.ANS:
ANS:
Указанные
R = 5M
V = 6 м / с
Формула для линейной скорости
V = R ω
Ω = V / R
Ω = 6/5
Ω = 1.2
Советы по изучению формулы линейной скорости
Понимание формулы линейной скорости стало проще благодаря приведенному выше содержанию исследования. Студенты должны были привить уверенность в этой теме.
Подготовка к таким темам для многих может оказаться сложной задачей.Однако тот, кто открывает правильный способ понять, применить и подготовиться к этому, может творить чудеса. На пути вы всегда будете сталкиваться с трудностями. Некоторые люди склонны сдаваться в таких ситуациях, но вам не обязательно быть одним из них.
 Вы должны вкладывать свою энергию в поиск наилучшего решения каждой проблемы, потому что по мере продвижения вперед эти препятствия будут становиться намного легче. Экзаменационного стресса и беспокойства невозможно избежать, но, безусловно, можно изучить вещи, которые помогут вам успокоиться.При этом вы также сможете делать вещи, которые помогут вам обрести больше уверенности.
Вы должны вкладывать свою энергию в поиск наилучшего решения каждой проблемы, потому что по мере продвижения вперед эти препятствия будут становиться намного легче. Экзаменационного стресса и беспокойства невозможно избежать, но, безусловно, можно изучить вещи, которые помогут вам успокоиться.При этом вы также сможете делать вещи, которые помогут вам обрести больше уверенности.Давайте познакомимся с некоторыми приемами яркого пересмотра темы.
Эта техника поможет вам оставаться сосредоточенным и достигать поставленных целей. У вас может быть много способов облегчить себе подготовку, например, составлять списки или следовать контрольному списку и т. д. Как только это войдет в привычку, вы можете предпринять следующие шаги по планированию на неделю и даже на месяц вперед. Убедитесь, что вы можете выделить нужное время для каждой из тем.
Способность анализировать и оценивать последствия, прежде чем планировать свой день или готовиться к какому-либо заданию, является важным навыком, которым должны обладать студенты.
 Ответы на такие вопросы, как результат или окончательные результаты, помогут вам сделать ваш учебный график более эффективным и действенным.
Ответы на такие вопросы, как результат или окончательные результаты, помогут вам сделать ваш учебный график более эффективным и действенным.Две основные области, над которыми вам следует работать, если вы хотите добиться хороших результатов, — это работа над темами, которые оказывают большее влияние, и работа над своими слабостями.Обе области требуют одинакового времени, усилий и внимания. Учащиеся должны следить за тем, чтобы их внимание было сосредоточено, чтобы иметь возможность достичь того, о чем они мечтали.
Подготовиться перед началом — самая большая задача, но она также обязательна. Вы можете очистить свое окружение и оптимизировать свое учебное пространство. Кроме того, не забудьте избавиться от всех отвлекающих факторов вокруг вас. Сделайте свое окружение позитивным и продуктивным. Избавьтесь от всех негативных мыслей и дайте ему толчок. Учащиеся должны понимать, что не только важно поставить себя на работу, но и подготовиться и повысить свою умственную энергию.



 9.2 Угловая и линейная скорости вращения
9.2 Угловая и линейная скорости вращения



 Гравитация Земли вызывает на Луне центростремительное ускорение, которое всегда направлено к Земле.
Гравитация Земли вызывает на Луне центростремительное ускорение, которое всегда направлено к Земле. Это метод Ньютона.
Это метод Ньютона. Под вертикалью всегда понимают направление от спутника к центру притягивающего тела.
Под вертикалью всегда понимают направление от спутника к центру притягивающего тела.

 Таким образом, для объекта, такого как луна, находящегося на круговой орбите, центростремительное ускорение объекта
дан кем-то
𝑎=𝑣𝑟,
где 𝑣 — линейная скорость Луны, а 𝑟 — радиус орбиты.
Таким образом, для объекта, такого как луна, находящегося на круговой орбите, центростремительное ускорение объекта
дан кем-то
𝑎=𝑣𝑟,
где 𝑣 — линейная скорость Луны, а 𝑟 — радиус орбиты. Помните, что это соотношение применяется только в случае круговых орбит,
где орбитальная скорость постоянна; некруговые орбиты не подчиняются этому уравнению.
Помните, что это соотношение применяется только в случае круговых орбит,
где орбитальная скорость постоянна; некруговые орбиты не подчиняются этому уравнению. 97×10 кг для массы Земли
и 6,67×10 м 3 /кг⋅с 2 для значения всемирного тяготения
постоянный. Дайте ответ с точностью до метра в секунду.
97×10 кг для массы Земли
и 6,67×10 м 3 /кг⋅с 2 для значения всемирного тяготения
постоянный. Дайте ответ с точностью до метра в секунду. В зависимости от того, какая информация предоставлена, мы можем изменить уравнение орбитальной скорости, чтобы решить другую величину, помимо
𝑣.Например, в следующем примере мы вычислим радиус орбиты для системы.
В зависимости от того, какая информация предоставлена, мы можем изменить уравнение орбитальной скорости, чтобы решить другую величину, помимо
𝑣.Например, в следующем примере мы вычислим радиус орбиты для системы. 9/=17900/.kmsms
9/=17900/.kmsms


 То
зависимость описывается как обратная, потому что увеличение одной величины вызывает уменьшение другой — помните, что
увеличение знаменателя соответствует уменьшению общего значения, а уменьшение знаменателя соответствует увеличению
в общей стоимости.Если спутник приблизить к Земле, мы знаем, что радиус орбиты уменьшится, поэтому мы можем
предсказывают, что орбитальная скорость увеличится.
То
зависимость описывается как обратная, потому что увеличение одной величины вызывает уменьшение другой — помните, что
увеличение знаменателя соответствует уменьшению общего значения, а уменьшение знаменателя соответствует увеличению
в общей стоимости.Если спутник приблизить к Земле, мы знаем, что радиус орбиты уменьшится, поэтому мы можем
предсказывают, что орбитальная скорость увеличится.
 Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.
Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой. Преобразование выглядит следующим образом:
241×601×601=86400.часыденьминутычасысекундыминутысекундыдень
Преобразование выглядит следующим образом:
241×601×601=86400.часыденьминутычасысекундыминутысекундыдень
 Это изменение может быть мгновенным или может происходить в течение определенного периода времени. Когда линейная скорость измеряется в течение очень короткого интервала, она называется мгновенной линейной скоростью, а когда она измеряется в течение заданного периода времени, она называется средней линейной скоростью.Однако, когда линейная скорость измеряется в течение короткого интервала времени, она является более точной.
Это изменение может быть мгновенным или может происходить в течение определенного периода времени. Когда линейная скорость измеряется в течение очень короткого интервала, она называется мгновенной линейной скоростью, а когда она измеряется в течение заданного периода времени, она называется средней линейной скоростью.Однако, когда линейная скорость измеряется в течение короткого интервала времени, она является более точной.
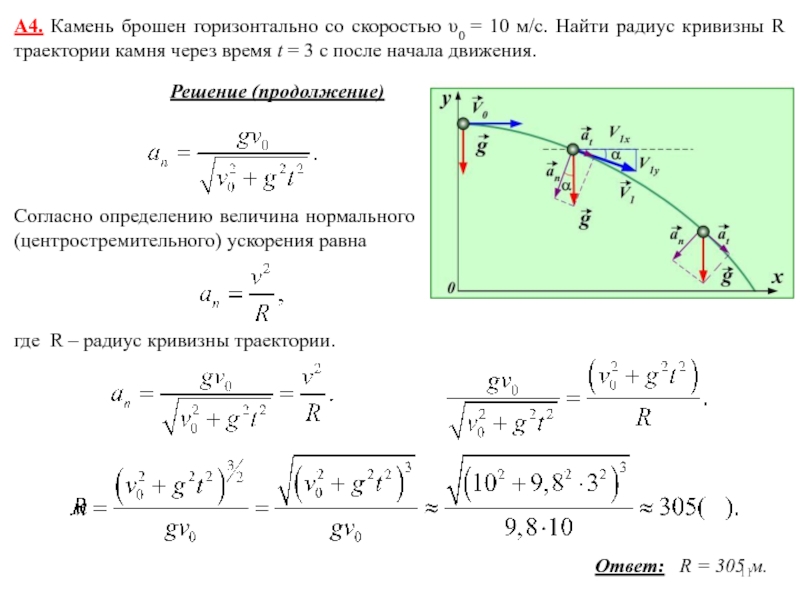 Линейная скорость отвечает за движение тела. Без наличия линейной скорости круговое движение прекратится. Без наличия угловой скорости круговое движение было бы нарушено и движение продолжилось бы в тангенциальном направлении. Следовательно, оба компонента одинаково важны для ограничения движения тела по круговой траектории.
Линейная скорость отвечает за движение тела. Без наличия линейной скорости круговое движение прекратится. Без наличия угловой скорости круговое движение было бы нарушено и движение продолжилось бы в тангенциальном направлении. Следовательно, оба компонента одинаково важны для ограничения движения тела по круговой траектории. Найдите линейную скорость тела через 6 с.
Найдите линейную скорость тела через 6 с. Мальчик вращает йо-йо в радиусе 5 м. Если линейная или тангенциальная скорость йо-йо равна 6 м/с, найдите угловую скорость йо-йо.
Мальчик вращает йо-йо в радиусе 5 м. Если линейная или тангенциальная скорость йо-йо равна 6 м/с, найдите угловую скорость йо-йо. Вы должны вкладывать свою энергию в поиск наилучшего решения каждой проблемы, потому что по мере продвижения вперед эти препятствия будут становиться намного легче. Экзаменационного стресса и беспокойства невозможно избежать, но, безусловно, можно изучить вещи, которые помогут вам успокоиться.При этом вы также сможете делать вещи, которые помогут вам обрести больше уверенности.
Вы должны вкладывать свою энергию в поиск наилучшего решения каждой проблемы, потому что по мере продвижения вперед эти препятствия будут становиться намного легче. Экзаменационного стресса и беспокойства невозможно избежать, но, безусловно, можно изучить вещи, которые помогут вам успокоиться.При этом вы также сможете делать вещи, которые помогут вам обрести больше уверенности. Ответы на такие вопросы, как результат или окончательные результаты, помогут вам сделать ваш учебный график более эффективным и действенным.
Ответы на такие вопросы, как результат или окончательные результаты, помогут вам сделать ваш учебный график более эффективным и действенным.