5 фактов, которые вы должны знать
Центростремительная сила отвечает за центростремительное движение объекта, а действующая против нее центробежная сила препятствует встрече объекта с центром окружности.
Центростремительное ускорение и радиус, очевидно, связаны друг с другом, так как объект, движущийся по круговой траектории с приложением центростремительной силы, сохраняет ускорение объекта по радиусу окружности. Оба вектора остаются в уникальном направлении.
Как центростремительное ускорение связано с радиусом?Центростремительное ускорение проявляется, когда объект совершает круговое движение и проходит путь по окружности определенного радиуса.
Объект, движущийся по кругу, ускоряется, поддерживая постоянное расстояние от центра, которое является радиусом кругового пути. Направление центростремительного ускорения объекта действует к центру кругового пути, прочерченного объектом по радиусу окружности.
Сила, удерживающая тело в круговом движении, называется центростремительной силой. Но это не только ответственность за движение объекта по круговой траектории. Сила действует против центростремительной силы и препятствует их падению внутрь. Сила, удерживающая их на месте при движении по круговой траектории, называется центробежной силой.
Но это не только ответственность за движение объекта по круговой траектории. Сила действует против центростремительной силы и препятствует их падению внутрь. Сила, удерживающая их на месте при движении по круговой траектории, называется центробежной силой.
На объект, ускоряющийся при круговом движении, действует центростремительная сила. Центростремительная сила, ускоряющая тело со скоростью v, определяется выражением:
F = mv2/r
Здесь m — масса объекта, а
r – радиус кругового пути.
Since F=ma from Newton’s second law of motion. Using this in the above equation, we get:
ма=мв2/r
Следовательно, формула для нахождения центростремительного ускорения объекта при круговом движении дается как:
a=mv2/r
Согласно этому уравнению, центростремительное ускорение объекта составляет половину квадрата скорости объекта. Линейная скорость всегда перпендикулярна центростремительному ускорению, действующему внутрь.
Приведенное выше уравнение ясно показывает, что угловое ускорение обратно пропорциональна радиусу кругового пути. Отсюда следует, что наибольшее центростремительное ускорение объекта мы будем иметь для объекта, распространяющегося по окружностям малого радиуса.
График центростремительного ускорения и радиусаТеперь давайте поймем обратную зависимость между центростремительным ускорением и радиусом круговой траектории, работая на одном простом примере.
Предположим, что в какое-то место привозят разные карусели с разными радиусами для изучения влияния радиуса вращающегося колеса на скорость движения. центростремительное ускорение карусели. Крутящий момент прикладывается ко всем каруселям поочередно, поддерживая постоянную скорость 3 м/с.
карусель; Кредит изображения: pixabayFor the first merry-go-round, the radius r=1 m, hence the центростремительное ускорение для этого колеса,
a1=мв2/r
=
The second merry-go-round has a radius r=2 m, hence the centripetal acceleration for this wheel is,
a2=v2/r
The third merry-go-round has a radius r=3 m, hence the centripetal acceleration for this wheel is,
a3=v2/r
The fourth merry-go-round has a radius r=4 m, hence the centripetal acceleration for this wheel is,
a4=v2/r
The fifth merry-go-round has a radius r=5 m, hence the centripetal acceleration for this wheel is,
a5=v2/r
Полученные данные заносятся в таблицу ниже:
| № карусели | Радиус (м) | Центростремительное ускорение (м/с2) |
| 1st | 1 | 3 |
| 2nd | 2 | 1. 5 5 |
| 3rd | 3 | 1 |
| 4th | 4 | 0.75 |
| 5th | 5 | 0.6 |
Построим график зависимости центростремительного ускорения от радиуса/с для приведенных выше данных.
Из приведенного выше графика можно сказать, что центростремительное ускорение объекта при круговом движении экспоненциально убывает с увеличением радиуса. Величина центростремительного ускорения уменьшается по радиусу.
Следовательно, чтобы сохранить центростремительное ускорение, скорость объекта должна увеличиваться по мере увеличения окружности пути, пройденного объектом.
Это связано с тем, что с увеличением радиуса центростремительная сила, действующая на объект, уменьшается. Мы можем связать это с кулоновской силой между двумя разноименными зарядами. По мере увеличения линейного расстояния между ними величина силы уменьшается.
Что произойдет с центростремительным ускорением, если радиус увеличить вдвое?Центростремительное ускорение объекта больше для малого радиуса круга по сравнению с большими радиусами.
Если радиус кругового пути удвоить, сохраняя радиальную скорость объекта постоянной, то центростремительное ускорение объекта уменьшится вдвое.
Если объект движется со скоростью u по круговой траектории радиуса r, а тот же объект движется по другой круговой траектории радиусом 2r со скоростью v, то изменение центростремительное ускорение равно
Это уравнение дает изменение центростремительное ускорение тела, движущегося с разными скоростями при движении по разным круговым дорожкам разного радиуса.
Чему равно центростремительное ускорение автомобиля, движущегося по круговой дорожке стадиона со скоростью 20 км/ч? Диаметр стадиона составляет 70 метров.Данный: Скорость автомобиля равна,
Диаметр стадиона d= 70 м.
Следовательно, радиус стадиона равен r = 35 м.
Игровой автомат формула для расчета центростремительного ускорения машины вдоль стадиона есть,
а=в2/r
Подставляя значения в это уравнение, мы получаем,
Hence, the centripetal acceleration of a car is 0.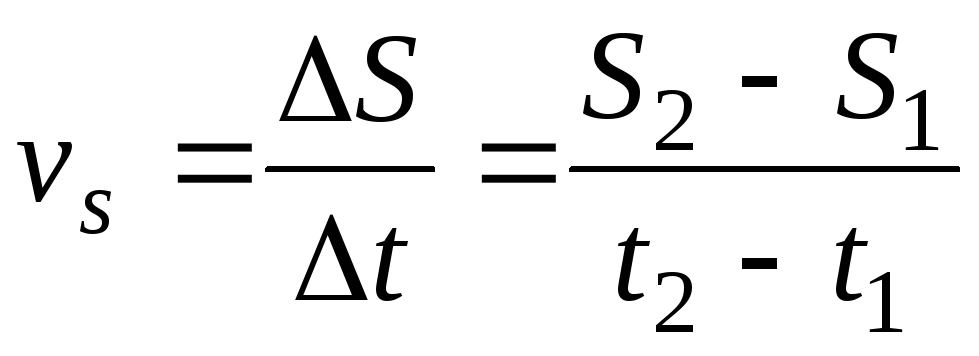 86 m/s2 во время движения по стадиону.
86 m/s2 во время движения по стадиону.
Данный: The initial length of the rope is, l1=100 cm = 1 m
The final length of the rope is, l2=100/2 cm = 50 cm = 0.5 m[/latex].
Let the initial velocity of the object be ‘u’ and the final velocity be ‘v’. The final velocity is doubled the initial velocity, hence, v=2u.
Начальная центростремительное ускорение объекта,
Окончательное центростремительное ускорение тела равно
Отсюда мы видим, что ускорение объекта увеличивается в 16 раз больше, чем начальное центростремительное ускорение объекта после уменьшения длины веревки вдвое.
ЗаключениеЦентростремительное ускорение объекта, движущегося по круговой траектории, зависит от радиуса окружности. центростремительное ускорение направлен внутрь по радиусу окружности. 2/R
2/R
Следовательно,при увеличении радиуса,ускорение уменьшится.
Похожие вопросы
Сила 15 Н действует на тело массой 0.5 кг. какая сила сообщит такое же ускорение телу массой 2 кг?
решение с дано, найти и системой СИ…
Какова масса груза подвешенного на пружине жесткостью 100Н/м если она удлиннилась на 5 см…
Якщо відкриту каструлю з водою поставити на плиту, то:…
В соревновании по перетягиванию каната участвуют четыре человека. Двоек из них, прикладывая силы 350 H и 150 H, тянут канат вправо, а двое других с силами 400 H и 200 H , влево. Какова равнодействующая этих сил ? В каком направлении будет перемещаться канат ?.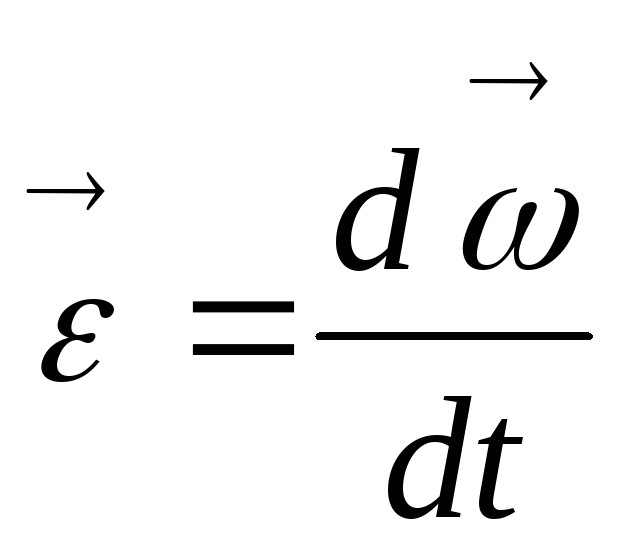
Какова плотность жидкости если она весит 400Н а вместимостью сосуда 50л…
СРОЧНО!
Сформулируйте условие статистического равновесия для вращательного движения….
Математика
Литература
Русский язык
Геометрия
Английский язык
Химия
Биология
Другие предметы
История
Обществознание
География
Українська мова
Українська література
Қазақ тiлi
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 5Следующая ⇒
v=dr/dt a=dv/dt Скорость характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной. Ускорение – векторная физическая величина, характеризующая быстроту изменения скорости.
Нормальное и тангенциальное ускорение.
Тангенциальное ускорение – ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении. Нормальное ускорение – ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении. где ω — угловая скорость относительно центра вращения, а r — радиус окружности.
Связь угла поворота, угловой скорости и углового ускорения.
Угловая скорость — векторная физическая величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения в единицу времени: , а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Угловое ускорение — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости материальной точки. При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости по времени, то есть , и направлен по касательной к годографу вектора в соответствующей его точке.
Связь угловых и линейных величин. Законы Ньютона.
1) Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения. 2) В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. 3) Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: 7. Силы в механике (вид, к чему приложена, куда направлена, чему равна). Сюда относятся силы упругости, сила трения, сила тяжести, вес. Сила – физическая величина, являющаяся количественной мерой воздействия одного тела на другое, в результате которого тело приобретает ускорение или деформируется. Сила упругости — сила, возникающая при деформации тела и противодействующая этой деформации. Действует в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. Вектор силы противоположен направлению деформации тела (смещению его молекул). Закон Гука: Силой трения– сила, которая возникает при движении одного тела по поверхности другого. Сила трения всегда направлена вдоль поверхности соприкосновения в сторону, противоположную движению. Сила трения прямо пропорциональна весу тела (P) и силе нормальной реакции (N) и зависит от того, насколько сильно тела прижаты друг к другу. Сила тяжести – сила, действующая на тело со стороны Земли и сообщающая телу ускорение свободного падения (Fт=mg). Направление силы тяжести – вертикаль в данной точке земной поверхности. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести Fт=GMm/R2 . СИЛА ТЯЖЕСТИ, сила P, действующая на любое тело, находящееся вблизи земной поверхности, и определяемая как геометрическая сумма силы притяжения Земли F и центробежной силы инерции Q, учитывающей эффект суточного вращения Земли. Вес тела – сила, в которой вследствие притяжения к Земле тело действует на свою опору или подвес.
Закон всемирного тяготения. Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.
⇐ Предыдущая12345Следующая ⇒ Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 891; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
домашнее задание и упражнения – Радиус центростремительного ускорения
Вопрос задан
Изменено 2 года, 11 месяцев назад
Просмотрено 16 тысяч раз
$\begingroup$
Предположим, вы движетесь по кругу радиусом $r$. Так что должно быть центростремительное ускорение к центру. Теперь вы хотите уменьшить радиус круга, поэтому кто-то должен приложить большее центростремительное ускорение, чтобы уменьшить ваш радиус. Но я читал, что с увеличением радиуса увеличивается центростремительное ускорение. Какое правильное объяснение без использования формулы? Делая это более ясным: «Моя интуиция подсказывает мне, что если я уменьшу центральную силу, действующую на объект в равномерном круговом движении, радиус круга должен увеличиться?»
- домашние задания и упражнения
- ньютоновская механика
- кинематика
- ускорение
- вращательная кинематика
$\endgroup$
3
$\begingroup$
Все зависит от того, что остается неизменным при изменении радиуса. Если вы поддерживаете постоянную угловую скорость (что то же самое, что поддерживаете постоянную частоту вращения или период), то центростремительное ускорение будет увеличиваться. Примером этого может быть удаление от центра вращающейся карусели.
Если вы поддерживаете постоянную угловую скорость (что то же самое, что поддерживаете постоянную частоту вращения или период), то центростремительное ускорение будет увеличиваться. Примером этого может быть удаление от центра вращающейся карусели.
Если вы поддерживаете постоянную скорость и увеличиваете радиус, то центростремительное ускорение уменьшится. Примером этого может быть движение по кривой с увеличивающимся радиусом (спираль) с постоянной скоростью.
Чтобы понять почему, вспомните, что ускорение — это скорость изменения скорости. Давайте пока предположим, что мы думаем о круговом движении с постоянной скоростью, поэтому ускорение будет результатом изменения направления скорости. Рассмотрим объект, проходящий половину круга. За это время направление его движения изменится на 180 градусов, величина изменения его скорости будет в два раза больше величины его начальной скорости. Например, если он первоначально двигался на восток со скоростью 10 м/с, а в итоге движется на запад со скоростью 10 м/с, его скорость изменилась на 20 м/с. Большее ускорение может возникнуть двумя способами: либо из-за большего изменения скорости, либо из-за изменения скорости за более короткий промежуток времени.
Большее ускорение может возникнуть двумя способами: либо из-за большего изменения скорости, либо из-за изменения скорости за более короткий промежуток времени.
В первом примере (постоянная угловая скорость) увеличение радиуса не меняет время, необходимое для прохождения половины пути. Люди, находящиеся в середине или на внешнем краю карусели, совершают половину оборота за одно и то же время, но люди с большим радиусом, находящиеся у края, должны двигаться быстрее. Они проходят больший круг за то же время. Это означает, что изменение скорости для людей с большим радиусом больше, и, следовательно, их центростремительное ускорение больше. 92}{r}$$
Если вы хотите уменьшить радиус $r$, на первый взгляд кажется, что у вас есть два варианта:
Но никогда не будьте столь строги в своих мыслях. Например:
Я хочу уменьшить $r$, поэтому я также уменьшаю $v$. Но если я недостаточно уменьшу $v$, то я должен немного уменьшить и $a$, чтобы уравнение оставалось верным.
 Теперь уменьшение как $a$, так и $v$ по-прежнему дает правильное уменьшение $r$.
Теперь уменьшение как $a$, так и $v$ по-прежнему дает правильное уменьшение $r$.Но если я уменьшу $v$ слишком сильно, то $a$ придется немного увеличьте , чтобы уравнение было верным. Тогда уменьшение $v$, но увеличение $a$ дает правильное уменьшение $r$.
Итог: Вы в первую очередь должны знать взаимосвязь между параметрами, которые пытаетесь изменить. Знание отношения показывает, что задействовано больше параметров, чем просто два $a$ и $r$.
И тогда вы должны знать , если какой-либо из этих параметров остается постоянным ! Потому что, если это не так, все параметры могут измениться одновременно. А когда есть более одного параметра, можно сказать что угодно и ничего нельзя сказать наверняка, потому что многие настройки этих параметров могут заставить его работать. Тогда вы не можете знать, что увеличивается или уменьшается, чтобы получить уменьшенный $r$.
Итак, будьте в курсе ситуации и условий. Утверждения, на которые вы ссылаетесь, тоже требуют этих знаний – иначе они бесполезны.
Утверждения, на которые вы ссылаетесь, тоже требуют этих знаний – иначе они бесполезны.
$\endgroup$
3
$\begingroup$
Для любых двух ситуаций, когда объект движется по окружности, при условии, что линейная скорость в обоих случаях одинакова, больший радиус требует меньшей центростремительной силы, чтобы объект двигался по окружности.
Возможно, повседневным примером этого является движение по кривой автомагистрали. Когда вы едете по кривой, вы чувствуете «инерционную» или «фиктивную» центробежную силу, которая ощущается сильнее, когда у вас большее центростремительное ускорение. Так что если вы идете по кривой малой кривизны – а значит и малого радиуса – вы чувствуете, что вас вот-вот выбросит из машины (фиктивная сила), а значит у вас более сильное центростремительное ускорение. Однако, если бы вы ехали с той же скоростью по кривой с большим радиусом, вы бы не чувствовали столько силы инерции, и, следовательно, центростремительное ускорение было бы меньше.
$\endgroup$
4
$\begingroup$
В ваших двух противоречивых “объяснениях” отсутствует ключевой момент:
Пока вы меняете радиус, вы не двигаетесь по кругу вокруг исходной центральной точки. Вы движетесь по какой-то спирали .
Подумайте о камне, привязанном к веревке, которая вращается по кругу. Если вы потянете за нить сильнее, чтобы укоротить ее, камень начнет закручиваться внутрь, а струна применит тангенциальная сила к камню, а также радиальная сила, вызывающая центростремительное ускорение. Тангенциальная сила увеличит скорость движения камня по окружности по мере уменьшения радиуса.
Таким образом, есть два изменения, которые оказывают противоположное влияние на натяжение струны. Уменьшение радиуса и сохранение всего остального без изменений уменьшит центростремительное ускорение, но увеличение скорости и сохранение всего остального без изменений увеличит его.
Чтобы узнать, какой эффект “победит”, вам нужно немного посчитать, но вы сказали, что вам не нужна “формула”.
Также в вопросе говорится, что “вы” движетесь по кругу, но не сказано, как к вам прилагается центростремительная сила, которая заставляет вас двигаться по кругу.
Итак, вы не полностью описали реальную систему и не хотите использовать лучший способ (математику) для моделирования ее поведения. Следовательно, это не полный ответ!
$\endgroup$
$\begingroup$
Возьмем классический пример: мячик вращается вокруг ваших пальцев на натянутой струне.
Нить натянута, потому что мяч движется по кругу. Сила натяжения постоянно заставляет мяч ускоряться по направлению к вашим пальцам. Мяч всегда стремится двигаться по касательной прямо от вашей руки. Напряжение постоянно препятствует этому. Напряжение связано с 3 вещами; масса мяча, скорость мяча и радиус струны.
Если вы увеличите массу мяча, увеличится натяжение, чтобы удержать его на орбите с его текущей скоростью и радиусом, потому что требуется больше силы, чтобы удержать большую массу на существующей орбите.
Если вы увеличите радиус орбиты и сохраните скорость и массу прежними, то орбита станет более крупной и более плавной. Вы можете увеличить радиус настолько, что кривая будет ОЧЕНЬ плавной и теоретически приблизится к касательной линии, по которой мяч действительно хочет следовать. Этот увеличенный радиус и результирующая более плавная кривая приводят к УМЕНЬШЕНИЮ ограничивающего напряжения. Если вы УМЕНЬШАЕТЕ радиус при тех же обстоятельствах, кривая настолько крутая и такое отклонение от желаемой касательной линии, что мяч хочет следовать, то ограничивающее напряжение должно УВЕЛИЧИТЬСЯ, чтобы выполнить это .
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Определение радиуса поворота и поперечного ускорения транспортного средства с помощью датчика GNSS/INS
. 2022 16 марта; 22 (6): 2298.
2022 16 марта; 22 (6): 2298.
дои: 10.3390/s22062298.
Юрай Ягельчак 1 , Йозеф Гнап 1 , Ондрей Куба 1 , Ярослав Фрнда 2 , Мариуш Костшевский 3
Принадлежности
- 1 Кафедра дорожного и городского транспорта, факультет эксплуатации и экономики транспорта и коммуникаций Жилинского университета, 010 26 Жилина, Словакия.
- 2 Кафедра количественных методов и экономической информатики, факультет эксплуатации и экономики транспорта и коммуникаций Жилинского университета, 010 26 Жилина, Словакия.

- 3 Отдел строительства и эксплуатации транспортных средств, факультет транспорта, Варшавский технологический университет, ул. Кошикова 75, 00-662 Варшава, Польша.
- PMID: 35336468
- PMCID: PMC8950859
- DOI: 10.3390/с22062298
Бесплатная статья ЧВК
Юрай Ягельчак и др. Датчики (Базель). .
Бесплатная статья ЧВК
. 2022 16 марта; 22 (6): 2298.
2022 16 марта; 22 (6): 2298.
дои: 10.3390/s22062298.
Авторы
Юрай Ягельчак 1 , Йозеф Гнап 1 , Ондрей Куба 1 , Ярослав Фрнда 2 , Мариуш Костшевский 3
Принадлежности
- 1 Кафедра дорожного и городского транспорта, факультет эксплуатации и экономики транспорта и коммуникаций Жилинского университета, 010 26 Жилина, Словакия.
- 2 Кафедра количественных методов и экономической информатики, факультет эксплуатации и экономики транспорта и коммуникаций Жилинского университета, 010 26 Жилина, Словакия.

- 3 Отдел строительства и эксплуатации транспортных средств, факультет транспорта, Варшавский технологический университет, ул. Кошикова 75, 00-662 Варшава, Польша.
- PMID: 35336468
- PMCID: PMC8950859
- DOI: 10,3390/с22062298
Абстрактный
В этой статье мы рассматриваем определение радиуса поворота и поперечного ускорения, действующего на транспортное средство полной массой до 3,5 т (GVM) и груз в кривых на основе радиуса поворота и скорости. Датчик глобальной навигационной спутниковой системы с инерциальной навигационной системой (GNSS/INS) с двумя антеннами используется для измерения ускорения, скорости и положения транспортного средства, чтобы определить радиус поворота и определить правильную формулу для расчета длинного среднего поперечного ускорения, действующего на транспортное средство и груз. Были применены два метода автоматического выбора событий на основе стабильного значения поперечного ускорения и среднеквадратичной ошибки (MSE) радиусов поворота. Модели расчета радиуса поворота справедливы для радиуса поворота в пределах 5-70 м для обоих методов автоматического отбора событий со среднеквадратичной ошибкой (СКО) 1,88 м и 1,32 м. Модели расчета бокового ускорения действительны при средних значениях СКО 0,022 g и 0,016 g для обоих методов автоматического выбора событий. Результаты статьи могут быть применены при планировании и реализации процедур упаковки и крепления грузов для расчета среднего поперечного ускорения, действующего на транспортное средство и груз, исходя из радиуса поворота и скорости для транспортных средств полной разрешенной массой до 3,5 т. Результаты потенциально могут быть применены для развертывания автономных транспортных средств в решениях, объединенных термином «Логистика 4.0».
Были применены два метода автоматического выбора событий на основе стабильного значения поперечного ускорения и среднеквадратичной ошибки (MSE) радиусов поворота. Модели расчета радиуса поворота справедливы для радиуса поворота в пределах 5-70 м для обоих методов автоматического отбора событий со среднеквадратичной ошибкой (СКО) 1,88 м и 1,32 м. Модели расчета бокового ускорения действительны при средних значениях СКО 0,022 g и 0,016 g для обоих методов автоматического выбора событий. Результаты статьи могут быть применены при планировании и реализации процедур упаковки и крепления грузов для расчета среднего поперечного ускорения, действующего на транспортное средство и груз, исходя из радиуса поворота и скорости для транспортных средств полной разрешенной массой до 3,5 т. Результаты потенциально могут быть применены для развертывания автономных транспортных средств в решениях, объединенных термином «Логистика 4.0».
Ключевые слова: датчики ГНСС/ИНС; груз; крепление груза; боковое ускорение; радиус поворота; средство передвижения.
Заявление о конфликте интересов
Авторы заявляют об отсутствии конфликта интересов.
Цифры
Рисунок 1
Влияние времени оценки на…
Рисунок 1
Влияние времени оценки на поперечное ускорение, полученное от IMU во время…
фигура 1Влияние времени оценки на поперечное ускорение, полученное от IMU во время движения автомобиля на повороте (необработанные данные ayRAW, ay80, ay300, ay1000 — время оценки 80, 300 и 1000 мс).
Рисунок 2
Радиус поворота R 2 от…
Рисунок 2
Радиус поворота R 2 от описанной окружности треугольника, определяемого тремя…
фигура 2 Радиус поворота R2 от описанной окружности треугольника, определяемого тремя точками на кривой.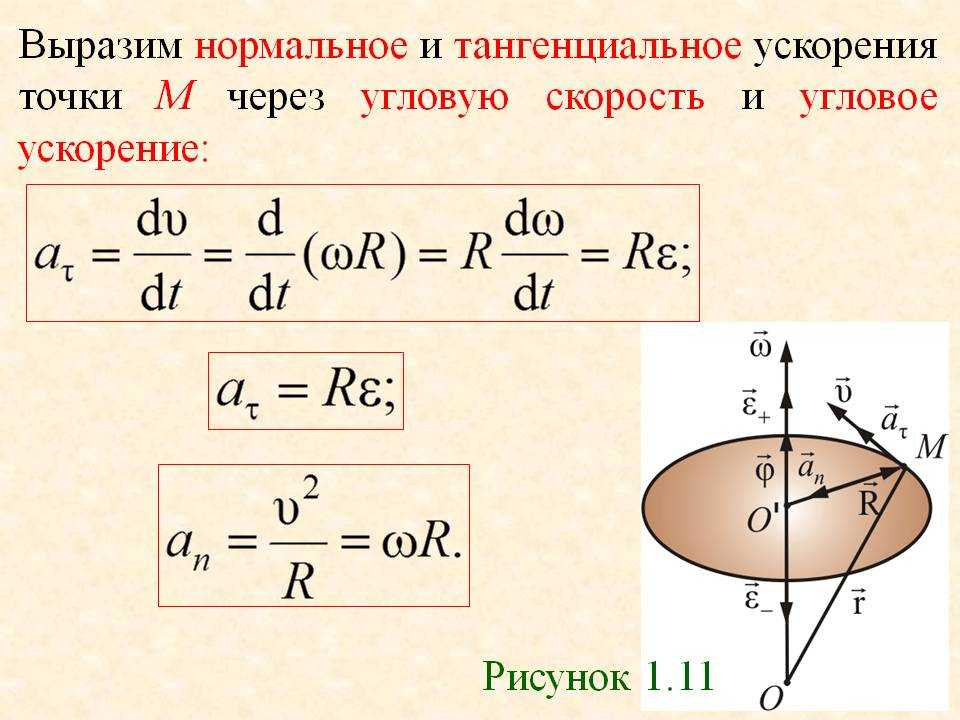
Рисунок 3
Пример автоматического выбора…
Рисунок 3
Пример автоматического выбора событий на основе устойчивых боковых ускорений.
Рисунок 3Пример автоматического выбора событий на основе устойчивых боковых ускорений.
Рисунок 4
Пример автоматического выбора…
Рисунок 4
Пример автоматического выбора событий на основе MSE R 1 и…
Рисунок 4 Пример автоматического выбора событий на основе MSE R 1 и R 2.
Рисунок 5
Фургон V7 ( левый…
Рисунок 5
Фургон V7 ( левый фото ) и автопоезд V10 ( правый…
Рисунок 5Автомобиль-фургон V7 ( левое фото ) и автопоезд V10 ( правое фото ) использовались в испытаниях.
Рисунок 6
Схема установки тестовой установки.
Рисунок 6
Схема установки тестовой установки.
Рисунок 6 Схема установки тестовой установки.
Рисунок 7
Тестовый маршрут TR1 в городе…
Рисунок 7
Тестовый маршрут TR1 в городе Жилина на слое карты OpenStreetMap (OSM).
Рисунок 7Тестовый маршрут TR1 в городе Жилина на слое карты OpenStreetMap (OSM).
Рисунок 8
Тестовый маршрут TR2 в городе…
Рисунок 8
Тестовый маршрут TR2 в городе Жилина на улице Высокошколаков на OSM…
Рисунок 8 Тестовый маршрут TR2 в городе Жилина на улице Высокошколаков на слое карты OSM с 4 проходами трех круговых развязок.
Рисунок 9
Радиус поворота R 1 против…
Рисунок 9
Радиус поворота R 1 и R 2 событий для SEL 1.
Рисунок 9Радиус поворота R1 и R2 событий для SEL 1.
Рисунок 10
Радиус поворота R 1 против…
Рисунок 10
Радиус поворота R 1 против R 2 событий для SEL2.
Рисунок 10Радиус поворота R1 и R2 событий для SEL2.
Рисунок 11
Рассчитано a y C против…
Рисунок 11
Расчетное значение a y C в сравнении с измеренным значением a y M событий для SEL1.
Расчетное значение ayC в сравнении с измеренным значением ayM событий для SEL1.
Рисунок 12
Рассчитано a y C против…
Рисунок 12
Расчетное значение a y C в сравнении с измеренным значением a y M событий для SEL2.
Рисунок 12Расчетное значение ayC в сравнении с измеренным значением ayM событий для SEL2.
Рисунок 13
Максимальное поперечное ускорение a y…
Рисунок 13
Максимальное поперечное ускорение a y Максимальное поперечное ускорение в зависимости от среднего поперечного ускорения a…
Рисунок 13 Максимальное поперечное ускорение ayMax в сравнении со средним боковым ускорением ayM событий для SEL1.
Рисунок 14
Максимальное поперечное ускорение a y…
Рисунок 14
Максимальное поперечное ускорение a y Максимальное поперечное ускорение в зависимости от среднего поперечного ускорения a…
Рисунок 14Максимальное боковое ускорение ayMax в сравнении со средним боковым ускорением ayM событий для SEL2.
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Расчет среднего бокового ускорения автомобиля на малых кольцевых развязках.
Ягельчак Й, Гнап Й, Костржевски М, Куба О, Фрнда Й. Ягельчак Дж. и соавт.
 Датчики (Базель). 2022 1 июля; 22 (13): 4978. дои: 10.3390/s22134978.
Датчики (Базель). 2022.
PMID: 35808473
Бесплатная статья ЧВК.
Датчики (Базель). 2022 1 июля; 22 (13): 4978. дои: 10.3390/s22134978.
Датчики (Базель). 2022.
PMID: 35808473
Бесплатная статья ЧВК.Исследование практических последствий использования одноантенных и двухантенных датчиков GNSS/INS в приложениях UAS-Lidar.
Brazeal RG, Wilkinson BE, Benjamin AR. Бразил Р.Г. и др. Датчики (Базель). 2021 9 августа; 21 (16): 5382. дои: 10.3390/s21165382. Датчики (Базель). 2021. PMID: 34450824 Бесплатная статья ЧВК.
Внедрение и анализ тесно связанной глобальной навигационной спутниковой системы точного позиционирования / инерциальной навигационной системы (GNSS PPP / INS) с недостаточным количеством спутников для навигации наземных транспортных средств.
Лю Ю, Лю Ф, Гао Ю, Чжао Л.
 Лю Ю и др.
Датчики (Базель). 2018 6 декабря; 18 (12): 4305. дои: 10.3390/s18124305.
Датчики (Базель). 2018.
PMID: 30563255
Бесплатная статья ЧВК.
Лю Ю и др.
Датчики (Базель). 2018 6 декабря; 18 (12): 4305. дои: 10.3390/s18124305.
Датчики (Базель). 2018.
PMID: 30563255
Бесплатная статья ЧВК.Оптические датчики и датчики массового расхода для облегчения навигации транспортных средств в условиях, когда GNSS запрещена.
Мусса М., Захран С., Мостафа М., Мусса А., Эль-Шейми Н., Эльхабиби М. Мусса М. и др. Датчики (Базель). 2020 17 ноября; 20 (22): 6567. дои: 10.3390/s20226567. Датчики (Базель). 2020. PMID: 33212949 Бесплатная статья ЧВК.
Применение датчиков MEMS для оценки динамики крепления грузов на дорожных транспортных средствах.
Гнап Ю., Ягельчак Ю., Мариенко П., Франчак М., Костржевски М. Гнап Дж. и др. Датчики (Базель).
 2021 20 апреля; 21 (8): 2881. дои: 10.3390/s21082881.
Датчики (Базель). 2021.
PMID: 33924081
Бесплатная статья ЧВК.
2021 20 апреля; 21 (8): 2881. дои: 10.3390/s21082881.
Датчики (Базель). 2021.
PMID: 33924081
Бесплатная статья ЧВК.
Посмотреть все похожие статьи
Цитируется
Обнаружение многолучевости/NLOS на основе кластеризации K-средних для тесно связанной системы GNSS/INS в городских районах.
Ван Х, Пан С, Гао В, Ся И, Ма С. Ван Х и др. Микромашины (Базель). 2022 17 июля; 13 (7): 1128. дои: 10.3390/ми13071128. Микромашины (Базель). 2022. PMID: 35888947 Бесплатная статья ЧВК.
Расчет среднего бокового ускорения автомобиля на малых кольцевых развязках.
Ягельчак Й, Гнап Й, Костржевски М, Куба О, Фрнда Й. Ягельчак Дж. и соавт. Датчики (Базель). 2022 1 июля; 22 (13): 4978.
 дои: 10.3390/s22134978.
Датчики (Базель). 2022.
PMID: 35808473
Бесплатная статья ЧВК.
дои: 10.3390/s22134978.
Датчики (Базель). 2022.
PMID: 35808473
Бесплатная статья ЧВК.Интегрированная система внутреннего позиционирования тепличного робота на основе UWB/IMU/ODOM/LIDAR.
Лонг Зи, Сян И, Лэй Икс, Ли И, Ху Зи, Дай Икс. Лонг З. и др. Датчики (Базель). 2022 25 июня; 22 (13): 4819. дои: 10.3390/s22134819. Датчики (Базель). 2022. PMID: 35808314 Бесплатная статья ЧВК.
использованная литература
- EN 12642:2016 Безопасность дорожного движения на дорожных транспортных средствах — Конструкция кузова коммерческих транспортных средств — Минимальные требования. [(по состоянию на 7 февраля 2022 г.)]. Доступно онлайн: https://standards.iteh.ai/catalog/standards/cen/cfb5d8a8-67c0-46fc-8b51-….

- EN 12642:2016 Безопасность дорожного движения на дорожных транспортных средствах — Конструкция кузова коммерческих транспортных средств — Минимальные требования. [(по состоянию на 7 февраля 2022 г.)]. Доступно онлайн: https://standards.iteh.ai/catalog/standards/cen/cfb5d8a8-67c0-46fc-8b51-….
- EN 17321:2020 Интермодальные грузовые единицы и грузовые автомобили. Транспортная устойчивость упаковок. Минимальные требования и испытания. [(по состоянию на 7 февраля 2022 г.)]. Доступно в Интернете: https://standards.iteh.ai/catalog/standards/sist/545c1b9f-c7d0-4196-aec8….
- Алонсо М., Мантарас Д.А., Луке П. К методологии оценки безопасности транспортного средства. Саф. науч. 2019;119:133–140. doi: 10.1016/j.ssci.2019.01.012. – DOI
- Бираль Ф., да Лио М., Бертолацци Э. Объединение запасов безопасности и предпочтений пользователя в критерий вождения для оптимального расчета эталонных маневров на основе управления для ADAS следующего поколения; Материалы симпозиума IEEE Intelligent Vehicles 2005; Лас-Вегас, Невада, США.
 6–8 июня 2005 г.; Пискатауэй, Нью-Джерси, США: IEEE; 2005. С. 36–41.
–
DOI
6–8 июня 2005 г.; Пискатауэй, Нью-Джерси, США: IEEE; 2005. С. 36–41.
–
DOI
- Бираль Ф., да Лио М., Бертолацци Э. Объединение запасов безопасности и предпочтений пользователя в критерий вождения для оптимального расчета эталонных маневров на основе управления для ADAS следующего поколения; Материалы симпозиума IEEE Intelligent Vehicles 2005; Лас-Вегас, Невада, США.
- Алонсо М., Мантарас Д.А., Луке П. Методология определения запаса прочности в реальном времени в дорожном транспортном средстве. трансп. Рез. Процессия. 2018; 33:331–338. doi: 10.1016/j.trpro.2018.10.110. – DOI
термины MeSH
Грантовая поддержка
- 2/KCMD/2021/Жилинский университет
Центростремительное ускорение
| Результат | х |
Для расчета: | Радиус скорости ускорения | |
Скорость: | ft/hrft/minft/sin/hrin/minin/secnmach[M]m/hrcm/hrkm/hr m/mincm/min km/min m/scm/mscm/sm/mskm/mskm/smphmpmmpsyd/hryd/minyd /с | |
Радиус | mcmfthminkmmilemmyd | |
Ускорение: | fph/minfph/sfpm/sft/hr²ft/min²ft/s²galgalileogravityGiph/miniph/sipm/sin/hr²in/min²in/s²kn/hrkn/minkn/skn/msm/hr²mm/hr²cm/hr²km/hr²m/min²mm/min²cm/min²km/ мин²м/с²мм/с²см/с²км/с²ми/ч²ми/мин²ми/с² | |
⚠️ Сообщить о проблеме
Слово «центростремительный» подразумевает все, что направлено к центру. Очевидно, этот термин применим к любому объекту, который находится в круговом движении.
Очевидно, этот термин применим к любому объекту, который находится в круговом движении.
Что такое центростремительное ускорение?
Рассмотрим камень, привязанный к веревке и удерживаемый вашей рукой. Если вращать, крепко удерживая его рукой, камень движется по круговой траектории с радиусом, равным длине струны. Нить, крепко удерживаемая вашей рукой, воздействует на камень с силой, называемой центростремительной силой.
Согласно второму закону Ньютона, каждый объект испытывает ускорение, направленное в направлении силы, действующей на него. Здесь сила направлена к центру. Следовательно, камень испытывает ускорение, называемое центростремительным ускорением, направленное к центру, то есть к вашей руке.
Центростремительное ускорение – это ускорение, которое тело, движущееся по окружности, испытывает под действием центростремительной силы.
Если вы внезапно покидаете камень, когда он движется по круговой траектории, он движется по прямой линии, касательной к этой точке в этот момент. Скорость, с которой он покидает круговой путь, называется тангенциальной скоростью «v».
Скорость, с которой он покидает круговой путь, называется тангенциальной скоростью «v».
Какие типы ускорений испытывает тело при движении по окружности?
Объект, движущийся по круговой траектории, испытывает три типа ускорений:
- Угловое ускорение: α = Δω Δt
- Тангенциальное ускорение: at = rα в м с 2
- Центростремительное ускорение: ac = vt 2 r = rω 2 .
В то время как угловое ускорение является угловой величиной, остальные две величины являются линейными величинами.
Какова формула центростремительного ускорения?
Для тела массой m, движущегося по окружности радиусом r с тангенциальной скоростью v, центростремительное ускорение определяется выражением: ac = v 2 / r
В терминах линейной скорости можно рассчитать центростремительное ускорение как ac= ω 2 r, так как мы знаем, что v=rω
Центростремительное ускорение также определяется как скорость изменения тангенциальной скорости: ac= Lim (Δv→0)[(Δvt/Δt)]
Замечания о центростремительном ускорении
- Центростремительное ускорение всегда направлено радиально внутрь к центру окружности, по которой он движется.

- Тело, движущееся по окружности, испытывает как центростремительное ускорение, так и угловое ускорение. Таким образом, чистое ускорение, которое испытывает тело, определяется как корень суммы квадратов обоих ускорений.
- Луна, которая движется вокруг Земли, является лучшим примером объекта, движущегося по круговой траектории. Гравитация Земли вызывает на Луне центростремительное ускорение, которое всегда направлено к Земле.
- Если угловую скорость оставить постоянной, а радиус изменить, центростремительное ускорение изменится; если радиус уменьшается, центростремительное ускорение увеличивается и наоборот.
- Центростремительное ускорение может измениться двумя способами: либо из-за огромного изменения центростремительной скорости за заданное время, либо из-за внезапного изменения центростремительной скорости за короткий промежуток времени.
- Центростремительное ускорение и тангенциальное ускорение всегда перпендикулярны друг другу; потому что в то время как центростремительное ускорение направлено к радиусу, тангенциальное ускорение направлено к мгновенной касательной.
 Мы знаем, что радиус и касательная всегда перпендикулярны в данной точке окружности.
Мы знаем, что радиус и касательная всегда перпендикулярны в данной точке окружности.
Примечание. Объект, движущийся по круговой траектории, может иметь нулевое тангенциальное ускорение, но не нулевое центростремительное ускорение. Если тангенциальное ускорение тела равно нулю, значит, оно движется с постоянной угловой скоростью и угловое ускорение также равно нулю.
Но если тело, движущееся по круговой траектории, имеет нулевое центростремительное ускорение, это означает, что его тангенциальная скорость не меняется, что означает, что оно вообще не движется по окружности.
Луна притягивается к Земле и под действием силы тяжести постоянно отклоняется от прямолинейного движения и удерживается на своей орбите.
– Исаак Ньютон
Применение центростремительного ускорения в повседневной жизни
Устройство под названием «Центрифуга» работает по принципу центростремительного ускорения. Центрифуга — это устройство, которое используется в лабораториях и на производстве для отделения частиц различной плотности, в основном из жидкостей.
Центрифуга Контейнер, содержащий жидкость, вращается с высокой скоростью и прикладывает усилие, перпендикулярное оси вращения. В результате более плотные частицы движутся наружу, а более легкие – к центру.
Этот принцип центрифуги обычно используется в следующих отраслях промышленности:
- Сепаратор сливок на молочных заводах
- Установки для переработки отходов для отделения взвешенных веществ и жидкостей различной плотности.
- Для имитации атмосферы высокой гравитации для обучения пилотов и военнослужащих.
- Стиральные машины также работают по принципу центрифуги.
Вы знаете?
Для проверки уровней толерантности космонавтов человеческие центрифуги спроектированы с чрезвычайно большими значениями ускорений, которые часто во много раз превышают силу тяжести Земли.
Человеческие центрифуги, чрезвычайно большие центрифуги, использовались для проверки устойчивости астронавтов к воздействию ускорений, превышающих гравитацию Земли.
Как вам поможет калькулятор центростремительного ускорения CalculatorHut?
Используя бесплатный онлайн-калькулятор центростремительного ускорения CalculatorHut, вы можете рассчитать любой параметр, связанный с центростремительным ускорением – радиус, скорость и центростремительное ускорение. Это очень удобный инструмент для студентов, чтобы проверить правильность своих расчетов.
CalculatorHut — это универсальное хранилище научных и ненаучных онлайн-калькуляторов, которое бесплатно удовлетворит все ваши потребности в онлайн-калькуляторах. Все калькуляторы удобны в использовании и дают результаты с точностью до многих знаков после запятой.
CalculatorHut также предлагает широкий выбор из более чем 100 калькуляторов на различные темы — калькуляторы здоровья, финансовые калькуляторы, калькуляторы транспортных средств, калькуляторы физики, калькуляторы химии, математические калькуляторы и многие другие онлайн-калькуляторы для научных исследований бесплатно.

 Смысл скорости и ускорения.
Смысл скорости и ускорения. Все правила по сольфеджио
Все правила по сольфеджио


 Природа упругих сил электромагнитная.
Природа упругих сил электромагнитная.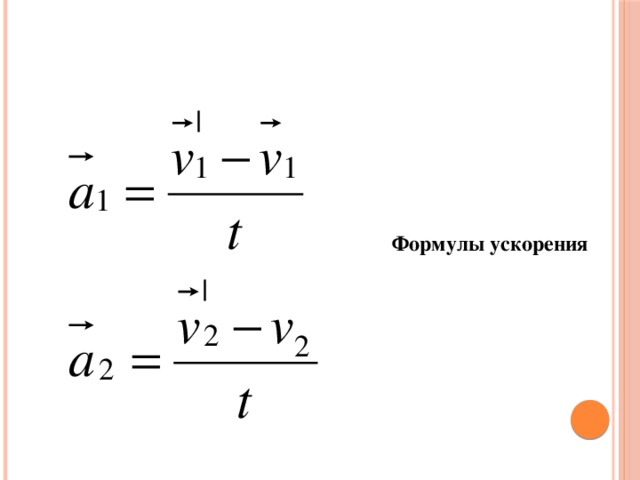 В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес – это упругая сила, приложенная к опоре или подвесу (т. е. к связи). Вес тела направлен в одну сторону с силой тяжести и равен P=m(g±a).
В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес – это упругая сила, приложенная к опоре или подвесу (т. е. к связи). Вес тела направлен в одну сторону с силой тяжести и равен P=m(g±a). su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.005 с.) Теперь уменьшение как $a$, так и $v$ по-прежнему дает правильное уменьшение $r$.
Теперь уменьшение как $a$, так и $v$ по-прежнему дает правильное уменьшение $r$.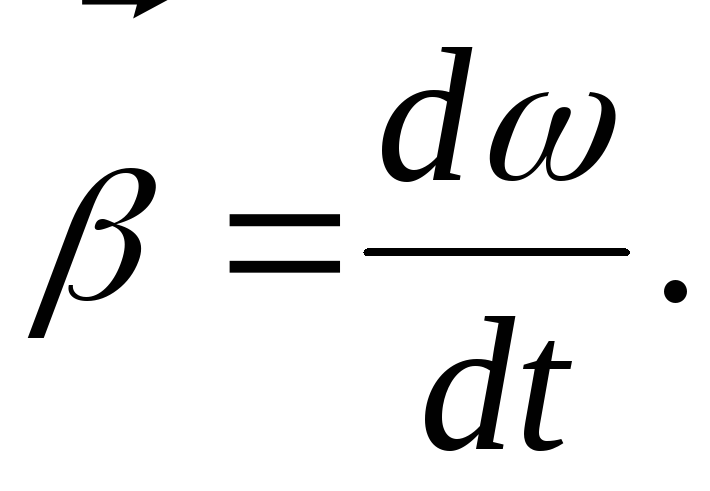

 Датчики (Базель). 2022 1 июля; 22 (13): 4978. дои: 10.3390/s22134978.
Датчики (Базель). 2022.
PMID: 35808473
Бесплатная статья ЧВК.
Датчики (Базель). 2022 1 июля; 22 (13): 4978. дои: 10.3390/s22134978.
Датчики (Базель). 2022.
PMID: 35808473
Бесплатная статья ЧВК. Лю Ю и др.
Датчики (Базель). 2018 6 декабря; 18 (12): 4305. дои: 10.3390/s18124305.
Датчики (Базель). 2018.
PMID: 30563255
Бесплатная статья ЧВК.
Лю Ю и др.
Датчики (Базель). 2018 6 декабря; 18 (12): 4305. дои: 10.3390/s18124305.
Датчики (Базель). 2018.
PMID: 30563255
Бесплатная статья ЧВК. 2021 20 апреля; 21 (8): 2881. дои: 10.3390/s21082881.
Датчики (Базель). 2021.
PMID: 33924081
Бесплатная статья ЧВК.
2021 20 апреля; 21 (8): 2881. дои: 10.3390/s21082881.
Датчики (Базель). 2021.
PMID: 33924081
Бесплатная статья ЧВК. дои: 10.3390/s22134978.
Датчики (Базель). 2022.
PMID: 35808473
Бесплатная статья ЧВК.
дои: 10.3390/s22134978.
Датчики (Базель). 2022.
PMID: 35808473
Бесплатная статья ЧВК.
 6–8 июня 2005 г.; Пискатауэй, Нью-Джерси, США: IEEE; 2005. С. 36–41.
–
DOI
6–8 июня 2005 г.; Пискатауэй, Нью-Джерси, США: IEEE; 2005. С. 36–41.
–
DOI
 Мы знаем, что радиус и касательная всегда перпендикулярны в данной точке окружности.
Мы знаем, что радиус и касательная всегда перпендикулярны в данной точке окружности.