ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4.  Скользящие и приложенные векторные величины. Скользящие и приложенные векторные величины.6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме.  4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения. 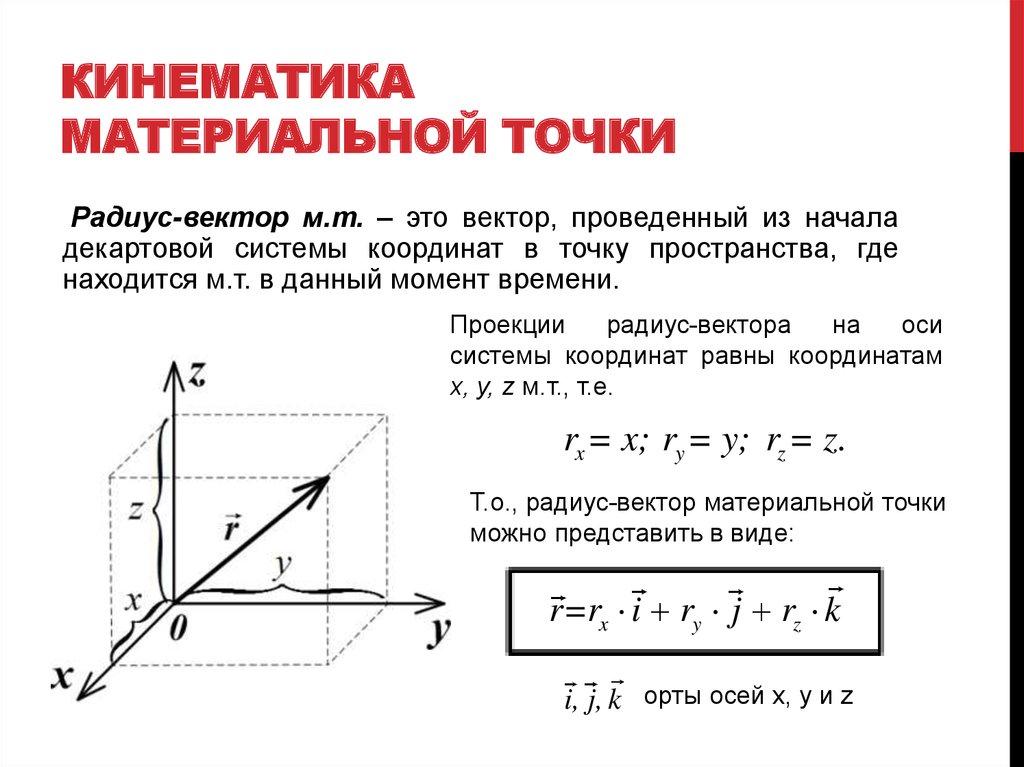 § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. § 2. Произведения пяти и шести векторов 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов.  4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 4. Основные задачи, связанные с произведениями трех и более векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 7. Связь дифференциала вектора с его приращением. § 3. Формула Тейлора Глава VIII.  ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ§ 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 5. Бинормаль и кручение. Третья основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3. 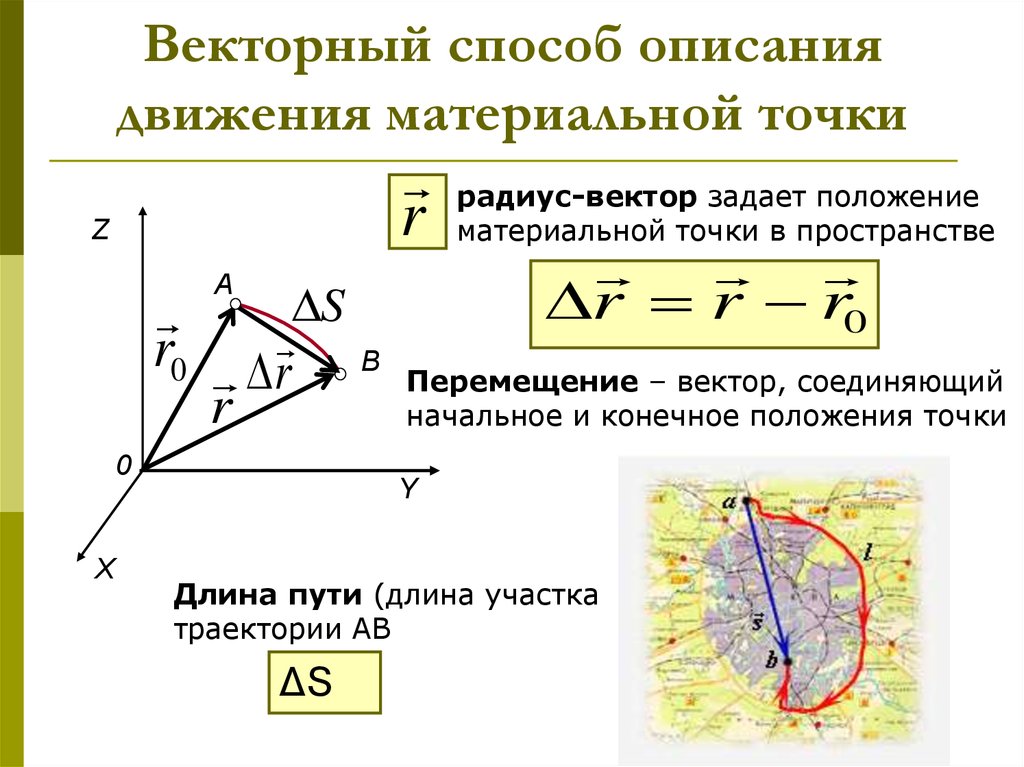 Круг кривизны Круг кривизны§ 4. Эволюта Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности.  5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2.  3. Основные свойства криволинейного интеграла. 4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV.  ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ§ 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII.  ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ§ 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах.  § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты |
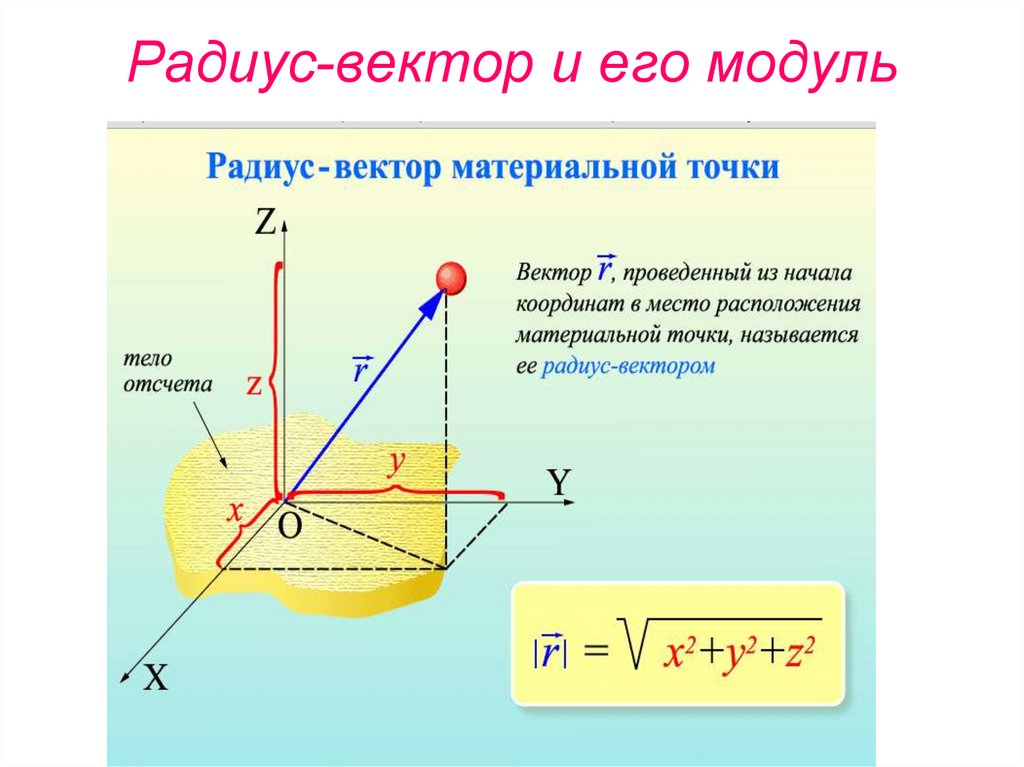
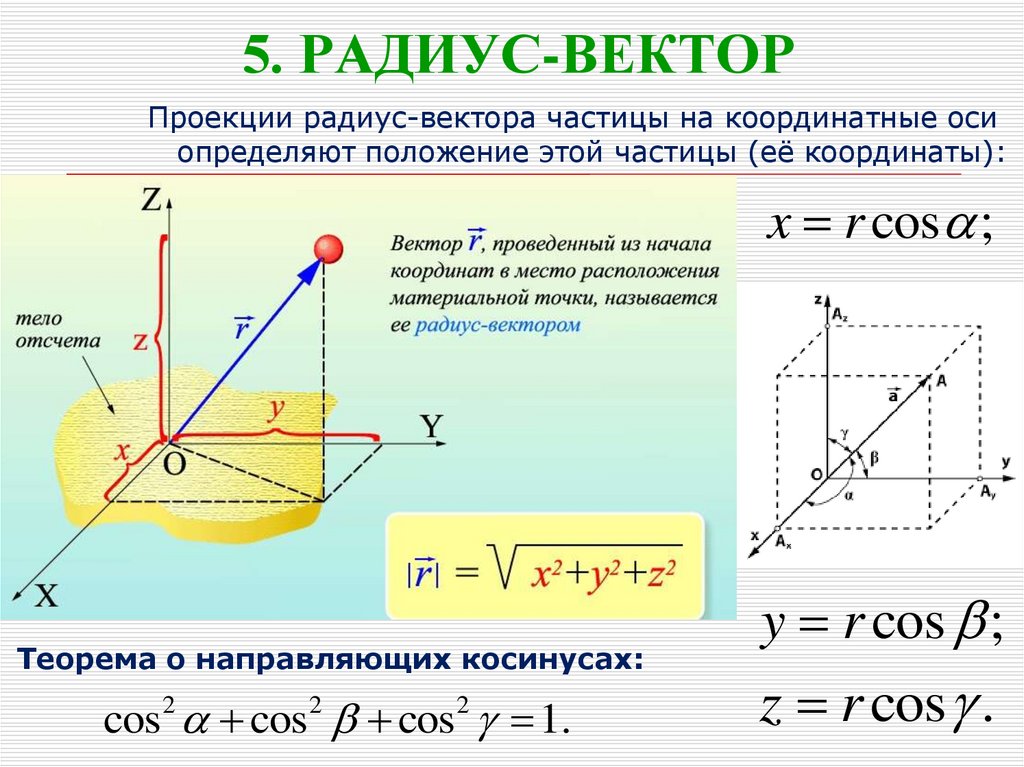
1.1. Радиус-вектор материальной точки
Рассмотрим движение материальной точки М в прямоугольной системе координат, поместив начало коородинат в точку О на Земле.
Положение точки М относительно системы отсчета можно задать не только с помощью трех декартовых координат , но также с помощью одной векторной величины – радиуса-вектора точки М, проведенного в эту точку из начала системы координат (рис. 1.1). Если – единичные вектора (орты) осей прямоугольной декартовой системы координат, то
(1. |
Векторы вдоль соответствующих осей координат. Проекции .
1.2.Кинематические уравнения движения материальной точки
При движении материальной точки М ее координаты и радиус-вектор изменяются с течением времени t.
Поэтому для задания закона движения м.т. необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:
(1.2) |
либо зависимость от времени радиус-вектора этой точки
(1.3) |
Три скалярных
уравнения (1.2) или эквивалентное им одно
векторное уравнение (1.3) называются
кинематическими уравнениями движения
материальной точки.
1.3. Траектория материальной точки
Траекторией материальной точки называется линия, описываемая пространстве этой точкой при ее движении. В зависимости от формы траектории различают прямолинейное и криволинейное движения точки. Если все участки траектории точки лежат в одной плоскости, то движение точки называют плоским.
Уравнения (1.2) и (1.3) задают траекторию точки в так называемой параметрической форме. Роль параметра играет время t. Решая эти уравнения совместно и исключая из них время t, найдем уравнение траектории.
Длина пути. Длиной пути материальной точки называют сумму длин всех участков траектории, пройденных точкой за рассматриваемый промежуток времени.
1.4.Вектор перемещения
.
Вектором перемещения материальной
точки за время от , т.е. приращение радиуса-вектора точки за рассматриваемый промежуток времени
(1. |
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории. Из того, что перемещение является вектором, следует подтверждающийся на опыте закон независимости движений: если материальная точка участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме ее перемещений, совершаемых ею за тоже время в каждом из движений порознь.
1.5. Скорость
Для характеристики движения материальной точки вводят векторную физическую величину – скорость, определяющую как быстроту движения, так и направление движения в данный момент времени.
Пусть материальная точка движется по криволинейной траектории МN так, что в момент времени t она находится в т.М, а в момент времени в т. N. Радиус-векторы точек М и N соответственно равны, а длина дуги МN равна(рис. 1.3).
Вектором средней скорости точки в интервале времени отt до t+Δt называют отношение приращения радиуса-вектора точки за этот промежуток времени к его величине:
(1. |
Вектор средней скорости направлен также, как вектор перемещения т.е. вдоль хорды МN.
Мгновенная скорость или скорость в данный момент времени. Если в выражении (1.5) перейти к пределу, устремляя к нулю, то мы получим выражение для вектора скорости м.т. в момент времени t прохождения ее через т.М траектории.
(1.6) |
В процессе уменьшения
величины точка
N приближается к т.М, и хорда МN, поворачиваясь
вокруг т.М, в пределе совпадает по
направлению с касательной к траектории
в точке М. Поэтому вектори
скорость v движущейся точки направлены
по касательной траектории в сторону
движения. Вектор скорости v материальной
точки можоразложить на три составляющие,
направленные вдоль осей прямоугольной
декартовой системы координат.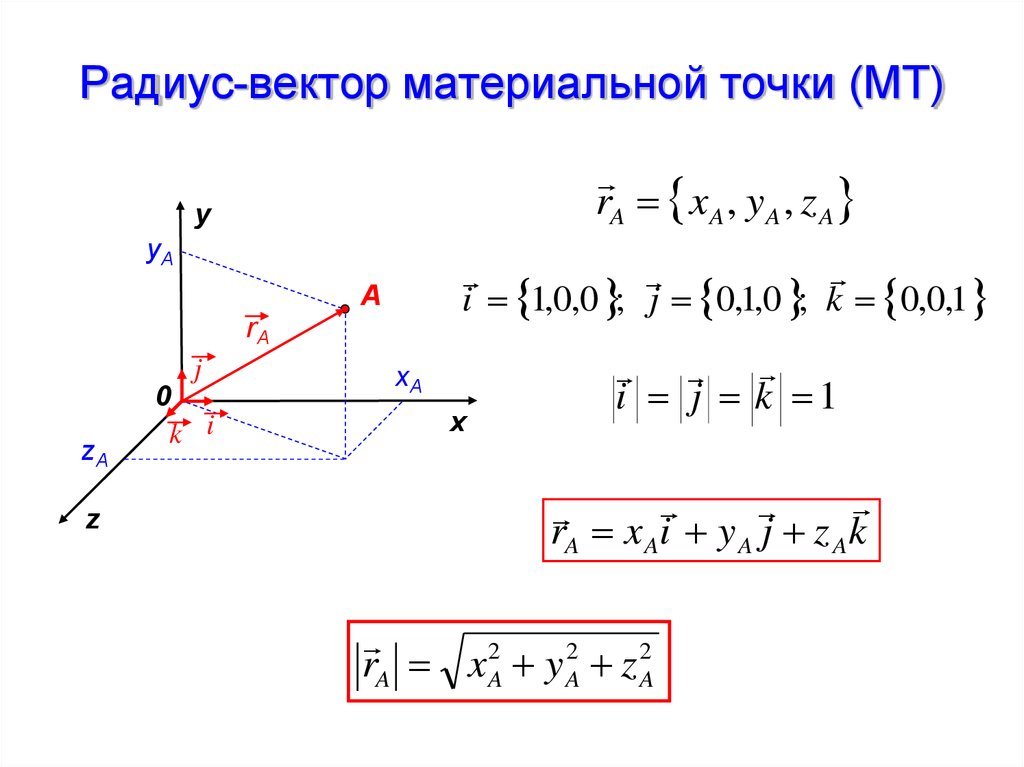
(1.7) |
где – проекции вектора скорости на оси координат х, у, z.
Подставляя в (1.6) значения для радиус-вектора материальной точки (1.1) и выполнив почленное дифференцирование, получим:
(1.8) |
Из сопоставления выражений (1.7) и (1.8) следует, что проекции скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки:
(1. |
Поэтому численное значение скорости:
(1.10) |
Движение, при котором направление скорости материальной точки не изменяется, называется прямолинейным. Если численное значение мгновенной скорости точки остается во время движения неизменным, то такое движение называется равномерным.
Если же за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным.
В этом случае часто пользуются скалярной величиной , называемой средней путевой скоростью неравномерного движения на данном участкетраектории. Она равна численному значению скорости такого равномерного движения, при котором на прохождение путизатрачивается то же время, что и при заданном неравномерном движении:
(1. |
Т.к. только в случае прямолинейного движения с неизменной по направлению скоростью, то в общем случае:
.
Закон сложения скоростей. Если материальная точка одновременно участвует в нескольких движениях, то результирующее перемещения в соответствии с законом независимости движения, равно векторной (геометрической) сумме элементарных перемещений, обусловленных каждым из этих движений в отдельности:
В соответствии с определением (1.6):
(1.12) |
Таким образом, скорость результирующего движения равна геометрической сумме скоростейвсех движений, в которых участвует материальная точка, (это положение носит название закона сложения скоростей).
Радиус-вектор точки A относительно начала координат изменяется со временем t как vec r = at hat i
A2Z-ОБЩАЯ КИНЕМАТИКА И ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ-Главный тест
21 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Обновлено: 27-06-2022
Text Solution
A
y=−ba2x2
B
y=ba2x2
3
2 y = −2ba2x2
D
y = 2ba2x2
Ответ
Правильный ответ –
Решение
→ R = ATˆi -BT2 j
x = atandy = -bt2
⇒t = (xa) ии = y = y = y = y = y = y = ay = −b(xa)2⇒y=−ba2x2.
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Похожие видео
Найдите единичный вектор, перпендикулярный каждому из векторов (→a+→b) и (→a−→b), где →a=ˆi+ˆj+ˆk,→b=ˆi+2ˆj+3ˆk .
Найдите единичный вектор, перпендикулярный обоим векторам →a+→b и →а−→б где →a=ˆi+ˆj+ˆk,→b=ˆi+2ˆj+3ˆk.
Частица движется в плоскости x−y так, что вектор ее положения изменяется со временем как →r=(2sin3t)ˆj+2(1−cos3t)ˆj. Найдите уравнение траектории частицы.
11296089
Вектор положения частицы определяется как vec(r ) = k cos omega hat(i) + k sin omega hat(j) = x hat(i) + yhat(j) , где k и omega константы и время t. Найдите угол между вектором положения и вектором скорости. Также определите траекторию частицы.
13025350
Вектор ardius точки A относительно начала координат изменяется со временем t как →r=atˆj−bt2ˆj, где a и b — константы. Найдите уравнение траектории точки.
Найдите уравнение траектории точки.
15088846
Найти проекцию вектора (→b+→a) на вектор →a, где →a=2i−j+2kand→b=j+2k
121711152
Для заданных векторов →a=j+2i−ˆ 2ˆk и →b=−ˆi+ˆj−ˆk, найти единичный вектор в направлении вектора →a+→b.
425867376
यदि सदिशों → B = 2ˆi+ˆj और → C = ˆi+ˆj+ˆk के में एक इक इक सदिश।। इस प्रकार है कि →a∧→b=→a∧→d जहाँ →d=ˆj+2ˆk तो ˆa है
643222336
Текст Решение
Частица движется в плоскости x−y таким образом, что вектор ее положения изменяется со временем как →r=(2sin3t)ˆj+2(1−cos3t)ˆj. Найдите уравнение траектории частицы.
644099998
Радиус-вектор точки A относительно начала координат изменяется со временем t как →r=atˆi−bt2ˆj, где a и b постоянны. Уравнение траектории точки есть.
644112405
Найдите единичный вектор, перпендикулярный каждому из векторов →a+→b и →a−→b, где →a=ˆi+ˆj+k и →b=ˆi+2ˆj+3k.
644962815
Найдите вектор →b такой, что →a×→b=→c и →a. →b=3, где →a=ˆi+ˆj+ˆk,→c=ˆj−ˆk.
→b=3, где →a=ˆi+ˆj+ˆk,→c=ˆj−ˆk.
645602315
Найдите единичный вектор, перпендикулярный каждому из векторов →a+→b и →a−→b, где →a=ˆi+ˆj+k и →b=ˆi+2ˆj+3k.
645602316
Вектор положения →r частицы изменяется со временем t по закону →r=(12t2)ˆi−(43t1,5)ˆj+(2t)ˆk, где r в метрах, t в секундах. Найдите подходящее выражение для его скорости и ускорения как функции времени. 9(3))hat(j)+(2t)hat(k) , где r в метрах, а t в секундах. Найдите подходящее выражение для его скорости и ускорения как функции времени
645855617
Направление вектора угловой скорости
Направление вектора угловой скорости идея
угловой скорости , которая является вращательным эквивалентом линейной скорости. Угловая скорость обычно измеряется в радианах в секунду, где радианы являются более естественным измерением угла, чем более привычные градусы. Но так же, как линейная скорость является вектором и, следовательно, имеет направление, угловая скорость тоже имеет направление. Итак, как направлен вектор угловой скорости?
Итак, как направлен вектор угловой скорости?Взаимосвязь между линейной скоростью и угловой скоростью
Как мы видели в блоге, где я ввел понятие угловой скорости, ее можно определить просто как угол, перемещаемый в единицу времени, или
, что, конечно же, приводит к тому, что она обычно измеряется в радианах в секунду. Однако мы также можем записать угловую скорость в терминах линейной скорости. Чтобы увидеть, как это сделать, давайте вспомним определение радиан , более естественную единицу измерения угла. Как я представил в этом блоге, измерение угла в радианах просто означает деление длины дуги на радиус окружности.
Угол, измеряемый в радианах, представляет собой просто длину дуги, деленную на радиус
Мы можем написать, что угол, измеренный в радианах, равен
. Но линейная скорость просто определяется как расстояние, деленное на время, поэтому мы можем написать
. как
Используя это для, мы можем записать угловую скорость как
Направление вектора угловой скорости
Записав это в терминах векторов и помня, что деление векторов не определено, вместо этого мы напишем, что
, где векторное произведение (или кросс-произведение), как я обсуждал в этом блоге здесь.
Направление радиус-вектора от центра окружности, а направление линейной скорости для объекта, движущегося против часовой стрелки, соответствует направлению, показанному на диаграмме ниже, по касательной к окружности, то есть под прямым углом к радиальный вектор .
Направление радиус-вектора от центра окружности, направление линейной скорости для объекта, движущегося против часовой стрелки, как показано, под прямым углом к радиус-вектору.
Чтобы найти направление , мы можем использовать правило правой руки , как показано на рисунке ниже.
Правило правой руки для определения направления результата векторного произведения
В нашем примере здесь наш первый палец находится в направлении радиального вектора, а наш второй палец находится в направлении линейной скорости, что приводит к тому, что угловая скорость (представленная большим пальцем) направлена наружу или к нам, как показано на рисунке ниже.

 1)
1) 4)
4) 5)
5) 9)
9) 11)
11)