Связь между координатами вектора и координатами его начала и конца 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 27.
Связь между координатами вектора и координатами его начала и конца.
Ты уже знаком с понятием координат вектора. Ими называют коэффициенты разложения данного вектора по единичным координатным векторам i⃗ и j⃗.
Сегодня мы ответим на вопрос «Как связаны координаты вектора с координатами его начала и конца?».
Но для начала вернёмся к координатам точки в прямоугольной системе координат.
Напомним, что для их определения нужно опустить перпендикуляры из данной точки к осям.
Точки пересечения данных прямых с осями обозначим как M1 и M2.
Абсциссой точки М является число x, которое является длиной отрезка OM1. А ординатой — число y, которое является длиной отрезка OM2.
M(x; y) x = OM1, y = OM2
Мы вспомнили, как определять координаты точек, а теперь вернёмся к общему случаю и, уже рассмотренной, точке M.
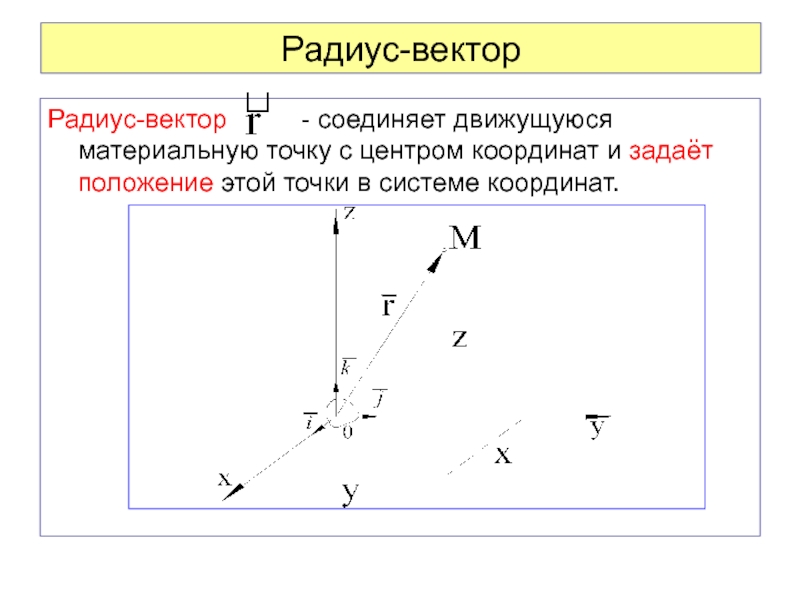
Проведём вектор из точки O к точке M. Запомни, вектор OM⃗ называют радиус-вектором точки M.
Сейчас докажем следующее утверждение: координаты точки M равны соответствующим координатам её радиус-вектора.
Доказать: M(x;y)=OM⃗x;y
Понятно, что вектор OM⃗=ОM1⃗+ОM2⃗ по правилу параллелограмма.
Теперь необходимо доказать, что вектор
OM1⃗=xi⃗, а вектор OM2⃗=yj⃗
Тем самым мы докажем, что вектор OM⃗x;y.
Если x > 0, то x = OM1, а векторы OM1⃗ и i⃗ сонаправлены, поэтому
OM1⃗=OM1∙i⃗=xi⃗
Если x x = OM1, а векторы OM1⃗ и i⃗ противоположно направлены.
Наконец, если x = 0
OM1⃗=0⃗ и равенство OM1=xi⃗ в этом случае так же справедливо. Таким образом, в любом случае ОM1⃗=xi⃗. Аналогично доказывается, что ОM2⃗=yj⃗.
Следовательно,OM⃗=ОM1⃗+ОM2⃗=xi⃗+yj⃗
Отсюда следует, что координаты радиус-вектора OM равны (x; y), то есть равны соответствующим координатам точки M
Пользуясь доказанным утверждением, выразим координаты вектора AB⃗ через координаты его начала A и конца B. Пусть точка A имеет координаты x1;y1, а точка B – координаты x2;y2.
Вектор AB⃗ равен разности векторов OB⃗ и OA⃗, поэтому его координаты равны разностям соответствующих координат векторов OB⃗ и OA⃗. Но OB⃗ и OA⃗ – радиус-векторы точек B и A, и, значит, OB⃗ имеет координаты x2;y2, а OA⃗ имеет координаты x1;y1. Следовательно, вектор AB⃗ имеет координаты x2-x1;y2-y1.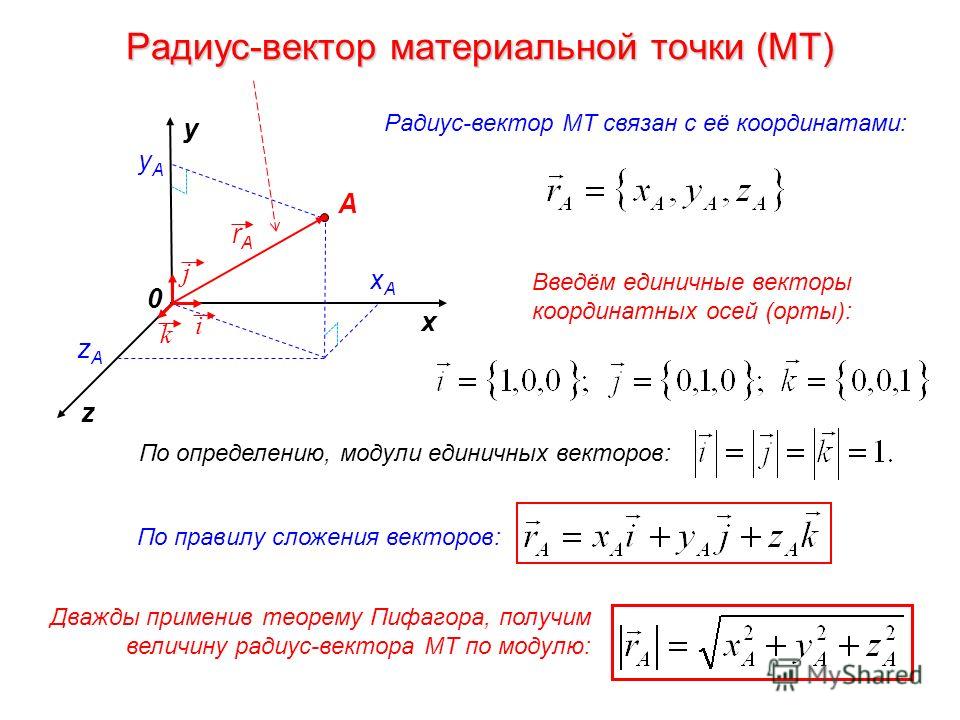
Таким образом, каждая координата вектора равна разности соответствующих координат его конца и начала.
Введение системы координат дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат.
Рассмотрим три вспомогательные задачи:
-
Как найти координаты середины отрезка.
Пусть в системе координат Oxy точка A имеет координаты x1;y1, а точка B – координаты x2;y2. Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка
OC⃗=12OA⃗+OB⃗.
x=x1+x22; y=y1+y22
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов.

-
Вычисление длины вектора по его координатам.
Пусть вектор a⃗x;y, тогда длина вектора вычисляется по формуле:
a⃗=x2+y2
-
Вычисление расстояния между двумя точками. Пусть точка M1 имеет координаты (x1; y1), точка
Рассмотрим вектор M1M2⃗. Его координаты равны x2-x1;y2-y1. Следовательно, длина этого вектора может быть найдена по формуле:
M1M2⃗=x2-x12+y2-y12
Пример:
-
Найти длину вектора a⃗-3;4
a⃗=x2+y2=-32+42=25=5
Ответ: 5
-
Найти расстояние между точкой A(2; 7) и точкой B(-2; 7)
Ответ: 4
Радиус-вектор инерции – Энциклопедия по машиностроению XXL
Из формулы (6. 22) следует, что главный вектор сил инерции ротора перпендикулярен его оси вращения у, т. е. расположен в плоскости 0x2, перпендикулярной к указанной оси. Обозначая через радиус-вектор частицы (этот вектор на рисунке не показан), находим момент силы инерции частицы относительно выбранного центра О
[c.97]
22) следует, что главный вектор сил инерции ротора перпендикулярен его оси вращения у, т. е. расположен в плоскости 0x2, перпендикулярной к указанной оси. Обозначая через радиус-вектор частицы (этот вектор на рисунке не показан), находим момент силы инерции частицы относительно выбранного центра О
[c.97]Задача динамической балансировки заключается в подборе масс т и т и противовесов и их радиус-векторов pj и рЬ в плоскостях I Vi II таким образом, чтобы центробежные силы инерции этих масс
Центром инерции системы называется геометрическая точка С пространства, определяемая радиусом-вектором [c.70]
Рассмотрим эллипсоид инерции, построенный для неподвижной точки О (рис. V.10). Назовем мгновенным полюсом Р точку, в которой мгновенная ось пересекает этот эллипсоид инерции, обозначим через Гр радиус-вектор точки Р и положим [c.198]
Здесь за независимую переменную принято безразмерное время т = ШоЗ, где и>о — угловая скорость орбитальною движения центра масс системы О.
Радиус-вектор и все длины в эллипсоиде инерции Коши имеют, размерностью величину, обратную квадратному корню из размерности момента инерции, что вносит ряд осложнений, особенно в графические построения. Значительно удобнее откладывать вдоль [c.341]
Радиус-вектор 124 Радиус инерции 337 Разложение движения точки 130 Разложение силы на составляющие 37,
Радиус-вектор 17 Радиус инерции 107 [c.301]
Обозначим X радиус-вектор точки пересечения главной оси с эллипсоидом инерции. Тогда, согласно определению главной оси и в соответствии с теоремой 1.8.4, будем иметь [c.49]
Но г X е есть произведение модуля г радиуса-вектора на синус угла между г и е, что представляет собой расстояние 0. между осями. Как следствие отметим, что момент инерции относительно оси, проходящей через центр масс, меньше момента инерции относительно любой другой параллельной оси.
[c.53]
между осями. Как следствие отметим, что момент инерции относительно оси, проходящей через центр масс, меньше момента инерции относительно любой другой параллельной оси.
[c.53]
Теорема 1.10.4. Если направление ег — главное для центрального эллипсоида инерции, то оно будет главным и для любой точки О, определенной радиусом-вектором г = гвг при произвольном значении г. И наоборот, если направление вг не было главным для центрального эллипсоида инерции, то оно не может стать главным пи при каком значении г.
Доказательство. Пусть рассматриваемая ось проходит через точки 0 и О2, заданные соответственно радиусами-векторами ri и Г2, имеющими начало в центре масс С. Эллипсоид инерции для точки Oi обозначим Эь Эллипсоид инерции для точки О2 обозначим Э2. Сравним векторы zi(x) и Z2(x) для эллипсоидов 9i и Э2. По теореме 1.10.3 будем иметь [c.56]
Таким образом операция удобна при вычислении тензоров инерции множества точечных масс, если радиусы-векторы точек выражаются как линейные комбинации других каких-нибудь векторов.

Пусть плоскость Ре имеет нормаль е и проходит через полюс О. Моментом инерции относительно плоскости Те множества точечных масс т, с радиусами-векторами г, называется величина [c.61]
Пусть г — радиус-вектор, имеющий начало в точке О и конец в центре масс множества Q точечных масс. А, В, С — главные центральные моменты инерции множества Q. Найти момент инерции множества Q относительно оси с направляющим вектором е, проходящей через точку О. [c.74]
Назовем апексом точку, в которой луч, выходящий из неподвижной точки О коллинеарно вектору о , пересекает эллипсоид инерции. Пусть г — радиус-вектор апекса. [c.467]
Первые два члена этой формулы постоянны при фиксированном радиусе орбиты и потому не существенны. Выражение в скобках у третьего члена есть момент инерции спутника относительно оси с направляющим вектором Оз, т.е. относительно радиуса-вектора центра [c.506]
Теорема 6.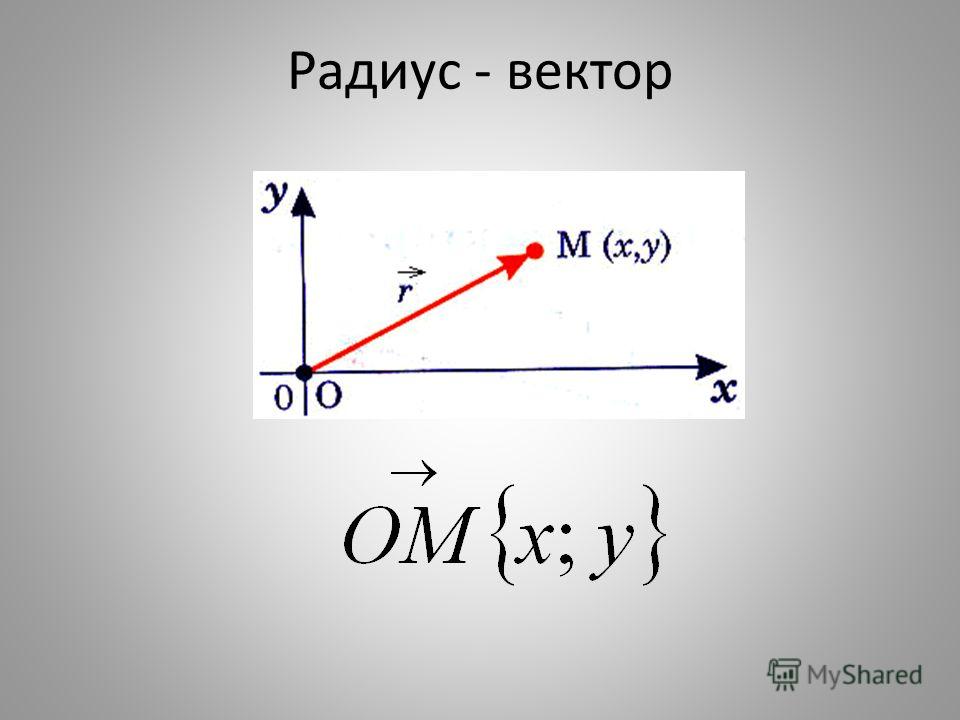 13.1. В принятых предположениях сумма потенциальных энергий гравитационных сил и сил инерции принимает минимальное значение, когда наибольшая ось эллипсоида инерции направлена вдоль радиуса-вектора центра масс, а наименьшая — по нормали к плоскости орбиты.
[c.508]
13.1. В принятых предположениях сумма потенциальных энергий гравитационных сил и сил инерции принимает минимальное значение, когда наибольшая ось эллипсоида инерции направлена вдоль радиуса-вектора центра масс, а наименьшая — по нормали к плоскости орбиты.
[c.508]
Из поверхностей второго порядка этому условию удовлетворяет только одна, а именно эллипсоид. Найденный эллипсоид называют эллипсоидом инерции для данного тела в точке О. Очевидно, эллипсоид инерции для данного тела можно построить в любой точке пространства. Поэтому эллипсоидом инерции для данного тела в какой-либо точке называют эллипсоид с центром в этой точке, центральные радиусы-векторы точек которого равны обратным значениям квадратных корней из моментов инерции тела относительно осей, направленных по этим радиусам-векторам. [c.249]
Подставляя в (29) У = У,, получим только два независимых уравнения для определения координат точки х, у, г эллипсоида инерции, соответствующих главной оси инерции. Для которой главный момент инерции есть Третье уравнение системы будет следствием двух других уравнений, так как определитель этой системы равен нулю. Из (29) можно найти только две величины, например х/г и у г. Они определят направление вектора г, вдоль главной оси инерции, момент инерции относительно которой есть Модуль радиус-вектора п остается неопределенным. Аналогично определяются направления векторов Гд и Гд вдоль двух других главных осей инерции, для которых главные моменты инерции равны У.2 и Уд. Можно доказать, что векторы г,, и Гд, направленные вдоль главных осей инерции, взаимно перпендикулярны.
[c.277]
Для которой главный момент инерции есть Третье уравнение системы будет следствием двух других уравнений, так как определитель этой системы равен нулю. Из (29) можно найти только две величины, например х/г и у г. Они определят направление вектора г, вдоль главной оси инерции, момент инерции относительно которой есть Модуль радиус-вектора п остается неопределенным. Аналогично определяются направления векторов Гд и Гд вдоль двух других главных осей инерции, для которых главные моменты инерции равны У.2 и Уд. Можно доказать, что векторы г,, и Гд, направленные вдоль главных осей инерции, взаимно перпендикулярны.
[c.277]
Для выражения центробежных моментов инерции через главные моменты инерции используем формулы преобразования координат точек тела при повороте осей координат вокруг точки О (рис. 36). Эти формулы получим проецированием на оси Охуг радиус-вектора точки М , разложенного предварительно на составляющие, параллельные осям двух систем осей координат в точке О.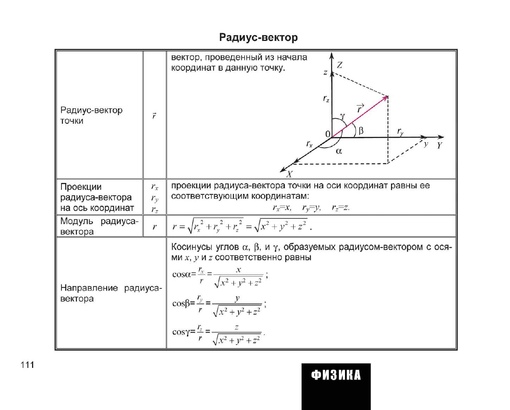 Имеем
[c.278]
Имеем
[c.278]
Геометрическая точка, для которой сумма произведений масс всех материальных точек, образующих механическую систему, на их радиусы-векторы, проведённые из этой точки, равна нулю (то же, что и центр инерции). [c.98]
Эллипсоид с центром в данной точке, для которого квадрат радиуса-вектора каждой его точки, проведённого из этого центра, обратно пропорционален моменту инерции механической системы относительно оси, направленной вдоль радиуса-вектора. [c.104]
Применим к системе параллельных сил m,w формулу (III. 56) первого тома. Тогда после очевидных упрощений найдем, что радиус-вектор центра инерции системы материальных точек определяется формулой [c.41]
Здесь г — радиус-вектор точки относительно центра инерции системы. Согласно формуле (I. 49) имеем [c.55]
Здесь Гс — относительный радиус-вектор центра инерции,Ус — относительная скорость центра инерции.
 [c.55]
[c.55]Если Х( Ф Ха, то второй множитель в левой части равенства (к) равен нулю. Однако этот множитель является скалярным произведением радиусов-векторов точек пересечения двух главных осей с эллипсоидом инерции. Следовательно, направления этих главных осей ортогональны. [c.83]
Здесь Г — радиусы-векторы точек системы относительно ее центра инерции, Пг — потенциальная энергия в относительных координатах, -с — ускорение центра инерции. [c.101]
Таким образом, приходим к следующей, полученной Пуансо, геометрической интерпретации движения твердого тела в случае Эйлера эллипсоид инерции для неподвижной точки катится без скольжения по плоскости, неподвижной в пространстве-, эта плоскость перпендикулярна кинетическому моменту угловая скорость тела пропорциональна длине радиуса-вектора точки касания, а по направлению с ним совпадает. [c.162]
Формулами (5) и (6) определяются соответственно радиус-вектор или координаты центра масс центра инерции) тела.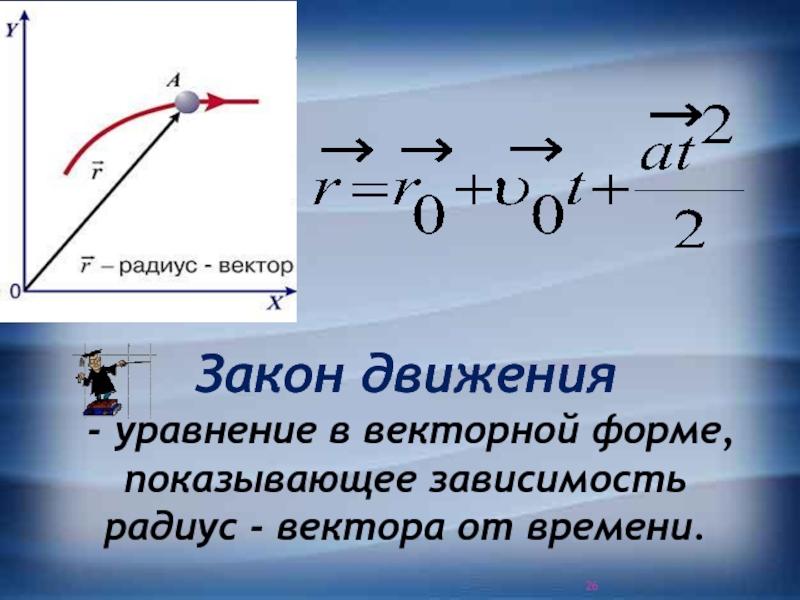 Как видно из этих формул, положение центра масс зависит только от распределения масс в объеме, занимаемом телом. Понятие о центре масс является более общим, чем понятие о центре тяжести, так как оно имеет смысл не только для одного твердого тела, но и для любой механической системы кроме того, это понятие не связано с тем, находится тело в поле тяжести или нет. Для тела, находящегося в однородном поле тяжести (в поле тяжести, где -= onst), положения центра тяжести и центра масс совпадают.
[c.213]
Как видно из этих формул, положение центра масс зависит только от распределения масс в объеме, занимаемом телом. Понятие о центре масс является более общим, чем понятие о центре тяжести, так как оно имеет смысл не только для одного твердого тела, но и для любой механической системы кроме того, это понятие не связано с тем, находится тело в поле тяжести или нет. Для тела, находящегося в однородном поле тяжести (в поле тяжести, где -= onst), положения центра тяжести и центра масс совпадают.
[c.213]
Радиус-вектор г — Г1е 1 -Ь Г2в2 -Ь гзе , точки на полодии должен удовлетворять как уравнению эллипсоида инерции [c.468]
В общем случае полодия служит пересечением эллипсоида инерции и конуса второго порядка, имеющего те же плоскости симметрии, что и эллипсоид. Она состоит из двух различных замкнутых ветвей, симметричных друг к другу относительно неподвижной точки и одной из главных плоскостей эл.липсоида, и обладает четырьмя вер-щинами, для которых радиус-вектор г, выходящий из неподвижной точки, имеет максимум или минимум модуля. При движении одна из ветвей полодии катится по неподвижной плоскости Р. Вторая ветвь катится по плоскости, симметричной Р относительно неподвижной точки. Общий вид расположения полодий на эл.липсоиде инерции представлен на рис. 6.7.1. Имеем однопараметрическое по В семейство кривых.
[c.469]
При движении одна из ветвей полодии катится по неподвижной плоскости Р. Вторая ветвь катится по плоскости, симметричной Р относительно неподвижной точки. Общий вид расположения полодий на эл.липсоиде инерции представлен на рис. 6.7.1. Имеем однопараметрическое по В семейство кривых.
[c.469]
Из центра О Земли проведем радиус-вектор Н центра масс спутника. Выберем вращающийся репер Ое /е2ез так, чтобы ось 03 была коллинеарна К, ось е о — параллельна скорости V центра масс, ось е” — перпендикулярна к плоскости орбиты и составляла с указанными двумя правую тройку. Относительно абсолютного (см. 3.14) репера 0010203 репер О0 /020з вращается с постоянной угловой скоростью а — ь/К вокруг вектора е” = 01- Найдем условие, при котором спутник будет находиться в равновесии относительно вращающегося репера Ое е е под действием сил тяготения и сил инерции цент1ю-бежных и кориолисовых. [c.504]
Если оси координат Ox y z являются главными осями инерции, то радиус-вектор г точки М эллипсоида инерции, расположенной на главной оси инерции, например оси Oz (рис. 35), направлен по нормали к эллипсоиду, т. е. параллельно вектору grad ф, который, согласно его определению, вычисляется по формуле
[c.276]
35), направлен по нормали к эллипсоиду, т. е. параллельно вектору grad ф, который, согласно его определению, вычисляется по формуле
[c.276]
Легко видеть, что в тех случаях, когда одна ось системы координат совпадает с одной из главных осей инерции, два соответствующих центробежных момента инерции обращаются в нуль. Действительно, в точке пересечения главной оси с поверхностью эллипсоида радиус-вектор, проведенный из начала координат, и орт нормали к поверхности эллипсоида коллинеариы (рис. 13). [c.81]
Yt Мп(у1 +г1),пред.ставляег собой сумму произведений каждой массы на квадрат ее расстояния от оси вращения поэтому мы его называем моментом инерции относительно оси . Если р(г) представляет собой плотность тела в точке, радиус-вектор [c.248]
Решение. Найдем величину радиуса-вектора центра масс R= = 0С как функцию обобщенной координаты ф, ф — угол между вертикалью и отрезком ОС (рис. 3.18). Пусть а, Ь — стороны угла, Ь>а. Тогда / =72Уа Ч-Ь (а+6) . Момент инерции относительно осп, проходящей через точку 0,/gg = — (а + 6 ) (а +. Ки-
[c.215]
Тогда / =72Уа Ч-Ь (а+6) . Момент инерции относительно осп, проходящей через точку 0,/gg = — (а + 6 ) (а +. Ки-
[c.215]
Элементарная математика
Пусть – угол между подвижным радиус-вектором OM= { x, y} и его начальным положением OA.
а) Синусом угла называется отношение ординаты y конца подвижного радиус-вектора r = OM к длине r = | r | этого радиус-вектора, т.е.
б) Косинусом угла называется отношение абсциссы x конца подвижного радиус-вектора r = OM к длине r = | r | этого радиус-вектора, т. е.
е.
в) Тангенсом угла называется отношение ординаты y к абсциссе x
конца подвижного радиус-вектора OM . т.е.
г) Котангенсом угла называется отношение абсциссы x к ординате y
конца подвижного радиус-вектора OM , т.е.
д) Функции секанс и косеканс определяются соотношениями
Подчеркнем, что отношения
зависят только от величины угла и не зависят от длины r радиус-вектора OM. Это означает, что тригонометрические функции
являются функциями только угла . При этом угол часто называют аргументом тригонометрических функций.
При вычислении тригонометрических функций можно пользоваться подвижными радиус-векторами длины r = 1. Концы таких векторов лежат на единичной окружности . В этом случае
Концы таких векторов лежат на единичной окружности . В этом случае
Векторное Произведение Векторов. Свойства, определение
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.

Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
, где
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
или
- Сочетательное свойство
или
, где λ произвольное действительное число.

Для большей ясности докажем свойство антикоммутативности векторного произведения.
По определению
и
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
Как решаем:
а) По условию требуется найти длину векторного произведения.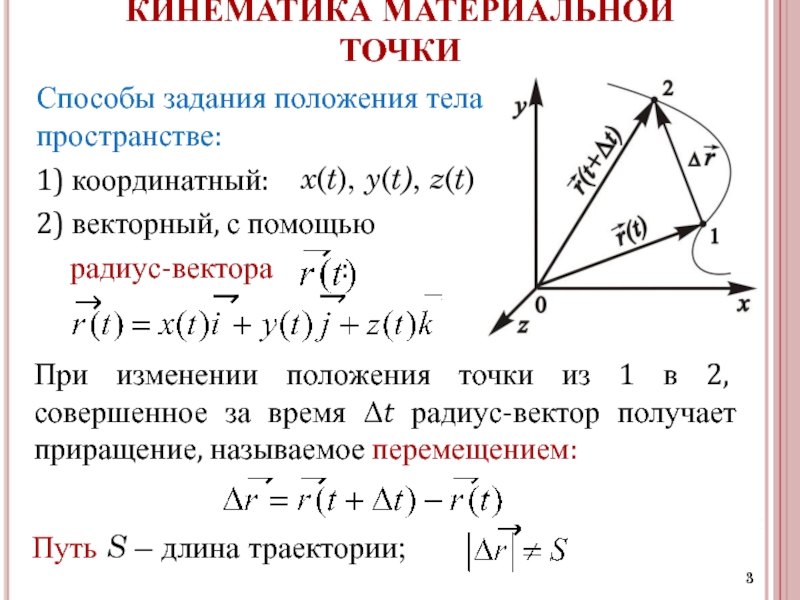 Подставляем данные в формулу:
Подставляем данные в формулу:
Ответ:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Ответ:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
Как решаем:
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Ответ:
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Как решаем:
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Ответ:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Операции с векторами, сложение векторов, умножение вектора на действительное число.
Рассмотрим вектор v с начальной точкой в начале координат в любой координатной системе x-y и с конечной точкой в (a,b). Мы говорим, что вектор находится в стандартном положении и ссылаемся на него как на радиус-вектор. Обратите внимание, что пара точек определяет этот вектор. Таким образом, мы можем использовать это для обозначения вектора. Чтобы подчеркнуть, что мы имеем в виду вектор, и, чтобы избежать путаницы, как правило, пишут:
v = .
Координата a есть скаляром горизонтальной компоненты вектора, и координата b есть скаляром вертикальной компоненты вектора. Под скаляром мы подразумеваем численное количество, а не векторную величину. Таким образом, это рассматривается как компонентная форма v. Обратите внимание, что a и b НЕ вектора и их не надо путать с определением компонента вектора.
Теперь рассмотрим с A = (x1, y1) и C = (x2, y2). Давайте рассмотрим, как найти радиус вектор, эквивалентный . Как Вы видите на рисунке внизу, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся вычитанием координат A из координат C. Таким образом, P = (x2 – x1, y2 – y1) и радиус вектор есть .
Давайте рассмотрим, как найти радиус вектор, эквивалентный . Как Вы видите на рисунке внизу, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся вычитанием координат A из координат C. Таким образом, P = (x2 – x1, y2 – y1) и радиус вектор есть .
Можно показать, что и имеют одну и ту же величину и направление, и поэтому эквивалентны. Таким образом, = = 2 – x1, y2 – y1 >.
Компонентная форма с A = (x1, y1) и C = (x2, y2) есть
= 2 – x1, y2 – y1 >.
Пример 1 Найдите компонентную форму если C = (- 4, – 3) и F = (1, 5).
Решение Мы имеем
= = .
Обратите внимание, что вектор есть равным радиус-вектору , как показано на рисунке вверху.
Теперь, когда мы знаем, как записать вектор в компонентной форме, давайте изложим некоторые определения.
Длину вектора v легко определить, когда известны компоненты вектора. Для v = 1, v2 >, мы имеем
|v|2 = v21 + v22 Используя теорему Пифагора
|v| = √v21 + v22.
Длина, или величина ветктора v = 1, v2 > находится как |v| = √v21 + v22.
Два вектора равны или эквивалентны, если они имеют одну и ту же величину и одно и то же направление.
Пусть u = 1, u2 > и v = 1, v2 >. Tогда
1, u2 > = 1, v2 > только если u1 = v1 and u2 = v2.
Операции с векторами
Чтобы умножить вектор V на положительное число, мы умножаем его длину на это число. Его направление остается прежним. Когда вектор V умножается на 2, например, его длина увеличивается в два раза, но его направление не изменяется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор V на отрицательное действительное число, умножаем его длину на это число и изменяем направление на противоположное. Например, Когда вектор умножается на (-2), его длина увеличивается в два раза и его направление изменяется на противоположное.
Так как действительные числа работают как скалярные множители в умножении векторов, мы называем их скаляры и произведение kv называется скалярные кратные v.
Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор V на отрицательное действительное число, умножаем его длину на это число и изменяем направление на противоположное. Например, Когда вектор умножается на (-2), его длина увеличивается в два раза и его направление изменяется на противоположное.
Так как действительные числа работают как скалярные множители в умножении векторов, мы называем их скаляры и произведение kv называется скалярные кратные v.
Для действительного числа k и вектора v = 1, v2 >, скалярное произведение k и v есть
kv = k.1, v2 > = 1, kv2 >.
Вектор kv есть скалярным кратным вектора v.
Пример 2 Пусть u = и w = . Найдите – 7w, 3u и – 1w.
Решение
– 7w = – 7. = ,
3u = 3. = ,
– 1w = – 1. = .
Теперь мы можем сложить два вектора, используя компоненты. Чтобы сложить два вектора в компонентной форме, мы складываем соответствующие компоненты. Пусть u = 1, u2 > и v = 1, v2 >. Тогда
Чтобы сложить два вектора в компонентной форме, мы складываем соответствующие компоненты. Пусть u = 1, u2 > и v = 1, v2 >. Тогда
u + v = 1 + v1, u2 + v2 >
Например, если v = и w = , тогда
v + w = =
Если u = 1, u2 > и v = 1, v2 >, тогда
u + v = 1 + v1, u2 + v2 >.
Перед тем, как мы определим вычитание векторов нам нужно дать определение – v. Противоположный вектору v = 1, v2 >, изображенному внизу, есть
– v = (- 1).v = (- 1)1, v2 > = 1, – v2 >
Вычитание векторов, такое как u – v вовлекает вычитание соответствующих компонент. Мы покажем это представлением u – v как u + (- v). Если u = 1, u2 > и v = 1, v2 >, тогда
u – v = u + (- v) = 1, u2 > + 1, – v2 > = 1 + (- v1), u2 + (- v2) > = 1 – v1, u2 – v2 >
Мы можем проиллюстрировать вычитание векторов с помощью параллелограмма , как мы это делали для сложения векторов.
Вычитание векторов
Если u = 1, u2 > и v = 1, v2 >, тогда
u – v = 1 – v1, u2 – v2 >.
Интересно сравнить суммы двух векторов с разницей тех же двух векторов в одном параллелограмме. Векторы u + v и u – v есть диагоналями параллелограмма.
Пример 3 Сделайте следующие вычисления, где u = и v = .
a) u + v
b) u – 6v
c)3u + 4v
d)|5v – 2u|
Решение
a) u + v = + = = ;
b)u – 6v = – 6. = – = ;
c) 3u + 4v = 3. + 4. = + = ;
d) |5v – 2u| = |5. – 2.| = | – | = || = √(- 29)2 + 212 = √1282 ≈ 35,8
Прежде чем сформулировать свойства векторного сложения и умножения, мы должны дать определение еще одному специальному вектору – нулевому вектору. Вектор, чья начальная точка совпадает с конечной точкой, называется нулевым вектором, обозначается O, или . Его величина равна 0. В сложении векторов:
v + O = v. 1, v2 > + = 1, v2 >
1, v2 > + = 1, v2 >
Операции над векторами обладают те же самыми свойствами, что и операции над вещественными числами.
Для всех векторов u, v, и w, и для всех скаляров b и c:
1. u + v = v + u.
2. u + (v + w) = (u + v) + w.
3. v + O = v.
4 1.v = v; 0.v = O.
5. v + (- v) = O.
6. b(cv) = (bc)v.
7. (b + c)v = bv + cv.
8. b(u + v) = bu + bv.
Орты
Вектор величиной, или длиной 1 называется орт. Вектор v = есть орт, потому что
|v| = || = √(- 3/5)2 + (4/5)2 = √9/25 + 16/25 = √25/25 = √1 = 1.
Пример 4 Найдите орт, который имеет то же самое направление, что и вектор w = .
Решение Найдем сначала длину w:
|w| = √(- 3)2 + 52 = √34. Таким образом, мы ищем вектор, с длиной 1/√34 от w и с таким же самым направлением, что и вектор w. Этот вектор есть
u = w/√34 = /√34 = 34, 5/√34 >.
Вектор u есть орт, потому что
|u| = |w/√34| = = √34/34 = √1 = 1.
Если v есть вектор и v ≠ O, тогда
(1/|v|)• v, or v/|v|,
есть орт в направлении v.
Хотя орты могут иметь любое направление, орты, параллельные осям x и y особенно полезны. Они определяются как
i = and j = .
Любой вектор может быть выражен как линейная комбинация орта i и j. Например, пусть v = 1, v2 >. Tогда
v = 1, v2 > = 1, 0 > + 2 > = v1 + v2 = v1i + v2j.
Пример 5 Выразите вектор r = как линейную комбинацию i и j.
Решение
r = = 2i + (- 6)j = 2i – 6j.
Пример 6 Запишите вектор q = – i + 7j в компонентной форме.
Решениеq = – i + 7j = -1i + 7j =
Векторные операции могут быть также выполнены, когда векторы записаны как линейные i и j.
Пример 7 Если a = 5i – 2j и b = -i + 8j, найдите 3a – b.
Решение
3a – b = 3(5i – 2j) – (- i + 8j) = 15i – 6j + i – 8j = 16i – 14j.
Углы обзора
Конечная точка P орты в стандартной позиции есть точкой на единичной окружности, определенной (cosθ, sinθ). Таким образом, орт может быть выражен в компонентной форме,
u = ,
или как линейная комбинация орт i и j,
u = (cosθ)i + (sinθ)j,
где компоненты u есть функциями угла обзора θ измеряемого против часовой стрелки от оси x к этому вектору. Так как θ изменяется от 0 до 2π, точка P отслеживает круг x2 + y2 = 1. Это охватывает все возможные направления ортов и тогда уравнение u = (cosθ)i + (sinθ)j описывает каждый возможный орт на плоскости.
Пример 8 Вычислите и сделайте эскиз орта u = (cosθ)i + (sinθ)j для θ = 2π/3. Изобразите единичную окружность на эскизе.
Решение
u = (cos(2π/3))i + (sin(2π/3))j = (- 1/2)i + (√3/2)j
Пусть v = 1, v2 > с углом обзора θ. Используя определение функции тангенса, мы можем определить угол обзора их компонент v:
Пример 9 Определите угол обзора θ вектора w = – 4i – 3j.
Решение Мы знаем, что
w = – 4i – 3j = .
Таким образом, имеем
tanθ = (- 3)/(- 4) = 3/4 и θ = tan– 1(3/4).
Так как w находится в третьем квадранте, мы знаем, что θ есть углом третьего квадранта. Соответствующий угол есть
tan– 1(3/4) ≈ 37°, и θ ≈ 180° + 37°, или 217°.
Это удобно для работы с прикладными задачами, а в последующих курсах, чтобы иметь способ выразить вектор так, чтобы его величина и направление могли быть легко определены или прочитаны. Пусть v это вектор. Тогда v/|v| есть орт в том же самом направлении, что и v. Таким образом, мы имеем
v/|v| = (cosθ)i + (sinθ)j
v = |v|[(cosθ)i + (sinθ)j] Умножая на |v|
v = |v|(cosθ)i + |v|(sinθ)j.
Углы между векторами
Когда вектор умножается на скаляр, результатом есть вектор. Когда складываются два вектора, результатом также есть вектор. Таким образом, мы могли бы ожидать, что произведение двух векторов есть вектор, но это не так. Скалярное произведение двух векторов есть действительное число или скаляр. Этот результат полезен в нахождении угла между двумя векторами и в определении, являются ли два вектора перпендикулярными.
Скалярное произведение двух векторов есть действительное число или скаляр. Этот результат полезен в нахождении угла между двумя векторами и в определении, являются ли два вектора перпендикулярными.
Скалярное произведение двух векторов u = 1, u2 > и v = 1, v2 > is
u • v = u1.v1 + u2.v2
(Обратите внимание, что u1v1 + u2v2 есть скаляром, а не вектором.)
Пример 10Найдите скалярное произведение, когда
u = , v = и w = .
a)u • w
b)w • v
Решение
a) u • w = 2(- 3) + (- 5)1 = – 6 – 5 = – 11;
b) w • v = (- 3)0 + 1(4) = 0 + 4 = 4.
Скалярное произведение может быть использовано для нахождения угла между двумя векторами. Угол между двумя векторами это самый маленький положительный угол, образованный двумя направленными отрезками. Таким образом, θ между u и v это тот же самый угол, что и между v и u, и 0 ≤ θ ≤ π.
Если θ есть углом между двумя ненулевыми векторами u и v, тогда
cosθ = (u • v)/|u||v|.
Пример 11Найдите угол между u = и v = .
Решение Начнем с нахождения u • v, |u|, и |v|:
u • v = 3(- 4) + 7(2) = 2,
|u| = √32 + 72 = √58, and
|v| = √(- 4)2 + 22 = √20.
Tогда
cosα = (u • v)/|u||v| = 2/√58.√20
α = cos– 1(2/√58.√20)
α ≈ 86,6°.
Равновесие сил
Когда несколько сил действуют на одну и ту же точку на объекте, их векторная сумма должна быть равна нуля, для того, чтобы был баланс. Когда есть баланс сил, то объект является стационарным или движется по прямой линии, без ускорения. Тот факт, что векторная сумма должна быть равна нулю вывода для получения баланса, и наоборот, позволяет решать нам многие прикладные задачи с участием сил.
Пример 12 Подвесной блок 350- фунтовый блок подвешен с помощью двух кабелей. осталось. В точке А есть три силы, действующие так: W блок тянет вниз, а R и S (два кабеля) тянут вверх и наружу. Найдите нагрузку каждого кабеля.
Найдите нагрузку каждого кабеля.
Решение Нарисуем диаграмму с начальными точками каждого вектора в начале кооординат. Для баланса, сумма векторов должна быть равна О:
R + S + W = О.
Мы можем выразить каждый вектор через его величину и угол обзора :
R = |R|[(cos125°)i + (sin125°)j],
S = |S|[(cos37°)i + (sin37°)j], и
W = |W|[(cos270°)i + (sin270°)j]
= 350(cos270°)i + 350(sin270°)j
= -350j cos270° = 0; sin270° = – 1.
Заменяя R, S, и W in R + S + W + O, мы имеем
[|R|(cos125°) + |S|(cos37°)]i + [|R|(sin125°) + |S|(sin37°) – 350]j = 0i + 0j.
Это дает нам систему уравнений:
|R|(cos125°) + |S|(cos37°) = 0,
|R|(sin125°) + |S|(sin37°) – 350 = 0.
Решая эту систему, мы получаем
|R| ≈ 280 и |S| ≈ 201.
Таким образом, нагрузка на кабели 280 фунтов и 201 фунт.
Момент вектора силы – определение и свойства
Момент вектора силы — Введение
Физическая величина «Момент вектора силы» имеет прямое отношение к вращательному движению и входит в состав одного важного соотношения, называемого уравнением моментов. Но давайте разбираться по порядку. Для начала нам необходимо провести ряд построений, без которых определение момента вектора силы будет неясным.Пусть существует некоторая точка О. Относительно этой точки, называемой началом или полюсом, мы будем рассматривать (а правильнее будет сказать находить или определять) момент вектора силы (моментом силы ), а так же момент импульса (момент импульса ).
Но давайте разбираться по порядку. Для начала нам необходимо провести ряд построений, без которых определение момента вектора силы будет неясным.Пусть существует некоторая точка О. Относительно этой точки, называемой началом или полюсом, мы будем рассматривать (а правильнее будет сказать находить или определять) момент вектора силы (моментом силы ), а так же момент импульса (момент импульса ).
Построим из обозначенного нами полюса (точки О) радиус вектор к точке приложения силы . Обратите внимание на рисунок приведенный выше — он иллюстрирует все наши рассуждения.
Момент вектора силы — Определение
Выполнив все вышеперечисленное, мы можем приступить к нахождению момента вектора силы (момента ). Итак, момент вектора силы это вектор, получаемый при векторном перемножении и . Обозначать момент силы мы будем через . Ниже приведена формула, соответствующая приведенному определению.
Как видно из формулы, направление вектора зависит от положения выбранного полюса (может быть изменено направление вектора ) и от направления вектора силы .
Момента вектора силы — Свойства
- Момент вектора силы не изменяется при переносе точки приложение силы вдоль линии действия этой силы.
- Момент вектора силы относительно выбранного полюса для нескольких сил равен геометрической сумме моментов сил, рассчитанных для каждой силы по отдельности.
Докажем справедливость первого пункта. Длина вектора , полученного нами, равна площади параллелограмма OABC (школьный курс математики). Если мы сместим вектор силы вдоль линии ее действия (смотри рисунок в выше), то мы получим параллелограмм ОА’B‘C, площадь которого равна площади первого параллелограмма. А дочитав правила векторного умножения до конца, вы поймете, что и направление вектора осталось прежним.
Справедливость второго пункта можно доказать вспомнив еще одно свойство векторного умножения — .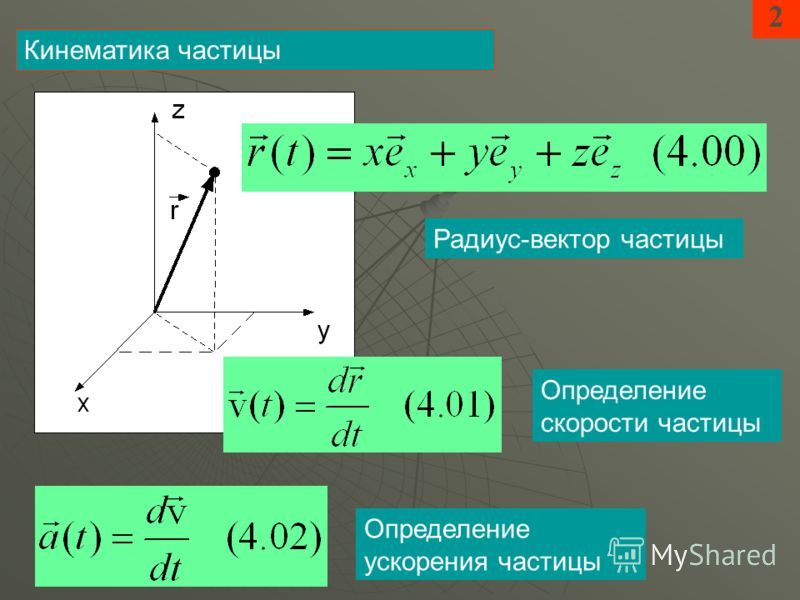 Заменив векторные произведения их значениями, мы получим математическое выражение для второго свойства момента вектора сил.
Заменив векторные произведения их значениями, мы получим математическое выражение для второго свойства момента вектора сил.
Post Views: 11 067
ПохожееКомплексная плоскость | Математика, которая мне нравится
Рассмотрим координатную плоскость и поставим в соответствие каждому комплексному числу точку с координатами . Тогда устанавливается взаимно однозначное соответствие между полем и множеством точек координатной плоскости. Координатную плоскость в этом случае будем называть комплексной плоскостью. Ось абсцисс будем называть вещественной осью, а ось ординат — мнимой осью.
С каждой точкой комплексной плоскости можно связать вектор, идущий из нуля в эту точку (радиус-вектор). Координаты этого вектора — вещественная и мнимая части его конца.
Радиус-вектор числа равен сумме радиус-векторов чисел и .
Аналогично с вычитанием.
Полярная система координат
Выберем в плоскости точку (полюс) и луч с началом в точке (полярную полуось). Тогда положение любой точки плоскости , отличной от точки , однозначно характеризуется двумя числами: длиной отрезка (полярный радиус точки ) и величиной угла, образованного лучом с полярной полуосью (полярный угол точки ). При этом полярный угол отсчитывается в некотором фиксированном направлении, одном и том же для всех точек.
Тогда положение любой точки плоскости , отличной от точки , однозначно характеризуется двумя числами: длиной отрезка (полярный радиус точки ) и величиной угла, образованного лучом с полярной полуосью (полярный угол точки ). При этом полярный угол отсчитывается в некотором фиксированном направлении, одном и том же для всех точек.
Полярный угол определен с точностью до . Полярный радиус точки считается равным нулю, а полярного угла у нее нет.
Модуль и аргумент комплексного числа
Модулем комплексного числа называется расстояние от до нуля на комплексной плоскости.
Обозначение. . (Модуль — длина радиус-вектора.) Если , это определение не противоречит определению модуля вещественного числа.
Пусть и — комплексные числа. — длина радиус-вектора числа — длина вектора — расстояние между и на комплексной плоскости.
Пусть . Тогда Следовательно, .
Теорема. .
Доказательство.
Теорема.
Доказательство аналогично.
Теорема.
Доказательство. Следует из определения модуля и геометрического смысла сложения и вычитания комплексных чисел.
Определение. Пусть — комплексное число, не равное нулю, пусть , тогда
Следовательно, точка лежит на единичной окружности с центром в нуле.
Существует вещественное число такое, что
Таких чисел бесконечно много, и любые два из них различаются на , где — произвольное целое число. Любое такое число называется аргументом числа .
Обозначение. .
Итак, любое комплексное число можно представить в виде
где .
Такое представление комплексного числа называется его тригонометрической формой.
Формула Муавра
Абрахам де Муавр (1667–1754) был выходцем из Франции, прожил долгую жизнь в Англии и умер в Лондоне.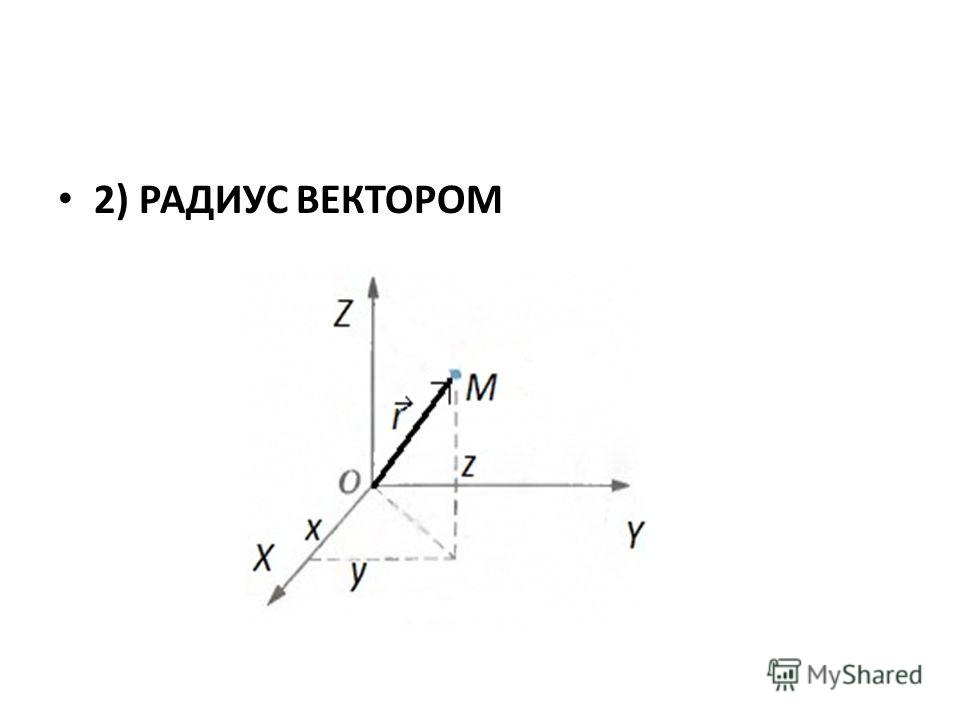 Однажды, незадолго до смерти, Муавр заявил, что ему необходимо ежедневно увеличивать время сна на 10–15 минут. Достигнув, таким образом, в сумме продолжительность сна более 23 часов, он на следующие сутки проспал все 24 часа и умер во сне.
Однажды, незадолго до смерти, Муавр заявил, что ему необходимо ежедневно увеличивать время сна на 10–15 минут. Достигнув, таким образом, в сумме продолжительность сна более 23 часов, он на следующие сутки проспал все 24 часа и умер во сне.
С именем Муавра связаны правила возведения в -ю степень и извлечения корня -й степени для комплексных чисел. Муавр много занимался исследованием рядов и доказал частный случай предельной теоремы в теории вероятностей.
Лемма. Пусть , где . Тогда .
Доказательство.
Пусть . Тогда . Но
Следовательно, числам и соответствует одна и та же точка числовой окружности. Значит, . Значит, — одно из значений .
Теорема. Пусть . Тогда .
Доказательство. Представим и в тригонометрической форме:
Тогда
Так как , то можно применить лемму. — одно из значений .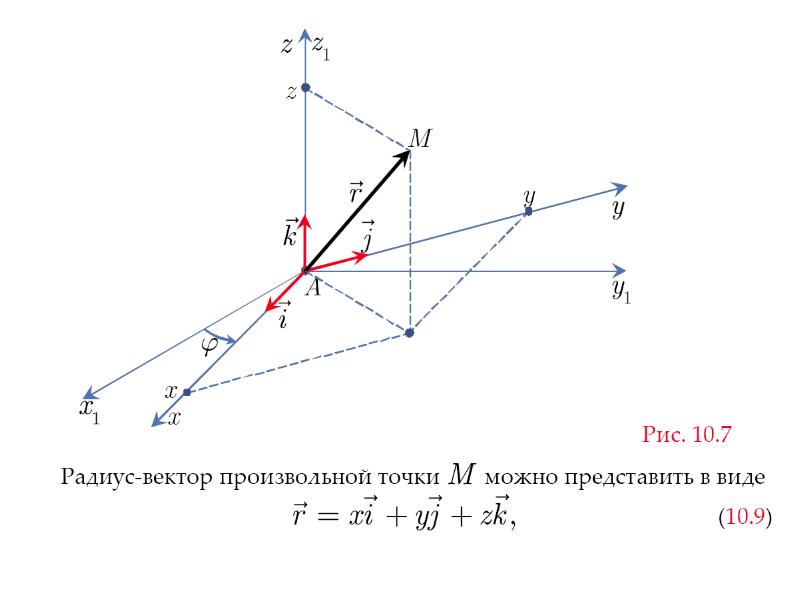
Следствие.
— формула Муавра.
Следствие. В условиях теоремы .
Доказательство.
Пусть . По теореме
Следствие. Формула Муавра верна для любого целого показателя (целая отрицательная и нулевая степень для комплексных чисел вводится так же, как и для вещественных).
Доказательство. Пусть .
Следствие.
Доказательство.
Задачи.
1. Изобразите на комплексной плоскости числа
1)
2) ;
3) .
2. Найдите модуль и аргумент чисел
1) ;
2) ;
3) ;
4) .
3. Изобразите на комплексной плоскости множество точек z, задаваемых условиями
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) и .
4. Найдите множество значений функций с областью определения :
1) , ;
2) , .
5. Используйте тригонометрическую форму и формулу Муавра для вычисления значений:
1) ;
2) ;
3) ;
4) .
13.3: Длина дуги и кривизна
В этом разделе мы изучаем формулы, относящиеся к кривым как в двух, так и в трех измерениях, и видим, как они связаны с различными свойствами одной и той же кривой. Например, предположим, что вектор-функция описывает движение частицы в пространстве. Мы хотели бы определить, какое расстояние прошла частица за заданный интервал времени, который можно описать длиной дуги пути, по которому она следует. Или предположим, что вектор-функция описывает дорогу, которую мы строим, и мы хотим определить, насколько круто изгибается дорога в данной точке.{b}_{a} \|\vecs r′(t)\|dt . \label{Arc3D} \end{align}\]
\label{Arc3D} \end{align}\]
Эти две формулы очень похожи; они отличаются только тем, что пространственная кривая имеет три составляющие функции вместо двух. Обратите внимание, что формулы определены для гладких кривых: кривых, где вектор-функция \(\vecs r(t)\) дифференцируема с ненулевой производной. Условие гладкости гарантирует, что кривая не имеет точек возврата (или углов), которые могли бы сделать формулу проблематичной.
Пример \(\PageIndex{1}\): определение длины дуги
Вычислите длину дуги для каждой из следующих вектор-функций:
- \(\vecs r(t)=(3t−2) \,\hat{\mathbf{i}}+(4t+5) \,\hat{\mathbf{j}},\quad 1≤t ≤5\)
- \(\vecs r(t)=⟨t\cos t,t\sin t,2t⟩,0≤t≤2 \pi \)
Раствор
- Используя уравнение \ref{Arc2D}, \(\vecs r′(t)=3 \,\hat{\mathbf{i}}+4 \,\hat{\mathbf{j}}\), поэтому
\[\begin{align*} s &=\int^{b}_{a} \|\vecs r′(t)\|dt \\[4pt] &=\int^{5}_{1 } \sqrt{3^2 + 4^2} dt \\[4pt] &=\int^{5}_{1} 5 dt = 5t\big|^{5}_{1} = 20.
 {3/2})≈37,785\) единиц
{3/2})≈37,785\) единицВернемся к спирали, представленной ранее в этой главе. Вектор-функцию, описывающую спираль, можно записать в виде
\[\vecs r(t)=R \cos \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{i}} +R \sin \left(\dfrac{2πNt} {h}\right) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}},0≤t≤h, \nonumber\]
, где \(R\) представляет собой радиус спирали, \(h\) представляет собой высоту (расстояние между двумя последовательными витками), а спираль завершает \(N\) витков.2}.\end{выравнивание*}\]
Это дает формулу для длины проволоки, необходимой для формирования спирали с \(N\) витками, которая имеет радиус \(R\) и высоту \(h\).
Параметризация длины дуги
Теперь у нас есть формула для длины дуги кривой, заданной вектор-функцией. Давайте сделаем еще один шаг вперед и рассмотрим, что такое функция длины дуги .
Если векторнозначная функция представляет положение частицы в пространстве как функцию времени, то функция длины дуги измеряет, как далеко эта частица проходит как функцию времени.
 {t}_{ a} ‖\vecs r′(u)‖du \bigg] \\[4pt] &=\|\vecs r′(t)\|.{t}_{a} ‖\vecs r′(u)‖\,du\]
{t}_{ a} ‖\vecs r′(u)‖du \bigg] \\[4pt] &=\|\vecs r′(t)\|.{t}_{a} ‖\vecs r′(u)‖\,du\]Кроме того,
\[\dfrac{ds}{dt}=‖\vecs r′(t)‖>0. \номер\]
Если \(‖\vecs r′(t)‖=1\) для всех \(t≥a\), то параметр \(t\) представляет собой длину дуги от начальной точки в \(t=a\ ).
Полезным применением этой теоремы является нахождение альтернативной параметризации данной кривой, называемой параметризацией длины дуги . Напомним, что любую вектор-функцию можно перепараметрировать заменой переменных.Например, если у нас есть функция \(\vecs r(t)=⟨3 \cos t,3 \sin t⟩,0≤t≤2π\), которая параметризует окружность радиуса 3, мы можем изменить параметр с \(t\) в \(4t\), получив новую параметризацию \(\vecs r(t)=⟨3 \cos 4t,3 \sin 4t⟩\). Новая параметризация по-прежнему определяет окружность радиуса 3, но теперь нам нужно использовать только значения \(0≤t≤π/2\), чтобы пройти круг один раз.
Предположим, что мы нашли функцию длины дуги \(s(t)\) и можем решить эту функцию для \(t\) как функцию от \(s\) .
 Затем мы можем перепараметрировать исходную функцию \(\vecs r(t)\), подставив выражение для \(t\) обратно в \(\vecs r(t)\). Теперь вектор-функция записывается в терминах параметра \(s\) . Поскольку переменная \(s\) представляет длину дуги, мы называем это параметризацией длины дуги исходной функции \(\vecs r(t)\). Одним из преимуществ нахождения параметризации длины дуги является то, что расстояние, пройденное вдоль кривой, начиная с \(s=0\), теперь равно параметру \(s\).Параметризация длины дуги также появляется в контексте кривизны (которую мы рассмотрим позже в этом разделе) и линейных интегралов.
Затем мы можем перепараметрировать исходную функцию \(\vecs r(t)\), подставив выражение для \(t\) обратно в \(\vecs r(t)\). Теперь вектор-функция записывается в терминах параметра \(s\) . Поскольку переменная \(s\) представляет длину дуги, мы называем это параметризацией длины дуги исходной функции \(\vecs r(t)\). Одним из преимуществ нахождения параметризации длины дуги является то, что расстояние, пройденное вдоль кривой, начиная с \(s=0\), теперь равно параметру \(s\).Параметризация длины дуги также появляется в контексте кривизны (которую мы рассмотрим позже в этом разделе) и линейных интегралов.Пример \(\PageIndex{2}\): поиск параметризации длины дуги
Найдите параметризацию длины дуги для каждой из следующих кривых:
- \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+ 4 \sin t \,\hat{\mathbf{j}},\quad t≥0\)
- \(\vecs r(t)=⟨t+3,2t−4,2t⟩,\quad t≥3\)
Раствор
- Сначала мы находим функцию длины дуги, используя уравнение \ref{arclength3}:
\[\begin{align*} s(t) &= \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_0^t ‖⟨−4 \sin u, 4 \cos u⟩‖ \,du \\[4pt] &= \int_0^t \sqrt{(−4 \sin u)^2+(4 \cos u)^2} \,du \\[4pt] &= \int_0^t \sqrt{16 \sin ^2 u+16 \cos ^2 u} \,du \\[4pt] &= \int_0^t 4\,du = 4t, \end{align*} \]
- , который дает связь между длиной дуги \(s\) и параметром \(t\) как \(s=4t;\), то есть \(t=s/4\).
 Далее заменяем переменную \(t\) в исходной функции \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf {j}}\) с выражением \(s/4\), чтобы получить
Далее заменяем переменную \(t\) в исходной функции \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf {j}}\) с выражением \(s/4\), чтобы получить\[\vecs r(s)=4 \cos\left(\frac{s}{4}\right) \,\hat{\mathbf{i}} + 4 \sin\left(\frac{s} {4}\справа) \,\шляпа{\mathbf{j}}. \номер\]
Это параметризация длины дуги \(\vecs r(t)\). Поскольку исходное ограничение на \(t\) было задано как \(t≥0\), ограничение на s становится \(s/4≥0\) или \(s≥0\).t 3 \,du \\[4pt] &= 3t – 9. \end{align*}\] Следовательно, связь между длиной дуги \(s\) и параметром \(t\) равна \(s=3t−9\), поэтому \(t= \frac{s}{3}+3\). Подстановка этого в исходную функцию \(\vecs r(t)=⟨t+3,2t−4,2t⟩ \) дает\[\vecs r(s)=⟨\left(\frac{s}{3}+3\right)+3,\,2\left(\frac{s}{3}+3\right)− 4,\,2\влево(\frac{s}{3}+3\вправо)⟩=⟨\frac{s}{3}+6, \frac{2s}{3}+2,\frac{2s {3}+6⟩.\номер\]
Это параметризация длины дуги \(\vecs r(t)\).Исходное ограничение на параметр \(t\) было \(t≥3\), поэтому ограничение на \(s\) равно \((s/3)+3≥3\) или \(s≥0 \).
Упражнение \(\PageIndex{2}\)
Найдите функцию длины дуги для спирали
\[\vecs r(t)=⟨3 \cos t, 3 \sin t,4t⟩,\quad t≥0. \номер\]
Затем используйте связь между длиной дуги и параметром \(t\), чтобы найти параметризацию длины дуги для \(\vecs r(t)\).
- Подсказка
Начните с нахождения функции длины дуги.
- Ответить
\(s=5t\) или \(t=s/5\). Подстановка этого в \(\vecs r(t)=⟨3 \cos t,3 \sin t,4t⟩\) дает
\[\vecs r(s)=⟨3 \cos\left(\frac{s}{5}\right),3 \sin\left(\frac{s}{5}\right),\frac{ 4s}{5}⟩,\quad s≥0 \nonumber\]
Кривизна
Кривизна является важной темой, связанной с длиной дуги. Понятие кривизны позволяет измерить, насколько резко поворачивает гладкая кривая.Окружность имеет постоянную кривизну. Чем меньше радиус окружности, тем больше кривизна.

Представьте, что вы едете по дороге. Предположим, что дорога лежит на дуге большого круга. В этом случае вам едва ли придется крутить руль, чтобы оставаться на дороге. Теперь предположим, что радиус меньше. В этом случае вам нужно будет поворачивать более резко, чтобы остаться на дороге. В случае кривой, отличной от окружности, часто полезно сначала вписать окружность в кривую в данной точке так, чтобы она касалась кривой в этой точке и «обнимала» кривую как можно теснее в заданной точке. окрестности точки (рис. \(\PageIndex{1}\)).Затем кривизна графика в этой точке определяется как такая же, как кривизна вписанной окружности.
Рисунок \(\PageIndex{1}\): График представляет кривизну функции \(y=f(x).\) Чем круче поворот на графике, тем больше кривизна и меньше радиус вписанный круг.Определение: кривизна
Пусть \(C\) — гладкая кривая на плоскости или в пространстве, заданная формулой \(\vecs r(s)\), где \(s\) — параметр длины дуги. Кривизна \(κ\) в точке \(s\) равна
\[κ =\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}=‖\vecs T′(s)‖.
 \]
\]Посмотрите это видео, чтобы узнать больше о кривизне пространственной кривой.
Формула определения кривизны не очень полезна с точки зрения расчета. В частности, напомним, что \(\vecs T(t)\) представляет собой единичный касательный вектор к заданной вектор-функции \(\vecs r(t)\), а формула для \(\vecs T(t) \) это
\[\vecs T(t)=\frac{\vecs r′(t)}{∥\vecs r′(t)∥}.\]
Чтобы использовать формулу кривизны, сначала необходимо выразить \(\vecs r(t)\) через параметр длины дуги \(s\), затем найти единичный касательный вектор \(\vecs T( s)\) для функции \(\vecs r(s)\), то возьмем производную от \(\vecs T(s)\) по \(s\).Это утомительный процесс. К счастью, существуют эквивалентные формулы для кривизны.
Теорема: альтернативные формулы кривизны
Если \(C\) — гладкая кривая, заданная \(\vecs r(t)\), то кривизна \(κ\) кривой \(C\) в точке \(t\) определяется выражением
\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}. \метка{EqK2} \]
Если \(С\) — трехмерная кривая, то кривизна может быть задана формулой
\[κ =\dfrac{‖\vecs r′(t)×\vecs r′′(t)‖}{‖\vecs r′(t)‖^3}.
 {3/2}}.\метка{EqK4}\]
{3/2}}.\метка{EqK4}\]Доказательство
Первая формула следует непосредственно из цепного правила:
\[\dfrac{d\vecs{T}}{dt} = \dfrac{d\vecs{T}}{ds} \dfrac{ds}{dt}, \nonumber\]
, где \(s\) – длина дуги вдоль кривой \(C\). Разделив обе стороны на \(ds/dt\) и взяв величину обеих сторон, мы получим
.\[\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}= \left\lVert\frac{\vecs T'(t)}{\dfrac{ds} {dt}}\right\rVert.\nonumber\]
Поскольку \(ds/dt=‖\vecs r′(t)‖\), это дает формулу кривизны \(κ\) кривой \(C\) в терминах любой параметризации \(C\ ):
\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}.3}.\номер\]
Это доказывает \(\ref{EqK3}\). Чтобы доказать \(\ref{EqK4}\), мы начнем с предположения, что кривая \(C\) определяется функцией \(y=f(x)\). Тогда мы можем определить mathbf{k}}\). Используя предыдущую формулу кривизны:
\[\begin{align*} \vecs r'(t) &=\,\hat{\mathbf{i}}+f'(x)\,\hat{\mathbf{j}} \\[4pt ] \vecs r″(t) &=f″(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r′(t)×\vecs r″(t) &= \begin {vmatrix} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ 1 & f'(x) & 0 \\ 0 & f”( х) & 0 \end{vmatrix} = f″(x)\,\hat{\mathbf{k}}.
 {3/2}}≈0,0059\)
{3/2}}≈0,0059\)Нормальные и бинормальные векторы
Мы видели, что производная \(\vecs r′(t)\) вектор-функции является касательным вектором к кривой, заданной \(\vecs r(t)\), а единичный касательный вектор \ (\vecs T(t)\) можно рассчитать, разделив \(\vecs r′(t)\) на его величину. При изучении движения в трех измерениях для описания движения частицы вдоль траектории в пространстве полезны два других вектора: вектор главной единичной нормали и бинормальный вектор .
Определение: бинормальные векторы
Пусть \(C\) трехмерная гладкая кривая, представленная \(\vecs r\) на открытом интервале \(I\) . Если \(\vecs T′(t)≠\vecs 0\), то главный единичный вектор нормали в точке \(t\) определяется как
\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \метка{EqNormal}\]
Вектор бинормалей в точке \(t\) определяется как
\[\vecs B(t)=\vecs T(t)×\vecs N(t),\label{EqBinormal}\]
, где \(\vecs T(t)\) – единичный касательный вектор.

Обратите внимание, что бинормали по определению ортогональны как единичному касательному вектору, так и вектору нормали. Кроме того, \(\vecs B(t)\) всегда является единичным вектором. Это можно показать, используя формулу для величины векторного произведения.
\[‖\vecs B(t)‖=‖\vecs T(t)×\vecs N(t)‖=‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta,\ ]
, где \(\theta\) — угол между \(\vecs T(t)\) и \(\vecs N(t)\). Поскольку \(\vecs N(t)\) является производной единичного вектора, свойство (vii) производной вектор-функции говорит нам, что \(\vecs T(t)\) и \(\vecs N(t)\) ортогональны друг другу, поэтому \(\theta=π/2\).Кроме того, они оба являются единичными векторами, поэтому их величина равна 1. Следовательно, \(‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta=(1)(1) \sin (π/ 2)=1\) и \(\vecs B(t)\) – единичный вектор.
Вычисление главного единичного вектора нормали может оказаться сложной задачей, поскольку единичный вектор касательной включает частное, а это частное часто имеет квадратный корень в знаменателе.
 2\,\hat{\mathbf{j}}−8t\,\hat{\mathbf {к}}\)
2\,\hat{\mathbf{j}}−8t\,\hat{\mathbf {к}}\)
Раствор
- Эта функция описывает окружность.2 t}} \\[4pt]
&=− \cos t\,\hat{\mathbf{i}}+ \sin t\,\hat{\mathbf{j}}. \конец{выравнивание*}\]Обратите внимание, что единичный касательный вектор и главный единичный вектор нормали ортогональны друг другу для всех значений \(t\):
\[\begin{align*} \vecs T(t)·\vecs N(t) &=⟨− \sin t,− \cos t⟩·⟨− \cos t, \sin t⟩ \\[4pt ] &= \sin t \cos t−\cos t \sin t \\[4pt] &=0. \конец{выравнивание*}\]
Кроме того, главный единичный вектор нормали указывает к центру окружности из каждой точки окружности.2−3t)\,\hat{\mathbf{i}}+(4t+1)\,\hat{\mathbf{j}}\) и вычислить его при \(t=2\).
- Подсказка
Сначала найдите \(\vecs T(t)\), затем используйте \(\ref{EqNormal}\).
- Ответить
\(\vecs N(2)=\dfrac{\sqrt{2}}{2}(\,\hat{\mathbf{i}}−\,\hat{\mathbf{j}})\)
Для любой гладкой кривой в трех измерениях, заданной вектор-функцией, теперь у нас есть формулы для единичного касательного вектора \(\vecs T\), единичного вектора нормали \(\vecs N\) и бинормали вектор \(\vecs B\).
Рисунок \(\PageIndex{2}\): На этом рисунке показана система отсчета Френе.В каждой точке \(P\) на трехмерной кривой вектора единичной касательной, единичной нормали и бинормали образуют трехмерную систему отсчета. Единичный вектор нормали и вектор бинормали образуют плоскость, перпендикулярную кривой в любой точке кривой, называемую плоскостью нормали. Кроме того, эти три вектора образуют систему отсчета в трехмерном пространстве, называемую системой отсчета Френе (также называемой системой отсчета TNB ) (рис. \(\PageIndex{2}\)). Наконец, плоскость, определяемая векторами \(\vecs T\) и \(\vecs N\), образует соприкасающуюся плоскость \(C\) в любой точке \(P\) на кривой.
Единичный вектор нормали и вектор бинормали образуют плоскость, перпендикулярную кривой в любой точке кривой, называемую плоскостью нормали. Кроме того, эти три вектора образуют систему отсчета в трехмерном пространстве, называемую системой отсчета Френе (также называемой системой отсчета TNB ) (рис. \(\PageIndex{2}\)). Наконец, плоскость, определяемая векторами \(\vecs T\) и \(\vecs N\), образует соприкасающуюся плоскость \(C\) в любой точке \(P\) на кривой.Предположим, мы образуем окружность в соприкасающейся плоскости \(C\) в точке \(P\) на кривой. Предположим, что окружность имеет ту же кривизну, что и кривая в точке \(P\), и пусть окружность имеет радиус \(r\). Тогда кривизна круга определяется как \(\frac{1}{r}\).
Рисунок \(\PageIndex{3}\): В этой соприкасающейся окружности окружность касается кривой \(C\) в точке \(P\) и имеет ту же кривизну. Мы называем \(r\) радиусом кривизны кривой, и он равен обратной величине кривизны.Если эта окружность лежит на вогнутой стороне кривой и касается кривой в точке \(P\), то эта окружность называется соприкасающейся окружностью кривой \(C\) в \(P\), как показано на рисунке \(\PageIndex{3}\).
Мы называем \(r\) радиусом кривизны кривой, и он равен обратной величине кривизны.Если эта окружность лежит на вогнутой стороне кривой и касается кривой в точке \(P\), то эта окружность называется соприкасающейся окружностью кривой \(C\) в \(P\), как показано на рисунке \(\PageIndex{3}\).Для получения дополнительной информации о соприкасающихся окружностях см. эту демонстрацию кривизны и кручения, эту статью о соприкасающихся окружностях и это обсуждение формул Серре.{3/2}}.\]
Это дает \(κ=6\). Следовательно, радиус соприкасающейся окружности определяется выражением \(R=\frac{1}{κ}=\dfrac{1}{6}\). Далее мы вычисляем координаты центра круга. Когда \(x=1\), наклон касательной равен нулю. Следовательно, центр соприкасающейся окружности находится прямо над точкой на графике с координатами \((1,−1)\). Центр расположен в точке \((1,−\frac{5}{6})\).
 2=\frac{1}{16}\).
2=\frac{1}{16}\).16.6 Векторные функции для поверхностей
Мы много работали с векторными уравнениями для кривых, ${\bf r}(t)=\langle x(t),y(t),z(t)\rangle$. Аналогичная техника может использоваться для представления поверхностей в более общем виде, чем уравнения для поверхностей, которые мы использовали до сих пор. Напомним, что когда мы используем ${\bf r}(t)$ для представления кривой, мы представляем себе вектор ${\bf r}(t)$ хвостом в начале координат, а затем следуем за головой стрелки при изменении $t$.Вектор «рисует» кривую через пространство при изменении $t$.
Предположим, что вместо этого у нас есть векторная функция двух переменных, $${\bf r}(u,v)=\langle x(u,v),y(u,v),z(u,v)\rangle.$$ Как и $u$, и $v$ меняются, мы снова представляем себе вектор ${\bf r}(u,v)$ с хвостом в происхождение, и его голова выметает поверхность в космосе. Полезный аналогом является технология ЭЛТ-видеоэкранов, в которой электрон пушка стреляет электронами в сторону экрана.
 пистолет
направление перемещается по горизонтали и вертикали, чтобы «раскрасить» экран
с желаемым изображением.На практике пушка перемещается горизонтально
через всю строку, затем перемещается по вертикали на следующую строку и
повторяет операцию. Точно так же может быть полезно представить
фиксируя значение $v$ и позволяя ${\bf r}(u,v)$ заметать кривую как
$u$ меняется. Тогда $v$ может немного измениться, и ${\bf r}(u,v)$ заметает
новая кривая очень близка к первой. Положите достаточно этих кривых
вместе, и они образуют поверхность.
пистолет
направление перемещается по горизонтали и вертикали, чтобы «раскрасить» экран
с желаемым изображением.На практике пушка перемещается горизонтально
через всю строку, затем перемещается по вертикали на следующую строку и
повторяет операцию. Точно так же может быть полезно представить
фиксируя значение $v$ и позволяя ${\bf r}(u,v)$ заметать кривую как
$u$ меняется. Тогда $v$ может немного измениться, и ${\bf r}(u,v)$ заметает
новая кривая очень близка к первой. Положите достаточно этих кривых
вместе, и они образуют поверхность.Пример 16.6.1. Рассмотрим функцию ${\bf r}(u,v)=\langle v\cos u,v\sin u, v\rangle$.Для фиксированного значения $v$, когда $u$ изменяется от 0 до $2\pi$, это описывает окружность радиуса $v$ на высоте $v$ над Плоскость $x$-$y$. Сложите много-много всего этого вместе, и они образуют конус, как на рисунке 16.6.1. В качестве альтернативы мы можем зафиксировать $u$, и поскольку $v$ варьируется от $0$ до бесконечности, ${\bf r}(u,v)$ отслеживает вне линии; примеры этих линий можно увидеть в стенке конуса или в одиночку на третьем графике рисунка.
 $\квадрат$
$\квадрат$Рис. 16.6.1. Трассировка поверхности.
Пример 16.6.2. Пусть ${\bf r}=\langle v\cos u, v\sin u, u\rangle$. Если $v$ постоянной, результирующая кривая представляет собой спираль (как в рисунок 13.1.1). Если $u$ постоянна, результирующая кривая представляет собой прямую линию на высоте $u$ в направлении $u$ радиан от положительная ось $x$. Обратите внимание на рисунок 16.6.2, как спирали и линии окрашивают одну и ту же поверхность по-разному. $\квадрат$
Рисунок 16.6.2. Трассировка поверхности.
Этот метод позволяет нам представлять намного больше поверхностей, чем ранее.
Пример 16.6.3. Кривая, заданная выражением $${\bf r}=\langle (2+\cos(3u/2))\cos u, (2+\cos(3u/2))\sin u, \sin(3u/2)\rangle$$ называется узел-трилистник. Напомним, что из векторного уравнения кривой мы можем вычислить единичный тангенс $\bf T$, единичная нормаль $\bf N$ и бинормальный вектор ${\bf B}={\bf T}\times{\bf N}$; ты можешь хотите просмотреть раздел 13.
 3. бинормаль
является
перпендикулярно обоим $\bf T$ и $\bf N$; один из способов интерпретировать это
состоит в том, что ${\bf N}$ и ${\bf B}$ определяют плоскость, перпендикулярную $\bf
T$, т. е. перпендикулярно кривой; поскольку ${\bf N}$ и ${\bf B}$
перпендикулярны друг другу, они могут функционировать как $\bf i$ и
$\bf j$ do для плоскости $x$-$y$.Конечно, $\bf N$ и $\bf B$
функции от $u$, изменяющиеся по мере движения вдоль кривой ${\bf r}(u)$.
Так, например, ${\bf c}(u,v)={\bf N}\cos v+{\bf B}\sin v$
векторное уравнение для единичного круга на плоскости
перпендикулярно кривой, описываемой $\bf r$, за исключением того, что обычно
интерпретация $\bf c$ поместила бы его центр в начало координат. Мы можем
исправить это, просто добавив $\bf c$ к исходному $\bf r$:
пусть ${\bf f}={\bf r}(u) +{\bf c}(u,v)$. Для
фиксированный $u$ рисует окружность вокруг точки ${\bf r}(u)$; как $u$
меняется, мы получаем последовательность таких окружностей вокруг кривой $\bf r$,
то есть трубка радиуса 1 с $\bf r$ в центре.
3. бинормаль
является
перпендикулярно обоим $\bf T$ и $\bf N$; один из способов интерпретировать это
состоит в том, что ${\bf N}$ и ${\bf B}$ определяют плоскость, перпендикулярную $\bf
T$, т. е. перпендикулярно кривой; поскольку ${\bf N}$ и ${\bf B}$
перпендикулярны друг другу, они могут функционировать как $\bf i$ и
$\bf j$ do для плоскости $x$-$y$.Конечно, $\bf N$ и $\bf B$
функции от $u$, изменяющиеся по мере движения вдоль кривой ${\bf r}(u)$.
Так, например, ${\bf c}(u,v)={\bf N}\cos v+{\bf B}\sin v$
векторное уравнение для единичного круга на плоскости
перпендикулярно кривой, описываемой $\bf r$, за исключением того, что обычно
интерпретация $\bf c$ поместила бы его центр в начало координат. Мы можем
исправить это, просто добавив $\bf c$ к исходному $\bf r$:
пусть ${\bf f}={\bf r}(u) +{\bf c}(u,v)$. Для
фиксированный $u$ рисует окружность вокруг точки ${\bf r}(u)$; как $u$
меняется, мы получаем последовательность таких окружностей вокруг кривой $\bf r$,
то есть трубка радиуса 1 с $\bf r$ в центре. Мы можем легко
изменить радиус; например ${\bf r}(u) +a{\bf c}(u,v)$
дает радиус трубы $a$; мы можем изменить радиус, как мы
двигаться по кривой с ${\bf r}(u) +g(u){\bf c}(u,v)$,
где $g(u)$ — функция от $u$.
Как показано в
16.6.3, трудно увидеть, что простой узел
завязанный; трубка делает структуру очевидной. Есть конечно
ничего особенного в узле-трилистнике в этом примере; мы можем поставить
трубка вокруг (почти) любой кривой таким же образом.
$\квадрат$
Мы можем легко
изменить радиус; например ${\bf r}(u) +a{\bf c}(u,v)$
дает радиус трубы $a$; мы можем изменить радиус, как мы
двигаться по кривой с ${\bf r}(u) +g(u){\bf c}(u,v)$,
где $g(u)$ — функция от $u$.
Как показано в
16.6.3, трудно увидеть, что простой узел
завязанный; трубка делает структуру очевидной. Есть конечно
ничего особенного в узле-трилистнике в этом примере; мы можем поставить
трубка вокруг (почти) любой кривой таким же образом.
$\квадрат$Рисунок 16.6.3. Трубки вокруг узла-трилистника радиусом $1/2$ и $3\cos(u)/4$.
Ранее мы рассматривали поверхности, заданные в виде $f(x,y)$. Иногда бывает полезно представить такие поверхности в более общая векторная форма, которая довольно проста: ${\bf r}(u,v)=\langle u,v,f(u,v)\rangle$. Имена переменных не важны, конечно; вместо того, чтобы маскировать $x$ и $y$, мы можно просто написать ${\bf r}(x,y)=\langle x,y,f(x,y)\rangle$.
Ранее мы также имели дело с поверхностями, которые не являются функциями $x$ и $y$; многие из них легко представить в векторной форме.
 2}$ вокруг оси $z$ на высоте $v$.
Мы могли бы также взять пример со сферических координат и написать
$\langle \sin u\cos v,\sin u\sin v,\cos u\rangle$, где фактически
$u$ и $v$ — это замаскированные $\phi$ и $\theta$.
2}$ вокруг оси $z$ на высоте $v$.
Мы могли бы также взять пример со сферических координат и написать
$\langle \sin u\cos v,\sin u\sin v,\cos u\rangle$, где фактически
$u$ и $v$ — это замаскированные $\phi$ и $\theta$.В Sage очень просто построить любую поверхность, для которой у вас есть векторное представление. Иногда использование различных векторных функций дает разные сюжеты, потому что Мудрец, по сути, рисует поверхность, удерживая одну переменную постоянной, а затем другую. За например, на рисунке 16.6.2 кривые на двух правых графиках наложены на левый график; график поверхности – это просто комбинация два набора кривых с пробелами, заполненными цветом.
Вот простой, но яркий пример: плоскость $x+y+z=1$ может быть вполне естественно представляется как $\langle u,v,1-u-v\rangle$. Но мы можно также подумать о том, чтобы нарисовать один и тот же самолет, выбрав конкретный точку на плоскости, скажем, $(1,0,0)$, а затем рисование кругов или эллипсы (или любые другие кривые), как если бы эта точка была происхождение в плоскости.
 Например, $\langle 1-v\cos u-v\sin u,v\sin
u,v\cos u\rangle$ — одна из таких векторных функций. Обратите внимание, что, хотя это может
не очевидно, откуда это взялось, довольно легко увидеть, что
сумма компонент $x$, $y$ и $z$ вектора всегда равна
1. Показана компьютерная визуализация самолета с использованием этих двух функций.
на рисунке 16.6.4.
Например, $\langle 1-v\cos u-v\sin u,v\sin
u,v\cos u\rangle$ — одна из таких векторных функций. Обратите внимание, что, хотя это может
не очевидно, откуда это взялось, довольно легко увидеть, что
сумма компонент $x$, $y$ и $z$ вектора всегда равна
1. Показана компьютерная визуализация самолета с использованием этих двух функций.
на рисунке 16.6.4.Рисунок 16.6.4. Два изображения одной плоскости.
Предположим, мы знаем, что плоскость содержит определенную точку $(x_0,y_0,z_0)$ и два вектора ${\bf u}=\langle u_0,u_1,u_2\rangle$ и ${\bf v}=\langle v_0,v_1,v_2\rangle$ параллельны плоскости, но не друг другу разное.Мы знаем, как получить уравнение плоскости в виде $ax+by+cz=d$, сначала вычислив ${\bf u}\times{\bf v}$. это даже проще получить векторное уравнение: $${\bf r}(u,v) = \langle x_0,y_0,z_0\rangle + u{\bf u} + v{\bf v}.$$ Первый вектор попадает в точку $(x_0,y_0,z_0)$ и затем, варьируя $u$ и $v$, $u{\bf u} + v{\bf v}$ попадают в каждую точку плоскости.

Возвращаясь к $x+y+z=1$, точки $(1,0,0)$, $(0,1,0)$ и $(0,0,1)$ все в самолете. Вычитая координаты, мы видим, что $\langle -1,0,1\rangle$ и $\langle -1,1,0\rangle$ параллельны плоскости, поэтому третья векторная форма для этой плоскости $$\langle 1,0,0\rangle + u\langle -1,0,1\rangle + v\langle -1,1,0\угол = \langle 1-u-v,v,u\rangle.$$ Это явно очень похоже на первую найденную нами форму.
Мы уже видели (раздел 15.4) как найти площадь поверхности, если она определяется в виде $f(x,y)$. Нахождение площади, когда поверхность в виде векторной функции очень похож. Глядя на сюжеты поверхностей, которые мы только что видели, очевидно, что два набора кривых которые заполняют поверхность, делят ее на сетку, и что пробелы в сетке примерно параллелограммы. Как и прежде, это ключ: мы можем записать площадь типичного маленького параллелограмма и сложите их все с интегралом.
Предположим, мы хотим аппроксимировать площадь поверхности ${\bf r}(u,v)$ вблизи ${\bf r}(u_0,v_0)$.
 Функции ${\bf r}(u,v_0)$ и ${\bf
r}(u_0,v)$ определяют две кривые, пересекающиеся в точке ${\bf
г}(и_0,v_0)$. Производные от $\bf r$ дают нам векторы, касающиеся
эти две кривые: ${\bf r}_u(u_0,v_0)$ и ${\bf r}_v(u_0,v_0)$, и
тогда ${\bf r}_u(u_0,v_0)\,du$ и ${\bf r}_v(u_0,v_0)\,dv$
два малых касательных вектора, длины которых можно использовать в качестве
длины сторон приближающего параллелограмма.2}\,dv\,du={\pi\sqrt2\over2}+
{\ пи \ пер (\ sqrt2 + 1) \ более 2}. $ $
$\квадрат$
Функции ${\bf r}(u,v_0)$ и ${\bf
r}(u_0,v)$ определяют две кривые, пересекающиеся в точке ${\bf
г}(и_0,v_0)$. Производные от $\bf r$ дают нам векторы, касающиеся
эти две кривые: ${\bf r}_u(u_0,v_0)$ и ${\bf r}_v(u_0,v_0)$, и
тогда ${\bf r}_u(u_0,v_0)\,du$ и ${\bf r}_v(u_0,v_0)\,dv$
два малых касательных вектора, длины которых можно использовать в качестве
длины сторон приближающего параллелограмма.2}\,dv\,du={\pi\sqrt2\over2}+
{\ пи \ пер (\ sqrt2 + 1) \ более 2}. $ $
$\квадрат$Упражнения 16.6
Вы можете использовать эти ячейки Sage для графических поверхностей. Первый пример представляет собой трубку вокруг узла Трилистник, второй представляет собой конус.
Пример 16.6.1 Опишите или зарисуйте поверхность с заданной векторной функцией.
а. ${\bf r}(u,v) = \langle u+v,3-v,1+4u+5v\rangle$
б. ${\bf r}(u,v) = \langle 2\sin u, 3\cos u, v\rangle$
в.2$. (отвечать)
Пример 16.6.16 Поверхность $f(x,y)$ может быть представлена вектором функция $\langle x,y,f(x,y)\rangle$.
 Настройте интеграл площади поверхности, используя
эту векторную функцию и сравнить с интегралом от
раздел 15.4.
Настройте интеграл площади поверхности, используя
эту векторную функцию и сравнить с интегралом от
раздел 15.4.Формула радиуса кривизны – Узнайте формулу для радиуса кривизны
Радиусом кривизны кривой называется любой приблизительный радиус окружности в любой данной точке. По мере движения по кривой радиус кривизны изменяется.Формула радиуса кривизны обозначается как «R». Величина, на которую кривая превращается из плоской в кривую и из кривой обратно в прямую, называется кривизной. Это скалярная величина. Радиус кривизны обратно пропорционален кривизне. Радиус кривизны — это не реальная форма или фигура, а воображаемый круг. Давайте подробно разберем формулу радиуса кривизны, используя решенные примеры в следующем разделе.
Что такое радиус формулы кривизны?
Расстояние от вершины до центра кривизны известно как радиус кривизны (обозначается R).{2}} |}\)
- Что такое вектор положения?
- Как найти вектор положения
- Пусть u = (-1, 4 , 5).
 Определите вектор положения, представленный UV .
Определите вектор положения, представленный UV . - Пусть u = (-1, 4) и v = (2, 5). Определите вектор положения, представленный VU .
- Пусть v = (3, 5) и VM = (-6, 3). Найдите вектор положения точки m.
- Учитывая b = (3,2,5), определите его вектор положения, R. Затем найдите длину вектора
- Пусть вектор AB начинается в a = (1, 2) и заканчивается в б = (2, 3). Определите его вектор положения и его длину.
- Пусть вектор OB начинается в точке o = (0,0) и заканчивается в точке b = (-2, 6). Определите вектор его положения.
- УФ = (3,1). Направление UV — на 3 единицы вправо по оси X и на 1 единицу вверх.
- ВУ = (-3,-1). Направление ВУ на 3 единицы влево по оси абсцисс и на 1 единицу вниз. Два вектора УФ и ВУ, противоположны по направлению.
 2)) для расчета длины, радиуса вектора эллипса от центра в заданном направлении – это расстояние между центром и точкой, чья линия, соединяющая центр и эту точку составляет угол тета.Длина обозначается символом L .
2)) для расчета длины, радиуса вектора эллипса от центра в заданном направлении – это расстояние между центром и точкой, чья линия, соединяющая центр и эту точку составляет угол тета.Длина обозначается символом L .Как рассчитать радиус-вектор эллипса от центра в заданном направлении с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для радиуса-вектора эллипса от центра в заданном направлении, введите большую полуось (a) , малую полуось (b) и угол (α) и нажмите кнопку расчета. Вот как вычисление вектора радиуса эллипса от центра в заданном направлении можно объяснить с заданными входными значениями -> 0.2)) .
сфер, касательных плоскостей в 3-х пространствах
сфер, касательных плоскостей в 3-х пространствахСФЕРЫ И КАСАТЕЛЬНЫЕ ПЛОСКОСТИ В ТРЕХПРОСТРАНСТВЕ Примечания и примеры
Темы этого урока
1) Уравнения сфер в трехмерном пространстве
2) Уравнения касательных плоскостей к Сферам в трехмерном пространстве
.

Уравнения сфер в трехмерном пространстве
Сфера — это просто трехмерный круг, поэтому он определяется как круг
по центральной точке и радиусу , поскольку сфера является геометрическим местом всех точек
это точное расстояние радиуса от центральной точки..
Стандартная форма уравнения сферы
Учитывая центр ( x o , y o , z o ) и радиус = r 91 сферы как утверждение о квадрате радиуса, так как мы не хотим
иметь дело с этим большим старым уродливым квадратным корнем в формуле расстояния.Тогда уравнение сферы будет таким:
( х – х или ) ² + ( у – у или ) ² + ( z – z или ) ² =
94
, в котором говорится, что квадрат расстояния от любой точки
на сфере к центру равно квадрату радиуса .
.
Пример 1: Напишите уравнение сферы с центром (-1, 3, 6) и радиусом = 5.
решение: ( х + 1 ) ² + ( у – 3) ² + ( z – 6) ² = 25.
пример 2: Запишите уравнение сферы с центром (- 4, 3, 7) через начало координат.
решение: сначала мы должны найти квадрат радиуса который является расстоянием
между центральной точкой и началом координат.r² = 16 + 9 + 49 = 74 с использованием формулы расстояния (которая на самом деле является пифагорейской).
поэтому уравнение сферы ( x + 4 ) ² + ( y – 3) ² + ( z – 7) ² = 74..
Общая форма уравнения сферы
Чтобы получить общую форму, мы просто расширяем оператор стандартной формы, чтобы получить
x² + y² + z² – 2 x O x – 2 y O Y – 2 Z O Z + [( x o ) ² + ( y о )² + ( z о )² – r² ] = 0.

Теперь мы собираем константы ( x O ) ² + ( y O ) ² + ( Z O ) ² – R² и установить их = D
Коэффициенты x, y и z , равные -2 (координаты центра), называются a, b и c .
Теперь уравнение становитсяx² + y² + z² + a x + by + c z + d = 0
Итак, координаты центра из общего вида, равны ( -½ a, -½ b, -½ c )
и когда у нас есть центр, мы находим радиус, используя d = ( x o )² + ( y o )² + ( z o )² 911Примечание: коэффициенты x², y² и z² должны = 1 , чтобы это работало.Если они не = 1,
разделите уравнение на то, что они есть, затем используйте этот подход..
пример 3: найти центр и радиус сферы
решение: центр равен ( -½ а, -½ b, -½ c ) = ( -1, 4, -6 )
Так как d = 69 = ( -1 )² + ( 4 )² + ( -6 )² – r ² находим r и получаем r = 4 941
Стандартная форма уравнения этой сферы: ( x + 1) ² + ( y – 4) ² + ( z + 6) ² = 16Если бы уравнение примера 3 было представлено в виде
3 x² + 3 y² + 3 z² + 6 x – 24 y + 36 Z +
0 217 = 0
мы бы разделили уравнение на 3.
.
Уравнение касательной плоскости к сфере с заданной точкой касания
Поскольку касательная плоскость перпендикулярна радиусу сферы к точке касания, радиус-вектор служит нормалью для касательной плоскости.Как только мы узнаем точку контакта и координаты центра сферы, у нас есть вектор нормали и точка на плоскости, поэтому мы можем найти ее уравнение.
.
Пример 4: Напишите уравнение касательной плоскости к сфере
с уравнением ( х + 1) ² + ( у – 4) ² + ( z + 6) ² = 16 в точке P (- 4, 4, – 10).решение: Центр C равен ( -1, 4, -6 ).Радиус-вектор или нормаль CP = .
Вектор в искомой плоскости равен v = . Поскольку нормаль — это плоскость z, n $ v = 0 .
Итак,
Уравнение касательной плоскости: – 3x – 4z – 52 = 0 .
Следовательно, чтобы найти уравнение касательной плоскости к заданной сфере, надо поставить точки над радиус-вектором любого вектора плоскости, приравнять его к нулю.
 Мы просто пишем уравнение плоскости через точку P с вектором нормали, равным вектору, соединяющему центр сферы с точкой касания.
Мы просто пишем уравнение плоскости через точку P с вектором нормали, равным вектору, соединяющему центр сферы с точкой касания..
Практика
1/ а) Найдите уравнение сферы с диаметрами в концах А (2, 3, 1) и В (-2, 1, 3).
б) Найдите уравнение касательной к этой сфере в точке В.
.
2/ Найдите центр и радиус этих сфер:
а) x² + y² + z² + 4x – 6z = 0 б) х² + у² + z² – 2х + 4у = 0 в) x² + y² + z² + 6x + 2z + 7 = 0 .
3/ Напишите уравнения этих сфер: (C – центральная точка)
а) С (4, 3, 12) через начало координат. б) С (4, 3, 12) по (0, 0, 2). 
c) C (1, 2, 3) касательной к плоскости xy . d) C (1, – 2, 1) по касательной к оси z . e) радиус = 2, центр в октанте-1, касательная ко всем трем координатным плоскостям. .
4/ Найдите уравнение касательной плоскости к x² + y² + z² – 2x – 4y -4 = 0 в P (0, 0, 2).
.
.
Решения
1/ а) C (0, 2, 2), радиус = , поэтому ( x – 0 )² + ( y – 2 )² + ( z – 2 )² = 6
б) Касательная плоскость имеет нормаль n = , а точка касания (- 2, 1, 3), поэтому:
Уравнение плоскости 2( x + 2) + ( y – 1) – ( z – 3) = 0
2х + у – г + 6 = 0
.
2/
а) С (-2, 0, 3), радиус = б) С (1, – 1, 0), радиус = в) С (0, – 3, – 1), радиус = .

3/
а) ( x – 4 ) ² + ( y – 3) ² + ( z – 12 ) ² = 169 b) ( x – 1 ) ² + ( y – 2) ² + z ² = 9 c) ( x – 1 ) ² + ( 0 1 ) ² + ( + ( z – 3 ) ² = 9 d) ( x – 1 ) ² + ( y + 2) ² + ( z – 1 ) ² = 5 e) C равно (2, 2, 2) u ( x – 2 ) ² + ( г – 2) ² + ( z – 2 ) ² = 4 .
4/ Центр C ( 1, 2, 0 ). Радиус/нормальный вектор равен CP = .
Любой вектор в плоскости через (0, 0, 2) равен = . Расставьте точки и установите = 0
Итак,
Уравнение этой касательной плоскости: x + 2y – 2z + 4 = 0 .

где K — кривизна кривой, K = dT/ds, (функция тангенса)
R радиус кривизны
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронируйте бесплатный пробный урок
Давайте быстро рассмотрим пару примеров, чтобы лучше понять формулу радиуса кривизны.{2}} |}\).
Кривизна плоских кривых
Пусть плоская кривая \(C\) параметрически задана радиус-вектором \(\mathbf{r}\left( t \right).\), а точка \(M\) движется по кривой \(C\ ), направление касательной меняется (рис. \(1\)).
Рис. 1.Кривизну кривой можно определить как отношение угла поворота касательной \(\Delta \varphi\) к длине пройденной дуги \(\Delta s = M{M_1}.\) Это отношение \(\frac{{\Delta \varphi}}{{\Delta s}}\) называется средней кривизной кривой.Когда точка \({M_1}\) приближается к точке \(M,\), мы получаем кривизну кривой в точке \(M:\)
\[k = \lim\limits_{\Delta s \to 0} \frac{{\Delta \varphi}}{{\Delta s}} = \frac{{d\varphi}}{{ds}}. \]
Ясно, что кривизна \(к\) в общем случае может быть как положительной, так и отрицательной в зависимости от направления вращения касательной. {\prime\prime}\) — первая и вторая производные радиус-вектора.{\ гидроразрыва {3} {2}}}}}.\]
{\prime\prime}\) — первая и вторая производные радиус-вектора.{\ гидроразрыва {3} {2}}}}}.\]
Обратная величина кривизны называется радиусом кривизны:
\[R = \frac{1}{{\left| к \право|}}.\]
Окружность с таким радиусом и центром, расположенным на внутренней нормали, будет наиболее точно аппроксимировать плоскую кривую в данной точке (рис. \(2\)).
Рис. 2.Такой круг называется соприкасающимся кругом.
См. решенные проблемы на стр. 2.
Вектор положения – объяснение и примеры
Мы можем использовать вектор положения , чтобы сообщить нам положение одного объекта относительно другого.В частности, вектор положения:
«Вектор, который указывает местоположение или положение данной точки относительно произвольной контрольной точки, такой как начало координат».
В этом разделе мы обсудим следующие аспекты векторов положения:
Что такое вектор положения?
Часто векторы, которые начинаются в начале координат и заканчиваются в любой произвольной точке, называются векторами положения. Они используются для определения положения точки относительно начала координат.
Они используются для определения положения точки относительно начала координат.
Направление вектора положения указывает от начала координат к заданной точке. В декартовой системе координат, если точка O является началом координат, а Q является некоторой точкой (x1, y1), то вектор положения, направленный из точки O в точку Q, представляется как OQ . В трехмерном пространстве, если O = (0,0,0) и Q = (x1, y1, z1), то вектор положения r точки Q представляется следующим образом:
r = x1i + y1j + z1k
Предположим, у нас есть два вектора, A и B, с векторами положения a = (2,4) и b = (3, 5) соответственно.Тогда мы можем записать координаты векторов A и B как:
A = (2,4), B = (3, 5)
определяя вектор положения точки, нам сначала нужно определить координаты этой точки.
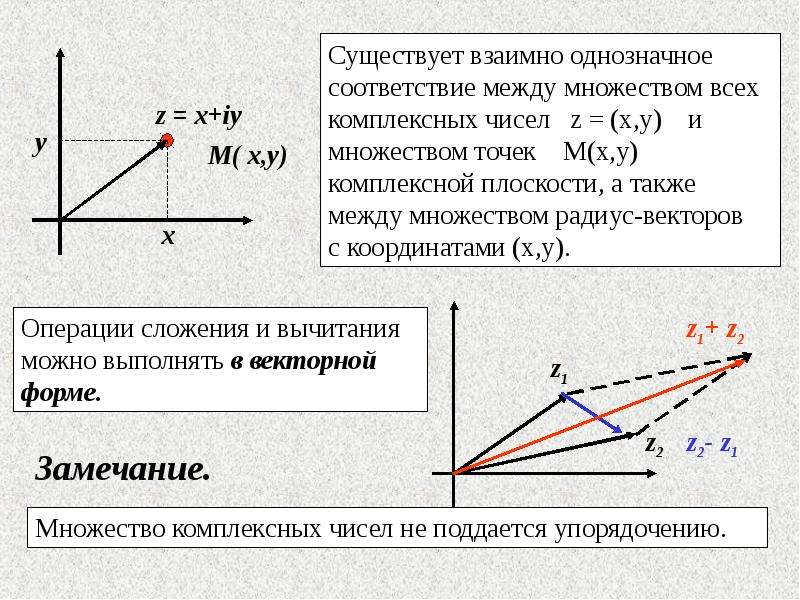 Предположим, у нас есть две точки, M и N, где M = (x1, y1) и N = (x2, y2). Далее мы хотим найти вектор положения из точки M в точку N, вектор MN . Чтобы определить этот вектор положения, мы вычитаем соответствующие компоненты M из N :
Предположим, у нас есть две точки, M и N, где M = (x1, y1) и N = (x2, y2). Далее мы хотим найти вектор положения из точки M в точку N, вектор MN . Чтобы определить этот вектор положения, мы вычитаем соответствующие компоненты M из N :MN = (x2-x1, y2-y1)
Формула вектора положения
Используя приведенную выше информацию, мы можем обобщить формула, которая будет определять вектор положения между двумя точками, если бы мы знали положение точек в плоскости xy.
Например, рассмотрим точку P с координатами (xk, yk) в плоскости xy и другую точку Q с координатами (xk+1, yk+1). Формула для определения вектора положения от P до Q:
PQ = ((xk+1)-xk, (yk+1)-yk)
Помните вектор положения PQ относится к вектору, который начинается в точке P и заканчивается в точке Q. Аналогично, если мы хотим найти вектор положения из точки Q в точку P, мы можем написать:
QP = (xk – (xk+1), yk – (yk+1))
Примеры
В этом разделе мы обсудим некоторые примеры задач вектора положения и их пошаговые решения. Это поможет глубже понять векторы положения.
Это поможет глубже понять векторы положения.
Пример 1
Для двух точек A = (-4, 6) и B = (5, 12) определите вектор положения AB. Затем , вычисляют величину вектора AB .
Решение
Имея две точки в системе координат xy, мы можем использовать следующую формулу для нахождения вектора положения AB :
AB = (x2-x1, y2-y1)
3
3 x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Таким образом, просто подставив значения точек A и B в приведенное выше уравнение, мы можем найти вектор положения AB : AB = (5-(-4), 12-6)
AB = ((5+ 4), 12-6)
AB = (9, 6)
Таким образом, вектор положения AB эквивалентен вектору, начинающемуся в начале координат и направленному в точку на расстоянии 9 единиц от вправо по оси x и на 6 единиц вверх по оси y. 2
2
| АВ | = √81 + 36
| АВ | = √117
| АВ | = 3√13
Пример 2
Имея две точки A = (-4, 6) и B = (5, 12), определите вектор положения BA. Затем вычислите модуль вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .
Решение
Имея две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения BA :
BA = (x1-x2, y1-y2)
3
3 x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Обратите внимание, что вектор положения BA представляет собой вектор, направленный от точки B к точке A. Он отличается от вектора положения AB, , который направлен от A к B. Таким образом, просто поставив значения точек A и B в приведенном выше уравнении мы можем найти вектор положения BA: BA = (-4-5), 6-12)
BA = (-9, -6)
Таким образом, вектор положения BA эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц влево по оси x и на 6 единиц вниз по оси y. 2
2
| ВА | = √81 + 36
| ВА | = √117
| ВА | = 3√13
Напомним, что в первом примере мы нашли вектор положения AB для тех же точек, а в этом примере мы определили вектор положения BA. Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, соотношение между ними:
BA = -1*(9, 6)
BA = -1* AB
BA = – 5 Таким образом, два вектора положения параллельны друг другу и противоположны друг другу.То есть они являются негативами друг друга.
Пример 3
Учитывая, что вектор положения точки S1 равен OS1 = (2, 3) и что вектор S1S2 = (-3, 6), определите вектор положения точки точка S2, OS2 .
Решение
Сначала мы наносим вектор OS1 с начальной точкой в начале координат (0,0) и конечной точкой в (2,3). Мы также наносим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x,y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает отношение между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. На изображении ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1
Мы также наносим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x,y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает отношение между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. На изображении ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1
Подставляя данные значения в это уравнение, получаем:
OS2 = (-3, 6) – (2, 3)
OS2 = (-3, 6) + ( -2, -3)
OS2 = (-3-2, 6-3)
OS2 = (-5, 3)
Таким образом, OS2 =(-5, 3) есть вектор положения точки S2.
Пример 4
Имея две точки M = (4, m) и Q = (-n, -3), определите вектор положения QM.
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу для определения вектора положения Q :
QM = (-n-4, -3-m) .
Поскольку нам неизвестны координаты QM или значения n и m, мы не можем упростить уравнение.2
| Р | = √100 + 25 + 9
| Р | = √100 + 25 + 9
| Р | = √134
Пример 6
Учитывая точки c = 5i + 6j +3k и d = 2i +5j – 2k в ортогональной системе, определите вектор положения между этими двумя точками, CD.
Решение
Учитывая две точки, мы можем использовать следующую формулу для определения вектора положения CD :
CD = (2-5, 5-5, -2-3)
CD = (-3, 0, -5)
CD = -3i + 0j -5k
Практические вопросы
Ответы
 2
2BA = (-4-5), 6-12)
BA = (-9, -6)
Таким образом, вектор положения BA эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц влево по оси x и на 6 единиц вниз по оси y. 2
2
| ВА | = √81 + 36
| ВА | = √117
| ВА | = 3√13
Напомним, что в первом примере мы нашли вектор положения AB для тех же точек, а в этом примере мы определили вектор положения BA. Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, соотношение между ними:
BA = -1*(9, 6)
BA = -1* AB
BA = – 5 Таким образом, два вектора положения параллельны друг другу и противоположны друг другу.То есть они являются негативами друг друга. Пример 3 Учитывая, что вектор положения точки S1 равен OS1 = (2, 3) и что вектор S1S2 = (-3, 6), определите вектор положения точки точка S2, OS2 . Решение Сначала мы наносим вектор OS1 с начальной точкой в начале координат (0,0) и конечной точкой в (2,3). Мы также наносим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x,y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает отношение между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. На изображении ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1
Мы также наносим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x,y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает отношение между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. На изображении ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1
Подставляя данные значения в это уравнение, получаем:
OS2 = (-3, 6) – (2, 3)
OS2 = (-3, 6) + ( -2, -3)
OS2 = (-3-2, 6-3)
OS2 = (-5, 3)
Таким образом, OS2 =(-5, 3) есть вектор положения точки S2.
Пример 4
Имея две точки M = (4, m) и Q = (-n, -3), определите вектор положения QM.
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу для определения вектора положения Q :
QM = (-n-4, -3-m) .
Поскольку нам неизвестны координаты QM или значения n и m, мы не можем упростить уравнение.2
| Р | = √100 + 25 + 9
| Р | = √100 + 25 + 9
| Р | = √134
Пример 6
Учитывая точки c = 5i + 6j +3k и d = 2i +5j – 2k в ортогональной системе, определите вектор положения между этими двумя точками, CD.
Решение
Учитывая две точки, мы можем использовать следующую формулу для определения вектора положения CD :
CD = (2-5, 5-5, -2-3)
CD = (-3, 0, -5)
CD = -3i + 0j -5k
Практические вопросыОтветы



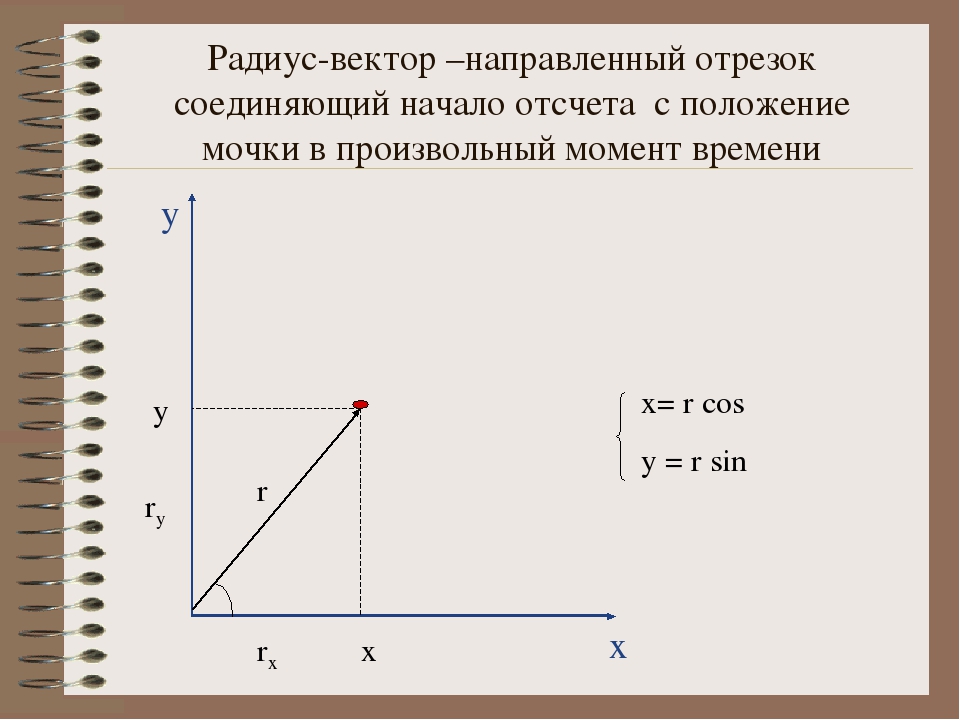
 {3/2})≈37,785\) единиц
{3/2})≈37,785\) единиц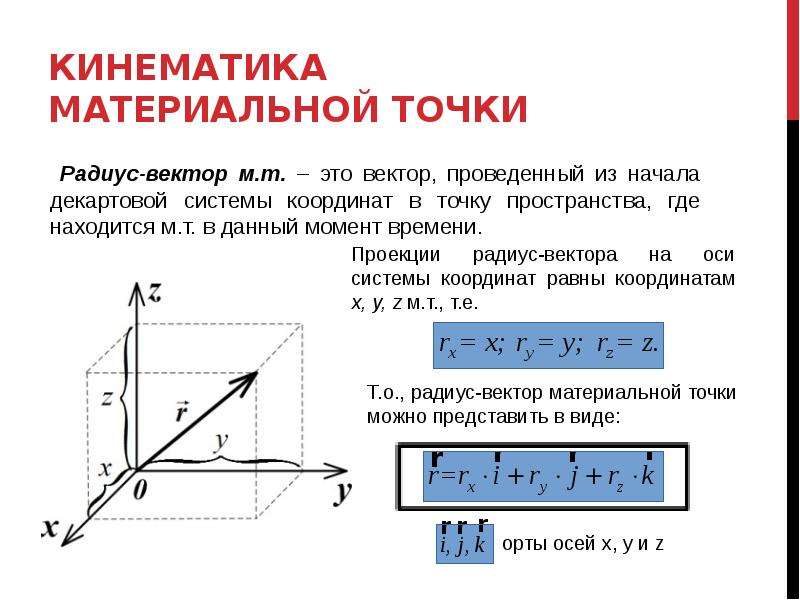 {t}_{ a} ‖\vecs r′(u)‖du \bigg] \\[4pt] &=\|\vecs r′(t)\|.{t}_{a} ‖\vecs r′(u)‖\,du\]
{t}_{ a} ‖\vecs r′(u)‖du \bigg] \\[4pt] &=\|\vecs r′(t)\|.{t}_{a} ‖\vecs r′(u)‖\,du\] Затем мы можем перепараметрировать исходную функцию \(\vecs r(t)\), подставив выражение для \(t\) обратно в \(\vecs r(t)\). Теперь вектор-функция записывается в терминах параметра \(s\) . Поскольку переменная \(s\) представляет длину дуги, мы называем это параметризацией длины дуги исходной функции \(\vecs r(t)\). Одним из преимуществ нахождения параметризации длины дуги является то, что расстояние, пройденное вдоль кривой, начиная с \(s=0\), теперь равно параметру \(s\).Параметризация длины дуги также появляется в контексте кривизны (которую мы рассмотрим позже в этом разделе) и линейных интегралов.
Затем мы можем перепараметрировать исходную функцию \(\vecs r(t)\), подставив выражение для \(t\) обратно в \(\vecs r(t)\). Теперь вектор-функция записывается в терминах параметра \(s\) . Поскольку переменная \(s\) представляет длину дуги, мы называем это параметризацией длины дуги исходной функции \(\vecs r(t)\). Одним из преимуществ нахождения параметризации длины дуги является то, что расстояние, пройденное вдоль кривой, начиная с \(s=0\), теперь равно параметру \(s\).Параметризация длины дуги также появляется в контексте кривизны (которую мы рассмотрим позже в этом разделе) и линейных интегралов. Далее заменяем переменную \(t\) в исходной функции \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf {j}}\) с выражением \(s/4\), чтобы получить
Далее заменяем переменную \(t\) в исходной функции \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf {j}}\) с выражением \(s/4\), чтобы получить
 \]
\]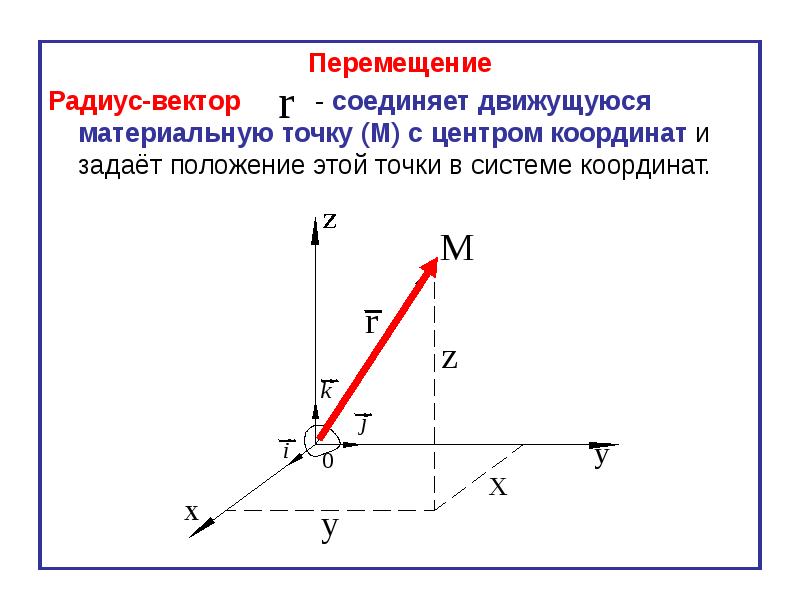 {3/2}}.\метка{EqK4}\]
{3/2}}.\метка{EqK4}\]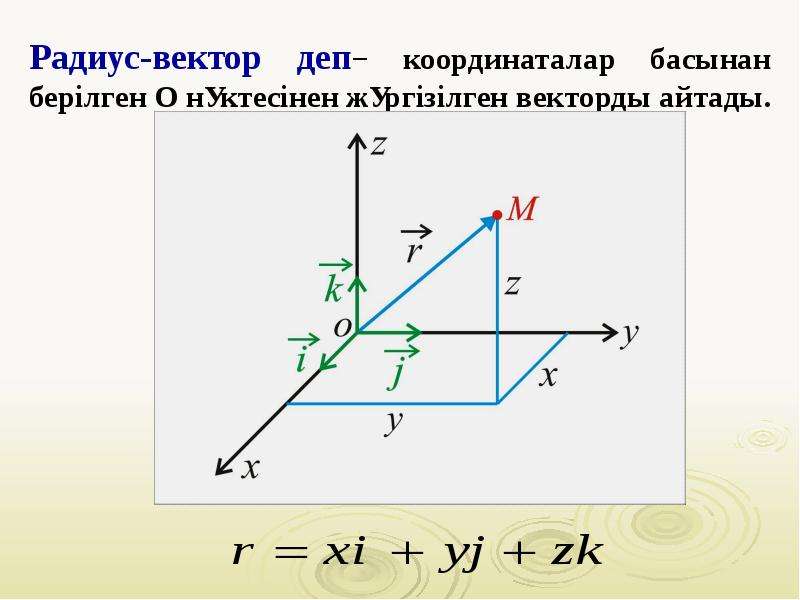 {3/2}}≈0,0059\)
{3/2}}≈0,0059\)
 2\,\hat{\mathbf{j}}−8t\,\hat{\mathbf {к}}\)
2\,\hat{\mathbf{j}}−8t\,\hat{\mathbf {к}}\) Единичный вектор нормали и вектор бинормали образуют плоскость, перпендикулярную кривой в любой точке кривой, называемую плоскостью нормали. Кроме того, эти три вектора образуют систему отсчета в трехмерном пространстве, называемую системой отсчета Френе (также называемой системой отсчета TNB ) (рис. \(\PageIndex{2}\)). Наконец, плоскость, определяемая векторами \(\vecs T\) и \(\vecs N\), образует соприкасающуюся плоскость \(C\) в любой точке \(P\) на кривой.
Единичный вектор нормали и вектор бинормали образуют плоскость, перпендикулярную кривой в любой точке кривой, называемую плоскостью нормали. Кроме того, эти три вектора образуют систему отсчета в трехмерном пространстве, называемую системой отсчета Френе (также называемой системой отсчета TNB ) (рис. \(\PageIndex{2}\)). Наконец, плоскость, определяемая векторами \(\vecs T\) и \(\vecs N\), образует соприкасающуюся плоскость \(C\) в любой точке \(P\) на кривой.-reshenie-zadacha-8.jpg) Мы называем \(r\) радиусом кривизны кривой, и он равен обратной величине кривизны.Если эта окружность лежит на вогнутой стороне кривой и касается кривой в точке \(P\), то эта окружность называется соприкасающейся окружностью кривой \(C\) в \(P\), как показано на рисунке \(\PageIndex{3}\).
Мы называем \(r\) радиусом кривизны кривой, и он равен обратной величине кривизны.Если эта окружность лежит на вогнутой стороне кривой и касается кривой в точке \(P\), то эта окружность называется соприкасающейся окружностью кривой \(C\) в \(P\), как показано на рисунке \(\PageIndex{3}\). 2=\frac{1}{16}\).
2=\frac{1}{16}\). пистолет
направление перемещается по горизонтали и вертикали, чтобы «раскрасить» экран
с желаемым изображением.На практике пушка перемещается горизонтально
через всю строку, затем перемещается по вертикали на следующую строку и
повторяет операцию. Точно так же может быть полезно представить
фиксируя значение $v$ и позволяя ${\bf r}(u,v)$ заметать кривую как
$u$ меняется. Тогда $v$ может немного измениться, и ${\bf r}(u,v)$ заметает
новая кривая очень близка к первой. Положите достаточно этих кривых
вместе, и они образуют поверхность.
пистолет
направление перемещается по горизонтали и вертикали, чтобы «раскрасить» экран
с желаемым изображением.На практике пушка перемещается горизонтально
через всю строку, затем перемещается по вертикали на следующую строку и
повторяет операцию. Точно так же может быть полезно представить
фиксируя значение $v$ и позволяя ${\bf r}(u,v)$ заметать кривую как
$u$ меняется. Тогда $v$ может немного измениться, и ${\bf r}(u,v)$ заметает
новая кривая очень близка к первой. Положите достаточно этих кривых
вместе, и они образуют поверхность. $\квадрат$
$\квадрат$ 3. бинормаль
является
перпендикулярно обоим $\bf T$ и $\bf N$; один из способов интерпретировать это
состоит в том, что ${\bf N}$ и ${\bf B}$ определяют плоскость, перпендикулярную $\bf
T$, т. е. перпендикулярно кривой; поскольку ${\bf N}$ и ${\bf B}$
перпендикулярны друг другу, они могут функционировать как $\bf i$ и
$\bf j$ do для плоскости $x$-$y$.Конечно, $\bf N$ и $\bf B$
функции от $u$, изменяющиеся по мере движения вдоль кривой ${\bf r}(u)$.
Так, например, ${\bf c}(u,v)={\bf N}\cos v+{\bf B}\sin v$
векторное уравнение для единичного круга на плоскости
перпендикулярно кривой, описываемой $\bf r$, за исключением того, что обычно
интерпретация $\bf c$ поместила бы его центр в начало координат. Мы можем
исправить это, просто добавив $\bf c$ к исходному $\bf r$:
пусть ${\bf f}={\bf r}(u) +{\bf c}(u,v)$. Для
фиксированный $u$ рисует окружность вокруг точки ${\bf r}(u)$; как $u$
меняется, мы получаем последовательность таких окружностей вокруг кривой $\bf r$,
то есть трубка радиуса 1 с $\bf r$ в центре.
3. бинормаль
является
перпендикулярно обоим $\bf T$ и $\bf N$; один из способов интерпретировать это
состоит в том, что ${\bf N}$ и ${\bf B}$ определяют плоскость, перпендикулярную $\bf
T$, т. е. перпендикулярно кривой; поскольку ${\bf N}$ и ${\bf B}$
перпендикулярны друг другу, они могут функционировать как $\bf i$ и
$\bf j$ do для плоскости $x$-$y$.Конечно, $\bf N$ и $\bf B$
функции от $u$, изменяющиеся по мере движения вдоль кривой ${\bf r}(u)$.
Так, например, ${\bf c}(u,v)={\bf N}\cos v+{\bf B}\sin v$
векторное уравнение для единичного круга на плоскости
перпендикулярно кривой, описываемой $\bf r$, за исключением того, что обычно
интерпретация $\bf c$ поместила бы его центр в начало координат. Мы можем
исправить это, просто добавив $\bf c$ к исходному $\bf r$:
пусть ${\bf f}={\bf r}(u) +{\bf c}(u,v)$. Для
фиксированный $u$ рисует окружность вокруг точки ${\bf r}(u)$; как $u$
меняется, мы получаем последовательность таких окружностей вокруг кривой $\bf r$,
то есть трубка радиуса 1 с $\bf r$ в центре. Мы можем легко
изменить радиус; например ${\bf r}(u) +a{\bf c}(u,v)$
дает радиус трубы $a$; мы можем изменить радиус, как мы
двигаться по кривой с ${\bf r}(u) +g(u){\bf c}(u,v)$,
где $g(u)$ — функция от $u$.
Как показано в
16.6.3, трудно увидеть, что простой узел
завязанный; трубка делает структуру очевидной. Есть конечно
ничего особенного в узле-трилистнике в этом примере; мы можем поставить
трубка вокруг (почти) любой кривой таким же образом.
$\квадрат$
Мы можем легко
изменить радиус; например ${\bf r}(u) +a{\bf c}(u,v)$
дает радиус трубы $a$; мы можем изменить радиус, как мы
двигаться по кривой с ${\bf r}(u) +g(u){\bf c}(u,v)$,
где $g(u)$ — функция от $u$.
Как показано в
16.6.3, трудно увидеть, что простой узел
завязанный; трубка делает структуру очевидной. Есть конечно
ничего особенного в узле-трилистнике в этом примере; мы можем поставить
трубка вокруг (почти) любой кривой таким же образом.
$\квадрат$ 2}$ вокруг оси $z$ на высоте $v$.
Мы могли бы также взять пример со сферических координат и написать
$\langle \sin u\cos v,\sin u\sin v,\cos u\rangle$, где фактически
$u$ и $v$ — это замаскированные $\phi$ и $\theta$.
2}$ вокруг оси $z$ на высоте $v$.
Мы могли бы также взять пример со сферических координат и написать
$\langle \sin u\cos v,\sin u\sin v,\cos u\rangle$, где фактически
$u$ и $v$ — это замаскированные $\phi$ и $\theta$. Например, $\langle 1-v\cos u-v\sin u,v\sin
u,v\cos u\rangle$ — одна из таких векторных функций. Обратите внимание, что, хотя это может
не очевидно, откуда это взялось, довольно легко увидеть, что
сумма компонент $x$, $y$ и $z$ вектора всегда равна
1. Показана компьютерная визуализация самолета с использованием этих двух функций.
на рисунке 16.6.4.
Например, $\langle 1-v\cos u-v\sin u,v\sin
u,v\cos u\rangle$ — одна из таких векторных функций. Обратите внимание, что, хотя это может
не очевидно, откуда это взялось, довольно легко увидеть, что
сумма компонент $x$, $y$ и $z$ вектора всегда равна
1. Показана компьютерная визуализация самолета с использованием этих двух функций.
на рисунке 16.6.4.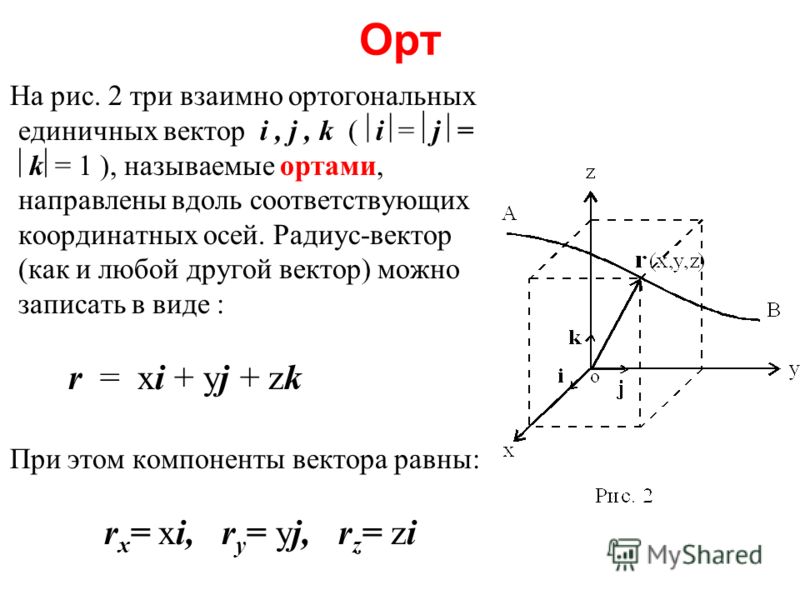
 Функции ${\bf r}(u,v_0)$ и ${\bf
r}(u_0,v)$ определяют две кривые, пересекающиеся в точке ${\bf
г}(и_0,v_0)$. Производные от $\bf r$ дают нам векторы, касающиеся
эти две кривые: ${\bf r}_u(u_0,v_0)$ и ${\bf r}_v(u_0,v_0)$, и
тогда ${\bf r}_u(u_0,v_0)\,du$ и ${\bf r}_v(u_0,v_0)\,dv$
два малых касательных вектора, длины которых можно использовать в качестве
длины сторон приближающего параллелограмма.2}\,dv\,du={\pi\sqrt2\over2}+
{\ пи \ пер (\ sqrt2 + 1) \ более 2}. $ $
$\квадрат$
Функции ${\bf r}(u,v_0)$ и ${\bf
r}(u_0,v)$ определяют две кривые, пересекающиеся в точке ${\bf
г}(и_0,v_0)$. Производные от $\bf r$ дают нам векторы, касающиеся
эти две кривые: ${\bf r}_u(u_0,v_0)$ и ${\bf r}_v(u_0,v_0)$, и
тогда ${\bf r}_u(u_0,v_0)\,du$ и ${\bf r}_v(u_0,v_0)\,dv$
два малых касательных вектора, длины которых можно использовать в качестве
длины сторон приближающего параллелограмма.2}\,dv\,du={\pi\sqrt2\over2}+
{\ пи \ пер (\ sqrt2 + 1) \ более 2}. $ $
$\квадрат$ Настройте интеграл площади поверхности, используя
эту векторную функцию и сравнить с интегралом от
раздел 15.4.
Настройте интеграл площади поверхности, используя
эту векторную функцию и сравнить с интегралом от
раздел 15.4. Определите вектор положения, представленный UV .
Определите вектор положения, представленный UV . 2)) для расчета длины, радиуса вектора эллипса от центра в заданном направлении – это расстояние между центром и точкой, чья линия, соединяющая центр и эту точку составляет угол тета.Длина обозначается символом L .
2)) для расчета длины, радиуса вектора эллипса от центра в заданном направлении – это расстояние между центром и точкой, чья линия, соединяющая центр и эту точку составляет угол тета.Длина обозначается символом L .


 Мы просто пишем уравнение плоскости через точку P с вектором нормали, равным вектору, соединяющему центр сферы с точкой касания.
Мы просто пишем уравнение плоскости через точку P с вектором нормали, равным вектору, соединяющему центр сферы с точкой касания.

