Радиус вектора формула: Mathway | Популярные задачи - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )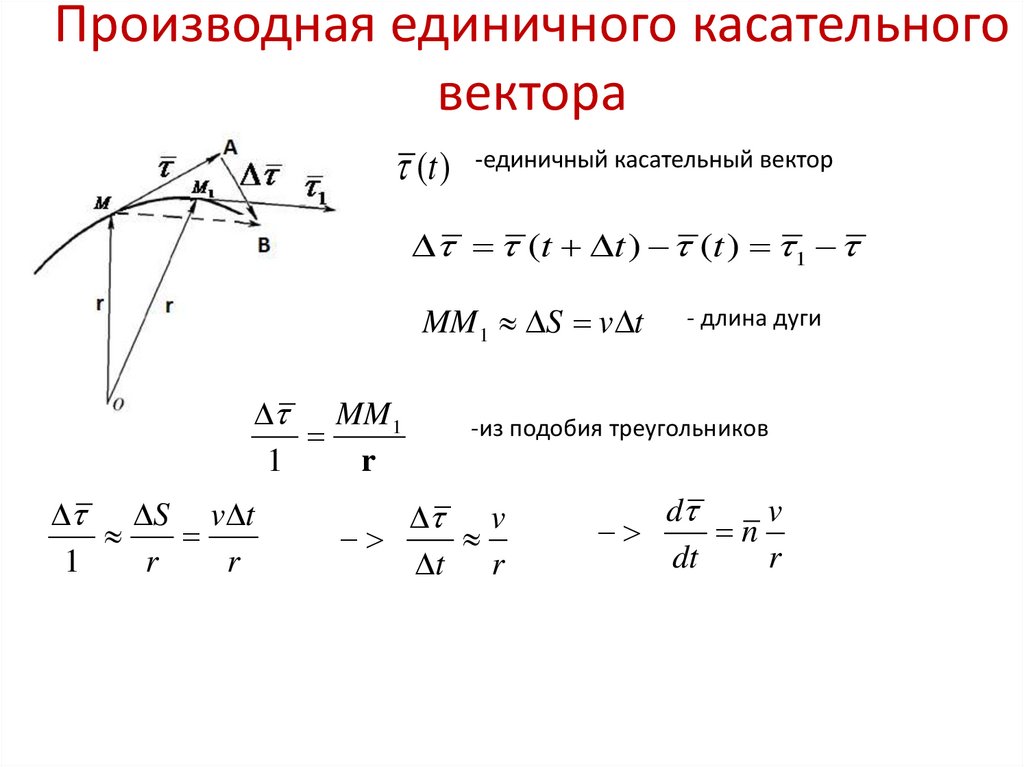
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Как найти радиус вектор точки

Радиус-вектор в декартовых координатах

Радиус-вектор точки — это называется вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.

Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат (рис. 17).

Введение понятия радиус-вектора оказалось чрезвычайно плодотворным при изучении различных физических явлений. В частности, это понятие широко используется в механике.

Как известно, положение точки можно задать с помощью ее координат. Так, если известны координаты x₁ и y₁ точки В или координаты x₂ и y₂ точки С, то мы легко находим положения этих точек на плоскости. Этот способ определения положения точки с помощью ее координат называется координатным способом.

Модуль радиус-вектора

— по теореме Пифагора.

Механическое движение. Система отсчета. Материальная точка.

Механическое движение – это процесс изменения положения данного тела в пространстве с течением времени относительно другого тела, которое мы считаем неподвижным.

Тело, условно принятое за неподвижное – тело отсчета.

Тело отсчета – это тело, относительно которого опре-деляется положение другого тела.

Обычно в качестве тела отсчета выбирается земля, но может быть и движущийся относительно земли предмет: автомобиль, лодка, самолет и т.д.

Система отсчета – это тело отсчета, система координат, жестко связанная с ним, и прибор для измерения времени движения.

Простейшей системой координат является прямоугольная декартова система (рис. 2). Система координат нужна для определения положения тела относительно тела отсчета. Выбор системы отсчета зависит от условий дан-ной задачи.

Движение реальных тел, как правило, сложное. Для упрощения рас-смотрения движений пользуются моделями. Одними из первых моделей реальных тел являются абсолютное твердое тело и материальная точка.

Материальной точкой называется тело, размерами и формой которого можно пренебречь в данной задаче. Данное понятие является математической абстракцией. Одно и то же тело в одних задачах можно рассматривать как материальную точку, а в других задачах – нельзя. Например, радиус Земли RЗемли равен 6400 км, расстояние между Солнцем и Землей L равно 150 000 000 км (L >> RЗемли). Рассматривая движение Земли относительно Солнца, радиусом Земли можно пре-небречь и считать, что Земля – материальная точка. Однако если нужно выяснить причины смены времен года, то Землю уже нельзя считать матери-альной точкой, а надо учитывать ее размеры, вращение вокруг оси и т.д. Мы будем изучать механическое движение материальной точки для того, чтобы потом определить движение реального тела.

Радиус-вектор. Проекции радиус-вектора. Модуль радиус-вектора.

Ра?диус-ве?ктор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки, называемой началом координат.

Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.

Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.

На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.

Радиус-вектор в декартовых координатах

Радиус-вектор точки — это называется вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.

Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат (рис. 17).

Введение понятия радиус-вектора оказалось чрезвычайно плодотворным при изучении различных физических явлений. В частности, это понятие широко используется в механике.

Как известно, положение точки можно задать с помощью ее координат. Так, если известны координаты x1 и y1 точки В или координаты x2 и y2 точки С, то мы легко находим положения этих точек на плоскости. Этот способ определения положения точки с помощью ее координат называется координатным способом.

— по теореме Пифагора.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10572 — | 7332 — или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Физика и техника.

Физика тесно связана и с техникой, причем эта связь имеет двусторонний характер.

Физика выросла из потребностей техники. Так, развитие механики у древних греков было вызвано запросами строительной и военной техники того времени.

Развитие техники, в свою очередь, определяет направление физических исследований. Например, в свое время задача создания наиболее экономичных тепловых двигателей вызвала бурное развитие термодинамики. А началось все с того, что Джеймс Уатт заметил, что крышка кипящего чайника немного приподнимается под действием пара.

С другой стороны, от развития физики зависит технический уровень производства.

Физика лежит в основе создания новых отраслей техники (электронная техника, ядерная техника и др.).

Бурный темп развития физики, растущие связи ее с техникой указывают на значительную роль курса физики во втузе.

Физика является фундаментальной основой для теоретической подготовки инженера, без которой его успешная практическая деятельность невозможна.

Развитие механики как науки начинается с III в. до н. э., когда древнегреческий ученый Архимед (287—212 до н. э.) сформулировал закон равновесия рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564—1642) и окончательно сформулированы английским ученым И. Ньютоном (1643—1727).

Механическим движением называется изменение положения тела относительно других тел с течением времени.

Материальной точкой называется тело, размерами и формой которого в данных условиях можно пренебречь.

Положение материальной точки указывается при помощи радиус-вектора , соединяющего начало системы координат с данной точкой:

, (1.1)

где — единичные векторы, направленные вдоль соответствующих осей координат: OX, OY, OZ. Значения координат данной материальной точки определяют проекции радиус-вектора на оси координат.

Модуль радиус-вектора вычисляется по формуле:

. (1.2)

Единичным вектором в направлении вектора называется вектор вида

. (1.3)

Если положение точки в пространстве изменяется, то радиус-вектор зависит от времени:

. (1.4)

Это векторная форма кинематического закона движения точки.

Конец радиус-вектора при движении точки описывает в пространстве кривую, называемую траекторией движения точки. Зависимость (1.4) эквивалентна системе уравнений:

(1.5)

Зависимость вида (1.5) называется координатной формой кинематического закона движения точки.

Расстояние между двумя положениями 1 и 2 материальной точки в пространстве определяется по формуле:

, (1.6)

где , , — разности координат материальной точки, отсчитанные вдоль осей OX, OY и OZ. Вектор, соединяющий точки 1 и 2, называется вектором перемещения. Он равен разности радиус-векторов точек 2 и 1:

. (1.7)

Действительно, из рисунка 1.1 видно, что вектор равен геометрической сумме векторов и : . Из последнего уравнения и следует выражение (1.7).

С другой стороны вектор перемещения может быть представлен через разности координат:

. (1.8)

Поэтому модуль вектора перемещения из точки 1 в точку 2 определяется по формуле (1.6).

Изменение положения материальной точки с течением времени характеризуется вектором мгновенной скорости, который определяется как производная от радиус-вектора материальной точки по времени[1]:

(1. 9)

Вектор мгновенной скорости точки направлен по касательной к траектории в сторону движения точки. Его можно представить в виде:

, (1.10)

где проекции , и вектора мгновенной скорости на соответствующие оси координат вычисляются по формулам:

. (1.11)

С другой стороны, радиус-вектор материальной точки можно представить в виде:

где — единичный вектор, совпадающий по направлению с радиус-вектором точки. Тогда, в соответствии с формулой (1.9), вектор мгновенной скорости точки равен:

Первая составляющая: — направлена вдоль радиус-вектора и характеризует быстроту изменения его модуля.

Вторая составляющая: — связана с быстротой изменения направления радиус-вектора. Дело в том, что единичный вектор по величине не может изменяться и единственным способом его изменения является вращение вокруг некоторой оси. Поэтому производная от единичного вектора по времени равна произведению угловой скорости вращения радиус-вектора на перпендикулярный к нему единичный вектор , направленный в сторону возрастания угла :

В целях наглядности, рассмотренные кинематические характеристики , и , возникающие, например, при движении материальной точки в плоскости x, y по некоторой криволинейной траектории, представлены на рисунке 1.2.

Модуль вектора мгновенной скорости определяется следующим образом:

. (1.12)

Направление вектора мгновенной скорости определяется при помощи направляющих косинусов:

. (1.13)

Средняя скорость перемещения материальной точки за время от до определяется по формуле:

, (1.14)

где — вектор перемещения точки за то же время.

Из предыдущей формулы следует, что перемещение можно выразить через среднюю скорость перемещения:

. (1.15)

Путь определяют как длину дуги между точками 1 и 2. При смещении материальной точки вдоль траектории на бесконечно малую величину, ее путь можно записать следующим образом:

Проинтегрировав полученное выражение по времени от до , найдем, что:

, (1. 16)

где — производная от по , — производная от по , и — значения координаты в моменты времени и , соответственно. Зависимость называют естественной формой кинематического закона движения точки.

Изменение вектора скорости с течением времени характеризуется вектором мгновенногоускорения, который определяется как производная от вектора скорости по времени:

. (1.17)

Вектор ускорения материальной точки можно представить в виде:

, (1.18)

где , и — проекции вектора ускорения на соответствующие оси координат.

Модуль вектора ускорения вычисляется следующим образом:

. (1.19)

Направляющие косинусы вектора ускорения равны

. (1.20)

Ускорение характеризует изменение величины и направления скорости в целом. Оно может быть представлено в виде векторной (геометрической) суммы тангенциального и нормального ускорений:

. (1.21)

Модуль ускорения выражается через модули тангенциального и нормального ускорений при помощи теоремы Пифагора:

. (1.22)

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9465 — | 7448 — или читать все.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .

Векторы i → и j → называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.

Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .

Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .

O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .

По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .

Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.

Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .

Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .

Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .

Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .

По условию известно, что A B → = ( 2 , 0 , — 2 ) .

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2

Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5

Ответ: B ( 5 , 5 , 5 ) .

Длина вектора — как найти? Формулы и примеры

Что такое векторы и какими они бывают

Как обычно, мы начнем с самого важного: с определения.

Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.

Вектор обозначают знаком →, например . Как вы заметили, вектор можно выразить одной латинской буквой, а можно — сочетанием двух букв, которыми мы назовем точками начала и конца вектора.

Нулевой вектор — вектор, начало которого совпадает с его концом. Обозначается он так: .

Как вы уже знаете, векторы бывают коллинеарными и неколлинеарными, сонаправленными и противоположно направленными. Теперь давайте подумаем, что объединяет все виды векторов без исключения. Правильно, у всех есть длина! О том, что это такое, мы и поговорим дальше.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Длина вектора

Длиной или модулем вектора называется длина направленного отрезка, определяющего вектор.

Иногда в математике длину вектора называют модулем. Это легко запомнить, так как длина вектора обозначается с помощью знака | |. Например: . Альтернативное название длины вектора дает нам отличную подсказку: она не может быть отрицательной, в какую бы сторону вектор ни был направлен. А вот нулевой — пожалуйста!

Длина нулевого вектора всегда равна нулю.

Здесь вам может стать интересно, зачем нам нужно знать, как найти длину вектора, и это очень хороший вопрос. Причин может быть множество, но мы выделим несколько главных:

Чтобы определить равенство векторов, необходимо знать их длины. Векторы являются равными, если равны их длины, и сами векторы — сонаправленные.
Вычислив модуль вектора, мы можем рассчитать другие величины.
Например, в физике сила — это векторная величина, т. е. имеет направление. Если вычислить модуль силы, мы можем рассчитать массу тела, его ускорение и т. д.
В геометрии с помощью длины векторов мы можем определить угол между ними, их скалярное произведение.

Достаточно весомые аргументы для нахождения этой величины, правда? Самое время перейти от слов к делу: давайте научимся вычислять длину вектора через свои координаты!

Как можно найти длину вектора по его координатам

Используя прямоугольную систему координат, нарисуем вектор АВ (х, у) из точки (0; 0). Тогда его можно будет считать радиус-вектором для векторов АВ₁ и АА₁.

Давайте обозначим длину вектора |АВ₁| = у, длину вектора |АА₁| = х. Треугольники АА₁В и АВ₁В являются прямоугольными, где АВ — гипотенуза. Теперь вспомните, как можно найти длину гипотенузы, зная длины катетов. Верно, через теорему Пифагора! Составим выражение для АВ:

Это значит, чтобы найти длину вектора нужно взять квадратный корень из суммы квадратов его координат. В общем виде эту формулу для длины вектора записывают так — длина вектора :

Если мы будем рассматривать векторы в трехмерном пространстве, формулу нахождения длины вектора можно рассчитать так:

Давайте разберемся, как работают эти формулы для нахождения длины вектора, на примерах. Вы можете решать задания самостоятельно, а потом свериться с нами: так будет еще эффективнее!

Пример № 1

Найдите модуль вектора .

Решение:

Ответ:

Пример № 2

Проведите вычисление длины вектора по его координатам {-2; 0; 5}.

Решение:

Ответ:

Пример № 3

Определите координату х вектора , если его координата по у равна 6, а длина вектора 10.

Решение:

Ответ: .

Уверены, что у вас все блестяще получилось!

Как найти длину вектора по двум точкам

Давайте подумаем, как решать задачи, если нам не даны координаты вектора. Для этого нужно понять, как найти длину вектора по двум точкам — координатам начала и конца. Вспомним: координаты вектора с точкой А (х_а; у_а) и В (х_в; у_в) можно рассчитать так: (х_в – х_а; у_в – у_а). А значит, длину вектора мы определим, если подставим эти выражения в формулу для ее нахождения:

Пример № 4

Найти длину вектора , если В (4; 6), С (-2; 0).

Решение:

Ответ:

Как найти длину вектора по теореме косинусов

Пришло время разобраться, как длина вектора связана с теоремой косинусов. К сожалению, не во всех задачах дано нужное количество информации, чтобы определить длину вектора — тут-то нам и поможет теорема.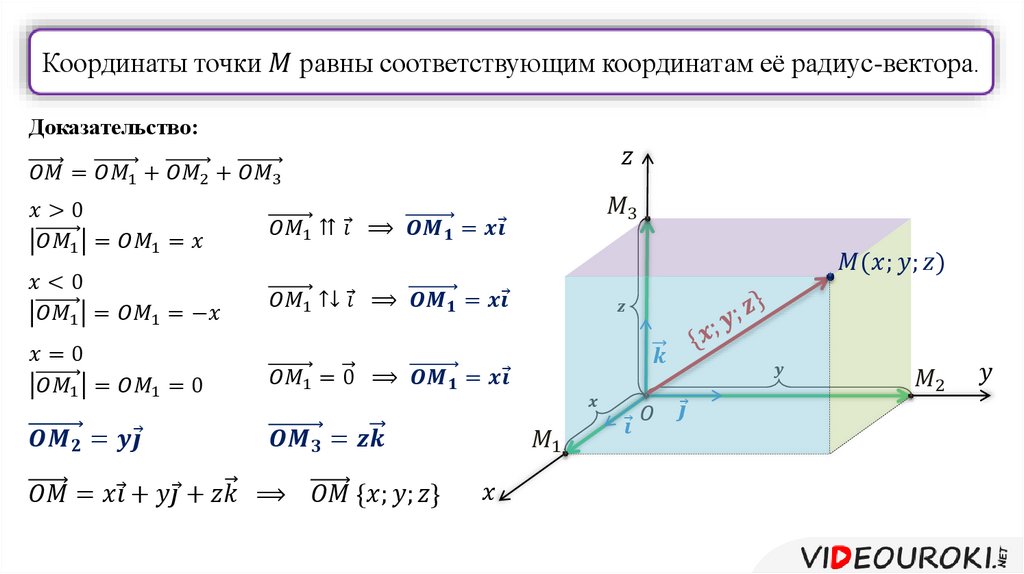 Вспомним ее!

Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Итак, чтобы определить длину стороны треугольника, нужно сложить квадраты двух других сторон, вычесть удвоенное произведение длин сторон на косинус угла между ними и взять корень из полученного числа. Так мы получим формулу нахождения длины вектора через теорему косинусов.

Предположим, что нам необходимо узнать длину вектора или . Тогда, чтобы воспользоваться теоремой косинусов, нам нужно найти длину векторов и и угол между ними.

Пример № 5

Длины векторов и равны 5 и 12 соответственно, а угол между ними равен π/3. Проведите вычисление длины вектора .

Решение:

Ответ:

Сегодня мы обсудили с вами все основные моменты, которые касаются длины вектора: изучили теорию и дополнили ее базовыми задачами. Дело осталось за малым — выучить весь материал и практиковаться! В этом вам помогут курсы по профильной математике в школе Skysmart.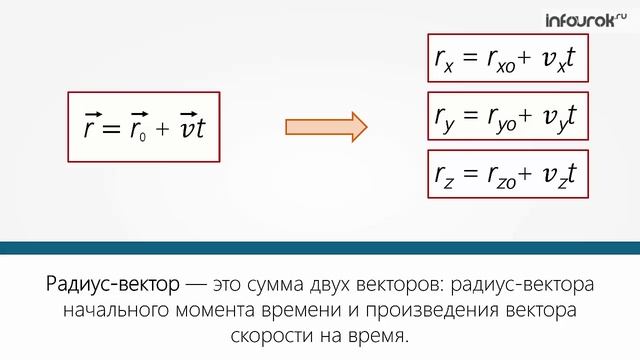 Уникальная платформа, учителя-профессионалы, индивидуальная программа — уроки просто созданы для того, чтобы стать уверенными в математике. Ждем вас на занятиях и до новых встреч!

Связь между координатами вектора и координатами его начала и конца 9 класс онлайн-подготовка на Ростелеком Лицей |

Тема 27.

Связь между координатами вектора и координатами его начала и конца.

Ты уже знаком с понятием координат вектора. Ими называют коэффициенты разложения данного вектора по единичным координатным векторам i⃗ и j⃗.

Сегодня мы ответим на вопрос «Как связаны координаты вектора с координатами его начала и конца?».

Но для начала вернёмся к координатам точки в прямоугольной системе координат.

Напомним, что для их определения нужно опустить перпендикуляры из данной точки к осям.

Точки пересечения данных прямых с осями обозначим как M₁ и M₂.

Абсциссой точки М является число x, которое является длиной отрезка OM₁. А ординатой — число y, которое является длиной отрезка OM₂.

M(x; y) x = OM₁, y = OM₂

Мы вспомнили, как определять координаты точек, а теперь вернёмся к общему случаю и, уже рассмотренной, точке M.

Проведём вектор из точки O к точке M. Запомни, вектор OM⃗ называют радиус-вектором точки M.

Сейчас докажем следующее утверждение: координаты точки M равны соответствующим координатам её радиус-вектора.

Доказать: M(x;y)=OM⃗x;y

Понятно, что вектор OM⃗=ОM1⃗+ОM2⃗ по правилу параллелограмма.

Теперь необходимо доказать, что вектор

OM1⃗=xi⃗, а вектор OM2⃗=yj⃗

Тем самым мы докажем, что вектор OM⃗x;y.

Если x > 0, то x = OM₁, а векторы OM1⃗ и i⃗ сонаправлены, поэтому

OM1⃗=OM1∙i⃗=xi⃗

Если x x = OM₁, а векторы OM1⃗ и i⃗ противоположно направлены. Поэтому OM1⃗=-OM1∙i⃗=xi⃗.

Наконец, если x = 0

OM1⃗=0⃗ и равенство OM1=xi⃗ в этом случае так же справедливо. Таким образом, в любом случае ОM1⃗=xi⃗. Аналогично доказывается, что ОM2⃗=yj⃗.

Следовательно,OM⃗=ОM1⃗+ОM2⃗=xi⃗+yj⃗

Отсюда следует, что координаты радиус-вектора OM равны (x; y), то есть равны соответствующим координатам точки M.

Пользуясь доказанным утверждением, выразим координаты вектора AB⃗ через координаты его начала A и конца B. Пусть точка A имеет координаты x1;y1, а точка B – координаты x2;y2.

Вектор AB⃗ равен разности векторов OB⃗ и OA⃗, поэтому его координаты равны разностям соответствующих координат векторов OB⃗ и OA⃗. Но OB⃗ и OA⃗ – радиус-векторы точек B и A, и, значит, OB⃗ имеет координаты x2;y2, а OA⃗ имеет координаты x1;y1. Следовательно, вектор AB⃗ имеет координаты x2-x1;y2-y1.

Таким образом, каждая координата вектора равна разности соответствующих координат его конца и начала.

Введение системы координат дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат.

Рассмотрим три вспомогательные задачи:

Как найти координаты середины отрезка.

Пусть в системе координат Oxy точка A имеет координаты x1;y1, а точка B – координаты x2;y2. Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то

OC⃗=12OA⃗+OB⃗.

x=x1+x22; y=y1+y22

Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Вычисление длины вектора по его координатам.

Пусть вектор a⃗x;y, тогда длина вектора вычисляется по формуле:

a⃗=x2+y2
Вычисление расстояния между двумя точками. Пусть точка M₁ имеет координаты (x₁; y₁), точка M₂ – координаты (x₂; y₂). Выразим расстояние d между точками M₁ и M₂ через их координаты.

Рассмотрим вектор M1M2⃗. Его координаты равны x2-x1;y2-y1. Следовательно, длина этого вектора может быть найдена по формуле:

M1M2⃗=x2-x12+y2-y12

Пример:

Найти длину вектора a⃗-3;4

a⃗=x2+y2=-32+42=25=5

Ответ: 5
Найти расстояние между точкой A(2; 7) и точкой B(-2; 7)

d=-2-22+7-72=16=4

Ответ: 4

Скорость через радиус вектор

Содержание:

1 Основные формулы кинематики материальной точки
2 Радиус-вектор и траектория точки
3 Скорость материальной точки
- 3. 1 Касательная к траектории
4 Ускорение материальной точки
- 4.1 Тангенциальное (касательное) и нормальное ускорения
  - 4.1.1 Тангенциальное (касательное) ускорение
  - 4.1.2 Радиус кривизны траектории
  - 4.1.3 Нормальное ускорение

Ра́диус-ве́ктор (обычно обозначается r → <displaystyle <vec >> или просто r <displaystyle mathbf> ) — вектор, задающий положения точки в пространстве (например, евклидовом) относительно некоторой заранее фиксированной точки, называемой началом координат.

Для произвольной точки в пространстве радиус-вектор — это вектор, идущий из начала координат в эту точку.

Длина, или модуль радиус-вектора — расстояние, на котором точка находится от начала координат, стрелка вектора — указывает направление на эту точку пространства.

Радиус-вектор точки — это вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.

Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат

Ра́диус-ве́ктор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки , называемой началомкоординат.

Скорость – это векторная физическая величина, которая определяет как быстроту движения, так и его направление в данный момент времени. Мгновенная скорость материальной точки – это средняя скорость за бесконечно малый интервал времени, определяемая как векторная величина, равная первой производной по времени от радиус-вектора rрассматриваемой точки:

v=lim(∆t→0) ∆r/∆t=dr/dt=r’ Вектор мгновенной скорости направлен по касательной к траектории в сторону движения.

Кинематический закон движения– это функция, выражающая положение точки в любой момент времени: r = r(t) (2.1)

Уравнение (2.1) является векторной формой закона. Движение материальной точки полностью определено, если координаты материальной точки заданы в зависимости от времени: x = x(t), y = y(t), z = z(t) . (2.2)

Траектория– это кривая, которую описывает радиус-вектор r(t) координат материальной точки (или тела) с течением времени.

Вектор перемещения∆r = r — r_{– это вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиус-вектора точки за рассматриваемый промежуток времени):}

∆r = r — r_{= r(t) — r(t_{) . В пределе ∆t→0 модуль элементарного перемещения равен элементарному пути: |dr| =ds .}}

Вектор угловой скорости w характеризует быстроту изменения угла поворота и определяется как

w =d(фи)/dt (2.15) где dt – промежуток времени, за которое тело совершает поворот d(фи) ; w =|фи’|.

Единицаугловой скорости в СИ – радиан на секунду (рад/с).

Аксиальные векторы– это векторы, направление которых связывают с направлением вращения. Начало вектора w можно совместить с любой точкой, принадлежащей оси вращения. Вектор w совпадает с наравлением вектора w и является аксиальным вектором.

Изменение вектора wсо временем характеризуют вектором углового ускорения(бета):

(бета)=dw/dt=w’=d 2 (фи’)/dt₂ .Единицауглового ускорения в СИ – радиан на секунду в квадрате (рад/с 2 ).

Равномерное вращение характеризуется периодом вращенияТ – временем, за которое точка совершает один полный оборот: T=2П/w.

Частота вращения– число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени: n=1/T=w/2П.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8946 — | 7616 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Основные формулы кинематики материальной точки

Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.

Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz :
,
где – единичные векторы (орты) в направлении осей x, y, z .

Скорость точки:
;
.
.
Единичный вектор в направлении касательной к траектории точки:
.

Тангенциальное (касательное) ускорение:
;
;
.

Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.

Радиус кривизны траектории:
.

Далее приводится вывод этих формул и изложение теории кинематики материальной точки.

Радиус-вектор и траектория точки

Рассмотрим движение материальной точки M . Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O . Тогда положение точки M однозначно определяются ее координатами ( x, y, z ) . Эти координаты являются компонентами радиус-вектора материальной точки.

Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M .
,
где – единичные векторы в направлении осей x, y, z .

При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.

Траектория материальной точки – это линия, вдоль которой происходит движение точки.

Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями

В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .

Скорость материальной точки

Согласно определению скорости и определению производной:

Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:

,
где
,
,

– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.

Таким образом
.
Модуль скорости:
.

Касательная к траектории

С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.

Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .

При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.

Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.

Тогда вектор скорости точки можно представить в виде:
.

Далее мы считаем, что если над буквой векторной величины не стоит стрелка, то это обозначает модуль вектора.

Ускорение материальной точки

Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.

Тангенциальное (касательное) и нормальное ускорения

Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.

Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?

Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают скалярное произведение векторов. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.

Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к касательной.

Тангенциальное (касательное) ускорение

Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили:
.
Отсюда видно, что тангенциальное ускорение равно проекции полного ускорения на направление касательной к траектории или, что тоже самое, на направление скорости точки.

Тангенциальное (касательное) ускорение материальной точки – это проекция ее полного ускорения на направление касательной к траектории (или на направление скорости).

Символом мы обозначаем вектор тангенциального ускорения, направленный вдоль касательной к траектории. Тогда – это скалярная величина, равная проекции полного ускорения на направление касательной. Она может быть как положительной, так и отрицательной.

Подставим в формулу:
.
Тогда:
.
То есть тангенциальное ускорение равно производной по времени от модуля скорости точки. Таким образом, тангенциальное ускорение приводит к изменению абсолютной величины скорости точки.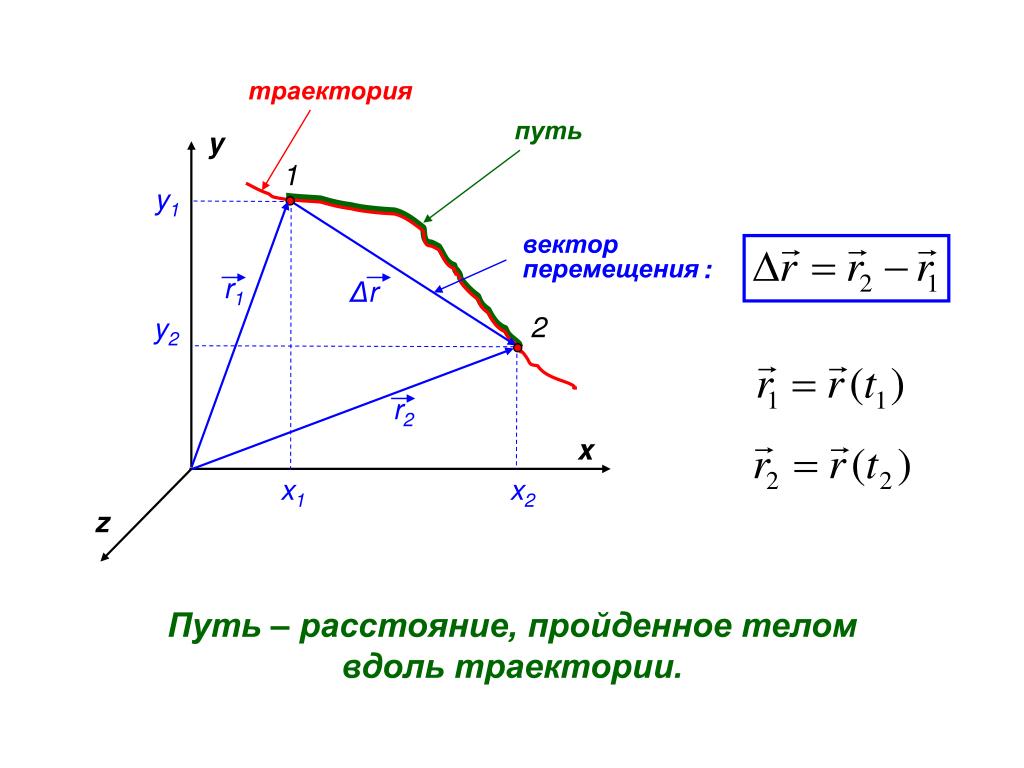 При увеличении скорости, тангенциальное ускорение положительно (или направлено вдоль скорости). При уменьшении скорости, тангенциальное ускорение отрицательно (или направлено противоположно скорости).

Радиус кривизны траектории

Теперь исследуем вектор .

Рассмотрим единичный вектор касательной к траектории . Поместим его начало в начало системы координат. Тогда конец вектора будет находиться на сфере единичного радиуса. При движении материальной точки, конец вектора будет перемещаться по этой сфере. То есть он будет вращаться вокруг своего начала. Пусть – мгновенная угловая скорость вращения вектора в момент времени . Тогда его производная – это скорость движения конца вектора. Она направлена перпендикулярно вектору . Применим формулу для вращающегося движения. Модуль вектора:
.

Теперь рассмотрим положение точки для двух близких моментов времени. Пусть в момент времени точка находится в положении , а в момент времени – в положении . Пусть и – единичные векторы, направленные по касательной к траектории в этих точках. Через точки и проведем плоскости, перпендикулярные векторам и . Пусть – это прямая, образованная пересечением этих плоскостей. Из точки опустим перпендикуляр на прямую . Если положения точек и достаточно близки, то движение точки можно рассматривать как вращение по окружности радиуса вокруг оси , которая будет мгновенной осью вращения материальной точки. Поскольку векторы и перпендикулярны плоскостям и , то угол между этими плоскостями равен углу между векторами и . Тогда мгновенная скорость вращения точки вокруг оси равна мгновенной скорости вращения вектора :
.
Здесь – расстояние между точками и .

Таким образом мы нашли модуль производной по времени вектора :
.
Как мы указали ранее, вектор перпендикулярен вектору . Из приведенных рассуждений видно, что он направлен в сторону мгновенного центра кривизны траектории. Такое направление называется главной нормалью.

Нормальное ускорение

направлено вдоль вектора . Как мы выяснили, этот вектор направлен перпендикулярно касательной, в сторону мгновенного центра кривизны траектории.
Пусть – единичный вектор, направленный от материальной точки к мгновенному центру кривизны траектории (вдоль главной нормали). Тогда
;
.
Поскольку оба вектора и имеют одинаковое направление – к центру кривизны траектории, то
.

Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.

Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.

Нормальное ускорение материальной точки – это проекция ее полного ускорения на направление, перпендикулярное к касательной к траектории.

Подставим . Тогда
.
То есть нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.

Отсюда можно найти радиус кривизны траектории:
.

И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.

Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.

Автор: Олег Одинцов . Опубликовано: 09-02-2016 Изменено: 19-02-2016

примеры и решения, формулы и теоремы

Длина вектора – основные формулы

Длину вектора a→ будем обозначать a→. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат Oxy. Пусть в ней задан некоторый вектор a→ с координатами ax;ay. Введем формулу для нахождения длины (модуля) вектора a→ через координаты ax и ay.

От начала координат отложим вектор OA→=a→. Определим соответственные проекции точки A на координатные оси как Ax и Ay .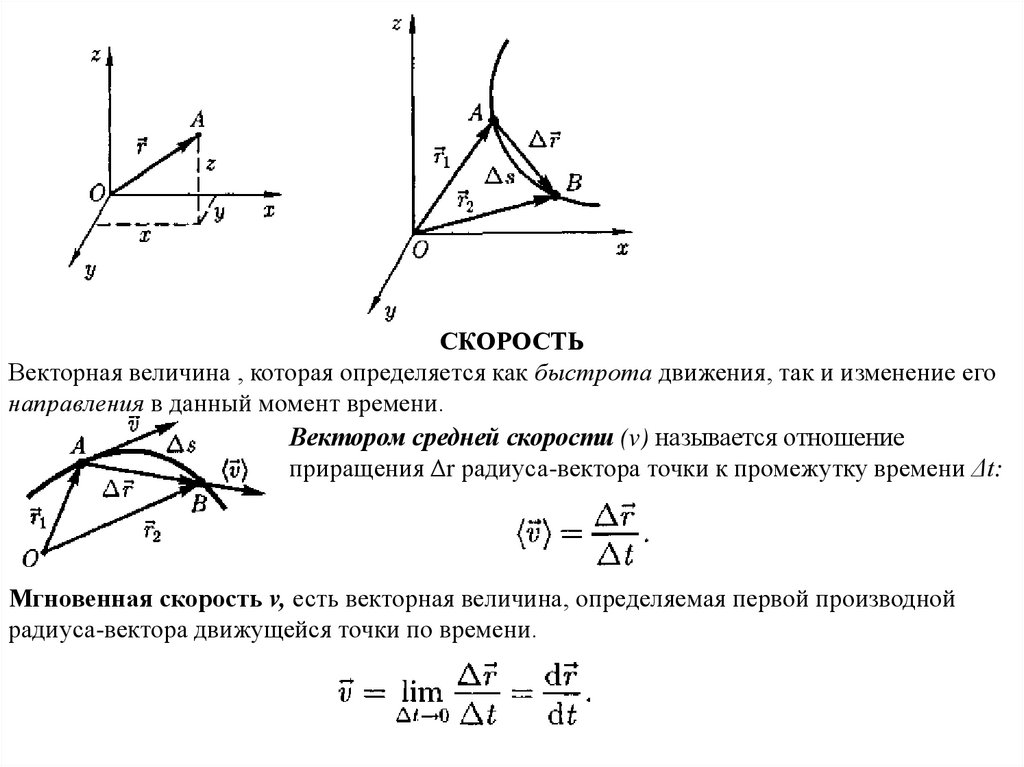 Теперь рассмотрим прямоугольник OAxAAy с диагональю OA.

Из теоремы Пифагора следует равенство OA2=OAx2+OAy2, откуда OA=OAx2+OAy2. Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что OAx2=ax2 и OAy2=ay2, а по построению длина OA равна длине вектора OA→, значит, OA→=OAx2+OAy2.

Отсюда получается, что формула для нахождения длины вектора a→=ax;ay имеет соответствующий вид: a→=ax2+ay2.

Если вектор a→ дан в виде разложения по координатным векторам a→=ax·i→+ay·j→, то вычислить его длину можно по той же формуле a→=ax2+ay2, в данном случае коэффициенты ax и ay выступают в роли координат вектора a→ в заданной системе координат.

Пример 1

Вычислить длину вектора a→=7;e, заданного в прямоугольной системе координат.

Решение

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатамa→=ax2+ay2: a→=72+e2=49+e

Ответ: a→=49+e.

Формула для нахождения длины вектора a→=ax;ay;az по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае OA2=OAx2+OAy2+OAz2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда OA=OAx2+OAy2+OAz2. Из определения координат вектора можем записать следующие равенства OAx=ax; OAy=ay; OAz=az; , а длина ОА равна длине вектора, которую мы ищем, следовательно, OA→=OAx2+OAy2+OAz2.

Отсюда следует, что длина вектора a→=ax;ay;az равна a→=ax2+ay2+az2.

Пример 2

Вычислить длину вектора a→=4·i→-3·j→+5·k→, где i→,j→,k→ – орты прямоугольной системы координат.

Решение

Дано разложение вектора a→=4·i→-3·j→+5·k→, его координаты равны a→=4,-3,5. Используя выше выведенную формулу получим a→=ax2+ay2+az2=42+(-3)2+52=52.

Ответ:a→=52.

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A(ax;ay) и B(bx;by), отсюда вектор AB→ имеет координаты (bx-ax; by-ay)значит, его длина может быть определена по формуле: AB→=(bx-ax)2+(by-ay)2

А если даны точки с заданными координатами A(ax;ay;az) и B(bx;by;bz) в трехмерном пространстве, то длину вектора AB→ можно вычислить по формуле

AB→=(bx-ax)2+(by-ay)2+(bz-az)2

Пример 3

Найти длину вектора AB→, если в прямоугольной системе координат A1, 3, B-3, 1.

Решение

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим AB→=(bx-ax)2+(by-ay)2: AB→=(-3-1)2+(1-3)2=20-23.

Второй вариант решения подразумевает под собой применение данных формул по очереди: AB→=(-3-1; 1-3)=(-4; 1-3); AB→=(-4)2+(1-3)2=20-23.-

Ответ: AB→=20-23.

Пример 4

Определить, при каких значениях длина вектора AB→ равна 30, еслиA(0, 1, 2); B(5, 2, λ2) .

Решение

Для начала распишем длину вектора AB→ по формуле: AB→=(bx-ax)2+(by-ay)2+(bz-az)2=(5-0)2+(2-1)2+(λ2-2)2=26+(λ2-2)2

Затем полученное выражение приравняем к 30, отсюда найдем искомые λ:

26+(λ2-2)2=3026+(λ2-2)2=30(λ2-2)2=4λ2-2=2 или λ2-2=-2 λ1=-2, λ2=2, λ3=0.

Ответ: λ1=-2, λ2=2, λ3=0.

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов AB→, AC→ и угол между ними (или косинус угла), а требуется найти длину вектора BC→ или CB→. В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ABC, вычислить длину стороны BC, которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Пример 5

Длины векторов AB→ и AC→ равны 3 и 7 соответственно, а угол между ними равен π3. Вычислить длину вектора BC→.

Решение

Длина вектора BC→ в данном случае равна длине стороны BC треугольника △ABC. Длины сторон AB и AC треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов:BC2=AB2+AC2-2·AB·AC·cos∠(AB,→AC→)=32+72-2·3·7·cosπ3=37 ⇒BC=37 Таким образом, BC→=37.

Ответ:BC→=37.

Итак, для нахождения длины вектора по координатам существуют следующие формулы a→=ax2+ay2 или a→=ax2+ay2+az2, по координатам точек начала и конца вектора AB→=(bx-ax)2+(by-ay)2 или AB→=(bx-ax)2+(by-ay)2+(bz-az)2, в некоторых случаях следует использовать теорему косинусов.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.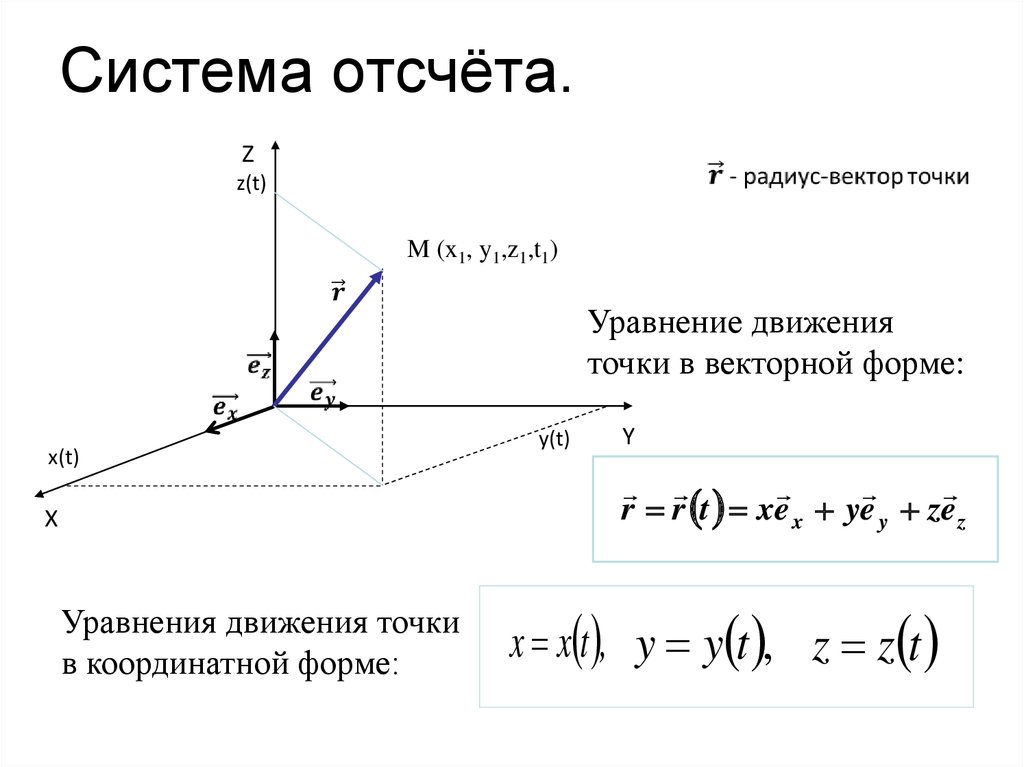 Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Формула радиуса кривизны – Выучить формулу радиуса кривизны

Радиусом кривизны кривой называется любой примерный радиус окружности в любой заданной точке. {2}} |}\) 9{2}} |}\)

где K — кривизна кривой, K = dT/ds, (функция тангенса-вектора)

R — радиус кривизны

Разбор сложных понятий с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Закажите бесплатный пробный урок

Давайте быстро рассмотрим пару примеров, чтобы лучше понять формулу радиуса кривизны. 9{2}} |}\).

13.3: Длина дуги и кривизна

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2596

Гилберт Странг и Эдвин «Джед» Герман
OpenStax

Цели обучения

Определить длину пути частицы в пространстве с помощью функции длины дуги.
Объясните значение кривизны кривой в пространстве и назовите ее формулу.
Объясните значение векторов нормали и бинормалей кривой в пространстве.

В этом разделе мы изучаем формулы, относящиеся к кривым как в двух, так и в трех измерениях, и видим, как они связаны с различными свойствами одной и той же кривой. Например, предположим, что вектор-функция описывает движение частицы в пространстве. Мы хотели бы определить, какое расстояние прошла частица за заданный интервал времени, который можно описать длиной дуги пути, по которому она следует. Или предположим, что вектор-функция описывает дорогу, которую мы строим, и мы хотим определить, насколько круто изгибается дорога в данной точке. Это описывается кривизной функции в этой точке. В этом разделе мы исследуем каждую из этих концепций. 9{b}_{a} \|\vecs r′(t)\|dt . \label{Arc3D} \end{align} \]

Эти две формулы очень похожи; они отличаются только тем, что пространственная кривая имеет три составляющие функции вместо двух. Обратите внимание, что формулы определены для гладких кривых: кривых, где вектор-функция $\vecs r(t)$ дифференцируема с ненулевой производной. Условие гладкости гарантирует, что кривая не имеет точек возврата (или углов), которые могли бы сделать формулу проблематичной.

Пример $\PageIndex{1}$: определение длины дуги 9{3/2})≈37,785\) единиц

Вернемся к спирали, представленной ранее в этой главе. Вектор-функцию, описывающую спираль, можно записать в виде

\[\vecs r(t)=R \cos \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf {i}} +R \sin\left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}},0≤t ≤h, \nonumber \]

где $R$ представляет радиус спирали, $h$ представляет высоту (расстояние между двумя последовательными витками), а спираль завершает $N$ витков. Давайте выведем формулу для длины дуги этой спирали, используя уравнение \ref{Arc3D}. Во-первых, 92}.\end{align*}\]

Это дает формулу для длины провода, необходимой для формирования спирали с $N$ витками, которая имеет радиус $R$ и высоту $h$ .

Параметризация длины дуги

Теперь у нас есть формула для длины дуги кривой, определяемой векторнозначной функцией. Давайте сделаем еще один шаг вперед и рассмотрим, что такое функция длины дуги .

Если векторнозначная функция представляет положение частицы в пространстве как функцию времени, то функция длины дуги измеряет, как далеко эта частица проходит как функцию времени. Формула для функции длины дуги непосредственно следует из формулы для длины дуги: 92} дю. \label{arclength3} \]

Если кривая имеет два измерения, то под квадратным корнем внутри интеграла появляются только два члена. Причина использования независимой переменной u состоит в том, чтобы различать время и переменную интегрирования. Поскольку $s(t)$ измеряет пройденное расстояние как функцию времени, $s′(t)$ измеряет скорость частицы в любой момент времени. Поскольку у нас есть формула для $s(t)$ в уравнении \ref{arclength3}, мы можем дифференцировать обе части уравнения: 9{t}_{a} ‖\vecs r′(u)‖\,du \nonumber \]

Кроме того,

\[\dfrac{ds}{dt}=‖\vecs r′(t)‖> 0. \nonumber \]

Если $‖\vecs r′(t)‖=1$ для всех $t≥a$, то параметр $t$ представляет собой длину дуги от начальной точки в \ (т=а\).

Полезным применением этой теоремы является нахождение альтернативной параметризации данной кривой, называемой параметризацией длины дуги . Напомним, что любую вектор-функцию можно перепараметрировать заменой переменных. Например, если у нас есть функция $\vecs r(t)=⟨3 \cos t,3 \sin t⟩,0≤t≤2π$, которая параметризует окружность радиуса 3, мы можем изменить параметр с $t$ в $4t$, получив новую параметризацию $\vecs r(t)=⟨3 \cos 4t,3 \sin 4t⟩$. Новая параметризация по-прежнему определяет окружность радиуса 3, но теперь нам нужно использовать только значения $0≤t≤π/2$, чтобы пройти круг один раз.

Предположим, что мы нашли функцию длины дуги $s(t)$ и можем решить эту функцию для $t$ как функцию от $s$ . Затем мы можем перепараметрировать исходную функцию $\vecs r(t)$, подставив выражение для $t$ обратно в $\vecs r(t)$. Теперь вектор-функция записывается в терминах параметра $s$ . Поскольку переменная $s$ представляет длину дуги, мы называем это параметризацией длины дуги исходной функции $\vecs r(t)$. Одним из преимуществ нахождения параметризации длины дуги является то, что расстояние, пройденное вдоль кривой, начиная с $s=0$, теперь равно параметру $s$. Параметризация длины дуги также появляется в контексте кривизны (которую мы рассмотрим позже в этом разделе) и линейных интегралов.

Пример $\PageIndex{2}$: поиск параметризации длины дуги

Найдите параметризацию длины дуги для каждой из следующих кривых:

$\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+ 4 \sin t \,\hat{\mathbf{j}},\quad t≥0$
$\vecs r(t)=⟨t+3,2t−4,2t⟩,\quad t≥3$

Решение

Сначала найдем функцию длины дуги, используя уравнение \ref{arclength3}:
\[\begin{align*} s(t) &= \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_0^t ‖⟨−4 \sin u, 4 \cos u⟩‖ \,du \\[4pt] &= \int_0^t \sqrt{(−4 \sin u)^2+(4 \cos u)^2} \,du \\[4pt] &= \int_0^t \sqrt{16 \sin ^2 u+16 \cos ^2 u} \,du \\[4pt] &= \int_0^t 4\,du = 4t, \end{align*} \]
, который дает связь между длиной дуги $s$ и параметром $t$ как $s=4t;$, то есть $t=s/4$. Далее заменяем переменную $t$ в исходной функции $\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf {j}}$ с выражением $s/4$, чтобы получить
\[\vecs r(s)=4 \cos\left(\frac{s}{4}\right) \,\hat{\mathbf{i}} + 4 \sin\left(\frac{s} {4}\справа) \,\шляпа{\mathbf{j}}. \номер\]
Это параметризация длины дуги $\vecs r(t)$. Поскольку исходное ограничение на $t$ было задано выражением $t≥0$, ограничение на 9t 3 \,du \\[4pt] &= 3t – 9. \end{align*}\]
Следовательно, связь между длиной дуги $s$ и параметром $t$ равна $s=3t−9$, поэтому $t= \frac{s}{3}+3$. Подстановка этого в исходную функцию $\vecs r(t)=⟨t+3,2t−4,2t⟩ $ дает
\[\vecs r(s)=⟨\left(\frac{s}{3}+3\right)+3,\,2\left(\frac{s}{3}+3\right)− 4,\,2\влево(\frac{s}{3}+3\вправо)⟩=⟨\frac{s}{3}+6, \frac{2s}{3}+2,\frac{2s {3}+6⟩.\номер\]
Это параметризация длины дуги $\vecs r(t)$. Исходное ограничение на параметр $t$ было $t≥3$, поэтому ограничение на $s$ равно $(s/3)+3≥3$ или $s≥0 $.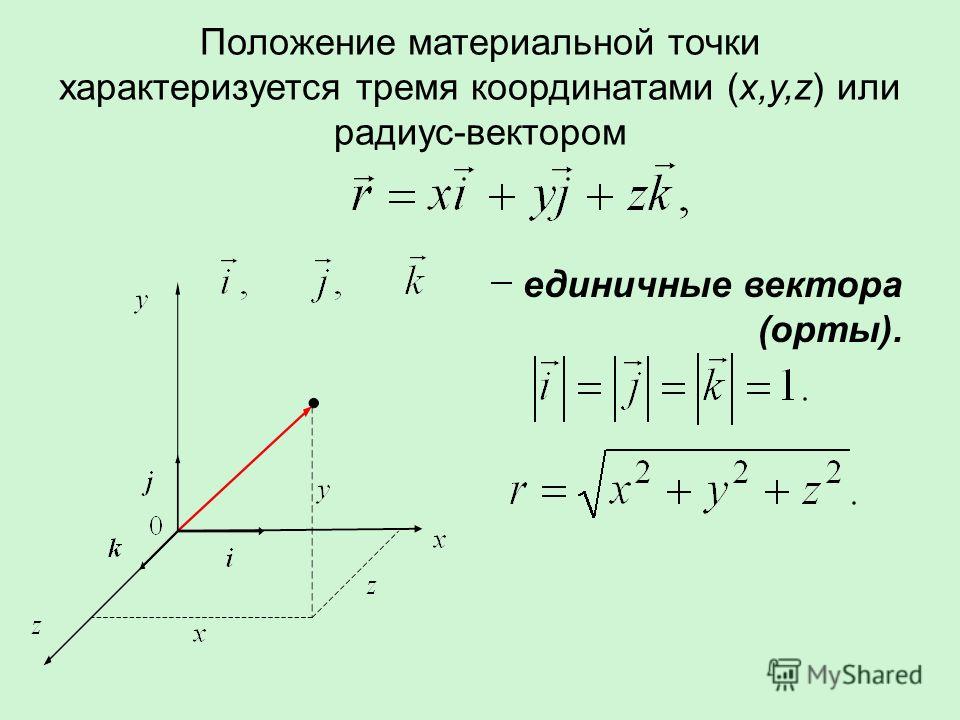

Упражнение $\PageIndex{2}$

Найдите функцию длины дуги для спирали

\[\vecs r(t)=⟨3 \cos t, 3 \sin t,4t⟩,\quad т≥0. \nonumber \]

Затем используйте связь между длиной дуги и параметром $t$, чтобы найти параметризацию длины дуги для $\vecs r(t)$.

Подсказка

Начните с нахождения функции длины дуги.

Ответить

$s=5t$ или $t=s/5$. Подстановка этого в $\vecs r(t)=⟨3 \cos t,3 \sin t,4t⟩$ дает

\[\vecs r(s)=⟨3 \cos\left(\frac{s}{5}\right),3 \sin\left(\frac{s}{5}\right),\frac{ 4s}{5}⟩,\quad s≥0 \nonumber \]

Кривизна

Важным вопросом, связанным с длиной дуги, является кривизна. Понятие кривизны позволяет измерить, насколько резко поворачивает гладкая кривая. Окружность имеет постоянную кривизну. Чем меньше радиус окружности, тем больше кривизна.

Представьте, что вы едете по дороге. Предположим, что дорога лежит на дуге большого круга. В этом случае вам едва ли придется крутить руль, чтобы оставаться на дороге. Теперь предположим, что радиус меньше. В этом случае вам нужно будет поворачивать более резко, чтобы остаться на дороге. В случае кривой, отличной от окружности, часто бывает полезно сначала вписать окружность в кривую в заданной точке так, чтобы она касалась кривой в этой точке и «обнимала» кривую как можно ближе в заданной точке. окрестности точки (рис. $\PageIndex{1}$). Затем кривизна графика в этой точке определяется как такая же, как кривизна вписанной окружности.

Определение: кривизна

Пусть $C$ — гладкая кривая на плоскости или в пространстве, заданная формулой $\vecs r(s)$, где $s$ — параметр длины дуги. Кривизна $κ$ в точке $s$ равна

\[κ =\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}=‖\vecs T «(с)».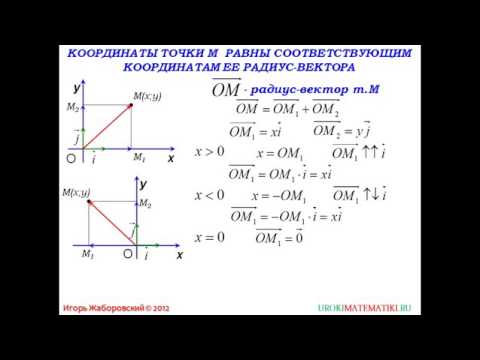 \nonumber \]

Посмотрите это видео, чтобы узнать больше о кривизне пространственной кривой.

Формула определения кривизны не очень полезна с точки зрения вычислений. В частности, напомним, что $\vecs T(t)$ представляет собой единичный касательный вектор к заданной вектор-функции $\vecs r(t)$, а формула для $\vecs T(t) $ равно

\[\vecs T(t)=\frac{\vecs r′(t)}{∥\vecs r′(t)∥}. \nonumber \]

Чтобы использовать формулу для кривизны, сначала необходимо выразить $\vecs r(t)$ через параметр длины дуги $s$, затем найти единичный касательный вектор \ (\vecs T(s)\) для функции $\vecs r(s)$, то возьмем производную от $\vecs T(s)$ по $s$. Это утомительный процесс. К счастью, существуют эквивалентные формулы для кривизны. 9{3/2}}.\label{EqK4} \]

Доказательство

Первая формула непосредственно следует из цепного правила:

\[\dfrac{d\vecs{T}}{dt} = \dfrac{ d\vecs{T}}{ds} \dfrac{ds}{dt}, \nonumber \]

где $s$ – длина дуги вдоль кривой $C$. Разделив обе стороны на $ds/dt$ и взяв величину обеих сторон, мы получим

\[\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}= \left\lVert\frac{\vecs T'(t)}{\dfrac{ds}{dt}}\right\rVert.\nonumber \]

Так как $ds/dt=‖\vecs r'(t )‖$, это дает формулу кривизны $κ$ кривой $C$ в терминах любой параметризации $C$: 93}.\nonumber \]

Это доказывает $\ref{EqK3}$. Чтобы доказать $\ref{EqK4}$, мы начнем с предположения, что кривая $C$ определяется функцией $y=f(x)$. Затем мы можем определить $\vecs r(t)=x \,\hat{\mathbf{i}}+f(x) \,\hat{\mathbf{j}}+0 \,\hat{\ mathbf{k}}$. Используя предыдущую формулу для кривизны:

\[\begin{align*} \vecs r′(t) &=\,\hat{\mathbf{i}}+f′(x)\,\hat{\mathbf {j}} \\[4pt] \vecs r″(t) &=f″(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r′(t)×\vecs r ″(t) &= \begin{vmatrix} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ 1 & f'(x) & 0 \\ 0 & f”(x) & 0 \end{vmatrix} =f”(x)\,\hat{\mathbf{k}}. \end{выравнивание*}\] 9{3/2}}≈0,0059\)

Нормальный и бинормальный векторы

Мы видели, что производная $\vecs r′(t)$ вектор-функции является касательным вектором к кривой, заданной $\vecs r(t) $, а единичный касательный вектор $\vecs T(t)$ можно рассчитать, разделив $\vecs r′(t)$ на его величину.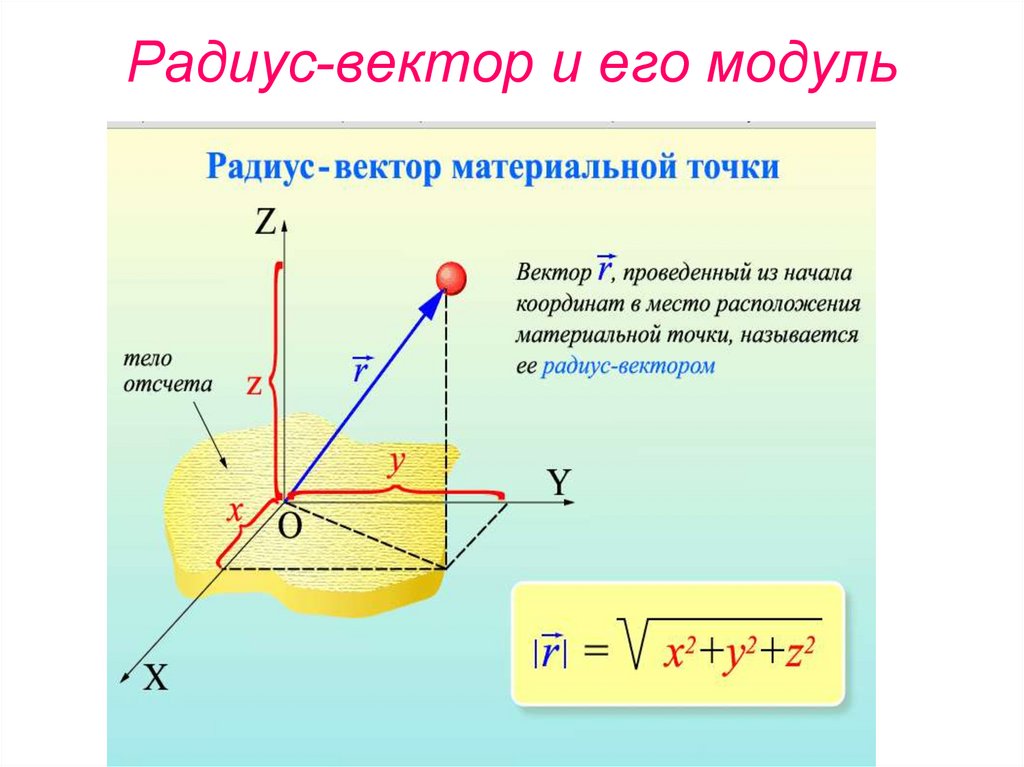 При изучении движения в трех измерениях для описания движения частицы по траектории в пространстве полезны два других вектора: главный единичный вектор нормали и вектор бинормальный вектор .

Определение: бинормальные векторы

Пусть $C$ – трехмерная гладкая кривая, представленная $\vecs r$ на открытом интервале $I$ . Если $\vecs T′(t)≠\vecs 0$, то главный единичный вектор нормали в точке $t$ определяется как

\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \label{EqNormal} \]

Вектор бинормалей в точке $t$ определяется как

\[\vecs B(t)=\vecs T(t)×\vecs N(t),\label{EqBinormal } \]

где $\vecs T(t)$ – единичный касательный вектор.

Обратите внимание, что бинормали по определению ортогональны как единичному касательному вектору, так и вектору нормали. Кроме того, $\vecs B(t)$ всегда является единичным вектором. Это можно показать, используя формулу для величины векторного произведения.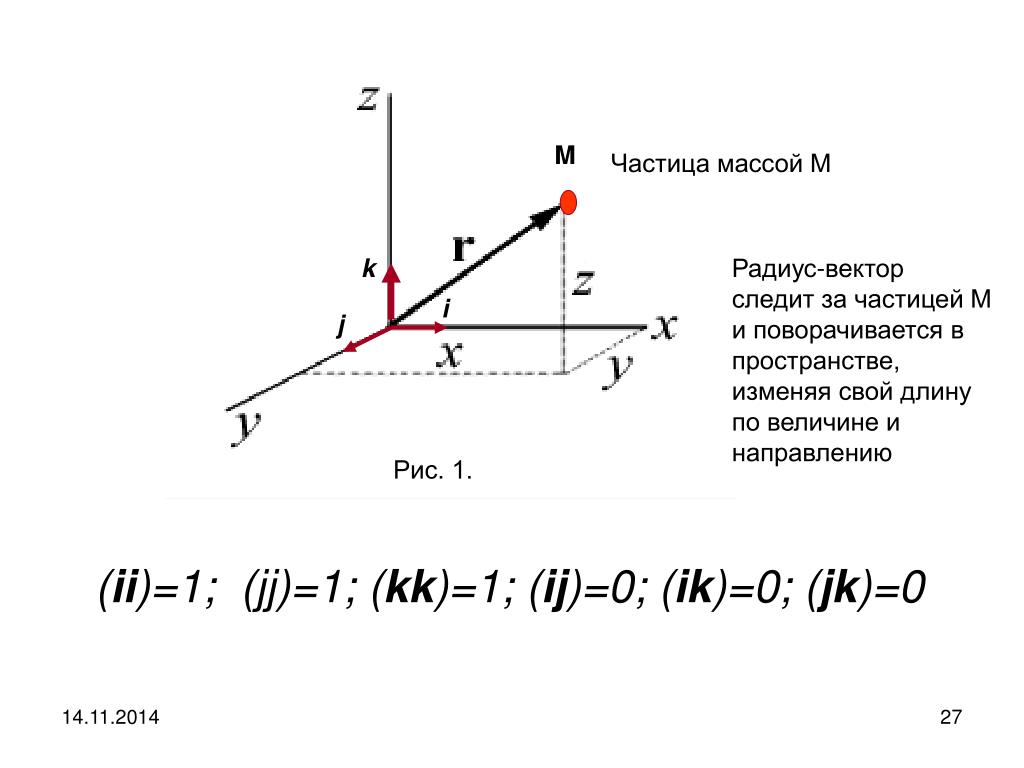

\[‖\vecs B(t)‖=‖\vecs T(t)×\vecs N(t)‖=‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta, \nonumber \]

где $\theta$ – угол между $\vecs T(t)$ и $\vecs N(t)$. Поскольку $\vecs N(t)$ является производной единичного вектора, свойство (vii) производной вектор-функции говорит нам, что $\vecs T(t)$ и $\vecs N(t)$ ортогональны друг другу, поэтому $\theta=π/2$. Кроме того, они оба являются единичными векторами, поэтому их величина равна 1. Следовательно, $‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta=(1)(1) \sin (π/ 2)=1$ и $\vecs B(t)$ – единичный вектор.

Главный единичный вектор нормали может быть сложным для вычисления, поскольку единичный вектор касательной включает частное, а это частное часто имеет квадратный корень в знаменателе. В трехмерном случае нахождение векторного произведения единичного касательного вектора и единичного вектора нормали может быть еще более громоздким. К счастью, у нас есть альтернативные формулы для нахождения этих двух векторов, и они представлены в разделе «Движение в пространстве».

Пример $\PageIndex{4}$: нахождение вектора нормали к главной единице и вектора бинормали 92 t}} \\[4pt]

Обратите внимание, что единичный вектор касательной и главный единичный вектор нормали ортогональны друг другу для всех значений $t$:

\[\begin{align*} \vecs T (t)·\vecs N(t) &=⟨− \sin t,− \cos t⟩·⟨− \cos t, \sin t⟩ \\[4pt] &= \sin t \cos t−\cos т \sin т \\[4pt] &=0. \end{align*}\]

Кроме того, главный единичный вектор нормали указывает к центру окружности из каждой точки окружности. Поскольку $\vecs r(t)$ определяет кривую в двух измерениях, мы не можем вычислить вектор бинормалей. 92−3t)\,\hat{\mathbf{i}}+(4t+1)\,\hat{\mathbf{j}}\) и оценить его при $t=2$.

Подсказка: Сначала найдите $\vecs T(t)$, затем используйте $\ref{EqNormal}$.
Ответить: $\vecs N(2)=\dfrac{\sqrt{2}}{2}(\,\hat{\mathbf{i}}−\,\hat{\mathbf{j}})$

Для любой гладкой кривой в трех измерениях, заданной вектор-функцией, теперь у нас есть формулы для единичного касательного вектора $\vecs T$, единичного вектора нормали $\vecs N$ и бинормальный вектор $\vecs B$. Единичный вектор нормали и вектор бинормали образуют плоскость, перпендикулярную кривой в любой точке кривой, называемую плоскостью нормали. Кроме того, эти три вектора образуют систему отсчета в трехмерном пространстве, называемую 9.0531 Система координат Френе (также называемая системой координат TNB ) (рис. $\PageIndex{2}$). Наконец, плоскость, определяемая векторами $\vecs T$ и $\vecs N$, образует соприкасающуюся плоскость $C$ в любой точке $P$ на кривой.

$P$

на трехмерной кривой вектора единичной касательной, единичной нормали и бинормали образуют трехмерную систему отсчета.

Предположим, мы образуем окружность в соприкасающейся плоскости $C$ в точке $P$ на кривой. Предположим, что окружность имеет ту же кривизну, что и кривая в точке $P$, и пусть окружность имеет радиус $r$. Тогда кривизна круга определяется как $\frac{1}{r}$. Мы называем $r$ радиусом кривизны кривой, и он равен обратной величине кривизны. Если эта окружность лежит на вогнутой стороне кривой и касается кривой в точке $P$, то эта окружность называется соприкасающийся круг из $C$ в точке $P$, как показано на рисунке $\PageIndex{3}$.

и имеет ту же кривизну.

Для получения дополнительной информации о соприкасающихся окружностях см. эту демонстрацию кривизны и кручения, эту статью о соприкасающихся окружностях и это обсуждение формул Серре.

Чтобы найти уравнение соприкасающейся окружности в двух измерениях, нам нужно найти только центр и радиус окружности. 9{3/2}}. \nonumber \]

Это дает $κ=6$. Следовательно, радиус соприкасающейся окружности определяется выражением $R=\frac{1}{κ}=\dfrac{1}{6}$. Далее мы вычисляем координаты центра круга. Когда $x=1$, наклон касательной равен нулю. 2=\frac{1}{36}\). График и его соприкасающийся круг показаны на следующем графике. 9{3/2}}\)

В точке $x=1$ кривизна равна $4$. Следовательно, радиус соприкасающейся окружности равен $\frac{1}{4}$.

Далее появится график этой функции:

Вершина этой параболы находится в точке $(1,3)$. Кроме того, центр соприкасающейся окружности находится прямо над вершиной. Следовательно, координаты центра равны $(1,\frac{13}{4})$. Уравнение соприкасающейся окружности

Вектор нормали к главной единице
$\vecs N(t)=\frac{\vecs T′(t)}{‖\vecs T′(t)‖}$
Вектор бинормалей
$\vecs B(t)=\vecs T(t)×\vecs N(t)$

Глоссарий

функция длины дуги: функция $s(t)$, которая описывает длину дуги кривой $C$ как функцию $t$

параметризация длины дуги: репараметризация вектор-функции, в которой параметр равен длине дуги

бинормальный вектор: единичный вектор, ортогональный единичному касательному вектору и единичному вектору нормали

кривизна: производная единичного касательного вектора по параметру длины дуги

Система координат Френе: (кадр TNB) система отсчета в трехмерном пространстве, образованная единичным касательным вектором, единичным вектором нормали и вектором бинормалей

обычная плоскость: плоскость, перпендикулярная кривой в любой точке кривой

соприкасающийся круг: окружность, касающаяся кривой $C$ в точке $P$ и имеющая ту же кривизну

соприкасающаяся плоскость: плоскость, определяемая единичной касательной и единичным вектором нормали

вектор нормали к главной единице: вектор, ортогональный единичному касательному вектору, определяемый формулой $\frac{\vecs T'(t)}{‖\vecs T'(t)‖}$

радиус кривизны: обратная кривизна

гладкая: кривых, где вектор-функция $\vecs r(t)$ дифференцируема с ненулевой производной

Эта страница под названием 13. 3: Длина и кривизна дуги распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
ОпенСтакс
Лицензия
CC BY-NC-SA
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать страницу TOC
нет
Метки
1. Длина дуги
2. функция длины дуги
3. параметризация длины дуги
4. автор @ Эдвин «Джед» Герман
5. автор@Гилберт Странг
6. бинормальный бинормальный вектор
7. кривизна
8. Система отсчета Френе
9. обычный самолет
10. соприкасающийся круг
11. соприкасающаяся плоскость
12. вектор нормали к главной единице
13. радиус кривизны
14. гладкая
15. источник@https://openstax. org/details/books/calculus-volume-1

16.6 Векторные функции для поверхностей

Мы много работали с векторными уравнениями для кривых, ${\bf r}(t)=\langle x(t),y(t),z(t)\rangle$. Аналогичная техника может использоваться для представления поверхностей в более общем виде, чем уравнения для поверхностей, которые мы использовали до сих пор. Напомним, что когда мы используем ${\bf r}(t)$ для представления кривой, мы представляем себе вектор ${\bf r}(t)$ хвостом в начале координат, а затем следуем за головой стрелки при изменении $t$. Вектор «рисует» кривую через пространство при изменении $t$.

Предположим, что вместо этого у нас есть векторная функция двух переменных, $${\bf r}(u,v)=\langle x(u,v),y(u,v),z(u,v)\rangle.$$ Как и $u$, и $v$ меняются, мы снова представляем себе вектор ${\bf r}(u,v)$ с хвостом в происхождение, и его голова выметает поверхность в космосе. Полезный аналогом является технология ЭЛТ-видеоэкранов, в которой электрон пушка стреляет электронами в сторону экрана.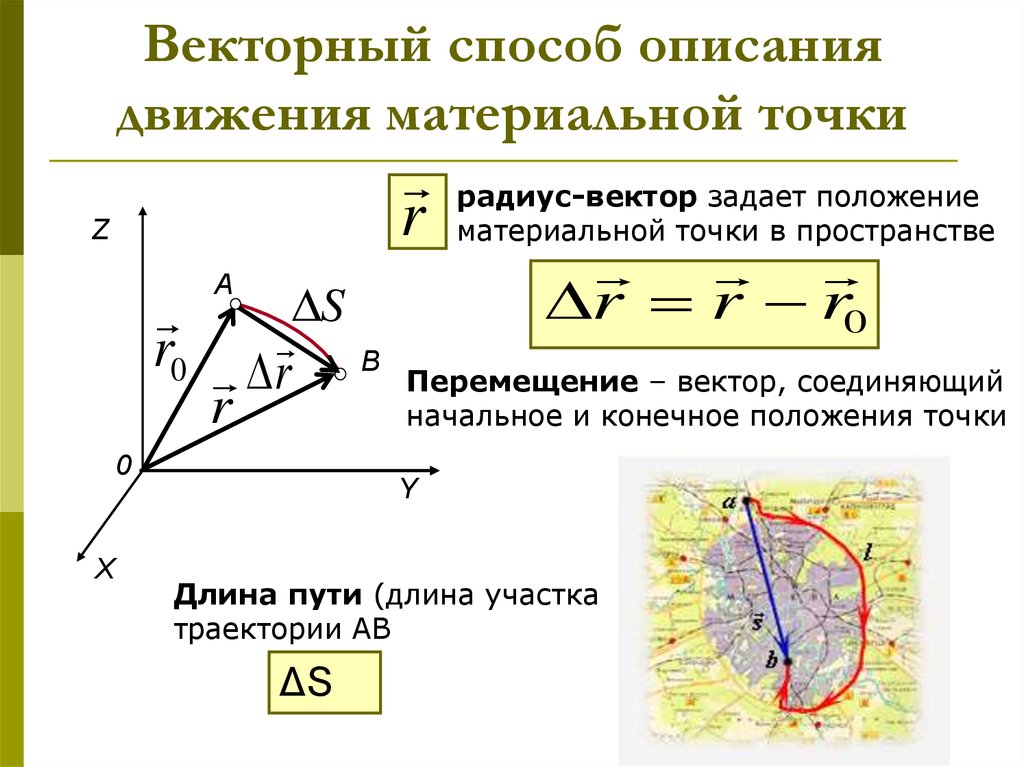 пистолет направление перемещается по горизонтали и вертикали, чтобы «раскрасить» экран с желаемым изображением. На практике пушка перемещается горизонтально через всю строку, затем перемещается по вертикали на следующую строку и повторяет операцию. Точно так же может быть полезно представить фиксируя значение $v$ и позволяя ${\bf r}(u,v)$ заметать кривую как $u$ меняется. Тогда $v$ может немного измениться, и ${\bf r}(u,v)$ заметает новая кривая очень близка к первой. Положите достаточно этих кривых вместе, и они образуют поверхность.

Пример 16.6.1. Рассмотрим функцию ${\bf r}(u,v)=\langle v\cos u,v\sin u, v\rangle$. Для фиксированного значения $v$, когда $u$ изменяется от 0 до $2\pi$, это описывает окружность радиуса $v$ на высоте $v$ над Плоскость $x$-$y$. Сложите много-много всего этого вместе, и они образуют конус, как на рисунке 16.6.1. В качестве альтернативы мы можем зафиксировать $u$, и поскольку $v$ варьируется от $0$ до бесконечности, ${\bf r}(u,v)$ отслеживает вне линии; примеры этих линий можно увидеть в стенке конуса или в одиночку на третьем графике рисунка. $\квадрат$

Рисунок 16.6.1. Трассировка поверхности.

Пример 16.6.2. Пусть ${\bf r}=\langle v\cos u, v\sin u, u\rangle$. Если $v$ постоянной, результирующая кривая представляет собой спираль (как в рисунок 13.1.1). Если $u$ постоянна, результирующая кривая представляет собой прямую линию на высоте $u$ в направлении $u$ радиан от положительная ось $x$. Обратите внимание на рисунок 16.6.2, как спирали и линии окрашивают одну и ту же поверхность по-разному. $\квадрат$

Рисунок 16.6.2. Трассировка поверхности.

Этот метод позволяет нам представлять намного больше поверхностей, чем ранее.

Пример 16.6.3. Кривая, заданная выражением $${\bf r}=\langle (2+\cos(3u/2))\cos u, (2+\cos(3u/2))\sin u, \sin(3u/2)\rangle$$ называется узел-трилистник. Напомним, что из векторного уравнения кривой мы можем вычислить единичный тангенс $\bf T$, единичная нормаль $\bf N$ и бинормальный вектор ${\bf B}={\bf T}\times{\bf N}$; вы можете хотите просмотреть раздел 13. 3. бинормаль является перпендикулярно обоим $\bf T$ и $\bf N$; один из способов интерпретировать это состоит в том, что ${\bf N}$ и ${\bf B}$ определяют плоскость, перпендикулярную $\bf T$, т. е. перпендикулярно кривой; поскольку ${\bf N}$ и ${\bf B}$ перпендикулярны друг другу, они могут функционировать как $\bf i$ и $\bf j$ do для плоскости $x$-$y$. Конечно, $\bf N$ и $\bf B$ функции от $u$, изменяющиеся по мере движения вдоль кривой ${\bf r}(u)$. Так, например, ${\bf c}(u,v)={\bf N}\cos v+{\bf B}\sin v$ векторное уравнение для единичного круга на плоскости перпендикулярно кривой, описываемой $\bf r$, за исключением того, что обычно интерпретация $\bf c$ поместила бы его центр в начало координат. Мы можем исправить это, просто добавив $\bf c$ к исходному $\bf r$: пусть ${\bf f}={\bf r}(u) +{\bf c}(u,v)$. Для фиксированный $u$ рисует окружность вокруг точки ${\bf r}(u)$; как $u$ меняется, мы получаем последовательность таких окружностей вокруг кривой $\bf r$, то есть трубка радиуса 1 с $\bf r$ в центре.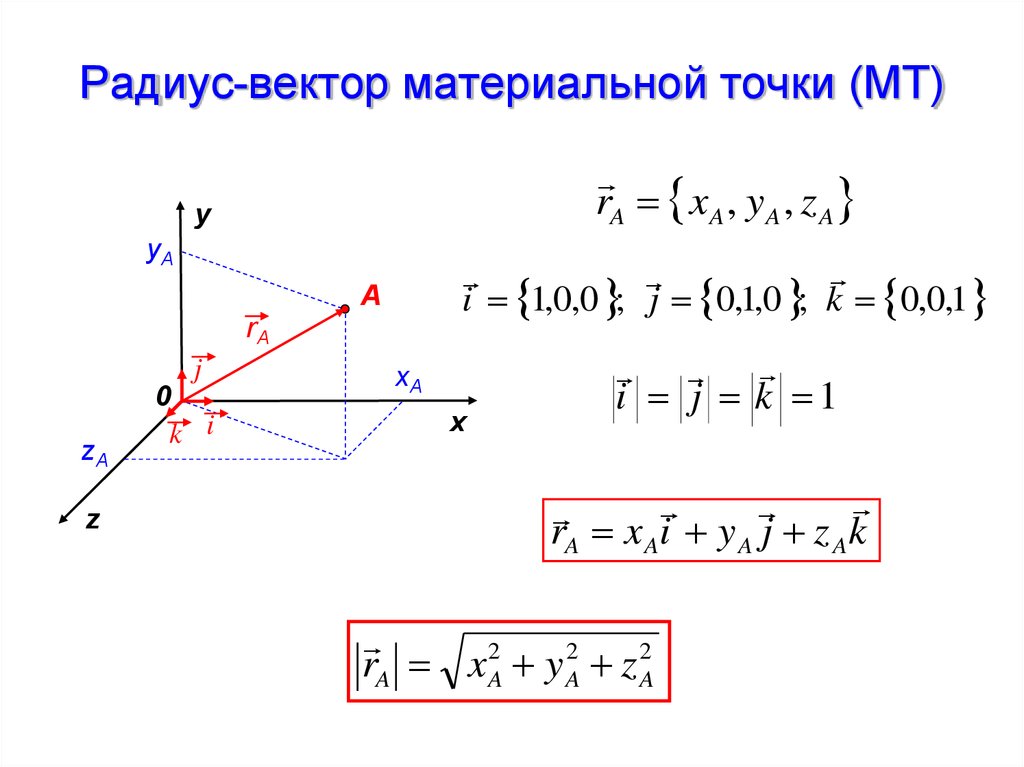 Мы можем легко изменить радиус; например ${\bf r}(u) +a{\bf c}(u,v)$ дает радиус трубы $a$; мы можем изменить радиус, как мы двигаться по кривой с ${\bf r}(u) +g(u){\bf c}(u,v)$, где $g(u)$ — функция от $u$. Как показано в 16.6.3, трудно увидеть, что простой узел завязанный; трубка делает структуру очевидной. Есть конечно ничего особенного в узле-трилистнике в этом примере; мы можем поставить трубка вокруг (почти) любой кривой таким же образом. $\квадрат$

Рисунок 16.6.3. Трубки вокруг узла-трилистника радиусом $1/2$ и $3\cos(u)/4$.

Ранее мы рассматривали поверхности, заданные в виде $f(x,y)$. Иногда бывает полезно представить такие поверхности в более общая векторная форма, которая довольно проста: ${\bf r}(u,v)=\langle u,v,f(u,v)\rangle$. Имена переменных не важны, конечно; вместо того, чтобы маскировать $x$ и $y$, мы можно просто написать ${\bf r}(x,y)=\langle x,y,f(x,y)\rangle$.

Ранее мы также имели дело с поверхностями, которые не являются функциями $x$ и $y$; многие из них легко представить в векторной форме. 2, v \ rangle $. 92}$ вокруг оси $z$ на высоте $v$. Мы могли бы также взять пример со сферических координат и написать $\langle \sin u\cos v,\sin u\sin v,\cos u\rangle$, где фактически $u$ и $v$ — это замаскированные $\phi$ и $\theta$.

В Sage очень просто построить любую поверхность, для которой у вас есть векторное представление. Иногда использование различных векторных функций дает разные сюжеты, потому что Мудрец, по сути, рисует поверхность, удерживая одну переменную постоянной, а затем другую. За пример на рис. 16.6.2 кривые на двух правых графиках наложены на левый график; график поверхности – это просто комбинация два набора кривых с пробелами, заполненными цветом.

Вот простой, но яркий пример: плоскость $x+y+z=1$ может быть вполне естественно представляется как $\langle u,v,1-u-v\rangle$. Но мы можно также подумать о том, чтобы нарисовать один и тот же самолет, выбрав конкретный точку на плоскости, скажем, $(1,0,0)$, а затем рисование кругов или эллипсы (или любые другие кривые), как если бы эта точка была происхождение в плоскости. Например, $\langle 1-v\cos u-v\sin u,v\sin u,v\cos u\rangle$ — одна из таких векторных функций. Обратите внимание, что, хотя это может не очевидно, откуда это взялось, довольно легко увидеть, что сумма компонент $x$, $y$ и $z$ вектора всегда равна 1. Показана компьютерная визуализация самолета с использованием этих двух функций. на рисунке 16.6.4.

Рисунок 16.6.4. Два изображения одной плоскости.

Предположим, мы знаем, что плоскость содержит определенную точку $(x_0,y_0,z_0)$ и два вектора ${\bf u}=\langle u_0,u_1,u_2\rangle$ и ${\bf v}=\langle v_0,v_1,v_2\rangle$ параллельны плоскости, но не друг другу Другой. Мы знаем, как получить уравнение плоскости в виде $ax+by+cz=d$, сначала вычислив ${\bf u}\times{\bf v}$. это даже проще получить векторное уравнение: $${\bf r}(u,v) = \langle x_0,y_0,z_0\rangle + u{\bf u} + v{\bf v}.$$ Первый вектор попадает в точку $(x_0,y_0,z_0)$ и затем, варьируя $u$ и $v$, $u{\bf u} + v{\bf v}$ попадают в каждую точку плоскости.

Возвращаясь к $x+y+z=1$, точки $(1,0,0)$, $(0,1,0)$ и $(0,0,1)$ все в самолете. Вычитая координаты, мы видим, что $\langle -1,0,1\rangle$ и $\langle -1,1,0\rangle$ параллельны плоскости, поэтому третья векторная форма для этой плоскости $$\langle 1,0,0\rangle + u\langle -1,0,1\rangle + v\langle -1,1,0\угол = \langle 1-u-v,v,u\rangle.$$ Это явно очень похоже на первую найденную нами форму.

Мы уже видели (раздел 15.4) как найти площадь поверхности, если она определяется в виде $f(x,y)$. Нахождение площади, когда поверхность в виде векторной функции очень похож. Глядя на сюжеты поверхностей, которые мы только что видели, очевидно, что два набора кривых которые заполняют поверхность, делят ее на сетку, и что пробелы в сетке примерно параллелограммы. Как и прежде, это ключ: мы можем записать площадь типичного маленького параллелограмма и сложите их все с интегралом.

Предположим, мы хотим аппроксимировать площадь поверхности ${\bf r}(u,v)$ вблизи ${\bf r}(u_0,v_0)$.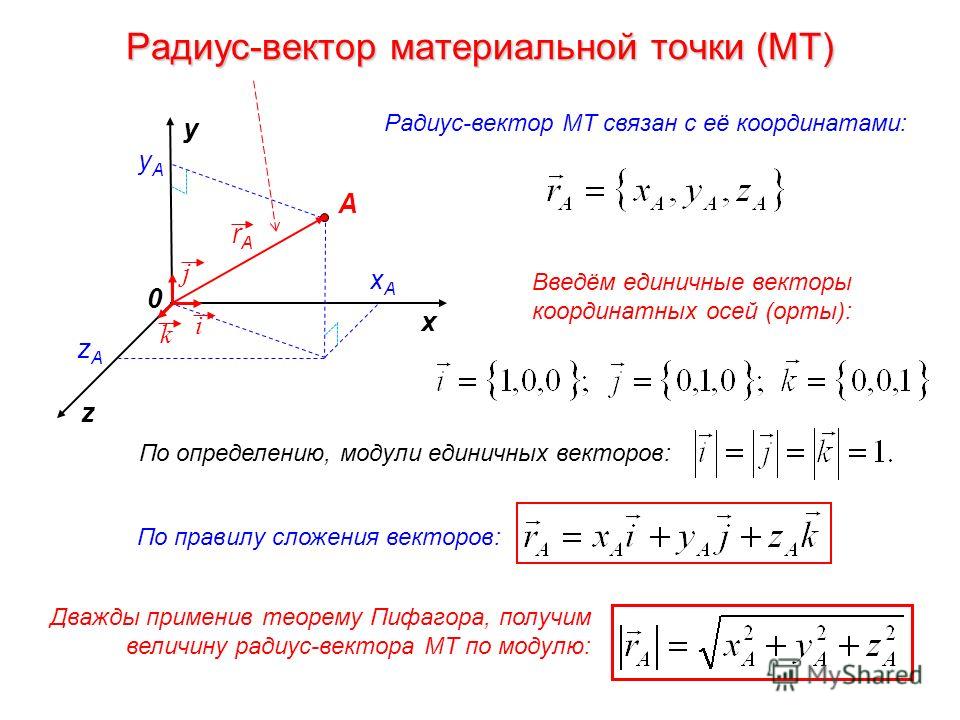 2 \ rangle $ 92$. (отвечать)

Пример 16.6.16 Поверхность $f(x,y)$ может быть представлена вектором функция $\langle x,y,f(x,y)\rangle$. Настройте интеграл площади поверхности, используя эту векторную функцию и сравнить с интегралом от раздел 15.4.

Калькулятор угловой скорости

Создано Wojciech Sas, PhD кандидатом

Отредактировано Bogna Szyk и Jack Bowater

Последнее обновление: 15 декабря 2021 г.

Что такое угловая скорость?
Формулы угловой скорости
Единицы измерения угловой скорости
Зависимость угловой скорости от угловой частоты
Как найти угловую скорость Земли?
Физические величины, зависящие от угловой скорости
Сохранение углового момента

Этот калькулятор угловой скорости представляет собой простой в использовании инструмент, который дает немедленный ответ на вопрос «Как найти угловую скорость?». В тексте вы найдете несколько формул угловой скорости, узнаете о различных единицах измерения угловой скорости и, наконец, оцените угловую скорость Земли! Вы когда-нибудь задумывались, какова связь между угловой скоростью и угловой частотой или где применяется угловая скорость? Читайте дальше, чтобы узнать, и стать экспертом в области кругового движения.

Что такое угловая скорость?

Угловая скорость описывает вращательное движение тел. Он измеряет, насколько быстро они движутся вокруг некоторого центра вращения. Мы можем думать о двух разных видах вращения. Первый описывает движение центра масс данного объекта вокруг определенной точки в пространстве , которую можно описать как начало координат. Некоторые примеры включают планеты, движущиеся вокруг Солнца, или автомобиль, съезжающий с шоссе.

Второй рассказывает о вращение тела вокруг собственного центра масс – спин (не путать с квантовым свойством частиц, также называемым спином). Наверняка вы видели, как баскетболист крутит мяч на пальце.

В целом можно сказать, что чем быстрее движение, тем выше угловая скорость. Чтобы определить некоторые конкретные значения, мы должны перейти к уравнениям угловой скорости, описанным в следующем разделе.

Формулы угловой скорости

В этом калькуляторе угловой скорости мы используем две разные формулы угловой скорости, в зависимости от того, какие у вас есть входные параметры.

Первое уравнение угловой скорости аналогично уравнению для линейной скорости:

ω = (α₂ - α₁) / t = Δα / t ,

где α₁ и α₂ два угла на круг, а Δα — их разность. t – время, за которое происходит изменение угла. Как видите, для нормальной скорости есть отношение изменения положения за период, а здесь мы используем угол вместо расстояния.

Вторая формула угловой скорости может быть получена из соотношения линейной скорости и радиуса с использованием векторного произведения, которое равно:

v знак равно ω × r .

Мы можем переписать это выражение, чтобы получить уравнение угловой скорости:

ω = r × v / |r|² ,

где все эти переменные являются векторами , а |r| обозначает абсолютное значение радиуса. Фактически угловая скорость представляет собой псевдовектор, направление которого перпендикулярно плоскости вращательного движения.

Единицы измерения угловой скорости

Существует несколько единиц измерения угловой скорости, и те, которые используются в нашем калькуляторе угловой скорости, перечислены ниже:

рад/с или радиан в секунду – определение, вытекающее прямо из первой формулы угловой скорости. Он показывает, насколько велик поворот (или угол), на который тело движется за заданное время,
об/мин или оборотов в минуту – единица, наиболее часто встречающаяся в практическом применении. С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между 10 и 100 об/мин .
Гц или герц — те же единицы, которые используются для частоты, но редко используются в контексте угловой скорости. Это чем-то похоже на об/мин , говоря нам, сколько полных оборотов делается за заданное время.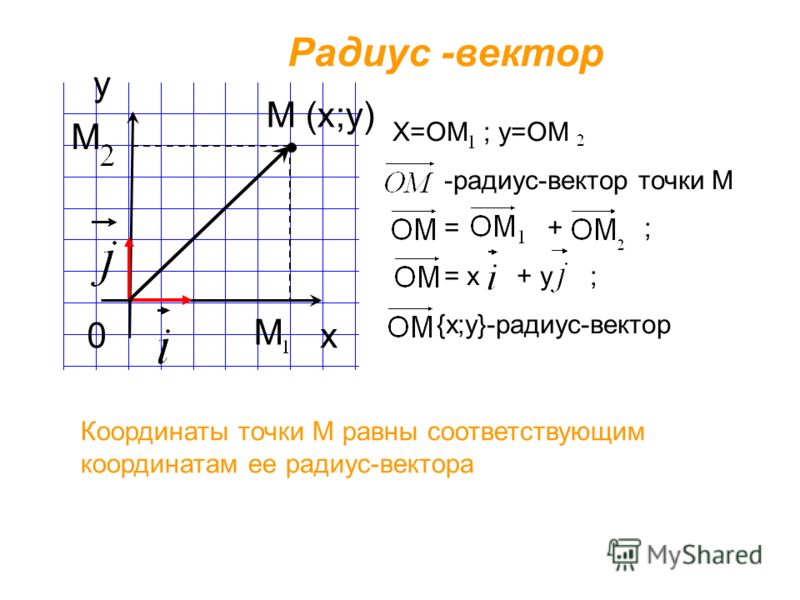 Разница в том, что раньше основной единицей времени была минута, а здесь – секунда.

Естественно, все эти единицы угловой скорости преобразуются между собой с использованием следующих соотношений:

1 RMP = 0,10472 рад/с = 0,01667 Гц ,

или наоборот:

1 Гц = 6,283 рад/с = 60 об/мин .

Угловая скорость в зависимости от угловой частоты

Посмотрите на определение угловой частоты:

ω = 2 * π * f ,

, где f — частота. Как мы видим, он обозначается той же буквой. Кроме того, единицей измерения угловой частоты является рад/с , точно такая же, как и для угловой скорости. Поэтому может возникнуть вопрос: «Чем отличается угловая скорость от угловой частоты?».

Ответ относительно прост. Связь между угловой частотой и угловой скоростью аналогична связи между скоростью и скоростью . Первый является величиной последнего, или, другими словами, угловая частота является скаляром, тогда как угловая скорость является (псевдо)вектором.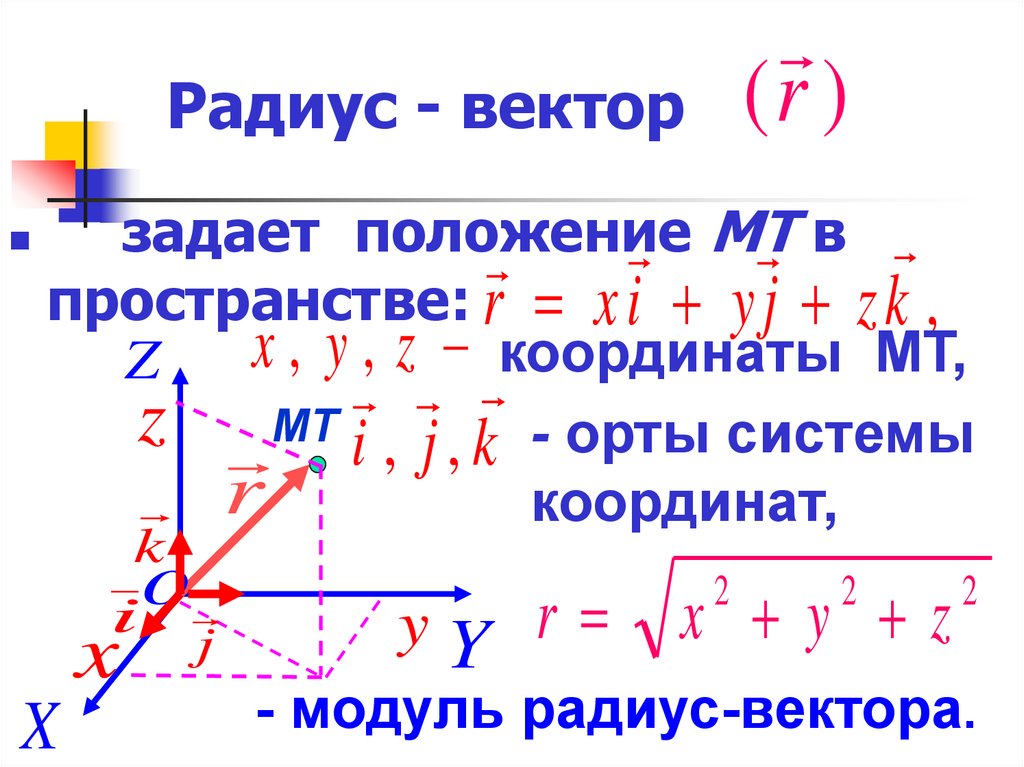

Угловая частота обычно используется, когда речь идет о гармоническом движении, примером которого является простой маятник. Как вы понимаете, движение не обязательно должно быть представлено стандартным вращением, а просто движением, которое периодически повторяет свое положение. Однако угловая скорость строго связана с движением вокруг некоторой точки. Поэтому можно сказать, что угловая частота является более общей величиной и может использоваться для описания широкого круга физических задач, тогда как угловая скорость включает только вращательное движение.

🙋 У нас есть специальный инструмент, который объясняет, как рассчитать угловую частоту. Обязательно проверьте и его!

Как найти угловую скорость Земли?

Как насчет того, чтобы воспользоваться нашим калькулятором угловой скорости? Оценим угловую скорость Земли! Во-первых, мы учитываем скорость вращения. Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за 23 ч 56 мин 4 с , что примерно составляет 23,934 ч . Полное вращение – угол 2π RAD , поэтому получающаяся угловая скорость составляет:

ω₁ = 2π Rad/23,934 H = 0,2625 RAD/H = 0,00007292 RAD/S ,

или 7.292 * 10⁻⁵ рад/с ,

или 7.292 * 10⁻⁵ Rad. /s (в экспоненциальном представлении).

Теперь, когда мы знаем угловую скорость вращения Земли, мы можем оценить ее линейную скорость на экваторе. Для этого нам нужен радиус Земли, который примерно равен 91 189 6 371 км 91 190 . Нам осталось только подставить значения во вторую формулу угловой скорости:

v₁ = r₁ * ω₁ = 6 371 км * 7,292 * 10⁻⁵ рад/с = 0,4646 км/с = 464,6 м/с .

Чтобы вычислить линейную скорость относительно центра Земли, все, что вам нужно сделать, это умножить этот результат на косинус широты вашего города. Кстати, вы когда-нибудь задумывались, почему ракеты обычно стартуют с космодромов, расположенных вблизи экватора, а не с полюсов? Ну почти 500 м/с разгон в начале составляет немалую долю его конечной скорости. Таким образом, перемещение точки старта как можно ближе к экватору уменьшает количество топлива, необходимого для разгона ракеты.

После этого можно еще раз спросить, как найти угловую скорость Земли, но на этот раз орбитальную. Все расчеты аналогичны, но мы должны изменить время с 23,943 ч на один год, что составляет примерно 365,25 дней. Изменение угла такое же, полный оборот.

ω₂ = 2π рад / 23,934 ч = 0,0000001991 рад/с = 1,991 * 10⁻⁷ рад/с ,

и линейная скорость Земли относительно Солнца (для среднего радиуса 1,496 * 10⁸ км ) равно:

v₂ = 1,496 * 10⁸ км * 1,991 * 10⁻⁷ рад/с = 29,785 км/с .

Мы движемся довольно быстро, не так ли?

Физические величины, зависящие от угловой скорости

Существует множество физических величин, связанных с угловой скоростью, некоторые из которых перечислены ниже:

Угловое ускорение – описывает, как угловая скорость изменяется со временем. Чем выше разность угловых скоростей, тем больше значение углового ускорения.
Кинетическая энергия вращения – мера энергии при круговом движении. Как и в случае с кинетической энергией, зависимость (угловой) скорости является квадратичной.
Центробежная сила – ее можно почувствовать в машине, когда она поворачивается. Чем быстрее вы проходите поворот или чем он круче, тем выше становится центробежная сила, что отчетливо ощущается.
Эффект Кориолиса – заставляет объекты вращаться, если они помещены на вращающееся тело (например, на Земле), вместо того, чтобы двигаться по прямой линии.
Система шкивов – это не физическая величина, точнее говоря, а интересное устройство, все дело в угловой скорости. Простейшая система состоит из двух шкивов, обычно с разными окружностями или радиусами. Они соединены ремнем, поэтому их линейные скорости идентичны , но так как они разного размера, их угловые скорости изменяются пропорционально . 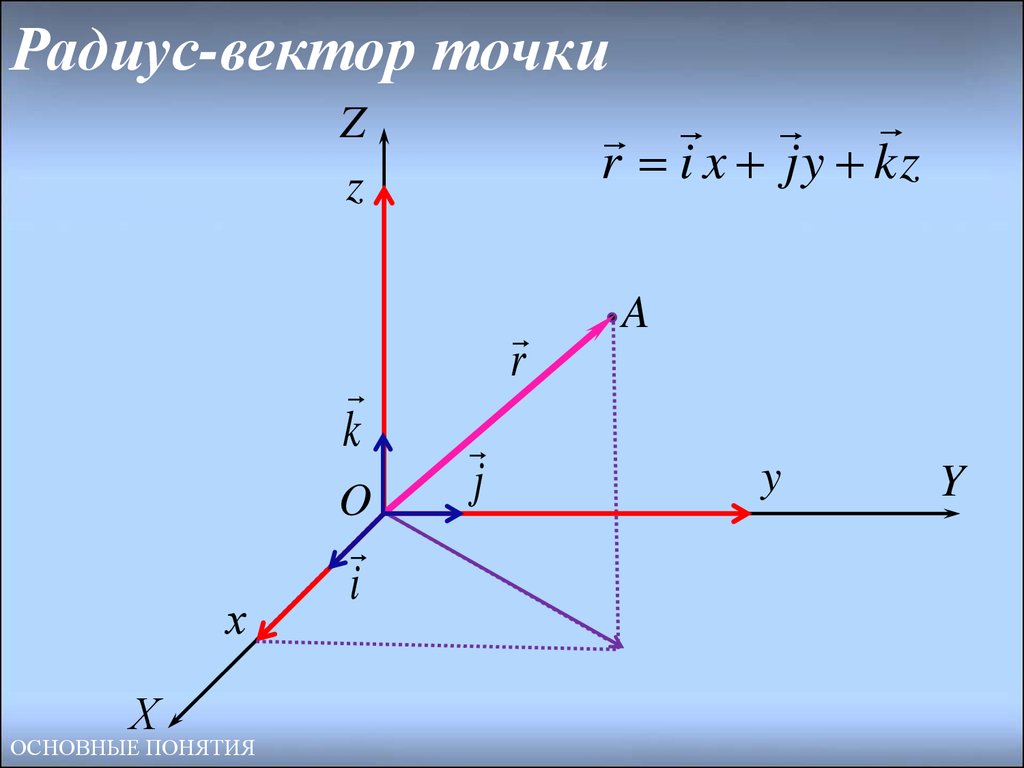Зная это и имея некоторый двигатель с четко определенной скоростью вращения, мы можем с хорошей точностью задать угловую скорость выходного элемента, просто регулируя его размер.

Сохранение углового момента

Есть несколько фундаментальных правил, которые говорят нам о величинах, сохраняющихся в изолированных системах. Наиболее известными являются закон сохранения энергии и закон сохранения импульса. Вместе с ними существует также закон сохранения момента импульса . Если мы представим два момента времени, правило можно записать так:

I₁ * ω₁ = I₂ * ω₂ ,

, где I₁ и I₂ — начальный и конечный моменты инерции соответственно, величины, описывающие распределение массы относительно центра тел.

Мы видим, что при увеличении момента инерции угловая скорость уменьшается, и наоборот . Итак, каковы последствия этого явления? Представим, что вы фигурист. Когда вы вращаетесь, вы обладаете некоторой угловой скоростью. Если ваши руки широко раскрыты, момент инерции масс относительно велик . Затем вы приближаете руки к остальной части тела. Как следствие, ваш момент инерции уменьшается на , поэтому из-за того, что общий угловой момент должен сохраняться, ваша угловая скорость увеличивается на – это означает, что вы будете вращаться быстрее! Это не магия, просто физика!

Если вам не нравится кататься на коньках, можно попробовать проверить правило на обычном вращающемся стуле. Просто помните, безопасность превыше всего! Убедитесь, что есть достаточно места для проведения этого эксперимента. После этого просто начните вращаться и посмотрите, как изменится ваша угловая скорость, когда вы двигаете руками вперед и назад. Кроме того, вы можете усилить эффект, используя гантели. В результате вы можете совместить и тренировки, и развлечения в одно целое!

Войцех Сас, кандидат наук

#1 Разность углов

Изменение угла (Δα)

Время (t)

Угловая скорость Радиус (ω)

#2 Радиальная скорость

Скорость )

Угловая скорость (ω)

Ознакомьтесь с 19 похожими калькуляторами вращательного и периодического движения 🌎

Угловое ускорениеУгловое смещениеУгловая частота… Еще 16

Объяснение урока: Момент силы относительно точки в 2D: векторы

В этом объяснителе мы научимся находить момент плоской системы сил, действующих на тело относительно точки как вектор.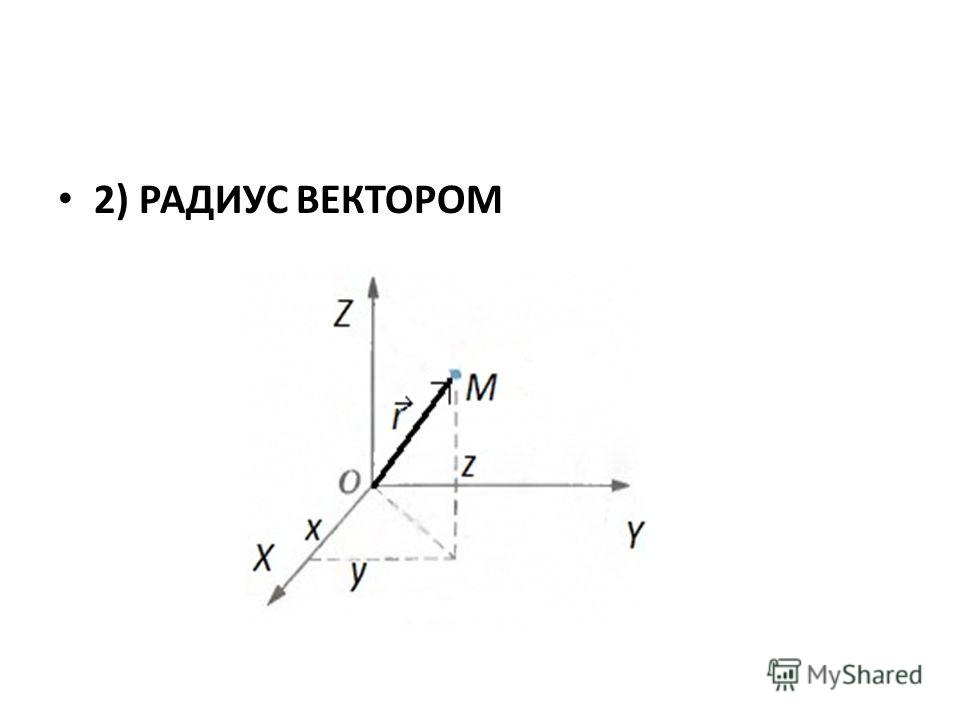

Мы знаем, что сила или система сил может оказывать вращательное действие на тело, которое описывается моментом сила или система сил относительно точки. Напомним, что при плоском движении момент 𝑀 силы ⃑𝐹 о точке определяется как скаляр, величина которого определяется выражением |𝑀|=‖‖⃑𝐹‖‖𝑑,⟂ где 𝑑⟂ – перпендикулярное расстояние между точкой и линией действия силы ⃑𝐹. Затем мы можем определить знак момента, рассмотрев, является ли эффект вращения идет по часовой стрелке или против часовой стрелки. По соглашению мы определяем момент с действием против часовой стрелки как положительный, что означает, что момент с эффектом вращения по часовой стрелке определяется как отрицательный.

Хотя это определение хорошо подходит для плоского движения, оно недостаточно, когда мы рассматриваем движение с трехмерным пространство, потому что понятие записи по часовой стрелке или против часовой стрелки здесь не работает. Следовательно, мы хотели бы расширить определение момента для трехмерного движения из скалярного момента, определенного для плоского движения. Чтобы сохранить понятия ориентации вращения, мы определяем момент как вектор следующим образом.

Определение: момент силы

Момент силы ⃑𝐹, действующей на тело относительно точки 𝑂, определяется выражением 𝑀=⃑𝑟×⃑𝐹, где 𝑟 – вектор положения 𝐴, точки приложения силы ⃑𝐹.

В этом определении мы видим, что система координат выбрана так, что ее начало совпадает с точкой около что мы принимаем момент. Если бы мы хотели вычислить момент силы ⃑𝐹 относительно точки 𝑃 это не источник, то мы просто заменим ⃑𝑟 на 𝑃𝐴: 𝑀=𝑃𝐴×⃑𝐹.

Буква 𝑃 была добавлена в качестве нижнего индекса к 𝑀, чтобы указать, что момент взят около точки 𝑃.

В нашем первом примере мы будем использовать эту формулу для вычисления векторного момента силы на плоскости относительно точки.

Пример 1. Нахождение момента вектора силы относительно точки

Если на точку действует сила ⃑𝐹=−5⃑𝑖+𝑚⃑𝑗 𝐴(7,3), определить момент ⃑𝐹 относительно точки 𝐵(7,−2).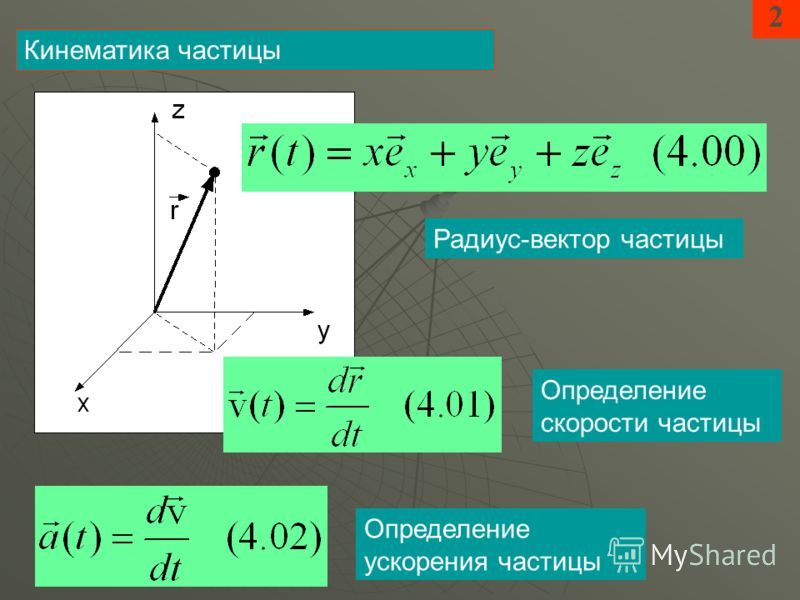

Ответ

В этом примере нам нужно найти момент плоской силы относительно точки. Напомним, что векторный момент силы ⃑𝐹, действующий в точке 𝐴 относительно точки 𝐵, определяется выражением 𝑀=𝐵𝐴×⃑𝐹.

Начнем с нахождения вектора 𝐵𝐴: 𝐵𝐴=(7,3,0)−(7,−2,0)=(0,5,0).

Мы можем написать ⃑𝐹 как ⃑𝐹=−5⃑𝑖+𝑚⃑𝑗+0⃑𝑘=(−5,𝑚,0).

Взяв векторное произведение, 𝐵𝐴×⃑𝐹=||||⃑𝑖⃑𝑗⃑𝑘050−5𝑚0||||=(5×0−0×𝑚)⃑𝑖−(0×0−0×(−5))⃑𝑗+(0×𝑚−5×( −5))⃑𝑘=25⃑𝑘.

Заметим, что неизвестная константа 𝑚 в силе ⃑𝐹 сокращалась, когда мы вычислили перекрестное произведение. Следовательно, момент ⃑𝐹 относительно точки 𝐵 равен 25⃑𝑘.

В предыдущем примере мы вычислили векторный момент плоской силы относительно точки по формуле 𝑀=⃑𝑟×⃑𝐹.

Мы видим, что результирующий вектор векторного произведения содержит только компонент ⃑𝑘, а компоненты ⃑𝑖 и ⃑𝑗 исчезли. Это не удивительно, если мы рассмотрим геометрическое свойство перекрестного произведения.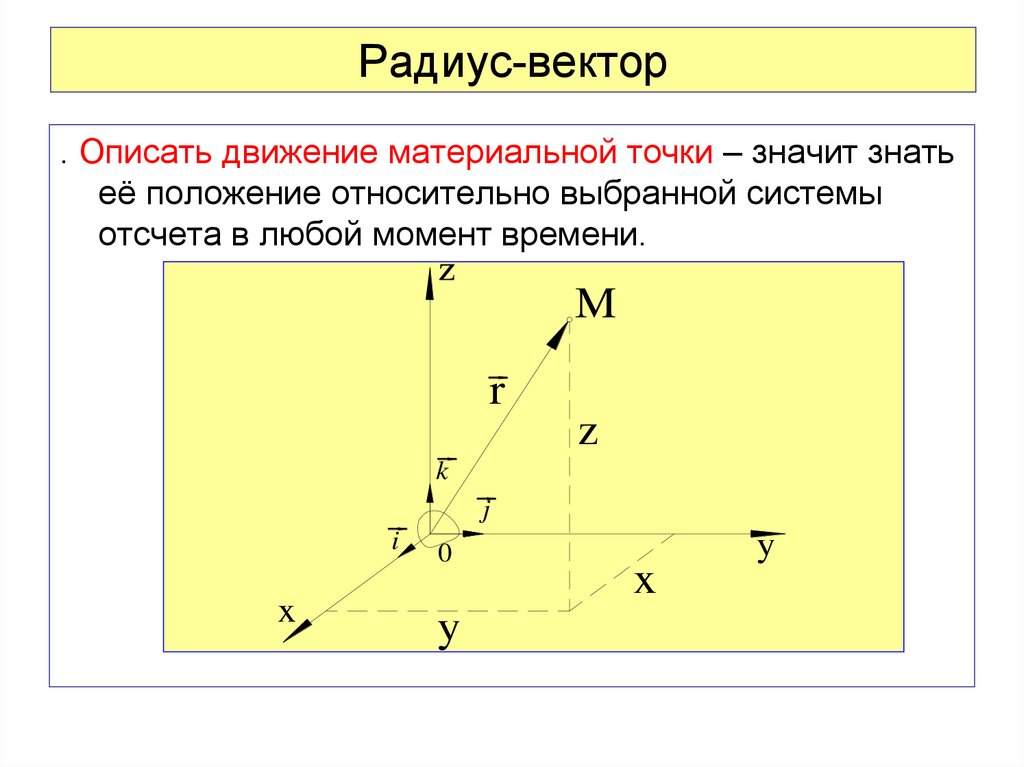 Напомним, что вектор, полученный в результате перекрестного произведения двух векторов должны быть перпендикулярны двум векторам. Поскольку 𝑀 определяется как крест произведение векторов ⃑𝑟 и ⃑𝐹, оно должно быть перпендикулярно обоим векторы. Мы знаем, что ⃑𝑟 и ⃑𝐹 оба лежат на 𝑥𝑦-плоскость, поэтому 𝑀 должна быть перпендикулярна 𝑥𝑦-плоскости. Вектор, перпендикулярный плоскости 𝑥𝑦, должен быть параллелен единичному вектору ⃑𝑘 в трехмерной системе координат. Это означает ⃑𝑟×⃑𝐹=𝑐⃑𝑘 для некоторого скаляра 𝑐. Поскольку это всегда так, мы можем упростить вычисление этого перекрестного произведения на используя двумерное перекрестное произведение.

Определение: двумерное перекрестное произведение

Для двух двумерных векторов (𝑎,𝑏) и (𝑐,𝑑), двумерное перекрестное произведение определяется как (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Как мы видим, двумерное перекрестное произведение вычисляется быстрее. Мы будем использовать эту формулу для вычисления перекрестного произведения двухмерных векторы для оставшейся части этого объяснения.

Далее обсудим величину момента, которая равна величине векторного произведения: ‖‖𝑀‖‖=‖‖⃑𝑟×⃑𝐹‖‖.

Напомним, что перекрестное произведение двух векторов дает площадь параллелограмма, две смежные стороны которого образованы два вектора. Проследим это, используя следующую схему.

На приведенной выше диаграмме площадь выделенной области представляет собой величину векторного произведения ⃑𝑟×⃑𝐹 и, следовательно, величину момента 𝑀. Мы также можем найти площадь этого параллелограмма геометрически, используя геометрическую формулу длина основанияперпендикулярвысота×.

На схеме основание этого параллелограмма образовано вектором ⃑𝐹, а высота равна перпендикулярное расстояние от начала координат до линии действия ⃑𝐹, которое обозначается 𝑑⟂.

Это приводит к следующей формуле для величины векторного момента для двумерной силы относительно точки.

Свойство: Величины векторного момента силы

Величина векторного момента плоской силы ⃑𝐹 относительно точки определяется выражением ‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝑑,⟂ где 𝑑⟂ — перпендикулярное расстояние между точкой и линией действия силы ⃑𝐹.

Мы видим, что приведенная выше величина векторного момента равна величине скалярного момента. Следовательно, величина векторного момента согласуется с величиной скалярного момента для плоского движения.

Когда мы переформулируем это уравнение, мы получим полезную формулу для вычисления перпендикулярного расстояния между точкой и линией действия силы.

Формула: Расстояние по перпендикуляру между точкой и линией действия

Пусть 𝑀 векторный момент силы или системы сил на плоскости относительно точки. Тогда перпендикулярное расстояние между точкой и линией действия силы определяется выражением 𝑑=‖‖𝑀‖‖‖‖⃑𝐹‖‖.⟂

В следующем примере мы вычислим момент плоской силы относительно точки, а затем воспользуемся этой формулой, чтобы найти перпендикулярное расстояние между точкой и линией действия силы.

Пример 2. Нахождение вектора момента силы, действующей в точке, и перпендикуляра между моментом и линией Действие Силы

Учитывая, что сила ⃑𝐹=4⃑𝑖−3⃑𝑗 действует через точки 𝐴(3,6), определить момент 𝑀 относительно происхождение 𝑂 силы ⃑𝐹. Кроме того, вычислить перпендикуляр расстояние 𝐿 между 𝑂 и линией действия силы.

Ответ

В этом примере сначала нужно найти момент 𝑀 относительно 𝑂 силы ⃑𝐹, а затем рассчитайте перпендикулярное расстояние между 𝑂 и линией действие ⃑𝐹. Начнем с поиска момента. Напомним, что векторный момент силы ⃑𝐹, действующий в точке 𝐴 относительно начала координат 𝑂, определяется выражением 𝑀=𝑂𝐴×⃑𝐹.

Нам даны координаты 𝐴, значит, 𝑂𝐴 — это позиция вектор, заданный 𝑂𝐴=(3,6).

Мы можем записать ⃑𝐹 в компонентной форме как ⃑𝐹=4⃑𝑖−3⃑𝑗=(4,−3).

Теперь мы готовы вычислить перекрестное произведение 𝑂𝐴×⃑𝐹. Напомним, что векторное произведение двумерных векторов определяется формулой (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Применяя эту формулу, получаем 𝑂𝐴×⃑𝐹=(3,6)×(4,−3)=(3×(−3)−6×4)⃑𝑘=−33⃑𝑘.

Следовательно, момент ⃑𝐹 относительно начала координат равен −33⃑𝑘.

Далее найдем перпендикулярное расстояние между началом координат и линией действия для ⃑𝐹. Напомним, что модуль векторного момента плоской силы ⃑𝐹 относительно точки определяется выражением ‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝐿, где 𝐿 – перпендикулярное расстояние между точкой и линией действия силы ⃑𝐹. Мы можем изменить это уравнение, чтобы написать 𝐿=‖‖𝑀‖‖‖‖⃑𝐹‖‖.

Поскольку мы знаем, что 𝑀=−33⃑𝑘, мы можем получить ‖‖𝑀‖‖=33. Найдем ‖‖⃑𝐹‖‖: ‖‖⃑𝐹‖‖=4+(−3)=√25=5.

Подставив эти значения в формулу для 𝐿, получим 𝐿=335=6,6.

Следовательно, 𝑀=−33⃑𝑘,𝐿=6.6.lengthunits

Мы отметили, что момент силы относительно точки приводит к вектору, параллельному единичному вектору ⃑𝑘. Другими словами, существует некоторый скаляр 𝑐 такой, что 𝑀=𝑐⃑𝑘.

Кроме того, мы заметили, что величина момента равна величине скалярного момента |𝑀|. Это означает, что либо 𝑐=𝑀, либо 𝑐=−𝑀. Чтобы определить, какой из них верен, нам нужно проверить, соответствует ли знак 𝑐 знаку скалярного момента. 𝑀.

Свойства векторного произведения позволяют нам сначала заключить, что 𝑀 является вектором, перпендикулярным плоскость, определяемая ⃑𝑟 и ⃑𝐹. Направление 𝑀 определяется по правилу правой руки. Это правило иногда объясняют ссылкой на вращение винта: направление вектора ⃑𝐴×⃑𝐵 соответствует направление движения (вверх или вниз) крышки бутылки или гайки, которое можно было бы повернуть в том же направлении вращения, что и при переходе от от ⃑𝐴 до ⃑𝐵, как показано на следующей диаграмме.

Помните, что у нас есть 𝑀=⃑𝑟×⃑𝐹=𝑐⃑𝑘.

Если 𝑐>0, вектор момента будет выходить из плоскости (вверх), что соответствует направлению против часовой стрелки вращение в соответствии с рисунком выше. Если 𝑐0, то вектор момента ушел бы в плоскость (вниз), что указывает на вращение по часовой стрелке. Напомним, что для скалярного момента 𝑀 ориентация против часовой стрелки соответствует к положительному знаку, а вращение по часовой стрелке приводит к отрицательному знаку. Это говорит нам о том, что знак скалярного момента 𝑀 согласуется со знаком скаляра 𝑐. Таким образом, мы показали, что 𝑐=𝑀.

Свойство: двумерный векторный момент силы

Пусть 𝑀 и 𝑀 будут скалярным и векторным моментами силы или системой сил, на плоскости около точки. Затем, 𝑀=𝑀⃑𝑘.

Это свойство твердо устанавливает, почему этот векторный момент является разумным расширением скалярного момента для плоской силы. Кроме того, векторный момент можно обобщить, чтобы представить момент общей трехмерной силы относительно точки, поскольку он получен используя перекрестное произведение.

Из этого свойства можно сделать несколько полезных выводов. Во-первых, мы знаем, что скалярный момент не зависит от положение точки, на которую действует сила, если точка лежит на одной линии действия силы. Это потому что скалярный момент получается только с использованием величины силы ‖‖⃑𝐹‖‖ и перпендикулярное расстояние 𝑑⟂. Это означает, что векторный момент также не зависит от местоположения точки, на которую действует сила. Мы сможем понять это лучше, если сравним величину момента, когда мы переместите эту точку вдоль линии действия.

Мы видим, что площади обоих параллелограммов равны, так как длина основания ‖‖⃑𝐹‖‖ и высота 𝑑⟂ одинаковы для обоих параллелограммы. Это говорит нам о том, что величина момента для этих двух систем одинакова. Кроме того, мы можем видеть что обе системы будут вызывать вращение по часовой стрелке вокруг начала координат, а это означает, что знак момента будет одинаковым для обе системы. Следовательно, векторный момент одинаков для этих двух систем. Это приводит к следующему полезному свойству.

Свойство: Векторный момент силы

Векторный момент 𝑀 силы относительно точки не зависит от точки, в которой сила действует до тех пор, пока точка лежит на одной линии действия.

В следующем примере мы найдем векторный момент плоской силы относительно точки, когда начальная точка 𝐴 не дается.

Пример 3. Определение момента вектора силы, действующего в точке

Конец 𝐴 из 𝐴𝐵 находится в точке (−6,7) и 𝐴𝐵 имеет середину 𝐷(−7,1). Если линия действия силы ⃑𝐹=−2⃑𝑖−6⃑𝑗 делит пополам 𝐴𝐵, определить момент ⃑𝐹 относительно точки 𝐵.

Ответ

В этом примере нам нужно найти момент плоской силы относительно точки. Напомним, что векторный момент силы ⃑𝐹, действующий в точке 𝑃 относительно точки 𝑂, определяется выражением 𝑀=𝑂𝑃×⃑𝐹.

Хотя нам не известна точка, в которой действует сила, нам известно, что линия действия силы ⃑𝐹 делит 𝐴𝐵 пополам. Это означает, что линия действия проходит через середину 𝐷 отрезка 𝐴𝐵. Напомним, что векторный момент 𝑀 силы, приложенной к точке, не зависит от начальной точки, если точка лежит в той же линии действия. Следовательно, мы можем вычислить момент, считая, что начальная точка находится в точке 𝐷(−7,1). Это означает, что момент ⃑𝐹 о 𝐵 дается 𝑀=𝐵𝐷×⃑𝐹.

Начнем с поиска вектора 𝐵𝐷. Так как 𝐷 является серединой 𝐴, мы знаем, что ‖‖𝐴𝐷‖‖=‖‖𝐵𝐷‖‖.

Также эти векторы имеют противоположное направление, а значит 𝐵𝐷=−𝐴𝐷.

Мы можем найти 𝐴𝐷, используя координаты точек 𝐴 и 𝐷: 𝐴𝐷=(−7,1)−(−6,7)=(−1,−6).

Следовательно, 𝐵𝐷=-(-1,-6)=(1,6).

Теперь мы готовы вычислить векторное произведение 𝐵𝐷×⃑𝐹. Напомним, что векторное произведение двумерных векторов определяется формулой (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Применяя эту формулу, получаем 𝐵𝐷×⃑𝐹=(1,6)×(−2,−6)=(1×(−6)−6×(−2))⃑𝑘=6⃑𝑘.

Следовательно, момент ⃑𝐹 относительно точки 𝐵 равен 6⃑𝑘.

В следующем примере мы найдем момент системы плоских сил, действующих в одной точке относительно другой точки, сначала найти равнодействующую сил.

Пример 4: Расчет момента трех сил, действующих на одну точку относительно данной точки, и расстояния между точками

Учитывая, что ⃑𝐹=−2⃑𝑖+2⃑𝑗, ⃑𝐹=−3⃑𝑖−⃑𝑗, и ⃑𝐹=⃑𝑖−4⃑𝑗 действуют в точке 𝐴(2,3), определить момент ⃑𝑚 равнодействующей сил относительно точки 𝐵(−2,−1) и вычислить длину перпендикулярной линии 𝐿 соединение точки 𝐵 с результирующей линией действия.

Ответ

В этом примере нам дана система плоских сил, действующих в одной и той же точке. Начнем с нахождения равнодействующей силы. Напомним, что равнодействующая системы сил, действующих в одной точке, равна сумме всех векторов сил в система. Следовательно, результирующая ⃑𝐹 определяется выражением ⃑𝐹 = ⃑𝐹+⃑𝐹+⃑𝐹 =  -2⃑𝑖+2⃑𝑗+ -3⃑𝑖 – ⃑𝑗+⃑𝑖 -4⃑𝑗 =  -2⃑𝑖 -3⃑𝑖+⃑𝑖+2⃑𝑗 -4⃑𝑗 = −4⃑𝑖 -3⃑𝑗. 

Это говорит нам о том, что равнодействующая сил равна ⃑𝐹=−4⃑𝑖−3⃑𝑗. Далее найдем момент ⃑𝑚 равнодействующей около точки 𝐵(−2,−1). Напомним, что векторный момент силы ⃑𝐹, действующей в точке 𝐴 о точке 𝐵 дается 𝑀=𝐵𝐴×⃑𝐹.

Используя координаты 𝐴 и 𝐵, мы можем найти 𝐵𝐴=(2,3)−(−2,−1)=(4,4).

Теперь мы готовы вычислить перекрестное произведение 𝐵𝐴×⃑𝐹. Напомним, что перекрестное произведение двумерных векторов определяется выражением (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Это приводит к 𝐵𝐴×⃑𝐹=(4,4)×(−4,−3)=(4×(−3)−4×(−4))⃑𝑘=4⃑𝑘.

Следовательно, момент равнодействующей сил относительно точки 𝐵 равен 4⃑𝑘.

Далее найдем длину перпендикуляра 𝐿, соединяющего точку 𝐵 с результирующая линия действия. Эта длина 𝐿 также известна как перпендикулярное расстояние между точкой 𝐵 и результирующая линия действия. Чтобы вычислить эту длину, вспомним, что величина векторный момент плоской силы ⃑𝐹 относительно точки определяется выражением ‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝐿, где 𝐿 — перпендикулярное расстояние между точкой и линией действия для ⃑𝐹. Мы можем изменить это уравнение, чтобы написать 𝐿=‖‖𝑀‖‖‖‖⃑𝐹‖‖.

Поскольку мы знаем, что 𝑀=4⃑𝑘, мы можем получить ‖‖𝑀‖‖=4. Найдем ‖‖⃑𝐹‖‖: ‖‖⃑𝐹‖‖=(−4)+(−3)=√25=5.

Подставляя эти значения в формулу для 𝐿, получаем 𝐿=45=0,8.

Следовательно, 𝑀=4⃑𝑘,𝐿=0,8.lengthunit

В предыдущем примере мы нашли момент системы плоских сил, действующих в той же точке относительно другой точки. Мы можем отметить что процесс нахождения момента для системы сил такой же, как и для одной силы, если силы действуют в тот же пункт.

Рассмотрим теперь задачу нахождения момента системы плоских сил, когда силы не действуют в одной и той же точке.

Определение: Момент системы плоских сил

Рассмотрим систему сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹, действующий в 𝐴, 𝐴, …, и 𝐴 соответственно. Чтобы найти момент этой системы сил относительно точки 𝑂, найдем нужно найти моменты 𝑀, 𝑀, …, и 𝑀 сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹 о пункте 𝑂. Тогда, момент система 𝑀 относительно точки 𝑂 задается формулой 𝑀=𝑀+𝑀+⋯+𝑀.

Это определение говорит нам, что момент системы сил равен сумме отдельных моментов каждой силы в система примерно в том же месте.

В нашем последнем примере мы найдем неизвестные константы сил в системе, действующей в разных точках, когда нам задано момент системы сил относительно двух различных точек.

Пример 5. Нахождение неизвестных компонентов двух сил по сумме их моментов относительно двух точек ⃑𝐹 — две силы, действующие в точках 𝐴(3,1) и 𝐵(−1,−1) соответственно. Сумма моментов относительно точки начала равна нулю.

Ответ

В этом примере нам нужно найти неизвестные константы 𝑚 и 𝑛 в силах ⃑𝐹 и ⃑𝐹, когда нам известно, что сумма моменты двух сил относительно начала координат, а также относительно точки 𝐶 равны нулю. Мы можем найти неизвестные константы путем идентификации пары одновременных уравнений с участием 𝑚 и 𝑛. Мы получим первое уравнение, вычислив сумму моментов ⃑𝐹 и ⃑𝐹 о происхождении и приравнивании их к нулю.

Напомним, что векторный момент силы ⃑𝐹, действующей в точке 𝑃 относительно точка 𝑄 задается 𝑀=⃑𝑟×⃑𝐹, где ⃑𝑟 — вектор из точки 𝑄 в точку 𝑃. Позволь нам сначала найдите момент ⃑𝐹 о происхождении. С ⃑𝐹 действует в точке 𝐴, мы можем написать ⃑𝑟=𝑂𝐴=(3,1).

Мы можем записать ⃑𝐹 в компонентной форме как ⃑𝐹=𝑚⃑𝑖+⃑𝑗=(𝑚,1).

Теперь мы готовы вычислить перекрестное произведение 𝑂𝐴×⃑𝐹. Напомним, что перекрестное произведение двумерных векторов определяется выражением (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Это приводит к ⃑𝑟×⃑𝐹=(3,1)×(𝑚,1)=(3×1−1×𝑚)⃑𝑘=(3−𝑚)⃑𝑘.

Далее найдем момент ⃑𝐹 относительно начала координат . С ⃑𝐹 действует в точке 𝐵, мы можем написать ⃑𝑟=𝑂𝐵=(−1,−1).

Мы можем записать ⃑𝐹 в компонентной форме как ⃑𝐹=𝑛⃑𝑖−5⃑𝑗=(𝑛,−5).

Взяв векторное произведение, ⃑𝑟×⃑𝐹=(−1,−1)×(𝑛,−5)=(−1×(−5)−(−1)×𝑛)⃑𝑘=(5+𝑛)⃑𝑘.

Тогда сумма этих двух моментов относительно начала координат равна (3−𝑚)⃑𝑘+(5+𝑛)⃑𝑘=(8−𝑚+𝑛)⃑𝑘.

Так как нам дано, что сумма этих моментов должна равняться нулю, то получаем

8−𝑚+𝑛=0.

(1)

Это дает нам одно уравнение, включающее 𝑚 и 𝑛. Мы можем повторить это вычисление на данный момент о точке 𝐶, чтобы получить другое уравнение, но мы также можем найти второе уравнение, используя свойства моменты. Найдем момент ⃑𝐹 относительно точки 𝐶: ⃑𝑟=𝐶𝐴=(3,1)−(1,2)=(2,−1).

Взяв векторное произведение, ⃑𝑟×⃑𝐹=(2,−1)×(𝑚,1)=(2×1−(−1)×𝑚)⃑𝑘=(2+𝑚)⃑𝑘.

Далее, на момент ⃑𝐹 о 𝐶, ⃑𝑟=𝐶𝐵=(−1,−1)−(1,2)=(−2,−3).

Взяв векторное произведение, ⃑𝑟×⃑𝐹=(−2,−3)×(𝑛,−5)=(−2×(−5)−(−3)×𝑛)⃑𝑘=(10+3𝑛)⃑𝑘.

Суммируя эти два моменты про 𝐶, (2+𝑚)⃑𝑘+(10+3𝑛)⃑𝑘=(12+𝑚+3𝑛)⃑𝑘.

Так как нам дано, что сумма этих моментов должна равняться нулю, то получаем

12+𝑚+3𝑛=0.

(2)

Теперь, когда мы получили два уравнения для 𝑚 и 𝑛, запишем уравнения (1) и (2) здесь: 8−𝑚+𝑛=0,12+𝑚+3𝑛=0.

Мы можем сложить два уравнения, чтобы исключить 𝑚. Это ведет к 20+4𝑛=0.

Преобразование этого уравнения таким образом, что 𝑛 является субъектом, дает нам 𝑛=−5. Мы можем заменить это значение в уравнение (1), чтобы записать 8−𝑚−5=0.

Преобразование этого уравнения таким образом, что 𝑚 является субъектом, приводит к 𝑚=3. Следовательно, у нас есть 𝑚=3,𝑛=−5.

Давайте закончим повторением нескольких важных понятий из этого объяснения.

Ключевые точки

Вектор момента силы ⃑𝐹, действующей в точке 𝐴 относительно точки 𝑂 дается 𝑀=⃑𝑟×⃑𝐹, где ⃑𝑟 — вектор из точки 𝑂 в точку 𝐴.
Величина векторного момента плоской силы ⃑𝐹 относительно точки определяется выражением ‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝑑,⟂ где 𝑑⟂ — перпендикулярное расстояние между точкой и линией действия силы ⃑𝐹.
Векторный момент 𝑀 силы относительно точки не зависит от начальной точки, пока точка лежит на одной линии действия.
Пусть 𝑀 и 𝑀 — скалярный и векторный моменты силы, или система сил на плоскости относительно точки. Затем, 𝑀=𝑀⃑𝑘.
Вычисление перекрестного произведения ⃑𝑟×⃑𝐹 для вычисления момент 𝑀 плоской силы относительно точки можно упростить, используя двумерное перекрестное произведение, которое определяется формулой (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.
Рассмотрим систему сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹 действующие в 𝐴, 𝐴, … и 𝐴 соответственно. Чтобы найти момент этой системы сил относительно точки 𝑂, нужно найти моменты 𝑀, 𝑀, … и 𝑀 сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹 о пункте 𝑂. Тогда, момент система 𝑀 относительно точки 𝑂 задается формулой 𝑀=𝑀+𝑀+⋯+𝑀.

6.1 Угол поворота и угловая скорость

Цели обученияУгол вращенияУгловая скоростьРешение задач, связанных с углом вращения и угловой скоростьюПрактические задачиПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее: своему линейному аналогу

Опишите угловую скорость и свяжите ее с ее линейным эквивалентом
Решение задач на угол поворота и угловую скорость

Основные термины раздела
угол поворота	угловая скорость	длина дуги
круговое движение	радиус кривизны	вращательное движение
вращение	тангенциальная скорость

Угол поворота

Что именно мы подразумеваем под круговым движением или вращением ? Вращательное движение – это круговое движение объекта вокруг оси вращения. Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, мчащийся по круговой кривой, игрушку, прикрепленную к веревке, которая качается по кругу вокруг вашей головы, или круговое движение. 0242 петля-петля на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, Земля, вращающаяся вокруг своей оси, колесо, вращающееся вокруг своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступление на Олимпиаде. Иногда объекты будут вращаться во время кругового движения, например Земля, вращающаяся вокруг своей оси, вращаясь вокруг Солнца, но мы сосредоточимся на этих двух движениях отдельно.

При решении задач, связанных с вращательным движением, мы используем переменные, аналогичные линейным переменным (расстояние, скорость, ускорение и сила), но учитывающие кривизну или вращение движения. Здесь мы определяем угол поворота, который является угловым эквивалентом расстояния; и угловая скорость, которая является угловой эквивалентностью линейной скорости.

Когда объекты вращаются вокруг какой-либо оси — например, когда диск на рис. 6.2 вращается вокруг своего центра — каждая точка объекта движется по круговой траектории.

Рис. 6.2. Все точки на компакт-диске движутся по круговым траекториям. Ямки (точки) вдоль линии от центра к краю перемещаются на один и тот же угол ΔθΔθ за время ΔtΔt.

Длина дуги , , это расстояние, пройденное по круговой траектории. Радиус кривизны, r , является радиусом кругового пути. Оба показаны на рис. 6.3.

Рис. 6.3 Радиус ( r ) окружности повернут на угол ΔθΔθ. Длина дуги, ΔsΔs, представляет собой расстояние, пройденное по окружности.

Рассмотрим линию от центра компакт-диска до его края. В заданное время каждая яма (используемая для записи информации) на этой линии перемещается на один и тот же угол. Угол поворота представляет собой величину поворота и является угловым аналогом расстояния. Угол поворота ΔθΔθ — это длина дуги, деленная на радиус кривизны.

Δθ=ΔсрΔθ=Δср

Угол поворота часто измеряется в радианах. (Радианы на самом деле безразмерны, потому что радиан определяется как отношение двух расстояний, радиуса и длины дуги.) Оборот — это один полный оборот, когда каждая точка на окружности возвращается в исходное положение. Один оборот покрывает 2π2π радиан (или 360 градусов) и, следовательно, имеет угол поворота 2π2π радиан и длину дуги, равную длине окружности. Мы можем преобразовать радианы, обороты и градусы, используя соотношение

1 оборот = 2π2πрад = 360°. См. Таблицу 6.1 для преобразования градусов в радианы для некоторых распространенных углов.

6,12π рад=360°1 рад=360°2π≈57,3°2π рад=360°1 рад=360°2π≈57,3°

Градусы	Радианные меры
30∘30∘	π6π6
60∘60∘	π3π3
90∘90∘	π2π2
120∘120∘	2π32π3
135∘135∘	3π43π4
180∘180∘	ππ

Таблица 6. 1 Обычно используемые углы в градусах и радианах

Угловая скорость

Как быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Сначала рассмотрим угловую скорость (ω)(ω) — скорость изменения угла поворота. В форме уравнения угловая скорость равна

6.2ω=ΔθΔt,ω=ΔθΔt,

, что означает, что угловой поворот (Δθ)(Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота за заданное время, он имеет большую угловую скорость. Единицами угловой скорости являются радианы в секунду (рад/с).

Теперь давайте рассмотрим направление угловой скорости, а значит мы теперь должны называть его угловой скоростью. Направление угловой скорости вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость направлена от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.

Угловая скорость (ω) является угловой версией линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта, находящегося во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим ямку на вращающемся компакт-диске. Эта яма движется по дуге (Δs)(Δs) за короткое время (Δt)(Δt), поэтому ее тангенциальная скорость равна

6.3 v=ΔsΔt.v=ΔsΔt.

Из определения угла поворота Δθ=ΔsrΔθ=Δsr видно, что Δs=rΔθΔs=rΔθ. Подставляя это в выражение для v дает

v=rΔθΔt=rω.v=rΔθΔt=rω.

Уравнение v=rωv=rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем краю компакт-диска (с большими r ), чем для точки ближе к центру компакт-диска (с меньшими r ). Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. рисунок 6.4.

Рисунок 6.4 Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ), но точка 2 перемещается по большей дуге (Δs2Δs2), поскольку она находится дальше от центра вращения.

Теперь рассмотрим другой пример: шина движущегося автомобиля (см. рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое против , потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет производить большую линейную (тангенциальную) скорость в, на машину. Это связано с тем, что больший радиус означает, что более длинная дуга должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.

Рис. 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят на домкрат и колеса крутились, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад относительно оси с тангенциальной скоростью v=rωv=rω, где r – радиус шины. Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.

Однако бывают случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда колеса автомобиля крутятся на льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля по льду длина дуги, по которой перемещаются протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или вращение педалей на велотренажере; вы буквально никуда не денетесь.

Советы по достижению успеха

Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны указать величину и направление. Направление угловой скорости находится вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.

Рис. 6.6 Когда муха на краю старой виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена по касательной к кругу. В этом случае направление угловой скорости находится на странице.

Watch Physics

Взаимосвязь между угловой скоростью и скоростью

В этом видео рассматривается определение и единицы измерения угловой скорости, а также их связь с линейной скоростью. Он также показывает, как конвертировать между оборотами и радианами.

Проверка захвата
Для объекта, движущегося по круговой траектории с постоянной скоростью, изменится ли линейная скорость объекта при увеличении радиуса траектории?
Да, потому что тангенциальная скорость не зависит от радиуса.
Да, потому что тангенциальная скорость зависит от радиуса.
Нет, так как тангенциальная скорость не зависит от радиуса.
Нет, так как тангенциальная скорость зависит от радиуса.
Решение задач на угол поворота и угловую скорость
Snap Lab
Измерение угловой скорости
В этом упражнении вы создадите и измерите равномерное круговое движение, а затем сопоставите его с круговыми движениями с разными радиусами.
Материалы
Одна струна (длиной 1 м)
Один предмет (резиновая пробка с двумя отверстиями) для привязки к концу
Один таймер
Процедура
Привяжите объект к концу нити.
Раскачайте предмет по горизонтальному кругу над головой (раскачивание запястьем). Важно, чтобы круг был горизонтальным!
Поддерживайте постоянную скорость объекта при его раскачивании.
Таким образом измерьте угловую скорость объекта. Измерьте время в секундах, за которое объект совершает 10 оборотов. Разделите это время на 10, чтобы получить угловую скорость в оборотах в секунду, которую вы можете преобразовать в радианы в секунду.
Какова приблизительная линейная скорость объекта?
Поднимите руку вверх по веревке так, чтобы длина веревки составила 90 см. Повторите шаги 2–5.
Переместите руку вверх по веревке так, чтобы ее длина составила 80 см. Повторите шаги 2–5.
Переместите руку вверх по веревке так, чтобы ее длина составила 70 см. Повторите шаги 2–5.
Переместите руку вверх по веревке так, чтобы ее длина составила 60 см. Повторите шаги 2–5
Переместите руку вверх по веревке так, чтобы ее длина составила 50 см. Повторите шаги 2–5
Постройте графики зависимости угловой скорости от радиуса (т.е. длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.
Проверка захвата
Если вы медленно качаете объект, он может вращаться со скоростью менее одного оборота в секунду. Каковы были бы обороты в секунду для объекта, который делает один оборот за пять секунд? Какова будет его угловая скорость в радианах в секунду?
Объект будет вращаться со скоростью 15 об/с. Угловая скорость объекта будет 2π5 рад/с.
Объект будет вращаться со скоростью 15 об/с. Угловая скорость объекта будет π5 рад/с.
Объект будет вращаться со скоростью 5 об/с. Угловая скорость объекта будет 10πрад/с.
Объект будет вращаться со скоростью 5 об/с. Угловая скорость объекта будет 5πрад/с.
Теперь, когда у нас есть понимание концепций угла поворота и угловой скорости, мы применим их к реальным ситуациям башни с часами и вращающейся шины.
Рабочий пример
Угол поворота на башне с часами
Часы на башне с часами имеют радиус 1,0 м. а) На какой угол поворачивается часовая стрелка часов, когда она движется с 12 часов дня до 12 часов дня. до 15:00? (b) Какова длина дуги по внешнему краю часов между часовой стрелкой в эти два времени?
Стратегия
Мы можем вычислить угол поворота, умножив полный оборот (2π2π радиан) на долю 12 часов, покрываемых часовой стрелкой при переходе от 12 к 3. Получив угол поворота, мы можно определить длину дуги, переформулировав уравнение Δθ=ΔsrΔθ=Δsr, поскольку радиус задан.
Решение задачи (a)
При переходе от 12 к 3 часовая стрелка покрывает 1/4 из 12 часов, необходимых для совершения полного оборота. Следовательно, угол между часовой стрелкой в положении 12 и 3 равен 14×2π рад=π214×2π рад=π2 (т. е. 90 градусов).
Решение (б)
Преобразовывая уравнение
6.4Δθ=Δsr,Δθ=Δsr,
получаем
6.5Δs=rΔθ.Δs=rΔθ.
Подстановка известных значений дает длину дуги
6,6Δs=(1,0 м)(π2 рад)=1,6 мΔs=(1,0 м)(π2 рад)=1,6 м
Обсуждение
Мы смогли убрать радианы из окончательного решения в часть (b), поскольку радианы на самом деле безразмерны. Это связано с тем, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.
Рабочий пример
Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с (около 54 км/ч). Смотрите этот рисунок.
Стратегия
В этом случае скорость протектора шины относительно оси шины равна скорости автомобиля относительно дороги, поэтому мы имеем v = 15,0 м/с. Радиус шины r = 0,300 м. Поскольку мы знаем v и r , мы можем изменить уравнение v=rωv=rω, чтобы получить ω=vrω=vr и найти угловую скорость.
Решение
Для нахождения угловой скорости используем соотношение: ω=vrω=vr.
Вставка известных количеств дает
6,7ω=15,0 м/с0,300 м=50,0 рад/с.ω=15,0 м/с0,300 м=50,0 рад/с.
Обсуждение
Когда мы отбрасываем единицы измерения в приведенном выше расчете, мы получаем 50,0/с (т. е. 50,0 в секунду, что обычно записывается как 50,0 с ⁻¹ ). Но угловая скорость должна иметь единицы рад/с. Поскольку радианы безразмерны, мы можем подставить их в ответ для угловой скорости, потому что мы знаем, что движение является круговым. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. У них будет угловая скорость
6,8ω=15,0 м/с1,20 м=12,5 рад/сω=15,0 м/с1,20 м=12,5 рад/с
Практические задачи
Чему равен угол в градусах между часовой и минутной стрелками часов, показывающих 9 часов утра?
0°
90°
180°
360°
Каково приблизительное значение длины дуги между часовой и минутной стрелками часов, показывающих 10:00, если радиус часов равен 0,2 м?
0,1 м
0,2 м
0,3 м
0,6 м
Проверьте свое понимание
Упражнение 1
Что такое круговое движение?
Круговое движение — это движение объекта по линейной траектории.
Круговое движение — это движение объекта по зигзагообразной траектории.
Круговое движение — это движение объекта по круговой траектории.
Круговое движение – это движение объекта по окружности окружности или вращение по круговой траектории.
Упражнение 2
Что подразумевается под радиусом кривизны при описании вращательного движения?
Радиус кривизны — это радиус кругового пути.
Радиус кривизны — это диаметр кругового пути.
Радиус кривизны – это длина окружности кругового пути.
Радиус кривизны – это площадь кругового пути.
Упражнение 3
Что такое угловая скорость?
Угловая скорость – это скорость изменения диаметра кругового пути.
Угловая скорость – это скорость изменения угла, образуемого круговой траекторией.
Угловая скорость — это скорость изменения площади кругового пути.
Угловая скорость – это скорость изменения радиуса кругового пути.
Упражнение 4
Какое уравнение определяет угловую скорость ω? Предположим, что r — радиус кривизны, θ — угол, t — время.
ω=ΔθΔt
ω=ΔtΔθ
ω=ΔrΔt
ω=ΔtΔr
Упражнение 5
Найдите три примера объекта, движущегося по кругу.
искусственный спутник Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и волчок, вращающийся вокруг своей оси
искусственный спутник на орбите Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и электрон, движущийся по круговой орбите вокруг ядра
Земля, вращающаяся вокруг своей оси, гоночный автомобиль, движущийся по круговой гоночной трассе, и электрон, движущийся по круговой орбите вокруг ядра.

Mathway | Популярные задачи

Как найти радиус вектор точки

Длина вектора — как найти? Формулы и примеры

Что такое векторы и какими они бывают

Длина вектора

Как можно найти длину вектора по его координатам

Как найти длину вектора по двум точкам

Как найти длину вектора по теореме косинусов

Связь между координатами вектора и координатами его начала и конца 9 класс онлайн-подготовка на Ростелеком Лицей |

Скорость через радиус вектор

Основные формулы кинематики материальной точки

Радиус-вектор и траектория точки

Скорость материальной точки

Касательная к траектории

Ускорение материальной точки

Тангенциальное (касательное) и нормальное ускорения

Тангенциальное (касательное) ускорение

Радиус кривизны траектории

Нормальное ускорение

примеры и решения, формулы и теоремы

Длина вектора – основные формулы

Длина вектора через координаты точек его начала и конца

Нахождение длины вектора по теореме косинусов

Формула радиуса кривизны – Выучить формулу радиуса кривизны

13.3: Длина дуги и кривизна

Цели обучения

Пример \(\PageIndex{1}\): определение длины дуги 9{3/2})≈37,785\) единиц

Параметризация длины дуги

Пример \(\PageIndex{2}\): поиск параметризации длины дуги

Упражнение \(\PageIndex{2}\)

Кривизна

Доказательство

Нормальный и бинормальный векторы

Пример \(\PageIndex{4}\): нахождение вектора нормали к главной единице и вектора бинормали 92 t}} \\[4pt]

Глоссарий

16.6 Векторные функции для поверхностей

Калькулятор угловой скорости

Что такое угловая скорость?

Формулы угловой скорости

Единицы измерения угловой скорости

Угловая скорость в зависимости от угловой частоты

Как найти угловую скорость Земли?

Физические величины, зависящие от угловой скорости

Сохранение углового момента

Объяснение урока: Момент силы относительно точки в 2D: векторы

Определение: момент силы

Пример 1. Нахождение момента вектора силы относительно точки

Ответ

Определение: двумерное перекрестное произведение

Свойство: Величины векторного момента силы

Формула: Расстояние по перпендикуляру между точкой и линией действия

Пример 2. Нахождение вектора момента силы, действующей в точке, и перпендикуляра между моментом и линией Действие Силы

Ответ

Свойство: двумерный векторный момент силы

Свойство: Векторный момент силы

Пример 3. Определение момента вектора силы, действующего в точке

Ответ

Пример 4: Расчет момента трех сил, действующих на одну точку относительно данной точки, и расстояния между точками

Ответ

Определение: Момент системы плоских сил

Ответ

Ключевые точки

6.1 Угол поворота и угловая скорость

Цели обучения

Угол поворота

Угловая скорость

Советы по достижению успеха

Watch Physics

Взаимосвязь между угловой скоростью и скоростью

Решение задач на угол поворота и угловую скорость

Snap Lab

Измерение угловой скорости

Рабочий пример

Угол поворота на башне с часами

Стратегия

Рабочий пример

Как быстро вращается автомобильная шина?

Стратегия

Практические задачи

Проверьте свое понимание