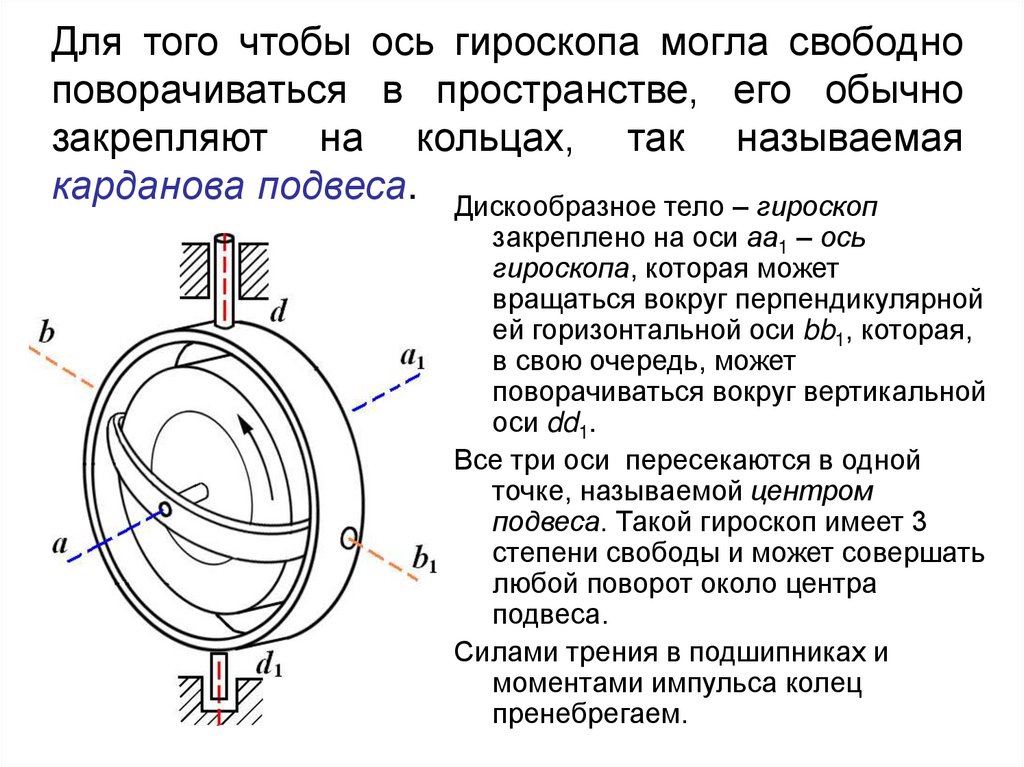
Расчет реакции гироскопа на заданный тестовый входной сигнал
Цель данного этапа исследований – увидеть, как меняется сигнал на выходе гироскопа при быстых (резких) и медленных (плавных) изменениях измеряемой угловой скорости .
Для проведения такого анализа задается некоторый тестовый закон изменения входного сигнала по времени и рассчитываются реакции линейной и нелинейной моделей гироскопа на этот сигнал.
Входной тестовый сигнал формируется с использованием блока Signal Builder (построитель сигнала), который берется из раздела Sources (источники сигналов), и Gain (усилитель сигнала), который берется из раздела Math Operations (математические действия).
Чтобы сравнивать входной сигнал и соответствующие ему выходы линейной и нелинейной моделей, все три сигнала строятся на одном графике. Такое построение достигается с использованием блока Mux.
Входной текстовый сигнал формируется в окне блока Signal Builder.
Формирование сигнала в этом окне выполняется в следующей последовательности:
На линейке команд окна выбираем кнопку Axes/Change time range (Оси/Изменить интервал времени) и задаем требуемый интервал времени моделирования (в нашем случае от 0 до 10 сек).

Командой Axes/Set Y display limit (задать диапазон отображения сигнала по оси Y) задаем диапазон возможных значений сигнала на выходе блока.
Нажав на клавиатуре клавишу Shift и кликнув мышью на оси времени, намечаем точки изломов на линейных участках сигнала.
Двигая с помощью мыши точки или участки между точками, формируем требуемый профиль входного тестового сигнала.
Чтобы сравнивать входной и выходные сигналы на одном графике, в программе используется блок Mux из раздела Signal Routing. Этот блок используется для объединения трех скалярных сигналов (входа и двух выходов гироскопа) в один векторный сигнал, состоящий из трех компонентов, который подается в блок построения графиков Scope.
График при анализе входа и выхода гироскопа по времени.
Целью
данного этапа исследований является
сопоставление переходных процессов на
выходе модели гироскопа, заданной в
виде «черного ящика», и аналогичной
модели с параметрами, оцененными на
этапах 1-2 выполнения задания. В
В
результате сопоставления можно увидеть, насколько точно были оценены параметры модели гироскопа по результатам расчета статической характеристики и переходных процессов.
Для получения графиков следует сформировать программу моделирования, показанную на рисунке. Параметры тестирующей модели rate gyro test model задаются в окне настройки. С помощью составленной программы сопоставим переходные процессы в системе. При значительном расхождении следует добиться приблизительного соответствия графиков переходных процессов в нелинейных моделях варьированием значения постоянной времени Т и коэффициента демпфирования гироскопа в окне настройки тестовой модели.
Параметры | Стат.хар-ки | Переходный процесс | Уточнённые параметры |
К | 0.4 | ||
Umin зона нечувст-ти | 0. | 0.12 | |
Umax насыщ | 36 | 36 | 36 |
Wвх | 93 град/с | 93 | 93 |
Uзаброс | 37.5 | 37.5 | |
Uуст | 37 | 37 | |
σ | 1.3 | 1.3 | |
Ξ | 0.87 | 0.87 | |
Tп.п. | 0.65 | 0.65 | |
T | 0. | 0.07 | |
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего
профессионального образования
«Московский авиационный институт»
(национальный исследовательский университет) (МАИ)
Кафедра «Системный анализ и управление»
РАСПРЕДЕЛЕНИЕ АМПЛИТУДЫ ОПТИЧЕСКОГО ПОЛЯ НА ТРАНСПАРАНТЕ ОПТИКО-ЭЛЕКТРОННОЙ СИСТЕМЫ ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ВИБРОПОДСТАВКИ В ЛАЗЕРНОМ ГИРОСКОПЕ
doi: 10.17586/2226-1494-2018-18-2-197-204
УДК 621.375.826:681.2.084
Читать статью полностью
Язык статьи – русский
Ссылка для цитирования: Авиев А.А., Енин В.Н. Распределение амплитуды оптического поля на транспаранте оптико-электронной системы для измерения параметров виброподставки в лазерном гироскопе // Научно-технический вестник информационных технологий, механики и оптики. 2018. Т. 18. № 2. С. 197–204. doi: 10.17586/2226-1494-2018-18-2-197-204
2018. Т. 18. № 2. С. 197–204. doi: 10.17586/2226-1494-2018-18-2-197-204
Аннотация
Предмет исследования. Исследована оптико-электронная система, позволяющая измерять параметры колебаний виброподставки в кольцевом лазерном гироскопе и служащая для компенсации составляющей его выходного сигнала, обусловленной этими колебаниями. Рассмотрен процесс прохождения лазерного излучения через элементы системы, получено распределение амплитуды оптического поля в плоскости ее транспаранта. Проанализировано распределение амплитуды при малом линейном сдвиге и малом наклоне объектива. Методы. Использованы элементы методики расчета полей в оптических системах чтения и записи информации на цифровых дисках. Исходные параметры лазерного излучения определены исходя из паспортных характеристик источника излучения. Преобразование излучения оптическими элементами системы осуществлялось путем трассировки лучей с использованием лучевых пакетов. Распределение амплитуды оптического поля в плоскости транспаранта вычислялось при помощи дифракционного интеграла с учетом аберраций.
Ключевые слова: лазерный гироскоп, кольцевой лазер, виброподставка, оптико-электронная измерительная система, оптическое поле, аберрации, дифракция
Список литературы
-
Aronovitz F.
 Fundamentals of the ring laser gyro // Optical Gyros and their Application. RTO-AG-339. 1999. P. 3-1–3-45.
Fundamentals of the ring laser gyro // Optical Gyros and their Application. RTO-AG-339. 1999. P. 3-1–3-45. -
Пешехонов В.Г. Современное состояние и перспективы развития гироскопических систем // Гироскопия и навигация. 2011. № 1. С. 3–16.
-
Лукьянов Д.П., Филатов Ю.В., Голяев Ю.Д. и др. 50 лет лазерному гироскопу // ХХ Санкт-Петербургская международная конференция по интегрированным навигационным системам. Санкт-Петербург, 2013. С. 7–21.
-
Лукьянов Д.П., Распопов В.Я., Филатов Ю.В. Основы теории гироскопов. СПб.: ОАО«Концерн«ЦНИИ«Электроприбор», 2015. 339 с.
-
Ljung B.H.G. Dither pick-off transducer for ring laser gyroscope. ПатентUS4406965. Опубл. 27.09.83.
-
Зюзев Г.Н. О компенсации частотной подставки лазерного датчика абсолютной угловой скорости // Труды МВТУ. 1982.
 № 385. С. 10–16.
№ 385. С. 10–16. -
-
Chen A., Li J., Chu Z. Dither signal removal of ring laser gyro POS based on combined digital filter // Proc. 8th IEEE Int. Symposium on Instrumentation and Control Technology. London, 2012. P. 178–182.
-
Климкович Б.В., Толочко А.М. Корректирующий фильтр для одноосного кольцевого лазерного гироскопа на виброподставке // Гироскопия и навигация. 2016. T. 24. № 2. С. 41–55. doi: 10.17285/0869-7035.2016.24.2.041-055
-
Авиев А.А. Оптико-электронная система для измерения параметров колебаний виброподставки в кольцевом лазерном гироскопе // Известия ТулГУ. Техническиенауки. 2016. № 6. С. 14–25.
-
Фролов М.Е. Проектирование и расчет высокоапертурных лазерных систем устройств хранения информации на цифровых оптических дисках: дис.
 … канд. техн. наук. Москва, 2008. 177 с.
… канд. техн. наук. Москва, 2008. 177 с. -
Звелто О. Принципы лазеров. М.: Мир, 1990. 560 с.
-
Пахомов И.И. Расчет преобразования лазерного пучка в оптических системах. М.: МВТУ, 1984. 54 с.
-
Носов П.А., Пахомов И.И., Ширанков А.Ф. Состояние и перспективы развития методов расчета преобразования лазерного излучения оптическими системами // Инженерный журнал: наука и инновации. 2012. № 9. С. 166–177. doi: 10.18698/2308-6033-2012-9-363
-
Пахомов И.И., Цибуля А.Б. Расчет оптических систем лазерных приборов. М.: Радио и связь, 1986. 152 с.
-
DiMarzio C.A. Optics for Engineers. Boca Raton: CRC Press, 2011. 564 p.
-
Борн М., Вольф Э. Основы оптики. М.: Наука, 1973. 720 с.
This work is licensed under a Creative
Commons Attribution-NonCommercial 4. 0 International License
0 International License
11.5: Прецессия гироскопа
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4037
- OpenStax
- OpenStax
Цели обучения
- Описать физические процессы, лежащие в основе явления прецессии
- Рассчитать угловую скорость прецессии гироскопа
На рисунке \(\PageIndex{1}\) показан гироскоп, определяемый как вращающийся диск, в котором ось вращения может принимать любую ориентацию. При вращении ориентация оси вращения не зависит от ориентации окружающего ее тела. Тело или транспортное средство, окружающее гироскоп, можно перемещать с места на место, а ориентация оси вращения останется прежней. Это делает гироскопы очень полезными в навигации, особенно там, где нельзя использовать магнитные компасы, например, в пилотируемых и беспилотных космических кораблях, межконтинентальных баллистических ракетах, беспилотных летательных аппаратах и спутниках, таких как космический телескоп Хаббла.
Это делает гироскопы очень полезными в навигации, особенно там, где нельзя использовать магнитные компасы, например, в пилотируемых и беспилотных космических кораблях, межконтинентальных баллистических ракетах, беспилотных летательных аппаратах и спутниках, таких как космический телескоп Хаббла.
Мы иллюстрируем прецессию гироскопа на примере волчка на следующих двух рисунках. Если волчок поместить на плоскую поверхность у поверхности Земли под углом к вертикали и не вращаться, он упадет из-за силы тяжести, создающей крутящий момент, действующий на его центр масс. Это показано на рисунке \(\PageIndex{2a}\). Однако, если волчок вращается вокруг своей оси, а не опрокидывается из-за этого крутящего момента, он прецессирует относительно вертикали, как показано в \(\PageIndex{2b}\). Это связано с моментом на центре масс, обеспечивающим изменение углового момента.
На рисунке \(\PageIndex{3}\) показаны силы, действующие на волчок. Создаваемый крутящий момент перпендикулярен вектору углового момента. Это изменяет направление вектора углового момента \(\vec{L}\) в соответствии с d\(\vec{L}\) = \(\vec{\tau}\)dt, но не его величину. Вершина прецессирует вокруг вертикальной оси, поскольку крутящий момент всегда горизонтален и перпендикулярен \(\vec{L}\). Если вершина , а не , он приобретает угловой момент в направлении крутящего момента и вращается вокруг горизонтальной оси, падая, как и следовало ожидать.
Рисунок \(\PageIndex{3}\): Сила тяжести, действующая на центр масс, создает крутящий момент \(\vec{\tau}\) в направлении, перпендикулярном \(\vec{L}\). Величина \(\vec{L}\) не меняется, но меняется ее направление, и вершина прецессирует вокруг оси z.
Мы можем испытать это явление на собственном опыте, взяв вращающееся велосипедное колесо и попытавшись повернуть его вокруг оси, перпендикулярной оси вращения. Как показано на рисунке \(\PageIndex{4}\), человек прикладывает силы, перпендикулярные оси вращения, пытаясь повернуть колесо, но вместо этого ось колеса начинает менять направление влево из-за приложенного крутящего момента.
Рисунок \(\PageIndex{4}\): (a) Человек, держащий вращающееся колесо велосипеда, поднимает его правой рукой и нажимает левой рукой, пытаясь повернуть колесо. Это действие создает крутящий момент прямо к ней. Этот крутящий момент вызывает изменение углового момента \(\Delta \vec{L}\) точно в том же направлении. (b) Векторная диаграмма, показывающая, как \(\Delta \vec{L}\) и \(\vec{L}\) складываются, создавая новый угловой момент, направленный больше к человеку. Колесо движется к человеку перпендикулярно силам, которые она на него оказывает. Все мы знаем, как легко велосипед может опрокинуться, если сидеть на нем в состоянии покоя. Но при езде на велосипеде в хорошем темпе его труднее опрокинуть, потому что мы должны изменить вектор углового момента вращающихся колес.
Но при езде на велосипеде в хорошем темпе его труднее опрокинуть, потому что мы должны изменить вектор углового момента вращающихся колес.
Примечание
Посмотрите это видео о прецессии гироскопа, чтобы полностью продемонстрировать прецессию велосипедного колеса.
Кроме того, когда вращающийся диск помещается в коробку, например, в проигрыватель Blu-Ray, попробуйте переместить его. Коробку легко сдвинуть в заданном направлении, но трудно повернуть вокруг оси, перпендикулярной оси вращающегося диска, поскольку мы прикладываем к коробке крутящий момент, который вызовет прецессию вектора углового момента вращающегося диска. .
Мы можем рассчитать скорость прецессии вершины на рисунке \(\PageIndex{3}\). Из рисунка \(\PageIndex{3}\) мы видим, что величина крутящего момента составляет
.\[\тау = rMg \sin \тета \ldotp\]
Таким образом,
\[dL = rMg \sin \theta dt \ldotp\]
Угол прецессии вершины за время dt равен
\[d \phi = \frac{dL}{L \sin \theta} = \frac{rMg \sin \theta}{L \sin \theta} dt = \frac{rMg}{L} dt \ldotp\ ]
Угловая скорость прецессии равна \(\omega_{P} = \frac{d \phi}{dt}\), и из этого уравнения мы видим, что
\[\omega_{P} = \frac{rMg}{L} \ldotp\]
или, поскольку L = I\(\omega\),
\[\omega_{P} = \frac{rMg}{I \omega} \ldotp \label{11. 12}\]
12}\]
В этом выводе мы предполагали, что \(\omega_{P}\) << \(\omega\), то есть что угловая скорость прецессии много меньше угловой скорости диска гироскопа. Угловая скорость прецессии добавляет небольшую составляющую к угловому моменту вдоль оси z. Это проявляется в легком покачивании вверх и вниз по мере прецессии гироскопа, что называется нутацией.
Сама Земля действует как гигантский гироскоп. Его угловой момент направлен вдоль его оси и в настоящее время указывает на Полярную звезду. Но Земля медленно прецессирует (примерно раз в 26 000 лет) из-за крутящего момента Солнца и Луны на ее несферической форме.
Пример \(\PageIndex{1}\): период прецессии
Гироскоп вращается кончиком на земле и вращается с пренебрежимо малым сопротивлением трения. Диск гироскопа имеет массу 0,3 кг и вращается со скоростью 20 об/с. Его центр масс находится на расстоянии 5,0 см от оси вращения, а радиус диска равен 5,0 см. Что такое прецессионный период гироскопа? 9{2})(125,66\; рад/с)} = 3,12\; рад/с \ldotp \nonumber\]
Период прецессии гироскопа равен
\[T_{P} = \frac{2 \pi}{3.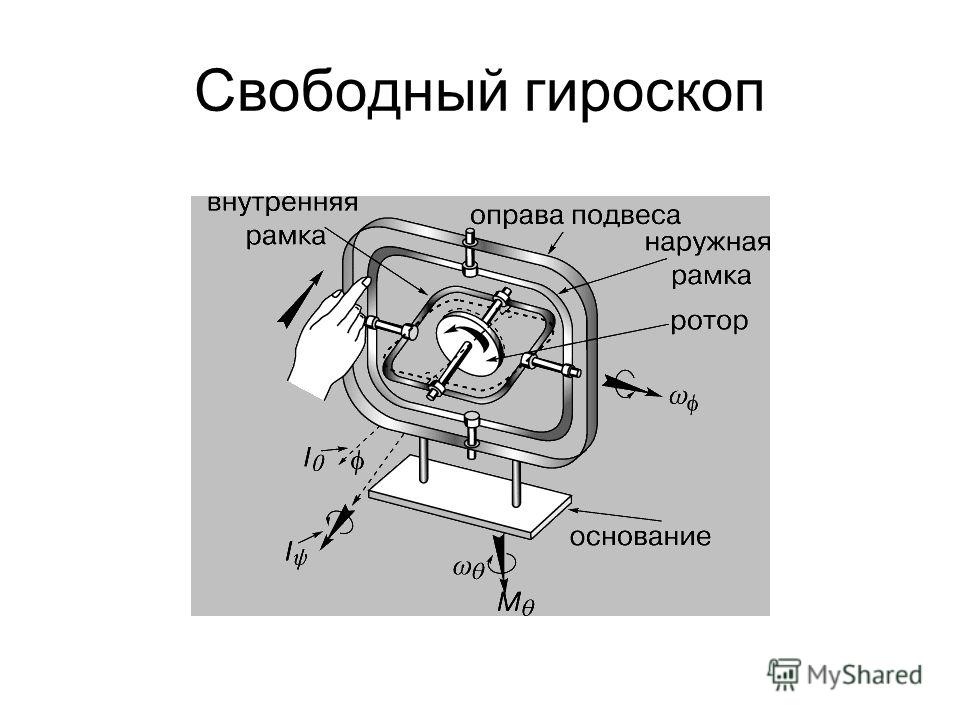 12\; рад/с} = 2,0\; s \ldotp \nonumber\]
12\; рад/с} = 2,0\; s \ldotp \nonumber\]
Значение
Угловая частота прецессии гироскопа, 3,12 рад/с, или около 0,5 об/с, много меньше угловой скорости 20 об/с диска гироскопа. Поэтому мы не ожидаем, что большая составляющая углового момента возникнет из-за прецессии, и уравнение 11.12 является хорошим приближением угловой скорости прецессии.
Упражнения \(\PageIndex{1}\)
Вулкан имеет частоту прецессии 5,0 рад/с на Земле. Какова его частота прецессии на Луне?
Эта страница под названием 11.5: Прецессия гироскопа распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа ООР или издатель
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Гироскопы
- прецессия
- источник@https://openstax.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1
Роберт М. Бил (май 2003 г.) Уравнения, встречающиеся в этом документе, были взяты из различные разделы учебника Инженерная механика – Статика и Dynamics , третье издание, Р. К. Хиббелер (ISBN 0-02-354140-7), прежде всего из глав 20 и 21 раздела «Динамика»; если читатель хочет углубиться в тему или нуждается в разъяснениях по части этот документ, я отсылаю вас к учебнику Хиббелера. Я собрал уравнения, со случайными изменениями и мои собственные комментарии, чтобы (надеюсь) обеспечить гладкое плавный вывод уравнений гироскопического движения, начиная с самое основное уравнение динамики, F = ma, и продолжается непрерывно к заявленной цели. Начнем с хорошо известного и принятого уравнения Ньютона.
отношение силы ( F ) к массе (м) и ускорение ( a ). Это уравнение утверждает, что сумма внешних сила, действующая на частицу, равна произведению массы частицы на ее ускорение. На самом деле первоначальная формулировка Ньютона связывала внешние силы с частица линейный импульс : Здесь v скорость, v скорость времени изменения скорости (d v /dt) , а m v ‘ – скорость изменение линейного количества движения. Если мы выбрали точку отсчета O и r — вектор положения частицы , мы можем взять векторное произведение обоих сторон этого уравнения, чтобы получить выражение, связывающее момент силы ( M o ), действующие на частицу угловой момент ( H o ) частицы относительно к контрольной точке О: Учитывая, что r x S F это Сумма Моментов ( S M o ) сил, действующих на частицу относительно точки отсчета O, мы можем написать: Поскольку угловой момент частицы равен Н о = г х м в , если мы возьмем производную момента количества движения по времени, мы имеем: H ‘ o = r ‘ x м v + р х м в ‘ Признавая, что v = d r /dt = r ‘, имеем: Поскольку перекрестное произведение двух эквивалентных векторов равно нулю, r ‘ x м r ‘ = m( r ‘ x r ‘) = 0 , следовательно: Подставляя в уравнение для суммы моментов, у нас есть: То есть для движущейся частицы сумма моментов относительно
точка O равна скорости изменения углового момента частицы во времени. Для системы частиц суммируем моменты сил всех частиц. В следующем уравнении S f есть внутренняя сила, действующая на i -ю частицу за счет всех другие частицы в системе: пары внутренних сил равны по величине и противоположны по направлению, следовательно, S i ( r x S f ) i = 0 , и полученное уравнение для системы частиц имеет тот же вид, что и уравнение для одной частицы: S M о = Н ‘ о На словах это означает, что сумма моментов относительно точки O
за счет внешних сил, действующих на систему частиц, равно
скорость изменения углового момента системы частиц около
этот же ориентир О. Мы признаем, что любое твердое тело представляет собой систему частиц, поэтому это уравнение применимо к анализу гироскопа. Теперь нам нужно выражение для углового момента H o или его производная по времени H ‘ o , имеющая атрибуты, которые мы можем физически измерить, такие как масса, радиус, угловой скорость и угловое ускорение. Если мы рассмотрим частицу в теле с приращенной массой Dm и угловая скорость w относительно точка отсчета O, так как v = w x r , мы можем написать: [D H o ] i = [ R x ( W x R )] i Dm i Суммируя все дополнительные угловые моменты для всех частиц в теле, имеем: Если мы приблизим D к 0, то
Дм i становятся дифференциалами, а
мы можем заменить S i с интеграцией. H o = z m r x ( w x r ) дм Если мы поместим опорные координатные оси xyz в точку O, мы можем определить H o , r и w через i , j и k следующие компоненты: г = х i + у j + г к w = w x i + w y j + w z k Подставляя в приведенное выше интегральное выражение для H или , у нас есть: z м (x i + y j + z k ) x [(w x i + w y j + w z k ) x (x i + y j + z k ) ]дм Вычисление векторных произведений и объединение членов дает: [w x z m (y 2 +z 2 )dm – w y z m xy dm – w z z m xz dm] i + [ – W x Z M XY DM + W Y Z M (x 2 + Z 2 ) DM – W Z 662626261111111111111111111111111111111111111111111111111111111111111111111111Р1н. 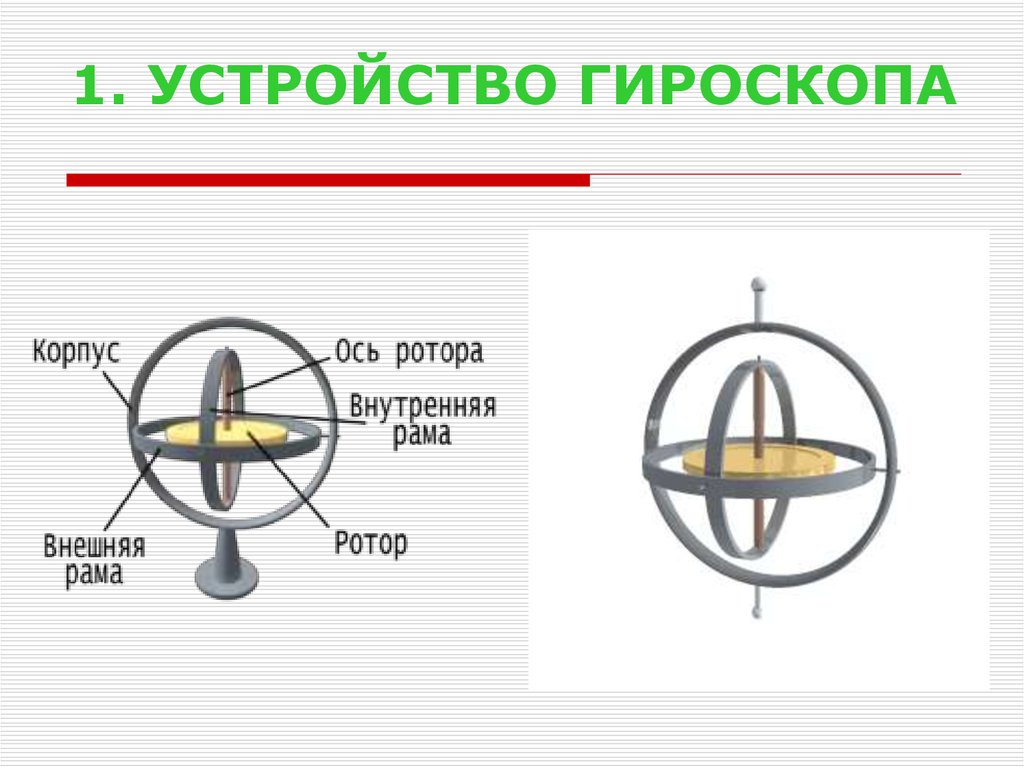 + [ – W x Z M ZX DM – W Y Z M YZ DM + W Z Z M (x 2 + Y M (x 2 + y M (x 2 + y 9 2 0 2 2) 2 2). Признавая, что приведенные выше интегралы равны моментов инерции и произведений инерции , мы можем записать вышеизложенное в следующем виде скалярных уравнений : 2 H 63 = w ° W 26266 2. yy w y – I yz w z H z = – I zx w x – I zy w y + I zz w z Если мы выберем такую систему координат, что хотя бы два из три ортогональные плоскости, определяемые системой координат, являются осями симметрии для тела, то все произведения инерции обращаются в нуль, и наши уравнения сократить до: H y = I yy w y H z = I zz w z Если оси выбраны, как описано выше, они называются главные оси инерции . Наш анализ гироскопа значительно упростится, если мы
выбрать такую систему координат, что хотя бы две из трех ортогональных
плоскости, заданные системой координат, являются осями симметрии для
гироскоп. Если система координат выбрана в соответствии с этим критерием, то все
произведения инерции станут равными нулю, и нам останется только учесть моменты
инерции в наших расчетах. Для этого мы будем использовать вращающийся стержень .
система координат с началом в точке вращения гироскопа.
вращающаяся система координат будет следовать за нутацией и прецессией гироскопа, но
не его спина. Назовем угловую скорость вращающегося отсчета Вт = нутация + прецессия = к ‘ + ф ‘
и обозначьте оси вращения как оси xyz. Поскольку оси xyz вращаются относительно фиксированных осей ABC, необходимо оценить H ‘ o с учетом того, что блок векторов i, j и k не являются постоянными, поскольку они изменяются направление. Тогда мы имеем: где ( H ‘ или ) ABC это время
производная момента количества движения относительно неподвижных осей АВС. d j /dt = Вт x j d k /dt = Вт x k Уравнение суммы моментов можно записать следующим образом: Таблицы моментов инерции для тел
различные геометрические формы для главных осей инерции и
обычно указываются как I xx , I yy и I zz .
Так как центр тяжести маховика нашего автожира лежит на расстоянии R
от начала O наших осей координат, оси x и y не являются главными
осей инерции, но они параллельны главным осям инерции
маховик. I y = I yy + mR 2 I z 4 2 = I z 4 2 = I z 9026 2 Принимая во внимание отношения между I x , I y , I z и I xx , я гг , I zz , теперь мы можем выразить угловой момент гироскопа как: H y = I y w y H z = I z w z Подстановка вышесказанного в уравнение суммы моментов и взятие указанных производных по времени дает: SM x i + SM y y + SM z k = Вычисляя векторные произведения и комбинируя члены, мы получаем следующий скаляр уравнения для суммы моментов: SM y = I y w’ y – I z W x w z + I x W z w x SM z = I z w’ z – I x W y w x + I y W x ш г Ссылаясь на рис. Ш = Ш x i + Ш y j + Ш z k W = q’ i + (f’sinq) j + (f’cosq) k w = q ‘ + f ‘ + y ‘ Замена компонентов W и w в приведенный выше скаляр Сумма моментов уравнения и вычисление указанных производных по времени дает: SM y = I y (f’q’cosq + f”sinq) – I z q'(f’cosq + y’) + I x f’q’cosq SM z = I z (- f’q’sinq + f”cosq + y”) – I x f’q’sinq + I y f’q’sinq В общем, было бы очень трудно прийти к решению, которое
однако удовлетворяет этим уравнениям в конкретном случае, когда прецессия
f’ постоянна, спин
y’ постоянна, а угол нутации
д = 90 0 — константа
90 градусов, как показано на рис. В этом случае имеем: е” = 0 г” = 0 потому что (90 0 ) = 0 грех(90 0 ) = 1 и уравнения суммы моментов сводятся к: СМ у = 0 СМ z = 0 так что единственный момент в данном случае это момент относительно оси x. В этом уравнении нет отрицательных знаков и мы последовательно использовали правило правой руки при выражении всех векторных величин, следовательно, все векторы – сумма моментов относительно оси x (SM x ), прецессия гироскопа вокруг оси Y (f’), а вращение маховика вокруг оси z (y’) все действуют вдоль своих соответствующих положительных осей как показано на рис. 3. Наш анализ гироскопа, лежащего на 90 0 сводится к следующему важному результату: Если единственным моментом относительно оси X является момент, возникающий в результате от веса маховика (мы предполагаем, что вес вала пренебрежимо мал), а если маховик находится на расстоянии R от точки поворота (начало O), и учитывая, что I z = I zz , имеем: , где m — масса маховика, а g —
ускорение силы тяжести. Для сплошного круглого диска I zz = 1/2mr 2 где r — радиус диска. Если вместо этого мы сосредоточим большую часть массы по внешнему краю, затем по тонкому круговому кольцу, I zz = мистер 2 : тонкое круглое кольцо: mgR = mr 2 f’y’ Для противодействия моменту mgR, гироскоп, использующий сплошной круглый диск в качестве маховика
будет прецессировать в два раза быстрее, чем гироскоп, использующий тонкое круглое кольцо (при условии, что оба маховика
имеют одинаковую массу m и радиус r). |


 12
12 16
16 Fundamentals of the ring laser gyro // Optical Gyros and their Application. RTO-AG-339. 1999. P. 3-1–3-45.
Fundamentals of the ring laser gyro // Optical Gyros and their Application. RTO-AG-339. 1999. P. 3-1–3-45. № 385. С. 10–16.
№ 385. С. 10–16. … канд. техн. наук. Москва, 2008. 177 с.
… канд. техн. наук. Москва, 2008. 177 с. org/details/books/university-physics-volume-1
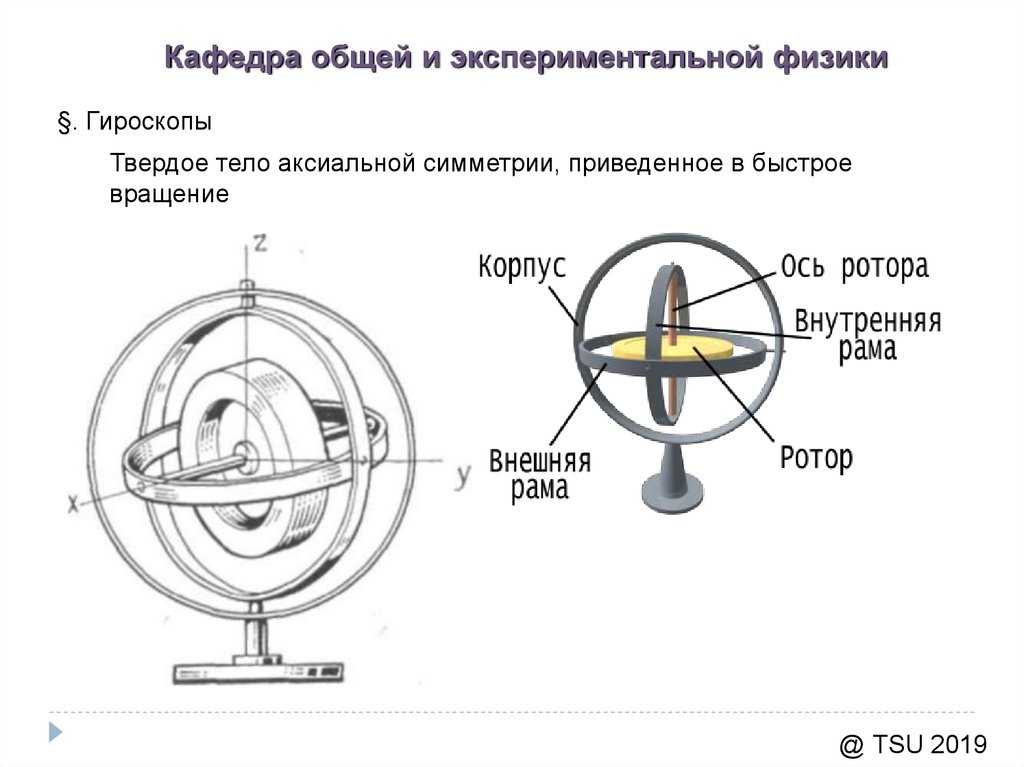
org/details/books/university-physics-volume-1 Для частицы это (жирным шрифтом обозначена векторная величина):
Для частицы это (жирным шрифтом обозначена векторная величина):
 Я буду использовать z вместо обычного знака интеграла
просто потому, что у меня нет обычного знака интеграла:
Я буду использовать z вместо обычного знака интеграла
просто потому, что у меня нет обычного знака интеграла: Теперь мы имеем угловой момент H o в полезной форме, так как угловая скорость может быть
измеренных и моментов инерции (I), которые зависят только от
массу и физические размеры тела можно посмотреть в таблице или
рассчитывается вручную.
Теперь мы имеем угловой момент H o в полезной форме, так как угловая скорость может быть
измеренных и моментов инерции (I), которые зависят только от
массу и физические размеры тела можно посмотреть в таблице или
рассчитывается вручную.  У нас также будет фиксированная
эталонная система координат, которая также будет иметь свое начало в точке поворота
точка гироскопа, и мы будем называть это осями ABC. Угловая скорость
гироскоп относительно неподвижных осей ABC будет w = нутация + прецессия + спин = к ‘ + ф ‘
+ y ‘ (см. рис. 1 и рис. 2). Углы к , ф ,
и y называются углами Эйлера после
швейцарский математик Леонард Эйлер .
У нас также будет фиксированная
эталонная система координат, которая также будет иметь свое начало в точке поворота
точка гироскопа, и мы будем называть это осями ABC. Угловая скорость
гироскоп относительно неподвижных осей ABC будет w = нутация + прецессия + спин = к ‘ + ф ‘
+ y ‘ (см. рис. 1 и рис. 2). Углы к , ф ,
и y называются углами Эйлера после
швейцарский математик Леонард Эйлер .
 Поэтому мы можем использовать теорему о параллельных осях для
свяжите компоненты x и y моментов инерции с
I xx и I yy моменты инерции как
показано ниже. я z не представляет проблемы, поскольку
ось Z проходит через центр тяжести маховика, поэтому является главной осью
инерции:
Поэтому мы можем использовать теорему о параллельных осях для
свяжите компоненты x и y моментов инерции с
I xx и I yy моменты инерции как
показано ниже. я z не представляет проблемы, поскольку
ось Z проходит через центр тяжести маховика, поэтому является главной осью
инерции: 2, мы можем выразить компоненты xyz
угловая скорость Вт вращающихся осей
и компоненты xyz угловой скорости w гироскопа следующим образом:
2, мы можем выразить компоненты xyz
угловая скорость Вт вращающихся осей
и компоненты xyz угловой скорости w гироскопа следующим образом: 3 ниже, решение становится довольно простым:
3 ниже, решение становится довольно простым:  Это уравнение говорит нам, что если маховик находится в
90 0 на расстоянии R от точки вращения
а маховик вращается с постоянной угловой скоростью
y’, то гироскоп не опрокинется, как могло бы быть.
ожидалось, но вместо этого он будет прецессировать вокруг положительной оси Y с постоянной
угловая скорость f’.
Это уравнение говорит нам, что если маховик находится в
90 0 на расстоянии R от точки вращения
а маховик вращается с постоянной угловой скоростью
y’, то гироскоп не опрокинется, как могло бы быть.
ожидалось, но вместо этого он будет прецессировать вокруг положительной оси Y с постоянной
угловая скорость f’.