Раскрытие неопределенностей — Мегаобучалка
При определении пределов часто возникают ситуации, называемые неопределенностями. Мы рассмотрим неопределенности следующих видов
1) – неопределенность “ноль делить на ноль”.
2) – неопределенность “бесконечность делить на бесконечность”.
3) –неопределенность “ноль умножить на бесконечность”.
Нахождение пределов в этих случаях называется раскрытием неопределенностей.
Рассмотрим некоторые приемы раскрытия каждой неопределенности в отдельности.
Неопределенность появляется при нахождении предела отношения двух бесконечно малых функций .
Пример 1.4
.
Здесь = 4 – 10 + 6 = 0 и = 0. Числитель и знаменатель дроби являются бесконечно малыми при , т.е. имеет место неопределенность . Для раскрытия неопределенности в рассматриваемом случае числитель и знаменатель дроби разложим на множители и сократим на величину , дающую 0 в числителе и знаменателе:
= = = = = – .
Пример 1.5
Найти предел: .
Решение
Здесь также имеем дело с неопределенностью . Для раскрытия этой неопределенности умножим числитель и знаменатель дроби на выражение , которое называется сопряженным выражению , тогда
= = = =
= = = .
Для раскрытия неопределенности в некоторых случаях могут быть полезны следующие определения и теоремы.
Определение 1.1. Пусть и две БМ при . Если
| , | (1.1) |
то БМ и называются эквивалентными. Эквивалентность БМ и обозначается .
Теорема 1.1. (Первый замечательный предел). Можно показать
[ ], что
| , | (1.2) |
Предел (1.2) называется первым замечательным пределом. Из теоремы 1.1 и определения 1.1 следует, что . Приведем еще некоторые примеры эквивалентных БМ при a® 0:
Таблица 1. 1
1
| 1. | sina ~ | a |
| 2. | a | |
| 3. | ||
| 4. | a | |
| 5. | a | |
| 6. | a |
Теорема 1.2.
Предел отношения двух бесконечно малых величин равен пределу отношения бесконечно малых, эквивалентных данным.
Поясним, что утверждает теорема. Пусть и две бесконечно малые функции. Известны еще две БМ и , причем и . Тогда .
Доказательство:
= , что и требовалось. доказать.
Каждый из пределов в рамках равен единице, т.к. это пределы отношений эквивалентных бесконечно малых.
Пример 1.6
Найти .
Решение
Здесь имеет место неопределенность , которая раскрывается
переходом к эквивалентным величинам: sin5x~5x, sin3x~3x, по теореме 1. 2 получаем:
2 получаем:
= = = .
Неопределенность появляется при нахождении предела отношения двух бесконечно больших .
Пример 1.7
Найти .
Решение
Здесь имеет место неопределенность . Отметим, что самая большая степень, в которой переменная входит в числитель и знаменатель дроби. Для раскрытия неопределенности вынесем за скобки и в числителе и в знаменателе и сократим. Получим
= =
= .
Отметим, что в данном примере высшая степень в числителе равна высшей степени в знаменателе. Предел равен отношению коэффициентов при высших степенях в числителе и знаменателе.
Пример 1.8
= = = = 0.
Отметим, что в данном примере высшая степень в числителе меньше высшей степени в знаменателе. Предел равен нулю.
Пример 1.9
= = =
= = .
В данном примере высшая степень в числителе больше высшей степени в знаменателе. Предел равен бесконечности. В результате рассмотрения примеров 1.7, 1.8 и 1.9 сформулируем общее правило нахождения предела вида
Предел равен бесконечности. В результате рассмотрения примеров 1.7, 1.8 и 1.9 сформулируем общее правило нахождения предела вида
=
=
Пример 1.10
.
Решение
Здесь , , , поэтому предел равен :
.
1.3 Раскрытие неопределенности вида ∞-∞.
Такую
неопределенность фиксируем, если имеем
разность двух бесконечно больших
функций, которые стремятся к бесконечности
с «примерно» одинаковой скоростью.
Например, в разности нет неопределенности ∞-∞.
Несмотря на то, что и ,
и при
,
но они стремятся к бесконечности с
разной скоростью (очевидно, что при
достаточно больших
выражение
гораздо больше, чем ).
Поэтому здесь уменьшаемое «подавляет»
вычитаемое, и такая разность будет
стремиться к +∞. А вот в выражении снова и
,
и оба стремятся к бесконечности, но порядок
их стремления «примерно» одинаков,
равен
(у
подкоренного выражения старшая степень,
определяющая рост —
,
так как «довесок»
очень незначительная прибавка по
сравнению с
,
и ей можно пренебречь; поэтому выражение
стремится к бесконечности «приблизительно»
как ).
Неопределенность такого вида возникает, как правило, либо при исследовании разности двух дробей (в этом случае нужно привести дроби к общему знаменателю), либо при рассмотрении разности двух иррациональных выражений. В последнем случае нужно домножить и разделить на выражение «сопряженное» к данному, то есть добавить до формулы разности квадратов или до разности (суммы) кубов, чтобы избавиться от корней, создающих неопределенность.
Пример 1.4. Вычислить
Решение. При числитель стремится к -∞, а в знаменателе стоит разность двух слагаемых и , которые стремятся к бесконечности «примерно» одинаково как , так как -3 и +3 не играют существенной роли на бесконечности. Поэтому в знаменателе фиксируем неопределенность ∞-∞, и нам нужно сначала избавиться от нее. Для этого преобразуем знаменатель (раскроем скобки), получим
Теперь
видно, что знаменатель тоже стремится
к -∞, а, значит, во всей дроби неопределенность
. Мы уже знаем, для того чтобы от нее
избавиться нужно вынести за скобку в
числителе и знаменателе неизвестное в
наибольшей степени:
Мы уже знаем, для того чтобы от нее
избавиться нужно вынести за скобку в
числителе и знаменателе неизвестное в
наибольшей степени:
Пример 1.5. Вычислить
Решение. Здесь имеем дело с разностью двух слагаемых, которые стремятся к бесконечности. При этом скорость роста первого слагаемого определяет (мы уже отмечали, что в выражении вторым слагаемым можно пренебречь, так как при оно незначительно по сравнению с ). Следовательно, в этом примере также неопределенность
Тогда в числителе мы искусственно создали формулу разности квадратов, применяя ее, получим
Теперь,
очевидно, числитель и знаменатель
стремятся к бесконечности. Значит,
пришли к неопределенности
. Действуем далее как обычно при такой
неопределенности, выносим в числителе
и знаменателе неизвестное в наибольшей
степени. В числителе это
,
в знаменателе вынесем старшую степень
сначала под корнем .
Теперь под корнем стоит произведение,
и мы можем воспользоваться свойством
арифметического корня, о котором уже
вспоминали выше:
.
Получим .
В знаменателе теперь два слагаемых и
,
они оба стремятся к бесконечности со
скоростью
.
Тогда
Действуем далее как обычно при такой
неопределенности, выносим в числителе
и знаменателе неизвестное в наибольшей
степени. В числителе это
,
в знаменателе вынесем старшую степень
сначала под корнем .
Теперь под корнем стоит произведение,
и мы можем воспользоваться свойством
арифметического корня, о котором уже
вспоминали выше:
.
Получим .
В знаменателе теперь два слагаемых и
,
они оба стремятся к бесконечности со
скоростью
.
Тогда
Пример 1.6. Вычислить:
Решение. Перед
нами снова разность двух бесконечно
больших последовательностей, у которых
скорость стремления к бесконечности .
То есть, имеем дело с неопределенностью
∞-∞. Так как заданное выражение содержит
иррациональность (корень кубический),
то для избавления от неопределенности
дополним исходное выражение до формулы
разности кубов .
Для этого домножим и разделим (чтобы
ничего не изменилось) на выражение,
представляющее собой неполный квадрат
суммы для и .
Свернем числитель по формуле разности кубов
Теперь числитель и знаменатель дроби стремятся к бесконечности, то есть пришли к неопределенности . Вынесем за скобку в знаменателе под каждым корнем старшую степень
Далее разобьем корень из произведения на произведение корней
Подставляя полученное преобразование в знаменатель дроби, получим
Так как при , то , , . Следовательно, знаменатель стремится к 3, при этом числитель к бесконечности. Значит, последнее равенство справедливо, так как .
философия науки – Подразумевает ли бесконечность неопределенность? (Или наоборот?)
Неопределенность и бесконечность связаны, но это разные понятия.
С одной стороны, неопределенность представляет собой понятие, выражающее состояние модальности, то есть является ли знание или информация полным или достоверным. Это связано с такими понятиями, как вероятность и детерминизм. Бесконечность — это понятие, связанное с кардинальностью и порядковостью, то есть подсчетом и упорядочением.
Это связано с такими понятиями, как вероятность и детерминизм. Бесконечность — это понятие, связанное с кардинальностью и порядковостью, то есть подсчетом и упорядочением.
Точность — это понятие, объединяющее эти два понятия посредством выражения модальности числовой величины. Квадратный корень из двух служит прекрасным примером для объяснения того, как связаны модальность, точность и количество.
В общем, квадратный корень из двух — это число, которое определяется как операция, выполняемая над натуральным числом. По сути, математическая философия утверждает, что квадратный корень из двух иррационален, то есть не может быть выражен как отношение двух целых чисел, и поэтому любая попытка его найти должна быть неконечной и неповторяющейся десятичной дробью. (Обратите внимание, что неконечные повторяющиеся десятичные знаки могут быть выражены в виде дробей.)
Однако на практике, скажем, строят ферму для крыши, где угол коньковой доски составляет 45 градусов, необходимо фактически обрезать стропила и нижний пояс, и так имея длину пиломатериала и вырезав квадратный корень из двух нужно и можно сделать. Имеет ли значение обсуждение корня из 2 как математического объекта и практического измерения с помощью линейки с ограниченной точностью? Абсолютно. Часто говорят, что инженер — это математик, который округляет числа, а в компьютерных науках неправильное построение схемы для выполнения операций с плавающей запятой может привести к ошибкам в вычислениях.
Имеет ли значение обсуждение корня из 2 как математического объекта и практического измерения с помощью линейки с ограниченной точностью? Абсолютно. Часто говорят, что инженер — это математик, который округляет числа, а в компьютерных науках неправильное построение схемы для выполнения операций с плавающей запятой может привести к ошибкам в вычислениях.
Здесь вступает в действие понятие точности. Точность измерения — это величина, выражающая степень уверенности в измерении. Если хорду необходимо сократить до относительной длины квадратного корня из двух, квадратный корень из двух может быть выражен в некоторой степени или числе знаков после запятой. Например, если длина стропил составляет 1000 м, то хорда может быть разрезана с точностью до 1,4 м, 1,41 м или даже 1,414 м. Чем точнее измерение, тем больше уверенности в том, что разрез будет работать в системе.
Отвечая на вторую часть вашего вопроса, да, определенность и дискретность связаны, потому что чем точнее измерение, тем больше информации вы имеете. Небольшие различия в измерениях могут привести к большим различиям в результатах построенных физических систем. Вот почему НАСА использует несколько команд, каждая из которых выполняет расчеты с максимально возможной точностью, а иногда и усредняет свои результаты.
Небольшие различия в измерениях могут привести к большим различиям в результатах построенных физических систем. Вот почему НАСА использует несколько команд, каждая из которых выполняет расчеты с максимально возможной точностью, а иногда и усредняет свои результаты.
Поскольку все измерения имеют степень точности, они по определению также имеют степень неточности. Вопрос о том, насколько точность необходима или возможна, является предметом споров о природе бесконечности, причем некоторые люди отвергают ее (бесконечности нет), некоторые признают, что она возникает в практическом, физическом контексте и ограничена (потенциальная бесконечность), а третьи считают бесконечность действительной характеристикой самой вселенной (фактическая бесконечность).
Математики наводят мосты между бесконечностью и физическим миром
Натали Волховер
Наука
Удивительное новое доказательство помогает соединить физический математический мир бесконечности.
Уайли Беккерт для журнала Quanta
С помощью удивительного нового доказательства два молодых математика нашли мост через конечно-бесконечную пропасть, помогая в то же время нанести на карту эту странную границу.
Граница не проходит между каким-то огромным конечным числом и следующим, бесконечно большим. Скорее, он разделяет два вида математических утверждений: «финитистские», которые можно доказать, не прибегая к понятию бесконечности, и «бесконечные», которые основаны на допущении — неочевидном в природе — существования бесконечных объектов.
Журнал Quanta
О
Оригинальная история перепечатана с разрешения Журнала Quanta , редакционно независимого подразделения Фонд Саймонса , чья миссия состоит в том, чтобы улучшить общественное понимание науки, освещая исследовательские разработки и тенденции в математике, физических науках и науках о жизни. профессор математики Калифорнийского университета в Беркли. Это стремление ведет непосредственно к вопросам математической объективности, смысла бесконечности и отношения между математикой и физической реальностью.
профессор математики Калифорнийского университета в Беркли. Это стремление ведет непосредственно к вопросам математической объективности, смысла бесконечности и отношения между математикой и физической реальностью.
Более конкретно, новое доказательство разрешает вопрос, который ускользал от ведущих экспертов в течение двух десятилетий: классификация утверждения, известного как «теорема Рамзи для пар», или RT 2 2 . В то время как можно показать, что почти все теоремы эквивалентны одной из нескольких основных систем логики — наборам исходных предположений, которые могут включать или не включать бесконечность и охватывать конечно-бесконечное деление — RT 2 2 попадает между этими линии. «Это исключительно исключительный случай», — сказал Ульрих Коленбах, профессор математики Технического университета Дармштадта в Германии. — Вот почему это так интересно.
В новом доказательстве 34-летний Кейта Ёкояма, математик из Японского передового института науки и технологий, и Людовик Патей, 27 лет, компьютерщик из Парижского университета Дидро, определяют логическую силу числа RT 2 2 — но не на уровне, которого ожидало большинство людей.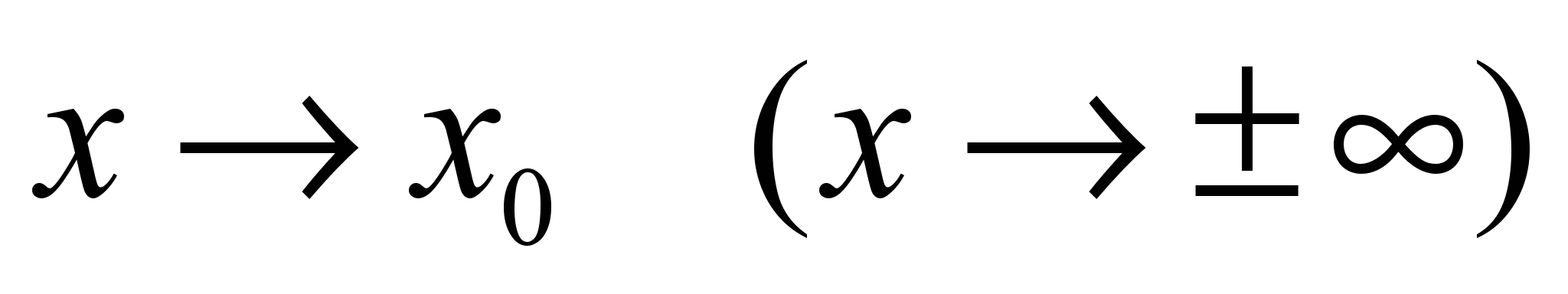 Теорема якобы является утверждением о бесконечных объектах. И все же Ёкояма и Пэти обнаружили, что она «финитивно редуцируема»: по силе она эквивалентна системе логики, которая не обращается к бесконечности. Этот результат означает, что бесконечный аппарат в RT 2 2 можно использовать для доказательства новых фактов в финитной математике, образуя удивительный мост между конечным и бесконечным. «Результат Пати и Йокоямы — действительно прорыв», — сказал Андреас Вейерманн из Гентского университета в Бельгии, чья собственная работа над RT 2 2 открыла один шаг к новому доказательству.
Теорема якобы является утверждением о бесконечных объектах. И все же Ёкояма и Пэти обнаружили, что она «финитивно редуцируема»: по силе она эквивалентна системе логики, которая не обращается к бесконечности. Этот результат означает, что бесконечный аппарат в RT 2 2 можно использовать для доказательства новых фактов в финитной математике, образуя удивительный мост между конечным и бесконечным. «Результат Пати и Йокоямы — действительно прорыв», — сказал Андреас Вейерманн из Гентского университета в Бельгии, чья собственная работа над RT 2 2 открыла один шаг к новому доказательству.
Людовик Патей (слева) и Кейта Йокояма совместно разработали доказательство долгожданной классификации теоремы Рамсея для пар. Предоставлено Людовиком Пати и Кейтой Йокогамой
Теорема Рамсея для пар считается самым сложным утверждением о бесконечности, которое, как известно, финитно приводимо. Он предлагает вам представить, что у вас в руках бесконечное множество объектов, например, множество всех натуральных чисел. Каждый объект в наборе связан со всеми другими объектами. Затем вы окрашиваете каждую пару объектов в красный или синий цвет в соответствии с некоторым правилом. (Правило может быть таким: для любой пары чисел A < B , раскрасьте пару синим цветом, если B < 2 A , и красным в противном случае.) Когда это сделано, RT 2 2 утверждает, что будет существовать бесконечное монохроматическое подмножество: множество, состоящее из бесконечно много чисел, так что все пары, которые они составляют со всеми другими числами, одного цвета. (Ёкояма, работая со Сламаном, теперь обобщает доказательство, чтобы оно было верным для любого количества цветов.)
Каждый объект в наборе связан со всеми другими объектами. Затем вы окрашиваете каждую пару объектов в красный или синий цвет в соответствии с некоторым правилом. (Правило может быть таким: для любой пары чисел A < B , раскрасьте пару синим цветом, если B < 2 A , и красным в противном случае.) Когда это сделано, RT 2 2 утверждает, что будет существовать бесконечное монохроматическое подмножество: множество, состоящее из бесконечно много чисел, так что все пары, которые они составляют со всеми другими числами, одного цвета. (Ёкояма, работая со Сламаном, теперь обобщает доказательство, чтобы оно было верным для любого количества цветов.)
Самые популярные
Раскрашиваемые делимые бесконечные множества в RT 2 2 — это абстракции, не имеющие аналога в реальном мире. И все же доказательство Йокоямы и Пати показывает, что математики могут свободно использовать этот бесконечный аппарат для доказательства утверждений финитной математики, включая правила чисел и арифметики, которые, возможно, лежат в основе всей математики, необходимой в науке, не опасаясь, что полученные теоремы основываются на логически шатком понятии бесконечности. Это потому, что все финитные последствия RT 2 2 являются «истинными» с бесконечностью или без нее; они гарантированно доказуемы каким-то другим, чисто финитистским способом. Бесконечные структуры RT 2 2 «могут упростить поиск доказательства, — объяснил Сламан, — но в конце концов они вам не понадобились. Вы могли бы дать что-то вроде нативного доказательства — [финитистского] доказательства».
Это потому, что все финитные последствия RT 2 2 являются «истинными» с бесконечностью или без нее; они гарантированно доказуемы каким-то другим, чисто финитистским способом. Бесконечные структуры RT 2 2 «могут упростить поиск доказательства, — объяснил Сламан, — но в конце концов они вам не понадобились. Вы могли бы дать что-то вроде нативного доказательства — [финитистского] доказательства».
Когда Ёкояма нацелился на RT 2 2 четыре года назад в качестве исследователя с докторской степенью, он ожидал, что все обернется иначе. «Честно говоря, я думал, что на самом деле это не финитно редуцируется», — сказал он.
Люси Ридинг-Икканда для журнала Quanta
Частично это было связано с тем, что более ранняя работа доказала, что теорема Рамсея для троек, или RT 2 3 , не является финитистски редуцируемой: подмножество троек, которое, по словам RT 2 3 , вы получите, слишком сложная бесконечность, чтобы сводить ее к финитным рассуждениям. То есть по сравнению с бесконечностью в RT 2 2 , тот, что в RT 2 3 , так сказать, более безнадежно бесконечен.
То есть по сравнению с бесконечностью в RT 2 2 , тот, что в RT 2 3 , так сказать, более безнадежно бесконечен.
Пока математики, логики и философы продолжают анализировать тонкие следствия результата Пати и Йокоямы, это триумф «частичной реализации программы Гильберта» — подхода к бесконечности, отстаиваемого математиком Стивеном Симпсоном из Университета Вандербильта. Программа заменяет ранее недостижимый план действий великого математика Давида Гильберта, который в 1921 приказал математикам полностью вплести бесконечность в лоно финитной математики. Гильберт видел в финитистской сводимости единственное средство от скептицизма, окружавшего новую математику бесконечного. Как Симпсон описал ту эпоху: «Были вопросы о том, уходит ли математика в сумеречную зону».
Восход бесконечности
Философия бесконечности, изложенная Аристотелем в четвертом веке до нашей эры. царил практически безраздельно до 150 лет назад. Аристотель принял «потенциальную бесконечность» — обещание числовой прямой (например) продолжаться вечно — как вполне разумную концепцию в математике. Но он отверг как бессмысленное понятие «актуальной бесконечности» в смысле полного множества, состоящего из бесконечно многих элементов.
Но он отверг как бессмысленное понятие «актуальной бесконечности» в смысле полного множества, состоящего из бесконечно многих элементов.
Различие Аристотеля удовлетворяло потребности математиков вплоть до XIX века. До этого «математика была в основном вычислительной», — сказал Джереми Авигад, философ и математик из Университета Карнеги-Меллона. Евклид, например, вывел правила построения треугольников и биссектрис — полезные для строительства мостов, — а гораздо позже астрономы использовали инструменты «анализа» для расчета движения планет. Реальная бесконечность, которую невозможно вычислить по самой своей природе, была мало полезна. Но 19В 20-м веке произошел сдвиг от расчетов к концептуальному пониманию. Математики начали изобретать (или открывать) абстракции — прежде всего, бесконечные множества, впервые введенные в 1870-х годах немецким математиком Георгом Кантором. «Люди пытались найти способы пойти дальше, — сказал Авигад. Теория множеств Кантора оказалась новой мощной математической системой. Но такие абстрактные методы вызывали споры. «Люди говорили, что если вы приводите аргументы, которые не говорят мне, как считать, это не математика».
Но такие абстрактные методы вызывали споры. «Люди говорили, что если вы приводите аргументы, которые не говорят мне, как считать, это не математика».
Подробнее Quanta
И, что тревожно, предположение о существовании бесконечных множеств привело Кантора прямо к некоторым неинтуитивным открытиям. Он обнаружил, что бесконечные множества входят в бесконечный каскад размеров — башня бесконечности, не имеющая связи с физической реальностью. Более того, теория множеств дала доказательства теорем, которые было трудно проглотить, таких как парадокс Банаха-Тарского 1924 года, в котором говорится, что если разбить сферу на части, каждая из которых состоит из бесконечно плотного разброса точек, можно сложить части вместе по-другому, чтобы создать две сферы того же размера, что и оригинал. Гильберт и его современники беспокоились: была ли бесконечная математика последовательной? Было ли это правдой?
Более того, теория множеств дала доказательства теорем, которые было трудно проглотить, таких как парадокс Банаха-Тарского 1924 года, в котором говорится, что если разбить сферу на части, каждая из которых состоит из бесконечно плотного разброса точек, можно сложить части вместе по-другому, чтобы создать две сферы того же размера, что и оригинал. Гильберт и его современники беспокоились: была ли бесконечная математика последовательной? Было ли это правдой?
Самые популярные
Среди опасений, что теория множеств содержит действительное противоречие — доказательство 0 = 1, которое сделает недействительной всю конструкцию — математика столкнулась с экзистенциальным кризисом. Вопрос, как сформулировал Симпсон, заключался в следующем: «В какой степени математика на самом деле говорит о чем-то реальном? [Это] речь идет о каком-то абстрактном мире, который далек от реального мира вокруг нас? Или математика в конечном счете имеет свои корни в реальности?»
Хотя Гильберт и его современники ставили под сомнение ценность и непротиворечивость бесконечной логики, Гильберт и его современники не хотели отказываться от таких абстракций — мощных инструментов математического мышления, которые в 1928 г.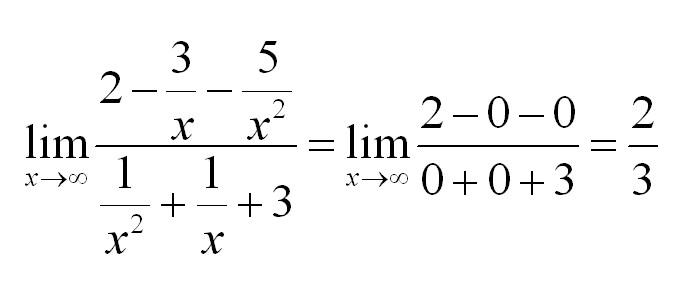 устанавливает по желанию. «Никто не изгонит нас из рая, созданного для нас Кантором», — сказал Гильберт в лекции 1925 года. Он надеялся остаться в канторовском раю и получить доказательства того, что он стоит на устойчивой логической основе. Гильберт поручил математикам доказать, что теория множеств и вся инфинитистская математика финитивно сводимы и, следовательно, заслуживают доверия. «Мы должны знать; мы узнаем!” он сказал в 19Адрес 30 в Кенигсберге – слова, позже выгравированные на его могиле.
устанавливает по желанию. «Никто не изгонит нас из рая, созданного для нас Кантором», — сказал Гильберт в лекции 1925 года. Он надеялся остаться в канторовском раю и получить доказательства того, что он стоит на устойчивой логической основе. Гильберт поручил математикам доказать, что теория множеств и вся инфинитистская математика финитивно сводимы и, следовательно, заслуживают доверия. «Мы должны знать; мы узнаем!” он сказал в 19Адрес 30 в Кенигсберге – слова, позже выгравированные на его могиле.
Однако австрийско-американский математик Курт Гёдель в 1931 году показал, что на самом деле мы этого не сделаем. В шокирующем результате Гёдель доказал, что никакая система логических аксиом (или исходных предположений) никогда не может доказать свою непротиворечивость; чтобы доказать, что система логики непротиворечива, вам всегда нужна другая аксиома вне системы. Это означает, что в математике нет окончательного набора аксиом — теории всего. Когда вы ищете набор аксиом, который дает все истинные математические утверждения и никогда не противоречит сам себе, вам всегда нужна еще одна аксиома. Теорема Гёделя означала, что программа Гильберта была обречена: аксиомы финитной математики не могут даже доказать свою непротиворечивость, не говоря уже о непротиворечивости теории множеств и математики бесконечности.
Теорема Гёделя означала, что программа Гильберта была обречена: аксиомы финитной математики не могут даже доказать свою непротиворечивость, не говоря уже о непротиворечивости теории множеств и математики бесконечности.
Это могло бы вызывать меньше беспокойства, если бы можно было ограничить неопределенность, связанную с бесконечными множествами. Но вскоре оно начало просачиваться в царство конечного. Математики начали придумывать бесконечные доказательства конкретных утверждений о натуральных числах — теорем, которые предположительно могли бы найти применение в физике или информатике. И это нисходящее рассуждение продолжалось. В 1994 году Эндрю Уайлс использовал инфинитистскую логику, чтобы доказать Великую теорему Ферма, великую проблему теории чисел, о которой Пьер де Ферма в 1637 году загадочно заявил: «Я обнаружил поистине чудесное доказательство этого, которое слишком узко, чтобы вместить его». Можно ли доверять 150-страничному, пронизанному бесконечностью доказательству Уайлса?
Имея в виду такие вопросы, такие логики, как Симпсон, сохраняли надежду, что программа Гильберта может быть реализована хотя бы частично. Хотя не вся инфинитистская математика может быть сведена к финитистским рассуждениям, они утверждают, что наиболее важные части можно укрепить. Симпсон, приверженец философии Аристотеля, который отстаивал эту идею с 1970-х годов (вместе с Харви Фридманом из Университета штата Огайо, который первым ее предложил), считает, что около 85 % известных математических теорем можно свести к финитным системам логики. «Значение этого, — сказал он, — состоит в том, что наша математика таким образом связана посредством финитной сводимости с реальным миром».
Хотя не вся инфинитистская математика может быть сведена к финитистским рассуждениям, они утверждают, что наиболее важные части можно укрепить. Симпсон, приверженец философии Аристотеля, который отстаивал эту идею с 1970-х годов (вместе с Харви Фридманом из Университета штата Огайо, который первым ее предложил), считает, что около 85 % известных математических теорем можно свести к финитным системам логики. «Значение этого, — сказал он, — состоит в том, что наша математика таким образом связана посредством финитной сводимости с реальным миром».
Исключительный случай
Почти все тысячи теорем, изученных Симпсоном и его последователями за последние четыре десятилетия, оказались (несколько загадочным образом) сводимыми к одной из пяти систем логики, охватывающих обе стороны конечно-бесконечного разделять. Например, в 1972 году было показано, что теорема Рамсея для троек (и всех упорядоченных множеств, содержащих более трех элементов) относится к третьему уровню иерархии, который является бесконечным. «Мы очень четко понимали закономерности, — сказал Генри Тауснер, математик из Пенсильванского университета. «Но люди посмотрели на теорему Рэмси для пар, и она выбила все из колеи».
«Мы очень четко понимали закономерности, — сказал Генри Тауснер, математик из Пенсильванского университета. «Но люди посмотрели на теорему Рэмси для пар, и она выбила все из колеи».
Прорыв произошел в 1995 году, когда британский логик Дэвид Ситапун, работая со Сламаном в Беркли, доказал, что RT 2 2 логически слабее RT 2 3 и, следовательно, ниже третьего уровня в иерархии. Точка разрыва между RT 2 2 и RT 2 3 возникает из-за того, что для построения бесконечных монохроматических наборов троек требуется более сложная процедура раскраски, чем бесконечные монохроматические наборы пар.
Самые популярные
Люси Ридинг-Икканда для журнала Quanta
«С тех пор было опубликовано много основополагающих статей, касающихся RT 2 2 », — сказал Вейерманн, — наиболее важно то, что результат 2012 года, проведенный Цзяи Лю (в сочетании с результатом Карла Йокуша из 1960-х годов), показал, что RT 2 2 не может доказать и не быть доказанным логической системой, расположенной на втором уровне иерархии, на одну ступеньку ниже RT 2 3 . Известно, что система второго уровня финитически сводится к «примитивно-рекурсивной арифметике» — набору аксиом, который многие считают самой сильной финитистской системой логики. Вопрос был в том, RT 2 2 также может быть сведена к примитивно-рекурсивной арифметике, несмотря на то, что она не принадлежит ко второму уровню иерархии или требует более сильных, бесконечных аксиом. «Окончательная классификация RT 2 2 казалась недостижимой», — сказал Вейерманн.
Известно, что система второго уровня финитически сводится к «примитивно-рекурсивной арифметике» — набору аксиом, который многие считают самой сильной финитистской системой логики. Вопрос был в том, RT 2 2 также может быть сведена к примитивно-рекурсивной арифметике, несмотря на то, что она не принадлежит ко второму уровню иерархии или требует более сильных, бесконечных аксиом. «Окончательная классификация RT 2 2 казалась недостижимой», — сказал Вейерманн.
Но затем, в январе, Патей и Йокояма, молодые стрелы, которые встряхнули поле с их совместным опытом в теории вычислимости и теории доказательств, соответственно, объявили о своем новом результате на конференции в Сингапуре. Используя множество методов, они показали, что RT 2 2 действительно равна по логической силе примитивно-рекурсивной арифметике и, следовательно, финитически приводима.
«Все спрашивали их: „Что вы сделали, что вы сделали? ». «Ёкояма очень скромный парень. Он сказал: «Ну, мы не сделали ничего нового; все, что мы сделали, это использовали метод индикаторов, и мы использовали эту другую технику», и он продолжил перечислять практически все техники, которые кто-либо когда-либо разрабатывал для работы над такого рода проблемами».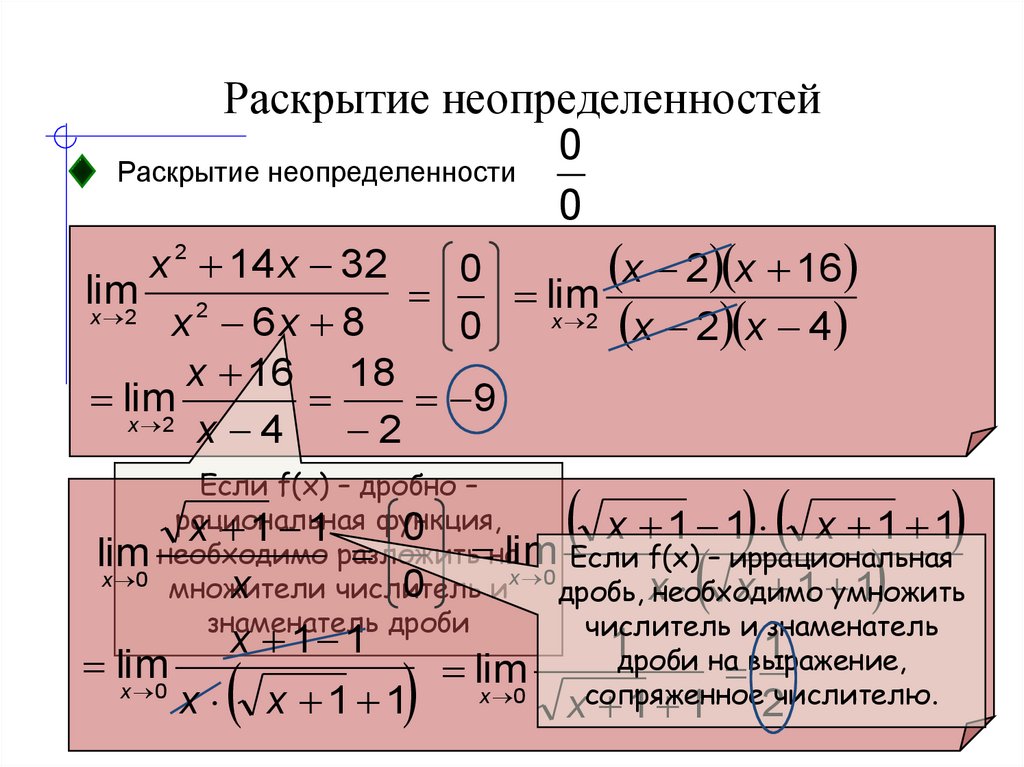
На одном ключевом этапе дуэт смоделировал бесконечное монохроматическое множество пар в RT 2 2 , используя конечное множество, элементы которого являются «нестандартными» моделями натуральных чисел. Это позволило Пэти и Йокояме перевести вопрос о силе RT 2 2 в размер конечного множества в их модели. «Мы напрямую вычисляем размер конечного множества, — сказал Ёкояма, — и если оно достаточно велико, то мы можем сказать, что оно не финитно приводимо, а если оно достаточно мало, мы можем сказать, что оно финитивно приводимо». Он был достаточно мал.
RT 2 2 имеет многочисленные финитистские следствия, утверждения о натуральных числах, которые, как теперь известно, выражаются в примитивно-рекурсивной арифметике и, таким образом, несомненно, логически непротиворечивы. Более того, эти утверждения — которые часто можно представить в виде «для каждого числа X существует другое число Y , такое что…» — теперь гарантированно содержат примитивно-рекурсивные алгоритмы, связанные с ними для вычисления Y . «Это более прикладное прочтение нового результата», — сказал Коленбах. В частности, он сказал, RT 2 2 может привести к новым ограничениям на алгоритмы «перезаписи терминов», устанавливая верхний предел количества раз, когда результаты вычислений могут быть дополнительно упрощены.
«Это более прикладное прочтение нового результата», — сказал Коленбах. В частности, он сказал, RT 2 2 может привести к новым ограничениям на алгоритмы «перезаписи терминов», устанавливая верхний предел количества раз, когда результаты вычислений могут быть дополнительно упрощены.
Самые популярные
Некоторые математики надеются, что другие инфинитистские доказательства могут быть переработаны на языке RT 2 3 2 90 и последовательно показаны в виде RT 04 2 3 2 90. Надуманный пример — доказательство Уайлса Великой теоремы Ферма, которое такие исследователи, как Симпсон, рассматривают как святой Грааль. «Если бы кто-нибудь обнаружил доказательство теоремы Ферма, которое является финитистским, за исключением некоторых умных приложений RT 2 2, — сказал он, — тогда результат Пати и Йокоямы подскажет нам, как найти чисто финистичное доказательство того же самого доказательства». теорема».
Симпсон считает раскрашиваемые делимые бесконечные множества в RT 2 2 «удобными фикциями», которые могут открыть новые истины о конкретной математике. Но может возникнуть вопрос, может ли вымысел быть настолько удобным, чтобы о нем можно было думать как о факте? Придает ли финитистская сводимость какую-либо «реальность» бесконечным объектам — актуальной бесконечности? Среди специалистов нет единого мнения. У Авигада двоякое мнение. В конечном счете, говорит он, нет необходимости решать. «Существует постоянное противоречие между идеализацией и конкретной реализацией, и мы хотим и того, и другого», — сказал он. «Я рад принять математику за чистую монету и сказать: смотрите, бесконечные множества существуют в той мере, в какой мы знаем, как рассуждать о них. И они играют важную роль в нашей математике. Но в то же время, думаю, полезно подумать, ну а как именно они играют роль? И какая связь?»
Но может возникнуть вопрос, может ли вымысел быть настолько удобным, чтобы о нем можно было думать как о факте? Придает ли финитистская сводимость какую-либо «реальность» бесконечным объектам — актуальной бесконечности? Среди специалистов нет единого мнения. У Авигада двоякое мнение. В конечном счете, говорит он, нет необходимости решать. «Существует постоянное противоречие между идеализацией и конкретной реализацией, и мы хотим и того, и другого», — сказал он. «Я рад принять математику за чистую монету и сказать: смотрите, бесконечные множества существуют в той мере, в какой мы знаем, как рассуждать о них. И они играют важную роль в нашей математике. Но в то же время, думаю, полезно подумать, ну а как именно они играют роль? И какая связь?»
С такими открытиями, как финитистская сводимость RT 2 2 — самого длинного моста между конечным и бесконечным — математики и философы постепенно приближаются к ответам на эти вопросы. Но путешествие длилось уже тысячи лет и вряд ли закончится в ближайшее время.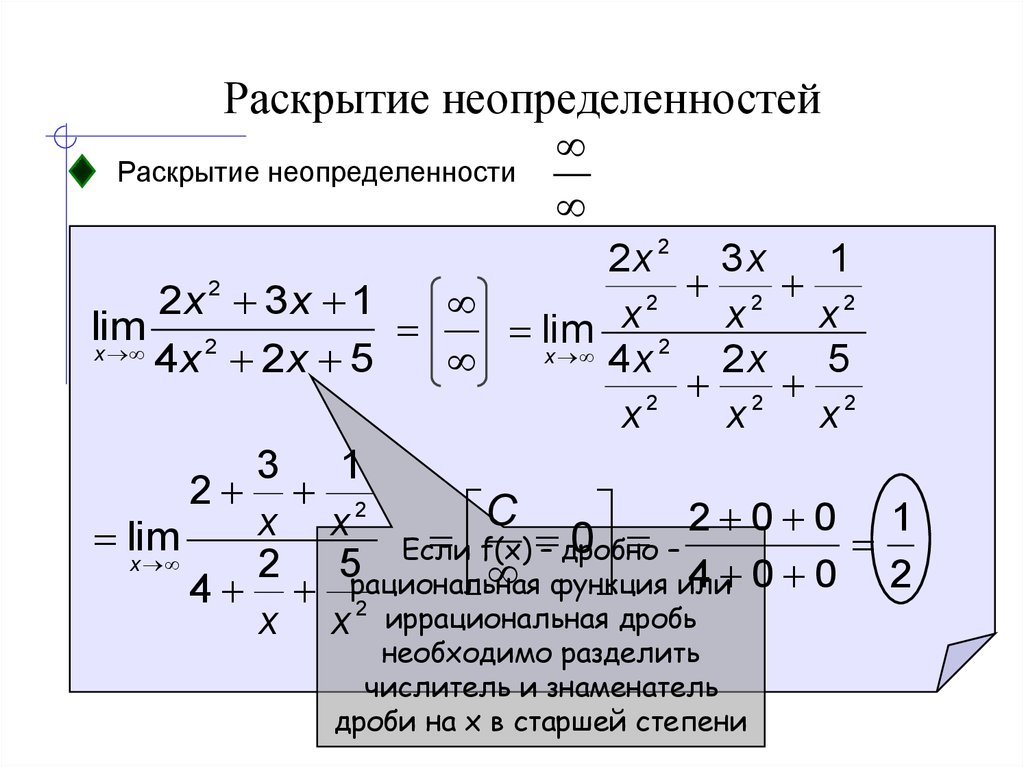

 Erica Klarreich ##### Математики открыли главный заговор
Erica Klarreich ##### Математики открыли главный заговор wired.com/photos/w_200,h_200/wp -content/uploads/2015/12/4Theorists_1200-200×200-e1450390345967.jpg” alt=”Отряд математиков соединяет теорию чисел и геометрию” itemprop=”image”>
Кевин Хартнетт ##### Отряд математиков связывает теорию чисел и геометрию
wired.com/photos/w_200,h_200/wp -content/uploads/2015/12/4Theorists_1200-200×200-e1450390345967.jpg” alt=”Отряд математиков соединяет теорию чисел и геометрию” itemprop=”image”>
Кевин Хартнетт ##### Отряд математиков связывает теорию чисел и геометрию