Все другие выражения не являются неопределенностями и принимают какое-то конкретное конечное или бесконечное значение.
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
Основные пределы
1. Первый замечательный предел: $\lim _{x \rightarrow 0} \frac{\sin x}{x}=1$
Пример
Задание. Вычислить предел $\lim _{x \rightarrow 0} \frac{\sin 3 x}{\arcsin 7 x}$
Решение. Получим неопределенность, сделаем замену. При $x \rightarrow 0$: $\sin x \sim x$, $\arcsin x \sim x$
$\lim _{x \rightarrow 0} \frac{\sin 3 x}{\arcsin 7 x}\left[\frac{0}{0}\right]=\lim _{x \rightarrow 0} \frac{3 x}{7 x}=\lim _{x \rightarrow 0} \frac{3}{7}=\frac{3}{7}$
Ответ. $\lim _{x \rightarrow 0} \frac{\sin 3 x}{\arcsin 7 x}=\frac{3}{7}$
2. Второй замечательный предел: $\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^{x}=e$
Слишком сложно?
Основные неопределенности и способы их раскрытия не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. {2}-5 x+6}=-4$
{2}-5 x+6}=-4$
Читать дальше: понятие непрерывности функции в точке.
Анализ простейших правил раскрытия неопределенностей
Библиографическое описание:Юлдашева, С. Б. Анализ простейших правил раскрытия неопределенностей / С. Б. Юлдашева. — Текст : непосредственный // Молодой ученый. — 2020. — № 52 (342). — С. 4-9. — URL: https://moluch.ru/archive/342/76887/ (дата обращения: 30.08.2021).
Значительное место в школьном курсе математики занимают элементы математического анализа, в том числе и пределы функций с раскрытием неопределенностей. Целью изучения в школьной программе этой темы является формирование интеллектуального развития учащихся, формирование качеств мышления, необходимых человеку для свободной ориентации в современном мире; овладение математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования. Но как показывает опыт преподавания учителей в школе, вычисление пределов вызывает большие затруднения у школьников по сравнению с другими темами.Вразделе «Предел функции и непрерывность» заметен высокий уровень научности и строгости понятий предела и непрерывности функции. Раскрытие неопределенностей — методы вычисления пределов функций, заданных формулами, которые теряют смысл в результате формальной подстановки в них предельных значений аргумента, то есть переходят в выражения
.
Но как показывает опыт преподавания учителей в школе, вычисление пределов вызывает большие затруднения у школьников по сравнению с другими темами.Вразделе «Предел функции и непрерывность» заметен высокий уровень научности и строгости понятий предела и непрерывности функции. Раскрытие неопределенностей — методы вычисления пределов функций, заданных формулами, которые теряют смысл в результате формальной подстановки в них предельных значений аргумента, то есть переходят в выражения
.
Вопрос решения пределов является достаточно обширным и является объектом интереса современных направлений математики. Существуют десятки нюансов и хитростей, позволяющих решить данный предел. Объектом нашего исследования правила раскрытия неопределенностей и правила Лопиталя. Можно привести огромный список литературы, в которой изучаются пределы, способы их вычислений. Вместе с тем, при изучении нами различных публикаций по данной тематике выявлена относительная недостаточность данных в курсе школьной математики.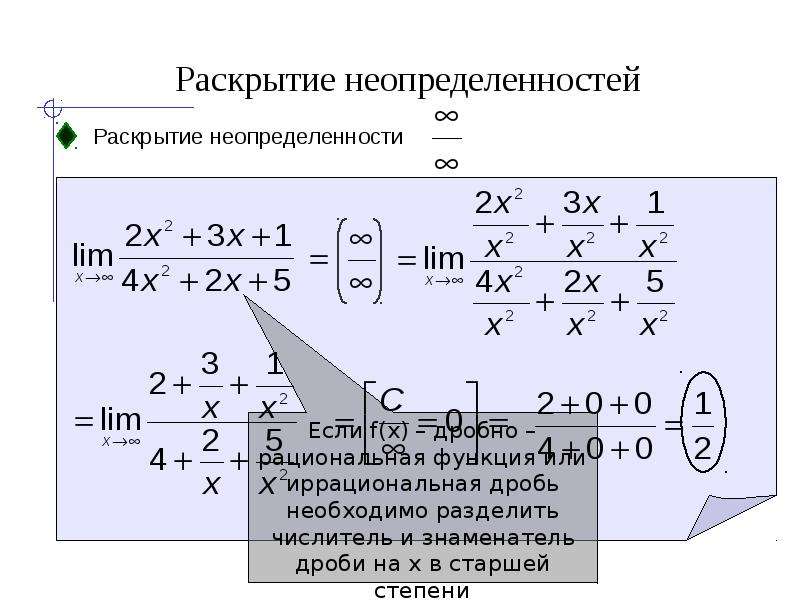
1. Предел функции
Вспомним определения:
1) Число L называется пределом функции f(x) при x a , если для любого сколь угодно малого числа найдется число N такое, что при . Символически записывают так:
2) Число L называется пределом функции f(x) при x , если для любого сколь угодно малого числа найдется такое число , что для любого x>N выполняется неравенство Пишут:
Отыскание предела функции по определению — это довольно трудоемкий процесс. Поэтому на практике удобнее пользоваться следующими теоремами о пределах.
Теорема. Если функции имеют пределы при
, то существует
1) предел суммы этих функций, причем
2) предел произведения этих функций, причем
3) предел их отношения
4) постоянный множитель можно выносить за знак предела:
Некоторые методы и приемы вычисления пределов.
Пример 1.Найти предел:
Пример 2.Найти предел:
Пример 3.Найти предел:
Пример 4.Найти предел:
2. Раскрытие неопределенностей
Нужно иметь в виду, что знак — это только символ для обозначения бесконечно большой величины. Он не обладает свойствами числа и в арифметических действиях не участвует. В следствие этого возникают различного рода неопределённости. Основные виды неопределенностей:
Вычисление пределов в этих случаях называют «раскрытием неопределенности».
Пример 1.Найти предел:
Решение. Теорему о пределе частного применять нельзя, так как числитель и знаменатель дроби конечного предела не имеют. Имеем неопределенность вида . Для избавления от неопределенности вынесем за скобки в числителе и знаменателе дроби переменную в старшей степени:
Пример 2.Найти предел:
Решение. Числитель и знаменатель дроби при х 0 стремятся к нулю, следовательно, имеем неопределенность вида . Для того, чтобы вычислить предел, перенесем иррациональность в знаменатель, умножив для этого числитель и знаменатель дроби на . Тогда
Пример 3.Найти предел:
Решение.Неопределенность здесь можно раскрыть, сделав замену переменной , тогда
Пример 4.Найти предел:
Решение. При вычислении данного предела применять теорему о пределе частного нельзя, так и числитель, и знаменатель равны 0. Воспользуемся разложением многочленов числителя и знаменателя на множители по формуле
где
Воспользуемся разложением многочленов числителя и знаменателя на множители по формуле
где
. Тогда
3. Замечательные пределы
Пределы функций, в которых участвуют тригонометрические выражения, обычно сводятся к первому замечательному пределу
Также используют несколько его следствий:
, , , ,
Пример 5.Найти предел:
Решение. Для избавления неопределенности воспользуемся первым замечательным пределом
Пример 6.Найти предел:
Решение. Произведя следующие преобразования, имеем
Пример 7. Найти предел:
Решение. Так как , то
Пример 8.Найти предел:
Решение. В этом примере получаем неопределенность вида . Приведем выражение под знаком предела к общему знаменателю.
Пример 9. Найти предел:
Найти предел:
Решение. Неопределенность вида сведем к неопределенности , тогда
Сделаем замену переменных , тогда и
Заключение
Таким образом, в процессе раскрытия неопределенностей можно выделить следующие основные этапы:
1) подготовка выражения под знаком предела к устранению неопределенности путем применения преобразований;
2) переход (в случае необходимости) к неопределенности или — переход от одной функции к другой.
Литература:
- Абылкасымова А. Е., Кучер Т. П., Корчевский В. Е., Жумагулова З. А., Алгебра и начала анализа: Учебник для 10 класса ЕМН, Алматы: Мектеп, 2019;
- Темиргалиев Н., Введение в математический анализ, Астана, 2015;
- Круглов Е. В., Мамаева Н. А., Таланова Е. А., Некоторые приемы вычисления пределов Нижний Новгород, 2018;
- Матвеева Т. А., Рыжкова Н. Г., Математический анализ, Екатеринбург, 2017;
- Самочернова Л.

- Альпин Т. Ю., Егоров А. И., Кашаргин П. Е., Сушков С. В., Практические занятия по математическому анализу, Казань, 2013.
Основные термины (генерируются автоматически): предел, знаменатель дроби, неопределенность вида, предел функции, раскрытие неопределенностей, решение, вычисление пределов, замечательный предел, малое число, предел функций.
6.2. Раскрытие неопределенностей различных типов
Далеко не всякая подстановка предельного значения в функцию вместо независимой переменной может сразу привести к нахождению предела. Случаи, в которых подстановка предельного значения в функцию не дает значения предела, называют
Устранить
неопределенность удается часто с
помощью алгебраических преобразований.
6.12. Найти
Решение. Имеем неопределенность вида [–]. Вынесем за скобкухв наибольшей степени:
х4является бесконечно большой величиной прих . По теоремам о пределах
так как иприх являются бесконечно малыми величинами, а предел постоянной равен самой постоянной (единице). По свойству бесконечно большихявляется бесконечно большой величиной, т.е. искомый предел равен.
Ответ данной задачи и приведенные в решении выкладки будем использовать при решении следующих примеров как заранее известные факты. Рассмотрим несколько типов примеров, классифицируя их по виду неопределенности и предельному значению х.
1-й
тип. Рассмотрим примеры видас
неопределенностью вида,
гдеf(x)и(х)в общем
случае – сложные степенные или
показательные функции. В случае степенных
функций необходимо выносить за скобку
в числителе и знаменателе дробихс наибольшим показателем степени среди
всех слагаемых дроби; в случае
показательных функций за скобку
выносится наиболее быстро возрастающее
слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность
устраняется.
После сокращения дроби неопределенность
устраняется.
6.13. Найти
Решение. Вынося за скобку и в числителе и в знаменателехв наибольшей степени, получим
так как ,,, – величины бесконечно малые прих .
6.17. Найти
Решение. Припоказательная функция, пристремится к. Быстрее будет возрастать та функция, у которой основание больше, поэтому в нашем случае выносим за скобки:
так как при и при.
Найти пределы:
6.18.
6.19.
6.20.
6.21.
6.22.
6.23.
6.24.
6.25.
6.26.
2-й тип. Рассмотрим примеры
вида с неопределенностью видаВ этом случае необходимо разложить на
множители и числитель, и знаменатель
дроби или домножить и числитель, и
знаменатель дроби на одно и то же
выражение, приводящее к формулам
сокращенного умножения. Неопределенность
устраняется после сокращения дроби.
Рассмотрим примеры
вида с неопределенностью видаВ этом случае необходимо разложить на
множители и числитель, и знаменатель
дроби или домножить и числитель, и
знаменатель дроби на одно и то же
выражение, приводящее к формулам
сокращенного умножения. Неопределенность
устраняется после сокращения дроби.
6.45.Найти
Решение.Имеем неопределенность видаРазложим числитель и знаменатель дроби на множители: числитель – по формуле сокращенного умноженияа знаменатель – по формуле разложения квадратного трехчлена на множители при
где
Получим
После сокращения дроби следует подставить предельное значение хв сокращенную дробь. Получим
6.46. Найти
Решение.1-й способ. Имеем неопределенность видаДополним числитель до разности квадратова знаменатель до разности кубовПолучим
2-й способ. Сделаем замену переменной:тогдааприт.е.Теперь
Сделаем замену переменной:тогдааприт.е.Теперь
Найти пределы:
6.47.
6.48.
6.49.
6.50.
6.51.
6.52.
6.53.
6.54.
6.55.
6.56.
6.57.
6.58.
3-й тип. Рассмотрим примеры
с неопределенностью вида [∞ – ∞].
Если функция, стоящая под знаком предела,
представляет собой алгебраическую
сумму дробей, то неопределенность
устраняется или приводится ко 2-му типу
после приведения дробей к общему
знаменателю. Если упомянутая функция
представляет собой алгебраическую
сумму иррациональных выражений, то
неопределенность или устраняется, или
приводится к 1-му типу путем домножения
и деления функции на одно и то же
(сопряженное) выражение, приводящее к
формулам сокращенного умножения.
6.68. Найти
Решение. Имеем неопределенность вида [∞ – ∞]. Приведем дроби к общему знаменателю:
Имеем предел 2-го типа, необходимо разложить на множители числитель дроби. Получим
6.69. Найти
Решение.Имеем неопределенность вида [∞ – ∞]. Домножим и разделим функцию, стоящую под знаком предела на сопряженное выражение, приводящее к разности квадратов:
Имеем предел 1-го типа.
При по определению модуля; поэтому
так как при – бесконечно малые величины.
Найти пределы:
6.70.
6.71.
6.72.
6.73.
6.74.
6. 75.
75.
6.76.
6.77.
6.78.
6.79.
6.80.
6.81.
6.82.
6.83.
6.84.
6.85.
6.86.
6.87.
6.3. Замечательные пределы
К пределам 4-го типаотнесем примеры с неопределенностью вида. В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела» .
6.97. Найти
Решение.Имеем неопределенность вида, так как
Выделим целую часть дроби
является бесконечно малой величиной
прих → ∞. Домножим показатель
степени наэто действие не нарушает знака равенства:
Домножим показатель
степени наэто действие не нарушает знака равенства:
ибо НайдемИмеем неопределенность видапредел 1-го типа. Вынесем за скобких2, так как вторая степень наибольшая:
так как Таким образом предел равен
6.99. Найти
Решение.Имеем неопределенность видапреобразуем ее в неопределенность вида, пользуясь свойствами логарифмов:
Получим
Учитывая непрерывность логарифмической функции, символы limиlnможно переставить , получим
так как по формуле
Найти пределы:
6.100.
6.101.
6.102.
6.103.
6.104.
6.105.
6.106.
6.107.
6.108.
5-й тип.К этому типу отнесем функции, сводящиеся к первому замечательному пределу (6.1):
6.121. Найти
Решение.
Первый сомножитель представляет собой первый замечательный предел и равен 1, второй сомножитель представляет предел, равный . Таким образом, искомый предел равен 11 = 1.
6.122. Найти
Решение.Имеем неопределенность видаСделаем замену переменной:
arcsin х=у; тогдах = sinу; прих→ 0,у→0; получим
Имеем первый замечательный предел, следовательно искомый предел равен 1, что и требовалось доказать.
Найти пределы:
6.124.
6.125.
6. 126.
126.
6.127.
6.128.
6.129.
6.130.
6.131.
6.132.
6.133.
6.134.
6.135.
He рассмотренные в этой главе неопределенности видов [0], [0°] и [°] могут быть устранены при помощи правила Лопиталя, которое будет рассмотрено в главе 8.
Переменная величина. Предел функции. Раскрытие простейших неопределенностей. Правило Лопиталя
· Переменная величина – величина, которая принимает различные численные
значения, в противном случае она называется постоянной. Перемен величины: x, y, z, u.
постоянные:a, b, c. Множиство всех числовых занчений переменной величины
наз обл измен этой переменной.(х=const, для всевозможн α есть отрезок [-1;1]).
Упорядоченная переменная величина – когда и область изменения переменной x и
порядок в котором она принемает свои значения Xn=1/n. -k=1/x – график – гипербола. Y=sin x , y=cos x – тригонометрические ф-ции график синусоида и
косинусоида. Y=√x – обратная функция. Y=log(a)x – логарифмическая.
-k=1/x – график – гипербола. Y=sin x , y=cos x – тригонометрические ф-ции график синусоида и
косинусоида. Y=√x – обратная функция. Y=log(a)x – логарифмическая.
· Предел ф-ции: число b наз приделом ф-ции y=f(x) при х стремящимуся к a если для любого Е ≥ 0 cущ число δ(Е) ≥ 0 ткое что для всех х≠а удовл неравенству /х-а/≤δ вып неравенства /f(x)-b/≤Е (функция стремится к b при х стремящимуся к а)
Ф-ция наз бесконечно малой при х стремящимся к а(∞) если
lim f(x)= 0
если при
Х .Стремящимся к а (∞) f(x) стремится к ∞ то такая ф-ция наз
бесконечно
большой.
1) Ф-ция обратная по величине бесконечно большой есть бесконечно малая
Ф-ция
f(x) обратная по величине бесконечно малой отлчной от 0
есть бесконечно большая т. 0=1
(x→1)
0=1
(x→1)
3) lim arcsin x = arcsin √2/2 = π/4 (x→1)
4) lim ln(x-2) = ln(3-2)=ln1= 0 (x→3)
5) lim F(u(x) = F(lim u(x) , F(u(x) – сложная ф-ция, (x→a)
· Раскрытие простейших неопределенностей: вида 0/0 функция есть отношение двух бесконечно малых ф-ций (х→а или ∞) lim f(x)=lim f(a) (x→a)
1) разложить на множители числит и знаменат и при наличии одинаковых множит стремящ к нулю дробь на них сократить.
2) Избавится от иррациональности в числители или знаменат и при наличии одинаковых бесконечно малых мнозит дробь на них сократить.
3) Исп первый замечат придел: lim (sin x/x)=1
Неопред вида ∞/∞ : когда ф-ция есть отношение двух бесконечнобольших ф-ций (х→∞,а)
1) при наличии многочленов делят почленно и числит и знам на старшую степень независемой переменной
2)
предел и числителя и знамо пред
пределами старшей степени и делят на числит и знам и на переем в старшей
степени.
·
Производная ф-ции– пусть ∆х
приращение аргумента х тогда х+∆х новое значение аргумента , а ∆f(x)=f(x+∆x)-f(x) –
соответств приращение ф-ции f(x) ∆f(x)/∆x производная – основное
понятие дифференциального исчисления,
характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента
к нулю (если таковой предел существует). Функцию,
имеющую конечную производную, называют дифференцируемой. Процесс вычисления
производной называется дифференцированием. Пусть ∆х→0, тогда lim ∆f(x)/ ∆x =f (x) наз производной f(x) в
точке х. Если указ придел сущь то ф-ция наз диф в данной точеке х, если произв
рана ∞, то такая ф-ция имеет бесконечную произв. Геометр смысл :f (x)=tg α- угол наклона касательной проведенной к кривой f(x) в
точке х к положительному направлению оси Ох. Физический смысл: Пусть
тело движется прямолинейно и закон его движения по времени задан уравнен s(t)
тогда производная s(t) есть мнгновенная скорость в момент t
т. е. v(t)=S (t).
е. v(t)=S (t).
·
·
·
· Основные правила дифф. Элементарные ф-ции: Пусть u и v существуют тоесть их ф-ции диф. Дифференцирование любой функции ведется путем сведения дифференцирования данной функции с помощью свойств производных к дифференцированию некой преобразованной функции, составленной из табличных элементарных функций.
Практическая работа Вычисление пределов
Просмотр содержимого документа
«Практическая работа Вычисление пределов»
Практическая работа
Вычисление пределов
Цель: формирование умений вычислять пределы последовательностей и функций,
раскрывать в простейших случаях неопределенности.
Методические рекомендации для выполнения практической работы по теме: Пределы числовых последовательностей
Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого 0 можно найти такое число N, что начиная с n N все члены последовательности расположены внутри интервала ( a a ). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
Последовательность называется ограниченной, если существует такое число M, что | un | Mдля всех n . Возрастающая или убывающая последовательность называется монотонной.
Основные свойства пределов. Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.
Если { un } и { vn } две сходящиеся последовательности, то:
Если члены последовательностей { un }, { vn }, { wn } удовлетворяют неравенствам
Замечательные пределы
Предел функции. Число L называется пределом функции y = f ( x ) при x, стремящемся к a :
Число L называется пределом функции y = f ( x ) при x, стремящемся к a :
если для любого 0 найдётся такое положительное число = ( ), зависящее от , что из условия | x – a | следует | f ( x ) – L | .
ПРИМЕР. Найти
Решение. Подставляя x = 3 в выражение получим не имеющее смысла выражение . Поэтому решим по-другому:
Сокращение дроби в данном случае корректно, так как x 3 , он лишь приближается к 3. Теперь мы имеем:
поскольку, если x стремится к 3, то x + 3 стремится к 6 .
Замечательные пределы
Бесконечно малая и бесконечно большая величины. Если предел некоторой переменной равен 0, то эта переменная называется бесконечно малой.
1.Найдите пределы последовательностей:
; 3) ;
; 4) .
2.Найдите пределы функций:
;
;
;
;
.
3. Раскрытие неопределенностей вида . Найдите пределы:
; ;
; .
Раскрытие неопределенностей вида . Найдите пределы:
; .
4
Свойства пределов. Простейшие пределы.
Практическое вычисление пределов основывается на следующих свойствах.
Если существуют конечные пределы , , то:
1.
2.
3. т.е.
4. Для
5. Если предел одной или нескольких функций равен бесконечности, то можно воспользоваться следующим соотношениями:
для
6. Если предел функции равен 0, то
Если предел функции равен 0, то
Для того, чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражение функции вместо аргумента подставить его предельное значение.
Примеры.
1.
2. т.к. при является б.б.в., то при является б.м.в., тогда по определению бесконечно малой величины. Или ;
3. т.к. при является бесконечно малой величиной, тогда -бесконечно большая величина; т.е. функция является бесконечно большой величиной, т.е. по определению бесконечно большой величины.
Или
Раскрытие неопределенностей различных типов.
Случаи, в которых подстановка предельного значения в функцию не дает значения предела называют неопределенностями; к ним относят неопределенности видов:
Устранить неопределенность удается часто с помощью алгебраических преобразований.
Пример.
Найти
РЕШЕНИЕ
Ответ данной задачи будем использовать далее как заранее известный факт.
2.2.1. Раскрытие неопределенности типа .
В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби x с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое, среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.
Пример.
Задания для самостоятельной работы
2.2.2. Раскрытие неопределенности типа .
В этом случае обычно используются следующие приемы:
a) алгебраические преобразования числителя и знаменателя дроби, приводящие к формулам сокращенного умножения; неопределенность устраняется после сокращения дроби;
b) вынесение в числителе и знаменателе дроби степени х с наименьшим показателем;
c) Деление числителя дроби на ее знаменатель;
d) Эквивалентность бесконечно малых величин;
e) Первый замечательный предел.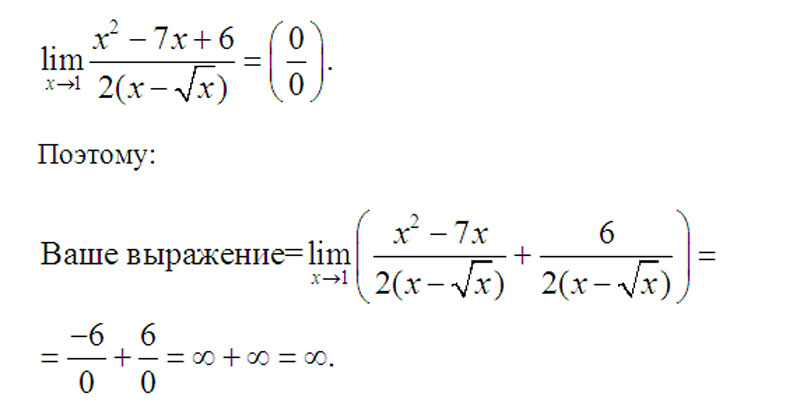
Примеры.
a)
(дополнили числитель до разности квадратов , а знаменатель до разности кубов ).
b)
c)
d) Примеры эквивалентных бесконечно малых величин при :
Предел отношения двух бесконечно малых величин не изменится, если эти бесконечно малые величины заменить им эквивалентными.
Пример.
e) – первый замечательный предел.
Примеры.
1)
2)
2.2.3. Раскрытие неопределенности типа .
В этом случае выражение, стояще под знаком предела представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи «второго замечательного предела».
Неопределенность устраняется при помощи «второго замечательного предела».
1) ; 2)
Примеры
1)
2)
3)
2.2.4. Раскрытие неопределенности типа
Если функция, стоящая под знаком предела представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится к неопределенности после приведения дробей к общему знаменателю. Если функция представляет собой сумму иррациональных выражений, то неопределенность или устраняется, или приводится к виду путем домножения и деления функции на одно и то же (сопряженное выражение), приводящее к формулам сокращенного умножения.
Примеры.
1)
2)
Задания для самостоятельной работы
Практическая работа №4 по теме: «Вычисление пределов»
Дисциплина «МАТЕМАТИКА»
Курс -2
Семестр -3
Практическая работа №4 по теме:
«Вычисление пределов»
Цель: формирование умений вычислять пределы последовательностей и функций,
раскрывать в простейших случаях неопределенности.
Методические рекомендации для выполнения
практической работы №4 по теме:
Пределы числовых последовательностей
Числовые последовательности. Формула общего члена.
Предел числовой последовательности. Сходящаяся и
расходящаяся последовательности. Ограниченная
последовательность. Монотонная последовательность.
Теорема Вейерштрасса. Основные свойства пределов.
Некоторые замечательные пределы.
Последовательности. Рассмотрим ряд натуральных чисел:
1, 2, 3, … , n –1, n, … .
Если заменить каждое натуральное число n в этом ряду некоторым числом un , следуя некоторому закону, то мы получим новый ряд чисел:
u1 , u2 , u3 , …, un 1 , un , …, кратко обозначаемый { un }
и называемый числовой последовательностью. Величина un называется общим членом последовательности. Обычно числовая последовательность задаётся некоторой формулой un = f ( n ), позволяющей найти любой член последовательности по его номеру n ; эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов (см. ниже последний пример).
Величина un называется общим членом последовательности. Обычно числовая последовательность задаётся некоторой формулой un = f ( n ), позволяющей найти любой член последовательности по его номеру n ; эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов (см. ниже последний пример).
П р и м е р ы числовых последовательностей:
1, 2, 3, 4, 5, … ряд натуральных чисел ;
2, 4, 6, 8, 10, … ряд чётных чисел;
1.4, 1.41, 1.414, 1.4142, … числовая последовательность
приближённых значений
с увеличивающейся точностью.
В последнем примере невозможно дать формулу общего члена последовательности, тем не менее эта последовательность описана полностью.
Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала ( a a ). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
Последовательность называется ограниченной, если существует такое число M, что | un | Mдля всех n . Возрастающая или убывающая последовательность называется монотонной.
Теорема Вейерштрасса. Всякая монотонная и ограниченная последовательность имеет предел (эта теорема даётся в средней школе без доказательства).
Основные свойства пределов. Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.
Если { un } и { vn } две сходящиеся последовательности, то:
Если члены последовательностей { un }, { vn }, { wn } удовлетворяют неравенствам
Замечательные пределы
- Пределы функций
Предел функции. Некоторые замечательные пределы.
Некоторые замечательные пределы.
Бесконечно малая и бесконечно большая величины.
Конечный предел. Бесконечный предел.
Понятие бесконечности.
Предел функции. Число L называется пределом функции y = f ( x ) при x, стремящемся к a :
если для любого > 0 найдётся такое положительное число = ( ), зависящее от , что из условия | x – a | < следует | f ( x ) – L | < .
Это определение означает, что L есть предел функции y = f ( x ), если значение функции неограниченно приближается к L , когда значение аргумента x приближается к a. Геометрически это значит, что для любого > 0 можно найти такое число , что если x находится в интервале ( a – , a + ), то значение функции лежит в интервале ( L – , L + ). Отметим, что в соответствии с этим определением аргумент функции лишь приближается к a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.
Отметим, что в соответствии с этим определением аргумент функции лишь приближается к a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.
П р и м е р . Найти
Р е ш е н и е . Подставляя x = 3 в выражение получим не имеющее смысла выражение . Поэтому решим по-другому:
Сокращение дроби в данном случае корректно, так как x 3 , он лишь приближается к 3. Теперь мы имеем:
поскольку, если x стремится к 3, то x + 3 стремится к 6 .
Замечательные пределы
Бесконечно малая и бесконечно большая величины. Если предел некоторой переменной равен 0, то эта переменная называется бесконечно малой.
П р и м е р . Функция y = является бесконечно малой при x,
cтремящемся к 4, так как
Если абсолютное значение некоторой переменной неограниченно возрастает, то эта переменная называется бесконечно большой.
Бесконечно большая величина не имеет конечного предела, но она имеет так называемый бесконечный предел, что записывается как:
Символ ( “бесконечность” ) не означает некоторого числа, он означает только, что дробь неограниченно возрастает при x, стремящемся к 3. Следует отметить, что дробь может быть как положительной ( при x > 3 ), так и отрицательной ( при x < 3 ). Если бесконечно большая величина может быть только положительной при любых значениях x, это отражается в записи. Например, при x 0 функция y = x2 бесконечно большая, но она положительна как при x > 0, так и при x < 0 ; это выражается так:
Наоборот, функция y = x 2 всегда отрицательна, поэтому
В соответствии с этим, результат в нашем примере можно записать так:
Практическая работа №4 по теме:
«Вычисление пределов»
Вариант 1.
1.Найдите пределы последовательностей:
; 3) ;
; 4) .
2.Найдите пределы функций:
;
;
;
;
.
3. Раскрытие неопределенностей вида . Найдите пределы:
; 3) ;
2) ; 4) .
4. Раскрытие неопределенностей вида . Найдите пределы:
1) ; 2) .
На войне – Раскрытие погрешностей измерений
| КРАТКАЯ ИНФОРМАЦИЯ |
|
ДЖЕРРИ Л. АРНОЛЬД, CPA, PhD, является
Доцент бухгалтерского учета Южного университета
Калифорния, Лос-Анджелес. УИЛЬЯМ У. ХОЛДЕР, CPA, PhD, является Эрнст энд Янг, профессор бухгалтерского учета и директор SEC и Институт финансовой отчетности USC. |
I Не секрет, что пользователи финансовой отчетности уже давно обеспокоен раскрытием неопределенности измерения в GAAP заявления, чтобы помочь инвесторам, кредиторам и другим лицам оценить неопределенность некоторых проводок в финансовой отчетности. Недавний заявления требуют раскрытия дополнительной информации о различных неопределенности.Эти мандаты – в сочетании с существующими требованиями – добавляют до сложного набора стандартов, которые часто сбивают с толку и компаниям сложно подать заявку. Несмотря на их сложность, факт то, что эти стандарты были утверждены вообще, подтверждает точку зрения разработчики стандартов, о которых финансовая отчетность не раскрыла должным образом степень неопределенности многих учетных измерений.
И FASB, и AcSEC призвали компании раскрыть бухгалтерский учет. неопределенности измерения.Однако сроки раскрытия такой информации и
их природа и масштабы сильно различаются. Эти вариации существуют, несмотря на
процесс утверждения новых стандартов AcSEC, который обеспечивает некоторую степень
согласования с FASB. (Если большинство членов FASB не
возражать против предлагаемого стандарта AcSEC, стандарт считается
одобрены FASB.) В результате компании могут быть
требуется для раскрытия обширной информации, когда мало
неопределенности и, наоборот, раскрывать относительно мало информации в
условия большой неопределенности.В некоторых случаях стандарты требуют
различное раскрытие информации об аналогичных экономических явлениях, что сбивает с толку
пользователи финансовой отчетности, составители и подтверждающие.
неопределенности измерения.Однако сроки раскрытия такой информации и
их природа и масштабы сильно различаются. Эти вариации существуют, несмотря на
процесс утверждения новых стандартов AcSEC, который обеспечивает некоторую степень
согласования с FASB. (Если большинство членов FASB не
возражать против предлагаемого стандарта AcSEC, стандарт считается
одобрены FASB.) В результате компании могут быть
требуется для раскрытия обширной информации, когда мало
неопределенности и, наоборот, раскрывать относительно мало информации в
условия большой неопределенности.В некоторых случаях стандарты требуют
различное раскрытие информации об аналогичных экономических явлениях, что сбивает с толку
пользователи финансовой отчетности, составители и подтверждающие.
| Шаги по улучшению финансовой отчетности “5. Улучшить раскрытие информации о неопределенности
измерения определенных активов и обязательств. «Сумма наличных денег на балансе дата составления отчета может быть известна точно, но начисленное обязательство затраты на очистку окружающей среды могут быть очень неточными.Пользователи хотите лучше понять неопределенность, присущую определенные измерения, чтобы лучше судить о доходах, денежный поток, возможности и риск. “Потому что измерения часто различаются по точности, компаниям следует указать в примечаниях к финансовой отчетности конкретные виды активы и обязательства, подлежащие значительному измерению неопределенности. По этим активам и обязательствам компании должен раскрывать, как были получены указанные суммы, и объяснять рассматриваемые оценки, допущения и суждения в их измерении.” Источник: AICPA Special
Комитет по финансовой отчетности, Улучшение бизнеса
Отчетность – ориентация на клиента. |
КОНЦЕПТУАЛЬНЫЕ ОСНОВЫ
В бухгалтерской литературе термин измерение
неопределенности описывает суммы финансовой отчетности, которые
по своей сути неточны и должны быть оценены. FASB четко признает
что многие цифры в финансовой отчетности являются неточными оценками и
что передача этой неточности пользователям – важная особенность
финансовый отчет.Чтобы понять проблему раскрытия информации, CPA должны
знать, насколько современные стандарты соответствуют концептуальным целям и
характеристики финансовой отчетности и действующие стандарты
для регистрации и представления неопределенностей. Заявление FASB о концепциях №
1, Цели финансовой отчетности коммерческих предприятий, говорит, что, «несмотря на ауру точности, которая может показаться
окружают финансовую отчетность в целом и финансовую отчетность в
в частности, за некоторыми исключениями, меры (в финансовой отчетности)
являются приближениями, которые могут быть основаны на правилах и соглашениях,
а не точные меры. “Еще раз подчеркивая важность
оценок, Заявление о концепциях нет. 2, Качественный
«Характеристики бухгалтерской информации», утверждает, что
“отчетность по бухгалтерским номерам как определенным и точным, если они
не является отрицанием достоверной отчетности “.
“Еще раз подчеркивая важность
оценок, Заявление о концепциях нет. 2, Качественный
«Характеристики бухгалтерской информации», утверждает, что
“отчетность по бухгалтерским номерам как определенным и точным, если они
не является отрицанием достоверной отчетности “.
В течение многих лет Положение FASB No. 5, Учет
Непредвиденные расходы, был наиболее полным стандартом по
сообщение о неопределенностях измерения. Требуется CPA для оценки
вероятность того, что неопределенное условие отрицательно повлияет на организацию и
сумма (или диапазон) любых связанных убытков.(Получите также непредвиденные расходы
должны быть раскрыты, но обычно упоминаются только в общих чертах
условий.) В то время как финансовая отчетность, соответствующая этому стандарту,
рассматриваются как исторические по своей природе, в действительности они обычно включают
предсказания неопределенных будущих событий и условий. Например,
оценки безнадежных долгов, устаревших запасов, доходов от продаж и
надбавки, гарантийные обязательства и даже амортизация и
Амортизация требует, чтобы CPA предсказывали будущие события.
Заявление №5 говорит, что компания должна понести убыток за счет списания доход при соблюдении двух условий:
1. Вероятно, что актив был обесценен или обязательство понесенные на дату составления финансовой отчетности.
2. Размер ущерба можно обоснованно оценить.
Заявление № 5, в интерпретации, говорит, что второе условие выполняется, если
диапазон потерь можно оценить. Компания должна раскрыть этот диапазон.
Интересно, однако, что в стандарте говорится, что раскрытие природы
начисления, а в некоторых случаях начисленная сумма “ может быть необходимо для финансовой отчетности.
вводящие в заблуждение »(курсив добавлен).Таким образом, Заявление № 5 не
требуют раскрытия этих относительно неопределенных измерений, хотя
он явно предвидит начисление сумм, которые только возможно
существовать. Исследования показывают, что большинство практиков понимают этот термин вероятный означает примерно 70% или 80% вероятность
вхождение.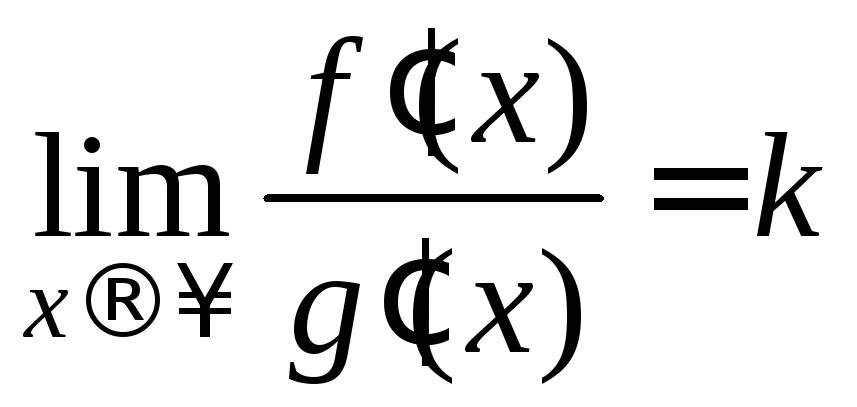 Это означает, что даже те суммы, которые CPA кладет на
финансовая отчетность может быть неопределенной.
Это означает, что даже те суммы, которые CPA кладет на
финансовая отчетность может быть неопределенной.
Учитывая важность неопределенностей измерения в финансовых отчетности, внимание, которое разработчики стандартов уделяли этому вопросу в последнее время заявления уместны.Возникновение двух заметно Несогласованные системы, описанные ниже, тем не менее, вызывают беспокойство.
ВАРИАЦИИ В РАСКРЫТИИ НЕОПРЕДЕЛЕННОСТЕЙ
Последнее заявление FASB, требующее от компаний
Раскрытие неопределенности измерений – это Заявление № 132, Раскрытие работодателями информации о пенсиях и других мероприятиях после выхода на пенсию
Преимущества . Это требует от компаний раскрытия предположений
они используют при оценке своих чистых обязательств по пенсиям и другим
пособия после трудоустройства.Приложение 1 справа резюмирует Положение №
132 и другие нормативные акты FASB, требующие неопределенности
раскрытие информации. Каждый стандарт в Приложении 1 требует регулярного раскрытия
информация, идентифицированная безотносительно к измерениям
относительная неопределенность.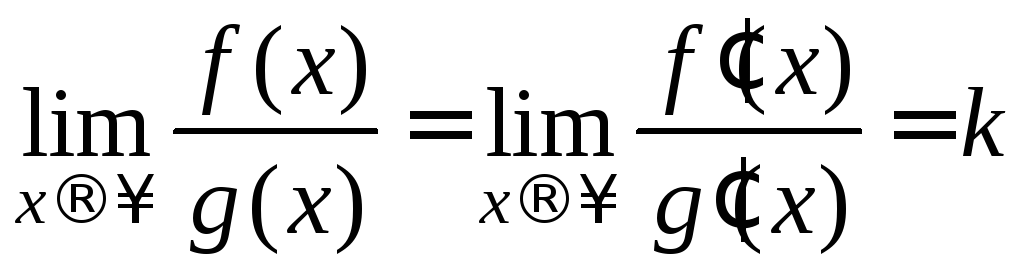 Ясно, что FASB начал требовать от компаний
раскрывать бухгалтерские оценки в гораздо большей степени, чем в
мимо.
Ясно, что FASB начал требовать от компаний
раскрывать бухгалтерские оценки в гораздо большей степени, чем в
мимо.
SOP 94-6, Раскрытие определенных значительных рисков и Неопределенности, использует другой подход.В нем говорится, что компании должен раскрывать существование неопределенностей измерения, если это разумно возможно, что лежащая в основе бухгалтерская оценка может измениться в течение года после даты финансовой отчетности в такой степени, что существенно повлиять на финансовую отчетность.
Противопоставление результатов двух подходов и утверждения нет. 5
резюмируются на Приложении 2, стр. 103. На Приложении 2 также показаны
обстоятельства, требующие раскрытия информации, и возникающие в результате различия
от тех стандартов.Эти различия и присущие им трудности
применения нескольких стандартов легко увидеть в
лечение обесценения долгосрочных активов. Заявление FASB № 121, Учет обесценения долгосрочных активов и
Долгосрочные активы, подлежащие выбытию, требует раскрытия информации
всякий раз, когда компания признает существенный убыток от обесценения. Интересно, что выписки нет. 121 использует конкретное «событие»
триггер, чтобы решить, когда компании необходимо признать обесценение
вместо использования вероятностного теста, требуемого Положением №5 и
СОП 94-6. Компаниям трудно понять, насколько
при каких обстоятельствах СОП 94-6 потребует от них раскрытия
возможное обесценение долгосрочного актива. Согласно Заявлению № 121,
Убыток от обесценения не будет признан.
Интересно, что выписки нет. 121 использует конкретное «событие»
триггер, чтобы решить, когда компании необходимо признать обесценение
вместо использования вероятностного теста, требуемого Положением №5 и
СОП 94-6. Компаниям трудно понять, насколько
при каких обстоятельствах СОП 94-6 потребует от них раскрытия
возможное обесценение долгосрочного актива. Согласно Заявлению № 121,
Убыток от обесценения не будет признан.
Следующие ниже примеры дополнительно иллюстрируют различия в отчетности. между стандартами FASB и SOP 94-6.
| Приложение 1: Раскрытие информации о неопределенности, требуемое FASB | ||
| Standard | Subject | Требуемые раскрытия информации |
| Заявление №107 | Финансовые инструменты – только раскрытие информации – нет корректировка финансовой отчетности. | Для всех
финансовые инструменты: справедливая стоимость, методы и существенные
предположения, использованные для оценки. |
| Номер ведомости 121 | Долгожитель ресурсы. | По списанным долгосрочным активам в связи с обесценением: «как была определена справедливая стоимость». |
| Номер ведомости 123 | Компенсация на основе запасов. | метод и существенные допущения, использованные в течение года для оценить справедливую стоимость опционов, включая определенные элементы. |
| Номер ведомости 124 | Учет инвестиций в некоммерческих организациях организации. | Методы и значимые допущения, использованные для оценки справедливой стоимости инвестиций кроме финансовых инструментов (например, нефтегазовых и недвижимость). |
| Номер ведомости 125 | Право на ипотечное обслуживание. | Справедливая стоимость капитализированного ипотечного обслуживания
права, а также методы и существенные допущения, использованные для
оценить эту справедливую стоимость. |
| Номер ведомости 132 | Поправки
к Положению № 106: Обязательства по выплате пособий по окончании трудовой деятельности Другое
чем пенсии. Поправки к Положению № 87: Пенсия с установленными выплатами планы. | Допущения по ставке дисконтирования, ставке увеличения компенсации, долгосрочная доходность по плану активы, ставка, используемая для измерения затрат на получение прибыли, и определенные информация о допущениях, связанных с чувствительностью. |
Пример 1. Постановление FASB № 107, Раскрытие информации о справедливой стоимости финансовых инструментов, требует, чтобы компании раскрыть справедливую стоимость долгосрочного долга и соответствующие методы и существенные допущения, использованные при оценке.Оценка справедливая стоимость долговых инструментов, не обращающихся активно (например, нот кредиторская задолженность перед банками и задолженность непубличных компаний) проста и простой. Например, если кредитоспособность компании не изменились с момента выпуска долга, может потребоваться только определить процентную ставку, которую кредитор будет взимать за аналогичный заем дату баланса и примените эту ставку к будущему инструмента денежные потоки. Хотя итоговая оценка может не подлежать значительная неопределенность, раскрытие информации, тем не менее, будет существенные и выходящие за рамки оценки справедливой стоимости, включая методы и существенные допущения.
| Приложение 2: Раскрытие информации о неопределенностях бухгалтерского учета | |||
| Стандарт | |||
| Выпуск | FASB Заявление № 5 | СОП 94-6 | Последние заявления FASB |
| Условия, требующие раскрытия информации | Разумно возможные убытки. Вероятная потеря с возможностью оценки только диапазона потерь. Прирост непредвиденных обстоятельств. | Бухгалтерский учет оценка, которая может существенно измениться в в ближайшем будущем из-за одного или нескольких будущих подтверждающих событий. | Простое наступление транзакции или события. |
| Требуется раскрытие информации | Характер и сумма возможных убытков или заявление о том, что
сумма не может быть обоснованно оценена. Диапазон потерь. Общего характера (неспецифический). | Природа
неопределенности. Указание на то, что по крайней мере разумно возможно изменение оценки произойдет в ближайшее время. | Существенные допущения. Используемые методы. |
Пример 2. С другой стороны, рассмотрим раскрытие стандарты, применимые к ответственности за гарантии на продукцию. Несмотря на то что сумма, которую накапливает компания, может быть значительно больше обсуждается неуверенность, чем долгосрочный потенциал изменения срочного долга выше, раскрытие информации не требуется, если только финансовые Составитель выписки считает, что существуют определенные условия.В частности, он или она должна сделать вывод, основываясь на известной информации, что это разумно возможно, что сумма, начисляемая компанией, изменится в в ближайшем будущем из-за одного или нескольких «будущих подтверждающих событий» и что такое изменение будет существенным для финансовой отчетности. Даже если эти условия соблюдены, раскрытие информации в соответствии с СОП 94-6 распространяется только на характер неопределенности и указание на то, что она не менее разумно возможное изменение оценки произойдет в ближайшее время. Заявление №5, с другой стороны, призывает компанию раскрывать диапазон условных убытков, если одноточечная оценка не возможный. Однако в заявлении не рассматривается вероятность необходимо установить такой диапазон. СОП 94-6 призывает компании к раскрыть наличие любых разумно возможных вариаций материала в сумме, начисленной по Выписке № 5. Требуемое раскрытие информации, тем не менее, не распространяются на то, как была сделана оценка, или на использованные допущения.
Кажется в лучшем случае нелогичным, что при сравнении примеров пример 2, что может включать гораздо больший уровень неопределенности, приводит к существенно меньше информации о методах и предположениях, которые используются для оценки неопределенности.
Вид ТРЦ. В то время как непубличные компании не требуется применять положения SEC к своей финансовой отчетности, эти заявления действительно имеют косвенное влияние на общие финансовые составление отчетов; отсюда их актуальность. Сотрудники SEC подчеркнули необходимость раскрытия дополнительной информации об ответственности за качество продукции в бухгалтерском учете персонала Бюллетень (САБ) № 92, Учет и раскрытие информации, относящейся к убыткам Непредвиденные обстоятельства. Персонал выпускает бюллетени только тогда, когда верит необходимо дополнительное практическое руководство.SAB нет. 92 говорит: ” персонал считает, что обязательства по продукту (и окружающей среде) обычно имеют такое значение, что подробное раскрытие информации о суждения и допущения, лежащие в основе признания и оценки обязательства необходимы “.
Некоторые примеры конкретного раскрытия информации, которое может сделать компания включить
- Обстоятельства, влияющие на надежность и точность потерь оценки.
- Степень отражения незаявленных требований при начислении или может повлиять на размер непредвиденных обстоятельств.
- Срок, в течение которого начисленные или в настоящее время непризнанные суммы могут быть выплачены.
- Существенные компоненты начислений и существенные допущения лежащие в основе оценок.
Другие несоответствия. Еще один пример, казалось бы, непоследовательные требования к раскрытию информации касаются различных активов. Заявление FASB № 125, Учет переводов и обслуживания Финансовые активы и погашение обязательств (который Заменено Положение FASB №122, Учет ипотеки Права на обслуживание ), требует, чтобы обслуживающие ссуды раскрывали методы и существенные допущения, которые они используют для оценки стоимости права на ипотечное обслуживание, отраженные как активы в их финансовых заявления. Хотя многие из этих оценок довольно точны и не связано с большой неопределенностью, раскрытие информации требуется во всех случаях в котором сообщается о правах на обслуживание ипотеки.
Напротив, рассмотрите необходимость оценок при оценке инвентарь производителя, оптового или розничного продавца.GAAP требует эти запасы оцениваются по наименьшей из рыночных или рыночных затрат. Верхний граница рынка – это чистая цена продажи – расчетная цена продажи за вычетом стоимость завершения продажи. Таким образом, стоимость, присвоенная инвентарю на баланс подлежит бухгалтерской оценке во всех случаях. Что то есть оценки будущих событий необходимы для определения рынка, и стоимость должна быть связана с рынком, чтобы определить текущую стоимость инвентаризация финансовой отчетности. Однако СОП 94-6 не требовать от компаний раскрытия этого факта, если только на основании известных информации, вполне возможно, что оценка изменится в в ближайшем будущем из-за одного или нескольких будущих подтверждающих событий и эффекта изменения будут существенными.Ни в коем случае СОП 94-6 не требует компании раскрыть методы и существенные допущения, использованные для оценить стоимость инвентаря.
Мы полагаем, что раскрытие информации связано с этими двумя оценками Стоимость активов непоследовательна и, возможно, сбивает с толку. Это не делает ощущение, что более общая и более неопределенная оценка требует меньше раскрытие информации и в меньшем количестве обстоятельств, чем при более общей оценке это менее неопределенно.
ДЕЙСТВИЯ ПО УЛУЧШЕНИЮ ПРАКТИКИ
Раскрытие информации о неопределенностях оценки в финансовых стандартах GAAP.
Заявления регулируются рядом сложных стандартов,
иногда несовместимые друг с другом, требуют существенного
профессиональное суждение и может привести к нелогичным результатам.Мы верим
разработчики стандартов должны применять комплексный подход, требующий
компаниям раскрывать информацию о неопределенностях измерения. Хотя концептуальный
основы для каждого из стандартов FASB и AcSEC можно понять
по отдельности, вместе они запутывают пользователей финансовой информации и
другие. В крайних случаях они могут даже ввести в заблуждение
выводы. Неопределенности измерения пронизывают финансовую отчетность и
относятся к наиболее важной информации в заявлениях.
Все разработчики стандартов должны принять единую систему раскрытия только
насколько неточные цифры финансовой отчетности вместо разрозненных
подход сейчас используется.Независимо от того, какой стандарт выбирают установщики системы,
его следует применять ко всем статьям финансовой отчетности.
Специальный комитет AICPA по финансовой отчетности изучил это тема интенсивно. Его отчет Улучшение бизнес-отчетности – A Ориентация на клиента, была основана на обширной работе с большим количеством пользователей финансовой информации. Рекомендовано
- Указание в примечаниях к финансовой отчетности конкретных видов активы и обязательства, подлежащие значительному измерению неопределенности.
- Раскрытие – для активов и обязательств, подверженных значительным неопределенности измерения – как были получены указанные суммы и объяснение оценок, предположений и суждений о будущем события, учитываемые при их измерении.
Специальный комитет основывал свои рекомендации частично на исследование потребностей инвесторов и кредиторов. Обе группы сказали раскрытие неопределенностей измерений и допущений и им были бы полезны методы, используемые для получения исходных оценок. в прогнозировании будущих доходов и денежных потоков и в оценке обоснованность бухгалтерских цифр в финансовой отчетности.В Рекомендации специального комитета представляют собой смесь двух принципов раскрытия информации. системы, описанные ранее. Как и SOP 94-6, не все измерения неопределенности требуют раскрытия. Критерии, подобные тем, которые указаны в СОП определит, насколько степень неопределенности и связанные с ней необходимо раскрыть существенность бухгалтерской оценки. Когда Компания считает, что раскрытие информации необходимо, однако раскрытие информации специальный комитет рекомендует распространить на методы и существенные допущения, использованные при оценке.Этот тип информация была отличительной чертой последних стандартов FASB, но заметно отсутствует в СОП 94-6.
Каждый из последних четырех стандартов FASB требует раскрытия методы и существенные допущения для оценок в тех стандарты, независимо от присущей степени неопределенности. Но многие предыдущие стандарты FASB не содержат таких требований к раскрытию информации даже хотя важные оценки, основанные на прогнозе будущих событий, часто необходимо при их применении.Примеры включают оценки необходимо для соблюдения этих положений FASB:
- Заявление № 13, Учет аренды.
- Заявление № 43, Учет компенсированного отсутствия.
- Заявление № 67, Учет затрат и начальных операций проектов недвижимости.
- Заявление № 91, Учет невозмещаемых комиссий и затрат Связанные с предоставлением или получением ссуд и первоначальным прямым Стоимость аренды.
Кроме того, стандарты бухгалтерского учета, установленные предшественником организации, устанавливающие стандарты (Совет по принципам бухгалтерского учета AICPA и комитет по бухгалтерскому учету) имеют аналогичные характеристики в что они требуют большого количества бухгалтерских оценок, но не раскрытие информации о существовании этих оценок или методов и существенные допущения, использованные при их применении. Мы верим различия в стандартах бухгалтерского учета, о которых говорилось выше, приводят к раскрытие излишне сложной информации в финансовой отчетности, которая непоследовательны и могут запутать пользователей финансовой отчетности.Чтобы решить эту проблему проблема, FASB должен предпринять проект по унификации или гармонизации раскрытие информации о неопределенностях оценки в финансовой отчетности.
W После принятия рекомендаций специального комитета будет существенно улучшить раскрытие неопределенностей измерений, это не решит всех связанных с этим проблем. Специальный комитет рекомендуется раскрывать только некоторые существенные оценки в зависимости от является ли неопределенность измерения особенно чувствительной к относительно небольшие изменения в предположении, вероятность того, что будущее события могут сильно отличаться от предполагаемых будущих событий или наличие возможных изменений в смете в связи с изменением предположения о будущем.Эти критерии аналогичны критериям в СОП 94-6 и дайте CPAs переменные, чтобы решить, раскрывать ли особая неопределенность. Таким критериям подчиняются разные интерпретации; профессионалы, находящиеся в аналогичном положении, с одинаковыми фактами могут прийти к разным выводам о необходимости раскрытия информации в конкретная практическая ситуация. Таким образом, критерии не могут привести к аналогичная информация при аналогичных обстоятельствах отчетности. Действительно, исследования показывают, что практикующим врачам трудно добиться последовательного суждения о том, следует ли раскрывать неопределенности в соответствии с Положением №5.
Наконец, раскрытие информации в СОП 94-6 основано на известной информации. к менеджменту. Большинство стандартов бухгалтерского учета устанавливают измерение или стандарта раскрытия информации и неявно требуют от руководства получения информация, необходимая для его применения. СОП 94-6 является явным исключением из это практика. Не требуя от руководства получения достаточных сведения о неточности учета измерений, СОП отличается от аналогичных стандартов.
Различные управления могут накапливаться и обладать самыми разными уровни информации.Одним из следствий этого является то, что хорошо информированные менеджеры раскрывают больше информации о неопределенности измерений, чем меньше информированные менеджеры. В результате финансовая отчетность компаний с более информированным руководством кажутся более неопределенными и неточными когда на самом деле может быть наоборот.
В свете текущего проекта FASB по раскрытию эффективности и беспокойство других о возможности стандартов и чрезмерное раскрытие информации, призыв к дополнительному раскрытию информации не может быть сделан слегка.Тем не менее, как Ассоциация по управлению инвестициями и исследовательский позиционный документ Финансовая отчетность в 1990-х и Beyond и специальный комитет признают, что больше информация о неопределенностях измерения в финансовой отчетности будут хорошо приняты. Следовательно, в зависимости от решения FASB проект повышения эффективности раскрытия информации, мы считаем, что компании должны раскрывать существенные неопределенности оценки, и что раскрываемая информация включает: методы и существенные допущения.Такое требование было бы
- Уменьшите количество суждений, которые компании должны принимать при принятии решения о том, для раскрытия неопределенностей измерений.
- Привести к раскрытию большего количества аналогичной информации в аналогичных фактических ситуациях.
- Уменьшить количество заявлений о ненадлежащем раскрытии неопределенностей на потенциальные тяжущиеся стороны.
- Существенно не увеличивает затраты на подготовку финансовой заявления.
КАКОЙ ЦЕНОЙ?
Расходы на сбор и раскрытие информации.
рекомендованный выше не будет большим.Практически во всех случаях при изготовлении
исходные оценки компании уже разработали
информация, необходимая для раскрытия рекомендуемой информации. В то время как другие
затраты, особенно вопросы конкуренции, следует учитывать, это
трудно представить, что стоимость может сделать эту рекомендацию
непомерно. Более единообразное применение правил раскрытия информации
улучшить процесс принятия решений, и выгоды будут значительно превосходить любые
расходы на внедрение и соблюдение нормативных требований. FASB, следовательно, должен двигаться
быстро обобщить стандарты раскрытия бухгалтерской информации
их уже начали выпускать.
Комиссия по ценным бумагам и биржам США, пересмотр MD&A – Акцент на раскрытие информации о неопределенностях в будущем | Locke Lord LLP
Комиссия по ценным бумагам и биржам продолжила свои усилия по обновлению и упорядочению требований к раскрытию информации для подачи заявок в SEC. В ноябре Комиссия по ценным бумагам и биржам приняла поправки к правилам обсуждения и анализа руководством и соответствующего раскрытия финансовой информации. [1] MD&A, в силу своей принципиальной природы, является одним из самых сложных требований к раскрытию информации. В рамках MD&A рассмотрение «известных тенденций или неопределенностей», поскольку требования основаны не только на принципах, но и ориентированы на будущее, может быть особенно сложной задачей.В последних поправках Комиссия по ценным бумагам и биржам, хотя и не изменяет напрямую свои предыдущие интерпретации в отношении раскрытия известных тенденций или неопределенностей, которые беспокоили практикующих специалистов на протяжении многих лет, предоставляет полезные рекомендации, которые должны согласовывать конкретные требования с подходами, применяемыми на практике.
MD&A, как того требует пункт 303 Положения S-K, уже давно является частью требуемого раскрытия информации. Он призван придать дополнительный смысл необходимой финансовой информации и поместить эту информацию в контекст «глазами руководства».«Частью обеспечения этого контекста является раскрытие известных тенденций, требований, обязательств, событий или неопределенностей, которые оказали или могли бы разумно оказать существенное влияние на финансовое состояние, денежный поток или результаты операций компании таким образом, чтобы это оставило прошлое финансовая информация не обязательно указывает на будущее состояние или результаты.
В 1989 году SEC установила двухэтапный тест для определения того, требуется ли раскрытие известной тенденции или неопределенности [2]. Во-первых, руководство должно определить, вероятно ли возникновение известной тенденции или неопределенности – если оно определяет, что это маловероятно, раскрытие информации не требуется.Если он не может сделать это определение, он должен перейти к следующему этапу, который заключается в объективной оценке существенности известной тенденции или неопределенности, исходя из предположения, что она произойдет. В таком случае требуется раскрытие информации, если только руководство не определит, что эффект вряд ли будет существенным. Этот двухэтапный отрицательный тест на презумпцию вызвал беспокойство у практикующих. Несмотря на комментарии, выражающие эту озабоченность, Комиссия решила подтвердить двухэтапный тест 1989 г., утверждая, что формулировка пункта 303 с поправками кодифицировала эту позицию.В то же время, однако, Комиссия предоставила руководство при принятии релиза о том, как применять двухэтапный тест при принятии решений о раскрытии, которые должны согласовывать требования пункта 303 с тем, как он обычно применяется на практике.
Во-первых, Комиссия включила в Пункт 303 (a) общие концепции, применимые к MD&A, которые ранее появлялись в качестве руководства в инструкциях и интерпретациях. Хотя положения пункта 303 (а) обычно применяются как юридические требования, из-за их общности положения пункта 303 (а) вряд ли будут применяться таким образом.Комиссия также разъясняет в утвержденном релизе, что MD&A должны включать вдумчивое обсуждение и анализ факторов, характерных для бизнеса конкретной компании, которые с точки зрения руководства необходимы для понимания финансового состояния компании, изменений в финансовом состоянии и результатов операций. Комиссия подчеркивает, что существенность является всеобъемлющим принципом раскрытия информации о МиД.
В отношении известных тенденций и неопределенностей поправки к пункту 303 устанавливают последовательный стандарт «разумно вероятный» в отличие от стандарта «будет» или «разумно ожидаемого».Требуемый анализ должен основываться на «оценке руководства», которая должна быть «объективно разумной». Затем Комиссия поясняет, что при применении двухэтапного теста для оценки того, требуется ли раскрытие известной тенденции или неопределенности, анализ должен основываться на «существенности», как обычно понимается как то, что разумный инвестор сочтет важным. при принятии решения о голосовании или инвестировании. Применяя двухэтапный тест в соответствии со стандартом «разумной вероятности», компания сначала должна объективно оценить вероятность того, что это произойдет.Если известная тенденция или неопределенность не являются отдаленными или если руководство не может сделать это определение, руководство должно затем на объективной основе рассмотреть, окажет ли известная тенденция или неопределенность существенное влияние в случае возникновения известной тенденции или неопределенности. В таком случае раскрытие информации потребовалось бы, если упущение информации могло бы существенно изменить набор информации, которую разумный инвестор сочтет важной, с целью предоставить инвесторам понимание существенных последствий известных прогнозных тенденций или неопределенностей.Комиссия категорически отклонила использование в этом контексте стандарта вероятности / величины Basic для оценки существенности [3].
Хотя двухэтапный тест на отрицательную презумпцию подтверждается, руководство Комиссии помещает его в контекст, который должен дать компаниям несколько больше свободы действий при оценке существенности для инвесторов далеко не известных тенденций или неопределенностей и большего комфорта в достижении добросовестного и вдумчивого раскрытия информации. решения.
Прочие изменения
Ниже приводится краткое изложение некоторых других изменений, внесенных SEC:
- Пункт 301, требующий выборочной таблицы финансовых данных за пять лет, исключается в связи с признанием того, что финансовая информация появляется в других документах.
- Пункт 302, требующий представления ежеквартальной финансовой информации в табличной форме за два предыдущих финансовых года и любой последующий квартальный период, который применяется к годовому отчету по форме 10-K и определенным регистрационным отчетам по форме S-1, изменен таким образом, чтобы требовать раскрытия только в случае предварительного изменения в отчете о прибылях и убытках за эти периоды были существенными, что привело к замене основанного на принципах подхода на техническое требование, которое воспроизводит информацию, в основном имеющуюся в других документах.
- В дополнение к добавлению нового пункта 303 (a) под названием «Цель», требования к анализу и обсуждению ликвидности, капитальных ресурсов и результатов операций в пункте 303 (b) (1) и (2) для полных финансовых лет а в отношении существенных изменений финансового состояния и результатов операций за промежуточные периоды были пересмотрены, чтобы «модернизировать, улучшить и прояснить» и, в некоторых случаях, упростить требования к раскрытию информации. Однако они в значительной степени требуют той же основной информации, основанной на принципах, которая и требовалась.Что касается информации за промежуточный период, SEC добавила гибкости, чтобы позволить компаниям адаптировать раскрытие информации к своей ситуации, выбрав традиционное сравнение в годовом исчислении или последовательное сравнение кварталов. Если компания меняет подход, она должна объяснить причину и предоставить оба сравнения в первой измененной документации.
- Вместо отдельного положения о забалансовых соглашениях заменяется инструкция по обсуждению существенных обязательств и обязательств, возникающих из этих забалансовых соглашений, в контексте обсуждения MD&A.
- Требование о включении таблицы договорных обязательств отменено в пользу более подробного раскрытия информации о ликвидности и капитальных обязательствах, существенных денежных обязательствах из обязательств, включая договорные обязательства.
- Новый пункт 303 (b) (3) добавлен для кодификации указаний Комиссии по ценным бумагам и биржам по критически важным оценкам бухгалтерского учета, чтобы прояснить, что обсуждение не должно повторять примечание к финансовому отчету по важным учетным политикам. Вместо этого обсуждение должно предоставить качественную и количественную информацию, необходимую инвестору для понимания неопределенности тех учетных оценок, отраженных в финансовой отчетности, которые связаны со значительной неопределенностью и могут оказать существенное влияние на финансовое состояние или результаты деятельности.
- Соответствующие изменения внесены в требования к небольшим отчитывающимся компаниям и иностранным частным эмитентам, наряду с другими изменениями в правилах и формах, чтобы отразить эти поправки.
Дата вступления в силу и переход.
Поправки вступают в силу через 30 дней после публикации в Федеральном реестре, но изменения применяются только к заявкам, начинающимся в первый финансовый год, заканчивающийся не позднее 210 дней после публикации в Федеральном реестре (для компаний календарного года, которым будет финансовый год, заканчивающийся в декабре). 31, 2021).Компании могут использовать новые правила в любое время после их вступления в силу, если они полностью соответствуют пункту (например, пункту 303).
* * *
[1] Обсуждение и анализ руководством, отдельные финансовые данные и дополнительная финансовая информация, версия № 33-10890 (19 ноября 2020 г.).
[2] Обсуждение и анализ руководством финансового состояния и результатов деятельности; Некоторые раскрытия информации об инвестиционных компаниях, выпуск №33-6835 (18 мая 1989 г.)
[3] Basic, Inc. против Левинсона , 485 U. S. 224 (1988).
Сообщение SEC «Пересмотр MD&A – Фокус на раскрытие информации о неопределенностях в будущем» впервые появилось на страницах «Рынки капитала».
Неопределенность измерений в финансовой отчетности: что нужно учитывать и как лучше всего сообщать об этом
В целом, «неопределенность» означает состояние ограниченного знания, при котором невозможно или практически невозможно точно описать существующее состояние или будущий результат. 1 Неопределенность существует в финансовой отчетности, где измерения «в значительной степени… основаны на оценках, суждениях и моделях, а не на точных представлениях». 2 По мере увеличения уровня неопределенности могут возникать проблемы:
- Составители финансовой отчетности для оценки будущих результатов неопределенностей, присущих многим бизнес-операциям,
- аудиторов для проверки субъективных суждений об этих неопределенностях, а
- инвесторов, чтобы понять эти неопределенности и оценить их потенциальное влияние на будущую прибыль или денежные потоки.
Например, кажущиеся небольшими изменения от выбранных руководством исходных данных, используемых для определения справедливой стоимости, могут оказать существенное влияние на отчетный результат на любую конкретную дату. Например, когда оценка справедливой стоимости определяется в основном на основе анализа дисконтированных денежных потоков, использование ставки дисконтирования, которая отличается на 100 базисных пунктов, может означать разницу между существенными убытками от обесценения гудвилла или отсутствие разницы вообще.
В этом круглом столе соберутся инвесторы, составители отчетов и аудиторы, которые предоставят информацию о тех измерениях (и связанных с ними раскрытиях), результат которых зависит от будущих событий, которые по определению в настоящее время неизвестны.В качестве первого шага в сборе мнений по этой теме обсуждение за круглым столом будет сосредоточено на:
- Оценка и признание – предоставляют ли измерения, связанные с неопределенностью, инвесторам полезную информацию.
- Раскрытие информации – информация, которую инвесторы считают важной для понимания и оценки неопределенностей измерений, а также проблем или препятствий, с которыми сталкиваются составители отчетов при предоставлении этой информации.
- Возможность аудита – роль и ответственность аудитора за представление финансовой отчетности с неопределенностями измерения.
Некоторые недавние стандарты бухгалтерского учета увеличили степень неопределенности оценки в финансовой отчетности 3 , а некоторые стандарты попытались повысить прозрачность неопределенности измерения, лежащей в основе статей финансовой отчетности. 4 Тем не менее, вопросы о признании и измерении неопределенности остаются; раскрытие информации, необходимое для понимания неопределенности измерения; и как неопределенность влияет на возможность аудита.
Концептуальная основа финансовой отчетности FASB гласит: «Если уровень неопределенности… достаточно велик, эта оценка не будет особенно полезной». 5 Характер и степень неопределенности оценки зависят от экономических явлений, которые должна отражать соответствующая статья финансовой отчетности. Некоторые задаются вопросом, каков правильный баланс и предоставляется ли достаточная информация для понимания природы и степени неопределенности измерений.
Для изучения этой темы может быть полезно проиллюстрировать некоторые из различных методов бухгалтерского учета, которые в настоящее время включают неопределенность.Например,
- Некоторые неликвидные финансовые активы, отражаемые по оценочной справедливой стоимости, корректируются в большую или меньшую сторону с учетом изменений оценочной справедливой стоимости; однако нефинансовые активы (например, гудвил) корректируются только в том случае, если отраженная сумма превышает справедливую стоимость в определенный момент времени.
- Условные обязательства признаются, когда существует вероятность того, что убыток был понесен и может быть обоснованно оценен, и оцениваются как единичная оценка. Если одноточечная оценка находится в пределах диапазона, необходимо раскрыть дополнительную максимальную подверженность убыткам.
- Некоторые гарантии оцениваются на основе ожидаемых будущих результатов, взвешенных с учетом вероятности.
- Влияние неопределенных налоговых позиций на финансовую отчетность признается, когда с учетом технических достоинств более вероятно, что эти позиции будут поддержаны после проверки, и оцениваются как наибольшая сумма, вероятность того, что осуществленный.
- Некоторые неликвидные финансовые активы оцениваются по приведенной стоимости на основе дисконтированных будущих денежных потоков, независимо от достоверности этих денежных потоков.
- Приобретенные идентифицируемые нематериальные активы признаются без учета неопределенности измерения. Однако большинство нематериальных активов внутренней разработки (например, исследования и разработки и гудвил) никогда не признаются в финансовой отчетности, поскольку будущие выгоды считаются слишком неопределенными.
- Когда есть существенные сомнения в способности предприятия продолжать непрерывно свою деятельность, финансовая отчетность, как правило, не корректируется для отражения неопределенности.Вместо этого раскрывается информация, которая включает, среди прочего, информацию о неопределенности, возмещаемости и классификации зарегистрированных сумм активов, а также суммах или классификации обязательств.
Панельные обсуждения
Панельные дискуссии будут сосредоточены на следующих вопросах. Экспертам будет предложено указать, где это применимо, тему – финансовые инструменты, гудвилл, непредвиденные убытки и т. Д. – к которой относятся их комментарии.
- Просьба предоставить отзывы по темам, в которых степень неопределенности менее полезна для инвесторов и почему более точные измерения были бы предпочтительнее.Точно так же предоставьте комментарии по тем темам, по которым оценка с неопределенностью дает инвесторам более полезную информацию и почему она предпочтительнее более точного измерения.
- Для тех тем, где неопределенные измерения полезны для инвесторов, как следует включить неопределенности в меру? Пожалуйста, объясните причины выбранных вами методов измерения.
- Какую информацию используют инвесторы, чтобы понять неопределенность? Опишите, почему такая информация полезна, и, если она не раскрыта в финансовой отчетности, укажите ее источник.
- Какие трудности возникают перед инвесторами в понимании природы и степени неопределенности измерения?
- По мере увеличения неопределенности измерения, пожалуйста, объясните, меняет ли это (и как, если применимо) ожидания инвестора в отношении составителей отчетности и аудиторов.
- Для составителей отчетности, каковы проблемы или препятствия на пути к предоставлению инвесторам информации для понимания характера и степени неопределенностей измерения?
- Какие проблемы возникают у аудиторов при оценке суждений руководства, связанных с неопределенностями измерения?
- Прокомментируйте, может ли (и как) изменение ответственности или роли аудитора улучшить понимание инвестором природы и степени неопределенности оценки.
- Пожалуйста, предоставьте любые дополнительные комментарии или предложения, относящиеся к тому, насколько неопределенность следует распознать и как лучше всего сообщить о ней.
Был выпущен отдельный запрос на комментарии для общественности, чтобы оставить отзыв по вышеуказанным вопросам. Публичные ответы могут быть предоставлены через веб-сайт SEC www.sec.gov.
Дополнительные ресурсы
Персонал Комиссии считает, что следующие ресурсы могут содержать дополнительную справочную информацию, относящуюся к теме неопределенности измерений.
- http://americanassembly.org/publication/future-accounting-profession
- http://www.aicpa.org/interestareas/frc/accountingfinancialreporting/
Enhancedbusinessreporting / pages / jenkinscommittee.aspx – См. Рекомендацию 5 – Улучшить раскрытие информации о неопределенности измерений определенных активов и обязательств. - Christensen, Glover et al. «Крайняя неопределенность оценок справедливой стоимости: последствия для аудиторской уверенности.» Аудит: журнал практики и теории. Готовится к выпуску http://ssrn.com/abstract=1916336
- «Будущее счетов: Истинные и честные – это не сложно и быстро. Чтобы счета отражали реальность, они должны быть более изменчивыми и менее точными. »Экономист. 24 апреля 2003 г. http://www.economist.com/node/1730918
- Schuetze, Уолтер П. «Аудит: объективные свидетельства против субъективных суждений». Фонд бухгалтерского образования, Общество бухгалтеров штата Нью-Йорк.Нью-Йорк. 9 сентября 2003 г. Документ для обсуждения Совета по международным стандартам бухгалтерского учета
- : «Основы оценки для финансового учета – оценка при первоначальном признании». Пункты 205-215. Ноябрь 2005 г.
http://www.iasb.org/NR/rdonlyres/E1A542DB-3A19-47AC-B995-EFCFA044F3EC/0/MeasurementBasesforFinancialAccountingDPfullversion.pdf
- Джерри Л. Арнольд и Уильям У. Холдер. «На войне – раскрытие погрешностей измерений». Бухгалтерский журнал., декабрь 1998 г. http://www.journalofaccountancy.com/Issues/1998/Dec/arnold.htm
- Публикация FR-60 Комиссии по ценным бумагам и биржам, «Предупреждающие советы относительно раскрытия информации о важнейших учетных политиках», 12 декабря 2001 г.
http://www.sec.gov/rules/other/33-8040.htm
- Выписка Комиссии по ценным бумагам и биржам FR-72, «Рекомендации комиссии относительно обсуждения и анализа руководством финансового состояния и результатов деятельности», 19 декабря 2003 г.
http://www.sec.gov/rules/interp/33-8350.htm
- Проект Совета по стандартам финансового учета (FASB): «Принципы раскрытия информации». http://www.fasb.org/cs/ContentServer?c=FASBContent_C&pagename=FASB%2FFASBContent_C%2FProjectUpdatePage&cid=1176156344894
- Совместный проект FASB и IASB: «Концептуальные основы». http://www.fasb.org/cs/ContentServer?c=FASBContent_C&pagename=FASB%2FFASBContent_C%2FProjectUpdatePage&cid=
0011090
- Публикация концепции Совета по надзору за бухгалтерским учетом публичных компаний (PCAOB) о возможных изменениях стандартов PCAOB, касающихся отчетов о проверенных финансовых отчетах, и соответствующих поправках к стандартам PCAOB. http://pcaobus.org/Rules/Rulemaking/Pages/Docket034.aspx
1 См. Дуглас Хаббард. «Как измерить что угодно: определение ценности нематериальных активов в бизнесе», John Wiley & Sons, 2007.
2 Изложение концепций финансового учета № 8, параграф OB 11.
3 Например, ASC Topic 825-10, Опция справедливой стоимости . Этот стандарт расширил использование показателей справедливой стоимости, которые могут быть определены с использованием ненаблюдаемых исходных данных.
4 Например, ASC 820-10, Оценка справедливой стоимости. Настоящий стандарт определяет справедливую стоимость, устанавливает основу для оценки справедливой стоимости и расширяет раскрытие информации об оценке справедливой стоимости.
5 Изложение концепций финансового учета № 8, пункт QC 16.
Определение, пример и роль в инвестировании
Что такое неопределенность?
Неопределенность просто означает отсутствие уверенности в событии.В бухгалтерском учете Бухгалтерский учет и финансы В этом руководстве будет сравниваться бухгалтерский учет и финансы по различным аспектам. Бухгалтерский учет ориентирован на регистрацию и отчетность о том, как бизнес вел себя в прошлом, в то время как финансы сосредоточены на анализе и прогнозировании ожидаемых результатов деятельности компании в будущем. Под неопределенностью понимается неспособность предсказать последствия или результаты из-за отсутствия знаний или баз, на которых можно делать какие-либо прогнозы.
Этот термин часто широко используется в финансовой отчетности, особенно потому, что существует множество событий, находящихся вне контроля компании, которые могут сильно повлиять на ее операции.Поскольку в периоды неопределенности принимать финансовые решения намного сложнее, многие владельцы компаний воздерживаются от их принятия, чтобы не создавать проблем.
Сравнение риска и неопределенности
Нередко можно встретить людей, которые путают риск и неопределенность. Хотя некоторые организацииТипы организаций В этой статье о различных типах организаций исследуются различные категории, на которые могут подпадать организационные структуры. Организационные структуры и эксперты в финансовом мире считают эти два термина взаимозаменяемыми, на самом деле понятия различаются следующим образом:
- Риском проще и легче управлять, особенно при соблюдении надлежащих мер.Неопределенность, как широко известно, связана с незнанием будущих событий.
- Согласно американскому экономисту Фрэнку Найту, риск – это то, что можно измерить и измерить, и от чего берущий может принять меры, чтобы защитить себя. С другой стороны, неопределенность не позволяет предпринимать такие шаги, поскольку никто не может точно предсказать будущие события.
- Риск можно пойти или нет, в то время как неопределенность – это обстоятельство, с которым должны столкнуться владельцы бизнеса и люди в финансовом мире.
- Принятие риска может привести либо к прибыли, либо к убытку, потому что вероятные результаты известны, а неопределенность связана с неизвестными вероятностями.
Пример риска и неопределенности
Чтобы проиллюстрировать различия между риском и неопределенностью, давайте рассмотрим следующий пример.
Допустим, садовник помещает два разных растения в два горшка и маркирует их А и Б. Теперь он звонит ученику садовника и говорит ему, что нужно делать с посадкой А, в том числе ставить его на солнце на несколько часов в день. ежедневно, поливая два раза в день и прополивая через день.С другой стороны, он говорит, что не следует делать ничего из этого с другим растением, но будет давать ему органические удобрения, чтобы помочь ему расти.
Затем он спрашивает, кто из двоих, вероятно, будет жить и процветать. Конечно, учитывая опыт и знания того, что будет делать садовник, ученик может взвесить, какое из двух растений, скорее всего, вырастет. Это пример риска.
Теперь, что, если садовник скажет, что ничего не сделает ни с одним из растений, и спросит ученика, который, по его мнению, скорее всего, выживет? Ответ будет неопределенным из-за отсутствия достаточной информации и невозможности предсказать результат.
Неопределенность и инвестиции
Неопределенность – это одно из понятий в финансах и бухгалтерском учете, которое следует глубоко понять. Владельцы бизнеса, а также инвесторы хотят получить доступ к достоверным и честным финансовым отчетам. Три финансовых отчета. Три финансовых отчета – это отчет о прибылях и убытках, баланс и отчет о движении денежных средств. Эти три основных утверждения относятся к временам неопределенности.
Посредством общепринятых принципов бухгалтерского учета GAAPGAAP, Общепринятые принципы бухгалтерского учета, представляет собой признанный набор правил и процедур, регулирующих корпоративный бухгалтерский и финансовый учет, в том числе принятые Советом по стандартам финансового учета, теперь существуют процессы, которые можно использовать для определения, записывать и раскрывать неопределенность.Последовательное использование принципов бухгалтерского учета позволяет сравнивать финансовые записи за разные периоды.
Как превратить неопределенность в преимущество
Единственное, что можно сказать о неопределенности – это то, что она может произойти в любое время, и когда это произойдет, ни одна компания не застрахована от ощущения ее последствий. Поэтому самое эффективное – подготовиться к этому и превратить это в преимущество. Вот как это сделать:
1. Прогнозирование необходимо
Компании, которые полагаются на годовые бюджеты, в настоящее время оказываются на мелководье, потому что цифры могут быть неприменимы даже до того, как закончится конкретный финансовый год.Вот почему так важно регулярно составлять прогнозы и обновлять планы.
2. Переход к автоматизации
Ручной сбор данных занимает больше времени, чем их анализ, поэтому часто бывает слишком поздно обнаруживать проблемы. Бизнес-организациям следует перейти на автоматизацию, поскольку это сокращает время, необходимое для сбора и анализа данных.
3. Эффективная финансовая отчетность
Автоматизация также способствует созданию эффективных и точных финансовых отчетов.
4. Самообслуживание – ключ к успеху
Заинтересованные стороны – важный компонент организации, поэтому предоставление приложений самообслуживания полезно. Например, пользователи могут использовать специальное приложение, которое позволяет им открывать свои учетные записи и самостоятельно оценивать данные. Это не только дает им свободу делать это в любое удобное для них время, но также освобождает работу ИТ-отдела организации, позволяя им сосредоточиться на более важных процессах.
Дополнительные ресурсы
CFI является официальным поставщиком аналитики финансового моделирования и оценки (FMVA) ™. Стать сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® Сертификация CFI по анализу финансового моделирования и оценки (FMVA) ® поможет вам получить необходимую уверенность в своей финансовой карьере.Запишитесь сегодня! программа сертификации, призванная превратить любого в финансового аналитика мирового уровня.
Чтобы продолжить изучение и развитие своих знаний в области финансового анализа, мы настоятельно рекомендуем дополнительные ресурсы CFI, указанные ниже:
- Не склонен к риску Определение, не склонное к риску Человек, не склонный к риску, имеет характерную черту, предпочитающую избегать потерь, а не получать прибыль. Эта характеристика обычно присваивается инвесторам или участникам рынка, которые предпочитают инвестиции с более низкой доходностью и относительно известными рисками инвестициям с потенциально более высокой доходностью, но также с более высокой неопределенностью и большим риском.
- Safe HarborSafe Harbour Безопасная гавань – это положение закона или нормативного акта, которое обеспечивает защиту от ответственности или штрафов или снижает ответственность при соблюдении определенных условий.
- Системный риск Системный риск Системный риск можно определить как риск, связанный с крахом или банкротством компании, отрасли, финансового учреждения или всей экономики. Это риск серьезного сбоя финансовой системы, когда возникает кризис, когда поставщики капитала теряют доверие к пользователям капитала. конкретная компания или частное лицо.Систематический риск вызывается внешними по отношению к организации факторами. Все инвестиции или ценные бумаги подвержены систематическому риску и, следовательно, не подлежат диверсификации.
(PDF) Раскрытие важных бухгалтерских суждений и основных источников неопределенности оценок в финансовой отчетности компаний в Нигерии
Journal of Finance and Accounting 2019; 7 (1): 22-31 25
при существенной корректировке балансовой стоимости активов и
обязательств в течение следующего финансового года.
Совет по финансовой отчетности [9] Великобритании провел
тематический обзор опубликованной годовой финансовой отчетности
британских компаний в соответствии с требованиями суждений и оценок
, т.е. IAS 1: 122 и IAS 1: 125 соответственно. . Обзор
сообщил о своих выводах под тремя заголовками; (a)
дифференциация суждений от оценок, (b) суждений
и (c) оценок. Что касается отдельного раскрытия информации о
суждениях от оценок, исследование показало, что треть из
проверенных компаний не различает суждения
от оценок.Еще 15% классифицировали оценки
, включающие суждения как «суждения», а не оценки,
, что привело к меньшему раскрытию информации в отношении конкретных сумм риска
, а также чувствительности и диапазона результатов соответствующих сумм
. Что касается судебных решений, исследование
показало, что пятая из рассмотренных компаний использовала шаблонный текст в
раскрытии по крайней мере некоторых из своих ключевых суждений.Эти
относились к конкретным статьям в счетах, но не содержали
подробных сведений о субъективных аспектах или основания для суждения руководства
. Что касается оценок, исследование
сделало несколько выводов: Во-первых, более двух третей из
компаний рассмотрели раскрытые оценки, которые, хотя
относились к существенным суммам, не имели существенного риска
привести к существенным корректировка до
балансовой стоимости активов и обязательств вообще.Типичным примером
было раскрытие оценок обесценения гудвила
. В соответствующем примечании указано, что
директора не считали, что существует разумная возможность того, что изменение
ключевых допущений, на которых основана возмещаемая стоимость, составляла
, привело бы к превышению балансовой стоимости над возмещаемой стоимостью
. Во-вторых, Совет по финансовой отчетности
[9] обнаружил, что треть выборки использовала шаблонный язык
при раскрытии оценок.Чаще всего
выявляют примеры этого, связанные с налогообложением,
полезной экономической жизни, а также резервы по дебиторам и запасам. Во многих случаях
раскрытие информации могло применяться к любой отчитывающейся организации, а
не давало дополнительной полезной информации пользователям счетов
. Кроме того, только 40% опрошенных компаний
последовательно определили конкретные суммы, подверженные риску существенного искажения
, возникающих из расчетных сумм
в течение следующего финансового года.В-третьих, допущения
, лежащие в основе оценок, не были определены количественно. Было
ситуаций, когда необходимо было количественно оценить допущения порядка
, чтобы инвесторы могли понять позиции, занятые руководством
. Это было особенно актуально в отраслях
, где определенные факторы могли быть значительными источниками неопределенности оценки
для всех участников отрасли и где
инвесторы хотели бы проводить сравнения между компаниями.
Около 90% опрошенных компаний предоставили информацию о чувствительности
или диапазоне раскрытия результатов по крайней мере для некоторых из раскрытых оценок
. Однако, как правило, это было только в областях
, где раскрытие этой информации требовалось другим стандартом бухгалтерского учета
, таких как обесценение и пенсии.
Хотя налоговые активы и обязательства были вторым наиболее распространенным источником неопределенности оценок
, было отмечено, что
только две из рассмотренных компаний предоставили какую-либо чувствительность
или диапазон информации о результатах в этой области.Ни одна из
проверенных компаний не раскрыла информацию о чувствительности в отношении
сроков полезного использования, несмотря на то, что это обычно упоминаемый источник неопределенности оценки
. Наконец, если изменение прошлых допущений
привело к значительному изменению учетной оценки
, МСФО (IAS) 8 требует раскрытия характера
и суммы изменения. Однако из проанализированных компаний
только две раскрыли существенные изменения в учетной оценке
, а еще три раскрыли более
незначительные изменения в допущениях.Только один представил всю
необходимую информацию, требуемую МСФО 8.
Ирландский орган по надзору за аудитом и бухгалтерским учетом
(IAASA) [12] также провел кабинетное исследование по вопросам
, идентифицированным компаниями как критически важные для бухгалтерского учета
постановлений. Исследование IAASA [12] было основано на ежегодных финансовых отчетах
, опубликованных 20 случайно выбранными ирландскими
корпорациями, охватывающими широкий круг секторов промышленности,
варьируются с точки зрения рыночной капитализации, от более крупных
до более мелких. размерные объекты.Основная цель исследования
заключалась в определении критических бухгалтерских суждений, которые
выбранные корпорации сочли наиболее значимыми при подготовке финансовой отчетности за 2014/15 год.
Исследование выявило в общей сложности 108 критически важных бухгалтерских суждений
областей суждений, из которых наиболее распространенными критическими
бухгалтерскими суждениями были: (a) налогообложение, (b)
пенсионные обязательства (c) обесценение гудвила и
( г) Положения.Количество критически важных бухгалтерских суждений
, раскрытых и представленных корпорациями, варьировалось от трех
в одной финансовой отчетности до десяти в другой. В отношении
, где были раскрыты важнейшие бухгалтерские суждения (т. Е.
, была ли отчетность представлена отдельным примечанием в финансовой отчетности
, в примечании к учетной политике, или
встроено в соответствующее примечание к финансовой отчетности),
важнейшие бухгалтерские суждения были раскрыты в виде отдельного примечания
в финансовой отчетности (60%), в примечании к учетной политике
(25%) и в соответствующем примечании к
бухгалтерской отчетности (15%).
Майорга и Сидху [13] исследовали соответствие нормативным требованиям
20 крупнейших
компаний, котирующихся в Австралии, чтобы раскрыть ключевые предположения и основные источники неопределенностей оценок
и обнаружили, что, хотя фирмы предоставляют
некоторую информацию, эта информация была недостаточно
информативно, чтобы дать пользователям содержательную информацию. В целом, уровень раскрытия информации
не соответствовал требованиям соответствующих требований
.Еще одно рассмотренное эмпирическое исследование
ежегодно проводится Ernest and Young [14], международной бухгалтерской фирмой
. Эрнест и Янг [14] внимательно следят за
Комиссией по ценным бумагам и биржам (SEC).
сотрудников комментируют документы публично подотчетных организаций, чтобы предоставить
информацию о сферах деятельности Комиссии по ценным бумагам и биржам. Эрнест и Янг [14]
подтвердили два условия, требующие раскрытия критических
бухгалтерских оценок и суждений, а именно: (i) существенность
характера оценок или допущений в отношении уровней
субъективности и необходимых суждений. учитывать
очень неопределенных вопросов, подверженных изменениям; и (ii)
существенности влияния оценок и допущений на
финансовую отчетность.Эрнест и Янг [14] сообщили о SEC
«Риск раскрытия микроданных» в JSTOR
. АбстрактныйСтатистические агентства, предоставляющие микроданные для общего пользования, стремятся свести к минимуму риск раскрытия конфиденциальной информации. Однако оценить величину риска раскрытия информации непросто. Будет ли пользователь данных или злоумышленник пытаться получить конфиденциальную информацию из общедоступного файла, зависит от предполагаемых затрат на идентификацию записи, предполагаемой вероятности успеха и ожидаемой информации.В этой статье разрабатывается теоретическая основа принятия решений для оценки риска, которая включает цели и стратегию злоумышленника для компрометации базы данных и информации, полученной злоумышленником. Различают два вида раскрытия микроданных – раскрытие личности респондента и раскрытие атрибутов респондента в результате несанкционированной идентификации. Приводится формула риска раскрытия личности и оценивается ее простое приближение.
Информация о журналеЖурнал деловой и экономической статистики (JBES) издается ежеквартально с 1983 года Американской статистической ассоциацией.Он служит уникальным местом встречи для прикладных экономистов, эконометристов и статистиков, разрабатывающих соответствующие эмпирические методологии для широкого круга тем в бизнесе и экономике. Согласно недавним опросам, он неизменно входит в десятку лучших экономических журналов. Охват включает прогнозирование, качество данных, оценку политики, все темы эмпирической экономики, финансов, маркетинга и т. Д. Публикация обычно требует значительного методологического вклада и существенного практического применения.Однако JBES также будет публиковаться в областях вычислений, моделирования, сетей и графики, если предполагаемые приложения тесно связаны с общими темами, представляющими интерес для журнала.
Информация об издателеОсновываясь на двухвековом опыте, Taylor & Francis быстро выросла за последние два десятилетия и стала ведущим международным академическим издателем. Группа издает более 800 журналов и более 1800 новых книг каждый год, охватывая широкий спектр предметных областей и включая журнал. отпечатки Routledge, Carfax, Spon Press, Psychology Press, Martin Dunitz и Taylor & Francis.Taylor & Francis полностью привержена публикации и распространению научной информации высочайшего качества, и сегодня это остается основной целью.
Теория уменьшения неопределенности – Определение и примеры
Теория уменьшения неопределенности исследует начальное взаимодействие между людьми, которое происходит до фактического процесса коммуникации, и, следовательно, также известна как теория начального взаимодействия.
Он был разработан Чарльзом Бергером и Ричардом Калабрезе в 1975 году.Они хотели объяснить, как межличностное общение используется для уменьшения неопределенности между незнакомцами во время первоначального взаимодействия. Бергер говорит: «По мере того, как способность людей предсказывать, какая альтернатива или альтернативы могут возникнуть в следующий раз, уменьшается, неопределенность увеличивается».
Допущения теории уменьшения неопределенности
Теория уменьшения неопределенности основана на центральном предположении, что основная задача незнакомцев при первоначальном взаимодействии – уменьшить неопределенность и повысить предсказуемость.Другие предположения, связанные с этой теорией:
- Люди чувствуют себя неуверенно в начальном межличностном общении.
- Неопределенность может заставить людей избегать ситуации или поведения (аверсивное состояние) и вызывать когнитивный стресс.
- Незнакомцы хотят уменьшить неопределенность / повысить предсказуемость при первоначальном взаимодействии.
- Межличностное общение можно разбить на этапы.
- Межличностное общение ведет к снижению неопределенности.
- Люди со временем меняют количество и характер информации, которой они делятся.
- Можно предсказать поведение людей.
Основные концепции теории уменьшения неопределенности
Теория гласит, что людям нужна предварительная информация о других, чтобы уменьшить свою неуверенность. Людям неприятно, когда они не уверены в поведении или действиях другого человека, поэтому они пытаются уменьшить неуверенность посредством межличностного общения.
Бергер предложил семь аксиом (самоочевидных истин) относительно этой начальной неопределенности.
Устное общение
Уровень начальной неуверенности для каждого человека снижается с началом вербального общения.Кроме того, коммуникация увеличивается по мере уменьшения неопределенности.
Невербальная теплота
По мере увеличения невербальной аффилиативной выразительности, такой как зрительный контакт, кивки головой, улыбки, уменьшается неуверенность.
Ищу информацию
Потребность в поиске информации уменьшается по мере уменьшения неуверенности в отношении другого человека.
Самораскрытие
Люди раскрывают интимную информацию, поскольку чувствуют, что уровень неопределенности снижается.
Взаимность
Неопределенность прямо пропорциональна взаимности.При первоначальном взаимодействии люди, как правило, обмениваются личными данными, чтобы они соответствовали друг другу. По мере уменьшения неопределенности они не чувствуют необходимости быстро обмениваться деталями.
Сходство
Когда люди понимают, что их интересы совпадают с интересами другого человека, неопределенность уменьшается.
Нравится
Неопределенность уменьшается по мере того, как увеличивается чувство одобрения между отдельными людьми.
Мотивация к снижению неопределенности
Люди чувствуют необходимость уменьшить неопределенность только при определенных обстоятельствах.Бергер выделил три условия, которые побуждают нас уменьшить неопределенность.
Ожидание будущего взаимодействия
Мы хотим уменьшить неуверенность, когда знаем, что снова увидим другого человека.
Поощрительная стоимость
Нам нужна информация от людей, которые имеют или контролируют то, что мы хотим.
Отклонение
Поведение людей отклоняется от общепринятых норм.
Типы неопределенности
По словам Бергера, незнакомцы сталкиваются с двумя видами неуверенности, отправляясь на первую встречу.Их:
Когнитивная неопределенность
Когнитивная неопределенность означает неопределенность, связанную с убеждениями и отношениями людей. Незнакомцы не осведомлены об убеждениях и отношении друг друга при первоначальном взаимодействии, поэтому на данный момент существует высокая степень неопределенности.
Неопределенность поведения
Поведенческая неопределенность возникает, когда люди пытаются предсказать действия других в данной ситуации. Неопределенность высока, когда люди игнорируют социальные нормы (как от человека должны действовать) в начальных взаимодействиях.Это снижает вероятность будущих разговоров.
Этапы начального взаимодействия
Бергер и Калабрезе разделили процесс развития отношений на три стадии, каждая из которых включает в себя поведение, указывающее на симпатию или неприязнь.
Начальный этап
Люди начинают общение, руководствуясь поведенческими нормами, такими как приветствие и обмен демографической информацией (возраст, род занятий, родной город).
Персональный этап
По мере дальнейшего общения они делятся большей личной информацией, и один будет искать признаки ценностей, взглядов и морали у другого.
Выходной этап
Они будут выбирать, продолжать ли отношения, основываясь на уровне удовлетворения от межличностного общения.
Критика теории снижения неопределенности
Несмотря на широкое влияние, теория уменьшения неопределенности не обходится без критики. Вот некоторые из них:
- Некоторые исследователи утверждают, что снижение неопределенности не всегда является мотивирующим фактором для общения. Часто возникает искреннее желание познакомиться с другим человеком.
- Бергер и Калабрезе включили в свою выборку только белых людей среднего класса.
- Теория может быть легко опровергнута из-за большого объема ее аксиом.




 Авторские права (c) 1994 г.
AICPA.
Авторские права (c) 1994 г.
AICPA.