Криволинейное движение. Равномерное движение точки по окружности.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Криволинейное движение. Равномерное движение…
| Криволинейное движение. | |
| При криволинейном движении вектор скорости всегда направлен по касательной к траектории движения. Любое криволинейное движение можно представить в виде суммы прямолинейных движений и движений по окружностям разных радиусов.Скорость изменяется как по величине, так и по направлению. Вектор ускорения направлен под углом к вектору скорости. | |
| РАВНОМЕРНОЕ ДВИЖЕНИЕ ТОЧКИ ПО ОКРУЖНОСТИ. | |
Равномерное движение точки по окружности – движение точки с постоянной по модулю скоростью (v=const) по траектории, представляющей собой окружность. В этом случае скорость точки называется линейной скоростью (ℓ–длина дуги). Вектор линейной скорости направлен по касательной к окружности в данной точке. | |
Можно характеризовать изменение положения тела с помощью углового перемещения (угла поворота) φ. Возьмем несколько концентрических окружностей и построим для всех центральный угол φ так, чтобы радиусы этих окружностей, образующие угол, накладывались друг на друга. Из рисунка видно, что одному и тому же углу Единица измерения угла в этом случае наз. радианом(сокращение – рад). | |
Центральный угол равен одному радиану, если длина дуги равна радиусу окружности. Если точка совершила полный оборот, то длина дуги равна длине окружности. Следовательно: – полный оборот точки соответствует | |
Равномерное движение точки по окружности – это движение, при котором точка за любые равные промежутки времени совершает одинаковые угловые перемещения (поворачивается на одинаковые углы). Если характеризовать движение углом поворота, то удобно ввести угловую скорость: – угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ – рад/с. | |
| Можно сказать, что равномерным движением по окружности наз. движение с постоянной угловой скоростью. Линейная и угловая скорости связаны между собой: , т.е. . | |
К важным характеристикам вращательного движения относятся частота и период. Период– физическая величина, показывающая, чему равно время, за которое точка совершает один полный оборот. Если обозначить N – число оборотов, а Т – период, то: . Единица измерения в СИ – с. Т.к. за период точка поворачивается на угол Частота – количество оборотов, которое совершила точка за единицу времени: .
Единица измерения в СИ – Гц (герц). Частота равна одному герцу, если за 1 секунду точка совершает один полный оборот (1Гц=1с-1). Частота и период – взаимно обратные величины: . |
|
Теги:
конспект
Вопрос 1. Механическое движение. Система отсчёта. Путь, перемещение, траектория. Расчёт пути при равноускоренном движении.
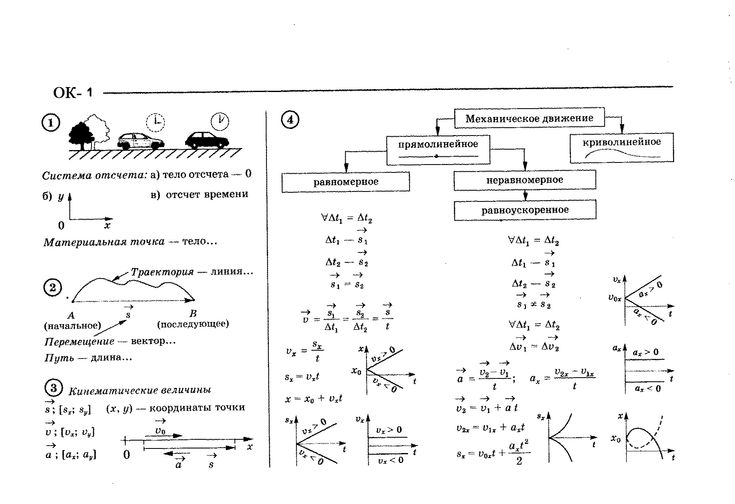
Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.
Механика Галилея-Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Законы движения тел со скоростями, сравнимыми со скоростью света, изучаются релятивистской механикой.
Движение
тел происходит в пространстве и во
времени. Положение материальной точки
определяется по отношению к какому-либо
другому телу, называемому телом отсчёта.
С ним связана система отсчета –
совокупность системы координат и часов,
связанных с телом отсчета.
Траектория движения материальной точки – линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Длина участка АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути и является скалярной функцией времени: . Вектор , проведенный из начального положения движущейся точки в положение ее в данный момент времени называется перемещением.
Равноускоренное движение – движение точки с постоянным ускорением. Ускорение – величина, характеризующая быстроту изменения скорости. В равноускоренном движении . Формула расчета скорости при равноускоренном движении в момент времени:
Проинтегрируем эту формулу: – путь при равноускоренном движении.
Вопрос 2. Кинематика поступательного движения. Скорость мгновенная, средняя. Модуль скорости. Ускорение и его составляющие.
Поступательное
движение — это движение, при котором
любая прямая, жестко связанная с
движущимся телом, остается параллельной
своему первоначальному положению.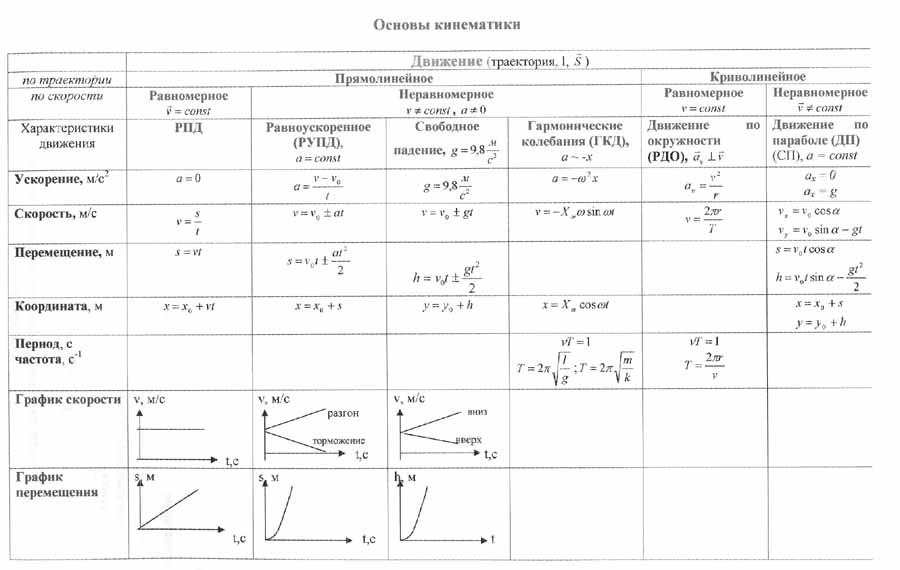 При
поступательном движении все точки тела
движутся одинаково, поэтому достаточно
изучить движение одной какой-то
произвольной точки тела (например,
движение центра масс тела). Так же при
поступательном движении тело не изменяет
ни своего вида, ни строения, одновременные
скорости всех точек равны и сонаправлены.
При
поступательном движении все точки тела
движутся одинаково, поэтому достаточно
изучить движение одной какой-то
произвольной точки тела (например,
движение центра масс тела). Так же при
поступательном движении тело не изменяет
ни своего вида, ни строения, одновременные
скорости всех точек равны и сонаправлены.
Мгновенная скорость (скорость) — предел отношения вектора перемещения к промежутку времени, за который это перемещение произошло, при стремлении длительности промежутка времени к нулю. Модуль мгновенной скорости равен первой производной пути по времени.
Средняя скорость (средняя путевая скорость) – отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.
Средняя
путевая скорость, в отличие от мгновенной
скорости не является векторной величиной.
Средняя скорость равна среднему
арифметическому от скоростей тела во
время движения только в том случае,
когда тело двигалось с этими скоростями
одинаковые промежутки времени.
В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.
Ускорение – величина, характеризующая быстроту изменения скорости по величине и направлению. Ускорение – векторная величина, состоит из двух составляющих – тангенциальной составляющей и нормальной.
Тангенциальная составляющая характеризует изменение скорости по величине и направлена по направлению вектора скорости (если движение равноускоренное) или противоположно вектору скорости (равнозамедленное движение), равна:
Вторая составляющая ускорения называется нормальной и направлена по нормали к траектории к центру ее кривизны (центростремительное ускорение):
Равноускоренное движение: Определение | StudySmarter
Все мы знакомы со знаменитой сказкой о яблоке, падающем с дерева, которая легла в основу ранней фундаментальной работы Исаака Ньютона по теории гравитации.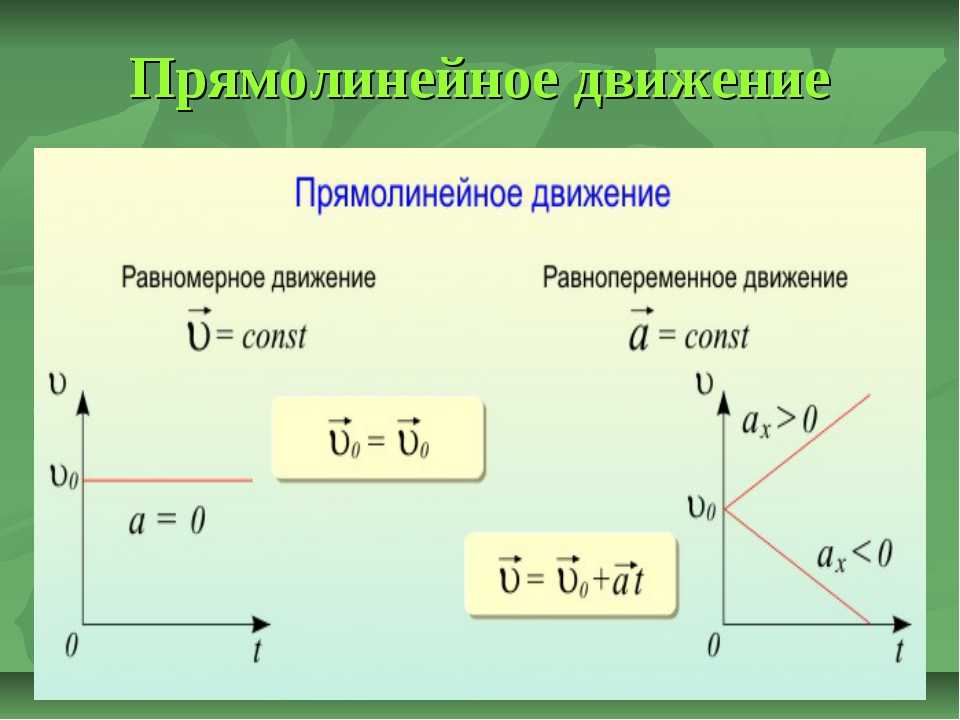 Любознательность и стремление Ньютона понять это, казалось бы, неинтересное падающее движение изменили большую часть нашего нынешнего понимания движущегося мира и Вселенной вокруг нас, включая явление равномерного ускорения из-за гравитации, постоянно происходящее вокруг нас.
Любознательность и стремление Ньютона понять это, казалось бы, неинтересное падающее движение изменили большую часть нашего нынешнего понимания движущегося мира и Вселенной вокруг нас, включая явление равномерного ускорения из-за гравитации, постоянно происходящее вокруг нас.
В этой статье мы углубимся в определение равноускоренного движения, в соответствующие формулы, которые нужно знать, как идентифицировать и исследовать связанные графики, а также в пару примеров. Давайте начнем!
Равномерно ускоренное движение Определение
Пока мы знакомились с кинематикой, мы столкнулись с несколькими новыми переменными и уравнениями для решения задач движения в одном измерении. Мы уделили пристальное внимание смещению и скорости, а также изменениям этих величин и тому, как различные начальные условия влияют на общее движение и результат системы. Но как насчет ускорения?
Наблюдение и понимание ускорения движущихся объектов так же важно в нашем начальном изучении механики. Возможно, вы заметили, что до сих пор мы в основном изучали системы, в которых ускорение равно нулю, а также системы, в которых ускорение остается постоянным в течение некоторого периода времени. Мы называем это равноускоренным движением.
Возможно, вы заметили, что до сих пор мы в основном изучали системы, в которых ускорение равно нулю, а также системы, в которых ускорение остается постоянным в течение некоторого периода времени. Мы называем это равноускоренным движением.
Равноускоренное движение — это движение объекта с постоянным ускорением, которое не меняется со временем.
Сила притяжения приводит к равномерному ускорению падения парашютиста, Creative Commons CC0
Другими словами, скорость движущегося объекта равномерно изменяется со временем, а ускорение остается постоянной величиной. Ускорение под действием силы тяжести, наблюдаемое при падении парашютиста, яблока с дерева или упавшего на пол телефона, является одной из наиболее распространенных форм равномерного ускорения, которые мы наблюдаем в нашей повседневной жизни. Математически мы можем выразить равномерное ускорение как:
\begin{align*}a=\mathrm{const.}\end{align*}
Вычисление определения ускорения
Напомним, что мы можем вычислить ускорение \(a\) движущегося объекта, если мы знаем начало и конечные значения как для скорости, так и для времени:
\begin{align*}a_{avg}=\frac{\Delta v}{\Delta t}=\frac{v_1-v_0}{t_1-t_0}\end {align*}
где \(\Delta v\) — изменение скорости, а \(\Delta t\) — изменение времени. Однако это уравнение дает нам среднее ускорение 92}\end{align*}
Однако это уравнение дает нам среднее ускорение 92}\end{align*}
То есть ускорение математически определяется как первая производная скорости и вторая производная положения по времени.
Формулы равномерно ускоренного движения
Оказывается, вы уже знаете формулы равноускоренного движения — это уравнения кинематики, которые мы выучили для движения в одном измерении! Когда мы ввели основные уравнения кинематики, мы предполагали, что все эти формулы точно описывают движение объекта, движущегося в одном измерении , пока ускорение остается постоянным . Раньше это был в значительной степени аспект, который мы подразумевали и не углублялись в него.
Давайте изменим наши уравнения кинематики и выделим переменную ускорения. Таким образом, мы можем легко использовать любую из наших формул для определения значения ускорения при различных начальных условиях для запуска. Начнем с формулы \(v=v_0+at\).
Значение постоянного ускорения с учетом начальной скорости, конечной скорости и времени: 92}{2 \Delta x}, \\ \Delta x \neq 0. \end{align*}
\end{align*}
Возможно, вы помните, что существует уравнение, не зависящее от ускорения, связанное с кинематикой, но это уравнение здесь не имеет значения, поскольку переменная ускорения не включено.
Хотя здесь мы изолировали переменную ускорения в каждом кинематическом уравнении, помните, что вы всегда можете перестроить свое уравнение, чтобы найти другое неизвестное — вы часто будете использовать известное значение ускорения вместо его решения!
Равномерное движение и равномерное ускорение
Равномерное движение, равномерное ускорение — есть ли разница между ними? Ответ, как ни странно, да! Поясним, что мы понимаем под равномерным движением.
Равномерное движение — объект, совершающий движение с постоянной или неизменной скоростью.
Хотя определения равномерного движения и равномерно ускоренного движения звучат похоже, здесь есть тонкая разница! Напомним, что для объекта, движущегося с постоянной скоростью, ускорение должно быть равно нулю согласно определению скорости.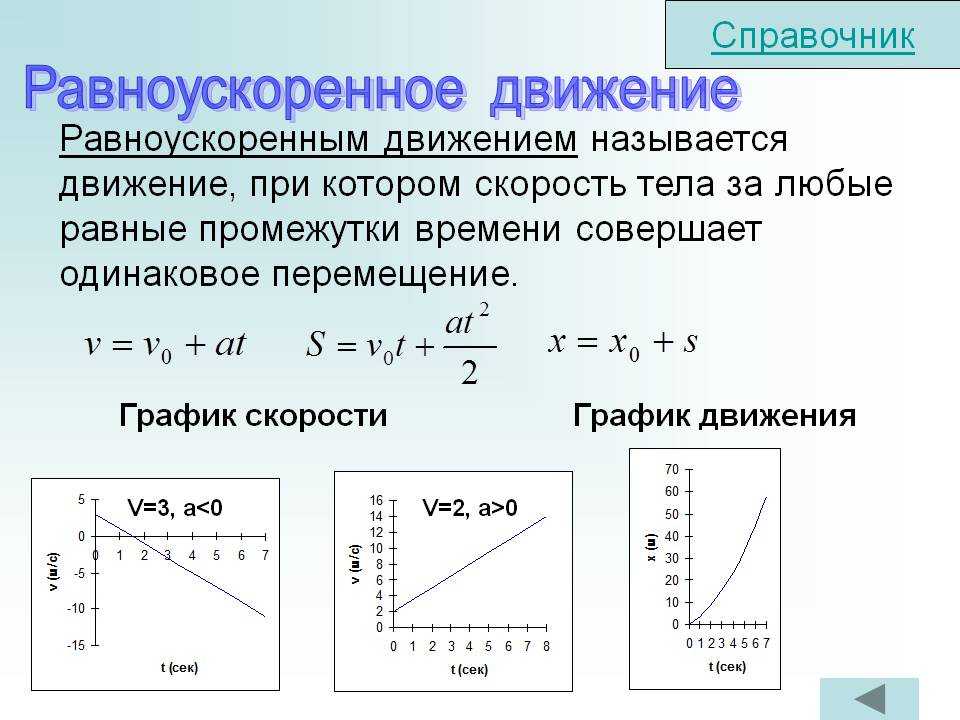 Следовательно, равномерное движение , а не также подразумевает равномерное ускорение, поскольку ускорение равно нулю. С другой стороны, равноускоренное движение означает, что скорость не постоянна, а само ускорение.
Следовательно, равномерное движение , а не также подразумевает равномерное ускорение, поскольку ускорение равно нулю. С другой стороны, равноускоренное движение означает, что скорость не постоянна, а само ускорение.
Графики равномерно ускоренного движения
Ранее мы рассмотрели несколько графиков движения в одном измерении — теперь вернемся к графикам равномерно ускоренного движения более подробно.
Равномерное движение
Мы только что обсудили разницу между равномерным движением и равноускоренным движением . Здесь у нас есть набор из трех графиков, которые визуализируют три разные кинематические переменные для объекта, совершающего равномерное движение в течение некоторого периода времени \(\Delta t\):
Мы можем визуализировать равномерное движение с помощью трех графиков: перемещение, скорость и ускорение , MikeRun через Wikimedia Commons CC BY-SA 4.0
На первом графике мы видим, что смещение или изменение положения относительно начальной точки линейно увеличивается со временем. Это движение имеет постоянную скорость во времени. Кривая скорости на втором графике имеет нулевой наклон, поддерживаемый постоянным значением \(v\) в \(t_0\). Что касается ускорения, то это значение остается равным нулю в течение того же периода времени, как и следовало ожидать. 9{t_2} v(t)\,\mathrm{d}t\end{align*}
Это движение имеет постоянную скорость во времени. Кривая скорости на втором графике имеет нулевой наклон, поддерживаемый постоянным значением \(v\) в \(t_0\). Что касается ускорения, то это значение остается равным нулю в течение того же периода времени, как и следовало ожидать. 9{t_2} v(t)\,\mathrm{d}t\end{align*}
Другими словами, мы можем проинтегрировать функцию скорости между нижним и верхним пределом времени, чтобы найти изменение смещения, которое произошло в течение этого временной период.
Равномерное ускорение
Мы можем изобразить те же три типа графиков для исследования равномерно ускоренного движения. Давайте посмотрим на график зависимости скорости от времени:
Линейное увеличение скорости со временем в соответствии с функцией скорости v(t)=2t, с площадью под кривой, равной смещению, StudySmarter Originals
Здесь у нас есть простая функция скорости \(v(t)=2t\), построенная от \(t_0=0\,\mathrm{s}\) до \(t_1=5\,\mathrm{s} \). Поскольку изменение скорости не равно нулю, мы знаем, что ускорение также будет ненулевым. 2}} \end{align* }
2}} \end{align* }
Теперь давайте посмотрим на график ускорение-время:
Графики ускорение-время для равноускоренного движения имеют нулевой наклон. Площадь под этой кривой равна изменению скорости во временном интервале, StudySmarter Originals
На этот раз график зависимости ускорения от времени показывает постоянное, ненулевое значение ускорения \(2\,\mathrm{\frac{m} {с}}\). Вы могли заметить, что площадь под кривой зависимости ускорения от времени равна изменению скорости 9{5}2\,\mathrm{d}t = 2t \\\Delta v = 2(5)-2(0) \\ \Delta v = 10\, \mathrm{\frac{m}{s}} \end{align*}
Наконец, мы можем продолжить работу в обратном направлении, чтобы вычислить изменение смещения в метрах, даже если перед нами нет графика для этой переменной. Вспомним следующее соотношение между смещением, скоростью и ускорением:
\begin{align*} \Delta s = \int v(t)\,\mathrm{d}t = \iint a(t)\,\mathrm{ d}t \end{align*}
Хотя мы знаем функции как для скорости, так и для ускорения, интегрировать функцию скорости здесь проще всего: 92 \\ \Delta s = 25\, \mathrm{m} \end{align*}
Помните, что этот расчет дает нам чистое смещение за пятисекундный период времени, в отличие от общей функции смещения. Графики могут многое рассказать нам о движущемся объекте, особенно если нам дают минимум информации в начале задачи!
Графики могут многое рассказать нам о движущемся объекте, особенно если нам дают минимум информации в начале задачи!
Примеры равномерно ускоренного движения
Теперь, когда мы знакомы с определением и формулами равноускоренного движения, давайте рассмотрим пример задачи.
Ребенок роняет мяч из окна на расстоянии \(11,5\, \mathrm{м}\) от земли. Пренебрегая сопротивлением воздуха, через сколько секунд мяч падает до удара о землю?
Может показаться, что здесь нам дали недостаточно информации, но мы подразумеваем значения некоторых переменных в контексте задачи. Нам нужно вывести некоторые начальные условия на основе рассматриваемого сценария:
- Мы можем предположить, что ребенок не задал начальную скорость, когда отпускал мяч (например, бросая его вниз), поэтому начальная скорость должна быть \(v_0= 0 \, \ mathrm {\ frac {m} {s}} \). 92}}}} \\ t=1.53\, \mathrm{s} \end{align*}
Путь мяча к земле длится \(1.53 \, \mathrm{s}\), равномерно ускоряясь при этом падении .

Прежде чем мы завершим наше обсуждение, давайте рассмотрим еще один пример равномерно ускоренного движения, на этот раз применяя уравнения кинематики, которые мы рассмотрели ранее.
Частица движется согласно функции скорости \(v(t)=4,2t-8\). Каково чистое смещение частицы после перемещения в течение \(5,0\, \mathrm{s}\)? Каково ускорение частицы в этот период времени? 92}{10}-8(5)-0\\ \Delta x= 12,5\, \mathrm{m} \end{align*}
С исчислением нам не нужно строить график нашей функции скорости, чтобы найти смещение, но визуализация проблемы может помочь нам проверить, имеют ли наши ответы смысл. Построим график \(v(t)\) от (\(t_0=0\, \mathrm{s}\) до (\(t_1=5\, \mathrm{s}\).
Функция скорости частицы с изменением направления непосредственно перед t = 2 секунды Эта отрицательная площадь приводит к меньшему чистому смещению за временной интервал, StudySmarter Originals
Мы можем наблюдать некую “отрицательную область” во время первой части его движения.
 Другими словами, частица в это время имела отрицательную скорость и направление движения. Поскольку чистое смещение учитывает направление движения, мы вычитаем эту площадь, а не прибавляем. Скорость точно равна нулю при:
Другими словами, частица в это время имела отрицательную скорость и направление движения. Поскольку чистое смещение учитывает направление движения, мы вычитаем эту площадь, а не прибавляем. Скорость точно равна нулю при:\begin{align*}0=4.2t-8 \\ t=1.9\, \mathrm{s} \end{align*}
или точнее, \(\frac{ 40}{21}\, \mathrm{s} \). Мы можем быстро перепроверить нашу интеграцию выше, вычислив площадь каждого треугольника вручную:
\begin{align*}\mathrm{A_1=\frac{1}{2}\cdot \frac{40}{21}\, s \cdot -8\, \frac{m}{s} = \ frac{-160}{21}\, м} \\ \mathrm{A_2=\frac{1}{2} \cdot (5\, с-\frac{40}{21}\, с) \cdot 13 \, \frac{m}{s} = \frac{845}{42} m} \\ \mathrm{A_{net}= \Delta x= \frac{845}{42}\, m-\frac{ 160}{21}\, m =12.5\, m} \end{align*}
Получим то же смещение, что и ожидалось. Наконец, мы можем рассчитать значение ускорения, используя наше уравнение кинематики с начальной скоростью, конечной скоростью и временем: 92}} \end{align*}
Равномерно ускоренное движение является важным компонентом наших ранних исследований в области кинематики и механики, физики движения, которая определяет большую часть нашего повседневного опыта.
 Знание того, как распознать равномерное ускорение, а также как подходить к этим проблемам, — это первый шаг к лучшему пониманию Вселенной в целом!
Знание того, как распознать равномерное ускорение, а также как подходить к этим проблемам, — это первый шаг к лучшему пониманию Вселенной в целом!Равномерно ускоренное движение — ключевые выводы
- Ускорение математически определяется как первая производная скорости по времени и вторая производная положения по времени.
- Равномерное движение — это движение объекта, скорость которого постоянна, а ускорение равно нулю.
- Равноускоренное движение — это движение объекта, ускорение которого не меняется с течением времени.
- Ускорение вниз под действием силы тяжести падающих предметов является наиболее распространенным примером равномерно ускоренного движения.
- Площадь под графиком скорость-время дает нам изменение смещения, а площадь под графиком ускорение-время дает нам изменение скорости.
Равноускоренное движение – Определение и ПРИМЕРЫ
Эта статья будет о Равноускоренном движении, основных характеристиках этого движения, с примерами и формулами.

Быстрый доступ
!Нажмите на кнопки ниже, чтобы перейти прямо к разделу статьи, которую вы ищете!
Определение равноускоренного движения
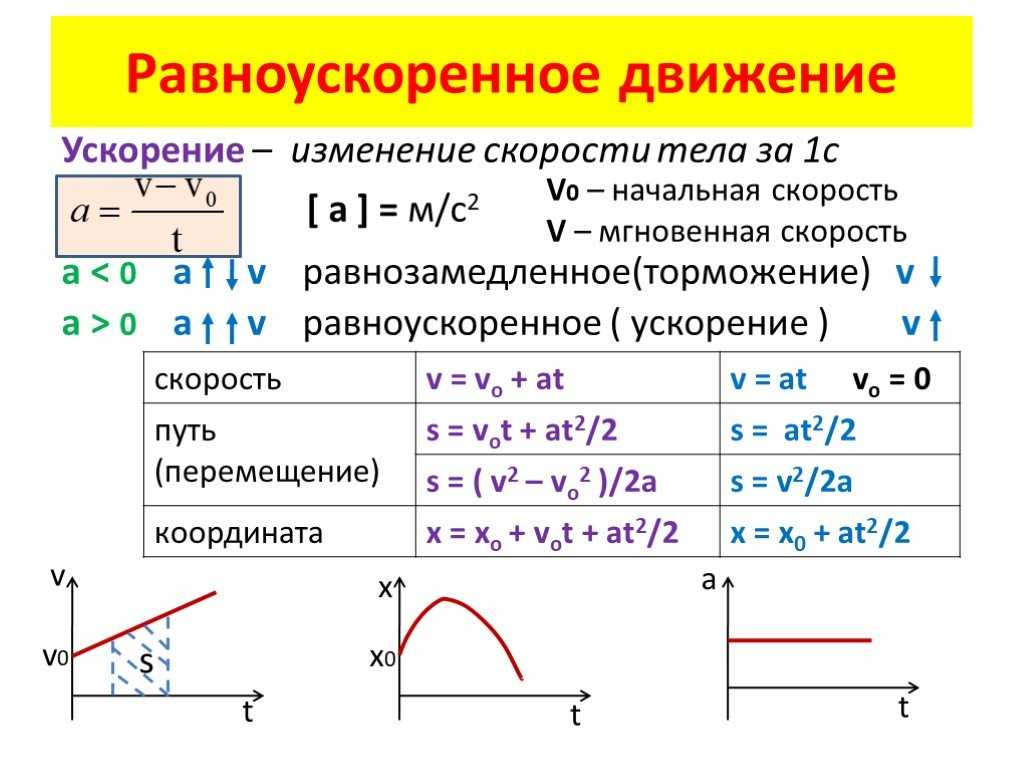
Равноускоренное движение есть движение, характеризующееся наличием прямолинейного движения с постоянным и отличным от нуля ускорением, поэтому скорость объекта при этом движении постоянно изменяется в зависимости по направлению скорости.
Основные характеристики равноускоренного движения: чтобы определить, когда речь идет о равноускоренном движении необходимо знать параметры этого движения: Его траектория прямолинейна что означает, что это движение, которое движется только в одном измерении. Его ускорение отличается от нуля , и в этом основное отличие этого движения от движения с постоянной скоростью. Его скорость постоянно меняется , из-за ускорения скорость постоянно увеличивается или уменьшается, поэтому в задачах об этом движении всегда будет начальная скорость и конечная скорость.

Ускорение – это постоянное изменение скорости. Знак или направление, которое имеет скорость или ускорение, может дать представление о том, на что будет похоже движение, если и ускорение, и скорость имеют один и тот же знак, то объект будет увеличивать скорость каждую секунду, но если эта величина имеют разные знаки (например, положительную скорость и отрицательное ускорение), то объект начнет замедляться каждую секунду, пока не остановится.
Положительное ускорение
Отрицательное ускорение
Поведение равномерно ускоренного движения
В системе отсчета мы обычно принимаем направления вверх и вправо как положительные, а направления вниз и влево — как отрицательные, поэтому, если объект начинается с состояния покоя, а затем мы приложим к нему положительное ускорение, объект начнет продвигаться вправо, но если мы приложим отрицательное ускорение, то объект начнет продвигаться влево.
Когда объект в равномерно ускоренном движении имеет ускорение в направлении, противоположном скорости, , то скорость объекта начнет уменьшаться, пока он не останется в состоянии покоя , после этого момента объект начнет двигаться в противоположном направлении, например, когда мы что-то подбрасываем, мы применяем скорость к объекту но из-за гравитации он начинает уменьшать свою скорость и какое-то время находится в покое, но затем он снова падает на землю, давайте вспомним, что гравитация – это ускорение, которое влияет на каждый объект на земле.

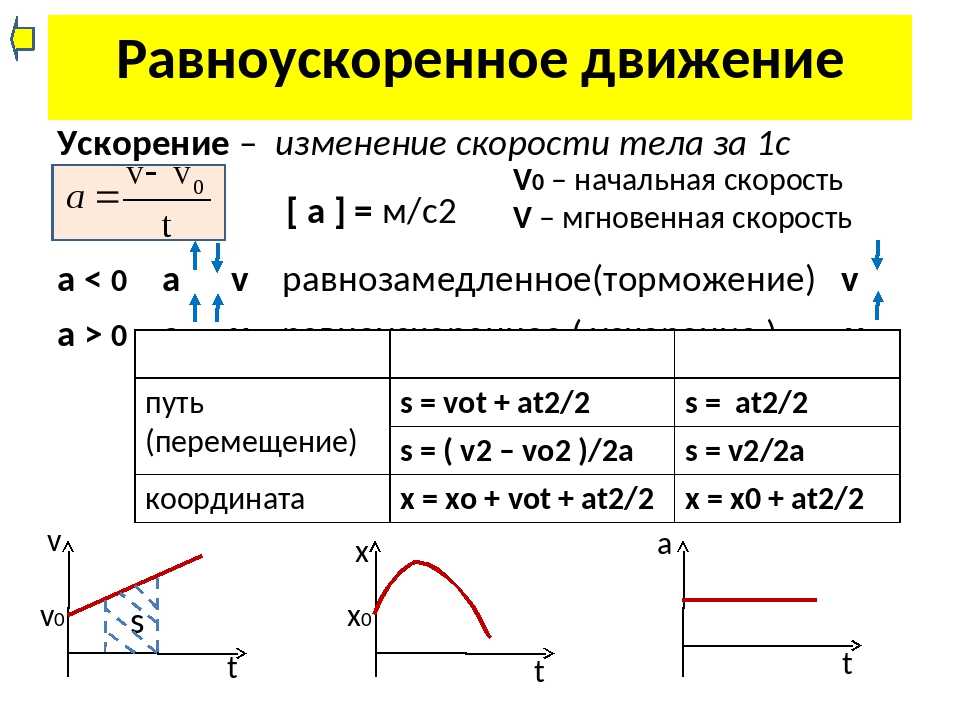
Формулы равноускоренного движения
Существует 5 формул для решения любой задачи равномерно ускоренного движения, из которых мы можем использовать любую из них для нахождения переменной, но мы должны знать, какую из них использовать, потому что есть некоторые задачи, которые дают только определенные данные, но задача не дает никаких данных, которые мы можем использовать в уравнении, поэтому мы должны очень тщательно выбирать, какое уравнение мы собираемся использовать.
Vo = начальная скорость, Vf = конечная скорость, a = ускорение, d = расстояние
- vf = vo + a * t
- d = vo * t + 1/2a * t 2
- вф 2 = во 2 + 2а * д
- во 2 = вф 2 – 2а * д
- d =
v o + v f /2
* t
Например, если в задаче мы должны найти конечную скорость объекта и у нас есть начальная скорость, ускорение и расстояние, первое уравнение для этого не подойдет, потому что для этого нам нужно время, формула которую нам пришлось бы использовать, — это третья формула, потому что она имеет те же самые переменные, что и мы.

Равноускоренная движущаяся графика
Позиционная графика
Является положительной частью параболы.
График скорости
Линейный график.
График ускорения
Является постоянным графиком.
Примеры равноускоренного движения
Приведенные данные Данные для поиска
Пример 1: Находящийся в состоянии покоя автомобиль начинает ускоряться со скоростью 2 м/с, если он продолжает ускоряться в течение 10 секунд, определите скорость, с которой машина доедет.
Данные
Vo = 0 a = 2 м/с t = 10 с Vf = ?
- Сначала мы пишем уравнение для использования
- v f = v o + a * t
- В этом примере нам не нужно очищать уравнение
- v f = 0 + 2 * 10 с
- Итак, мы решаем это напрямую
- v f = 20
Иисус любит тебя
Иисус — сын Божий, который был послан на смерть, чтобы каждый, кто верит в него, имел жизнь вечную.

Узнать больше
Пример 2: Человек, начавший идти со скоростью 1 м/с, начал ускоряться и через 30 секунд этот человек уже бежит со скоростью 5 м/с, ¿какое расстояние преодолел этот человек бегать?.
Данные
Vo = 1 м/с vf = 5 м/с t = 30 с d = ?
- Запишем формулу
- d =
v o + v f /2
* t - Затем заменить данные и решить
- д =
1 + 5/2
* 30 - д =
6/2
* 30 - д = 3*30
- д = 90
Пример 3: Автомобиль, движущийся со скоростью 33,2 м/с, начинает замедляться и в конце концов останавливается, если мы знаем, что приложенное ускорение составляло -2 м/с машина накрыта?
Данные
Vo = 33,2 м/с Vf = 0 м/с a = -2 м/с d = ?
- Напишите формулу
- вф 2 = во 2 + 2а * д
- Затем расчищаем дистанцию
- d =
v f 2 – v o 2 /2a
- затем заменить данные и решить
- d =
0 – 33,2 2 /2(-2)
- d =
-33,2 2 /-4
- d =
-1102,24/-4
- д = 275,56
Пример 4: легкий самолет летит со скоростью 12 м/с, если он ускоряется и достигает скорости 20 м/с, и если мы знаем, что между этим он преодолел расстояние 300 метров, то какова была время и какое ускорение.

Данные
Vo = 12 м/с Vf = 20 м/с d = 300 t = ? а = ?
- Запишем пятую формулу
- д =
v о + v f /2
* т - Затем очищаем время и решаем
- t =
2d/v o + v f
- т =
2(300)/12 + 20
- т =
600/32
- т = 18,75 с
- Теперь, когда у нас есть время, пишем первую формулу и очищаем ускорение
- v f = v o + a * t
- а =
v ф – в или /т
- Затем заменить данные и решить
- а =
20 – 12/18,75
- а =
8/18,75
- а = 0,43
Пример 5: к объекту прикладывалось ускорение 3 м/с в течение 9 секунд, если мы знаем, что объект преодолел расстояние 103 метра, рассчитайте конечную скорость и начальную скорость.

Данные
a = 3 м/с d = 103 м t = 9 с Vo = ? Вф = ?
- Напишите формулу
- d = v о * t + 1/2a * t 2
- Очистить начальную скорость
- v o =
d – 1/2a * t 2 /t
- И решить
- v o =
103 – 1/2(3) * (9) 2 /9
- v o =
103 – 1/2(3) * (81)/9
- v o =
103 – 1/2(243)/9
- v o =
103 – 121,5/9
- v o =
-18,5/9
- v o = -2,06
- Напишите первую формулу
- v f = v o + a * t
- Затем замените формулу и решите
- v f = -2,06 + 3 * 9
- в ф = -2,06 + 27
- v f = 24,94
Ejercicio 6: В парке аттракционов есть американские горки, где первые 140 метров проходят по прямой, если с начала, когда автомобиль находится в состоянии покоя, и до достижения им 140 метров происходит постоянное ускорение 7,5 м.
 /с, рассчитайте время, за которое автомобиль преодолел 140 м, и конечную скорость.
/с, рассчитайте время, за которое автомобиль преодолел 140 м, и конечную скорость.Datos
Vo = 0 м/с d = 140 м a = 7,5 м/с t = ? Вф = ?
- Напишите уравнение
- вф 2 = во 2 + 2а * д
- Заменить данные и решить
- вф 2 = во 2 + 2а * д
- vf 2 = 0 + 2(7,5) * 140
- vf 2 = 0 + 15 * 140
- vf = √ 2100
- vf = 45,82
- Теперь найдем время
- вф = во + а * т
- t =
v f – v o /a
- т =
45,82 – 0/7,5
- т = 6,11
Пример 7: Спутник в космосе, находящийся в состоянии покоя, изменит свое положение, двигаясь по прямой линии, если он достигнет скорости 3000 м/с всего за 0,9 с, какое ускорение было приложено и определите расстояние.

Данные
Vf = 3000 м/с Vo = 0 t = 0,9 с d = ? а = ?
- Сначала найдем расстояние по пятой формуле
- d =
v o + v f /2
* t - d =
0 + 3000/2
* 0,9 - д = 1500*0,9
- д = 1350
- И затем мы собираемся вычислить ускорение
- v f = v o + a * t
- а =
v f – v о /т
- а =
3000/0,9
- а = 3333,33
Пример 8: Лодка, плывущая по озеру, движется со скоростью 5 м/с, но если она ускоряется на 1 м/с на протяжении 40 метров, рассчитайте время, за которое она ускорилась.
Данные
d = 40 м Vo = 5 м/с a = 1 м/с t = ?
Этот пример можно решить разными способами, потому что если мы посмотрим в формулах ту, которая позволяет нам найти время, имея расстояние, начальную скорость и ускорение, есть только одно и второе уравнение, но очистить время в этой формуле – непростая работа, поэтому самый простой способ сделать это – сначала найти другие данные с другими уравнениями, например, мы могли бы найти начальную скорость с помощью первого уравнения, а затем использовать первую или пятую формулу, чтобы найти время, но в этом случае мы собираемся решить это трудным путем.


 Но, т.к. скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Значит равномерное движение по окружности –
Но, т.к. скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Значит равномерное движение по окружности – 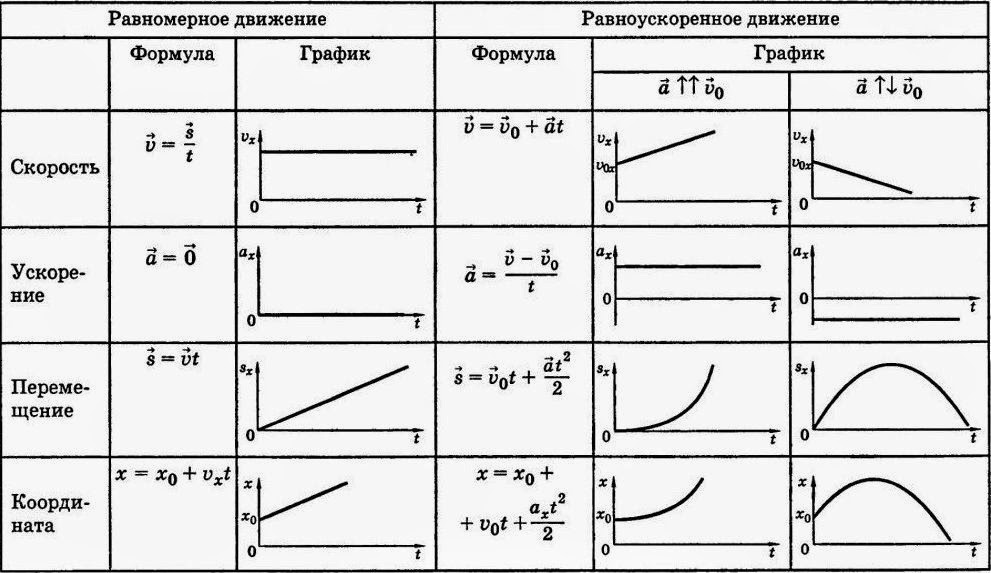 За меру угла можно принять отношение длины дуги к радиусу:.
За меру угла можно принять отношение длины дуги к радиусу:.
 Следовательно: .
Следовательно: .
 Другими словами, частица в это время имела отрицательную скорость и направление движения. Поскольку чистое смещение учитывает направление движения, мы вычитаем эту площадь, а не прибавляем. Скорость точно равна нулю при:
Другими словами, частица в это время имела отрицательную скорость и направление движения. Поскольку чистое смещение учитывает направление движения, мы вычитаем эту площадь, а не прибавляем. Скорость точно равна нулю при: Знание того, как распознать равномерное ускорение, а также как подходить к этим проблемам, — это первый шаг к лучшему пониманию Вселенной в целом!
Знание того, как распознать равномерное ускорение, а также как подходить к этим проблемам, — это первый шаг к лучшему пониманию Вселенной в целом!




 /с, рассчитайте время, за которое автомобиль преодолел 140 м, и конечную скорость.
/с, рассчитайте время, за которое автомобиль преодолел 140 м, и конечную скорость.
