Разделить матрицу на матрицу: 4. Деление матриц:

python – Разделение матрицы на подматрицы

Вопрос задан 1 год 6 месяцев назад

Изменён 1 год 6 месяцев назад

Просмотрен 509 раз

Вводится N – размер матрицы, K – размер подматриц.
Далее вводится матрица
Допустим N = 3, K = 2

Наша матрица N*N

1 2 1
1 1 2
1 1 1

Все подматрицы размера K*K:

[1 2
 1 1]
[2 1
 1 2]
[1 1
 1 1]
[1 2
 1 1]

Как сделать такое же нахождение подматриц? От чего отталкиваться? Единственное что сделал – создание трёхмерного массива матриц k*k заполненных нулями.

• python
• матрицы
• олимпиада

3

если в лоб, то так:

matrix = [[1, 2, 3, 'a'], [4, 5, 6, 'b'], [7, 8, 9, 'c'], [10, 11, 12, 'd']]
size = (3, 2)
for j in range(len(matrix) - size[1] + 1):
    for i in range(len(matrix[j]) - size[0] + 1):
        for y in range(size[1]):
            line = []
            for x in range(size[0]):
                line.  append(matrix[j + y][i + x])
            print(line)
        print()

грубо говоря вам надо пройтись по матрице так чтобы 1 элемент подматрицы был в диапазоне: matrix_width - submatrix_width, matrix_height - submatrix_height

а дальше используя координаты первого элемента находите все остальные элементы подматрицы в матрице

или если это записать на уровне формулы, то:

submatrix[x][y] = matrix[i + x][j + y]

где (i, j) – координаты первого (левый верхний) элемента подматрицы в матрице

P.S.

код можно чуть-чуть упростить (для любителей разврата):

[[[print([matrix[j + y][i + x] for x in range(size[0])]) for y in range(size[1])] + [print()] for i in range(len(matrix[j]) - size[0] + 1)] for j in range(len(matrix) - size[1] + 1)]

Если исходную матрицу представить в виде планарного списка, то решение довольно простое и укладывается в одну строку.

matrix = [1, 2, 1,
          1, 1, 2,
          1, 1, 1]
N = int(len(matrix)**0. 5)
K = N - 1
k_matrixes = [sum((matrix[rr*N+c:rr*N+c+K] for rr in range(r,r+K)), []) for r in range(N-K+1) for c in range(N-K+1)]
print(k_matrixes)

[[1, 2, 1, 1], [2, 1, 1, 2], [1, 1, 1, 1], [1, 2, 1, 1]]

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Деление матриц – онлайн калькулятор на Calculators.

byМатрица А
(3×3)

Размер Матрицы А: кол-во строк:       23456
кол-во столбцов:123456

+-×

Матрица B
(3×3)

Размер Матрицы B: кол-во строк:       23456
кол-во столбцов:123456

Можно ли делить матрицы?

Пользуясь удобным средством вычисления на сайте, выполняйте точное деление матриц онлайн. Обратите внимание на особенности этой процедуры, чтобы получить корректный итог.

Делить матрицы невозможно! Так считает теория высшей математики, и для этого утверждения есть веские основания. Принято считать, что деление строк матриц нецелесообразно, так как дает 0, а на него нельзя совершать эту операцию. Но, если задуматься, везде есть свои нюансы и особенности. Такое явление, как матричные таблицы, конечно, обладает своей спецификой. Поэтому здесь можно посмотреть на этот вопрос под другим углом.

Оказывается, деление в данном случае все-таки возможно. Но как это сделать, если оно противоречит принципам матрицы? Согласно учебникам, такая операция просто-напросто отсутствует в рабочем арсенале математика.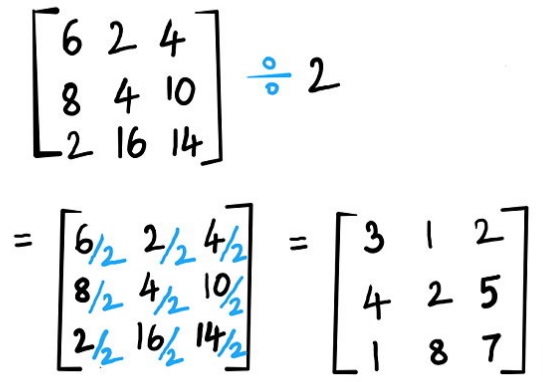 Но есть хитрость: здесь идет фактически замена деления одной таблички на другую на операцию перемножения.

Как же это работает? Ведь если совершить умножение, то результат произведения не сойдется с тем, что может быть с делением. Делается это так: заменяется разделение на умножение матриц друг на друга, но вторая из них должна быть обратной второй.

Стоит присмотреться в данном случае ко второй участнице этого нестандартного умножения. Вторая из матриц должна быть, если все верно, квадратной самой себе. Но что делать, если она не соответствует этому критерию либо ее математический определитель вообще равен 0?

В этом случае надо признать решение следующим: в этом расчете нет однозначного и точного решения. Если есть альтернатива, то следует высчитать матричный определитель и действовать дальше, в соответствии со следующим шагом. То есть найти обратное значение элемента В, далее перемножить его с А.

Важный момент: согласно известной аксиоме, от перемены мест произведение не меняется. В данном случае матричные уравнения подбрасывает нам «сюрприз». Согласно данному порядку, менять местами участников процедуры умножения нельзя ни при каких обстоятельствах. Иначе есть риск получить неодинаковые результаты при одинаковых данных. Здесь стоит проявить внимательность, используя калькулятор деления матриц.

Если матрицу можно инвертировать, она получает статус «невырожденной», то есть регулярной. Если инвертирование недоступно, то перед нами «вырожденная» таблица, либо сингулярная.

Формула

Как это выглядит в виде формулы: А:В – неверное представление, такая форма вычисления как раз и запрещена в силу своей несостоятельности. Нужно сделать обмен на следующий вариант: А*В.

Обе формулы будут как бы равнозначны по смыслу, если используются величины скалярного типа. В теории это и будет называться как «деление», но ели быть корректными, то это перемножение одной таблицы на обратную ей самой.

Теперь, зная, что такое суть «деления матриц», можно приступить к совершению подобного расчета и попробовать что-то вычислить. Всегда слово, обозначающее «деление», следует ставить в кавычки, указывая на условность этого обозначения. Оно применяется для удобства, фактически этого действия не существует в математической реальности.

Но итог, если дойти до итогов, будет тем же, что и первая версия данного расчета. Вот почему признается равенство разделительного действия и перемножения, при условии использования обратного значения второго операнда.

Правильная запись такого типа вычислений будет выглядеть следующим образом: [A]*[B]^-1 или [B]^–* [A].

Традиционно такие методы используют для расчетов в линейных системах. В этом случае тоже выручит, как и при делении матриц онлайн калькулятор.

Примеры решений

Теперь проверим возможность делимости на практических примерах математических вычислений. Согласно теории, невозможно сделать это прямым способом, только при обратной версии второго операнда. Следует учесть, что А*В^-1 отличается от В^-1*А, данные действия разные по своей сути. Можно провести разные действия, чтобы просчитать все ответы и версии решения.

Пример можно привести на разделении простых чисел: 10:5.

Итак, мы не можем напрямую получить ожидаемое 2, так как действие неактуально. Значит, нужно найти обратные числа по отношению к 5. Это будет 5^-1 (либо ¹/_5). Теперь осуществляется замена на операцию умножения и получается: 10*5^-1.

Таким образом и будем действовать при своем расчете:

Нам нужно перемножить две таблицы:

(13 26) : (7 4)

(39 13)    (2 3)

Правильной будет следующая версия записи:

(13 26) * (7 4)^-1

(39 13)       (2 3)

Вычисление делается согласно правилам в следующем порядке, если нужен другой итог:

(7 4)^-1 (13 26) *

(2 3)    (39 13)

Вот таким образом выполняется на бумаге и на калькуляторе интересная и неоднозначная расчетная операция – деление матриц. Не стоит забывать о такой опции, как инвертирование – то есть поиск обратной версии таблицы, она должна иметь черты квадратной, то есть обладать равным количеством строчек и столбиков. В случае несоответствия данному условию не будет одного точного решения ни при каких условиях. Для получения корректных результатов важно точно и внимательно вводить данные на онлайн-калькуляторе, тогда искажений не последует.

матриц – Разделить матрицу на обе части уравнения

$\begingroup$

Вот вопрос, который я должен решить:

Найдите значение $x$, если
$$ \begin{bmatrix} 1 и х и 1 \end{bmatrix} \begin{bmatrix} 1 и 3 и 2 \\ 2 и 5 и 1 \\ 15 и 3 и 2\\ \end{bmatrix} \begin{bmatrix} 1\\ 2\\ Икс\\ \end{bmatrix} =0 $$

Моя попытка:
Я разделил обе части уравнения на $\begin{bmatrix} 1 и 3 и 2 \\ 2 и 5 и 1 \\ 15 и 3 и 2\\ \end{bmatrix}$, чтобы получить: $$\фракция{ \begin{bmatrix} 1 и х и 1 \end{bmatrix} \begin{bmatrix} 1 и 3 и 2 \\ 2 и 5 и 1 \\ 15 и 3 и 2\\ \end{bmatrix} \begin{bматрица} 1\\ 2\\ Икс\\ \end{bmatrix}}{\begin{bmatrix} 1 и 3 и 2 \\ 2 и 5 и 1 \\ 15 и 3 и 2\\ \end{bmatrix}} = \frac{0}{\begin{bmatrix} 1 и 3 и 2 \\ 2 и 5 и 1 \\ 15 и 3 и 2\\ \end{bmatrix}}$$ Который дает: $$ \begin{bmatrix} 1 и х и 1 \end{bmatrix} \begin{bmatrix} 1\\ 2\\ Икс\\ \end{bmatrix} = 0$$ Решение этого: \начать{выравнивать} (1)(1)+(2)(х)+(1)(х) &= 0 \\ 1 + 2х + х &= 0 \\ 3x &= -1 \\ х &= \фракция{-1}{3} \\ \end{выравнивание} .

.. это неправильный ответ. 9{-1} М \begin{bmatrix} 1\\ 2\\ Икс\\ \end{bmatrix}=0$$

как вы, кажется, сделали

$\endgroup$

4

Калькулятор деления матрицы – символьный

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Matrix Division

Инструмент для расчета матричного деления двух матриц (2×2, 3×3, 4×4, 5×5, …). Деление матрицы состоит из умножения на инвертированную матрицу.

Результаты

Matrix Division – dCode

Метки: Matrix

Поделиться

dCode и многое другое проблемы, которые нужно решить каждому день!

Предложение ? обратная связь? Жук ? идея ? Запись в dCode !

Раздел матрицы

Деление 2-х матриц

Matrix M1

Загрузка…
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

Matrix M2

Загрузка. {-1} $$ 9{-1} $$ полученный результат является результатом деления матрицы.

Пример: Деление матриц 2×2 $$ \begin{bmatrix} 0 & 1 \\ 2 & 3 \end{bmatrix} / \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 0 и 1 \\ 2 и 3 \end{bmatrix} . \left( \frac{1}{2} \begin{bmatrix} -4 & 2 \\ 3 & -1 \end{bmatrix} \right) = \frac{1}{2} \begin{bmatrix} 3 & -1 \\ 1 & 1 \end{bmatrix} $$

Чтобы произвести деление, необходимо соблюдать правила умножения матриц: $M_1$ должно иметь такое же количество $n$ столбцов, как и количество строк матрицы $M_2$. Более того, чтобы быть обратимой матрицей, матрица $M_2$ должна быть квадратной и, следовательно, иметь размер $n\times n$.

Как разделить матрицу на скаляр?

Делением матрицы $M=[a_{ij}]$ на скаляр $\lambda$ является матрица того же размера, что и $M$ (исходная матрица), причем каждый элемент матрицы делится на $ \лямбда $.

$$ \frac{M}{\lambda} = [ a_{ij} / \lambda ] $$

Пример:

$$ \begin{bmatrix} 0 & 2 \\ 4 & 6 \end{bmatrix } / 2 = \begin{bmatrix} 0 & 1 \\ 2 & 3 \end{bmatrix} $$

Исходный код

dCode сохраняет право собственности на исходный код Matrix Division. За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Matrix Division», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, взломщик, транслятор) или «Matrix Функции разделения» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт или доступ к API для «Matrix Division» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!

Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы “Matrix Division” или любых ее результатов разрешено (даже в коммерческих целях) при условии, что вы цитируете dCode!
Бесплатный экспорт результатов в виде файла .