Скорость при неравномерном движении – формула
4.7
Средняя оценка: 4.7
Всего получено оценок: 284.
4.7
Средняя оценка: 4.7
Всего получено оценок: 284.
Равномерное движение – нечастое явление в Природе. Большинство движений является неравномерными, и формулы параметров такого движения иные. Рассмотрим особенности определения скорости при неравномерном движении.
Скорость неравномерного движения
Из самого названия неравномерного движения ясно, что его скорость непостоянна. Если для равномерного движения вычисление скорости в любой отрезок времени будет давать одно и то же значение, то для неравномерного движения это не так. Формула скорости при неравномерном движении будет давать различные значения для различных моментов времени.
Рис. 1. Неравномерное движение.Для вычисления скорости неравномерного движения используются следующие способы.
Мгновенная скорость
Первый способ заключается в том, чтобы измерять скорость на малых участках.
Например, можно измерить (с помощью стробоскопа), за какое время падающее тело пролетает один сантиметр в конце первого метра падения, второго и третьего и вычислить получающуюся скорость:
S(м) | t(мс) | Δt(мс) | v(м/с) |
1 | 451.5 | ||
1.01 | 453.8 | 2.252 | 0.444 |
1.02 | 456.0 | 2.241 | 0.446 |
2 | 638.6 | ||
2.01 | 640.1 | 1.594 | 0.627 |
2.02 | 641.7 | 1.590 | 0.629 |
3 | 782.1 | ||
3. | 783.4 | 1.302 | 0.768 |
3.02 | 784.7 | 1.300 | 0.769 |
01Можно видеть, что время прохождения (Δt) соседних сантиметров в конце каждого метра – отличаются очень незначительно (единицы процентов и менее), хотя разница времени между группами значений – гораздо больше. Вычисленная скорость также между соседними сантиметрами почти не отличается, хотя в конце каждого метра отличие значительное.
Если взять не сантиметры, а миллиметры – отличия между соседними миллиметрами будут еще меньше, хотя разница между концами пройденных метров – сохранится.
Хотя на далеких участках скорость при неравномерном движении различна, при стягивании измеряемого участка в точку, скорость на нем будет почти не отличаться от скорости на соседних таких же участках, и ее можно будет считать постоянной.
Скорость, измеренная таким образом, называется мгновенной скоростью.
$$v_{мгнов}= {ΔS\over {Δt}}, при ΔS \rightarrow 0,Δt\rightarrow 0$$
Направление мгновенной скорости всегда совпадает с направлением перемещения, и является касательной к траектории пути. Мгновенная скорость наиболее точно отражает изменения перемещения в каждый момент времени, и в общем случае постоянно меняется.
Рис. 2. Мгновенная скорость.Средняя скорость
Вычисление мгновенной скорости требует большого числа измерений и операций, либо учета дополнительных условий и использовании формул высшей математики. Однако, во многих случаях точность мгновенной скорости не нужна.
Если для решения задачи важен общий результат движения, то можно не учитывать изменения мгновенной скорости в процессе движения. В этом случае достаточно найти отношение всего пути к полному времени его прохождения. Такая скорость называется средней:
$$v_{ср}= {s_{общ}\over t_{общ}}$$
Средняя скорость не учитывает изменения, происходящие во время пути, она лишь дает «результирующую картину» движения, и считается постоянной на всем пройденном пути.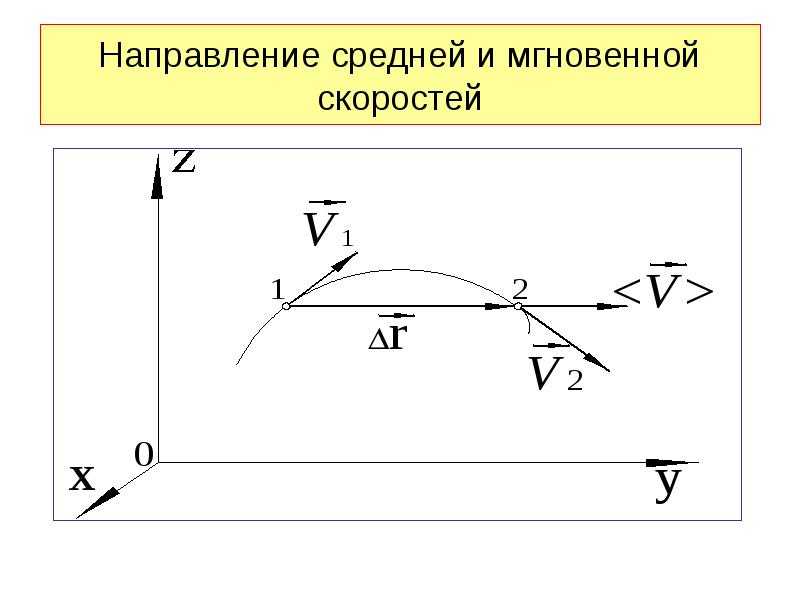
Что мы узнали?
Скорость при неравномерном движении может быть описана двумя способами. Можно найти мгновенную скорость, для этого разбить весь путь на очень короткие участки, и считать скорость на каждом из них. А можно найти среднюю скорость, для этого вычислить отношение всего пути ко времени его прохождения.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 284.
А какая ваша оценка?
Основные кинематические характеристики – Механика (Физика)
Основные кинематические характеристики.
1) Вектор элементарного перемещения.
Предположим, что в некоторой системе отсчета происходит движение материальной точки. В момент времени t – ее радиус-вектор .
В момент времени t+→. Вектором элементарного перемещения называется вектор
Перемещение за некоторый промежуток времени – вектор, соединяющий начальное и конечное положение и направленный начального к конечному положению.
Причем, необходимо различать путь и перемещение . Путь – это длина траектории (расстояние)и скаляр. Перемещение – вектор, характеризующийся точкой приложения, направлением и модулем. Длина пути и перемещения не совпадают. Но иногда совпадает длина пути с модулем перемещения (в случае прямолинейного движения, если нет поворотов).
2) Скорость.
а) средняя – это величина, характеризующая изменение положения частицы в пространстве. Вектор средней скорости при перемещении между двумя точками определяется как вектор, совпадающий по направлению с перемещением и равный:
, где
Средняя скорость характеризует движение за какой-то промежуток времени. – вектор, но иногда среднюю скорость определяют как скалярную величину.
При неограниченном уменьшении Δt, стремится к ее предельному значению, равному мгновенной скорости.
б) мгновенная скорость. Понимается предел, к которому стремится при устремлении промежутка времени Δt к нулю:
,
где – вектор элементарного перемещения.
Это выражение представляет собой производную функции от переменной t.
Представим в декартовой системе координат:
Поскольку , , постоянны, то
Направление задается направляющими косинусами:
;
Следовательно, компоненты скорости:
Если движение задано через параметры траектории, то известны траектория и зависимость пути от времени. Следовательно, . Тогда:
– вектор, касательный к траектории, – проекция на касательную.
Направление вектора мгновенной скорости.
Если , то точка 2 будет приближаться к точке 1 и вектор будет иметь одну общую точку с траекторией. Следовательно, v в точке направлена по касательной.
можно представить следующим образом:
,
где – единичный вектор касательной к траектории, .
3) Ускорение – скорость изменения скорости. Пусть в момент t и t+Δt скорости равны соответственно , то
а) средним ускорением называется:
Будем изображать векторы в различные промежутки времени, исходящими из одного начала.
Конец вектора при движении материальной точки опишет кривую, которая называется годографом вектора скорости. Понятие годографа было введено английским ученым Гамильтоном.
При , учитывая, что
В прямоугольной декартовой системе координат компоненты вектора скорости запишутся следующим образом:
Необходимо определить ориентировку вектора ускорения относительно скорости и траектории движения.
В отличие от скорости , который всегда направлен по касательной к траектории, вектор ускорения может занимать любую ориентацию по отношению к ней.
Т.к.
Первое слагаемое – составляющая ускорения, направленная вдоль скорости и характеризующая изменение модуля скорости.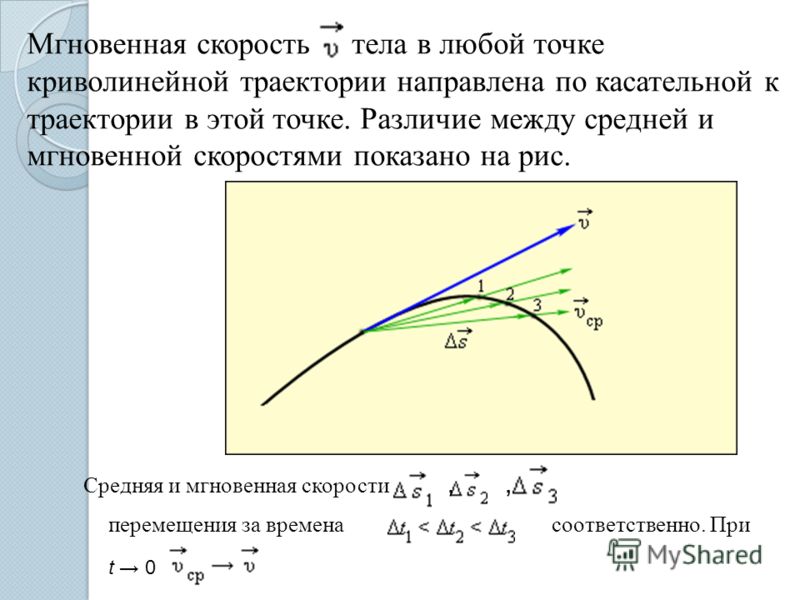
Эта составляющая называется касательным, или тангенциальным ускорением:
Выясним, что представляет собой второе слагаемое.
Пусть за малый промежуток времени материальная точка переместилась из 1 в 2. Изображены единичные касательные векторы .
Если , то ;
Перенесем в точку 1. Малый участок любой кривой можно представить как малую дугу некоторой окружности. В соответствие с этим, участок траектории между 1 и 2 представляется дугой окружности с радиусом R и центром в точке О. Тогда α – угол, под которым видна дуга окружности. Угол между и равен α. Угол α – малая величина, следовательно .
Тогда .
Если v – скорость движения, то ;
Из рисунка видно, что по мере того, как точка перемещается из 2 в 1, разность направлена к центру окружности, которая заменяет участок кривой. Значит, вторая составляющая вектора ускорения, направленная перпендикулярно касательной к кривой, т.е. к вектору тангенциального ускорения:
, где – единичный вектор, перпендикулярный .
Определить направление этой составляющей ускорения, можно воспользовавшись равенством:
Согласно тому, что , – нормальное ускорение.
Ещё посмотрите лекцию “Содержание и условные обозначения” по этой теме.
Оно определяет, как быстро изменяет вектор касательной свое направление в пространстве (или характеризует изменение скорости по направлению).
Следовательно, вектор ускорения в общем случае равен:
Длина вектора
Таким образом, вектор перпендикулярен и сонаправлен с вектором , т.е. направлен по нормали которая называется главной, вдоль которой направлен . Плоскость в которой лежат и называется соприкасающейся.
При движении точки по окружности нормальное ускорение называется центростремительным, поскольку центр кривизны траектории для всех ее точек одинаковый и совпадающий с центром окружности.
Acceleration and Velocity Essay – 823 Words
Равномерное ускорение Лабораторная работа Цель: Определить тип движения тележки, катящейся по склону.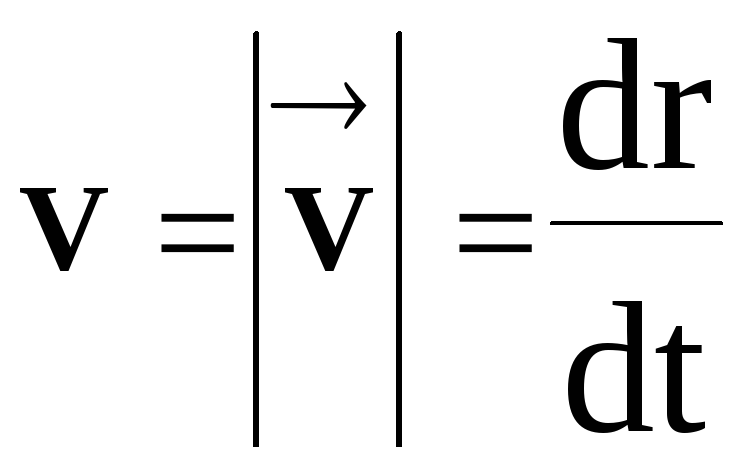
Теория: В этом эксперименте необходимо определить тип движения тележки при скатывании по склону. Это будет сделано путем изучения положения тележки относительно верхней части пандуса в течение определенного периода времени.
Используя положение тележки во времени, будут определены перемещение, скорость и ускорение. Прямая линия на графике зависимости положения от времени будет представлять равномерное движение. Прямая линия на графике зависимости скорости от времени представляет равномерное ускорение.
Позиция — это расстояние от точки отсчета до объекта, включая направление. Смещение — это изменение положения объекта, измеряемое в см. Скорость — это изменение положения объекта с течением времени, измеряемое в см/с. Мгновенная скорость — это мера скорости объектов в определенное время, вычисляемая по наклону касательной в каждый конкретный момент времени на графике зависимости положения от времени. Ускорение — это изменение скорости объекта во времени, измеряемое в м/с2, которое можно найти, рассчитав наклон линии на графике зависимости скорости от времени.
Оборудование: тележка, бегущий таймер, бегущая лента 2,0 м, малярная лента, наклонная рампа 2,0 м, кирпичи/учебники.
Рисунок 1: Устройство
Процедура:
1) Устройство было установлено, как показано выше на рисунке 1; верх пандуса был поднят примерно на 25 см над землей с помощью учебников.
2) Тикерная лента была пропущена через бегущую строку таймера и приклеена к тележке с помощью малярной ленты.
3) Тележка и бегущая строка были размещены наверху рампы.
4) Тикерный таймер установлен на 60 Гц
5) Таймер бегущей строки был включен, когда тележка была освобождена от вершины рампы.
6) Данные были собраны с бегущей строки после завершения движения тележки.
Следующие данные были собраны с бегущей строки, которая измеряла положение тележки в каждый временной интервал.
Таблица 1: Данные бегущей строки
Время (с)
Положение (см [Н])
Перемещение (см [Н])
Средняя скорость (см/с [Н])
Мгновенная скорость (см/с [Н] ])
Acceleration (m/s2 [N])
0
0
0
0
0
0
0.1
0.9
0.9
9.0
0.9
0.2
2.7
1.9
19.0
1.00
0.3
4.8
2.0
20.0
0.10
0.4
3.1
31.0
1.70
0.5
13.1
5.2
52.0
1.50
0.6
20.5
7.4
74.0
83.3
2.20
0.7
30.1
9.6
96.0
2.20
0,8
41.7
11.6
116.0
120.0
2.00
0.9
55.2
13.5
135.0
1.90
1.0
70.5
15.3
153.0
166.7
1.80
1.1
87.7
17.2
172.0
1.90
1.2
107.1
19.4
194.0
2.20
1.3
128.3
21.
2
212.0
1.80
1.4
151.6
23.3
2.10
1.5
176.3
24.7
247.0
1.40
Следующие графики представляют положение, скорость и ускорение тележки во времени.
Расчеты:
Обсуждение: График зависимости положения от времени показал возрастающую чашевидную форму, которая представляет собой ускорение. Это можно интерпретировать таким образом, потому что наклон линии увеличивается с течением времени, а это означает, что тележка двигаться быстрее и преодолевать большее расстояние за каждый временной интервал. График зависимости скорости от времени показал возрастающую прямую линию, которая представляет возрастающую скорость и постоянное ускорение. Наклон этой линии представляет собой среднее ускорение тележки. Среднее значение скорости и мгновенное значение скорости были
Физика: График Энергии и Скорости Время Примеры сочинений
Общие науки-МеханикаРасстояние, скорость, время (DVT)
Расстояние — это мера того, насколько далеко находится точка.
Измеряется в м/км
Скорость — это мера того, насколько быстро движется объект. Измеряется в мс-1/км/ч-1
Время является мерой продолжительности периода. Измеряется в секундах/час
Графики DVT. Мы можем представить информацию в виде графиков, которые многое говорят нам о том, как движется объект.
Чем круче прямая линия, тем «выше» постоянная скорость
Градиент прямой линии на графике расстояния и времени дает скорость v=d/t ИЛИ v=подъем/бег
«Плоская линия» означает объект остановлен/неподвижен
Кривая линия (вверх) ускорение от начальной точки
Кривая линия (вниз) замедление/замедление
Графики скорости, времени
График скорость-время с наклоном больше нуля показывает объект ускорение
Графики, которые показывают прямую линию, означают, что поддерживается постоянная скорость
Графики, которые показывают положительный наклон, означают, что объект ускоряется
Графики, которые показывают отрицательный наклон, означают, что объект замедляется
Чем круче наклон, тем быстрее он либо ускоряется, либо замедляется
Расчет ускорения
Чтобы рассчитать ускорение по графику скорость-время, вы должны рассчитать наклон так же, как вы бы нашли график средней скорости-расстояния-время
Наклон Y2-Y1= Y/X2-X1= X
Градиент= подъем/спуск
Расстояние от области под графиком
Общая площадь под уклоном представляет общее расстояние
Площадь треугольника= ½ x длина x высота
Площадь квадрата = длина х высота
Расстояние и время – пересмотр
Движение – это то, как что-то движется.
Движение объекта, такого как автомобиль/теннисный мяч, описывается с помощью таких величин, как время, расстояние, скорость и ускорение
Время (T), секунды (S), расстояние (D), метры (M)
Скорость
Средняя скорость – это мера пройденного расстояния каждый час/мин/сек
Средняя скорость = пройденное расстояние/затраченное время
V= d/t
Мгновенная скорость – это фактическая скорость в любой момент. Спидометр (спидометр) в автомобиле измеряет мгновенную скорость
Графики расстояние-время- Показывает время, затраченное на преодоление определенного расстояния. Наклон (градиент) графика дает информацию о скорости.
Наклон (градиент) = изменение переменной оси Y/ изменение переменной оси X
Slope= d/ t= Пройденное расстояние/затраченное время
Ускорение – когда скорость объекта изменяется либо за счет замедления/ускорения объекта
Среднее ускорение – измеряет, насколько скорость изменяется каждый час/мин. /сек
Графики скорость-время – дают информацию об ускорении
Наклон (градиент) графика зависимости скорости от времени находится из наклона = v/ t = изменение скорости/затраченного времени = ускорение.
Наклон представляет собой ускорение.
Сила
Сила может быть определена как толкание/тяга/крутка
Измеряется в ньютонах (Н)
Ньютон эквивалентен перемещению массы 1 кг на 1 метр
Сила = масса x ускорение
Н= кг x мс-2
Уравновешенные и неуравновешенные силы
Уравновешенные силы
Равные силы, действующие на один объект в противоположных направлениях
Ускорение равно нулю
Скорость постоянна
Суммарные силы = 0 (без заряда в движении)
Силы рисования на диаграмме
Сила, масса, ускорение
Чем тяжелее объект, тем больше силы требуется для ускорения
Ускорение-гравитация-10мс-2 материя в объекте, измеряемая в килограммах (кг)
Вес – мера силы, действующей на объект из-за ускорения, вызванного гравитацией, измеряемой в ньютонах (Н)
Трение
Трение возникает, когда объект движется относительно другого. Трение всегда препятствует движению объекта (или останавливает его).