Реферат по информатике система счисления: Реферат на тему: Система счисления - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Реферат на тему: Система счисления

У вас нет времени на реферат или вам не удаётся написать реферат? Напишите мне в whatsapp — согласуем сроки и я вам помогу!

В статье «Как научиться правильно писать реферат», я написала о правилах и советах написания лучших рефератов, прочитайте пожалуйста.

Собрала для вас похожие темы рефератов, посмотрите, почитайте:

Реферат на тему: Источники права
Реферат на тему: Инфаркт миокарда
Реферат на тему: Мировые религии
Реферат на тему: Гепатиты

Введение

На протяжении всей жизни мы сталкиваемся с числами и выполняем с ними арифметические операции. Это нас не удивляет. Мы принимаем это как факт. И откуда взялись цифры и результат? Что такое цифровая система? Где мы теперь с ними встретимся? Мне было очень интересно, поэтому я решил изучить этот предмет.

Эта тема интересна и для меня, так как двоичная система счисления в настоящее время стала очень важной в связи с ее использованием в электронных компьютерах.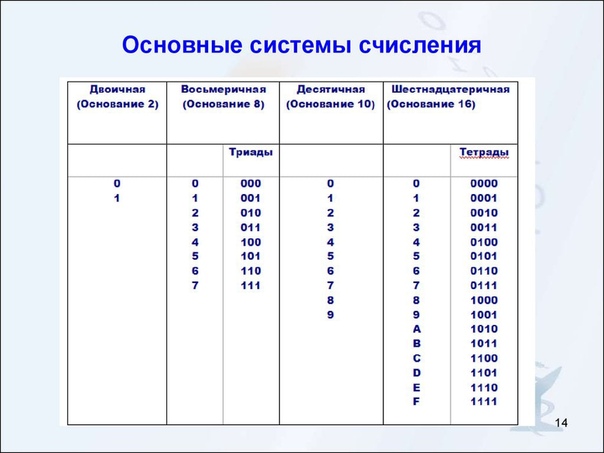

Численные системы с базами 8 и 16 используются в программировании различных процессов на компьютерах.

Я поставил перед собой цель: познакомиться с историей возникновения счетных и числовых систем, изучить числовые системы, используемые в вычислениях, позиционные и непозиционные числовые системы, а также арифметические действия в различных системах. В данной диссертации рассматриваются различные вычислительные системы.

История происхождения систем счисления

В древние времена людям приходилось рассчитывать на пальцы. Кроме пальцев, нужно было сосчитать много испытуемых, на счету было больше участников. Один считал единицы, второй — дюжины, третий — сотни. Очевидно, что такой расчет лег в основу принятой почти всеми народами системы вычислений, называемой десятичной системой. Расчет с базовой десяткой также применим к восточным славянам.

Там, где люди ходили босиком, их пальцы легко сосчитать до 20. Следы использования при подсчете до 20, например, во французском число 80 в буквальном переводе на русский звучит как «четырежды двадцать».

Были также распределены десятки аккаунтов, т.е. аккаунт, на котором использовалась система базы 12. Его происхождение связано с 12 фалангами на четырех пальцах (кроме большого). Даже сейчас некоторые пункты все еще считаются десятками. Столовые приборы состоят из полдюжины или дюжины комплектов.

В древнем Вавилоне, где математика была очень высоко развита, существовала очень сложная шестнадцатеричная система счисления. В настоящее время мы также используем эту систему. Например: 1 час=60 минут; 1 минута=60 секунд.

Самой старой из систем пальцев считается система с пятью пальцами. Эта система родилась и наиболее широко используется в Америке. Его происхождение восходит к эпохе, когда человек считал на пальцах одной руки. До недавнего времени некоторые племена сохранили пятипальцевую систему счисления в чистом виде.

Таким образом, все системы (пятикратные, двенадцатикратные, двадцати четырехкратные) соединены одним или другим способом счета пальцев ног (или рук и ног). Переход человека к счету пальцев привел к созданию различных систем подсчета. /1/

Численные системы, используемые в компьютерных технологиях

Система счисления — это система методов и правил, позволяющих установить взаимосогласованную связь между любым числом и его представлением в виде набора конечного числа символов. Многие символы, используемые для этого представления, называются цифрами.

В зависимости от того, как отображаются номера, они делятся на номера элементов и номера без элементов.

В непозиционных системах каждое число определяется как особая функция числовых значений набора чисел, представляющих это число. Числа в непозиционных системах счисления соответствуют некоторым фиксированным числам. Исторически сложилось так, что первыми вычислительными системами были непозиционные системы. Одним из главных недостатков является сложность написания больших чисел. Написание больших чисел в таких системах либо очень громоздко, либо системный алфавит чрезвычайно велик.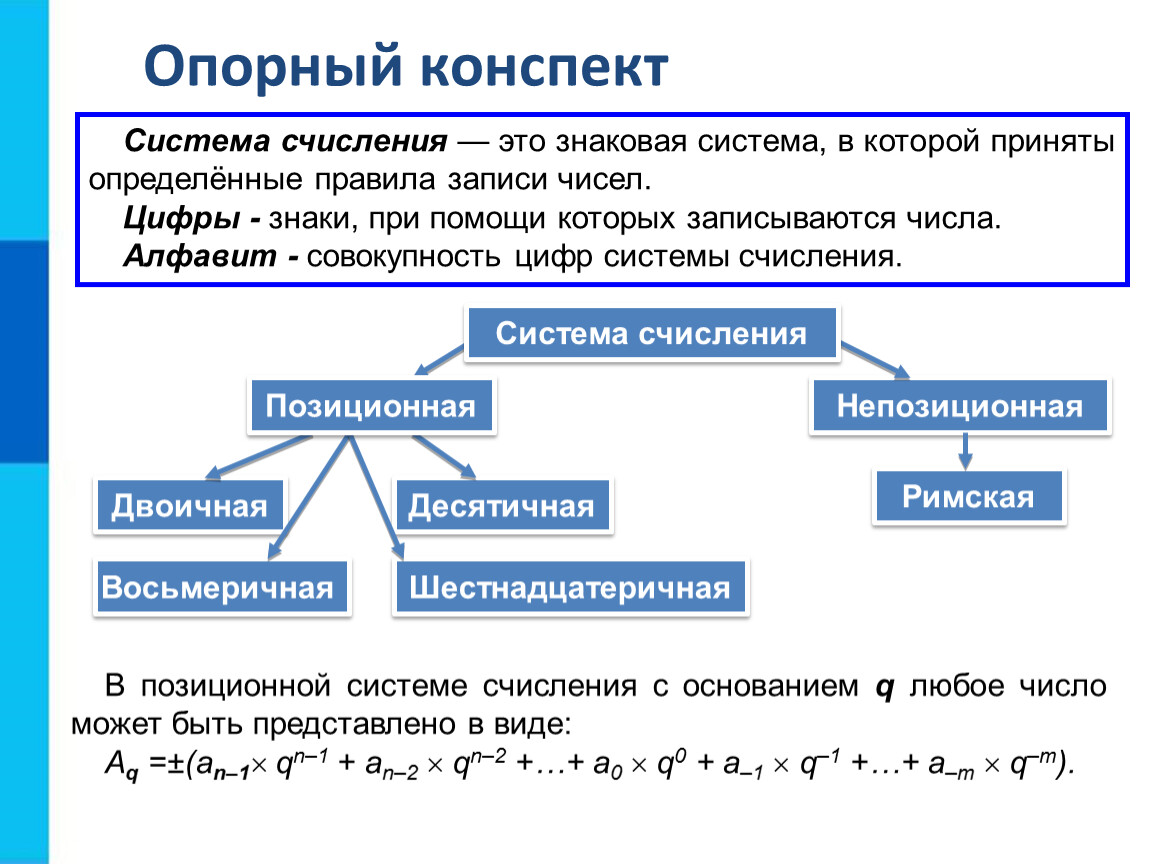 Не-позиционные системы не используются в компьютерных технологиях.

Система счисления называется позиционной, когда одна и та же цифра может принимать различные числовые значения в зависимости от того, какая позиция цифры присутствует в наборе цифр, представляющих определенное число. Примером такой системы является арабская десятичная система счисления.

Фактические количества и количественные пропорции могут быть отображены различными способами. Основа системы нумерации элементов определяет их название. В вычислениях используются двоичная, восьмеричная, десятичная и шестнадцатеричная системы. Чтобы явно указать используемую систему счисления, заключим номер в скобки и укажем основу системы счисления в нижнем индексе. Каждая числовая позиция соответствует коэффициенту положения (цифра) или весу.

В настоящее время позиционные системы охлаждения встречаются чаще, чем непозиционные. Это связано с тем, что они позволяют писать большие числа относительно небольшим количеством символов. Еще более важным преимуществом систем позиционирования является простота и легкость арифметических операций по сравнению с числами, написанными в этих системах.

Преобразование чисел в десятичную систему осуществляется путем суммирования последовательностей степеней, основанных на системе, из которой переводится число. Затем вычисляется суммарное значение.

Как правило, вычислительные машины могут быть встроены в любую систему счисления. Но такая общая десятичная система крайне непрактична для нас. Если в механических вычислительных машинах с десятичной системой достаточно использовать только один элемент с множеством состояний (колесо с десятью зубцами), то в электронных машинах в цепях необходимо иметь 10 различных потенциалов.

Системы без номеров позиций

В настоящее время как позиционные, так и непозиционные системы расчета широко используются как в технологии, так и в быту.

В системах без вычисления позиции вес фигуры не зависит от позиции, которую она занимает в номере.

Примером непозиционной системы счисления является римская система счисления. Он появился в Древнем Риме и существует по сей день. Традиционно используется для нумерации веков или для создания оглавления печатных произведений. Римские цифры можно найти на циферблатах часов.

В современной жизни наиболее показательным вариантом использования системы непозиционного учета являются денежные отношения. Мы сталкиваемся с ними каждый день. Никому не приходит в голову, что сумма, которую мы тратим на еду в магазине, может зависеть от того, в каком порядке мы поставим монеты на стол. Номинальная стоимость монеты не зависит от порядка, в котором она была взята из кошелька. Это классический пример непозиционной системы подсчета.

Это означает, что в настоящее время наиболее широко используется система позиционирования чисел.

Позиционные номера

В системах подсчета позиций вес каждой цифры изменяется в зависимости от ее положения в последовательности цифр, представляющих число. Каждая система позиций характеризуется своей базой. Основой системы нумерации элементов является количество различных символов или символов, используемых для представления цифр в этой системе. Любое натуральное число — два, три, четыре, шестнадцать и т.д. — может быть принято за основу. Следовательно, возможны бесконечные системы позиций: двоичные, состоящие из чисел 0 и 1; троичные, состоящие из чисел 0,1,2; и так далее.

Системы позиционирования удобны тем, что позволяют захватывать большие числа с небольшим количеством символов при выполнении простых и легко выполняемых арифметических операций.

Десятичная система счисления

Основой десятичной системы числа 10 является число 10, которое является единицей второй цифры, единицей третьей цифры будет 100 = 102, в общем случае единица каждой следующей цифры в десять раз больше, чем единица предыдущей цифры (предполагается, что выбор в качестве основы D. S. числа 10 связан с подсчетом на пальцах).

Д.

С. С. основывается на принципе положения, т.е. один и тот же знак (число) имеет разное значение в зависимости от места его расположения. Поэтому только первые 10 цифр нуждаются в специальных символах, чтобы покрыть все цифры. Эти символы, которые обозначаются символами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называются цифрами. Для захвата числа вы определяете, сколько единиц наибольшей цифры в нем содержится; остальное определяется как количество единиц наибольшей цифры, на единицу меньше, и т.д. Полученные цифры записываются бок о бок: например, 4×102 + 7×101 + 3×100 = 473.

При этом действия выполняются над числами в цифрах, т.е. отдельно над числами каждой цифры; если при этом числа складываются более чем до 10 (в случае сложения, умножения), то к следующей, более высокой цифре прибавляется одна или несколько единиц; в случае деления и вычитания, цифры должны быть разбиты на более мелкие.

Двоичная система счисления

Двоичная система счисления, система счисления, основанная на позиционном принципе записи чисел, с основой 2 Двоичная система счисления использует только два символа, цифры 0 и 1, и, как и в любой позиционной системе, значение цифры также зависит от ее позиции. Цифра 2 считается единицей 2-й цифры и записывается следующим образом: 10 (читать: «один, ноль»). Каждая единица следующей цифры в два раза больше предыдущей, т.е. эти единицы образуют последовательность цифр 2, 4, 8, 16, … , 2n.

По числу, записанному в десятичной системе в D. S., он поочередно делится на 2, а получившиеся остатки 0 и 1 записываются в порядке от последнего к первому, например: 43 = 21-2 +1; 21 = 10-2 +1; 10 = 5-2 +0; 5 = 2-2 +1; 2 = 1-2 + 0; 1 = 0-2 + 1; таким образом, двоичный вход числа 43 равен 101011. Таким образом, в EPS 101011 обозначает 1-20+1-21 + 0×22 +1×23 + 0-24 + 1-25.

В D. S. все арифметические операции особенно просты: например, таблица умножения сводится к равенству 1-1 = 1. Однако, запись в D.S. очень громоздка: например, число 9000 будет иметь 14 цифр.

В связи с тем, что двоичная система счисления использует только две цифры, она часто полезна в теоретических вопросах и для вычислений на ДЦК.

Восьмикратная числовая система

Восьмая система счисления — это система позиционных целых чисел с базой 8. Для представления чисел используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Число 1 в нижней цифре означает только одну, как и в десятичной системе счисления. То же число 1 в следующей цифре означает 8, следующие 64 и так далее. Число 100 (восьмеричное) не более 64 (десятичное). Например, чтобы перевести число 611 (восьмеричное) в двоичную систему, каждая цифра должна быть заменена соответствующей двоичной триадой (три цифры). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричной системе необходимо разделить его на триады справа налево и заменить каждую триаду соответствующим восьмеричным числом.

Восьмая система наиболее часто используется в областях, связанных с цифровым оборудованием. Например, восьмеричная система счисления служит самым простым языком общения человека с компьютером.

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления (шестнадцатеричные числа) — Позиционная система счисления на целочисленном базисе 16 Запись чисел в восьмеричной системе счисления достаточно компактна, но еще более компактна в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцати десятичных цифр берутся обычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а в качестве остальных 6 цифр используются первые буквы латинского алфавита: A, B, C, D, E, F. Номер 1, написанный нижней цифрой, означает только один. Одна и та же цифра 1 в следующей — 16 (после запятой), следующая — 256 (после запятой) и т.д. Цифра F, записанная внизу цифры, означает 15 (десятичная).

Преобразование из шестнадцатеричной системы в двоичную и наоборот осуществляется таким же образом, как и для восьмеричной системы.

Шестнадцатеричная система счисления на сегодняшний день является самой популярной компактной программой записи двоичных чисел. Он широко использовался при разработке и проектировании цифровых технологий и, как восьмеричная система счисления, является простейшим языком для общения человека с компьютером.

Заключение

В соответствии с целью исследований в работе я ознакомился с историей зарождения исчисления и систем нотации, изучил системы нотации, используемые в компьютерной технике, позиционные и непозиционные системы нотации, а также арифметические действия в различных системах нотации.

После знакомства с компьютерными системами я узнал много нового и полезного, и считаю, что эта наука необходима для развития общества. Трудно представить мир без компьютеров. Это связано с тем, что именно бинарная система получила широкое распространение в различных областях техники, особенно в современных компьютерах и калькуляторах.

Система позиционирования номера состоит в использовании ограниченного числа цифр, но положение каждой цифры в номере обеспечивает значение (вес) этой цифры Положение цифры в числе называется цифрой в математическом языке.

Основой системы нумерации элементов является количество различных символов или символов (чисел), используемых для представления чисел в определенной системе.

Двоичная система счисления — наиболее широко используемая в компьютерах, так как одна цифра двоичного числа соответствует одному биту — минимальной единице информации в компьютерной технике

Для того, чтобы двоичные числа, которые достаточно сильно отличаются друг от друга по длине, более воспринимаемые и легче представляемые, сжимаются в восьмеричные и шестнадцатеричные числа.

В компьютерных технологиях все виды информации кодируются только числами, точнее числами, представленными в двоичной системе счисления — метод представления любого числа двумя символами (числами) по позиционному принципу.

Шестнадцатеричная система счисления широко используется как в низкоуровневом программировании, так и в компьютерной документации. Система восьмеричных чисел также иногда используется в компьютерах — по-видимому, чаще всего в определении прав в Unix-подобных операционных системах. Когда-то были компьютеры, которые использовали 24-битные и 36-битные слова. Шестизначная система счисления широко используется для подсчета минут и секунд. /4/. В целом, восьмеричная и шестнадцатеричная системы счисления являются самым простым языком общения человека с компьютером.

Я думаю, что у моей работы есть перспективы, потому что тема числовых систем достаточно сложна и обширна и может быть использована в реальной жизни. В моей работе собраны и систематизированы все материалы на эту тему.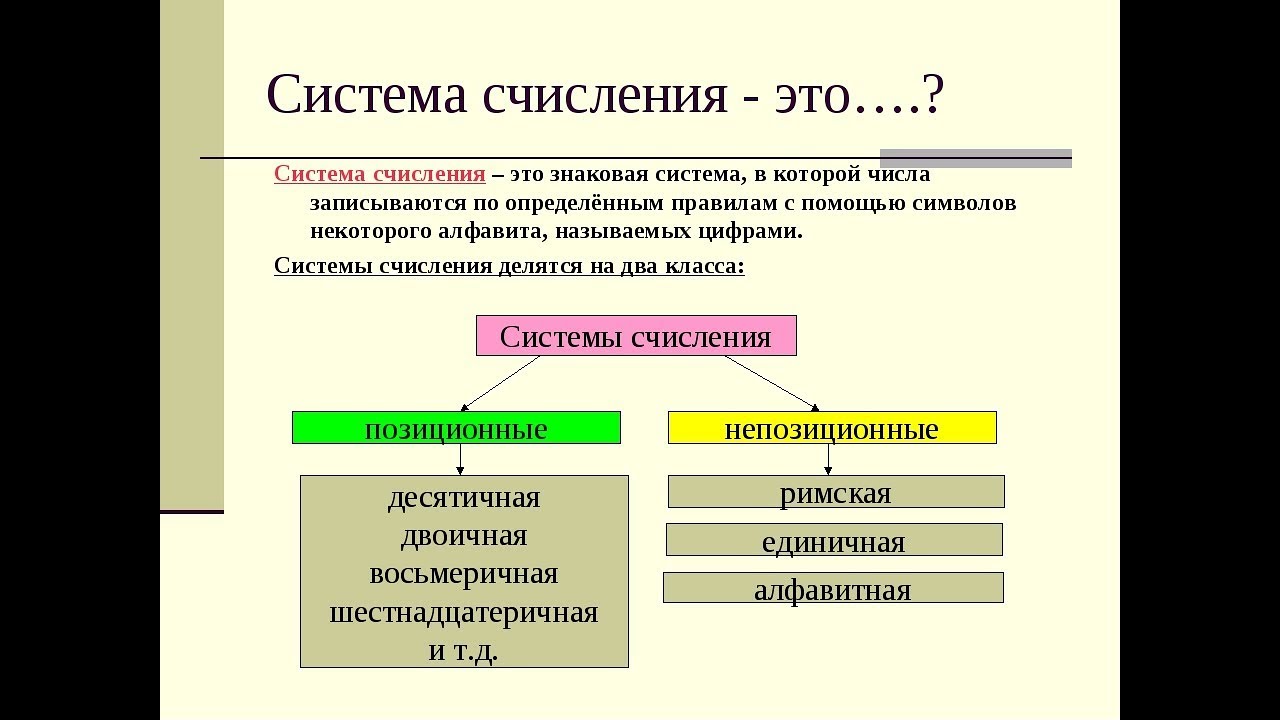

Надеюсь, что мою работу будут применять не только учителя, но и студенты.

Список литературы

ФоминС.В. Числовые системы, издание 1987 г. Главная редакцияфизико-математической литературыиздательства»Наука».
ГашковС.Б. Вычислительные системы и их применение, 2014 . Публикация: ICNSM.
КовриженкоГ.А. Числовые системы и двоичная арифметика, 1983.
Базовыекомпьютерные системы/Хабрахабр.
Фринландский университет. Вычислительная техника. М., 2003.
Сидоров В.К. Численные системы // Наука и жизнь 2000. №2.
Радюк Л. алгоритм трансляции в двоичную систему счисления и из нее // Наука и жизнь. 2003. №1.
РасселДжесси — Система двоичных чисел, 2014-е издание: Книгаспроса.
КолмогоровА.Н. Система чисел, 1973 Издатель «Академия наук СССР
Алексеев Е.Г., Богатырев С.Д. Информатика. Мультимедийный электронный учебник.

Помощь студентам в учёбе от Людмилы Фирмаль

Здравствуйте!

Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.

Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.

У меня конфиденциальность и безопасность высокого уровня. Никто не увидит Ваше задание, кроме меня и моих преподавателей, потому что WhatsApp и Gmail — это закрытые от индексирования системы , в отличие от других онлайн-сервисов (бирж и агрегаторов), в которые Вы загружаете своё задание, и поисковые системы Yandex и Google индексируют всё содержимое файлов, и любой пользователь сможет найти историю Вашего заказа, а значит, преподаватели смогут узнать всю историю заказа. Когда Вы заказываете у меня — Вы получаете максимальную конфиденциальность и безопасность.

Моё видео:

Как вы работаете?

Вам нужно написать сообщение в WhatsApp (Контакты ➞ тут) . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.

Сколько может стоить заказ?

Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения заказа?

Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить заказ?

Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Какие гарантии и вы исправляете ошибки?

В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.

Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.

Теперь напишите мне в Whatsapp или почту (Контакты ➞ тут) и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.

Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.

После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.

Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.

В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!

Жду ваших заказов!

С уважением

Пользовательское соглашение

Политика конфиденциальности

Помощь студентам в учёбе от Людмилы Фирмаль

Здравствуйте!

Моё видео:

Как вы работаете?

Сколько может стоить заказ?

Какой срок выполнения заказа?

Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить заказ?

Какие гарантии и вы исправляете ошибки?

Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.

Жду ваших заказов!

С уважением

Пользовательское соглашение

Политика конфиденциальности

Помощь студентам в учёбе от Людмилы Фирмаль

Здравствуйте!

Моё видео:

Как вы работаете?

Сколько может стоить заказ?

Какой срок выполнения заказа?

Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить заказ?

Какие гарантии и вы исправляете ошибки?

Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.

Жду ваших заказов!

С уважением

Пользовательское соглашение

Политика конфиденциальности

Реферат

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Геоинформационных систем

по дисциплине Информатика

Системы счисления. Описание понятия. Позиционные и непозиционные системы. Принципы перевода из одной системы счисления в другую.

Выполнили:

студенты гр. ИСТ-111

Абрамов С. А.

Проверил преподаватель:

Васильева М.И.

Уфа 2007

Содержание.

1 Введение_____________________________________________________3

2 Непозиционные системы счисления______________________________3

3 Позиционные системы счисления________________________________3

3.1 Введение___________________________________________________3

3.2 Преобразование чисел________________________________________4

3.3 Шестидесятеричная система счисления__________________________6

4 Двоичная система счисления____________________________________7

5 Восьмеричная и шестнадцатеричная системы счислений____________10

6 Перевод из одной системы счисления в другую____________________12

7 Список используемой литературы_______________________________14

Введение.

Для начала проведем границу между числом и цифрой. Число это некоторая абстрактная сущность для описания количества. Цифры это знаки используемые для записи чисел. Цифры бывают разные, самыми распространенными являются арабские цифры, они представляются известными знаками от нуля (0) до девяти (9), еще распространены римские цифры, мы их можем иногда встретить на циферблате часов или в обозначении века (IXX век).

Итак запомним: число, это абстрактная мера количества, цифра это знак для записи числа.

Существует множество способов записи чисел с помощью цифр. Эти способы грубо можно разделить на две части:

Позиционные системы счислений мы рассмотрим более подробно ниже. Расскажем вкратце о непозиционных системах счислениях.

Непозиционные системы счислений.

В непозиционной системе счисления величина числа не зависит от положения цифры в представлении числа. Если бы мы перемешали цифры в числе 603121200000, то мы бы не смогли понять сколько стоит пылесос, в непозиционной системе такого не случиться. Ярким примером непозиционной системы счисления является римская система.

Позиционные системы счислений. Введение.

Чем хороши позиционные системы счисления? Тем, что они позволяют легко производить арифметические расчеты. Попробуйте считать используя, например римские цифры. Сколько будет ? То-то, а вот достаточно представить эти числа арабскими цифрами и мы легко сможем посчитать в столбик.

Представление чисел с помощью арабских цифр самая распространенная позиционная система счисления, она называется «десятичной системой счисления». Десятичной системой она называется потому, что использует десять цифр. Вот эти цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Внимательно их пересчитайте – их ровно десять. Замете: максимальная цифра (9) на единичку меньше количества цифр (10).

Компьютер, в отличии от человека, хорошо разбирается в двоичной системе, он использует цифры: 0 и 1. Обратите внимание, что и здесь: система двоичная, а максимальная цифра 1.

Программисты пользуются, для упрощения себе жизни, еще восьмеричной и шестнадцатеричной системами счисления.

Количество цифр используемых в системе счисления называется «основанием». В десятичной системе основание равно десяти, в двоичной системе основание равно двум, ну а в восьмеричной и шестнадцатеричной соответственно восьми и шестнадцати.

В общем случае в позиционной системе счисления числа представляются следующим образом: (a_na_n_{− 1}…a₀)_f, где a₀,a₁,…,a_n – цифры, а f – основание системы счисления. Если используется десятичная система, то f – можно опустить.

Примеры чисел:

11001₂ – число в двоичной системе счисления, a₀ = 1,a₁ = 0,a₂ = 0,a₃ = 1,a₄ = 1;
221₃ – число в троичной системе счисления, a₀ = 1,a₁ = 2,a₂ = 2;
31₈ – число в восьмеричной системе счисления, a₀ = 1,a₁ = 3;
25₁₀ – число в десятичной системе счисления, a₀ = 5,a₁ = 2;

Реферат

Муниципальное бюджетное образовательное учреждение Пеновская средняя общеобразовательная школа имени Е.И. Чайкиной. РЕФЕРАТ по информатике Системы счисления работу выполнил: обучающийся 8Б класса МБОУ Пеновская СОШ имени Е.И. Чайкиной Тиккер Алексей. Руководитель работы: учитель математики и информатики Рябочкина С.В. п. Пено, 2017 СОДЕРЖАНИЕ ВВЕДЕНИЕ…………………………………………………………………… 3 ОСНОВНАЯ ЧАСТЬ: 4 1.1. Что такое система счисления…………………………………………… 5 1.2. История возникновения систем счисления………………………….. 6 1.3. Системы счисления: древние и современные……………………….. 11 1.4. Перевод целых чисел из одних систем счисления в другие……….. 14 ЗАКЛЮЧЕНИЕ………………………………………………………………. СПИСОК ЛИТЕРАТУРЫ…………………………………………………… 15 2 Введение В коробке лежит 31 шар. Среди них 12 красных и 17 синих. Может ли такое быть? На первый взгляд такой вопрос может показаться странным, и даже любой первоклассник ответит на него отрицательно. Но это только на первый взгляд. В привычной для нас десятичной системе счисления это утверждение верным назвать нельзя, но если посмотреть на это равенство в другой системе счисления, оно вполне может оказаться верным. Цель моего реферата: изучение возникновения и развития числа, системы счисления, правил перевода целых чисел из одной системы в другую. Задачи: с историей числа Познакомиться Изучить Изучить правило перевода целых чисел из одной системы счисления в другую. различные и системы счисления. счисления. системы виды 3 Что такое система счисления Система счисления совокупность правил наименования и изображения чисел с помощью набора символов, называемых цифрами. Количество цифр (знаков), называют основанием системы счисления. используемых для представления чисел Различные системы счисления, которые существовали раньше и которые используются в настоящее время, делятся на две группы: позиционные и непозиционные. Наиболее совершенными являются позиционные системы счисления, т.е. системы записи чисел, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число. Например, наша привычная десятичная система является позиционной: в числе 34 цифра 3 обозначает количество десятков и “вносит” в величину числа 30, а в числе 304 та же цифра 3 обозначает количество сотен и “вносит” в величину числа 300. Системы счисления, в которых каждой цифре соответствует величина, не зависящая от её места в записи числа, называются непозиционными. Примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы: V 5 X 10 L 50 I 1 В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются. C 100 500 1000 D M VI=5+1=6 IV= 5 – 1=4 Позиционные системы счисления результат длительного исторического развития непозиционных систем счисления. 4 История возникновения систем счисления Потребность в записи чисел появилась в очень древние времена, как только люди начали считать. Количество предметов изображалось нанесением чёрточек или засечек на какой либо твёрдой поверхности: камне, глине, дереве (до изобретения бумаги было ещё очень и очень далеко). Каждому предмету в такой записи соответствовала одна чёрточка. Археологами найдены такие “записи” при раскопках культурных слоёв, относящихся к периоду палеолита (10 11 тысяч лет до н.э.). Учёные назвали этот способ записи чисел единичной (“палочной” или унарной) системой счисления. В ней для записи чисел применялся только один вид знаков “палочка”. Каждое число в такой системе счисления обозначалось с помощью строки, составленной из палочек, количество которых и равнялось обозначаемому числу. Неудобства такой системы записи чисел и ограниченность её применения очевидны: чем большее число надо записать, тем длиннее строка из палочек. Да и при записи большого числа легко ошибиться, нанеся лишнее количество палочек или, наоборот, не дописав их. Древние люди добывали себе пищу главным образом охотой. На крупного зверя – бизона или лося – приходилось охотиться всем племенем. Чтобы добыча не ушла, ее надо было окружить, но вот хотя бы так: пять человек справа, слева. Даже в те времена, когда человек не знал таких слов, как “пять” или ”семь”, он мог показать числа на пальцах рук. Так начинали учиться считать, пользуясь тем, что дала сама природа, собственной пятерней. четыре семь сзади, Пальцы оказались прекрасной вычислительной машиной. С их помощью можно было считать до 5, а если взять две руки, то и до 10. В странах, где люди ходили босиком, по пальцам легко было считать до 20. Научившись считать по пальцам до десяти, люди стали считать десятками. Таким путем, основой счисления чаще всего становились числа 5, 10 или 20. Понятно, что системы счисления с более высоким основанием возникли позже, чем с низшим. Благодаря связям между племенами, усилению обмена между ними, наименования числительных и систем счислении объединялись. Системы с низшим основанием оказались менее пригодными, чем десятичная. С другой стороны, и системы с высоким основанием как двадцатеричная система, не оправдывались на практике, ибо они требовали запоминания большого числа особых слов – названий низших числительных. Таким образом, в процессе естественного отбора в подавляющем большинстве случаев выжила система счисления с основанием «средней» величины десятичная. 5 Системы счисления: древние и современные В мире существовали и существуют различные виды систем счисления. Например, система счисления племени Майя включала позиционность и нуль. Первые девятнадцать чисел системы счисления были представлены точками и черточками, согласно следующей таблице: Нуль записывался как символ, похожий на раковину (домик улитки). Многозначные числа большие 19, записывались вертикально, начиная с единиц высшего разряда сверху вниз. Это двадцатеричная система счисления. В древнем Вавилоне примерно за 40 веков до нашего времени создалась позиционная нумерация, то есть такой способ записи чисел, при котором одна и та же цифра может обозначать разные числа, смотря по месту, занимаемому этой цифрой. Для малых чисел вавилонская система счисления в основных чертах напоминала египетскую. 1 10. Например число 23 записывалось так : Но для записи чисел больше 59 древние вавилоняне впервые использовали новый принцип – одно из самых выдающихся достижений в развитии систем обозначений чисел – принцип позиционности, т.е. зависимости значения символа от его местоположения в записи числа. Вавилоняне заметили, что в качестве коллективных символов более высокого порядка можно применять уже ранее использованные символы, если они будут занимать в записи числа новое положение левее предыдущих символов. Так, один клиновидный знак мог использоваться для обозначения и 1, и 60, и 602, и 603, в зависимости от занимаемого им в записи числа положения, подобно тому, как единица в наших обозначениях используется в записях и 10, и 6 102, и 103. При обозначении чисел больше 60 знаки, выступающие в новом качестве, отличались от старых тем, что символы разбивались на «места», или «позиции», и единицы более высокого порядка располагались слева, с небольшими пробелами между ними. При таком способе записи для обозначения сколь угодно больших чисел уже не нужно было других символов, кроме уже известных. Так, например, число 302 будет иметь вид: 302 = 5 х 60 + 2 то есть А число 3725: Это шестидесятеричная система счисления. Встречается шестидесятеричная система счисления и в наше время: 1 час = 60 минут = 3600 секунд, окружность делят на 360, то есть 6*60 градусов, градус на 60 минут, а минуту на шестьдесят секунд. то есть 3725 = 1 х 60 х 60 + 2 х 60 + 5 У ряда африканских племен была распространена пятеричная система счисления. Долгое время пользовались пятеричной системой счисления и в Китае. Очевидна связь этой системы счисления со строением человеческой руки. Расшифровка системы счисления, созданной в Египте во времена первой династии, была существенно облегчена тем, что иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. 1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки. Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем должно быть столько же палочек сколько и в верхнем, или на одну больше. 10. Такими путами египтяне связывали коров Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам. 100. Это мерная веревка, которой измеряли земельные участки после разлива Нила. 1 000. Вы когданибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка. 7 10 000. “В больших числах будь внимателен!” говорит поднятый вверх указательный палец. 100 000. Это головастик. Обычный лягушачий головастик. 1 000 000. Увидев такое число обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф 10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца. Серьезным соперником десятичной системы счисления оказалась двенадцатерична, которая имела довольно широкое распространение. Вместо десятков применяли при счете дюжины, т.е. группы из двенадцати предметов. Происхождение её тоже связано со счётом на пальцах. Считали большой палец руки и фаланги остальных четырёх пальцев: всего их 12. Элементы двенадцатеричной системы счисления сохранилась в Англии в системе мер (1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам). Нередко и мы сталкиваемся в быту с двенадцатеричной системой счисления: чайные и столовые сервизы на 12 персон, комплект носовых платков – 12 штук. В году 12 месяцев, сутки составляют 24 часа=12*2. В середине V в. до н. э. появилась запись чисел нового типа, так называемая алфавитная нумерация. В этой системе записи числа обозначались при помощи букв алфавита: первые девять букв обозначали числа от 1 до 9, следующие девять числа 10, 20, 30, …, 90, и следующие девять числа 100, 200, …, 900. Алфавитная система была принята и в Древней Руси. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой Если посмотреть внимательно, то увидим, что после “а” идет буква “в”, а не “б” как следует по славянскому алфавиту, то есть используются только буквы, которые есть в греческом алфавите. записью чисел. 8 До XVII века эта форма записи чисел была официальной на территории Белоруссии, До сих пор православные церковные книги используют эту нумерацию. Сербии и Хорватии. Венгрии, Украины, Болгарии, В России славянская нумерация сохранилась до конца XVII века. При Петре I возобладала так называемая арабская нумерация. Арабская самая распространенная на сегодняшний день нумерация. Название “арабская” для нее не совсем верно, поскольку хоть и завезли ее в Европу из арабских стран, но там она тоже была не родной. Настоящая родина этой нумерации – Индия. Применяемые в настоящее время цифры 1234567890 сложились в Индии около 400 г.н.э. Форма индийских цифр претерпевала многообразные изменения. Марокканский историк Абкелькари Боужибар считает, что арабским цифрам в их первоначальном варианте было придано значение в строгом соответствии с числом углов, которые образуют фигуры. Так, единица создает лишь один угол, тройка три, пятерка пять и т.п. нуль не образует никакого угла, поэтому он не имеет никакого содержания. Та форма, которой мы сейчас пользуемся, установилась в XVI веке. В конце ХХ века, века компьютеризации, человечество пользуется двоичной системой ежедневно, так как вся информация, обрабатываемая современными ЭВМ, хранится в них в двоичном виде. В современные компьютеры мы можем вводить текстовую информацию, числовые значения, а также графическую и звуковую информацию. Количество информации, хранящейся в ЭВМ, измеряется ее «длиной» (или «объемом»), которая выражается в битах (от английского binary digit – двоичная цифра). Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Некоторые идеи, лежащие в основе двоичной системы, по существу были известны в Древнем Китае. Идея двоичной 9 системы была известна и древним индусам. Представление информации в двоичной системе использовалось человеком с давних времен. Так, жители островов Полинезии передавали необходимую информацию при помощи барабанов: чередование звонких и глухих ударов. Звук над поверхностью воды распространялся на достаточно большое расстояние, таким образом «работал» полинезийский телеграф. В телеграфе в XIX–XX веках информация передавалась с помощью азбуки Морзе – в виде последовательности из точек и тире. Часто мы договариваемся открывать входную дверь только по «условному сигналу» – комбинации коротких и длинных звонков. В 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем. Двоичная система счисления (Бинарная система счисления, binary) позиционная система счисления с основанием 2. Для представления чисел используются символы 0 и 1. Восьмеричная — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры 0 до 7. Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Ранее широко использовалась в программировании и компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной. Шестнадцатеричная (наиболее распространена в программировании, а также в шрифтах) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15. Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Этих систем счисления обычно хватает для полноценной работы, как человека, так и вычислительной машины, однако иногда в силу различных обстоятельств, всетаки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32. 10 Перевод целых чисел из одних систем счисления в другие Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики: Х2= Аn∙2n1 + Аn1∙2n2 + Аn2∙2n3 +…+А2∙21 + А1∙20 При переводе удобно пользоваться таблицей степеней двойки: n(степень) 2n 0 1 1 2 2 4 3 8 4 5 6 7 8 9 10 16 32 64 128 256 512 1024 Пример: Число 111010002 перевести в десятичную систему счисления: 111010002= 1∙27 + 1∙26 + 1∙25 +0∙24 + 1∙23+0∙22+0∙21+0∙20=23210 Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и 11 соответствующей степени числа 8, и вычислить по правилам десятичной арифметики: Х8= Аn∙8n1 + Аn1∙8n2 + Аn2∙8n3 +…+А2∙81 + А1∙80 При переводе удобно пользоваться таблицей степеней восьмерки: n(степень) 8n 0 1 1 8 2 3 4 5 6 64 512 4096 32768 262144 Пример: Число 750138 перевести в десятичную систему счисления: 750138= 7∙84 + 5∙83+ 0∙82 +1∙81 + 3∙80=3124310 Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики: Х16= Аn∙16n1 + Аn1∙16n2 + Аn2∙16n3 +…+А2∙161 + А1∙160 При переводе удобно пользоваться таблицей степеней числа 16: n(степень) 16n 0 1 1 16 2 3 4 5 6 256 4096 65536 1048576 16777216 Пример: Число FDA116 перевести в десятичную систему счисления: FDA116= 15∙163 + 13∙162 + 10∙161 +1∙160=6492910 Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке. Пример: Число 2210 перевести в двоичную систему счисления: 2210 = 101102 Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке. Пример: Число57110 перевести в восьмеричную систему счисления. 57110=10738 Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке. 12 Пример: Число746710 перевести в шестнадцатеричную систему счисления. 746710=1D2B16 Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой. При переводе необходимо пользоваться двоичновосьмеричной таблицей: 2ная 000 8ная 0 001 1 010 2 011 3 100 4 101 5 110 6 111 7 Пример: Число 1001011 перевести в восьмеричную систему счисления: 001 001 0112=1138 Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой. При переводе необходимо пользоваться двоичношестнадцатеричной таблицей: 2ная 0000 0001 0010 0011 0100 0101 0110 0111 16ная 0 1 2 3 4 5 6 7 2ная 1000 1001 1010 1011 1100 1101 1110 1111 16ная 8 9 A B C D E F Пример: Число 1011100011 перевести в шестнадцатеричную систему счисления: 0010 1110 00112=2E316 Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой. Пример: Число 5318 перевести в двоичную систему счисления: 5318=101 011 0012 Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой. Пример: Число ЕЕ816 перевести в двоичную систему счисления: ЕЕ816=1110111010002 При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему. Пример 1: Число FEA16 перевести в восьмеричную систему счисления: FEA16=1111111010102=111 111 101 0102=77528 13 Пример 2: Число 66358 перевести в шестнадцатеричную систему счисления: 66358=1101100111012=1101 1001 11012=D9D16 Заключение Работая над рефератом по теме «Системы счисления», я узнал много новых и интересных фактов о происхождении чисел и систем счисления, о том, как люди в разные эпохи учились считать, как изображали цифры и числа, что люди пользовались различными системами счисления, позиционными и непозиционными. Многие системы счисления имеют анатомическое происхождение. Элементы некоторых систем счисления имеют практическое применение в наши дни. Общеупотребительной системой счисления стала десятичная система счисления. Но и другие системы счисления имеют практическое применение, например системы счисления с основаниями 2, 8, 16 широко используются в программировании и в компьютерной документации. 14 Материал данного реферата как на уроках информатики в качестве дополнительного, так и на уроках математики. Ксати, задачка, данная во введении, имеет решение в восьмеричной системе счисления. может быть использован Надеюсь, что и Вам данный реферат был интересен, и, прочитав нижеследующее стихотворение, Вы не будете рисовать в своем воображении монстра. Ей было 1100 лет. Она в 101 класс ходила. В портфеле по 100 книг носила. Всё это правда, а не бред. Когда, пыля десятком ног, Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато стоногий. Она ловила каждый звук Своими десятью ушами, И 10 загорелых рук Портфель и поводок держали. И 10 тёмно синих глаз Оглядывали мир привычно. Но станет всё совсем обычным, Когда поймете наш рассказ. Список литературы 1. Гашков С.Б. Системы счисления и их применение. МЦНМО, 2004. 2. Глейзер Г. И.. История математики в школе. М.: Просвещение, 1964. 3. Кессельман В.С. Занимательная математика. М.:АСТ: Астрель, 2008. 4. Симонович С. В. Практическая информатика. Учебное пособие для средней школы. Универсальный курс. – М.: АСТПРЕСС. Инфорком – Пресс, 1999 . Фомин С.В. Системы счисления, М.: Наука, 1987. 5. 15 16

Реферат По Информатике 8 Класс Система Счисления – Telegraph

>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<

Реферат По Информатике 8 Класс Система Счисления
История создания систем счисления. Системы счисления, используемые в вычислительной технике. Сравнение непозиционных и позиционных систем счисления. Изучение основных правил десятичной, двоичной, восьмеричной и шестнадцатиричной систем счисления.
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Негосударственное образовательное учреждение
высшего профессионального образования
«Санкт-Петербургский университет управления и экономики»
Институт гуманитарных и социальных наук
Кафедра Информационных технологий и математики
по дисциплине «Компьютерный практикум»
Выполнила: Студентка группы _3041-1
система счисление вычислительный техника
1. История создания систем счисления
2. Системы счисления, используемые в вычислительной технике
8. Шестнадцатиричная система счисления
9. Перевод из одной системы счисления в другую
На протяжении всей своей жизни мы сталкиваемся с числами и выполняем над ними арифметические действия. Нас это не удивляет. Мы воспринимаем это, как факт, как само собой разумеющееся. А откуда возникли числа и счет? Что такое система счисления? Где сейчас мы сталкиваемся с ними? Мне стало очень интересно, и я решила изучить эту тему.
Данная тема мне интересна еще и потому, что в настоящее время двоичная система счисления приобрела большое значение в связи с ее применением в электронных вычислительных машинах. Системы счисления с основанием 8 и 16 применяются в программировании различных процессов на вычислительной технике.
Я поставила перед собой цель: познакомиться с историей возникновения счета и систем счисления, изучить системы счисления, используемые в вычислительной технике, позиционные и непозиционные системы счисления и арифметические действия в различных системах. В данной работе будут рассмотрены разные системы счисления.
1. История создания систем счисления
В древности людям приходилось считать на пальцах. Кроме пальцев считать нужно было много предметов, к счету привлекали больше участников. Один считал единицы, второй – десятки, третий – сотни. Очевидно, такой счет лег в основу системы счисления, принятой почти у всех народов, она называется десятичной системой. Счет с основанием десять применяли и у восточных славян.
Где люди ходили босиком, по пальцам легко было считать до 20. Сохранились следы использования при счете основания двадцать. Например, во французском языке число 80 в дословном переводе на русский язык звучит как «четырежды двадцать».
Так же был распространен счет дюжинами, то есть счет, при котором пользовались системой с основанием 12. Её происхождение связано с 12 фалангами на четырёх пальцах руки (кроме большого). Еще и сейчас некоторые предметы принято считать дюжинами. Столовые приборы состоят из полудюжины или дюжины комплектов.
В древнем Вавилоне, где математика была очень высоко развита, существовала весьма сложная шестидесятеричная система счисления. В наше время мы тоже используем эту систему. Например: 1 час=60 минут; 1 минута=60 секунд.
Самой древней из пальцевых систем счисления считается пятеричная. Эта система зародилась, и наибольшее распространение получила в Америке. Ее создание относится к эпохе, когда человек считал по пальцам одной руки. До последнего времени у некоторых племен пятеричная система счисления сохранилась еще в чистом виде.
Таким образом, все системы (пятеричная, двенадцатеричная, двадцатеричная) связаны с тем или иным способом счёта по пальцам рук (или рук и ног). Переход человека к пальцевому счету привел к созданию различных систем счисления./1/
2. Системы счисления, используемые в вычислительной технике
Системой счисления называют систему приемов и правил, позволяющих устанавливать взаимнооднозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов. Множество символов, используемых для такого представления, называют цифрами.
В зависимости от способа изображения чисел с помощью цифр системы счисления делятся на позиционные и непозиционные.
В непозиционных системах любое число определяется как некоторая функция от численных значений совокупности цифр, представляющих это число. Цифры в непозиционных системах счисления соответствуют некоторым фиксированным числам. Исторически первыми системами счисления были именно непозиционные системы. Одним из основных недостатков является трудность записи больших чисел. Запись больших чисел в таких системах либо очень громоздка, либо алфавит системы чрезвычайно велик. В вычислительной технике непозиционные системы не применяются.
Систему счисления называют позиционной, если одна и та же цифра может принимать различные численные значения в зависимости от номера разряда этой цифры в совокупности цифр, представляющих заданное число. Пример такой системы – арабская десятичная система счисления.
Количества и количественные составляющие, существующие реально могут отображаться различными способами. Основание позиционной системы счисления определяет ее название. В вычислительной технике применяются двоичная, восьмеричная, десятичная и шестнадцатеричная системы. В дальнейшем, чтобы явно указать используемую систему счисления, будем заключать число в скобки и в нижнем индексе указывать основание системы счисления. Каждой позиции в числе соответствует позиционный (разрядный) коэффициент или вес./2/
В настоящее время позиционные системы счисления более широко распространены, чем непозиционные. Это объясняется тем, что они позволяют записывать большие числа с помощью сравнительно небольшого числа знаков. Еще более важное преимущество позиционных систем – это простота и легкость выполнения арифметических операций над числами, записанными в этих системах.
Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
В целом вычислительные машины могут быть построены в любой системе счисления. Но столь привычная для нас десятичная система окажется крайне неудобной. Если в механических вычислительных устройствах, использующих десятичную систему, достаточно просто применить элемент со множеством состояний (колесо с десятью зубьями), то в электронных машинах надо было бы иметь 10 различных потенциалов в цепях./3/
В настоящее время и в технике и в быту широко используются как позиционные, так и непозиционные системы счисления.
В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Пример непозиционной системы счисления – римская система счисления. Возникшая в древнем Риме она просуществовала до наших дней. Традиционно применяют ее при нумерации веков или при составлении оглавлений печатных трудов. Римские цифры можно встретить на циферблатах часов.
В современной жизни наиболее яркий вариант использования непозиционной системы счисления – это денежные отношения. Мы с ними сталкиваемся каждый день. Здесь никому не приходит в голову, что сумма, которую мы выкладываем в магазине за продукты, может зависеть от того, в каком порядке мы расположим монеты на столе. Номинал монеты не зависит от того, в каком порядке она была вынута из кошелька. Это классический пример непозиционной системы счисления.
Таким образом, в настоящее время позиционная система счисления является наиболее распространенной.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число – два, три, четыре, шестнадцать и т.д. Следовательно, возможно бесконечное множество позиционных систем: двоичная, состоящая из цифр 0 и 1; троичная, состоящая из цифр 0,1,2; и так далее.
Таким образом, позиционные системы удобны тем, что они позволяют записывать большие числа с помощью небольшого числа знаков, просто и легко выполняются арифметические действия. /4/
Пришла в Европу из Индии, где она появилась не позднее VI века н.э. Основанием десятичной системы счисления является число 10, которое образует единицу 2-го разряда, единицей 3-го разряда будет 100 = 102, вообще единица каждого следующего разряда в 10 раз больше единицы предыдущего (полагают, что выбор в качестве основания Д. с. с. числа 10 связан со счётом на пальцах).
Д. с. с. основана на позиционном принципе, т. е. в ней один и тот же знак (цифра) имеет различные значения в зависимости от того места, где он расположен. В связи с этим для записи всех чисел нуждаются в особых символах только первые 10 чисел. Символы эти, обозначаемые знаками 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называются цифрами. Для записи числа определяют, сколько в нём содержится единиц наивысшего разряда; затем в остатке определяют число единиц разряда, на единицу меньшего, и т.д. Полученные цифры записывают рядом: например 4Ч102 + 7Ч101 + 3Ч100 = 473.
Таким образом, действия над числами производятся поразрядно, т. е. отдельно над цифрами каждого разряда; если при этом получаются числа больше 10 (при сложении, умножении), то прибавляют одну или несколько единиц к следующему, более высокому разряду; при делении и вычитании приходится разбивать разряды на более мелкие./4/
Двоичная система счисления, система счисления, построенная на позиционном принципе записи чисел, с основанием 2. В двоичной системе счисления используются только два знака — цифры 0 и 1; при этом, как и во всякой позиционной системе, значение цифры зависит дополнительно от занимаемого ею места. Число 2 считается единицей 2-го разряда и записывается так: 10 (читается: “один, нуль”). Каждая единица следующего разряда в два раза больше предыдущей, т. е. эти единицы составляют последовательность чисел 2, 4, 8, 16,…, 2n,…
Для того чтобы число, записанное в десятичной системе счисления, записать в Д. с. с., его делят последовательно на 2 и записывают получающиеся остатки 0 и 1 в порядке от последнего к первому, например: 43 = 21·2 +1; 21 = 10·2 +1; 10 = 5·2+0; 5=2·2+1; 2 = 1·2+ 0; 1 =0·2 + 1; итак, двоичная запись числа 43 есть 101011. Т. о., 101011 в Д. с. с. обозначает 1·20+1·21 + 0Ч22 +1Ч23 + + 0·24 + 1·25.
В Д. с. с. особенно просто выполняются все арифметические действия: например, таблица умножения сводится к одному равенству 1·1 = 1. Однако запись в Д. с. с. очень громоздка: например, число 9000 будет 14-значным.
Благодаря тому, что в двоичной системе счисления используются лишь две цифры, она часто бывает полезной в теоретических вопросах и при вычислениях на ЦВМ./5/
Восьмеричная система счисления – позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает – как и в десятичном числе – просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т.д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмиричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.
Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Таким образом, восьмеричная система счисления выступает в качестве простейшего языка общения человека с ЭВМ. /5/
8. Шестнадцатиричная система счисления
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означат просто единицу. Та же цифра 1 в следующем – 16 (десятичное), в следующем – 256 (десятичное) и т.д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное).
Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
Шестнадцатеричная система счисления, на сегодняшний день является наиболее популярным средством компактной записи двоичных чисел. Она очень широко используется при разработке и проектировании цифровой техники, и как восьмеричная система счисления служит человеку в качестве простейшего языка общения с ЭВМ. /6/
9. Перевод из одной системы счисления в другую
1. Перевод из любой системы счисления в десятичную систему счисления
Для перевода целого числа из любой системы счисления в десятичную, необходимо записать данное число в общем виде:
anbn+an-1bn-1+an-2bn-2+…+a2b2+a1b1+a0b0
Например: переведем число 12568 в десятичную систему счисления.
12568=1·83+2·82+5·81+6·80=1·512+2·64+5·8+6·1=68610
2. Правило перевода числа из десятичной системы счисления в другую систему.
2.1 Делим данное число на основание той системы, в которую необходимо перевести число.
2.2 Полученное число делим аналогично на основание системы, в которую необходимо перевести число.
2.3 Пункт 2 повторяем до тех пор пока, полученное частное не будет меньше основания.
2.4 Выписываем остатки от деления в порядке от последнего к первому./7/
3.1 Разбиваем число по три цифры на группы начиная с младшего разряда.
Если не хватает до целой тройки цифр, то добавляем необходимое количество нулей справа.
3.2 Каждую полученную тройку цифр заменяем цифрой из восьмеричной системы счисления.
(Можно использовать “Таблицу Систем Счисления” – первым смотрим столбик А2, затем – столбик А8).
3.3 Дробную часть разбиваем на тройки вправо от запятой.
Если не хватает цифр, то припысываем нули справа./7/
4.1 Разбиваем число по четыре цифры на группы начиная с младшего разряда.
Если не хватает до целой четверки цифр, то добавляем необходимое количество нулей слева.
4.2 Каждую полученную четверку цифр заменяем цифрой из восьмеричной системы счисления.
(Можно использовать “Таблицу Систем Счисления” – первым смотрим столбик А2, затем – столбик А16).
4.3 Дробную часть разбиваем на четверки вправо от запятой.
Если не хватает цифр, то припысываем нули справа./7/
Заменяем каждую цифру данного восьмеричного числа соответсвующим ей двоичным эквивалентом.
(Можно использовать “Таблицу Систем Счисления” – первым смотрим столбик А8, затем – столбик А2).
Если до полной тройки не хватает цифр, то в данной тройке добавлем недостающее количество нулей слева.
Заменяем каждую цифру данного шестнадчатиричного числа соответсвующим ей двоичным эквивалентом.
(Можно использовать “Таблицу Систем Счисления” – первым смотрим столбик А8, затем – столбик А2).
Если до полной четверки не хватает цифр, то в данной четверке добавлем недостающее количество нулей справа./7/
Согласно цели исследований в работе, я познакомилась с историей возникновения счета и систем счисления, изучила системы счисления, используемые в вычислительной технике, позиционные и непозиционные системы счисления и арифметические действия в различных системах счисления.
Познакомившись с системами счисления, я узнала очень много нового и полезного, и считаю, что эта наука необходима для развития общества. Сложно представить мир без вычислительной техники. Ведь именно двоичная система получила широкое распространение в различных областях техники, в особенности в современных вычислительных машинах и компьютерах.
Так же, подводя итоги работы, можно сделать следующие выводы:
1. Позиционная система счисления состоит в использовании ограниченного числа цифр, зато позиция каждой цифры в числе обеспечивает значимость (вес) этой цифры. Позиция цифры в числе на математическом языке называется разрядом.
Основание позиционной системы счисления – это количество различных знаков или символов (цифр), используемых для отображения чисел в данной системе.
2. Двоичная система счисления – наиболее широко используется в компьютерах, так как один разряд двоичного числа соответствует одному биту – минимальной единице информации в компьютерной технике.
3. Для того чтобы двоичные числа, отличающиеся довольно значительной длиной, было легче воспринимать и отображать, их сжимают в восьмеричную и шестнадцатеричную системы счисления.
4. В компьютерных технологиях все виды информации кодируются только цифрами или, точнее, числами, которые представляются в двоичной системе счисления – способе представления любых чисел с помощью двух знаков (цифр) по позиционному принципу.
5. Шестнадцатеричная система счисления широко используется в низкоуровневом программировании, а также в компьютерной документации. Также, восьмеричная система счисления иногда используется в компьютерах – по видимому, чаще всего при определении прав в Unix-подобных операционных системах. Когда-то были компьютеры, в которых использовались 24-х и 36-битные слова. Шестидесятеричная система счисления широко используется при подсчёте минут и секунд. /4/. В общем, восьмеричная и шестнадцатеричная системы счисления выступают в качестве простейшего языка общения человека с ЭВМ.
Я считаю, что у моей работы есть перспективы, так как тема системы счисления достаточно сложна, обширна и может использоваться в настоящей жизни. В моей работе собран и систематизирован весь материал по данной теме.
Надеюсь, что моя работа найдет применение не только среди преподавателей, но и среди учеников.
1. Фомин С. В. Системы счисления, 1987 г. Издание: Главная редакция физико-математической литературы издательства “Наука”.
2. Гашков С. Б. Системы счисления и их применение, 2012 г. Издание: МЦНМО.
3. Ковриженко, Г.А. Системы счисления и двоичная арифметика, 1984 г.
4. Основы систем счисления / Хабрахабр [http://habrahabr.ru/post/124395/].
5. Фринланд А.Я. Информатика. М., 2005.
6. Сидоров В.К. Системы счисления.//Наука и жизнь 2000. №2.
7. Радюк Л. Алгоритм перевода в двоичную и из двоичной системы счисления.// Наука и жизнь. 2005. №1.
8. Рассел Джесси – Двоичная система счисления, 2012 г. Издание: Книга по Требованию.
9. Колмогоров А.Н. Система счисления, 1970 г. Издательство “Академия Наук СССР”.
10. Алексеев Е.Г., Богатырев С.Д. Информатика. Мультимедийный электронный учебник. [http://inf.e-alekseev.ru/text/Schisl_perevod.html].
Порождение целых чисел в позиционных системах счисления. Почему мы пользуемся десятичной системой, а компьютеры – двоичной (восьмеричной и шестнадцатеричной)? Перевод чисел из одной системы в другую. Математические действия в различных системах счисления.

конспект произведения [971,1 K], добавлен 31.05.2009

Система счисления как способ записи (изображения) чисел. История появления и развития различных систем счисления: двоичная, восьмеричная, десятичная и шестнадцатеричная. Основные принципы и правила алгоритма перевода из одной системы счисления в другую.

курсовая работа [343,1 K], добавлен 11.11.2014

История систем счисления, позиционные и непозиционные системы счисления. Двоичное кодирование в компьютере. Перевод чисел из одной системы счисления в другую. Запись цифр в римской нумерации. Славянская нумерация, сохранившаяся в богослужебных книгах.

презентация [516,8 K], добавлен 23.10.2015

Определение понятия и видов систем счисления – символического метода записи чисел, представления чисел с помощью письменных знаков. Двоичные, смешанные системы счисления. Перевод из одной системы счисления в другую и простейшие арифметические операции.

курсовая работа [232,6 K], добавлен 16.01.2012

Исследование истории развития систем счисления. Изучение математического аспекта теории информатики. Характеристика информационных систем счисления. Основные операции над двоичными числами. Разработка программного обеспечения для проведения тестирования.

курсовая работа [995,4 K], добавлен 24.05.2015

Работы в архивах красиво оформлены согласно требованиям ВУЗов и содержат рисунки, диаграммы, формулы и т.д.
PPT, PPTX и PDF-файлы представлены только в архивах.
Рекомендуем скачать работу.
© 2000 — 2020, ООО «Олбест» Все права защищены

Системы счисления | РЕФЕРАТ
Доклад Системы счисления по информатике 5, 8 класс…
Система счисления
Реферат по информатике и информационно-коммуникационным…
Реферат : Системы счисления – BestReferat.ru
Свобода И Ответственность Примеры Для Эссе
Сочинение На Тему Фантазия По Тексту Железникова
Реферат По Истории Столетняя Война В Европе
Наука 21 Века Эссе
Отчет По Практике По Музею

Системы счисления

Обзор

Студенты будут изучать свойства систем счисления, эффективно изобретая систему счисления с основанием 3, используя круги, треугольники и квадраты в качестве символов вместо арабских цифр. Учащимся предлагается создать правила, объясняющие, как каждое расположение символов может быть сгенерировано или предопределено как упорядоченный, логический ряд. Цель состоит в том, чтобы понять, что вы можете представить любое число любым согласованным набором символов, которые появляются в согласованном порядке.Это верно как для кругов, треугольников и квадратов, так и для цифр 0–9 или систем счисления, которые мы обычно видим в информатике (двоичных и шестнадцатеричных).

Назначение

В информатике принято перемещаться между разными представлениями чисел. Обычно мы видим числа, представленные в десятичном (основание-10), двоичном (основание-2) и шестнадцатеричном (основание-16) виде. Символы десятичной системы счисления (с основанием 10) – 0 1 2 3 4 5 6 7 8 9 – настолько знакомы, что может быть сложно мысленно отделить написанные символы от абстрактных значений, которые они представляют.В результате использование цифр 0 и 1 может отвлекать при первоначальном изучении двоичного кода, поэтому в этом уроке мы этого не делаем.

Мы хотим раскрыть тот факт, что сами числа (количества) являются законами природы, но символы, которые мы используем для представления чисел, являются произвольной абстракцией, созданной руками человека. Иногда студенты запоминают преобразование одной системы счисления в другую, не понимая, почему. Цель этого урока – эффективно изобрести свою собственную систему счисления с основанием 3, чтобы студенты увидели, что все системы счисления имеют схожие свойства и функционируют одинаково.Пока у вас есть 1) набор различных символов 2) соглашение о том, как эти символы должны быть упорядочены, вы можете представлять ими любое число.

Повестка дня

Начало работы (5 минут)

Активность (30 минут)

Заключение

Оценка

Расширенное обучение

Посмотреть на Code Studio

Цели

Студенты смогут:

Рассуждения о паттернах и символах как о произвольных абстрактных понятиях, которые можно использовать для представления чисел.
Изобретите свою собственную «систему счисления» с символами и правилами для перехода от одного шаблона к другому.

Препарат

Ссылки

Внимание! Сделайте копии всех документов, которыми вы планируете поделиться со студентами.

Учителю

Студентам

Начало работы (5 минут)

Сколько способов вы можете представить «7»?

Цель обсуждения

Это обсуждение направлено на то, чтобы подготовить студентов различать знакомые символы, которые мы используем для представления чисел, и величины, которые мы фактически представляем.

Например, если на столе семь яблок, мы можем представить этот факт, написав «семь», «7», «VII», «*******», семь подсчетов, семь рисунков яблок и т. Д. на.

Подсказка :

«Сколько разных способов вы можете представить количество« 7 »? Выделите одну минуту, чтобы записать свои идеи, прежде чем поделиться с соседями. »

Дайте учащимся около минуты для молчаливой работы, а затем поделитесь идеями из класса.Мы рекомендуем просто написать их где-нибудь, чтобы их мог видеть весь класс.

Обсудить

Предлагаемые подсказки:

«Если мы продолжим, сколько способов представления« 7 », по вашему мнению, мы могли бы придумать? »
- Существует бесконечное количество представлений.
«Как вы думаете, почему мы используем символы для обозначения чисел? Кто это решил? »
«Если бы мы собирались разработать новую систему для представления чисел, какие функции она должна была бы иметь? »
- Ответ на этот вопрос – предмет сегодняшнего урока.

Переходные примечания

В предыдущих уроках вы все изобрели способы представления набора сообщений с помощью битов. Сегодня мы сосредоточимся на представлении чисел. К концу урока вы придумаете свою собственную систему счисления.

Активность (30 минут)

Уголок содержания

Цель использования этих трех символов (в отличие от цифр или букв алфавита) – сделать упражнение более подходящим для решения проблем или головоломки.Фигур в большинстве случаев достаточно, чтобы вырвать учащихся из контекста математического класса и по-настоящему изобрести собственную систему счисления, не осознавая этого поначалу.

Даже если учащиеся могут не придумать системы, которые мы бы считали “общими”, творчество следует поощрять. Можно изобрести всевозможные правила, чтобы переходить от одного паттерна к другому.

Дело в том, что системы счисления – это созданные человеком наборы символов и правил.

Круг-Треугольник-Квадрат Упражнение – Создайте систему счисления с помощью символов

Препарат :

Формируйте команды по 2 или 3 студента в каждой.
Раздать руководство по деятельности – Системы счисления: круг-треугольник-квадрат – Рабочий лист
Каждой группе должны быть предоставлены бумажные фигурки (не менее семи штук каждой). В качестве альтернативы, предоставьте учащимся материалы для изготовления своих собственных или используйте забавные винки, фишки для покера или любые другие маленькие бабочки, которые вы можете найти, если есть три разных типа объектов.

Учебный совет

В этой деятельности есть два основных момента:

Откройте для себя все трехместные узоры
Придумайте способ упорядочить их, чтобы последовательность была предсказуемой.

Студенты должны открыть в общей сложности 27 уникальных узоров.

Когда учащиеся записывают все рисунки, которые они придумали, на бумаге и пронумеровывают их, это предвещает присвоение числового значения определенному набору символов.

Возможно, вам потребуется подчеркнуть, что цель упражнения – не просто перечислить все 27 шаблонов, но и разработать набор правил, которым можно было бы следовать, чтобы сгенерировать все из них.

Некоторые студенты могут быстро распознать, что существует 27 различных групп.Однако их упорядочивание часто является проблемой для студентов, потому что вне контекста математического класса они могут не сразу применить то, что они уже знают о системах счисления, особенно о числовых значениях.

Тем не менее следует поощрять творчество. Можно изобрести всевозможные правила, чтобы переходить от одного паттерна к другому.

Хорошие вопросы, которые помогут ученикам думать таким образом, включают:

Не могли бы вы сказать мне, какой узор будет следующим?
Может ли одноклассник легко следовать вашим правилам, чтобы сгенерировать такой же порядок?
Были бы ваши правила по-прежнему работать, если бы я только попросил вас сделать все шаблоны длины 2? Что, если бы я попросил вас сделать все выкройки длиной 4 или 5?

Действие: круг-треугольник-квадрат

Инструкции: (из руководства по деятельности: Руководство по деятельности – Системы счисления: Круг-Треугольник-Квадрат – Рабочий лист)

Имея 3 места для работы, сделайте как можно больше уникальных узоров, используя только круги, треугольники и квадраты.

На диаграмме справа показано несколько примеров некоторых трехзначных паттернов. ПРИМЕЧАНИЕ. Порядок имеет значение, например: Круг-Треугольник-Квадрат – это другой шаблон, чем Квадрат-Круг-Треугольник, хотя оба имеют по одной из возможных форм.

Задание 1 – Найдите все трехместные шаблоны

Запишите все уникальных трехместных шаблонов, которые вы можете найти в шаблоне, начатом ниже.
Сколько их там? Пронумеруйте каждую, чтобы отслеживать.(Обратите внимание, что общих шаблонов может быть больше или меньше, чем предусмотрено пробелов)
Предложение : постарайтесь найти закономерности каким-то организованным или систематическим способом, а не просто случайным образом.

 ____ ____ ____

____ ____ ____

____ ____ ____

...

Задача 2 – создать систему для генерации всех шаблонов

Теперь, когда вы перечислили все трехместные узоры кругов, треугольников и квадратов, давайте расположим их в систематическом порядке.Вы можете использовать любую систему, которая вам нравится, при условии, что вы создаете четкий набор правил перехода от одной строки к другой и следуете им.

Запишите ниже правила вашей системы.
Предложение : чтобы проверить ваши правила, попросите кого-нибудь следовать им, чтобы увидеть, смогут ли они воссоздать ваш организованный список, указанный выше.

Время работы

Дайте учащимся достаточно времени, чтобы они разбились на группы и начали расставлять фигуры.Они должны пытаться обнаружить закономерности и правила, чтобы найти все возможные уникальные конфигурации.

Студентам нужно будет сделать три вещи:

Используйте вырезанные формы, чтобы исследовать и создавать все возможные узоры.
Организуйте набор выкроек в упорядоченную систему собственной разработки.
Запишите правила их системы заказа; хороший набор правил позволит кому-то еще предсказать или сгенерировать каждую последующую перестановку в списке.

Заключение

Учебный совет

Взгляните на следующий урок, посвященный двоичным числам, чтобы понять, насколько глубоко вам нужно углубиться в системы счисления для этого. Возможно, вы сможете более плавно совместить конец этого урока с началом следующего.

Уголок содержания

На схеме справа (щелкните, чтобы развернуть) показан метод создания всех уникальных узоров с 3 формами.Эта стратегия имитирует то, как мы обычно считаем в большинстве систем счисления. Затем вместо фигур, если вы просто скажете круг = 0, треугольник = 1 и квадрат = 2, вы сможете увидеть, как можно представить любой узор с помощью трех цифр.

Настоящая школьная система счисления круг-треугольник-квадрат

Используйте операцию совместного использования, чтобы студенты могли поделиться своими системами со своими одноклассниками. Либо в группах, либо в классе ученики должны прочитать правила своих одноклассников, оценить, понятны ли они, и проверить их, чтобы увидеть, насколько они похожи или отличаются от их собственных правил и шаблонов, которые они генерируют.

Примечания

Вы только что создали систему счисления!

Если у вас есть хорошее правило для создания всех шаблонов и перехода от одного шаблона к другому, и вы пронумеровали каждый шаблон, чтобы у вас было преобразование символа в число, у вас есть начало системы счисления!

Вспомните: сколько разных способов можно было написать цифру 7? Что ж, теперь у вас есть другой способ использования системы, которую вы только что создали.

Цель обсуждения

Цель этого заключительного обсуждения – установить общие свойства всех систем счисления.Вы можете выдвинуть идею о том, что системы, разработанные студентами, могут быть такими же законными, как и те, которые они используют каждый день, – но это не является общепринятым. Единственные требования для разработки системы счисления:

У вас должен быть набор уникальных символов
Вы должны согласиться с основным порядком расположения этих символов. Например: круг идет перед треугольником, треугольник перед квадратом. (аналогично: 0 стоит перед 1, 1 перед 2 и т. д.)
Если он у вас есть, то вы можете считать и представлять любое число.

Обсудите правила, созданные для систем счисления

Подсказки :

Было ли легче использовать одни наборы правил, чем другие? Если да, то что, по вашему мнению, привело к такой разнице?
Как вы думаете, есть ли ограничения на количество символов, которые мы можем использовать для представления чисел?

Подключение к системам счисления и двоичным числам

В конце урока можно выполнить подключение к системам счисления в целом и к двоичным числам в частности.

Например, после демонстрации правила для системы счисления круга, треугольника, квадрата вы можете спросить:

«Что, если бы у нас было только два символа: круг и квадрат? Могли бы мы по-прежнему составить систему счисления?»
Конечно, да, и именно так работают двоичные числа (подробнее мы увидим в следующем уроке)

Затем вы можете задать соответствующий вопрос:

«Что, если бы у нас было 10 символов: круг, треугольник, квадрат, звезда и так далее…Можем ли мы все же сделать систему счисления? »
Этот вопрос должен помочь понять суть – если бы у вас было 10 различных форм, вы могли бы просто заставить их работать как цифры 0-9.

Если это будет полезно, вы можете показать виджет Двоичный одометр – Code Studio, который появится на следующем уроке.

ПРИМЕЧАНИЕ :

К концу этого урока студентам НЕ нужно знать двоичную систему счисления или уметь переводить из десятичной в двоичную.Мы рассмотрим двоичные числа в следующем уроке гораздо более конкретно, включая идею значения разряда . Необходимо только общее понимание концепции систем счисления.

Оценка

Code Studio: Контрольные вопросы доступны в Code Studio

Экспертная оценка: Для взаимной оценки студентов раздайте студентам карточки для заметок или чистые листы бумаги и попросите их написать на них первые несколько вариантов своей системы.Затем они обменяются своими бумагами с другой группой и посмотрят, сможет ли другая группа предсказать следующие две перестановки в системе.

Расширенное обучение

Расширение до 4-х символьной системы: вырежьте одну или несколько дополнительных фигур, чтобы предоставить учащимся. Попросите учащихся расширить свои системы счисления, чтобы учесть эту дополнительную форму.
Попытайтесь определить, какое число представляет случайная перестановка, не считая всех перестановок, которые появляются перед ней.Можете ли вы разработать какие-нибудь правила?
Питер Деннинг объясняет, как «представление информации лежит в основе вычислений» в этой статье: «Вычисления: новый путь науки». Предлагаемое задание: поручите учащимся прочитать и обобщить содержание. Проведите обсуждение в классе.

(PDF) Система счисления

КОМПЬЮТЕРНАЯ СИСТЕМА НОМЕРА

Система счисления

Система счисления в компьютерной идеологии рассматривается как метод или система нумерации

и представления цифр во «внутренней» компьютерной системе.Другими словами, это метод

, используемый для представления чисел в архитектуре компьютерной системы. Цифровой компьютер

представляет все виды данных и информации в двоичных числах. Это означает, что каждое значение / число

, которое вы сохраняете или вводите / извлекаете из системной памяти компьютера,

имеет определенную систему счисления. Подача значений / данных в / выборка из может включать, но не ограничивается

: аудио, графику, видео, текстовый файл, числа и т. Д.Общее количество цифр, используемых в системе числа

, называется его основанием или основанием. Основание пишется после числа как нижний индекс; например

10001102 (1000110 с основанием 2), 5610 (от 56 до основания 10), 718 (71 с основанием 8) и т. д.

Архитектура компьютера поддерживает следующие системы счисления.

и. Двоичная система счисления (База 2)

ii. Восьмеричная система счисления (база 8)

iii. Десятичная система счисления (основание 10)

iv. Шестнадцатеричная система счисления (Base 16)

1) Двоичная система счисления

В двоичной системе счисления всего две цифры: 0 и 1.Каждое число (значение) –

, представленное 0 и 1 в этой системе счисления. Основание двоичной системы счисления – 2, потому что

состоит только из двух цифр. Хотя DECIMAL (№ 3) чаще используется в представлении Number

, BINARY – это форма системы счисления, которую принимает система / машина.

2) Восьмеричная система счисления

Восьмеричная система счисления имеет только восемь (8) цифр от 0 до 7. Каждое число (значение) представлено

с 0,1,2,3,4,5,6 и 7 дюймов эта система счисления.Основание восьмеричной системы счисления – 8, потому что

состоит только из 8 цифр.

3) Десятичная система счисления

Десятичная система счисления состоит только из десяти (10) цифр от 0 до 9. Каждое число (значение) –

, представленное как 0,1,2,3,4,5,6, 7, 8 и 9 в этой системе счисления. Основание десятичной системы числа

равно 10, потому что оно состоит всего из 10 цифр.

Абстракция

Абстракция
CPSC 110-08: Вычисления на мобильных телефонах

Spring 2012
Алгоритмы преобразования чисел
Принципы CS
Это упражнение знакомит с концепцией, на которой построены абстракции. двоичные последовательности могут использоваться для представления всех цифровых данных .Здесь также представлена концепция алгоритма . Это фокусируется на следующих целях обучения:
Задача обучения 5: Учащийся может описать комбинацию абстракций, используемых для представления данных.
Задача обучения 6: Учащийся может объяснить, как двоичные последовательности используются для представления цифровых данных.
16а. Использование естественного языка, псевдокода, визуального или текстового языка программирования для выражения алгоритма.
16б. Объяснение того, как алгоритм представлен на естественном языке, псевдокоде, визуальном или текстовом языке программирования.
16с. Объяснение того, как язык, используемый для выражения алгоритма, может влиять на такие характеристики, как ясность или удобочитаемость.
16д. Краткое изложение цели алгоритма.
Вступление
Позиционные системы счисления
Наша десятичная система счисления (а также двоичная и шестнадцатеричная) – это частный пример более общей абстракции, позиционный система счисления.
В позиционной системе счисления один и тот же символ может представлять разные значения в зависимости от его места в цифре.Например, в 91 цифре 9 соответствует 90 (10-е место), а в 19 – 9. (одно место). Сравните это с римскими цифрами, где X всегда представляет 10.
Основание числа
Основание числовой системы представляет количество цифр:
Десятичный (основание 10) имеет 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двоичный (основание 2) имеет 2 цифры: 0 и 1
Восьмеричный (основание 8) имеет 8 цифр: 0,1,2,3,4,5,6,7
Шестнадцатеричный (основание 16) имеет 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.Здесь вы можете видеть, что A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
Значение места
Позиционные системы счисления используют возведение в степень для определения значения цифры в количестве в зависимости от его места. Во всех случаях значение цифры – это умноженная на цифру цифру. по стоимости его места. Например,
Десятичное (основание 10) 104 = (1 × 10 ²) + (0 × 10 ¹) + (4 × 10 ⁰) = 100 + 0 + 4 = 104
Двоичный (основание 2) 111 = (1 × 2 ²) + (1 × 2 ¹) + (1 × 2 ⁰) = 4 + 2 + 1 = 7
Восьмеричный (основание 8) 104 = (1 × 8 ²) + (0 × 8 ¹) + (4 × 8 ⁰) = 64 + 0 + 4 = 68
Шестнадцатеричный (основание 16) FEC = (F × 16 ²) + (E × 16 ¹) + (C × 8 ⁰) = 15 × 256 + 14 × 16 + 12 × 1 = 3840 + 224 + 12 = 4076.
Алгоритмы преобразования
Алгоритм – это пошаговая процедура для выполнения вычисление. Давайте посмотрим на некоторые алгоритмы выполнения номера конверсии. Запишем алгоритмы в псевдокоде , a язык программирования, более формальный, чем английский, но менее формальный чем язык программирования.
Алгоритм преобразования любой системы счисления в десятичную систему счисления
Пусть n будет количеством цифр в номере.Например, 104 состоит из 3 цифр, поэтому n = 3 .
Пусть b будет основанием числа. Например, 104 является десятичным, поэтому b = 10 .
Пусть s будет промежуточной суммой, изначально равной 0.
Для каждой цифры в номере, работая слева направо, выполните:
Вычтем 1 из n .
Умножьте цифру на b ⁿ и прибавьте к s .
Когда вы закончите со всеми цифрами в номере, его десятичное значение будет s
Попробуем на двоичном числе 1011.
Пусть n = 4. Пусть b = 2. Пусть s = 0. Первая цифра, 1: n = 3, 1 × b ⁿ равно 1 × 2 ³ = 8. Итак, s = 8. Вторая цифра, 0: n = 2, 0 × b ⁿ равно 0 × 2 ² = 0. Итак, s = 8. Третья цифра, 1, n = 1, 1 × b ⁿ равно 1 × 2 ¹ = 2. Итак, s = 10. Последняя цифра, 1, n = 0, 1 × b ⁿ равно 1 × 2 ⁰ = 1. Таким образом, s = 11
Попробуем на шестнадцатеричном числе 7E.
Пусть n = 2. Пусть b = 16.Пусть s = 0. Первая цифра, 7: n = 1, 7 × b ⁿ равно 7 × 16 ¹ = 7 × 16 = 112. Итак, s = 112. Последняя цифра, E: n = 0, 14 × b ⁿ равно 14 × 16 ⁰ = 14. Итак, s = 112 + 14 = 126. Итак, s = 126.
Давайте попробуем на восьмеричном числе 124.
Пусть n = 3. Пусть b = 8. Пусть s = 0. Первая цифра, 1: n = 2, 1 × b ⁿ равно 1 × 8 ² = 1 × 64 = 64. Итак, s = 64. Вторая цифра, 2: n = 1, 2 × b ⁿ равно 2 × 8 ¹ = 2 × 8 = 16.Итак, s = 64 + 16 = 80. Последняя цифра, 4: n = 0, 4 × b ⁿ равно 4 × 8 ⁰ = 4. Итак, s = 80 + 4 = 84. Итак, s = 84.
Алгоритм преобразования десятичного числа в другое основание
Пусть n будет десятичным числом.
Пусть m будет числом, изначально пустым, в которое мы конвертируем. Мы будем составлять его справа налево.
Пусть b будет основанием числа, в которое мы конвертируем.
Повторяйте, пока n не станет 0
Разделите n на b , пусть результат будет d , а остаток будет r .
Запишите остаток r как крайнюю левую цифру от b .
Пусть d будет новым значением n .
Воспользуемся алгоритмом для преобразования 45 в двоичную форму.
Пусть n = 45. Пусть b = 2. Повторить 45, деленное на b, составляет 45/2 = 22, остаток 1. Таким образом, d = 22 и r = 1 . Итак, m = 1 , а новое n равно 22. 22, деленное на b, составляет 22/2 = 11 остаток 0. Таким образом, d = 11 и r = 1 .Таким образом, m = 01 , а новое значение n равно 11. Деление 11 на b дает 11/2 = 5 остаток 1. Таким образом, d = 5 и r = 1 . Итак, m = 101 , а новый n равен 5. Деление 5 на b дает 5/2 = 2 остатка 1. Таким образом, d = 2 и r = 1 . Итак, m = 1101 , а новое n равно 2. 2, деленное на b, составляет 2/2 = 1 остаток 0. Таким образом, d = 1 и r = 0 . Таким образом, m = 01101 и новый n равен 1. 1, деленное на b, равно 1/2 = 0, остаток 1.Итак, d = 0 и r = 1 . Итак, m = 101101 , а новый n равен 0. Итак, m = 101101.
Давайте воспользуемся им для преобразования 99 в двоичную форму.
Пусть n = 99. Пусть b = 2. Повторить 99 деленное на b дает 99/2 = 49 остаток 1. Таким образом, d = 49 и r = 1 . Итак, m = 1 , а новое n - 49. 49, деленное на b, составляет 49/2 = 24 остатка 1. Таким образом, d = 24 и r = 1 . Итак, m = 11 , а новое n равно 24.24, деленное на b, составляет 24/2 = 12, остаток 0. Таким образом, d = 12 и r = 0 . Итак, m = 011 , а новое n равно 12. Деление 12 на b дает 12/2 = 6 остаток 0. Таким образом, d = 6 и r = 0 . Итак, m = 0011 , а новый n равен 6. 6, деленное на b, составляет 6/2 = 3 остатка 0. Таким образом, d = 3 и r = 0 . Таким образом, m = 00011 , а новый n равен 3. 3, деленное на b, составляет 3/2 = 1 остаток 1. Таким образом, d = 1 и r = 1 .Таким образом, m = 100011 , а новое значение n равно 1. 1, деленное на b, равно 1/2 = 0, остаток 1. Таким образом, d = 0 и r = 1 . Таким образом, m = 1100011 , а новое значение n равно 0. Таким образом, m равно 1100011.
Давайте воспользуемся им для преобразования 45 в шестнадцатеричное.
Пусть n = 45. Пусть b = 16. Повторить 45, деленное на b, составляет 45/16 = 2 остатка 13. Таким образом, d = 2 и r = 13 . Таким образом, m = D , а новый n равен 2. 2, деленное на b, равно 2/16 = 0, остаток 2.Итак, d = 0 и r = 2 . Итак, m = 2D , а новое значение n равно 0. Таким образом, m равно 2D.
Давайте воспользуемся им для преобразования 99 в шестнадцатеричное.
Пусть n = 99. Пусть b = 16. Повторить 99, деленное на b, дает 99/16 = 6 остаток 3. Таким образом, d = 6 и r = 3 . Итак, m = 3 , а новое n равно 6. 6, деленное на b, составляет 6/16 = 0 остаток 6. Таким образом, d = 0 и r = 6 . Таким образом, m = 63 , а новое значение n равно 0.Итак, m - 63.
Домашние упражнения (срок сдачи)
Преобразуйте следующие числа в десятичную систему.
Двоичное число 111.
Двоичное число 1011.
Двоичное число 1011 1011.
Шестнадцатеричное число 61.
Шестнадцатеричное число DA.
Шестнадцатеричное число FEE.
Преобразуйте следующие числа, как показано.
Преобразуйте следующие 12 в двоичную форму.
Преобразуйте следующие 44 в двоичные.
Преобразуйте следующие 254 в шестнадцатеричный.
Преобразует следующие 16 в шестнадцатеричный.
Задача: преобразовать 125 в восьмеричную систему счисления .
Сочетание абстракций и символов в компьютере

2.1.1. Какая абстракция используется для представления чисел и символов на компьютере?
Словарь
I.Как абстрагируются данные
Абстракция данных обеспечивает четкое разделение между абстрактными свойствами типа данных и конкретными деталями его реализации. К абстрактным свойствам относятся те, которые видны клиентскому коду, который использует тип данных , интерфейс к типу данных, в то время как конкретная реализация остается полностью закрытой и действительно может изменяться, например, для включения улучшений эффективности с течением времени.
Компьютерные науки представляют уровни абстракции, в которых каждый уровень представляет разные модели, которые включают в себя одни и те же процессы и информацию, но использует систему выражения, которая включает уникальный набор объектов и композиций, применимых к определенной области .Существует три разных уровня абстракции; Физический уровень (самый низкий уровень), логический уровень (следующий более высокий уровень) и уровень обзора (самый высокий уровень). Физический уровень – это самый низкий уровень абстракции, который описывает, как работает система, как она хранит данные; этот уровень подробно описывает сложные низкоуровневые структуры данных. Следующий более высокий уровень – это логический уровень, который описывает, какие данные хранятся в базе данных, и отношения, существующие между этими данными. По сути, он описывает всю базу данных в виде небольшого числа в относительно небольших структурах.Самый высокий уровень абстракции – это уровень представления, который описывает только часть всей базы данных. Хотя он использует более простые структуры, сложность остается из-за разнообразия информации, хранящейся в большой базе данных. Уровень просмотра существует только для упрощения взаимодействия пользователей с системой.
II. Системы счисления, используемые в компьютере
Мы используем две основные системы: десятичную и двоичную.Двоичная система представляет числовые значения с использованием двух символов: обычно 0 и 1. Обычная система с основанием 2 – это позиционная система счисления с основанием 2. Числа, представленные в этой системе, обычно называются двоичными числами . Из-за простой реализации в цифровых электронных схемах с использованием логических вентилей, двоичная система используется внутри почти всех современных компьютеров и компьютерных устройств, таких как мобильные телефоны. Десятичная система – это система классификации проприетарной библиотеки.Классификация была известна в свое время тем, что в ней были введены понятия относительного местоположения и относительного индекса . Он использует трехзначные арабские цифры для основных классов с десятичными знаками в качестве расширений для более подробной информации.
Числовые системы и информатика Пример бесплатного эссе
Сравните различные форматы представления чисел в компьютерах. Кратко обсудите с помощью примеров.Назовите наиболее популярное представление чисел и почему вы так думаете
Система счисления – это способ представления чисел. Мы привыкли использовать десятичную систему счисления (основание 10). Другие распространенные системы счисления включают шестнадцатеричную (основание 16), восьмеричную (основание 8) и двоичную (основание 2). Что касается компьютерных систем, системы счисления можно разделить на четыре категории:
Десятичная система счисления
Двоичная система счисления
Восьмеричная система счисления
Шестнадцатеричная система счисления
Десятичная система счисления
Термин «десятичный» происходит от латинского префикса «deci», что означает «десять».
Сдавайте бумагу самого высокого качества
Обратитесь к квалифицированному писателю, который поможет вам с
«Системы счисления и информатика»
Получите качественную бумагу
НОВИНКА! AI сопоставление с писателями
Десятичная система счисления состоит из десяти цифр от 0 до 9. Потому что в этой системе десять цифр; ее также называют десятичной или десятичной системой счисления. Десятичное число всегда следует записывать с нижним индексом 10, например. X10. Но поскольку это наиболее широко используемая система счисления в мире, нижний индекс обычно понимается и игнорируется в письменной работе.
Однако, когда многие системы счисления рассматриваются вместе, всегда следует ставить нижний индекс, чтобы различать системы счисления.
Двоичная система счисления
Для обозначения чисел используются две цифры, а именно 1 и 0. В отличие от десятичных чисел, где значение разряда увеличивается в десять раз, в двоичной системе значения разряда увеличиваются в 2 раза, двоичные числа записываются как X2, рассмотрим двоичное число, такое как 10112. разрядное значение 1–20, в то время как крайнее левое имеет разрядное значение 1–23.
Узнайте смету стоимости вашей бумаги
«Вы должны согласиться с условиями предоставления услуг и политикой конфиденциальности»
Восьмеричная система счисления
Состоит из восьми цифр в диапазоне от 0 до 7. Разряд восьмеричных чисел увеличивается в восемь раз справа налево.
Шестнадцатеричная система счисления
Это система счисления с основанием 16, которая состоит из шестнадцати цифр от 0 до 9 и букв A-F, где A эквивалентно 10, от B до 11 до F, что эквивалентно 15 в системе с основанием десять.Разрядность шестнадцатеричных чисел увеличивается в шестнадцать раз.
Шестнадцатеричное число может быть обозначено с помощью нижнего индекса 16 или заглавной буквы H справа от числа. Например, 94B можно записать как 94B16 или 94BH.
Самое популярное представление номера
Самым популярным представлением чисел среди вышеперечисленных четырех, на мой взгляд, является десятичная система счисления. Это потому, что он не ограничивает нас в использовании его нижнего индекса 10, например X10, как и другие системы счисления.Как это понимает большинство из нас.
Что вы подразумеваете под точностью представления числа с плавающей запятой в стандарте IEEE? Объясните на небольшом примере
IEEE стандартизировал компьютерное представление двоичных чисел с плавающей запятой в IEEE 754 (также известном как IEC 60559) в 1985 году. Новая версия IEEE 754-2008 была опубликована в августе 2008 года после семилетнего процесса пересмотра под председательством Дэна. Зурас и отредактированный Майком Коулишоу. Он заменил как IEEE 754-1985 (двоичная арифметика с плавающей запятой), так и стандарт IEEE 854-1987 для Radix-независимой арифметики с плавающей запятой.Текущая версия IEEE 754-2019, опубликованная в июле 2019 года, является производной и заменяет IEEE 754-2008 после процесса пересмотра, начатого в сентябре 2015 года под председательством Дэвида Г. Хоу и отредактированным Майком Коулишоу. Он включает в себя в основном пояснения и исправления, но также включает некоторые новые рекомендуемые операции. Стандарт предусматривает множество тесно связанных форматов, три из которых особенно широко используются в компьютерном оборудовании и языках:
одинарной точности
Одинарная точность обычно используется для представления типа «float» в семействе языков C (хотя это не гарантируется).Это двоичный формат, занимающий 32 бита (4 байта), а его значащий формат имеет точность 24 бита (около 7 десятичных цифр).
Двойная точность
Двойная точность обычно используется для представления типа «double» в семействе языков C (хотя это не гарантируется). Это двоичный формат, занимающий 64 бита (8 байтов), а его значащий формат имеет точность 53 бита (около 16 десятичных цифр).
Двойной удлиненный
Двойной расширенный также называется форматом «расширенной точности».Это двоичный формат, который занимает не менее 79 бит (80, если правило скрытых / неявных битов не используется), а его значащий формат имеет точность не менее 64 бит (около 19 десятичных цифр). Формат, удовлетворяющий минимальным требованиям (64-битная точность, 15-битная экспонента, что соответствует 80 битам), обеспечивается архитектурой x86. Как правило, на таких процессорах этот формат может использоваться с «длинным двойным» в семействе языков C (стандарты C99 и C11 «Расширение арифметических операций с плавающей запятой IEC 60559 – Приложение F» рекомендуют использовать 80-битный расширенный формат как «Длинный дубль», если таковой имеется).
Например, если b = 10, p = 7 и e-max = 96, то e-min =? 95, значащее удовлетворяет 0? с? 9,999,999, а показатель степени удовлетворяет? 101? д? 90. Следовательно, наименьшее ненулевое положительное число, которое может быть представлено, равно 1 × 10 × 101, а наибольшее – 9999999 × 1090 (9,999999 × 1096), поэтому полный диапазон чисел составляет от? 9,999999? 1096 до 9,999999? 1096. . Числа? B1? Emax и b1? Emax (здесь? 1? 10? 95 и 1? 10? 95) являются наименьшими (по величине) нормальными числами; ненулевые числа между этими наименьшими числами называются субнормальными числами.
Компьютерные науки
Приложения в наши дни, где CS / SE движется к
Информатика – это изучение компьютеров и вычислительных систем. В отличие от инженеров-электриков и компьютерных инженеров, компьютерные ученые в основном занимаются программным обеспечением и программными системами; это включает их теорию, дизайн, разработку и применение. Основные области изучения компьютерных наук включают искусственный интеллект, компьютерные системы и сети, безопасность, системы баз данных, взаимодействие человека с компьютером, зрение и графику, численный анализ, языки программирования, программную инженерию, биоинформатику и теорию вычислений.
Хотя умение программировать необходимо для изучения информатики, это только один элемент области знаний. Ученые-информатики разрабатывают и анализируют алгоритмы для решения программ и изучают производительность компьютерного оборудования и программного обеспечения. Проблемы, с которыми сталкиваются компьютерные ученые, варьируются от абстрактных (определение того, какие проблемы могут быть решены с помощью компьютеров и сложности алгоритмов, которые их решают), до материальных (создание приложений, которые хорошо работают на портативных устройствах, которые просты в использовании и которые соблюдать меры безопасности.Его области можно разделить на теоретические и практические дисциплины. Теория вычислительной сложности очень абстрактна, в то время как компьютерная графика делает упор на реальные приложения.
Разница между CS / SE / CE
Компьютерная инженерия (CE)
Он занимается проектированием, разработкой и эксплуатацией компьютерных систем. По своей сути, компьютерная инженерия концентрируется на цифровых аппаратных устройствах и компьютерах, а также на программном обеспечении, которое ими управляет. Компьютерная инженерия делает упор на решение проблем с цифровым оборудованием и программно-аппаратным интерфейсом.
Программная инженерия (SE)
Занимается созданием и обслуживанием программных систем. Он больше ориентирован на программное обеспечение и уделяет больше внимания крупным программным приложениям, чем компьютерная инженерия. Он более прикладной, чем информатика, уделяя больше внимания всему процессу разработки программного обеспечения, от идеи до конечного продукта.
Компьютерные науки
Он фокусируется на понимании, проектировании и разработке программ и компьютеров. По своей сути компьютерные науки концентрируются на данных, преобразовании данных и алгоритмах.На курсах продвинутого уровня представлены специализированные методы программирования и конкретные области применения. Программа CS менее структурирована, чем программы CE и SE, что дает студентам большую гибкость для углубления и расширения в различных областях приложений или в основах компьютерных наук.
Работа в Интернете
Когда вы вводите слова на веб-странице поисковой системы, она так быстро возвращает вам результаты. (Алгоритмы поиска, параллельные вычисления)
Играя в компьютерные науки
Современные игры выглядят потрясающе, со всеми их крутыми трехмерными эффектами, и все это визуализируется в реальном времени, когда вы играете и постоянно меняете игровую среду.(Компьютерная графика)
Враги в игре кажутся «умными» и могут учиться на ваших действиях. (Искусственный интеллект)
Мы и десятки других игроков можем играть онлайн одновременно, и при этом большую часть времени игра будет отзывчивой. (Сеть, архитектура клиент-сервер)
Загрузка носителя (юридически)
Программы обмена файлами, такие как Bit-Torrent, могут работать намного быстрее, чем простая загрузка с веб-сайта.(Сеть, распределенные алгоритмы)
Разве не удивительно, что когда вы загружаете файл, он всегда попадает на ваш компьютер в первозданном виде, даже несмотря на то, что ему пришлось пройти тысячи миль по ненадежным медным проводам? (Надежные сетевые протоколы, обнаружение и исправление ошибок)
Высококачественные фотографии, аудио и видео можно сильно сжать (от 1/10 до 1/100 исходного размера) без большой потери качества. (Алгоритмы сжатия потерь)
Покупки в Интернете
Вы можете быть уверены в том, что никто не украдет номер вашей кредитной карты, пока вы делаете покупки в Интернете.(Сетевая безопасность, криптография)
Продавец может отслеживать, какие товары есть в наличии, и сообщать о результатах в режиме реального времени на своем веб-сайте. (Базы данных, веб-программирование)
Некоторые другие приложения информатики: использование наших мобильных телефонов, невротическое обновление ваших страниц в Facebook, Instagram, Twitter и отслеживание профилей других людей и путешествия в самолете.
Будущее компьютерных наук
Будущее информатики может быть не слишком светлым.Компьютеры стали настолько широко распространенной технологией, что я думаю, что изучение вычислительной техники может скоро быть отнесено к другим академическим предметам, и компьютерная наука может потерять свою независимость как академический предмет. Меня не удивит, если через 20 лет отделы информационных технологий вымрут. Вычислительная техника уже породила несколько академических факультетов, таких как информационные технологии, программная инженерия и компьютерная инженерия, которые редко интегрируются в учебную программу факультета компьютерных наук. В последнее время возникли и другие вычислительные дисциплины, такие как научные вычисления / вычислительная наука, наука об управлении, цифровая графика и компьютерные игры / виртуальная реальность.
двоичный – Computer Science Wiki
из вики по информатике
Перейти к навигации Перейти к поиску
Это основная концепция информатики
В математике и цифровой электронике двоичное число – это число, выраженное в двоичной системе счисления или системе счисления с основанием 2, которое представляет числовые значения с использованием двух разных символов: обычно 0 (ноль) и 1 (единица). Система с основанием 2 – это позиционная система счисления с основанием 2.Благодаря простой реализации в цифровых электронных схемах с использованием логических вентилей, двоичная система используется внутри почти всех современных компьютеров и компьютерных устройств. Каждая цифра называется битом. ^[1]
Это одно из лучших видео о двоичных файлах, которые я видел. Содержание используется с благодарностью и разрешением: ^[2]

Основные определения [править]
бит : бит представляет логическое состояние с одним из двух возможных значений
байт : Группа из 8 смежных двоичных цифр (8 бит), на которой компьютер работает как единое целое
двоичная : двоичная система счисления является системой счисления с основанием 2.
денарная / десятичная : десятичная система счисления (также называемая основанием 10 или иногда денарная) имеет основу десять. ^[3]
шестнадцатеричный : В математике и вычислительной технике шестнадцатеричный (также основание 16 или шестнадцатеричный) – это позиционная система счисления с основанием 16 ^[4]. Щелкните здесь, чтобы посмотреть отличное видео о шестнадцатеричной системе счисления
Таблица двоичного преобразования [править]
Я считаю полезным нарисовать эту таблицу, когда мне нужно преобразовать двоичный код в базу 10.Это также помогает при просмотре видео выше.
Полезная шпаргалка [править]

Как сложить два двоичных числа [править]
Добавить двоичный файл очень просто. Выровняйте числа, как если бы вы складывали числа с основанием 10.
Запомните это:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10, поэтому напишите 0 и перенесите 1 в следующий столбец.
Что вы должны знать [править]
Вы должны уметь правильно ответить на следующие вопросы:
Определите термин: бит
Определите термин: байт
Определите термин: двоичный
Определите термин: десятичный / десятичный (они относятся к одному и тому же)
Определите термин: шестнадцатеричный
Почему это так важно? [Править]
Если мы можем представить числа как 1 и 0 , почему бы не представить числа как вкл и выкл ? Если мы можем представить буквы как числа (A = 65, B = 66), не могли бы мы также сказать, что A = 01000001 и B = 01000010? Мы можем следовать этому образу мышления и делать север / юг, вверх / вниз и вниз / вверх.Простые конструкции, которые мы можем использовать для представления более сложных чисел и даже букв.
Двоичное представление – это суть работы компьютеров.
Ресурсы [править]
Щелкните здесь, чтобы просмотреть слайды, которые хорошо освещают эту тему.
Ссылки [править]
Двоичные числа и работа компьютеров
Хотя для изучения компьютерного программирования необязательно обладать обширными знаниями математики, это, безусловно, помогает иметь базовые знания в некоторых основах математики, которые делают вычисления возможными.А что может быть более фундаментальным для современных вычислений, чем двоичная математика?
Термин «двоичный» означает что-то, что имеет только два возможных объекта или состояния. В двоичной системе счисления этими двумя объектами являются числа 0 и 1 . Эти два числа могут обозначать разные вещи.
Например, в компьютерной логике 0 представляет «ложь», а 1 представляет «истину». Или они могут использоваться для представления обычных чисел в виде комбинаций единиц и нулей.Примером этого может быть представление чисел 0, 1, 2, 3 и 4 в виде трех двоичных цифр 000, 001, 010, 011 и 100 соответственно.
Но что все это означает на фундаментальном уровне вычислений? Почему двоичная система счисления используется в качестве основы для всех наших вычислений?
Возможно, будет легче понять все это, если мы сможем понять основы работы компьютеров на машинном уровне.
Комбинации 0 и 1: Интерпретация работы компьютерных схем
компьютеры работают с электрическими сигналами, генерируемыми этими схемами.Чтобы спроектировать компьютер, который работает эффективно, нам нужна система, которая может интерпретировать электрические сигналы упрощенным и эффективным способом.
Хороший способ сделать это – интерпретировать электрические сигналы как двоичные значения: 0 для низкого значения напряжения и 1 для высокого значения напряжения. Более простой способ подумать об этом – представить лампочку. Если лампочка находится в положении от , это состояние интерпретируется как имеющее значение 0 . Если это на , это интерпретируется как имеющее значение 1.
Интерпретация состояний лампочки в двоичном формате
Это широкое обобщение сокращает диапазон интерпретации каждого электрического сигнала до двух различных значений вместо бесконечного диапазона непрерывных значений напряжения.
Имея этот метод работы и интерпретации электронных схем, мы можем приступить к разработке кодированных систем на основе двоичных разрядов, чтобы помочь в наших вычислительных задачах. Эти системы могут быть двоичной логикой (ограничены только значениями истинных или ложных ), представлением числовых значений с основанием 2 или другими системами, которые полагаются на серию двоичных чисел для представления текста, изображений или звуков.
По сути, наши компьютеры используют серию электрических сигналов высокого и низкого напряжения (двоичные значения) для представления всего, от текста и чисел до изображений и звуков. Существуют специальные электронные схемы, такие как триггеры и другие схемы, которые могут «хранить» или сохранять эти конкретные образцы электрических сигналов для длительного использования.
Например, один триггер может иметь несколько входов, которые в настоящее время имеют выход высокого напряжения (который мы интерпретируем как 1 ).Предположим, что следующие два триггера имеют низковольтные выходы 0 . Мы могли бы объединить эти три вывода, чтобы получить значение 100 , которое в двоичном формате совпадает с числом 4 .
Понимание двоичных чисел, таким образом, может помочь нам понять некоторые основы компьютерных операций на достаточно абстрактном уровне , даже если наш слабый человеческий интеллект никогда не позволит нам понять всю сложность компьютерных операций.
И это также хорошо, что для работы с упрощенными и абстрактными концепциями компьютерных операций нам, изучающим информатику, более чем достаточно.В следующих разделах мы кратко рассмотрим некоторые из различных способов, которыми компьютеры используют двоичные символы для выполнения некоторых из своих самых фундаментальных операций.
Логическая логика: использование двоичных чисел для понимания компьютерной логики
Компьютерные программы используют очень специфическую систему логики для выполнения своих инструкций. Это известно как булева логика, сформулированная английским математиком Джорджем Булем в XIX веке.
Boole разработал систему арифметических и логических операций, использующих двоичную систему чисел.Логическая логика имеет дело только с двумя возможными значениями: истинно или ложно . Истинный представлен 1 , а ложный представлен 0 . Все логические операции приводят к получению только одного из этих двух двоичных значений.
Современные компьютеры постоянно используют эту форму логики для принятия решений. Эти решения приводят к тому, что наши компьютеры принимают определенный образ действий вместо другого.
Принятие решений на компьютерах
Чтобы понять, насколько важна эта система для компьютеров, не нужно смотреть дальше существования логических операторов в большинстве языков программирования: операторов AND, OR и NOT.
Эти операторы взяты непосредственно из операций И, ИЛИ и НЕ из логической логики. И любой, кто имеет поверхностные познания в программировании, знает, что эти операции являются центральными в программировании.
Но на этом влияние работы Буля не заканчивается. Фактически, многие языки программирования имеют тип данных с именем boolean , который может хранить только «истина» или «ложь», то есть 1 или 0.
Эти логические переменные и логические операторы являются фундаментальными компонентами, используемыми при реализации условных операторов и управления. операторы на языках программирования.В результате их важность невозможно переоценить, поскольку это Programming 101.
Есть также много других, более творческих и более сложных способов использования двоичных чисел в языках программирования. Однако это сообщение в блоге служит простым обзором некоторых вещей, для которых можно использовать двоичные числа.
Таким образом, мы не будем вдаваться в подробности технического программирования. Возможно, я рассмотрю эти темы в следующих статьях блога. А пока давайте просто рассмотрим более простую тему числовых представлений в компьютерах.
Представление числовых значений в системе счисления с основанием 2
Числовые значения представлены в наших компьютерных системах в некоторой форме системы счисления с основанием 2. Обычные числа, которые мы используем в повседневной жизни, – это десятичная система счисления. Например, число 135 дает нам сто тридцать пять.
Значения десятичных разрядов
Как видно из изображения выше, каждая цифра, начиная с правой стороны, умножается на 10, начиная с (10 ^ 0 = 1) , затем (10 ^ 1 = 10) и, наконец, (10 ^ 2 = 100) .Чем больше цифр, тем больше последовательность степеней 10. Вот почему эта система счисления называется системой счисления с основанием 10.
Система счисления с основанием 2 работает таким же образом, за исключением того, что мы умножаем каждый бит (двоичную «цифру») на последовательные степени 2. В качестве примера возьмем число с основанием 2 1011 и увидим какое число по основанию 10 он представляет.
Значение двоичного разряда
Как мы видим, двоичное число 1011 эквивалентно числу одиннадцать (11) в базе 10.
Конечно, имеет значение и способ группировки двоичных чисел. Мы знаем, что 1011 представляет собой число 11 по основанию 10. Но что, если мы сгруппируем ту же последовательность битов, что и 10 11? Это два разных числа: 10 и 11? Или это единое число 1011?
Это показывает нам важность того, как мы группируем наши числа. А в компьютерах числа сгруппированы по-разному. Например, целочисленный тип данных int в C ++ хранит одно число в серии из 32 двоичных чисел.Таким образом, число с основанием 10 0 представлено серией из 32 нулей, а число 1 представлено единицей, перед которой слева стоит 31 ноль.
Текстовое и символьное представление
Мы видели, что система счисления с основанием 2 формирует основу числового представления в наших электронных устройствах. И хотя это верно для систем текстового представления, их работа совершенно другая.
Наиболее распространенными системами представления символов являются ASCII, (американский стандартный код для обмена информацией) и Unicode, (расширение ASCII).Эти системы присваивают символам уникальные числовые значения и хранят их в двоичном формате.
Например, система ASCII изначально использовала 7 бит для представления символа. В настоящее время он расширен до 8 бит. Например, символ A представлен числовым значением 65 в ASCII. Двоичный код для 65 – 1000001 . Обратите внимание, что двоичное представление состоит из 7 бит. В расширенном ASCII это будет сохранено как 01000001 , так что общее количество бит равно 8.
Точно так же код ASCII для символа a – 97 , и он представлен как 01100001 в расширенном ASCII. Есть также очень специальные символы, которые представлены 0 , 1 , 2 и так далее. И они представлены как 00000000 , 00000001 , 00000010 и так далее.
Эта система хорошо подходит для представления английских и некоторых европейских символов и символов, но, к сожалению, не подходит для представления символов из языков всего мира.Для размещения дополнительных символов был разработан Unicode .
Unicode изначально использовал 21 бит на символ, в отличие от 7 битов, изначально используемых в ASCII. Это значительно расширяет диапазон значений, которые можно использовать для представления символов. Исходные коды ASCII размещены в системе Unicode.
В настоящее время система кодирования на основе Unicode, называемая UTF-8 , является наиболее часто используемой системой кодирования в веб-приложениях. UTF-8 может использовать до 32 бит на символ, что означает, что он может представлять еще большее количество символов.
Пиксели и изображения
Неудивительно, что изображения также часто представлены числами. В компьютерах изображения чаще всего создаются с помощью крошечных цветных квадратов, называемых пикселями. Подумайте о мозаике в реальной жизни: изображение или узор создается путем объединения множества маленьких цветных кусочков. Или пазл, в котором мы объединяем более мелкие части, чтобы создать более крупное и законченное изображение.
Пиксели работают аналогично. Тысячи крошечных цветных квадратов составляют изображения, которые отображаются на наших экранах.Есть много способов кодирования цветов в пикселях, но наиболее часто используемый код – это код RGB (красный, зеленый, синий).
Коды
RGB работают путем комбинирования красного, зеленого и синего цветов для получения всех оттенков цветов, которые мы видим в наших современных устройствах. Каждый из трех компонентов цвета кодируется числом, значения которого находятся в диапазоне от 0 до 255. Таким образом, существует три набора чисел, которые описывают пиксель.
В качестве примера рассмотрим цвет, представленный кодом RGB (142, 150, 123).Этот цветовой код состоит из 3 компонентов: Красный = 142 , Зеленый = 150 и Синий = 123 .
Внутри наших компьютеров каждый из этих цветовых компонентов представлен своими двоичными эквивалентами с использованием 8 бит, а затем объединяется вместе. Например, двоичный код для 142 (красный компонент) – 10001110, двоичный для 150 – 10010110, а двоичный для 123 – 1111011.
Красный = 142 = 10001110
Зеленый = 150 = 10010110
Синий = 123 = 01111011
Компьютер объединяет эти числа слева направо, чтобы сохранить код RGB в своей памяти.
Полный код RGB = 100011101001011001111011
Работа кода RGB
Таким образом, мы видим, что даже изображения представлены в двоичном формате. Фактически, знание двоичных кодов пикселей изображения открывает двери для забавных небольших приложений манипулирования изображениями, таких как сокрытие одного изображения внутри другого. Я уже писал о простом методе сокрытия изображений в моем предыдущем блоге «Стеганография: скрытие информации внутри изображений». Вы можете проверить это на предмет практического применения двоичных чисел в информатике.
Заключительные мысли и выводы
Двоичные числа составляют одну из основных основ современных вычислений. И хотя мы вкратце рассмотрели некоторые способы использования двоичных чисел в наших компьютерах, мы также упустили многое, поскольку исчерпывающий список приложений и пояснений выходит за рамки этого блога.
При этом мы рассмотрели довольно много интересных тем, хотя они могут быть базовыми. Мы видели, что
физических действий компьютерных схем интерпретируются с использованием двоичной записи i.е. в одной цепи значения низкого напряжения интерпретируются как 0 , а значения высокого напряжения интерпретируются как 1 . Компьютеры
используют логическую логику, интерпретируя 1 как истинный и 0 как ложный при выполнении логических операций. Числа
представлены в формате base-2 в различных группах битов в зависимости от приложения (некоторые числа представлены 16 битами, другие 32 битами, а некоторые другие 64 битами).
символам и тексту присваиваются уникальные числовые значения, которые затем преобразуются в формат base-2 в группах по 7 или 8 битов (ASCII) или 32 бита (UTF-8) .
изображений представлены группами крошечных цветных квадратов, называемых пикселями, каждый из которых закодирован в числах, которые в конечном итоге преобразуются в двоичные
И это завершает этот блог, и я надеюсь, что пролил свет на то, почему двоичные числа так важно для вычислений.