Действительные числа
СОДЕРЖАНИЕ.
Введение…………………………………………………………
Глава 1. Зарождение и развитие понятия числа………………………………3
1.1.Числовые системы и
история их появления…………………………
1.2 История появления дробных чисел………………………………………..6
1.3 Предпосылки зарождения
«действительных чисел»……………………
1.4 Парадоксы………………………………………………………
1.5 Теория предела…………………………………………
Глава 2. Создание теории действительного числа…………………………….15
2.1 Карл Вейерштрасс……………………………………
2.2 Георг Кантор………………………………………………
Глава 3. Действительные числа…………………………………………………21
3.1 Бесконечные десятичные дроби…………………………………………….21
3.2 Определение иррациональности числа……………………………………..23
Заключение……………………………………………………
Список литературы…………………………………………………… 26
26
Введение.
Темой данной курсовой работы является раскрытие и донесение понятия «Действительные числа», а так же их роль в математическом анализе.
В первой главе рассматриваются вопросы, связанные с понятием «Числа», его историей и путями развития.
Понятия числа являются первичным и основным в математике. Это понятие прошло длительный путь исторического развития.
Множество натуральных чисел появилось в связи со счетом предметов. Затем под влиянием потребностей практики и развития самой математики были введены целые числа и рациональные числа где.
Для однозначности записи рационального числа будем считать, что дробь не сократима, если не будет делаться оговорки на этот счет.
Вторая и третья главы реферата посвящены теории действительных чисел и математических моделей их применения.
Действительные числа. Приближение
действительных чисел конечными десятичными
дробями.
Вещественное, или действительное число – математическая абстракция, возникшая из потребности человека в измерении геометрических и физических величин окружающего материального мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений [2, стр. 28] . Если «Натуральные числа» возникли в процессе счета, «Рациональные числа» возникли – из потребности оперировать частями целого, то «Вещественные числа» – предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.
Глава 1. Зарождение и развитие понятия числа
В основе
математики лежит понятие числа, одно
из самых ранних и самых абстрактных. Оно
возникло как обобщение счета отдельных
предметов. Счет присущ не только человеку,
но и, в некоторой форме, и животным, например
кошке, которая чувствует наличие при
себе всех своих котят.
Наиболее ранняя форма счета носит конкретно-чувственный характер. Такой счет можно обнаружить у первобытных людей и у животных. Однако нельзя с уверенностью сказать, что только человек способен к абстрактному счету. Есть данные о способности приматов к символизации счета «Приматы способны распознавать и обобщать признак «число элементов», устанавливать соответствие между этим отвлеченным признаком и ранее нейтральными для них стимулами — арабскими цифрами. Оперируя цифрами как символами, они способны ранжировать множества и упорядочивать их по признаку «число», а также совершать число действий, соответствующее цифре. Наконец, они способны к выполнению операций, изоморфных сложению, но этот вопрос требует более точных исследований.»[12]. Там же отмечается высокая способность к символизации и обобщении по признаку «количества» у врановых.
Переход
от «чувственного счета» к абстрактному
осуществляется при помощи взаимооднозначного
соответствия между двумя множествами,
одно из которых позже принимается как
бы за эталон.

1.1. Числовые системы и история их появления
Современная десятичная система появилась в результате развития древних систем счисления. К системам счисления предшествующим десятичной относятся:
Иероглифические непозиционные системы. К ней относится Римская система. В ней числа формируется из набора узловых чисел обозначенных иероглифами. Число образуется из этого набора путем дописывания справа или слева узлового числа других узловых чисел. Значения числа вычисляется по аддитивному или субстрактивному принципу.
Алфавитные системы счисления. Здесь числа записываются при помощи букв. Чтобы отличить буквы от чисел, каждой букве приписывается отличительный признак. Буквы используемые для записи чисел берутся в группы по 9 штук. Для записи единиц десятков и сотен используются разные группы букв, что существенно осложняет ее использование.
Почти
одновременно со счетом зарождаются математические
операции сложения и вычитания(когда уменьшаемое
больше вычитаемого).
Однако
даже в математике Древней Греции не было
единого представления о том, что такое
число. Так в школе Пифагора и Платона
считали единицу не числом, а «эмбрионом
числа». Стоит отметить, что мифологическое
сознание древнегреческого общества еще
не до конца воспринимало математические
и философские абстракции. «Наименее доступны
пониманию широких кругов были именно
числа, эти наиболее абстрактные элементы
науки того времени»[7, стр. 83]. По этим и
другим причинам математика, ее методы
и результаты выглядели мистически. Наиболее
развитым и философски обоснованным мистическим
взглядом на числа были пифагорейство
и неопифагорейство. Упрощая, можно сказать,
что пифагореизм в основе гармонии мира
видел число, для пифагореизма все числа
имели мистический смысл. Подобные взгляды
можно встретить и сегодня.
Однако следует признать, что проникновение
в философию понятий математики чаще всего
было плодотворным. В качестве примера
можно привести категорию «Количество»
в философии Канта и в диалектической
логике, а также парадоксы теории множеств.
«Наименее доступны
пониманию широких кругов были именно
числа, эти наиболее абстрактные элементы
науки того времени»[7, стр. 83]. По этим и
другим причинам математика, ее методы
и результаты выглядели мистически. Наиболее
развитым и философски обоснованным мистическим
взглядом на числа были пифагорейство
и неопифагорейство. Упрощая, можно сказать,
что пифагореизм в основе гармонии мира
видел число, для пифагореизма все числа
имели мистический смысл. Подобные взгляды
можно встретить и сегодня.
Однако следует признать, что проникновение
в философию понятий математики чаще всего
было плодотворным. В качестве примера
можно привести категорию «Количество»
в философии Канта и в диалектической
логике, а также парадоксы теории множеств.
Первоначально понятие
нуля возникло в качестве обозначения
нулевого разряда в записи чисел. Первое
достоверное использование нуля обнаружено
в Индии и относится к IX веку. Однако точное
происхождение цифры ноль в позиционных
системах не известно.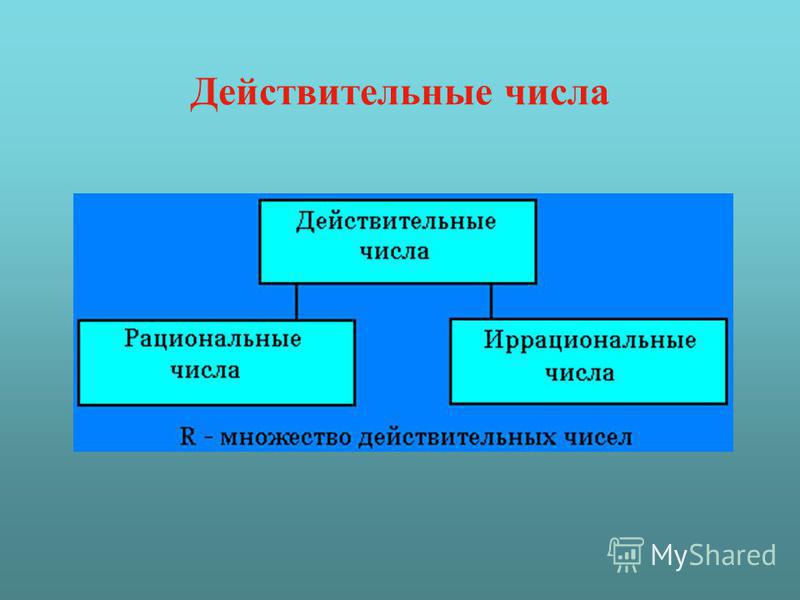
Также в индийской математике было наиболее отчетливое представление об отрицательных числах. «Индийские математики, начиная с Брахмагунты(VII в.н.э.), систематически пользовались отрицательными числами и трактовали положительное число как имущество, а отрицательное как долг»[10, стр. 190], хотя мы не можем утверждать, что отрицательные числа впервые появились в Индии. Было установлено, что квадрат отрицательного числа — число положительное, также ставились вопросы о наличии квадратного корня из отрицательного числа. Действиям с отрицательными числами посвящена целая глава в произведении Бхаскары «Виджаганита».
Менее ясные представления
об отрицательных числах были и у китайцев.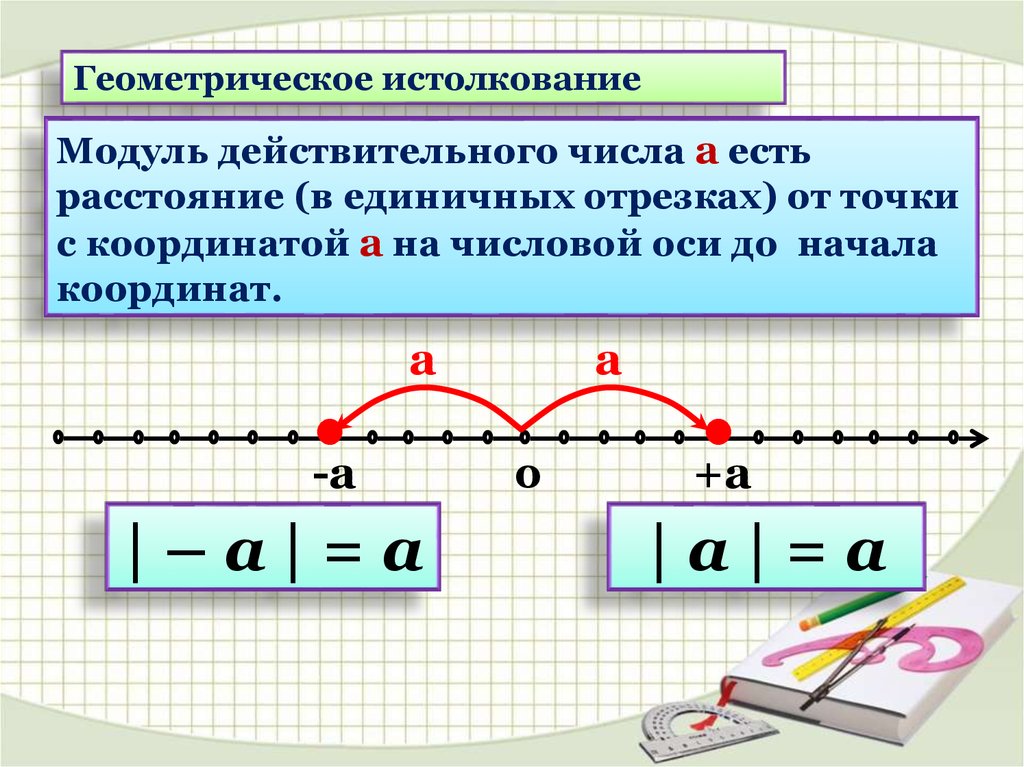 Их появление было связано с задачами,
которые сегодня называются системы линейных
уравнений. «Так как все вычисления, в
том числе и преобразования матрицы, производились
на счетной доске, то для обозначения отрицательных
чисел применялись счетные палочки другого
цвета или формы, а в случае записи применялись
иероглифы разных цветов»[11, стр.84]. Юшкевич
высказывает предположение о том, что
представление об отрицательных числах
имел Диофант [10, стр. 145].
Их появление было связано с задачами,
которые сегодня называются системы линейных
уравнений. «Так как все вычисления, в
том числе и преобразования матрицы, производились
на счетной доске, то для обозначения отрицательных
чисел применялись счетные палочки другого
цвета или формы, а в случае записи применялись
иероглифы разных цветов»[11, стр.84]. Юшкевич
высказывает предположение о том, что
представление об отрицательных числах
имел Диофант [10, стр. 145].
Интерпретация отрицательного
числа как «долга» у индусов переняли
арабы, использование отрицательных чисел
встречается в работах арабского математика
Абу-л-Вафы. Считается, что термин долг
был заимствован математиком Средневековья
Леонардо Пизанским(ок. 1170-после 1250, известен
как Фибоначчи) у арабов. Кроме «долга»
существовал термин «меньше, чем ничто».
Зачатки геометрической интерпретации
отрицательных чисел появляется в работе
М. Штифеля «Полная арифметика», но только
после работ Ферма и Декарта отношение
к отрицательным числам кардинально изменилось. Применение отрицательных чисел и нуля
сыграло важную роль в математике, позволило
обобщить многие задачи, упростить некоторые
вычисления и формализовать многие алгоритмы.
Применение отрицательных чисел и нуля
сыграло важную роль в математике, позволило
обобщить многие задачи, упростить некоторые
вычисления и формализовать многие алгоритмы.
1.2 История появления дробных чисел
Как было отмечено ранее, дроби
появились намного раньше чем целые числа
() и даже раньше чем операция деления.
Они возникли из потребности делить целое
на части, а также выражать величину через
ее части. Дроби вида называемые долями
известны человечеству со времен зарождения
математического знания. Так египтяне
имели обозначения для дробей вида (единичные),
а также для , однако если им встречались
дроби другого вида, они раскладывали
их на сумму единичных дробей. Единичные
дроби использовались на ранних этапах
греками и шумерами. Дроби общего вида
появляются в Греции, хотя изначально
не принимаются как числа. Греки впервые
построили, по нашим понятиям группу положительных
рациональных чисел. «Только в Греции
начали оперировать с дробями вида , причем
умели производить с ними все действия
арифметики с тем ограничением, что вычитать
можно было из большего меньшее»[10, стр. 71].
71].
Дроби также были издавна известны в Индии, упоминания о таких дробях как относятся к середине II тысячелетия до н.э. Причем индийцы записывали их способом, напоминающий современный: числитель над знаменателем, но без разделительной черты. Также указывались правила обращения с такими объектами, аналогичные современным правилам обращения с дробями.
Несколько слов стоит сказать
о происхождении десятичных дробей. Прообразом
для десятичных дробей послужили шестидесятиричные
дроби, используемые вавилонянами. Она
напоминала современный способ записи
дробей тем, что позволяла записывать
целю и дробную часть однотипно, что значительно
упрощало вычисления. Постепенно, возникают
догадки,что это удобство не связано с
какими-то особенными свойствами число
60. «Зреет мысль о том, что в основу системы
таких дробей может быть положено и другое
число…Понимание этой мысли можно видеть
уже в учебнике арифметики середины XII
в., приписываемом Иоанну Севильскому. Иордан Немораррий(XIII в.) дает даже специальное
название таким систематическим дробям,
аналогичным шестидесятеричным»[6, стр.
240]. Идея десятичных дробей использовалась
некоторыми математиками, но до XIV века
строгого их построения не было. В середине
XIV в. французский математик Бонфис сделал
попытку развить идею десятичного числа.
Однако его работа носила эскизный характер
и не была опубликована.
Иордан Немораррий(XIII в.) дает даже специальное
название таким систематическим дробям,
аналогичным шестидесятеричным»[6, стр.
240]. Идея десятичных дробей использовалась
некоторыми математиками, но до XIV века
строгого их построения не было. В середине
XIV в. французский математик Бонфис сделал
попытку развить идею десятичного числа.
Однако его работа носила эскизный характер
и не была опубликована.
В первой половине XV теорию десятичного числа построил самаркандский математик Джемшид Гиясэддином ал-Каши. Он описал десятичную записи числа и описал правила обращения с десятичными дробями. Однако работы ал-Каши оставались неизвестными вплоть до середины XX века.
В Европе десятичные дроби появились
благодаря инженеру Симону Стевину(1548-1620).
Он объединил отдельные идеи и представления
о десятичных дробях и пламенно их пропагандировал.
Большой интерес матетиков вызвали периодические
дроби. Они были впервые обнаружены арабским
матетиком ал-Марадини в XV в.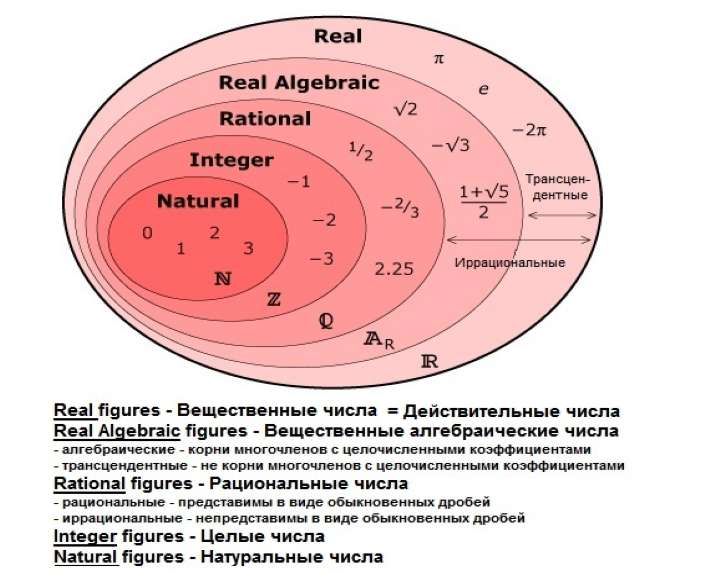 В Европе вопрос
о периодических дробях был серьезно рассмотрен
Валлисом в 1676 в трактате по алгебре. Вопросами
периодических дробей занимались также
Лейбниц, Ламберт, Эйлер, Бернулли, Гаусс
и др.
В Европе вопрос
о периодических дробях был серьезно рассмотрен
Валлисом в 1676 в трактате по алгебре. Вопросами
периодических дробей занимались также
Лейбниц, Ламберт, Эйлер, Бернулли, Гаусс
и др.
1.3 Предпосылки зарождения «действительных чисел»
Как видно из предыдущего исторического
экскурса, твердого понимания что такое
число долгое время не было. С точки зрения
древних греков, числом было только натуральное
число большее единицы. Несколько более
прогрессивная система счисления была
у вавлонян, использущих шестидесятиричные
дроби. Вавилоняне знали теорему Пифагора
и сталкивались с проблемой извлечения
корней из чисел не имеющих точного квадрата.
Однако, нет данных о том, рассматривали
ли они этот вопрос теоретически. «Обладание
подобной [шестидесятиричной] системой
и вытекающая отсюда уверенность в числовых
расчетах неизбежно приводили к «наивному»
понятию действительного числа, почти
совпадающему с тем, которое в наши дни
можно встретить в элементарных учебниках
математики (связанное с десятичной системой
счисления) или у физиков и инженеров. Это понятие не поддается точному определению,
но его можно выразить, сказав, что число
рассматривается как определенное благодаря
возможности получать его приближенные
значения и вводить их в вычисления.»[2,
стр. 146].
Это понятие не поддается точному определению,
но его можно выразить, сказав, что число
рассматривается как определенное благодаря
возможности получать его приближенные
значения и вводить их в вычисления.»[2,
стр. 146].
3.5. Действительные числа
В математике существуют различные построения теории действительного числа:
– по Дедекинду (построение действительного числа с помощью сечений на множестве рациональных чисел),
– по Вейерштрассу (представление действительного числа как бесконечного десятичного ряда),
– по Кантору (построение действительного числа с помощью фундаментальных последовательностей рациональных чисел)…
Но эти построения весьма сложны (не случайно в математике они оформились во второй половине 19 века).
Понятие «действительное
число» (как и понятие «бесконечная
десятичная дробь»), основные положения
теории действительного числа вполне
доступны учащимся 7 класса. В настоящее
время существует тенденция более раннего
изучения действительных чисел, что
ускоряет создание цельной системы
знаний учащихся о числе, облегчает
потребности практики вычислений,
позволяет строже изложить некоторые
вопросы фундаментальной теории…
В настоящее
время существует тенденция более раннего
изучения действительных чисел, что
ускоряет создание цельной системы
знаний учащихся о числе, облегчает
потребности практики вычислений,
позволяет строже изложить некоторые
вопросы фундаментальной теории…
Понятие «иррациональное число» появляется в учебниках 8 класса.
Мотивация введения действительных чисел опирается на внутренние потребности математики, а не на практику. Учащиеся убеждаются в необходимости введения новых чисел при решении следующих задач:
– Решить уравнение: х2 = 2.
– Найти отношение длины дуги окружности к ее диаметру.
– Найти сторону квадрата, если его площадь 3 см2.
– Решить графически уравнение: х2 = 3.
– К множеству каких чисел относятся числа 2, 56565…; 7,23233233…; 0, 123123412345…?
Определение
иррационального числа дается через
отрицание.
Пример: Алгебра – 8(С.А. Теляковский)
Доказывается, что «среди рациональных чисел нет такого числа, квадрат которого равен 2».
Вводится понятие «действительное число»: «Если к положительным бесконечным десятичным дробям присоединить противоположные им числа и нуль, то получим множество чисел, которые называют действительными числами».
Дается определение иррациональных чисел: «Каждую бесконечную десятичную периодическую дробь можно записать в виде отношения m /n, где m – целое число, n – натуральное число. Бесконечные десятичные непериодические дроби представляют числа, не являющиеся рациональными. Их называют иррациональными числами (приставка «ир» означает отрицание). Иррациональные числа нельзя представить в виде отношения m /n. Таким образом, множество действительных чисел состоит из рациональных и иррациональных чисел.
 ».
».Приводятся примеры иррациональных чисел.
Вводятся «действия» над числами. В школьном курсе действия с иррациональными числами сводятся к операциям с их рациональным приближениями по недостатку и по избытку5.
Остановимся более подробно на методике изучения иррациональных чисел.
Рациональные и иррациональные числа
В 5 – 6 классах учащиеся познакомились с обыкновенными дробями. Перед изучением иррациональных чисел целесообразно обобщить эти знания и на новом уровне рассмотреть множество рациональных чисел Q.
В множестве натуральных чисел N операция деления имеет ограниченный характер: если а и в натуральные числа, то не всегда найдется натуральное число х такое, чтобы
ах = в (приведите примеры). Другими словами, в
том случае, когда в не делится нацело на а,
уравнение ах
= в неразрешимо. Чтобы устранить это несовершенство,
вводятся дроби, записываемые в виде
отношения m/n,
где m,n – натуральные числа. При этом число m называют
числителем, а число n знаменателем
дроби m/n.
Вспомним правила действий с дробями:
Чтобы устранить это несовершенство,
вводятся дроби, записываемые в виде
отношения m/n,
где m,n – натуральные числа. При этом число m называют
числителем, а число n знаменателем
дроби m/n.
Вспомним правила действий с дробями:
(1)
Правило позволяет «сокращать» дробь на общий для числителя множитель. Например,. Как видим, равные дроби могут очень различаться по внешнему виду. (Убедитесь, что дробии- равные дроби.) Натуральное числоn можно считать частным случаем дроби, отождествляя его с .
Построенное
расширение натурального ряда обозначим
через Q+ – этоположительные
рациональные числа (от латинского ratio
– отношение). Умножение в Q+ ассоциативно и коммутативно, уравнения
вида ах = в,
где а и в – любые числа из Q+,
разрешимы (решением будет х =
).
Следовательно, (Q+,. )
–коммутативная группа, это –
мультипликативная группа положительных
рациональных чисел (от латинского
multiplication
– умножение). Деление в ней осуществляется
неограниченно.
)
–коммутативная группа, это –
мультипликативная группа положительных
рациональных чисел (от латинского
multiplication
– умножение). Деление в ней осуществляется
неограниченно.
Если ноль и отрицательные числа сначала появились как математические абстракции и лишь впоследствии нашли им содержательное толкование, то дроби были известны с древнейших времен:
– Распределение некоторого общего достояния на индивидуальные доли было повседневной практикой (см., например, в библейской книге Чисел стихи 25 – 46 главы 31).
– Другим видом деятельности, приводившим к дробям, были измерения: если, например, стандарт длины не укладывался между двумя данными точками целое число раз, приходилось прибегать к более мелким его частям6
Присоединяя к
положительным рациональным числам
противоположные им величины и ноль,
получаем все множество рациональных
чисел Q.
Оно состоит, таким образом, из нуля,
положительных и отрицательных целых
чисел, положительных и отрицательных
дробей. Сложение, умножение и деление
в Q
выполняются по формуле (1), вычитание
осуществляется по правилу.
Сложение, умножение и деление
в Q
выполняются по формуле (1), вычитание
осуществляется по правилу.
(Выполните действия с рациональными числами: ,, -…. )
В множестве Q рациональных чисел все четыре арифметических операции выполняются беспрепятственно за одним досадным исключением: нельзя делить на ноль (один из доводов в пользу того, что 0 –«ненастоящее» число). Следовательно, в этом множестве разрешимы уравнения вида а + х = в при любых а, в и уравнения вида ах = в при всех а0 и при всехв. Таким образом, множество Q является кольцом, а его ненулевые элементы образуют коммутативную группу по умножению. Кольца, обладающие этим свойством, называются полями.
Мы построили поле рациональных чисел (Q+,.). Оно расширяет кольцо целых чисел (Z,+,.), позволяя неограниченно выполнять операцию деления (кроме деления на ноль).
Поле рациональных
чисел бесконечно, но существуют и
конечные поля. Таковым будет, например,
любое кольцо Zp остатков от деления натуральных чисел
на простое число p.
Имея перед собой таблицу умножения поля
Z5,
легко решить в нем уравнения
Таковым будет, например,
любое кольцо Zp остатков от деления натуральных чисел
на простое число p.
Имея перед собой таблицу умножения поля
Z5,
легко решить в нем уравнения
2х = 1, 3х = 4, 4х= 5. А вот в кольце Z6 эти уравнения не имеют корней.
В поле рациональных чисел разрешимо любое уравнение ах + в = 0,решением будет
х = – . Поле рациональных чисел всюду плотно, так как между любыми двумя рациональными числамиr1и r2можно указать рациональное число (r1+ r2):2 и даже бесконечное множество рациональных чисел.
Наглядное
представление о рациональных числах
дает координатная ось. На некоторой
прямой линии выбирается точка 0 – начало
отсчета, указывается единица масштаба,
направление. Если дано положительное
рациональное число
,то
единица масштаба делится на n равных частей и вправо от нуля эта доля
откладывается m раз. Полученная точка и есть изображение
числа
.
Если число отрицательное – откладывание
производят влево от нуля. Например,
Полученная точка и есть изображение
числа
.
Если число отрицательное – откладывание
производят влево от нуля. Например,
-2/3 5/3
—–!–.—.—!–.—.–!–.—.–!———>
-1 0 1 2
Построив числовое множество Q (поле рациональных чисел), в котором разрешимо любое линейное алгебраическое уравнение ах + в =о, естественно перейти к исследованию квадратных уравнений ах2 + вх + с = 0. В простейшем случае х2 – 1 = 0, т.е. х2 = 1, имеет два решения (корня): х1 =1, х2 = -1. Однако уже следующий напрашивающийся шаг заводит нас в тупик.
Теорема 1. Уравнение х2 = 2 не имеет решений в поле рациональных
чисел.
Теорема 2. Диагональ квадрата несоизмерима с его стороной.
Необходимо самостоятельно познакомиться с доказательствами этих теорем, приводимыми авторами школьных учебников.
Т
Рис. 1.
еоремы 1 и 2 при всем внешнем несходстве
представляют собой лишь разные
интерпретации одного и того же
математического факта: одна на языке
алгебры, другая – в геометрических
терминах. (В математике это обычное
явление.) Обратимся теперь к координатной
оси. Если взять на ней точки, соответствующие
рациональным числама и в (пусть а < в), то
середина отрезка
выражается
числомс = (а + в): 2.
Это тоже рациональное число, так что
между любыми двумя рациональными числами
лежит еще одно. Деля пополам отрезки
и,
получим еще два рациональных числа
междуа и в и т.д. Поскольку этот процесс деления
пополам (дихотомия) можно продолжать
неограниченно, приходим к выводу, что
между произвольными рациональными
числами а и в находится
бесконечно много других рациональных
чисел. Представив себе все это, мы могли
бы прийти к заключению, что рациональные
числа заполняют сплошь числовую ось.
Но нет – если от точки 0 отложить
вправо диагональ единичного квадрата,
то согласно теореме 2 другой конец
диагонали не попадет ни в какую
рациональную точку. (См. рис. 1) Аналогично
строится точка.
Вот эти «дыры» на числовой прямой и были
интерпретированы как иррациональные
числа. (В словаре: «иррациональный – не
постигаемый разумом, такой, который не
может быть выражен в логических понятиях».
Повседневный математический смысл
проще: иррациональное число – это число,
не являющееся рациональным.)
Представив себе все это, мы могли
бы прийти к заключению, что рациональные
числа заполняют сплошь числовую ось.
Но нет – если от точки 0 отложить
вправо диагональ единичного квадрата,
то согласно теореме 2 другой конец
диагонали не попадет ни в какую
рациональную точку. (См. рис. 1) Аналогично
строится точка.
Вот эти «дыры» на числовой прямой и были
интерпретированы как иррациональные
числа. (В словаре: «иррациональный – не
постигаемый разумом, такой, который не
может быть выражен в логических понятиях».
Повседневный математический смысл
проще: иррациональное число – это число,
не являющееся рациональным.)
Иррациональных чисел тоже бесконечно много: если – иррациональное, аа – рациональное число, то сумма а и произведениеа (при а) тоже будет иррациональное число (иначе, например,оказалось бы рациональным).
Первый конкретный
пример иррационального числа – это
длина диагонали единичного квадрата,
т.е. положительный корень уравнения х2 = 2, обозначаемый
через. Рассуждения, проведенные в доказательстве
теоремы 1, могут быть дословно повторены
и для уравнений х2 = 3, х3 =5, что доказывает иррациональность
чисел
.
Рассуждения, проведенные в доказательстве
теоремы 1, могут быть дословно повторены
и для уравнений х2 = 3, х3 =5, что доказывает иррациональность
чисел
.
Изобразив действительные числа на координатной прямой, мы получим, что каждой точке координатной прямой соответствует действительное число (прямая без «дырок») и каждому действительному числу отвечает точка на прямой. Координатная прямая, на которой изображено множество действительных чисел, называется числовой прямой, поле действительных чисел стало непрерывным, то есть отношения и алгебраические операции с действительными числами сводятся к одноименным отношениям и операциям с их рациональными приближениями по недостатку и избытку.
После введения
действительных чисел появилась
возможность дать общую запись для
решений любого квадратного уравнения ах2 + вх + с = 0 с
использованием радикала (знака извлечения
корня), а именно х =
или х =.
Если величина D = в2– 4ас (дискриминант) положительна, уравнение имеет два корня, рациональных или иррациональных в зависимости от того, является дискриминант полным квадратом или нет.
Золотым сечением называется деление отрезка длины 1 на две части, большая из которых х является средней пропорциональной величиной между всем отрезком и его меньшей частью 1 – х, то есть принцип золотого сечения (название ввел Леонардо да Винчи в конце 15 века) составлял, в частности, теоретическую основу архитектурных композиций классической древности и эпохи Возрождения. Для нахождения х необходимо решить квадратное уравнение х2 + х – 1 = 0, откуда х = (отрицательный корень отбрасываем). Для нас иррациональность этого числа очевидна, в древности же она была установлена весьма сложным путем, а сам факт её существования произвел удручающее впечатление.
Пример квадратного
уравнения возбудил надежду на то, что
алгебраические уравнения и всех других,
более высоких степеней, окажутся
разрешимыми в радикалах, то есть корни
можно будет выразить с помощью
арифметических операций и извлечения
корней. В середине 16 века итальянские
математики Тарталья, Кардано и Феррари
нашли подобные формулы для кубического
уравнения четвертой степени. (Происходило
это в атмосфере ожесточенной полемики
о приоритете, с публичными состязаниями
в решении соответствующих задач,
проклятиями и покаяниями.) В почти три
последующие столетия существенных
продвижений в этом вопросе не было, и
лишь в 1826 году норвежский математик
Нильс Хенрик Абель (1802 – 1829) доказал,
что для каждого натурального числа n>4
существует алгебраическое уравнение n степени с
целыми коэффициентам, неразрешимыми в
радикалах (например, х5 – 4х – 2 = 0). Окончательное решение
проблемы, занимавшей умы лучших
математиков, принадлежит французу
Эваристу Галуа (1811 – 1832). Он ввел понятие
группы и показал, что каждому алгебраическому
уравнению соответствует некоторая
группа, по свойствам которой и можно
судить, разрешимо или нет уравнение в
радикалах.
В середине 16 века итальянские
математики Тарталья, Кардано и Феррари
нашли подобные формулы для кубического
уравнения четвертой степени. (Происходило
это в атмосфере ожесточенной полемики
о приоритете, с публичными состязаниями
в решении соответствующих задач,
проклятиями и покаяниями.) В почти три
последующие столетия существенных
продвижений в этом вопросе не было, и
лишь в 1826 году норвежский математик
Нильс Хенрик Абель (1802 – 1829) доказал,
что для каждого натурального числа n>4
существует алгебраическое уравнение n степени с
целыми коэффициентам, неразрешимыми в
радикалах (например, х5 – 4х – 2 = 0). Окончательное решение
проблемы, занимавшей умы лучших
математиков, принадлежит французу
Эваристу Галуа (1811 – 1832). Он ввел понятие
группы и показал, что каждому алгебраическому
уравнению соответствует некоторая
группа, по свойствам которой и можно
судить, разрешимо или нет уравнение в
радикалах.
Н. Абель и Э. Галуа
ушли из жизни совсем молодыми (первый
скончался от туберкулеза, второй был
убит на дуэли), их идеи не были должным
образом восприняты современниками, но
впоследствии оказали огромное влияние
на развитие важнейших разделов математики. Имена этих выдающихся ученых носят
многие математические объекты, например,
абелевыми называются коммутативные
группы, а конечные поля – полями Галуа.
Имена этих выдающихся ученых носят
многие математические объекты, например,
абелевыми называются коммутативные
группы, а конечные поля – полями Галуа.
Задания к лекции
Путь построения числового множества в науке отличается от соответствующего пути, принятого в школьной математике. Укажите эти отличия, вскройте их причины.
Проанализируйте методический подход к введению модуля числа, данный в учебниках математики Н.Я. Виленкина. Сравните этот подход с другими, встречающимися в методической и учебной литературе.
3. Познакомьтесь с операциями на множестве Rи разработайте беседу для учащихся 9 класса на тему «Отношения и операции на множестве действительных чисел».
4.Подберите материал и наметьте план беседы для учащихся 9 класса о развитии понятия числа.
Указание1. Большую роль в беседе
следует отвести историческим сведениям
о развитии понятия числа. 2. Постарайтесь
аргументированно обосновать необходимость
расширения числовых множеств, показывая
при этом потребности практики и науки.
2. Постарайтесь
аргументированно обосновать необходимость
расширения числовых множеств, показывая
при этом потребности практики и науки.
5. Сделайте обзор литературы, которая может быть использована а) учителем для проведения элективного курса по изучению комплексных чисел, б) учеником для самостоятельного чтения при изучении комплексных чисел.
Вещественные и комплексные числа – 840 слов
Содержание
- Введение
- Вещественные числа
- Комплексные числа
- Ссылки
Чтобы лучше понять значения, придаваемые действительным и комплексным числам, в этом эссе мы сосредоточимся на кратких, но подробных сравнениях между двумя классами чисел в математике. Кроме того, в эссе будут использованы некоторые графические представления теоретических объяснений для улучшения понимания.
Кроме того, в эссе будут использованы некоторые графические представления теоретических объяснений для улучшения понимания.
Вещественные числа
Вещественное число — это любое количественное представление в континууме (Denlinger, 2010, стр. 3). Лучшей демонстрацией действительных чисел является одномерная числовая прямая. К действительным числам относятся целые числа, дроби, которые являются рациональными числами, но не целыми числами, десятичные дроби, квадратные корни и некоторые алгебраические выражения. На рисунке ниже показаны некоторые распространенные действительные числа.
Некоторые из самых основных свойств действительных чисел включают рациональность и иррациональность, а также алгебраичность или трансцендентность. Рациональные числа также могут быть положительными, отрицательными или нулевыми. Важно отметить, что действительные числа в основном измеряют непрерывные величины. Одним из отличительных свойств действительных чисел являются биномы действительных чисел. С помощью биномиальной теоремы можно доказать, что степень «r» является действительным числом, используя выражения, подобные приведенному ниже.
С помощью биномиальной теоремы можно доказать, что степень «r» является действительным числом, используя выражения, подобные приведенному ниже.
f (х) = (1+х) R = A 0 + A 1 x + A 2 x 2 + A 3 x 3 … .A K x K ……
Completry Numbers
8 K
……Completry Numbers
8 K
……Комплекс
8 K
……Комплексы
K …. Действительные числа составляют важную часть комплексных чисел. Согласно Касане (2005, стр. 2) комплексные числа представляют собой пары упорядоченных действительных чисел. Проще говоря, комплексные числа состоят из действительного числа и мнимого числа, для завершения которого требуется математическое решение. В то время как действительные числа прямолинейны, комплексные системы счисления чаще всего представляют собой выражение формы. Например, a+bi представляет собой сложное выражение, где «a» и «b» — действительные числа, а «i» представляет собой воображаемую единицу, значение которой поможет решить сложное выражение. Любое число, квадрат которого является действительным числом меньше нуля, является мнимым числом. Квадрат мнимого числа всегда отрицателен. Когда мнимое число, например, «би» прибавляется к действительному числу, получается комплексное число. Поэтому правильно утверждать, что мнимые числа — это ненулевые комплексные числа с нулем в качестве действительной части. Ниже приведены некоторые примеры комплексных чисел.
Любое число, квадрат которого является действительным числом меньше нуля, является мнимым числом. Квадрат мнимого числа всегда отрицателен. Когда мнимое число, например, «би» прибавляется к действительному числу, получается комплексное число. Поэтому правильно утверждать, что мнимые числа — это ненулевые комплексные числа с нулем в качестве действительной части. Ниже приведены некоторые примеры комплексных чисел.
2 + 5 i , 6 +22 i , 12 – i
«i» в комплексных числах недействительны. Определение мнимой единицы выглядит следующим образом:
Затем
Одно из наиболее заметных различий между системами действительных чисел и системами комплексных чисел заключается в сложности комплексного числа, увековеченного его частями.
Одним из наиболее часто используемых выражений в математике является a+bi=z. Это выражение составляет типичное комплексное число. Действительная числовая часть приведенного выше выражения — это «а», которую математики называют действительной частью «z». Другое действительное число «b» является мнимой частью комплексного числа.
Другое действительное число «b» является мнимой частью комплексного числа.
Однако, несмотря на различия, и вещественные, и комплексные числа неразрывно взаимодействуют в математических операциях. В то время как операции с действительными числами кажутся простыми, операции с комплексными числами весьма сложны. Операции, включающие как сложение, так и вычитание действительных и мнимых частей слагаемых, составляют основную процедуру. Следующее выражение иллюстрирует определение сложения операций с комплексными числами.
(a+bi) + (c+di) = (a+c) + (b=d)i
Графическое представление, например, суммы 3 + i и –1 + 2i, ответ которой равен 2 + 3i, будет следующим;
Рисунок 1: Графическое сложение комплексных чисел.Формула умножения комплексных чисел в основном использует квадрат мнимой единицы. Следующее выражение показывает определение умножения комплексных чисел (Касана, 2005, стр. 2).
(a+bi)(c+di) = (ac-bd) + (bc+ad)i. Например,
Результат умножения (3 + 2i) на (4 + 5i) будет следующим:
(3 + 2i)(4 + 5i) = (3 × 4) + (3 × (5i)) + ((2i) × 4) + ((2i) × (5i))
= 12 + 15i + 8i + 10i ²
= 12 + 23i -10 (Обратите внимание, что 10i ² = 10(-1) = -10)
= 2 + 23i
Следовательно, (3 + 2i)(4 + 5i) = 2 +23i.
Следующая графическая иллюстрация умножения комплексных чисел в уравнении (1+i)*(-1+i)=-2
Рисунок 2 Графическая иллюстрация умножения комплексных чисел.Одним из наиболее существенных различий между действительными и комплексными числами является их использование и представление на числовой прямой. В отличие от действительных чисел комплексные системы счисления позволяют расширить одномерную числовую строку. В то время как действительные числа используют обычную числовую прямую, комплексные числа используют двумерную комплексную плоскость, которую иллюстрирует диаграмма Аргана.
Диаграмма Аргана.Короче говоря, любой анализ двух систем счисления обнаружит гораздо больше различий и сходств, источником которых являются операции с числами в двух системах. Следовательно, это был теоретический подход, который дает сравнение только по номинальной стоимости.
Ссылки
Denlinger, C. (2010). Элементы реального анализа . Нью-Йорк: обучение Джонса и Бартлетта.
Нью-Йорк: обучение Джонса и Бартлетта.
Касана, Х.С. (2005). Комплексные переменные: теория и приложения 2-е изд. . Лондон: PHI Learning Pvt.
Это эссе о действительных и комплексных числах было написано и представлено вашим коллегой ученик. Вы можете использовать его для исследовательских и справочных целей, чтобы написать свою собственную статью; однако ты должны цитировать его соответственно.
Запрос на удаление
Если вы являетесь владельцем авторских прав на эту статью и больше не хотите, чтобы ваша работа публиковалась на IvyPanda.
Запросить удаление
Нужен пользовательский Образец эссе , написанный с нуля
профессиональный специально для вас?
801 сертифицированный писатель онлайн
ПОЛУЧИТЬ ПИСЬМЕННУЮ ПОМОЩЬ
Математический обзор операций с вещественными числами
Математический обзор операций с действительными числами https://schooltutoring. com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg
150
150 Дебора Дебора https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g
com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg
150
150 Дебора Дебора https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g
Обзор
Действительные числа включают рациональные и иррациональные числа, целые числа, положительные и отрицательные целые числа, а также число 0. Их можно использовать в таких операциях, как сложение, вычитание, умножения и деления, а также в выражениях с переменными.
Вещественные числа
Вещественные числа включают множество различных типов чисел, которые хорошо знакомы, например, положительные и отрицательные целые числа, расположенные вдоль числовой прямой. Рациональные числа, такие как 3/5, также включены, а также иррациональные числа, такие как π, √7 и √2. Представление бесконечности ∞ не является ни действительным числом, ни мнимыми числами.
Рисунок 1: Содержимое набора действительных чисел.
Сложение действительных чисел
Поскольку действительные числа попадают на числовую прямую, их можно складывать, используя модель числовой прямой. Например, чтобы добавить 3 + 2, перейдите от 0 к 3 в числовой строке, а затем переместите 2 пробела вперед до 5. Аналогичным образом, добавив -2 + -5, перейдите влево в числовой строке на 2 пробела до -2, а затем перейдите осталось еще 5, до -7. Дроби можно складывать, находя наименьший общий знаменатель, а затем складывая их с помощью числовой прямой, потому что дроби — это рациональные числа.
Рисунок 2: Сложение действительных чисел с использованием модели числовой прямой.
Вычитание действительных чисел
Вычитание — это то же самое, что сложение аддитивной обратной величины вычитаемого числа. В символьной форме для любых двух чисел a и b, a – b равнозначно a + (-b). Напомним, что аддитивная инверсия числа является противоположностью этого числа, так что a + (-a) = 0 и b + (-b) = 0. Вычитание также можно продемонстрировать с использованием линейной модели действительных чисел, так что вычитание 7-6 означает, что нужно начать с 0 и пройти 7 делений до 7, а затем перейти на 6 делений влево до 1.
Вычитание также можно продемонстрировать с использованием линейной модели действительных чисел, так что вычитание 7-6 означает, что нужно начать с 0 и пройти 7 делений до 7, а затем перейти на 6 делений влево до 1.
Рисунок 3: Определение вычитания в символьной форме.
Умножение и деление действительных чисел
При умножении чисел следует помнить два важных правила. Произведение двух положительных чисел или двух отрицательных чисел является положительным числом. Произведение положительного числа на отрицательное число есть отрицательное число. Например, 6∙ 2 равно 12 как произведение двух положительных чисел. Точно так же -5 ∙ -6 равно 30 как произведение двух отрицательных чисел. Однако -7 ∙ 3 равно -21, как произведение отрицательного числа и положительного числа, а 4 ∙ -7 равно -28, как произведение положительного числа и отрицательного числа. Правила деления чисел аналогичны. Если оба числа положительны, то и частное будет положительным, если оба числа отрицательны, то и частное положительно.
