Релятивистская механика | это… Что такое Релятивистская механика?
Релятивистская механика — раздел физики, рассматривающий законы механики (законы движения тел и частиц) при скоростях, сравнимых со скоростью света. При скоростях значительно меньших скорости света переходит в классическую (ньютоновскую) механику.
|
Содержание
|
Общие принципы
Релятивистская механика — теория, в которой, в отличие от классической механики, где пространственные координаты и время являются независимыми, при отсутствии голономных связей зависящих от времени, (время является абсолютным, то есть течёт одинаково во всех системах отсчёта) и действуют преобразования Галилея, события происходят в четырёхмерном пространстве, объединяющем физическое трёхмерное пространство и время (пространство Минковского) и действуют преобразования Лоренца.
Основные законы релятивистской механики — релятивистское обобщение второго закона Ньютона и релятивистский закон сохранения энергии-импульса являются следствием такого «смешения» пространственных и временной координат при преобразованиях Лоренца.
Сила определяется как , также известно выражение для релятивистского импульса:
Взяв для определения силы производную по времени от последнего выражения, получим:
где введены обозначения: и .
В результате выражение для силы приобретает вид:
Отсюда видно, что в релятивистской механике в отличие от нерелятивистского случая ускорение не обязательно направлено по силе, в общем случае ускорение имеет также и составляющую, направленную по скорости.
Функция Лагранжа свободной частицы в релятивистской механике
Запишем интеграл действия, исходя из принципа наименьшего действия: , где -положительное число.
Как известно из специальной теории относительности (СТО) , подставляя в интеграл движения, находим: . Но, с другой стороны, интеграл движения, можно выразить через функцию Лагранжа: . Сравнивая последние два выражения, нетрудно понять, что подынтегральные выражения должны быть равны, то есть:
.
Далее, разложим последнее выражение по степеням , получим:
, первый член разложения не зависит от скорости, а значит не вносит никаких изменений в уравнения движения. Тогда, сравнивая с классическим выражением функции Лагранжа: , нетрудно определить константу :
. Таким образом, окончательно получаем вид функции Лагранжа свободной частицы:
.
Рассуждения, приведенные выше, можно рассматривать не только для частицы, но и для произвольного тела, лишь бы его части двигались как одно целое.
Поскольку квадрат 4-вектора импульса является постоянной величиной:
то релятивистская частица может рассматриваться как механическая система с неголономной связью в 4-мерном псевдоевклидовом пространстве[1][2][3].
Источники
- ↑ O. Krupková and J. Musilová, «The relativistic particle as a mechanical system with non-holonomic constraints», J. Phys. A: Math. Gen. 34 (2001) 3859-3876.
- ↑ O. Krupkova, J. Musilova, «The relativistic mechanics in a nonholonomic setting: A unified approach to particles with non-zero mass and massless particles» arXiv:0904.2933.
- ↑ V.E. Tarasov «Relativistic non-Hamiltonian mechanics» Annals of Physics. Vol.325. No.10.(2010) p.2103-2119.
См. также
- Специальная теория относительности
- Теория относительности
- Релятивистски равноускоренное движение
Литература
- Паули В. Теория относительности. М.: Наука, 1991. 328 с.
- Принцип относительности. Сборник работ по специальной теории относительности. М.: Атомиздат, 1973.
- Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 3-е, переработанное. — М.: Физматгиз, 1960. — 512 с. — («Теоретическая физика», том II).
- Уиттекер Э. История теории эфира и электричества. Современные теории 1900—1926. Пер с англ. Москва, Ижевск: ИКИ, 2004. 464с. ISBN 5-93972-304-7 (Глава 2)
Релятивистская механика | это… Что такое Релятивистская механика?
Релятивистская механика — раздел физики, рассматривающий законы механики (законы движения тел и частиц) при скоростях, сравнимых со скоростью света. При скоростях значительно меньших скорости света переходит в классическую (ньютоновскую) механику.
|
Содержание
|
Общие принципы
Релятивистская механика — теория, в которой, в отличие от классической механики, где пространственные координаты и время являются независимыми, при отсутствии голономных связей зависящих от времени, (время является абсолютным, то есть течёт одинаково во всех системах отсчёта) и действуют преобразования Галилея, события происходят в четырёхмерном пространстве, объединяющем физическое трёхмерное пространство и время (пространство Минковского) и действуют преобразования Лоренца.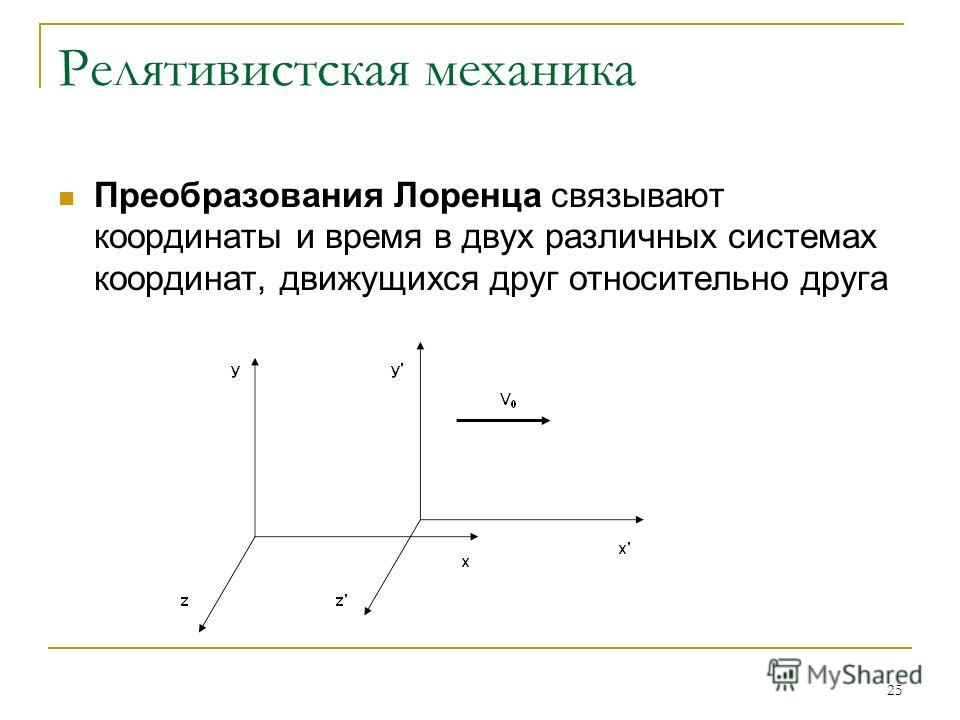
Таким образом, в отличие от классической механики, одновременность событий зависит от выбора системы отсчёта.
Основные законы релятивистской механики — релятивистское обобщение второго закона Ньютона и релятивистский закон сохранения энергии-импульса являются следствием такого «смешения» пространственных и временной координат при преобразованиях Лоренца.
Сила определяется как , также известно выражение для релятивистского импульса:
Взяв для определения силы производную по времени от последнего выражения, получим:
где введены обозначения: и .
В результате выражение для силы приобретает вид:
Отсюда видно, что в релятивистской механике в отличие от нерелятивистского случая ускорение не обязательно направлено по силе, в общем случае ускорение имеет также и составляющую, направленную по скорости.
Функция Лагранжа свободной частицы в релятивистской механике
Запишем интеграл действия, исходя из принципа наименьшего действия: , где -положительное число.
Как известно из специальной теории относительности (СТО) , подставляя в интеграл движения, находим: . Но, с другой стороны, интеграл движения, можно выразить через функцию Лагранжа: . Сравнивая последние два выражения, нетрудно понять, что подынтегральные выражения должны быть равны, то есть:
.
Далее, разложим последнее выражение по степеням , получим:
, первый член разложения не зависит от скорости, а значит не вносит никаких изменений в уравнения движения. Тогда, сравнивая с классическим выражением функции Лагранжа: , нетрудно определить константу :
. Таким образом, окончательно получаем вид функции Лагранжа свободной частицы:
.
Рассуждения, приведенные выше, можно рассматривать не только для частицы, но и для произвольного тела, лишь бы его части двигались как одно целое.
Поскольку квадрат 4-вектора импульса является постоянной величиной:
то релятивистская частица может рассматриваться как механическая система с неголономной связью в 4-мерном псевдоевклидовом пространстве[1][2][3].
Источники
- ↑ O. Krupková and J. Musilová, «The relativistic particle as a mechanical system with non-holonomic constraints», J. Phys. A: Math. Gen. 34 (2001) 3859-3876.
- ↑ O. Krupkova, J. Musilova, «The relativistic mechanics in a nonholonomic setting: A unified approach to particles with non-zero mass and massless particles» arXiv:0904.2933.
- ↑ V.E. Tarasov «Relativistic non-Hamiltonian mechanics» Annals of Physics. Vol.325. No.10.(2010) p.2103-2119.
См. также
- Специальная теория относительности
- Теория относительности
- Релятивистски равноускоренное движение
Литература
- Паули В. Теория относительности. М.: Наука, 1991. 328 с.
- Принцип относительности. Сборник работ по специальной теории относительности. М.: Атомиздат, 1973.
- Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 3-е, переработанное. — М.: Физматгиз, 1960. — 512 с. — («Теоретическая физика», том II).
- Уиттекер Э. История теории эфира и электричества. Современные теории 1900—1926. Пер с англ. Москва, Ижевск: ИКИ, 2004. 464с. ISBN 5-93972-304-7 (Глава 2)
Relativistic Mechanics by Ron Kurtus
SfC Home > Physics > Mechanics >
Рона Куртуса (обновлено 9 января 2023 г.)
Релятивистская механика — также известная как Relativity — касается изучения движения объектов. и задействованные силы. Он разделен на две области: Специальная теория относительности и Общая теория относительности 9.0013 .
Объекты имеют размеры от нормальных до очень больших и движутся со скоростью, близкой к скорости света. Согласно Теории Относительности, при таких высоких скоростях меняются физические законы.
Альберт Эйнштейн был лидером в разработке теорий относительности.
У вас могут возникнуть следующие вопросы:
- Что такое относительность?
- Что такое специальная теория относительности?
- Что такое Общая теория относительности?
Этот урок ответит на эти вопросы.
Полезный инструмент: Преобразование единиц
Относительность
Основная идея относительности заключается в том, что движение всегда относительно некоторой системы отсчета.
Например, когда вы идете по тротуару, вы двигаетесь относительно неподвижной земли, которая является системой отсчета. Однако, когда вы не идете и видите проезжающую мимо машину, она движется относительно вас. Точно так же человек, сидящий в машине, также движется относительно вас, но остается неподвижным относительно системы отсчета автомобиля.
Основная предпосылка изучения теории относительности заключается в том, что не существует фиксированной системы отсчета, относительно которой все движется. Все в пространстве движется относительно других объектов, и в пространстве нет фиксированной точки отсчета.
Это вызывает вопросы о том, меняются ли законы физики и какова скорость света относительно движущихся объектов. Это изучается в специальной теории относительности .
Специальная теория относительности
Специальная теория относительности касается систем отсчета, которые не испытывают никакого ускорения. Они называются инерциальными системами отсчета.
Первый постулат
Первый постулат теории утверждает, что законы физики имеют одинаковую форму во всех инерциальных системах отсчета. Другими словами, результат эксперимента, проведенного в автобусе, движущемся с постоянной скоростью, будет таким же, как и в неподвижном транспортном средстве.
Второй постулат
Второй постулат утверждает, что свет распространяется через пустое пространство с постоянной скоростью, не зависящей от скорости источника или наблюдателя.
Результаты второго постулата заключаются в том, что время замедляется при высоких скоростях, а длины сокращаются, когда скорость объекта приближается к скорости света.
Другой фактор заключается в том, что когда объект приближается к скорости света, его масса приближается к бесконечной массе.
Общая теория относительности
Общая теория относительности касается того, что произойдет, если объекты или системы отсчета будут ускорены.
Одна из концепций состоит в том, что все системы отсчета, подвергающиеся одинаковому ускорению, эквивалентны друг другу.
Ускорение и гравитация
Теория гласит, что локальные наблюдения в ускоряющейся системе отсчета нельзя отличить от наблюдений, сделанных в классическом или ньютоновском гравитационном поле. Одним из результатов является то, что наблюдатели не могут экспериментально определить, ускоряются ли они или находятся в гравитационном поле.
Кривизна пространства
Общая теория относительности утверждает, что массивные объекты вызывают искривление пространства и времени (пространство-время). Таким образом, гравитация является следствием искривления пространства-времени.
Это понятие отличается от определения гравитации как силы, действующей на расстоянии.
Резюме
Альберт Эйнштейн был лидером в разработке релятивистской механики или теории относительности, которая касается изучения движения объектов и задействованные силы.
Специальная теория относительности касается законов физики, когда система отсчета не ускоряется. В нем также говорится, что скорость света не зависит от скорости источника или наблюдателя.
Общая теория относительности утверждает, что гравитацию нельзя отличить от ускорения и что большие массы искривляют пространство, вызывая гравитационную силу.
Используйте свое воображение для решения задач
Ресурсы и ссылки
Ron Kurtus’ Credentials
Websites
Relativistic mechanics – Wikipedia
Mechanics outline – HyperPhysics
Einstein’s Theory of Special Relativity – Space.
com
Einstein’s Theory of General Relativity – Space.com
Ресурсы по физике
Книги
(Примечание: Школа чемпионов может получать комиссионные за покупку книг)
Книги с самым высоким рейтингом по физике механики
Поделитесь этой страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
mechanics_relativistic.htm .
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Где ты сейчас?
Школа чемпионов
Темы по физике
Релятивистская механика
17.
1: Введение в релятивистскую механику
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 9663
- Дуглас Клайн
- Университет Рочестера
Ньютоновская механика включает в себя ньютоновскую концепцию полного разделения пространства и времени. Эта теория господствовала с самого начала, в 1687 году, до ноября 1905 года, когда Эйнштейн разработал специальную теорию относительности. Релятивистская механика подрывает ньютоновские концепции абсолютности времени, присущие ньютоновской формулировке, а также переработанные в лагранжевой и гамильтоновой формулировках классической механики. Релятивистская механика оказала глубокое влияние на физику и философию науки двадцатого века.
Классическая механика — это приближение релятивистской механики, справедливое для скоростей, намного меньших скорости света в вакууме. Термин «относительность» относится к тому факту, что физические измерения всегда производятся относительно некоторой выбранной системы отсчета. Наивно можно подумать, что преобразование между различными системами отсчета тривиально и содержит мало физических данных. Однако Эйнштейн показал, что результаты измерений зависят от выбора системы координат, что произвело революцию в наших представлениях о пространстве и времени.
Работа Эйнштейна по релятивистской механике включала в себя два основных достижения. Первым достижением является Специальная теория относительности 1905 года , которая относится к неускоряющимся системам отсчета. Вторым крупным достижением стала Общая теория относительности 1916 года , которая рассматривает ускоряющиеся системы отсчета и их связь с гравитацией. Специальная теория является предельным случаем общей теории относительности.
Математически сложная Общая теория относительности требуется для описания ускоряющихся систем отсчета, гравитации, а также смежных тем, таких как черные дыры, или чрезвычайно точных измерений времени, присущих Глобальной системе позиционирования. Настоящее обсуждение будет сосредоточено главным образом на математически простой специальной теории относительности, поскольку она охватывает большую часть физики, встречающейся в атомной, ядерной физике и физике высоких энергий. В этой главе используются основные понятия специальной теории относительности для исследования следствий распространения ньютоновской, лагранжевой и гамильтоновой формулировок классической механики на релятивистскую область. Лоренц-инвариантные расширенные гамильтоновы и лагранжевы формализмы вводятся, поскольку они применимы к специальной теории относительности. Общая теория относительности включает гравитационную силу как геодезическое явление в четырехмерную рейманову структуру, основанную на пространстве, времени и материи.