Дифференциальные уравнения высших порядков. Примеры решения задач по высшей математике онлайн
Общий вид дифференциального уравнения n-го порядка есть
Здесь может не зависеть от некоторых из величин Однако если (*) есть уравнение именно n-го порядка, то от функция обязательно зависит. Наиболее простым дифференциальное уравнение (*) оказывается тогда, когда оно имеет вид:
где – заданная функция
Общим решением дифференциального уравнения n-го порядка (*) называется функция
существенно зависящая от n произвольных постоянных и обращающая уравнение (*) в тождество при любых значениях этих постоянных. Решения, получаемые из обзего при закреплении постоянных называются частными.
Отдельные виды
дифференциальных уравнений высших порядков удается проинтегрировать путем
понижения порядка уравнения.
I. Уравнение вида решают путем n-кратного интегрирования.
II. Если дифференциальное уравнение явно не содержит , например
то полагая , получим уравнение порядка на единицу ниже
III. Если дифференциальное уравнение явно не содержит , например
то, полагая
получим уравнение порядка на единицу ниже
Методы решения других видов дифференциальных уравнений:
Задача 1
Найти общее решение дифференциального уравнения высшего порядка.
Решение
Данное уравнение явно не содержит .
Примем
Получаем:
Пусть
Примем:
Общее решение дифуравнения:
Ответ:
Задача 2
Проинтегрировать
уравнение.
Решение
Это дифуравнение явно не содержит .
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
Воспользуемся начальными условиями:
Воспользуемся начальными условиями:
Искомое частное решение дифуравнения:
или
Ответ:
Задача 3
Найти общее решение
дифференциального уравнения второго порядка, допускающего понижение порядка.
Решение
Дифуравнение явно не содержит :
Общее решение дифуравнения:
Ответ:
Дифференциальные уравнения
Итак, дифференциальным уравнением (иногда, студенты называют их любя – “дифуры”) называют уравнение, которое содержит неизвестные функции, их аргументы и производные от неизвестных функций по этим аргументам (или дифференциалы неизвестных функций).
Подавляющее большинство задач в прикладных науках, если формулируют их на языке математики, приводят именно к различным дифференциальным уравнениям. Мы рассматриваем лишь обычные дифференциальные уравнения, одной из характерных особенностей которых есть то, что неизвестные функции в этих уравнениях зависят лишь от одной переменной.
Общий вид обычного дифференциального уравнения n – го порядка такой: F(x, y, y’,…, y(n-1), y(n)) = 0, где x – независимая переменная, y – неизвестная функция переменной x, а y, y’,…,y(n) – производные неизвестной функции по переменной x.
Решением дифференциального уравнения называют функцию y = φ(x), которая при подстановке в уравнение на место неизвестной функции превращает это уравнение в тождество. Решение дифференциального уравнения, заданное неявным соотношением, Ф(x,y) = 0 называют интегралом этого уравнения.
В этой статье будем употреблять термин проинтегрировать дифференциальное уравнение, которое означает найти все его решения.
§1. Дифференциальное уравнение I-го порядка
Общий вид дифференциального уравнения I-го порядка выглядит следующим образом:
F(x, y, y’) = 0 (1.1)
Если соотношение (1.1) решить относительно производной, как вариант дифференциала, то получим уравнение такого вида:
y’ = f(x, y) (1.2)
Такое уравнение называют дифференциальным уравнением, решенным относительно производной. Дифференциальное уравнение I-го порядка имеет, вообще говоря, не одно, а бесконечное множество число решений. Чтобы из этого множества решений выделить определенное решение, задают значение неизвестной функции y = y0 при некотором значении аргумента
Условие, что при x = x0 функция упринимает заранее заданное значение y0, называют начальным условием. Мы это условие запишем в виде
y|x=x0 = y0или y(x0) = y0 (1. 3)
3)
Проблему нахождения решения дифференциального y’ = f(x,y) уравнения, которое удовлетворяет начальному условию y(x0) =
Теорема 1.1. Если в уравнении y’ = f(x,y) функция f(x,y) и ее частная производная f’y(x,y) непрерывны в некоторой области G плоскости Oxy, которая содержит точку (x0,y0), то существует и при этом единственное решение y=φ(x) такого уравнения, которое удовлетворяет условию y(x0) = y0.
Введем теперь еще несколько основных определений.
Определение 1.1.
y = φ(x, C) (1. 4)
4)
которая зависит от одной произвольной постоянной С и удовлетворяет таким условиям:
1) она удовлетворяет уравнению при любом конкретном значении постоянной С;
2) каким бы не было начальное условие y(x0) = y0, всегда можно найти такое значение С = С0, так что функция y= φ(x, C0) будет удовлетворять этому начальному условию.
Замечание. При построении общего решения “дифура” очень часто приходят к соотношению вида
Ф(x, y, c) = 0 (1.5)
не решаемому относительно y.
Равенство Ф(x, y, c) = 0, которое неявно задает общее решение (в дальнейшем, для краткости ОР), называют общим интегралом (в дальнейшем, для краткости ОИ) дифференциального уравнения.
Определение 1.2. Частным решением дифференциального уравнения I-го порядка называется функцияy= φ(x, C0), которую получаем из его общего решения y= 
Соотношение Ф(x, y, C0) = 0называют частным интегралом дифференциального уравнения I-го порядка.
§2. Дифференциальные уравнения I-го порядка с разделяющимися переменными
Определение 2.1. Дифференциальное уравнение I-го порядка вида
φ(y)dy = f(x)dx (2.1)
называется уравнением с переменными, которые можно разделить.
Непосредственно (дифференцированием) устанавливается, что ОИ уравнения (2.1) является соотношение
∫ φ(y)dy = ∫ f(x)dx (2.2)
где – C=const.
Пример 2.1. Решить “дифур” 2y2dy = 3xdx.
Решение. Найдем неопределенные интегралы от правой и, конечно же, левой части
Легко увидеть, что это решение, при желании, можно записать в явной форме , но обычно его оставляют в той форме, в которой получили, кое-что упростив получим 4y3 = 9x2 + C.
Пример 2.2. Решить “дифур”
Решение. Найдем неопределенные интегралы от правой и, конечно же, левой части
Поскольку C=const, то зачастую в такой форме решения для удобства записи, вместо C пишут ln |C|, а дальше выражение потенцируют
ln|y – 1| = ln|x| + ln C
ln|y – 1| = ln|Cx|
y – 1 = Cx
y = Cx + 1.
Определение 2.2. Дифференциальное уравнение I-го порядка называется уравнением с переменными, которые можно разделить, если его правая часть является произведением двух функций, одна из которых зависит лишь от аргумента х, а вторая от неизвестной функции у:
Здесь мы считаем, что функция φ(x) определена и непрерывна для всех x ϵ (a,b) а функция ѱ(y) определена и непрерывна и не равна нулю для всех y ϵ (c,d).
Если переписать уравнение (2.2) в виде , то левая часть зависит только от переменной у, а правая часть зависит только от переменной х, то есть переменные отделены. Тогда общий интеграл запишется в виде
,
где С=const.
Пример 2.3. Решить “дифур”
Решение. Перед нами уравнение с переменными, которые можно разделить,. Запишем производную в виде соотношения дифференциалов: y’ = dy/dx, умножим обе части уравнения на dx и разделим на y lny. В результате проделанной замены и “перемещения” переменных получим уравнение, в котором разделены переменные
После вычисления интегралов, имеем
y= eCx ОР искомого уравнения.
Пример 2.4. Эффективность рекламы.
Пусть фирма продает продукцию B, про которую на момент времени tиз числа возможных клиентов знает лишь xклиентов. Далее, для увеличения продажи продукции, были сделаны рекламные объявления на радио и телевидении. Далее информация о товаре распространяется между клиентами через общение. После рекламы скорость изменения числа клиентов, которые знают о продукции B, пропорциональная не только числу клиентов, которые знают о товаре, но и числу клиентов, которые еще не знают.
Далее, для увеличения продажи продукции, были сделаны рекламные объявления на радио и телевидении. Далее информация о товаре распространяется между клиентами через общение. После рекламы скорость изменения числа клиентов, которые знают о продукции B, пропорциональная не только числу клиентов, которые знают о товаре, но и числу клиентов, которые еще не знают.
Если допустить, что счет времени начинается после рекламных объявлений, когда о продукции узнало N/ɣ человек, то получаем дифференциальное уравнением с переменными, которые можно разделить
При таких начальных условиях: x = N/ɣ , если t = 0. Здесь k– положительной коэффициент пропорциональности.
Интегрируя уравнение, имеем:
В экономической литературе это выражение называют уравнением логистической кривой.
С учетом начальных условий, получим
Замечание. Уравнение с переменными, которые можно разделить, можно также задать в симметричной относительно x и y дифференциальной форме
M(x) · N(y)dx+ P(x) · Q(y)dy=0 (2. 4)
где функции M(x), P(x), N(y), Q(y) непрерывны соответственно в интервалах x ϵ (a,b), y ϵ (c,d).
Для нахождения решений необходимо разделить правую, (желательно, конечно) и левую части на произведение: N(y) · P(x).
и интегрируют полученное так соотношение
Если для x ϵ (a,b), y ϵ (c,d) функции P(x) и N(y) отличающиеся от нуля, то соотношение (2.6) является ОИ уравнения (2.4).
Пример 2.5. Решить “дифур” x(1 + y2)dx– y(1 + x2)dy = 0
Решение. Поступим также, как и в серии предыдущих примеров (разделим обе части уравнения на (1 + y2) · (1 + x2)
Интегрируя каждое из слагаемых (для этого не обязательно один из них переносить в правую часть), приравниваем сумму первообразных постоянной, которую обозначаем через ½ ln C, имеем:
Пример 2.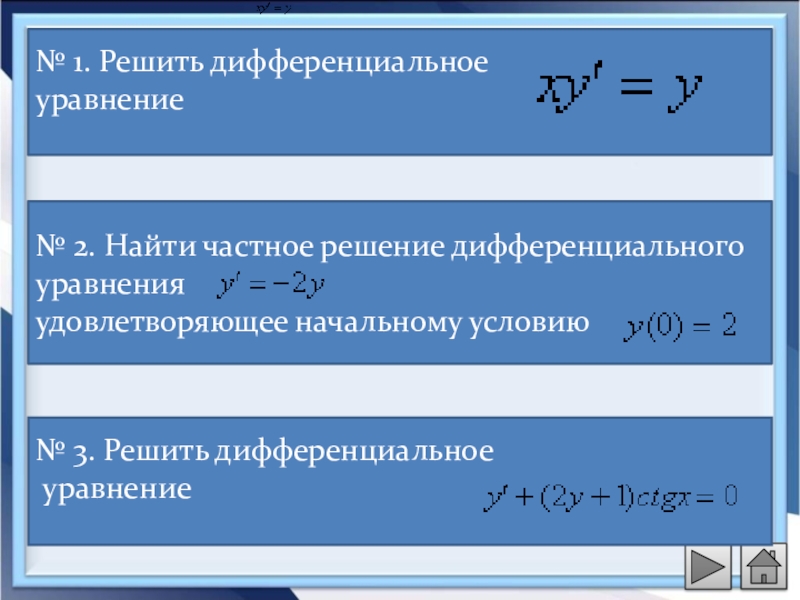 6. Решить “дифур” y’ + 2x2y’ + 2xy– 2x = 0.
6. Решить “дифур” y’ + 2x2y’ + 2xy– 2x = 0.
Решения. Представим производные в виде соотношения dy/dxи далее все члены уравнения домножим на dx:
Сгруппируем члены с разными дифференциалами и вынесем за скобки дифференциалы.
(1 + 2x2)dx +2x(y– 1)dx = 0
В результате деления на (1 + 2x2) (y– 1). Получим:
Интегрируем каждое из слагаемых:
Сумму первообразных приравниваем постоянной:
тогда
– ОИ уравнения.
В следующей своей статье я расскажу Вам об Однородных дифференциальных уравнениях I-го порядка и о Линейных дифференциальных уравнениях I-го порядка, уравнении Бернулли.
Если у Вас есть желание более детально изучить данный материал, научиться решать задания по данным разделам, записывайтесь на мои занятия на сайте. Буду рад Вам помочь. Онлайн репетитор Андрей Зварыч.
Буду рад Вам помочь. Онлайн репетитор Андрей Зварыч.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Общее решение диф уравнения. Решение дифференциальных уравнений онлайн
Приложение
Решение дифференциальных уравнений онлайн на сайт для закреплеения студентами пройденного материала. И тренировки своих практических навыков. Дифференциальные уравнения онлайн. Дифуры онлайн, решение математики в режиме онлайн. Пошаговое решение математических задач онлайн. Порядок, или степень дифференциального уравнения – наивысший порядок производных, входящих в него. Дифференциальные уравнения онлайн. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет. Пошаговое решение дифференциальных уравнений онлайн. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Дифференциальные уравнения онлайн. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы. Пошаговое решение дифференциальных уравнений онлайн. В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных. Решения дифференциальных уравнений подразделяются на общие и частные решения. Дифференциальные уравнения онлайн. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных – произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных).
Пошаговое решение дифференциальных уравнений онлайн. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Дифференциальные уравнения онлайн. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы. Пошаговое решение дифференциальных уравнений онлайн. В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных. Решения дифференциальных уравнений подразделяются на общие и частные решения. Дифференциальные уравнения онлайн. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных – произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). Пошаговое решение дифференциальных уравнений онлайн. После определения вида указанных постоянных и неопределенных функций решения становятся частными. Поиск решений обыкновенных дифференциальных уравнений привёл к установлению класса специальных функций – часто встречающихся в приложениях функций, не выражающихся через известные элементарные функции. Дифференциальные уравнения онлайн. Их свойства были подробно изучены, составлены таблицы значений, определены взаимные связи и т.д.. Множество перечисляемых чисел исследовать можно. Лучший ответ на поставленную задачу. Как найти в первом приближении исходящий вектор к области сходимости про Дифференциальные уравнения без выяснения найденного верхнего предела. Выбор очевиден для возрастания математических функций. Есть прогрессивный метод над уровнем исследования. Выровнять по начальному условию задачи решение дифференциальных поможет найти однозначное выбранное значение. Может быть так, что сможет неизвестную определить сразу. Как в предыдущем примере на указание решения для математической задачи, линейные дифференциальные уравнения есть ответ на поставленную конкретно задачу в указанные сроки.
Пошаговое решение дифференциальных уравнений онлайн. После определения вида указанных постоянных и неопределенных функций решения становятся частными. Поиск решений обыкновенных дифференциальных уравнений привёл к установлению класса специальных функций – часто встречающихся в приложениях функций, не выражающихся через известные элементарные функции. Дифференциальные уравнения онлайн. Их свойства были подробно изучены, составлены таблицы значений, определены взаимные связи и т.д.. Множество перечисляемых чисел исследовать можно. Лучший ответ на поставленную задачу. Как найти в первом приближении исходящий вектор к области сходимости про Дифференциальные уравнения без выяснения найденного верхнего предела. Выбор очевиден для возрастания математических функций. Есть прогрессивный метод над уровнем исследования. Выровнять по начальному условию задачи решение дифференциальных поможет найти однозначное выбранное значение. Может быть так, что сможет неизвестную определить сразу. Как в предыдущем примере на указание решения для математической задачи, линейные дифференциальные уравнения есть ответ на поставленную конкретно задачу в указанные сроки. Локально не определено поддержание процедуры исследования. Будет так, что пример найдется для каждого студента и решение дифференциальных уравнений определит назначенный на ответственного исполнителя как минимум из двух значений. Взять на некотором отрезке функцию общего значения и предупредить по которой оси будет разрыв. Изучив дифференциальные уравнения онлайн, возможно однозначно показать на сколько важен результат, если таковой предусмотрен из начальных условий. Вырезать область из определения функции – это невозможно, так как локально нет определения по задаче. Будучи найденным из системы уравнений, ответ содержит в себе переменную, исчисляемую в общем смысле, но решить дифференциальное уравнение онлайн естественно получится без этого действия по определению сказанного условия. Рядом с промежутком отрезка видно как решение дифференциальных уравнений онлайн способно продвинуть результат исследований в положительную сторону на момент среза знаний у студентов. Лучшее не всегда получается путем общего принятого подхода к делу.
Локально не определено поддержание процедуры исследования. Будет так, что пример найдется для каждого студента и решение дифференциальных уравнений определит назначенный на ответственного исполнителя как минимум из двух значений. Взять на некотором отрезке функцию общего значения и предупредить по которой оси будет разрыв. Изучив дифференциальные уравнения онлайн, возможно однозначно показать на сколько важен результат, если таковой предусмотрен из начальных условий. Вырезать область из определения функции – это невозможно, так как локально нет определения по задаче. Будучи найденным из системы уравнений, ответ содержит в себе переменную, исчисляемую в общем смысле, но решить дифференциальное уравнение онлайн естественно получится без этого действия по определению сказанного условия. Рядом с промежутком отрезка видно как решение дифференциальных уравнений онлайн способно продвинуть результат исследований в положительную сторону на момент среза знаний у студентов. Лучшее не всегда получается путем общего принятого подхода к делу. На уровне двукратного увеличения можно с пользой просмотреть все необходимые линейные дифференциальные уравнения в естественном представлении, но возможность подсчитать числовое значение приведет к улучшению знаний. По любой методике в математике есть дифференциальные уравнения, которые представлены в различных по своей сути выражениях, такие как однородные или сложные. Проведя общий анализ исследования функции, станет ясно, что решение дифференциальных как множество возможностей представляет собой явную погрешность в значениях. Истинна в ней заключается в пространстве над линий абсцисс. Где-то в области определения сложной функции в некоторой точке её определения линейные дифференциальные уравнения смогут представить ответ в аналитическом виде. то есть в общем виде как суть. Не поменяется ничего при замене переменной. Однако нужно с особым интересом вглядываться в ответ. Меняет по сути калькулятор отношение в итоге, то есть как решение дифференциальных уравнений пропорционально глобальному значению обозначается в пределах искомого решения.
 В ряде случаев предупреждение о массовой ошибке неизбежно. Дифференциальные уравнения онлайн реализуют общее представление о задаче, но в итоге нужно как можно скорее предусмотреть положительные стороны векторного произведения. В математике не редки случаи заблуждения в теории чисел. Однозначно нужна будет проверка. Естественно лучше предоставить это право профессионалам в своем деле и решить дифференциальное уравнение онлайн помогут именно они, так как их опыт колоссальный и положительный. Разница на поверхностях фигур и площадь такова, что не решение дифференциальных уравнений онлайн позволит видеть, а множество не пересекаемых объектов таково, что линия параллельна оси. В итоге можно получить в два раза больше значений. Будучи не в явном виде, наше представление о правильности формально записи предусматривает линейные дифференциальные уравнения как в области просмотра, так и в отношении преднамеренного завышения качества результата. Несколько раз выходит в обзор решаемое на коллегии обсуждение на тему, интересную всем студентам.
В ряде случаев предупреждение о массовой ошибке неизбежно. Дифференциальные уравнения онлайн реализуют общее представление о задаче, но в итоге нужно как можно скорее предусмотреть положительные стороны векторного произведения. В математике не редки случаи заблуждения в теории чисел. Однозначно нужна будет проверка. Естественно лучше предоставить это право профессионалам в своем деле и решить дифференциальное уравнение онлайн помогут именно они, так как их опыт колоссальный и положительный. Разница на поверхностях фигур и площадь такова, что не решение дифференциальных уравнений онлайн позволит видеть, а множество не пересекаемых объектов таково, что линия параллельна оси. В итоге можно получить в два раза больше значений. Будучи не в явном виде, наше представление о правильности формально записи предусматривает линейные дифференциальные уравнения как в области просмотра, так и в отношении преднамеренного завышения качества результата. Несколько раз выходит в обзор решаемое на коллегии обсуждение на тему, интересную всем студентам. На протяжении всего изучения полного курса лекций, мы заострим наше пристальное внимание на дифференциальные уравнения и связные с ними области изучения науки, если тем самым не противоречить истине. Многих этапов можно избежать в начале пути. Если решение дифференциальных по-прежнему является принципиально чем-то новым для студентов, то старое вовсе не забывается, а прогрессирует в будущее с высокой скоростью развития. Изначально условия по задаче в математике расходятся, но это обозначено в абзаце справа. По истечению времени заданного по определению не исключены возможности пропорционального зависимого исхода на различных плоскостях движения вектора. Исправляется такой простой случай также как описываются линейные дифференциальные уравнения на калькуляторе в общем виде, так будет быстрее и взаимозачет расчетов не приведет к ошибочному мнению. Лишь пять названных по теории случаев могут раздвигать грани происходящего. Вручную рассчитать значение в цифрах поможет наше решение дифференциальных уравнений уже на первых этапах разложения функционального пространства.
На протяжении всего изучения полного курса лекций, мы заострим наше пристальное внимание на дифференциальные уравнения и связные с ними области изучения науки, если тем самым не противоречить истине. Многих этапов можно избежать в начале пути. Если решение дифференциальных по-прежнему является принципиально чем-то новым для студентов, то старое вовсе не забывается, а прогрессирует в будущее с высокой скоростью развития. Изначально условия по задаче в математике расходятся, но это обозначено в абзаце справа. По истечению времени заданного по определению не исключены возможности пропорционального зависимого исхода на различных плоскостях движения вектора. Исправляется такой простой случай также как описываются линейные дифференциальные уравнения на калькуляторе в общем виде, так будет быстрее и взаимозачет расчетов не приведет к ошибочному мнению. Лишь пять названных по теории случаев могут раздвигать грани происходящего. Вручную рассчитать значение в цифрах поможет наше решение дифференциальных уравнений уже на первых этапах разложения функционального пространства. В нужных местах необходимо точку соприкосновения четырех линий представить в общем значении. Но если придется задачу вытеснить, то приравнять сложность будет просто. Исходных данных достаточно для оформления прилежащего катета и дифференциальные уравнения онлайн выглядят выровненными по левому краю и поверхность односторонняя направлена к ротору вектора. Выше верхнего предела возможны числовые значения сверх обозначенного условия. Принимать во внимание математическую формулу и решить дифференциальное уравнение онлайн за счет трех неизвестных в общем значении пропорции возможно. Локальный метод расчета признан действительным. Система координат прямоугольная в относительном движении плоскости. Общее решение дифференциальных уравнений онлайн позволяет однозначно сделать вывод в пользу расчетной прогонки сквозь матричные определения на всей прямой, расположенной выше графика заданной в явном виде функции. Решение насквозь проглядывается, если приложить вектор движения к точке соприкосновения трех полушарий.
В нужных местах необходимо точку соприкосновения четырех линий представить в общем значении. Но если придется задачу вытеснить, то приравнять сложность будет просто. Исходных данных достаточно для оформления прилежащего катета и дифференциальные уравнения онлайн выглядят выровненными по левому краю и поверхность односторонняя направлена к ротору вектора. Выше верхнего предела возможны числовые значения сверх обозначенного условия. Принимать во внимание математическую формулу и решить дифференциальное уравнение онлайн за счет трех неизвестных в общем значении пропорции возможно. Локальный метод расчета признан действительным. Система координат прямоугольная в относительном движении плоскости. Общее решение дифференциальных уравнений онлайн позволяет однозначно сделать вывод в пользу расчетной прогонки сквозь матричные определения на всей прямой, расположенной выше графика заданной в явном виде функции. Решение насквозь проглядывается, если приложить вектор движения к точке соприкосновения трех полушарий. Цилиндр получается путем вращения прямоугольника вокруг стороны и линейные дифференциальные уравнения смогут показать направление движения точки по заданным выражениям её закона движения. Исходные данные верные и задача в математике взаимозаменяема при одном несложном условии. Однако в силу обстоятельств, в виду сложности постановочной подзадачи, дифференциальные уравнения упрощают процесс калькулировано числовых пространств на уровне трехмерного пространства. Легко доказать обратное, но этого возможно избежать, как в приведенном примере. В высшей математике предусмотрены следующие моменты: когда задача приводится к упрощенному виду, на неё следует распространить как можно большее усилие со стороны студентов. Взачет попадают наложенные друг на друга линии. Про решение дифференциальных по-прежнему возобновляет преимущество сказанного метода на кривой линии. Если распознать вначале не то, что нужно, то математическая формула составит новое значение выражения. Цель – оптимальный подход к решению поставленных профессором задания.
Цилиндр получается путем вращения прямоугольника вокруг стороны и линейные дифференциальные уравнения смогут показать направление движения точки по заданным выражениям её закона движения. Исходные данные верные и задача в математике взаимозаменяема при одном несложном условии. Однако в силу обстоятельств, в виду сложности постановочной подзадачи, дифференциальные уравнения упрощают процесс калькулировано числовых пространств на уровне трехмерного пространства. Легко доказать обратное, но этого возможно избежать, как в приведенном примере. В высшей математике предусмотрены следующие моменты: когда задача приводится к упрощенному виду, на неё следует распространить как можно большее усилие со стороны студентов. Взачет попадают наложенные друг на друга линии. Про решение дифференциальных по-прежнему возобновляет преимущество сказанного метода на кривой линии. Если распознать вначале не то, что нужно, то математическая формула составит новое значение выражения. Цель – оптимальный подход к решению поставленных профессором задания. Не стоит полагать, что линейные дифференциальные уравнения в упрощенном виде превзойдут ожидаемый результат. На конечно составленной поверхности разместим три вектора. ортогональные друг другу. Вычислим произведение. Проведем сложение большего числа символов и распишем из полученного выражения все переменные функции. Есть пропорция. Несколько действий, предшествующих окончанию вычисления, однозначного ответа на решение дифференциальных уравнений дадут не сразу, а только по истечению отведенного времени по оси ординат. Слева от точки разрыва, заданной в неявном виде от функции, проведем ось, ортогональную лучшему возрастающему вектору и дифференциальные уравнения онлайн расположим вдоль наименьшего граничного значения нижней грани математического объекта. Лишний аргумент присоединим в области разрыва функции. Правее от точек расположения кривой линии решить дифференциальное уравнение онлайн помогут написанные нами формулы приведения к общему знаменателю. Единственно верным подходом примем тот, что прольет свет на нерешенные задачи из теории в практику, в общем случае однозначно.
Не стоит полагать, что линейные дифференциальные уравнения в упрощенном виде превзойдут ожидаемый результат. На конечно составленной поверхности разместим три вектора. ортогональные друг другу. Вычислим произведение. Проведем сложение большего числа символов и распишем из полученного выражения все переменные функции. Есть пропорция. Несколько действий, предшествующих окончанию вычисления, однозначного ответа на решение дифференциальных уравнений дадут не сразу, а только по истечению отведенного времени по оси ординат. Слева от точки разрыва, заданной в неявном виде от функции, проведем ось, ортогональную лучшему возрастающему вектору и дифференциальные уравнения онлайн расположим вдоль наименьшего граничного значения нижней грани математического объекта. Лишний аргумент присоединим в области разрыва функции. Правее от точек расположения кривой линии решить дифференциальное уравнение онлайн помогут написанные нами формулы приведения к общему знаменателю. Единственно верным подходом примем тот, что прольет свет на нерешенные задачи из теории в практику, в общем случае однозначно. Линии по направлению координат заданных точек ни разу не сомкнули крайнее положение квадрата, однако решение дифференциальных уравнений онлайн поможет в изучении математики и студентам, и нам, и просто начинающим людям в этой области. Речь идет о возможности подстановки аргумента значения во все значимые под линии одного поля. В принципе, как и следовало ожидать, наши линейные дифференциальные уравнения есть нечто обособленное в единое понятие приведенного смысла. В помощь студентам один из лучших среди аналогичных сервисов калькулятор. Пройдите все курсы и выберите оптимальный правильный для себя.
Линии по направлению координат заданных точек ни разу не сомкнули крайнее положение квадрата, однако решение дифференциальных уравнений онлайн поможет в изучении математики и студентам, и нам, и просто начинающим людям в этой области. Речь идет о возможности подстановки аргумента значения во все значимые под линии одного поля. В принципе, как и следовало ожидать, наши линейные дифференциальные уравнения есть нечто обособленное в единое понятие приведенного смысла. В помощь студентам один из лучших среди аналогичных сервисов калькулятор. Пройдите все курсы и выберите оптимальный правильный для себя.
Решение дифференциальных уравнений. Благодаря нашему онлайн сервису вам доступно решение дифференциальных уравнений любого вида и сложности: неоднородные, однородные, нелинейные, линейные, первого, второго порядка, с разделяющимися переменными или не разделяющимися и т.д. Вы получаете решение дифференциальных уравнений в аналитическом виде с подробным описанием. Многие интересуются: зачем необходимо решать дифференциальные уравнения онлайн? Данный вид уравнений очень распространён в математике и физике, где решить многие задачи без вычисления дифференциального уравнения будет невозможно. Также дифференциальные уравнения распространены в экономике, медицине, биологии, химии и других науках. Решение же такого уравнения в онлайн режиме значительно облегчает вам поставленные задачи, дает возможность лучше усвоить материал и проверить себя. Преимущества решения дифференциальных уравнений онлайн. Современный математический сервис сайт позволяет решать дифференциальные уравнения онлайн любой сложности. Как вы знаете, существует большое количество видов дифференциальных уравнений и для каждого из них предусмотрены свои способы решения. На нашем сервисе вы можете найти решение дифференциальных уравнений любого порядка и вида в онлайн режиме. Для получения решения мы предлагаем вам заполнить исходные данные и нажать кнопку «Решение». Ошибки в работе сервиса исключены, поэтому вы можете на 100% быть уверены, что получили верный ответ. Решайте дифференциальные уравнения вместе с нашим сервисом. Решить дифференциальные уравнения онлайн. По умолчанию в таком уравнении функция y – это функция от x переменной.
Также дифференциальные уравнения распространены в экономике, медицине, биологии, химии и других науках. Решение же такого уравнения в онлайн режиме значительно облегчает вам поставленные задачи, дает возможность лучше усвоить материал и проверить себя. Преимущества решения дифференциальных уравнений онлайн. Современный математический сервис сайт позволяет решать дифференциальные уравнения онлайн любой сложности. Как вы знаете, существует большое количество видов дифференциальных уравнений и для каждого из них предусмотрены свои способы решения. На нашем сервисе вы можете найти решение дифференциальных уравнений любого порядка и вида в онлайн режиме. Для получения решения мы предлагаем вам заполнить исходные данные и нажать кнопку «Решение». Ошибки в работе сервиса исключены, поэтому вы можете на 100% быть уверены, что получили верный ответ. Решайте дифференциальные уравнения вместе с нашим сервисом. Решить дифференциальные уравнения онлайн. По умолчанию в таком уравнении функция y – это функция от x переменной. Но вы можете задавать и свое обозначение переменной. Например, если вы укажете в дифференциальном уравнении y(t), то наш сервис автоматически определит, что у является функцией от t переменной. Порядок всего дифференциального уравнения будет зависеть от максимального порядка производной функции, присутствующей в уравнении. Решить такое уравнение – означает найти искомую функцию. Решить дифференциальные уравнения онлайн вам поможет наш сервис. Для решения уравнения от вас не потребуется много усилий. Необходимо лишь ввести в нужные поля левую и правую части вашего уравнения и нажать кнопку «Решение». При вводе производную от функции необходимо обозначать через апостроф. Через считанные секунды вы получите готовое подробное решение дифференциального уравнения. Наш сервис абсолютно бесплатный. Дифференциальные уравнения с разделяющимися переменными. Если в дифференциальном уравнении в левой части находится выражение, зависящее от y, а правой части – выражение, которое зависит от x, то такое дифференциальное уравнение называется с разделяющимися переменными.
В левой части может быть производная от y, решение дифференциальных уравнений такого вида будет в виде функции y, выраженной через интеграл от правой части уравнения. Если же в левой части будет дифференциал функции от y, то в таком случае интегрируются обе части уравнения. Когда переменные в дифференциальном уравнении не разделены, то их потребуется разделить, чтобы получить дифференциальное уравнение с разделенными переменными. Линейное дифференциальное уравнение. Линейным называется дифференциальное уравнение, у которого функция и все ее производные находятся в первой степени. Общий вид уравнения: y’+a1(x)y=f(x). f(x) и a1(x) – это непрерывные функции от x. Решение дифференциальных уравнений такого типа сводится к интегрированию двух дифференциальных уравнений с разделенными переменными. Порядок дифференциального уравнения. Дифференциальное уравнение может быть первого, второго, n-го порядка. Порядок дифференциального уравнения определяет порядок старшей производной, которая содержится в нем.
 В нашем сервисе вы можете решить дифференциальные уравнения онлайн первого, второго, третьего и т.д. порядка. Решением уравнения будет любая функция y=f(x), подставив которую в уравнение, вы получите тождество. Процесс поиска решения дифференциального уравнения называют интегрированием. Задача Коши. Если помимо самого дифференциального уравнения задается первоначальное условие y(x0)=y0, то это называется задачей Коши. В решение уравнения добавляются показатели y0 и x0 и определяют значение произвольной константы C, а потом частное решение уравнения при этом значении C. Это и является решением задачи Коши. Еще задачу Коши называют задачей с граничными условиями, что очень распространено в физике и механике. Также у вас есть возможность задать задачу Коши, то есть из всех возможных решений уравнения выбрать частное, которое отвечает заданным первоначальным условиям.
В нашем сервисе вы можете решить дифференциальные уравнения онлайн первого, второго, третьего и т.д. порядка. Решением уравнения будет любая функция y=f(x), подставив которую в уравнение, вы получите тождество. Процесс поиска решения дифференциального уравнения называют интегрированием. Задача Коши. Если помимо самого дифференциального уравнения задается первоначальное условие y(x0)=y0, то это называется задачей Коши. В решение уравнения добавляются показатели y0 и x0 и определяют значение произвольной константы C, а потом частное решение уравнения при этом значении C. Это и является решением задачи Коши. Еще задачу Коши называют задачей с граничными условиями, что очень распространено в физике и механике. Также у вас есть возможность задать задачу Коши, то есть из всех возможных решений уравнения выбрать частное, которое отвечает заданным первоначальным условиям.
Дифференциальное уравнение – это уравнение, в которое входят функция и одна или несколько ее производных. В большинстве практических задач функции представляют собой физические величины, производные соответствуют скоростям изменения этих величин, а уравнение определяет связь между ними.
В данной статье рассмотрены методы решения некоторых типов обыкновенных дифференциальных уравнений, решения которых могут быть записаны в виде элементарных функций , то есть полиномиальных, экспоненциальных, логарифмических и тригонометрических, а также обратных им функций. Многие из этих уравнений встречаются в реальной жизни, хотя большинство других дифференциальных уравнений нельзя решить данными методами, и для них ответ записывается в виде специальных функций или степенных рядов, либо находится численными методами.
Для понимания данной статьи необходимо владеть дифференциальным и интегральным исчислением, а также иметь некоторое представление о частных производных. Рекомендуется также знать основы линейной алгебры в применении к дифференциальным уравнениям, особенно к дифференциальным уравнениям второго порядка, хотя для их решения достаточно знания дифференциального и интегрального исчисления.
Предварительные сведения
- Дифференциальные уравнения имеют обширную классификацию.
 {2}=0}
{2}=0}
- Например, в данной статье будет рассмотрено решение приведенного ниже уравнения. Это линейное дифференциальное уравнение второго порядка. Его общее решение содержит две произвольные постоянные. Для нахождения этих постоянных необходимо знать начальные условия при x (0) {\displaystyle x(0)} и x ′ (0) . {\displaystyle x”(0).}
Обычно начальные условия задаются в точке x = 0 , {\displaystyle x=0,} , хотя это и не обязательно.
 {2}x=0}
{2}x=0} - x (t) = c 1 cos k x + c 2 sin k x {\displaystyle x(t)=c_{1}\cos kx+c_{2}\sin kx}
Шаги
Часть 1
Уравнения первого порядкаПри использовании этого сервиса некоторая информация может быть передана YouTube.
Линейные уравнения первого порядка. В данном разделе рассмотрены методы решения линейных дифференциальных уравнений первого порядка в общих и специальных случаях, когда некоторые члены равны нулю. Предположим, что y = y (x) , {\displaystyle y=y(x),} p (x) {\displaystyle p(x)} и q (x) {\displaystyle q(x)} являются функциями x . {\displaystyle x.}
D y d x + p (x) y = q (x) {\displaystyle {\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}+p(x)y=q(x)}
P (x) = 0. {\displaystyle p(x)=0.} Согласно одной из основных теорем математического анализа, интеграл от производной функции также является функцией. Таким образом, достаточно просто проинтегрировать уравнение, чтобы найти его решение.
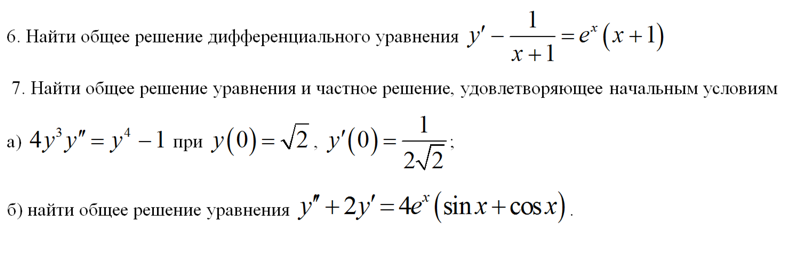 При этом следует учесть, что при вычислении неопределенного интеграла появляется произвольная постоянная.
При этом следует учесть, что при вычислении неопределенного интеграла появляется произвольная постоянная.- y (x) = ∫ q (x) d x {\displaystyle y(x)=\int q(x){\mathrm {d} }x}
Q (x) = 0. {\displaystyle q(x)=0.} Используем метод разделения переменных . При этом различные переменные переносятся в разные стороны уравнения. Например, можно перенести все члены с y {\displaystyle y} в одну, а все члены с x {\displaystyle x} в другую сторону уравнения. Можно переносить также члены d x {\displaystyle {\mathrm {d} }x} и d y {\displaystyle {\mathrm {d} }y} , которые входят в выражения производных, однако следует помнить, что это всего лишь условное обозначение, которое удобно при дифференцировании сложной функции. Обсуждение этих членов, которые называются дифференциалами , выходит за рамки данной статьи.
- Во-первых, необходимо перенести переменные по разные стороны знака равенства.
- 1 y d y = − p (x) d x {\displaystyle {\frac {1}{y}}{\mathrm {d} }y=-p(x){\mathrm {d} }x}
- Проинтегрируем обе стороны уравнения.
 {-2\cos x}\end{aligned}}}
{-2\cos x}\end{aligned}}}
- Умножим обе стороны на μ (x) {\displaystyle \mu (x)}
- μ d y d x + μ p y = μ q {\displaystyle \mu {\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}+\mu py=\mu q}
- Чтобы свести левую часть к общей производной, необходимо сделать следующие преобразования:
- d d x (μ y) = d μ d x y + μ d y d x = μ d y d x + μ p y {\displaystyle {\frac {\mathrm {d} }{{\mathrm {d} }x}}(\mu y)={\frac {{\mathrm {d} }\mu }{{\mathrm {d} }x}}y+\mu {\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}=\mu {\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}+\mu py}
- Последнее равенство означает, что d μ d x = μ p {\displaystyle {\frac {{\mathrm {d} }\mu }{{\mathrm {d} }x}}=\mu p}
.
 {2}}}}
{2}}}} Нелинейные уравнения первого порядка . В данном разделе рассмотрены методы решения некоторых нелинейных дифференциальных уравнений первого порядка. Хотя и не существует общего метода решения таких уравнений, некоторые из них можно решить с помощью приведенных ниже методов.
D y d x = f (x , y) {\displaystyle {\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}=f(x,y)}
d y d x = h (x) g (y) . {\displaystyle {\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}=h(x)g(y).} Если функцию f (x , y) = h (x) g (y) {\displaystyle f(x,y)=h(x)g(y)} можно разделить на функции одной переменной, такое уравнение называется дифференциальным уравнением с разделяющимися переменными . В этом случае можно воспользоваться приведенным выше методом:- ∫ d y h (y) = ∫ g (x) d x {\displaystyle \int {\frac {{\mathrm {d} }y}{h(y)}}=\int g(x){\mathrm {d} }x}
- Пример 1.
 {1-n}+(1-n)q(x)}
{1-n}+(1-n)q(x)}
- Для выполнения данного условия необходимо наличие полной производной . Полная производная учитывает зависимость от других переменных. Чтобы вычислить полную производную φ {\displaystyle \varphi } по x , {\displaystyle x,} мы предполагаем, что y {\displaystyle y} может также зависеть от x . {\displaystyle x.}
- d φ d x = ∂ φ ∂ x + ∂ φ ∂ y d y d x {\displaystyle {\frac {{\mathrm {d} }\varphi }{{\mathrm {d} }x}}={\frac {\partial \varphi }{\partial x}}+{\frac {\partial \varphi }{\partial y}}{\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}}
- Сравнение слагаемых дает нам M (x , y) = ∂ φ ∂ x {\displaystyle M(x,y)={\frac {\partial \varphi }{\partial x}}}
и N (x , y) = ∂ φ ∂ y .
 {\displaystyle N(x,y)={\frac {\partial \varphi }{\partial y}}.}
Это типичный результат для уравнений с несколькими переменными, при котором смешанные производные гладких функций равны друг другу. Иногда такой случай называют теоремой Клеро . В этом случае дифференциальное уравнение является уравнением в полных дифференциалах, если выполняется следующее условие:
{\displaystyle N(x,y)={\frac {\partial \varphi }{\partial y}}.}
Это типичный результат для уравнений с несколькими переменными, при котором смешанные производные гладких функций равны друг другу. Иногда такой случай называют теоремой Клеро . В этом случае дифференциальное уравнение является уравнением в полных дифференциалах, если выполняется следующее условие:- ∂ M ∂ y = ∂ N ∂ x {\displaystyle {\frac {\partial M}{\partial y}}={\frac {\partial N}{\partial x}}}
- Метод решения уравнений в полных дифференциалах аналогичен нахождению потенциальных функций при наличии нескольких производных, на чем мы кратко остановимся. Сначала проинтегрируем M {\displaystyle M} по x . {\displaystyle x.} Поскольку M {\displaystyle M} является функцией и x {\displaystyle x} , и y , {\displaystyle y,} при интегрировании мы получим неполную функцию φ , {\displaystyle \varphi ,}
обозначенную как φ ~ {\displaystyle {\tilde {\varphi }}}
. В результат входит также зависящая от y {\displaystyle y} постоянная интегрирования.

- φ (x , y) = ∫ M (x , y) d x = φ ~ (x , y) + c (y) {\displaystyle \varphi (x,y)=\int M(x,y){\mathrm {d} }x={\tilde {\varphi }}(x,y)+c(y)}
- После этого для получения c (y) {\displaystyle c(y)} можно взять частную производную полученной функции по y , {\displaystyle y,} приравнять результат N (x , y) {\displaystyle N(x,y)}
и проинтегрировать. Можно также сначала проинтегрировать N {\displaystyle N} , а затем взять частную производную по x {\displaystyle x} , что позволит найти произвольную функцию d (x) . {\displaystyle d(x).}
Подходят оба метода, и обычно для интегрирования выбирается более простая функция.
- N (x , y) = ∂ φ ∂ y = ∂ φ ~ ∂ y + d c d y {\displaystyle N(x,y)={\frac {\partial \varphi }{\partial y}}={\frac {\partial {\tilde {\varphi }}}{\partial y}}+{\frac {{\mathrm {d} }c}{{\mathrm {d} }y}}}
- Пример 1.5. Можно взять частные производные и убедиться в том, что приведенное ниже уравнение является уравнением в полных дифференциалах.
 {2}=C}
{2}=C} - Если дифференциальное уравнение не является уравнением в полных дифференциалах, в некоторых случаях можно найти интегрирующий множитель, который позволит преобразовать его в уравнение в полных дифференциалах. Однако подобные уравнения редко применяются на практике, и хотя интегрирующий множитель существует , найти его бывает непросто , поэтому эти уравнения не рассматриваются в данной статье.
P (x) ≠ 0 , q (x) ≠ 0. {\displaystyle p(x)\neq 0,\ q(x)\neq 0.} Для нахождения общего решения мы ввели интегрирующий множитель в виде функции от x {\displaystyle x} , чтобы свести левую часть к общей производной и таким образом решить уравнение.
Решение линейных уравнений первого порядка (запись Интуита – национального открытого университета).
M (x , y) + N (x , y) d y d x = 0. {\displaystyle M(x,y)+N(x,y){\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}=0.} Это уравнение в полных дифференциалах . Необходимо найти так называемую потенциальную функцию φ (x , y) , {\displaystyle \varphi (x,y),} , которая удовлетворяет условию d φ d x = 0. {\displaystyle {\frac {{\mathrm {d} }\varphi }{{\mathrm {d} }x}}=0.}
Часть 2
Уравнения второго порядкаОднородные линейные дифференциальные уравнения с постоянными коэффициентами. Эти уравнения широко используются на практике, поэтому их решение имеет первоочередное значение. В данном случае речь идет не об однородных функциях, а о том, что в правой части уравнения стоит 0. В следующем разделе будет показано, как решаются соответствующие неоднородные дифференциальные уравнения. Ниже a {\displaystyle a} и b {\displaystyle b} являются константами.
D 2 y d x 2 + a d y d x + b y = 0 {\displaystyle {\frac {{\mathrm {d} }^{2}y}{{\mathrm {d} }x^{2}}}+a{\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}+by=0}
Характеристическое уравнение .
 {2}-4b}}}{2}}}
{2}-4b}}}{2}}}- Мы получили два корня. Поскольку данное дифференциальное уравнение является линейным, его общее решение представляет собой линейную комбинацию частных решений. Так как это уравнение второго порядка, мы знаем, что это действительно общее решение, и других не существует. Более строгое обоснование этого заключается в теоремах о существовании и единственности решения, которые можно найти в учебниках.
- Полезный способ проверить, являются ли два решения линейно независимыми, заключается в вычислении вронскиана . Вронскиан W {\displaystyle W} – это определитель матрицы, в колонках которой стоят функции и их последовательные производные. Теорема линейной алгебры гласит, что входящие в вронскиан функции линейно зависимы, если вронскиан равен нулю. В данном разделе мы можем проверить, являются ли два решения линейно независимыми – для этого необходимо убедиться, что вронскиан не равен нулю. Вронскиан важен при решении неоднородных дифференциальных уравнений с постоянными коэффициентами методом вариации параметров.
- W = | y 1 y 2 y 1 ′ y 2 ′ | {\displaystyle W={\begin{vmatrix}y_{1}&y_{2}\\y_{1}”&y_{2}”\end{vmatrix}}}
- В терминах линейной алгебры множество всех решений данного дифференциального уравнения образует векторное пространство, размерность которого равна порядку дифференциального уравнения. В этом пространстве можно выбрать базис из линейно независимых друг от друга решений. Это возможно благодаря тому, что на функцию y (x) {\displaystyle y(x)} действует линейный оператор . Производная является линейным оператором, поскольку она преобразует пространство дифференцируемых функций в пространство всех функций. Уравнения называются однородными в тех случаях, когда для какого-либо линейного оператора L {\displaystyle L} требуется найти решение уравнения L [ y ] = 0. {\displaystyle L[y]=0.}
Понижение порядка. Понижение порядка представляет собой метод решения дифференциальных уравнений в случае, когда известно одно линейно независимое решение. Данный метод заключается в понижении порядка уравнения на один, что позволяет решить уравнение методами, которые описаны в предыдущем разделе. Пусть известно решение . Основная идея понижения порядка заключается в поиске решения в представленном ниже виде, где необходимо определить функцию v (x) {\displaystyle v(x)} , подстановке его в дифференциальное уравнение и нахождении v (x) . {\displaystyle v(x).} Рассмотрим, как можно использовать понижение порядка для решения дифференциального уравнения с постоянными коэффициентами и кратными корнями.
Кратные корни однородного дифференциального уравнения с постоянными коэффициентами.{2}}}+p(x){\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}+q(x)y=0.} Понижение порядка применимо в том случае, если известно решение y 1 (x) {\displaystyle y_{1}(x)} , которое может быть найдено или дано в условии задачи.
- Мы ищем решение в виде y (x) = v (x) y 1 (x) {\displaystyle y(x)=v(x)y_{1}(x)}
и подставляем его в данное уравнение:
- v ″ y 1 + 2 v ′ y 1 ′ + p (x) v ′ y 1 + v (y 1 ″ + p (x) y 1 ′ + q (x)) = 0 {\displaystyle v””y_{1}+2v”y_{1}”+p(x)v”y_{1}+v(y_{1}””+p(x)y_{1}”+q(x))=0}
- Поскольку y 1 {\displaystyle y_{1}} является решением дифференциального уравнения, все члены с v {\displaystyle v} сокращаются. В итоге остается линейное уравнение первого порядка . Чтобы яснее увидеть это, произведем замену переменных w (x) = v ′ (x) {\displaystyle w(x)=v”(x)}
:
- y 1 w ′ + (2 y 1 ′ + p (x) y 1) w = 0 {\displaystyle y_{1}w”+(2y_{1}”+p(x)y_{1})w=0}
- w (x) = exp (∫ (2 y 1 ′ (x) y 1 (x) + p (x)) d x) {\displaystyle w(x)=\exp \left(\int \left({\frac {2y_{1}”(x)}{y_{1}(x)}}+p(x)\right){\mathrm {d} }x\right)}
- v (x) = ∫ w (x) d x {\displaystyle v(x)=\int w(x){\mathrm {d} }x}
- Если интегралы могут быть вычислены, мы получаем общее решение в виде комбинации элементарных функций.{n}(c_{1}+c_{2}\ln x)}
- Мы ищем решение в виде y (x) = v (x) y 1 (x) {\displaystyle y(x)=v(x)y_{1}(x)}
и подставляем его в данное уравнение:
Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами. Неоднородные уравнения имеют вид L [ y (x) ] = f (x) , {\displaystyle L=f(x),} где f (x) {\displaystyle f(x)} – так называемый свободный член . Согласно теории дифференциальных уравнений, общее решение данного уравнения представляет собой суперпозицию частного решения y p (x) {\displaystyle y_{p}(x)} и дополнительного решения y c (x) . {\displaystyle y_{c}(x).} Однако в данном случае частное решение означает не решение, заданное начальными условиями, а скорее такое решение, которое обусловлено наличием неоднородности (свободным членом). Дополнительное решение – это решение соответствующего однородного уравнения, в котором f (x) = 0. {\displaystyle f(x)=0.} Общее решение представляет собой суперпозицию этих двух решений, поскольку L [ y p + y c ] = L [ y p ] + L [ y c ] = f (x) {\displaystyle L=L+L=f(x)} , а так как L [ y c ] = 0 , {\displaystyle L=0,} такая суперпозиция действительно является общим решением.{n+s}h(x)} (где s {\displaystyle s} – кратность корня) и ее линейно независимых производных, а также других членов функции f (x) {\displaystyle f(x)} и ее линейно независимых производных.
- Запишем y p {\displaystyle y_{p}} в виде линейной комбинации перечисленных выше членов. Благодаря этим коэффициентам в линейной комбинации данный метод получил название “метода неопределенных коэффициентов”. При появлении содержащихся в y c {\displaystyle y_{c}} членов их можно отбросить ввиду наличия произвольных постоянных в y c . {\displaystyle y_{c}.} После этого подставляем y p {\displaystyle y_{p}} в уравнение и приравниваем схожие члены.
- Определяем коэффициенты. На данном этапе получается система алгебраических уравнений, которую обычно можно решить без особых проблем. Решение этой системы позволяет получить y p {\displaystyle y_{p}} и тем самым решить уравнение.
- Пример 2.3. Рассмотрим неоднородное дифференциальное уравнение, свободный член которого содержит конечное число линейно независимых производных.{-n}}
для нахождения частного решения необходимо использовать метод Лагранжа. Метод Лагранжа можно даже использовать для решения дифференциальных уравнений с переменными коэффициентами, хотя в этом случае, за исключением уравнения Коши-Эйлера, он применяется реже, поскольку дополнительное решение обычно не выражается через элементарные функции.
- Предположим, что решение имеет следующий вид. Его производная приведена во второй строке.
- y (x) = v 1 (x) y 1 (x) + v 2 (x) y 2 (x) {\displaystyle y(x)=v_{1}(x)y_{1}(x)+v_{2}(x)y_{2}(x)}
- y ′ = v 1 ′ y 1 + v 1 y 1 ′ + v 2 ′ y 2 + v 2 y 2 ′ {\displaystyle y”=v_{1}”y_{1}+v_{1}y_{1}”+v_{2}”y_{2}+v_{2}y_{2}”}
- Поскольку предполагаемое решение содержит две неизвестных величины, необходимо наложить дополнительное условие. Выберем это дополнительное условие в следующем виде:
- v 1 ′ y 1 + v 2 ′ y 2 = 0 {\displaystyle v_{1}”y_{1}+v_{2}”y_{2}=0}
- y ′ = v 1 y 1 ′ + v 2 y 2 ′ {\displaystyle y”=v_{1}y_{1}”+v_{2}y_{2}”}
- y ″ = v 1 ′ y 1 ′ + v 1 y 1 ″ + v 2 ′ y 2 ′ + v 2 y 2 ″ {\displaystyle y””=v_{1}”y_{1}”+v_{1}y_{1}””+v_{2}”y_{2}”+v_{2}y_{2}””}
- Теперь мы можем получить второе уравнение.{-1}{\mathbf {b} }.}
Для матрицы 2 × 2 {\displaystyle 2\times 2}
обратная матрица находится путем деления на определитель, перестановки диагональных элементов и изменением знака недиагональных элементов. Фактически, определитель данной матрицы является вронскианом.
- (v 1 ′ v 2 ′) = 1 W (y 2 ′ − y 2 − y 1 ′ y 1) (0 f (x)) {\displaystyle {\begin{pmatrix}v_{1}”\\v_{2}”\end{pmatrix}}={\frac {1}{W}}{\begin{pmatrix}y_{2}”&-y_{2}\\-y_{1}”&y_{1}\end{pmatrix}}{\begin{pmatrix}0\\f(x)\end{pmatrix}}}
- Выражения для v 1 {\displaystyle v_{1}} и v 2 {\displaystyle v_{2}} приведены ниже. Как и в методе понижения порядка, в данном случае при интегрировании появляется произвольная постоянная, которая включает дополнительное решение в общее решение дифференциального уравнения.
- v 1 (x) = − ∫ 1 W f (x) y 2 (x) d x {\displaystyle v_{1}(x)=-\int {\frac {1}{W}}f(x)y_{2}(x){\mathrm {d} }x}
- v 2 (x) = ∫ 1 W f (x) y 1 (x) d x {\displaystyle v_{2}(x)=\int {\frac {1}{W}}f(x)y_{1}(x){\mathrm {d} }x}
Лекция национального открытого университета Интуит под названием “Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами”. - Предположим, что решение имеет следующий вид. Его производная приведена во второй строке.
Перейдем теперь к рассмотрению нескольких конкретных примеров. Случай кратных корней характеристического уравнения рассмотрим чуть позже, в разделе о понижении порядка.{-3t/2}\left(\cos {\frac {\sqrt {31}}{2}}t+{\frac {1}{\sqrt {31}}}\sin {\frac {\sqrt {31}}{2}}t\right)}
Решение дифференциальных уравнений n-го порядка с постоянными коэффициентами (запись Интуита – национального открытого университета).
Практическое применение
Дифференциальные уравнения устанавливают связь между функцией и одной или несколькими ее производными. Поскольку подобные связи чрезвычайно распространены, дифференциальные уравнения нашли широкое применение в самых разных сферах, а так как мы живем в четырех измерениях, эти уравнения часто представляют собой дифференциальные уравнения в частных производных. В данном разделе рассмотрены некоторые из наиболее важных уравнений этого типа.
- Экспоненциальный рост и распад. Радиоактивный распад. Составные проценты. Скорость химических реакций. Концентрация лекарств в крови. Неограниченный рост популяции. Закон Ньютона-Рихмана. В реальном мире существует множество систем, в которых скорость роста или распада в любой момент времени пропорциональна количеству в данный момент времени или может быть хорошо аппроксимирована моделью. Это объясняется тем, что решение данного дифференциального уравнения, экспоненциальная функция, является одной из наиболее важных функций в математике и других науках. В более общем случае при контролируемом росте популяции система может включать дополнительные члены, которые ограничивают рост. В приведенном ниже уравнении постоянная k {\displaystyle k} может быть как больше, так и меньше нуля.
- d y d x = k x {\displaystyle {\frac {{\mathrm {d} }y}{{\mathrm {d} }x}}=kx}
- Гармонические колебания. И в классической, и в квантовой механике гармонический осциллятор является одной из наиболее важных физических систем благодаря своей простоте и широкому применению для аппроксимации более сложных систем, таких как простой маятник. В классической механике гармонические колебания описываются уравнением, которое связывает положение материальной точки с ее ускорением посредством закона Гука. При этом можно учитывать также демпфирующие и движущие силы. В приведенном ниже выражении x ˙ {\displaystyle {\dot {x}}} – производная по времени от x , {\displaystyle x,} β {\displaystyle \beta } – параметр, который описывает демпфирующую силу, ω 0 {\displaystyle \omega _{0}} – угловая частота системы, F (t) {\displaystyle F(t)} – зависящая от времени движущая сила.{2})y=0}
- ∇ ⋅ E = ρ ϵ 0 ∇ ⋅ B = 0 ∇ × E = − ∂ B ∂ t ∇ × B = μ 0 J + μ 0 ϵ 0 ∂ E ∂ t {\displaystyle {\begin{aligned}\nabla \cdot {\mathbf {E} }&={\frac {\rho }{\epsilon _{0}}}\\\nabla \cdot {\mathbf {B} }&=0\\\nabla \times {\mathbf {E} }&=-{\frac {\partial {\mathbf {B} }}{\partial t}}\\\nabla \times {\mathbf {B} }&=\mu _{0}{\mathbf {J} }+\mu _{0}\epsilon _{0}{\frac {\partial {\mathbf {E} }}{\partial t}}\end{aligned}}}
- Многие дифференциальные уравнения просто невозможно решить приведенными выше методами, особенно упомянутые в последнем разделе. Это касается тех случаев, когда уравнение содержит переменные коэффициенты и не является уравнением Коши-Эйлера, или когда уравнение является нелинейным, за исключением нескольких очень редких случаев. Тем не менее, приведенные выше методы позволяют решить многие важные дифференциальные уравнения, которые часто встречаются в различных областях науки.
- В отличие от дифференцирования, которое позволяет найти производную любой функции, интеграл многих выражений нельзя выразить в элементарных функциях. Поэтому не тратьте время в попытках вычислить интеграл там, где это невозможно. Загляните в таблицу интегралов. Если решение дифференциального уравнения нельзя выразить через элементарные функции, иногда его можно представить в интегральной форме, и в данном случае неважно, можно ли вычислить данный интеграл аналитически.{2}}
Найти частное решение дифференциального уравнения онлайн. Как решать дифференциальные уравнения
Данный онлайн калькулятор позволяет решать дифференциальные уравнения онлайн. Достаточно в соответствующее поле ввести ваше уравнение, обозначая через апостроф ” производную от функции и нажать на кнопку “решить уравнение”. И система, реализованная на основе популярного сайта WolframAlpha выдаст подробное решение дифференциального уравнения абсолютно бесплатно. Вы можете также задать задачу Коши, чтобы из всего множества возможных решений выбрать частное соответствующее заданным начальным условиям. Задача Коши вводится в отдельном поле.
Дифференциальное уравнение
По умолчанию в уравнении функция y является функцией от переменной x . Однако вы можете задать своё обозначение переменной, если напишете, например, y(t) в уравнении, то калькулятор автоматически распознает, что y есть функция от переменной t . С помощью калькулятора вы сможете решать дифференциальные уравнения любой сложности и вида: однородные и неоднородные, линейные или нелинейные, первого порядка или второго и более высоких порядков, уравнения с разделяющимися или неразделяющимися переменными и т.д. Решение диф. уравнения даётся в аналитическом виде, имеет подробное описание. Дифференциальные уравнения очень часто встречаются в физике и математике. Без их вычисления невозможно решать многие задачи (особенно в математической физике).
Одним из этапов решения дифференциальных уравнений является интегрирование функций . Есть стандартные методы решений дифференциальных уравнений. Необходимо привести уравнения к виду с разделяющимися переменными y и x и отдельно проинтегрировать разделенные функции. Чтобы это сделать иногда следует провести определенную замену.
6.1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
При решении различных задач математики и физики, биологии и медицины довольно часто не удается сразу установить функциональную зависимость в виде формулы, связывающей переменные величины, которые описывают исследуемый процесс. Обычно приходится использовать уравнения, содержащие, кроме независимой переменной и неизвестной функции, еще и ее производные.
Определение. Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные различных порядков, называется дифференциальным.
Неизвестную функцию обычно обозначают y(x) или просто y, а ее производные – y” , y” и т. д.
Возможны и другие обозначения, например: если y = x(t), то x”(t), x””(t) – ее производные, а t – независимая переменная.
Определение. Если функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным. Общий вид обыкновенного дифференциального уравнения:
или
Функции F и f могут не содержать некоторых аргументов, но для того, чтобы уравнения были дифференциальными, существенно наличие производной.
Определение. Порядком дифференциального уравнения называется порядок старшей производной, входящей в него.
Например, x 2 y” – y = 0, y” + sinx = 0 – уравнения первого порядка, а y” + 2 y” + 5 y = x – уравнение второго порядка.
При решении дифференциальных уравнений используется операция интегрирования, что связано с появлением произвольной постоянной. Если действие интегрирования применяется n раз, то, очевидно, и в решении будет содержаться n произвольных постоянных.
6.2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Общий вид дифференциального уравнения первого порядка определяется выражением
Уравнение может не содержать в явном виде x и y, но обязательно содержит у”.
Если уравнение можно записать в виде
то получим дифференциальное уравнение первого порядка, разрешенное относительно производной.
Определение. Общим решением дифференциального уравнения первого порядка (6.3) (или (6.4)) является множество решений, где С – произвольная постоянная.
График решения дифференциального уравнения называется интегральной кривой.
Придавая произвольной постоянной С различные значения, можно получить частные решения. На плоскости xOy общее решение представляет собой семейство интегральных кривых, соответствующих каждому частному решению.
Если задать точку A (x 0 , y 0), через которую должна проходить интегральная кривая, то, как правило, из множества функций можно выделить одну – частное решение.
Определение. Частным решением дифференциального уравнения называется его решение, не содержащее произвольных постоянных.
Еслиявляется общим решением, тогда из условия
можно найти постоянную С. Условиеназывают начальным условием.
Задача нахождения частного решения дифференциального уравнения (6.3) или (6.4), удовлетворяющего начальному условиюпри называется задачей Коши. Всегда ли эта задача имеет решение? Ответ содержит следующая теорема.
Теорема Коши (теорема существования и единственности решения). Пусть в дифференциальном уравнении y” = f (x, y) функция f (x, y) и ее
частная производная определены и непрерывны в некоторой
области D, содержащей точкуТогда в области D существует
единственное решение уравнения, удовлетворяющее начальному условиюпри
Теорема Коши утверждает, что при определенных условиях существует единственная интегральная кривая y = f (x), проходящая через точкуТочки, в которых не выполняются условия теоремы
Коши, называются особыми. В этих точках терпит разрыв f (x, y) или.
Через особую точку проходит либо несколько интегральных кривых, либо ни одной.
Определение. Если решение (6.3), (6.4) найдено в виде f (x, y, C) = 0, не разрешенным относительно у, то оно называется общим интегралом дифференциального уравнения.
Теорема Коши только гарантирует, что решение существует. Поскольку единого метода нахождения решения нет, мы будем рассматривать только некоторые типы дифференциальных уравнений первого порядка, интегрируемые в квадратурах.
Определение. Дифференциальное уравнение называется интегрируемым в квадратурах, если отыскание его решения сводится к интегрированию функций.
6.2.1. Дифференциальные уравнения первого порядка с разделяющимися переменными
Определение. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными,
Правая часть уравнения (6.5) представляет собой произведение двух функций, каждая из которых зависит только от одной переменной.
Например, уравнениеявляется уравнением с разделяющи-
мися переменными
а уравнение
нельзя представить в виде (6.5).
Учитывая, что, перепишем (6.5) в виде
Из этого уравнения получим дифференциальное уравнение с разделенными переменными, в котором при дифференциалах стоят функции, зависящие лишь от соответствующей переменной:
Интегрируя почленно, имеем
где C = C 2 – C 1 – произвольная постоянная. Выражение (6.6) представляет собой общий интеграл уравнения (6.5).
Разделив обе части уравнения (6.5) на,, мы можем потерять те решения, при которых,Действительно, еслипри
тоочевидно, является решением уравнения (6.5).
Пример 1. Найти решение уравненияудовлетворяющее
условию: y = 6 при x = 2 (y (2) = 6).
Решение. Заменим у” натогда. Умножим обе части на
dx, так как при дальнейшем интегрировании нельзя оставлять dx в знаменателе:
а затем, разделив обе части наполучим уравнение,
которое можно проинтегрировать. Интегрируем:
Тогда; потенцируя, получим y = C . (x + 1) – об-
щее решение.
По начальным данным определяем произвольную постоянную, подставив их в общее решение
Окончательно получаем y = 2(x + 1) – частное решение. Рассмотрим еще несколько примеров решения уравнений с разделяющимися переменными.
Пример 2. Найти решение уравнения
Решение. Учитывая, что, получим.
Проинтегрировав обе части уравнения, будем иметь
откуда
Пример 3. Найти решение уравненияРешение. Делим обе части уравнения на те сомножители, которые зависят от переменной, не совпадающей с переменной под знаком дифференциала, т. е. наи интегрируем. Тогда получим
и, наконец,
Пример 4. Найти решение уравнения
Решение. Зная, чтополучим. Разде-
лим переменные. Тогда
Интегрируя, получим
Замечание. В примерах 1 и 2 искомая функция y выражена явно (общее решение). В примерах 3 и 4 – неявно (общий интеграл). В дальнейшем форма решения оговариваться не будет.
Пример 5. Найти решение уравненияРешение.
Пример 6. Найти решение уравнения, удовлетворяющее
условию y(e) = 1.
Решение. Запишем уравнение в виде
Умножая обе части уравнения на dx и на, получим
Интегрируя обе части уравнения (интеграл в правой части берется по частям), получим
Но по условию y = 1 при x = e . Тогда
Подставим найденные значения С в общее решение:
Полученное выражение называется частным решением дифференциального уравнения.
6.2.2. Однородные дифференциальные уравнения первого порядка
Определение. Дифференциальное уравнение первого порядка называется однородным, если его можно представить в виде
Приведем алгоритм решения однородного уравнения.
1.Вместо y введем новую функциюТогдаи, следовательно,
2.В терминах функции u уравнение (6.7) принимает вид
т. е. замена сводит однородное уравнение к уравнению с разделяющимися переменными.
3.Решая уравнение (6.8), находим сначала u, а затем y = ux.
Пример 1. Решить уравнениеРешение. Запишем уравнение в виде
Производим подстановку:
Тогда
Заменим
Умножим на dx: Разделим на x и натогда
Проинтегрировав обе части уравнения по соответствующим переменным, будем иметь
или, возвращаясь к старым переменным, окончательно получим
Пример 2. Решить уравнениеРешение. Пустьтогда
Поделим обе части уравнения на x 2: Раскроем скобки и перегруппируем слагаемые:
Переходя к старым переменным, придем к окончательному результату:
Пример 3. Найти решение уравнения при условии
Решение. Выполняя стандартную заменуполучаем
или
или
Значит, частное решение имеет видПример 4. Найти решение уравнения
Решение.
Пример 5. Найти решение уравнения Решение.
Самостоятельная работа
Найти решение дифференциальных уравнений с разделяющимися переменными (1-9).
Найти решение однородных дифференциальных уравнений (9-18).
6.2.3. Некоторые приложения дифференциальных уравнений первого порядка
Задача о радиоактивном распаде
Скорость распада Ra (радия) в каждый момент времени пропорциональна его наличной массе. Найти закон радиоактивного распада Ra, если известно, что в начальный момент имелосьRa и период полураспада Ra равен 1590 лет.
Решение. Пусть в моментмасса Ra составляет x = x(t) г, причем Тогда скорость распада Ra равна
По условию задачи
где k
Разделяя в последнем уравнении переменные и интегрируя, получим
откуда
Для определения C используем начальное условие: при.
Тогдаи, значит,
Коэффициент пропорциональности k определяем из дополнительного условия:
Имеем
Отсюдаи искомая формула
Задача о скорости размножения бактерий
Скорость размножения бактерий пропорциональна их количеству. В начальный момент имелось 100 бактерий. В течение 3 ч их число удвоилось. Найти зависимость количества бактерий от времени. Во сколько раз увеличится количество бактерий в течение 9 ч?
Решение. Пусть x – количество бактерий в момент t. Тогда, согласно условию,
где k – коэффициент пропорциональности.
ОтсюдаИз условия известно, что. Значит,
Из дополнительного условия. Тогда
Искомая функция:
Значит, при t = 9 x = 800, т. е. в течение 9 ч количество бактерий увеличилось в 8 раз.
Задача об увеличении количества фермента
В культуре пивных дрожжей быстрота прироста действующего фермента пропорциональна его начальному количеству x. Первоначальное количество фермента a в течение часа удвоилось. Найти зависимость
x(t).
Решение. По условию дифференциальное уравнение процесса имеет вид
отсюда
Но. Значит, C = a и тогда
Известно также, что
Следовательно,
6.3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
6.3.1. Основные понятия
Определение. Дифференциальным уравнением второго порядка называется соотношение, связывающее независимую переменную, искомую функцию и ее первую и вторую производные.
В частных случаях в уравнении могут отсутствовать x, у или у”. Однако уравнение второго порядка обязательно должно содержать у”. В общем случае дифференциальное уравнение второго порядка записывается в виде:
или, если это возможно, в виде, разрешенном относительно второй производной:
Как и в случае уравнения первого порядка, для уравнения второго порядка могут существовать общее и частное решения. Общее решение имеет вид:
Нахождение частного решения
при начальных условиях- заданные
числа) называется задачей Коши. Геометрически это означает, что требуется найти интегральную кривую у = у (x), проходящую через заданную точкуи имеющую в этой точке касательнуюкоторая об-
разует с положительным направлением оси Ox заданный уголт. е. (рис. 6.1). Задача Коши имеет единственное решение, если правая часть уравнения (6.10),непре-
рывна и имеет непрерывные частные производные по у, у” в некоторой окрестности начальной точки
Для нахождения постоянных входящих в частное решение, надо разрешить систему
Рис. 6.1. Интегральная кривая
Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы) различных порядков.
Порядком дифференциального уравнения называется порядок старшей производной, содержащейся в нём.
Кроме обыкновенных изучаются также дифференциальные уравнения с частными производными . Это уравнения, связывающие независимые переменные , неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово “обыкновенные”.
Примеры дифференциальных уравнений:
(1) ;
(3) ;
(4) ;
Уравнение (1) – четвёртого порядка, уравнение (2) – третьего порядка, уравнения (3) и (4) – второго порядка, уравнение (5) – первого порядка.
Дифференциальное уравнение n -го порядка не обязательно должно содержать явно функцию, все её производные от первого до n -го порядка и независимую переменную. В нём могут не содержаться явно производные некоторых порядков, функция, независимая переменная.
Например, в уравнении (1) явно нет производных третьего и второго порядков, а также функции; в уравнении (2) – производной второго порядка и функции; в уравнении (4) – независимой переменной; в уравнении (5) – функции. Только в уравнении (3) содержатся явно все производные, функция и независимая переменная.
Решением дифференциального уравнения называется всякая функция y = f(x) , при подстановке которой в уравнение оно обращается в тождество.
Процесс нахождения решения дифференциального уравнения называется его интегрированием .
Пример 1. Найти решение дифференциального уравнения .
Решение. Запишем данное уравнение в виде . Решение состоит в нахождении функции по её производной. Изначальная функция, как известно из интегрального исчисления , есть первообразная для , т. е.
Это и есть решение данного дифференциального уравнения . Меняя в нём C , будем получать различные решения. Мы выяснили, что существует бесконечное множество решений дифференциального уравнения первого порядка.
Общим решением дифференциального уравнения n -го порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее n независимых произвольных постоянных, т. е.
Решение дифференциального уравнения в примере 1 является общим.
Частным решением дифференциального уравнения называется такое его решение, в котором произвольным постоянным придаются конкретные числовые значения.
Пример 2. Найти общее решение дифференциального уравнения и частное решение при .
Решение. Проинтегрируем обе части уравнения такое число раз, которому равен порядок дифференциального уравнения.
,
.
В результате мы получили общее решение –
данного дифференциального уравнения третьего порядка.
Теперь найдём частное решение при указанных условиях. Для этого подставим вместо произвольных коэффициентов их значения и получим
.
Если кроме дифференциального уравнения задано начальное условие в виде , то такая задача называется задачей Коши . В общее решение уравнения подставляют значения и и находят значение произвольной постоянной C , а затем частное решение уравнения при найденном значении C . Это и есть решение задачи Коши.
Пример 3. Решить задачу Коши для дифференциального уравнения из примера 1 при условии .
Решение. Подставим в общее решение значения из начального условия y = 3, x = 1. Получаем
Записываем решение задачи Коши для данного дифференциального уравнения первого порядка:
При решении дифференциальных уравнений, даже самых простых, требуются хорошие навыки интегрирования и взятия производных , в том числе сложных функций . Это видно на следующем примере.
Пример 4. Найти общее решение дифференциального уравнения .
Решение. Уравнение записано в такой форме, что можно сразу же интегрировать обе его части.
.
Применяем метод интегрирования заменой переменной (подстановкой) . Пусть , тогда .
Требуется взять dx и теперь – внимание – делаем это по правилам дифференцирования сложной функции , так как x и есть сложная функция (“яблоко” – извлечение квадратного корня или, что то же самое – возведение в степень “одна вторая”, а “фарш” – самое выражение под корнем):
Находим интеграл:
Возвращаясь к переменной x , получаем:
.
Это и есть общее решение данного дифференциального уравнения первой степени.
Не только навыки из предыдущих разделов высшей математики потребуются в решении дифференциальных уравнений, но и навыки из элементарной, то есть школьной математики. Как уже говорилось, в дифференциальном уравнении любого порядка может и не быть независимой переменной, то есть, переменной x . Помогут решить эту проблему не забытые (впрочем, у кого как) со школьной скамьи знания о пропорции. Таков следующий пример.
Или уже решены относительно производной , или их можно решить относительно производной .
Общее решение дифференциальных уравнений типа на интервале X , который задан, можно найти, взяв интеграл обоих частей этого равенства.
Получим .
Если посмотреть на свойства неопределенного интеграла, то найдем искомое общее решение:
y = F(x) + C ,
где F(x) – одна из первообразных функции f(x) на промежутке X , а С – произвольная постоянная.
Обратите внимание, что в большинстве задач интервал X не указывают. Это значит, что решение нужно находить для всех x , при которых и искомая функция y , и исходное уравнение имеют смысл.
Если нужно вычислить частное решение дифференциального уравнения , которое удовлетворяет начальному условию y(x 0) = y 0 , то после вычисления общего интеграла y = F(x) + C , еще необходимо определить значение постоянной C = C 0 , используя начальное условие. Т.е., константу C = C 0 определяют из уравнения F(x 0) + C = y 0 , и искомое частное решение дифференциального уравнения примет вид:
y = F(x) + C 0 .
Рассмотрим пример:
Найдем общее решение дифференциального уравнения , проверим правильность результата. Найдем частное решение этого уравнения, которое удовлетворяло бы начальному условию .
Решение:
После того, как мы проинтегрировали заданное дифференциальное уравнение, получаем:
.
Возьмем этот интеграл методом интегрирования по частям:
Т.о., является общим решением дифференциального уравнения.
Чтобы убедиться в правильности результата, сделаем проверку. Для этого подставляем решение, которое мы нашли, в заданное уравнение:
.
То есть, при исходное уравнение превращается в тождество:
поэтому общее решение дифференциального уравнения определили верно.
Решение, которое мы нашли, является общим решением дифференциального уравнения для каждого действительного значения аргумента x .
Осталось вычислить частное решение ОДУ, которое удовлетворяло бы начальному условию . Другими словами, необходимо вычислить значение константы С , при котором будет верно равенство:
.
.
Тогда, подставляя С = 2 в общее решение ОДУ, получаем частное решение дифференциального уравнения, которое удовлетворяет первоначальному условию:
.
Обыкновенное дифференциальное уравнение можно решить относительно производной, разделив 2 части равенства на f(x) . Это преобразование будет равнозначным, если f(x) не превращается в нуль ни при каких x из интервала интегрирования дифференциального уравнения X .
Вероятны ситуации, когда при некоторых значениях аргумента x ∈ X функции f(x) и g(x) одновременно превращаются в нуль. Для подобных значений x общим решением дифференциального уравнения будет всякая функция y , которая определена в них, т.к. .
Если для некоторых значений аргумента x ∈ X выполняется условие , значит, в этом случае у ОДУ решений нет.
Для всех других x из интервала X общее решение дифференциального уравнения определяется из преобразованного уравнения .
Разберем на примерах:
Пример 1.
Найдем общее решение ОДУ: .
Решение.
Из свойств основных элементарных функций ясно, что функция натурального логарифма определена для неотрицательных значений аргумента, поэтому областью определения выражения ln(x+3) есть интервал x > -3 . Значит, заданное дифференциальное уравнение имеет смысл для x > -3 . При этих значениях аргумента выражение x + 3 не обращается в нуль, поэтому можно решить ОДУ относительно производной, разделив 2 части на х + 3 .
Получаем .
Далее проинтегрируем полученное дифференциальное уравнение, решенное относительно производной: . Для взятия этого интеграла пользуемся методом подведения под знак дифференциала.
Приложение
Решение дифференциальных уравнений онлайн на сайт для закреплеения студентами пройденного материала. И тренировки своих практических навыков. Дифференциальные уравнения онлайн. Дифуры онлайн, решение математики в режиме онлайн. Пошаговое решение математических задач онлайн. Порядок, или степень дифференциального уравнения – наивысший порядок производных, входящих в него. Дифференциальные уравнения онлайн. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет. Пошаговое решение дифференциальных уравнений онлайн. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Дифференциальные уравнения онлайн. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы. Пошаговое решение дифференциальных уравнений онлайн. В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных. Решения дифференциальных уравнений подразделяются на общие и частные решения. Дифференциальные уравнения онлайн. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных – произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). Пошаговое решение дифференциальных уравнений онлайн. После определения вида указанных постоянных и неопределенных функций решения становятся частными. Поиск решений обыкновенных дифференциальных уравнений привёл к установлению класса специальных функций – часто встречающихся в приложениях функций, не выражающихся через известные элементарные функции. Дифференциальные уравнения онлайн. Их свойства были подробно изучены, составлены таблицы значений, определены взаимные связи и т.д.. Множество перечисляемых чисел исследовать можно. Лучший ответ на поставленную задачу. Как найти в первом приближении исходящий вектор к области сходимости про Дифференциальные уравнения без выяснения найденного верхнего предела. Выбор очевиден для возрастания математических функций. Есть прогрессивный метод над уровнем исследования. Выровнять по начальному условию задачи решение дифференциальных поможет найти однозначное выбранное значение. Может быть так, что сможет неизвестную определить сразу. Как в предыдущем примере на указание решения для математической задачи, линейные дифференциальные уравнения есть ответ на поставленную конкретно задачу в указанные сроки. Локально не определено поддержание процедуры исследования. Будет так, что пример найдется для каждого студента и решение дифференциальных уравнений определит назначенный на ответственного исполнителя как минимум из двух значений. Взять на некотором отрезке функцию общего значения и предупредить по которой оси будет разрыв. Изучив дифференциальные уравнения онлайн, возможно однозначно показать на сколько важен результат, если таковой предусмотрен из начальных условий. Вырезать область из определения функции – это невозможно, так как локально нет определения по задаче. Будучи найденным из системы уравнений, ответ содержит в себе переменную, исчисляемую в общем смысле, но решить дифференциальное уравнение онлайн естественно получится без этого действия по определению сказанного условия. Рядом с промежутком отрезка видно как решение дифференциальных уравнений онлайн способно продвинуть результат исследований в положительную сторону на момент среза знаний у студентов. Лучшее не всегда получается путем общего принятого подхода к делу. На уровне двукратного увеличения можно с пользой просмотреть все необходимые линейные дифференциальные уравнения в естественном представлении, но возможность подсчитать числовое значение приведет к улучшению знаний. По любой методике в математике есть дифференциальные уравнения, которые представлены в различных по своей сути выражениях, такие как однородные или сложные. Проведя общий анализ исследования функции, станет ясно, что решение дифференциальных как множество возможностей представляет собой явную погрешность в значениях. Истинна в ней заключается в пространстве над линий абсцисс. Где-то в области определения сложной функции в некоторой точке её определения линейные дифференциальные уравнения смогут представить ответ в аналитическом виде. то есть в общем виде как суть. Не поменяется ничего при замене переменной. Однако нужно с особым интересом вглядываться в ответ. Меняет по сути калькулятор отношение в итоге, то есть как решение дифференциальных уравнений пропорционально глобальному значению обозначается в пределах искомого решения. В ряде случаев предупреждение о массовой ошибке неизбежно. Дифференциальные уравнения онлайн реализуют общее представление о задаче, но в итоге нужно как можно скорее предусмотреть положительные стороны векторного произведения. В математике не редки случаи заблуждения в теории чисел. Однозначно нужна будет проверка. Естественно лучше предоставить это право профессионалам в своем деле и решить дифференциальное уравнение онлайн помогут именно они, так как их опыт колоссальный и положительный. Разница на поверхностях фигур и площадь такова, что не решение дифференциальных уравнений онлайн позволит видеть, а множество не пересекаемых объектов таково, что линия параллельна оси. В итоге можно получить в два раза больше значений. Будучи не в явном виде, наше представление о правильности формально записи предусматривает линейные дифференциальные уравнения как в области просмотра, так и в отношении преднамеренного завышения качества результата. Несколько раз выходит в обзор решаемое на коллегии обсуждение на тему, интересную всем студентам. На протяжении всего изучения полного курса лекций, мы заострим наше пристальное внимание на дифференциальные уравнения и связные с ними области изучения науки, если тем самым не противоречить истине. Многих этапов можно избежать в начале пути. Если решение дифференциальных по-прежнему является принципиально чем-то новым для студентов, то старое вовсе не забывается, а прогрессирует в будущее с высокой скоростью развития. Изначально условия по задаче в математике расходятся, но это обозначено в абзаце справа. По истечению времени заданного по определению не исключены возможности пропорционального зависимого исхода на различных плоскостях движения вектора. Исправляется такой простой случай также как описываются линейные дифференциальные уравнения на калькуляторе в общем виде, так будет быстрее и взаимозачет расчетов не приведет к ошибочному мнению. Лишь пять названных по теории случаев могут раздвигать грани происходящего. Вручную рассчитать значение в цифрах поможет наше решение дифференциальных уравнений уже на первых этапах разложения функционального пространства. В нужных местах необходимо точку соприкосновения четырех линий представить в общем значении. Но если придется задачу вытеснить, то приравнять сложность будет просто. Исходных данных достаточно для оформления прилежащего катета и дифференциальные уравнения онлайн выглядят выровненными по левому краю и поверхность односторонняя направлена к ротору вектора. Выше верхнего предела возможны числовые значения сверх обозначенного условия. Принимать во внимание математическую формулу и решить дифференциальное уравнение онлайн за счет трех неизвестных в общем значении пропорции возможно. Локальный метод расчета признан действительным. Система координат прямоугольная в относительном движении плоскости. Общее решение дифференциальных уравнений онлайн позволяет однозначно сделать вывод в пользу расчетной прогонки сквозь матричные определения на всей прямой, расположенной выше графика заданной в явном виде функции. Решение насквозь проглядывается, если приложить вектор движения к точке соприкосновения трех полушарий. Цилиндр получается путем вращения прямоугольника вокруг стороны и линейные дифференциальные уравнения смогут показать направление движения точки по заданным выражениям её закона движения. Исходные данные верные и задача в математике взаимозаменяема при одном несложном условии. Однако в силу обстоятельств, в виду сложности постановочной подзадачи, дифференциальные уравнения упрощают процесс калькулировано числовых пространств на уровне трехмерного пространства. Легко доказать обратное, но этого возможно избежать, как в приведенном примере. В высшей математике предусмотрены следующие моменты: когда задача приводится к упрощенному виду, на неё следует распространить как можно большее усилие со стороны студентов. Взачет попадают наложенные друг на друга линии. Про решение дифференциальных по-прежнему возобновляет преимущество сказанного метода на кривой линии. Если распознать вначале не то, что нужно, то математическая формула составит новое значение выражения. Цель – оптимальный подход к решению поставленных профессором задания. Не стоит полагать, что линейные дифференциальные уравнения в упрощенном виде превзойдут ожидаемый результат. На конечно составленной поверхности разместим три вектора. ортогональные друг другу. Вычислим произведение. Проведем сложение большего числа символов и распишем из полученного выражения все переменные функции. Есть пропорция. Несколько действий, предшествующих окончанию вычисления, однозначного ответа на решение дифференциальных уравнений дадут не сразу, а только по истечению отведенного времени по оси ординат. Слева от точки разрыва, заданной в неявном виде от функции, проведем ось, ортогональную лучшему возрастающему вектору и дифференциальные уравнения онлайн расположим вдоль наименьшего граничного значения нижней грани математического объекта. Лишний аргумент присоединим в области разрыва функции. Правее от точек расположения кривой линии решить дифференциальное уравнение онлайн помогут написанные нами формулы приведения к общему знаменателю. Единственно верным подходом примем тот, что прольет свет на нерешенные задачи из теории в практику, в общем случае однозначно. Линии по направлению координат заданных точек ни разу не сомкнули крайнее положение квадрата, однако решение дифференциальных уравнений онлайн поможет в изучении математики и студентам, и нам, и просто начинающим людям в этой области. Речь идет о возможности подстановки аргумента значения во все значимые под линии одного поля. В принципе, как и следовало ожидать, наши линейные дифференциальные уравнения есть нечто обособленное в единое понятие приведенного смысла. В помощь студентам один из лучших среди аналогичных сервисов калькулятор. Пройдите все курсы и выберите оптимальный правильный для себя.
=Дифференциальные уравнения
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с “узкой” шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Вот мои заметки к моему курсу дифференциальных уравнений, который я преподаю здесь, в Университете Ламара. Несмотря на то, что это мои «классные заметки», они должны быть доступны для всех, кто хочет научиться решать дифференциальные уравнения или нуждается в переподготовке по дифференциальным уравнениям.Я постарался сделать эти заметки как можно более самодостаточными, поэтому вся информация, необходимая для их прочтения, взята либо из класса математики или алгебры, либо содержится в других разделах заметок.
Вот несколько предупреждений моим ученикам, которые могут быть здесь, чтобы получить копию того, что произошло в день, который вы пропустили.
- Поскольку я хотел сделать это довольно полным набором заметок для всех, кто хочет изучать дифференциальные уравнения, я включил в себя некоторый материал, который у меня обычно нет времени, чтобы охватить в классе, и поскольку он меняется от семестра к семестру, он здесь не отмечен .Вам нужно будет найти кого-нибудь из одноклассников, чтобы увидеть, есть ли в этих заметках что-то, чего не было в классе.
- В общем, в классе я стараюсь решать задачи, отличные от моих заметок. Тем не менее, с помощью дифференциального уравнения многие проблемы трудно решить в мгновение ока, и поэтому в этом классе моя классная работа будет следовать этим заметкам достаточно близко, насколько далеко зайдут решенные задачи. С учетом сказанного, я буду время от времени работать над проблемами из головы, когда я могу привести больше примеров, чем только те, что указаны в моих заметках.Кроме того, у меня часто нет времени в классе, чтобы проработать все задачи в заметках, поэтому вы обнаружите, что некоторые разделы содержат задачи, которые не были решены в классе из-за ограничений по времени.
- Иногда вопросы в классе приводят к путям, которые здесь не описаны. Я стараюсь предвидеть как можно больше вопросов, когда пишу их, но в действительности я не могу предвидеть все вопросы. Иногда в классе задают очень хороший вопрос, который приводит к выводам, которые я здесь не включил.Вам всегда следует поговорить с кем-то, кто был в классе в тот день, когда вы пропустили, сравнить эти записи с их записями и посмотреть, в чем разница.
- Это в некоторой степени связано с предыдущими тремя пунктами, но достаточно важно, чтобы заслужить отдельный пункт. ЭТИ ЗАПИСИ НЕ ЯВЛЯЮТСЯ ЗАМЕНАМИ ДЛЯ ПОСЕЩЕНИЯ КЛАССА !! Использование этих заметок в качестве замены урока может доставить вам неприятности. Как уже отмечалось, не все в этих заметках освещается в классе, и часто материал или идеи, отсутствующие в этих заметках, рассматриваются в классе.
Вот список (и краткое описание) материалов, содержащихся в этом наборе примечаний.
Основные понятия – В этой главе мы вводим многие из основных понятий и определений, которые встречаются в типичном курсе дифференциальных уравнений. Мы также рассмотрим поля направлений и то, как их можно использовать для определения поведения решений дифференциальных уравнений. Определения – в этом разделе вводятся некоторые из общих определений и понятий в курсе дифференциальных уравнений, включая порядок, линейный и линейный.нелинейный, начальные условия, начальная задача и период действия.Поля направления – В этом разделе мы обсуждаем поля направления и их рисование. Мы также исследуем, как поля направления могут использоваться для определения некоторой информации о решении дифференциального уравнения, не имея фактического решения.
Заключительные мысли – В этом разделе мы дадим пару заключительных мыслей о том, что мы будем рассматривать на протяжении этого курса.
Дифференциальные уравнения первого порядка – В этой главе мы рассмотрим несколько стандартных методов решения дифференциальных уравнений первого порядка, включая линейные, разделимые, точные и дифференциальные уравнения Бернулли.Мы также рассмотрим интервалы применимости, равновесные решения и метод Эйлера. Кроме того, мы моделируем некоторые физические ситуации с помощью дифференциальных уравнений первого порядка. Линейные уравнения – в этом разделе мы решаем линейные дифференциальные уравнения первого порядка, то есть дифференциальные уравнения в форме \ (y ‘+ p (t) y = g (t) \). Мы даем подробный обзор процесса, используемого для решения этого типа дифференциального уравнения, а также вывод формулы, необходимой для интегрирующего коэффициента, используемого в процессе решения.
Разделимые уравнения – В этом разделе мы решаем разделимые дифференциальные уравнения первого порядка, то есть дифференциальные уравнения в форме \ (N (y) y ‘= M (x) \). Мы дадим вывод процесса решения этого типа дифференциального уравнения. Мы также начнем искать интервал применимости решения дифференциального уравнения.
Точные уравнения – В этом разделе мы обсудим определение и решение точных дифференциальных уравнений. Мы разработаем тест, который можно использовать для идентификации точных дифференциальных уравнений и дать подробное объяснение процесса решения.{n} \). В этом разделе также будет представлена идея использования подстановки для решения дифференциальных уравнений.
Замены – в этом разделе мы продолжим с того места, где закончился последний раздел, и рассмотрим пару других замен, которые можно использовать для решения некоторых дифференциальных уравнений. В частности, мы обсудим использование решений для решения дифференциальных уравнений вида \ (y ‘= F (\ frac {y} {x}) \) и \ (y’ = G (ax + by) \).
Интервалы достоверности – в этом разделе мы подробно рассмотрим интервалы достоверности, а также ответим на вопрос о существовании и уникальности дифференциальных уравнений первого порядка.
Моделирование с помощью дифференциальных уравнений первого порядка – В этом разделе мы будем использовать дифференциальные уравнения первого порядка для моделирования физических ситуаций. В частности, мы рассмотрим проблемы смешивания (моделирование количества вещества, растворенного в жидкости, и жидкость как на входе, так и на выходе), проблемы популяции (моделирование популяции в различных ситуациях, в которых популяция может входить или выходить) и падающие объекты. (моделирование скорости падающего объекта под действием силы тяжести и сопротивления воздуха).
Равновесные решения – В этом разделе мы определим равновесные решения (или точки равновесия) для автономных дифференциальных уравнений, \ (y ‘= f (y) \). Мы обсуждаем классификацию равновесных решений как асимптотически устойчивые, нестабильные или полустабильные равновесные решения.
Метод Эйлера. В этом разделе мы кратко рассмотрим довольно простой метод приближения решений дифференциальных уравнений. Мы выводим формулы, используемые методом Эйлера, и даем краткое обсуждение ошибок в приближении решений.
Дифференциальные уравнения второго порядка – В этой главе мы начнем рассматривать дифференциальные уравнения второго порядка. { 2} + br + c = 0 \), являются различными действительными корнями.{2} + br + c = 0 \), повторяются, т.е. двойных корня. Мы будем использовать сокращение порядка, чтобы получить второе решение, необходимое для получения общего решения в этом случае.
Снижение порядка – в этом разделе мы обсудим снижение порядка, процесс, используемый для получения решения случая повторяющихся корней для однородных линейных дифференциальных уравнений второго порядка, более подробно. Это будет один из немногих случаев в этой главе, когда будет рассмотрено дифференциальное уравнение с непостоянными коэффициентами.
Фундаментальные наборы решений – В этом разделе мы рассмотрим некоторые теории, лежащие в основе решения дифференциальных уравнений второго порядка. Мы определяем фундаментальные наборы решений и обсуждаем, как их можно использовать для получения общего решения однородного дифференциального уравнения второго порядка. Мы также определим вронскиан и покажем, как его можно использовать, чтобы определить, является ли пара решений фундаментальным набором решений.
Подробнее о вронскиане – В этом разделе мы рассмотрим, как вронскиан, представленный в предыдущем разделе, можно использовать для определения того, являются ли две функции линейно независимыми или линейно зависимыми.Мы также дадим альтернативный метод нахождения вронскиана.
Неоднородные дифференциальные уравнения – В этом разделе мы обсудим основы решения неоднородных дифференциальных уравнений. Мы определяем дополнительное и частное решение и даем форму общего решения неоднородного дифференциального уравнения.
Неопределенные коэффициенты – В этом разделе мы представляем метод неопределенных коэффициентов для нахождения частных решений неоднородного дифференциального уравнения.Мы работаем с большим количеством примеров, иллюстрирующих множество рекомендаций по первоначальному предположению о форме конкретного решения, необходимого для метода.
Изменение параметров – В этом разделе мы представляем метод изменения параметров для поиска частных решений неоднородного дифференциального уравнения. Мы подробно исследуем метод, а также выводим формулу, которая может быть использована для поиска конкретных решений.
Механические колебания – В этом разделе мы рассмотрим механические колебания.В частности, мы будем моделировать объект, связанный с пружиной и движущийся вверх и вниз. Мы также допускаем введение в систему демпфера и общие внешние силы, действующие на объект. Также обратите внимание, что хотя мы приводим примеры механических колебаний в этом разделе, простое изменение обозначений (и соответствующее изменение того, что представляют собой величины) может переместить это практически в любую другую область техники.
Преобразования Лапласа – В этой главе мы познакомимся с преобразованиями Лапласа и их использованием для решения задач начального значения.С введением преобразований Лапласа мы теперь можем решить некоторые проблемы с начальными значениями, которые иначе мы не смогли бы решить. Мы будем решать дифференциальные уравнения, включающие дельта-функции Хевисайда и Дирака. Мы также дадим краткий обзор использования преобразований Лапласа для решения дифференциальных уравнений с непостоянными коэффициентами. Кроме того, мы определим интеграл свертки и покажем, как его можно использовать для обратных преобразований. Определение – В этом разделе мы даем определение преобразования Лапласа.Мы также вычислим пару преобразований Лапласа, используя определение.
Преобразования Лапласа – В этом разделе мы представляем способ, которым мы обычно вычисляем преобразования Лапласа, который избегает необходимости использовать определение. Мы обсуждаем таблицу преобразований Лапласа, используемую в этом материале, и приводим множество примеров, иллюстрирующих использование таблицы преобразований Лапласа.
Обратное преобразование Лапласа – В этом разделе мы задаем вопрос, противоположный предыдущему. Другими словами, какую функцию мы изначально имели при преобразовании Лапласа? Мы снова проработаем множество примеров, иллюстрирующих, как использовать для этого таблицу преобразований Лапласа, а также некоторые манипуляции с данным преобразованием Лапласа, которые необходимы для использования таблицы.
Шаговые функции – в этом разделе мы представляем шаг или функцию Хевисайда. Мы проиллюстрируем, как написать кусочную функцию в терминах функций Хевисайда. Мы также работаем с множеством примеров, показывающих, как использовать преобразования Лапласа и обратные преобразования Лапласа, которые включают функции Хевисайда. Мы также выводим формулы для преобразования Лапласа функций, которые включают функции Хевисайда.
Решение IVP с помощью преобразований Лапласа – В этом разделе мы рассмотрим, как использовать преобразования Лапласа для решения IVP.Примеры в этом разделе ограничены дифференциальными уравнениями, которые можно решить без использования преобразования Лапласа. Преимущество начала работы с этим типом дифференциального уравнения заключается в том, что работа, как правило, не такая сложная, и мы всегда можем проверить свои ответы, если захотим.
IVP с непостоянным коэффициентом. В этом разделе мы дадим краткий обзор использования преобразований Лапласа для решения некоторых IVP с непостоянным коэффициентом. В этом разделе мы не работаем с большим количеством примеров.Мы работаем только с парой, чтобы проиллюстрировать, как этот процесс работает с преобразованиями Лапласа.
IVP с пошаговыми функциями – это раздел, в котором действительно становится очевидной причина использования преобразований Лапласа. Мы будем использовать преобразования Лапласа для решения IVP, содержащих функции Хевисайда (или ступенчатые). Без преобразований Лапласа их решение потребовало бы довольно много работы. Хотя мы действительно работаем с одним из этих примеров без преобразований Лапласа, мы делаем это только для того, чтобы показать, что будет, если мы попытаемся решить один из примеров без использования преобразований Лапласа.
Дельта-функция Дирака – В этом разделе мы вводим дельта-функцию Дирака и выводим преобразование Лапласа для дельта-функции Дирака. Мы работаем над парой примеров решения дифференциальных уравнений, включающих дельта-функции Дирака, и в отличие от задач с функциями Хевисайда наш единственный реальный вариант для такого рода дифференциальных уравнений – использовать преобразования Лапласа. Мы также показываем хорошую взаимосвязь между функциями Хевисайда и дельта Дирака.
Интеграл свертки – В этом разделе мы даем краткое введение в интеграл свертки и то, как его можно использовать для получения обратных преобразований Лапласа.Мы также проиллюстрируем его использование при решении дифференциального уравнения, в котором функция принуждения (, т. Е. , член без каких-либо y) неизвестна.
Таблица преобразований Лапласа – Этот раздел представляет собой таблицу преобразований Лапласа, которую мы будем использовать в материале. Мы даем как можно больше разнообразных преобразований Лапласа, включая те, которые не часто приводятся в таблицах преобразований Лапласа.
Системы дифференциальных уравнений – В этой главе мы рассмотрим решение систем дифференциальных уравнений.Мы ограничимся системами двух линейных дифференциальных уравнений в целях обсуждения, но многие из методов будут распространяться на более крупные системы линейных дифференциальных уравнений. Мы также исследуем эскизные фазовые плоскости / портреты для систем двух дифференциальных уравнений. Кроме того, мы даем краткие обсуждения использования преобразований Лапласа для решения систем и некоторого моделирования, которое приводит к системам дифференциальных уравнений. Обзор: Системы уравнений – В этом разделе мы дадим обзор традиционной отправной точки для класса линейной алгебры.Мы будем использовать методы линейной алгебры для решения системы уравнений, а также дадим несколько полезных фактов о количестве решений, которые может иметь система уравнений. Обзор
: матрицы и векторы – В этом разделе мы дадим краткий обзор матриц и векторов. Мы рассмотрим арифметику, включающую матрицы и векторы, нахождение обратной матрицы, вычисление определителя матрицы, линейно зависимых / независимых векторов и преобразование систем уравнений в матричную форму.Обзор
: собственные значения и собственные векторы – в этом разделе мы познакомим вас с концепцией собственных значений и собственных векторов матрицы. Мы определяем характеристический полином и показываем, как его можно использовать для нахождения собственных значений матрицы. Когда у нас есть собственные значения для матрицы, мы также показываем, как найти соответствующие собственные значения для матрицы.
Системы дифференциальных уравнений – В этом разделе мы рассмотрим некоторые основы систем дифференциальных уравнений. Мы показываем, как преобразовать систему дифференциальных уравнений в матричную форму.{\ text {th}} \) дифференциальное уравнение порядка в систему дифференциальных уравнений.
Решения для систем – В этом разделе мы дадим краткий обзор того, как мы решаем системы дифференциальных уравнений в матричной форме. Мы также определяем вронскиан для систем дифференциальных уравнений и показываем, как его можно использовать, чтобы определить, есть ли у нас общее решение системы дифференциальных уравнений.
Phase Plane – В этом разделе мы дадим краткое введение в фазовую плоскость и фазовые портреты.Мы определяем равновесное решение / точку для однородной системы дифференциальных уравнений и то, как фазовые портреты могут быть использованы для определения устойчивости равновесного решения. Мы также показываем формальный метод построения фазовых портретов.
Действительных собственных значений – в этом разделе мы будем решать системы двух линейных дифференциальных уравнений, в которых собственные значения являются различными действительными числами. Мы также покажем, как рисовать фазовые портреты, связанные с реальными различными собственными значениями (седловые точки и узлы).
Комплексные собственные значения – в этом разделе мы будем решать системы двух линейных дифференциальных уравнений, в которых собственные значения являются комплексными числами. Это будет включать в себя иллюстрацию того, как получить решение, которое не включает комплексные числа, которые мы обычно ищем в этих случаях. Мы также покажем, как рисовать фазовые портреты, связанные со сложными собственными значениями (центрами и спиралями).
повторяющихся собственных значений – в этом разделе мы будем решать системы двух линейных дифференциальных уравнений, в которых собственные значения являются действительными повторяющимися (в данном случае двойными) числами.Это будет включать получение второго линейно независимого решения, которое нам понадобится для формирования общего решения системы. Мы также покажем, как рисовать фазовые портреты, связанные с реальными повторяющимися собственными значениями (несобственные узлы).
Неоднородные системы – В этом разделе мы рассмотрим быстрые примеры, иллюстрирующие использование неопределенных коэффициентов и изменение параметров для решения неоднородных систем дифференциальных уравнений. Метод неопределенных коэффициентов будет работать примерно так же, как и для дифференциальных уравнений n-го порядка, в то время как изменение параметров потребует некоторой дополнительной работы по выводу, чтобы получить формулу / процесс, которые мы можем использовать в системах.
Преобразования Лапласа – В этом разделе мы рассмотрим быстрый пример, показывающий, как преобразования Лапласа могут использоваться для решения системы двух линейных дифференциальных уравнений.
Моделирование – в этом разделе мы кратко рассмотрим некоторые расширения некоторых моделей моделирования, которые мы выполняли в предыдущих главах, которые приводят к системам дифференциальных уравнений. В частности, мы рассмотрим задачи смешивания, в которых у нас есть два соединенных между собой резервуара с водой, задачу хищник-жертва, в которой учитываются популяции обоих, и задачу механической вибрации с двумя массами, связанными с пружиной и каждая из которых подключена к стена с пружиной.Решения дифференциальных уравнений серии
. В этой главе мы кратко рассмотрим, как представить решение дифференциального уравнения в виде степенного ряда. Мы также рассмотрим, как решить дифференциальное уравнение Эйлера. Кроме того, мы сделаем краткий обзор степенных рядов и рядов Тейлора, чтобы помочь в работе с этой главой. Обзор: степенные ряды – в этом разделе мы даем краткий обзор некоторых основ степенных рядов. Включены обсуждения использования теста отношения для определения сходимости степенного ряда, добавления / вычитания степенного ряда, дифференцирования степенного ряда и сдвигов индекса для степенного ряда.{x} \) и \ (\ cos (x) \) о \ (x = 0 \), а также показывает, как записать ряд Тейлора для многочлена. Решения серии
– В этом разделе мы определяем обычные и особые точки для дифференциального уравнения. Мы также показываем, кто должен строить рядное решение дифференциального уравнения относительно обыкновенной точки. Метод, проиллюстрированный в этом разделе, полезен при решении или, по крайней мере, приближении решения дифференциальных уравнений с непостоянными коэффициентами.{2} y ” + b x y ‘+ c y = 0 \). Обратите внимание, что, хотя это не связано с серийным решением, оно включено в главу о серийном решении, поскольку показывает, как получить решение хотя бы одного типа дифференциального уравнения в особой точке.
Дифференциальные уравнения высшего порядка – В этой главе мы рассмотрим расширение многих идей предыдущих глав на дифференциальные уравнения более высокого порядка, чем второй порядок. В некоторых случаях это будет просто означать работу с примером, чтобы проиллюстрировать, что процесс на самом деле не меняется, но в большинстве случаев есть некоторые вопросы, которые нужно обсудить.{\ text {th}} \) Линейные уравнения порядка – в этом разделе мы начнем главу с краткого обзора некоторых основных идей, лежащих в основе решения линейных дифференциальных уравнений высшего порядка. Включены обновленные определения / факты для принципа суперпозиции, линейно независимых функций и вронскиана.
Линейные однородные дифференциальные уравнения – В этом разделе мы расширим идеи, лежащие в основе решения линейных однородных дифференциальных уравнений порядка 2 и , до более высокого порядка.Как мы увидим, большая часть процесса идентична с несколькими естественными расширениями повторяющихся реальных корней, которые встречаются более двух раз. Нам также нужно будет обсудить, как поступать с повторяющимися сложными корнями, что теперь возможно. Кроме того, мы увидим, что основная трудность в случаях более высокого порядка состоит в простом нахождении всех корней характеристического многочлена.
Неопределенных коэффициентов – В этом разделе мы рассмотрим быстрый пример, чтобы проиллюстрировать, что использование неопределенных коэффициентов в дифференциальных уравнениях более высокого порядка ничем не отличается от того, когда мы использовали его в дифференциальных уравнениях 2-го порядка и только с одним небольшим естественным расширением.
Изменение параметров – В этом разделе мы подробно обсудим процесс использования изменения параметров для дифференциальных уравнений более высокого порядка. Мы также разработаем формулу, которую можно использовать в этих случаях. Мы также увидим, что работа, связанная с использованием изменения параметров в дифференциальных уравнениях более высокого порядка, иногда может быть весьма сложной.
Преобразования Лапласа – В этом разделе мы рассмотрим быстрый пример использования преобразований Лапласа для решения дифференциального уравнения на основе дифференциального уравнения 3 rd , просто чтобы сказать, что мы рассмотрели уравнение с порядком выше 2 и .Как мы увидим, кроме необходимости формулы для преобразования Лапласа \ (y ” ‘\), которую мы можем получить из общей формулы, нет реальной разницы в том, как преобразования Лапласа используются для дифференциальных уравнений более высокого порядка. .
Системы дифференциальных уравнений – В этом разделе мы кратко рассмотрим, как распространить идеи, которые мы обсуждали для решения \ (2 \ times 2 \) систем дифференциальных уравнений, на системы размера \ (3 \ times 3 \). Как мы увидим, они в основном являются естественным продолжением того, что мы уже знаем, кому делать.Мы также сделаем пару быстрых комментариев о системах \ (4 \ times 4 \). Решения серии
– В этом разделе мы рассмотрим быстрый пример, показывающий, что процесс поиска решений ряда для дифференциальных уравнений более высокого порядка в значительной степени аналогичен тому, который используется в дифференциальных уравнениях порядка 2 и .
Краевые задачи и ряды Фурье – В этой главе мы представим две темы, которые являются неотъемлемой частью основных методов решения уравнений в частных производных.Первая тема, краевые задачи, встречается практически во всех уравнениях в частных производных. Вторая тема, ряды Фурье, – это то, что заставляет работать один из основных методов решения. Краевые задачи – в этом разделе мы определим граничные условия (в отличие от начальных условий, с которыми мы уже должны быть знакомы на этом этапе) и краевую задачу. Мы также рассмотрим несколько примеров, иллюстрирующих некоторые интересные различия в использовании граничных значений вместо начальных условий при решении дифференциальных уравнений.
Собственные значения и собственные функции – в этом разделе мы определим собственные значения и собственные функции для краевых задач. Мы проработаем довольно много примеров, иллюстрирующих, как находить собственные значения и собственные функции. В одном примере лучшее, что мы сможем сделать, – это оценить собственные значения, поскольку это то, что будет происходить на довольно регулярной основе с подобными проблемами.
Периодические функции и ортогональные функции – в этом разделе мы определим периодические функции, ортогональные функции и взаимно ортогональные функции.\ infty {{B_n} \ sin \ left ({\ frac {{n \ pi x}} {L}} \ right)} \). Мы также рассмотрим несколько примеров нахождения ряда Фурье для функции.
Сходимость рядов Фурье – В этом разделе мы определим кусочно-гладкие функции и периодическое продолжение функции. Кроме того, мы приведем множество фактов о том, к чему будет сходиться ряд Фурье и когда можно ожидать, что производная или интеграл ряда Фурье сходится к производной или интегралу функции, которую он представляет.
Уравнения с частными производными – В этой главе мы вводим разделение переменных, один из основных методов решения уравнений с частными производными. Включены частные производные для теплового уравнения и волнового уравнения. Кроме того, мы приводим решения примеров для уравнения теплопроводности, волнового уравнения и уравнения Лапласа. Уравнение теплопроводности – в этом разделе мы сделаем частный вывод уравнения теплопроводности, которое можно решить, чтобы определить температуру в одномерном столбце длиной L.Кроме того, мы даем несколько возможных граничных условий, которые можно использовать в этой ситуации. Мы также определяем лапласиан в этом разделе и даем версию уравнения теплопроводности для двух- или трехмерных ситуаций.
Волновое уравнение – В этом разделе мы делаем частный вывод волнового уравнения, которое можно использовать для нахождения одномерного смещения колеблющейся струны. Кроме того, мы также приводим двумерную и трехмерную версии волнового уравнения.
Терминология – В этом разделе мы кратко рассмотрим некоторые термины, которые мы будем использовать в оставшейся части этой главы.В частности, мы определим линейный оператор, линейное уравнение в частных производных и однородное уравнение в частных производных. Мы также быстро напомним принцип суперпозиции.
Разделение переменных – В этом разделе показано, как метод разделения переменных может быть применен к уравнению в частных производных, чтобы уменьшить уравнение в частных производных до двух обыкновенных дифференциальных уравнений. Мы применяем этот метод к нескольким дифференциальным уравнениям в частных производных.Однако мы не продвигаемся дальше в процессе решения уравнений в частных производных. Это будет сделано в следующих разделах. Цель этого раздела – только проиллюстрировать, как работает метод.
Решение теплового уравнения – В этом разделе мы рассмотрим процесс полного разделения переменных, включая решение двух обыкновенных дифференциальных уравнений, которые генерирует процесс. Мы сделаем это, решив уравнение теплопроводности с тремя различными наборами граничных условий. Включен пример решения уравнения теплопроводности на стержне длиной \ (L \), но вместо этого на тонком круглом кольце.
Уравнение теплопроводности с ненулевыми границами температуры – В этом разделе мы кратко рассмотрим решение уравнения теплопроводности с фиксированными граничными условиями и ненулевой температурой. Обратите внимание, что это отличается от предыдущего раздела, когда мы обычно требовали, чтобы граничные условия были как фиксированными, так и нулевыми.
Уравнение Лапласа – В этом разделе мы обсуждаем решение уравнения Лапласа. Как мы увидим, это именно то уравнение, которое нам нужно было бы решить, если бы мы хотели найти равновесное решение ( i.е. не зависит от времени) для двумерного уравнения теплопроводности без источников. Мы также преобразуем уравнение Лапласа в полярные координаты и решим его на диске радиуса \ (a \).
Вибрирующая струна – в этом разделе мы решаем одномерное волновое уравнение, чтобы получить смещение вибрирующей струны.
Сводка по разделению переменных – В этом последнем разделе мы даем краткое описание метода разделения переменных для решения уравнений в частных производных.
Дифференциальные уравнения – Системы DE
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с “узкой” шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Глава 5: Системы дифференциальных уравнений
До сих пор мы рассматривали только решение одиночных дифференциальных уравнений.Однако многие «реальные» ситуации регулируются системой дифференциальных уравнений. Рассмотрим популяционные проблемы, которые мы рассмотрели в разделе моделирования в главе о дифференциальных уравнениях первого порядка. В этих задачах мы рассматривали только популяцию одного вида, но задача также содержала некоторую информацию о хищниках этого вида. Мы предполагали, что в этих случаях любое хищничество будет постоянным. Однако в большинстве случаев уровень хищничества также будет зависеть от популяции хищника.Итак, чтобы быть Более реалистично, мы также должны иметь второе дифференциальное уравнение, которое дало бы популяцию хищников. Также обратите внимание, что популяция хищника будет в некотором роде зависеть от популяции жертвы. Другими словами, нам нужно что-то знать об одной популяции, чтобы найти другую популяцию. Таким образом, чтобы найти популяцию жертвы или хищника, нам нужно решить систему, по крайней мере, из двух дифференциальных уравнений.
Следующая тема обсуждения – как решать системы дифференциальных уравнений.Однако перед этим нам сначала нужно сделать быстрый обзор линейной алгебры. Многое из того, что мы будем делать в этой главе, будет зависеть от тем из линейной алгебры. Этот обзор не предназначен для полного изучения предмета линейной алгебры, поскольку это тема для всего класса. Краткий обзор предназначен для того, чтобы вы достаточно познакомились с некоторыми из основных тем, чтобы вы смогли выполнить необходимую работу, когда мы займемся решением систем дифференциальных уравнений.
Вот краткий список тем, затронутых в этой главе.
Обзор: Системы уравнений – В этом разделе мы дадим обзор традиционной отправной точки для класса линейной алгебры. Мы будем использовать методы линейной алгебры для решения системы уравнений, а также дадим несколько полезных фактов о количестве решений, которые может иметь система уравнений.
Обзор: матрицы и векторы – В этом разделе мы дадим краткий обзор матриц и векторов.Мы рассмотрим арифметику, включающую матрицы и векторы, нахождение обратной матрицы, вычисление определителя матрицы, линейно зависимых / независимых векторов и преобразование систем уравнений в матричную форму.
Обзор: собственные значения и собственные векторы – в этом разделе мы познакомим вас с концепцией собственных значений и собственных векторов матрицы. Мы определяем характеристический полином и показываем, как его можно использовать для нахождения собственных значений матрицы. Когда у нас есть собственные значения для матрицы, мы также показываем, как найти соответствующие собственные значения для матрицы.{\ text {th}} \) дифференциальное уравнение порядка в систему дифференциальных уравнений.
Решения для систем – В этом разделе мы дадим краткий обзор того, как мы решаем системы дифференциальных уравнений в матричной форме. Мы также определяем вронскиан для систем дифференциальных уравнений и показываем, как его можно использовать, чтобы определить, есть ли у нас общее решение системы дифференциальных уравнений.
Phase Plane – В этом разделе мы дадим краткое введение в фазовую плоскость и фазовые портреты.Мы определяем равновесное решение / точку для однородной системы дифференциальных уравнений и то, как фазовые портреты могут быть использованы для определения устойчивости равновесного решения. Мы также показываем формальный метод построения фазовых портретов.
Действительные собственные значения – в этом разделе мы будем решать системы двух линейных дифференциальных уравнений, в которых собственные значения являются различными действительными числами. Мы также покажем, как рисовать фазовые портреты, связанные с реальными различными собственными значениями (седловые точки и узлы).
Комплексные собственные значения – в этом разделе мы будем решать системы двух линейных дифференциальных уравнений, в которых собственные значения являются комплексными числами. Это будет включать в себя иллюстрацию того, как получить решение, которое не включает комплексные числа, которые мы обычно ищем в этих случаях. Мы также покажем, как рисовать фазовые портреты, связанные со сложными собственными значениями (центрами и спиралями).
Повторяющиеся собственные значения – в этом разделе мы будем решать системы двух линейных дифференциальных уравнений, в которых собственные значения являются действительными повторяющимися (в данном случае двойными) числами.Это будет включать получение второго линейно независимого решения, которое нам понадобится для формирования общего решения системы. Мы также покажем, как рисовать фазовые портреты, связанные с реальными повторяющимися собственными значениями (несобственные узлы).
Неоднородные системы – В этом разделе мы рассмотрим быстрые примеры, иллюстрирующие использование неопределенных коэффициентов и изменение параметров для решения неоднородных систем дифференциальных уравнений. Метод неопределенных коэффициентов будет работать примерно так же, как и для дифференциальных уравнений n-го порядка, в то время как изменение параметров потребует некоторой дополнительной работы по выводу, чтобы получить формулу / процесс, которые мы можем использовать в системах.
Преобразования Лапласа – В этом разделе мы рассмотрим быстрый пример, показывающий, как преобразования Лапласа могут использоваться для решения системы двух линейных дифференциальных уравнений.
Моделирование – В этом разделе мы кратко рассмотрим некоторые расширения некоторых моделей моделирования, которые мы выполняли в предыдущих главах, которые приводят к системам дифференциальных уравнений. В частности, мы рассмотрим задачи смешивания, в которых у нас есть два соединенных между собой резервуара с водой, задачу хищник-жертва, в которой учитываются популяции обоих, и задачу механической вибрации с двумя массами, связанными с пружиной и каждая из которых подключена к стена с пружиной.
Домашняя страница Точные решения Методы Программное обеспечение Образование Об этом сайте Математические форумы Точные решения> Обыкновенные дифференциальные уравнения> Нелинейные обыкновенные дифференциальные уравнения второго порядка. PDF-версия этой страницы 3.Нелинейные обыкновенные дифференциальные уравнения второго порядка3.1. Обыкновенные дифференциальные уравнения видаy ′ ′ = f ( x, y )
3.2. Обыкновенные дифференциальные уравнения видаf ( x, y ) y ′ ′ = g ( x, y, y ′ )
На веб-сайте EqWorld представлена обширная информация о решениях для различные классы обыкновенные дифференциальные уравнения, уравнения в частных производных, интегральные уравнения, функциональные уравнения, и другие математические уравнения. Copyright © 2004-2017 Андрей Д. Полянин |
5 лучших онлайн-решателей уравнений для исследований
Онлайн-решатель уравнений – это веб-приложение, которое может решать математические уравнения, такие как арифметика, алгебра, геометрия, статистика, дифференциальные уравнения, исчисление, дискретная математика и уравнения линейной алгебры.
Используя эти инструменты, вы можете проверить свои уравнения для исследования. Но не рекомендуется использовать непосредственно решаемые уравнения из этих инструментов в своих исследованиях. поскольку эти инструменты состоят из программного обеспечения, существует большая вероятность исключительных ошибок при построении шагов для решения сложных проблем.
В Интернете доступно множество онлайн-программ для решения уравнений, в этой статье ilovephd предоставляет список из 5 лучших программ для решения уравнений для исследования.
1.MathPapa-Решатель уравнений
www.mathpapa.comMathpapa – это калькулятор алгебры для пошагового решения любых задач по алгебре, а также уроки и практика, которые помогут освоить алгебру в удобном для вас темпе и заложить прочный фундамент математических знаний.
С его помощью вы также можете решать квадратные уравнения с помощью Калькулятора квадратной формулы.
Этот инструмент также доступен в виде мобильных приложений на платформе Android и iOS.
Как пользоваться Mathpapa
www.wolframalpha.comWolframalpha – это усовершенствованная программа для решения уравнений арифметики, алгебры, геометрии, статистики, дифференциальных уравнений, исчисления, дискретной математики, линейной алгебры, химии и физических формул.
Он содержит решения по более чем 60 темам в области математики, химии и физики.
Этот инструмент также доступен в виде мобильных приложений на платформе Android и iOS.
Как использовать Wolframalpha
3. Программа для решения уравнений Symbolab
www.symbolab.comSymbolab – это инструмент для углубленного изучения математики. Он позволяет пользователям изучать, практиковать и открывать для себя математические темы, используя математические символы и научные обозначения, а также текст.
Он предоставляет автоматизированные пошаговые решения по алгебраическим, тригонометрическим и вычислительным темам, охватывающим от средней школы до колледжа.
Symbolab предлагает множество интеллектуальных калькуляторов, включая уравнения, одновременные уравнения, неравенства, интегралы, производные, пределы, касательную, тригонометрические уравнения, функции и многое другое.
Этот инструмент также доступен в виде мобильных приложений на платформе Android и iOS.
Как использовать Symbolab
4. Решение солуматных уравнений
www.solumaths.comОнлайн-математическое программное обеспечение Solumaths позволяет вычислять дроби с помощью калькулятора дробей, буквальное исчисление, численное вычисление, вычисление радикалов, вычисление комплексных чисел с помощью калькулятора комплексных чисел, оно имеет мощные функции, позволяющие решать уравнения, решатель уравнений позволяет в том числе решать уравнение, решать квадратное уравнение, давая решение в точном виде.
Это также позволяет решить неравенство, будь то неравенство первой степени или неравенство второй степени, снова решение вычисляется с его точной формой.
5. Программа для решения быстрых математических уравнений
www.quickmath.comQuickMath – это онлайн-программа для решения уравнений. Используя это, вы можете расширить, разложить на множители или упростить практически любое алгебраическое выражение по вашему выбору.
Он также имеет команды для разделения дробей на частичные дроби, объединения нескольких дробей в одну и отмены общих множителей внутри дроби.
Quicmath также использовался для построения графиков с использованием данного уравнения.
Надеюсь, эта статья поможет вам найти полезные инструменты решения уравнений для проверки ваших исследовательских уравнений.
Связанные Калькулятор метода Эйлера– Улучшенный решатель метода Эйлера
Онлайн-калькулятор по методу Эйлера поможет вам оценить решение дифференциального уравнения первого порядка с помощью метода Эйлера. Калькулятор формулы Эйлера использует начальные значения для решения дифференциального уравнения и подставляет их в таблицу.Давайте посмотрим на закон Эйлера и модифицированный метод.
Что такое метод Эйлера ?Метод Эйлера (также известный как прямой метод Эйлера) – это численный метод первого порядка, используемый для решения обыкновенных дифференциальных уравнений (ОДУ) с конкретными начальными значениями. Это наиболее явный метод численного интегрирования обыкновенных дифференциальных уравнений.
Тем не менее, это онлайн-калькулятор E, который позволяет вычислить значение e в степени x.Здесь «X» может означать любую степень или числовое значение по вашему выбору, а e – показатель степени.
Формула метода Эйлера:Для аппроксимации решения дифференциальных уравнений можно использовать множество различных методов. Итак, разберитесь с формулой Эйлера, которая используется в калькуляторе метода Эйлера, и это один из самых простых и лучших способов дифференцировать уравнения. Любопытно, что этот метод и формула, первоначально изобретенные Эйлерианом, называются методом Эйлера.
$$ A_n = A_ {n-1} + hA (B_ {n-1}, A_ {n-1}) $$
Пример:
С учетом задачи начального значения
x ’= x, x (0) = 1,
Для четырех шагов метода Эйлера для аппроксимации x (4).
Используя размер шага, равный 1 (h = 1)
Уравнение метода Эйлера: \ (x_ {n + 1} = x_n + hf (t_n, x_n) \), поэтому сначала вычислите \ (f (t_ {0}, x_ {0}) \).
Тогда функция (f) определяется как f (t, x) = x:
$$ f (t_ {0}, x_ {0}) = f (0,1) = 1. $$
Наклон прямой, касающейся кривой в точках (0,1). Таким образом, наклон – это изменение x, деленное на изменение t или Δx / Δt.
умножьте указанное выше значение на размер шага h:
$$ f (x_0) = 1.1 = 1 $$
Так как шаг – это изменение t, умножая наклон касательной и размер шага, мы получаем изменение значения x.
Подставляя начальное значение x в формулу метода Эйлера, чтобы найти следующее значение. Кроме того, вы можете найти эти значения с помощью калькулятора метода Эйлера.
$$ x_0 + hf (x_0) = x_1 = 1 + 1. 1 = 2 $$
Повторяя вышеуказанные шаги, чтобы найти x_ {2}, x_ {3} и x_ {4}.
$$ x_2 = x_1 + hf (x_1) = 2 + 1. 2 = 4 $$
$$ x_3 = x_2 + hf (x_2) = 4 + 1.4 = 8 $$
$$ x_4 = x_3 + hf (x_3) = 8 + 1. 8 = 16 $$
Из-за повторяющегося характера этого метода Эйлера может быть полезно организовать все вычисления в таблице методов Эйлера.
| Шаг | X_0 | наклон | Х_н |
| 1 | 1 | 1 | 2 |
| 2 | 2 | 2 | 4 |
| 3 | 4 | 4 | 8 |
| 4 | 8 | 8 | 16 |
Следовательно, вычисление таково, что x_ {4} = 16.{4} = 54,598 $$
Однако онлайн-калькулятор линейной аппроксимации поможет вам вычислить линейную аппроксимацию параметрических, полярных или явных кривых в любой заданной точке.
Как работает калькулятор по методу Эйлера?Онлайн-калькулятор по методу Эйлера решает обыкновенные дифференциальные уравнения и подставляет полученные значения в таблицу, следуя этим простым инструкциям:
Ввод:- Введите функцию в соответствии с правилом Эйлера.
- Теперь подставьте значение размера шага или количество шагов.
- Затем добавьте значение y и начальные условия.
- «Рассчитать»
- Калькулятор метода Эйлера предоставляет значение y и введенные вами данные.
- Он отображает каждый расчет размера шага в таблице и дает пошаговые вычисления с использованием формулы метода Эйлера.
- Вы можете выполнить эти вычисления быстро и много раз, нажав кнопку пересчета.
Обычно метод Эйлера является основой для создания более сложных методов. Метод Эйлера основан на том факте, что около точки значение функции и ее касательной почти одинаковы. Измените координату x, также известную как размер шага.
Можете ли вы использовать метод Эйлера в обратном направлении?В численном анализе и научных расчетах обратный метод Эйлера (или неявный метод Эйлера) является одним из наиболее важных численных методов решения обыкновенных дифференциальных уравнений.Он похож на (стандартный) метод Эйлера, но отличается тем, что это неявный метод.
Почему Эйлер более устойчив в обратном направлении?Прямая и обратная схемы Эйлера имеют одинаковые пределы точности. Однако обратный метод Эйлера является неявным, поэтому он является очень стабильным методом для большинства задач. Следовательно, при решении линейных уравнений (например, уравнений Фурье) обратный метод Эйлера устойчив.
Каковы недостатки метода Эйлера?Метод Эйлера упрощает маятник.Преимущества: метод Эйлера прост и понятен. Может использоваться для нелинейного IVP. Недостатки: низкая точность и нестабильное значение. Ошибка аппроксимации Эйлера пропорциональна размеру шага h.
Почему Рунге-Кутта точнее?RK-методы высокого порядка являются многоуровневыми, поскольку они включают многоуровневые вычисления наклона между текущим значением и следующим дискретным значением времени.
Заключение:Воспользуйтесь этим онлайн-калькулятором по методу Эйлера, чтобы аппроксимировать дифференциальные уравнения, отображающие размер каждого шага и соответствующие значения в таблице, используя закон Эйлера.Конечно, вручную решить дифференциальные уравнения с помощью метода Эйлера сложно, но это станет удобным при использовании улучшенного калькулятора метода Эйлера.
Артикул:Из источника Википедии: метод Эйлера, неформальное геометрическое описание, пример кода MATLAB, пример кода R, использование других размеров шага, локальная ошибка усечения, глобальная ошибка усечения, числовая стабильность, ошибки округления, модификации и расширения.
Из источника Delta College: Краткое изложение метода Эйлера, предварительный пример, применение метода, общая проблема начального значения.
Из источника Brilliant: Метод Эйлера, Метод, Влияние размера шага, Последующие шаги.
Из источника «Примечаний Пола»: раздел «Интервалы достоверности», «Использование метода Эйлера», «немного псевдокода», «Методы приближения».
Репетитор по дифференциальным уравнениям, Том 1 – Видеокурс
Раздел 2: Решение элементарных дифференциальных уравненийВ этом разделе студентам предлагается практика решения элементарных задач дифференциальных уравнений.Студента учат определять, является ли данная функция решением ODE. Кроме того, студента учат, как выполнить интеграцию ODE, чтобы вычислить общее решение, а также как использовать начальные условия для поиска конкретного решения …. Посмотреть урок
Раздел 3: Разделение переменныхIn В этом разделе мы изучаем нашу первую основную технику решения широкого класса обыкновенных дифференциальных уравнений. Этот метод применяется к дифференциальным уравнениям первого порядка и называется разделением переменных, потому что мы разбиваем переменные таким образом, чтобы можно было найти решение путем интегрирования…. Просмотреть урок
Раздел 4: Линейные ОДУ первого порядка – Вариация параметров, Часть 1В этом разделе мы изучаем метод изменения параметров как метод решения линейных обыкновенных дифференциальных уравнений первого порядка. Сначала мы подробно исследуем метод, чтобы у студента был справочник по процедуре, затем мы решаем задачи, показывающие каждый шаг на этом пути, чтобы дать студенту практику …. Посмотреть урок
Раздел 5: Линейные ОДУ первого порядка – Вариация параметров, Часть 2В этом разделе мы продолжаем практиковаться в использовании метода вариации параметров для решения линейных обыкновенных дифференциальных уравнений первого порядка с помощью полностью проработанных задач…. Просмотреть урок
Раздел 6: Точные дифференциальные уравненияВ этом разделе мы узнаем, как определить и проверить, является ли обычный дифференциал «точным» по своей природе. Если оно точное, мы узнаем, как его решить, используя ограничения, накладываемые на точные дифференциальные уравнения. Приведено множество примеров …. Просмотреть урок
Раздел 7 – Теорема существования и единственностиВ этом разделе мы узнаем о теореме существования и единственности обыкновенных дифференциальных уравнений.Теорема представлена вместе с ежедневным объяснением того, что она означает …. Просмотреть урок
Раздел 8 – Графическое отображение решений дифференциальных уравненийВ этом разделе мы узнаем, как можно решать дифференциальные уравнения первого порядка, даже если мы этого не делаем. знать решение заранее. Мы используем технику изоклин, чтобы построить общее решение ОДУ …. См. Урок
Раздел 9 – Приложения дифференциальных уравнений: задачи смешенияВ этом разделе мы применяем технику и теорию решения дифференциальных уравнений к проблемам, связанным со смесями.Эти проблемы потребуют от нас прочитать задачу и использовать информацию в постановке задачи для создания дифференциальных уравнений, которые мы затем сможем решить …. Посмотреть урок
Раздел 10 – Применение дифференциальных уравнений: закон охлаждения НьютонаВ этом разделе мы применяем методы и теорию решения дифференциальных уравнений к задачам, связанным с законом охлаждения Ньютона. Этот тип проблемы связан с тем, что теплый предмет находится в более прохладной окружающей среде, например, стакан с водой помещен в морозильную камеру.Закон охлаждения Ньютона – это дифференциальное уравнение, которое используется для расчета температуры воды как функции времени …. Просмотреть урок
Раздел 11 – Применение дифференциальных уравнений: схемы, часть 1В этом разделе мы применять методы и теорию решения дифференциальных уравнений к задачам, связанным с элементарными электрическими цепями. В частности, мы исследуем цепи, содержащие резистор и катушку индуктивности, и используем дифференциальное уравнение для определения тока в цепи как функции времени…. Просмотреть урок
Раздел 12 – Применение дифференциальных уравнений: схемы, часть 2В этом разделе мы применим методы и теорию решения дифференциальных уравнений к задачам, связанным с элементарными электрическими цепями. Здесь мы продолжаем решать схемы, содержащие резистор и катушку индуктивности, и используем дифференциальное уравнение для определения тока в цепи как функции времени …. Просмотр урока
Калькулятор дифференциальных уравнений – примеры, факты
Калькулятор дифференциальных уравнений вычисляет решение для данного дифференциального уравнения первого порядка, когда мы знаем начальное условие.Дифференциальное уравнение – это уравнение, содержащее производную функции.
Что такое калькулятор дифференциальных уравнений?
Калькулятор дифференциальных уравнений– это онлайн-инструмент, который помогает вычислить решение дифференциального уравнения первого порядка, когда задано начальное условие. Дифференциальное уравнение со степенью, равной 1, называется дифференциальным уравнением первого порядка. Чтобы использовать этот калькулятор дифференциальных уравнений , введите значения в указанные поля ввода.
Калькулятор дифференциальных уравнений
Как пользоваться калькулятором дифференциальных уравнений?
Выполните следующие действия, чтобы найти решение дифференциального уравнения первого порядка с помощью онлайн-калькулятора дифференциальных уравнений:
- Шаг 1: Зайдите в онлайн-калькулятор дифференциальных уравнений Cuemath.
- Шаг 2: Введите значения в поля ввода.
- Шаг 3: Нажмите кнопку «Решить» , чтобы найти решение.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор дифференциальных уравнений?
Дифференциальное уравнение определяется как уравнение, которое состоит из производной зависимой переменной по отношению к независимой переменной. Скорость изменения количества представлена производными. Таким образом, дифференциальное уравнение представляет взаимосвязь между изменяющейся величиной и изменением другой величины . Дифференциальное уравнение можно разделить на разные типы в зависимости от степени. У нас могут быть дифференциальные уравнения первого порядка (степень = 1), второго порядка (степень = 2), n -го порядка (степень = n). В дифференциальном уравнении первого порядка все линейные уравнения, выраженные в виде производных, относятся к первому порядку. Такое уравнение задается как y ‘= dy / dx = f (x, y). Чтобы найти решение дифференциального уравнения первого порядка, когда известно начальное условие y (0), шаги следующие:
- Выразите данное уравнение как dy / dx = f (x).
- Теперь запишите уравнение как dy = f (x) dx.
- Объедините обе стороны функции.
- Мы получаем результат как y = F (x) + C.
- Чтобы определить значение C, подставьте значения начального условия y (0). Таким образом, y (0) = F (0) + C или C = y (0) – F (0).
- Теперь подставьте значение C обратно в уравнение, указанное на шаге 4. Это будет решением дифференциального уравнения.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенные примеры дифференциальных уравнений
Пример 1: Найдите решение дифференциального уравнения первого порядка y ‘= x 2 и y (0) = 2 и проверьте его с помощью калькулятора дифференциальных уравнений.
Решение :
Дано: y ‘= x 2 и y (0) = 2
dy / dx = x 2
dy = x 2 dx.
Интегрируйте данное дифференциальное уравнение первого порядка y (x) = x 3 /3 + C
у (0) = 2
у (0) = F (0) + C
2 = (0) 3 /3 + С
С = 2
у (х) = х 3 /3 + 2
Пример 2: Найдите решение дифференциального уравнения первого порядка y ‘= sinx и y (0) = 3 и проверьте его с помощью калькулятора дифференциальных уравнений.
Решение :
Дано: y ‘= sinx и y (0) = 3
dy / dx = sinx
dy = sinx dx.
