Калькулятор Второй Производной – Mathcracker.Com
Инструкции: Используйте калькулятор второй производной для вычисления второй производной (то есть производной от производной) любой дифференцируемой функции, которую вы предоставите, показывая все шаги. Пожалуйста, введите функцию в поле формы ниже.
Подробнее о вторых производных
Этот калькулятор поможет вам вычислить вторую производную любой заданной вами функции, показывая все этапы процесса. Все, что вам нужно сделать, это предоставить действительную дифференцируемую функцию.
Допустимой функцией может быть f(x) = x*tan(x), или f(x) = 3x^3 + 2x – 1 и т. д. Это может быть любая действительная функция, и она не обязательно должна быть упрощенной, поскольку калькулятор упростит ее, если это потребуется.
д. Это может быть любая действительная функция, и она не обязательно должна быть упрощенной, поскольку калькулятор упростит ее, если это потребуется.
После того, как вы предоставили действительную функцию, вы можете нажать кнопку “Рассчитать”, чтобы получить все вычисления и шаги, показанные на рисунке.
Вторые производные имеют огромное практическое значение во многих приложениях, особенно в Calculus, с тестом второй производной на максимизацию и минимизацию, чтобы оценить, является ли критическая точка максимумом, минимумом или нет.
Что такое вторая производная
Проще говоря, вторая производная – это просто производная от производной.
Идея второй производной также применима к частные производные и соответствует производной дважды, но в этом случае она может быть вычислена относительно разных переменных.
Этапы вычисления второй производной
- Шаг 1: Определите функцию f(x), которую вы хотите дифференцировать дважды, и упростить как можно раньше
-
Шаг 2:
Продифференцируем один раз, чтобы получить производную f'(x).
 При необходимости упростите полученную производную.
При необходимости упростите полученную производную.
- Шаг 3: Дифференцируйте теперь f'(x), чтобы получить вторую производную f”(x)
Шаги кажутся простыми, но в зависимости от заданной функции, количество алгебраические вычисления может быть большим.
Обозначение второй производной
Наиболее распространенное обозначение для второй производной – \(f”(x)\), что хорошо отражает тот факт, что операция производной, обозначаемая ‘, применяется к функции дважды. 2} = \displaystyle \frac{d}{dx} \left(\frac{dy}{dx}\right) \]
2} = \displaystyle \frac{d}{dx} \left(\frac{dy}{dx}\right) \]
Этапы вычисления вторых производных для неявных функций
- Шаг 1: Определите уравнение, включающее x и y
- Шаг 2: Дифференцируйте обе части равенства. Каждая сторона потенциально может зависеть от x, y и y’. Упростите очевидные термины, но это не обязательно
-
Шаг 3:
Снова продифференцируем обе части равенства.
 2 = 1\).
2 = 1\).
Вторая производная в точке
Как и производная, вторая производная – это функция, определяемая по точкам. Обратите внимание, что распространенной ошибкой студентов является мысль о том, что раз я хочу дифференцировать в точке, а функция, оцениваемая в точке, постоянна, то и ее производная должна быть постоянной. НЕВЕРНО. Сначала вычислить производную , а потом оцениваете.
Пример: вычисление второй производной
Вычислите вторую производную от : \(f(x) = \cos(x^2)\)
Отвечать: В этом примере мы вычислим вторую производную функции \(\displaystyle f(x)=\cos\left(x^2\right)\).
 2\right)\]
2\right)\]
Пример: больше вторых производных
Для следующей функции : \(f(x) = x \cos(x)\), вычислите ее вторую производную
Отвечать: Теперь проделаем то же самое в tis \(\displaystyle f(x)=x\cos\left(x\right)\), для которого нужно вычислить его производную.
Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:
\( \displaystyle \frac{d}{dx}\left(x\cos\left(x\right)\right)\)
Using the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \cdot \frac{d}{dx}\left(\cos\left(x\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \cdot \frac{d}{dx}\left(\cos\left(x\right)\right)\)
Directly differentiating: \(\frac{d}{dx}\left( \cos\left(x\right) \right) = -\sin\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \left(-\sin\left(x\right)\right)\)
which then leads to
\( \displaystyle = \,\,\)
\(\displaystyle x\cdot \left(-\sin\left(x\right)\right)+\cos\left(x\right)\)
By reorganizing/simplifying/expanding the terms that are amenable to
\( \displaystyle = \,\,\)
\(\displaystyle -x\sin\left(x\right)+\cos\left(x\right)\)
Вычисление Второй Производной: Следующим шагом является дифференцирование производной, полученной на предыдущих этапах:
\( \displaystyle \frac{d^2f}{dx^2} = \frac{d}{dx}\left(-x\sin\left(x\right)+\cos\left(x\right)\right)\)
By linearity, we know \(\frac{d}{dx}\left( (-1)x\sin(x)+\cos(x) \right) = \frac{d}{dx}\left((-1)x\sin(x)\right)+\frac{d}{dx}\left(\cos(x)\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(\left(-1\right)x\sin\left(x\right)\right)+\frac{d}{dx}\left(\cos\left(x\right)\right)\)
Directly differentiating: \(\frac{d}{dx}\left( \cos\left(x\right) \right) = -\sin\left(x\right)\) and we can use the Product Rule: \(\frac{d}{dx}\left( \left(-1\right)x\sin\left(x\right) \right) = \frac{d}{dx}\left(\left(-1\right)x\right) \cdot \sin\left(x\right)+\left(-1\right)x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(\left(-1\right)x\right) \cdot \sin\left(x\right)+\left(-1\right)x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\)
Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\) and directly we get: \(\frac{d}{dx}\left( \left(-1\right)x \right) = -1\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(-1\right) \sin\left(x\right)+\left(-1\right)x \cdot \cos\left(x\right)-\sin\left(x\right)\)
and then we get
\( \displaystyle = \,\,\)
\(\displaystyle \left(-1\right)x\cos\left(x\right)+\left(-1\right)\sin\left(x\right)+\left(-\sin\left(x\right)\right)\)
Reducing the multiplication by ones in \(\left(-1\right)x\cos\left(x\right) = \left(-1\right)x\cos\left(x\right)\) and
\( \displaystyle = \,\,\)
\(\displaystyle \left(-1\right)x\cos\left(x\right)-\sin\left(x\right)+\left(-\sin\left(x\right)\right)\)
Simplifying:
\( \displaystyle = \,\,\)
\(\displaystyle -x\cos\left(x\right)-2\sin\left(x\right)\)
Вывод Второй Производной : Делаем вывод, что вторая производная данной функции равна a:
\[f”(x) = -x\cos\left(x\right)-2\sin\left(x\right)\]
Пример: вторая производная и неявное дифференцирование
Используя неявное дифференцирование, вычислите вторую производную y по x для \( x^2 + y^2 = 1\).
 2}{y} \]
2}{y} \]
чем завершается расчет.
Другие производные калькуляторы
Когда нахождение производной функции, естественно подумать о том, чтобы повторить процесс, который заключается в нахождении производной производной, и это именно то, что это калькулятор второй производной делает.
Понятие второй производной весьма полезно в исчислении, особенно во время максимизации или минимизации функций.
 Вторая производная дает вам информацию о вогнутости функции, что также важно в то время, чтобы понять форму
график функции
.
Вторая производная дает вам информацию о вогнутости функции, что также важно в то время, чтобы понять форму
график функции
.
Вторые производные можно вычислять как для обычных производных, так и для неявное дифференцирование , в котором вы дважды вычисляете правило неявного дифференцирования.
Калькулятор неявной дифференциации с шагами
Введение в калькулятор неявной дифференциации?
Калькулятор неявного дифференцирования — это онлайн-инструмент, с помощью которого можно вычислить любую производную функцию через x и y.
 Калькулятор неявной производной с шагами позволяет крупным производителям быстро освоить это, выполняя вычисления во время выполнения. Пошаговые результаты калькулятора неявной производной заставят вас выполнить конкретную задачу в рамках менуэта.
Калькулятор неявной производной с шагами позволяет крупным производителям быстро освоить это, выполняя вычисления во время выполнения. Пошаговые результаты калькулятора неявной производной заставят вас выполнить конкретную задачу в рамках менуэта.Интегрирование и дифференцирование обратны друг другу. Вы можете найти полезные калькуляторы интеграции на этом веб-сайте, а также полезные блоги.
Что такое неявное дифференцирование?
В исчислении слово неявный используется для функций, которые могут быть выражены как x, так и y. Неявное дифференцирование — это процесс, в котором мы находим производную зависимой переменной. Это делается с помощью
Раздельного дифференцирования каждого члена
Выражения производной зависимой переменной в виде символа 92 \right) = \frac{d}{dx} (1) $$
Этот веб-сайт предлагает другие полезные инструменты дифференцирования, например, вы можете использовать калькулятор дифференцирования на главной странице или калькулятор частных производных, чтобы получить мгновенное решение.
 вашей проблемы.
вашей проблемы.Преимущества использования калькулятора неявных функций
Всегда лучше использовать онлайн-инструмент, чем ручной метод. Вот некоторые из основных преимуществ калькулятора dy/dx с шагами:
- Он экономит ваше время, которое вы тратите на ручные вычисления.
- Неявный калькулятор прост и удобен в использовании.
- Обеспечивает точные и пошаговые результаты.
- Вы можете увидеть график и возможные промежуточные шаги неявного дифференцирования.
- Калькулятор неявной производной с шагами поможет вам попрактиковаться в Интернете, чтобы закрепить свои концепции.
Помимо этого калькулятора неявного дифференциала, вы также можете использовать калькулятор аппроксимации касательной для нахождения производной наклона или кривой.
Преимущества использования калькулятора dy dx
Использование калькулятора второй неявной производной с шагами для обучения и практики всегда полезно и разумно.
 Вот некоторые из основных преимуществ этого решателя неявного дифференцирования:
Вот некоторые из основных преимуществ этого решателя неявного дифференцирования:- Он экономит ваше время, затрачиваемое на ручные вычисления.
- Этот неявный калькулятор с шагами прост и удобен в использовании.
- Вы можете попрактиковаться, чтобы закрепить свои концепции неявной дифференциации.
- Предоставляет пошаговые точные результаты.
- Вы можете найти график и возможные промежуточные шаги неявного дифференцирования.
- Вам не нужна плата или подписка, чтобы использовать калькулятор производной неявной функции.
Связанный: Также найдите сопутствующие инструменты, такие как калькулятор производных частных, и бесплатно найдите производные с помощью калькулятора правил произведения.
Как пользоваться калькулятором неявной дифференциации?
Наш калькулятор неявного дифференцирования с шагами очень прост в использовании. Просто выполните следующие действия, чтобы получить точные результаты.
 Эти шаги:
Эти шаги:1. Введите функцию в основной ввод или загрузите пример.
2. Выберите переменную, относительно которой вы хотите произвести оценку.
3. Подтвердите в предварительном просмотре правильность функции или переменной.
4. Нажмите кнопку “РАССЧИТАТЬ”, чтобы получить пошаговый ответ.
Надеемся, вам понравился наш калькулятор неявных функций. На этом веб-сайте есть и другие полезные онлайн-инструменты, которые вы можете использовать, такие как калькулятор третьей производной или калькулятор цепного правила с шагами. Такие инструменты могут сэкономить ваше время, которое вы тратите на ручные вычисления.
Часто задаваемые вопросы
Является ли неявное дифференцирование тем же, что и частичное дифференцирование?
При неявном дифференцировании функция дифференцируется по одной переменной, но в конце другая переменная исчезает.
В то время как при частичном дифференцировании функция дифференцируется одновременно по двум переменным.
 Используйте калькулятор неявных частных производных, чтобы получить точные результаты онлайн.
Используйте калькулятор неявных частных производных, чтобы получить точные результаты онлайн.Что такое производная неявной функции?
Неявное дифференцирование, функция дифференцируется по одной переменной, рассматривая другую как функцию первой переменной. При оценке вторая переменная изолируется от решения. Вы можете использовать калькулятор производной неявной функции, чтобы получить мгновенные и точные результаты.
Что такое неявная функция дифференцирования?
Функция называется неявной функцией, если одна из ее переменных записана в виде функции другой переменной. Например, х 2 +xy=0 является неявной функцией, поскольку одна переменная является зависимой, то есть функцией независимой переменной. Между тем, вы можете вычислить эти функции и уравнения, шаг за шагом используя калькулятор производной неявной функции.
Как найти производную неявной функции?
Мы можем легко дифференцировать неявную функцию. Например, чтобы найти y’ для xy=1, мы можем выполнить следующие шаги.

xy=1
Так как y является функцией x, то
$$ xy(x) \;=\; 1 \подразумевает y(x) \;=\; \frac{1}{x} $$ 92} $$
Также найдите другие производные инструменты для обучения и практики.
Алан Уокер
Последнее обновление 28 февраля, 2023Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.
Вторая, третья и другие производные
Исследование Математика 9Константы: пи Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Функция
Максимальное число производных
900 04 Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.Синтаксис формулы функции
В записи функции вы можете использовать одну переменную (всегда используйте x ), скобки, число пи ( 9 .

Вы можете использовать следующие общие функции: sqrt – квадратный корень, exp – степень экспоненты, lb – логарифм по основанию 2, lg – логарифм по основанию 10, ln – логарифм по основанию e , sin – синус, cos – косинус, tg – тангенс, ctg – котангенс, sec – секанс, cosec – косеканс, arcsin – арксинус, arccos – арккосинус, arctg – арктангенс, arcctg – арккотангенс, arcsec – арксеканс, arccosec – арккосеканс, версин – версинус, веркос – веркосинус, гаверсин – гаверсинус , exsec – экссекант, exsc – экссеканс, sh – гиперболический синус, ch – гиперболический косинус, th – гиперболический тангенс, cth – гиперболический котангенс, sech – гиперболический секанс, csch – гиперболический cosec муравей, абс – модуль, sgn – signum (знак), log__ p – логарифм по основанию p , f.

 При необходимости упростите полученную производную.
При необходимости упростите полученную производную.
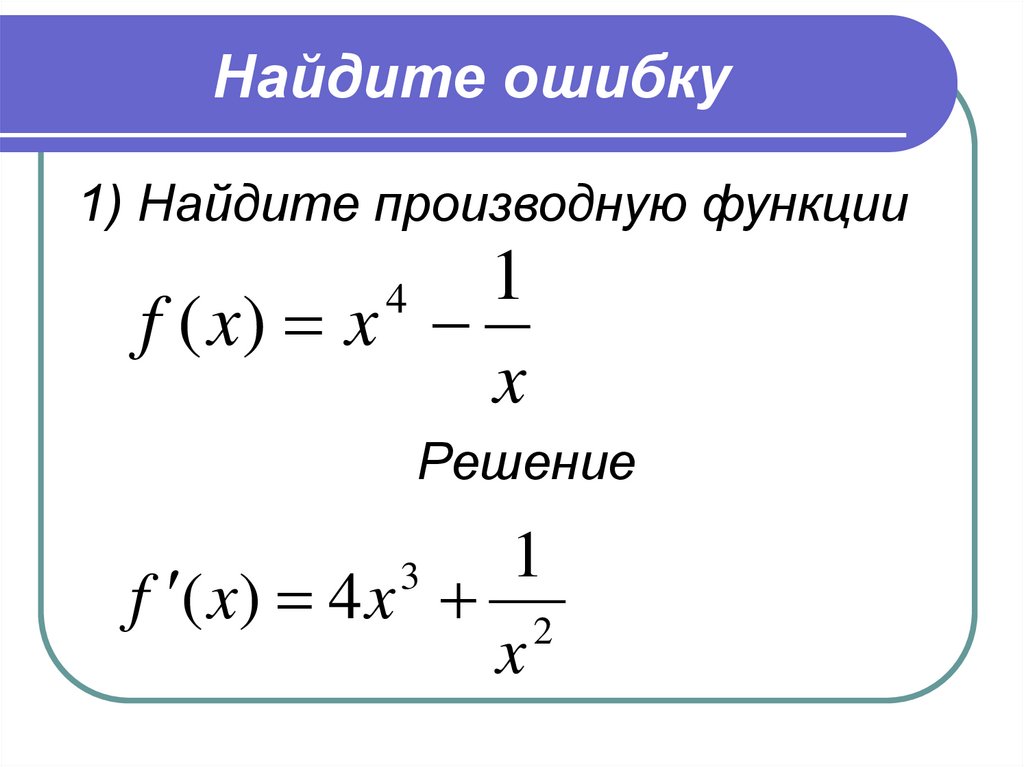 2 = 1\).
2 = 1\).
 2\right)\]
2\right)\]
 2}{y} \]
2}{y} \]
 Вторая производная дает вам информацию о вогнутости функции, что также важно в то время, чтобы понять форму
график функции
.
Вторая производная дает вам информацию о вогнутости функции, что также важно в то время, чтобы понять форму
график функции
.
 Калькулятор неявной производной с шагами позволяет крупным производителям быстро освоить это, выполняя вычисления во время выполнения. Пошаговые результаты калькулятора неявной производной заставят вас выполнить конкретную задачу в рамках менуэта.
Калькулятор неявной производной с шагами позволяет крупным производителям быстро освоить это, выполняя вычисления во время выполнения. Пошаговые результаты калькулятора неявной производной заставят вас выполнить конкретную задачу в рамках менуэта. вашей проблемы.
вашей проблемы. Вот некоторые из основных преимуществ этого решателя неявного дифференцирования:
Вот некоторые из основных преимуществ этого решателя неявного дифференцирования: Эти шаги:
Эти шаги: Используйте калькулятор неявных частных производных, чтобы получить точные результаты онлайн.
Используйте калькулятор неявных частных производных, чтобы получить точные результаты онлайн.

