Урок 26. уравнение. решение уравнений подбором неизвестного числа – Математика – 2 класс
Математика, 2 класс
Урок №26. Уравнение. Решение уравнений подбором неизвестного числа
Перечень вопросов, рассматриваемых в теме:
– Что такое уравнение, корень уравнения?
– Как решить уравнение?
Глоссарий по теме:
Уравнение – равенство, содержащее неизвестное число, которое надо найти.
Корень уравнения – это значение буквы, при котором из уравнения получается верное равенство.
Решить уравнение, значит найти его корни.
Основная и дополнительная литература по теме урока
1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1.– 8-е изд. – М.: Просвещение, 2017. – С. 80-81.
2. Моро М. И., Бантова М. А. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций.
3. Моро М. И., Волкова С. И. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. 9-е изд. – М.: Просвещение, 2014. – С. 60.
Теоретический материал для самостоятельного изучения
Вы умеете читать буквенные выражения. Например:
Вы уже знаете, что равенства бывают верные и неверные.
Рассмотрим верное равенство с окошком: + 4 = 12
Запишем вместо окошка маленькую латинскую букву , как в буквенное выражение. Какое число надо поместить вместо буквы х, чтобы равенство стало верным?
Это число 8. Получили верное равенство: сумма чисел 8 и 4 равна 12.
х + 4 = 12
х = 8
8 + 4 = 12
Равенство с буквой , которое мы записали – это уравнение.
Неизвестное число обозначается маленькими латинскими буквами, как и в буквенном выражении.
Решить уравнение – значит найти все такие значения х (если они есть), при которых равенство будет верным. Значение буквы, при котором из уравнения получается верное равенство, называется корень уравнения.
Решим уравнение 10 – d = 6 способом подбора.
Возьмём число 5. Сейчас проверим, верно ли подобрали число. Заменим d в уравнении числом 5. Получим равенство: 10 – 5 = 6. Оно неверно. Значит, число подобрали неверно.
Попробуем взять другое число. Например, 4. При подстановке его вместо d получили верное равенство: 10 – 4 = 6. Значит, число четыре – корень уравнения, его решение.
Сейчас мы с вами рассмотрим, как по схеме составить уравнение. Перед нами такая схема. Изучим, что обозначает каждое число в схеме. Число 27 обозначает «целое». Оно состоит из двух частей. Первая «часть» – это число

20 х
27
Воспользуемся правилом,
ЧАСТЬ + ЧАСТЬ = ЦЕЛОЕ
Запишем равенства:
20 + x = 27
27 – x = 20
Рассмотрим другой пример. Перед вами другая схема. Изучим, где на схеме целое, а где части: х – это «целое», а 30 и 6 – это части.
30 6
х
Воспользуемся правилом,
Вывод:
Тренировочные задания.
- Соедините уравнение с его решением.
Правильные ответы:
2. Выберите и подчеркните среди математических записей уравнения.
15 + 6 = 21
17 – d
b + 3 = 12
3 + 5 > 6
48 – a = 8
9 + e < 39
k – 4 = 10
Правильные ответы:
15 + 6 = 21
17 – d
b + 3 = 12
3 + 5 > 6
48 – a = 8
9 + e < 39
k – 4 = 10
Базовые методы решения уравнений и неравенств – Математика – Теория, тесты, формулы и задачи
Знание базовых методов решения уравнений и неравенств является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Базовые методы решения уравнений и неравенств, которые надежно усвоены и отработаны учеником – это один из основных инструментов, которым он должен оперировать при решении математических задач. На этой странице сайта представлены примеры применения базовых методов решения уравнений и неравенств из школьной математики.
Базовые методы решения уравнений и неравенств, которые надежно усвоены и отработаны учеником – это один из основных инструментов, которым он должен оперировать при решении математических задач. На этой странице сайта представлены примеры применения базовых методов решения уравнений и неравенств из школьной математики.
Изучать базовые методы решения уравнений и неравенств из школьной математики онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности.

- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
как их понимать, разбирать и решать
У меня есть книга о том, как решать математические задачи на этом уровне, которую, надеюсь, вы найдете полезной.
Решение домашних заданий – важная часть настоящего изучения высшей математики, пишет Анна Евкова evkova.org/vyisshaya-matematika. Она показывает, что вы можете не только “ходить”, но и “говорить”, и, в частности, показывает, какие у вас есть слабые места в материале. Стоит потрудиться, чтобы понять, как решить эти проблемы, а не только ради сиюминутной цели получить хорошую оценку. Если вам трудно решить домашнее задание, то в дальнейшем или на следующем курсе вам может быть еще труднее.
Даже после того, как вы решили проблему, “игра” с ней может быть очень полезной для понимания механизма решения. Например, попытаться убрать некоторые гипотезы или попытаться доказать более сильный вывод.
Также важно помнить, что получение решения является лишь краткосрочной целью при решении математической задачи. Долгосрочная цель – улучшить ваше понимание. Хорошее эмпирическое правило гласит: если вы не можете полностью объяснить решение своим одноклассникам, значит, вы сами не понимаете решения. В связи с этим частичный прогресс в решении проблемы следует оценивать как ступеньку к полному решению (и как важное средство углубления понимания проблемы).
Долгосрочная цель – улучшить ваше понимание. Хорошее эмпирическое правило гласит: если вы не можете полностью объяснить решение своим одноклассникам, значит, вы сами не понимаете решения. В связи с этим частичный прогресс в решении проблемы следует оценивать как ступеньку к полному решению (и как важное средство углубления понимания проблемы).
Как изучать высшую математику
Высшая математика – это предмет, который невозможно обойти стороной. Некоторые люди любят ее, но, честно говоря, большинство людей ненавидят изучать математику. Математика важна для студентов как никогда – предметы являются основой завтрашних технологий. Большинство университетских курсов включают математику, а большинство профессий используют математику в той или иной форме на ежедневной основе. Проблема для многих студентов заключается в том, что они не знают, как изучать математику, чтобы получать хорошие оценки.
Высшая математика – один из тех предметов, на изучение которых можно потратить часы, но в итоге ничего не получить. Неважно, сколько вы готовились, если вы не сможете решить задачи в день экзамена, вам конец. К счастью, существуют способы изучения математики, которые вы можете применять независимо от вашего уровня знаний. К концу этой статьи вы, возможно, даже поймете, что любите математику.
Неважно, сколько вы готовились, если вы не сможете решить задачи в день экзамена, вам конец. К счастью, существуют способы изучения математики, которые вы можете применять независимо от вашего уровня знаний. К концу этой статьи вы, возможно, даже поймете, что любите математику.
7 советов по решению математических задач
1. Практика, практика и еще раз практика
Вы не можете выучить математику должным образом, просто читая или слушая. Чтобы выучить математику, вам нужно засучить рукава и решать задачи. Чем больше вы практикуетесь в решении математических задач, тем лучше у вас получается. Каждая задача имеет свои особенности, и перед экзаменом важно решить их разными способами. От этой реальности никуда не деться. Для того чтобы получить хороший результат на экзамене по математике, необходимо предварительно многократно решать математические задачи.
2. Просмотрите ошибки
При отработке этих задач важно отработать каждое решение. Вы должны проанализировать все допущенные вами ошибки и понять, где ваши навыки решения проблем не сработали. Понимание того, как вы подошли к решению проблемы и где ошиблись, – отличный способ стать сильнее и избежать повторения ошибок в будущем.
Вы должны проанализировать все допущенные вами ошибки и понять, где ваши навыки решения проблем не сработали. Понимание того, как вы подошли к решению проблемы и где ошиблись, – отличный способ стать сильнее и избежать повторения ошибок в будущем.
3. Овладейте ключевыми концепциями
Не пытайтесь запомнить процесс. Это контрпродуктивно. В конечном счете, гораздо лучше и полезнее сосредоточиться на понимании процесса и логики. Это поможет вам понять, как справиться с этими проблемами, если они возникнут.
Важно помнить, что математика – это непрерывный предмет. Важно хорошо понимать ключевые понятия, лежащие в основе математических тем, прежде чем переходить к другим, более сложным решениям, основанным на базовом понимании.
4. Разберитесь в своих сомнениях
Иногда учащиеся застревают, пытаясь решить часть математической задачи, и им трудно перейти к следующему этапу. Многие студенты часто пропускают эту задачу и переходят к следующей. Чтобы избежать этого, следует уделить время пониманию процесса решения проблем. Если вы поняли исходную проблему, вы можете использовать ее как трамплин для перехода к остальным проблемам.
Чтобы избежать этого, следует уделить время пониманию процесса решения проблем. Если вы поняли исходную проблему, вы можете использовать ее как трамплин для перехода к остальным проблемам.
Помните, что для овладения математикой требуется время и терпение.
Лучше всего заниматься с другом, с которым можно обсудить и обменяться идеями по решению сложных задач.
5. Создайте учебную среду, свободную от отвлекающих факторов
Высшая математика – это предмет, который требует большей концентрации внимания, чем любой другой. При решении сложных уравнений и задач по геометрии, алгебре и тригонометрии решающее значение имеют подходящая учебная среда и свободное пространство, не отвлекающее внимание.
Обучающая музыка помогает создать расслабляющую атмосферу и стимулировать поток информации. Соответствующая фоновая музыка поможет вам сосредоточиться. Конечно, лучше избегать Pitbull и Eminem. Инструментальная музыка – лучшая в наши дни.
6. Создайте математический словарь
Высшая математика имеет свою специфическую терминологию и большой словарный запас. Мы рекомендуем вам сделать блокнот или карточку со всеми необходимыми понятиями, терминами и определениями. Покажите смысл, ключевые моменты и даже примеры решений, чтобы вы могли в любой момент обсудить и обобщить их.
7. Применяйте математику к реальным задачам
Приступая к изучению математики, старайтесь как можно чаще применять реальные задачи. Поскольку математика настолько абстрактна, поиск практических приложений может изменить вашу точку зрения и помочь вам по-другому воспринимать идеи.
Вероятность можно использовать в повседневной жизни, например, для предсказания исхода событий или для принятия решения о том, стоит ли рисковать, например, покупать лотерейный билет или играть в азартные игры.
И помните, что также важно быть уверенным в себе и сдавать экзамены, зная, что вы правильно подготовились.
Ресурс по объяснению решения задач по высшей математике
Анна Евкова разработала ресурс для объяснения решению задач по высшей математике, предлагая предлагаемые занятия, которые позволяют ученикам продемонстрировать свои математические знания в реальной жизни и на работе.
Ключевые особенности ресурса:
- Он побуждает учеников решать задачи, определяя, какая математика необходима и как ее следует использовать.
- Это позволяет ученикам устанавливать связи между различными направлениями математических знаний и понимания для решения проблемы.
- Это дает ученикам возможность работать индивидуально или совместно, чтобы найти решение.
- Он побуждает учеников задуматься над тем, какие методы и стратегии они использовали, и нашли ли они решение.
- Хотя материалы по решению проблем не всегда сосредоточены на одной конкретной области знаний и понимания, они сгруппированы на вкладках ниже по направлениям, которым уделяется больше внимания.

Задачи по высшей математике также имеют связанные с ними рейтинги сложности, который обозначается кружками – переход от одного кружка к самому сложному, четырем кружкам. Указание сложности можно найти в конце каждой строки ниже. Обратите внимание, что в связи с добавлением новых менее сложных задач рейтинг сложности для каждой задачи был изменен.
Решение задач по математике
Решение задач по математике
(смотрите также решение задач по химии)
Сложно представить себе человека старше 12 лет, не умеющего считать на бытовом уровне. Ещё сложнее представить себе человека старше 6 лет, не умеющего пользоваться калькулятором. Однако бытовые подсчёты – это совсем не та математика, которая преподаётся в старших классах, а тем более в ВУЗах.
В начальной школе у нормального ребёнка математика проблем вызвать в принципе не должна. Но вот позже, как только начинается более сложная математика – алгебра, геометрия, основы математического анализа – возможны варианты.
Пример оформления контрольной работы по высшей математике нашими специалистами:
Люди, как известно, разные. Не все склонны к точным расчётам и вниманию к каждому символу, усвоению правил и методов. Уже в этом возрасте можно определить «технарей» и «гуманитариев». И хотя математика нужна всем, некоторым из нас она пригодится лишь на бытовом уровне. Для более сложных задач целесообразно будет заказать решение задач по математике у специалистов.
Конечно, далеко не всем подойдёт такой способ решения проблем. Если одним математика нужна просто как учебный предмет, то другим – программистам, экономистам, инженерам – она необходима как рабочий инструмент. Всё-таки в основе любых расчётов лежат именно математические модели, и, не освоив математику, невозможно ими пользоваться, а тем более строить самостоятельно.
Ещё один важнейший фактор при освоении математики – ваша склонность к ней. Некоторые люди умеют видеть в математике красоту решений, исчислений, функций и склонны заниматься ей просто для удовольствия. Некоторые другие не могут себе представить, как это – орудовать в голове точными абстракциями.
Некоторые другие не могут себе представить, как это – орудовать в голове точными абстракциями.
В ВУЗе математика не спрашивает вас, нравится ли она вам. Она просто стоит в учебном плане и занимает ваше время. Иногда это долгие часы, иногда – дни и даже недели, которые нужны для усвоения отдельных курсов и решения задач. Не лучше ли в этом случае провести простые арифметические расчёты и прикинуть: может, будет целесообразнее поискать решение задач по математике на заказ в Интернете?
Это особенно актуально, если вы работаете и вынуждены обеспечивать себя работой. И вдвойне актуально, если эта работа связана с вашей будущей специальностью: ведь в таком случае время надо уделять и работе, и учёбе по профилирующим предметам.
Математику не случайно называют «царицей наук»: как известно, точность – королевская вежливость, а в математике точность превыше всего. Поэтому если вы решились заказать решение задач по математике, обращаться для этого надо к проверенным специалистам. У нас практически любой студент сможет найти для себя нечто полезное. Это может быть и типовое решение типовых примеров, и решение вашей конкретной задачи под заказ, и индивидуальные консультации по выбранной тематике.
У нас практически любой студент сможет найти для себя нечто полезное. Это может быть и типовое решение типовых примеров, и решение вашей конкретной задачи под заказ, и индивидуальные консультации по выбранной тематике.
Поскольку наши сотрудники сами являются бывшими (а чаще – действующими) преподавателями различных учебных заведений (университетов, академий, колледжей), они не только разбираются в математике, но и способны оформить решение задач по математике в соответствии с требованиями вашего ВУЗа.
Одно из важнейших отличий нашей работы – то, что решение задач сопровождается комментариями, поясняющими ход решения, выбор метода и значение ответа. Таким образом, вы не просто получаете готовое решение, но и сможете прокомментировать его преподавателю. У этого подхода есть и ещё один эффект: вы сможете для себя глубже усвоить материал и лучше понять его.
Ведь просто предложить готовое решение – это, скажем прямо, не самый честный путь. Но мы хотим стать не вашими соучастниками в обмане преподавателей, а вашими соучителями. И решение задач по математике, правильно оформленное и прокомментированное – наш способ делать это.
И решение задач по математике, правильно оформленное и прокомментированное – наш способ делать это.
Разумеется, мы гарантируем оперативное, грамотное и точное решение задач, с учётом вашей специфики. По ходу работы мы постоянно остаёмся на связи, что позволяет оперативно корректировать действия.
Заказать нам работу!
Математики нашли проблему в знаменитых уравнениях для описания жидкостей / Хабр
Два математика доказали, что при определённых экстремальных условиях уравнения Навье-Стокса выдают бессмыслицу
Уравнения Навье-Стокса
при помощи нескольких лаконичных членов описывают одно из самых распространённых явлений физического мира: течение жидкостей. Сегодня эти уравнения, появившиеся ещё в 1820-х, используются для описания всего, от океанских течений и турбулентности, следующей за самолётом до потока крови в сердце.
Хотя физики считают эти уравнения надёжными, как молоток, математики относятся к ним с недоверием. Для математика то, что эти уравнения вроде бы работают, мало что значит. Им нужны доказательства того, что уравнения безошибочны: что для любой жидкости и для долгосрочного прогноза, распространённого сколь угодно далеко в будущее, математика уравнений не подведёт. Такую гарантию оказалось нелегко отыскать. Первый человек или команда, которая сумеет доказать, что уравнения Навье-Стокса будут работать всегда — или представить пример, доказывающий, что они не работают — сможет получить награду за решение одной из “Задач тысячелетия”, анонсированных математическим институтом Клэя, и миллионом долларов в придачу [по состоянию на 2017 год только одна из семи задач тысячелетия (гипотеза Пуанкаре) решена Григорием Перельманом / прим. перев.].
Им нужны доказательства того, что уравнения безошибочны: что для любой жидкости и для долгосрочного прогноза, распространённого сколь угодно далеко в будущее, математика уравнений не подведёт. Такую гарантию оказалось нелегко отыскать. Первый человек или команда, которая сумеет доказать, что уравнения Навье-Стокса будут работать всегда — или представить пример, доказывающий, что они не работают — сможет получить награду за решение одной из “Задач тысячелетия”, анонсированных математическим институтом Клэя, и миллионом долларов в придачу [по состоянию на 2017 год только одна из семи задач тысячелетия (гипотеза Пуанкаре) решена Григорием Перельманом / прим. перев.].
Математики разработали множество способов для решения этой задачи. Новая работа, опубликованная в сентябре, ставит серьёзные вопросы по поводу того, сможет ли добиться успеха один из самых популярных подходов к задаче, разрабатываемый в течение многих лет. Работа, которую написали Тристан Бакмастер и Влад Викол из Принстонского университета, представляет собой первый результат, показывающий, как при определённых условиях уравнения Навье-Стокса дают противоречивое описание физического мира.
«Мы пытаемся понять определённые проблемы, присущие этим уравнениям, и то, почему людям, вероятно, придётся их переосмыслить», — говорит Бакмастер.
Работа Бакмастера и Викола показывает, что, если принять при решении уравнений Навье-Стокса очень грубые допущения, они начинают выдавать бессмыслицу: утверждают, что одна и та же жидкость с одними и теми же начальными условиями может прийти в два или более различных состояний. Она может течь одним образом, или же совершенно другим. Если так, то эти уравнения не могут надёжно описывать физический мир, для которого они были разработаны.
Взрывая уравнения
Чтобы понять, как уравнения могут сломаться, представьте себе океанское течение. В его рамках могут существовать локальные течения, в результате чего некоторые его части могут перемещаться в одном направлении и с одной скоростью, а другие — в другом направлении с другой скоростью. Локальные течения взаимодействуют друг с другом в постоянном взаимном действии трения и давления воды, определяющих её поток.
Математики моделируют это взаимодействие при помощи карты, сообщающей вам о направлениях и скорости потока в любой точке жидкости. Эта карта, называемая векторным полем — снимок внутренней динамики жидкости. Уравнения Навье-Стокса берут этот снимок и воспроизводят его, как видео, сообщая, как именно будет выглядеть векторное поле в каждый последующий момент времени.
Карта ветров (windy.com) работает похожим на векторное поле образом. В каждой точке у ветра есть определённое направление и сила
Эти уравнения работают. Они описывают течение жидкости так же надёжно, как уравнения Ньютона предсказывают будущие положения планет; физики постоянно используют их, и они постоянно совпадают с результатами экспериментов. Однако математикам нужно нечто большее, чем эпизодическое подтверждение — им нужно доказательство того, что уравнения не нарушаются, что вне зависимости от того, с какого векторного поля вы начнёте, и от того, как далеко в будущее вы будете его воспроизводить, уравнения всегда дадут вам новое, уникальное векторное поле.
Это и есть тема Задачи тысячелетия, спрашивающей, есть ли у уравнений Навье-Стокса решения (решение, по сути, и есть векторное поле) для всех начальных точек во все моменты времени. Эти решения должны обеспечить точное направление и силу потока в каждой точке жидкости. Решения, дающие информацию с таким бесконечно мелким разрешением, называются «гладкими». У гладкого решения каждая точка поля имеет связанный с ней вектор, позволяющий вам «гладко» путешествовать по полю, не застревая в точках, где вектор отсутствует — в точке, дальнейшее движение из которой вам будет непонятно.
Гладкие решения — полное представление физического мира, но с математической точки зрения они могут существовать не всегда. Математики, работающие над уравнениями, подобными этим, переживают по поводу такой ситуации: вы запускаете уравнения Навье-Стокса и наблюдаете за изменениями векторного поля. По прошествии какого-то конечного времени уравнения говорят вам, что некая частица жидкости двигается с бесконечной скоростью. Тогда у вас будут проблемы. В уравнения входит измерение изменений таких свойств, как давление, трение, скорость жидкости — говоря жаргонным языком, они берут производные этих величин — но производную от бесконечной величины взять не проще, чем поделить на ноль. Так что если уравнения выдают бесконечное значение, можно сказать, что они отказали вам, или «взорвались». Они уже не могут описывать последующие состояния вашей жидкости.
Тогда у вас будут проблемы. В уравнения входит измерение изменений таких свойств, как давление, трение, скорость жидкости — говоря жаргонным языком, они берут производные этих величин — но производную от бесконечной величины взять не проще, чем поделить на ноль. Так что если уравнения выдают бесконечное значение, можно сказать, что они отказали вам, или «взорвались». Они уже не могут описывать последующие состояния вашей жидкости.
Такой «взрыв» — свидетельство того, что в уравнениях не хватает описания каких-то свойств физического мира, который они должны описывать. «Возможно, уравнения охватывают не все эффекты реальной жидкости, поскольку в реальной жидкости мы не ожидаем» бесконечной скорости движения частиц, как говорит Бакмастер.
Решение Задачи тысячелетия состоит либо в том, чтобы показать, что уравнения Навье-Стокса никогда не взрываются, либо найти условия, при которых это происходит. Одна из стратегий, используемых математиками — смягчить требования к тому, как точно эти уравнения должны описывать требуемые решения.
Нарушение потока
Уравнения Навье-Стокса должны описывать течение любой жидкости, с любыми начальными условиями, и распространять описание бесконечно далеко в будущее. Пытаясь доказать эту их способность, математики иногда «ослабляют», то есть, используют приближённые описания векторных полей, описывающих жидкость. Но с этим возникают трудности.
В идеале, математики хотят доказать, что применение уравнений Навье-Стокса к любой непрерывной, «гладкой» жидкости выдаст один уникальный результат.
Однако проще работать со «слабыми», не такими детализированными векторными полями. И вот математики обнаружили, что некоторые слабые описания выдают неуникальные результаты — позволяют одной и той же жидкости в одних и тех же начальных условиях течь двумя способами.
От слабых к гладким
Когда математики изучают такие уравнения, как эти, они иногда начинают расширять определение того, что считается решением. Гладким решениям требуется максимум информации — в случае с Навье-Стоксом им требуется, чтобы в каждой точке векторного поля, связанного с жидкостью, существовал вектор. Но что, если ослабить требования, и сказать, что вам нужно подсчитывать вектора только для некоторых точек поля, или нужно получить только примерные значения векторов? Такие решения называют «слабыми». Они позволяют математикам почувствовать поведение уравнения без утомительной работы по поиску абсолютно всех решений (что на практике может оказаться и невозможным).
Но что, если ослабить требования, и сказать, что вам нужно подсчитывать вектора только для некоторых точек поля, или нужно получить только примерные значения векторов? Такие решения называют «слабыми». Они позволяют математикам почувствовать поведение уравнения без утомительной работы по поиску абсолютно всех решений (что на практике может оказаться и невозможным).
Тристан Бакмастер, математик из Принстонского университета
«С какой-то точки зрения слабые решения ещё легче описать, чем реальные, поскольку знать нужно гораздо меньше», — сказал Камилло Де Леллис, в соавторстве с Лазло Щекелихиди написавший несколько важных работ, заложивших фундамент для работы Бакмастера и Викола.
Слабые решения бывают разной градации. Если представить себе гладкое решение в виде математического изображения жидкости с бесконечным разрешением, то слабые решения будут представлять собой нечто вроде 32-битных, 16-битных или 8-битных версий этого изображения.
В 1934 году французский математик Жан Лере определил важный класс слабых решений. Вместо работы с точными векторами, «решения Лере» берут среднее значение векторов в небольшой окрестности векторного поля. Лере доказал, что всегда можно решить уравнения Навье-Стокса, позволяя вашим решениям принимать форму такого вида. Иначе говоря, решения Лере не взрываются.
Вместо работы с точными векторами, «решения Лере» берут среднее значение векторов в небольшой окрестности векторного поля. Лере доказал, что всегда можно решить уравнения Навье-Стокса, позволяя вашим решениям принимать форму такого вида. Иначе говоря, решения Лере не взрываются.
Достижение Лере определило новый подход к задаче Навье-Стокса: начать с решений Лере, о существовании которых уже известно, и посмотреть, можно ли превратить их в гладкие решения, существование которых вы хотите доказать. Этот процесс напоминает тот, где вы начинаете с грубой картинки, и смотрите, нельзя ли постепенно подкрутить разрешение, чтобы достичь идеального изображения реальности.
«Одна из возможных стратегий — показать, что эти слабые решения Лере гладкие, и если вы сможете показать, что они гладкие — вы решите Задачу тысячелетия», — сказал Бакмастер.
Влад Вкол представляет собой половину команды, вскрывшей проблемы в подходе к проверке уравнений Навье-Стокса.
Есть и ещё один подвох. Решения уравнений Навье-Стокса соответствуют реальным физическим событиям, а физические события происходят одним возможным образом. Учитывая это, хотелось бы, чтобы у ваших уравнений был только один набор уникальных решений. Если уравнения дают вам множество возможных решений, они не справляются со своей задачей.
Решения уравнений Навье-Стокса соответствуют реальным физическим событиям, а физические события происходят одним возможным образом. Учитывая это, хотелось бы, чтобы у ваших уравнений был только один набор уникальных решений. Если уравнения дают вам множество возможных решений, они не справляются со своей задачей.
Поэтому математики смогут использовать решения Лере для решения Задачи тысячелетия, только если решения Лере уникальны. Неуникальные решения Лере будут означать, что, согласно правилам Навье-Стокса, одна и та же жидкость с одними и теми же начальными условиями может прийти к двум разным физическим состояниям, что не имеет физического смысла, и подразумевает, что уравнения на самом деле не описывают то, что должны.
Новый результат Бакмастера и Викола — первый намёк на то, что для определённых определений слабых решений может происходить именно это.
Множество миров
В своей новой работе Бакмастер и Викол рассматривают ещё более слабые решения, чем решения Лере — решения, в которых используется тот же принцип усреднения, что у и Лере, но ослаблено ещё одно дополнительное требование (известное, как неравенство энергий). Они используют метод «выпуклого интегрирования», берущий начало из работ по геометрии математика Джона Нэша, и позднее привлечённый к изучению жидкостей Де Леллисом и Щекелихиди.
Они используют метод «выпуклого интегрирования», берущий начало из работ по геометрии математика Джона Нэша, и позднее привлечённый к изучению жидкостей Де Леллисом и Щекелихиди.
Используя такой подход, Бакмастер и Викол доказывают, что эти очень слабые решения уравнений Навье-Стокса неуникальны. Они, к примеру, демонстрируют, что если начать с полностью спокойной жидкости, к примеру, со стакана с водой рядом с кроватью, возможны два вида развития событий. Первый очевиден: вода начинает со спокойного состояния и остаётся спокойной всегда. Второй фантастичный, но математически возможный: вода начинает со спокойного состояния, взрывается в середине ночи, а затем возвращается в спокойное состояние.
«Это доказывает отсутствие уникальности, поскольку из начальных данных можно сконструировать по меньшей мере два объекта», — говорит Викол.
Бакмастер и Викол доказали существование множества неуникальных слабых решений (не только тех двух, что описаны выше) уравнений Навье-Стокса. Важность этого доказательства ещё предстоит понять. В какой-то момент слабые решения могут стать настолько слабыми, что они перестанут быть связанными с более гладкими решениями, которые должны имитировать. Если так и есть, тогда результат, полученный Бакмастером и Виколом, мало к чему приведёт.
Важность этого доказательства ещё предстоит понять. В какой-то момент слабые решения могут стать настолько слабыми, что они перестанут быть связанными с более гладкими решениями, которые должны имитировать. Если так и есть, тогда результат, полученный Бакмастером и Виколом, мало к чему приведёт.
«Такой результат однозначно является предупреждением, но можно спорить о том, что это предупреждение касается самой слабой идеи слабых решений. Существует множество слоёв более сильных решений, на гораздо лучшее поведение которых можно возлагать надежду» в случае уравнений Навье-Стокса, — говорит Де Леллис.
Бакмастер и Викол также мыслят в терминах слоёв, и он нацелились на решения Лере — на доказательство того, что и те допускают множественную физику, в которой одна и та же жидкость из одного и того же состояния может прийти к разным формам в будущем.
«Мы с Тристаном считаем, что решения Лере неуникальны. Мы пока этого не доказали, но наша работа закладывает плацдарм для атаки на эту задачу», — сказал Викол.
Правила решения уравнений с одним неизвестным
Текст ниже готовила, чтобы объяснить своему ребёнку шаг за шагом что такое уравнение и как оно решаются, чтобы у него сведения выстроились хоть в какую-то систему. Примеры ниже я комментировала, а вместо Васи и Маши были ты да я.
Что такое равенство и неравенство
Неравенство
У Васи — 4 яблока. У Маши — 3 яблока. У кого больше яблок? У кого меньше яблок?
У Васи больше яблок, чем у Маши: 4> 3 У Васи и Маши неравное количество яблок. Это неравенство (четыре не равно трём): 4≠ 3
У Маши меньше яблок, чем у Васи: 3< 4 У Васи и Маши неравное количество яблок. Это неравенство (три не равно четырём): 3≠ 4
Равенство
У Васи — 4 яблока. У Маши — 4 яблока. У кого больше яблок? У кого меньше яблок?
У Васи и Маши равное количество яблок. Это равенство (четыре равно четырём): 4= 4
У Васи — 2 красных яблока и 3 зелёных. У Маши — 5 яблок. У кого больше яблок? У кого меньше яблок?
У Васи и Маши равное количество яблок.Это равенство (два плюс три равно пяти): 2 + 3= 5
У Васи и Маши равное количество яблок. Это равенство (пять равно сумме чисел два плюс три): 5= 2 + 3
Что такое сложение и вычитание
Сложение
У Васи — 2 яблока. У Маши — 3 яблока. Сколько всего яблок у ребят?
У Васи и Маши на двоих 5 яблок: 2 первое слагаемое+ 3 второе слагаемое= 5 сумма От перемены мест слагаемых сумма не меняется [a + b = b + a]: 3+ 2= 5
У Васи — 2 яблока. У Маши — 2 красных яблока и 1 зелёное. Сколько всего яблок у ребят?
У Васи и Маши на двоих 5 яблок (примеры с несколькими арифметическими действиями выполняются поэтапно): 2+ 2 + 1 = 2 + (2 + 1) = 2 + 3 = 5 Сумма не зависит от группировки её слагаемых [(a + b) + c = a + (b + c)]: 2+ 2 + 1 = (2 + 2) + 1 = 4 + 1 = 5
Вычитание
У Васи было 5 яблок. Он подарил Маше 3 яблока. Сколько яблок осталось у Васи?
У Васи осталось 2 яблока: 5 уменьшаемое- 3 вычитаемое= 2 разность
У Васи было 3 яблока. Он подарил Маше 3 яблока и пообещал принести ещё 5. Сколько яблок осталось у Васи?
Он подарил Маше 3 яблока и пообещал принести ещё 5. Сколько яблок осталось у Васи?
У Васи нет яблок, он ещё должен принести 5 яблок, у него -5 яблок (числа могут быть отрицательными) [a − b = a + (−b)]: 3- 3 - 5= (3 - 3) - 5 = 0 - 5 = 0 + (-5) = -5
Вася должен Пете 5 яблок. Маше подарили 3 яблока. Сколько всего яблок у ребят?
У Васи и Маши на двоих -2 яблока [a - (b + c) = a - b - c]: -5+ 3= 3 + (-5) = 3 - 5 = 3 - (3 + 2) = 3 - 3 - 2 = (3 - 3) - 2 = - 2
Связь сложения и вычитания
У Васи — 2 яблока. У Маши — 3 яблока. Всего: 5 яблок. Придумай условия задачи и 4-е варианта решения.
Сколько яблок у ребят? 2+ 3= 5 Сколько яблок у Васи (если из суммы двух слагаемых вычесть одно из них, то получится второе слагаемое)? 5 - 3= 2 Сколько яблок у Маши? 5 - 2= 3 Сколько яблок у ребят (если к разности прибавить вычитаемое, то получится уменьшаемое)? 3+ 2= 5
Что такое уравнение
Уравнение – это равенство, содержащее неизвестное число, которое надо найти.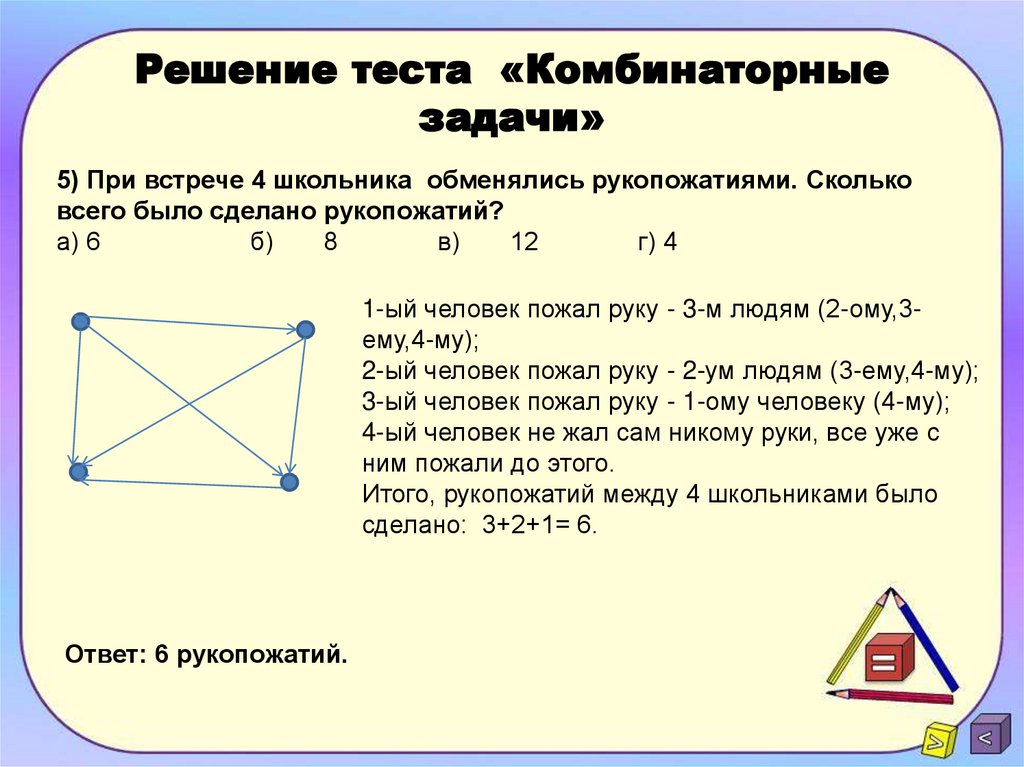 Неизвестное число обозначают латинской буквой, чаще всего x.
Неизвестное число обозначают латинской буквой, чаще всего x.
Решение задачи с одним неизвестным методом подбора
Всего у ребят 5 яблок, 3 из которых съест Маша. Сколько съест Вася?
x+ 3= 5 Если x = 4, то 4 + 3 = 7 7 ≠ 5 (неверно) Если x = 3, то 3 + 3 = 6 6 ≠ 5 (неверно) Если x = 2, то 2 + 3 = 5 5 = 5 (правильно) Ответ: Вася съест 2 яблока
Сложение или вычитание с неизвестным
Всего у ребят 5 яблок, 3 из которых съест Маша. Сколько съест Вася?
Положительное число можно перенести за знак равно, поменяв его знак: x+ 3= 5 x = 5 - 3 = 2 Проверка: 2 + 3 = 5 (правильно) Ответ: Вася съест 2 яблока Правило: чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.
Вася подарил Маше 2 яблока. У него осталось 3 яблока. Сколько яблок было у Васи?
Отрицательное число можно перенести за знак равно, поменяв его знак: x- 2= 3 x = 3 + 2 = 5 Проверка: 5 - 2 = 3 (правильно) Ответ: у Васи было 5 яблок Правило: чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
У Васи было 5 яблок. После того, как он поделился с Машей, у него осталось 3 яблока. Сколько яблок подарил Вася?
Отрицательное число можно перенести за знак равно, поменяв его знак: 5- x= 3 5 = 3 + x 5 - 3 = x 2 = x Проверка: 5 - 2 = 3 (правильно) Ответ: Вася подарил 2 яблока Правило: чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.
Анекдот в тему. Профессор жалуется коллеге: До чего же глупые у меня студенты. Раз объясняю — не понимают, второй раз объясняю — снова не понимают, третий раз объясняю — сам уже начинаю понимать, а они всё не понимают!
Найди закономерность и продолжи ряд — математические закономерности
Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.
В чем смысл игры?
Игры такого рода развивают умение выделять закономерности в последовательном ряде элементов. Для этого сначала нужно внимательно рассмотреть задание: сравнить соседние объекты и попробовать определить правило закономерности.
Для этого сначала нужно внимательно рассмотреть задание: сравнить соседние объекты и попробовать определить правило закономерности.
Решить задачу можно с помощью простого счета, обобщения по какому-либо признаку или простого анализа рисунка, текста или схемы.
Как научить ребенка находить закономерности?
Маленьким детям, для решения задач на поиски закономерностей, понадобится только смекалка и воображение. Достаточно лишь объяснить, как можно установить закономерность между звеньями ряда. Если задачу решить не получается, то вместо прямых подсказок следует задать дополнительные вопросы, не раскрывая решение задачи полностью.
В любом случае, пользы будет больше, если ребенок решит, хотя бы одну задачу самостоятельно, нежели взрослый просто расскажет, как её решать.
Рассмотрим способы, которые помогут ребенку понять закономерности и последовательности в заданиях.
Инструкция по решению числовых последовательностей:
- Найти разницу между двумя рядом стоящими числами
- Определить алгоритм построения последовательности
- Применить алгоритм к следующей паре чисел
- Использовать алгоритм для определения следующего числа в ряду
Инструкция по нахождению закономерностей в заданиях с геометрическими фигурами:
- Рассмотреть фигуры и разделить их, на повторяющиеся группы
- Определить какой элемент изменился в группе
- Решить, какая именно фигура отсутствует или является лишней.

Задания для 1 класса
Задание 1
Раскрась дорожки для зайчика и белочки, сохраняя закономерность.
Решение: Белочка и зайчик бегут по разным дорожкам. У каждой дорожки есть своя закономерность. У зайчика повторяется 3 цвета на дорожке: красный, голубой, жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый, жёлтый.
В этом задании можно обратить внимание на то, что обе дорожки состоят из 12 кругов. Но количество повторяющихся цветов разное.
Задание 2
Найди закономерность в ряду геометрических фигур.
Решение: В этом ряду нужно обратить внимание на размеры фигур, а не на цвет и форму. Сначала идет одна большая фигура, а за ней две маленькие, далее они повторяются.
Задание 3
Нарисуйте в четвертом квадрате правильный ответ.
Решение: Рассмотрев внимательно рисунок, мы увидим, что круги в квадратах исчезают по одному, против часовой стрелки. В этой задаче имеет значение только расположение кругов квадрате. Таким образом, в последний квадрат мы должны нарисовать один синий круг в нижнем левом углу.
В этой задаче имеет значение только расположение кругов квадрате. Таким образом, в последний квадрат мы должны нарисовать один синий круг в нижнем левом углу.
Задание 4
Соблюдая закономерность, продолжи ряд чисел до 10. Сформулируй правило, которое действует в этой закономерности. Используя это правило, придумай свою закономерность.
Решение: В этом ряду каждая цифра увеличивается на 2 относительно предыдущей – мы вычислили правило для данной закономерности. Значит, чтобы продолжить ряд, мы прибавим к каждой следующей цифре по 2. Ответ будет выглядеть так: 2,4,6,8,10.
Чтобы придумать подобную закономерность, нужно использовать сформулированное выше правило: например, 1,3,5,7,9.
Задания для 2 класса
Задание 1
Найди закономерность и в пустом квадрате нарисуй нужное количество кругов.
Решение: В таблице в первом горизонтальном ряду количество кругов увеличивается на 1. Во втором ряду увеличивается на 2. Таким образом, можно предположить, что в третьем ряду количество кругов будет увеличиваться на 3 и ответ будет 9. Можно заметить, что и в вертикальных рядах эта закономерность повторяется.
Таким образом, можно предположить, что в третьем ряду количество кругов будет увеличиваться на 3 и ответ будет 9. Можно заметить, что и в вертикальных рядах эта закономерность повторяется.
Задание 2
В цепочке чисел найди закономерность и вставь пропущенные числа
- 95, 90, 85, 80, 75,_, 65,_, _,50
Решение: В цепочке чисел можно выделить пары: 95 -90, 85 – 80 и далее. Каждый раз, в паре, число уменьшается на 5. Значит, после 75 запишем 70, после 65 — 60, а затем 55 .
Задание 3
Найди закономерность и продолжи последовательность.
- 2, 3, 5, 8, …, …, …, …
Решение: В этой цепочке чисел к каждому последующему числу прибавляется предыдущее. 2+3=5+3=8+5=13+8=21+13=34 и далее.
Задание 4
В поезде едут геометрические фигуры. Нарисуйте фигуры, в четвёртом вагоне, соблюдая закономерность их расположения.
Решение: В поезде едут геометрические фигуры: квадрат, треугольник, прямоугольник и круг. В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.
В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.
Задания для 3 класса
Задание 1
Рассмотрите картинку и найдите закономерность в задаче.
Решение: В таблице мы увидим такую закономерность:
8-5=3, то есть число увеличилось на 3; далее 14-8=6, соответственно, число увеличилось на 6. В последней связке 23-14=9 число увеличилось на 9. Мы делаем вывод, что каждое следующее число увеличивается на предыдущее значение+3. Таким образом, следующее число увеличивается на 9+3=12. 23 + 12 = 35. Ответ: 35.
Задание 2
В пустые клетки вставьте геометрические фигуры, сохраняя закономерность.
Решение: Чтобы выполнить задание, нужно фигуры расставить по порядку, друг за другом, соблюдая последовательность. Значит, после прямоугольника стоит круг, треугольник и квадрат и т. д.
д.
Задание 3
Найди закономерность и продолжи ряды:
- 12, 23, 34, 45, 56…
- 13, 24, 35, 46…
Решение: В этой задаче каждая последующая цифра увеличивается так: десятки на один десяток и единицы на одну единицу. 12=10+2, 23=20+3, 34=30+5 и т. д.
Задание 4
Продолжи ряд, сохраняя закономерность.
- 12, 36, 13, 39, 14, 42, 15,…
Решение: В числовой цепочке выделяем пары чисел. Первая пара:12 и 36. 12×3=36, далее по порядку: 13×3=39. Умножая каждый раз на 3, цифры, следующие по порядку (12,13,14,15…), мы продолжаем последовательный ряд. Ответ: 45.
Задания для 4 класса
Задание 1
Найди ошибку в бусах.
Решение: В первых бусах повторяются квадрат и круг, значит лишний шестой круг. Во вторых бусах, повторяется закономерность: круг, два треугольника, два круга, лишний – восьмой, по счету, круг.
Задание 2
Определите закономерность. Найдите лишнее число.
- 8, 16, 20, 24, 32, 40, 48, 56, 64, 72.
Решение: В этом числовом ряду таблица умножения на 8. Ответ: число 20 – лишнее.
Задание 3
Каких геометрических фигур не хватает? Дорисуй их, соблюдая закономерность в таблице:
Решение: Определить, какой элемент изменился во втором и последующих рядах, можно, выделив последовательность: ромб, трапеция, шестиугольник и параллелограмм. Во втором ряду недостает шестиугольника, в третьем — ромба, в четвертом – параллелограмма и трапеции.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнееКакое решение по математике
Какое решение по математике
Какое решение по математике? Математический термин для решения. Решение – это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям. В зависимости от степени уравнения численные решения равны степени уравнения. Пример: (i) Для линейного уравнения количество решений равно одному.
Решение – это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям. В зависимости от степени уравнения численные решения равны степени уравнения. Пример: (i) Для линейного уравнения количество решений равно одному.
Что представляет собой пример уравнения с одним решением в математике?
Линейные уравнения с решением Пример 1. Рассмотрим уравнение 7 x 35 = 0.При решении они имеют 7 x = 35 или x = 5. Вышеупомянутое линейное уравнение верно, только если x = 5, и, следовательно, данное линейное уравнение имеет разрешение только x = 5.
Как найти набор решений уравнения?
Чтобы найти набор решений для набора подстановки, вставьте каждое значение в набор подстановки и оцените обе стороны уравнения. Если обе стороны равны, то уравнение правильное и, следовательно, значение является решением. Пример 1. Найдите набор решений 11 5w = 1 набора перестановок {0, 2, 4}.
Что означает набор решений в математике?
В математике набор решений – это набор значений, которые удовлетворяют определенному набору уравнений или неравенств.
Что означает в математике термин «решить»?
Решить (глагол) Найдите значения переменных, которые удовлетворяют системе уравнений и / или неравенств. решить (глагол) Алгебраически манипулирует уравнением или неравенством таким образом, чтобы изолировать выбранную переменную с одной стороны так, чтобы другая сторона состояла из выражения, которое можно использовать для генерации решений.
Что такое уравнение и решение в математике?
Уравнение – это алгебраическое выражение, которое связывает обычно неизвестные переменные с другими переменными или константами. Например, x + 2 = 15 – это уравнение, как и y 2 = 4. Решение или квадратный корень уравнения – это значение или набор значений, которые можно вставить в уравнение, чтобы сделать утверждение.
Что такое «набор решений» в математике?
Ряд решений. Любое значение переменных, удовлетворяющее уравнению, неравенству, системе уравнений или системе неравенств.В системе уравнений или системе неравенств набор решений – это набор, содержащий значение (значения) переменной (переменных), которые удовлетворяют всем уравнениям и / или неравенствам в системе.
Какое определение решения в математике?
Решение – это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям. В зависимости от степени уравнения численные решения равны степени уравнения. Пример: (i) Для линейного уравнения количество решений равно одному.
Что значит иметь решение в математической формуле
Решение – это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям. В зависимости от степени уравнения численные решения равны степени уравнения.
Что такое определение бесконечных решений?
Бесконечные решения будут означать, что каждое значение переменной делает уравнение истинным. Давайте посмотрим на следующее уравнение: Обратите внимание, что у вас есть переменные с обеих сторон уравнения.Итак, мы собираемся вычесть обе части, чтобы исключить правую часть уравнения.
Какое решение?
Раствор – это смесь одного вещества, растворенного в другом, поэтому его свойства везде одинаковы.
Раствор состоит из растворенного вещества и растворителя. Растворенное вещество – это вещество, которое растворяется, а растворитель – это часть раствора, которая растворяется.
Что значит иметь решение в математическом примере
Решение – это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям.В зависимости от степени уравнения численные решения равны степени уравнения. Пример: (i) Для линейного уравнения количество решений равно одному. (ii) Для квадратного уравнения численное решение равно двум и так далее.
Что означает набор решений в математических примерах
Определение набора решений уравнения обычно включает в себя три шага: сначала вы решаете уравнение одной переменной для другой, по соглашению нужно решить для y относительно x.Затем определите, какие значения x могут быть частью вашего набора решений. Наконец, подставьте значения x в уравнение, чтобы найти соответствующие значения y.
Как рассчитывается решение?
Расчет концентрации раствора Метод 1 из 3: Использование уравнения массы к объему. Найдите массу растворенного вещества, смешанного с растворителем. Метод 2/3: Найдите концентрацию в процентах или частях на миллион. Найдите массу растворенного вещества в граммах. Метод 3 из 3: Рассчитайте молярность.Сложите атомные массы растворенного вещества, чтобы найти молярную массу.
Каково определение решения уравнения?
Решение уравнения. Решение уравнения – это набор всех значений, которые при замене неизвестными делают уравнение истинным. Для уравнений неизвестной мощности используются два основных правила алгебры для определения их решений, включая свойство аддитивности и свойство мультипликативности.
Что значит иметь решение в математических задачах
Во-первых, решение уравнения или неравенства – это любое число, которое, будучи связанным с уравнением / неравенством, удовлетворяет уравнению / неравенству.
Что вы имеете в виду под удовлетворением? Давайте рассмотрим два примера, чтобы проиллюстрировать это.
Как создать линейное уравнение?
Шаги Убедитесь, что линейное уравнение имеет вид y = mx + b. Представьте себе число b на оси Y. Преобразуйте m в дроби. Продолжайте линию от точки b, начиная на склоне или в гору. Продолжайте вытягивать линию с помощью линейки, не забывая использовать наклон m в качестве ориентира.
Как найти значение переменной?
Для большинства простых событий используйте формулу ожидания для биномиальной случайной величины или формулу ожидания для нескольких событий.Формула математического ожидания для биномиальной случайной величины: P (x) * X. X – количество попыток, а P (x) – вероятность успеха.
Каково математическое определение решения?
Математический термин для решения. Решение – это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям. В зависимости от степени уравнения численные решения равны степени уравнения.
Пример: (i) Для линейного уравнения количество решений равно одному.(ii) Для квадратного уравнения численное решение равно двум и так далее.
Каково определение одного решения в математике?
Решение. Уравнение выкупа возникает, когда уравнение имеет только одно решение. Это означает, что при решении уравнения переменную можно заменить всего ОДНОЙ цифрой.
Что представляет собой пример уравнения с одним решением в математических десятичных дробях
Давайте рассмотрим несколько примеров добавления десятичных знаков. Пример 1: Сложение + Пример 2: Сложение + 5.Пример 3: Добавление ,, Решение: Пусть ,, y.
Как решить уравнение с десятичными знаками?
Итак, для уравнения с десятичными числами вы можете использовать тот же метод, который вы использовали для очистки дробей: умножьте обе части уравнения на наименьший общий делитель. Принимать решение:. Посмотрите на десятичные дроби и подумайте о соответствующих дробях.
Обратите внимание, что на ЖК-дисплее 100.
Есть ли только одно решение уравнения x?
Итак, есть только одно решение – ВРЕМЯ.x = 8. a Укажите в линейном уравнении ниже, имеет ли уравнение ровно одно решение, бесконечное количество решений или нет решений. Используйте свойство распределения. найти одинаковый коэффициент для x с обеих сторон.
Как решить уравнение с дробью?
КАК: Решите уравнения с дробными коэффициентами, исключив дроби. Найдите наименьший общий делитель всех дробей в уравнении. Умножьте обе части уравнения на этот ЖК-дисплей. Это исключит дроби.
Как найти количество решений линейного уравнения?
Следующая таблица помогает им найти количество решений линейного уравнения с одной переменной. В приведенном ниже линейном уравнении укажите, имеет ли уравнение решение, бесконечное количество решений или нет решения. Добавьте по 3 с обеих сторон. Оттянитесь по 2 раза с каждой стороны. Разделите каждую сторону на 2. Подставим в это уравнение x = 8.
Разделите каждую сторону на 2. Подставим в это уравнение x = 8.
Что такое уравнение решения
Решение уравнения – это значение переменной, которая делает утверждение истинным при включении в уравнение.Нахождение решения уравнения называется решением уравнения. Найти решение уравнения – это значит найти значение переменной, которая делает уравнение истинным. Что такое калькулятор переменных?
Что значит найти решение уравнения?
В математике решение уравнения означает нахождение его решений, которые являются значениями (числами, функциями, величинами и т. Д.), Удовлетворяющими условию, заданному уравнением, которое обычно состоит из двух выражений, связанных равными подписать.При поиске решения одна или несколько свободных переменных идентифицируются как неизвестные.
Как найти решение уравнения?
Чтобы решить эту проблему, сначала необходимо объединить s в правой части уравнения. Это даст вам.
Затем вычтите y из обеих частей уравнения, чтобы получить. Наконец, разделите обе части на числа, чтобы получить ответ.
Каково решение уравнения с двумя переменными?
Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо.В этом примере упорядоченная пара (4.7) (4, 7) является решением линейной системы уравнений. Вы можете проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
Как рассчитать систему уравнений?
Решение умножением Запишите одно уравнение поверх другого. Умножайте одно или оба уравнения до тех пор, пока одна из переменных в двух членах не будет иметь равные коэффициенты. Сложите или вычтите уравнения. Решайте до конца срока.Вставьте член обратно в уравнение, чтобы найти значение первого члена. Проверьте свой ответ.
Что представляет собой пример уравнения с одним решением в листах математики
Линейные уравнения с примером решения 1: Рассмотрим уравнение 7x – 35 = 0. При решении они имеют 7 x = 35 или x = 5. Приведенное выше линейное уравнение верно только если x = 5 и, следовательно, данное линейное уравнение имеет разрешение только x = 5.
При решении они имеют 7 x = 35 или x = 5. Приведенное выше линейное уравнение верно только если x = 5 и, следовательно, данное линейное уравнение имеет разрешение только x = 5.
Имеет ли уравнение одно истинное решение?
Однако возможно, что уравнение не может иметь более одного решения, или бесконечное число решений, или вообще не иметь решения.Отсутствие решения означает, что уравнение не имеет ответа, а бесконечные решения уравнения означают, что любое значение переменной делает уравнение истинным.
Когда системы уравнений имеют одно решение?
Решение Уравнение выкупа – это когда уравнение имеет только одно решение. Когда уравнение имеет бесконечное количество решений, это означает, что если бы переменная была преобразована в число, уравнение было бы либо истинным, либо истинным, независимо от числа или значения.Уравнение без решения – это когда, несмотря ни на что, никакое число не делает уравнение истинным.
Как вы решаете уравнения?
Решение уравнений с одной переменной Напишите задачу. Определите, хотите ли вы выделить переменный член путем сложения или вычитания. Добавление или вычитание константы из обеих частей уравнения. Исключите коэффициент переменной делением или умножением. Найдите переменную.
Определите, хотите ли вы выделить переменный член путем сложения или вычитания. Добавление или вычитание константы из обеих частей уравнения. Исключите коэффициент переменной делением или умножением. Найдите переменную.
Каково решение уравнений?
Решение уравнения – это набор всех значений, которые при замене неизвестными делают уравнение истинным.Для уравнений с неизвестной в единственной степени для определения их решений используются два основных правила алгебры, включая свойство сложения и свойство мультипликативности.
Ситуационное уравнение
Ситуационное уравнение – это уравнение, которое представляет ситуацию повествовательной задачи. Уравнение решения – это уравнение, которое представляет операцию, необходимую для решения переменных. Переменная представляет собой букву, представляющую неизвестное число.
Какие примеры уравнений?
Уравнение – это утверждение, которое выражает равенство двух математических выражений.
У уравнения есть знак равенства, выражение справа и выражение слева. Примеры уравнений. 3x + 3 = 2x + 4: левая часть уравнения равна 3x + 3, а правая часть – 2x + 4.
Какой пример уравнения?
Уравнение определяется как состояние равенства и часто представляется как математическое выражение с равными значениями с обеих сторон или относится к проблеме, требующей учета множества факторов.Пример уравнения: 2 + 2 = 3 + 1.
Что такое среднее уравнение?
Уравнение – это математическое утверждение, что две вещи равны. Он состоит из двух выражений, по одному с каждой стороны от знака равенства.
Какое определение ситуации?
Определение ситуации. общее состояние стечения обстоятельств в любой момент времени, сложившаяся международная ситуация опасна; кто-то задается вопросом, как возникло это состояние; Вечные истины не являются истинными или вечными, если они не приводят к новому настроению Франклина для каждой новой социальной ситуации.
Что представляет собой пример уравнения с одним решением в математике, который показывает
Существует только одно решение для одной переменной. Например, уравнение x + 2 = 0 имеет только одно решение, такое как x = 2. Но в случае линейного уравнения с двумя переменными решения вычисляются как декартовы координаты точки на евклидовой плоскости.
Что такое ситуационное уравнение
Ситуационное уравнение – это уравнение, которое представляет ситуацию повествовательной задачи.Уравнение решения – это уравнение, которое представляет операцию, необходимую для решения переменных. Переменная представляет собой букву, представляющую неизвестное число.
Что представляет собой пример уравнения с одним решением в математическом определении
В случае переменной существует только одно решение, поэтому x + 2 = 0. Однако в случае линейного уравнения с двумя переменными решения вычисляются как декартовы координаты точки на евклидовой плоскости.
Что такое определение линейных уравнений и примеров? Уравнение с максимальным порядком 1 называется линейным уравнением.
Сколько решений имеет уравнение?
Система двух линейных уравнений может иметь одно решение, бесконечное число решений или не иметь решения. Системы уравнений можно классифицировать по количеству решений.
Какие примеры нелинейных уравнений?
Примерами нелинейных дифференциальных уравнений являются уравнения Навье-Стокса в гидродинамике и уравнения Лотки-Вольтерра в биологии. Одна из самых больших проблем с нелинейными задачами состоит в том, что обычно невозможно объединить известные решения в новые решения.
Какие есть три метода решения системы уравнений?
Три наиболее часто используемых метода решения систем уравнений – это подстановка, исключение и расширенные матрицы.
Как вы проверяете решение системы уравнений?
Чтобы проверить систему уравнений с помощью подстановки, замените значения x и y в исходных уравнениях. Если оба упрощенных выражения верны, ваш ответ правильный. Например: чтобы проверить, было ли (2, −3) правильным решением для системы уравнений: y = −2x + 1 и y = x – 5, замените x на 2 и y на 3 в каждом уравнении.
Если оба упрощенных выражения верны, ваш ответ правильный. Например: чтобы проверить, было ли (2, −3) правильным решением для системы уравнений: y = −2x + 1 и y = x – 5, замените x на 2 и y на 3 в каждом уравнении.
Каковы этапы решения уравнения?
Решение линейного уравнения: пять шагов к успеху.
Шаг 1 : Найдите распределение для ().
Шаг 2 : Объедините одинаковые термины с каждой стороны знака =.
Шаг 3 : Сложите или вычтите термины из переменных, чтобы все переменные находились по одну сторону от знака =.
Как правильно решить уравнение?
Чтобы решить уравнение, используйте свойство суммирования тяги, чтобы преобразовать данное уравнение в эквивалентное уравнение формы x = a, из которого вы можете проверить, чтобы найти решение.Пример 3 Решите 2x + 1 = x 2.
Каковы шаги для решения уравнения?
Используйте следующую процедуру для решения уравнений. Этапы решения уравнений
Шаг 1 : Очистите дробные и десятичные дроби путем умножения каждого члена в уравнении с помощью дисплея наименьшего общего делителя (ЖКД).
Шаг 2 : Снимите скобы при электромонтаже.
Шаг 3 : объединяет все похожие термины на одной странице.
Как решить уравнение со ступенями?
ШАГИ ДЛЯ РАЗРЕШЕНИЯ УРАВНЕНИЙ В НЕСКОЛЬКО ШАГОВ.
Шаг 1 Используйте свойство распределения.
Шаг 2 Выровняйте одинаковые элементы с каждой стороны.
Шаг 3 Переместите переменные в одну часть уравнения.
Шаг 4 Отменить сложение или вычитание.
Шаг 5 Отмените умножение или деление.
Как вы решаете уравнения с помощью подстановки?
Замена – это метод решения системы уравнений путем исключения всех переменных, кроме одной, в одном из уравнений и последующего решения этого уравнения.Это достигается путем выделения другой переменной в одно уравнение и последующей подстановки значений этих переменных в другое уравнение.
Какое решение системы уравнений?
Решение системы уравнений – это набор значений одной переменной, которым одновременно удовлетворяют все уравнения. Чтобы решить систему уравнений, вы должны найти все наборы значений переменных, которые представляют решения системы.
Чтобы решить систему уравнений, вы должны найти все наборы значений переменных, которые представляют решения системы.
Как найти решение уравнения на два
1) Сначала сложите обе части линейного уравнения с одинаковым числом.2) Во-вторых, умножьте или разделите обе части линейного уравнения на одно и то же число. 3) * вместо
step # 2 всегда умножайте обе части уравнения на обратную величину коэффициента переменной. Пример 1. Решите следующее уравнение в два этапа.
Что такое решение системы уравнений?
Система уравнений – это набор из двух или более уравнений с одним и тем же набором неизвестных. Решая систему уравнений, они пытаются найти значения для каждой из неизвестных, которые удовлетворяют всем уравнениям в системе.Уравнения системы могут быть линейными или нелинейными.
Что такое два линейных уравнения?
- Убедитесь, что линейное уравнение имеет вид y = mx + b.
- Нарисуйте число b на оси Y.
 Ваш b всегда будет рациональным числом.
Ваш b всегда будет рациональным числом. - Преобразовать м в дроби.
- Начните удлинение линии от точки b вверх по склону или вверх по склону.
- Продолжайте вытягивать линию с помощью линейки, не забывая использовать наклон m в качестве ориентира.
Какое уравнение не имеет решения?
Иногда уравнения не имеют решения.Это означает, что независимо от того, какое значение вставлено перед переменной, вы всегда будете получать противоречие. Ознакомьтесь с этим руководством, чтобы узнать, что нужно сделать, чтобы ваше уравнение оставалось неразрешенным.
Как найти решение уравнения на основе
Вы можете решить систему уравнений, заменив значение y второго уравнения первым. Пересечение первых двух прямых равно (1,1). Теперь вы можете найти пересечение второй и третьей линий.
Какой пример набора решений?
Ряд решений.Фамилия. Определение набора решений – это группа чисел, которая может удовлетворять уравнению.
Примерный диапазон решений: 0, 1 и 2 для 4×4. <4.
Какое решение задается в математике?
В математике набор решений – это набор значений, которые удовлетворяют определенному набору уравнений или неравенств.
Что означает одно решение в математике?
Решение Уравнение выкупа – это когда уравнение имеет только одно решение. Это означает, что при решении уравнения переменную можно заменить всего ОДНОЙ цифрой.
Каково определение решения в математике?
Ряд решений. Любое значение переменной или переменных, которые удовлетворяют уравнению, неравенству, системе уравнений или системе неравенств. В системе уравнений или системе неравенств набор решений – это набор, содержащий значение (значения) переменной (переменных), которые удовлетворяют всем уравнениям и / или неравенствам в системе.
Значение приостановки в науке
Что такое приостановка? Суспензия определяется как гетерогенная смесь, в которой твердые частицы распределены в жидкости, но не растворяются в ней. Суспензия определяется как гомогенная смесь частиц диаметром более 1000 нм, так что частицы видны невооруженным глазом.
Суспензия определяется как гомогенная смесь частиц диаметром более 1000 нм, так что частицы видны невооруженным глазом.
Что означает отстранение с точки зрения науки?
Суспензия – это смесь, в которой мелкие частицы взвешены в жидкости, где они переносятся плавучестью (химическим составом), веществом, состоящим из двух или более веществ, смешанных вместе (не в твердых телах и без химической связи).
Что означает «приостановлено» с точки зрения науки?
В науке суспензия – это смесь, в которой мелкие частицы вещества диспергированы в газе или жидкости.
Что такое приостановка в науке?
Определение подвески. В химии суспензия – это гетерогенная смесь твердых и жидких частиц. Чтобы быть суспензией, частицы не должны растворяться в жидкости.
Какой пример суспензии в химии?
Частицы и жидкость смешиваются так, что частицы диспергируются в жидкости. Они взвешены в жидкости. Важной характеристикой раствора является то, что твердые частицы со временем оседают и оседают, если их оставить в покое.Примером затирки является смесь воды и песка.
Они взвешены в жидкости. Важной характеристикой раствора является то, что твердые частицы со временем оседают и оседают, если их оставить в покое.Примером затирки является смесь воды и песка.
Что означает набор решений в математических неравенствах
Набор решений – это набор значений, удовлетворяющих заданному неравенству. Это означает, что каждое значение в наборе решений удовлетворяет неравенству, и никакое другое значение не удовлетворяет неравенству. Как найти набор решений? Набор замены – это набор значений, которые можно заменить переменной.
Каково решение этого неравенства?
Набор решений – это набор значений, удовлетворяющих заданному неравенству.Это означает, что каждое значение в наборе решений удовлетворяет неравенству, и никакое другое значение не удовлетворяет неравенству.
Какое множество решений уравнения x = 0?
Набор решений единственного уравнения x = {displaystyle x = 0} – это набор {0}. 2. Для любого ненулевого многочлена f {стиль отображения f} над комплексными числами в переменной множество решений состоит из конечного числа точек.
Как решить систему неравенства?
Система неравенств очень похожа, за исключением того, что вы работаете с неравенствами вместо уравнений! Чтобы решить такую систему, вы должны найти значения переменных, которые делают каждое неравенство одновременно истинным.Это руководство познакомит вас с системами неравенства.
Какой пример решения в науке?
Раствор представляет собой гомогенную смесь двух или более компонентов с размером частиц менее 1 нм. Распространенными примерами растворов являются растворы сахара в воде и соли в воде, газированной воде и т. Д. В растворе все компоненты имеют форму ступени. Есть однородность частиц. Частицы распределены равномерно.
Каковы характеристики решения в науке?
- Раствор – это однородная смесь двух или более веществ.
- Растворенные в растворе частицы не видны невооруженным глазом.
- Раствор не рассеивает световые лучи.
- Решение стабильное.
- Вещество, растворенное в растворе, не может быть отделено фильтрованием (или механическим способом).

- Состоит из фазы.
Какое простое решение в науке?
Simple Solutions Science предлагает мини-классы обучения и основана на стандартах академического содержания, общих в большинстве штатов.Эта серия поддерживает получение степени магистра в четырех областях: научные исследования, науки о Земле и космосе, науки о жизни и физика. Долгосрочная лояльность – это цель ежедневной распределенной практики, основанной на подходе простых решений.
В чем научный смысл решения?
В химии раствор – это особый вид гомогенной смеси двух или более веществ.
Как найти набор решений?
Чтобы найти набор решений уравнения с определенным диапазоном, необходимо сначала вставить каждое значение диапазона в уравнение, чтобы получить соответствующие значения диапазона.Составьте упорядоченные пары этих значений и запишите их как набор. Этот набор – ваш ответ!
Какие есть примеры решений в химии?
- Вода
- Этанол
- Метанол
- Н-пропанал
- Бутанол
- Эфир
- Дихлорметан
- сероуглерод
- глицерин
- Ацетон
Какие бывают типы растворов в химии?
Растворы, в которых растворителем является жидкость, а растворенное вещество – газ, жидкость или твердое вещество, широко используются.
Есть три типа растворов: газообразные растворы, жидкие растворы и твердые растворы. газообразные растворы.
Какое значение имеют растворы в химии?
Растворы играют очень важную роль во многих биологических, лабораторных и промышленных химикатах. Особый интерес представляют растворы с веществами, растворенными в воде или водных растворах. Решения – это системы равновесия, и выводы предыдущей главы снова будут представлять особый интерес.
Что означает в химии слово раствор?
Раствор: в химии однородная смесь двух или более веществ в относительных количествах, которые могут непрерывно изменяться до так называемого предела растворимости. Термин «раствор» часто используется для обозначения жидкого состояния, но также возможны растворы газов и твердых веществ.
Что такое решение по математической алгебре
Чувство. Решение. плюс Одно или несколько значений, которые можно использовать для замены переменной (например, x), которая делает сравнение истинным. Пример: x + 2 = 7. Если вы замените 5 на x, вы получите: 5 + 2 = 7,5 + 2 = 7 истинно, тогда x = 5 – решение. См .: переменная.
Пример: x + 2 = 7. Если вы замените 5 на x, вы получите: 5 + 2 = 7,5 + 2 = 7 истинно, тогда x = 5 – решение. См .: переменная.
Как мне решать алгебру?
Решите двухэтапное уравнение, умножая вместо деления в конце. Принцип решения этого типа уравнения тот же: используйте арифметику для соединения констант, изолировать переменную-член, а затем изолировать переменную, не являющуюся членом. Предположим, вы работаете с уравнением x / 5 + 7 = 3.
Что такое подстановка в алгебре?
Подстановка – это фундаментальная операция в алгебре.В системах компьютерной алгебры это часто называют pod или pod. Распространенным случаем подстановки являются полиномы, когда замена числового значения неопределенным (одномерным) полиномом сводится к вычислению полинома на этом значении.
Какое решение в математическом построении графиков
Иллюстрированное определение решения: значение или значения, заменяющие переменную (например, x), которая делает уравнение истинным.
Что такое решение в математическом определении
Определение решения (иллюстрированный математический словарь) Иллюстрированное определение решения: значение или значения, которые можно заменить переменной (например, x), которая делает уравнение истинным.
Есть ли решение для каждой математической задачи?
У каждой проблемы есть решение, но не совсем. Вы должны решить проблему и принять реальность. Математика не может научить их, как добавить любви или уменьшить ненависть. Но это дает им все основания надеяться, что для каждой проблемы есть решение.
Что такое решение в математике
Другими словами, решение – это значение или набор значений (по одному для каждого неизвестного), так что когда уравнение заменяется неизвестными, оно становится равенством.Решение уравнения часто называют корнем уравнения, особенно, но не только для полиномиальных уравнений.
Что такое решение в математических терминах
Определение решения (иллюстрированный математический словарь) Иллюстрированное определение решения: значение или значения, которые вы можете подставить вместо переменной (например, x), которая делает уравнение истинным.
Алгебра – Решения и наборы решений
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с “узкой” шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-1: Решения и наборы решений
Мы начнем эту главу с довольно короткого раздела с некоторой базовой терминологией, которую мы довольно регулярно используем при решении уравнений и неравенств. ? 0 \\ 9–9 & = 0 \\ 0 & = 0 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
? 0 \\ 9–9 & = 0 \\ 0 & = 0 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
Итак, мы спрашиваем, равна ли правая сторона левой стороне после того, как мы подключим предложенное решение. В этом смысл символа «?» над знаком равенства в первой строке.
Поскольку правая и левая части совпадают, мы говорим, что \ (x = 3 \) удовлетворяет уравнению.
b \ (y = 8 \) in \ (3 \ left ({y + 1} \ right) = 4y – 5 \) Показать решение
Итак, мы хотим увидеть, удовлетворяет ли \ (y = 8 \) уравнению.? 4 \ left (8 \ right) – 5 \\ 27 & = 27 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
Итак, \ (y = 8 \) удовлетворяет уравнению и, следовательно, является решением.
c \ (z = 1 \) in \ (2 \ left ({z – 5} \ right) \ le 4z \) Показать решение
В этом случае мы имеем неравенство, и в этом случае «удовлетворить» означает что-то немного другое. В этом случае мы будем говорить, что число будет удовлетворять неравенству, если после его подключения мы получим в результате истинное неравенство. ? 4 \ left ({- 5} \ right) \\ – 20 & \ le – 20 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
? 4 \ left ({- 5} \ right) \\ – 20 & \ le – 20 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
В этом случае -20 меньше или равно -20 (в данном случае оно равно), и поэтому мы снова получаем истинное неравенство, и поэтому \ (z = – 5 \) удовлетворяет неравенству и поэтому будет решением.
Мы также должны сделать быстрый пример чисел, которые не являются решением, чтобы мы могли увидеть, как они будут работать.
Пример 2 Покажите, что следующие числа не являются решениями данного уравнения или неравенства.- \ (y = – 2 \) в \ (3 \ left ({y + 1} \ right) = 4y – 5 \)
- \ (z = – 12 \) в \ (2 \ left ({z – 5} \ right) \ le 4z \)
В этом случае мы делаем то же самое, что и в предыдущем примере.? 4 \ left ({- 2} \ right) – 5 \\ – 3 & \ ne – 13 \, \, \, \, {\ mbox {НЕ ОК}} \ end {align *} \]
Итак, -3 – это не то же самое, что -13, и поэтому уравнение не выполняется. ? 4 \ left ({- 12} \ right) \\ – 34 \ require {cancel} & \ bcancel {\ le} – 48 \, \, \, \, {\ mbox {NOT OK}} \ end {align * } \]
? 4 \ left ({- 12} \ right) \\ – 34 \ require {cancel} & \ bcancel {\ le} – 48 \, \, \, \, {\ mbox {NOT OK}} \ end {align * } \]
В этом случае -34 НЕ меньше или равно -48, поэтому неравенство не выполняется.2} – 9 = 0 \). В этом случае \ (x = – 3 \) также является решением.
Мы называем полный набор всех решений набором решений для уравнения или неравенства. Есть также некоторые формальные обозначения для наборов решений, хотя мы не будем часто их использовать в этом курсе. Несмотря на это, мы все равно должны это признать.
Для уравнений мы обозначаем множество решений, заключая все решения в фигурные скобки, \ (\ left \ {{} \ right \} \). Вот наборы решений для двух уравнений, которые мы рассмотрели выше.2} – 9 & = 0 & \ hspace {0,25 дюйма} & {\ mbox {Набор решений}}: \, \, \, \ left \ {{- 3,3} \ right \} \ end {align *} \]
Для неравенств используются аналогичные обозначения. В зависимости от сложности неравенства набор решений может быть одним числом или диапазоном чисел. Если это одно число, мы используем те же обозначения, что и для уравнений. Если набор решений представляет собой диапазон чисел, как тот, который мы рассмотрели выше, мы будем использовать так называемую нотацию конструктора наборов .Вот набор решений для неравенства, которое мы рассмотрели выше.
Если это одно число, мы используем те же обозначения, что и для уравнений. Если набор решений представляет собой диапазон чисел, как тот, который мы рассмотрели выше, мы будем использовать так называемую нотацию конструктора наборов .Вот набор решений для неравенства, которое мы рассмотрели выше.
Это читается как: «Множество всех \ (z \) таких, что \ (z \) больше или равно -5».
Большинство неравенств, которые мы будем рассматривать, будут иметь достаточно простые наборы решений, которые мы часто сокращаем как
\ [z \ ge – 5 \]Есть еще одна последняя тема, которую мы должны затронуть в отношении наборов решений, прежде чем покинуть этот раздел.2} &
Если мы ограничимся только реальными решениями (что мы не всегда будем делать), тогда у уравнения не будет решения. Возведение в квадрат \ (x \) делает \ (x \) больше нуля, затем добавление 1 к этому означает, что левая часть гарантированно будет не меньше 1. Другими словами, у этого уравнения нет реального решения. По той же основной причине нет решения неравенства. Возведение любого вещественного \ (x \) в квадрат делает его положительным или нулевым, и поэтому никогда не будет отрицательным.
Другими словами, у этого уравнения нет реального решения. По той же основной причине нет решения неравенства. Возведение любого вещественного \ (x \) в квадрат делает его положительным или нулевым, и поэтому никогда не будет отрицательным.
Нам нужен способ обозначить тот факт, что здесь нет решений.В обозначении набора решений мы говорим, что набор решений пустой , и обозначаем его символом: \ (\ emptyset \). Этот символ часто называют пустым набором .
Теперь нам нужно сделать пару заключительных замечаний, прежде чем покинуть этот раздел.
В приведенном выше обсуждении пустых множеств мы предполагали, что ищем только реальные решения. Хотя это то, что мы будем делать с неравенствами, мы не будем ограничиваться реальными решениями с уравнениями.2} + 1 = 0 \) действительно имеет сложные решения.
Наконец, как отмечалось выше, мы не будем часто использовать нотацию набора решений в этом курсе. Это хорошее обозначение, которое иногда может использоваться, особенно для сложных решений. Однако для подавляющего большинства уравнений и неравенств, которые мы будем рассматривать, будут достаточно простые наборы решений, так что их будет проще записать и отпустить. Следовательно, это то, что мы не будем использовать для обозначений наших наборов решений.Однако вы должны знать обозначения и понимать, что они означают.
Это хорошее обозначение, которое иногда может использоваться, особенно для сложных решений. Однако для подавляющего большинства уравнений и неравенств, которые мы будем рассматривать, будут достаточно простые наборы решений, так что их будет проще записать и отпустить. Следовательно, это то, что мы не будем использовать для обозначений наших наборов решений.Однако вы должны знать обозначения и понимать, что они означают.
Mathematical Solution – обзор
5.8. Неравновесные жидкостные системы и наш космологический «двигатель»
С другой стороны, мы можем посмотреть на «тепловое ощущение» наших планетных экосистем, которое, как правило, зависит от расположения в межзвездном пространстве [9, 191]. Ни одна планета не является замкнутой системой и не находится в контакте с двумя или более термальными ваннами. Каждая планета контактирует с горячим излучателем (солнце ∼ 5800 K) и стоками холодной радиации (космическое пространство ∼ 2.75 К). Таким образом, каждая планета реализует своего рода «особый космологический двигатель». Сфера имеет решающее значение из-за ее режимов вращения и вращения с наклонной осью, которые ответственны за богатство и сложность поведения, вызванного солнечным притоком. Движение атмосферной жидкости добавляет изюминку хаоса, так что термодинамические события, происходящие на планете, поддерживаются неравновесными потоками, которые должны подчиняться фундаментальным законам неравновесной термодинамики.
Сфера имеет решающее значение из-за ее режимов вращения и вращения с наклонной осью, которые ответственны за богатство и сложность поведения, вызванного солнечным притоком. Движение атмосферной жидкости добавляет изюминку хаоса, так что термодинамические события, происходящие на планете, поддерживаются неравновесными потоками, которые должны подчиняться фундаментальным законам неравновесной термодинамики.
Если бы наша атмосфера была жесткой, ее термодинамика не содержала бы никаких хаотических явлений. Если бы Земля была твердой однородной сферой без атмосферы и, следовательно, без альбедо или нисходящей диффузии, прямой приток Солнца можно было бы рассчитать без каких-либо специальных экспериментальных измерений. В каждую точку поверхности приток солнечного света будет равен тригонометрическому коэффициенту, умноженному на солнечную постоянную, строго изменяющемуся вдоль открытой поверхности. Соседняя планета Марс активна таким образом, поэтому, если бы мы ее колонизировали, нам нужно было бы сначала создать ее альбедо, создав ретроактивно отражающую атмосферу при введении CO 2 из минеральных источников или просто доставив «земной тип». загрязнение »(как в нашей атмосфере), необходимое для повышения температуры поверхности и обеспечения возможности таяния и испарения воды, погребенной в почве.Этот процесс может быть относительно коротким по сравнению со следующим этапом, которым должно быть создание пригодной для жизни среды с помощью соответствующего процесса (посадки) для введения кислорода. Однако есть много других препятствий, которые необходимо преодолеть, например, слишком высокий уровень опасной радиации (которая экранируется от Земли ее экраном из магнитного поля). Поверхность планеты Венера, напротив, чрезвычайно горячая, потому что ее атмосфера плотная и непрозрачная из-за высокой концентрации отражающих назад компонентов и частиц (содержащих даже капли H 2 SO 4 ), которые, следовательно, демонстрируют: чрезвычайно сильное атмосферное движение.Из-за очень особой природы внешнего космологического состояния граничные условия для планет определяют возможность существования экосистемы, а именно диссипативной системы с устойчиво поддерживаемой жизнеспособностью.
загрязнение »(как в нашей атмосфере), необходимое для повышения температуры поверхности и обеспечения возможности таяния и испарения воды, погребенной в почве.Этот процесс может быть относительно коротким по сравнению со следующим этапом, которым должно быть создание пригодной для жизни среды с помощью соответствующего процесса (посадки) для введения кислорода. Однако есть много других препятствий, которые необходимо преодолеть, например, слишком высокий уровень опасной радиации (которая экранируется от Земли ее экраном из магнитного поля). Поверхность планеты Венера, напротив, чрезвычайно горячая, потому что ее атмосфера плотная и непрозрачная из-за высокой концентрации отражающих назад компонентов и частиц (содержащих даже капли H 2 SO 4 ), которые, следовательно, демонстрируют: чрезвычайно сильное атмосферное движение.Из-за очень особой природы внешнего космологического состояния граничные условия для планет определяют возможность существования экосистемы, а именно диссипативной системы с устойчиво поддерживаемой жизнеспособностью. Мы можем ожидать очень сложную циркуляцию доступности по планете. Мы можем определить глобальную физическую экосистему как систему, которая удовлетворяет следующим свойствам: она замкнута в отношении массообмена (занимает конечную область), но открыта в отношении энергии (исходящий поток соответствует полученному) и является в глобальном устойчивом состоянии в течение более длительного периода (энергетический баланс).
Мы можем ожидать очень сложную циркуляцию доступности по планете. Мы можем определить глобальную физическую экосистему как систему, которая удовлетворяет следующим свойствам: она замкнута в отношении массообмена (занимает конечную область), но открыта в отношении энергии (исходящий поток соответствует полученному) и является в глобальном устойчивом состоянии в течение более длительного периода (энергетический баланс).
Пока что космическая экосистема предлагает только один пример, Землю, и это может быть ее только одна реализация . Земля развивалась как гетерогенная термодинамическая система, состоящая из многих компонентов во всех трех фазах – газа, жидкости и твердого тела, и с их межфазными границами сложного характера. Его математическое решение, даже категорически сокращенное, бесконечно сложно: либо простейшее, использующее только один компонент и одну фазу в однородном виде, либо другое, с двумя несмешивающимися компонентами, предполагая гетерогенную концепцию, или многие другие, включая химические реакции и сложные оценки с помощью конечных элементов, решеток и т. д.. Дополнительное разнообразие биохимических циклов стало таким же сложным, как определение самой жизни. Проблемы предсказуемости со все более сложными нелинейными моделями всегда чрезвычайно раздуваются.
д.. Дополнительное разнообразие биохимических циклов стало таким же сложным, как определение самой жизни. Проблемы предсказуемости со все более сложными нелинейными моделями всегда чрезвычайно раздуваются.
Рис. 28. Слева показано соотношение энтропии между Солнцем и Землей, в то время как правый эскиз предлагает проблемы с энтропией, которые приводят к тому, что наш мир находится в постепенном, но повторяющемся спиралевидном развитии. В центре показано глобальное представление энергии, получаемой от Солнца, в сравнении с одноразовыми капитальными ресурсами энергии, доступными на Земле, как схематично показано кубами, связанными друг с другом (на вставке показан исходный спектр, запускаемый Солнцем и его ступенчатые изменения при достижении внешней атмосферы и в конечном итоге собираются на уровне моря).
Например, давайте посмотрим на температурное поле и его уменьшение и проследим за температурой в данном пространственном элементе. Мы ожидаем, что после периода в один год или в среднем за десять лет или около того, эта температура повторится с определенной точностью. Нарушения его ожидания можно отнести к локальным хаотическим взаимодействиям (быстрые неоднородности), глобальным хаотическим взаимодействиям (медленные неоднородности) и, наконец, к антропогенным модификациям энергетического баланса, таким как введение избыточного CO 2 на земную поверхность. .Теперь, учитывая поле плотности других компонентов (SO 2 , аэрозоли) и его уменьшение методом конечных элементов, мы снова ожидаем лишь небольших изменений; в противном случае Земля стала бы термически или химически отравленной. Конечно, это может стать результатом резкого извержения вулкана или внезапного удара метеорита, но в последнее время стабильно обеспечивается человеком, который, таким образом, является странным обитателем Экосистемы и, в то же время, наиболее гибким и очень уязвимым. . Он не переносит перепадов давления, химического состава окружающей среды и особенно температуры.Разница в температуре здорового тела составляет около одного градуса, поэтому человеку нужна сложная система контроля тела, а также укрытие – дом и одежда.
Нарушения его ожидания можно отнести к локальным хаотическим взаимодействиям (быстрые неоднородности), глобальным хаотическим взаимодействиям (медленные неоднородности) и, наконец, к антропогенным модификациям энергетического баланса, таким как введение избыточного CO 2 на земную поверхность. .Теперь, учитывая поле плотности других компонентов (SO 2 , аэрозоли) и его уменьшение методом конечных элементов, мы снова ожидаем лишь небольших изменений; в противном случае Земля стала бы термически или химически отравленной. Конечно, это может стать результатом резкого извержения вулкана или внезапного удара метеорита, но в последнее время стабильно обеспечивается человеком, который, таким образом, является странным обитателем Экосистемы и, в то же время, наиболее гибким и очень уязвимым. . Он не переносит перепадов давления, химического состава окружающей среды и особенно температуры.Разница в температуре здорового тела составляет около одного градуса, поэтому человеку нужна сложная система контроля тела, а также укрытие – дом и одежда. Существует очевидная разница между живым существом (саморазвитая система управления) и всей экосистемой Земли (определяется солнечным излучением).
Существует очевидная разница между живым существом (саморазвитая система управления) и всей экосистемой Земли (определяется солнечным излучением).
Мощность на квадратный метр поверхности Земли – не большая цифра, но этот скромный дар – то, что дала нам природа. Любое особенно стабильное общество могло уживаться; поколения динозавров жили в равновесии с этим числом в течение ста миллионов лет, человечество также управляло в течение нескольких тысячелетий, пока не начало увеличивать свою популяцию и продвигать свои технологии.Наконец, в последнее столетие, страдающее от жажды, мгновение в отношении истории, небольшой процент человечества развил тенденцию к потреблению ископаемой энергии, которая не соответствует естественным порядкам величины мощности, которые, вероятно, решила космическая эволюция. дать нам. Иногда трудно поверить, что мы недостаточно умны, действуем без научной совести, а просто движимы соблазном ускоряющегося роста.
В первом приближении рассмотрим Солнце как стабильный источник распределенных Планка фотонов при температуре T s = 5800 K на его внешнем радиусе R s . Фотоны, которые покидают Солнце, движутся во всех направлениях и без взаимодействия погружаются на бесконечность или, лучше сказать, приходят в равновесие с ископаемым источником при температуре около 2,7 К. Мы можем определить температуру T d , на расстоянии d, которое равно T d = T s √ (d / R s ) > 1. Для энтропийного излучения Солнца выполняется аналогичное соотношение: S d ./S s . = √ (d / R s ) > 1.Если бы твердая Земля была черной жесткой сферой с радиусом R E и с прозрачной атмосферой, потоки внутрь и наружу задавались бы простыми граничными условиями T и R. Относительное движение Земли и Солнца дает периодическую функцию f с периодом p, которая воплощает непрерывность массы, уравнение Навье-Стокса и соотношения энергетического баланса для атмосферы, которые все еще очень далеки от достоверности. Стационарное распределение устойчивых равновесий соответствует мощности механической мощности, которая может быть выражена распределением бесконечного числа двигателей Карно, глобальная эффективность которых может быть сформулирована в общих терминах с помощью математики.
Фотоны, которые покидают Солнце, движутся во всех направлениях и без взаимодействия погружаются на бесконечность или, лучше сказать, приходят в равновесие с ископаемым источником при температуре около 2,7 К. Мы можем определить температуру T d , на расстоянии d, которое равно T d = T s √ (d / R s ) > 1. Для энтропийного излучения Солнца выполняется аналогичное соотношение: S d ./S s . = √ (d / R s ) > 1.Если бы твердая Земля была черной жесткой сферой с радиусом R E и с прозрачной атмосферой, потоки внутрь и наружу задавались бы простыми граничными условиями T и R. Относительное движение Земли и Солнца дает периодическую функцию f с периодом p, которая воплощает непрерывность массы, уравнение Навье-Стокса и соотношения энергетического баланса для атмосферы, которые все еще очень далеки от достоверности. Стационарное распределение устойчивых равновесий соответствует мощности механической мощности, которая может быть выражена распределением бесконечного числа двигателей Карно, глобальная эффективность которых может быть сформулирована в общих терминах с помощью математики. Он аппроксимируется соотношением, η global = ∫ [λ (T 1 -T 2 ) 2 / max (T 1 .T 2 )] dS / R 2 δT 4 , где λ и δ – соответственно общая теплопроводность Ньютона (фиксированная как 8 Вт / м 2 K) и радиационные постоянные Стефана-Больцмана (обеспечивая δT 4 ≈ 1384 Вт / м 2 ). Вычисленные значения η global находятся в районе сотых.
Он аппроксимируется соотношением, η global = ∫ [λ (T 1 -T 2 ) 2 / max (T 1 .T 2 )] dS / R 2 δT 4 , где λ и δ – соответственно общая теплопроводность Ньютона (фиксированная как 8 Вт / м 2 K) и радиационные постоянные Стефана-Больцмана (обеспечивая δT 4 ≈ 1384 Вт / м 2 ). Вычисленные значения η global находятся в районе сотых.
Биологическая сеть взаимодействует с термодинамической экосистемой (фактически является «термодинамически живой»), так что это не пассивная стадия, а архитектура жизнеобеспечения. Глобальный подход способствует лучшему пониманию концепции глобальной устойчивости, регулирующей распределение локальных неравновесий. Если бы Земля имела нерегулярную орбиту, проблема не допускала бы глобального устойчивого решения, и если бы, помимо суточной и годовой периодичности, были бы дополнительные нерегулярные движения, не было бы ни глобальной устойчивости, ни менее ограничивающего свойства глобального периодичность. Серьезным осложнением является изменение либо солнечного излучения, либо геометрии взаимной орбиты, что подразумевает изменения входных условий для экосистемы Земли и, как известно, происходит в определенные часто повторяющиеся короткие (30, 70 или 150 лет) или длительные ( тысячи и миллионы лет) интервалы, зависящие в основном от Солнца, но также имеющие много хаотических компонентов (извержений).
Серьезным осложнением является изменение либо солнечного излучения, либо геометрии взаимной орбиты, что подразумевает изменения входных условий для экосистемы Земли и, как известно, происходит в определенные часто повторяющиеся короткие (30, 70 или 150 лет) или длительные ( тысячи и миллионы лет) интервалы, зависящие в основном от Солнца, но также имеющие много хаотических компонентов (извержений).
Отметим, что орбита Земли, к счастью, близка к круговой, но не полностью. Его эллиптичность меняется в течение года, но его влияние слишком слабое (3%), чтобы вызывать мгновенные сезоны, но достаточно сильное по своей строгости, регрессируя примерно на один полный день каждые 58 лет.Земля достигает перигелия (ближайшей точки к Солнцу) в начале января, но эта дата не остается фиксированной, а медленно регрессирует. Тропический год измеряется между двумя весенними равноденствиями (являющимися основой нашего григорианского календаря), в то время как между двумя перигелиями лежит аномальный год (примерно на 25 минут дольше), который полностью проходит через тропический год примерно за 21000 лет. Большая часть этой разницы связана с небольшим изменением направления оси вращения Земли в космосе, называемым прецессией, которая наклонена от нормали к плоскости орбиты под углом 23 градуса и прецессирует каждые 23000 лет.Эксцентриситет земной орбиты периодически изменяется с временной шкалой около 100 000 лет, так что климатологически он может стать императивным, если положительно модулировать вместе с 21 000 циклом перигелия. Еще одна вариация за 41 000 лет – наклон, отличный от прецессии. Эти астрономические фазы часто называют циклами Миланковича, циклами (по теории сербского инженера-строителя), но их истинное влияние на климатические изменения еще не ясно.
Большая часть этой разницы связана с небольшим изменением направления оси вращения Земли в космосе, называемым прецессией, которая наклонена от нормали к плоскости орбиты под углом 23 градуса и прецессирует каждые 23000 лет.Эксцентриситет земной орбиты периодически изменяется с временной шкалой около 100 000 лет, так что климатологически он может стать императивным, если положительно модулировать вместе с 21 000 циклом перигелия. Еще одна вариация за 41 000 лет – наклон, отличный от прецессии. Эти астрономические фазы часто называют циклами Миланковича, циклами (по теории сербского инженера-строителя), но их истинное влияние на климатические изменения еще не ясно.
Однако в космологическом масштабе концепция изолированной системы становится неосуществимой, потому что определение даже границ нашего соседства сложно (поскольку Солнце окружено далеко идущим дисперсным слоем, полным водоворотов и ужасных струй, а также нашей земной атмосферой. диффузный и полный движения, содержащий разреженные ионы со сверхбыстрыми потоками наружу), и уравнения движения жидкости не выполняются. Эти изменения входных условий вызывают еще один динамический режим атмосферных и океанических движений (помимо изменений в составе, структуре и т. Д.). Поскольку эти модификации снова являются нелинейными, никто не может предсказать или знать, каким может быть результирующий эффект по отношению к тому, что мы испытали или можем решить из истории.
Эти изменения входных условий вызывают еще один динамический режим атмосферных и океанических движений (помимо изменений в составе, структуре и т. Д.). Поскольку эти модификации снова являются нелинейными, никто не может предсказать или знать, каким может быть результирующий эффект по отношению к тому, что мы испытали или можем решить из истории.
Перейдем к примеру возобновляемого двигателя, а для этого рассмотрим термодинамику Земли. Это система, находящаяся примерно в глобальном устойчивом неравновесном состоянии, что означает, что более или менее уравновешиваются входящие и исходящие потоки излучения.Можно вспомнить стандартный термодинамический подход для рассмотрения пространственной области, Ом, с элементарным объемом d 3 v → с координатами, v → (x, y, z), граница, Ω B , и время t, принимая плотность, ρ (v → , t), скорость жидкости , v ( v → , t), и температуру, T ( v → , t), , которые не все локально стационарны. Диссипация энергии w (необратимость или производство энтропии) происходит от теплопроводности (∇T) и вязкого сдвига (тензор, σ ij ) и содержит сложный поддерживаемый поток неравновесий, которому соответствует рассеиваемая доступность для естественная система , w d n = σ ij ∂v i / ∂x (k) + λ (∇T) 2 / T (указано в [ Вт / м 3 ]). Плотность мощности постоянно создается и рассеивается, и это мощность, заключенная в естественном движении.Если мы знаем решение естественной динамики, мы могли бы построить величину w, вычислить ее численно, и это будет оценка рассеиваемой мощности Земли. Его интеграл по объему был бы фундаментальным глобальным числом, определяющим стационарные глобальные условия планеты, так сказать, ее «здоровье». На самом деле это продолжение истории классического двигателя, который производит механическую работу, и эта работа немедленно превращается в тепло.
Диссипация энергии w (необратимость или производство энтропии) происходит от теплопроводности (∇T) и вязкого сдвига (тензор, σ ij ) и содержит сложный поддерживаемый поток неравновесий, которому соответствует рассеиваемая доступность для естественная система , w d n = σ ij ∂v i / ∂x (k) + λ (∇T) 2 / T (указано в [ Вт / м 3 ]). Плотность мощности постоянно создается и рассеивается, и это мощность, заключенная в естественном движении.Если мы знаем решение естественной динамики, мы могли бы построить величину w, вычислить ее численно, и это будет оценка рассеиваемой мощности Земли. Его интеграл по объему был бы фундаментальным глобальным числом, определяющим стационарные глобальные условия планеты, так сказать, ее «здоровье». На самом деле это продолжение истории классического двигателя, который производит механическую работу, и эта работа немедленно превращается в тепло. Бензин – это солнечное излучение, и окружающая среда совпадает с двигателем, потому что нет «внешнего» для глобального окружения.Правую часть вышеупомянутого уравнения можно разделить на две части, первая – это доступность сдвига, а вторая – доступность Карно. Для активной системы (обычно называемой «доступностью ветряной мельницы») второй термин объединяется с термином «механическая мощность», давая w a = λ (∇T) 2 / T + v → ∇ P, , который технически является источником энергии подходящих плотин, ветряных мельниц и т. Д., Построенных человеком, в то время как остающееся рассеивание, σ ij ∂v i / ∂x (k) , кроме незначительная задержка ничего не меняет в естественном кровообращении.Таким образом, мы можем рассматривать естественные движения как петлю, питаемую доступностью, которая создает движение, которое, в свою очередь, создает доступность, которая, в свою очередь, рассеивается и снова создает движение, и так далее.
Бензин – это солнечное излучение, и окружающая среда совпадает с двигателем, потому что нет «внешнего» для глобального окружения.Правую часть вышеупомянутого уравнения можно разделить на две части, первая – это доступность сдвига, а вторая – доступность Карно. Для активной системы (обычно называемой «доступностью ветряной мельницы») второй термин объединяется с термином «механическая мощность», давая w a = λ (∇T) 2 / T + v → ∇ P, , который технически является источником энергии подходящих плотин, ветряных мельниц и т. Д., Построенных человеком, в то время как остающееся рассеивание, σ ij ∂v i / ∂x (k) , кроме незначительная задержка ничего не меняет в естественном кровообращении.Таким образом, мы можем рассматривать естественные движения как петлю, питаемую доступностью, которая создает движение, которое, в свою очередь, создает доступность, которая, в свою очередь, рассеивается и снова создает движение, и так далее. Естественная и активная системы действительно разные.
Естественная и активная системы действительно разные.
Их совместное рассмотрение эквивалентно рассмотрению сжигания определенного количества бензина в природе, и посмотреть, что произойдет, если мы сожжем его внутри двигателя. Эти движения могут быть периодическими (или, лучше сказать, хаотическими) в зависимости от температурных градиентов.В тех местах, где (λ (∇T) 2 / T) и (v → ∇ P ) особенно велики, может произойти выброс механической энергии, обычно в виде пузырьков роста в горшок с горячей вулканической магмой. Он многому нас учит. Мы узнали, что в растянутый период солнечное излучение непостоянно, а его диаграмма излучения частично периодична, а частично хаотична. Конечным результатом является то, что экосистема Земли имеет чрезвычайно сложную термодинамическую конфигурацию [191, 192] с наличием хаоса, перекрывающего преобладающую периодичность.Это показывает физический факт, что фундаментальные числа возникли в результате чистого использования глобальной формулировки; в общем, это в основном температура Солнца, разделительное расстояние и сфероидичность Земли. Данная доступность на самом деле является оболочкой или, лучше сказать, явлением интерфейса, особенно при введении в модель изучения химических реакций и детального движения жидкости, которые обязательно сходятся вместе, потому что подавляющее большинство процессов происходит в жидком состоянии.Непонятно, какое количество химических реакций следует учитывать в описании, по крайней мере, биофизический цикл CO 2 (рост → 6CO 2 + 6H 2 O = C 6 H 12 O 6 + 6O 2 ← горение) является наиболее важным. Фактически сама природа изобрела сверхсложные химические циклы, и теперь человек в своей богатой империи пытается развить какие-то невежественные и аналогичные нарушения.
Данная доступность на самом деле является оболочкой или, лучше сказать, явлением интерфейса, особенно при введении в модель изучения химических реакций и детального движения жидкости, которые обязательно сходятся вместе, потому что подавляющее большинство процессов происходит в жидком состоянии.Непонятно, какое количество химических реакций следует учитывать в описании, по крайней мере, биофизический цикл CO 2 (рост → 6CO 2 + 6H 2 O = C 6 H 12 O 6 + 6O 2 ← горение) является наиболее важным. Фактически сама природа изобрела сверхсложные химические циклы, и теперь человек в своей богатой империи пытается развить какие-то невежественные и аналогичные нарушения.
Понятно, что хорошие идеи для теории экологического укрытия человека могут возникнуть в результате изучения диссипативных обучающих систем, т.е.е. такие адаптивные системы, которые пригодны для выживания. Земля обладает необходимой жизнеспособностью, сложностью и равновесной стабильностью, что является предпосылкой для ее выживания. Иерархия взаимодействий может помочь сформулировать концепцию, согласно которой человек – это не детерминированная система, а скорее финалистическая система или, лучше сказать, система контроля. Таким образом, экосистема видов имеет более простое внешнее взаимодействие, а экосистема, как гигантский двигатель, очень сложный внутри, имеет довольно упрощенное и почти ничтожное взаимодействие с самой Вселенной, что позволяет рассматривать ее как все же детерминированный мир.Следовательно, увидеть существование островов порядка, которые питают возможность разумной жизни, является глубокой тайной. Изучение и более широкое применение истинно неравновесной термодинамики и теории хаоса имеет смысл, но есть большая, неизученная область, помимо той, которая касается, в частности, неравновесной термодинамики самой среды Земли.
Иерархия взаимодействий может помочь сформулировать концепцию, согласно которой человек – это не детерминированная система, а скорее финалистическая система или, лучше сказать, система контроля. Таким образом, экосистема видов имеет более простое внешнее взаимодействие, а экосистема, как гигантский двигатель, очень сложный внутри, имеет довольно упрощенное и почти ничтожное взаимодействие с самой Вселенной, что позволяет рассматривать ее как все же детерминированный мир.Следовательно, увидеть существование островов порядка, которые питают возможность разумной жизни, является глубокой тайной. Изучение и более широкое применение истинно неравновесной термодинамики и теории хаоса имеет смысл, но есть большая, неизученная область, помимо той, которая касается, в частности, неравновесной термодинамики самой среды Земли.
Решение линейных уравнений с нулевым Солнцем, без Солнца и «Все-x» Солнцем
Purplemath
Есть три типа решений, которые могут вызвать путаницу. Мы рассмотрим по одному примеру каждого из них, и я объясню различия. Затем мы поработаем над смесью типов уравнений, чтобы вам было удобнее различать типы решений.
Мы рассмотрим по одному примеру каждого из них, и я объясню различия. Затем мы поработаем над смесью типов уравнений, чтобы вам было удобнее различать типы решений.
Чтобы решить это уравнение, мне сначала нужно упростить левую часть, взяв «минус» в скобки и объединив «похожие» термины:
MathHelp.com
5 – (3 x + 4)
5 – 1 (3 x ) – 1 (+4)
5 – 3 x – 4
5 – 4 – 3 x
1-3 x
Теперь я могу решить обычным способом:
1–3x = 1
-1 -1
———–
-3x = 0
— –
-3-3
х = 0
Является ли « x = 0» допустимым решением? Да, действительно, потому что ноль – допустимое число. Дело не в том, что решение – «ничто»; дело в том, что решение – это «что-то», а это «что-то» равно нулю. Итак, мой ответ:
Дело не в том, что решение – «ничто»; дело в том, что решение – это «что-то», а это «что-то» равно нулю. Итак, мой ответ:
Студенты, как правило, могут привыкнуть к тому, что ноль является решением уравнения, но разница между решением «ноль» (это решение является числовым значением) и «ничего» (возможно, является физической мерой чего-то вроде «без яблок» или «нет денег») может вызвать недоумение.
Убедитесь, что вы понимаете, что «ноль» сам по себе не является «ничем». Ноль – это числовое значение, которое (в «реальной жизни» или в контексте словесной проблемы) может означать , что означает «ничего» чего-то или другого, но ноль сам по себе является реальной вещью; это существует; это что-то”.
Решить 11 + 3
x -7 = 6 x + 5-3 x
Во-первых, объедините одинаковые термины; затем решите:
Гм. .. подожди минутку …
.. подожди минутку …
С каких это пор четыре когда-либо равно пяти? Никогда! Существует ли какое-нибудь возможное значение x , которое «исправит» это уравнение, чтобы оно говорило что-то, имеющее какой-то смысл? Будет ли любое значение x когда-либо заставить это уравнение работать?
Нет; это просто невозможно. Я выполнил все свои шаги правильно, но эти шаги привели к уравнению (а) не содержало переменных и (б) не имело смысла.Поскольку не существует значения x , которое заставило бы это уравнение работать, то и решения этого уравнения нет. Вот мой ответ на это упражнение:
. Вот логика для приведенного выше примера: когда вы пытаетесь решить уравнение, вы исходите из (неустановленного) предположения, что на самом деле – это решение. Когда вы в конечном итоге получаете бессмыслицу (например, бессмысленное уравнение «4 = 5» выше), это означает, что ваше первоначальное предположение (а именно, что исходное уравнение действительно имело решение) было неверным; на самом деле решения нет. Поскольку утверждение «4 = 5» совершенно неверно, и с момента нет значения x, которое когда-либо могло бы сделать его истинным , то это уравнение не имеет решения.
Поскольку утверждение «4 = 5» совершенно неверно, и с момента нет значения x, которое когда-либо могло бы сделать его истинным , то это уравнение не имеет решения.
Advisory: этот ответ полностью отличается от ответа на первое упражнение в верхней части этой страницы, где было , значение x , что будет работать (это значение решения равно нулю). Не путайте эти две очень разные ситуации : «решение существует и имеет нулевое значение» никоим образом не то же самое, что «никакого значения решения не существует вообще».
И не путайте приведенное выше уравнение типа «без решения» со следующим типом уравнения:
Решить 6
x + 5-2 x = 4 + 4 x + 1
Сначала я объединю похожие термины; тогда решу:
Для предыдущего уравнения я получил «5 = 4», и не было значения x , которое могло бы сделать уравнение истинным. Этот результат противоположен этому. Для этого уравнения существует ли какое-либо возможное значение x , которое могло бы сделать приведенное выше утверждение ложным? Нет; 5 – это , всегда будет равно 5. Фактически, поскольку в последней строке вычислений нет « x », значение x явно не имеет отношения к уравнению; x может быть чем угодно, и уравнение останется верным. Итак, решение:
Этот результат противоположен этому. Для этого уравнения существует ли какое-либо возможное значение x , которое могло бы сделать приведенное выше утверждение ложным? Нет; 5 – это , всегда будет равно 5. Фактически, поскольку в последней строке вычислений нет « x », значение x явно не имеет отношения к уравнению; x может быть чем угодно, и уравнение останется верным. Итак, решение:
Это решение также может быть указано как «все действительные числа», «все действительные числа», «вся числовая строка», «(–∞, + ∞)» или « x ∈ & reals;» (последнее означает « x является членом набора действительных чисел»).Вы должны ожидать увидеть некоторые вариации в жаргоне от одного учебника к другому, поэтому не удивляйтесь различиям в форматировании.
Обратите внимание, что, если бы я решил уравнение, вычтя 5 из любой части исходного уравнения, я бы получил:
Другими словами, я бы получил еще одно тривиально верное утверждение. Я также мог бы вычесть 4 x с любой стороны, или я мог бы разделить обе стороны приведенного выше уравнения на 4, или я мог бы разделить на 4, а затем вычесть x с любой стороны, или я мог бы вычесть и 4 x , и 5 с обеих сторон исходного уравнения.Каждый из них – это еще один способ получить другой тривиально верный результат, например «0 = 0». Но независимо от конкретных предпринятых шагов результат (тривиально верное уравнение) всегда будет одним и тем же, и решение останется тем же: «все x ».
Я также мог бы вычесть 4 x с любой стороны, или я мог бы разделить обе стороны приведенного выше уравнения на 4, или я мог бы разделить на 4, а затем вычесть x с любой стороны, или я мог бы вычесть и 4 x , и 5 с обеих сторон исходного уравнения.Каждый из них – это еще один способ получить другой тривиально верный результат, например «0 = 0». Но независимо от конкретных предпринятых шагов результат (тривиально верное уравнение) всегда будет одним и тем же, и решение останется тем же: «все x ».
Поскольку (как я перечислил выше) существует множество способов прийти к одному и тому же выводу для этого типа уравнения, вы не должны удивляться, если для уравнений «все действительные числа» или «без решения» вы не используйте те же шаги, что и некоторые из ваших одноклассников.Существует бесконечно много всегда верных уравнений (например, «0 = 0») и бесконечно много бессмысленных уравнений (например, «3 = 4»), также будет много способов (правильно) прийти к этим ответам.
Основным выводом из приведенных выше примеров должны быть следующие правила:
x = 0: регулярное решение регулярного уравнения
ерунда (например, 3 = 4): нет решения
тривиально истинно (например, 0 = 0): решение – все действительные числа
К сожалению, хотя вы почти наверняка встретите хотя бы один из этих вопросов «нет решения» или «все реально» в следующем тесте (и, вероятно, также в финале), обычно их не так много в наборе домашних заданий, и ваш инструктор, вероятно, предоставил только по одному образцу каждого типа.Это не дает вам большой практики в интерпретации решений такого типа, поэтому давайте еще несколько примеров.
Сначала я умножу 3 на скобку в левой части. Потом решу.
3x + 12 = 3x + 11
-3x -3x
——————
12 = 11
Моя математика верна, но результат – ерунда. Двенадцать никогда не будет равняться одиннадцати. Итак, мой ответ:
Двенадцать никогда не будет равняться одиннадцати. Итак, мой ответ:
Решите 6 – 2 (
x + 3) = –2 x
Я буду умножать и упрощать в левой части. Потом решу.
6-2 (x + 3) = -2x
6 – 2x – 6 = -2x
6-6 – 2x = -2x
0 – 2x = -2x
-2x = -2x
+ 2x + 2x
———
0 = 0
Ноль всегда будет равняться нулю, и в последней строке моей работы нет даже какой-либо переменной, поэтому переменная явно не имеет значения.Это уравнение верно независимо от значения x . Итак, мой ответ:
Решите 2 (
x + 1) + x = 3 ( x + 2) – 2
Мне нужно будет умножить и упростить каждую часть этого уравнения.
2 (х + 1) + х = 3 (х + 2) – 2
2х + 2 + х = 3х + 6-2
2х + х + 2 = 3х + 4
3х + 2 = 3х + 4
-3x -3x
———————-
2 = 4
Нет; никогда не правда.
Решить 5
x + 7 = 4 (2 x + 1) – 3 x -2
Мне нужно упростить правую часть, а затем посмотреть, к чему это приведет.
5x + 7 = 4 (2x + 1) – 3x – 2
5х + 7 = 8х + 4 – 3х – 2
5x + 7 = 8x – 3x + 4-2
5х + 7 = 5х + 2
-5x -5x
——————
7 = 2
Нет; никогда не правда.
Я разверну левую часть и решу.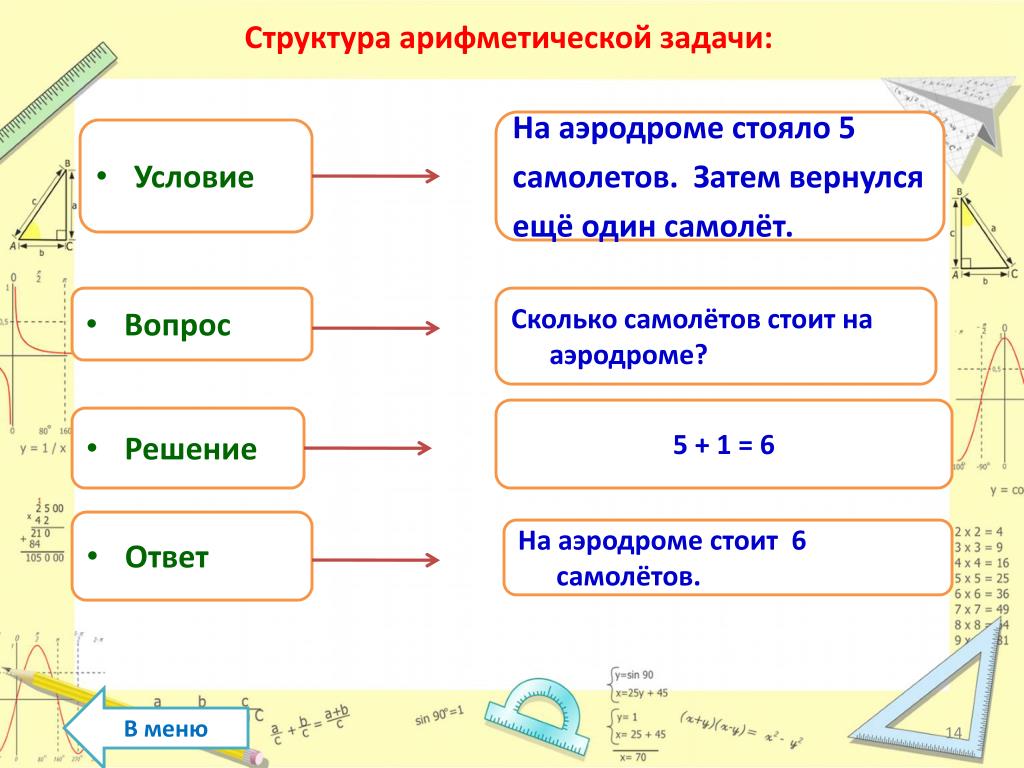
8 (x + 2) = 2x + 16
8х + 16 = 2х + 16
-2x -2x
——————
6х + 16 = 16
-16 -16
——————
6x + 0 = 0
—— –
6 6
х = 0
Это уравнение имеет значение решения, равное нулю.
Решить 1,5
x + 4 = 4 ( x + 1) – 2,5 x
Я расширяю и упрощаю в правой части, а затем решаю.
1,5x + 4 = 4 (x + 1) – 2,5x
1,5x + 4 = 4x + 4 – 2,5x
1,5x + 4 = 4x – 2,5x + 4
1.5х + 4 = 1,5х + 4
-1,5x -1,5x
——————–
4 = 4
Это всегда так, поэтому мой ответ:
Я разверну левую часть и решу.
2 (х + 5) = 2x + 5
2х + 10 = 2х + 5
-2x -2x
—————–
10 = 5
Нет; никогда не правда.
URL: https://www.purplemath.com/modules/solvelin5.htm
Обучение математике с использованием нескольких методов решения: влияние типов решений и активности учащихся
Эйнсворт, С. (2006). DeFT: концептуальная основа для рассмотрения обучения с несколькими представлениями. Обучение и инструктаж, 16 , 183–198. DOI: 10.1016 / j.learninstruc.2006.03.001.
Артикул Google Scholar
Эйнсворт, С., Бибби, П., и Вуд, Д. (2002). Изучение эффектов различных множественных репрезентативных систем в изучении начальной математики. Журнал научных исследований, 11 , 25–61.
Журнал научных исследований, 11 , 25–61.
Артикул Google Scholar
Ангилери, Дж., Бейшуйзен, М., и Ван Путтен, К. (2002). От неформальных стратегий к структурированным процедурам: помните о пробелах! Образовательные занятия по математике, 49 , 149–170.
Артикул Google Scholar
Аткинсон, Р. К., Дерри, С. Дж., Ренкл, А., и Уортэм, Д. У. (2000). Учимся на примерах: обучающие принципы на основе исследования отработанных примеров. Обзор исследований в области образования, 70 , 181–214.DOI: 10.3102 / 00346543070002181.
Артикул Google Scholar
Аткинсон, Р. К., Ренкл, А., & Меррилл, М. М. (2003). Переход от изучения примеров к решению проблем: сочетание угасания с подсказками способствует обучению. Журнал педагогической психологии, 95 , 774–783. DOI: 10.1037 / 0022-0663.95.4.774.
Журнал педагогической психологии, 95 , 774–783. DOI: 10.1037 / 0022-0663.95.4.774.
Артикул Google Scholar
Бандура, А., И Локк, Э. А. (2003). Еще раз об отрицательной самоэффективности и целевых эффектах. Журнал прикладной психологии, 88 , 87–99. DOI: 10.1037 / 0021-9010.88.1.87.
Артикул Google Scholar
Бергер Р. (1989). Prozent – und Zinsrechnen in der Hauptschule – Didaktische Analysen und empirische Ergebnisse zu Schwierigkeiten, Lösungsverfahren und Selbstkorrekturverhalten der Schüler am Didde Calzec, анализ результатов средней школы и процентного отношения к результатам оценки и процентного отношения к результатам оценки 9114 в средней школе, а также анализ проблем, связанных с решением 911-й средней школы, а также процентное решение проблем, связанных с решением 911-й средней школы, а также анализом процентного отношения к результатам средней школы44 методы и самокоррекция поведения учащихся по окончании общеобразовательной школы. Регенсбург: С. Родерер.
Регенсбург: С. Родерер.
Bortz, J. (1993). Statistik für Sozialwissenschaftler [Статистика для социологов] . Берлин: Springer.
Google Scholar
Коллинз А., Браун Дж. С. и Ньюман С. Е. (1989). Познавательное обучение. Обучение чтению, письму и математике. В Л. Б. Резник (ред.), Знание, обучение и наставление (стр. 453–493). Хиллсдейл, Нью-Джерси: Эрлбаум.
Google Scholar
Инициатива Common Core State. (2012). Математика . Получено 21 января 2014 г. с сайта http://www.corestandards.org/Math.
Деци, Э. Л., и Райан, Р. М. (1993). Die Selbstbestimmungstheorie der Motivation und ihre Bedeutung für die Pädagogik [Теория самоопределения мотивации и ее значение для педагогики]. Zeitschrift für Pädagogik, 39 , 223–238.
Google Scholar
Gigerenzer, G. , & Hoffrage, U. (1995). Как улучшить байесовские рассуждения без инструкции: частотные форматы. Психологическое обозрение, 102 , 684–704.
, & Hoffrage, U. (1995). Как улучшить байесовские рассуждения без инструкции: частотные форматы. Психологическое обозрение, 102 , 684–704.
Артикул Google Scholar
Große, C. S. (2005). Lernen mit multiplen Lösungswegen [Обучение с использованием нескольких методов решения] .Мюнстер: Waxmann.
Google Scholar
Große, C. S., & Renkl, A. (2006). Эффекты множественных методов решения в обучении математике. Обучение и инструктаж, 16 , 122–138. DOI: 10.1016 / j.learninstruc.2006.02.001.
Артикул Google Scholar
Хэтти, Дж. И Тимперли, Х. (2007). Сила обратной связи. Обзор исследований в области образования, 77 , 81–112. DOI: 10.3102 / 003465430298487.
Артикул Google Scholar
Йоханнинг Д. И. (2004). Поддержка развития алгебраического мышления в средней школе: более пристальный взгляд на неформальные стратегии учащихся. Журнал математического поведения, 23 , 371–388.
И. (2004). Поддержка развития алгебраического мышления в средней школе: более пристальный взгляд на неформальные стратегии учащихся. Журнал математического поведения, 23 , 371–388.
Артикул Google Scholar
Калюга, С., Эйрес, П., Чендлер, П., и Свеллер, Дж. (2003). Эффект отмены экспертизы. Психолог-педагог, 38 , 23–31.
Артикул Google Scholar
Кёдингер, К. Р. и Натан, М. Дж. (2004). Реальная история проблем истории: влияние представлений на количественные рассуждения. Журнал научных исследований, 13 , 129–164.DOI: 10.1207 / s15327809jls1302_1.
Артикул Google Scholar
Koedinger, K. R., & Tabachneck, H. J. M. (1994). Две стратегии лучше, чем одна: Использование нескольких стратегий для решения словесных задач. Представлено на ежегодном собрании Американской ассоциации исследований в области образования , Новый Орлеан, Луизиана.
Представлено на ежегодном собрании Американской ассоциации исследований в области образования , Новый Орлеан, Луизиана.
Math Warehouse. (нет данных). Система линейных уравнений с 2-мя переменными. Получено 21 января 2014 г. с http: // www.mathwarehouse.com/algebra/linear_equation/systems-of-equation/index.php.
Мец, М. Л. (2010). Использование стандартов GAISE и NCTM в качестве основы для обучения теории вероятностей и статистики учителям математики начальных и средних школ. Journal of Statistics Education [онлайн], 18. Получено 20 января 2014 г. с http://www.amstat.org/publications/jse/v18n3/metz.pdf.
NCTM. (2014). Принципы и стандарты школьной математики. Получено 21 января 2014 г. с сайта http://www.nctm.org/standards/content.aspx?id=312.
Нойбранд, Дж., И Нойбранд, М. (2000). Эффект мультипликатора Lösungsmöglichkeiten: Beispiele aus einer japanischen Mathematikstunde [Эффекты нескольких решений: примеры урока японской математики]. В C. Selter & G. Walther (Eds.), Mathematikdidaktik als design science (стр. 148–158). Лейпциг: Клетт.
В C. Selter & G. Walther (Eds.), Mathematikdidaktik als design science (стр. 148–158). Лейпциг: Клетт.
Google Scholar
Паас, Ф., Ренкл А. и Свеллер Дж. (2003). Теория когнитивной нагрузки и учебный дизайн: последние разработки. Психолог-педагог, 38 , 1–4.
Артикул Google Scholar
Предигер, С. (2004). «Darf man denn das so rechnen?» – Vielfalt im Mathematikunterricht [«Можно ли использовать этот метод решения?» – Разнообразие в математическом образовании]. Фридрих Ярешефт, 22 , 86–89.
Google Scholar
Ренкл А. (1997). Учимся на отработанных примерах: исследование индивидуальных различий. Когнитивная наука, 21 , 1–29.
Артикул Google Scholar
Ренкл, А. (1999). Изучение математики на основе разработанных примеров: анализ и содействие самооценкам. Европейский журнал психологии образования, 14 , 477–488.
(1999). Изучение математики на основе разработанных примеров: анализ и содействие самооценкам. Европейский журнал психологии образования, 14 , 477–488.
Артикул Google Scholar
Ренкл А., Аткинсон Р. К. и Гроссе К. С. (2004). Как работает постепенное исчезновение шагов решения – перспектива когнитивной нагрузки. Instructional Science, 32 , 59–82.
Артикул Google Scholar
Ренкл А., Аткинсон Р. К. и Майер У. Х. (2000). От изучения примеров до решения проблем: постепенное исчезновение проработанных шагов решения помогает учиться.В Л. Глейтман и А. К. Джоши (ред.), Труды 22-й ежегодной конференции Общества когнитивных наук (стр. 393–398). Махва, Нью-Джерси: Эрлбаум.
Ренкл А., Аткинсон Р. К., Майер У. Х. и Стейли Р. (2002). От учебного примера к решению проблем: плавные переходы помогают в обучении. Журнал экспериментального образования, 70 , 293–315.
Журнал экспериментального образования, 70 , 293–315.
Артикул Google Scholar
Райнберг, Ф.(2004). Motivationsdiagnostik [Диагностика мотивации] . Геттинген: Hogrefe.
Google Scholar
Риттл-Джонсон, Б., & Стар, Дж. Р. (2007). Облегчает ли сравнение методов решения концептуальные и процедурные знания? Экспериментальное исследование по обучению решению уравнений. Журнал педагогической психологии, 99 , 561–574. DOI: 10.1037 / 0022-0663.99.3.561.
Артикул Google Scholar
Риттл-Джонсон, Б., & Стар, Дж. Р. (2009). По сравнению с чем? Влияние различных сравнений на концептуальные знания и процедурную гибкость при решении уравнений. Журнал педагогической психологии, 101 , 529–544. DOI: 10.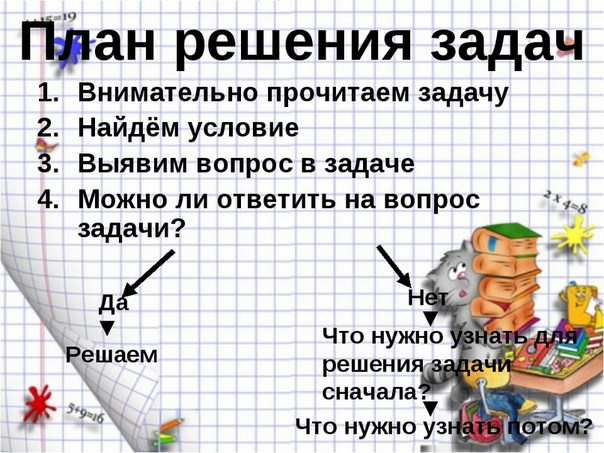 1037 / a0014224.
1037 / a0014224.
Артикул Google Scholar
Риттл-Джонсон, Б., Стар, Дж. Р., и Дуркин, К. (2009). Важность предварительных знаний при сравнении примеров: влияет на концептуальные и процедурные знания о решении уравнений. Журнал педагогической психологии, 101 , 836–852. DOI: 10.1037 / a0016026.
Артикул Google Scholar
Риттл-Джонсон, Б., Стар, Дж. Р., и Дуркин, К. (2012). Развитие процедурной гибкости: готовы ли новички учиться на сравнении процедур? Британский журнал педагогической психологии, 82 , 436–455. DOI: 10.1111 / j.2044-8279.2011.02037.x.
Артикул Google Scholar
Sedlmeier, P. (1999). Улучшение статистических рассуждений – теоретические модели и практическое применение . Махва, Нью-Джерси: Эрлбаум.
Google Scholar
Sedlmeier, P. , & Gigerenzer, G. (2001). Обучение байесовскому мышлению менее чем за два часа. Журнал экспериментальной психологии: Общие, 130 , 380–400.DOI: 10.1037 / 0096-3445.130.3.380.
, & Gigerenzer, G. (2001). Обучение байесовскому мышлению менее чем за два часа. Журнал экспериментальной психологии: Общие, 130 , 380–400.DOI: 10.1037 / 0096-3445.130.3.380.
Артикул Google Scholar
Сютс, Дж. (2002). Unterschiedliche mentale Konstruktionen beim Aufgabenlösen — Eine Fallstudie zur Ma-tematik als Werkzeug zur Wissenspräsentation [Различные мысленные конструкции для решения проблем – Пример использования математики как инструмента для представления знаний]. Journal für Mathematik-Didaktik, 23 , 106–128.
Артикул Google Scholar
Спиро, Р.Дж., Фельтович, П. Дж., Якобсон, М. Дж., И Коулсон, Р. Л. (1991). Когнитивная гибкость, конструктивизм и гипертекст: инструкция произвольного доступа для получения дополнительных знаний в плохо структурированных областях. Образовательные технологии, 31 , 24–33.
Google Scholar
Спиро, Р. Дж., И Дженг, Дж. К. (1990). Когнитивная гибкость и гипертекст: теория и технология нелинейного и многомерного обхода сложных предметов.В Д. Никс и Р. Дж. Спиро (ред.), Познание, образование и мультимедиа: изучение идей в высоких технологиях (стр. 163–205). Хиллсдейл, Нью-Джерси: Эрлбаум.
Google Scholar
Стар, Дж. Р. и Риттл-Джонсон, Б. (2008). Гибкость в решении проблем: случай решения уравнений. Обучение и инструктаж, 18 , 565–579. DOI: 10.1016 / j.learninstruc.2007.09.018.
Артикул Google Scholar
Стар, Дж.Р., и Риттл-Джонсон, Б. (2009). Стоит сравнивать: экспериментальное исследование вычислительной оценки. Журнал экспериментальной детской психологии, 102 , 408–426. DOI: 10.1016 / j. jecp.2008.11.004.
jecp.2008.11.004.
Артикул Google Scholar
Старк Р. (1999). Lernen mit Lösungsbeispielen. Der Einfluss unvollständiger Lösungsschritte auf Beispiel-development, Motivation und Lernerfolg [Обучение на рабочих примерах.Влияние неполных примеров на разработку примеров, мотивацию и результаты обучения] . Геттинген: Hogrefe.
Google Scholar
Старк Р., Грубер Х., Ренкл А. и Мандл Х. (2000). Instruktionale Effekte einer kombinierten Lernme-thode: Zahlt sich die Kombination von Lösungsbeispielen und Problemlöseaufgaben aus? [Учебные эффекты комбинированного метода обучения: окупается ли комбинация проработанных примеров и задач?]. Zeitschrift für Pädagogische Psychologie, 14 , 206–218.
Артикул Google Scholar
Staub, F. C., & Reusser, K. (1995). Роль презентационных структур в понимании и решении математических текстовых задач. В C. A. Weaver, S. Mannes, & C. R. Fletcher (Eds.), Понимание дискурса. Очерки в честь Вальтера Кинча (стр. 285–305). Хиллсдейл, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.
В C. A. Weaver, S. Mannes, & C. R. Fletcher (Eds.), Понимание дискурса. Очерки в честь Вальтера Кинча (стр. 285–305). Хиллсдейл, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.
Google Scholar
Стерн, Э. (1993). Что делает некоторые арифметические задачи, связанные со сравнением наборов, такими трудными для детей? Журнал педагогической психологии, 85 , 7–23.
Артикул Google Scholar
Табачнек, Х. Дж. М., Кёдингер, К. Р., и Натан, М. Дж. (1994). К теоретическому учету использования стратегии и осмысления решения математических задач. Материалы 16-й ежегодной конференции Общества когнитивных наук (стр. 836–841). Хиллсдейл, Нью-Джерси: Эрлбаум.
Trafton, J. G., & Reiser, B.J. (1993). Вклад изучения примеров и решения проблем в приобретение навыков. В М. Полсоне (ред.), Труды 15-й ежегодной конференции Общества когнитивных наук . Хиллсдейл, Нью-Джерси: Эрлбаум.
Хиллсдейл, Нью-Джерси: Эрлбаум.
Ван Амером Б.А. (2003). Сосредоточение внимания на неформальных стратегиях при увязке арифметики с ранней алгеброй. Образовательные занятия по математике, 54 , 63–75.
Артикул Google Scholar
Ван Мерриенбоер, Дж. Дж. Г. (1990). Стратегии обучения программированию в средней школе: завершение программы по сравнению с генерацией программы. Журнал образовательных компьютерных исследований, 6 , 265–285.
Артикул Google Scholar
Ван Мерриенбор, Дж.Дж. Г. и де Крук, М. Б. М. (1992). Стратегии для обучения программированию на компьютере: завершение программы по сравнению с генерацией программы. Журнал образовательных компьютерных исследований, 8 , 365–394.
Google Scholar
Обоснование решения
На этой странице
Учителя математики должны побуждать учеников сосредоточиться не только на правильном ответе; учащимся необходимо понимать процесс и лежащие в основе концепции, чтобы получить правильный ответ (Johnson & Watson, 2011). Другими словами, учащимся нужно найти и обосновать свои решения.
Другими словами, учащимся нужно найти и обосновать свои решения.
Чтобы обосновать решение, учащиеся должны уметь использовать соответствующий математический язык для обоснования конкретного подхода, используемого для решения проблемы. Каждый раз, когда ученик предлагает «решение» в попытке решить проблему, это «решение» должно быть обосновано. То есть ученик должен объяснить, откуда он знает, что его «решение» правильное.
Обоснование решения также может возникнуть в контексте обсуждения математики в классе, когда учащимся нужно будет объяснить свои решения устно.
Понимание этой стратегии
Чтобы помочь учащимся обосновать свои решения, учитель может:
- иметь класс обсуждение того, что значит оправдать решение
предоставить учащимся задачу и попросить их решить ее, записав свои обоснования.
попросите учащихся работать в парах, чтобы обосновать свои решения.
попросите пары поделиться и предоставить конструктивную обратную связь об оправданиях друг друга.
Учитель может попросить некоторых учеников обрисовать в общих чертах, как они могут обосновать конкретное решение из предыдущего урока.
Может быть полезно обсудить ключевую терминологию, относящуюся к изучаемой математической теме, чтобы поддержать студентов в их обсуждении.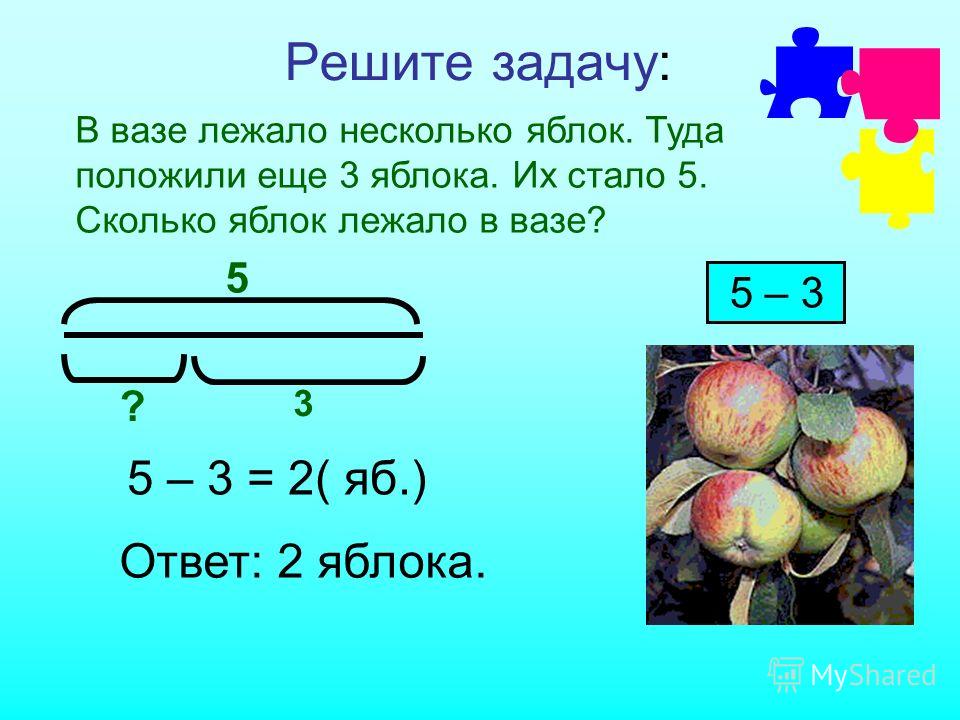 Эти ключевые термины можно найти в классе и записать на доске.
Эти ключевые термины можно найти в классе и записать на доске.
Пример использования выравнивания
В приведенном ниже примере показано, как эту стратегию можно применить к классу 10 года по линейным уравнениям.
Сценарий: начисление платы за выполнение задачи
Сравните следующие два расчета начисления платы за услугу, где C – стоимость (в долларах) на выполнение задачи, а t – время, затраченное (в часах) на выполнение задачи. выполнить задание:
Определите, когда первое уравнение дешевле второго
C = 25t + 200
C = 30t +150
Разработка решения
Студенты будут работать над решением задачи. Графически или решая одновременные уравнения, время, при котором затраты равны, составляет 10 часов.
Графически или решая одновременные уравнения, время, при котором затраты равны, составляет 10 часов.
Примечание. Время, в течение которого первая скорость меньше второй, – это любое время, превышающее 10 часов.
Обсуждение в классе
Обсудите в классе, что значит оправдать решение. Попросите некоторых студентов обрисовать в общих чертах, как они могли бы оправдать свое конкретное решение.
Ключевые термины для обсуждения могут включать фиксированные затраты, переменные затраты, почасовую оплату и т. Д.
Обоснование решения
Попросите учащихся работать в парах, чтобы обосновать свои решения.
Студенты обмениваются решениями с другой парой и добавляют предложения по улучшению решений.
Обоснование решения будет включать следующее:
- проверка решения одновременных уравнений, возможно, путем замены
- объяснение с использованием графиков или численных примеров того, почему решение t> 10 часов
Приведенный выше пример ссылается на
VCMNA335, а также является частью
Рассуждение на уровне владения математикой, где учащиеся «обосновывают стратегии и сделанные выводы» (VCAA, n. d.)
d.)
Видео «Грамотность на практике»: математика
В этом видео Эндрю Витт обсуждает, как дать студентам навыки для решения сформулированных задач и прикладных задач по математике.
21-значное решение многолетней проблемы предполагает, что существует гораздо больше решений – ScienceDaily
Что вы будете делать после решения ответа на вопрос о жизни, Вселенной и всем остальном? Если вы математики Дрю Сазерленд и Энди Букер, вы решите более сложную задачу.
В 2019 году Букер из Бристольского университета и Сазерленд, главный научный сотрудник Массачусетского технологического института, первыми нашли ответ на 42. Число имеет значение для поп-культуры как вымышленный ответ на «главный вопрос жизни – Вселенная и все такое », как классно написал Дуглас Адамс в своем романе« Автостопом по Галактике ». Вопрос, который порождает 42, по крайней мере, в романе, удручающе, до смешного неизвестен.
Вопрос, который порождает 42, по крайней мере, в романе, удручающе, до смешного неизвестен.
В математике, совершенно случайно, существует полиномиальное уравнение, ответ на которое математикам не удавалось найти 42 в течение десятилетий.Уравнение x 3 + y 3 + z 3 = k известно как задача суммы кубов. Несмотря на кажущуюся простоту, уравнение становится экспоненциально сложным для решения, если его оформить как «диофантово уравнение» – проблема, которая требует, чтобы для любого значения k значения x, y и z каждое должны быть целыми числами.
Когда уравнение суммы кубов сформулировано таким образом, для определенных значений k целочисленные решения для x, y и z могут вырасти до огромных чисел. Числовое пространство, в котором математики должны искать эти числа, еще больше, что требует сложных и массивных вычислений.
На протяжении многих лет математикам приходилось решать уравнение различными способами, либо находя решение, либо определяя, что решение не должно существовать, для каждого значения k от 1 до 100, за исключением 42.
В сентябре 2019 года Букер и Сазерленд, используя совокупную мощность полумиллиона домашних компьютеров по всему миру, впервые нашли решение для 42. Широко известное открытие побудило команду взяться за еще более сложную и в некоторой степени более универсальная проблема: найти следующее решение для 3.
Букер и Сазерленд опубликовали решения для 42 и 3, а также несколько других чисел, превышающих 100, на этой неделе в Proceedings of the National Academy of Sciences .
Принимая вызов
Первые два решения уравнения x 3 + y 3 + z 3 = 3 могут быть очевидны для любого школьника, занимающегося алгеброй, где x, y и z могут быть либо 1, 1 и 1 или 4, 4 и -5.Однако поиск третьего решения на протяжении десятилетий ставил в тупик опытных теоретиков чисел, и в 1953 году эта загадка побудила математика-новатора Луиса Морделла задать вопрос: возможно ли вообще узнать, существуют ли другие решения для 3?
«Это было похоже на то, как Морделл бросил вызов», – говорит Сазерленд. «Интерес к решению этого вопроса заключается не столько в конкретном решении, сколько в том, чтобы лучше понять, насколько сложно решить эти уравнения. Это эталон, по которому мы можем измерить себя.«
«Интерес к решению этого вопроса заключается не столько в конкретном решении, сколько в том, чтобы лучше понять, насколько сложно решить эти уравнения. Это эталон, по которому мы можем измерить себя.«
По прошествии десятилетий без новых решений для 3, многие начали полагать, что их не найти. Но вскоре после того, как был найден ответ на 42, метод Букера и Сазерленда за удивительно короткое время нашел следующее решение для 3:
.569936821221962380720 3 + (−569936821113563493509) 3 + (−472715493453327032) 3 = 3
Это открытие явилось прямым ответом на вопрос Морделла: да, можно найти следующее решение для 3, и более того, вот это решение.И, возможно, более универсально, решение, включающее гигантские 21-значные числа, которые до сих пор было невозможно отсеять, предполагает, что существует больше решений для 3 и других значений k.
«В математическом и вычислительном сообществах возникли серьезные сомнения, потому что [вопрос Морделла] очень трудно проверить», – говорит Сазерленд. «Цифры так быстро становятся такими большими. Вы никогда не найдете ничего, кроме первых нескольких решений. Но что я могу сказать, так это то, что, найдя это единственное решение, я убежден, что существует бесконечно много других решений.«
«Цифры так быстро становятся такими большими. Вы никогда не найдете ничего, кроме первых нескольких решений. Но что я могу сказать, так это то, что, найдя это единственное решение, я убежден, что существует бесконечно много других решений.«
Изюминка решения
Чтобы найти решения для 42 и 3, команда начала с существующего алгоритма или преобразования уравнения суммы кубов в форму, которую, по их мнению, было бы легче решить:
k – z 3 = x 3 + y 3 = ( x + y ) ( x 2 – xy11 905 2 )
Этот подход был впервые предложен математиком Роджером Хит-Брауном, который предположил, что для каждого подходящего k должно быть бесконечно много решений.Команда дополнительно изменила алгоритм, представив x + y как единственный параметр d. Затем они сократили уравнение, разделив обе части на d и сохранив только остаток – математическая операция, называемая «по модулю d», – оставив упрощенное представление проблемы.
«Теперь вы можете думать о k как о кубическом корне из z по модулю d», – объясняет Сазерленд. “Итак, представьте, что вы работаете в системе арифметики, где вас интересует только остаток по модулю d, а мы пытаемся вычислить кубический корень из k.«
С этой более изящной версией уравнения исследователям нужно было бы только искать значения d и z, которые гарантировали бы нахождение окончательных решений для x, y и z при k = 3. Но все же пространство чисел, которое им пришлось бы перебирать, было бы бесконечно большим.
Итак, исследователи оптимизировали алгоритм, используя математические методы «просеивания», чтобы резко сократить пространство возможных решений для d.
«Это включает в себя довольно продвинутую теорию чисел, использующую структуру того, что мы знаем о числовых полях, чтобы не заглядывать туда, куда нам не нужно смотреть», – говорит Сазерленд.
Глобальная задача
Команда также разработала способы эффективного разделения поиска алгоритма на сотни тысяч параллельных потоков обработки.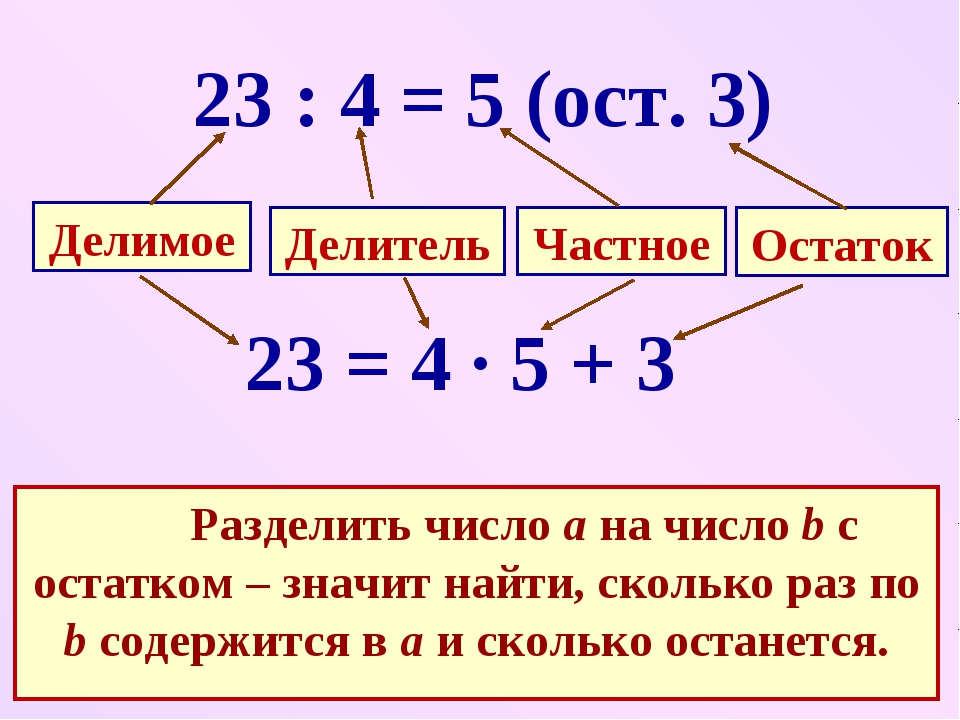 Если бы алгоритм запускался только на одном компьютере, на поиск решения k = 3 потребовались бы сотни лет. Разделив задание на миллионы более мелких задач, каждая из которых независимо запускается на отдельном компьютере, команда могла бы еще больше ускорить свой поиск.
Если бы алгоритм запускался только на одном компьютере, на поиск решения k = 3 потребовались бы сотни лет. Разделив задание на миллионы более мелких задач, каждая из которых независимо запускается на отдельном компьютере, команда могла бы еще больше ускорить свой поиск.
В сентябре 2019 года исследователи реализовали свой план с помощью Charity Engine – проекта, который можно загрузить в виде бесплатного приложения на любой персональный компьютер и который предназначен для использования любых свободных домашних вычислительных мощностей для коллективного решения сложных математических задач.В то время сеть Charity Engine включала более 400 000 компьютеров по всему миру, и Букер и Сазерленд смогли запустить свой алгоритм в сети в качестве теста новой программной платформы Charity Engine.
«Им говорят, что для каждого компьютера в сети ваша задача – искать d, простой фактор которых попадает в этот диапазон, при некоторых других условиях», – говорит Сазерленд. «И нам нужно было выяснить, как разделить задание примерно на 4 миллиона задач, на выполнение каждой из которых у компьютера уйдет около трех часов. «
«
Очень быстро глобальная сетка вернула самое первое решение для k = 42, и всего две недели спустя исследователи подтвердили, что нашли третье решение для k = 3 – веху, которую они отметили, частично, распечатав уравнение на футболках.
Тот факт, что существует третье решение для k = 3, предполагает, что исходная гипотеза Хита-Брауна была верной и что существует бесконечно больше решений, помимо этого новейшего. Хит-Браун также предсказывает, что расстояние между решениями будет экспоненциально расти вместе с их поисками.Например, вместо 21-значных значений третьего решения четвертое решение для x, y и z, скорее всего, будет включать числа с ошеломляющими 28 цифрами.
«Объем работы, которую вы должны выполнить для каждого нового решения, увеличивается более чем в 10 миллионов раз, поэтому для следующего решения для 3 потребуется 10 миллионов раз 400 000 компьютеров, и нет никакой гарантии, что этого достаточно», – Сазерленд говорит. «Я не знаю, узнаем ли мы когда-нибудь четвертое решение.




 Это равенство (два плюс три равно пяти):
2 + 3=
5
Это равенство (два плюс три равно пяти):
2 + 3=
5


 Раствор состоит из растворенного вещества и растворителя. Растворенное вещество – это вещество, которое растворяется, а растворитель – это часть раствора, которая растворяется.
Раствор состоит из растворенного вещества и растворителя. Растворенное вещество – это вещество, которое растворяется, а растворитель – это часть раствора, которая растворяется.
 Что вы имеете в виду под удовлетворением? Давайте рассмотрим два примера, чтобы проиллюстрировать это.
Что вы имеете в виду под удовлетворением? Давайте рассмотрим два примера, чтобы проиллюстрировать это. Пример: (i) Для линейного уравнения количество решений равно одному.(ii) Для квадратного уравнения численное решение равно двум и так далее.
Пример: (i) Для линейного уравнения количество решений равно одному.(ii) Для квадратного уравнения численное решение равно двум и так далее. Обратите внимание, что на ЖК-дисплее 100.
Обратите внимание, что на ЖК-дисплее 100. Затем вычтите y из обеих частей уравнения, чтобы получить. Наконец, разделите обе части на числа, чтобы получить ответ.
Затем вычтите y из обеих частей уравнения, чтобы получить. Наконец, разделите обе части на числа, чтобы получить ответ. У уравнения есть знак равенства, выражение справа и выражение слева. Примеры уравнений. 3x + 3 = 2x + 4: левая часть уравнения равна 3x + 3, а правая часть – 2x + 4.
У уравнения есть знак равенства, выражение справа и выражение слева. Примеры уравнений. 3x + 3 = 2x + 4: левая часть уравнения равна 3x + 3, а правая часть – 2x + 4.
 Что такое определение линейных уравнений и примеров? Уравнение с максимальным порядком 1 называется линейным уравнением.
Что такое определение линейных уравнений и примеров? Уравнение с максимальным порядком 1 называется линейным уравнением. Ваш b всегда будет рациональным числом.
Ваш b всегда будет рациональным числом. Примерный диапазон решений: 0, 1 и 2 для 4×4. <4.
Примерный диапазон решений: 0, 1 и 2 для 4×4. <4.

 Есть три типа растворов: газообразные растворы, жидкие растворы и твердые растворы. газообразные растворы.
Есть три типа растворов: газообразные растворы, жидкие растворы и твердые растворы. газообразные растворы.