Решение высшей математики онлайн
‹– Назад
При вычислении производной, наличие формул для производной суммы, разности, произведения, частного и композиции — всех тех операций, при помощи которых элементарные функции образуются из минимального набора — приводит к тому, что производная любой элементарной функции снова является элементарной функцией. При нахождении неопределённых интегралов, однако, формул для первообразной произведения, частного и композиции нет. Это приводит к такому положению, что отнюдь не для любой элементарной подынтегральной функции можно “взять интеграл”, то есть выразить некоторую первообразную для подынтегральной функции в виде некоторого выражения, использующего лишь элементарные функции. Дело не в том, что пока что не придумано способа это сделать, а в принципиальной невозможности: никакая из первообразных в случае “неберущегося” интеграла никаким образом не может быть выражена как комбинация элементарных функций, связанных знаками арифметических действий и знаками композиции.
Не следует думать, что если такое представление невозможно, то и функции такой нет1: можно считать, что для её выражения просто не хватает запаса рассматриваемых операций или запаса рассматриваемых исходных функций, и их надо расширить, то есть выйти за рамки множества функций, называемых элементарными2. В науке и её приложениях в технике, экономике и других дисциплинах применяются многие неэлементарные функции; часто их называют специальными. К специальным функциям относятся и многие первообразные для элементарных функций, причём часто не столь уж “сложной” структуры. Интегралы, выражающиеся через такие первообразные, называются (по традиции, берущей начало в 18 веке) неберущимися. Итак, интеграл не берётся, если функция не является элементарной. Приведём примеры неберущихся интегралов и названия первообразных — специальных функций, связанных с этими интегралами.
Пример 1.8 Неберущимся является интеграл
Здесь одна из первообразных, которую мы обозначили , выделяется из всего набора первообразных условием .
Функция называется функцией Лапласа. Она широко применяется в теории вероятностей, физике, математической и прикладной статистике и других разделах науки и её приложений. Для вычисления значений функции Лапласа составлены таблицы, имеющиеся во многих учебниках, задачниках и справочниках по теории вероятностей и статистике. Возможность вычисления предусмотрена также на многих моделях калькуляторов (не самых дешёвых) и уж, обязательно, на тех, что предназначены для статистической обработки числового материала. Так что, с практической точки зрения, пользоваться функцией Лапласа ничуть не сложнее, чем, скажем, синусом, арктангенсом или натуральным логарифмом, которые мы условно относим к элементарным функциям.
Пример 1.9 Не берётся также интеграл
Доопределим подынтегральную функцию , полагая её равной 1 при . В соответствии с тем, что , доопределённая функция будет непрерывна на всей числовой оси.
Среди её первообразных выделим ту, для которой . Эта неэлементарная функция называется интегральным синусом и обозначается . Именно её мы использовали в приведённой выше формуле.
Пример 1.10 Ещё один неберущийся интеграл:
Одна из первообразных — та, что мы использовали в правой части и обозначили — называется интегральным косинусом.
Пример 1.11
—
это тоже неберущийся интеграл. Одна из первообразных, которую мы обозначили , — специальная функция, называющаяся интегральной экспонентой.
Пример 1.12 Не берётся интеграл
(при
одна из первообразных, , называется интегральным логарифмом.
Используя специальные функции, заданные предыдущими примерами, мы с помощью изученных выше правил интегрирования можем выражать через эти функции и другие интегралы. Приведём такой пример.
Пример 1.13 Выразим через функцию Лапласа следующий интеграл:
Для этого сделаем замену переменного :
Заметим, что та первообразная для , для которой , обозначается . Функция называется в теории вероятностей и статистике функцией ошибок.
Упражнение 1.
3 Выразите функцию ошибок через функцию Лапласа и наоборот, функцию Лапласа через функцию ошибок.
Пример 1.14 К интегралу предыдущего примера можно свести и тем самым выразить через функцию Лапласа, например, такой интеграл:
Для вычисления мы применили формулу интегрирования по частям.
Пример 1.15 Вычислим интеграл от интегральной экспоненты . Заметим, что по определению первообразной. Применяя формулу интегрирования по частям, получаем:
Кроме приведённых выше, в приложениях встречаются и многие другие неберущиеся интегралы, например:
Эти четыре интеграла называются интегралами Френеля.
Упражнение 1.4 Сделав соответствующую замену переменного, выразите последние два из интегралов Френеля через функции и , которые стоят в правых частях первых двух интегралов Френеля.
Не берутся также интегралы
и многие другие.
Тем не менее, для многих классов интегралов, наиболее часто встречающихся в приложениях, первообразную всё же удаётся выразить через элементарные функции. В следующей главе мы изучим такие классы интегралов.
Упражнение 1.5 С помощью соответствующих замен переменного, докажите следующие соотношения:
(при (при
(на самом деле функции и определяются так, что обе постоянные равны 0).
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
11-а, Решение интегралов
Решение
интегралов.
Рассказываем, как решать
интегралы.
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое. Решение интегралов (интегрирование) есть операция обратная диференциированию. Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему. В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .
Так
вот площадь закрашенной области, есть
интеграл от функции в пределах от a до
b.
Не верится? Проверим на любой функции.
Возьмем простейшую у=3.
Ограничим функцию
значениями а=1 и b=2. Построим: Итак
ограниченная фигура прямоугольник.
Площадь прямоугольника равна произведению
длины на ширину. В наше случае длина 3,
ширина 1, площадь 3*1=3.
Попробуем решить
тоже самое не прибегая к построению,
используя интегрирование: Как
видите ответ получился тот же. Решение
интегралов – это собирание во едино
каких-либо элементарных частей. В случае
с площадью суммируются полоски бесконечно
малой ширины. Интегралы могут быть
определенными и неопределенными.
Решить
определенный интеграл значит найти
значение функции в заданных границах.
Решение неопределенного интеграла
сводиться к нахождению первообразной. F(x)
– первообразная. Дифференцируя
первообразую, мы получим исходное
подинтегральное выражение. Чтобы
проверить правильно ли мы решили
интеграл, мы дифференциируем полученный
ответ и сравниваем с исходным
выражением.
Основные функции и
первообразные для них приведены в
таблице:
Таблица первообразных для решения интегралов
Основные
приемы решения интегралов:
Решить
интеграл, значит проинтегрировать
функцию по переменной.
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные примеры решения интегралов. Приемы будет даны для общего ознакомления без примеров решения, чтобы не перегружать статью. Нужно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.
Основные приемы решения интегралов
1. Замена переменной. Для выполнения данного приема потребуется хороший навык нахождения производных.
2. Интегрирование по
частям.
Пользуются следующей
формулой. Применения
этой формулы позволяет казалось бы
нерешаемые интегралы привести к решению.
3. Интегрирование дробно-рациональных функций. – разложить дробь на простейшие – выделить полный квадрат. – создать в числителе дифференциал знаменателя.
4. Интегрирование дробно-иррациональных функций. – выделить под корнем полный квадрат – создать в числителе дифференциал подкоренного выважения. 5. Интегрирование тригонометрических функций. При интегрировании выражений вида применяет формулы разложения для произведения. Для выражений m-нечетное, n –любое, создаем d(cosx). Используем тождество sin2+cos2=1 m,n – четные, sin2x=(1-cos2x)/2 и cos2x=(1+cos2x)/2 Для выражений вида: – Применяем свойство tg2x=1/cos2x – 1
1. Разобраться
в сути интегралов.
Необходимо понять базовую сущность
интеграла и его решения. Интеграл по
сути есть сумма элементарных частей
объекта интегрирования.
Дополнительно после
решения интеграла на
первых этапах рекомендуется сверять
решение. Для этого мы дифференциируем
полученное выражение и сравниваем с
исходным интегралом.
Отработаем
основные моменты на нескольких примерах:Примеры решения интегралов
Пример 1: Решить интеграл: Интеграл неопределенный. Находим первообразную. Для этого интеграл суммы разложим на сумму интегралов. Каждый из интегралов табличного вида. Смотрим первообразные по таблице. Решение интеграла: Проверим решение(найдем производную):
Пример
2. Решаем интеграл Интеграл
неопределенный. Находим
первообразную.
Сравниваем с таблицей.
В таблице нет.
Разложить, пользуясь
свойствами, нельзя.
Смотрим приемы.
Наиболее подходит замена переменной.
Заменяем
х+5 на t
Пример
3.
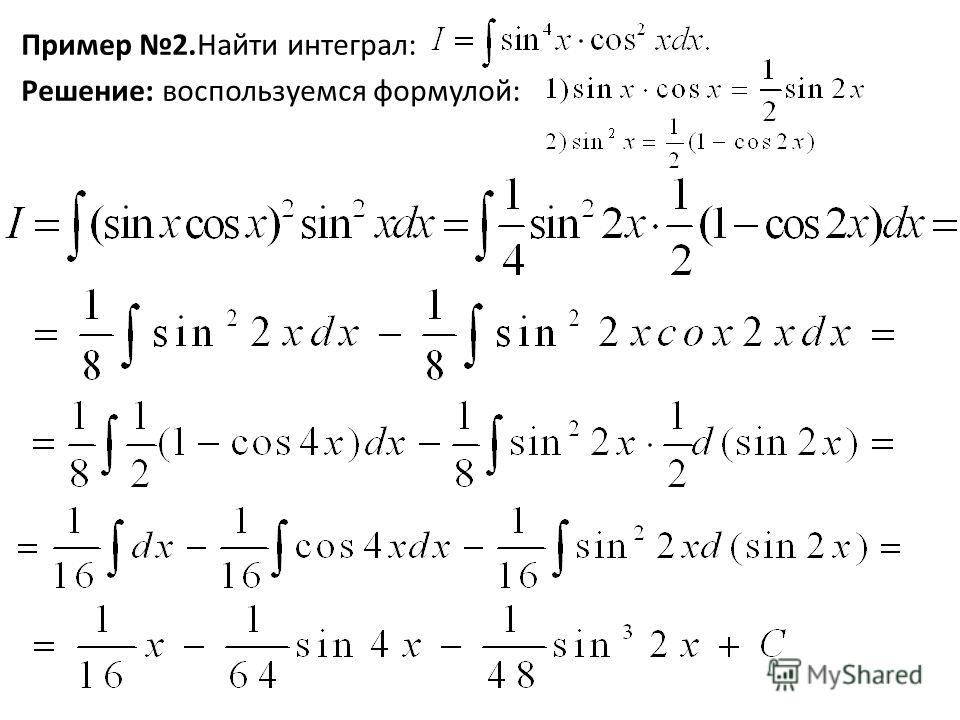Решение интеграла: Для
решения в этом случае необходимо выделить
полный квадрат. Выделяем:
В данном случае коэфециент ½ перед интегралом получился в результате замены dx на ½*d(2x+1). Если вы найдете производные x’ = 1 и ½*(2x+1)’= 1, то поймете почему так. В результате мы привели интеграл к табличному виду. Находим первообразную. В итоге получаем:
Исчисление II. Несобственные интегралы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.
t\\ & = \mathop {\lim }\limits_{t \to \infty} \left( {1 – \frac{1}{t}} \right) = 1\end{align*}\]
Итак, вот как мы будем поступать с этими типами интегралов в целом. Мы заменим бесконечность переменной (обычно \(t\)), сделаем интеграл, а затем возьмем предел результата, когда \(t\) стремится к бесконечности.
Кстати, обратите внимание, что площадь под кривой на бесконечном интервале не равна бесконечности, как мы могли предположить. На самом деле, это было удивительно мало. Конечно, так будет не всегда, но достаточно важно отметить, что не все области на бесконечном интервале дадут бесконечные области.
Давайте теперь разберемся с некоторыми определениями. Мы будем называть эти интегралы сходящимися , если связанный предел существует и является конечным числом (
Теперь формализуем метод работы с бесконечными интервалами.
2}}}\,dx}}\]
9t \\ & = \ mathop {\ lim} \ limit_ {t \ to \ infty} \ left ({\ cos 2 – \ cos t} \ right) \ end {align *} \]
Этот предел не существует, поэтому интеграл расходится.
В большинстве примеров класса Calculus II, которые работают с бесконечными интервалами, предел либо существует, либо бесконечен. Однако есть пределы, которых не существует, как показал предыдущий пример, так что не забывайте о них.
Разрывное интегральное число
Теперь нам нужно рассмотреть второй тип несобственных интегралов, который мы рассмотрим в этом разделе. Это интегралы, имеющие разрывные подынтегральные выражения. Процесс здесь в основном такой же, с одним небольшим отличием. Вот общие случаи, которые мы рассмотрим для этих интегралов. 9{{\,b}}{{е\влево( х \вправо)\,dx}}\]
Где \(c\) — любое число. Опять же, это требует, чтобы ОБА интеграла были сходящимися, чтобы этот интеграл также был сходящимся.
Обратите внимание, что ограничения в этих случаях действительно должны быть правосторонними или левосторонними.
2}}}\,dx}}\]
Показать решение
Это интеграл по бесконечному интервалу, который также содержит разрывную подынтегральную функцию. Чтобы сделать этот интеграл, нам нужно разделить его на два интеграла, чтобы каждый интеграл содержал только одну точку разрыва. Важно помнить, что все процессы, с которыми мы работаем в этом разделе, поэтому каждый интеграл содержит только одну проблемную точку.
Мы можем разделить его где угодно, но выбрать значение, которое будет удобно для целей оценки. 9+ }} \left( { – 1 + \frac{1}{t}} \right)\\ & = \infty \end{align*}\]
Итак, первый интеграл расходится, а значит, расходится и весь интеграл.
ОДУ: интегралы как решения
ОДУ первого порядка представляет собой уравнение вида
\begin{уравнение*} \frac{dy}{dx} = f(x,y) , \end{уравнение*}
или просто
\begin{уравнение*} у’ = f(х,у) . \end{уравнение*}
В общем, не существует простой формулы или процедуры, которой можно следовать, чтобы найти решение.
В следующих нескольких лекциях мы рассмотрим частные случаи, когда решение получить нетрудно. В этом разделе предположим, что \(f\) является функцией только \(x\), т. е. уравнение имеет вид
\begin{уравнение} y’ = f(x).\label{ias_inteq}\tag{1.1} \end{уравнение}
Мы могли бы просто проинтегрировать (антидифференцировать) обе части относительно \(x\text{.}\)
\begin{уравнение*} \int y'(x) \,dx = \int f(x) \,dx + C , \end{уравнение*}
это
\begin{уравнение*} y(x) = \int f(x) \,dx + C . \end{уравнение*}
Это \(y(x)\) на самом деле является общим решением. Таким образом, чтобы решить (1.1), мы находим некоторую первообразную от \(f(x)\), а затем добавляем произвольную константу, чтобы получить общее решение.
Сейчас самое время поговорить об обозначениях и терминологии исчисления. Учебники по математическому анализу мутят воду, говоря об интеграле прежде всего как о так называемом неопределенном интеграле. Неопределенный интеграл — это на самом деле первообразная (фактически все однопараметрическое семейство первообразных).
На самом деле существует только один интеграл, и это определенный интеграл. Единственная причина неопределенного обозначения интеграла состоит в том, что мы всегда можем записать первообразную как (определенный) интеграл. То есть по основной теореме исчисления мы всегда можем записать \(\int f(x) \,dx + C\) как 9х f(t) \,dt + С .
\end{уравнение*}
Отсюда и терминология для интеграции , когда мы действительно можем иметь в виду для антидифференцирования . Интегрирование — это всего лишь один из способов вычисления первообразной (и этот способ работает всегда, см. следующие примеры). Интеграция определяется как площадь под графиком, это происходит только для вычисления первообразных. Ради последовательности мы будем продолжать использовать обозначение неопределенного интеграла, когда нам нужна первообразная, и вы должны 9{x_0} f(x)\,dx + y_0 = y_0\text{.}\) Так и есть!
Обратите внимание, что определенный интеграл и неопределенный интеграл (антидифференцирование) — совершенно разные звери.
Определенный интеграл всегда дает число. Следовательно, (1.2) — это формула, которую мы можем вставить в калькулятор или компьютер, и он будет рад вычислить для нас конкретные значения. Мы легко сможем построить решение и работать с ним, как и с любой другой функцией. Не так важно всегда находить замкнутую форму первообразной. 92} \, дс + 1 .
\end{уравнение*}
Вот хороший способ подшутить над своими друзьями, сдающими математику за второй семестр. Скажите им найти решение в закрытой форме. Ха-ха-ха (плохая математическая шутка). Нельзя (в закрытом виде). Нет абсолютно ничего плохого в том, чтобы записать решение в виде определенного интеграла. Этот конкретный интеграл на самом деле очень важен в статистике.
Используя этот метод, мы также можем решить уравнения формы
\begin{уравнение*} у’ = f(y) . \end{уравнение*}
Запишем уравнение в системе обозначений Лейбница.
\begin{уравнение*} \frac{dy}{dx} = f(y) . \end{уравнение*}
Теперь мы используем теорему об обратной функции из исчисления, чтобы поменять местами \(x\) и \(y\), чтобы получить
\begin{уравнение*}
\frac{dx}{dy} = \frac{1}{f(y)} .