Решение линейных уравнений методом гаусса: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

3.2 Метод Гаусса для решения систем линейных уравнений (метод последовательного исключения)

Метод Гаусса заключается в следующем. Допустим, что в системе (5) коэффициент при первом неизвестном a₁₁ 0.

Исключим сначала неизвестное х₁ из всех уравнений системы (5), кроме первого. Для этого, прежде всего, разделим обе части первого уравнения на коэффициент a₁₁0; тогда получим новую систему, равносильную данной:

(6)

Умножим теперь первое уравнение системы (6) на a₂₁ и вычтем из второго уравнения. Затем умножим первое уравнение на a₃₁ и вычтем из третьего уравнения и т.д. В результате получим новую систему, также равносильную данной:

(7)

Здесь введены обозначения:

(8)

Разделим теперь второе уравнение системы (7) на коэффициент а’₂₂

, предполагая, что он отличен от нуля; затем умножим второе уравнение полученной системы последовательно на а’₃₂, . .., а’_i2…,…, а’_m2 и вычтем поочередно из соответствующих уравнений системы, кроме первого и второго.

Если, продолжая этот процесс, мы придем к системе, содержащей уравнение, в котором все коэффициенты левой части равны нулю, а свободный член отличен от нуля, то эта система несовместна. В том случае, когда система совместна, приходим либо к системе

(9)

(причем р < n), либо к системе

(10)

Система вида (9) называется ступенчатой, а система вида (10) — треугольной.

В случае треугольной системы из последнего уравнения находим x_п=β_n, затем, подставляя значение x_п в предыдущее уравнение, находим x_п-т, и т.д.

Таким образом, если данная система уравнений (5) после выполнения ряда элементарных преобразований приводится к треугольной системе (10), то это означает, что система (5) является совместной и определенной.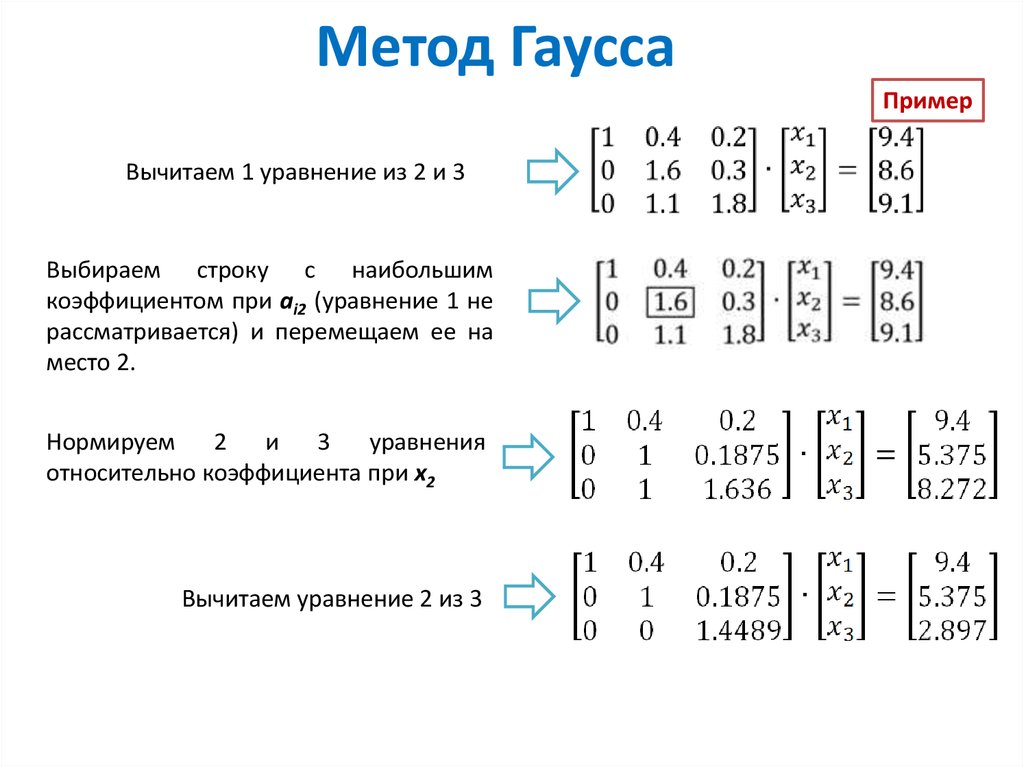

Если же данная система (5) после элементарных преобразований приводится к ступенчатой системе (9), то система (5) совместна и неопределенна.

Перенося в каждом из уравнений системы (10) члены с неизвестными x_p+1,…, x_n в правую часть, получим систему вида

(11)

Придавая неизвестным x_p+1,…, x_n ,которые называются свободными, произвольные значения , получим треугольную систему, из которой последовательно найдем все остальные неизвестные

x_p, x_p-1,…, x₁. Так как числа могут иметь различные значения, то исходная система (3.1) имеет бесчисленное множество решений.

Процесс нахождения коэффициентов треугольной системы (10) называется прямым ходом, а процесс получения ее решения – обратным ходом метода Гаусса.

Пример 3.1. Решить систему уравнений:

Решение.

Разделив все члены первого уравнения на коэффициент а₁₁=2 получаем систему

Сначала умножим все члены первого уравнения полученной системы на 3 и вычтем из второго уравнения; затем из третьего уравнения вычтем первое:

Разделим все члены второго уравнения на а’₂₂=0,5:

Умножим второе уравнение на –1,5 и вычтем из третьего. Тогда получим систему

из которой последовательно находим x₁=1; x

₂=2; x₃=3.

Решение треугольной системы, а, следовательно, и равносильной ей первоначальной –– x₁=1; x₂=2; x₃=3. Данная система является совместной и определенной.

Ответ: x₁=1; x₂=2; x₃=3.

При решении примеров методом Гаусса необходимости выписывать системы (3.1), (3.2), (3.3), (3.5) и (3.6) нет. Все преобразования можно проводить над матрицами, составленными из коэффициентов этих систем.

Системе (3.1) соответствуют две матрицы А и В:

(12)

Матрица А называется матрицей системы и состоит из коэффициентов системы, матрица В называется расширенной матрицей и отличается от матрицы системы столбцом, состоящим из свободных членов уравнений системы. При решении системы (5) методом Гаусса элементарные преобразования системы заменяются соответствующими элементарными преобразованиями, выполняемыми над ее расширенной матрицей В.

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями

¹ над строками приводят расширенную матрицу системы к ступенчатому виду:

а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:

Последний, (n + 1) столбец этой матрицы содержит решение системы.

Пример 3.2. Решить систему уравнений:

Решение.

Таблица 3.1

Шаг	a(k)i1	a(k)i2	a(k)i3	a( k)i4	a(k)i5	a(k)i6
	1	0,17	0,25	0,54	0,3	-1,76
I	0,47	1	0,67	-0,32	0,5	-2,32
	-0,11	0,35	1	-0,74	0,7	-1,20
	0,55	0,43	0,36	1	0,9	-3,24
	1	0,17	0,25	0,54	0,3	-1,76
II		0,9201	0,7875	-0,5738	0,3590	-1,4928
		0,3687	0,9725	0,6806	0,7330	-1,3936
		0,3365	0,4975	0,7030	0,7350	-2,2720
		1	0,8559	-0,6236	0,3902	-1,6224
III			0,6569	-0,4507	0,5891	-0,7954
			0,2095	0,9128	0,6037	-1,7261
IV			1	-0,6861	0,8968	-1,2108
				1,0565	0,4158	-1,4724
				1	0,3936	-1,3937
V			1		1,1668	-2,1670
		1			-0,3630	-0,6368
	1				0,4409	-1,4409

Порядок заполнения таблицы.

Прямой ход.

1. Записываем коэффицненты данной системы в четырех строках и пяти столбцах шага I.

2. Суммируем все коэффициенты по строке и записываем сумму с обратным знаком в последний столбец, т.е. . Тогда сумма всех элементов каждой из четырех начальных строк будет равна нулю.

3. Выбираем из первого столбца главный элемент и меняем местами строку, содержащую этот элемент, с первой. Пусть главным элементом будет a⁽⁰⁾₁₁. Делим все числа, стоящие в первой строке, на a⁽⁰⁾₁₁ и записываем в первую строку шага II.

4. По формулам

a^(k)_kj= a^(k-1)_kj/ a^(k-1)_kk, a^(k)_ij= a^(k-1)_ij – a^(k-1)_ik a^(k)_kj (13)

где k+1jn+1, k+1in, k=1.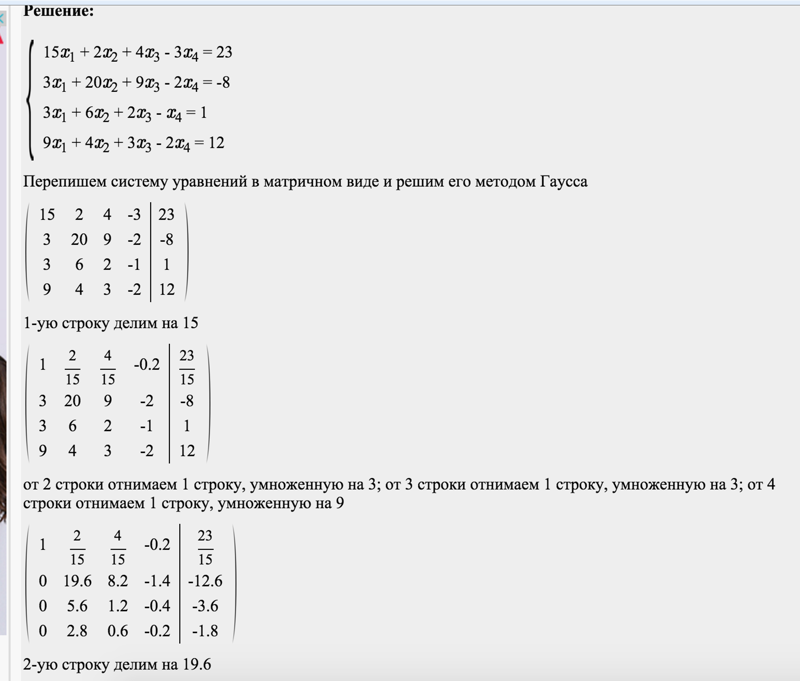 .n (^a(0)_ij=a_ij, i,j=1..n+1).

Вычисляем коэффициенты a⁽¹⁾_ij, i=2..4, j=2..6. Результаты записываем в соответствующие строки шага II. С элементами последнего столбца поступаем так же, как с элементами предыдущих столбцов.

5. Для проверки правильности вычислений находим сумму элементов каждой строки. Величина суммы должна отличаться от нуля в пределах ошибок округления. Большое отклоненне от нуля свидетельствует о наличии грубой ошибки в вычислениях.

6. Среди элементов a⁽¹⁾₂₂, a⁽¹⁾_32, a⁽¹⁾₄₂ выбираем главный элемент и поступаем, как в п. 3. Пусть a⁽¹⁾₂₂^— главный элемент. Делим на него вторую строку шага II и результаты записываем в первую строку шага III .

7. По формулам (13) вычисляем коэффицциенты a⁽²⁾_ij, i=3..4, j=3..6. Результаты записываем во вторую и третью строки шага III.

8. Проверяем правильность произведенных вычислений (см. п. 5).

9. Пусть a⁽²⁾₃₃ главный элемент. Делим на него вторую строку шага III и результаты записываем в первую строку шага IV.

10. По формулам (3.9) вычисляем a⁽³⁾_4j, j=4..6. Результаты записываем во вторую строку шага IV.

11. Проверяем правильность вычислений (см. п. 5).

Обратный ход.

1. В шаге V записываем единицы, как указано в табл. 4.

2. Вычисляем x₄= a⁽³⁾₄₅/a⁽³⁾₄₄, = a⁽³⁾₄₆/a⁽³⁾₄₄.

3. Для вычислений x₃, x₂, x₁ (,,) используются лишь первые строки шагов II, III. IV, т.е. строки, содержащие единицы:

4 Проверяем правильность вычислений. При отсутствии ошибок округлений сумма элементов в четырех строках шага V должна быть равна нулю. т.е. строки содержащие единицы:

x₃= a⁽³⁾₃₅–a⁽³⁾₃₄ x₄

x₂= a⁽²⁾₂₅–a⁽²⁾₂₃ x₃–a⁽²⁾₂₄ x₄

x₁= a⁽¹⁾₁₅-a⁽¹⁾₁₂ x₂-a⁽¹⁾₁₃ x₃– a⁽¹⁾₁₄ x₄

= a⁽³⁾₃₆-a⁽³⁾₃₄ x₄ (14)

= a⁽²⁾₂₆-a⁽²⁾₂₃ x₃-a⁽²⁾₂₄ x₄

= a⁽¹⁾₁₆-a⁽¹⁾₁₂ x₂-a⁽¹⁾₁₃ x₃– a⁽¹⁾₁₄ x₄

5 Решение исходной системы, округленное до двух десятичных знаков после запятой, таково:

x₁=0,44; x₂=-0,36; x₃=1,17; x₄=0,39

Ответ: x₁=0,44; x₂=-0,36; x₃=1,17; x₄=0,39

Решение системы линейных уравнений.

Метод Гаусса Решение системы линейных уравнений. Метод Гаусса

Метод Гаусса — метод решения системы линейных алгебраических уравнений (СЛАУ), заключающийся в постепенном понижении порядка системы и исключении неизвестного.

Решение СЛАУ методом Гаусса состоит из двух шагов:

1. На первом этапе (прямое исключение): с помощью элементарных преобразований по строкам система приводится к ступенчатой ​​или треугольной форме, либо устанавливается, что система несовместна. Выбрать ненулевой элемент из элементов первого столбца матрицы, переместить его в верхнюю позицию с помощью перестановки строк и вычесть первую строку, полученную после перестановки, из других строк; сначала пользователю нужно умножить эту строку на значение, равное отношению первого элемента каждой строки к первому элементу первой строки, тем самым обнулив столбец под этим элементом. Затем мысленно вычеркиваются первая строка и столбец. Продолжайте таким образом, пока не останется нулевая матрица. Если в ходе одной из итераций в первом столбце не найден ненулевой элемент, переходим к следующему столбцу и делаем то же самое.

2. На втором этапе используется обратная замена. Смысл этого шага состоит в том, чтобы выразить все выходные базисные переменные через небазисные и построить фундаментальную систему решений. Если все переменные основные, то необходимо выразить единственное решение системы линейных уравнений в численном виде. Эта процедура начинается с последнего уравнения. Это уравнение используется для выражения единственной соответствующей базовой переменной, которая должна быть заменена в предыдущих уравнениях. Продолжайте в том же духе, поднимаясь по «лестнице». Каждой строке соответствует только одна базовая переменная, поэтому на каждом шаге, кроме последнего, ситуация такая же, как и в случае с последней строкой.

Допустим, существует исходная система, которая выглядит следующим образом:

(1)

Матрица A называется главной матрицей системы, а матрица b называется столбцом свободных членов.

Используя свойство элементарных операций над строками, базовую матрицу можно преобразовать в ступенчатую матрицу. Те же операции следует применить к столбцу свободных членов:

Предположим, что главный минор (ненулевой минор максимального порядка) основной матрицы расположен в верхнем левом углу, т. е. содержит только коэффициенты при переменных x j1 , …, x jr . Этого положения минора можно добиться перестановкой столбцов основной матрицы и соответствующей перенумерацией переменных.

Следовательно, переменные x j1 , …, x jr называются основными переменными . Все остальные переменные называются свободными переменными .

Если хотя бы одно число β i   ≠ 0, где i > r рассматриваемая система несовместима.

Предположим, что β i   = 0 для любого i > r .

Вынести свободные переменные за знаки равенства и разделить каждое из уравнений системы на его крайний левый коэффициент (αij, i  = 1, …, r , где i — номер строки):

(2)

Где i  = 1, …, r , k  =  i  + 1, …, n .

Если присвоить свободным переменным системы (2) все возможные значения и решить новую систему относительно главных неизвестных снизу вверх (т. е. от нижнего уравнения к верхнему), то в результате все решения получаются такие СЛАУ. Так как эта система получена путем выполнения элементарных преобразований исходной системы (1), то в соответствии с теоремой эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, т. е. множества их решения совпадают.

Эффекты:

• Если все переменные совместно расположенной системы являются основными переменными, то система является определенной.

• Если в системе больше переменных, чем уравнений, система может быть либо неопределенной, либо несовместимой.

См. также:

Библиотека методов и моделей | ISmLinearEquations

15.4 Решение неоднородных уравнений: исключение Гаусса

15.4 Решение неоднородных уравнений: исключение Гаусса

Главная | 18. 022 | Глава 15 Инструменты    Индекс    Вверх    Предыдущий    Далее

Имея набор уравнений, можно выполнить несколько операций. на них, которые не влияют на их содержание.
Они:

1. Сложить кратное одно к другому (сложение левых сторон с левыми и правых на права.)

Доказательство

2. Переупорядочить их.

Комментарий

3. Умножьте обе части любого из них на ненулевое число.

Они называются элементарными операциями со строками .
Решение уравнений означает нахождение эквивалентной системы уравнений, имеющей очень простая форма: каждое уравнение имеет только одну переменную, ее коэффициент равно 1, и переменная появляется одна в левой части уравнения. Затем уравнение предоставляет явное выражение для соответствующей переменной.
Решаем линейные уравнения по выполняя последовательность элементарных операции со строками, которые преобразуют исходную матрицу коэффициентов в тождество матрица. Эта процедура называется Исключение Гаусса .

Обсуждение:

1. Предположим, у нас есть матрица коэффициентов 3 на 3 C , мы определяем столбец вектор v , чтобы правая часть j-го уравнения была его j-й составляющей, и пусть вектор-столбец r имеет компоненты x, y и z.
Тогда линейные уравнения принимают вид C r = v , где левая часть представляет матричное произведение матрицы 3 на 3 С и матрица 3 на 1 r .

2. Если матрица коэффициентов C является единичной матрицей, мы имеем решение: C = I подразумевает C r = I r = r = v .

3. Исключение Гаусса — это в точности обычный стандартный метод решения уравнений, что происходит следующим образом: решить первое уравнение для любой переменной, которая встречается в нем с точки зрения остальных.