Решение матриц методом гаусса: Метод Гаусса онлайн - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Метод Гаусса – примеры c решением, теоремы и формулы

Метод Гаусса – идеальный вариант для решения систем линейных алгебраических уравнений (далее СЛАУ). Благодаря методу Гаусса можно последовательно исключать неизвестные путём элементарных преобразований. Метод Гаусса – это классический метод решения СЛАУ, который и рассмотрен ниже.

Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ

Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.

Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений.

Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.

У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.

Определения и обозначения

Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.

Для начала систематизируем знания о системах линейных уравнений.

Обратите внимание!

СЛАУ в зависимости от её элементов может иметь:

Одно решение;
много решений;
совсем не иметь решений.

В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.

Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:

перемена мест уравнений системы;
почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
сложение к обеим частям одного из уравнений определённых частей другого уравнения.

Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.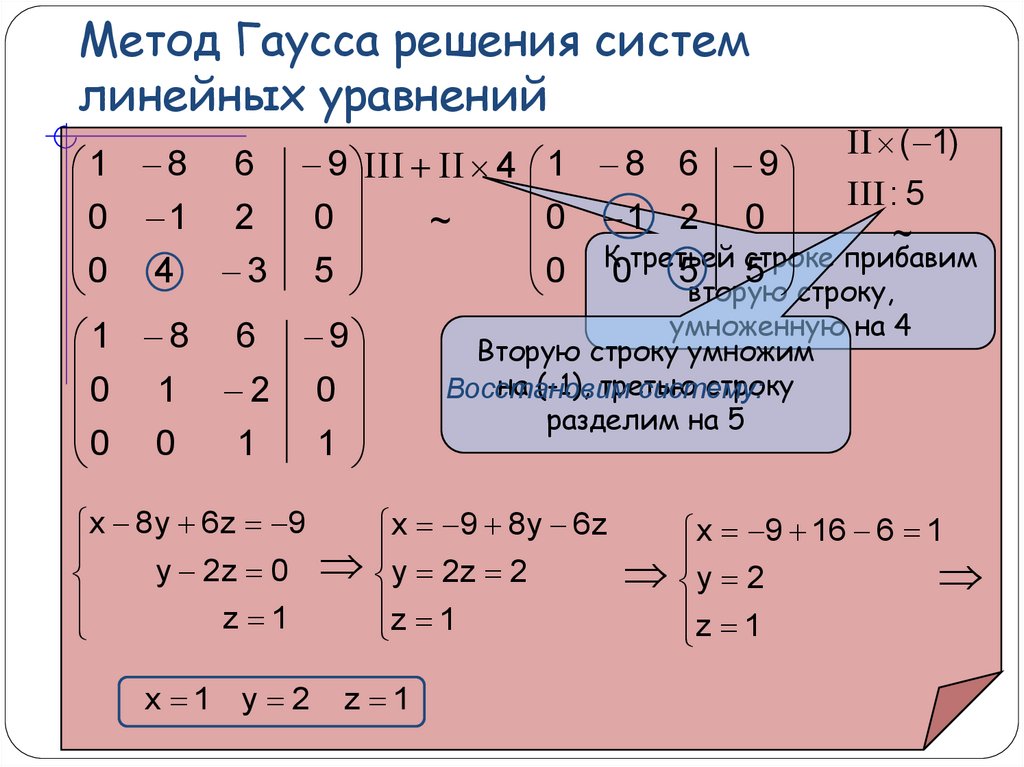

Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:

где а, в, с – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.

Если = = = , тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.

Множественные числа , , называются решением СЛАУ, если при подстановке , , в СЛАУ получим числовые тождества.

Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:

– это основная матрица СЛАУ.

– матрица столбец неизвестных переменных.

– матрица столбец свободных членов.

Если к основной матрице добавить в качестве – ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой , а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов.

То есть, расширенная матрица выглядит так:

Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.

Обратите внимание!

Если с системой уравнений:

Произвести такие действия:

умножать обе части любого из уравнений на произвольное и отличное от нуля число ;
менять местами уравнения;
к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число ,

тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.

Теперь можно перейти непосредственно к методу Гаусса.

Нужна работа? Есть решение!

Более 70 000 экспертов: преподавателей и доцентов вузов готовы помочь вам в написании работы прямо сейчас.

Подробнее Гарантии Отзывы

Простейшие преобразования элементов матрицы

Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:

Из уравнения запишем расширенную матрицу:

Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.

Определение

Матрица системы – это матрица, которая составляется исключительно с коэффициентами при неизвестных. Что касается расширенной матрицы системы, так, это такая матрица, в которой кроме коэффициентов записаны ещё и свободные члены. Любую из этих матриц называют просто матрицей.

На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:

1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:

2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).

3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.

4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.

5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:

Для удобства умножаем первую строку на (-3):

Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:

В итоге получилось такое преобразование:

Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:

В матрице верхняя строка преобразовалась:

Первую строку делим на и преобразовалась нижняя строка:

И верхнюю строку поделили на то же самое число :

Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты

Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:

Обратите внимание!

Если в примере приведены десятичные дроби, метод Гаусса в этом случае также поможет решить систему линейных алгебраических уравнений. Однако, не стоит забывать, что следует избегать приближённых вычислений, так как ответ будет неверным. Лучше всего использовать десятичные дроби, а от них переходить к обыкновенным дробям.

Алгоритм решения методом Гаусса пошагово

После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:

Шаг 1. Переписываем систему в виде матрицы

Записываем матрицу:

Шаг 2.

Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю

Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на .

Шаг 3. Приводим матрицу к ступенчатому виду

Теперь вторую строку можно поделить на 2 и получается:

Верхнюю строку делим на и приводим матрицу к ступенчатому виду:

Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.

Шаг 4. Записываем эквивалентную систему

После наших элементарных преобразований получилась эквивалентная система:

Шаг 5. Производим проверку (решение системы обратным путём)

Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки. :

находим : ,

После находим :

Тогда:

Как видим, уравнение решено правильно, так как ответы в системе совпадают.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений

Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.

Дана система уравнений:

Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.

Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную :

Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим . И последнее, находим первое уравнение .

Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.

Когда выражается через и в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:

берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на ,
берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на .

И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:

Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:

В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно , чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.

Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.

В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.

Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений

Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.

Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.

В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:

1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.

Например, вам попалась подобная система:

У нас получается такая ситуация

Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.

Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.

2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где – число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:

Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:

В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных , и , и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.

3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной . Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной . Если же уже исключались, тогда переходим к , и т. д.

Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :

Такая система уравнений после преобразования выглядит так:

Вы наверное уже обратили внимание, что вместе с исключились и . Поэтому решение методом Гаусса продолжаем исключением переменной из всех уравнений системы, а начнём мы с третьего уравнения:

Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:

Допусти, что система уравнений стала:

В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:

В нашем примере это , и . В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:

Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: , , , где , , – произвольные числа.

Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.

В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении: , а из первого уравнения получаем:

= =

В итоге, получился результат, который можно и записать.

Ответ

Примеры решения методом Гаусса

Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.

Пример 1

Задача

Решить систему линейных алгебраических уравнений методом Гаусса:

Решение

Выписываем матрицу, куда добавляем столбец свободных членов:

Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:

Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой превратился в . Для этого можно ко второй строке прибавить первую строку и умножить на .Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на (разрешающий элемент данного шага).

Соответственно, первая строка остаётся неизменной, а вторая поменяется:

Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на и только после этого ко второй строке прибавить изменённую после умножения на вторую строку. Вот что получилось:

. Теперь прибавляем со второй строки первую строку . У нас получился , который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:

Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.

Итак, у нас получился ступенчатый вид матрицы:

Записываем новую систему уравнений:

Для проверки решаем систему обратным ходом. Для этого находим сначала :

Так как найден, находим :

Подставляем в изначальную нашу систему уравнений найденные и :

и .

Как видите из решения, система уравнений решена верно. Запишем ответ.

Ответ

Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.

Пример 2

Задача

Решить систему уравнений методом Гаусса:

Решение

Составляем матрицу, куда вписываем и свободные члены:

Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку: . В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем , и . Аналогично, и . И умножаем свободный член . Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:

Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:

Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:

В результате получилась ступенчатая система уравнений:

Сначала находим : ,

Обратный ход:

Итак, уравнение системы решено верно.

Ответ

Пример 3

Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.

Задача

Решите систему уравнений методом Гаусса:

Решение

В уравнении , то есть – ведущий член и пусть ≠ 0

Из данного уравнения составим расширенную матрицу:

Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: , , . Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в теперь стоит 0.

Поменяем вторую и третью строку местами и получим:

Получилось так, что = b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную из третьей и четвёртой строк:

Получилась такая матрица:

Также, учитывая, что = , умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную и получаем новую систему уравнений:

Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,

из третьего: = = =

второе уравнение находим: = = = 2,

из первого уравнения: = .

Значит, решение системы такое: (1, 2, -1, -2).

Ответ

Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.

Пример 4

Задача

Решить систему уравнений методом Гаусса:

Решение

Записываем расширенную матрицу системы:

Сначала смотрим на левое верхнее число:

Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:

Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:

Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:

Получился ступенчатый вид уравнения:

Проверяем:

Ответ

Заключение

Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.

Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.

Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.

Литература для общего развития:

Умнов А. Е. Аналитическая геометрия и линейная алгебра, изд. 3: учеб. пособие – М. МФТИ – 2011 – 259 с.

Карчевский Е. М. Лекции по линейной алгебре и аналитической геометрии, учеб. пособие – Казанский университет – 2012 – 302 с.

Математика онлайн

Решение математики онлайн

Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.

Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.

Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.

О калькуляторах

По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.

Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту info@math34. biz

Преимущества

1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.

2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.

3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.

4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.

5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.

Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.

Метод Гаусса для решения матриц. Решение системы линейных уравнений методом Гаусса :: SYL.ru

Еще с начала XVI-XVIII веков математики усиленно начали изучать функции, благодаря которым так много в нашей жизни изменилось. Компьютерная техника без этих знаний просто не существовала бы. Для решения сложных задач, линейных уравнений и функций были созданы различные концепции, теоремы и методики решения. Одним из таких универсальных и рациональных способов и методик решения линейных уравнений и их систем стал и метод Гаусса. Матрицы, их ранг, детерминант – все можно посчитать, не используя сложных операций.

Что представляет собой СЛАУ

В математике существует понятие СЛАУ – система линейных алгебраических уравнений. Что же она собой представляет? Это набор из m уравнений с искомыми n неизвестными величинами, обычно обозначающимися как x, y, z, или x₁, x₂… x_n, или другими символами. Решить методом Гаусса данную систему – означает найти все искомые неизвестные. Если система имеет одинаковое число неизвестных и уравнений, тогда она называется системой n-го порядка.

Наиболее популярные методы решения СЛАУ

В учебных заведениях среднего образования изучают различные методики решения таких систем. Чаще всего это простые уравнения, состоящие из двух неизвестных, поэтому любой существующий метод для поиска ответа на них не займет много времени. Это может быть как метод подстановки, когда из одного уравнения выводится другое и подставляется в изначальное. Или метод почленного вычитания и сложения. Но наиболее легким и универсальным считается метод Гаусса. Он дает возможность решать уравнения с любым количеством неизвестных. Почему именно эта методика считается рациональной? Все просто. Матричный способ хорош тем, что здесь не требуется по несколько раз переписывать ненужные символы в виде неизвестных, достаточно проделать арифметические операции над коэффициентами – и получится достоверный результат.

Где используются СЛАУ на практике

Решением СЛАУ являются точки пересечения прямых на графиках функций. В наш высокотехнологический компьютерный век людям, которые тесно связаны с разработкой игр и прочих программ, необходимо знать, как решать такие системы, что они представляют и как проверить правильность получившегося результата. Наиболее часто программисты разрабатывают специальные программы-вычислители линейной алгебры, сюда входит и система линейных уравнений. Метод Гаусса позволяет высчитать все существующие решения. Также используются и другие упрощенные формулы и методики.

Критерий совместимости СЛАУ

Такую систему можно решить только в том случае, если она совместима. Для понятности представим СЛАУ в виде Ax=b. Она имеет решение, если rang(A) равняется rang(A,b). В этом случае (A,b) – это матрица расширенного вида, которую можно получить из матрицы А, переписав ее со свободными членами. Выходит, что решить линейные уравнения методом Гаусса достаточно легко.

Возможно, некоторые обозначения не совсем понятны, поэтому необходимо рассмотреть все на примере. Допустим, есть система: x+y=1; 2x-3y=6. Она состоит всего из двух уравнений, в которых 2 неизвестные. Система будет иметь решение только в том случае, если ранг ее матрицы будет равняться рангу расширенной матрицы. Что такое ранг? Это число независимых строк системы. В нашем случае ранг матрицы 2. Матрица А будет состоять из коэффициентов, находящихся возле неизвестных, а в расширенную матрицу вписываются и коэффициенты, находящиеся за знаком «=».

Почему СЛАУ можно представить в матричном виде

Исходя из критерия совместимости по доказанной теореме Кронекера-Капелли, систему линейных алгебраических уравнений можно представить в матричном виде. Применяя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ на всю систему. Если ранг обычной матрицы равняется рангу ее расширенной матрицы, но при этом меньше количества неизвестных, тогда система имеет бесконечное количество ответов.

Преобразования матриц

Прежде чем переходить к решению матриц, необходимо знать, какие действия можно проводить над их элементами. Существует несколько элементарных преобразований:

Переписывая систему в матричный вид и осуществляя ее решение, можно умножать все элементы ряда на один и тот же коэффициент.
Для того чтобы преобразовать матрицу в канонический вид, можно менять местами два параллельных ряда. Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся – нулями.
Соответствующие элементы параллельных рядов матрицы можно прибавлять один к другому.

Метод Жордана-Гаусса

Суть решения систем линейных однородных и неоднородных уравнений методом Гаусса в том, чтобы постепенно исключить неизвестные. Допустим, у нас есть система из двух уравнений, в которых две неизвестные. Чтобы их найти, необходимо проверить систему на совместимость. Уравнение методом Гаусса решается очень просто. Необходимо выписать коэффициенты, находящиеся возле каждого неизвестного в матричный вид. Для решения системы понадобится выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, тогда на место пропущенного элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, прибавление соответствующих элементов рядов друг к другу и другие. Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.

Простой пример решения системы 2х2

Для начала возьмем простенькую систему алгебраических уравнений, в которой будет 2 неизвестных.

Перепишем ее в расширенную матрицу.

Чтобы решить данную систему линейных уравнений, требуется проделать всего две операции. Нам необходимо привести матрицу к каноническому виду, чтобы по главной диагонали стояли единицы. Так, переводя с матричного вида обратно в систему, мы получим уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 – получившиеся ответы в процессе решения.

Первое действие при решении расширенной матрицы будет таким: первый ряд необходимо умножить на -7 и прибавить соответственно отвечающие элементы ко второй строке, чтобы избавиться от одного неизвестного во втором уравнении.
Так как решение уравнений методом Гаусса подразумевает приведение матрицы к каноническому виду, тогда необходимо и с первым уравнением проделать те же операции и убрать вторую переменную. Для этого вторую строку отнимаем от первой и получаем необходимый ответ – решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.

Как видим, наша система решена методом Жордана-Гаусса. Переписываем ее в необходимую форму: x=-5, y=7.

Пример решения СЛАУ 3х3

Предположим, что у нас есть более сложная система линейных уравнений. Метод Гаусса дает возможность высчитать ответ даже для самой, казалось бы, запутанной системы. Поэтому, чтобы более глубоко вникнуть в методику расчета, можно переходить к более сложному примеру с тремя неизвестными.

Как и в прежнем примере, переписываем систему в вид расширенной матрицы и начинаем приводить ее к каноническому виду.

Для решения этой системы понадобится произвести гораздо больше действий, чем в предыдущем примере.

Сначала необходимо сделать в первом столбце один единичный элемент и остальные нули. Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую – уже в измененном.
Далее убираем эту же первую неизвестную из третьего уравнения. Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья – уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
Теперь необходимо проделать операции и над другими элементами рядов. Третье и четвертое действие можно объединить в одно. Нужно разделить вторую и третью строку на -1, чтобы избавиться от минусовых единиц по диагонали. Третью строку мы уже привели к необходимому виду.
Дальше приведем к каноническому виду вторую строку. Для этого элементы третьего ряда умножаем на -3 и прибавляем их ко второй строчке матрицы. Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.
Чтобы из второго элемента строки сделать 0, необходимо умножить третью строку на -3 и прибавить ее к первому ряду.
Следующим решающим этапом будет прибавление к первой строке необходимые элементы второго ряда. Так мы получаем канонический вид матрицы, а, соответственно, и ответ.

Как видно, решение уравнений методом Гаусса довольно простое.

Пример решения системы уравнений 4х4

Некоторые более сложные системы уравнений можно решить методом Гаусса посредством компьютерных программ. Необходимо вбить в существующие пустые ячейки коэффициенты при неизвестных, и программа сама пошагово рассчитает необходимый результат, подробно описывая каждое действие.

Ниже описана пошаговая инструкция решения такого примера.

• В первом действии в пустые ячейки вписываются свободные коэффициенты и числа при неизвестных. Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.

• Далее меняются все строки местами, чтобы можно было выразить по главной диагонали единичные элементы.

• И производятся все необходимые арифметические операции, чтобы привести расширенную матрицу к каноническому виду. Необходимо понимать, что не всегда ответ на систему уравнений – это целые числа. Иногда решение может быть из дробных чисел.

Проверка правильности решения

Метод Жордана-Гаусса предусматривает проверку правильности результата. Для того чтобы узнать, правильно ли посчитаны коэффициенты, необходимо всего-навсего подставить результат в изначальную систему уравнений. Левая сторона уравнения должна соответствовать правой стороне, находящейся за знаком “равно”. Если ответы не совпадают, тогда необходимо пересчитывать заново систему или попробовать применить к ней другой известный вам метод решения СЛАУ, такой как подстановка или почленное вычитание и сложение. Ведь математика – это наука, которая имеет огромное количество различных методик решения. Но помните: результат должен быть всегда один и тот же, независимо от того, какой метод решения вы использовали.

Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ

Во время решения линейных систем уравнений чаще всего возникают такие ошибки, как неправильный перенос коэффициентов в матричный вид. Бывают системы, в которых отсутствуют в одном из уравнений некоторые неизвестные, тогда, перенося данные в расширенную матрицу, их можно потерять. В результате при решении данной системы результат может не соответствовать действительному.

Еще одной из главных ошибок может быть неправильное выписывание конечного результата. Нужно четко понимать, что первый коэффициент будет соответствовать первому неизвестному из системы, второй – второму, и так далее.

Метод Гаусса подробно описывает решение линейных уравнений. Благодаря ему легко произвести необходимые операции и найти верный результат. Кроме того, это универсальное средство для поиска достоверного ответа на уравнения любой сложности. Может быть, поэтому его так часто используют при решении СЛАУ.

Методические рекомендации к внеурочной самостоятельной работе “Решение систем уравнений методом Гаусса”

Самостоятельная работа №2

Решение систем уравнений методом Гаусса

Цель работы: овладеть методом Гаусса при решении систем линейных уравнений

Студент должен:

Знать:

символику и формы записи систем линейных уравнений
что такое совместная и несовместная система уравнений
методы решения СЛАУ(метод Гаусса)

Уметь:

КОНТРОЛЬНЫЕ ВОПРОСЫ:

В каком случае система имеет единственное решение?
В каком случае система имеет бесконечное множество решений?
В чем достоинство метода Гаусса по сравнению с другими методами?

Форма выполнения задания: решение задач (письменно)

Время выполнения 45 мин

Основной теоретический материал

Метод Гаусса. Этот способ заключается в обнулении элементов основной расширенной матрицы системы уравнений, находящихся под главной диагональю.

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы

Алгоритм метода Гаусса

На основании системы линейных уравнений составляем расширенную матрицу системы;
Приводим матрицу к “треугольному” виду;
Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через переменные которые могут принимать произвольные значения;

Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:

Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.

Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.

На первом этапе составляется расширенная матрица, состоящая из коэффициентов при неизвестных, и с помощью несложных математических преобразований она приводится к виду, когда диагональ, состоящая из единичек отсекает нули:

На втором этапе последовательно находятся все неизвестные, начиная с предпоследней.

Решение типовых заданий

Решить систему трех линейных уравнений методом Гаусса

Ответ: х=1, y=2, z=3.

Покажем, как методом Гаусса можно решить следующую систему:

Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на и , соответственно:

Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на :

В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

из третьего;

из второго, подставив полученное

из первого, подставив полученные и .

Ответ: (2; 3; -1).

Решить самостоятельно системы линейных уравнений по вариантам: 10 вариантов

Оформить отчет

Требования к оформлению самостоятельной работы

Расчетные задания должны быть выполнены в рабочей тетради

По результатам решения тренажера выставляется оценка, которая учитывается при приеме дифференцированного зачета.

Шкала оценки образовательных достижений

Процент результативности

(правильных ответов)

Интернет ресурсы

http://math2.ru/education/sys_lin_eq/gauss. html

http://www.bestreferat.ru/referat-180751.html

Оценка уровня подготовки
Балл (оценка)	Вербальный аналог
90-100	5	отлично
80-89	4	хорошо
70-79	3	удовлетворительно
менее 70	2	неудовлетворительно

Как решать матрицы методом гаусса. Метод Гаусса для решения матриц

Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Далее полезно изучить урок .

Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной ).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений? и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы : . По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .

На практике так подробно, конечно, не расписывают, а пишут короче: Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ : рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя! Вернемся к нашей системе . Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :

(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .

В нижнем уравнении у нас уже готовый результат: .

Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число: Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения . Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО :
А мысленный ход самих расчётов я уже рассмотрел выше.

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :
Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: Круто.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:

Ответ :

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Пример 2

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!

Пример 3

Решить систему линейных уравнений методом Гаусса

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:

Ответ : .

Пример 4

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.

В последней части рассмотрим некоторые особенности алгоритма Гаусса. Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например: Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули: Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .

Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.

Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:

Пример 5

Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными.

Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Желаю успехов!

Решения и ответы:

Пример 2: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Выполненные элементарные преобразования: (1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем! (2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее. (3) К третьей строке прибавили вторую строку, умноженную на 5. (4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход:

Ответ : .

Пример 4: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования: (1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке». (2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы (3) К третьей строке прибавили вторую, умноженную на –1. (4) Ко второй строке прибавили третью, умноженную на –3. Нужная вещь на второй ступеньке получена . (5) К третьей строке прибавили вторую, умноженную на 6. (6) Вторую строку умножили на –1, третью строку разделили на -83.

Обратный ход:

Ответ :

Пример 5: Решение : Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования: (1) Первую и вторую строки поменяли местами. (2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3. (3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1. (4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки. (5) К четвертой строке прибавили третью строку, умноженную на –5.

Обратный ход:

Ответ :

Что представляет собой СЛАУ

В математике существует понятие СЛАУ – система линейных алгебраических уравнений. Что же она собой представляет? Это набор из m уравнений с искомыми n неизвестными величинами, обычно обозначающимися как x, y, z, или x 1 , x 2 … x n, или другими символами. Решить методом Гаусса данную систему – означает найти все искомые неизвестные. Если система имеет одинаковое число неизвестных и уравнений, тогда она называется системой n-го порядка.

Наиболее популярные методы решения СЛАУ

Где используются СЛАУ на практике

Критерий совместимости СЛАУ

Почему СЛАУ можно представить в матричном виде

Преобразования матриц

Переписывая систему в матричный вид и осуществляя ее решение, можно умножать все элементы ряда на один и тот же коэффициент.
Для того чтобы преобразовать матрицу в канонический вид, можно менять местами два параллельных ряда. Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся – нулями.
Соответствующие элементы параллельных рядов матрицы можно прибавлять один к другому.

Метод Жордана-Гаусса

Простой пример решения системы 2х2

Для начала возьмем простенькую систему алгебраических уравнений, в которой будет 2 неизвестных.

Перепишем ее в расширенную матрицу.

Первое действие при решении расширенной матрицы будет таким: первый ряд необходимо умножить на -7 и прибавить соответственно отвечающие элементы ко второй строке, чтобы избавиться от одного неизвестного во втором уравнении.
Так как решение уравнений методом Гаусса подразумевает приведение матрицы к каноническому виду, тогда необходимо и с первым уравнением проделать те же операции и убрать вторую переменную. Для этого вторую строку отнимаем от первой и получаем необходимый ответ – решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.

Как видим, наша система решена методом Жордана-Гаусса. Переписываем ее в необходимую форму: x=-5, y=7.

Пример решения СЛАУ 3х3

Для решения этой системы понадобится произвести гораздо больше действий, чем в предыдущем примере.

Сначала необходимо сделать в первом столбце один единичный элемент и остальные нули. Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую – уже в измененном.
Далее убираем эту же первую неизвестную из третьего уравнения. Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья – уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
Теперь необходимо проделать операции и над другими элементами рядов. Третье и четвертое действие можно объединить в одно. Нужно разделить вторую и третью строку на -1, чтобы избавиться от минусовых единиц по диагонали. Третью строку мы уже привели к необходимому виду.
Дальше приведем к каноническому виду вторую строку. Для этого элементы третьего ряда умножаем на -3 и прибавляем их ко второй строчке матрицы. Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.
Чтобы из второго элемента строки сделать 0, необходимо умножить третью строку на -3 и прибавить ее к первому ряду.
Следующим решающим этапом будет прибавление к первой строке необходимые элементы второго ряда. Так мы получаем канонический вид матрицы, а, соответственно, и ответ.

Как видно, решение уравнений методом Гаусса довольно простое.

Пример решения системы уравнений 4х4

Ниже описана пошаговая инструкция решения такого примера.

В первом действии в пустые ячейки вписываются свободные коэффициенты и числа при неизвестных. Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.

И производятся все необходимые арифметические операции, чтобы привести расширенную матрицу к каноническому виду. Необходимо понимать, что не всегда ответ на систему уравнений – это целые числа. Иногда решение может быть из дробных чисел.

Проверка правильности решения

Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ

Одним из простейших способов решения системы линейных уравнений является прием, основанный на вычислении определителей (правило Крамера ). Его преимущество состоит в том, что он позволяет сразу провести запись решения, особенно он удобен в тех случаях, когда коэффициенты системы являются не числами, а какими-то параметрами. Его недостаток – громоздкость вычислений в случае большого числа уравнений, к тому же правило Крамера непосредственно не применимо к системам, у которых число уравнений не совпадает с числом неизвестных. В таких случаях обычно применяют метод Гаусса .

Системы линейных уравнений, имеющие одно и то же множество решений, называются эквивалентными . Очевидно, что множество решений линейной системы не изменится, если какие-либо уравнения поменять местами, или умножить одно из уравнений на какое-либо ненулевое число, или если одно уравнение прибавить к другому.

Метод Гаусса (метод последовательного исключения неизвестных ) заключается в том, что с помощью элементарных преобразований система приводится к эквивалентной системе ступенчатого вида. Сначала с помощью 1-го уравнения исключается x 1 из всех последующих уравнений системы. Затем с помощью2-го уравнения исключается x 2 из 3-го и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса , продолжается до тех пор, пока в левой части последнего уравнения останется только одно неизвестное x n . После этого производится обратный ход метода Гаусса – решая последнее уравнение, находим x n ; после этого, используя это значение, из предпоследнего уравнения вычисляем x n –1 и т.д. Последним находим x 1 из первого уравнения.

Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицами их коэффициентов. Рассмотрим матрицу:

называемую расширенной матрицей системы, ибо в нее, кроме основной матрицы системы, включен столбец свободных членов. Метод Гаусса основан на приведении основной матрицы системы к треугольному виду (или трапециевидному виду в случае неквадратных систем) при помощи элементарных преобразованиях строк (!) расширенной матрицы системы.

Пример 5.1. Решить систему методом Гаусса:

Решение . Выпишем расширенную матрицу системы и, используя первую строку, после этого будем обнулять остальные элементы:

получим нули во 2-й, 3-й и 4-й строках первого столбца:

Теперь нужно чтобы все элементы во втором столбце ниже 2-й строки были равны нулю. Для этого можно умножить вторую строку на –4/7 и прибавить к 3-й строке. Однако чтобы не иметь дело с дробями, создадим единицу во 2-й строке второго столбца и только

Теперь, чтобы получить треугольную матрицу, нужно обнулить элемент четвертой строки 3-го столбца, для этого можно умножить третью строку на 8/54 и прибавить ее к четвертой. Однако чтобы не иметь дело с дробями поменяем местами 3-ю и 4-ю строки и 3-й и 4-й столбец и только после этого произведем обнуление указанного элемента. Заметим, что при перестановке столбцов меняются местами, соответствующие переменные и об этом нужно помнить; другие элементарные преобразования со столбцами (сложение и умножение на число) производить нельзя!

Последняя упрощенная матрица соответствует системе уравнений, эквивалентной исходной:

Отсюда, используя обратный ход метода Гаусса, найдем из четвертого уравнения x 3 = –1; из третьего x 4 = –2, из второго x 2 = 2 и из первого уравнения x 1 = 1. В матричном виде ответ записывается в виде

Мы рассмотрели случай, когда система является определенной, т.е. когда имеется только одно решение. Посмотрим, что получится, если система несовместна или неопределенна.

Пример 5.2. Исследовать систему методом Гаусса:

Решение . Выписываем и преобразуем расширенную матрицу системы

Записываем упрощенную систему уравнений:

Здесь, в последнем уравнении получилось, что 0=4, т.е. противоречие. Следовательно, система не имеет решения, т.е. она несовместна . à

Пример 5.3. Исследовать и решить систему методом Гаусса:

Решение . Выписываем и преобразуем расширенную матрицу системы:

В результате преобразований, в последней строке получились одни нули. Это означает, что число уравнений уменьшилось на единицу:

Таким образом, после упрощений осталось два уравнения, а неизвестных четыре, т.е. два неизвестных “лишних”. Пусть “лишними”, или, как говорят, свободными переменными , будут x 3 и x 4 . Тогда

Полагая x 3 = 2a и x 4 = b , получим x 2 = 1–a и x 1 = 2b –a ; или в матричном виде

Записанное подобным образом решение называется общим , поскольку, придавая параметрам a и b различные значения, можно описать все возможные решения системы. à

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной ).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья . Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы :
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.

Существуют следующие элементарные преобразования:

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .

На практике так подробно, конечно, не расписывают, а пишут короче:

Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »

Элементарные преобразования не меняют решение системы уравнений

Вернемся к нашей системе . Она практически разобрана по косточкам.

(2) Делим вторую строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

В нижнем уравнении у нас уже готовый результат: .

Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:

И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:

Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения . Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Результат записываем во вторую строку:

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

А мысленный ход самих расчётов я уже рассмотрел выше.

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:

Ответ :

Пример 2

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Пример 3

Решить систему линейных уравнений методом Гаусса

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Ответ : .

Пример 4

Решить систему линейных уравнений методом Гаусса

В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:

Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:

Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Пример 5

Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Желаю успехов!

Решения и ответы:

Пример 2: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход:

Ответ : .

Пример 4: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы

(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
(3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.
(4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.
(5) К четвертой строке прибавили третью строку, умноженную на –5.

Обратный ход:

Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).

Мы знаем, что система линейных алгебраических уравнений может:

1) Не иметь решений (бытьнесовместной ).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.

Как мы помним,правило Крамера и матричный методнепригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений , который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.

Преобразования расширенной матрицы (это матрица системы – матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:

1) с троки матрицыможно переставлять местами.

2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следуетудалить из матрицы все эти строки кроме одной.

3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить .

4) строку матрицы можноумножить (разделить) на любое число,отличное от нуля.

5) к строке матрицы можноприбавить другую строку, умноженную на число , отличное от нуля.

В методе Гаусса элементарные преобразования не меняют решение системы уравнений.

Метод Гаусса состоит из двух этапов:

«Прямой ход» – с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:

Для этого выполним следующие действия:

1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х 1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х 1 , стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х 1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х 1 не будут иметь коэффициент 0.

2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х 2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х 2 во всех уравнениях будут нули.

3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.

«Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х n . Для этого решаем элементарное уравнение А*х n = В. В примере, приведенном выше, х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.

Пример.

Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
1 шаг . К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).

2 шаг . Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

3 шаг . Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

4 шаг . К третьей строке прибавили вторую строку, умноженную на 2.

5 шаг . Третью строку разделили на 3.

Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23) , и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:

x 3 = 1
x 2 = 3
x 1 + x 2 – x 3 = 1, следовательно x 1 + 3 – 1 = 1, x 1 = –1

Ответ 😡 1 = –1, x 2 = 3, x 3 = 1.

Решим эту же систему по предложенному алгоритму. Получаем

4 2 –1 1
5 3 –2 2
3 2 –3 0

Разделим второе уравнение на 5, а третье – на 3. Получим:

4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0

Умножим второе и третье уравнения на 4, получим:

4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0

Вычтем из второго и третьего уравнений первое уравнение, имеем:

4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1

Разделим третье уравнение на 0,64:

4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625

Умножим третье уравнение на 0,4

4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625

Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:

4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225

Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х 3 = 0,96 или приблизительно 1.

х 2 = 3 и х 1 = –1.

Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.

Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.

Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решение систем уравнений методом Гаусса | Проект по алгебре (8 класс) на тему:

МАОУ-лицей № 13 п. Краснообск, Рязанова М. «Решение систем уравнений методом Гаусса»

Муниципальное автономное общеобразовательное учреждение

Новосибирского района Новосибирской области –

лицей № 13 п. Краснообск

Решение систем уравнений

методом Гаусса

Работу выполнила:

Рязанова Мария

8Б класс

Руководитель:

учитель математики

Черемисина Галина Артуровна

2018

Содержание:

Введение…….…………………………………..…………….…..3
Немного из биографии Гаусса……………………………………4
Понятие матрицы и её преобразования ……………………….…5
Решение двойной системы уравнений………………….……….7
Решение тройной системы……………………………………….8
Заключение ………….…………………………….……………..9
Используемые ресурсы……………………………………….…10

Введение

Одной из основных задач алгебры является решение систем линейных алгебраических уравнений. Большая часть методов решения различных задач включает в себя решение систем линейных уравнений как один из шагов соответствующего алгоритма. Достаточно известным методом решения систем линейных уравнений является метод Гаусса. Это метод также называют методом последовательного исключения неизвестных Гаусса, который является одним из наиболее универсальных и эффективных методов решения линейных систем уравнений, известный в различных вариантах уже более 2000 лет.

Процесс решения по методу Гаусса состоит из двух этапов, называемых прямым и обратным ходом. На первом этапе система приводится к треугольному виду, а на втором (обратный ход) идет последовательное определение неизвестных из указанной треугольной системы.

Метод Гаусса – один из основных результатов линейной алгебры и аналитической геометрии, к нему сводятся множество других теорем и методов линейной алгебры. Поэтому поиск решения системы линейных уравнений методом Гаусса имеет не только важное значение, но и является частью алгоритма решения многих задач, что позволяет говорить об актуальности изучения метода Гаусса. В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных.

Цели и задачи

Цели проекта: ознакомить и научить одноклассников решать системы уравнений методом Гаусса.

Задачи проекта:

подобрать информацию по данной теме;
изучить метод Гаусса;
научиться самостоятельно решать системы уравнений методом Гаусса;
рассказать историю появления метода Гаусса, о самом Гауссе и его научных трудах;
показать преобразования матрицы одноклассникам;
подобрать и решить примеры систем уравнений этим методом;
применить метод Гаусса при решении систем уравнений вместе с одноклассниками.

Немного из биографии Гаусса

Иога́нн Карл Фри́дрих Га́усс (1777 — 1855) — немецкий математик, механик, физик, астроном и геодезист. Считается одним из величайших математиков всех времён, «королём математиков».

С именем Гаусса связаны фундаментальные исследования почти во всех основных областях математики: в алгебре, теории чисел, дифференциальной и неевклидовой геометрии, теории вероятностей, а также в механике, астрономии, физике и геодезии.

Гаусс чрезвычайно строго относился к своим печатным трудам и никогда не публиковал даже выдающиеся результаты, если считал свою работу над этой темой незавершённой. Изучение архива Гаусса показало, что он медлил с публикацией ряда своих открытий, и в результате его опередили другие математики. Вот неполный перечень упущенных им трудов.

Неевклидова геометрия
Эллиптические функции
Метод наименьших квадратов
Закон распределения простых чисел

Метод Гаусса

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, при котором с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида. Затем последовательно, начиная с последних (по номеру), находятся все переменные системы. Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах».

Понятие матрицы, её преобразования

Матрица (математика) — прямоугольная таблица элементов.

пример матрицы

Со строками матрицы мы можем выполнять следующие операции: деление; умножение на число, отличное от нуля; сложение; вычитание.

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:

2) Если в матрице есть пропорциональные (или одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу.

В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них:

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Нулевая строка – это строка, в которой одни нули.

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу:

Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:

Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.

Строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

Цель элементарных преобразований – привести матрицу к ступенчатому виду:

Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.

Решение системы уравнений с двумя переменными

Решим данную систему методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы,

которая представляет из себя коэффициенты чисел:

Умножаем первую строку на 2
К первой строке прибавляем вторую
Сокращаем первую строку на 5
Умножаем первую строку на 3
Из второй строки вычитаем первую
Первую строку сокращаем на 3, а вторую на 4

Ответ:

Решение системы уравнений с тремя переменными

Вычитаем из первой строки вторую
Вычитаем из первой строки первую строку, умноженную на 2. Из третьей строки вычитаем первую.

Третью строку умножаем на -1.
Ко второй строке прибавляем третью, умноженную на 7.

Вторую строку делим на -30.
Из первой строки вычитаем третью, умноженную на 3.

Из первой строки вычитаем вторую, умноженную на 13.
К третьей строке прибавляем вторую, умноженную на 7.

– решение системы уравнений

Ответ:

Заключение

Поработав с данным методом, я ощутила преимущество его применения по отношению к классическим приёмам решения систем уравнений. Надеюсь, знание этого метода мне поможет в будущем быстро решать системы уравнений с несколькими переменными, а также осуществлять проверку решений классическими способами.

Одной из целей моего проекта является научить одноклассников решать системы уравнений методом Гаусса, для чего на спецкурсе по математике я показала и рассказала им о своей работе и предложила совместно решить несколько систем, состоящих из двух строк, методом Гаусса. Ребят заинтересовал данный метод, они с интересом слушали меня, а потом совместно решали системы уравнений данным методом. Далее предложены системы уравнений и фотографии с нашего занятия.

Ответ: Ответ:

Ответ:

У меня получилось самой освоить данный метод и передать свои знания одноклассникам. Таким образом, поставленные мною цели и задачи выполнены. И ещё метод Гаусса прост тем, как мне кажется, что для его освоения не требуется много знаний. А также для матриц ограниченного размера метод Гаусса менее трудоёмкий по сравнению с другими методами, поэтому в будущем я планирую его активно применять при решении систем уравнений.

Используемые ресурсы:

Метод Гаусса. Решение системы линейных уравнений методом Гаусса и Жордана-Гаусса

Матрицы и системы уравнений

6.1 – Матрицы и системы уравнений

Определение матрицы

Прямоугольный массив действительных чисел
м строк по n столбцов
Обозначается заглавными буквами
Первый индекс – строка, второй индекс – столбец

Терминология

Матрица с m строк и n столбцами называется матрицей порядка m x n .
Квадратная матрица – это матрица с равным количеством строк и столбцов. Поскольку количество строки и столбцы одинаковы, говорят, что он имеет порядок n .
Главной диагональю квадратной матрицы являются элементы от верхнего левого угла до нижнего правого угла. матрица.
Матрица-строка – это матрица, состоящая только из одной строки.
Матрица столбцов – это матрица, имеющая только один столбец.
Матрица только с одной строкой или одним столбцом называется вектором.

Преобразование систем линейных уравнений в Матрицы

Каждое уравнение в системе превращается в строку. Каждая переменная в система становится колонной. Переменные отбрасываются, а коэффициенты помещаются в матрицу. Если правая часть включена, это называется расширенной матрицей. Если правая сторона отсутствует, это называется матрицей коэффициентов.

Система линейных уравнений …

 х + у - г = 1
3х - 2у + г = 3
4x + y - 2z = 9

становится расширенной матрицей…

х	л	z	пр.
1	1	-1	1
3	-2	1	3
4	1	-2	9

Операции с элементарными строками

Операции с элементарной строкой – это операции, которые могут быть выполнены с матрицей, которая даст эквивалентная строка матрица.Если матрица является расширенной матрицей, построенной из системы линейных уравнений, то эквивалентная строка матрица будет иметь то же решение, что и исходная матрица.

При работе с системами линейных уравнений вы могли выполнять три операции. что не повлияет на набор решений.

Поменяйте местами два уравнения.
Умножьте уравнение на ненулевую константу.
Умножьте уравнение на ненулевую константу и добавьте его к другому уравнению, заменив это уравнение.

Когда система линейных уравнений преобразуется в расширенную матрицу, каждое уравнение становится строка. Итак, теперь есть три элементарные операции со строками, которые производят эквивалент строки матрица.

Перестановка двухрядная
Умножить строку на ненулевую константу
Умножьте строку на ненулевую константу и добавьте ее в другую строку, заменив эту строку.

Формы рядов-эшелонов и сокращенных рядов-эшелонов

Это эквивалентные строкам формы матрицы.Несложно решить систему линейных уравнений когда матрицы находятся в одной из этих форм.

Форма рядного эшелона

Матрица находится в виде эшелона строк, когда выполняются следующие условия.

Если есть строка со всеми нулями, то она находится внизу матрицы.
Первый ненулевой элемент любой строки – это единица. Этот элемент называется ведущим.
Первая строка любой строки находится справа от первой строки предыдущей строки.

Банкноты

Первая строка в строке не обязательно должна быть рядом с , непосредственно справа от первой строки предыдущий ряд.
Матрица в виде эшелона строк будет иметь нули под ведущими.
Метод исключения Гаусса переводит матрицу в форму строки-эшелон, а затем выполняется обратная подстановка. требуется, чтобы завершить поиск решений системы.
Форма матрицы “строка-эшелон” не обязательно уникальна.

Форма Row-Echelon уменьшенная

Матрица находится в сокращенной форме строка-эшелон, когда выполняются все условия формы строка-эшелон. и все элементы выше и ниже, ведущие равны нулю.

Если есть строка со всеми нулями, то она находится внизу матрицы.
Первый ненулевой элемент любой строки – это единица. Этот элемент называется ведущим.
Первая строка любой строки находится справа от первой строки предыдущей строки.
Все элементы выше и ниже ведущего равны нулю.

Банкноты

Первая строка в строке не обязательно должна быть рядом с , непосредственно справа от первой строки предыдущий ряд.
Матрица в виде эшелона строк будет иметь нули как над, так и под ведущими.
Метод исключения Гаусса-Джордана переводит матрицу в сокращенную форму строки-эшелона.
Для завершения поиска решений в системе не требуется обратной замены.
Уменьшенная строковая форма матрицы уникальна.

Исключение по Гауссу

Запишите систему линейных уравнений в виде расширенной матрицы
Выполните элементарные операции со строками, чтобы преобразовать матрицу в эшелонированную форму строки
Преобразуйте матрицу обратно в систему линейных уравнений
Используйте обратную замену, чтобы получить все ответы

Гаусс-Джордан Ликвидация

Запишите систему линейных уравнений в виде расширенной матрицы
Выполните элементарные операции со строками, чтобы преобразовать матрицу в сокращенную форму строки-эшелона
Преобразуйте матрицу обратно в систему линейных уравнений
Обратной замены не требуется

Поворотный

Поворот – это процесс, который автоматизирует операции со строками, необходимые для размещения матрицы в рядный эшелон или редуцированный рядный эшелон формы
В частности, поворот превращает элементы выше или ниже ведущего в нули

Типы решений

Существует три типа решений, которые возможны при решении системы линейных уравнений.

Независимая

Согласованный
Уникальное решение
Матрица с сокращенной строкой имеет такое же количество ненулевых строк, что и переменные
Левая часть обычно представляет собой единичную матрицу, но не обязательно
Для получения независимого решения должно быть как минимум столько же уравнений, сколько переменных.

х	л	z	пр.
1	0	0	3
0	1	0	1
0	0	1	2

Когда вы конвертируете расширенную матрицу обратно в форму уравнения, вы получаете x = 3, y = 1 и z = 2.

Зависимые

Согласованный
Множество решений
Запишите ответ в параметрической форме
Матрица с сокращенной строкой содержит больше переменных, чем ненулевых строк
Ряд нулей быть не обязательно, но обычно он есть.
Это также может произойти, когда уравнений меньше, чем переменных.

х	л	z	пр.
1	0	3	4
0	1	-2	3
0	0	0	0

Первое уравнение будет x + 3z = 4.Решение относительно x дает x = 4 – 3z.

Второе уравнение будет y – 2z = 3. Решение для y дает y = 3 + 2z.

Столбец z не очищен (все нули, кроме одно число), поэтому другие переменные будут определены через z. Следовательно, z будет параметром t и решение …

x = 4 – 3t, y = 3 + 2t, z = t

Несоответствие

Нет решения
Матрица с сокращенной строкой имеет строку нулей слева, но правая часть не равна нулю.

х	л	z	пр.
1	0	3	4
0	1	-2	3
0	0	0	2

Тут решения нет.Вы можете записать это как нулевой набор Ø, пустой набор {} или нет решения.

Методы исключения Гаусса и матричные методы

Система линейных уравнений может быть помещены в матричную форму. Каждый уравнение становится строкой, и каждое переменная становится столбцом. An добавлен дополнительный столбец для справа.Система показаны линейные уравнения и результирующая матрица.

Система линейных уравнений …

 3x + 2y - 4z = 3
2х + 3у + 3z = 15
5x - 3y + z = 14

становится расширенной матрицей …

х	л	z	пр.
3	2	-4	3
2	3	3	15
5	-3	1	14

Цель при решении системы уравнений состоит в том, чтобы преобразовать расширенную матрицу в сокращенную форму строки-эшелона, если это возможно.

Есть три элементарных операции со строками, которые вы можете использовать для размещения матрицы в уменьшенная строчно-эшелонированная форма.

Каждое из требований сокращенной матрицы строка-эшелон может быть удовлетворено с использованием элементарной строки операции.

Если есть строка со всеми нулями, то она находится внизу матрицы.
Поменяйте местами две строки матрицы, чтобы переместить строку со всеми нулями вниз.
Первый ненулевой элемент любой строки – это единица.Этот элемент называется ведущим.
Умножьте (разделите) строку на ненулевую константу, чтобы превратить первый ненулевой элемент в один.
Первая строка любой строки находится справа от первой строки предыдущей строки.
Умножьте строку на ненулевую константу и добавьте ее в другую строку, заменив эту строку. В Смысл этой элементарной операции со строками состоит в том, чтобы преобразовать числа в нули. Сделав числа под ведущими в ноль, это заставляет первый ненулевой элемент любой строки быть справа от ведущей предыдущей строки.
Все элементы выше и ниже ведущего равны нулю.
Умножьте строку на ненулевую константу и добавьте ее в другую строку, заменив эту строку. В Смысл этой элементарной операции со строками состоит в том, чтобы преобразовать числа в ноль. Разница здесь в что вы очищаете (обнуляете) элементы выше ведущего, а не чуть ниже ведущий.

Что такое поворот?

Цель поворота – сделать элемент выше или ниже ведущего в ноль.

«Поворотный элемент» или «сводный элемент» – это элемент в левой части матрицы. что вы хотите элементы сверху и снизу равны нулю.

Обычно это один элемент. Если вы найдете книгу, в которой упоминается поворот, они обычно сказать вам, что вы должны повернуться на один. Если ограничиться тремя элементарными рядами операций, то это верное утверждение.

Однако, если вы хотите объединить вторую и третью элементарные операции со строками, вы придумать другую строковую операцию (не элементарную, но все еще действующую).

Вы можете умножить строку на ненулевую константу и добавить ее к ненулевому кратному другому. row, заменив эту строку.

И что? Если вам нужно повернуться на одном, то вам иногда придется использовать второй. элементарная операция со строкой и разделите строку на ведущий элемент, чтобы превратить ее в единицу. Деление приводит к дробям. Хотя дроби – ваши друзья, у вас меньше шансов ошибиться если вы их не используете.

В чем прикол? Если вы не остановитесь на одном, вы, вероятно, столкнетесь с большими числами. Наиболее люди готовы работать с большими числами, чтобы избежать дробей.

Процесс поворота

Pivoting работает, потому что общее кратное (не обязательно наименьшее общее кратное) двух чисел всегда можно найти, умножив два числа вместе. Давайте возьмем предыдущий пример и очистить первый столбец.

х	л	z	пр.
3	2	-4	3
2	3	3	15
5	-3	1	14

Полезные советы

Хотя вам не нужно поворачиваться на единицу, это очень желательно.Поворот на единицу означает, что вы умножаете на 1 (что легко сделать).
Поворот по главной диагонали – это хорошо, но не обязательно. Некоторым людям нравится начинать с левого верхнего угла и продвигаться вниз к Нижний правый.
Пока вы выполняете поворот только один раз для каждой строки и столбца, столбцы, которые были очищены, останутся очищенными.
Поскольку целью поворота является очистка столбца вращения, выбор столбец, в котором уже есть нули, экономит время, потому что у вас нет чтобы изменить строку, содержащую ноль.

Выбор оси

Выберите столбец с наибольшим количеством нулей.
Использовать строку или столбец только один раз
Поверните на единицу, если возможно
Поворот по главной диагонали
Никогда не поворачивайтесь на ноль
Никогда не поворачивайте вправо

Поскольку в первом ряду никого нет, у нас есть два варианта: либо мы первую строку делим на три и работаем дробями, либо делаем поворот на три и получите большие числа.Это вариант, который я собираюсь использовать. Я поверну на тройку в R ₁ C ₁. Обведите его как стержневой элемент. В зависимости от вашего браузера вы элементы поворота могут быть обведены красным кружком или просто отмечены знаком * перед ним.

х	л	z	пр.
* 3	2	-4	3
2	3	3	15
5	-3	1	14

Идея состоит в том, чтобы превратить числа в рамке (желтые) в ноль.Использование комбинированного рядная операция (это не элементарная операция), это может сделать 3R ₂ – 2R ₁ → R ₂ и 3R ₃ – 5R ₁ → R ₃.

Единственная строка, которая не изменяется, – это строка, содержащая элемент поворота ( 3). Весь смысл процесса поворота состоит в том, чтобы обнулить значения в рамке. Перепишите сводную строку и очистите (сделайте ноль) сводный столбец.

х	л	z	пр.
* 3	2	-4	3
0
0

Для замены значений в строке 2 каждый новый элемент получается путем умножения элемент, заменяемый во второй строке на 3 и вычитающий в 2 раза элемент в первой строка из того же столбца, что и заменяемый элемент.

Чтобы выполнить поворот, поместите один палец на шарнир (обведен кружком). номер) и один палец на заменяемом элементе. Умножьте эти два числа вместе. Теперь поместите один палец на номере в рамке в той же строке, что и элемент, который вы заменяя и другой палец в поворотном ряду и такой же столбец как номер, который вы заменяете. Умножьте эти два числа вместе. Возьмите продукт за шарнир и вычесть произведение без оси.

х	л	z	пр.
* 3	2	-4	3
2	3	3	15
5	-3	1	14

Чтобы заменить 3 в R ₂ C ₂, вы должны взять 3 (3) – 2 (2) = 9 – 4 = 5.

Чтобы заменить 3 в R ₂ C ₃, вы должны взять 3 (3) – 2 (-4) = 9 +8 = 17.

Чтобы заменить 15 в R ₂ C ₄, вы должны взять 3 (15) – 2 (3) = 45-6 = 39.

Чтобы заменить -3 в R ₃ C ₂, вы должны взять 3 (-3) – 5 (2) = -9-10 = -19.

Чтобы заменить 1 в R ₃ C ₃, вы должны взять 3 (1) – 5 (-4) = 3 + 20 = 23

Чтобы заменить 14 в R ₃ C ₄, вы должны взять 3 (14) – 5 (3) = 42-15 = 27.

Вот как выглядит процесс.

х	л	z	пр.
поворотный ряд, копия 3	поворотный ряд, копия 2	поворотный ряд, копия -4	поворотный ряд, копия 3
поворотная стойка, прозрачная 0	3 (3) – 2 (2) 5	3 (3) – 2 (-4) 17	3 (15) – 2 (3) 39
поворотная стойка, прозрачная 0	3 (-3) – 5 (2) -19	3 (1) – 5 (-4) 23	3 (14) – 5 (3) 27

Или, если убрать комментарии, матрица после первого поворота будет выглядеть так.

х	л	z	пр.
3	2	-4	3
0	5	17	39
0	-19	23	27

Пришло время повторить весь процесс.Мы проходим и выбираем другое место для поворота. Мы хотел бы, чтобы он был на главной диагонали, с единицей или с нулями в столбце. К сожалению, у нас не может быть ничего из этого. Но так как мы должны все умножить другие числа у оси, мы хотим, чтобы она была маленькой, поэтому мы перейдем к 5 дюймов R ₂ C ₂ и очистите 2 и -19.

х	л	z	пр.
3	2	-4	3
0	* 5	17	39
0	-19	23	27

Начните с копирования вниз сводной строки (2-я строка) и очистки сводного столбца (2-я строка). столбец).Ранее очищенные столбцы останутся очищенными.

х	л	z	пр.
	0
0	* 5	17	39
0	0

Вот вычисления, чтобы найти следующее взаимодействие.Обратите особое внимание в 3-ю строку, где мы вычитаем значение -19 раз. Поскольку мы вычитаем отрицательный, я записал его как плюс 19.

х	л	z	пр.
5 (3) – 2 (0) 15	поворотная стойка, прозрачная 0	5 (-4) – 2 (17) -54	5 (3) – 2 (39) -63
поворотный ряд, копия 0	поворотный ряд, копия 5	поворотный ряд, копия 17	поворотный ряд, копия 39
ранее погашено 0	поворотная стойка, прозрачная 0	5 (23) + 19 (17) 438	5 (27) + 19 (39) 876

И получившаяся матрица.

х	л	z	пр.
15	0	-54	-63
0	5	17	39
0	0	438	876

Обратите внимание, что все элементы в первой строке кратны 3 и все элементы в последней строке кратны 438.Разделим, чтобы сократить ряды.

х	л	z	пр.
5	0	-18	-21
0	5	17	39
0	0	1	2

Это имело дополнительное преимущество, давая нам 1, именно там, где мы хотим, чтобы это было вращаться.Итак, мы повернемся к 1 в R ₃ C ₃ и очистим -18 и 17. Обведите свою точку поворота и поместите остальные числа в рамку. этот столбец очистить.

х	л	z	пр.
5	0	-18	-21
0	5	17	39
0	0	* 1	2

Скопируйте сводную строку и очистите сводный столбец.Ранее очищенные столбцы останется очищенным до тех пор, пока вы не повернете строку или столбец дважды.

х	л	z	пр.
	0	0
0		0
0	0	* 1	2

Обратите внимание, что каждый раз приходится выполнять меньше вычислений.Вот расчеты для этой оси. Опять же, поскольку значение в сводном столбце в первая строка -18, и мы вычитаем, я записал это как + 18.

х	л	z	пр.
1 (5) +18 (0) 5	ранее погашено 0	поворотная стойка, прозрачная 0	1 (-21) + 18 (2) 15
ранее погашено 0	1 (5) – 17 (0) 5	поворотная стойка, прозрачная 0	1 (39) – 17 (2) 5
поворотный ряд, копия 0	поворотный ряд, копия 0	поворотный ряд, копия 1	поворотный ряд, копия 2

И получившаяся матрица.

х	л	z	пр.
5	0	0	15
0	5	0	5
0	0	1	2

Обратите внимание, что первая и вторая строки кратны 5, поэтому мы можем уменьшить их ряды.

х	л	z	пр.
1	0	0	3
0	1	0	1
0	0	1	2

И окончательный ответ: x = 3, y = 1 и z = 2.Вы также можете написать это как упорядоченный триплет {(3,1,2)}.

Надеюсь, вы заметили, что когда я работал над этим примером, я не следовал подсказкам Я дал. Это потому, что я хотел, чтобы вы увидели, что произойдет, если вы не повернетесь на один. В исходной матрице был один на главной диагонали, и Лучше было бы начать с этого.

Сводка

Выбирайте поворотный элемент с умом.
Выбор столбца с нулями означает меньший поворот.
Выбор единицы в качестве оси поворота уменьшает числа, упрощает умножение и оставляет ненулевые элементы в очищенном столбце такие же (без поворота)
Поворот по главной диагонали означает, что вам не придется переключать строки, чтобы поместить матрицу в уменьшенная строчно-эшелонированная форма.
Не поворачивайтесь на ноль.
Не поворачивайте вправо.
Используйте строку или столбец только один раз
Возьмите продукт с шарниром за вычетом продукта без шарнира

Особые случаи

Если вы получите строку из всех нулей, кроме правой, то система не имеет решения.

Если вы получили строку со всеми нулями, а количество ненулевых строк меньше, чем количество переменных, то система зависима, у вас будет много ответов, и вам нужно написать свой ответ в параметрической форме.

Содержание: Примечания по алгебре колледжа

Сайт Расс Фрит

Как решить линейные системы с помощью исключения Гаусса – Видео и стенограмма урока

Расширенная матрица

Помните, что матрица – это просто прямоугольный массив значений, помещенных в строки и столбцы.Сначала нам нужно превратить нашу линейную систему в матричную форму, превратив ее в расширенную матрицу. Расширенная матрица представляет собой комбинацию двух матриц. В нашем случае у нас есть матрица для коэффициентов левой части уравнения и еще одна матрица для правой части уравнения.

Напомним, что преобразование системы уравнений в матричную форму включает в себя выделение только коэффициентов вместе с их соответствующими знаками после их организации таким образом, что за членом x сначала следует член y , за которым следует член z , т.е. знак равенства, а затем константа.Мы можем использовать вертикальную линию или несколько точек на вертикальной линии, чтобы обозначить наш знак равенства. Наша линейная система уже организована должным образом, поэтому все, что нам нужно сделать, это выделить наши коэффициенты. В нашей первой строке будет 1, 1, 1, | а затем 5. Во второй строке 2, 0, -1, | и 4. В нашей третьей строке 0, 3, 1, | и 2. Наша матрица выглядит так:

Исключение Гаусса

Теперь мы можем использовать метод исключения Гаусса, чтобы помочь нам решить эту линейную систему.Исключение Гаусса – это манипулирование расширенной матрицей до тех пор, пока мы не получим матрицу, которая представляет левую часть уравнений в верхней треугольной форме . Это означает, что мы хотим, чтобы все нули находились ниже главной диагонали. Эта главная диагональ начинается в верхнем левом углу и заканчивается в правом нижнем углу матрицы коэффициентов. Другими словами, мы хотим манипулировать матрицей так, чтобы 2 во второй строке и 0 и 3 в третьей строке были равны 0.

Чтобы заменить эти числа на нули, мы будем использовать наши операции со строками матрицы.Чтобы превратить наши первые 2 в 0, мы умножаем нашу первую строку на -2, а затем добавляем ее ко второй строке, чтобы создать новую вторую строку. Получаем новую вторую строку 0, -2, -3, | и -6. Теперь, чтобы заменить 3 в третьей строке на 0, мы будем использовать эту новую вторую строку в сочетании с третьей строкой. Мы умножим вторую строку на 3 и прибавим ее к третьей строке, умноженной на 2. Мы получим новую третью строку из 0, 0, -7, | и -14.

Мы не переписывали первую строку, потому что нам не нужно менять это уравнение.Мы только умножили первую строку на 3, чтобы вычесть ее из второй строки. Помните, что в алгебре всякий раз, когда мы умножаем уравнение на любую константу, уравнение вообще не меняется; числа просто увеличиваются в несколько раз.

Теперь, когда у нас есть нули под главной диагональю, мы закончили с помощью исключения Гаусса. Теперь мы можем продолжить и решить нашу линейную систему.

Решение системы

Обратите внимание, как легко теперь решить эту проблему. Если мы выпишем наши линейные уравнения, мы получим x + y + z = 5, -2 y -3 z = -6 и -7 z = -14.Мы можем немедленно решить третье уравнение для z , чтобы получить z = -14 / -7 = 2. Затем мы можем заменить это значение на z во второе уравнение, чтобы найти следующую переменную, y . Получаем -2 y -3 (2) = -6. Получается -2 y -6 = -6. Чтобы найти y , мы прибавляем 6 к обеим сторонам и получаем -2 y = 0. Разделив обе стороны на -2, мы получаем y = 0. Итак, теперь у нас есть y = 0 и z = 2.Чтобы решить нашу последнюю переменную, x , мы можем использовать наше самое первое уравнение. Подставляя эти два значения, мы получаем x + 0 + 2 = 5. Решая это для x , мы получаем x = 3. Итак, наш окончательный ответ: x = 3, y = 0, и z = 2. Мы также можем записать это в точечной форме, например: (3, 0, 2).

Резюме урока

Давайте рассмотрим то, что мы узнали. Мы узнали, что линейных систем представляют собой наборы линейных уравнений.Линейная система имеет такое же количество уравнений, как и переменных, поскольку нам нужно по одному уравнению для каждой переменной, чтобы решить такую систему уравнений. Метод, о котором мы говорили в этом уроке, использует Исключение Гаусса , метод решения системы уравнений, который включает манипулирование матрицей так, чтобы все элементы ниже главной диагонали равнялись нулю. Верхний треугольник – это термин, используемый для описания матрицы, в которой все нули находятся под главной диагональю. Затем мы используем алгебру и подстановку, чтобы завершить решение нашей системы уравнений.

Результаты обучения

Завершение этого урока может подготовить вас к:

Чтению определений линейных систем, расширенной матрицы и верхней треугольной формы
Продемонстрировать использование метода исключения Гаусса для решения системы уравнений

Раздел 1.2 Исключение Гаусса – Матрицы

Определение: прямоугольная матрица находится в эшелоне формы (или эшелоне формы ), если она имеет следующие три свойства:

1.Все строки, полностью состоящие из нулей, находятся внизу.

2. Первой ненулевой записью в каждой ненулевой строке является 1

3. Каждая ведущая 1 находится справа от всех ведущих единиц в строках над ней.

Если матрица в форме эшелона удовлетворяет следующему дополнительному условию, то
она находится в форме сокращенного эшелона (или форме сокращенного эшелона строки):

4. Каждая ведущая единица является единственной ненулевой записью в своем столбце.

(B) Матрица эшелона (соответственно, матрица уменьшенного эшелона) – это матрица, которая имеет эшелонированную форму (соответственно, форму уменьшенного эшелона.)

Теорема (факт): Каждая матрица может быть приведена к (приведенной) эшелонированной форме с помощью последовательности элементарных операций со строками.

Теорема (факт): (Единственность приведенной формы эшелона)

Каждая матрица является строкой, эквивалентной одной и только одной матрице сокращенного эшелона.

Определение: Положение поворота в матрице [латекс] A [/ latex] – это место в [латексе] A [/ latex], которое соответствует ведущей 1 в форме уменьшенного эшелона [латекса] A [/ latex ]. Столбец поворота – это столбец [латекс] A [/ latex], который содержит положение поворота.

Определение: , ранг матрицы [латекс] A [/ latex] , , обозначенный ранг [латекс] A [/ latex], – это количество позиций поворота в любой эшелонированной матрице, полученной из [латекса] A [/ latex], выполняя элементарные операции со строками.

Определение: Предположим, что расширенная матрица линейной системы была
преобразована в эквивалентную сокращенную форму эшелона:

$$ \ left [\ begin {array} {cccc} 1 & 0 & -1 & 4 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 0 & 0 \ end {array} \ right] $$

Есть 3 переменные, потому что расширенная матрица имеет четыре столбца.Связанная система уравнений
– это

$$ \ begin {array} {ccc}
x_ {1} -x_ {3} & = & 4 \\
x_ {2} + 2x_ {3} & = & 3
\ end {array} $$

Переменные [latex] x_ {1} [/ latex] и [latex] x_ {2} [/ latex], соответствующие сводным столбцам в матрице, называются базовыми переменными . Другая переменная, [latex] x_ {3} [/ latex], называется свободной переменной . [латекс] x_ {3} [/ latex] бесплатно, [латекс] x_ {2} = 3-2x_ {3} [/ latex] и [латекс] x_ {1} = 4 + x_ {3} [/ latex] – это параметрическое описание наборов решений, в которых свободные переменные действуют как параметры.

Факт: Всякий раз, когда система непротиворечива, множество решений можно описать явно, решив сокращенную систему уравнений для основных переменных в терминах свободных переменных. Каждый разный выбор решения системы со свободной переменной, и каждое решение системы определяется выбором свободной переменной.

Определение: Решение линейной системы означает поиск параметрического описания набора решений или определение того, что набор решений пуст.

Факт: когда система согласована и имеет свободные переменные, набор решений имеет множество параметрических описаний. Когда система несовместима, набор решений пуст, даже если в системе есть свободные переменные. В этом случае набор решений не имеет параметрического представления.

Пример 1 : Решите линейную систему

$$ \ begin {array} {ccc}
x_ {1} + x_ {2} -x_ {3} & = & 2 \\
x_ {1} + 2x_ {2} -x_ {3} & = & 1 \\
2x_ {1} + 2x_ {2} -2x_ {3} & = & 2
\ end {array} $$

Упражнение 1 : Решите линейную систему

$$ \ begin {array} {ccc}
-x_ {1} + 2x_ {2} -x_ {3} & = & 1 \\
3x_ {1} -6x_ {2} + x_ {3} & = & -3 \\
2x_ {1} -4x_ {2} + 2x_ {3} & = & 1
\ end {array} $$

Теорема: теорема существования и единственности

Линейная система непротиворечива тогда и только тогда, когда крайний правый столбец расширенной матрицы не является сводным столбцом – i.е., если и только если эшелонированная форма расширенной матрицы не имеет строки вида [0. . . 0 b] с ненулевым b.

Исключение по Гауссу

Чтобы решить систему линейных уравнений, выполните следующие действия:

1 Перенести расширенную матрицу в матрицу сокращенного эшелона, используя
операций с элементарной строкой.

2 Если появляется строка вида [00 ··· 0 | 1], система несовместима.

3 В противном случае присвойте параметры, не являющиеся ведущими переменными (если они есть), и используйте уравнения, соответствующие сокращенной матрице строки-эшелон, чтобы найти ведущие переменные в терминах параметров.

Факт: Если линейная система непротиворечива, то множество решений содержит либо (i) единственное решение, когда нет свободных переменных, либо (ii) бесконечное множество решений, когда есть хотя бы одна свободная переменная.

Пример 2 : Решите линейную систему

$$ \ begin {array} {ccc}
x_ {1} -x_ {2} -x_ {3} & = & 2 \\
2x_ {1} -2x_ {2} -2x_ {3} & = & 4 \\
3x_ {1} -x_ {2} + x_ {3} & = & 1
\ end {array} $$

Упражнение 2 : Решите линейную систему

$$ \ begin {array} {ccc}
-2x_ {1} + 2x_ {2} -4x_ {3} & = & -4 \\
3x_ {1} -6x_ {2} + 3x_ {3} & = & -3 \\
x_ {1} -x_ {2} + 2x_ {3} & = & 2
\ end {array} $$

Пример 3 : Решите линейную систему

$$ \ begin {array} {ccc}
x_ {1} -x_ {2} -x_ {3} & = & 2 \\
2x_ {1} + x_ {2} -2x_ {3} & = & 4 \\
3x_ {1} -x_ {2} + x_ {3} & = & 1
\ end {array} $$

Упражнение 3 : Решите линейную систему

$$ \ begin {array} {ccc}
-2x_ {1} + x_ {2} -2x_ {3} & = & -4 \\
3x_ {1} -x_ {2} + x_ {3} & = & 1 \\
x_ {1} -x_ {2} + 2x_ {3} & = & 2
\ end {array} $$

GroupWork 1: Отметьте каждое утверждение как истинное или ложное.Обоснуйте каждый ответ.

а. Матрица может быть уменьшена до двух различных форм сокращенного эшелона с помощью различных операций со строками.

г. Мы можем применить алгоритм сокращения строк только к расширенной матрице линейной системы

г. Базовая переменная в линейной системе – это переменная, которая соответствует сводному столбцу
в матрице коэффициентов.

г. Нахождение параметрического описания множества решений линейной системы аналогично ее решению.

e. Если одна строка в эшелонированной форме расширенной матрицы равна [0 0 0 3 0], то
соответствующая линейная система несовместима.

GroupWork2: Предположим, что матрица коэффициентов [latex] 4 \ times 5 [/ latex] системы линейных уравнений имеет точку поворота в каждой строке. Последовательна ли система? Почему?

GroupWork3: Рассмотрим систему линейных уравнений с расширенной матрицей [латекс] A [/ латекс] и матрицей коэффициентов [латекс] C [/ латекс].В каждом случае либо докажите утверждение, либо приведите пример, показывающий, что оно ложно.

а. Если существует более одного решения, [latex] A [/ latex] содержит строку нулей.

г. Если решения нет, в строковой форме [latex] C [/ latex] есть ряд нулей.

г. Если в строковой форме [latex] C [/ latex] есть ряд нулей, решения нет.

г. Если система согласована для некоторого выбора констант, она непротиворечива для каждого выбора констант.

Теперь предположим, что расширенная матрица [latex] A [/ latex] имеет 3 строки и 5 столбцов.

e. Если система согласована, существует более одного решения.

ф. Ранг [латекса] A [/ latex] не выше 3.

г. Если rank [latex] A = 3 [/ latex], система согласована.

ч. Если ранг [латекс] C = 3 [/ latex], система согласована.

GroupWork4: Предположим, что матрица [latex] 4 \ times 6 [/ latex] дополнена системой линейных уравнений, 6-й столбец которой не является сводным столбцом.Последовательна ли система? Почему?

GroupWork5: сбалансировать указанную ниже химическую реакцию с участием олова (Sn),
водорода (H) и кислорода (O)

$$ xSnO_ {2} + yH_ {2} \ rightarrow zSn + wH_ {2} O $$

Алгоритм исключения Гаусса

Подраздел 2.5.1. Некоторые матрицы, связанная с ними система уравнений легко решается.

Элементарные операции со строками позволяют нам изменять матрицы и связанную с ними систему линейных уравнений без изменения решений этих уравнений.Цель состоит в том, чтобы получить матрицы, которые сделают эти общие решения очевидными. Вот несколько примеров.

Расширенная матрица
\ begin {уравнение *} \ left [\ begin {array} {cccc | c} 1 \ amp 0 \ amp 0 \ amp 0 \ amp 1 \\ 0 \ amp 1 \ amp 0 \ amp 0 \ amp 2 \\ 0 \ amp 0 \ amp 1 \ amp 0 \ amp 5 \\ 0 \ amp 0 \ amp 0 \ amp 1 \ amp -1 \ end {array} \ right] \ end {уравнение *}
соответствует системе линейных уравнений
\ begin {уравнение *} \ begin {array} {cccccc} x_1 \ amp \ amp \ amp \ amp = \ amp 1 \\ \ amp x_2 \ amp \ amp \ amp = \ amp 2 \\ \ amp \ amp x_3 \ amp \ amp = \ amp 5 \\ \ amp \ amp \ amp x_4 \ amp = \ amp -1 \ end {массив} \ end {уравнение *}
Сами уравнения фактически описывают единственное решение! Обратите внимание на структуру матрицы коэффициентов, которая делает это возможным.В каждой строке есть только одна ненулевая запись, ее значение равно 1, и при переходе от одной строки к другой ненулевой элемент перемещается на один столбец вправо.
Расширенная матрица
\ begin {уравнение *} \ left [\ begin {array} {cc | c} 1 \ amp 1 \ amp 4 \\ 0 \ amp 2 \ amp 6 \ end {array} \ right] \ end {уравнение *}
соответствует системе линейных уравнений
\ begin {уравнение *} \ begin {array} {rcc} x_1 + x_2 \ amp = \ amp 4 \\ 2x_2 \ amp = \ amp 6 \ end {массив} \ end {уравнение *}
Последнюю строку решить несложно: получаем \ (x_2 = 3 \ text {.} \) Используя это значение, также легко решить \ (x_1 + x_2 = x_1 + 3 = 4 \ text {,} \) или \ (x_1 = 1 \ text {.} \)
Расширенная матрица
\ begin {уравнение *} \ left [\ begin {array} {ccc | c} 1 \ amp 1 \ amp 1 \ amp 4 \\ 0 \ amp 0 \ amp 2 \ amp 6 \ end {array} \ right] \ end {уравнение *}
соответствует системе линейных уравнений
\ begin {уравнение *} \ begin {array} {rcc} x_1 + x_2 + x_3 \ amp = \ amp 4 \\ 2x_3 \ amp = \ amp 6 \ end {массив} \ end {уравнение *}
Как и раньше, получаем \ (x_3 = 3 \ text {.} \) У нас все еще есть две неопределенные переменные: мы назначаем параметр второй: \ (x_2 = t \ text {.} \) Используя это значение, мы имеем \ (x_1 + x_2 + x_3 = x_1 + t + 3 = 4 \ text {,} \) или \ (x_1 = 1-t \ text {.} \) Теперь мы знаем решения: \ (x_1 = 1-t \ text {,} \) \ (x_2 = t \ текст {,} \) \ (x_3 = 3 \) где \ (t \) может быть любым действительным числом. Фактически мы можем проверить этот результат с помощью первого уравнения: \ (x_1 + x_2 + x_3 = (1-t) + t + 3 = 4 \ text {.} \) Компактный способ записать это решение – \ ((x_1 , x_2, x_3) = (1-t, t, 3) \ text {.} \)

Из приведенных примеров ясно, что наличие большого количества нулей в матрице коэффициентов полезно для вычисления решений.Также ясно, что если первая ненулевая запись в строке – это единица, то вычисления проще. Наш план состоит в том, чтобы использовать элементарные операции со строками, чтобы преобразовать заданную матрицу коэффициентов в матрицу с этими свойствами, а затем описать все решения. Вот несколько наблюдений, которые нам помогут:

Если столбец имеет ненулевую запись, мы всегда можем сделать верхнюю запись ненулевой, поменяв местами строки, при необходимости используя \ (R_1 \ leftrightarrow R_i \) для некоторого \ (i> 1 \ text {.} \)
Если первая ненулевая запись строки \ (R_i \) – это \ (\ lambda \ text {,} \), мы можем превратить ее в 1, используя \ (R_i \ leftarrow \ tfrac 1 \ lambda R_i \ text { .} \)
Если две строки \ (R_i \) и \ (R_j \) имеют ненулевые записи в некотором столбце \ (k \ text {,} \), мы можем превратить запись \ (j, k \) в ноль, используя \ ( R_j \ leftarrow R_j – \ frac {a_ {j, k}} {a_ {i, k}} R_i \ text {.} \)

Подраздел 2.5.2 Форма эшелона строк

Теперь мы хотим определить общий класс матриц, соответствующая система линейных уравнений которых имеет решения, которые легко найти. Эти матрицы имеют особый образец нулей и единиц и, как говорят, находятся в форме эшелона строк.

Рисунок 2.5.1. Матрица в виде эшелона строк

Матрица выше дает представление о том, что мы хотим. Обратите внимание на то, что на линии лестницы, проведенной через матрицу, все записи под ней равны нулю. Записи, отмеченные знаком \ (* \), могут принимать любое значение.

Первая ненулевая запись в строке (если она есть) называется ведущей записью . Если он равен \ (1 \ text {,} \), то он называется ведущим .

Определение 2.5.2. Форма ступенчатого эшелона.

Матрица находится в эшелоне строк , форма , если

Каждая ведущая запись является ведущей.
Каждая запись ниже первой – \ (0 \ text {.} \)
По мере движения вниз по матрице ведущие перемещаются вправо.
Все нулевые строки находятся внизу.

Контрольная точка 2.5.3.

Какая из следующих матриц находится в форме эшелона строк?

\ (\ displaystyle \ begin {bmatrix} 1 \ amp2 \ amp3 \ amp4 \\ 0 \ amp5 \ amp6 \ amp7 \\ 0 \ amp0 \ amp8 \ amp9 \\ 0 \ amp0 \ amp0 \ amp10 \ end {bmatrix} \)
\ (\ displaystyle \ begin {bmatrix} 1 \ amp2 \ amp3 \ amp4 \\ 0 \ amp1 \ amp2 \ amp3 \\ 0 \ amp0 \ amp0 \ amp0 \\ 0 \ amp0 \ amp0 \ amp1 \ end {bmatrix} \)
\ (\ Displaystyle \ begin {bmatrix} 1 \ amp2 \ amp3 \ amp4 \\ 0 \ amp1 \ amp2 \ amp3 \\ 0 \ amp0 \ amp0 \ amp1 \\ 0 \ amp0 \ amp0 \ amp0 \ end {bmatrix} \)
\ (\ displaystyle \ begin {bmatrix} 1 \ amp2 \ amp3 \ amp4 \\ 0 \ amp1 \ amp6 \ amp7 \\ 0 \ amp0 \ amp1 \ amp1 \\ 0 \ amp0 \ amp1 \ amp1 \ end {bmatrix} \)
\ (\ displaystyle \ begin {bmatrix} 1 \ amp0 \ amp0 \ amp0 \\ 0 \ amp0 \ amp0 \ amp0 \\ 0 \ amp0 \ amp0 \ amp0 \\ 0 \ amp0 \ amp0 \ amp0 \ end {bmatrix} \)

Решение

Не в форме эшелона строк, потому что не каждая ведущая запись является \ (1 \ text {.} \)
Не в форме эшелона строк, потому что нулевая строка не находится внизу.
Форма рядного эшелона.
Форма Not row echelon, потому что у ведущей записи есть ненулевая запись под ней.
Форма рядного эшелона.

Подраздел 2.5.3 Алгоритм исключения Гаусса

План теперь начинается с расширенной матрицы и, используя последовательность операций с элементарными строками, изменяет ее на новую матрицу, в которой легко идентифицировать решения связанной системы линейных уравнений.Поскольку любая операция с элементарной строкой оставляет решения неизменными, решения окончательной системы линейных уравнений будут идентичны решениям исходной.

Работаем со столбцами матрицы слева направо и меняем матрицу следующим образом:

Начните с первого столбца. Если все записи равны нулю, перейдите к следующему столбцу справа.
Если столбец имеет ненулевые записи, при необходимости поменяйте строки местами, чтобы получить ненулевую запись наверху.
При необходимости измените верхнюю запись, сделав ее \ (1 \ text {.} \)
Для любой ненулевой записи ниже верхней используйте элементарную операцию со строкой, чтобы изменить ее на ноль.
Теперь рассмотрим часть матрицы ниже верхней строки и справа от рассматриваемого столбца: если таких строк или столбцов нет, остановитесь, поскольку процедура завершена. В противном случае выполните ту же процедуру с новой матрицей. .

Вот первый пример:

\ begin {уравнение *} \ begin {array} {r} 3x_1-2x_2-x_3 + x_4 = 1 \\ 6x_1-8x_2 + x_3 + 2x_4 = 4 \ end {массив} \ end {уравнение *}

имеет расширенную матрицу

\ begin {уравнение *} \ begin {bmatrix} 3 \ amp -2 \ amp -1 \ amp 1 \ amp 1 \\ 6 \ amp -8 \ amp 1 \ amp 2 \ amp 4 \ end {bmatrix}.\ end {уравнение *}

Нам не нужно обмениваться строками, чтобы сделать верхнюю запись первого столбца ненулевой, поэтому мы приступаем к созданию верхней записи \ (1 \), используя операцию элементарной строки \ (R_1 \ gets \ frac13R_1 \ text {.} \) Матрица принимает вид

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp – \ frac23 \ amp – \ frac13 \ amp \ frac13 \ amp \ frac13 \\ 6 \ amp -8 \ amp 1 \ amp 2 \ amp 4 \ end {bmatrix}. \ end {уравнение *}

Теперь мы должны сделать все записи ниже верхнего в столбце равными нулю.Конечно, есть только одна такая запись, и поэтому, используя \ (R_2 \ leftarrow R_2-6R_1 \ text {,} \), мы получаем

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp – \ frac23 \ amp – \ frac13 \ amp \ frac13 \ amp \ frac13 \\ 0 \ amp -4 \ amp 3 \ amp 0 \ amp 2 \ end {bmatrix} \ text {.} \ end {уравнение *}

Теперь мы закончили с первым столбцом, поэтому продолжаем ту же процедуру с матрицей, полученной удалением первой строки и первого столбца:

\ begin {уравнение *} \ begin {bmatrix} -4 \ amp 3 \ amp 0 \ amp 2 \ end {bmatrix}.\ end {уравнение *}

Поскольку есть только одна строка, нам нужно только изменить верхнюю запись на \ (1 \), используя деление на \ (- 4 \ text {,} \), то есть \ (R_1 \ gets – \ frac14R_1 \ text {. } \) Тогда получаем

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp – \ frac34 \ amp 0 \ amp – \ frac12 \ end {bmatrix}. \ end {уравнение *}

и, вставив обратно в исходную матрицу, получаем

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp – \ frac23 \ amp – \ frac13 \ amp \ frac13 \ amp \ frac13 \\ 0 \ amp 1 \ amp – \ frac34 \ amp 0 \ amp – \ frac12 \ end {bmatrix} \ end {уравнение *}

Матрица в виде эшелона строк.Теперь мы можем определить все решения исходной системы линейных уравнений. Первая ненулевая запись в первой строке находится в первом столбце, столбце, связанном с \ (x_1 \ text {.} \). Первая ненулевая запись во второй строке, аналогично, связана с \ (x_2 \ text {.} \) Мы назначаем параметры другим переменным: \ (x_3 = s \) и \ (x_4 = t \ text {.} \) Затем вторая строка сообщает нам, что \ (x_2- \ frac34s = – \ frac12 \ text { ,} \) или \ (x_2 = \ frac34s- \ frac12 \ text {.} \) Теперь, когда мы знаем \ (x_2 \ text {,} \), мы можем использовать первую строку, чтобы найти \ (x_1 \ text {: } \) получаем \ (x_1- \ frac23x_2- \ frac13s + \ frac13t = \ frac13 \ text {.} \) Мы подставляем известное значение для \ (x_2 \) в это уравнение, и после некоторого упрощения получаем \ (x_1 = \ tfrac56s- \ tfrac13t \ text {.} \) В итоге мы имеем: Все решения к

\ begin {уравнение *} \ begin {array} {r} 3x_1-2x_2-x_3 + x_4 = 1 \\ 6x_1-8x_2 + x_3 + 2x_4 = 4 \ end {массив} \ end {уравнение *}

имеют вид

\ begin {уравнение *} \ begin {array} {rcl} x_1 \ amp = \ amp \ tfrac56s- \ tfrac13t \\ x_2 \ amp = \ amp – \ tfrac12 + \ tfrac34 s \\ x_3 \ amp = \ amp s \\ x_4 \ amp = \ amp т \ end {массив} \ end {уравнение *}

где \ (s \) и \ (t \) – любые действительные числа.Более компактно запишем это как \ ((x_1, x_2, x_3, x_4) = \ tfrac56s- \ tfrac13t, – \ tfrac12 + \ tfrac34 s, s, t) \ text {.} \) Другими словами, для любого присваивая вещественные числа \ (s \) и \ (t \ text {,} \), мы получаем решение системы линейных уравнений.

Легко (и полезно) проверить, что замена \ (x_1, \ dots, x_4 \) в два уравнения действительно дает решение.

Теперь рассмотрим другой пример с уравнениями

\ begin {alignat *} {3} x_1 \ amp {} + 2x_2 \ amp {} – 2x_3 \ amp {} = \ amp {} – 1 \\ 3x_1 \ amp {} – 2x_2 \ amp {} – 4x_3 \ amp {} = \ amp {} 3 \\ 4x_1 \ amp \ amp {} – 2x_3 \ amp {} = \ amp {} – 2 \\ -x_1 \ amp {} -x_2 \ amp {} + 2x_3 \ amp {} = \ amp {} 0 \ end {alignat *}

и соответствующая ему расширенная матрица, измененная методом исключения Гаусса:

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 2 \ amp -2 \ amp -1 \\ 3 \ amp -2 \ amp -4 \ amp 3 \\ 4 \ amp 0 \ amp -2 \ amp -2 \\ -1 \ amp -1 \ amp 2 \ amp 0 \ end {bmatrix} \ begin {array} {c} \\ R_2 \ leftarrow R_2-3R_1 \\ R_3 \ получает R_3-4R_1 \\ R_4 \ получает R_4 + R_1 \ end {массив} \ end {уравнение *}

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 2 \ amp -2 \ amp -1 \\ 0 \ amp -8 \ amp 2 \ amp 6 \\ 0 \ amp -8 \ amp 6 \ amp 2 \\ 0 \ amp 1 \ amp 0 \ amp -1 \ end {bmatrix} \ begin {array} {c} R_2 \ получает- \ frac18 R_2 \\ R_3 \ получает R_3 + 8R_2 \\ R_4 \ получает R_4-R_2 \ end {массив} \ end {уравнение *}

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 2 \ amp -2 \ amp -1 \\ 0 \ amp 1 \ amp – \ frac14 \ amp – \ frac34 \\ 0 \ amp 0 \ amp 4 \ amp -4 \\ 0 \ amp 0 \ amp \ tfrac14 \ amp – \ tfrac14 \ end {bmatrix} \ begin {array} {c} R_3 \ получает \ frac14 R_3 \\ R_4 \ получает R_4- \ frac14 R_3 \ end {массив} \ end {уравнение *}

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 2 \ amp -2 \ amp -1 \\ 0 \ amp 1 \ amp – \ frac14 \ amp – \ frac34 \\ 0 \ amp 0 \ amp 1 \ amp -1 \\ 0 \ amp 0 \ amp 0 \ amp 0 \ end {bmatrix} \ end {уравнение *}

Последняя строка при любом выборе \ (x_1, x_2, x_3 \ text {,} \) сводится к \ (0 = 0, \), поэтому любое решение связанных первых трех уравнений также будет решением последнего один.Другими словами, последняя строка матрицы не влияет на набор решений и может быть удалена из матрицы. Третья строка дает \ (x_3 = -1. \) Вторая строка дает \ (x_2 = -1 \), а первая строка дает \ (x_1 = -1. \) Следовательно, есть одно решение: \ ((x_1, x_2, x_3) = (- 1, -1, -1). \)

Теперь очень немного изменим уравнения из последнего примера (правая часть последнего уравнения изменена с \ (0 \) на \ (1 \)):

Гауссово исключение почти идентично

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 2 \ amp -2 \ amp -1 \\ 3 \ amp -2 \ amp -4 \ amp 3 \\ 4 \ amp 0 \ amp -2 \ amp -2 \\ -1 \ amp -1 \ amp 2 \ amp 1 \ end {bmatrix} \ end {уравнение *}

уменьшено до

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 2 \ amp -2 \ amp -1 \\ 0 \ amp 1 \ amp – \ frac14 \ amp – \ frac34 \\ 0 \ amp 0 \ amp 1 \ amp -1 \\ 0 \ amp 0 \ amp 0 \ amp 1 \ end {bmatrix} \ end {уравнение *}

Теперь в последней строке написано \ (0x_1 + 0x_2 + 0x_3 = 1 \ text {,} \), что при любом выборе \ (x_1 \ text {,} \) \ (x_2 \) и \ (x_3 \ text { ,} \) сводится к \ (0 = 1 \) и никогда не является истинным.Это означает, что исходная система уравнений не имеет решений, то есть система несовместна.

Здесь мы можем сделать полезное наблюдение: если строка расширенной матрицы имеет вид

\ begin {уравнение *} \ begin {bmatrix} 0 \ amp 0 \ amp 0 \ amp \ cdots \ amp 0 \ amp * \ end {bmatrix} \ end {уравнение *}

, где \ (* \) либо ноль, либо ненулевое значение, тогда происходит одно из двух:

\ (* = 0 \), в этом случае строка может быть удалена из матрицы
\ (* \ not = 0 \) в этом случае решения нет.

Пример 2.5.4.

Рассмотрим систему линейных уравнений:

\ begin {уравнение *} \ begin {array} {rcl} х + у + г \ amp = \ amp 1 \\ 2x + y + z \ amp = \ amp 2 \\ 3x + ay + bz \ amp = \ amp c \ end {массив} \ end {уравнение *}

Мы хотим знать значения \ (a, \) \ (b \) и \ (c \), для которых нет решений, одно решение или более одного решения. Чтобы решить эту проблему, мы применяем метод исключения Гаусса к расширенной матрице:

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 1 \ amp 1 \ amp 1 \\ 2 \ amp 1 \ amp 1 \ amp 2 \\ 3 \ amp a \ amp b \ amp c \ end {bmatrix} \ begin {matrix} R_2 \ получает R_2-2R_1 \\ R_3 \ получает R_3-3 R_1 \ end {matrix} \ end {уравнение *}

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 1 \ amp 1 \ amp 1 \\ 0 \ amp -1 \ amp -1 \ amp 0 \\ 0 \ amp a-3 \ amp b-3 \ amp c-3 \ end { bmatrix} \ begin {matrix} R_2 \ gets -R_2 \\ R_3 \ gets R_3- (a-3) R_2 \ end {matrix} \ end {уравнение *}

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 1 \ amp 1 \ amp 1 \\ 0 \ amp 1 \ amp 1 \ amp 0 \\ 0 \ amp 0 \ amp b-a \ amp c-3 \ end {bmatrix} \ end {уравнение *}

Анализ последней строки говорит нам все: если \ (b-a \ not = 0, \), то есть ровно одно решение.Если \ (b-a = 0, \) и \ (c-3 \ not = 0, \), то решений нет. В противном случае (когда \ (b = a \) и \ (c = 3 \)) существует бесконечное количество решений.

Упражнения Упражнения

1.

Найдите все решения системы уравнений

\ begin {align *} х + 2у-z \ amp = 2 \\ х + у-z \ amp = 0 \\ 2x-y + z \ amp = 3 \ end {выровнять *}

Решение

Добавляем расширенную матрицу в форму эшелона строк:

\ begin {уравнение *} \ begin {bmatrix} 1 \ amp 2 \ amp -1 \ amp 2 \\ 1 \ amp 1 \ amp -1 \ amp 0 \\ 2 \ amp -1 \ amp 1 \ amp 3 \\ \ end {bmatrix} \\ \ begin {array} {l} R_2 \ получает R_2 – R_1 \\ R_3 \ получает R_3-2R_1 \ end {массив} \\ \ begin {bmatrix} 1 \ amp 2 \ amp -1 \ amp 2 \\ 0 \ amp -1 \ amp 0 \ amp -2 \\ 0 \ amp -5 \ amp 3 \ amp -1 \\ \ end {bmatrix} \\ \ begin {array} {l} R_2 \ получает -R_2 \\ \ end {массив} \\ \ begin {bmatrix} 1 \ amp 2 \ amp -1 \ amp 2 \\ 0 \ amp 1 \ amp 0 \ amp 2 \\ 0 \ amp -5 \ amp 3 \ amp -1 \\ \ end {bmatrix} \\ R_3 \ получает R_3 + 5R_2 \\ \ begin {bmatrix} 1 \ amp 2 \ amp -1 \ amp 2 \\ 0 \ amp 1 \ amp 0 \ amp 2 \\ 0 \ amp 0 \ amp 3 \ amp 9 \\ \ end {bmatrix} \\ R_3 \ получает \ frac13 R_3 \\ \ begin {bmatrix} 1 \ amp 2 \ amp -1 \ amp 2 \\ 0 \ amp 1 \ amp 0 \ amp 2 \\ 0 \ amp 0 \ amp 1 \ amp 3 \\ \ end {bmatrix} \ end {уравнение *}

Последняя строка дает \ (z = 3 \ text {.} \) Вторая строка дает \ (y = 2 \ text {.} \) Первая строка дает \ (x = 2-2y + z = 2-4 + 3 = 1 \ text {,} \) и поэтому там – единственное решение \ ((x, y, z) = (1,2,3) \ text {.} \)

Решающие системы с исключением Гаусса · Алгебра и тригонометрия

Решение систем с исключением Гаусса · Алгебра и тригонометрия

В этом разделе вы будете:

Напишите расширенную матрицу системы уравнений.
Напишите систему уравнений из расширенной матрицы.
Выполняет операции со строками в матрице.
Решите систему линейных уравнений с помощью матриц.

Карл Фридрих Гаусс жил в конце 18-го и начале 19-го веков, но до сих пор считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика.Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.

Мы впервые столкнулись с исключением Гаусса в Системах линейных уравнений: две переменные. В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.

Написание расширенной матрицы системы уравнений

Матрица может служить устройством для представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы.Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей .

Например, рассмотрим следующие 2 × 2

система уравнений.

3x + 4y = 74x − 2y = 5

Мы можем записать эту систему в виде расширенной матрицы:

[344−2 \ | 75]

Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов .

[344−2]

Трехкратная система уравнений , например

3x − y − z = 0 x + y = 5 2x − 3z = 2

имеет матрицу коэффициентов

[3−1−111020−3]

и представлена расширенной матрицей

[3−1−111020−3 \ | 052]

Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: x -термов идет в первый столбец, – -термов – во втором столбце и z -термов – в третьем столбце.Очень важно, чтобы каждое уравнение было записано в стандартной форме ax + by + cz = d

, чтобы переменные совпали. Если в уравнении отсутствует переменный член, коэффициент равен 0.

Для данной системы уравнений напишите расширенную матрицу.

Запишите коэффициенты членов x как числа в первом столбце.
Запишите коэффициенты членов и в виде чисел во втором столбце.
Если имеется z -термов, запишите коэффициенты в виде чисел в третьем столбце.
Нарисуйте вертикальную линию и напишите константы справа от нее.

Написание расширенной матрицы для системы уравнений

Напишите расширенную матрицу для данной системы уравнений.

x + 2y − z = 3 2x − y + 2z = 6 x − 3y + 3z = 4

Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.

[12−12−121−33 \ | 364]

Напишите расширенную матрицу данной системы уравнений.

4x − 3y = 113x + 2y = 4

[4−33 2 \ | 11 4]

Написание системы уравнений из расширенной матрицы

Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными. Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным.Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.

Написание системы уравнений из расширенной матричной формы

Найдите систему уравнений из расширенной матрицы.

[1−3−52−5−4−354 \ | -256]

Когда столбцы представляют переменные x,

и z,

[1−3−52−5−4−354 \ | −256] → x − 3y − 5z = −2 2x − 5y − 4z = 5−3x + 5y + 4z = 6

Напишите систему уравнений из расширенной матрицы.

[1−1 12−1 30 1 1 \ | 5 1-9]

x – y + z = 52x – y + 3z = 1 y + z = −9

Выполнение операций со строками в матрице

Теперь, когда мы можем записывать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками , которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.

Выполнение операций со строками в матрице – это метод, который мы используем для решения системы уравнений.Чтобы решить систему уравнений, мы хотим преобразовать матрицу в строковую форму , в которой есть единицы по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции. ниже главной диагонали, как показано.

Рядно-эшелонированная форма [1ab01d001]

Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, которая эквивалентна строкам в более простой форме. Вот рекомендации по получению формы рядного эшелона.

В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
Любые нулевые строки помещаются внизу матрицы.
Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.

Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в строковую форму и выполнить обратную подстановку, чтобы найти решение.

Поменять местами ряды. (Обозначение: Ri ↔ Rj
)
Умножьте строку на константу. (Обозначение: cRi
)
Добавить произведение одной строки на константу к другой строке. (Обозначение: Ri + cRj)

Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными. С помощью этих операций есть несколько ключевых ходов, которые быстро достигнут цели написания матрицы в виде эшелона строк.Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, так что строку 1 можно использовать для преобразования оставшихся строк.

Исключение по Гауссу

Метод исключения Гаусса относится к стратегии, используемой для получения матрицы в виде строки-эшелона. Цель – написать матрицу A

с цифрой 1 в начале главной диагонали и всеми нулями внизу.

A = [a11a12a13a21a22a23a31a32a33] → После исключения Гаусса A = [1 b12 b130 1 b230 0 1]

Первый шаг стратегии Гаусса включает получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.

Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».

Первое уравнение должно иметь старший коэффициент 1. Поменяйте местами строки или умножьте на константу, если необходимо.
Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
Используйте операции со строками, чтобы получить 1 в строке 2, столбец 2.
Используйте операции со строками, чтобы получить нули в нижнем столбце 2, под записью 1.
Используйте операции со строками, чтобы получить 1 в строке 3, столбец 3.
Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу не останутся только нули.
Если какие-либо строки содержат все нули, поместите их внизу.

Решение 2 × 2 Система методом исключения Гаусса

Решите данную систему методом исключения Гаусса.

2x + 3y = 6 x − y = 12

Во-первых, мы запишем это как расширенную матрицу.

[231−1 \ | 612]

Нам нужна 1 в строке 1, столбце 1. Этого можно добиться, поменяв местами строку 1 и строку 2.

R1↔R2 → [1−123 \ | 126]

Теперь у нас есть 1 как первая запись в строке 1, столбце 1.Теперь давайте получим 0 в строке 2, столбце 1. Этого можно добиться, умножив строку 1 на −2,

, а затем добавляем результат в строку 2.

−2R1 + R2 = R2 → [1−105 \ | 125]

У нас есть только один шаг, чтобы умножить строку 2 на 15.

15R2 = R2 → [1−101 \ | 121]

Использовать обратную замену. Вторая строка матрицы представляет y = 1.

Обратная замена y = 1

в первое уравнение.

х- (1) = 12 х = 32

Решением является точка (32,1).

Решите данную систему методом исключения Гаусса.

4x + 3y = 11 x − 3y = −1

(2, 1)

Использование исключения Гаусса для решения системы уравнений

Используйте исключения Гаусса , чтобы решить заданное 2 × 2

Система уравнений .

2x + y = 14x + 2y = 6

Запишите систему как расширенную матрицу .

[2142 \ | 16]

Получите 1 в строке 1, столбце 1.Этого можно добиться, умножив первую строку на 12.

12R1 = R1 → [11242 \ | 126]

Затем нам нужен 0 в строке 2, столбце 1. Умножим строку 1 на −4

и добавьте строку 1 к строке 2.

−4R1 + R2 = R2 → [11200 \ | 124]

Вторая строка представляет уравнение 0 = 4.

Следовательно, система непоследовательна и не имеет решения.

Решение зависимой системы

Решите систему уравнений.

3x + 4y = 126x + 8y = 24

Выполните строковых операций на расширенной матрице, чтобы попытаться получить строковую форму .

A = [3468 \ | 1224]

−12R2 + R1 = R1 → [0068 \ | 024] R1↔R2 → [6800 \ | 24 0]

Матрица заканчивается всеми нулями в последней строке: 0y = 0.

Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите относительно y.

3x + 4y = 12 4y = 12−3x y = 3−34x

Итак, решение этой системы – (x, 3−34x).

Выполнение операций со строками в расширенной матрице 3 × 3 для получения формы эшелона строк

Выполнить операции со строками для данной матрицы, чтобы получить форму строки-эшелона.

[1−342−56−334 \ | 366]

В первой строке уже есть 1 в строке 1, столбце 1. Следующим шагом будет умножение строки 1 на −2

и добавьте его во 2 ряд.Затем замените строку 2 результатом.

−2R1 + R2 = R2 → [1−3401−2−334 \ | 306]

Затем получить ноль в строке 3, столбце 1.

3R1 + R3 = R3 → [1−3401−20−616 \ | 3015]

Затем получить ноль в строке 3, столбце 2.

6R2 + R3 = R3 → [1−3401−2004 \ | 3015]

Последний шаг – получить 1 в строке 3, столбец 3.

14R3 = R3 → [1−3401−2001 \ | 3−6154]

Запишите систему уравнений в виде строк.

x − 2y + 3z = 9 −x + 3y = −42x − 5y + 5z = 17

[1−52 52 0 15 0 0 1 \ | 17292]

Решение системы линейных уравнений с использованием матриц

Мы видели, как написать систему уравнений с расширенной матрицей , а затем как использовать строковые операции и обратную подстановку для получения строковой формы . Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3.Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.

Решение системы линейных уравнений с помощью матриц

Решите систему линейных уравнений, используя матрицы.

x – y + z = 82x + 3y – z = −23x – 2y −9z = 9

Сначала мы пишем расширенную матрицу.

[1−1123−13−2−9 \ | 8−29]

Затем мы выполняем операции со строками, чтобы получить форму «строка-эшелон».

−2R1 + R2 = R2 → [1−1105−33−2−9 \ | 8−189] −3R1 + R3 = R3 → [1−1105−301−12 \ | 8−18−15]

Самый простой способ получить 1 в строке 2 столбца 1 – это поменять местами R2

и R3.

Развязки R2 и R3 → [1−11801−12−1505−3−18]

Затем

−5R2 + R3 = R3 → [1−1101−120057 \ | 8−1557] −157R3 = R3 → [1−1101−12001 \ | 8−151]

Последняя матрица представляет собой эквивалентную систему.

x − y + z = 8 y − 12z = −15 z = 1

Используя обратную подстановку, мы получаем решение как (4, −3,1).

Решение зависимой системы линейных уравнений с помощью матриц

Решите следующую систему линейных уравнений, используя матрицы.

−x − 2y + z = −1 2x + 3y = 2 y − 2z = 0

Напишите расширенную матрицу.

[−1−2123001−2 \ | -120]

Сначала умножьте строку 1 на −1

, чтобы получить 1 в строке 1, столбце 1. Затем выполните операций со строками , чтобы получить форму «строка-эшелон».

−R1 → [12−123001−2 \ | 120]

R2↔R3 → [12−101−2230 \ | 102]

−2R1 + R3 = R3 → [12−101−20−12 \ | 100]

R2 + R3 = R3 → [12−101−2000 \ | 210]

Последняя матрица представляет следующую систему.

x + 2y − z = 1 y − 2z = 0 0 = 0

Мы видим по тождеству 0 = 0

, что это зависимая система с бесконечным количеством решений. Затем мы находим общее решение.Решая второе уравнение относительно y

и подставив его в первое уравнение, мы можем решить для z

в пересчете на х.

x + 2y − z = 1 y = 2zx + 2 (2z) −z = 1 x + 3z = 1 z = 1 − x3

Теперь подставим выражение для z

во второе уравнение, чтобы найти y

в пересчете на х.

y − 2z = 0 z = 1 − x3 y − 2 (1 − x3) = 0 y = 2−2×3

Общее решение – (x, 2−2×3,1 − x3).

Решите систему, используя матрицы.

х + 4y − z = 42x + 5y + 8z = 15x + 3y − 3z = 1

(1, 1, 1)

Можно ли решить любую систему линейных уравнений методом исключения Гаусса?

Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.

Для данной системы уравнений решите с помощью матриц с помощью калькулятора.

Сохранить расширенную матрицу как матричную переменную [A], [B], [C],….
Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.

Решение систем уравнений с матрицами с помощью калькулятора

Решите систему уравнений.

5x + 3y + 9z = −1−2x + 3y − z = −2 − x − 4y + 5z = 1

Напишите расширенную матрицу для системы уравнений.

[539−23−1−1−45 \ | −1−2−1]

На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную [A].

[A] = [539−1−23−1−2−1−451]

Используйте функцию ref ( в калькуляторе, вызывая матричную переменную [A].

исх. ([A])

Оценить.

[1 35 95150 1 1321−470 0 1−24187] → x + 35y + 95z = −15 y + 1321z = −47 z = −24187

При использовании обратной подстановки решение: (61187, −

, −24187).

Применение матриц 2 × 2 к финансам

Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10.5% годовых, а другой – 12% годовых. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?

У нас есть система двух уравнений с двумя переменными. Пусть x =

сумма, вложенная под 10,5% годовых, а y =

сумма вложена под 12% годовых.

x + y = 12,0000,105x + 0,12y = 1,335

В качестве матрицы имеем

[110.1050.12 \ | 12,0001,335]

Умножить строку 1 на −0,105

и добавьте результат в строку 2.

[1100.015 \ | 12,00075]

Затем,

0,015y = 75 y = 5,000

Итак, 12 000–5 000 = 7 000.

Таким образом, 5000 долларов были инвестированы под 12% годовых и 7000 долларов под 10,5%.

Применение матриц 3 × 3 к финансам

Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5%, другой – 8%, а третий – 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше суммы, инвестированной под 5%. Сколько было вложено по каждой ставке?

У нас есть система трех уравнений с тремя переменными. Пусть x

– сумма, вложенная под 5% годовых, пусть y

будет сумма, вложенная под 8% годовых, и пусть z

– сумма, вложенная под 9% годовых. Таким образом,

х + у + г = 10,0000.05x + 0,08y + 0,09z = 770 2x − z = 0

В качестве матрицы имеем

[1110.050.080.0920−1 \ | 10,0007700]

Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.

−0.05R1 + R2 = R2 → [11100.030.0420−1 \ | 10,0002700] −2R1 + R3 = R3 → [11100.030.040−2−3 \ | 10,000270−20,000] 10.03R2 = R2 → [01101430 −2−3 \ | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 \ | 10,0009,000-2,000]

Третья строка говорит нам -13z = -2,000;

, таким образом, z = 6000.

Вторая строка говорит нам, что y + 43z = 9000.

Подставляем z = 6000,

получаем

y + 43 (6000) = 9000y + 8000 = 9000y = 1000

Первая строка сообщает нам, что x + y + z = 10,000.

Подставляем y = 1,000

и z = 6000,

получаем

х + 1,000 + 6,000 = 10,000 х = 3,000

Ответ: 3000 долларов вложены под 5% годовых, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.

Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.

150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%

Ключевые концепции

Расширенная матрица – это матрица, которая содержит коэффициенты и константы системы уравнений.См. [Ссылка].
Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. [Ссылка].
Операции со строками включают в себя умножение строки на константу, добавление одной строки к другой и замену строк местами.
Мы можем использовать метод исключения Гаусса для решения системы уравнений. См. [Ссылка], [ссылка] и [ссылка].
Операции со строками выполняются над матрицами для получения формы «строка-эшелон». См. [Ссылка].
Чтобы решить систему уравнений, запишите ее в форме расширенной матрицы.Выполните операции со строками, чтобы получить форму эшелона строк. Обратно-заменитель, чтобы найти решения. См. [Ссылка] и [ссылка].
Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. [Ссылка].
Многие реальные проблемы можно решить с помощью расширенных матриц. См. [Ссылка] и [ссылка].

Упражнения по разделам

Устный

Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как написать эту расширенную матрицу.

Да. Для каждой строки коэффициенты переменных записываются поперек соответствующей строки и помещается вертикальная черта; затем константы помещаются справа от вертикальной полосы.

Можно ли любую матрицу записать в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.

Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые могут быть использованы для решения расширенной матрицы [931−2 \ | 06].

Нет, существует множество правильных методов использования строковых операций над матрицей. Возможны два способа: (1) Поменять местами строки 1 и 2. Тогда R2 = R2−9R1.

(2) R2 = R1−9R2.

Затем разделите строку 1 на 9.

Можно ли решить матрицу, на диагонали которой стоит 0? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?

Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.

Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.

Алгебраические

Для следующих упражнений напишите расширенную матрицу линейной системы.

16y = 49x − y = 2

[0169−1 \ | 42]

3x + 2y + 10z = 3−6x + 2y + 5z = 13 4x + z = 18

x + 5y + 8z = 19 12x + 3y = 43x + 4y + 9z = −7

[1581230349 \ | 164-7]

6x + 12y + 16z = 4 19x − 5y + 3z = −9 x + 2y = −8

Для следующих упражнений запишите линейную систему из расширенной матрицы.

[−256−18 \ | 526]

−2x + 5y = 56x − 18y = 26

[320−1−94857 \ | 3−18]

3x + 2y = 13 − x − 9y + 4z = 538x + 5y + 7z = 80

[8291−175003 \ | 433810]

[45−2015887−3 \ | 122-5]

4x + 5y − 2z = 12 y + 58z = 28x + 7y − 3z = −5

Для следующих упражнений решите систему методом исключения Гаусса.

[−124−5 \ | −36]

(-1, -2)

2x − 3y = −95x + 4y = 58

(6,7)

2x + 3y = 12 4x + y = 14

(3,2)

−4x − 3y = −2 3x − 5y = −13

−5x + 8y = 3 · 10x + 6y = 5

(15,12)

3x + 4y = 12−6x − 8y = −24

−60x + 45y = 12 20x − 15y = −4

(х, 415 (5х + 1))

−1.06x − 2,25y = 5,51−5,03x − 1,08y = 5,40

34x − 35y = 414x + 23y = 1

(19639, −513)

[100011001 \ | 314587]

(31, -42,87)

[101110011 \ | 5020−90]

[123056008 \ | 479]

(2140,120,98)

[−0.10.3−0.1−0.40.20.10.60.10.7 \ | 0,20,8−0,8]

−2x + 3y − 2z = 3 4x + 2y − z = 9 4x − 8y + 2z = −6

(1813,1513, −1513)

x + y − 4z = −4 5x − 3y − 2z = 0 2x + 6y + 7z = 30

2x + 3y + 2z = 1 −4x − 6y − 4z = −2 10x + 15y + 10z = 5

(х, у, 12 (1−2x − 3y))

x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 5

x + 2y − z = 1 − x − 2y + 2z = −2 3x + 6y − 3z = 3

(х, −x2, −1)

Х + у = 2 х + г = 1-у-г = -3

x + y + z = 100 x + 2z = 125 − y + 2z = 25

(125, −25,0)

14x − 23z = −1215x + 13y = 4715y − 13z = 29

−12x + 12y + 17z = −5314 12x − 12y + 14z = 3 14x + 15y + 13z = 2315

(8,1, −2)

−12x − 13y + 14z = −296 15x + 16y − 17z = 431210−18x + 19y + 110z = −4945

Расширения

Для следующих упражнений используйте метод исключения Гаусса для решения системы.

х-17 + у-28 + г-34 = 0 х + у + г = 6 х + 23 + 2у + г-33 = 5

(1,2,3)

x − 14 − y + 14 + 3z = −1 x + 52 + y + 74 − z = 4 x + y − z − 22 = 1

x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 8 x + y + z = 1

(х, 3128−3×4,128 (−7x − 3))

x − 310 + y + 32−2z = 3 x + 54 − y − 18 + z = 32x − 14 + y + 42 + 3z = 32

x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 7 x + y + z = 1

Реальные приложения

Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.

Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если вкус шоколада в 3 раза популярнее, чем аромат ванили, сколько кексов продается в день?

В конкурирующем магазине кексов ежедневно продаются кексы на сумму 4520 долларов. Шоколадные кексы стоят 2,25 доллара, а кексы из красного бархата – 1,75 доллара. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?

860 красный бархат, 1340 шоколадный

Вы вложили 10 000 долларов в два счета: один с простой процентной ставкой 3%, а другой – с двумя.5% годовых. Если ваша общая выплата процентов по истечении одного года составила 283,50 доллара, какая сумма была на каждом счете по истечении года?

Вы инвестировали 2300 долларов на счет 1 и 2700 долларов на счет 2. Если общая сумма процентов по истечении одного года составляет 254 доллара, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.

4% на счет 1, 6% на счет 2

Bikes’R’Us производит велосипеды по 250 долларов.Он стоит производителю 180 долларов за велосипед плюс стартовый взнос в размере 3500 долларов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?

Крупный магазин бытовой техники рассматривает возможность приобретения пылесосов у небольшого производителя. Магазин сможет приобрести пылесосы по 86 долларов каждый, со стоимостью доставки 9 200 долларов, независимо от того, сколько пылесосов будет продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать плату за пылесосы?

Три самых популярных вкуса мороженого – это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого.Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?

В магазине мороженого возрастает спрос на три вкуса. В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы – на 20%.Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.

Банан – 3%, тыква – 7%, а каменистая дорога – 2%

Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек. Кешью весит 3 г, фисташки – 4 г, миндаль – 5 г. Если сумка весит 3.7 кг, узнайте, сколько орехов каждого вида в мешке.

Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля. Для начала выясните, сколько орехов каждого типа было в пакете.

100 миндальных орехов, 200 кешью, 600 фисташек

Глоссарий

расширенная матрица: матрица коэффициентов, примыкающая к столбцу констант, разделенному вертикальной линией в скобках матрицы

матрица коэффициентов: матрица, содержащая только коэффициенты из системы уравнений

Исключение по Гауссу: с использованием элементарных операций со строками для получения матрицы в виде строки-эшелона

главная диагональ: записей из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы

рядная форма: после выполнения строковых операций матричная форма, содержащая единицы по главной диагонали и нули в каждом пробеле ниже диагонали

эквивалент строки

две матрицы А

эквивалентны строкам, если один может быть получен из другого путем выполнения основных операций со строками

строковые операции: : добавление одной строки к другой, умножение строки на константу, перестановка строк и т. Д. С целью получения формы «строка-эшелон»

Эта работа находится под лицензией Creative Commons Attribution 4.0 Международная лицензия.

Вы также можете бесплатно скачать по адресу http://cnx.org/contents/[email protected]

Авторство:

Алгебра – расширенные матрицы

Решите каждую из следующих систем уравнений.

a \ (\ begin {align *} 3x + y – 2z & = 2 \\ x – 2y + z & = 3 \\ 2x – y – 3z & = 3 \ end {align *} \) Показать решение

Давайте сначала запишем расширенную матрицу для этой системы.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & 2 \\ 1 & {- 2} & 1 & 3 \\ 2 & {- 1} & {- 3} & 3 \ end {array}} \ right] \]

Как и в предыдущих примерах, мы помечаем красным цветом числа, которые мы хотим изменить на данном шаге.Первый шаг здесь – получить 1 в верхнем левом углу, и, опять же, у нас есть много способов сделать это. В этом случае мы заметим, что если мы поменяем местами первую и вторую строки, мы сможем получить 1 в этом месте с относительно небольшой работой.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & 2 \\ 1 & {- 2} & 1 & 3 \\ 2 & {- 1} & {- 3} & 3 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_1} \ leftrightarrow {R_2}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ {\ color {Red} 3} & 1 & {- 2} & 2 \\ {\ color {Red} 2} & {- 1} & {- 3} & 3 \ end {array}} \ right] \]

Следующий шаг – получить два числа под этой единицей равными нулю.Также обратите внимание, что это почти всегда требует выполнения операции третьей строки. Кроме того, мы можем сделать и то, и другое за один шаг следующим образом.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ {\ color {Red} 3} & 1 & {- 2} & 2 \\ {\ color {Red } 2} & {- 1} & {- 3} & 3 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} – 3 {R_1} \ to {R_2 }} \\ {{R_3} – 2 {R_1} \ to {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & {\ color {Red} 7} & {- 5} & {- 7} \\ 0 & 3 & {- 5} & {- 3} \ end {array}} \ right] \]

Затем мы хотим превратить 7 в 1.Мы можем сделать это, разделив вторую строку на 7.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & {\ color {Red} 7} & {- 5} & {- 7} \\ 0 & 3 & {- 5} & {- 3} \ end {array}} \ right] \ begin {array} {* {20} {c}} {\ frac {1} {7} {R_2}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & {- 1} \\ 0 & {\ color {Красный} 3} & {- 5} & {- 3} \ end {array}} \ right] \]

Итак, у нас есть дробь.Такое случается время от времени, так что не стоит сильно волноваться по этому поводу. Следующий шаг – заменить 3 под этой новой единицей на 0. Обратите внимание, что мы пока не будем беспокоиться о -2 над ней. Иногда так же легко превратить это в 0 на том же этапе. Однако в этом случае это, вероятно, так же легко сделать позже, как мы увидим.

Итак, используя операцию третьей строки, мы получаем

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & {- 1} \\ 0 & { \ color {Red} 3} & {- 5} & {- 3} \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_3} – 3 {R_2} \ в {R_3}} \\ \ в \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & { – 1} \\ 0 & 0 & {\ color {Red} – \ frac {{20}} {7}} & 0 \ end {array}} \ right] \]

Далее нам нужно преобразовать число в правом нижнем углу в 1.Мы можем сделать это с помощью операции второй строки.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & {- 1} \\ 0 & 0 & { \ color {Red} – \ frac {{20}} {7}} & 0 \ end {array}} \ right] \ begin {array} {* {20} {c}} {- \ frac {7} {{ 20}} {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & {\ color {Red} 1} & 3 \\ 0 & 1 & {\ цвет {Красный} – \ frac {5} {7}} & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \]

Теперь нам нужны нули над этой новой единицей.Итак, использование операции третьей строки дважды, как показано ниже, сделает то, что нам нужно.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & {\ color {Red} 1} & 3 \\ 0 & 1 & {\ color {Red} – \ frac {5] } {7}} & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} + \ frac {5} {7} { R_3} \ to {R_2}} \\ {{R_1} – {R_3} \ to {R_1}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {\ цвет {Красный} – 2} & 0 & 3 \\ 0 & 1 & 0 & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \]

Обратите внимание, что в этом случае последний столбец не изменился на этом этапе.Это произошло только потому, что последняя запись в этом столбце была нулевой. В общем, этого не произойдет.

Последний шаг – преобразовать -2 над 1 во втором столбце в ноль. Это легко сделать с помощью операции третьего ряда.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {\ color {Red} – 2} & 0 & 3 \\ 0 & 1 & 0 & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right ] \ begin {array} {* {20} {c}} {{R_1} + 2 {R_2} \ to {R_1}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \]

Итак, у нас есть расширенная матрица в окончательном виде и решение будет

\ [x = 1, \, \, \, y = – 1, \, \, \, z = 0 \]

Это можно проверить, подставив их во все три уравнения и убедившись, что все они удовлетворяются.

b \ (\ begin {align *} 3x + y – 2z & = – 7 \\ 2x + 2y + z & = 9 \\ – x – y + 3z & = 6 \ end {align *} \) Показать решение

Опять же, первый шаг – записать расширенную матрицу.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & {- 7} \\ 2 & 2 & 1 & 9 \\ {- 1} & { – 1} & 3 и 6 \ end {array}} \ right] \]

На этот раз мы не можем получить 1 в верхнем левом углу, просто поменяв местами строки.Мы могли бы поменять местами первую и последнюю строку, но это также потребовало бы другой операции, чтобы превратить -1 в 1. Хотя это несложно, это две операции. Обратите внимание, что мы можем использовать операцию третьей строки, чтобы получить 1 в этом месте следующим образом.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & {- 7} \\ 2 & 2 & 1 & 9 \\ {- 1} & { – 1} & 3 и 6 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_1} – {R_2} \ to {R_1}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ {\ color {Red} 2} & 2 & 1 & 9 \\ {\ color {Red} – 1 } & {- 1} & 3 & 6 \ end {array}} \ right] \]

Теперь мы можем использовать операцию третьей строки, чтобы превратить два красных числа в нули.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ {\ color {Red} 2} & 2 & 1 & 9 \\ { \ color {Red} – 1} & {- 1} & 3 & 6 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} – 2 {R_1} \ to {R_2 }} \\ {{R_3} + {R_1} \ to {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3 } & {- 16} \\ 0 & {\ color {Red} 4} & 7 & {41} \\ 0 & {- 2} & 0 & {- 10} \ end {array}} \ right] \]

Следующий шаг – получить 1 на месте, занимаемом красной 4.Мы могли бы сделать это, разделив всю строку на 4, но это добавило бы пару несколько неприятных дробей. Итак, вместо этого мы собираемся поменять местами вторую и третью строки. Причина этого станет очевидной достаточно скоро.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & {\ color {Red} 4} & 7 & {41 } \\ 0 & {- 2} & 0 & {- 10} \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} \ leftrightarrow {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & {\ color {Red} – 2} & 0 & {- 10 } \\ 0 и 4 и 7 и {41} \ end {array}} \ right] \]

Теперь, если мы разделим вторую строку на -2, мы получим 1 в том месте, которое нам нужно.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & {\ color {Red} – 2} & 0 & { – 10} \\ 0 & 4 & 7 & {41} \ end {array}} \ right] \ begin {array} {* {20} {c}} {- \ frac {1} {2} {R_2}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & {\ color {Red} 4} & 7 & { 41} \ end {array}} \ right] \]

Прежде чем перейти к следующему шагу, давайте заметим здесь пару вещей.Во-первых, нам удалось избежать дробей, что всегда хорошо, а во-вторых, эта строка готова. В конечном итоге нам понадобился бы ноль в этом третьем месте, и мы получили его бесплатно. Более того, это не изменится ни в одной из последующих операций. Это происходит не всегда, но если это произойдет, наша жизнь станет легче.

Теперь давайте воспользуемся операцией третьей строки, чтобы заменить красную 4 на ноль.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & {\ color {Red} 4} & 7 & {41} \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_3} – 4 {R_2} \ to {R_3}} \\ \ to \ end {массив } \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & {\ color {Red} 7} & {21} \ end {массив}} \ справа] \]

Теперь мы можем разделить третью строку на 7, чтобы получить число в правом нижнем углу в единицу.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & {\ color {Red} 7} & {21} \ end {array}} \ right] \ begin {array} {* {20} {c}} {\ frac {1} {7} {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {\ color {Red} – 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right] \]

Затем мы можем использовать операцию третьей строки, чтобы заменить -3 на ноль.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {\ color {Red} – 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end { array}} \ right] \ begin {array} {* {20} {c}} {{R_1} + 3 {R_3} \ to {R _ {\ kern 1pt}}}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {\ color {Red} – 1} & 0 & {- 7} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right] \]

Последний шаг – затем снова превратить -1 в 0, используя операцию третьей строки.

\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {\ color {Red} – 1} & 0 & {- 7} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right ] \ begin {array} {* {20} {c}} {{R_1} + {R_2} \ to {R _ {\ kern 1pt}}} \\ \ to \ end {array} \ left [{\ begin { array} {rrr | r} 1 & 0 & 0 & {- 2} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right] \]

Тогда решение этой системы:

\ [x = – 2, \, \, \, y = 5, \, \, \, z = 3 \] .

Метод Гаусса – примеры c решением, теоремы и формулы

Определения и обозначения

Простейшие преобразования элементов матрицы

Алгоритм решения методом Гаусса пошагово

Шаг 1. Переписываем систему в виде матрицы

Шаг 2.

Шаг 3. Приводим матрицу к ступенчатому виду

Шаг 4. Записываем эквивалентную систему

Шаг 5. Производим проверку (решение системы обратным путём)

Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений

Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений

Примеры решения методом Гаусса

Заключение

Математика онлайн

Метод Гаусса для решения матриц. Решение системы линейных уравнений методом Гаусса :: SYL.ru

Что представляет собой СЛАУ

Наиболее популярные методы решения СЛАУ

Где используются СЛАУ на практике

Критерий совместимости СЛАУ

Почему СЛАУ можно представить в матричном виде

Преобразования матриц

Метод Жордана-Гаусса

Простой пример решения системы 2х2

Пример решения СЛАУ 3х3

Пример решения системы уравнений 4х4

Проверка правильности решения

Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ

Методические рекомендации к внеурочной самостоятельной работе “Решение систем уравнений методом Гаусса”

Как решать матрицы методом гаусса. Метод Гаусса для решения матриц

Что представляет собой СЛАУ

Наиболее популярные методы решения СЛАУ

Где используются СЛАУ на практике

Критерий совместимости СЛАУ

Почему СЛАУ можно представить в матричном виде

Преобразования матриц

Метод Жордана-Гаусса

Простой пример решения системы 2х2

Пример решения СЛАУ 3х3

Пример решения системы уравнений 4х4

Проверка правильности решения

Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ

Решение систем уравнений методом Гаусса | Проект по алгебре (8 класс) на тему:

Метод Гаусса. Решение системы линейных уравнений методом Гаусса и Жордана-Гаусса

Похожие главы из других работ:

4.1 Метод Гаусса

Метод Гаусса

2.3.1 Метод Гаусса-Зайделя

6. Метод Гаусса-Зейделя

1.3 Метод Гаусса

1.1 Метод Гаусса

1.2 Метод Гаусса решения СЛУ

1.2 Метод Гаусса

1.3 Метод Гаусса в Excel

1.1 Метод Гаусса

1.1 Метод Гаусса

Метод Гаусса

Метод Гаусса

2.6 Метод Гаусса-Кронрода

2.6 Метод Гаусса-Кронрода

Матрицы и системы уравнений

Определение матрицы

Терминология

Преобразование систем линейных уравнений в Матрицы

Операции с элементарными строками

Формы рядов-эшелонов и сокращенных рядов-эшелонов

Форма рядного эшелона

Форма Row-Echelon уменьшенная

Исключение по Гауссу

Гаусс-Джордан Ликвидация

Поворотный

Типы решений

Методы исключения Гаусса и матричные методы

Что такое поворот?

Процесс поворота

Полезные советы

Выбор оси

Сводка

Особые случаи

Содержание: Примечания по алгебре колледжа

Как решить линейные системы с помощью исключения Гаусса – Видео и стенограмма урока