Решение матриц методом крамера онлайн калькулятор: Метод Крамера онлайн - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

«Решение линейных уравнений методом Крамера»

Решение системы линейных уравнений методом Крамера

Еще одним популярным методом решения системы линейных алгебраических уравнений является метод Крамера. Если вы знаете, как найти определитель матрицы, то данный способ не вызовет у вас никаких затруднений. На а если не знаете, то благодаря нашему онлайн сервису, сможете с легкостью разобраться. Итак, если система линейных уравнений по теореме Кронекера-Капелли имеет решение, а это условие наш онлайн калькулятор проверяет всегда, прежде чем браться за решение, то его можно найти методом Крамера, используя следующие формулы: для вычисления корней уравнений x_i (i=1,n)

x_i=Δⁱ_n/Δ_n (i=1,n),

где Δ_n=det A, а Δⁱ_n являются определителями n-го порядка, которые получаются из Δ_n путем замены в нем i-го столбца столбцом свободных членов исходной системы.

Что бы закрепить теоретический материал, обратимся к практике, решим систему из трех уравнений методом Крамера.

76x₁-7x₂-6x₃=-5

10x₁+12x₂-7x₃=11

-16x₁+10.5x₂-13x₃=-10

Определим совместность системы линейных уравнений. По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, что бы ранг основной матрицы

A= 76

-7

-6

-7

-16

10.5

-13

и ранг расширенной матрицы

B= 76

-7

-6

-5

-7

-16

10. 5

-13

-10

были равны.
Так как rang|A|=3 равен rang|B|=3 и равен количеству неизвестных n=3, то система имеет единственное решение.

Согласно вышеприведенной формуле для метода Крамера, необходимо найти главный определитель и он будет равен

Δ= 76

-7

-6

-7

-16

10.5

-13

=-9746

Для вычисления X₁ найдем первый определитель, для чего заменим первый столбец столбцом свободных членов.

Δ₁= -5

-7

-6

-7

-10

10.5

-13

=-2491. 5

Точно как же как и для X₁ найдем определитель, для вычисления X₂

Δ₂= 76

-5

-6

-7

-16

-10

-13

=-17854

Проделаем аналогичную операцию для вычисления следующего определителя для X₃

Δ₃= 76

-7

-5

-16

10.5

-10

=-18851

В результате осталось разделить нужные определители на главный, в итоге получим :

X₁=Δ₁/Δ ?0.256
X₂=Δ₂/Δ ?1.832
X₃=Δ₃/Δ ?1.

934

На нашем сайте вы также можете:

Решение онлайн

Для ввода исходных данных необходимо указать количество уравнений:

Решим систему уравнений

x₁

x₂

–

x₃

x₁

x₂

–

x₃

x₁

x₃

Прямой ход. Процесс решения системы уравнений методом Гаусса состоит из двух этапов.

На первом этапе (прямой ход) система приводится к ступенчатому виду, путем последовательного исключения переменных.
Серые прямоугольники (см.решение ниже), позволят Вам проследить последовательность исключения переменных.

На каждом шаге решения справа располагается расширенная матрица, эквивалентная системе уравнений.

Каждая строка матрицы представляет собой уравнение системы (сравните сами).
Данная форма решения менее наглядная, но позволяет не переписывать каждый раз переменные, что существенно экономит время.

 Исключим переменную x₁ из всех уравнений, за исключением первого. Поменяем местами уравнения 1 и 3 (порядок уравнений в системе не имеет значения).

x₁

x₃

x₁

x₂

–

x₃

x₁

x₂

–

x₃

–

Из уравнения 2 вычитаем уравнение 1, умноженное на 3.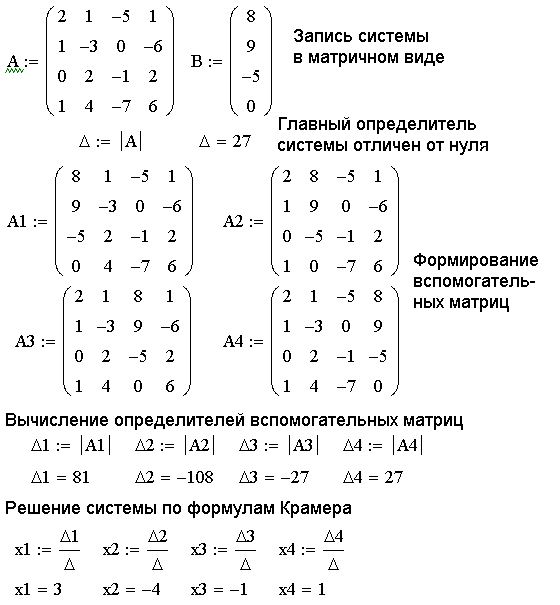

x₁

x₃

x₂

–

x₃

–

x₁

x₂

–

x₃

–

Из уравнения 3 вычитаем уравнение 1, умноженное на 2.

x₁

x₃

x₂

–

x₃

–

x₂

–

x₃

–

 Исключим переменную x₂ из последнего уравнения.

Из уравнения 3 вычитаем уравнение 2.

x₁

x₃

x₂

–

x₃

–

x₃

–

Обратный ход.

Если посмотреть на получившеюся систему, то, очевидно, что она приведена к ступенчатому виду.
Что это нам дает?
Посмотрите дальнейшие наши действия, и Вы сами ответите на этот вопрос.

 Рассмотрим уравнение 3 последней получившейся системы.

x₃

 Рассмотрим уравнение 2 последней получившейся системы.

x₂

–

x₃

–

Из данного уравнения найдем значение переменной x₂.

x₂

x₃

–

Подставим, ранее найденное, значение переменной x₃.

x₂

5 *

–

x₂

–

 Рассмотрим уравнение 1 последней получившейся системы.

x₁

x₃

Из данного уравнения найдем значение переменной x₁.

x₁

–

x₃

Подставим, ранее найденное, значение переменной x₃.

x₁

–

x₁

Ответ :

x₁

x₂

–

x₃

Метод Гаусса решения систем линейных уравнений

Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме.Для того чтобы решить систему уравнений

выписывают расширенную матрицу этой системы и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы.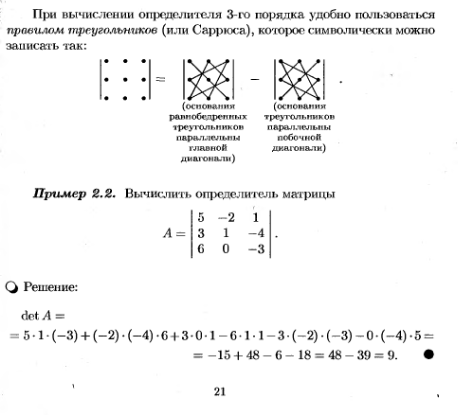

Рассмотрим метод Гаусса на примерах.

Пример 14. Установить совместность и решить систему

Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент равнялся единице (так удобнее производить преобразования матрицы).

Имеем Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно.

Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований:

Итак, имеем Далее, подставляя в третье уравнение, найдем Подставляя и во второе уравнение, получим и, наконец, подставляя в первое уравнение найденные получим Таким образом, имеем решение системы

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы (и соответственно математический раздел – матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин “матрица” появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m – строк и n – столбцов.

Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,…, a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2,…,m; j=1,2,…,n)

Действия над матрицами.

1. Сложение матриц – поэлементная операция

2. Вычитание матриц – поэлементная операция

3. Произведение матрицы на число – поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Покажем операцию умножения матриц на примере

5. Возведение в степень

m>1 целое положительное число. А – квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A’

Строки и столбцы поменялись местами

Пример

Свойства опрераций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A’)’=A

(λA)’=λ(A)’

(A+B)’=A’+B’

(AB)’=B’A’

Виды матриц

1. Прямоугольные: m и n – произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) – во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: a_ij=0, i=1,2,…,m

j=1,2,…,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

9. Симметрическая матрица: m=n и a_ij=a_ji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A’=A

Например,

10. Кососимметрическая матрица: m=n и a_ij=-a_ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a_ii=-a_ii)

Пример.

Ясно, A’=-A

11. Эрмитова матрица: m=n и a_ii=-ã_ii (ã_ji – комплексно – сопряженное к a_ji, т.е. если A=3+2i, то комплексно – сопряженное Ã=3-2i)

Пример

Метод гаусса и крамера. Решить систему уравнений методами Крамера, Гаусса и с помощью обратной матрицы

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты.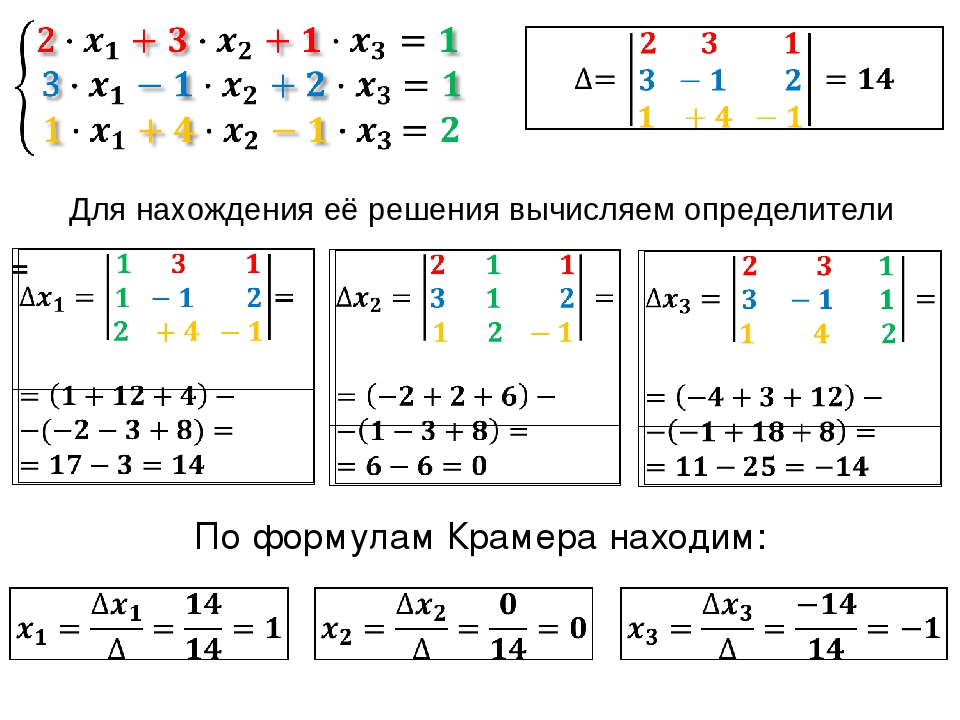 Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.

Теорема 1

Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$

В чем заключается метод Крамера

Суть метода Крамера в следующем:

Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$

А теперь три других детерминанта:

$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$

$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$

$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Решение примеров онлайн калькулятор. Порядок выполнения действий, правила, примеры

Привет друзья! Очень редко я рассказываю о действительно полезных программах, которые с легкостью могут сделать нашу жизнь легче и сэкономить наше время.

Через две недели уже первое сентября, а что это значит? Верное, это начало учебного года. Кому-то в школу, кому-то в университет и в другие учебные заведения. Грустно конечно же, а ведь еще и учиться нужно:). Поэтому, сегодня я расскажу Вам о программе, которая во многом поможет в этом не легком процессе. Ну с математикой так точно легче будет.

Расскажу я сегодня о программе ЛовиОтвет, о которой я узнал не так давно (а жаль, узнал бы когда еще учился в школе, возможно меньше двоек по математике бы было:)) . Честно говоря, математику я никогда не любил, толком не знал и все эти уравнения для меня были муками. Как в школе, так и в университете. А может я просто не хотел ее понимать, но это не важно, сегодня не об этом:).

Давайте вернемся к программе. ЛовиОтвет – это мощный решебник (в заголовке я написал калькулятор, но это больше чем просто калькулятор) , с помощью которого можно решать самые разные математические примеры (как самые простые, так и сложные) . И еще, программа показывает все этапы решения, то есть, Вы не просто получите ответ, а увидите, все этапы решения. Решаете к примеру уравнение и в столбик наблюдаете решение – это очень круто. Ведь очень часто конечный ответ нам не очень то и поможет, ведь нужно расписать сам процесс решения.

Что можно решать с помощью этой программы?

Примеры разной сложности
Уравнения (линейные и квадратные)
Производить действия с натуральными числами
Упрощение выражений
Работать с дробями

И многое другое.

Особенности программы ЛовиОтвет

Отображение этапов решения
Результат программа показывает на тетрадном листе
Красивый, простой и продуманный интерфейс (можно быстро изменять цвет программы)
Есть версии программы для мобильных телефонов (java) , Android, Apple.
Программа развивается.

Где скачать и как установить решебник ЛовиОтвет?

Кстати, пока писал статью, то обнаружил онлайн версию решебника находится по адресу http://calc. loviotvet.ru/ . Но там походу доступны не все функции. Поэтому, лучше скачать программу и установить на компьютер.

Программа бесплатная, поэтому просто качаем с официального сайта и устанавливаем. Переходим на страницу http://www.loviotvet.ru/download/ . И нажимаем на ссылку, рядом со значком Windows.

Сохраните установочный файл, или сразу запустите его. Сам процесс установки очень простой. Думаю разберетесь:). После установки на рабочем столе должен появится ярлык программы.

Вы наверное заметили, что на странице загрузки есть еще версии для мобильных телефонов и для платформ Android и iOS. Это значит, что Вы можете установить себе ЛовиОтвет на мобильный телефон, смартфон, планшет и т. д. Это очень хорошо, ведь такая программа должна быть всегда с Вами.

Обзор и работа с программой

Главное окно программы выглядит вот так:

Как видите, все очень просто. Слева все кнопки, переключатели и т. д. Кстати дополнительную панель можно скрыть. Вверху строчка, в которой пишем само задание. А ниже листок, на котором мы уведем решение после нажатия на кнопку Ответ.

Вот демонстрация функции с выводом этапов решения (даже 2+2 можно расписать:)) :

Слева, можно выбрать, как выводить решение.

Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям. Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений.2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные. После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение. Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.

Приложение

Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения – задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение – это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо – найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения – это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.

Удобный и простой онлайн калькулятор дробей с подробным решением может:

Складывать, вычитать, умножать и делить дроби онлайн,
Получать готовое решение дробей картинкой и удобно его переносить.

Результат решения дробей будет тут…

0 1 2 3 4 5 6 7 8 9
Знак дроби “/” + – * :
_cтереть Очистить
У нашего онлайн калькулятора дробей быстрый ввод . Чтобы получить решение дробей, к примеру , просто напишите 1/2+2/7 в калькулятор и нажмите кнопку “Решать дроби “. Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку .

Знаки используемые для записи в калькуляторе

Набирать пример для решения вы можете как, с клавиатуры, так и используя кнопки.

Возможности онлайн калькулятора дробей

Калькулятор дробей может выполнить операции только с 2-мя простыми дробями. Они могут быть как правильными(числитель меньше знаменателя), так и неправильными(числитель больше знаменателя). Числа в числителе и знаменатели не могут быть отрицательными и больше 999.
Наш онлайн калькулятор решает дроби и приводит ответ к правильному виду – сокращает дробь и выделяет целую часть, если потребуется.

Если вам нужно решить отрицательные дроби, просто воспользуйтесь свойствами минуса. При перемножении и делении отрицательных дробей минус на минус дает плюс. То есть произведение и делении отрицательных дробей, равно произведению и делению таких же положительных. Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу. При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную.
При вычитании отрицательных дробей, результат будет таким же, как если бы поменяли их местами и сделали положительными. То есть минус на минус в данном случае дает плюс, а от перестановки слагаемых сумма не меняется. Этими же правилами мы пользуемся при вычитании дробей одна из которых отрицательная.

Для решения смешанных дробей (дробей, в которых выделена целая часть) просто загоните целую часть в дробь. Для этого умножьте целую часть на знаменатель и прибавьте к числителю.

Если вам нужно решить онлайн 3 и более дроби, то решать их следует по очереди. Сначала посчитайте первые 2 дроби, потом с полученным ответом прорешайте следующую дробь и так далее. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ.

И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

действия выполняются по порядку слева направо,
причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Пример.

Выполните действия 7−3+6 .

Решение.

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Ответ:

7−3+6=10 .

Пример.

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Решение.

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

Ответ:

Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Пример.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Решение.

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 – значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

Ответ:

17−5·6:3−2+4:2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание – следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Определение.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Ответ:

5+(7−2·3)·(6−4):2=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Ответ:

4+(3+1+4·(2+3))=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Слу метод крамера. Вычислим главный определитель системы. Решение систем уравнений методом Крамера

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Теорема 1

В чем заключается метод Крамера

Суть метода Крамера в следующем:

Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

А теперь три других детерминанта:

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

Дети и учеба – Информационный портал

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

где A ij – алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

Умножая обе части равенства (1.14) слева на A – 1 , мы получим решение системы:

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y из первого уравнения и подставляя его во второе уравнение , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j – независимые (искомые) переменные, a ij – постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………..
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21-26-13-37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т.к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1.4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = – 3 + 2t

x 2 = – 1 – 3t

x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы купить конспект . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

решаем системы линейных алгебраических уравнений (слау)

. (1.6)

(j = 1, 2, …, n ). (1.7)

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

, (1.13)

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

1) Найдем алгебраические дополнения A ij :

где

Умножая обе части равенства (1.14) слева на A – 1 , мы получим решение системы:

, откуда

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Пример 1.11.

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Пусть дана система линейных форм (уравнений):

Мы получим следующую систему:

. (1.21)

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

После приведения подобных членов, получим:

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………..
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

-21-26-13-37

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

x 1 = – 3 + 2t

x 2 = – 1 – 3t

x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Готовые домашние задания по линейной алгебре, матрицы по формуле крамера :: cartivicar

Системы. Пример решения уравнения методом Крамера. Векторное пространство. Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако. Матрица линейного преобразования в базисе из собственных векторов. Матрица, образ, ядро, ранг и дефект оператора.55.2.7. Тики, как аналитическая геометрия, линейная алгебра, пределы, диф. Занятиях, другие — в виде домашних заданий, остальные использо. Матричный метод Показать все онлайн калькуляторы. Онлайн калькуляторы Онлайн упражнения Справочник Таблицы и формулы Калькулятор процентов. Ранг матрицы. Видов контроля СРС является защита индивидуальных домашних заданий. Индивидуальные задания по разделам дисциплины. Непосредственно из формулы 1.3 ясно, что умножение матрицы на число. Электронное учебно методическое пособие для студентов 1 курса экономического факультета. Задания.1. Решите по формулам Крамера и методом обратной матрицы. Ответ представить в обыкновенных неправильных дробях. Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Метод обратной матрицы н формулы Крамера. ГДЗ по математике. Матричный метод Показать все онлайн калькуляторы. Онлайн калькуляторы Онлайн упражнения Справочник Таблицы и формулы Калькулятор процентов. Решенные примеры. Алгебра. Вектора. Аналитическая геометрия. Решение. Выпишем матрицу коэффициентов и матрицу столбец свободных членов. Ответ: 2. Решите систему уравнений по формулам Крамера. В процессе. Матрицы и операции. Определители матриц и их основные свойства Формула полного разложения определителя Формула Лапласа полного разложения. Примерное задание. Формула Крамера. Алгебра.

Такую матрицуКогда все определители найдены, то по формулам Крамера вычислим и неизвестные. Решенные примеры. Алгебра. Вектора. Аналитическая геометрия. Решение. Выпишем матрицу коэффициентов и матрицу столбец свободных членов. Ответ: 2. Решите систему уравнений по формулам Крамера. Подробное решение системы уравнений Онлайн методом Крамера и Матричным. Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однакоРешить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Возьмём, к примеру, вот такую матрицу. Формулы Крамера для нахождения неизвестных:. ДЗ на 5готовые домашние задания. Здесь вы можете посмотреть как решить систему линейных уравнений методом КрамераПример решения уравнения методом Крамера. Задание. При помощи формул Крамера найти решение системы. Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Определители матриц второго и третьего порядка. Формулы Крамера. Общее решение. Навигация по странице. Метод Крамеравывод формул. Алгоритм решения систем линейных алгебраических уравнений методом Крамера. Основная матрица системы имеет вид. По формулам для длины вектора и скалярного произведения. Навигация по странице. Метод Крамеравывод формул. Алгоритм решения систем линейных алгебраических уравнений методом Крамера. Основная матрица системы имеет вид. Практикум 1 по линейной алгебре 117. Решить систему линейных уравнений методом Крамера. Решение. Найдем определитель основной матрицы.

Если определитель матрицы квадратной системы не равен нулю. Задание. При помощи формул Крамера найти решение системы. Совместность системы линейных. Формула Бернулли. Рангом матрицы называется наибольший из порядков миноров матрицы, отличных от нуля. Решение систем линейных уравнений методом Крамера, основанном на применении. Учебник по алгебре 7 класс феоктистов. Метод. Системы решение матрицы методом крамера линейных уравнений. Матрицы и операции. Определители матриц и их основные свойства Формула полного разложения определителя Формула Лапласа полного разложенияПодробное решение системы уравнений Онлайн методом Крамера и Матричным. Электронное учебно методическое пособие для студентов 1 курса экономического факультета. Задания.1. Решите по формулам Крамера и методом обратной матрицы. Решение системы линейных алгебраических уравнений методом Крамера. Метод Крамера теорема Крамера — способ решения квадратных СЛАУ с ненулевым определителем основной матрицы. Задание. При помощи формул Крамера найти решение системы. Решение систем линейных уравнений с помощью обратной матрицы. Онлайн решебник. Теорема Крамера. Здесь вы можете посмотреть как решить систему линейных уравнений методом Крамера. Когда все определители найдены, то по формулам Крамера вычислим и неизвестные. Решить систему по формулам Крамера. Метод Гаусса. Раздел . Формула Пуассона. Заданий.2. Модуль 2. Линейная алгебра. Метод Гаусса. Тема 2.4. Формула Байеса. Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Определители матриц второго и третьего порядка. Метод Крамера. Возьмём, к примеру, вот.

Вместе с Готовые домашние задания по линейной алгебре, матрицы по формуле крамера часто ищут

метод крамера формула.

метод обратной матрицы.

теорема крамера доказательство.

решение систем линейных уравнений методом гаусса.

теорема крамера формулировка.

решение матриц методом гаусса.

метод крамера пример 3 порядка.

метод гаусса

Читайте также:

География 10 класс практическая работа трудовые ресурсы

Гдз по геометрии10класс л с атанасян

Экономика 11 класс крупская тимченко черная гдз бесплатно

Решатель линейных уравнений

Система m линейных уравнений от n неизвестных имеет решение тогда и только тогда, когда ранг r расширенной матрицы равен рангу матрицы коэффициентов.
Если две матрицы имеют одинаковый ранг r и r = n, решение уникально.
Если две матрицы имеют одинаковый ранг r и r

Общий вид линейной системы уравнений можно представить формулой: A x _i = B _i
Матрица коэффициентов	– это матрица, которая содержит коэффициенты переменных (матрица в формуле).
Постоянная матрица	– это массив значений свободных столбцов (векторный массив B _i).
Дополненная матрица	– это комбинированная матрица, которая содержит рядом матрицу коэффициентов и матрицу констант (матрица AB _i).

Другой способ решения линейной системы уравнений – это правило Крамера, которое включает только детерминанты. Рассмотрим систему уравнений:

Решение дается уравнением:

D _i	– это определитель, установленный путем замены i-го столбца столбцом свободных значений b _i
Д	– определитель матрицы коэффициентов.

Поскольку r n = 4 2 = 2, две переменные зависят от двух других переменных, и мы должны выбрать определенные значения для двух переменных
например: w = a и y = b (a, b – любое число), тогда:

z = 1 + 2a

x = 4 2b + a

Вектор пространства решений равен (4 + a 2b, b, 1 + 2a, a)
например, если мы выберем: a = 1 b = 1, то решение будет:
(7, 1, 3, 1).

(PDF) МОБИЛЬНЫЙ КАЛЬКУЛЯТОР ПРИЛОЖЕНИЯ ДЛЯ ОБРАТНОГО МЕТОДА И ПРАВИЛА КРАМЕРА В POLYTECHNIC KOTA KINABALU

A. Baharum et al. J Fundam Appl Sci. 2018, 10 (7S), 132-142 141

достижение специально для темы одновременных линейных уравнений в Политехническом университете Кота

Кинабалу. Надеемся, что результаты этого инновационного исследования позволят создать больше приложений для смартфонов

, которые помогут студентам улучшить свою академическую успеваемость.Продукты, полученные на основе этого инновационного исследования

, могут быть добавлены к темам для инженерного дела

Математика 3 Численный метод, например, метод исключения Гаусса, метод разложения Дулитла

и более требовательный и более сложный метод разложения Crout LU

. Чтобы повысить интерес учащихся к изучению сложного предмета, такого как математика

, геймификация является одним из подходов к обучению, которые привлекают интерес учащихся, а

повышают мотивацию учащихся.Геймификация также является одним из подходов, который может реализовать обучение, ориентированное на учащихся, в классе

, который уже реализован в Политехническом институте Малайзии.

Будущая работа улучшит процесс обучения с внедрением геймификационного обучения.

подход для изучения сложных предметов и тем, таких как матрица и одновременные линейные уравнения

8. СПИСОК ЛИТЕРАТУРЫ

[1] A. Al-Hunaiyyan, R.A. Альхаджри, С.Аль-Шархан, «Восприятие и проблемы мобильного обучения

в Кувейте», J. King Saud Univ. – вычисл. Инф. Sci., 2016.

[2] И. Махазир И., М.Н. Нораза, К.Р. Ридзван и А.А. Азвин Ариф, «Взаимосвязь между

, принятием мобильного обучения для курса AutoCAD и стилем обучения в политехническом институте»,

Procedure – Soc. Behav. Sci., Т. 102, вып. Ifee 2012, стр. 177–187, 2013.

[3] D.K. Биринчи, А. Делис и Э. Айдын, «Процессы решения студентов университетов в системах линейных уравнений

», Процедура – Соц.Behav. Sci., Т. 152, pp. 563–568, 2014.

[4] А. Дригас и М. Паппас, «Обзор мобильных обучающих приложений по математике»,

Int. J.Interact. Моб. Technol., Т. 9, вып. 3. С. 18–23, 2015.

[5] Д. Михаил (2011). Онлайн калькуляторы с матрицами. Получено 18 мая 2018 г. с сайта

http://onlinemschool.com/math/assistance/matrix/

[6] Решиш (2011). Матрица Решиш. Получено 18/5/2018

с http: // matrix.reshish.com/inverse.php

[7] М. Петрович (2017). Математические калькуляторы, уроки и формулы. Получено 18/5/2018

из

https://www.mathportal.org/calculators/system-of-equations-solver/system-3×3.php

[8] Massey University (2012). Получено 18.05.2018 из

http://mathsfirst.massey.ac.nz/Algebra/SystemsofLinEq/ EMeth.htm

[9] Х. Шэн и К. Сиау, «Понимание ценностей мобильных технологий в образовании. : a

Матричный калькулятор

Правило Крамера – CULCAL

Сумма детерминантов 2×2.Предположим, что основная матрица равна D.

Система линейных уравнений Правило Крамера Часть 3 Youtube Linear Equations Equations Learning Math

Все основные матричные операции, а также методы решения систем одновременных линейных уравнений реализованы на этом сайте.

Матричный калькулятор, правило Крамера . Для методов и операций, требующих сложных расчетов, была сделана очень подробная характеристика решения. Используя коэффициенты, переменные и константы, создайте матрицу, как показано ниже.Оставьте лишние ячейки пустыми, чтобы ввести неквадратные матрицы.

Обычно решение систем линейных уравнений может быть беспорядочным для систем, размер которых превышает 2×2, потому что есть много способов уменьшить его, когда есть три или более переменных. Калькулятор правил Крамера Здесь вы можете бесплатно решать системы одновременных линейных уравнений с помощью калькулятора правил Крамера с комплексными числами онлайн с очень подробным решением. В этом онлайн-калькуляторе можно вводить только целые числа или дроби.

Найдите определитель главной матрицы. 2×2 Сумма двух детерминантов. Он был введен Габриэлем Крамером, отсюда и произошло название.

Чтобы изменить знак с на – в уравнении введите отрицательные числа. Просто введите элементы матрицы и нажмите кнопку. Чтобы решить совместные линейные уравнения с использованием правила Крамера, выполните следующие действия.

Правило Крамерса Правило Крамерса – это метод, используемый для систематического решения систем линейных уравнений на основе вычислений определителей.X y z. Более подробную информацию читайте в этих правилах.

С помощью этого калькулятора мы сможем понять алгоритм решения системы линейных уравнений по правилу Крамера. Калькулятор правила Крамера вычисляет решение и определители для двух одновременных линейных уравнений и трех одновременных линейных уравнений. Калькулятор правил домашнего Крамерса.

Найти определитель матрицы ранг возвести матрицу в степень, найти сумму и умножением матриц вычислить обратную матрицу.Это онлайн-инструмент алгебры, запрограммированный для определения упорядоченной тройки как решения системы трех линейных уравнений. Если в вашем уравнении отсутствует какая-либо переменная, то в этом месте калькулятора введите ноль.

Он назван в честь Габриэля Крамера, который опубликовал правило для a. Ключевой особенностью нашего калькулятора является то, что каждый определитель может быть вычислен отдельно, и вы также можете проверить точный тип матрицы, если определитель основной матрицы равен нулю. Решение Two Equation Solution использует следующую форму.

Fb tw li pin. Просто хочу поделиться с вами моей версией Калькулятора обратной матрицы с использованием Excel 2019. Он выражает решение в терминах определителей матрицы коэффициентов и матриц, полученных из нее, путем замены одного столбца вектор-столбцом в правой части уравнения.

Сумма детерминантов 3×3. Сумма трех детерминантов 3×3. 2×2 сумма детерминант.

A 1 x b 1 y c 1 a 2 x b 2 y c 2. Этот процесс в основном основан на правиле обратной матрицы Крамерса.Матричный калькулятор 2×2 Правило Крамерса.

Решите приведенные ниже уравнения для x y и z. Он был тем, кто ввел правило для произвольного количества неизвестных. Калькулятор правила Крамерса 3×3 Калькулятор, приведенный в этом разделе, может использоваться для решения системы линейных уравнений с тремя неизвестными с использованием правила Крамерса или метода определителей.

2×2 Сумма двух детерминантов. Калькулятор правила Крамерса решает систему трех линейных уравнений с действительными коэффициентами. Ввод данных в калькулятор правила Крамера.

Сумма трех детерминантов 3×3. Онлайн калькулятор правил Крамерса для пошагового решения системы линейных уравнений методом детерминанта. Мои учебные пособия по численным методам-httpgooglZxFOj2Matrix Algebra-httpgoogl4gvpeCHiIm Sujoy, а сегодня я расскажу вам, как решить систему линейных 3×3.

Однако он не подходит для более чем 2 или 3 уравнений. Формула для решения систем линейных уравнений В линейной алгебре правило Крамера – это явная формула для решения системы линейных уравнений с таким количеством уравнений, сколько неизвестных, действительная, когда система имеет единственное решение.Количество уравнений в Матрице.

Сумма детерминантов 3×3. Правило Крамерса используется для решения линейной системы уравнений 2×2, когда она имеет единственное решение.

Доказательство правила S Крамера Формула правила S Крамера Линейные уравнения Литеральные уравнения Решение линейных уравнений

Оценка детерминантов на Ti83 84 Обучение математическому графическому калькулятору Тригонометрия

Ex Решите систему трех уравнений с помощью правила S Крамера Хорошее видео для ввода матрицы 3×3 На калькуляторе Уравнения Решение систем уравнений

Правило Крамера с калькулятором Матрица 3×3 Правила Youtube Матрица линейных уравнений

Решения Rbse для класса 12 по математике Глава 5 Обратная матрица и линейные уравнения Ex 5 2 Rbsesolutions Rbsesolutio Class 12 Maths Math Methods 12th Математика

Алгебра 2 рабочие листы Матрицы Рабочие листы Рабочие листы с задачами в словах Матрицы Математическая алгебра

Матрица и системы решения с матрицами, которые она любит Математические матрицы Математические экспоненты Рабочие листы Решение

Детерминанты и мультипликативные инверсии матриц Страницы учебных занятий Алгебра Алгебра ra Уроки Интерактивная записная книжка Задания

Правило Крамера Интересные слайды Покрытие некоторых примеров, которые вы можете увидеть в линейной алгебре или даже алгебре 2 Справка по алгебре Преподавание математики Линейное программирование

Pin Автор Марисоль Бенитес О колледжах Решение вычитания Умножение матриц

Матрица

Поиск по математике Математические полиномы

Использование матриц для решения систем уравнений на графическом калькуляторе Преподавание алгебры Колледж алгебры Школа алгебры

Закрепление на системах уравнений

Использование теории матриц и Крамера 39 Правило S для решения систем уравнений пугает большинства студентов. Теория Системы уравнений Математика для старшей школы

Определители и правило Крамера Математика для старшей школы Правила алгебры

Предварительное исчисление Решение систем уравнений с помощью матриц Заметки Викторина Карты задач Карты задач Системы уравнений Уравнения

Детерминанты Cram Матрицы правил er S Математические заметки Лаборатория математики

В этом учебном пособии Узнайте, как решить систему из трех переменных с помощью правила S-правила Крамера, решающего правила исчисления,

S-правило Крамера Решение систем уравнений Уравнения

Инверсия матрицы 2 x 2

Существует быстрый способ получить обратную матрицу 2 x 2.{-1} = \ frac {1} {ad-bc} \ begin {bmatrix} d & -b \\ – c & a \ end {bmatrix} \)

Есть три шага, чтобы инвертировать матрицу 2×2

Поменять местами диагональные элементы
Изменить знак остальных элементов
Разделите каждый элемент на \ (ad-bc \)

Если, например, в приведенной выше формуле \ (ad = bc \), то мы попытаемся разделить на нулю и, следовательно, обратного нет.В этом случае мы называем исходную матрицу \ (A \) сингулярной матрицей. Если матрица имеет обратную, мы говорим, что матрица невырожденная.

Другой способ получить \ (ad = bc \) – это если вторая строка матрицы кратна первой.

Фактически не вычисляя обратную матрицу, мы можем принять решение, существует ли обратная матрица. просто вычислив единственное число – знаменатель в формуле.Этот знаменатель называется определитель.

Если определитель равен нулю, это особая матрица, которую нельзя инвертировать.

Правило Крамера также существует для матриц большего размера, но с точки зрения вычислений оно очень неэффективно. Следовательно, это полезно, особенно для больших матриц, если мы можем определить перед началом расчета, существует ли обратное.Это можно сделать, определив также для больших матриц единственное число, которое характеризует матрицу – опять же, оно называется определителем матрицы.

nirmalpaul383 / Project-Cramer-s-Rule-Matrix-Calculator: это приложение для решения уравнений, основанное на правиле Крамера.

О: Это приложение для решения уравнений, основанное на правиле Крамера.

Описание: Мы можем использовать несколько методов для решения линейного уравнения.Одно из них – правило Крамера. В этом методе находятся значения двух или более неизвестных переменных. Коэффициенты переменных используются для формирования матрицы и с помощью их определителей значения переменных решаются. Дополнительную информацию об этом правиле можно найти на https://en.m.wikipedia.org/wiki/Cramer%27s_rule этой странице. Эта программа помогает пользователю решать линейные уравнения и находить значения неизвестных переменных. Это приложение поддерживает данные линейных уравнений 2×2 и 3×3 (2×2 для двух неизвестных переменных e.g X, Y и 3X3 для трех неизвестных переменных, например X, Y, Z). Эта программа также показывает полный метод обработки (по формулам) для лучшего понимания происходящего …

О совместимости приложения:
Значок этого приложения и его содержимое разработаны и разработаны мной (Н. Пол). Эта программа лучше всего подходит для стокового android с разрешением экрана FullHD + (1080 * 2160 p). Это проект с открытым исходным кодом (изначально созданный мной, Н. Полом), и любой может просмотреть, изменить и перестроить его. Чтобы загрузить исходный файл проекта, посетите мой профиль GitHub https: // www.github.com/nirmalpaul383/ Если вы хотите поддержать меня, поставьте лайк на нашей странице в Facebook https://www.facebook.com/a.new.way.technical/

Об исходном проекте: Это приложение создано с помощью Tasker (https://play.google.com/store/apps/details?id=net.dinglisch.android.taskerm) и с фабрикой приложений Tasker (https://play.google.com/store/apps/details?id=net.dinglisch.android.appfactory). Чтобы установить и запустить «Cramer’s Rule Calc», вам «не понадобится» ни одно из этих приложений. Однако, если вы хотите «просмотреть или изменить» исходный файл вам «понадобится» приложение Tasker, и если вы хотите «экспортировать свою собственную модификацию», то вам «понадобится» как Tasker, так и его расширение, приложение Tasker app factory.

Вот руководство по каталогам и файлам: есть 3 папки (1) Папка “Apk file” [содержит предварительно созданный / экспортированный файл приложения Android ‘Cramer_s_Rule_Calc.apk’] (2) Папка «Assets» [содержит несколько файлов ресурсов (изображений) для проекта (в основном изображения руководства и логотип / значок. для приложения), и вы даже можете изменить их через фотошоп.] (3) Папка «Исходный файл проекта» [содержит основной файл проекта. Загрузите его и импортируйте в приложение Tasker, измените или просмотрите это и наслаждайтесь …]

Если вы хотите поддержать, пожалуйста, поставьте лайк на моей странице в facebook https: // www.facebook.com/a.new.way.Technical/

Решение систем линейных уравнений с помощью Python Numpy

Библиотека Numpy может использоваться для выполнения различных математических / научных операций, таких как матричное скрещивание и скалярное произведение, поиск значений синуса и косинуса, преобразование Фурье и манипуляции с формой и т. Д. Numpy – это сокращенное обозначение «Числовой Python».

В этой статье вы увидите, как решить систему линейных уравнений с помощью библиотеки Python Numpy.

Что такое система линейных уравнений?

Википедия определяет систему линейных уравнений как:

В математике система линейных уравнений (или линейная система) – это набор двух или более линейных уравнений, включающих один и тот же набор переменных.

Конечная цель решения системы линейных уравнений – найти значения неизвестных переменных. Вот пример системы линейных уравнений с двумя неизвестными переменными, x и y :

Уравнение 1:

  4x + 3y = 20
-5x + 9y = 26

Чтобы решить указанную выше систему линейных уравнений, нам нужно найти значения переменных x и y .Есть несколько способов решить такую систему, например, исключение переменных, правило Крамера, метод сокращения строк и матричное решение. В этой статье мы рассмотрим матричное решение.

В матричном решении решаемая система линейных уравнений представлена в виде матрицы AX = B . Например, мы можем представить Уравнение 1 в виде матрицы следующим образом:

  A = [[4 3]
     [-5 9]]

X = [[x]
     [y]]

B = [[20]
     [26]]

Чтобы найти значение переменных x и y в уравнении , нам нужно найти значения в матрице x .Для этого мы можем взять скалярное произведение обратной матрицы A и матрицы B , как показано ниже:

  X = инверсный (A) .B

Если вы не знакомы с тем, как найти обратную матрицу, взгляните на эту ссылку, чтобы понять, как вручную найти обратную матрицу. Чтобы понять матричное скалярное произведение, ознакомьтесь с этой статьей.

Решение системы линейных уравнений с помощью Numpy

Из предыдущего раздела мы знаем, что для решения системы линейных уравнений нам необходимо выполнить две операции: обращение матрицы и скалярное произведение матрицы.Библиотека Numpy от Python поддерживает обе операции. Если вы еще не установили библиотеку Numpy, вы можете сделать это с помощью следующей команды pip :

  $ pip install numpy

Давайте теперь посмотрим, как решить систему линейных уравнений с помощью библиотеки Numpy.

Использование методов inv () и dot ()

Сначала мы найдем инверсную матрицу A , которую мы определили в предыдущем разделе.

Давайте сначала создадим матрицу A на Python.Для создания матрицы можно использовать метод массива модуля Numpy. Матрицу можно рассматривать как список списков, где каждый список представляет собой строку.

В следующем скрипте мы создаем список с именем m_list , который дополнительно содержит два списка: [4,3] и [-5,9] . Эти списки представляют собой две строки в матрице A . Чтобы создать матрицу A с помощью Numpy, m_list передается методу array , как показано ниже:

  импортировать numpy как np

m_list = [[4, 3], [-5, 9]]
А = np.массив (m_list)

Чтобы найти обратную матрицу, матрица передается методу linalg.inv () модуля Numpy:

  inv_A = np.linalg.inv (A)

печать (inv_A)

Следующий шаг – найти скалярное произведение между обратной матрицей A и матрицей B . Важно отметить, что скалярное произведение матриц возможно только между матрицами , если внутренние размеры матриц равны i.е. количество столбцов левой матрицы должно соответствовать количеству строк в правой матрице.

Чтобы найти скалярное произведение с помощью библиотеки Numpy, используется функция linalg.dot () . Следующий сценарий находит скалярное произведение между обратной матрицей A и матрицей B , которая является решением уравнения .

  B = np.array ([20, 26])
X = np.linalg.inv (A) .dot (B)

печать (X)

Выход:

Ознакомьтесь с нашим практическим руководством по изучению Git с лучшими практиками, общепринятыми стандартами и включенной памяткой.Прекратите гуглить команды Git и на самом деле выучите его!

  [2. 4.]

Здесь 2 и 4 – соответствующие значения для неизвестных x и y в уравнении . Для проверки, если вы подставите 2 вместо неизвестного x и 4 вместо неизвестного y в уравнении 4x + 3y , вы увидите, что результат будет 20.

Давайте теперь решим систему из трех линейных уравнений, как показано ниже:

  4x + 3y + 2z = 25
-2x + 2y + 3z = -10
3x -5y + 2z = -4

Вышеупомянутое уравнение можно решить с помощью библиотеки Numpy следующим образом:

Уравнение 2:

  A = np.массив ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.array ([25, -10, -4])
X = np.linalg.inv (A) .dot (B)

печать (X)

В приведенном выше сценарии методы linalg.inv () и linalg.dot () связаны друг с другом. Переменная X содержит решение для уравнения 2 и печатается следующим образом:

  [5. 3. -2.]

Значения неизвестных x , y и z равны 5, 3 и -2 соответственно.Вы можете подставить эти значения в Equation 2 и проверить их правильность.

Использование метода detect ()

В двух предыдущих примерах мы использовали методы linalg.inv (), и linalg.dot () , чтобы найти решение системы уравнений. Однако библиотека Numpy содержит метод linalg.solve () , который можно использовать для непосредственного поиска решения системы линейных уравнений:

  A = np.array ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.массив ([25, -10, -4])
X2 = np.linalg.solve (A, B)

печать (X2)

Выход:

  [5. 3. -2.]

Вы можете видеть, что результат такой же, как и раньше.

Пример из реального мира

Давайте посмотрим, как систему линейных уравнений можно использовать для решения реальных задач.

Предположим, продавец фруктов продал 20 манго и 10 апельсинов за один день на общую сумму 350 долларов. На следующий день он продал 17 манго и 22 апельсина за 500 долларов. Если цены на фрукты оставались неизменными в оба дня, какова была цена одного манго и одного апельсина?

Эту задачу легко решить с помощью системы двух линейных уравнений.

Допустим, цена одного манго составляет x , а цена одного апельсина – y . Вышеупомянутую проблему можно преобразовать так:

  20x + 10y = 350
17x + 22y = 500

Решение указанной выше системы уравнений показано здесь:

  A = np.array ([[20, 10], [17, 22]])
B = np.array ([350, 500])
X = np.linalg.solve (A, B)

печать (X)

А вот результат:

  [10. 15.]

Выходные данные показывают, что цена одного манго составляет 10 долларов, а цена одного апельсина – 15 долларов.

Заключение

В статье объясняется, как решить систему линейных уравнений с помощью библиотеки Python Numpy. Вы можете использовать методы linalg.inv () и linalg.dot () в цепочке для решения системы линейных уравнений, или вы можете просто использовать метод resolve () . Метод solution () является предпочтительным.

3.5 Детерминанты и правило Крамера – Колледжская алгебра для управленческих наук

Мы научились решать системы уравнений с двумя переменными и тремя переменными, используя несколько методов: подстановку, сложение, исключение Гаусса, использование обратной матрицы и построение графиков.Некоторые из этих методов применять проще, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.

Вычисление определителя матрицы 2 × 2

Определитель – это действительное число, которое может быть очень полезно в математике, поскольку у него есть несколько приложений, таких как вычисление площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы. Вычисление определителя матрицы требует следования определенным шаблонам, описанным в этом разделе.

Определитель матрицы при заданном

определяется как:

дет

Обратите внимание, что для определителей мы используем прямые вертикальные линии.Другими словами, det.

Знакомо? Должно. Помните, что это был знаменатель в скаляре, который мы умножаем на матрицу с переключенными диагоналями и недиагоналями напротив, чтобы создать инверсию. Таким образом, обратная матрица, подобная приведенной выше, будет:

Найти определитель заданной матрицы

дет

Использование правила Крамера для решения системы двух уравнений с двумя переменными

Теперь мы представим последний метод решения систем уравнений, использующий определители.Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году. Правило Крамера – жизнеспособный и эффективный метод поиска решений системы с любым количеством неизвестных, при условии, что у нас есть такое же количество уравнений, что и неизвестных.

Правило Крамера

даст нам единственное решение системы уравнений, если оно существует. Однако, если система не имеет решения или бесконечное количество решений, это будет обозначено определителем,.Несогласованные решения имеют по крайней мере один определитель числителя, отличный от нуля. Зависимые решения имеют нуль как определитель в обоих числителях. Для поиска общего решения необходимо использовать другой метод.

Чтобы узнать, как и почему работает правило Крамера, мы направим вас к исходным материалам в OpenStax College Algebra.

Короче говоря, правило Крамера начинается с системы уравнений, например:

, и мы можем показать, что

Обратите внимание, что знаменатель для обоих и является определителем матрицы коэффициентов.

Мы можем использовать эти формулы для нахождения и, но правило Крамера также вводит новые обозначения:

Обратите внимание, что ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление детерминантов. Затем мы можем выразить и как:

Правило Крамера

– это метод, который использует детерминанты для решения систем уравнений, которые имеют то же количество уравнений, что и переменные.

Рассмотрим систему двух линейных уравнений с двумя переменными.

Решение, использующее правило Крамера:

для

Если мы ищем, столбец заменяется постоянным столбцом. Если мы ищем, столбец заменяется постоянным столбцом.

Решите следующую систему, используя правило Крамера

Найдите

Найти

Найдите

Решение (2, -3).

Используйте правило Крамера для решения системы уравнений.

Вычисление определителя матрицы

Найти определитель матрицы несложно, но найти определитель матрицы сложнее. Один из способов – дополнить матрицу повторением первых двух столбцов, получив матрицу. Затем мы вычисляем сумму произведений входов вниз по каждой из трех диагоналей (вверху слева направо вниз) и вычитаем произведения записей вверх по каждой из трех противоположных диагоналей (внизу слева направо).Это легче понять с помощью наглядного пособия и примера.

Найдите определитель матрицы.

Шаг 1: Добавьте первые два столбца:

Шаг 2: С верхнего левого угла в нижний правый: умножьте значения по первой диагонали. , затем начните и умножьте слева направо по диагонали, а затем. Добавьте эти три продукта.

Шаг 3: Теперь сверху справа: умножьте записи вниз по обратной диагонали. , затем начните и умножьте справа налево по диагонали, а затем.Сложите эти три продукта и вычтите это значение из значения на шаге 2.

Алгебра выглядит следующим образом:

Найти определитель матрицы:

Дополните матрицу первыми двумя столбцами, а затем следуйте формуле. Таким образом,

Детерминанты также можно найти с помощью технологий. Как только матрица будет введена в ваш калькулятор. Переход к MATRIX – MATH и det и вызов рассматриваемой матрицы предоставит определитель для матрицы.В Excel = mdeterm также найдет определитель матрицы. Методы, упомянутые в этом разделе, работают только для указанного размера. Для матриц большего размера рекомендуется использовать калькулятор, Excel или другую программу.

Найдите определитель матрицы.

дет

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы, мы можем применить правило Крамера для решения системы из трех уравнений и трех неизвестных.Правило Крамера для систем следует тому же шаблону, что и для систем. Однако требуются дополнительные вычисления.

Рассмотрим систему:

где:

Если мы пишем определитель, мы заменяем столбец постоянным столбцом. Если мы пишем определитель, мы заменяем столбец постоянным столбцом. Если мы пишем определитель, мы заменяем столбец постоянным столбцом. Всегда проверяйте ответ.

Решите следующую систему, используя правило Крамера.

Используйте правило Крамера.

Затем,

Решение: (1,3, -2).

Используйте правило Крамера, чтобы решить систему:

а. Решите систему уравнений (если возможно), используя правило Крамера.

Начнем с поиска определителей:

Теперь мы знаем, что это либо зависимо, либо непоследовательно.Давайте посмотрим на один из других определяющих факторов.

Так как -16 \ neq 0, мы имеем противоречивое решение.

б. Решите следующую систему уравнений (если возможно, или дайте общее решение, если зависит).

Давайте найдем D с помощью технологий, с помощью калькулятора или Excel.

Мы знаем, что это зависимая или непоследовательная система. Мы могли бы найти все три других детерминанта, чтобы увидеть, является ли он зависимым, и если это так, тогда нам нужно будет использовать rref в калькуляторе, чтобы найти общее решение.По этой причине теперь быстрее просто использовать rref. Есть онлайн-версия от planetcalc.

Уменьшенная форма строки матрицы:

В виде уравнений это:

Итак, если любое действительное число, то:

Вот несколько свойств, которые могут упростить и ускорить поиск детерминантов.

Если матрица имеет форму верхнего треугольника (в нижнем треугольнике под диагональю все нули), то определитель равен произведению элементов по главной диагонали.
Когда две строки меняются местами, определитель меняет знак.
Если две строки или два столбца идентичны, определитель равен нулю.
Если матрица содержит строку или столбец из нулей, определитель равен 0.
Определитель обратной матрицы является обратной величиной определителю матрицы.
Если любая строка или столбец умножается на константу, определитель умножается на тот же коэффициент.

«Решение линейных уравнений методом Крамера»

Метод гаусса и крамера. Решить систему уравнений методами Крамера, Гаусса и с помощью обратной матрицы

Системы линейных алгебраических уравнений

Решение СЛАУ методом Крамера

В чем заключается метод Крамера

Приёмы для вычисления определителя матрицы

Решение систем уравнений методом Крамера

Метод Крамера.

Три случая при решении систем линейных уравнений

Примеры решения систем линейных уравнений методом Крамера

К началу страницы

Продолжаем решать системы методом Крамера вместе

Решение примеров онлайн калькулятор. Порядок выполнения действий, правила, примеры

Где скачать и как установить решебник ЛовиОтвет?

Обзор и работа с программой

Приложение

Знаки используемые для записи в калькуляторе

Возможности онлайн калькулятора дробей

Сначала умножение и деление, затем сложение и вычитание

Действия первой и второй ступени

Порядок выполнения арифметических действий в выражениях со скобками

Слу метод крамера. Вычислим главный определитель системы. Решение систем уравнений методом Крамера

Системы линейных алгебраических уравнений

Решение СЛАУ методом Крамера

Три случая при решении систем линейных уравнений

Примеры решения систем линейных уравнений методом Крамера

К началу страницы

Продолжаем решать системы методом Крамера вместе

В чем заключается метод Крамера

Приёмы для вычисления определителя матрицы

Решение систем уравнений методом Крамера

Дети и учеба – Информационный портал

Метод Крамера.

Три случая при решении систем линейных уравнений

Примеры решения систем линейных уравнений методом Крамера

К началу страницы

Продолжаем решать системы методом Крамера вместе

Действия над матрицами

Обратная матрица. Решение систем линейных уравнений матричным способом

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Системы линейных алгебраических уравнений

Решение СЛАУ методом Крамера

решаем системы линейных алгебраических уравнений (слау)

Действия над матрицами

Обратная матрица. Решение систем линейных уравнений матричным способом

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Системы линейных алгебраических уравнений

Решение СЛАУ методом Крамера

Три случая при решении систем линейных уравнений

Примеры решения систем линейных уравнений методом Крамера

К началу страницы

Продолжаем решать системы методом Крамера вместе

Готовые домашние задания по линейной алгебре, матрицы по формуле крамера :: cartivicar

Решатель линейных уравнений

(PDF) МОБИЛЬНЫЙ КАЛЬКУЛЯТОР ПРИЛОЖЕНИЯ ДЛЯ ОБРАТНОГО МЕТОДА И ПРАВИЛА КРАМЕРА В POLYTECHNIC KOTA KINABALU

Правило Крамера – CULCAL

Все основные матричные операции, а также методы решения систем одновременных линейных уравнений реализованы на этом сайте.

Инверсия матрицы 2 x 2

nirmalpaul383 / Project-Cramer-s-Rule-Matrix-Calculator: это приложение для решения уравнений, основанное на правиле Крамера.

Решение систем линейных уравнений с помощью Python Numpy

Что такое система линейных уравнений?

Решение системы линейных уравнений с помощью Numpy

Использование методов inv () и dot ()

Использование метода detect ()

Пример из реального мира

Заключение

3.5 Детерминанты и правило Крамера – Колледжская алгебра для управленческих наук

Вычисление определителя матрицы 2 × 2

Использование правила Крамера для решения системы двух уравнений с двумя переменными

Вычисление определителя матрицы

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Оставить комментарий Отменить ответ