Решение матриц методом крамера: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Решить систему линейных уравнений методом крамера. Решить систему уравнений методами Крамера, Гаусса и с помощью обратной матрицы

Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.

Теорема 1

Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$

В чем заключается метод Крамера

Суть метода Крамера в следующем:

Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.

Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$

А теперь три других детерминанта:

$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$

$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$

$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы,

a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы,

X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы купить конспект . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Рассмотрим систему 3-х уравнений с тремя неизвестными

Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т. е.

(2.4)

если 0. Здесь

Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .

Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:

Решение . Находим определитель основной матрицы системы

Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:

Проверка:

Следовательно, решение найдено правильно. 

Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место

Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам

(2.5)

где  – определитель основной матрицы ,  i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .

Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.

Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.

2.4. Определители n-го порядка

Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .

Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя

Получаем



Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .

Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

(2.6)

Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:

т.е. алгебраические дополнения записывают в явном виде через миноры.

Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.



2.

5. Основные свойства определителей

Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.

Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т. е. при транспонировании матрицы :

Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.

Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).

Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .

Например,

Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .

Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число .

Например,

Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:

Как найти определитель матрицы 4х4 методом крамера. Правило Крамера. Метод обратной матрицы. Решение слау методом крамера

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

Теорема 1

В чем заключается метод Крамера

Суть метода Крамера в следующем:

Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

А теперь три других детерминанта:

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:

Пусть дана система трех линейных уравнений:

Для решения системы линейных уравнений методом Крамера из коэффициентов при неизвестных составляется главный определитель системы . Для системы (1) главный определитель имеет вид
.

Далее составляются определители по переменным
,,. Для этого в главном определителе вместо столбца коэффициентов при соответствующей переменной записывается столбец свободных членов, то есть

,
,
.

Тогда решение системы находится по формулам Крамера

,
,

Следует отметить, что система имеет единственное решение
, если главный определитель
. Если же
и
= 0,= 0,= 0, то система имеет бесчисленное множество решений, найти которые по формулам Крамера нельзя. Если же
и
0, или0,или0, то система уравнений несовместна, то есть решений не имеет.

Пример

Решение:

1) Составим и вычислим главный определитель системы, состоящий из коэффициентов при неизвестных.

Следовательно, система имеет единственное решение.

2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в  столбцом из свободных членов.

По формулам Крамера находим неизвестные:

,
,
.

Сделаем проверку, чтобы убедиться в правильности решения

Т.е.
.

, т.е.

Ответ: .

Пример

Решить систему уравнений методом Крамера:

Решение:

1) Составим и вычислим главный определитель системы из коэффициентов при неизвестных:

Следовательно, система не имеет единственного решения.

2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в  столбцом из свободных членов:

,
, следовательно, система несовместна.

Ответ: система несовместна .

Метод Гаусса

Метод Гаусса состоит из двух этапов. Первый этап заключается в последовательном исключении переменных из уравнений системы при помощи действий, не нарушающих равносильности системы. Например, рассмотрим два первых уравнения системы (1).

(1)

Необходимо путем сложения этих двух уравнений получить уравнение, в котором отсутствует переменная . Умножим первое уравнение на, а второе на (
) и сложим полученные уравнения

Заменим коэффициент перед y , z и свободный член на ,исоответственно, получим новую пару уравнений

Заметим, что во втором уравнении отсутствует переменная x .

Проведя аналогичные действия над первым и третьим уравнениями системы (1), а затем над полученными в результате сложения вторым и третьим уравнениями, преобразуем систему (1) к виду

(2)

Такой результат возможен, если система имеет единственное решение. В этом случае решение находится при помощи обратного хода метода Гаусса (второй этап). Из последнего уравнения системы (2) находим неизвестную переменную z , затем из второго уравнения находим y , а x соответственно из первого, подставляя в них уже найденные неизвестные.

Иногда в результате сложения двух уравнений суммарное уравнение может принять один из видов:

А)
, где
. Это означает, что решаемая система несовместна.

Б) , то есть
. Такое уравнение исключается из системы, в результате число уравнений в системе становится меньше, чем число переменных, и система имеет бесчисленное множество решений, нахождение которых будет показано на примере.

Пример

Решение:

Рассмотрим следующий способ осуществления первого этапа решения методом Гаусса. Запишем три строки коэффициентов при неизвестных и свободных членов, соответствующих трем уравнениям системы. Свободные члены отделим от коэффициентов вертикальной линией, а под третьей строкой проведем горизонтальную прямую.

Первую строку, которая соответствует первому уравнению системы, обведем – коэффициенты в этом уравнении останутся неизменными. Вместо второй строки (уравнения) надо получить строку (уравнение), где коэффициент при равен нулю. Для этого все числа первой строки умножим на (–2) и сложим с соответствующими числами второй строки. Полученные суммы запишем под горизонтальной чертой (четвертая строка). Для того чтобы вместо третьей строки (уравнения) также получить строку (уравнение), в которой коэффициент приравен нулю, умножим все числа первой строки на (–5) и сложим с соответствующими числами третьей строки. Полученные суммы запишем пятой строкой и проведем под ней новую горизонтальную черту. Четвертую строку (или пятую – по выбору) обведем. Выбирается строка с меньшими коэффициентами. В этой строке коэффициенты останутся неизменными. Вместо пятой строки надо получить строку, где уже два коэффициента равны нулю. Умножим четвертую строку на 3 и сложим с пятой. Сумму запишем под горизонтальной чертой (шестая строка) и обведем ее.

Все описанные действия изображены в таблице 1 при помощи арифметических знаков и стрелок. Обведенные в таблице строки запишем снова в виде уравнений (3) и, применив обратный ход метода Гаусса, найдем значения переменных x , y и z .

Таблица 1

Восстанавливаем систему уравнений, полученную в результате наших преобразований:

(3)

Обратный ход метода Гаусса

Из третьего уравнения
находим
.

Во второе уравнение системы
подставим найденное значение
, получим
или
.

Из первого уравнения
, подставляя уже найденные значения переменных, получаем
, то есть
.

Чтобы убедиться в правильности решения, проверку необходимо сделать во всех трех уравнениях системы.

Проверка:

, получим

Получим

значит, система решена верно.

Ответ:
,
,
.

Пример

Решить систему методом Гаусса:

Решение:

Порядок действий в этом примере аналогичен порядку в предыдущем примере, а конкретные действия указаны в таблице 2.

В результате преобразований получим уравнение вида , следовательно, заданная система несовместна.

Ответ: система несовместна .

Пример

Решить систему методом Гаусса:

Решение:

Таблица 3

В результате преобразований получим уравнение вида , которое исключается из рассмотрения. Таким образом, имеем систему уравнений, в которой число неизвестных 3, а число уравнений 2.

Система имеет бесчисленное множество решений. Чтобы отыскать эти решения, введем одну свободную переменную. (Число свободных переменных всегда равно разности между числом неизвестных и числом уравнений, оставшихся после преобразования системы. В нашем случае 3 – 2 = 1).

Пусть
– свободная переменная.

Тогда из второго уравнения найдем
, откуда
, а затем найдемx из первого уравнения
или
.

Таким образом,
;
;
.

Сделаем проверку в уравнениях, которые не участвовали в нахождении и, то есть во втором и в третьем уравнениях первоначальной системы.

Проверка:

или , получаем
.

Система решена верно. Давая произвольной постоянной различные значения, будем получать различные значенияx , y и z .

Ответ:
;
;
.

Решение матрицы методом крамера для чайников. Правило Крамера

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1. 8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

где A ij – алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

Умножая обе части равенства (1.14) слева на A – 1 , мы получим решение системы:

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1. 16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y из первого уравнения и подставляя его во второе уравнение , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j – независимые (искомые) переменные, a ij – постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1.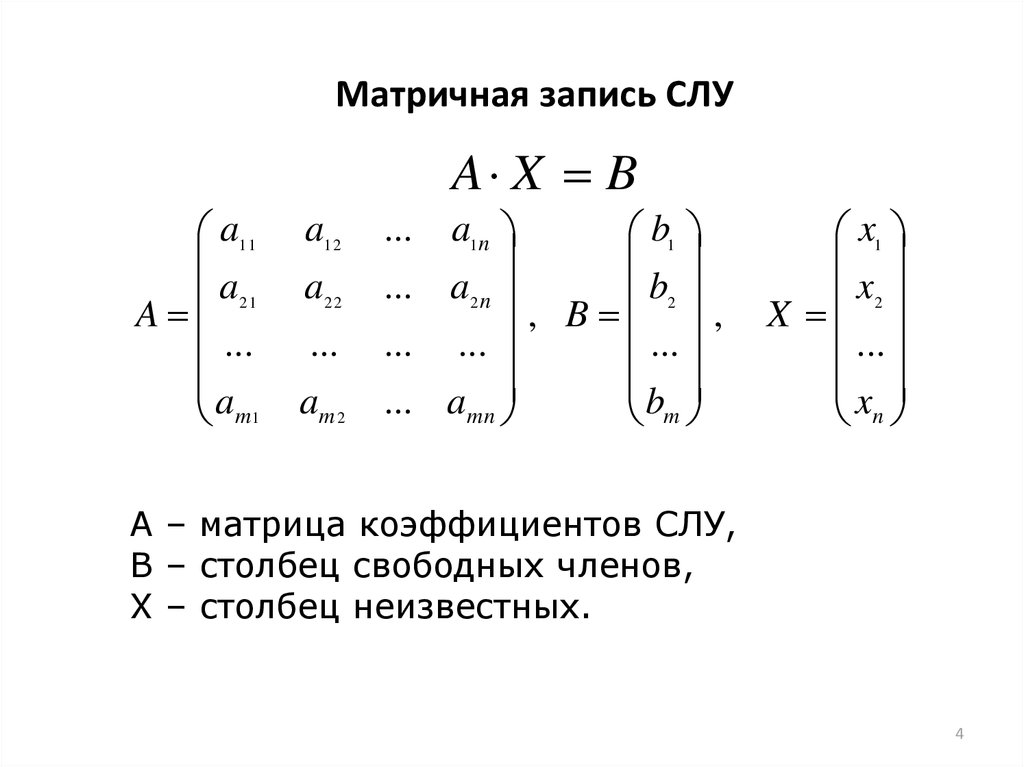 21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1. 1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1. 1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………. .
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21-26-13-37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т.к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1.4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = – 3 + 2t

x 2 = – 1 – 3t

x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

В нашем калькуляторе вы бесплатно найдете решение системы линейных уравнений методом Крамера онлайн с подробным решением и даже с комплексными числами . Каждый определитель, использованный в расчетах, можно просмотреть отдельно, а также проверить точный вид системы уравнений, если вдруг определитель основной матрицы оказался равен нулю.

Подробнее о том, как пользоваться нашим онлайн калькулятором, вы можете прочитать в инструкции .

О методе

При решении системы линейных уравнений методом Крамера выполняются следующие шаги.

Записываем расширенную матрицу.
Находим определитель основной (квадратной) матрицы.
Для нахождения i-ого корня подставляем столбец свободных членов в основную матрицу на i-ое место и находим ее определитель. Далее находим отношение полученного определителя к основному, это и есть очередное решение. Проделываем данную операцию для каждой переменной.
В случае, если основной определитель матрицы равен нулю, то система уравнений либо несовместна, либо имеет бесконечное множество решений. К сожалению метод Крамера не позволяет более точно ответить на этот вопрос. Тут вам поможет

Решение систем уравнений методом крамера эксель

Содержание

1 Варианты решений
- 1.1 Способ 1: матричный метод
- 1.2 Способ 2: подбор параметров
- 1.3 Способ 3: метод Крамера
- 1.4 Способ 4: метод Гаусса
2 Краткое описание метода Крамера
3 Решение уравнений методом Крамера в Excel

Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.

Решим систему из 3-х уравнений.

Запишем в ячейки основную матрицу системы и столбец свободных членов.

Определитель основной матрицы вычислим с помощью формулы =МОПРЕД(A11:C13)

Определитель =12, это означает, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера.

Теперь последовательно будем заменять столбцы матрицы А на столбец свободных членов и вычислять соответствующие определители полученных матриц. Отношение определителей позволяет вычислить переменные х.

В файле примера также приведено решение системы 4-х уравнений и прямая проверка решения.

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».

Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.

Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».

Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.

После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4.

Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

. Высчитываем соответствующее для него значение f(x), применив следующую формулу:

Вместо значения «X» подставляем адрес той ячейки, где расположено число , принятое нами за x.

Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».

Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за . После выполнения данных действий жмем на кнопку «OK».

После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».

Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».

Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.

Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».

Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.

Аналогичным образом производим подсчет определителей для остальных трех таблиц.

На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.

Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После этого копируем полученную строку и вставляем её в строчку ниже.

Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».

Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».

В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

Жмем привычное уже нам сочетание клавиш для применения формулы массива.

Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Одним из способов решения системы линейных уравнений является применение метода Крамера.
Давайте разберем принципы использования метода Крамера в Excel.

Краткое описание метода Крамера

Предположим у нас есть система из n линейных уравнений с n неизвестными.
Тогда, при определителе матрицы системы D, отличном от нуля, решение записывается в следующем виде:

Решение уравнений методом Крамера в Excel

Разберем систему из 3 линейных уравнений с 3 неизвестными и запишем систему линейных уравнений в матричном виде Ax = B.
Введем матрицы A (диапазон ячеек B3:D5) и B (диапазон ячеек G3:G5), для наглядности области ввода выделены зеленым цветом.
В ячейке B7, с помощью функции МОПРЕД, запишем расчет определителя матрицы A:

В случае если определитель системы не равен нулю, то система имеет единственное решение и систему можно решить методом Крамера.
Для поиска решения вычислим 3 дополнительных определителя матриц (диапазоны ячеек B9:D11, B13:D15 и B17:D19), в каждом из которых вместо одного из столбцов подставляется матрица B.
Например, вместо первого столбца (коэффициенты при переменной x1), ставим столбец матрицы B (свободные коэффициенты):

В ячейках F10, F14 и F18 рассчитываем определители матриц и записываем в ячейки I10, I14 и I18 (выделены голубым цветом) решение системы, по формуле Крамера получаем как отношение определителя дополнительных матриц к определителю матрицы системы (формулы =F10/B7, =F14/B7 и =F18/B7).

Решение СЛАУ методом Крамера для матриц большего размера (4×4, 5×5 и т.д.) аналогично рассмотренному выше.
Подробно ознакомиться с шаблоном решения для матриц 3×3 и 4×4 — скачать пример.

Метод Крамера — правило и примеры решения систем линейных уравнений » Kupuk.net

Распространённый в математике метод Крамера отлично себя зарекомендовал как способ поиска неизвестных величин из систем уравнений. Но использовать этот подход можно только тогда, когда число искомых значений эквивалентно реальному количеству алгебраических уравнений. Формируемая в системе основная матрица обязательно должна быть квадратной, наличие нулевых строчек просто недопустимо.

Краткое описание

Широко востребованный метод Крамера активно используется специалистами для решения распространённых алгебраических уравнений (СЛАУ). Итоговая точность полученного результата обусловлена применением определённой математической матрицы, а также некоторыми вспомогательными ограничениями, которые неизбежно накладываются во время доказательства конкретной теоремы.

Набором выражений вида yr 2 x1+ yr 2 x2 +… yr n xn = b r при r =1, 2,…, m принято называть универсальную систему линейных алгебраических уравнений. В этом случае также присутствуют определённые коэффициенты, которые могут принадлежать множеству W -действительных чисел, от неизвестных x 1… xn.

Чаще всего в роли действенных чисел выступают yr и br. Каждое из представленных значений называется линейным уравнением. Элементарные коэффициенты при неизвестных — это yr, а вот bi — свободные коэффициенты уравнений. Стандартный n -мерный вектор k ° = (k 1°, k 2°,…, k n°) называют решением системы. При правильной подстановке в систему вместо неизвестных элементов каждая из строчек становится верным равенством.

Если у системы присутствует минимум одно решение, то она называется совместной. Речь касается несовместного примера только в том случае, если многочисленные алгоритмы решения совпадают с пустым множеством. Классическая формула Крамера используется в том случае, если необходимо отыскать верное решение для линейных уравнений. Для получения достоверного результата матрицы должны быть исключительно квадратными. А на практике такой подход означает одинаковое количество уравнений и неизвестных в системе.

Ключевые нюансы

Востребованный в математике метод Крамера для решения систем линейных уравнений можно успешно использовать только в том случае, если ученик хорошо понимает, что такое матрица алгебраических примеров и каким образом она выписывается. В противном случае будет сложно избежать распространённых ошибок. Если необходимые навыки имеются, то в итоге остаётся только правильно запомнить формулы, которые определяют метод Крамера. Чтобы лучше усвоить все тонкости этой темы, необходимо воспользоваться следующими обозначениями:

Главный определитель совместности матрицы системы — Det.
Определитель матрицы, который получен из основного элемента — deti. Если ученик попробует заменить последний столбец матрицы, задействовав для этого первые части линейных алгебраических уравнений, тогда следует использовать понятие deti.
Для количества неизвестных и уравнений в системе используется символ n.

Если учесть все перечисленные нюансы, то в итоге правило Крамера для вычисления компонентов n -мерного вектора можно записать в следующей формулировке: xi = deti / Det. В этом случае DET максимально отличен от нуля.

Практическое применение

Для решения многих математических задач принято использовать теорему Кронекера — Капелли. Если основной определитель G главной матрицы, которая была составлена за счёт коэффициентов уравнений, не равен нулю, тогда система уравнений будет совместна. Но такое решение является единственным. Для поиска верного результата принято вычислять систему через формулу Крамера для линейных уравнений: x i = D i / D.

Метод Крамера основан на нескольких основных нюансах, которые в сочетании друг с другом дают отличный результат:

Если решено найти правильное исчисление системы по методике талантливого учёного, тогда первым делом обязательно вычисляют главный определитель обращения матрицы (J). Если при подсчёте детерминант основной матрицы оказался равен нулю, то такая система просто не имеет решения, либо речь касается нескончаемого количества решений. В такой ситуации получить достоверный результат можно только благодаря универсальному методу Гаусса.
На втором этапе ученику нужно постараться заменить крайний столбец главной матрицы столбцом свободных членов, чтобы отыскать определитель (J 1).
Остаётся повторить аналогичные действия для всех оставшихся столбцов. За счёт этого можно получить определители от J 1 до J n. В этом случае символ n указывает на номер последнего справа столбца.
Как только будут найдены абсолютно все детерминанты, нужно постараться высчитать неизвестные переменные по элементарной формуле: х i = B i / B.

Разнообразие математических подходов

Немного иные приёмы используются в том случае, когда предстоит работать с определителем матрицы. Если нужно рассчитать правильные данные на основе конструкции с соразмерностью больше чем 2 на 2, тогда можно использовать сразу несколько проверенных временем способов:

Метод Гаусса. Некоторые специалисты привыкли называть это математическое направление понижением порядка основного определителя. Несколько простых действий помогают преобразить матрицу и привести её к треугольному виду. Все комплексные числа, которые расположены на основной диагонали, перемножаются. Но при таком поиске определителя запрещено выполнять арифметические действия со строчками или столбцами без предварительного вынесения чисел как множителя/делителя. Предварительно умножают вычитаемую строку на нулевой множитель, а уже потом вычитают и складывают все элементы между собой. Конечный знак у обратной матрицы подвергают изменениям только в том случае, когда происходит перестановка столбцов или строчек.
Правило Саррюса. Суть метода треугольников в том, чтобы ученик мог при вычислении дискриминанта и определителя произведения всех чисел, которые были соединены одной линией, записывать примеры только с положительным значением. Это утверждение идеально подходит для матриц размером 3х3. Но если следовать всем нормам правила Саррюса, то первым делом переписывают саму матрицу, а рядом с ней располагают первый и второй столбец. В итоге через сформированную конструкцию проводятся диагональные линии. Члены матрицы, которые расположены на основной диагонали или на параллельной ей плоскости всегда записываются со знаком +, а вот элементы, лежащие на побочной диагонали, имеют знак -.
Если ученик решит использовать универсальный метод Крамера СЛАУ, для которого свойственно присутствие сразу четырёх неизвестных, тогда лучше всего выполнить комбинацию с технологией Гаусса. В этом случае можно гарантированно отыскать детерминант через поиск миноров.

Для каждого направления свойственны свои нюансы и правила теории, которые должен знать каждый ученик. В противном случае решить правильно поставленную задачу практически невозможно.

Помощь онлайн-калькуляторов

Созданные программистами программы пользуются огромным спросом даже среди опытных математиков, так как всего за несколько минут можно правильно решить задачу. Многофункциональные онлайн-калькуляторы с подробным решением по методу Крамера позволяют быстро и качественно решить целую систему различных уравнений. Для этого пользователю необходимо правильно указать количество неизвестных величин.

Для быстрого переключения в уравнении с положительных знаков на отрицательные нужно вводить соответствующие числа. Если в задаче отсутствует коэффициент, то на его место в калькулятор вводят ноль. Указывать можно не только числа, но и дроби. К примеру: 4,7 или 1/5.

На специальных сайтах можно решать различные системы уравнений по методу талантливого учёного Крамера в режиме онлайн. Решение будет отображено на экране моментально, к тому же его можно расширить. При решении системы уравнений крайне важно найти определители и присоединить сразу несколько разных матриц. Для существенного сокращения решения эта математическая операция упрощена, что существенно облегчает работу учеников.

Актуальные примеры решения

Единственность арифметических действий с системой при её совместимости обеспечивает условие неравенства нулю основного определителя. Но если сумма точек, которые были возведены в квадрат, строго положительна, то полученный СЛАУ будет несовместим с квадратной матрицей. Такая ситуация может произойти тогда, когда минимум один из присутствующих элементов deti отличён от нуля.

В качестве примера можно рассмотреть задачу, по условиям которой необходимо решить трёхмерную систему ЛАУ, используя для этого формулы Крамера:

x1 + 2 x2 + 4 x3 = 31.
5 x1 + x2 + 2 x3 = 29.
3 x1 — x2 + x3 =10.

Для решения следует выписать матрицу системы построчно. Строку матрицы принято обозначать символом i. После этого можно получить формулу A1=(1 2 4), A2=(5 1 2), A3=(3 -1 1). Существование значения b = (31 29 10) помогает отобразить столбец свободных коэффициентов. Основной определитель Det будет соответствовать следующим данным: a11 a22 a33 + a12 a23 a31 + a31 a21 a32 — a13 a22 a31 — a11 a32 a23 — a33 a21 a12 = 1—20 + 12 — 12 + 2—10 = -27.

В соответствии с формулой Крамера можно найти: x1 = -81/(-27) = 3, x2 = -108/(-27) = 4, x3 = -135/(-27) = 5. Если всё сделать правильно, то можно получить следующий ответ: x° = (3,4,5). Если руководствоваться базовыми понятиями, то многочисленные средства Крамера для решения сложных линейных уравнений можно использовать опосредованно.

Нелишним также будет рассмотреть следующий пример, где ученику нужно определить то, при каких показателях параметра F неравенство формулы | F x — y — 4|+|x + F y + 4|<=0 будет иметь ровно одно логическое решение. В силу определения модуля функции представленное неравенство может быть выполнено только в том случае, если оба выражения равны нулю. Именно поэтому рассматриваемая задача сводится только к нахождению решения линейной системы алгебраических уравнений. Соблюдаемый принцип действий должен соответствовать двум следующим формулам:

F x — y = 4.
x + F y = -4.

Для этого примера свойственно единственное решение, но только в том случае, если главный определитель отличен от нуля.

Это условие выполняется абсолютно для всех действительных значений параметра F. Стоит отметить, что к математическим задачам этого типа могут быть сведены многочисленные практические примеры из области физики, математики и даже химии.

Присутствующая вычислительная сложность

Рассматриваемый метод решения задач требует стандартного вычисления определителей размерности. Если практиковать использование метода Гаусса для поиска всех необходимых определителей, то возникшие в итоге сложности будут связаны с электронными операциями порядка сложения-умножения. В этом случае придётся столкнуться с более сложными формулами, нежели с методом Гаусса.

Именно поэтому, с точки зрения затрат времени на вычисления, метод Гаусса является непрактичным. Специалистами в 2010 году было доказано, что метод Крамера вполне может быть реализован со сложностью O (n 3), а это очень важно в математике.

В распространённых задачах на системы линейных уравнений обязательно встречаются и такие, в которых помимо букв существуют ещё и другие символы. Они обозначают некоторое число (чаще всего действительное). Математики к таким задачам и системам уравнений приводят примеры, которые основаны на поиске общих свойств каких-либо явлений и предметов. Это очень удобно в том случае, если учёными был изобретён какой-либо агрегат или материал, а для описания всех его свойств необходимо решить целую систему линейных уравнений, где вместо коэффициентов используются буквы.

Метод Крамера – правило и примеры решения систем линейных уравнений

Содержание

Краткое описание
Ключевые нюансы
Практическое применение
Разнообразие математических подходов
Помощь онлайн-калькуляторов
Актуальные примеры решения
Присутствующая вычислительная сложность

Краткое описание

Ключевые нюансы

Главный определитель совместности матрицы системы — Det.
Определитель матрицы, который получен из основного элемента — deti. Если ученик попробует заменить последний столбец матрицы, задействовав для этого первые части линейных алгебраических уравнений, тогда следует использовать понятие deti.
Для количества неизвестных и уравнений в системе используется символ n.

Если учесть все перечисленные нюансы, то в итоге правило Крамера для вычисления компонентов n -мерного вектора можно записать в следующей формулировке: xi = deti / Det. В этом случае DET максимально отличен от нуля.

Практическое применение

Если решено найти правильное исчисление системы по методике талантливого учёного, тогда первым делом обязательно вычисляют главный определитель обращения матрицы (J). Если при подсчёте детерминант основной матрицы оказался равен нулю, то такая система просто не имеет решения, либо речь касается нескончаемого количества решений. В такой ситуации получить достоверный результат можно только благодаря универсальному методу Гаусса.
На втором этапе ученику нужно постараться заменить крайний столбец главной матрицы столбцом свободных членов, чтобы отыскать определитель (J 1).
Остаётся повторить аналогичные действия для всех оставшихся столбцов. За счёт этого можно получить определители от J 1 до J n. В этом случае символ n указывает на номер последнего справа столбца.
Как только будут найдены абсолютно все детерминанты, нужно постараться высчитать неизвестные переменные по элементарной формуле: х i = B i / B.

Разнообразие математических подходов

Метод Гаусса. Некоторые специалисты привыкли называть это математическое направление понижением порядка основного определителя. Несколько простых действий помогают преобразить матрицу и привести её к треугольному виду. Все комплексные числа, которые расположены на основной диагонали, перемножаются. Но при таком поиске определителя запрещено выполнять арифметические действия со строчками или столбцами без предварительного вынесения чисел как множителя/делителя. Предварительно умножают вычитаемую строку на нулевой множитель, а уже потом вычитают и складывают все элементы между собой. Конечный знак у обратной матрицы подвергают изменениям только в том случае, когда происходит перестановка столбцов или строчек.
Правило Саррюса. Суть метода треугольников в том, чтобы ученик мог при вычислении дискриминанта и определителя произведения всех чисел, которые были соединены одной линией, записывать примеры только с положительным значением. Это утверждение идеально подходит для матриц размером 3х3. Но если следовать всем нормам правила Саррюса, то первым делом переписывают саму матрицу, а рядом с ней располагают первый и второй столбец. В итоге через сформированную конструкцию проводятся диагональные линии. Члены матрицы, которые расположены на основной диагонали или на параллельной ей плоскости всегда записываются со знаком +, а вот элементы, лежащие на побочной диагонали, имеют знак -.
Если ученик решит использовать универсальный метод Крамера СЛАУ, для которого свойственно присутствие сразу четырёх неизвестных, тогда лучше всего выполнить комбинацию с технологией Гаусса. В этом случае можно гарантированно отыскать детерминант через поиск миноров.

Для каждого направления свойственны свои нюансы и правила теории, которые должен знать каждый ученик. В противном случае решить правильно поставленную задачу практически невозможно.

Помощь онлайн-калькуляторов

Актуальные примеры решения

x1 + 2 x2 + 4 x3 = 31.
5 x1 + x2 + 2 x3 = 29.
3 x1 — x2 + x3 =10.

F x — y = 4.
x + F y = -4.

Для этого примера свойственно единственное решение, но только в том случае, если главный определитель отличен от нуля.

Присутствующая вычислительная сложность

Именно поэтому, с точки зрения затрат времени на вычисления, метод Гаусса является непрактичным. Специалистами в 2010 году было доказано, что метод Крамера вполне может быть реализован со сложностью O (n ³), а это очень важно в математике.

Предыдущая

МатематикаЛуч в математике – определение, форма и свойства

Следующая

МатематикаМатематические диктанты для 4 класса

Калькулятор правила Крамера

Вспомним пример путешествия из второго раздела и систему уравнений, которую мы получили из него после упрощения каждой строки:

x + y + z = 26 ;

у - 2з = 6 ; и

2x - z = 12 .

Напомним также расширенную матрицу коэффициентов:

⌈	1	1	1	⁞	26	⌉
\|	0	1	-2	⁞	6	~
⌊	2	0	-1	⁞	12	⌋

Прежде чем мы перейдем к построению четырех матриц, используемых в правиле Крамера для систем 3×3, давайте уделим некоторое время описанию того, как мы можем вводить данные в калькулятор правила Крамера 9. 0072 .

У нас есть три уравнения, поэтому давайте сообщим калькулятору, что , выбрав правильный вариант в поле ” Число уравнений “. Это превратит наш инструмент в средство решения системы уравнений с тремя переменными и покажет нам изображение того, как такая система выглядит , с несколькими загадочными символами, например a₁ или c₂ . Они обозначают коэффициенты нашей системы , т. е. числа, стоящие слева от переменных в каждой строке, и числа справа от = знак.

Это обозначение указано в калькуляторе , где вы можете ввести значения из задачи, которую хотите решить. и соответствуют номерам рядом с x , b — y , c — z , d . числа справа, а индексы сообщают нам номер строки. Обратите внимание, что наш калькулятор правила Крамера принимает только линейные уравнения . Это означает, что у нас не может быть, например, квадратного, или выражения с переменной под квадратным корнем.

Обратите внимание, что эти коэффициенты также находятся в нашей расширенной матрице коэффициентов . На самом деле достаточно скопировать их в калькулятор правила Крамера. Например, в первой строке матрицы есть числа 1 , 1 , 1 и 26 . Соответствует первому уравнению , коэффициенты которого обозначены индексом ₁ . Следовательно, имеем:

а₁ = 1 , b₁ = 1 , c₁ = 1 , d₁ = 26 .

Точно так же две другие строки дают нам:

a₂ = 0 , b₂ = 1 , c₂ = -2 , d₂ = 6 ; и

a₃ = 2 , b₃ = 0 , c₃ = -1 , d₃ = 12 .

Как только вы введете все эти данные в калькулятор правила Крамера, он должен выдать значения четырех определителей, а затем решение системы .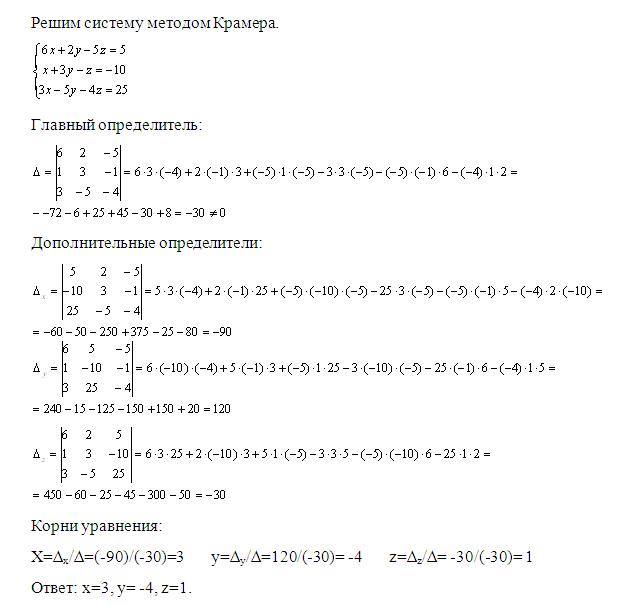 Посмотрим, как это выяснилось.

Как мы упоминали в предыдущем разделе, правило Крамера для систем 2×2 и 3×3 означает, что мы должны вычислить определители нескольких матриц . Первый, так называемый основной , представляет собой просто матрицу коэффициентов, которую мы определили во втором разделе:

		⌈	1	1	1	⌉
Вт	=	\|	0	1	-2	~
		⌊	2	0	-1	⌋

Чтобы построить остальные три, нам нужно заменить один столбец этой матрицы на четвертый дополнительный столбец расширенной матрицы коэффициентов , который в нашем случае имеет номера 26 , 6 и 12 . Чтобы получить Wₓ , матрицу x , мы подставляем эти числа вместо столбца, соответствующего переменной x , а именно первого:

		⌈	26	1	1	⌉
Втₓ	=	\|	6	1	-2	~
		⌊	12	0	-1	⌋

Аналогично получаем

		⌈	1	26	1	⌉
Втᵧ	=	\|	0	6	-2	~
		⌊	2	12	-1	⌋

		⌈	1	1	26	⌉
Ш _З	=	\|	0	1	6	~
		⌊	2	0	12	⌋

Все, что нам нужно сделать, это использовать формулу определителя из раздела выше для всех четырех матриц:

|W| = 1*1*(-1) + 1*(-2)*2 + 1*0*0 - 1*1*2 - 1*0*(-1) - 1*(-2)*0 = - 7 ,

|Втₓ| = 26*1*(-1) + 1*(-2)*12 + 1*6*0 - 1*1*26 - 1*6*(-1) - 26*(-2)*0 = - 56 ,

|Wᵧ| = 1*26*(-1) + 26*(-2)*2 + 1*0*12 - 1*6*2 - 26*0*(-1) - 1*(-2)*12 = - 98 ,

|W _z | = 1 1 12 + 1 6 2 + 26 0 0 - 26 1 2 - 1 0 12 - 1 6 0 = -28

`.`

Наконец, мы используем правило Крамера для систем 3x3 и получаем решение : x = |Wₓ| / |В| = -56 / (-7) = 8 , y = |Wᵧ| / |В| = -98 / (-7) = 14 , 93-8 9 Оценка квадратный корень из 12 10 Оценка квадратный корень из 20 11 Оценка квадратный корень из 50 94 18 Оценка квадратный корень из 45 19 Оценка квадратный корень из 32 20 Оценка квадратный корень из 18 92 Правило Крамера | GyanGossip Опубликовано: 14 фев 2022 г. Что такое правило Крамера и как решать задачи линейного уравнения с помощью правила Крамера? В математике для решения линейных уравнений используется матричная форма. Матрица представляет собой прямоугольный массив элементов, заключенных в квадратные скобки «[]». Есть некоторые методы и правила матрицы, используемые для решения линейных уравнений. Правило Кримера — одно из них. В этом правиле также используются определители. В этом посте мы изучим основную концепцию этого правила и используем несколько примеров, чтобы понять, как решать задачи линейных уравнений с помощью правила Крамера. Что такое правило Крамера? В матрицах правило Крамера используется для нахождения значений неизвестных переменных, присутствующих в линейных уравнениях. Для нахождения системы уравнений используется правило Крамера, и уравнения должны быть линейными. В этом методе все расчеты основаны на определителях, поэтому этот метод также называется методом определителей. Прямоугольный массив матриц не используется в правиле Крамера, поэтому мы используем форму квадратной матрицы. В квадратной матрице присутствует равное количество строк и столбцов. Поскольку определение матрицы гласит, что прямоугольный массив матрицы, то у ума должен возникнуть вопрос, почему мы используем квадратную матрицу для правила Крамера? Ответ заключается в том, что все квадратные матрицы в общем случае являются прямоугольными матрицами. Итак, мы всегда делаем вывод, что квадратная матрица прямоугольная. Формула правила Крамера Правило Крамера соответствует следующему уравнению: Ax = b -сторона линейного уравнения, а X - неизвестные переменные, которые необходимо найти. Уравнения принимаются в общем виде. A ₁ x + B ₁ y = C ₁ A ₂ x + B ₂ 90 линейная форма этой общей матрицы -матрица и y-матрица задаются как Первым шагом правила Крамера является преобразование матрицы в матричную форму. А затем найти определитель всех квадратных матриц, которые мы составили. Согласно правилу Крамера, если определитель квадратной матрицы равен нулю, то это правило неприменимо. Следующие формы используются для вычисления неизвестных переменных x и y линейных уравнений. Для определения значения x X = det[x]/det Для определения значения y y = det[y]/det Как решать линейные уравнения по правилу Крамера? Чтобы решить задачи линейного уравнения, вы должны быть знакомы с основной формулой и правилом Крамера. В правиле Крамера используются определители, определители должны быть рассчитаны с применением «||» для матриц вместо скобок []. Существует онлайн-калькулятор правила Крамера, который используется для таких вычислений, чтобы уменьшить сложность больших вычислений. Шаги для определения определителя для матриц 2x2 очень просты, просто следуйте данному методу. a b c d = (a x d) – (b x c) Шаги для определения определителя для матриц 3x3 довольно сложны и длительны, просто следуйте данному методу. Пример 1 Найдите неизвестные линейного уравнения, используя правило Крамера. 5x + 3y = 6 x + 3y = 2 Решение Шаг 1: Сначала напишите в форме AX = B. 5 3 1 3 x y = 6 2 Step 2: Find the determinant of square matrix A. A = 5 3 1 3 Step 3: Write the formula to determine the determinant of square matrix A. a b c d = (a x d) – (b x c) Шаг 4: Поместите значения каждого члена в приведенную выше формулу. 5 3 1 3 = (5 х 3) – (3 х 1) 5 3 1 3 = 15 - 3 5 3 1 3 = 12 DET A = 12 . первый столбец матрицы A и дайте имя значения x. X значений = 6 3 2 3 Шаг 6: Найдите определитель приведенной выше матрицы. 6 3 2 3 = (6 x 3) - (3 x 2) 6 3 2 3 = 18 - 6 6 3 2 77 3 2 77 3 2 77 3 9007 2 77778 3 9007 2 7 7 3 9007 2 7 7 9007 2 7 7 7 2 77778 3 2 = 12 det _x = 12 Шаг 7: Теперь возьмите значения b во втором столбце матрицы A и назовите значение y. Значения X = 5 6 1 2 Шаг 8: Найдите определитель приведенной выше матрицы. 5 6 1 2 = (5 x 2) – (6 x 1) 5 6 1 2 = 10 – 6 5 6 1 2 = 4 det _y = 4 Шаг 9 : По формуле правила Крамера для нахождения неизвестных переменных имеем. X = det _x /det Y = det _y /det Шаг 10: Подставьте значения рассчитанных определителей в приведенные выше формулы. X = 12/12 = 1 Y = 4/12 = 1/3 = 0,3333 Пример 2 5x – 4y = 6 3x + 9y = 2 Решение Шаг 1: Сначала запишите в форме AX = B. 5 -4 3 9 x y = 6 2 Step 2: Find the determinant of square matrix A. A = 5 -4 3 9 Step 3: Write the formula to determine the determinant of square matrix A. a b c d = (a x d) – (b x c) Step 4: Поместите значения каждого члена в приведенную выше формулу. 5 -4 3 9 = (5 x 9) – (3 x (-4)) 5 -4 3 9 = 45 – ( -12) 5 -4 3 9 = 45 + 12 5 -4 3 9 = 57 Det A = 57 Step 5 : Теперь возьмите значения b в первом столбце матрицы A и назовите значение x. Значения X = 6 -4 2 9 Шаг 6: Найдите определитель приведенной выше матрицы. 6 -4 2 9 = (6 x 9) – (-4 x 2) 6 -4 2 9 = 54 – (-8 ) 6 -4 2 9 = 54 + 8 6 -4 2 9 = 62 det _x = 62 Шаг 7: Теперь возьмите значения b во втором столбце матрицы A и назовите значение y. Значения X = 5 6 3 2 Шаг 8: Найдите определитель приведенной выше матрицы. 5 6 3 2 = (5 х 2) – (6 х 3) 5 6 3 2 = 10 -18 5 6 3 2 = -8 DET _Y = -8 . чтобы найти неизвестные переменные, мы имеем. X = det _x /det Y = det _y /det Шаг 10: Подставьте значения рассчитанных определителей в приведенные выше формулы. X = 62/57 = 1,0877 Y = -8/57 = -0,1404 Резюме Теперь вы усвоили все основы правила Крамера. Работать по этому правилу очень просто, требуется лишь некоторая практика, это правило также определено в ведической математике. Из приведенных примеров вы также можете решить правило Крамера для матриц 3x3, выполнив те же действия. Правило Крамера – объяснение и примеры Для решения системы уравнений мы в основном используем метод подстановки , метод исключения, или метод построения графиков. Мы также можем использовать матричную алгебру для решения системы уравнений. Такие процессы, как исключение Гаусса (также известное как исключение Гаусса-Джордана), могут помочь решить систему уравнений с $3$ или более неизвестными. Мы также можем использовать правило Крамера для решения системы. Что такое правило Крамера? Правило Крамера — это метод решения системы уравнений с использованием определителей. В этом уроке мы рассмотрим, что такое правило Крамера и как решить систему уравнений. Ниже приведены некоторые примеры и практические задачи. Что такое правило Крамера? Правило Крамера — это метод решения системы уравнений с использованием определителей. Это и есть красота правила Крамера. Мы можем найти значение одной переменной без решения всей системы (или других переменных). Помните определители? Рассмотрим матрицу $ 2 \times 2 $, показанную ниже: $ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} $ Определитель этой матрицы определяется выражением: $ det( A ) = | А | = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad – bc $ Примечание. Мы использовали обозначения $ 3 $ для обозначения определителя. Теперь рассмотрим матрицу $ 3 \times 3 $, показанную ниже: $ B = \begin{bmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \end {bmatrix} $ Определитель этой матрицы равен: $ det( B ) = | Б | = \begin{vmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \ end {vmatrix} = a \begin {vmatrix} { e } & f \\ h & i \end {vmatrix} – b \begin{vmatrix} d & f \\ g & i \end {vmatrix} + c \begin{vmatrix} d & e \\ g & h \end {vmatrix} $ Обратите внимание, что мы разбили матрицу $3\x 3$ на более мелкие матрицы $2\x 2$. Вертикальные черточки за пределами матриц $ 2 \times 2 $ указывают на то, что мы должны взять определитель. Зная определитель $ 2 \times 2 $ матриц, мы можем еще больше упростить формулу: $ det(B)=| Б | = a(ei-fh) – b(di – fg) + c(dh-eg) $ Рассмотрим систему уравнений, показанную ниже: $ \begin{align*} { 2x } + 3y &= \ , { 7 } \\ { – 3x } + 4y &= { 15 } \end{align*} $ Теперь мы назовем несколько матриц, которые помогут нам в дальнейшем использовать правило Крамера для решения этой системы. Следуя формуле определителя $ 2 \times 2 $, мы можем записать определяющую матрицу как: $ D = \begin{vmatrix} 2 & 3 \\ { – 3 } & 4 \end{vmatrix } $ Мы назвали его «D». Подставив постоянные коэффициенты из системы в первый столбец (вместо $ x $s), можно написать другую матрицу: $ D_{ x } = \begin{vmatrix} 7 & 3 \\ { 15 } & 4 \end{vmatrix} $ Мы назвали его «$ D_{ x } $» и назвали его x -матрица . Аналогично, подставив константы из системы во второй столбец (вместо $y$s), можно написать другую матрицу: $ D_{ y } = \begin{vmatrix} 2 & 7 \ \ { – 3 } & 15 \end{vmatrix} $ Мы обозначили его как «$ D_{ y } $» и назвали его y-матрицей . Теперь формула правила Крамера для решения переменных $ x $ и $ y $ показана ниже: $ x = \frac{ D_{ x } }{ D } = \frac{ \begin {vmatrix} 7 и 3 \\ { 15 } & 4 \end{vmatrix} }{ \begin{vmatrix} 2 & 3 \\ { – 3 } & 4 \end{vmatrix} } $ $ y = \frac { D_{ y } }{ D } = \frac{ \begin{vmatrix} 2 и 7 \\ { – 3 } & 15 \end{vmatrix} }{ \begin{vmatrix} 2 & 3 \\ { – 3 } & 4 \end{vmatrix} } $ В следующем разделе мы покажем, как на самом деле использовать правило и решить систему! Обратите внимание, что мы не может использовать правило Крамера, когда определитель матрицы равен $ 0 $! Нулевой определитель может означать: Система несовместна (не имеет решения) Система зависима (имеет бесконечные решения) В этом случае приходится полагаться на другие методы в решение системы, такой как метод замены/исключения или метод исключения Гаусса. Как пользоваться правилом Крамера? Давайте решим систему уравнений ( переменные $ 2 $ ), используя правило Крамера, чтобы увидеть концепцию в прямом эфире в действии! Решите приведенную ниже систему уравнений, используя правило Крамера: $ \begin{align*} { 2x } + y &= \, { 7 } \\ { 3x } – 2y &= { – 7 } \end{align*} $ Первым шагом является запись определителей этой системы уравнений, определителя ( $ D $ ), определителя $ x – $ ( $ D_ { x } ) и определителя $ y – $ ($D_{у}). Давайте воспользуемся выученной формулой и запишем их: $ D = \begin{vmatrix} 2 & 1 \\ { 3 } & { – 2 } \end{vmatrix} $ $ D_{ x } = \begin{vmatrix} 7 & 1 \\ { – 7 } & { – 2 } \end{vmatrix} $ $ D_{ y } = \begin{vmatrix} 2 & { 7 } \\ { 3 } & { – 7 } \end{vmatrix} $ Вспомните формулу для вычисления определителя $ 2 \times 2 $: Для матрицы $ 2 \times 2 $ — $ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} $ Определитель вычисляется как — $ det( A ) = | А | = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad – bc $ Вычислим определители: $ D = \begin{vmatrix} 2 & 1 \\ { 3 } & { – 2 } \end{vmatrix} = ( 2 )( – 2 ) – ( 1 )( 3 ) = – 4 – 3 = – 7 $ $ D_{ x } = \begin{vmatrix} 7 & 1 \\ { – 7 } & { – 2 } \end{vmatrix} = ( 7 )( – 2 ) – ( 1 )( – 7 ) = – 14 – ( – 7 ) = – 14 + 7 = – 7 $ $ D_{ y } = \begin{vmatrix} 2 & { 7 } \\ { 3 } & { – 7 } \end{vmatrix} = ( 2 )( – 7 ) – ( 7 )( 3 ) = -14 – 21 = – 35 $ Теперь мы можем использовать формулы и, таким образом, Правило Крамера , чтобы найти переменные $ x $ и $ y $. Ниже показано: $ x = \frac{ D_{ x } }{ D } = \ frac{ – 7 }{ – 7 } = 1 $ $ y = \ frac{D_{ y } }{ D } = \frac{ – 35 }{ – 7 } = 5 $ набор решений системы равен (1, 5) . Вы можете заметить, что если бы мы хотели решить только для $ 1 $ переменных, не решая всю систему, мы могли бы легко использовать формулу для одной переменной, чтобы найти ее. Правило Крамера — довольно изящный инструмент для поиска решений системы уравнений. Мы увидим несколько примеров, а также один с переменными $3$. Пример 1 Решите приведенную ниже систему уравнений, используя правило Крамера: $ \begin{align*} { – x } – y &= \, { 5 } \\ { 2x } + y &= { 4 } \end{align*} $ Решение Первым шагом является запись определителей этой системы уравнений, определитель ( $ D $ ), $ x – $ определитель ( $ D_ { x } ) и определитель $ y – $ ( $ D_{ y } ). Давайте воспользуемся выученной формулой и запишем их: $ D = \begin{vmatrix} – 1 & – 1 \\ { 2 } & { 1 } \end{vmatrix} $ $ D_{ x } = \begin{vmatrix} 5 & – 1 \\ { 4 } & { 1 } \end{vmatrix} $ $ D_{ y } = \begin{vmatrix} – 1 & { 5 } \\ { 2 } & { 4 } \end{vmatrix} $ используйте формулу для вычисления определителей матриц $2\times 2$ для вычисления матриц $D$, $D_{x}$ и $D_{y}$. $ D = \begin{vmatrix} – 1 & – 1 \\ { 2 } & { 1 } \end{vmatrix} = (– 1 )( 1 ) – ( – 1 )( 2 ) = – 1 + 2 = 1 9 долларов США0003 $ D_{ x } = \begin{vmatrix} 5 & – 1 \\ { 4 } & { 1 } \end{vmatrix} = ( 5 )( 1 ) – ( – 1 )( 4 ) = 5 + 4 = 9 $ $ D_{ y } = \begin{vmatrix} – 1 & { 5 } \\ { 2 } & { 4 } \end{vmatrix} = ( – 1 )( 4 ) – ( 5 )( 2 ) = – 4 – 10 = – 14 $ Теперь воспользуемся формулами, изученными в правиле Крамера, чтобы найти значения переменных: $ x = \frac{ D_{ x } }{ D } = \frac{ 9 }{ 1 } = 9 $ $ y = \frac{D_{ y } }{ D } = \frac{ – 14 }{ 1 } = – 14 $ Набор решений системы стоит $ (9, – 14) $ . Рассмотрим пример с переменными $3$. Пример 2 Решите приведенную ниже систему уравнений с помощью правила Крамера: – c &= 5 \\ a – 2b + 3c = 6 \end{align*} $ Решение Первый шаг – записать определители этой системы уравнений, определитель ($D$), $a – $детерминант ($D_{a}), $b–$ определитель ($D_{b}) и $c–$ определитель ($D_{c}). Давайте воспользуемся выученной формулой и запишем их: $ D = \begin{vmatrix} 2 & 1 & -2 \\ 3 & -3 & -1 \\ 1 & -2 & 3 \end{vmatrix} $ $ D_{ a } = \begin{ vmatrix} -1 & 1 & -2 \\ 5 & -3 & -1 \\ 6 & -2 & 3 \end{vmatrix} $ $ D_{ b } = \begin{vmatrix} 2 & -1 & -2 \\ 3 & 5 & -1 \\ 1 & 6 & 3 \end{vmatrix} $ $ D_{ c } = \begin{vmatrix} 2 & 1 & -1 \\ 3 & -3 & 5 \\ 1 & -2 & 6 \end{vmatrix} $ Для матрицы вида: $ B = \begin{bmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \end {bmatrix} $ Определитель вычисляется как : $ | Б | = a(ei-fh) – b(di – fg) + c(dh-eg) $ Теперь воспользуемся правилом Крамера и вычислим значения переменных $a $, $b$ и $c$ . Шаги показаны ниже (мы не показывали подробные шаги нахождения определителей $ 3 \times 3 $ матриц): $ a = \frac{ D_{ a } }{ D } = \frac{ \ begin{vmatrix} -1 & 1 & -2 \\ 5 & -3 & -1 \\ 6 & -2 & 3 \end{vmatrix} }{ \begin{vmatrix} 2 & 1 & -2 \\ 3 & -3 & -1 \\ 1 & -2 & 3 \end{vmatrix} } = \frac{-26}{-26} =1 $ $ b = \frac{D_{ b } }{D } = \frac{ \begin{vmatrix} 2 & -1 & -2 \\ 3 & 5 & -1 \\ 1 & 6 & 3 \end{ vmatrix} }{ \begin{vmatrix} 2 & 1 & -2 \\ 3 & -3 & -1 \\ 1 & -2 & 3 \end{vmatrix} } = \frac{26}{-26} = - 1 $ $ c = \frac{D_{c} }{D} = \frac{ \begin{vmatrix} 2 & 1 & -1 \\ 3 & -3 & 5 \\ 1 & -2 & 6 \ end{vmatrix} }{ \begin{vmatrix} 2 & 1 & -2 \\ 3 & -3 & -1 \\ 1 & -2 & 3 \end{vmatrix} } = \frac{-26}{-26 } = 1$ Набор решений системы равен $ (1, – 1,1) $. Практические вопросы Решите приведенную ниже систему уравнений, используя правило Крамера: &= { 20 } \end{align*} $ Решите приведенную ниже систему уравнений, используя правило Крамера: $ \begin{align*} 3x – 4y + z &= \, -5 \ \ x – y – z &= – 10 \\ 6x – 8y + 2z = 10 \end{align*} $ Ответы Первым шагом является запись определителей этой системы уравнений, определителя ( $ D $ ), $ x – $ определителя ( $ D_{ x } $ ) и $ y – $ определитель ($D_{y}$). Давайте воспользуемся выученной формулой и запишем их: $ D = \begin{vmatrix} 5 & 2 \\ { – 1 } & { 4 } \end{vmatrix} $ $ D_{ x } = \begin {vmatrix} 10 & 2 \\ { 20 } & { 4 } \end{vmatrix} $ $ D_{ y } = \begin{vmatrix} 5 & { 10 } \\ { – 1 } & { 20 } \ конец{vmatrix} $ Мы будем использовать формулу для вычисления определителей матриц $ 2 \times 2 $ для вычисления матриц $ D $, $ D_{ x } $ и $ D_ { y } $. 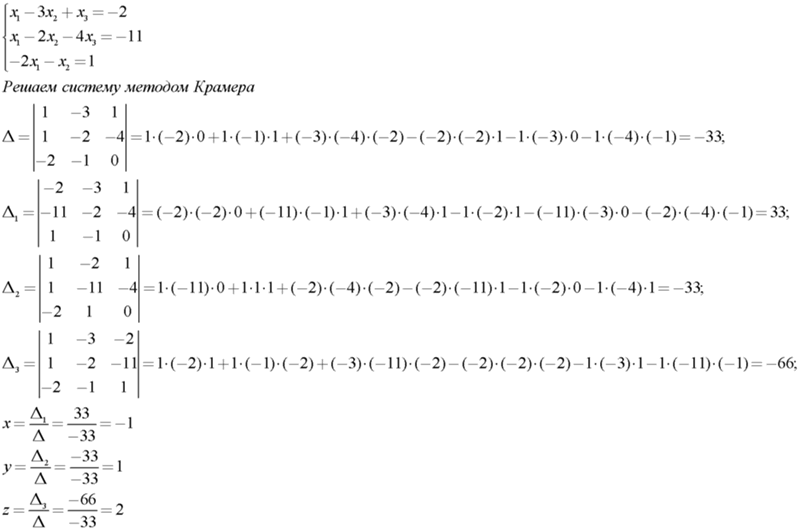$ D = \begin{vmatrix} 5 & 2 \\ { – 1 } & { 4 } \end{vmatrix} = ( 5 )( 4 ) – ( 2 )( -1 ) = 20 + 2 = 22 $ $ D_{x} = \begin{vmatrix} 10 & 2 \\ {20} & {4} \end{vmatrix} = (10)(4) – (2)(20) = 40 – 40 = 0 $ $ D_{ y } = \begin{vmatrix} 5 & {10} \\ {– 1} & {20} \end{vmatrix} = (5)(20) – (10)(-1) = 100 + 10 = 110 9 долл. США0003 Теперь воспользуемся формулами, изученными в правиле Крамера, чтобы найти значения переменных: $ x = \frac{ D_{ x } }{ D } = \frac{ 0 }{ 22 } = 0 $ $ y = \frac{D_{ y } }{D } = \frac{ 110 }{ 22 } = 5 $ набор решений системы равен $ (0, 5) $. Первый шаг - записать определители этой системы уравнений, определитель ($D$), $x – определитель $ ($D_{x} ), $y – определитель $ ($D_{y}) $, и определитель $ z – $ ( $ D_{ z } ) $. Давайте воспользуемся выученной формулой и запишем их: $ D = \begin{vmatrix} 3 & -4 & 1 \\ 1 & -1 & -1 \\ 6 & -8 & 2 \end{vmatrix} $ $ D_{ x } = \begin{ vmatrix} 5 & -4 & 1 \\ -10 & -1 & -1 \\ 10 & -8 & 2 \end{vmatrix} $ $ D_{ y } = \begin{vmatrix} 3 & 5 & 1 \\ 1 & -10 & -1 \\ 6 & 10 & 2 \end{vmatrix} $ $ D_{ z } = \begin{vmatrix} 3 & -4 & 5 \\ 1 & -1 & -10 \\ 6 & -8 & 10 \end{vmatrix} $ Напомним, что $ 3 \times 3 $ матрица вида: $ B = \begin{bmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \end {bmatrix} $ Имеет определитель, равный: $ | Б | = a(ei-fh) – b(di – fg) + c(dh-eg) $ Сначала найдем значение определителя $D$, $ D = \begin{vmatrix} 3 & -4 & 1 \\ 1 & -1 & -1 \\ 6 & -8 & 2 \end{vmatrix} = 3(-2-8) +4(2+6) +1(-8+6) = 3(-10) + 4(8) +1(-2) = 0 $ Определитель этой матрицы равен $ 0 $; таким образом, мы не можем решить систему, используя правило Крамера!! Предыдущий урок | Главная страница | Next Lesson Правило Крамера Redux Вот первый прием по использованию правила Крамера на матрицах 3 × 3. Это не работает для матриц 4 × 4 и больше, и, конечно, нам это не нужно для 2 × 2. Допустим, у нас есть эта дерзкая маленькая матрица 3 × 3, которую мы бы с удовольствием представили нашей подруге Крамер, если бы только она привела с собой свою подругу Детерминант. Вот что мы делаем, чтобы найти определитель матрицы 3 × 3. Сначала скопируйте левый и центральный столбцы справа от матрицы: Вы, конечно, помните, что метод Крамера 2 × 2 заставлял нас умножать по диагонали из левого верхнего угла в правый нижний, а затем вычитать из левого нижнего в верхний правый. Это на самом деле очень похоже. Главное — не перепутать столбцы, которые вы копируете повторно. Теперь, когда у нас есть наша матрица и левый и центральный столбцы из нее, скопированные за пределы полос, мы готовы вычислить определитель так же, как мы сделали 2 × 2. Сначала умножаем из левого верхнего угла в правый нижний, а затем складываем. Мы делаем это три раза — поэтому мы снова добавили первые два столбца: D = aei + bfg + cdh … Затем мы снова вычитаем из нижнего левого угла в верхний правый, точно так же, как мы делали раньше: D = aei + bfg + cdh – gec – hfa – idb 8 80002 Вот и все. Итак, в ситуации с реальными числами: Сначала мы скопируем первые два столбца снаружи и справа от полос: И с этого момента, это в основном plug 'n' chug: D = (4)(1)(4) + (1)(5)(3) + (0)(2)(0) – (3)(1)(0) – (0)(5) (4) – (4)(2)(1) = 16 + 15 + 0 – 0 – 0 – 8 = 23 Понятно. Пример задачи Теперь, поскольку мы знаем, как получить определитель для матрицы 3 × 3, вот как мы находим переменные с помощью правила Крамера, когда их три. Вот наши три счастливых холостяка: 2 x + Y -3 Z = 8 -3 x + 2 Y + Z = 10 x -3 y + 2 7777 x -3 y + 2 77777 x -3 y + 2 77777 x -3 y + 2 7777 x -3 Y + 2 777 x -3 . Первый шаг - найти D , определитель коэффициента. Мы только что узнали, как это сделать для матрицы 3 × 3, так что поехали. Сначала создайте матрицу коэффициентов: Ого! Вот оно. Далее находим D : Вспоминаем нашу маленькую хитрость, где мы снова копируем первые два столбца наружу и вправо от матрицы: Отлично, Смитерс. Теперь умножаем и прибавляем по диагонали сверху слева направо снизу: D = (2)(2)(2) + (1)(1)(1) + (-3)(-3)(- 3)… Затем мы умножаем и вычитаем по диагонали снизу слева направо вверх: D = (2)(2)(2) + (1)(1)(1) + (-3)( -3)(-3) – (1)(2)(-3) – (-3)(1)(2) – (2)(-3)(1) Итак: D = 8 + 1 + (-27) – (-6) – (-6) – (-6) = 0 Рух-рох, Лохматый! Когда D = 0, точных значений быть не может! (Вы помните?) Мы подумали, что эти уравнения выглядят подозрительно. Ну как насчет этих? Sample Problem Solve the following system of equations: 3 x – y – 4 z = 10 -2 x + 5 y + z = 9 -3 x + 4 y + 2 z = 8 Сначала мы разбиваем нашу матрицу коэффициентов: Вы устали от поиска D ? Ага, вы меня знаете: Копируем первые два столбца прямо снаружи и справа от матрицы: Затем пришло время умножать и прибавлять по диагонали сверху слева вниз справа и затем умножать и вычитать по диагонали снизу слева направо вверх: D = (3)(5)(2) + (-1)(1)(-3) + (-4)(-2)(4) – ( -3)(5)(-4) – (4)(1)(3) – (2)(-2)(-1) Отсюда математическое счастье: D = 30 + 3 + 32 – 60 – 12 – 4 = -11 Мы знаем, что D = -11, так что теперь мы ищем другие определители. Мы знаем, что эти три вещи верны: Мы знаем, что способ найти D _x состоит в том, чтобы подставить постоянные значения в смесь вместо значений x , а затем используйте наш трюк с копированием столбцов, чтобы получить числа. Время для большего количества подключи и пыхтение. Удалить x -значения: Замените их постоянными значениями: Скопируйте первые два столбца в нашей модифицированной матрице снаружи и справа: внизу справа, а затем умножить и вычесть по диагонали снизу слева направо вверх: D _x = (10)(5)(2) + (-1)(1)(8) + (-4) (9)(4) – (8)(5)(-4) – (4)(1)(10) – (2)(9)(-1) = 100 + (-8) + (-144 ) – (-160) – 40 – (-18) = 86 Далее. Ищем D _и . Вот оно, лишенное всех и -значений. Теперь мы подставляем постоянные значения и прокручиваем оттуда: Уловка столбца: Подключи и пыхти: D _y = (3)(9)(2) + (10)( 1)(-3) + (-4)(-2)(8) – (-3)(9)(-4) – (8)(1)(3) – (2)(-2)(10 ) = 54 + (-30) + 64 – 108 – 24 – (-40) = -4 Решите для y , пока мы здесь: Мы , так что почти готово. Итак, наша маленькая матрица, голая из всех z -значений: Подставляем постоянные значения: Ах, постоянные значения. Вы дополняете нас. Уловка с колонкой: Подключи и пей, детка: D _z = (3)(5)(8) + (-1)(9)(-3) + (10)(-2 )(4) – (-3)(5)(10) – (4)(9)(3) – (8)(-2)(-1) = 120 + 27 + (-80) – (-150) – 108 – 16 = 93 Еще одно торжество человеческого духа. Наконец, мы находим определитель z : Итак: Как и немецкая опера, они отнимают много времени и могут показаться повторяющимися, но отдача ощущается великолепно. А если вы ненавидите оперу или алгебру, расплата будет за то, что вы уйдете или закончите, так что это еще лучше. Изучите правила для матриц 2x2 и 3x3, формулы здесь 0 Сохранить Скачать публикацию в формате PDF Правило Крамера в матрицах представляет решение в терминах определителей матрицы коэффициентов и матриц, полученных заменой одного столбца на вектор-столбец правых частей уравнений. Правило Крамера возникает в матрицах и определителях. Всякий раз, когда система имеет единственное решение, правило Крамера будет самым надежным способом определить решение системы линейных уравнений, в которой столько уравнений, сколько неизвестных. По мере чтения статьи вы узнаете о формуле правила Крамера, концепции определителей, линейных уравнениях, условиях единственного решения в матрице, отсутствии условий решения и многом другом. Прежде чем перейти к обсуждению правила Крамера и его методов с решенными примерами, давайте узнаем о некоторых ключевых терминах. Правило Крамера Правило Крамера — это явный метод решения системы линейных уравнений с несколькими уравнениями и неизвестными, т. е. квадратной матрицы, действующий, когда система имеет единственное решение. Правило Крамера — это дополнительный подход, позволяющий решать системы линейных уравнений с использованием определителей. Он представляет решение через определители (квадратной матрицы) матрицы коэффициентов и матриц, полученных из нее заменой одного столбца на вектор правых частей уравнений. Правило Крамера для матрицы 2×2 Система линейных уравнений с двумя и тремя переменными может быть эффективно решена путем применения определителей. Ниже приведены формулы и шаги для определения решения системы линейных уравнений вместе с решенными примерами. \(\begin{array}{l} Рассмотрим\ линейную\ систему:\\ ax+by=p\ и\ cx+dy=q\ \\ \ эквивалентную\ матрицу\ form=\begin {bmatrix}a&b\\ c&d\end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}p\\ q\end{bmatrix}\\ Здесь,\ D=\begin{bmatrix}a&b\\ c&d\end{bmatrix}\\ Рассмотрим \det er\min ant\ отличен от нуля.\\ Тогда\ x\ и\ y\ можно\ вычислить\ по\ правилу Крамера\:\\ x=\frac{\begin{ vmatrix}p&b\\ q&d\end{vmatrix}}{\begin{vmatrix}a&b\\ c&d\end{vmatrix}}=\frac{\left(pd-bq\right)}{\left(ad- bc\right)}\\ Здесь,\ \left|D_x\right|=\begin{vmatrix}p&b\\ q&d\end{vmatrix}\\ y=\frac{\begin{vmatrix}a&p\\ c&q\end{vmatrix}}{\begin{vmatrix}a&b\\ c&d\end{vmatrix}}=\frac{\left(aq-pc\ right)}{\left(ad-bc\right)}\\ Здесь,\ \left|D_y\right|=\begin{vmatrix}a&p\\ c&q\end{vmatrix}\end{array} \ ) Узнайте больше о линейных неравенствах здесь. Пример правила Крамера 2×2 $\begin{array}{l}Рассмотрим\ линейную\ систему:\\ 4x-3y=11\ и\ 6x+5y=7\\ \эквивалентная\матрица\форма=\begin{bmatrix}4&-3\\ 6&\ 5\end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}11\\ 7\end{bmatrix}\\ D=\begin{bmatrix} 4&-3\\ 6&\ 5\end{bmatrix}\стрелка вправо\влево|D\вправо|=\begin{vmatrix}4&-3\\ 6&\ 5\end{vmatrix}=\left(4\times5 \right)-\left(-3\times6\right)\\ \left|D\right|=20+18=38\\ For\ x\\ D_x=\begin{bmatrix}11&-3\ \ 7&\ 5\end{bmatrix}\Стрелка вправо\влево|D_x\right|=\begin{vmatrix}11&-3\\ 7&\ 5\end{vmatrix}=55+21\\ \left|D_x\right|=76\\ x=\frac{\left|D_x\right|}{\left|D\right|}=\frac{76}{38}=2\\ Для \ y\\ D_y=\begin{bmatrix}4&11\\ 6&\ 7\end{bmatrix}\Стрелка вправо\влево|D_y\right|=\begin{vmatrix}4&11\\ 6&\ 7\end{vmatrix }=28-66=-38\\ y=\frac{\left|D_y\right|}{\left|D\right|}=\frac{-38}{38}=-1\\ ( x,y)=(2,−1)\end{array} $ Ознакомьтесь с этой статьей о системах счисления. Правило Крамера для матрицы 3×3 \(\begin{array}{l}Рассмотрим\ линейную\ систему:\\ ax+by+cz=p\ ,\ dx+ey+fz=q\ и\gx+hy+iz=r\\ \ эквивалентная\ матрица\ form=\begin{bmatrix}a&b&c\\ d&e&f\ \ g&h&i\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}=\begin{bmatrix}p\\ q\\ r\end{bmatrix}\\ Здесь \ D=\begin{bmatrix}a&b&c\\ d&e&f\\ g&h&i\end{bmatrix}and\ \left|D\right|=\begin{vmatrix}a&b&c\\ d&e&f\\ g&h&i\end {vmatrix}\\ Тогда\ значения\ x\, y\ и\ z\ вычисляются\ по\ правилу Крамера\:\\ x=\frac{\begin{vmatrix}p&b&c\\ q&e&f\\ r&h&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\ d&e&f\\ g&h&i\end{vmatrix}}\\ Здесь \ \left|D_x\right|=\begin{vmatrix}p&b&c\\ q&e&f\\ r&h&i\end{vmatrix}\\ y=\frac{\begin{vmatrix}a&p&c\\ d&q&f\\ g&r&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\ d&e&f\\ g&h&i\end{vmatrix}}\\ Здесь,\ \left|D_y\right|=\begin{vmatrix}a&p&c\ \ d&q&f\\ g&r&i\end{vmatrix}\\ z=\frac{\begin{vmatrix}a&b&p\\ d&e&q\\ g&h&r\end{vmatrix}}{\begin{vmatrix}a&b&c\\ d&e&f \\ g&h&i\end{vmatrix}}\\ Здесь,\ \left|D_z\right|=\begin{vmatrix}a&b&p\\ d&e&q\\ g&h&r\end{vmatrix}\end{array} \ ) $\begin{array}{l}Для\ упрощения\\ x=\frac{\begin{vmatrix}p&b&c\\ q&e&f\\ r&h&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\ d&e&f\\ g&h&i\end{vmatrix}}=\frac{\left|D_x\right|}{\left|D\right|} \\ Где\ D=\begin{vmatrix}a&b&c\\ d&e&f\\ g&h&i\end{vmatrix},\ D_x=\begin{vmatrix}p&b&c\\ q&e&f\\ r&h&i\end{vmatrix}\ \ y=\frac{\begin{vmatrix}a&p&c\\ d&q&f\\ g&r&i\end{vmatrix}}{\begin{vmatrix}a&b&c\\ d&e&f\\ g&h&i\end{vmatrix}}=\frac{\left|D_y\right|}{\left|D\right|}\\ Где\ D=\begin{vmatrix}a&b&c\\ d&e&f\\ g&h&i \end{vmatrix}\ ,\ D_y=\begin{vmatrix}a&p&c\\ d&q&f\\ g&r&i\end{vmatrix}\\ z=\frac{\begin{vmatrix}a&b&p\\ d&e&q\\ g&h&r\end{vmatrix}}{\begin{vmatrix}a&b&c\\ d&e&f\\ g&h&i\end{vmatrix}}=\frac{\left|D_z\right|}{\left|D\right|}\ \ Где\ D=\begin{vmatrix}a&b&c\\ d&e&f\\ g&h&i\end{vmatrix}\ ,\ D_z=\begin{vmatrix}a&b&p\\ d&e&q\\ g&h&r\end{vmatrix}\end {массив} $ Изучите концепции трехмерной геометрии здесь. Пример правила Крамера 3×3 \(\begin{array}{l}Рассмотрим\ линейную\ систему:\\ x+2y+3z=-5\ ,\ 3x+y-3z= 4\ и\ -3x+4y+7z=-7\\ \ Эквивалентная\ матрица\ form=\begin{bmatrix}1&2&3\\ 3&1&-3\\ -3&4&7\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}=\begin{bmatrix}-5\\ 4\\ -7 \end{bmatrix}\\ Здесь,\ D=\begin{bmatrix}1&2&3\\ 3&1&-3\\ -3&4&7\end{bmatrix}\\ \left|D\right|=\begin{vmatrix }1&2&3\\ 3&1&-3\\ -3&4&7\end{vmatrix}=40\\ D_x=\begin{bmatrix}-5&2&3\\ 4&1&-3\\ -7&4&7\end{bmatrix}\\ \влево|D_x\вправо|=-40\\ D_y=\begin{bmatrix}1&-5&3\\ 3&4&-3\\ -3&-7&7\end{bmatrix}\\ \left|D_y\right|=40\\ D_z=\begin{bmatrix }1&2&-5\\ 3&1&4\\ -3&4&-7\end{bmatrix}\\ \left|D_z\right|=-80\\ Тогда\ значение\ x\ ,y\ и\ z \ быть\ рассчитано\ по\ правилу Крамера\:\\ x=\frac{\left|D_x\right|}{\left|D\right|}=-\frac{40}{40}=-1\ \ y=\frac{\left|D_y\right|}{\left|D\right|}=\frac{40}{40}=1\\ z=\frac{\left|D_z\right| }{\left|D\right|}=\frac{-80}{40}=-2\\ (x,y,z)=(−1,1,−2)\end{array} \) Условия для правила Крамера Правило Крамера эффективно для решения небольших систем и может быть вычислено довольно быстро; но по мере роста системы определение новых детерминант может быть утомительным. Например, для системы уравнений с единственным решением определитель матрицы должен быть невырожденным, то есть его значение должно быть ненулевым. \(\begin{array}{l} Рассмотрим\ два\ уравнения:\\ ax_1+by_1=c_1\\ ax_2+by_2=c_2\\ Одно\ или\бесконечно\ много\ решений\ называются\ непротиворечивым\ решением.\\ Для\ единственного\ решения\левого (непротиворечивого\ и\независимого\правого)\ :\ \frac{a_1}{a_2}\ne\frac{b_1}{b_2}\ или\ \ a_1b_2-a_2b_1=0\\ Единственное\ решение\ представляет\ пересекающиеся\ линии.\\ Для\ Бесконечно\много\решений\слева(непротиворечивых\и\зависимых\справа):\\\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\\ Бесконечно\ много \решения\ представляют\ совпадающие\ линии.\\ Нет\ решения\ (несовместимые\ и\ независимые):\ \frac{a_1}{a_2}=\frac{b_1}{b_2}\ne\frac{c_1}{ с_2}\\ Нет\ решения\ представляют\ параллельные\ непересекающиеся\ линии.\end{массив}\) Если вы читаете Правило Крамера, вам также следует прочитать о Множествах здесь. Мы надеемся, что приведенная выше статья о правиле Крамера поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам. Часто задаваемые вопросы о правиле Крамера В.1 Как работает правило Крамера? Ответ 1 Правило Крамера — это метод, использующий детерминанты для решения систем уравнений, содержащих такое же количество уравнений, что и переменных. То есть он работает только с квадратными матрицами, имеющими ненулевой определитель и единственное решение. Q.2 Какие преимущества имеет правило Крамера? Ответ 2 Правило Крамера позволяет определить только одну искомую переменную, например, если у вас есть система с тремя переменными и тремя уравнениями и вы хотите найти только одну. Это позволяет нам делать это очень быстро и легко. Q.3 Что утверждает правило Крамера? Ответ 3 Правило Крамера в матрицах представляет решение через определители матрицы коэффициентов и матриц, полученных из нее заменой одного столбца на вектор-столбец правых частей уравнений. В.4 Как проверить правило Крамера? Ответ 4 Для получения n-го решения системы линейных уравнений по правилу Крамера заменяет n-й столбец основной матрицы вектором решения и оценивает его определитель. Затем разделите этот определитель на главный. В.5 Каковы ограничения правила Крамера? Ответ 5 Поскольку для получения результата мы делим на определитель, правило Крамера работает, только если det(A) не равно нулю. Если det(A) = 0, правило Крамера не может быть использовано, потому что единственного решения не существует, поскольку было бы бесконечно много решений или вообще не было бы решений.