Метод Гаусса
Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (быть несовместной).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений, который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.
Преобразования расширенной матрицы (это матрица системы – матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) строки матрицы можно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует
4) строку матрицы можно умножить (разделить) на любое число, отличное от нуля.
5) к строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» – с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду:
Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х1, стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0.
Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0.
2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную хn. Для этого решаем элементарное уравнение А*хn = В. В примере, приведенном выше, х3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной.
 Например, х2 – 4 = 1, т.е. х2
Например, х2 – 4 = 1, т.е. х2
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
1 шаг. К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по апробированной методике:
2 шаг. Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг. Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг. К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг. Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23), и, соответственно, 11x3 = 23, x3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x3 = 1
x2 = 3
x1 + x2 – x3 = 1, следовательно x1 + 3 – 1 = 1, x1 = –1
Ответ: x1 = –1, x2 = 3, x3 = 1.
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3. Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
Умножим второе и третье уравнения на 4, получим:
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0.4 –0.6 0.6
0 0. 64 –3 –1
64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х3 = 0,96 или приблизительно 1.
х2 = 3 и х1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Матрицы. Метод Гаусса. Формулы Крамера
1. Матрицы
Метод ГауссаФормулы Крамера
2. Матрица Определение
Прямоугольная таблица из m, n чисел, содержащая m – строк и n –столбцов, вида: a a a a
a 11a 12 a 1i a1n
2j
2n
21 22
a a a a
ij
in
a a a a
mj
mn
m1 m 2
называется
матрицей размера
m n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента аi j в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так:
A (aij ) ;
i 1, m;
j 1, n
3.
 Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)
Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)4. Метод Гаусса
Метод Гаусса — классический метод решения системылинейных алгебраических уравнений. Это метод последовательного
исключения переменных, когда с помощью элементарных
преобразований система уравнений приводится к равносильной
системе ступенчатого (или треугольного) вида, из которого
последовательно, начиная с последних (по номеру) переменных,
находятся все остальные переменные.
Система т линейных уравнений с п неизвестными имеет вид:
a11 x1 a12 x2 … a1n xn b1
a 21 x1 a 22 x2 … a 2 n xn b2
………………………………………..
a m1 x1 a m 2 x2 … am n xn bn
x1 , x2, …, xn – неизвестные.
ai j – коэффициенты при неизвестных.
bi – свободные члены (или правые части)
5. Типы уравнений
Система линейных уравнений называется совместной, если онаимеет решение, и несовместной, если она не имеет решения.

Совместная система называется определенной, если она имеет
единственное решение и неопределенной, если она имеет
бесчисленное множество решений.
Две совместные системы называются равносильными, если они
имеют одно и то же множество решений.
6. Элементарные преобразования
К элементарным преобразованиям системы отнесем следующее:1.
2.
3.
перемена местами двух любых уравнений;
умножение обеих частей любого из уравнений на
произвольное число, отличное от нуля;
прибавление к обеим частям одного из уравнений системы
соответствующих частей другого уравнения, умноженных на
любое действительное число.
7. Общий случай
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений стремя неизвестными в случае, когда существует единственное решение:
Дана система:
a11 x1 a12 x2 a13 x3 b1
a21 x1 a22 x2 a23 x3 b2
a x a x a x b
32 2
33 3
3
31 1
(1)
1-ый шаг метода Гаусса
На первом шаге исключим неизвестное х1 из всех уравнений системы (1), кроме
первого.
 Пусть коэффициент . Назовем его ведущим элементом. Разделим первое
Пусть коэффициент . Назовем его ведущим элементом. Разделим первоеуравнениеa системы (1) на аb11. Получим уравнение:
где
a1 j
(1)
1j
a11
;
j 1,2,3 ;
b1
(1)
1
a11
Исключим х1 из второго и третьего уравнений системы (1). Для этого вычтем из
них уравнение (2), умноженное на коэффициент при х1 (соответственно а21 и а31).
x a x a x b
(2)
Система примет вид:
(1)
1
12
(1)
2
13
(1)
3
1
Верхний индекс (1) указывает, что речь идет о коэффициентах первой
преобразованной системы. x a x a x b
a x a x b
(3)
(1)
1
12
(1)
22
(1)
2
2
13
(1)
23
(1)
3
3
1
(1)
2
a32 x2 a33 x3 b3
(1)
(1)
(1)
2-ой шаг метода Гаусса
На втором шаге исключим неизвестное х2 из третьего уравнения системы (3).
Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе
уравнение системы (3), получим уравнение: x a x b (4)
( 2)
2
где
a23
( 2)
a23
(1)
a22
(1)
;
b2
( 2)
b2
23
( 2)
3
2
(1)
a22
(1)
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на
Получим уравнение:
Предполагая, что
a33
( 2)
x3
b3
( 2)
находим
a33
( 2)
0,
x3
b3
( 2)
a33
( 2)
b3
3
(1)
a33 .

В результате преобразований система приняла вид:
x1 a12 (1) x 2 a13 (1) x3 b1 (1)
( 2)
( 2)
x 2 a 23 x3 b2
( 3)
x3 b3
(5)
Система вида (5) называется треугольной.
Процесс приведения системы (1) к треугольному виду (5)
(шаги 1 и 2) называют прямым ходом метода Гаусса.
Нахождение неизвестных из треугольной системы
называют обратным ходом метода Гаусса.
Для этого найденное значение х3 подставляют во второе
уравнение системы (5) и находят х2. Затем х2 и х3
подставляют в первое уравнение и находят х1.
Если в ходе преобразований системы получается противоречивое
уравнение вида 0 = b, где b 0, то это означает, что система несовместна и
решений не имеет.
В случае совместной системы после преобразований по методу Гаусса,
составляющих прямой ход метода, система т линейных уравнений с п
неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное
решение, которое находится в
x1 c12 x 2 .
 .. a1n x n d1
.. a1n x n d1x 2 … a 2 n x n d 2
…………….
xn d n
результате проведения обратного хода метода Гаусса.
Ступенчатая система имеет вид:
Такая система имеет бесчисленное
множество решений.
x1 c12 x2 … c1n xn d1
x2 … c2 n xn d 2
…………………
xk … ck n xn d k
11. Рассмотрим на примере
1.Покажем последовательность решения системы из трех уравнений методом Гаусса
Поделим первое уравнение на 2, затем вычтем его из второго (a21=1, поэтому
домножение не требуется) и из третьего, умножив предварительно на a31=3
2.
Поделим второе уравнение полученной системы на 2, а затем вычтем его из
третьего, умножив предварительно на 4,5 (коэффициент при x2)
3.
x3=-42/(-14)=3;
Тогда
x2=8-2×3=2
x1=8-0,5×2-2×3=1
12. Метод Крамера
Метод Крамера—способ решения квадратныхсистем линейных алгебраических уравнений с
ненулевым определителем основной матрицы.

Создан Габриэлем Крамером в 1751 году.
13. Габриэль Крамер (31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция)
14. Рассмотрим систему линейных уравнений с квадратной матрицей A , т.е. такую, у которой число уравнений совпадает с числом неизвестных:
Теорема. Cистемаa11x1+a12x2+…+a1nxn=b1
a21x1+a22x2+…+a2nxn=b2
…
…
an1x1+an2x2+…+annxn=bn
15. Имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля:
a11 a12 … a1na21 a22 … a2n
…
…
an1 an2 … ann
≠0
16. В этом случае решение можно вычислить по формуле Крамера
17. Для получения значения xk в числитель ставится определитель, получающийся из det(A) заменой его k-го столбца на столбец правых частей
Пример. Решить систему уравнений :18. Решение.
19. Найдите оставшиеся компоненты решения.
Формулы Крамера не представляют практического значения вслучае систем с числовыми коэффициентами: вычислять по
ним решения конкретных систем линейных уравнений
неэффективно, поскольку они требуют вычисления (n+1)-го
определителя порядка n , в то время как метод Гаусса
фактически эквивалентен вычислению одного определителя
порядка n .
 Тем не менее, теоретическое значение формул
Тем не менее, теоретическое значение формулКрамера заключается в том, что они дают явное
представление решения системы через ее коэффициенты.
Например, с их помощью легко может быть доказан результат
Решение системы линейных уравнений с квадратной
матрицей A является непрерывной функцией коэффициентов
этой системы при условии, что det A не равно 0 .
20. Найдите оставшиеся компоненты решения.
Кроме того, формулы Крамера начинают конкурировать по вычислительнойэффективности с методом Гаусса в случае систем, зависящих от параметра.
зависящей от параметра
решения:
, определить предел отношения компонент
21. Решение.
В этом примере определитель матрицысистемы равен
. По теореме Крамера
система совместна при
. Для случая
применением метода Гаусса убеждаемся,
что система несовместна. Тем не менее,
указанный предел существует. Формулы
Крамера дают значения компонент решения
в виде
и, хотя при
каждая из них имеет бесконечный предел, их
отношение стремится к пределу конечному.

22. Ответ.
Приведенный пример поясняет также каким образом система линейныхуравнений, непрерывно зависящая от параметра, становится
несовместной: при стремлении параметра к какому-то критическому
значению (обращающему в нуль определитель матрицы системы) хотя
бы одна из компонент решения «уходит на бесконечность».
23. Использованные источники
1.В.С. Щипачев, Высшая математика
2.
Ильин В. А., Позняк Э. Г. Линейная
алгебра: Учебник для вузов.
3.
Волков Е.А. Численные методы.
4.
В.Е. Шнейдер и др., Краткий курс
высшей математики,том I.
python – Numpy: решение системы линейных уравнений методом Гаусса
В конце приведена ссылка на jupyter notebook с более-менее полным решателем СЛАУ. Плюс трюк, как считать на pyton почти так же быстро, как на Фортране 🙂
Первоначальный ответ
Если не обращать внимание на возможное деление на ноль, то привидение к треугольному виду можно записать очень просто:
def gaussFunc(matrix):
# функция меняет матрицу через побочные эффекты
# если вам нужно сохранить прежнюю матрицу, скопируйте её np. copy
for nrow, row in enumerate(matrix):
# nrow равен номеру строки
# row содержит саму строку матрицы
divider = row[nrow] # диагональный элемент
# делим на диагональный элемент.
row /= divider
# теперь надо вычесть приведённую строку из всех нижележащих строчек
for lower_row in matrix[nrow+1:]:
factor = lower_row[nrow] # элемент строки в колонке nrow
lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
# все строки матрицы изменились, в принципе, можно и не возвращать
return matrix
copy
for nrow, row in enumerate(matrix):
# nrow равен номеру строки
# row содержит саму строку матрицы
divider = row[nrow] # диагональный элемент
# делим на диагональный элемент.
row /= divider
# теперь надо вычесть приведённую строку из всех нижележащих строчек
for lower_row in matrix[nrow+1:]:
factor = lower_row[nrow] # элемент строки в колонке nrow
lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
# все строки матрицы изменились, в принципе, можно и не возвращать
return matrix
Результат для вашего примера:
array([[ 1. , 1.76315789, -0.31578947, 1.36842105],
[-0. , 1. , 0.06800211, 0.49657354],
[ 0. , 0. , 1. , 0.09309401]])
В чём засада. В ходе вычислений может оказаться ноль на диагонали.
matrix = np.array([[1, 0, 0, 1],
[0, 0, 1, 2],
[0, 1, 0, 3]])
Насколько я помню, перед тем, как делить на диагональный элемент сначала просматривают все строки, начиная с текущей, вниз. Выбирают строку с максимальным значением в текущей колонке и переставляют с текущей. После чего продолжают.
Выбирают строку с максимальным значением в текущей колонке и переставляют с текущей. После чего продолжают.
Проверка результата.
Функция make_identity берёт матрицу, полученную методом Гаусса, и доводит её до единичной. Для этого строки перебираются снизу вверх и вычитаются из вышележащих строк, чтобы обнулить соответствующие колонки.
def make_identity(matrix):
# перебор строк в обратном порядке
for nrow in range(len(matrix)-1,0,-1):
row = matrix[nrow]
for upper_row in matrix[:nrow]:
factor = upper_row[nrow]
upper_row -= factor*row
return matrix
Результат для вашего примера:make_identity(gaussFunc(np.copy(matrix)))
array([[ 1. , 0. , 0. , 0.53344344],
[-0. , 1. , 0. , 0.49024295],
[ 0. , 0. , 1. , 0.09309401]])
Вырезаем последний столбец, получим строку корней: roots = make_identity(gaussFunc(np. copy(matrix)))[:,3]
copy(matrix)))[:,3]
array([0.53344344, 0.49024295, 0.09309401])
Умножаем найденные корни на исходную матрицу и сравниваем с последним столбцом исходной задачи: np.matmul(matrix[:,:3], roots.T) - matrix[:,3]
Результат вычисления array([ 0.00000000e+00, -4.44089210e-16, -2.22044605e-16])
Следовательно, корни найдены правильно. С чем и поздравляю.
UPDATE
Метод Гаусса с выбором главного элемента. Плюс добавлена обработка нуля на диагонали.
def gaussPivotFunc(matrix):
for nrow in range(len(matrix)):
# nrow равен номеру строки
# np.argmax возвращает номер строки с максимальным элементом в уменьшенной матрице
# которая начинается со строки nrow. Поэтому нужно прибавить nrow к результату
pivot = nrow + np.argmax(abs(matrix[nrow:, nrow]))
if pivot != nrow:
# swap
# matrix[nrow], matrix[pivot] = matrix[pivot], matrix[nrow] - не работает. # нужно переставлять строки именно так, как написано ниже
matrix[[nrow, pivot]] = matrix[[pivot, nrow]]
row = matrix[nrow]
divider = row[nrow] # диагональный элемент
if abs(divider) < 1e-10:
# почти нуль на диагонали. Продолжать не имеет смысла, результат счёта неустойчив
raise ValueError(f"Матрица несовместна. Максимальный элемент в столбце {nrow}: {divider:.3g}")
# делим на диагональный элемент.
row /= divider
# теперь надо вычесть приведённую строку из всех нижележащих строчек
for lower_row in matrix[nrow+1:]:
factor = lower_row[nrow] # элемент строки в колонке nrow
lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
# приводим к диагональному виду
make_identity(matrix)
return matrix
# нужно переставлять строки именно так, как написано ниже
matrix[[nrow, pivot]] = matrix[[pivot, nrow]]
row = matrix[nrow]
divider = row[nrow] # диагональный элемент
if abs(divider) < 1e-10:
# почти нуль на диагонали. Продолжать не имеет смысла, результат счёта неустойчив
raise ValueError(f"Матрица несовместна. Максимальный элемент в столбце {nrow}: {divider:.3g}")
# делим на диагональный элемент.
row /= divider
# теперь надо вычесть приведённую строку из всех нижележащих строчек
for lower_row in matrix[nrow+1:]:
factor = lower_row[nrow] # элемент строки в колонке nrow
lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
# приводим к диагональному виду
make_identity(matrix)
return matrix
В этой функции главный фокус в том, как переставлять строки. Простая формула matrix[nrow], matrix[pivot] = matrix[pivot], matrix[nrow] не работает.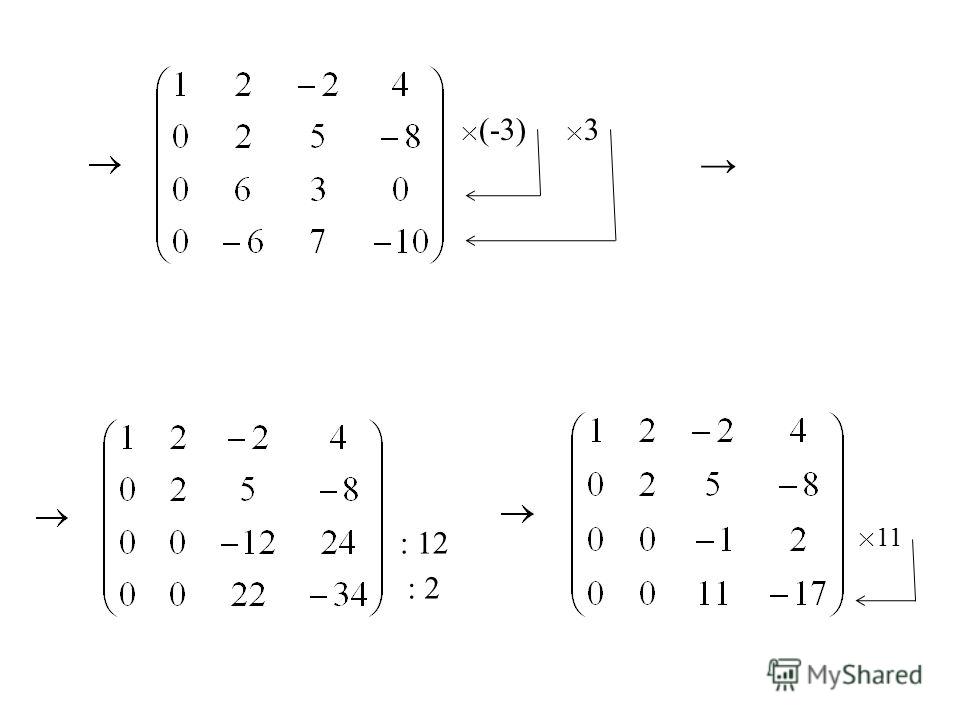 При таком присваивании справа стоят указатели на строку, а слева – адреса, куда нужно скопировать значения. То есть при первом присваивании в строку
При таком присваивании справа стоят указатели на строку, а слева – адреса, куда нужно скопировать значения. То есть при первом присваивании в строку nrow будет скопирована строка pivot, а в строку pivot – содержимое строки nrow — но оно уже переписано из строки pivot! То есть фактически строка pivot скопируется в саму себя. И вместо перестановки двух строк будет копия одной строки.
matrix[[nrow, pivot]] = matrix[[pivot, nrow]] – работает. И c явным копированием тоже работает: matrix[nrow], matrix[pivot] = matrix[pivot], np.copy(matrix[nrow])
UPDATE 2
Jupyter Notebook с кодом решателя СЛАУ
Помимо собственно решателя дано сравнение с Си-шным решателем numpy.linalg.solve и трюк как ускорить скорость счёта решателя на пайтоне в 20 раз, что почти так же быстро, как чисто Си-шный решатель.
Строго говоря, решатель в numpy даже не Си-шный, а фортрановский LAPACK gesv
Метод Гаусса-Джордана – обзор
Пример 2.2.3Обращение матрицы Гаусса-Жордана
Метод Гаусса-Джордана основан на том факте, что существуют матрицы M L , такие что произведение M L A оставит произвольную матрицу A без изменений, за исключением
- (a)
одна строка, умноженная на константу, или
- (b)
, одна строка заменена исходной строкой за вычетом числа, кратного другой ряд, или
- (c)
чередование двух рядов.
Используя эти преобразования, строки матрицы могут быть изменены (путем умножения матриц) теми же способами, которыми мы могли изменять элементы определителей, поэтому мы можем действовать аналогично тем, которые используются для редукции определителей по Гауссу. устранение. Если A неособое число, применение последовательности M L , т.е.е., M = (… ML′′ML′ML), может приводить A к единичной матрице:
MA = 1 или M = A − 1.
Таким образом, что нам нужно сделать, так это применить последовательные преобразования к A до тех пор, пока эти преобразования не уменьшат A до 1 , отслеживая продукт этих преобразований. Мы следим за последовательным применением преобразований к единичной матрице.Вот конкретный пример. Мы хотим инвертировать матрицу
A = (321231114).
Наша стратегия будет заключаться в том, чтобы записать рядом друг с другом матрицу A и единичную матрицу одинакового размера и выполнять одни и те же операции с каждой из них до тех пор, пока A не будет преобразована в единичную матрицу, что означает, что единичная матрица будет иметь изменен на A −1 .Начнем с(321231114) и (100010001).
Умножаем строки по мере необходимости, чтобы установить в единицу все элементы первого столбца левой матрицы:(1231313212114) и (13000120001).
Вычитая первую строку из второй и третьей строк, получаем(1231305616013113) и (1300−13120−1301).
Затем мы делим вторую строку (из обеих матриц ) на 56 и вычитаем ее в 23 раза из первой строки и в 13 раз из третьей строки. Результаты для обеих матриц равны(1015011500185) и (35-250-25350-15-151).
Мы делим третью строку (из обеих матриц ) на 185. Затем, в качестве последнего шага, 15 раз третья строка вычитается из каждой из первых двух строк (обеих матриц). Наша последняя пара –(100010001) и A − 1 = (1118−718−118−7181118−118−118−118518).
Мы можем проверить нашу работу, умножив исходное A на вычисленное A −1 , чтобы увидеть, действительно ли мы получаем единичную матрицу 1 . Линейная алгебра– зачем использовать исключение Гаусса-Джордана вместо исключения Гаусса, Различия
Следующий пример, часть Поиск последовательности элементарных матриц дополняет идею @ Xoque55
Целевая матрица $$ \левый[ \ begin {array} {cc | cc} 2 и 4 \\ 1 и 1 \\ \ end {массив} \верно] $$
Используйте элементарные операции со строками для исключения Гаусса.$ \ color {blue} {Blue} $ окрашивание обозначает измененные элементы в выходной матрице.
Рядный эшелон формы
Форма дополненной матрицы
$$ \левый[ \ begin {array} {c | c} \ mathbf {A} & b \ end {массив} \верно] знак равно \левый[ \ begin {array} {cc | c} 2 и 4 и b_ {1} \\ 1 & 1 & b_ {2} \\ \ end {массив} \верно] $
Нормализовать строку 1: $$ \левый[ \ begin {array} {cc} \ frac {1} {2} & 0 \\ 0 и 1 \\ \ end {массив} \верно] % \левый[ \ begin {array} {cc | c} 2 и 4 и b_ {1} \\ 1 & 1 & b_ {2} \\ \ end {массив} \верно] знак равно \левый[ \ begin {array} {cc | c} \ color {blue} {1} & \ color {blue} {2} & \ frac {1} {2} b_ {1} \\ 1 & 1 & b_ {2} \\ \ end {массив} \верно] $
Очистить столбец 1 $$ \левый[ \ begin {array} {rc} 1 & 0 \\ -1 и 1 \\ \ end {массив} \верно] % \левый[ \ begin {array} {cc | c} \ color {blue} {1} & \ color {blue} {2} & \ frac {1} {2} b_ {1} \\ 1 & 1 & b_ {2} \\ \ end {массив} \верно] знак равно \левый[ \ begin {array} {cr | c} 1 и 2 & \ frac {1} {2} b_ {1} \\ \ color {blue} {0} & \ color {blue} {- 1} & b_ {2} – \ frac {1} {2} b_ {1} \\ \ end {массив} \верно] $
Система может быть решена обратной заменой.
Редукционная форма ступени
Процесс восстановления $$ % \левый[ \ begin {array} {c | c} \ mathbf {A} & \ mathbf {I} \ end {массив} \верно] % \ qquad \ Rightarrow \ qquad % \левый[ \ begin {array} {c | c} \ mathbf {E_ {A}} и \ mathbf {R} \ end {массив} \верно] $
Форма дополненной матрицы
$$ \левый[ \ begin {array} {c | c} \ mathbf {A} & \ mathbf {I} \ end {массив} \верно] знак равно \левый[ \ begin {array} {cc | cc} 2 и 4 и 1 и 0 \\ 1 и 1 и 0 и 1 \\ \ end {массив} \верно] $
Нормализовать строку 1: $$ \левый[ \ begin {array} {cc} \ frac {1} {2} & 0 \\ 0 и 1 \\ \ end {массив} \верно] % \левый[ \ begin {array} {cc | cc} 2 и 4 и 1 и 0 \\ 1 и 1 и 0 и 1 \\ \ end {массив} \верно] знак равно \левый[ \ begin {array} {cc | cc} \ color {blue} {1} & \ color {blue} {2} & \ frac {1} {2} & 0 \\ 1 и 1 и 0 и 1 \\ \ end {массив} \верно] $
Очистить столбец 1 $$ \левый[ \ begin {array} {rc} 1 & 0 \\ -1 и 1 \\ \ end {массив} \верно] % \левый[ \ begin {array} {cc | cc} 1 и 2 & \ frac {1} {2} & 0 \\ 1 и 1 и 0 и 1 \\ \ end {массив} \верно] знак равно \левый[ \ begin {array} {cr | rc} 1 и 2 & \ frac {1} {2} & 0 \\ \ color {blue} {0} & \ color {blue} {- 1} & – \ frac {1} {2} & 1 \\ \ end {массив} \верно] $
Нормализовать строку 2 $$ \левый[ \ begin {array} {cr} 1 & 0 \\ 0 & -1 \\ \ end {массив} \верно] % \левый[ \ begin {array} {cc | cr} 1 и 2 & \ frac {1} {2} & 0 \\ 0 & 1 & \ frac {1} {2} & -1 \\ \ end {массив} \верно] знак равно \левый[ \ begin {array} {cc | cr} 1 и 2 & \ frac {1} {2} & 0 \\ \ color {blue} {0} & \ color {blue} {1} & \ frac {1} {2} & -1 \\ \ end {массив} \верно] $
Очистить столбец 2 $$ \левый[ \ begin {array} {cr} 1 & -2 \\ 0 и 1 \\ \ end {массив} \верно] % \левый[ \ begin {array} {cc | cr} 1 и 2 & \ frac {1} {2} & 0 \\ 0 & 1 & \ frac {1} {2} & -1 \\ \ end {массив} \верно] знак равно \левый[ \ begin {array} {cc | rr} \ color {blue} {1} & \ color {blue} {0} & – \ frac {1} {2} & 2 \\ 0 & 1 & \ frac {1} {2} & -1 \\ \ end {массив} \верно] $$ Результат $$ \левый[ \ begin {array} {c | c} \ mathbf {E_ {A}} и \ mathbf {R} \ end {массив} \верно] знак равно \левый[ \ begin {array} {cc | rr} 1 & 0 & – \ frac {1} {2} & 2 \\ 0 & 1 & \ frac {1} {2} & -1 \\ \ end {массив} \верно] $
Решение $$ \ mathbf {A} x = b \ quad \ Rightarrow \ quad х = \ mathbf {A} ^ {- 1} б \ quad \ Rightarrow \ quad x = \ frac {1} {2} \ left [ \ begin {array} {rr} -1 и 4 \\ 1 & -2 \\ \ end {массив} \верно] % \левый[ \ begin {array} {c} б_ {1} \\ Би 2} \\ \ end {массив} \верно] \ quad \ Rightarrow \ quad х = \левый[ \ begin {array} {l} – \ frac {1} {2} b_ {1} + 2b_ {2} \\ \ phantom {-} \ frac {1} {2} b_ {1} – b_ {2} \\ \ end {массив} \верно] $
Произведение матриц приведения
Произведение последовательности матриц редукции является обратным: $$ % четыре \левый[ \ begin {array} {cr} 1 & -2 \\ 0 и 1 \\ \ end {массив} \верно] % в третьих \левый[ \ begin {array} {cr} 1 & 0 \\ 0 & -1 \\ \ end {массив} \верно] % второй \левый[ \ begin {array} {rc} 1 & 0 \\ -1 и 1 \\ \ end {массив} \верно] % первый \левый[ \ begin {array} {cc} \ frac {1} {2} & 0 \\ 0 и 1 \\ \ end {массив} \верно] знак равно \левый[ \ begin {array} {rr} – \ frac {1} {2} & 2 \\ \ frac {1} {2} & -1 \\ \ end {массив} \верно] знак равно \ mathbf {A} ^ {- 1} $
Метод исключения Гаусса
Далее: Строка уменьшенная форма эшелона Up: Операции со строками и аналог Предыдущая: Операции со строками и аналог Содержание D EFINITION 2.2.10 (Метод прямого / исключения Гаусса) Исключение Гаусса – это метод решения линейной системы (состоящий из уравнения в неизвестные) путем приведения дополненной матрицы к верхнетреугольной форме Этот процесс исключения также называется методом прямого исключения.
Следующие примеры иллюстрируют процедуру исключения Гаусса.
E XAMPLE 2.2,11 Решите линейную систему по Гауссу метод устранения.Решение: В этом случае расширенная матрица Метод продолжается по следующие шаги.
- Развязка и уравнение (или ).
- Разделите уравнение (или ).
- Добавить раз уравнение уравнение (или ).
- Добавить раз уравнение уравнение (или ).
- Умножьте уравнение (или ).
Последнее уравнение дает второе уравнение теперь дает Наконец, первое уравнение дает Следовательно, множество решения УНИКАЛЬНЫЙ РЕШЕНИЕ .
E XAMPLE 2.2.12 Решите линейную систему по Гауссу метод устранения.Решение: В этом случае расширенная матрица и метод работает следующим образом:
- Добавить умножить первое уравнение на второе уравнение.
- Добавить умножить первое уравнение на третье уравнение.
- Добавить умножить второе уравнение на третье уравнение
Решение: В этом случае расширенная матрица и метод работает следующим образом:
- Добавить умножить первое уравнение на второе уравнение.
- Добавить умножить первое уравнение на третье уравнение.
- Добавить умножить второе уравнение на третье уравнение
Далее: Строка уменьшенная форма эшелона Up: Операции со строками и аналог Предыдущая: Операции со строками и аналог Содержание А К Лал 2007-09-12
Исключение Гаусса для разреженных матриц: введение
Страница из
НАПЕЧАТАНО ИЗ ОНЛАЙН-СТИПЕНДИИ ОКСФОРДА (Оксфорд.Universitypressscholarship.com). (c) Авторские права Oxford University Press, 2021. Все права защищены. Отдельный пользователь может распечатать одну главу монографии в формате PDF в OSO для личного использования. дата: 17 августа 2021 г.
- Глава:
- . (стр.89) 5 Исключение Гаусса для разреженных матриц: введение
- Источник:
- Прямые методы для разреженных матриц
- Автор (ы):
И.С. Дафф
А.М. Эрисман
Дж.К. Рейд
- Издатель:
- Oxford University Press
DOI: 10.1093 / acprof: oso / 9780198508380.003.0005
В этой главе представлено введение в использование метода исключения Гаусса для решения разреженных наборов линейных уравнений. Мы исследуем три основных этапа большинства компьютерных программ для этой задачи: АНАЛИЗ, ФАКТОРИЗАЦИЯ и РЕШЕНИЕ. Мы подчеркиваем важность допустимых накладных расходов и численной стабильности, но не касаемся алгоритмических деталей или деталей реализации, которые являются предметом последующих глав.
Ключевые слова: Разреженное исключение Гаусса, АНАЛИЗ, ФАКТОРИЗАЦИЯ, РЕШЕНИЕ, компьютерные программы
Для получения доступа к полному тексту книг в рамках службы для получения стипендииOxford Online требуется подписка или покупка. Однако публичные пользователи могут свободно искать на сайте и просматривать аннотации и ключевые слова для каждой книги и главы.
Пожалуйста, подпишитесь или войдите для доступа к полному тексту.
Если вы считаете, что у вас должен быть доступ к этой книге, обратитесь к своему библиотекарю.
Для устранения неполадок, пожалуйста, проверьте наш FAQs , и если вы не можете найти там ответ, пожалуйста свяжитесь с нами .
Исключение Гауссав Python: иллюстрация и реализация
Привет, кодеры !! В этой статье мы узнаем об исключении гаусса в Python. Сначала мы поймем, что это означает, изучим его алгоритм, а затем реализуем его на Python.Итак, приступим!
Что такое метод исключения Гаусса?
Исключение по Гауссу также известно как сокращение строки. Это алгоритм линейной алгебры, используемый для решения системы линейных уравнений. В основном последовательность операций выполняется над матрицей коэффициентов. Были задействованы следующие операции:
- Замена двух строк
- Умножение строки на ненулевое число
- Добавление кратного одной строки к другой строке
Эти операции выполняются до тех пор, пока нижний левый угол матрицы не заполнится нулями, насколько это возможно. возможно.
Иллюстрация исключения Гаусса на примере:
Рассмотрим следующую систему линейных уравнений:
- 2x + y – z = 8 ………………… .L1
- -3x – y + 2z = -11 ………… ..L2
- -2x + y + 2z = -3 ……… … ..L3
Расширенная матрица вышеуказанной системы уравнений будет иметь вид:
Наша цель – сделать нижний левый угол матрицы максимально заполненным нулями. Для этого выполним последовательность операций.
L2 + 3 / 2L1 -> L2
L3 + L1 -> L3
Когда мы выполняем приведенное выше уравнение для расширенной матрицы, мы получаем:
Теперь перейдем к следующему этапу работы со строками.
L3 + -4L2 -> L3
Выполняя указанную выше операцию, мы получаем в результате расширенную матрицу. Как видите, матрица теперь имеет эшелонированную форму (треугольную форму).
L2 + 1 / 2L3 -> L2
L1 – L3 -> L1
Выполнив указанную выше операцию, мы получим следующую матрицу:
Мы все еще можем добавить в эту матрицу больше нулей, так что продолжим.
2L2 -> L2
-L3 -> L3
При выполнении вышеуказанных операций получаем следующую матрицу:
L1 – L2 -> L1
1/2 L2 -> L1
В результате выполнения вышеуказанной строковой операции мы получаем следующий результат:
Поскольку мы не можем дальше уменьшать матрицу, мы останавливаем алгоритм. Решение вышеуказанных уравнений:
Реализация на Python:
импортировать numpy как np
import sys
n = int (input ('Введите количество неизвестных:'))
а = нп.нули ((n, n + 1))
x = np. нули (n)
print ('Введите коэффициенты расширенной матрицы:')
для i в диапазоне (n):
для j в диапазоне (n + 1):
a [i] [j] = float (input ('a [' + str (i) + '] [' + str (j) + '] ='))
для i в диапазоне (n):
если [i] [i] == 0.0:
sys.exit ('Обнаружено деление на ноль!')
для j в диапазоне (i + 1, n):
соотношение = a [j] [i] / a [i] [i]
для k в диапазоне (n + 1):
a [j] [k] = a [j] [k] - соотношение * a [i] [k]
x [n-1] = a [n-1] [n] / a [n-1] [n-1]
для i в диапазоне (n-2, -1, -1):
x [i] = a [i] [n]
для j в диапазоне (i + 1, n):
x [i] = x [i] - a [i] [j] * x [j]
x [i] = x [i] / a [i] [i]
print ('\ nРешение:')
для i в диапазоне (n):
print ('X% d =% 0.2f '% (i, x [i]), end =' \ t ')
Выход и пояснение:
Итак, это будет вывод вышеуказанного кода. Теперь позвольте мне объяснить вам этот код шаг за шагом.
- Сначала мы импортировали необходимые библиотеки, которые будем использовать в нашей программе.
- Затем мы спросили у пользователя количество неизвестных переменных, которые мы храним в переменной «n».
- После этого мы создали numpy-массив «a» размера nx (n + 1) и инициализировали его нулем. Мы будем хранить нашу расширенную матрицу в этом массиве.
- Другой массив «x» размера n также создается и инициализируется нулем. Мы будем использовать этот массив для хранения вектора решения.
- Затем мы использовали цикл для получения входных данных расширенной матрицы.
- После этого мы применили метод исключения Гаусса.
- Если какой-либо из коэффициентов равен 0, возникает ошибка, поскольку деление на ноль невозможно.
- После этого мы применяем метод обратной подстановки, чтобы получить желаемый результат.
Обязательно к прочтению
Вывод:
На этом мы подошли к концу данной статьи.Надеюсь, вы узнали об исключении Гаусса и его реализации на Python.
Однако, если у вас есть какие-либо сомнения или вопросы, дайте мне знать в разделе комментариев ниже. Я постараюсь помочь вам как можно скорее.
Счастливого питонинга!
| “” “ | |
| Исключение Гаусса с частичным поворотом. | |
| Этот модуль содержит 5 функций, которые процедурно решают | |
| линейная система Ax = b, A – матрица nxn, а b – матрица | |
| вектор-столбец с n строками. | |
| “” “ | |
| импортный номер | |
| импорт математики | |
| , точка поворота (A): | |
| “” “ | |
| Сводная матрица A – находит строку с максимальной первой записью | |
| и, если необходимо, меняет его местами с первой строкой. | |
| Входные аргументы | |
| ————— | |
| Расширенная матрица A | |
| Возвращает | |
| ——- | |
| Поворотная расширенная матрица A | |
| “” “ | |
| B = numpy.нули ((1,2)) | |
| B [0,0] = A.shape [0] | |
| B [0,1] = A.shape [1] | |
| nrows = B [0,0] # Здесь хранятся размеры | |
| ncols = B [0,1] # матрица в массиве | |
| pivot_size = numpy.abs (A [0,0]) | |
| # проверяет наибольшую первую запись и свопы | |
| pivot_row = 0; | |
| для i в диапазоне (int (0), int (nrows)): | |
| , если numpy.abs (A [i, 0])> pivot_size: | |
| pivot_size = numpy.abs (A [i, 0]) | |
| pivot_row = i | |
| , если pivot_row> 0: | |
| tmp = numpy.empty (ncols) | |
| tmp [:] = A [0 ,:] | |
| A [0 ,:] = A [pivot_row ,:] | |
| A [pivot_row ,:] = tmp [:] | |
| возврат | |
| # Тестирование функции | |
| , если __name__ == “__main__”: | |
| A = numpy.array ([[- 1., 1., 2., 1.], [3., – 1., 1., 1.], [- 1., 3., 4., 1.]]) | |
| печать ‘Testing pivot’ | |
| напечатайте ‘A перед поворотом \ n’, A | |
| напечатайте ‘A после поворота \ n’, поворот (A), ‘\ n’ | |
| def elim (A): | |
| “” “ | |
| elim (A) использует строковые операции для представления | |
| нуля под диагональю в первом столбце | |
| матрицы А | |
| Входной аргумент | |
| ————— | |
| Расширенная матрица A | |
| Возвращает | |
| ——- | |
| A с исключенной первой колонкой | |
| “” “ | |
| A = шарнир (A) | |
| B = numpy.нули ((1,2)) | |
| B [0,0] = A.shape [0] | |
| B [0,1] = A.shape [1] | |
| рядов = B [0,0] | |
| ncols = B [0,1] | |
| # рядные операции | |
| rpiv = 1./float(A[0ght[0]) | |
| для строк в диапазоне (int (1), int (nrows)): | |
| s = A [irow, 0] * rpiv | |
| для jcol в диапазоне (int (0), int (ncols)): | |
| A [irow, jcol] = A [irow, jcol] – s * A [0, jcol] | |
| возврат | |
| # Тестирование функции | |
| , если __name__ == “__main__”: | |
| A = numpy.array ([[- 1., 1., 2., 1.], [3., – 1., 1., 1.], [- 1., 3., 4., 1.]]) | |
| распечатка «Испытания на устранение» | |
| напечатайте ‘A до исключения \ n’, точка поворота (A) | |
| print ‘A после исключения \ n’, elim (pivot (A)), ‘\ n’ | |
| def backsub (A): | |
| “” “ | |
| Подставка | (A) решает верхнюю треугольную систему |
| Входной аргумент | |
| ————— | |
| Расширенная матрица A | |
| Возвращает | |
| ——- | |
| вектор b, решение линейной системы | |
| “” “ | |
| B = numpy.нули ((1,2)) | |
| B [0,0] = A.shape [0] | |
| B [0,1] = A.shape [1] | |
| n = B [0,0] | |
| ncols = B [0,1] | |
| x = numpy.zeros ((n, 1)) | |
| x [n-1] = A [n-1, n] / A [n-1, n-1] | |
| для i в диапазоне (int (n-1), int (-1), int (-1)): | |
| для j в диапазоне (int (i + 1), int (n)): | |
| A [i, n] = A [i, n] -A [i, j] * x [j] | |
| x [i] = A [i, n] / A [i, i] | |
| возврат x | |
| # Тестирование функции | |
| , если __name__ == “__main__”: | |
| A = numpy.array ([[- 1., 1., 2., 1.], [3., – 1., 1., 1.], [- 1., 3., 4., 1.]]) | |
| печать ‘Тестирование подкладки’ | |
| напечатайте ‘A перед backsub \ n’, A, ‘\ n’ | |
| выведите ‘A после backsub \ n’, backsub (A), ‘\ n’ | |
| по умолчанию (A): | |
| “” “ | |
| gaussfe (A) использует строковые операции для уменьшения A | |
| в верхнюю треугольную форму, вызвав elim и | |
| поворотный | |
| Входной аргумент | |
| ————— | |
| Расширенная матрица A | |
| Возвращает | |
| ——- | |
| A в верхнем треугольнике | |
| “” “ | |
| B = numpy.нули ((1,2)) | |
| B [0,0] = A.shape [0] | |
| B [0,1] = A.shape [1] | |
| рядов = B [0,0] | |
| ncols = B [0,1] | |
| для i в диапазоне (int (0), int (nrows-1)): | |
| A [i: nrows, i: ncols] = pivot (A [i: nrows, i: ncols]) | |
| A [i: nrows, i: ncols] = elim (A [i: nrows, i: ncols]) | |
| возврат | |
| # Тестирование функции | |
| , если __name__ == “__main__”: | |
| A = numpy.array ([[- 1., 1., 2., 1.], [3., – 1., 1., 1.], [- 1., 3., 4., 1.]]) | |
| принт ‘Testing gaussfe’ | |
| print ‘A до исключения Гаусса \ n’, gaussfe (pivot (A)) | |
| выведите ‘A после g.elimination \ n’, gaussfe (elim (pivot (A))), ‘\ n’ | |
| по умолчанию (A, b): | |
| “” “ | |
| Solve увеличивает матрицу A nxn и вектор-столбец b | |
| Затем | вызывает функции в этом модуле для решения |
| линейная система | |
| Входной аргумент | |
| ————— | |
| Матрица A nxn и вектор-столбец b | |
| Возвращает | |
| ——- | |
| x, решение линейной системы | |
| “” “ | |
| B = numpy.нули ((1,2)) | |
| B [0,0] = A.shape [0] | |
| B [0,1] = A.shape [1] | |
| рядов = B [0,0] | |
| ncols = B [0,1] | |
| Авг = numpy.zeros ((nrows, ncols + 1)) | |
| # эти 2 цикла дополняют матрицу вектором-столбцом | |
| для i в диапазоне (int (0), int (nrows)): | |
| для j в диапазоне (int (0), int (ncols)): | |
| Август [i, j] = A [i, j] | |
| для k в диапазоне (int (0), int (nrows)): | |
| Авг [k, ncols] = b [k] | |
| A = август | |
| A = gaussfe (A) | |
| x = задняя опора (A) | |
| х = х.Т | |
| возврат x | |
| # Специальное испытание | |
| , если __name__ == “__main__”: | |
| A = numpy.array ([[1., 1., 1.], [1., – 2., 2.], [1., 2., – 1.]]) | |
| b = numpy.array ([[0.], [4.], [2.]]) | |
| печать «Решение для тестирования» | |
| напечатайте ‘A is \ n’, A | |
| print ‘B is \ n’, b | |
| print ‘Решение \ n’, решите (A, b), ‘\ n \ n \ n’ | |
| # Общее тестирование функции | |
| , если __name__ == “__main__”: | |
| импортный номер | |
| импортное время | |
| print “Тесты для решения \ n \ n” | |
| п = 100 | |
| принт «Размер матрицы», № | |
| A = numpy.random.random ((n, n)) | |
| xe = numpy.random.random (n) | |
| b = numpy.dot (A, xe) | |
| resolve_start = time.clock () | |
| x = решить (A, b) | |
| выведите «время решения», str (time.clock () – resolve_start) | |
| err = numpy.max (numpy.абс (xe-x)) | |
| print «Ошибка», err, «\ n \ n» | |
| подтвердить ошибку <1e-10 | |
| распечатка «решите тест пройден». | |

 Например, х2 – 4 = 1, т.е. х2
Например, х2 – 4 = 1, т.е. х2  copy
for nrow, row in enumerate(matrix):
# nrow равен номеру строки
# row содержит саму строку матрицы
divider = row[nrow] # диагональный элемент
# делим на диагональный элемент.
row /= divider
# теперь надо вычесть приведённую строку из всех нижележащих строчек
for lower_row in matrix[nrow+1:]:
factor = lower_row[nrow] # элемент строки в колонке nrow
lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
# все строки матрицы изменились, в принципе, можно и не возвращать
return matrix
copy
for nrow, row in enumerate(matrix):
# nrow равен номеру строки
# row содержит саму строку матрицы
divider = row[nrow] # диагональный элемент
# делим на диагональный элемент.
row /= divider
# теперь надо вычесть приведённую строку из всех нижележащих строчек
for lower_row in matrix[nrow+1:]:
factor = lower_row[nrow] # элемент строки в колонке nrow
lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
# все строки матрицы изменились, в принципе, можно и не возвращать
return matrix
 # нужно переставлять строки именно так, как написано ниже
matrix[[nrow, pivot]] = matrix[[pivot, nrow]]
row = matrix[nrow]
divider = row[nrow] # диагональный элемент
if abs(divider) < 1e-10:
# почти нуль на диагонали. Продолжать не имеет смысла, результат счёта неустойчив
raise ValueError(f"Матрица несовместна. Максимальный элемент в столбце {nrow}: {divider:.3g}")
# делим на диагональный элемент.
row /= divider
# теперь надо вычесть приведённую строку из всех нижележащих строчек
for lower_row in matrix[nrow+1:]:
factor = lower_row[nrow] # элемент строки в колонке nrow
lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
# приводим к диагональному виду
make_identity(matrix)
return matrix
# нужно переставлять строки именно так, как написано ниже
matrix[[nrow, pivot]] = matrix[[pivot, nrow]]
row = matrix[nrow]
divider = row[nrow] # диагональный элемент
if abs(divider) < 1e-10:
# почти нуль на диагонали. Продолжать не имеет смысла, результат счёта неустойчив
raise ValueError(f"Матрица несовместна. Максимальный элемент в столбце {nrow}: {divider:.3g}")
# делим на диагональный элемент.
row /= divider
# теперь надо вычесть приведённую строку из всех нижележащих строчек
for lower_row in matrix[nrow+1:]:
factor = lower_row[nrow] # элемент строки в колонке nrow
lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
# приводим к диагональному виду
make_identity(matrix)
return matrix