Метод Крамера. Примеры решения систем линейных алгебраических уравнений методом Крамера.
Высшая математика » Системы линейных алгебраических уравнений » Метод Крамера
Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
- Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. $\Delta\neq 0$.
- Для каждой переменной $x_i$($i=\overline{1,n}$) необходимо составить определитель $\Delta_{x_i}$, полученный из определителя $\Delta$ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
- Найти значения неизвестных по формуле $x_i=\frac{\Delta_{x_{i}}}{\Delta}$ ($i=\overline{1,n}$).

Перед переходом к чтению примеров рекомендую ознакомиться с правилами вычисления определителей второго и третьего порядка, изложенными здесь.
Пример №1
Решить СЛАУ $\left\{\begin{aligned} & 3x_1+2x_2=-11;\\ & -x_1+5x_2=15. \end{aligned}\right.$ методом Крамера.
Решение
Матрица системы такова: $ A=\left( \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array} \right)$. Определитель этой матрицы:
$$\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|=3\cdot 5-2\cdot(-1)=17.$$
Как вычисляется определитель второго порядка можете глянуть здесь.
Так как определитель системы не равен нулю, то продолжаем решение методом Крамера. Вычислим значения двух определителей: $\Delta_{x_1}$ и $\Delta_{x_2}$. Определитель $\Delta_{x_1}$ получаем из определителя $\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|$ заменой первого столбца (именно этот столбец содержит коэффициенты при $x_1$) столбцом свободных членов $\left(\begin{array} {c} -11\\ 15\end{array}\right)$:
$$
\Delta_{x_1}=\left|\begin{array}{cc}-11&2\\15&5\end{array}\right|=-55-30=-85. $$
$$
Аналогично, заменяя второй столбец в $\Delta=\left|\begin{array}{cc}3&2\\-1&5\end{array}\right|$ столбцом свободных членов, получим:
$$ \Delta_{x_2}=\left|\begin{array} {cc} 3 & -11\\ -1 & 15\end{array}\right|=45-11=34. $$
Теперь можно найти значения неизвестных $x_1$ и $x_2$.
$$x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{-85}{17}=-5;\;x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{34}{17}=2.$$
В принципе, можно ещё проверить, правильно ли решена система методом Крамера. Подставим в заданную СЛАУ $x_1=-5$, $x_2=2$:
$$\left\{\begin{aligned} & 3x_1+2x_2=3\cdot(-5)+2\cdot{2}=-11;\\ & -x_1+5x_2=-(-5)+5\cdot{2}=15. \end{aligned}\right.$$
Проверка пройдена, решение системы уравнений методом Крамера найдено верно. Осталось лишь записать ответ.
Осталось лишь записать ответ.
Ответ: $x_1=-5$, $x_2=2$.
Пример №2
Решить СЛАУ $ \left\{\begin{aligned} & 2x_1+x_2-x_3=3;\\ & 3x_1+2x_2+2x_3=-7;\\ & x_1+x_3=-2. \end{aligned} \right.$, используя метод Крамера.
Решение
Определитель системы:
$$\Delta=\left| \begin{array} {ccc} 2 & 1 & -1\\ 3 & 2 & 2 \\ 1 & 0 & 1 \end{array}\right|=4+2+2-3=5.$$
Как вычисляется определитель третьего порядка можете глянуть здесь.
Заменяя первый столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_1}$:
$$ \Delta_{x_1}=\left| \begin{array} {ccc} 3 & 1 & -1\\ -7 & 2 & 2 \\ -2 & 0 & 1 \end{array}\right|=6-4-4+7=5. $$
Заменяя второй столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_2}$:
 $$
$$
Заменяя третий столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_3}$:
$$ \Delta_{x_3}=\left| \begin{array} {ccc} 2 & 1 & 3\\ 3 & 2 & -7 \\ 1 & 0 & -2 \end{array}\right|=-8-7-6+6=-15. $$
Учитывая все вышеизложенное, имеем:
Метод Крамера завершён. Можно проверить, верно ли решена система уравнений методом Крамера, подставив значения $x_1=1$, $x_2=-2$ и $x_3=-3$ в заданную СЛАУ:
$$\left\{\begin{aligned}
& 2x_1+x_2-x_3=2\cdot{1}+(-2)-(-3)=3;\\
& 3x_1+2x_2+2x_3=3\cdot{1}+2\cdot(-2)+2\cdot(-3)=-7;\\
& x_1+x_3=1+(-3)=-2. \end{aligned} \right.$$
\end{aligned} \right.$$
Проверка пройдена, решение системы уравнений методом Крамера найдено верно.
Ответ: $x_1=1$, $x_2=-2$, $x_3=-3$.
Пример №3
Решить СЛАУ $\left\{\begin{aligned} & 2x_1+3x_2-x_3=15;\\ & -9x_1-2x_2+5x_3=-7. \end{aligned}\right.$ используя метод Крамера.
Решение
Матрица системы $ \left( \begin{array} {ccc} 2 & 3 & -1\\ -9 & -2 & 5 \end{array} \right) $ не является квадратной. Однако это вовсе не означает, что решение системы уравнений методом Крамера невозможно. Преобразуем заданную СЛАУ, перенеся переменную $x_3$ в правые части уравнений:
Теперь матрица системы $ \left( \begin{array} {cc} 2 & 3 \\ -9 & -2 \end{array} \right) $ стала квадратной, и определитель её $\Delta=\left| \begin{array} {cc} 2 & 3\\ -9 & -2 \end{array}\right|=-4+27=23$ не равен нулю. Применим метод Крамера аналогично предыдущим примерам:
Применим метод Крамера аналогично предыдущим примерам:
$$ \begin{aligned} & \Delta_{x_1} =\left| \begin{array} {cc} x_3+15 & 3\\ -5x_3-7 & -2 \end{array}\right| =-2x_3-30-\left(-15x_3-21\right) =13x_3-9;\\ \\ & \Delta_{x_2} =\left| \begin{array} {cc} 2 & x_3+15\\ -9 & -5x_3-7 \end{array}\right| =-10x_3-14-\left(-9x_3-135\right) =-x_3+121. \end{aligned} $$ $$ x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{13x_3-9}{23};\; x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{-x_3+121}{23}. $$
Ответ можно записать в таком виде: $\left\{\begin{aligned}
& x_1=\frac{13x_3-9}{23};\\
& x_2=\frac{-x_3+121}{23};\\
& x_3\in R.
\end{aligned}\right.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.
Примечание
В подобных примерах возможна ситуация, когда после переноса переменной (или переменных) в правые части уравнений, определитель системы равняется нулю. В этом случае можно перенести в правую часть иную переменную (или переменные). Например, рассмотрим СЛАУ
$\left\{\begin{aligned}
& 2x_1-5x_2+10x_3=14;\\
& -4x_1+10x_2-7x_3=5.
\end{aligned}\right.$. Если перенести в правые части уравнений $x_3$, получим: $
\left\{\begin{aligned}
&2x_1-5x_2=-10x_3+14;\\
&-4x_1+10x_2=7x_3+5.
\end{aligned}\right.$. Определитель данной системы $\Delta=\left| \begin{array} {cc} 2 & -5\\ -4 & 10 \end{array}\right|=20-20=0$. Однако если перенести в правые части уравнений переменную $x_2$, то получим систему $
\left\{\begin{aligned}
&2x_1+10x_3=5x_2+14;\\
&-4x_1-7x_3=-10x_2+5.
\end{aligned}\right.$, определитель которой $\Delta=\left| \begin{array} {cc} 2 & 10\\ -4 & -7 \end{array}\right|=-14+40=26$ не равен нулю.
Пример №4
Решить СЛАУ
$$\left\{\begin{aligned} &x_1-5x_2-x_3-2x_4+3x_5=0;\\ &2x_1-6x_2+x_3-4x_4-2x_5=0; \\ &-x_1+4x_2+5x_3-3x_4=0. \end{aligned}\right.$$
методом Крамера.
Решение
Матрица системы $\left(\begin{array} {ccccc} 1 & -5 & -1 & -2 & 3 \\ 2 & -6 & 1 & -4 & -2 \\ -1 & 4 & 5 & -3 & 0 \end{array}\right)$ не является квадратной. Преобразуем заданную СЛАУ, перенеся переменные $x_4$, $x_5$ в правые части уравнений, и применим метод Крамера:
$$
\left\{\begin{aligned}
& x_1-5x_2-x_3=2x_4-3x_5;\\
& 2x_1-6x_2+x_3=4x_4+2x_5; \\
& -x_1+4x_2+5x_3=3x_4.
\end{aligned}\right.$$
$$
\begin{aligned}
& \Delta
=\left| \begin{array} {ccc} 1 & -5 & -1\\ 2 & -6 & 1\\-1 & 4 & 5 \end{array}\right|
=19;\\
\\
& \Delta_{x_1}
=\left| \begin{array} {ccc} 2x_4-3x_5 & -5 & -1\\ 4x_4+2x_5 & -6 & 1\\3x_4 & 4 & 5 \end{array}\right|
=-17x_4+144x_5;\\
\\
& \Delta_{x_2}
=\left| \begin{array} {ccc} 1 & 2x_4-3x_5 & -1\\ 2 & 4x_4+2x_5 & 1\\-1 & 3x_4 & 5 \end{array}\right|
=-15x_4+41x_5;\\
\\
& \Delta_{x_3}
=\left| \begin{array} {ccc} 1 & -5 & 2x_4-3x_5\\ 2 & -6 & 4x_4+2x_5\\-1 & 4 & 3x_4 \end{array}\right|
=20x_4-4x_5. \end{aligned}
$$
\end{aligned}
$$
Ответ таков: $\left\{\begin{aligned} & x_1=\frac{-17x_4+144x_5}{19};\\ & x_2=\frac{-15x_4+41x_5}{19};\\ & x_3=\frac{20x_4-4x_5}{19}; \\ & x_4\in R; \; x_5\in R. \end{aligned}\right.$ Переменные $x_1$, $x_2$, $x_3$ – базисные, переменные $x_4$, $x_5$ – свободные.
Естественно, что применение метода Крамера в случаях вроде того, что рассмотрен в примере №4, не всегда оправдано с точки зрения временных затрат. Мы ведь не можем гарантировать, что после переноса каких-либо переменных в правые части уравнений, определитель системы не будет равен нулю. А перебирать различные варианты – слишком долгий процесс. Гораздо удобнее в таком случае применить метод Гаусса. Я привёл пример №4 лишь с одной целью – показать, что метод Крамера применим вне зависимости от содержимого правых частей уравнений заданной СЛАУ (числа, переменные, функции – не имеет значения). Главное, чтобы определитель матрицы системы был отличен от нуля.
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Решить систему линейных уравнений (метод Крамера или метод Гаусса )
Пример 1:
Найти решение системы методом Крамера:
Решение от преподавателя:
Запишем систему в виде:
A = |
|
BT = (1,-3,0)
Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю.
Определитель:
∆ = 10*((-2)*5-1*(-7))-1*(1*5-1*4)+2*(1*(-7)-(-2)*4) = -29
Заменим 1-ый столбец матрицы А на вектор результата В.
1 | 1 | 4 |
-3 | -2 | -7 |
0 | 1 | 5 |
Найдем определитель полученной матрицы.
∆1 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 1*((-2)*5-1*(-7))-(-3)*(1*5-1*4)+0*(1*(-7)-(-2)*4) = 0
Заменим 2-ый столбец матрицы А на вектор результата В.
10 | 1 | 4 |
1 | -3 | -7 |
2 | 0 | 5 |
Найдем определитель полученной матрицы.
∆2 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 10*((-3)*5-0*(-7))-1*(1*5-0*4)+2*(1*(-7)-(-3)*4) = -145
Заменим 3-ый столбец матрицы А на вектор результата В.
10 | 1 | 1 |
1 | -2 | -3 |
2 | 1 | 0 |
Найдем определитель полученной матрицы.
∆3 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 10*((-2)*0-1*(-3))-1*(1*0-1*1)+2*(1*(-3)-(-2)*1) = 29
Выпишем отдельно найденные переменные Х
Проверка.
10*0+1*5+4*(-1) = 1
1*0-2*5-7*(-1) = -3
2*0+1*5+5*(-1) = 0
Пример 2:
Решить систему линейных уравнений (метод Крамера или метод Гаусса )
Решение от преподавателя:
Запишем систему в виде:
A = |
|
BT = (6,1,11)
Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю..png)
Определитель:
∆ = 2*((-1)*4-2*(-1))-1*(3*4-2*1)+5*(3*(-1)-(-1)*1) = -24
Заменим 1-й столбец матрицы А на вектор результата В.
6 | 3 | 1 |
1 | -1 | -1 |
11 | 2 | 4 |
Найдем определитель полученной матрицы.
∆1 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 6*((-1)*4-2*(-1))-1*(3*4-2*1)+11*(3*(-1)-(-1)*1) = -44
Заменим 2-й столбец матрицы А на вектор результата В.
2 | 6 | 1 |
1 | 1 | -1 |
5 | 11 | 4 |
Найдем определитель полученной матрицы.
∆2 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 2*(1*4-11*(-1))-1*(6*4-11*1)+5*(6*(-1)-1*1) = -18
Заменим 3-й столбец матрицы А на вектор результата В.
2 | 3 | 6 |
1 | -1 | 1 |
5 | 2 | 11 |
Найдем определитель полученной матрицы.
∆3 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 2*((-1)*11-2*1)-1*(3*11-2*6)+5*(3*1-(-1)*6) = -2
Выпишем отдельно найденные переменные Х
Пример 3:
Решить систему линейных уравнений
по формулам Крамера и методом Гаусса. Сравнить полученные результаты.
Сравнить полученные результаты.
Решение от преподавателя:
Пример 4:
Решить систему линейных уравнений по правилу Крамера:
Решение от преподавателя:
Пример 5:
Решить систему уравнений с помощью формул Крамера.
Решение от преподавателя:
Пример 6:
Решить систему линейных уравнений с помощью формул Крамера:
Решение от преподавателя:
Находим определитель матрицы системы:
В определителе матрицы системы последовательно меняем 1-й, 2-й, 3-й столбцы на столбец свободных членов и находим полученные определители:
Решение системы:
Ответ: (6; 2; – 4).
Пример 7:
Решить систему линейных уравнений (метод Крамера или метод Гаусса )
Решение от преподавателя:
Запишем систему в виде:
BT = (7,3,4)
Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю.
Определитель:
∆ = 2*(3*(-3)-(-2)*(-1))-7*((-1)*(-3)-(-2)*4)+5*((-1)*(-1)-3*4) = -154
Заменим 1-й столбец матрицы А на вектор результата В.
7 | -1 | 4 |
3 | 3 | -1 |
4 | -2 | -3 |
Найдем определитель полученной матрицы.
∆1 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 7*(3*(-3)-(-2)*(-1))-3*((-1)*(-3)-(-2)*4)+4*((-1)*(-1)-3*4) = -154
Заменим 2-й столбец матрицы А на вектор результата В.
2 | 7 | 4 |
7 | 3 | -1 |
5 | 4 | -3 |
Найдем определитель полученной матрицы.
∆2 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 2*(3*(-3)-4*(-1))-7*(7*(-3)-4*4)+5*(7*(-1)-3*4) = 154
Заменим 3-й столбец матрицы А на вектор результата В.
2 | -1 | 7 |
7 | 3 | 3 |
5 | -2 | 4 |
Найдем определитель полученной матрицы.
∆3 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 2*(3*4-(-2)*3)-7*((-1)*4-(-2)*7)+5*((-1)*3-3*7) = -154
Выпишем отдельно найденные переменные Х
Ответ:
Пример 8:
Решение от преподавателя:
а)
Ответ:X=1
Y=1
Z=1
б)
Из вышеизложенной таблицы следует:
X=1
Y=1
Z=1
Пример 9:
Решить систему линейных уравнений по правилу Крамера:
Решение от преподавателя:
Пример 10:
Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса и методом Крамера.
Решение от преподавателя:
Пример 11:
Решить сиситему методом Крамера и сдеать проверку:
Решение от преподавателя:
Запишем систему в виде:
A = |
|
BT = (3,-2,1)
Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю.
Определитель:
∆ = 1*(3*1-1*(-1))-(-2)*(5*1-1*1)+3*(5*(-1)-3*1) = -12
Заменим 1-й столбец матрицы А на вектор результата В.
3 | 5 | 1 |
-2 | 3 | -1 |
1 | 1 | 1 |
Найдем определитель полученной матрицы.
∆1 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 3*(3*1-1*(-1))-(-2)*(5*1-1*1)+1*(5*(-1)-3*1) = 12
Заменим 2-й столбец матрицы А на вектор результата В.
1 | 3 | 1 |
-2 | -2 | -1 |
3 | 1 | 1 |
Найдем определитель полученной матрицы.
∆2 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 1*((-2)*1-1*(-1))-(-2)*(3*1-1*1)+3*(3*(-1)-(-2)*1) = 0
Заменим 3-й столбец матрицы А на вектор результата В.
1 | 5 | 3 |
-2 | 3 | -2 |
3 | 1 | 1 |
Найдем определитель полученной матрицы.
∆3 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 1*(3*1-1*(-2))-(-2)*(5*1-1*3)+3*(5*(-2)-3*3) = -48
Выпишем отдельно найденные переменные Х
Проверка.
1*(-1)+5*0+1*4 = 3
-2*(-1)+3*0-1*4 = -2
3*(-1)+1*0+1*4 = 1
Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
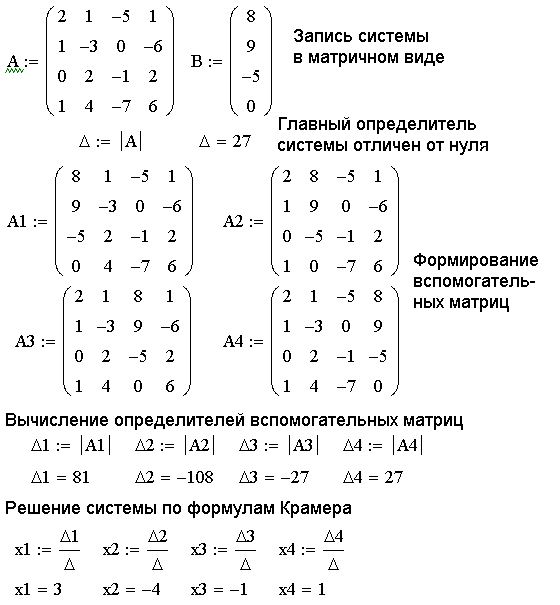
9.8: Решение систем с правилом Крамера
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1390
- OpenStax
- OpenStax
Цели обучения
- Оценить определители 2 × 2.
- Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
- Оценить 3 × 3 определителя.
- Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.

- Знать свойства определителей.
Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2 × 2
Определитель — это действительное число, которое может быть очень полезным в математике, поскольку оно имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
НАЙТИ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2 × 2
Определитель матрицы 2 × 2,
\(A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\)
равен определяется как
Обратите внимание на изменение обозначения. Есть несколько способов указать определитель, в том числе \(\det(A)\) и замена скобок в матрице прямыми, \(| A |\).
Пример \(\PageIndex{1}\): нахождение определителя матрицы \(2 × 2\)
Найдите определитель данной матрицы.
\(A=\begin{bmatrix}5&2\\−6&3\end{bmatrix}\)
Решение
\[\begin{align*} \det(A)&= \begin{vmatrix} 5&2\\-6&3\end{vmatrix}\\ &= 5(3)-(-6)(2)\\ &= 27 \end{align*}\]
Использование правила Крамера для решения системы двойки Уравнения с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители. Известен как Правило Крамера , этот метод восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году в . Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.
Известен как Правило Крамера , этот метод восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году в . Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.
Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.
\[\begin{align} a_1x+b_1y&= c_1 (1) \label{eq1}\\ a_2x+b_2y&= c_2 (2) \label{eq2}\\ \end{align}\]
Исключаем одну переменную, используя операции со строками, и решить для другой. Скажем, что мы хотим найти \(x\). Если уравнение \ref{eq2} умножается на коэффициент, противоположный коэффициенту \(y\) в уравнении \ref{eq1}, уравнение \ref{eq1} умножается на коэффициент \(y\) в уравнении \ref {eq2}, и мы добавим два уравнения, переменная \(y\) будет исключена.
Скажем, что мы хотим найти \(x\). Если уравнение \ref{eq2} умножается на коэффициент, противоположный коэффициенту \(y\) в уравнении \ref{eq1}, уравнение \ref{eq1} умножается на коэффициент \(y\) в уравнении \ref {eq2}, и мы добавим два уравнения, переменная \(y\) будет исключена.
\[\begin{align*} &b_2a_1x+b_2b_1y = b_2c_1 & \text{Умножить }R_1 \text{ на }b_2 \\ -&\underline{b_1a_2x-b_1b_2y=-b_1c_2} & \text{Умножить }R_2 \ text{ by }−b_1 \\ & b_2a_1x−b_1a_2x=b_2c_1−b_1c_2 \end{align*}\]
Теперь найдите \(x\).
\[\begin{align*} b_2a_1x−b_1a_2x &= b_2c_1−b_1c_2 \\ x(b_2a_1−b_1a_2) &= b_2c_1−b_1c_2 \\ x &= \dfrac{b_2c_1−b_1c_2}{b_2a_1−b_1a_2}=\ dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Аналогично, чтобы найти \(y\), мы исключим \(x\).
\[\begin{align*} & a_2a_1x+a_2b_1y = a_2c_1 & \text{Multiply }R_1 \text{ by }a_2 \\ -& \underline{a_1a_2x-a_1b_2y=-a_1c_2} & \text{Multiply }R_2 \text{ by }-a_1 \\ & a_2b_1y-a_1b_2y =a_2c_1-a_1c_2 \end{align*}\]
Решение для \(y\) дает
\[ \begin{align*} a_2b_1y-a_1b_2y &= a_2c_1−a_1c_2 \\ y(a_2b_1−a_1b_2) &= a_2c_1−a_1c_2 \\ y &= \dfrac{a_2c_1−a_1c_2}{a_2b_1−a_1b_2}=\dfrac{a_1c_2−a_2c_1}{a_1b_2−a_2b_1}=\dfrac{ \begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Обратите внимание, что знаменатель для \(x\) и \(y\) является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для вычисления \(x\) и \(y\), но правило Крамера также вводит новые обозначения: детерминанты. Тогда мы можем выразить \(x\) и \(y\) как частное двух определителей.
ПРАВИЛО КРАМЕРА ДЛЯ СИСТЕМ \(2×2\)
Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно количеству переменных.
Рассмотрим систему двух линейных уравнений с двумя переменными.
\[\begin{align*} a_1x+b_1y&= c_1\\ a_2x+b_2y&= c_2 \end{align*}\]
Решение с использованием правила Крамера дается как
\[\begin{align} x& = \dfrac{D_x}{D} = \dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0\\ y&= \dfrac{D_y}{D} = \dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix }}\; , D\neq 0 \end{align}\]
Если мы находим \(x\), столбец \(x\) заменяется столбцом констант. Если мы ищем \(y\), столбец \(y\) заменяется постоянным столбцом.
Пример \(\PageIndex{2}\): использование правила Крамера для решения системы \(2 × 2\)
Решите следующую систему \(2 × 2\), используя правило Крамера.
\[\begin{align*} 12x+3y&= 15\\ 2x-3y&= 13 \end{align*}\]
Решение
Найдите \(x\).
\[\begin{align*} x&= \dfrac{D_x}{D}\\ &= \dfrac{\begin{bmatrix}15&3\\13&-3\end{bmatrix}}{\begin{bmatrix} 12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{-45-39}{-36-6}\\ &= \dfrac{-84}{-42}\\ &= 2 \end{align*}\]
Найдите \(y\).
\[\begin{align*} y&= \dfrac{D_y}{D}\\ &= \dfrac{\begin{bmatrix}12&15\\2&13\end{bmatrix}}{\begin{bmatrix}12&3\ \2&-3\end{bmatrix}}\\ &= \dfrac{156-30}{-36-6}\\ &= -\dfrac{126}{42}\\ &= -3 \end{align *}\]
Решение: \((2,−3)\).
Упражнение \(\PageIndex{1}\)
Используйте правило Крамера для решения системы \(2 × 2\) уравнений.
\[\begin{align*} x+2y&= -11\\ -2x+y&= -13 \end{align*}\]
- Ответ
\((3,−7)\)
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но определить определитель матрицы 3 × 3 сложнее. Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем вычисляем сумму произведений записей вниз по по каждой из трех диагоналей (слева вверху справа внизу) и вычесть произведения записей вверх по по каждой из трех диагоналей (слева внизу справа вверху). Это легче понять с визуальным и пример.
Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем вычисляем сумму произведений записей вниз по по каждой из трех диагоналей (слева вверху справа внизу) и вычесть произведения записей вверх по по каждой из трех диагоналей (слева внизу справа вверху). Это легче понять с визуальным и пример.
Найдите определитель матрицы 3×3.
\(A=\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\)
- Дополнить \(A\) первыми двумя столбцами.
\(\det(A)=\left| \begin{array}{ccc|cc} a_1&b_1&c_1&a_1&b_1\\a_2&b_2&c_2&a_2&b_2\\a_3&b_3&c_3&a_3&b_3\end{array} \right|\)
- От верхнего левого угла к нижнему правому: умножьте числа по первой диагонали. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
- Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали.
 Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
Алгебра выглядит следующим образом:
\(| A |=a_1b_2c_3+b_1c_2a_3+c_1a_2b_3−a_3b_2c_1−b_3c_2a_1−c_3a_2b_1\)
Пример определения {3} × 3 Matrix
Найдите определитель матрицы \(3 × 3\) по данным
\(A=\begin{bmatrix}0&2&1\\3&−1&1\\4&0&1\end{bmatrix}\)
Решение
Дополните матрицу первыми двумя столбцами и следуйте формуле. Таким образом,
\[\begin{align*} | А | &= \влево| \begin{массив}{ccc|cc}0&2&1&0&2\\3&-1&1&3&-1\\4&0&1&4&0\end{массив}\right| \\ &= 0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3) (2) \\ &=0+8+0+4−0−6 \\ &= 6 \end{align*}\]
Упражнение \(\PageIndex{2}\)
Найдите определитель Матрица 3 × 3.
\(\det(A)=\begin{vmatrix}1&−3&7\\1&1&1\\1&−2&3\end{vmatrix}\)
- Ответ
\(−10\)
Вопросы и ответы: Можно ли использовать тот же метод для нахождения определителя матрицы большего размера?
Нет, этот метод работает только для матриц 2 × 2 и 3 × 3. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы \(3 × 3\), мы можем применить правило Крамера для решения системы трех уравнений с тремя переменные. Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц \(2 × 2\). Однако по мере увеличения порядка матрицы до \(3 × 3\) требуется гораздо больше вычислений.
Когда мы вычисляем определитель равным нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.
Рассмотрим систему уравнений \(3 × 3\).
\[\begin{align} a_1x+b_1y+c_1z &= \color{blue}d_1 \\ a_2x+b_2y+c_2z &= \color{blue}d_2 \\ a_3x+b_3y+c_3z &= \color{blue }d_3 \\ \end{align}\]
\(x=\dfrac{D_x}{D}\), \(y=\dfrac{D_y}{D}\), \(z=\dfrac{ D_z}{D}\), \(D≠0\)
где
\[D = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_x = \begin{vmatrix} \color{blue}d_1 & b_1 & c_1\\ \color{blue}d_2 & b_2 & c_2\\ \color{blue}d_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_y = \begin{vmatrix} a_1 & \color{blue}d_1 & c_1\\ a_2 & \color{blue}d_2 & c_2\\ a_3 & \color{blue}d_3 & c_3 \end{vmatrix}\; ,\; D_z = \begin{vmatrix} a_1 & b_1 & \color{blue}d_1\\ a_2 & b_2 & \color{blue}d_2\\ a_3 & b_3 & \color{blue}d_3 \end{vmatrix}\]
Если мы записываем определитель \(D_x\), мы заменяем столбец \(x\) постоянным столбцом. Если мы записываем определитель \(D_y\), мы заменяем их столбец y на постоянный столбец. Если мы записываем определитель \(D_z\), мы заменяем столбец \(z\) постоянным столбцом. Всегда проверяйте ответ.
Если мы записываем определитель \(D_y\), мы заменяем их столбец y на постоянный столбец. Если мы записываем определитель \(D_z\), мы заменяем столбец \(z\) постоянным столбцом. Всегда проверяйте ответ.
Пример \(\PageIndex{4}\): решение системы \(3 × 3\) с помощью правила Крамера
Найдите решение данной системы \(3 × 3\) с помощью правила Крамера.
\[\begin{align*} x+y-z&= 6\\ 3x-2y+z&= -5\\ x+3y-2z&= 14 \end{align*}\]
Решение
Используйте правило Крамера.
\(D=\begin{vmatrix}1&1&−1\\3&−2&1\\1&3&−2\end{vmatrix}\), \(D_x=\begin{vmatrix}6&1&−1\\−5&−2&1 \\14&3&-2\end{vmatrix}\), \(D_y=\begin{vmatrix}1&6&-1\\3&-5&1\\1&14&-2\end{vmatrix}\), \(D_z=\begin{ vmatrix}1&1&6\\3&-2&-5\\1&3&14\end{vmatrix}\)
Затем
\[\begin{align*} x&= \dfrac{D_x}{D}&= \dfrac{- 3}{-3}&= 1\\ y&= \dfrac{D_y}{D}&= \dfrac{-9}{-3}&= 3\\ z&= \dfrac{D_z}{D}&= \dfrac{6}{-3}&= -2\\ \end{align*}\]
Решение: \((1,3,−2)\).
Упражнение \(\PageIndex{3}\)
Используйте правило Крамера для решения матрицы \(3 × 3\).
\[\begin{align*} x-3y+7z&= 13\\ x+y+z&= 1\\ x-2y+3z&= 4 \end{align*}\]
- Ответ
\(\влево(−2,\dfrac{3}{5},\dfrac{12}{5}\вправо)\)
Пример \(\PageIndex{5A}\): использование правила Крамера для решения несогласованной системы
Решите систему уравнений с помощью правила Крамера.
\[\begin{align} 3x-2y&= 4 \label{eq3}\\ 6x-4y&= 0 \label{eq4}\end{align}\]
Решение
Начнем с нахождения определители \(D\), \(D_x\) и \(D_y\).
\(D=\begin{vmatrix}3&-2\\6&-4\end{vmatrix}=3(-4)−6(-2)=0\)
Мы знаем, что определитель нуля означает либо система не имеет решений, либо имеет бесконечное число решений. Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.
- Умножить уравнение \ref{eq3} на \(−2\).
- Добавьте результат к уравнению \ref{eq4}.
\[\begin{align*} &−6x+4y=−8 \\ &\;\;\;\underline{6x−4y=0} \\ &\;\;\;\;\;\ ;\;\;\;\; 0=−8 \end{align*}\]
Получаем уравнение \(0=−8\), которое неверно. Следовательно, система не имеет решения. График системы показывает две параллельные линии. См. рисунок \(\PageIndex{1}\).
Следовательно, система не имеет решения. График системы показывает две параллельные линии. См. рисунок \(\PageIndex{1}\).
Пример \(\PageIndex{5B}\): использование правила Крамера для решения зависимой системы
Решите систему с бесконечным числом решений.
\[\begin{align} x-2y+3z&= 0 \label{eq5}\\ 3x+y-2z&= 0 \label{eq6}\\ 2x-4y+6z&= 0 \label{eq7} \ end{align}\]
Решение
Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.
\(\left| \begin{array}{ccc|cc}1&−2&3&1&-2\\3&1&−2&3&1\\2&−4&6&2&-4\end{array}\right|\)
Затем
\(1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)( 1)−6(3)(−2)=0\)
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений. Мы должны выполнить исключение, чтобы узнать.
1. Умножьте уравнение \ref{eq5} на \(−2\) и добавьте результат к уравнению \ref{eq7}:
\[\begin{align*} &−2x+4y−6x=0 \ \ &\;\;\underline{2x−4y+6z=0} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;0=0 \end{align*}\]
2. Получение ответа \(0=0\), утверждение, которое всегда верно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой. См. рисунок \(\PageIndex{2}\).
Получение ответа \(0=0\), утверждение, которое всегда верно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой. См. рисунок \(\PageIndex{2}\).
Понимание свойств определителей
У определителей много свойств. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
- Если матрица имеет верхнетреугольную форму, определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.
- Если две строки или два столбца идентичны, определитель равен нулю. 9{−1}\) — величина, обратная определителю матрицы \(A\).
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Пример \(\PageIndex{6}\): Иллюстрация свойств определителей
Проиллюстрируйте каждое из свойств определителей.
Решение
Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов, расположенных вниз по главной диагонали.
\(A=\begin{bmatrix}1&2&3\\0&2&1\\0&0&-1\end{bmatrix}\)
Дополнить \(A\) первыми двумя столбцами.
\(A=\left[ \begin{array}{ccc|cc}1&2&3&1&2\\0&2&1&0&2\\0&0&−1&0&0\end{array}\right]\)
Затем
\[\begin{align* } \det(A)&= 1(2)(-1)+2(1)(0)+3(0)(0)-0(2)(3)-0(1)(1)+1 (0)(2)\\ &= -2 \end{align*}\]
Свойство 2 утверждает, что перестановка строк меняет знак. Учитывая
\[\begin{align*} A&=\begin{bmatrix}-1&5\\4&-3\end{bmatrix}\\ \det(A)&= (-1)(-3)-(4) (5)\\ &= 3-20\\ &= -17 \end{align*}\]
\[\begin{align*} B&= \begin{bmatrix}4&-3\\-1&5\end {bmatrix}\\ \det(B)&= (4)(5)-(-1)(-3)\\ &= 20-3\\ &= 17 \end{align*}\]
Свойство 3 утверждает, что если две строки или два столбца идентичны, определитель равен нулю.
\[\begin{align*} A&=\left[ \begin{array}{ccc|cc}1&2&2&1&2\\2&2&2&2&2\\-1&2&2&-1&2\end{массив}\right]\\ \det(A) &=1(2)(2)+2(2)(-1)+2(2)(2)+1(2)(2)-2(2)(1)-2(2)(2) \\ &=4-4+8+4-4-8\\ &=0 \end{align*}\] 9{-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \ end{align*}\]
Свойство 6 гласит, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,
Таким образом,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-2(3)\\ &= -2 \end{align*}\]
\[\begin{align*} B&=\begin{bmatrix}2(1)&2(2)\\3&4\end{bmatrix}\\ \det(B) &=2(4)-3(4)\\ &=-4 \end{align*}\]
Пример \(\PageIndex{7}\): использование правила Крамера и свойств определителя для решения системы
Найдите решение заданной системы \(3 × 3\).
\[\begin{align} 2x+4y+4z&=2 \label{eq8}\\ 3x+7y+7z&=-5 \label{eq9}\\ x+2y+2z&=4 \label{eq10} \end{align}\]
Решение
Используя правило Крамера, мы имеем
\(D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}\)
Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.
1. Умножьте уравнение \ref{eq10} на \(–2\) и добавьте результат к уравнению \ref{eq8}.
\[\begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}\]
Получение оператора, который является Противоречие означает, что система не имеет решения.
Медиа
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практических занятий по правилу Крамера.
- Решение системы двух уравнений с помощью правила Крамера
- Решите систему из трех уравнений, используя правило Крамера
Ключевые понятия
- Определитель для \(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) равен \(ad-bc\). См. пример \(\PageIndex{1}\).
- Правило Крамера заменяет столбец переменной столбцом константы. Решения: \(x=\dfrac{D_x}{D}\), \(y=\dfrac{D_y}{D}\). См. пример \(\PageIndex{2}\).
- Чтобы найти определитель матрицы \(3×3\), увеличьте первые два столбца. Сложите три диагональных элемента (слева вверху справа внизу) и вычтите три элемента по диагонали (слева внизу справа вверху). См. пример \(\PageIndex{3}\).
- Чтобы решить систему из трех уравнений с тремя переменными с помощью правила Крамера, замените столбец переменных столбцом констант для каждого требуемого решения: \(x=\dfrac{D_x}{D}\), \(y=\dfrac{ D_y}{D}\), \(z=\dfrac{D_z}{D}\).
 См. пример \(\PageIndex{4}\).
См. пример \(\PageIndex{4}\). - Правило Крамера также полезно для нахождения решения системы уравнений без решения или с бесконечным числом решений. См. Пример \(\PageIndex{5}\) и Пример \(\PageIndex{6}\).
- Некоторые свойства определителей полезны при решении задач. Например: 9{−1}\) — величина, обратная определителю матрицы \(A\).
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент. См. Пример \(\PageIndex{7}\) и Пример \(\PageIndex{8}\).
Эта страница под названием 9.8: Решающие системы с правилом Крамера распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- Правило Крамера
- Детерминанты
- источник@https://openstax.
 org/details/books/precalculus
org/details/books/precalculus
Determinant Calculator: Wolfram|Alpha
WolframAlpha
Take the determinant of matrices with Wolfram|Alpha
123321213
Math Input
Vectors & MatricesБольше, чем просто онлайн-калькулятор определителей
Wolfram|Alpha — идеальный ресурс для вычисления определителей матриц. Он также может вычислять матричные произведения, ранг, недействительность, сокращение строк, диагонализацию, собственные значения, собственные векторы и многое другое.
Он также может вычислять матричные произведения, ранг, недействительность, сокращение строк, диагонализацию, собственные значения, собственные векторы и многое другое.
Узнайте больше о:
- Определители »
Советы по вводу запросов
Для ввода запросов используйте простой английский или общепринятый математический синтаксис. Чтобы ввести матрицу, разделяйте элементы запятыми, а строки — фигурными скобками, скобками или круглыми скобками.
- определитель {{2, 3}, {4, 7}}
- определитель {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}
- найти определитель матрицы ((a, 3), (5, -7))
- |{{2/3, -5/7}, {-3, 4/9}}|
- определитель [[2, 3], [5, 6]]
- Просмотреть другие примеры »
Доступ к средствам мгновенного обучения
Получите немедленную обратную связь и рекомендации с помощью пошаговых решений и Генератора проблем Wolfram
Узнать больше о:
- Пошаговые решения »
- Генератор задач Wolfram »
База знаний об определителях
Определитель — это свойство квадратной матрицы.

Значение определителя имеет много значений для матрицы. Определитель, равный 0, означает, что матрица сингулярна и, следовательно, необратима. Систему линейных уравнений можно решить, создав матрицу из коэффициентов и взяв определитель; этот метод называется правилом Крамера и может использоваться только в том случае, если определитель не равен 0. Геометрически определитель представляет собой площадь параллелограмма со знаком, образованную векторами-столбцами, принятыми в качестве декартовых координат.
Существует множество методов вычисления определителя. Определения некоторых матриц, таких как диагональные или треугольные матрицы, можно вычислить, взяв произведение элементов на главной диагонали. Для матрицы 2 на 2 определитель вычисляется путем вычитания обратной диагонали из главной диагонали, что известно как формула Лейбница. Определитель произведения матриц равен произведению определителей этих матриц, поэтому может быть полезно разложить матрицу на более простые матрицы, вычислить отдельные определители, а затем умножить результаты.



 Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали. См. пример \(\PageIndex{4}\).
См. пример \(\PageIndex{4}\). org/details/books/precalculus
org/details/books/precalculus