Решение неопределенности онлайн: Решение пределов онлайн

Энни Дьюк – Принцип ставок. Как принимать решения в условиях неопределенности читать онлайн бесплатно

12 3 4 5 6 7 …62

Энни Дьюк

ПРИНЦИП СТАВОК

Как принимать решения в условиях неопределенности

Москва «Манн, Иванов и Фербер» 2019 * * *

Annie Duke

Thinking in Bets

Making Smarter Decisions When You Don’t Have All the Facts

Portfolio/Penguin

Научные редакторы Максим Мерзляков, Кирилл Чехов

Издано с разрешения Portfolio, an imprint of Penguin Publishing Group, a division of Penguin Random House LLC и литературного агентства Anna Jarota Agency

Благодарим за помощь в подготовке издания Яна Матвеева

Возрастная маркировка в соответствии с Федеральным законом от 29 декабря 2010 г. № 436-ФЗ: 12+

Все права защищены.

Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.

© 2018 by Annie Duke

All rights reserved including the right of reproduction in whole or in part in any form. This edition published by arrangement with Portfolio, an imprint of Penguin Publishing Group, a division of Penguin Random House LLC.

© Перевод на русский язык, издание на русском языке, оформление. ООО «Манн, Иванов и Фербер», 2019

* * *

ВВЕДЕНИЕ

Почему эта книга не о покере[1]

В двадцать шесть лет мне казалось, что мое будущее предопределено. Я окончила известную школу в Нью-Гэмпшире, где мой отец возглавлял английскую кафедру. Потом получила степени по английскому языку и психологии в Колумбийском университете. В аспирантуре Университета Пенсильвании я выиграла грант Национального научного фонда, училась в магистратуре и приступила к докторской диссертации по когнитивной психологии.

Диссертация была почти готова, когда я заболела и мне пришлось взять академический отпуск. В итоге я оставила университет, вышла замуж и переехала в небольшой городок в Монтане. Конечно, гранта не хватило: мне были нужны деньги. Мой брат Говард, профессиональный игрок в покер, на тот момент был участником финального стола Мировой серии (WSOP). Он предложил мне сыграть в легальном заведении — в подвале бара «Хрустальный салон». Атмосфера в нашей семье была пропитана соревновательным духом, мы обожали разные игры, и Говард несколько раз возил меня на каникулы в Лас-Вегас. Я наблюдала за его игрой и сама несколько раз сыграла по низким ставкам.

В покер я влюбилась сразу. Меня увлекли острые ощущения от игры и возможность проверить себя. Мне предстояло многому научиться, и это меня радовало. Я хотела заработать немного денег во время вынужденного перерыва. Затем планировала вернуться в аспирантуру, а покер остался бы моим хобби.

Этот «временный перерыв» обернулся двадцатилетней карьерой профессионального игрока. К ее завершению в моем арсенале были золотой браслет Мировой серии покера, победы в Турнире чемпионов WSOP и в Национальном чемпионате NBC по игре один на один.

В турнирах по покеру я выиграла более четырех миллионов долларов. Говард получил два браслета Мировой серии, пару титулов в чемпионате Hall of Fame Poker Classic, победил в двух турнирах World Poker Tour и выиграл свыше 6,4 миллиона долларов.

Я ушла из науки. Но скоро поняла, что просто занялась другими исследованиями, наблюдая, как люди учатся и принимают решения. Одна полная раздача (или «рука») в покере занимает около двух минут. За этот короткий промежуток я принимаю до двадцати решений. И каждая раздача заканчивается конкретным результатом: я выигрываю или теряю деньги, то есть сразу вижу эффективность решений. Но эта обратная связь неоднозначна: выигрыш и проигрыш — слабые индикаторы качества решений. Можно победить лишь благодаря везению. И можно проиграть при плохой раздаче, даже не допуская ошибок.

Я не хотела терять деньги и подошла к вопросу серьезно. Я училась у игроков мирового класса «справляться» с удачей и неопределенностью. Наставники помогли мне понять, что ставка — это решение о неопределенном будущем. Такой подход позволил мне избежать многочисленных ловушек на пути принятия решений, более рационально использовать собственный опыт и скрывать эмоции.

В 2002 году меня попросили выступить перед трейдерами и поделиться советами по игре, которые будут полезны в торговле ценными бумагами. С тех пор разным специалистам я рассказывала о том, как приемы покера помогают принимать решения в финансах, стратегическом планировании, в работе с персоналом, в вопросах права и предпринимательства.

Принцип ставок позволяет постоянно совершенствовать процесс принятия решений. Можно научиться отличать качество результата от качества решения, открыть потенциал фразы «Я не уверен», освоить стратегии планирования, контролировать свои реакции. Мы можем участвовать в объединениях, которые поддержат наш интерес к истине, помогут отточить рациональное мышление. Мы можем научиться «сотрудничать» с нашим прошлым и будущим, чтобы более осознанно действовать в настоящем.

Мышление по принципу ставок не сделало меня расчетливым флегматиком. Я совершаю немало ошибок. Промахи, эмоции, проигрыши неизбежны, потому что мы люди. Но принцип ставок помогает мне сохранять объективность, точность, непредвзятость. Этот подход применим в разных областях жизни и серьезно ее меняет. И моя книга не о стратегиях азартных игр. Она о том, чему научил меня покер: как осваивать новое и принимать решения. Жизнь определяется качеством наших решений и удачей. Главное — распознавать разницу между ними. И в этом суть принципа ставок.

ГЛАВА 1

Жизнь — это покер, а не шахматы

Пит Кэрролл и «кабинетные стратеги» на стадионе[2]

Одно из самых резонансных решений в истории Супербоула было принято в 2015 году. «Сиэтл Сихоукс» отставали на четыре очка. За 26 секунд до конца игры они получили мяч на второй попытке одноярдовой линии «Нью-Ингленд Пэтриотс». Все думали, что тренер «Сихоукс» Пит Кэрролл назначит выносной розыгрыш и отдаст мяч в руки бегущего Маршона Линча. Ситуация к этому располагала, а Линч был одним из лучших бегущих в Национальной футбольной лиге (НФЛ).

Но Кэрролл назначил пасовый розыгрыш в исполнении квотербека Расселла Уилсона. Соперники перехватили{1} мяч и спустя мгновение выиграли Супербоул. На следующий день решение тренера раскритиковали в прессе.

USA Today: «О чем думали „Сихоукс“, когда назначали худший розыгрыш в истории НФЛ?»

Washington Post: «Худшее назначение розыгрыша в истории Супербоула навсегда изменит отношение к „Сихоукс“ и „Пэтриотс“».

FoxSports.com: «Самое идиотское назначение в истории Супербоула может быть началом конца для „Сиэтл Сихоукс“».

Читать дальше

12 3 4 5 6 7 …62

Читать книгу «Управляй будущим. Как принимать решения в условиях неопределенности» онлайн полностью📖 — Максима Киселева — MyBook.

Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.

© ООО Издательство «Питер», 2017

© Серия «Практика лучших бизнес-тренеров России», 2017

Автор этой книги – преподаватель (с ученой степенью, прошу заметить). Я читаю студентам такие дисциплины, как «Рынок ценных бумаг», «Финансовые рынки», «Инвестиции», «Поведенческая экономика». При этом наряду с преподавательской деятельностью я всегда работал на финансовых рынках как практик, совершал сделки с акциями и облигациями, валютами, драгоценными металлами и нефтью (обычно эта деятельность называется биржевыми спекуляциями).

На протяжении всей карьеры я смутно осознавал, что выбранные мною два направления (теоретическое и практическое) хоть и относятся к одной области, но все же не совпадают. Более того, теория и практика противоречат друг другу. Дело в том, что главенствующая экономическая парадигма построена на нескольких аксиомах и одна из них – это теория рационального поведения экономических агентов (то есть нас с вами). Отцы-основатели экономической науки исходят из того, что люди точно знают, чего они хотят и как этого достичь. Другими словами, экономисты уверены, что у людей есть стабильные предпочтения, которые можно сравнить между собой и в отношении которых люди самостоятельно принимают решения, сколько и какого блага потребить. Например, в интерпретации экономистов, мы должны точно ответить на вопрос, какой велосипед (телефон, машину) мы хотим купить, почему и за какую цену. Кроме того, мы будто бы знаем, как изменится наше предпочтение, если цена велосипеда вырастет или упадет на 10 % либо на 10 % изменится стоимость его обслуживания.

Эта аксиома прочно встроена в фундамент современной экономической науки вот уже 250 лет и не подвергается сомнению в рамках главенствующей экономической парадигмы. Действительно, если мы откажемся от признания рационального характера наших экономических решений, придется придумывать новую теорию, чтобы объяснять поведение покупателей и продавцов, взаимодействие спроса и предложения, процессы ценообразования, реакции вкладчиков на рост процентных ставок и даже направления передвижения мирового финансового капитала.

Однако многолетняя работа в качестве участника торгов никак не позволяла мне согласиться с теорией рационального поведения, ибо на финансовых рынках наши решения почти всегда (то есть за редким исключением)… иррациональны. Это заявление я делаю совершенно ответственно, ибо имею за плечами 15-летний опыт деятельности трейдера и менеджера по работе с клиентами. Не только мой личный опыт совершения биржевых сделок свидетельствует о доминировании иррациональных решений, но также опыт сотен клиентов, с которыми я имел честь быть знаком. Я абсолютно уверен: именно иррациональные, более того – глупые и опрометчивые решения являются единственной причиной разорения биржевых трейдеров (а не заговор сильных мира сего, сломавшийся компьютер или манипуляции алчных банкиров).

Чем больше я об этом думал, тем яснее понимал: с теорией явно что-то не так. Традиционная экономическая наука утверждает, что если вы приняли решение начать бегать в шесть часов утра, то именно это и произойдет – завтра вы проснетесь в полшестого, а в шесть стартуете. И так поступят 100 % людей, принявших такое решение. На этом основании экономисты строят модели, формулы, теории, закономерности и – самое главное – прогнозы. С математической точки зрения вся эта надстройка безупречна. Но мы-то понимаем, что из 100 человек, принявших решение начать новую жизнь с завтрашнего дня, на беговую дорожку к шести утра выйдет лишь один, максимум – двое. Остальные отложат это решение на неопределенный срок. Другими словами, «Я» сегодня – это совсем не «Я» завтра. А как же тогда строить прогнозы, если у нас есть информация только о сегодняшнем «Я» и мы не знаем, каким это «Я» станет завтра?

Мы – преподаватели экономики – учим студентов тому, что поведение людей рационально, что на рынках царит совершенная конкуренция, что экономические агенты обладают всей необходимой информацией, что рынки находятся в равновесном состоянии и что рост спроса останавливается в итоге ростом цены. Но на самом-то деле все это не так! Наше поведение далеко от того, чтобы называться рациональным; поддавшись панике, мы сметаем товар с полок магазинов, даже если продавцы повышают цены; конкурентных рынков в природе нет и никогда не было; принимая решение купить тот или иной товар, мы ориентируемся на слухи и собственные эмоции, а не на факты… А если бы рыночное равновесие существовало, то кризисы были бы невозможны.

И вот у меня появилась задумка поглубже разобраться в данной проблеме. Через пару лет эта задумка воплотилась в книгу, которую вы сейчас держите в руках. Прочитав ее, вы, хочется надеяться, получите массу практических преимуществ. Ведь осознание собственной иррациональности, умение разобраться в факторах, толкающих нас на совершение поступков, о которых мы нередко потом сожалеем, – это и есть отправная точка, откуда можно начинать самосовершенствование и изменение жизни к лучшему. В этой книге вы найдете ответы на следующие вопросы:

‣ для чего так важно думать о том, как мы думаем;

‣ почему так важно насторожиться, если все складывается очень хорошо;

‣ где находится предел информации, необходимой для принятия решений;

‣ чем рациональное поведение отличается от иррационального;

‣ почему социопаты и аутисты – самые рациональные люди на свете;

‣ почему наши решения вовсе не наши;

‣ почему мы так любим прогнозировать и искать причины;

‣ как важно говорить: «Я не знаю»;

‣ почему мы так часто сожалеем о принятых решениях;

‣ что толкает людей покупать лотерейные билеты и играть на бирже.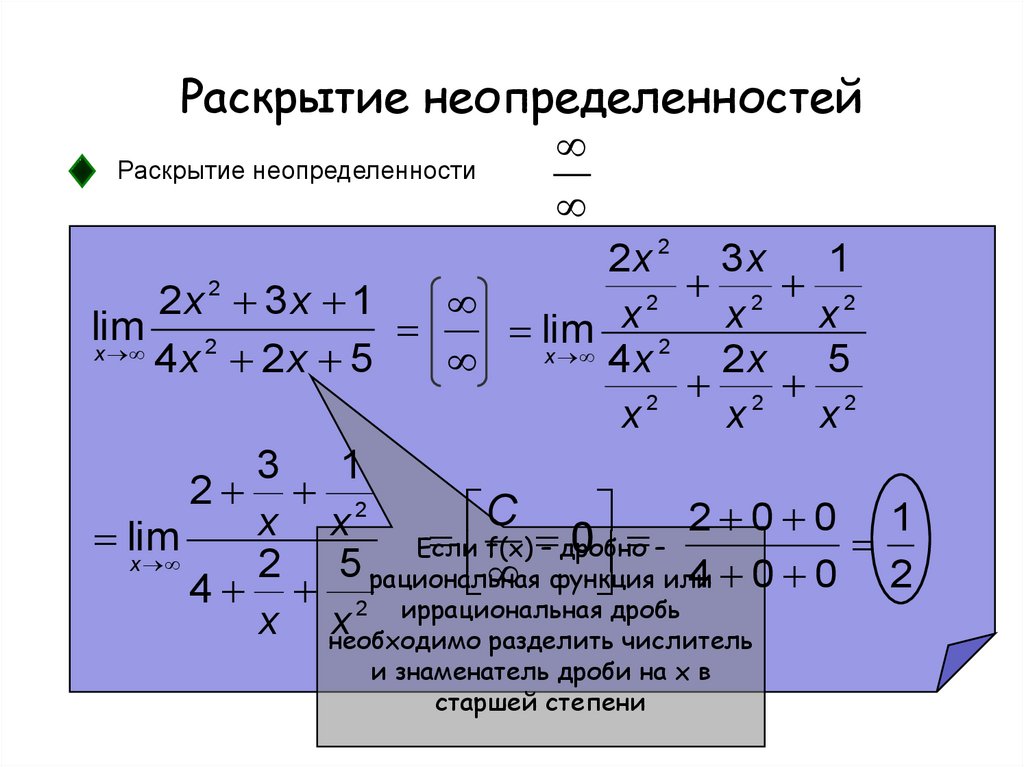

Ричард Фейнман, известный физик и популяризатор науки, как-то сказал, что каждая формула снижает число читателей книги в два раза. Поэтому я старался не нагружать вас математикой и статистикой. Так что в этой книге вы встретите только одну формулу, зато очень полезную.

Специально для вас я подготовил много интересных задач и примеров, экспериментов и кейсов, подсмотренных мною у других авторов или проделанных лично (благо поток студентов неисчерпаем).

Кроме того, в конце каждой главы я набросал несколько рекомендаций (нет-нет, я ни в коем случае не пытаюсь вас учить, как надо жить), которые помогут вам выбирать правильно.

Спасибо вам за то, что приобрели эту книгу. Я надеюсь, что она изменит вашу жизнь к лучшему. Ведь очень скоро вы узнаете, как мы осуществляем выбор – в быту, политике и, конечно же, на финансовых рынках (не забудьте, ведь моя профессия – биржевой спекулянт).

8 Бесплатное программное обеспечение для расчета погрешности, которое можно загрузить сейчас

Введение

Нужен калькулятор погрешности измерений?

Если вы являетесь лабораторией, аккредитованной в соответствии с ISO/IEC 17025, в ваших интересах иметь программное обеспечение для оценки неопределенности измерений. Кроме того, если вы похожи на меня, вы, скорее всего, искали в Интернете программное обеспечение для расчета неопределенности.

Нашли ли вы программное обеспечение для измерения погрешностей, которое вам нравится использовать?

Если так, отлично! Если нет, я здесь, чтобы помочь.

В этой статье я составил список из 8 бесплатных калькуляторов неопределенности, которые вы можете скачать и попробовать уже сегодня. Я даже даю вам ссылки, чтобы скачать их.
Кроме того, я включил снимки экрана и свой опыт работы с программным обеспечением, чтобы помочь вам решить, какой калькулятор вам стоит попробовать.

Теперь, если вам интересно, давайте начнем.

 

Справочная информация

В течение многих лет я искал программное обеспечение для расчета неопределенности, которое соответствовало бы моим требованиям.

Мне нужно было программное обеспечение для измерения неопределенности;
• Создание легко читаемых бюджетов неопределенности;
• Сохранение и архивирование результатов анализа неопределенности;
• Интеграция с программным обеспечением для управления калибровкой.

Итак, я искал в Интернете, звонил в компании и брал демонстрационное программное обеспечение на конференциях. Я перепробовал все, до чего мог дотянуться.

К сожалению, никто не делает программное обеспечение, отвечающее этим требованиям; в частности, интеграция с программным обеспечением для управления калибровкой.

Доверься мне. Я искал везде и не смог найти программное обеспечение, которое делало бы все три.

Я даже пытался сделать свою собственную программу измерения погрешности измерения; но я сдался, потратив месяцы на то, чтобы заставить его работать так, как я хотел.

Затем я реализовал новое решение (на тот момент), которым я поделюсь с вами позже в этом руководстве. А пока давайте поговорим о программном обеспечении для определения погрешности измерений.

Большинство калькуляторов неопределенности (из тех, что я нашел) позволяют создавать бюджеты неопределенности и сохранять результаты своей работы.

Это необходимо, если ваша лаборатория аккредитована по ISO/IEC 17025 или желает получить аккредитацию.

Чтобы получить аккредитацию, вам необходимо программное обеспечение для оценки неопределенности для вашей области аккредитации и результатов измерений. Кроме того, вам необходимо вести записи своих расчетов, чтобы показывать их оценщикам и делиться ими с коллегами.

Послушай меня. Вы не хотите вычислять неопределенность с помощью бумаги, ручки и калькулятора.

Итак, хватит тратить время, отложите калькулятор и давайте проверим какое-нибудь программное обеспечение для определения погрешности измерений.

 

Бесплатное программное обеспечение для расчета неопределенности

Ниже приведен список программ для расчета неопределенности, которые вы можете загрузить и установить на свой компьютер, чтобы приступить к оценке неопределенности.

В следующих разделах я расскажу вам больше об этом программном обеспечении и о том, где его можно скачать. Кроме того, я собираюсь рассказать вам, что я думал об этом программном обеспечении после его использования.

1. Gum Tree Calculator
2. QMSys GUM Standard
3. Metrodata GmbH GUM Workbench Pro
4. MUKit — комплект для измерения погрешности измерения
5. NIST Uncertainty Machine
6. Hewlett-Packard UnCal 3.2
7. Uncertainty Sidekick
8. Программное обеспечение NPL для измерения погрешности

 

Нажмите здесь, чтобы получить полный список из Бонус1: программное обеспечение для расчета неопределенности со ссылками для загрузки.

 
 

Калькулятор дерева GUM (GTC)

 

Описание

Первым калькулятором неопределенности в списке является калькулятор дерева GUM (GTC).

Он разработан Лабораторией эталонов Новой Зеландии (MSL) и представляет собой инструмент, предназначенный для упрощения применения международных рекомендаций по расчету неопределенности.

GUM Tree Calculator — это приложение командной строки без графического пользовательского интерфейса. Таким образом, знание программирования (на Python) является обязательным для вас, чтобы в полной мере использовать этот калькулятор неопределенности.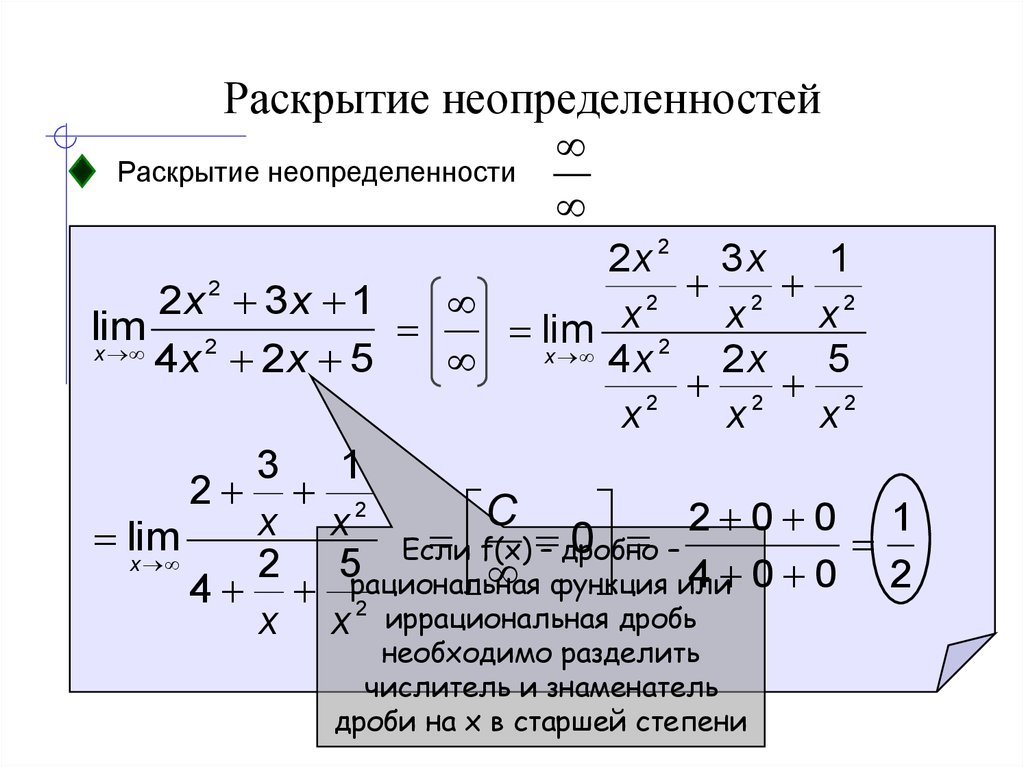

Если вы хотите скачать Калькулятор дерева ГУМ, вы можете заполнить заявку здесь.

 

Ключевые выводы

• Калькулятор командной строки
• Нет графического интерфейса пользователя (GUI)
• Требуется знание программирования на Python
• Трудно учиться

 

Краткий обзор

На мой взгляд, это может быть мощным калькулятором неопределенности, если вы знаете, как программировать на Python. В противном случае, я считаю, что кривая обучения будет трудной для большинства непрограммистов.

Лично я не умею программировать на Python. Таким образом, я мог использовать калькулятор только с ограниченными возможностями.

 

QMSys GUM Standard

 

Описание

QMSys GUM — это вычислитель неопределенности, разработанный в Болгарии и предназначенный для оценки неопределенности линейных процессов измерения по методу GUM.

Разработчик утверждает, что вам не нужно устанавливать это программное обеспечение на свой компьютер. Таким образом, вы можете использовать его на любом компьютере через USB-накопитель.

Если вы хотите попробовать программное обеспечение, производитель предлагает бесплатную 30-дневную пробную версию, которую вы можете запросить, нажав здесь.

 

Ключевые выводы

• Последняя версия — 2016
• Красивый пользовательский интерфейс
• Простота использования
• От базовых до расширенных параметров
• План бюджета большой неопределенности
• Текстовый редактор, аналогичный Microsoft Word

 

Краткий обзор

Попробовав этот калькулятор неопределенности, он мне очень понравился. Программное обеспечение было новее, чем остальные приложения в этом руководстве. У него приятный пользовательский интерфейс, и его было довольно легко освоить и начать оценивать неопределенность.

Кроме того, у него была отличная возможность добавлять примечания к вашему анализу неопределенности.

Наконец, мне понравилось представление бюджетов неопределенности. Они были хорошо отформатированы и просты для понимания, что очень важно, когда вы делитесь своими бюджетами с оценщиками.

 

Metrodata GmbH GUM Workbench Pro

 

Описание

GUM Workbench — это программное приложение, разработанное компанией Metrodata GmbH в Германии на основе Руководства по выражению неопределенности в измерениях. Его цель состоит в том, чтобы позволить пользователям систематически оценивать неопределенность измерения для одного и нескольких результатов.

 

Ключевые выводы

• Дружественный интерфейс
• Множество удобных функций и инструментов
• Комната для заметок
• Отлично подходит для моделей на основе уравнений
• Ввод данных может немного сбить с толку новичков
• Отличная презентация результатов

 

Краткий обзор

GUM Workbench был прекрасным инструментом для оценки неопределенности измерений. У него был простой пользовательский интерфейс с отличными инструментами, помогающими рассчитать неопределенность. Подобно QMSys GUM, он имел возможность добавлять примечания к вашему анализу неопределенности.

Однако ввод ваших данных для расчета неопределенности был немного запутанным. Учиться было несложно, и мне потребовалось некоторое время, чтобы привыкнуть.

Что мне больше всего понравилось в этом калькуляторе неопределенности, так это бюджеты неопределенности. Бюджеты имели отличный макет, который было легко читать и понимать.

 

MUKit – Комплект для определения погрешности измерения

 

Описание

Комплект для определения погрешности измерения (MUKit) представляет собой программное приложение для определения погрешности измерения, разработанное в Финляндии на основе Nordtest TR 537.

 

Ключевые выводы

• Не буду устанавливать
• Лучше подходит для химических и биологических лабораторий

 

Краткий обзор

К сожалению, мне не удалось протестировать этот калькулятор неопределенности. Что бы я ни пытался, программа не устанавливалась на мой компьютер. Я постоянно сталкивался с ошибкой за ошибкой.

Итак, я просмотрел руководство пользователя, снимки экрана и примерные бюджеты неопределенности, предоставленные разработчиком.

Судя по тому, что я просмотрел, это программное обеспечение было разработано для оценки неопределенности в химических, биологических и медико-биологических лабораториях. Мне не удалось найти примеров, связанных с калибровочными лабораториями.

В общем, я не могу рекомендовать вам эту программу, потому что не смог ее опробовать.

 

NIST Uncertainty Machine

 

Описание

NIST Uncertainty Machine — это программное приложение, разработанное в США для оценки неопределенности измерения модели измерения или математического уравнения.

Калькулятор погрешности анализирует погрешность измерения одним из следующих двух методов;
1. Метод GUM и NIST, Техническое примечание 1297.
2. Метод Монте-Карло, описанный в GUM Supplement 1.

Кроме того, чтобы использовать программное обеспечение NIST Uncertainty Machine, вам необходимо сначала загрузить программное обеспечение R.

 

Ключевые выводы

• Простой пользовательский интерфейс
• Вариантов немного
• Простота использования
• Лучше подходит для анализа неопределенностей уравнений
• Запутанный экран результатов с красивым графиком
• Результаты усечены до целых чисел

 

Краткий обзор

Я решил проверить это программное обеспечение после того, как Грег Страус из NIST порекомендовал мне попробовать его. Так я и сделал.

В целом, я не был впечатлен. Пользовательский интерфейс был довольно простым, а в программном обеспечении не было много опций.

Тем не менее, программное обеспечение было простым в использовании и генерировало несколько хороших графиков, которые вы можете или не можете использовать.

Больше всего меня расстроила неопределенность бюджетов.

Результаты были немного запутанными для понимания, и программное обеспечение сократило расчеты неопределенности до целых чисел. Это не очень хорошо для лабораторий, стремящихся получить аккредитацию ISO/IEC 17025.

Так что мне трудно рекомендовать его вам для расчета погрешности измерения (извините, Грег!).

 

Hewlett Packard UnCal 3.2

 

Описание

Калькулятор неопределенности 3.2 — это приложение для Windows 2000 (да, я сказал Windows 2000), разработанное Хьюстонской метрологической группой Hewlett-Packard Enterprise для простого расчета неопределенности для часто выполняемых измерений.

Методы, используемые для оценки неопределенности, основаны на Руководстве ISO по выражению неопределенности в измерениях и Техническом примечании NIST 1297.

Простота использования

Легко учиться

Множество функций

Не удалось сохранить или записать в Word или Excel

 

Краткий обзор

UnCal 3.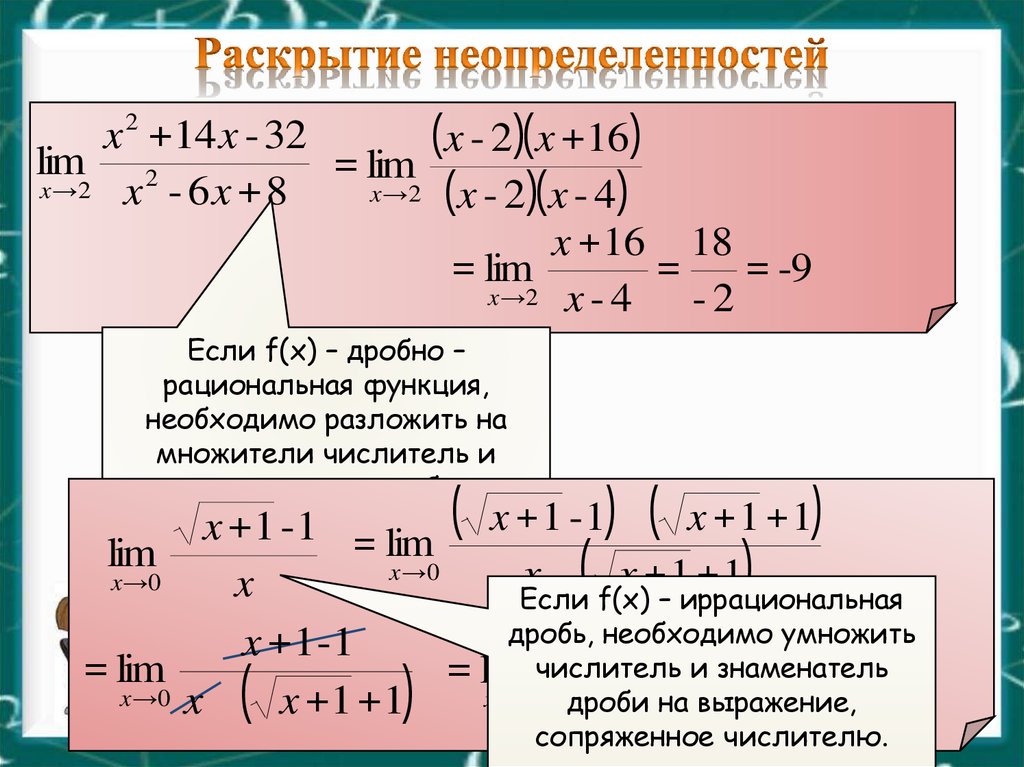 2 — это простой калькулятор неопределенности, который прост в использовании и освоении. Это может выглядеть не очень красиво, но со своей задачей справляется.

Это первое программное приложение для расчета неопределенности, которое я использовал, когда начинал вычислять неопределенность.

Эту программу мне порекомендовал коллега. Итак, я использовал его в течение нескольких лет, пока мне не надоело заново создавать каждый бюджет неопределенности, потому что программное обеспечение не сохраняло данные.

Это было неприятно.

Похоже, что разработчик добавил несколько новых функций, в том числе возможность сохранять вашу работу.

Если вы хотите рассчитать неопределенность как новичок (и не хотите перегружаться слишком большим количеством функций) или вам просто нужен простой работающий калькулятор неопределенности, UnCal 3.2 — это то, что вам нужно.

 

Неопределенность Sidekick от Integrated Sciences Group

 

Описание

Неопределенность Sidekick — это бесплатный калькулятор неопределенности, разработанный Integrated Sciences Group. Он был разработан для расчета и анализа неопределенности измерений с использованием методов и концепций, описанных в Руководстве ISO по выражению неопределенности в измерениях (GUM).

По словам разработчика, программное обеспечение предназначено для того, чтобы помочь вам в процессе оценки неопределенности результатов измерений.

 

Ключевые выводы

• Отличный пользовательский интерфейс
• Отличный пользовательский опыт (UX)
• Инструкции, которые помогут вам в процессе
• Простота использования

 

Краткий обзор

Неопределенность Sidekick — калькулятор неопределенности, разработанный доктором Говардом Кастрапом. Если вы не знаете, кто такой Говард, рекомендую зайти на его сайт.

Он и его жена Сьюзен написали много статей и сделали множество презентаций по неопределенности измерений.

Ховард также написал множество политик НАСА по оценке неопределенности измерений.

Можно сказать, что этот парень – гуру погрешности измерений!

Итак, мне пришлось попробовать его программу. Я должен сказать, что это очень хороший калькулятор неопределенности.

Он имеет множество функций (больше, чем вам может понадобиться). Однако больше всего мне понравилось представление результатов и диаграмма, помогающая пользователям ориентироваться в процессе.

Это отличная функция для новичков или любого пользователя.

Лично я не пользуюсь этим программным обеспечением, но определенно рекомендую его тем, кто ищет программное обеспечение для расчета неопределенности.

 

Программное обеспечение NPL для измерения погрешности измерения

 

Описание

NPLUnc_101 — это программное приложение, разработанное Национальной физической лабораторией (NPL) в Соединенном Королевстве для расчета погрешности измерения с использованием Руководства по выражению неопределенности в измерении (GUM).

Программное обеспечение также позволяет оценивать неопределенность с использованием метода Монте-Карло, описанного в GUM, Приложение 1.

Для использования программного обеспечения необходимо установить библиотеки MATLABS Component Runtime (MCR). Вы можете скачать программу установки MATLAB Runtime здесь.

 

Ключевые выводы

• Требуется программа установки MATLAB Runtime Installer
• Загрузка заняла много времени

 

Краткий обзор

После того, как я нашел программное обеспечение NPL для расчета неопределенности, мне не терпелось попробовать его.

К сожалению, я этого не сделал.

Программное обеспечение требует, чтобы вы установили MATLAB Runtime Installer, чтобы использовать программное обеспечение для измерения неопределенности. Когда я попытался загрузить программное обеспечение онлайн, это заняло целую вечность; даже при скорости соединения 100 Мбит/с.

Через 30 минут я отменил загрузку и сдался. Поэтому я не могу поделиться с вами своими мыслями о программном обеспечении.

Однако, если вы хотите попробовать его, воспользуйтесь приведенными выше ссылками, чтобы загрузить его самостоятельно.

Если вы попробуете и вам понравится, пришлите мне электронное письмо с вашим мнением и несколькими скриншотами, и я с радостью обновлю это руководство для других.

 

Дополнительное программное обеспечение для расчета неопределенности

Если вы заинтересованы в опробовании дополнительного программного обеспечения для расчета неопределенности, взгляните на этот список программного обеспечения для распространения неопределенности в Википедии.

Не все программное обеспечение в этом списке относится к метрологии. Однако это не означает, что вы не можете попробовать.

Вы можете случайно найти калькулятор неопределенности, который лучше всего подходит для вас.

 

Мой любимый калькулятор неопределенности

При расчете неопределенности я предпочитаю использовать Microsoft Excel.

Хотя некоторые люди могут не согласиться с моим выбором, Microsoft Excel делает все, что мне нужно.

Я могу быстро рассчитать неопределенность, поделиться своими расчетами с коллегами и оценщиками и могу интегрировать их в свои отчеты о калибровке (с некоторой дополнительной работой).

По моему мнению, программа расчета неопределенности должна помочь лабораториям выполнить требования стандарта ISO/IEC 17025 и политики ILAC P-14;
• Расчет неопределенности возможностей калибровки и измерения (CMC);
• Создание/обновление области аккредитации лаборатории;
• Объединение бюджетов неопределенностей в отчеты для аккредитационных аудитов;
• Расчет погрешности калибровки для отчетов о калибровке;

На сегодняшний день я не нашел программного обеспечения для расчета неопределенности, отвечающего этим требованиям.

Лично я думаю, что именно поэтому большинство калькуляторов неопределенности терпят неудачу как продукты. Они не решают проблем, с которыми лаборатории должны соответствовать требованиям ISO/IEC 17025!

Пока кто-нибудь не создаст калькулятор неопределенности, способный выполнять перечисленные выше задачи, я буду продолжать использовать Microsoft Excel.

Если вы согласны и используете Microsoft Excel для расчета неопределенности, воспользуйтесь моим калькулятором неопределенности для Microsoft Excel. Это не бесплатно, но по разумной цене.

 

Заключение

Программное обеспечение для расчета погрешности — это инструмент, необходимый большинству испытательных и калибровочных лабораторий для выполнения требований ISO/IEC 17025. Однако многие из доступных приложений не отвечают потребностям аккредитованных лабораторий.

Если вы ищете программное обеспечение только для расчета неопределенности, существует множество вариантов.

В этом руководстве я дал вам список программного обеспечения для расчета неопределенности, которое вы можете загрузить и попробовать в своей лаборатории.

Многие из перечисленных калькуляторов доступны бесплатно или в пробном режиме. Некоторые приложения могут потребовать, чтобы вы купили их, чтобы получить доступ ко всем функциям.

Итак, попробуйте эти калькуляторы неопределенности и оставьте комментарий, чтобы сообщить мне и другим, какой из них вам нравится больше всего.

Если вы найдете калькулятор неопределенности, который вам нравится, и вы хотите, чтобы я добавил его в этот список, пришлите мне электронное письмо и сообщите мне об этом.

Формула неопределенности | Расчет (примеры с шаблоном Excel)

Формула неопределенности (Содержание)

• Формула
• Примеры

На статистическом языке термин «неопределенность» связан с измерением, где он относится к ожидаемому изменению значения, полученному из среднего значения нескольких показаний, от истинного среднего значения набора данных или показаний. Другими словами, неопределенность можно рассматривать как стандартное отклонение среднего значения набора данных. Формула неопределенности может быть получена путем суммирования квадратов отклонения каждой переменной от среднего значения, затем деления результата на произведение количества показаний и числа показаний минус один, а затем вычисления квадратного корня результата. . Математически формула неопределенности представлена ​​​​как

Неопределенность (u) = √ [∑ (x _i – μ) ² / (n * (n – 1))]

, где

• x _I 07107107107107107107107107107070707071 гг. th чтение в наборе данных
• μ = Среднее значение набора данных
• n = количество показаний в наборе данных

Примеры формулы неопределенности (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять расчет неопределенности.

Вы можете скачать этот шаблон Excel с формулой неопределенности здесь — Шаблон Excel с формулой неопределенности

Формула неопределенности — Пример № 1

Возьмем в качестве примера забег на 100 м в школьных соревнованиях. Гонка измерялась с использованием пяти разных секундомеров, и каждый секундомер зафиксировал немного разное время. Показания составляют 15,33 секунды, 15,21 секунды, 15,31 секунды, 15,25 секунды и 15,35 секунды. Рассчитайте неопределенность времени на основе предоставленной информации и представьте время с уровнем достоверности 68%.

Решение:

Среднее значение рассчитывается как:

Теперь нам необходимо рассчитать отклонений каждого показания

Аналогично, рассчитайте для всех показаний

. Рассчитайте квадрат квадрат. отклонения каждого показания

Неопределенность рассчитывается по формуле, приведенной ниже

• Неопределенность = 0,03 секунд

68 % значений находятся в пределах 1 стандартного отклонения от среднего (-1 с <= X <= 1 с)

Итак, время при доверительном уровне 68 % = μ ± 1 * u

• Измерение при доверительном уровне 68 % = ( 15,29 ± 1 * 0,03) секунд
• Измерение при доверительном уровне 68% = (15,29 ± 0,03) секунд

Таким образом, погрешность набора данных составляет 0,03 секунды, а время можно представить как (15,29± 0,03) секунды при доверительном уровне 68%.

Формула неопределенности – Пример №2

Возьмем в качестве примера Джона, который решил продать свою недвижимость, представляющую собой бесплодную землю. Он хочет измерить доступную площадь собственности. По назначению геодезиста было снято 5 показаний – 50,33 акра, 50,20 акра, 50,51 акра, 50,66 акра и 50,40 акра. Выразите измерение земли с уровнем достоверности 95% и 99%.

Решение:

Среднее значение рассчитывается как:

Теперь нам нужно рассчитать отклонения каждого показания

Аналогичным образом рассчитайте для всех показаний

Рассчитайте квадрат отклонений каждого показания

Неопределенность рассчитывается по формуле, приведенной ниже 0,08 акра

95 % значений находятся в пределах 1,96 стандартных отклонений от среднего (-1,96 с <= X <= 1,96 с)

So Измерение с доверительной вероятностью 95 % = μ ± 2 * u

• Измерение с доверительной вероятностью 95 % = (50,42 ± 2 * 0,08) акра
• Измерение при доверительном уровне 95% = (50,42 ± 0,16) акров

99 % значений находятся в пределах 2,58 стандартных отклонений от среднего (-2,58 с <= X <= 2,58 с)

Измерение в 99% доверительный интервал = μ ± 3 * u

• Измерение при 99% доверительном уровне = (50,42 ± 3 * 0,08) акра
• Измерение при доверительном уровне 99% = (50,42 ± 0,24) акра

Таким образом, погрешность показаний составляет 0,08 акра, и измерение может быть представлено как (50,42 ± 0,16) акра и (50,42 ± 0,24) акра при уровне достоверности 95 % и 99 %.

Пояснение

Формулу неопределенности можно вывести, выполнив следующие шаги:

Шаг 1: Сначала выберите эксперимент и измеряемую переменную.

Шаг 2: Затем соберите достаточное количество показаний для эксперимента посредством повторных измерений. Показания будут формировать набор данных, и каждое показание будет обозначаться x _i .

Шаг 3: Затем определите количество показаний в наборе данных, которое обозначается n.

Шаг 4: Затем вычислите среднее значение показаний путем суммирования всех показаний в наборе данных, а затем разделите результат на количество показаний, доступных в наборе данных. Среднее значение обозначается μ.

μ = ∑ x _i / n

Шаг 5: Затем вычислите отклонение для всех показаний в наборе данных, которое представляет собой разницу между каждым показанием и средним значением, т. е. (x _i — мк) .

Шаг 6: Затем вычислите квадрат всех отклонений, т.е. (x _i – μ) ² .

Шаг 7: Затем просуммируйте все квадраты отклонений, т.е. ∑ (x _и – мк) ² .

Шаг 8: Затем вышеуказанная сумма делится на произведение количества показаний и числа показаний минус один, т.е. n * (n – 1) .

Шаг 9: Наконец, формула для неопределенности может быть получена путем вычисления квадратного корня из приведенного выше результата, как показано ниже.

Неопределенность (u) = √ (∑ (x _i – μ) ² ) / (n * (n-1))

Релевантность и использование формулы неопределенности

С точки зрения статистических экспериментов понятие неопределенности очень важно, поскольку оно помогает статистику определить изменчивость показаний и оценить измерение с определенным уровнем достоверности.