Главная
Решение онлайн матрицы методом крамера: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера

Решение онлайн матрицы методом крамера: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера

Содержание

Решение СЛАУ 3-его порядка методом Крамера, пример № 1

СЛАУ 3-его порядка: 1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9 – 10 – 11 – 12

Условие

 2x 1 + x 2 + 2x 3   =   1
 3x 1 – x 2 + 2x 3   =   1
 4x 1 – x 2 + 5x 3   =   -3

Решение системы линейных алгебраических уравнений методом Крамера

Для проверки ответов можете воспользоваться нашим онлайн сервисом – Решение системы линейных уравнений методом Крамера. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по математике и другим предметам!

Систему уравнений можно представить в матричной форме: Ax = B, где А – основная матрица (квадратная матрица), В – матрица свободных членов.

Теперь необходимо найти 4 определителя: определитель основной матрицы (определитель системы) и 3 определителя дополнительных матриц. Перед нахождением определителей советуем ознакомиться с теорией определителей матриц, а для нахождения определителей советуем использовать нашу программу – нахождение определителя матрицы.

Перепишем систему линейных алгебраических уравнений в матричную форму. Слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.


Найдем определитель основной матрицы:


Δ =  =  – 2 · 1 · 5 + 1 · 2 · 4 – 2 · 3 · 1 + 2 · 1 · 4 + 2 · 1 · 2 – 5 · 1 · 3 = -11

Определитель основной матрицы не равен нуля, значит система невырожденная.

Найдем определители 3 дополнительных матриц:

Дополнительная матрица получается из основной путем замены элементов одного из трех столбцов основной матрицы элементами матрицы свободных членов.


Δ 1 =  =  – 1 · 1 · 5 – 1 · 2 · 3 – 2 · 1 · 1 – 2 · 1 · 3 + 2 · 1 · 1 – 5 · 1 · 1 = -22

Δ 2 =  =  2 · 1 · 5 + 1 · 2 · 4 – 2 · 3 · 3 – 2 · 1 · 4 + 2 · 3 · 2 – 5 · 1 · 3 = -11

Δ 3 =  =  2 · 1 · 3 + 1 · 1 · 4 – 1 · 3 · 1 + 1 · 1 · 4 + 1 · 1 · 2 + 3 · 1 · 3 = 22

Найдем решения системы алгебраических уравнений:

х1 = Δ1/Δ = 2
х2

= Δ2/Δ = 1
х3 = Δ3/Δ = -2


Вы поняли, как решать? Нет?

Помощь с решением

1.3. Системы линейных уравнений.

Метод Крамера

Рассмотрим систему 3-х уравнений с тремя неизвестными

(1.3)

Используя определители 3-го порядка, решение такой системы можно записать в таком виде:

(1.4)

если 0. Здесь

(1.5)

Это есть формулы Крамерарешения системы трех линейных уравнений с тремя неизвестными.

Пример 1.6.Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель основной матрицы системы:

Поскольку 0, то для нахождения решения системы можно применить метод Крамера. Вычислим остальные определители:

Тогда

Проверка:

Следовательно, решение найдено правильно.

Теорема Крамера.Квадратная система линейных неоднородных уравнений n-го порядка с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение, и это решение вычисляется по формулам:

где  – определитель основной матрицы, i – определитель матрицы, полученной из основной, заменой i-го столбца столбцом свободных членов.

Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо вообще не имеет решений, либо имеет бесконечное множество решений.

1.4. Матричный метод. Обратная матрица

Матрица

А–1называетсяобратнойматрицей по отношению к матрицеА, если выполняется равенствоAA–1=A–1A=E. Только квадратные матрицы могут иметь обратные. Однако не каждая квадратная матрица имеет обратную. Для того чтобы матрицаАимела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля:detA0.

Пример 1.7.Решить систему линейных уравнений матричным методом (при помощи обратной матрицы).

Решение

. Запишем исходную систему уравнений в матричном виде:

.

Тогда решение можно формально записать в виде:

.

Таким образом, чтобы найти решение системы, нужно вычислить обратную матрицу

.

Найдем ее

1) Вычисляем определитель исходной матрицы: .

2) Транспонируем матрицу .

3) Находим все алгебраические дополнения транспонированной матрицы:

4) Составляем присоединенную матрицу, для этого вместо элементов транспонированной матрицы ставим найденные алгебраические дополнения:

5) Записываем обратную матрицу, для этого все элементы присоединенной матрицы делим на определитель исходной матрицы:

.

6) Сделаем проверку:

.

Следовательно, обратная матрица найдена правильно.

Теперь, используя найденную обратную матрицу можно найти решение исходной системы:

.

1.5. Метод Гаусса

Рассмотрим произвольную систему линейных уравнений

(1.5)

В общем случае

nm.

Задача теории систем линейных уравнений состоит в том, чтобы найти все решения системы. При этом возможны три случая. 1) Система вообще не имеет решений. Системы линейных уравнений, не имеющие ни одного решения, называются несовместными. 2) Система имеет хотя бы одно решение. такие системы называютсясовместными. 3) Система имеет только одно решение. Такие системы называютсяопределёнными.

Метод Гаусса (метод последовательного исключения неизвестных)заключается в том, что с помощью элементарных преобразований система приводится к эквивалентной системе ступенчатого вида.

Рассмотрим метод Гаусса на конкретных примерах.

Пример 1.8. Решить систему линейных уравнений методом Гаусса.

Решение.Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее к треугольному виду:

.

Теперь выписываем соответствующую укороченную систему уравнений. Из последнего уравнения находим значение z и подставляем его во второе уравнение. После этого из второго уравнения находим y. Найденные значения y и z подставляем в первое уравнение, из которого затем находим значение

x:

Эта тройка чисел будет являться единственным решением системы.

Пример 1.9.Решить систему методом Гаусса:

Решение. Выписываем и преобразуем расширенную матрицу системы

Записываем упрощенную систему уравнений:

Здесь, в последнем уравнении получилось, что 0=4, т. е. противоречие. Следовательно, система не имеет решения, т.е. она несовместна.

Пример

1.10. Найти общее решение методом Гаусса

Решение. Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее трапециевидной форме:

-1

4

3

3

:15

.

Теперь выписываем соответствующую укороченную систему уравнений:

Пусть переменные x4 и x5 будут свободными, тогда переменные x1, x2 и x3 будут основными (или базисными). Их мы оставим в левой части:

Разрешая эту систему относительно x1, x2 и x3 получим

Это есть общее решение системы. Запишем это решение в параметрическом виде. Пусть x4=a и x5=5b. Тогда общее решение системы запишется в виде:

Давая числам a и b различные значения, будем получать частные решения. Например, если a=0, b=1, то x1=–7, x2=–2, x3=4, x4=0, x5=5.

Решение линейных уравнений методом Крамера: правило и примеры.

Правило крамера.

Среди способов решения линейных уравнений — не только методика Гаусса и метод обратной матрицы, но и правило Крамера. Метод основан на работе с определителями и позволяет легко решить систему уравнений.

Следует отметить, что метод Крамера подходит только для тех ситуаций, когда определитель не равен нулю. В ином случае придется использовать метод Гаусса.

Итак, как же решается система линейных уравнений по методу Крамера?

Решение линейных уравнений по Крамеру.

Пример решения системы линейных уравнений методом Крамера.

Разберем на примере.

Первый этап работы — это вычислить главный определитель системы, в нашем случае:

Как уже было сказано, если определитель системы равен нулю, то метод Крамера не подходит для работы, поскольку выходит, что система или не имеет решений, или имеет бесконечное множество их. В таком случае используется метод Гаусса.

Если же определитель больше или меньше нуля, то методом Крамера мы можем вычислить единственное верное решение. Для этого необходимо найти еще два определителя системы:

Теперь остается лишь найти корни уравнения, а они рассчитываются по следующим формулам:

Рассмотрим еще один пример.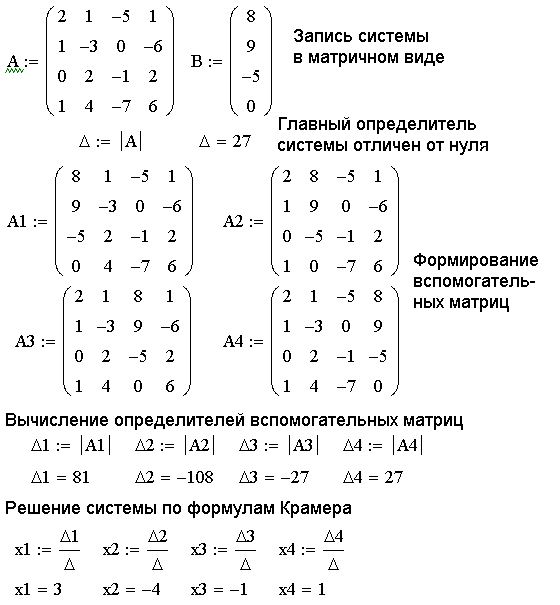 Возьмем систему линейных уравнений:

Метод Крамера – наиболее удобный метод как раз для работы со сложными уравнениями, включающими в себя десятичные дроби. Иные методы оказываются сложнее, да и в вычислениях можно просто запутаться. Здесь же все довольно просто. Находим главный определитель:

Определитель не равен нулю, следовательно, система имеет решение, и мы можем найти его методом Крамера.

Таким образом, получаем, что а = – 0,35, в = 37,77. Система линейных уравнений полностью решена, можно записывать ответ.

Похожие статьи

9.8: Решение систем с помощью правила Крамера

Цели обучения
  • Оцените детерминанты 2 × 2.
  • Используйте правило Крамера для решения системы уравнений с двумя переменными.
  • Оцените детерминанты 3 × 3.
  • Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
  • Знать свойства определителей.

Мы научились решать системы уравнений с двумя переменными и тремя переменными, используя несколько методов: подстановку, сложение, исключение Гаусса, использование обратной матрицы и построение графиков.Некоторые из этих методов применять проще, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.

Вычисление определителя матрицы 2 × 2

Определитель – это действительное число, которое может быть очень полезно в математике, поскольку оно имеет множество приложений, таких как вычисление площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы. Вычисление определителя матрицы требует следования определенным шаблонам, описанным в этом разделе.

НАЙТИ ОПРЕДЕЛЕНИЕ МАТРИЦЫ 2 × 2

Определитель матрицы 2 × 2, учитывая

\ (A = \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} \)

определяется как

Обратите внимание на изменение обозначений.Есть несколько способов указать определитель, включая \ (\ det (A) \) и замену скобок в матрице прямыми линиями, \ (| A | \).

Пример \ (\ PageIndex {1} \): поиск определителя матрицы \ (2 × 2 \)

Найдите определитель заданной матрицы.

\ (A = \ begin {bmatrix} 5 & 2 \\ – 6 & 3 \ end {bmatrix} \)

Решение

\ [\ begin {align *} \ det (A) & = \ begin {vmatrix} 5 & 2 \\ – 6 & 3 \ end {vmatrix} \\ & = 5 (3) – (- 6) (2) \\ & = 27 \ end {align *} \]

Использование правила Крамера для решения системы двух уравнений с двумя переменными

Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера , восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году в году. Courbes algébriques . Правило Крамера – это жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных, при условии, что у нас есть такое же количество уравнений, что и неизвестных.

Правило Крамера даст нам единственное решение системы уравнений, если оно существует.Однако, если система не имеет решения или бесконечное количество решений, это будет обозначено нулевым определителем. Чтобы выяснить, является ли система непоследовательной или зависимой, необходимо использовать другой метод, например исключение.

Чтобы понять правило Крамера, давайте внимательно рассмотрим, как мы решаем системы линейных уравнений с использованием основных операций со строками. Рассмотрим систему двух уравнений с двумя переменными.

\ [\ begin {align} a_1x + b_1y & = c_1 (1) \ label {eq1} \\ a_2x + b_2y & = c_2 (2) \ label {eq2} \\ \ end {align} \]

Мы исключаем одну переменную, используя операции со строками, и решаем для другой.Скажите, что мы хотим найти \ (x \). Если уравнение \ ref {eq2} умножается на коэффициент, противоположный коэффициенту \ (y \) в уравнении \ ref {eq1}, уравнение \ ref {eq1} умножается на коэффициент при \ (y \) в уравнении \ ref {eq2}, и мы добавляем два уравнения, переменная \ (y \) будет удалена.

\ [\ begin {align *} & b_2a_1x + b_2b_1y = b_2c_1 & \ text {Multiply} R_1 \ text {by} b_2 \\ – & \ underline {b_1a_2x − b_1b_2y = −b_1c_2} & \ text {Multiply} R_2 \ text {by} −b_1 \\ & b_2a_1x − b_1a_2x = b_2c_1 − b_1c_2 \ end {align *} \]

Теперь решите относительно \ (x \).

\ [\ begin {align *} b_2a_1x − b_1a_2x & = b_2c_1 − b_1c_2 \\ x (b_2a_1 − b_1a_2) & = b_2c_1 − b_1c_2 \\ x & = \ dfrac {b_2c_1 − b_1c_2} {b_2a_1 − b_1a_2} = \ dfrac {\ begin {bmatrix} c_1 & b_1 \\ c_2 & b_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end {bmatrix}} \ end {align *} \]

Аналогичным образом, чтобы найти \ (y \), мы исключим \ (x \).

\ [\ begin {align *} & a_2a_1x + a_2b_1y = a_2c_1 & \ text {Multiply} R_1 \ text {by} a_2 \\ – & \ underline {a_1a_2x − a_1b_2y = −a_1c_2} & \ text {Multiply} R_2 \ текст {by} −a_1 \\ & a_2b_1y − a_1b_2y = a_2c_1 − a_1c_2 \ end {align *} \]

Решение относительно \ (y \) дает

\ [\ begin {align *} a_2b_1y − a_1b_2y & = a_2c_1 − a_1c_2 \\ y (a_2b_1 − a_1b_2) & = a_2c_1 − a_1c_2 \\ y & = \ dfrac {a_2c_1 − a_1c_2} {a_2b_1 − a_1b_2} = \ dfrac {a_1c_2 − a_2c_1} {a_1b_2 − a_2b_1} = \ dfrac {\ begin {bmatrix} a_1 & c_1 \\ a_2 & c_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end {bmatrix}} \ end {align * } \]

Обратите внимание, что знаменатель для \ (x \) и \ (y \) является определителем матрицы коэффициентов.

Мы можем использовать эти формулы для решения относительно \ (x \) и \ (y \), но правило Крамера также вводит новые обозначения:

  • \ (D \): определитель матрицы коэффициентов
  • \ (D_x \): определитель числителя в решении \ (x \)

    \ [x = \ dfrac {D_x} {D} \]

  • \ (D_y \): определитель числителя в решении \ (y \)

    \ [y = \ dfrac {D_y} {D} \]

Ключ к правилу Крамера заключается в замене интересующего столбца переменной на столбец констант и вычислении детерминантов. Тогда мы можем выразить \ (x \) и \ (y \) как частное двух определителей.

ПРАВИЛО КРЕМЕРА ДЛЯ СИСТЕМ \ (2 × 2 \)

Правило Крамера – это метод, использующий детерминанты для решения систем уравнений, которые имеют то же количество уравнений, что и переменные.

Рассмотрим систему двух линейных уравнений с двумя переменными.

\ [\ begin {align *} a_1x + b_1y & = c_1 \\ a_2x + b_2y & = c_2 \ end {align *} \]

Решение, использующее правило Крамера, дается как

\ [\ begin {align} x & = \ dfrac {D_x} {D} = \ dfrac {\ begin {bmatrix} c_1 & b_1 \\ c_2 & b_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end { bmatrix}} \; , D \ neq 0 \\ y & = \ dfrac {D_y} {D} = \ dfrac {\ begin {bmatrix} a_1 & c_1 \\ a_2 & c_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end {bmatrix }} \; , D \ neq 0 \ end {align} \]

Если мы решаем для \ (x \), столбец \ (x \) заменяется постоянным столбцом.Если мы решаем для \ (y \), столбец \ (y \) заменяется постоянным столбцом.

Пример \ (\ PageIndex {2} \): Использование правила Крамера для решения системы \ (2 × 2 \)

Решите следующую систему \ (2 × 2 \), используя правило Крамера.

\ [\ begin {align *} 12x + 3y & = 15 \\ 2x-3y & = 13 \ end {align *} \]

Решение

Решите относительно \ (x \).

\ [\ begin {align *} x & = \ dfrac {D_x} {D} \\ & = \ dfrac {\ begin {bmatrix} 15 & 3 \\ 13 & -3 \ end {bmatrix}} {\ begin {bmatrix} 12 & 3 \\ 2 & -3 \ end {bmatrix}} \\ & = \ dfrac {-45-39} {- 36-6} \\ & = \ dfrac {-84} {- 42} \\ & = 2 \ end {align *} \]

Решите относительно \ (y \).

\ [\ begin {align *} y & = \ dfrac {D_y} {D} \\ & = \ dfrac {\ begin {bmatrix} 12 & 15 \\ 2 & 13 \ end {bmatrix}} {\ begin {bmatrix} 12 & 3 \\ 2 & -3 \ end {bmatrix}} \\ & = \ dfrac {156-30} {- 36-6} \\ & = – \ dfrac {126} {42} \\ & = -3 \ end {align * } \]

Решение: \ ((2, −3) \).

Упражнение \ (\ PageIndex {1} \)

Используйте правило Крамера для решения системы уравнений \ (2 × 2 \).

\ [\ begin {align *} x + 2y & = -11 \\ -2x + y & = -13 \ end {align *} \]

Ответ

\ ((3, −7) \)

Вычисление определителя матрицы 3 × 3

Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее.Один из способов – увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведения записей на каждой из трех диагоналей (нижний левый верхний правый). Это легче понять с помощью наглядного пособия и примера.

Найдите определитель матрицы 3 × 3.

\ (A = \ begin {bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \ end {bmatrix} \)

  1. Дополните \ (A \) первыми двумя столбцами.

    \ (\ det (A) = \ left | \ begin {array} {ccc | cc} a_1 & b_1 & c_1 & a_1 & b_1 \\ a_2 & b_2 & c_2 & a_2 & b_2 \\ a_3 & b_3 & c_3 & a_3 & b_3 \ end {array} \ right | \)

  2. С верхнего левого угла в нижний правый: умножение значений по первой диагонали. Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
  3. От левого нижнего угла к правому верхнему: вычтите произведение входов вверх по первой диагонали.Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.

Алгебра выглядит следующим образом:

\ (| A | = a_1b_2c_3 + b_1c_2a_3 + c_1a_2b_3 − a_3b_2c_1 − b_3c_2a_1 − c_3a_2b_1 \)

Пример \ (\ PageIndex {3} \): поиск определителя матрицы 3 × 3

Найти определитель матрицы \ (3 × 3 \) по заданному

\ (A = \ begin {bmatrix} 0 & 2 & 1 \\ 3 & −1 & 1 \\ 4 & 0 & 1 \ end {bmatrix} \)

Решение

Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,

\ [\ begin {align *} | А | & = \ left | \ begin {array} {ccc | cc} 0 & 2 & 1 & 0 & 2 \\ 3 & -1 & 1 & 3 & -1 \\ 4 & 0 & 1 & 4 & 0 \ end {array} \ right | \\ & = 0 (−1) (1) +2 (1) (4) +1 (3) (0) −4 (−1) (1) −0 (1) (0) −1 (3) (2) \\ & = 0 + 8 + 0 + 4−0−6 \\ & = 6 \ end {align *} \]

Упражнение \ (\ PageIndex {2} \)

Найдите определитель матрицы 3 × 3.

\ (\ det (A) = \ begin {vmatrix} 1 & −3 & 7 \\ 1 & 1 & 1 \\ 1 & −2 & 3 \ end {vmatrix} \)

Ответ

\ (- 10 \)

Q&A: Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?

Нет, этот метод работает только для матриц 2 × 2 и 3 × 3.Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы \ (3 × 3 \), мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера простое и соответствует шаблону, соответствующему правилу Крамера для матриц \ (2 × 2 \). Однако по мере увеличения порядка матрицы до \ (3 × 3 \) требуется гораздо больше вычислений.

Когда мы вычисляем детерминант, равный нулю, правило Крамера не дает никаких указаний на то, что у системы нет решения или есть бесконечное количество решений.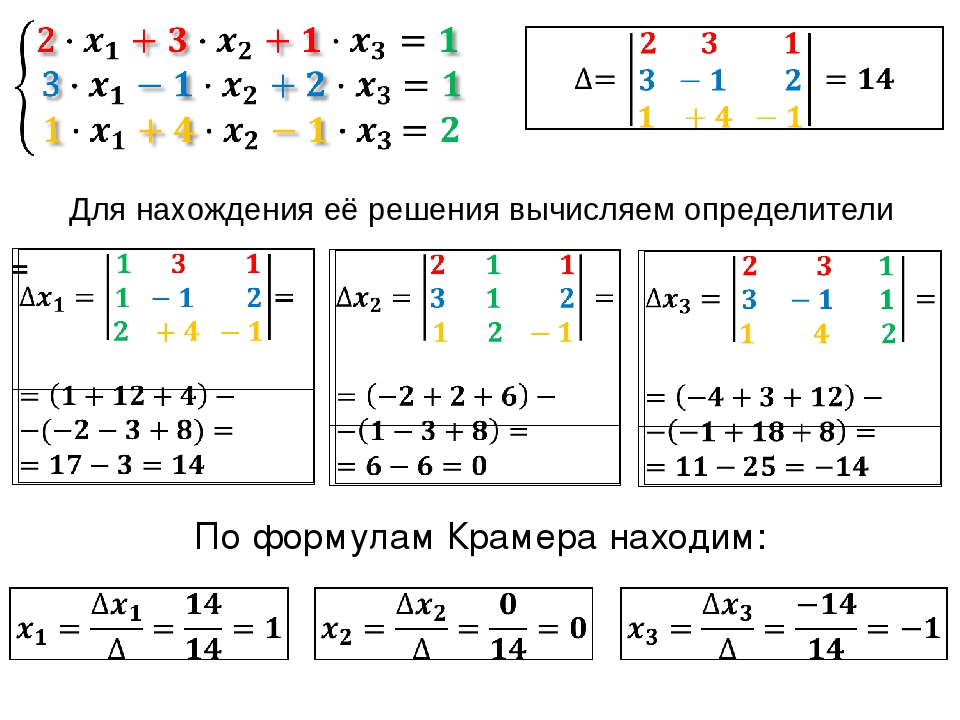 Чтобы выяснить это, мы должны выполнить устранение в системе.

Рассмотрим систему уравнений \ (3 × 3 \).

\ [\ begin {align} a_1x + b_1y + c_1z & = \ color {blue} d_1 \\ a_2x + b_2y + c_2z & = \ color {blue} d_2 \\ a_3x + b_3y + c_3z & = \ color {blue} d_3 \\ \ end {align} \]

\ (x = \ dfrac {D_x} {D} \), \ (y = \ dfrac {D_y} {D} \), \ (z = \ dfrac {D_z} {D} \), \ (D ≠ 0 \)

где

\ [D = \ begin {vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \ end {vmatrix} \; , \; D_x = \ begin {vmatrix} \ color {blue} d_1 & b_1 & c_1 \\ \ color {blue} d_2 & b_2 & c_2 \\ \ color {blue} d_3 & b_3 & c_3 \ end {vmatrix} \; , \; D_y = \ begin {vmatrix} a_1 & \ color {blue} d_1 & c_1 \\ a_2 & \ color {blue} d_2 & c_2 \\ a_3 & \ color {blue} d_3 & c_3 \ end {vmatrix} \; , \; D_z = \ begin {vmatrix} a_1 & b_1 & \ color {blue} d_1 \\ a_2 & b_2 & \ color {blue} d_2 \\ a_3 & b_3 & \ color {blue} d_3 \ end {vmatrix} \]

Если мы записываем определитель \ (D_x \), мы заменяем столбец \ (x \) постоянным столбцом. Если мы пишем определитель \ (D_y \), мы заменяем столбец y на столбец констант. Если мы пишем определитель \ (D_z \), мы заменяем столбец \ (z \) постоянным столбцом. Всегда проверяйте ответ.

Пример \ (\ PageIndex {4} \): решение системы \ (3 × 3 \) с использованием правила Крамера

Найдите решение данной системы \ (3 × 3 \), используя правило Крамера.

\ [\ begin {align *} x + y-z & = 6 \\ 3x-2y + z & = -5 \\ x + 3y-2z & = 14 \ end {align *} \]

Решение

Используйте правило Крамера.

\ (D = \ begin {vmatrix} 1 & 1 & −1 \\ 3 & −2 & 1 \\ 1 & 3 & −2 \ end {vmatrix} \), \ (D_x = \ begin {vmatrix} 6 & 1 & −1 \\ – 5 & −2 & 1 \ \ 14 & 3 & −2 \ end {vmatrix} \), \ (D_y = \ begin {vmatrix} 1 & 6 & −1 \\ 3 & −5 & 1 \\ 1 & 14 & −2 \ end {vmatrix} \), \ (D_z = \ begin {vmatrix } 1 & 1 & 6 \\ 3 & −2 & −5 \\ ​​1 & 3 & 14 \ end {vmatrix} \)

Тогда,

\ [\ begin {align *} x & = \ dfrac {D_x} {D} & = \ dfrac {-3} {- 3} & = 1 \\ y & = \ dfrac {D_y} {D} & = \ dfrac {-9} {- 3} & = 3 \\ z & = \ dfrac {D_z} {D} & = \ dfrac {6} {- 3} & = -2 \\ \ end {align *} \]

Решение: \ ((1,3, −2) \).

Упражнение \ (\ PageIndex {3} \)

Используйте правило Крамера, чтобы решить матрицу \ (3 × 3 \).

\ [\ begin {align *} x-3y + 7z & = 13 \\ x + y + z & = 1 \\ x-2y + 3z & = 4 \ end {align *} \]

Ответ

\ (\ left (−2, \ dfrac {3} {5}, \ dfrac {12} {5} \ right) \)

Пример \ (\ PageIndex {5A} \): Использование правила Крамера для решения несовместимой системы

Решите систему уравнений, используя правило Крамера.

\ [\ begin {align} 3x-2y & = 4 \ label {eq3} \\ 6x-4y & = 0 \ label {eq4} \ end {align} \]

Решение

Начнем с нахождения определителей \ (D \), \ (D_x \) и \ (D_y \).

\ (D = \ begin {vmatrix} 3 & −2 \\ 6 & −4 \ end {vmatrix} = 3 (−4) −6 (−2) = 0 \)

Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное количество решений. Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель – исключить одну из переменных.

  1. Умножьте уравнение \ ref {eq3} на \ (- 2 \).
  2. Добавьте результат в уравнение \ ref {eq4}.

\ [\ begin {align *} & −6x + 4y = −8 \\ & \; \; \; \ underline {6x − 4y = 0} \\ & \; \; \; \; \; \ ; \; \; \; \; 0 = −8 \ end {align *} \]

Получаем уравнение \ (0 = −8 \), которое неверно. Следовательно, у системы нет решения. График системы показывает две параллельные линии. См. Рисунок \ (\ PageIndex {1} \).

Рисунок \ (\ PageIndex {1} \)
Пример \ (\ PageIndex {5B} \): использование правила Крамера для решения зависимой системы

Решите систему с бесконечным количеством решений.

\ [\ begin {align} x-2y + 3z & = 0 \ label {eq5} \\ 3x + y-2z & = 0 \ label {eq6} \\ 2x-4y + 6z & = 0 \ label {eq7} \ end {align} \]

Решение

Давайте сначала найдем определитель. Создайте матрицу, дополненную первыми двумя столбцами.

\ (\ left | \ begin {array} {ccc | cc} 1 & −2 & 3 & 1 & -2 \\ 3 & 1 & −2 & 3 & 1 \\ 2 & −4 & 6 & 2 & -4 \ end {array} \ right | \)

Тогда,

\ (1 (1) (6) + (- 2) (- 2) (2) +3 (3) (- 4) −2 (1) (3) – (- 4) (- 2) (1 ) −6 (3) (- 2) = 0 \)

Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное количество решений. Чтобы выяснить это, нам нужно провести отбор.

1. Умножьте уравнение \ ref {eq5} на \ (- 2 \) и добавьте результат к уравнению \ ref {eq7}:

\ [\ begin {align *} & −2x + 4y − 6x = 0 \\ & \; \; \ underline {2x − 4y + 6z = 0} \\ & \; \; \; \; \; \ ; \; \; \; \; \; \; \; \; \; \; 0 = 0 \ end {align *} \]

2. Получение ответа \ (0 = 0 \), утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений. Изобразив систему, мы видим, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.См. Рисунок \ (\ PageIndex {2} \).

Рисунок \ (\ PageIndex {2} \)

Понимание свойств детерминантов

Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.

СВОЙСТВА ДЕТЕРМИНАНТОВ
  1. Если матрица имеет верхнюю треугольную форму, определитель равен произведению элементов по главной диагонали.
  2. Когда две строки меняются местами, определитель меняет знак. {−1} \) – величина, обратная определителю матрицы \ (A \).
  3. Если любая строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Пример \ (\ PageIndex {6} \): иллюстрация свойств детерминантов

Проиллюстрируйте каждое из свойств определителей.

Решение

Свойство 1 утверждает, что если матрица имеет верхнюю треугольную форму, определитель является произведением элементов по главной диагонали.

\ (A = \ begin {bmatrix} 1 & 2 & 3 \\ 0 & 2 & 1 \\ 0 & 0 & −1 \ end {bmatrix} \)

Дополните \ (A \) первыми двумя столбцами.

\ (A = \ left [\ begin {array} {ccc | cc} 1 & 2 & 3 & 1 & 2 \\ 0 & 2 & 1 & 0 & 2 \\ 0 & 0 & −1 & 0 & 0 \ end {array} \ right] \)

Затем

\ [\ begin {align *} \ det (A) & = 1 (2) (- 1) +2 (1) (0) +3 (0) (0) -0 (2) (3) -0 (1) (1) +1 (0) (2) \\ & = -2 \ end {align *} \]

Свойство 2 утверждает, что при смене строк меняется знак. Учитывая

\ [\ begin {align *} B & = \ begin {bmatrix} 4 & -3 \\ – 1 & 5 \ end {bmatrix} \\ \ det (B) & = (4) (5) – (- 1) (- 3) \\ & = 20-3 \\ & = 17 \ end {align *} \]

Свойство 3 утверждает, что если две строки или два столбца идентичны, определитель равен нулю.

\ [\ begin {align *} A & = \ left [\ begin {array} {ccc | cc} 1 & 2 & 2 & 1 & 2 \\ 2 & 2 & 2 & 2 & 2 \\ – 1 & 2 & 2 & -1 & 2 \ end {array} \ right] \\ \ det (A) & = 1 (2) (2) +2 (2) (- 1) +2 (2) (2) +1 (2) (2) -2 (2) (1) -2 (2) (2) \ \ & = 4-4 + 8 + 4-4-8 \\ & = 0 \ end {align *} \]

Свойство 4 утверждает, что если строка или столбец равны нулю, определитель равен нулю.{-1}) & = – 2 \ left (- \ dfrac {1} {2} \ right) – \ dfrac {3} {2} (1) \\ & = – \ dfrac {1} {2} \ конец {выравнивание *} \]

Свойство 6 утверждает, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,

Пример \ (\ PageIndex {7} \): Использование правила Крамера и определяющих свойств для решения системы

Найдите решение данной системы \ (3 × 3 \).

Решение

Используя правило Крамера, мы имеем

\ (D = \ begin {bmatrix} 2 & 4 & 4 \\ 3 & 7 & 7 \\ 1 & 2 & 2 \ end {bmatrix} \)

Обратите внимание, что второй и третий столбцы идентичны.Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо существует бесконечное число решений. Чтобы выяснить это, нам нужно провести отбор.

1. Умножьте уравнение \ ref {eq10} на \ (- 2 \) и добавьте результат в уравнение \ ref {eq8}.

Получение противоречивого утверждения означает, что система не имеет решения.

Медиа

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с правилом Крамера.

Ключевые понятия

  • Определитель для \ (\ begin {bmatrix} a & b \\ c & d \ end {bmatrix} \) равен \ (ad − bc \).См. Пример \ (\ PageIndex {1} \).
  • Правило Крамера заменяет переменный столбец постоянным столбцом. Решения: \ (x = \ dfrac {D_x} {D} \), \ (y = \ dfrac {D_y} {D} \). См. Пример \ (\ PageIndex {2} \).
  • Чтобы найти определитель матрицы \ (3 × 3 \), дополните ее двумя первыми столбцами. Сложите три диагональных записи (верхний левый нижний правый) и вычтите три диагональных входа (нижний левый верхний правый). См. Пример \ (\ PageIndex {3} \).
  • Чтобы решить систему трех уравнений с тремя переменными с использованием правила Крамера, замените столбец переменных столбцом констант для каждого желаемого решения: \ (x = \ dfrac {D_x} {D} \), \ (y = \ dfrac { D_y} {D} \), \ (z = \ dfrac {D_z} {D} \).См. Пример \ (\ PageIndex {4} \).
  • Правило Крамера также полезно для поиска решения системы уравнений без решения или с бесконечными решениями. См. Пример \ (\ PageIndex {5} \) и Пример \ (\ PageIndex {6} \).
  • Некоторые свойства определителей полезны для решения задач. Например:
    • Если матрица имеет верхнюю треугольную форму, определитель равен произведению элементов по главной диагонали.
    • Когда две строки меняются местами, определитель меняет знак.{−1} \) – величина, обратная определителю матрицы \ (A \).
    • Если любая строка или столбец умножается на константу, определитель умножается на тот же коэффициент. См. Пример \ (\ PageIndex {7} \) и Пример \ (\ PageIndex {8} \).

Авторы и авторство

% PDF-1.3 % 68 0 объект > эндобдж xref 68 192 0000000016 00000 н. 0000004189 00000 п. 0000004357 00000 н. 0000004386 00000 п. 0000005458 00000 п. 0000005752 00000 н. 0000005815 00000 н. 0000005994 00000 н. 0000006108 00000 п. 0000006220 00000 н. 0000006347 00000 н. 0000006473 00000 н. 0000006612 00000 н. 0000006779 00000 н. 0000006870 00000 н. 0000006962 00000 н. 0000007053 00000 н. 0000007144 00000 н. 0000007235 00000 н. 0000007326 00000 н. 0000007416 00000 н. 0000007506 00000 н. 0000007596 00000 п. 0000007686 00000 н. 0000007776 00000 н. 0000007866 00000 н. 0000007956 00000 н. 0000008046 00000 н. 0000008136 00000 н. 0000008226 00000 п. 0000008316 00000 н. 0000008406 00000 н. 0000008497 00000 н. 0000008588 00000 н. 0000008681 00000 п. 0000008774 00000 н. 0000008867 00000 н. 0000008960 00000 н. 0000009053 00000 п. 0000009146 00000 п. 0000009239 00000 п. 0000009332 00000 н. 0000009425 00000 н. 0000009518 00000 н. 0000009611 00000 н. 0000009704 00000 п. 0000009797 00000 н. 0000009889 00000 н. 0000009982 00000 н. 0000010075 00000 п. 0000010168 00000 п. 0000010261 00000 п. 0000010354 00000 п. 0000010447 00000 п. 0000010540 00000 п. 0000010633 00000 п. 0000010726 00000 п. 0000010819 00000 п. 0000010912 00000 п. 0000011005 00000 п. 0000011098 00000 п. 0000011191 00000 п. 0000011283 00000 п. 0000011377 00000 п. 0000011471 00000 п. 0000011565 00000 п. 0000011659 00000 п. 0000011753 00000 п. 0000011847 00000 п. 0000011941 00000 п. 0000012035 00000 п. 0000012129 00000 п. 0000012223 00000 п. 0000012317 00000 п. 0000012411 00000 п. 0000012505 00000 п. 0000012599 00000 н. 0000012693 00000 п. 0000012786 00000 п. 0000012878 00000 п. 0000012972 00000 п. 0000013066 00000 п. 0000013160 00000 п. 0000013254 00000 п. 0000013348 00000 п. 0000013442 00000 п. 0000013536 00000 п. 0000013630 00000 п. 0000013724 00000 п. 0000013818 00000 п. 0000013912 00000 п. 0000014006 00000 п. 0000014100 00000 п. 0000014193 00000 п. 0000014285 00000 п. 0000014379 00000 п. 0000014473 00000 п. 0000014567 00000 п. 0000014661 00000 п. 0000014755 00000 п. 0000014849 00000 п. 0000014943 00000 п. 0000015037 00000 п. 0000015131 00000 п. 0000015225 00000 п. 0000015319 00000 п. 0000015413 00000 п. 0000015507 00000 п. 0000015601 00000 п. 0000015695 00000 п. 0000015789 00000 п. 0000015883 00000 п. 0000015977 00000 п. 0000016071 00000 п. 0000016164 00000 п. 0000016256 00000 п. 0000016350 00000 п. 0000016444 00000 п. 0000016538 00000 п. 0000016632 00000 п. 0000016726 00000 п. 0000016820 00000 н. 0000016914 00000 п. 0000017008 00000 п. 0000017102 00000 п. 0000017195 00000 п. 0000017480 00000 п. 0000021320 00000 н. 0000021618 00000 п. 0000021931 00000 п. 0000022406 00000 п. 0000022562 00000 н. 0000022630 00000 н. 0000022949 00000 п. 0000023271 00000 п. 0000023442 00000 п. 0000023684 00000 п. 0000023851 00000 п. 0000024109 00000 п. 0000024418 00000 п. 0000024459 00000 п. 0000024660 00000 п. 0000024979 00000 п. 0000025304 00000 п. 0000026855 00000 п. 0000027216 00000 п. 0000027711 00000 п. 0000027976 00000 п. 0000028062 00000 н. 0000028358 00000 п. 0000028593 00000 п. 0000028789 00000 п. 0000029090 00000 н. 0000029158 00000 п. 0000034985 00000 п. 0000035413 00000 п. 0000035715 00000 п. 0000036207 00000 п. 0000036979 00000 п. 0000037506 00000 п. 0000037677 00000 п. 0000037918 00000 п. 0000038093 00000 п. 0000038413 00000 п. 0000038651 00000 п. 0000041214 00000 п. 0000041840 00000 п. 0000047041 00000 п. 0000047465 00000 п. 0000047533 00000 п. 0000047946 00000 н. 0000047970 00000 п. 0000060206 00000 п. 0000060230 00000 п. 0000072396 00000 п. 0000072420 00000 п. 0000084037 00000 п. 0000084061 00000 п. 0000096393 00000 п. 0000096417 00000 п. 0000109243 00000 п. 0000109267 00000 н. 0000120494 00000 н. 0000120518 00000 н. 0000132662 00000 н. 0000132686 00000 н. 0000145778 00000 н. 0000145857 00000 н. 0000148532 00000 н. 0000151530 00000 н. 0000004443 00000 н. 0000005436 00000 н. трейлер ] >> startxref 0 %% EOF 69 0 объект > эндобдж 70 0 объект [ 71 0 руб. ] эндобдж 71 0 объект > / Ж 81 0 Р >> эндобдж 258 0 объект > транслировать Hb“f`f“ Ā

Решение систем линейных уравнений с двумя переменными с использованием детерминантов – видео и стенограмма урока

Правило Крамера

Чтобы помочь вам решить эту систему, мы можем использовать правило Крамера. Правило Крамера говорит вам, как решить линейную систему, работая только с определителями. Сначала вы создаете матрицу коэффициентов, которая включает только коэффициенты в левой части уравнений. Затем вы найдете определитель этой матрицы.

Назовем этот определитель D . Затем для каждой переменной вы берете свою матрицу коэффициентов и подставляете постоянные числа, которые являются числами в правой части уравнения, в каждый столбец.

Итак, для переменной c вы подставляете постоянные числа в первый столбец матрицы коэффициентов.Для переменной d вы подставляете постоянные числа во второй столбец матрицы коэффициентов.

Затем вы найдете определители этих матриц. Для переменной c мы назовем определитель D sub c . Для переменной d мы назовем определитель D sub d .

Тогда решение находится делением. Решение c : c = D sub c / D .Решение d : d = D sub d / D . Поскольку у нас есть две переменные, нам нужно найти три детерминанта: один общий детерминант, а затем по одному определителю для каждой переменной.

Поиск детерминантов

Давайте теперь посмотрим на это в действии. Сначала мы создаем нашу матрицу коэффициентов:

Находя определитель, получаем 1 * 1 – 1 * -1 = 1 + 1 = 2.Итак, D = 2. Это наш общий определяющий фактор. Теперь нам нужны еще два определителя, по одному для каждой переменной. Затем для переменной c подставляем в первый столбец постоянные числа 50 и 30. Для матрицы получаем следующее:

Взяв определитель, мы получаем 50 * 1 – 1 * 30 = 50 – 30 = 20. Итак, D sub c равно 20. Затем мы заменяем второй столбец постоянными числами 50 и 30, чтобы найти D переходник d .Получаем для матрицы:

Взяв определитель этой матрицы, мы получаем 1 * 30 – 50 * -1 = 30 + 50 = 80. Итак, D sub d равно 80. Теперь у нас есть три определителя, которые нам нужно решить. наша система. Итак, помните, если у вас есть две переменные, вам понадобятся три детерминанта: один общий, а затем по одному для каждой переменной.

Поиск решения

Теперь все, что нам нужно сделать, чтобы найти ответ, – это разделить наши детерминанты.Решение c : c = D sub c / D = 20/2 = 10. Решение d : d = D sub d / D = 80/2 = 40.

Значит, у нас в зоомагазине 10 кошек и 40 собак. Мы успешно решили проблему и можем рассказать владельцу зоомагазина о том, что нашли.

Резюме урока

Давайте рассмотрим то, что мы узнали. Мы узнали, что линейная система с двумя переменными является обычным явлением в математике.Они представляют собой наборы двух уравнений с двумя переменными без показателей. Вы можете использовать правило Крамера, чтобы помочь вам решить такую ​​систему.

Чтобы использовать правило Крамера , сначала нужно найти определитель матрицы коэффициентов, D . Затем для каждой переменной вы заменяете соответствующий столбец матрицы коэффициентов постоянными числами.

Затем вы найдете определитель этих матриц. Вы получите D sub x и D sub y , по одному для каждой переменной.Тогда решение x будет D sub x / D , а решение y будет D sub y / D .

Результаты обучения

По завершении этого урока вы должны уметь:

  • Вспомнить правило Крамера
  • Определить и решить линейную систему с двумя переменными

Правило Крамера: 5. Используйте правило Крамера, чтобы найти x, y и z для следующей системы …

  • СИСТЕМА ИЗ 3 УРАВНЕНИЙ С 3 НЕИЗВЕСТНЫМИ ИСПОЛЬЗУЯ ПРАВИЛО КРАМЕРА, НАЙДИТЕ НАБОР РЕШЕНИЙ ДЛЯ СЛЕДУЮЩЕЙ СИСТЕМЫ УРАВНЕНИЙ: 4X -2Y -3Z = 8 5X + 3Y -4Z = 4 6X -4Y -5Z = 12 ТРЕБУЕТСЯ: Найдите набор решений {(x, y z)} для данной системы

    СИСТЕМА ИЗ 3 УРАВНЕНИЙ С 3 НЕИЗВЕСТНЫМИ ИСПОЛЬЗУЯ ПРАВИЛО КРАМЕРА, НАЙДИТЕ НАБОР РЕШЕНИЙ ДЛЯ СЛЕДУЮЩЕЙ СИСТЕМЫ УРАВНЕНИЙ: 4X -2Y -3Z = 8 5X + 3Y -4Z = 4 6X -4Y -5Z = 12 ТРЕБУЕТСЯ: Найдите набор решений {(x, y z)} для данной системы.

  • O СИСТЕМЫ УРАВНЕНИЙ И МАТРИЦ Использование правила Крамера для решения 3x … Español Используйте …

    O СИСТЕМЫ УРАВНЕНИЙ И МАТРИЦ Использование правила Крамера для решения 3x … Español Используйте правило Крамера, чтобы найти значение y, которое удовлетворяет уравнениям. 5y + z = 0 3x + 5y + 2z = -5 – 5x + y-2z = 0 Определитель матрицы коэффициентов равен D = Aa y D

  • Задачи тренировки (по 10 баллов). Для вопросов 11–12 рассмотрите следующую систему (x – 5y +…

    Задачи тренировки (по 10 баллов). Для вопросов 11-12 рассмотрите следующую систему (x – 5y + 3z = 2. 2x – 3y + 5z = 1. 2y + 5z = 6. 11. Найдите определитель матрицы коэффициентов, det (A) 12. Решите систему, используя правило Крамера.

  • 2x y5z 2 5x y 4x y 2z = – Используйте правило Крамера, чтобы решить систему уравнений справа. Если D 0, используйте другой метод …

    2x y5z 2 5x y 4x y 2z = – Используйте правило Крамера, чтобы решить систему уравнений справа. Если D 0, воспользуйтесь другим методом для завершения решения. Z = -4 L 8 Запишите дроби, используя правило Крамера в виде определителей. det det det det det y = Z = X = det 2x y5z 2 5x y 4x y 2z = – Используйте правило Крамера, чтобы решить систему уравнений справа. Если D 0, используйте другой …

  • 3. Напишите следующие системы линейных уравнений, используя расширенную матричную форму a. 6x + 7y = -9 X-y = …

    3. Напишите следующие системы линейных уравнений, используя расширенную матричную форму a.6x + 7y = -9 X-y = 5 б. 2x-5y = 4 4x + 3y = 5 C. x + y + z = 4 2x-y-z = 2 -x + 2y + 3z = 5 4. Решите следующие системы линейных уравнений, используя правило Крамера a. 6x-3y = -3 8x-4y = -4 б. 2x-5y = -4 4x + 3y = 5 в. 2x-3y + z = 5 X + 2y + z = -3 x-3y + 2z = 1

  • Решите следующую систему линейных уравнений 3×3, используя Правило Крамера. Используйте расширение несовершеннолетние …

    Решите следующую систему линейных уравнений 3×3, используя Правило Крамера.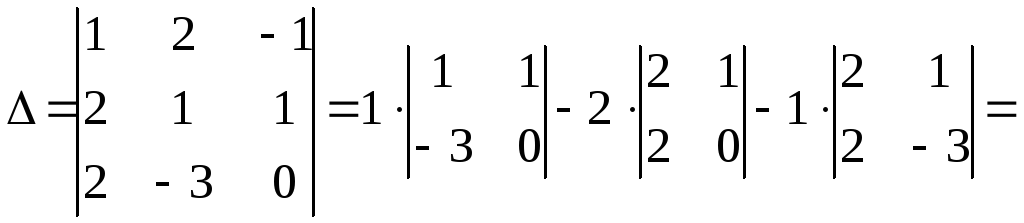 Используйте расширение метод несовершеннолетних для оценки детерминант.Найди раствор заказал тройку и проверил. Показать работы: 3х-2у + г = 12 х + 3у-2z = -9 2x-4y-3z = -4 [РАЗВЕРНУТЬ ПО СТРОКЕ 1] “|” просто я вручную создаю строки, чтобы показать шаги расширения x = | _______ | = | ________ | ______ | _____ | ______ | _____ | = ________ = _____ = y = | _______ | = | ________ | ______ | _____ | ______ | _____ | = ________ = _____ = z = | _______ | = | ________ | ______ | _____ | ______ | _____ | = ________ = _____ = заказанная тройка: {(__, __)} Включить проверки x, y, z извините, я попытался загрузить изображение проблемы, но это …

  • (1 балл) Решите систему, используя правило Крамера.1 53 + 5лет -5 5x + 5лет …

    (1 балл) Решите систему, используя правило Крамера. 1 53 + 5y -5 5x + 5y + 42 202 5 z IL || || 4 3 det = T = y = 2 = Примечание. Вы можете получить частичный балл по этой задаче.

  • Борюсь с этими двумя. Помоги мне, пожалуйста Используйте правило Крамера, чтобы решить (если возможно) систему .

    ..

    Борюсь с этими двумя. Помоги мне, пожалуйста Используйте правило Крамера для решения (если возможно) системы линейных уравнений. (Если невозможно, введите НЕВОЗМОЖНО.) 4x – 2y + 32 = -7 2x + 2y + 5z – 13 8x – 5y – 22 = 1 (x, y, z) = (НЕВОЗМОЖНО *) Нужна помощь? Прочтите, поговорите с преподавателем Отправить ответ Практика Другая версия 12.-14 баллов LarlinAlg8 3.4.027. Мои заметки Попросите учителя Воспользуйтесь правилом Крамера, чтобы решить …

  • 3. Решите систему уравнений 5x + 3y + z 23 3x + 4y-z 21 …

    3. Решите систему уравнений 5x + 3y + z 23 3x + 4y-z 21 4x + 5y 2z 26 4. Решите систему уравнений. 4x-2y + 3z 27 5x 7y + 4z 39

  • 4. Используйте обратный метод, чтобы решить систему и проверить свой результат, используя правило Крамера. 2x-y + 3z …

    4. Используйте обратный метод, чтобы решить систему и проверить свой результат, используя правило Крамера.2x-y + 3z = 9, x + y + z = 6, x-y + z = 2. [15 баллов 5. Покажите, что уравнения X1 + X2 + x, -6, x1 + 2×2 + 3×3 = 14, x1 + 4×2 + 7×3-30 [10 баллов] согласованы, и решите их.

    • Доля рынка цифровых медиакоммутаторов, размер и анализ, 2021-2026 гг.

    В этом отчете рассматривается текущее состояние и будущие перспективы глобального рынка цифровых медиа-коммутаторов на 2015–2026 годы.
    Отчет предлагает подробный обзор индустрии цифровых медиа-коммутаторов и основных тенденций рынка. Исследование рынка включает исторические и прогнозируемые рыночные данные, спрос, сведения о приложениях, ценовые тенденции и доли компаний в ведущих цифровых медиа-коммутаторах с разбивкой по географическому признаку.В отчете размер рынка разбивается по объему и стоимости в зависимости от типа приложения и географии.

    В этом отчете мы анализируем мировой рынок в 5 регионах: Азиатско-Тихоокеанский регион [Китай, Юго-Восточная Азия, Индия, Япония, Корея, Западная Азия], Европа [Германия, Великобритания, Франция, Италия, Россия, Испания, Нидерланды, Турция. , Швейцария], Северная Америка [США, Канада, Мексика], Ближний Восток и Африка [GCC, Северная Африка, Южная Африка], Южная Америка [Бразилия, Аргентина, Колумбия, Чили, Перу].

    Ключевые компании
    Crestron, Extron, AMX, Hitachi, Sony, Hill Residential Systems, TI, Barco, Kramer Electronics

    Сегменты рынка следующим образом:
    Рынок по типу заказа

    Интегрированные коммутаторы
    Модульные матричные коммутаторы
    Коммутаторы для мультимедийных презентаций
    Разбивка цифровых мультимедийных коммутаторов по приложениям
    Жилой дом
    Гостиничный бизнес
    Правительство
    Прочие

    Цифровые мультимедийные коммутаторы на рынке, сохраняя при этом свое конкурентное преимущество над конкурентами.Отчет предлагает подробную и важную информацию для понимания общего рыночного сценария.

    По регионам
    Азиатско-Тихоокеанский регион [Китай, Юго-Восточная Азия, Индия, Япония, Корея, Западная Азия]
    Европа [Германия, Великобритания, Франция, Италия, Россия, Испания, Нидерланды, Турция, Швейцария]
    Север Америка [США, Канада, Мексика]
    Ближний Восток и Африка [GCC, Северная Африка, Южная Африка]
    Южная Америка [Бразилия, Аргентина, Колумбия, Чили, Перу]

    Исследование дает ответы на следующие ключевые вопросы:
    • Каковы предполагаемые темпы роста, рыночная доля и размер рынка цифровых медиа-коммутаторов на прогнозный период 2021–2026 годов?
    • Каковы движущие силы рынка цифровых медиа-коммутаторов на прогнозный период 2021–2026 годов?
    • Кто являются выдающимися игроками на рынке и как они получили конкурентное преимущество перед другими конкурентами?
    • Какие рыночные тенденции влияют на развитие индустрии цифровых медиа-коммутаторов во всем мире?
    • Каковы основные проблемы и угрозы, сдерживающие развитие отрасли?
    • Какие возможности открывает рынок для видных игроков?

    Примечание. Чтобы обеспечить более точный прогноз рынка, все наши отчеты будут обновляться перед отправкой с учетом воздействия COVID-19.

    Запросить бесплатный образец

    Методология исследования

    Reports Insights предлагает технологические решения и их полную интеграцию в исследовательский процесс, чтобы быть квалифицированным на каждом этапе. Мы используем разнообразные активы для достижения наилучших результатов для наших клиентов. Успех исследовательского проекта полностью зависит от исследовательского процесса, принятого в компании. Reports Insights помогает своим клиентам распознавать возможности, исследуя мировой рынок и предлагая экономические идеи.Мы гордимся нашим обширным охватом, охватывающим понимание множества основных отраслевых областей.

    Reports Insights обеспечивает последовательность в нашем исследовательском отчете, а также мы предоставляем часть анализа прогнозов в широком диапазоне географических зон и покрытия. Исследовательские группы проводят первичные и вторичные исследования для реализации и разработки процедуры сбора данных. Затем исследовательская группа анализирует данные о последних тенденциях и основных проблемах в каждой отрасли и стране.Это помогает определить предполагаемые рыночные процедуры в будущем. Компания предлагает решения, основанные на технологиях, и их полное включение в метод исследования, чтобы быть квалифицированным на каждом этапе.

    Исследовательский процесс компании имеет следующие преимущества:

    1. Информационные закупки

    Этап включает получение рыночной информации или данных с использованием различных методологий и источников.

    1. Информационное расследование

    Этот шаг включает отображение и исследование всей информации, полученной на предыдущем шаге.Он также включает анализ различий в данных, наблюдаемых в многочисленных источниках данных.

    1. Высокоутентичный источник

    Мы предлагаем достоверную информацию из множества источников. Выполнять требование клиента.

    1. Формулировка рынка

    Этот шаг влечет за собой размещение точек данных на подходящих рыночных площадях, чтобы сделать возможные выводы. Точка зрения аналитика и изучение формы определения размера рынка, основанное на профильных специалистах, также играет важную роль на этом этапе.

    1. Проверка и публикация информации

    Проверка – важный этап процедуры. Валидация с помощью тщательно разработанной процедуры помогает нам сделать выводы о точках данных, которые будут использоваться для окончательных расчетов.

    .

    Оставить комментарий