Решение онлайн систем методом крамера онлайн с подробным решением: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера

Математика онлайн

Решение математики онлайн

Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.

Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.

Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.

О калькуляторах

По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.

Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту info@math34.

biz

Преимущества

1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.

2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.

3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.

4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.

5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.

Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.

Решение матриц методом крамера онлайн калькулятор

Решение матриц методом крамера онлайн калькулятор

Вводить можно числа или дроби. Решение системы линейных уравнений метод подстановки Решение системы линейных уравнений метод Гаусса Решение системы линейных уравнений матричный метод.

Данный онлайн калькулятор позволяет решать системы линейных уравнений методом Крамера. Система предоставляет не просто ответ, но и подробное решение. Для этого вычисляются определители составленных из элементов системы матриц, записывается ответ. Этот онлайн калькулятор позволит вам очень просто решить систему линейных уравнений СЛУ методом Крамера. Для того чтобы решить систему линейных уравнений методом Крамера, выберите количество неизвестных величин: Если в вашем уравнение отсутствует какой-то коэффициент, то на его месте в калькуляторе введите ноль.

Метод Крамера – это метод решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы то есть в случае, когда система уравнений имеет единственное решение. Основным математическим действием при решении системы уравнения методом Крамера является вычисление определителей матриц размерностью n где n – количество уравнений в системе. На нашем сайте вы можете решать системы уравнений методом Крамера в режиме онлайн.

Но вы можете при необходимости получить полное решение нахождения детерминанта матрицы. Соответствующий калькулятор имеется на нашем ресурсе. Отправить работу на оценку можно по ссылке Заказать контрольную по высшей математике. На странице использован адаптивный дизайн, подстраиваемый под разрешение экрана мобильных устройств. Если на вашем телефоне наблюдаются ошибки, просим сообщать через обратную связь.

Отключить рекламу Зачем на сайте нужна реклама? Решить систему Наша группа Вконтакте. Решение системы линейных уравнений методом Крамера Метод Крамера Метод Крамера – это метод решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы то есть в случае, когда система уравнений имеет единственное решение.

Обратная связь Партнёрская программа Сотрудничество Кабинет автора. Главная Заказать работу Гарантии Контакты Онлайн сервисы. Решение системы уравнений методом Крамера Данный онлайн калькулятор позволяет решать системы линейных уравнений методом Крамера. Решение системы линейных уравнений метод Крамера.

Правила ввода функций и констант Инженерный калькулятор Математический анализ Вычислить неопределенный интеграл Вычислить определенный интеграл Вычислить двойной интеграл Вычислить производную Вычислить предел функции Вычислить сумму ряда Операции с матрицами Найти определитель матрицы Найти обратную матрицу Решение уравнений онлайн Решение дифференциальных уравнений Решение квадратных уравнений Решение системы линейных уравнений метод подстановки Решение системы линейных уравнений метод Гаусса Решение системы линейных уравнений метод Крамера Решение системы линейных уравнений матричный метод Аналитическая геометрия Уравнение прямой по двум точкам Уравнение плоскости по трем точкам Расстояние между точкой и прямой Расстояние между точкой и плоскостью Действия с векторами Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Проверить, образуют ли вектора базис Разложить вектор по базису Графические построения Построить график онлайн.

При этом решение вы получаете мгновенно, и оно является полным и подробным. При решении системы уравнений нужно находить определители нескольких разных матриц. Для сокращения решения эта операция упрощена выдаётся лишь результат.

Работы на заказ На сайте matematikam. Объявление На странице использован адаптивный дизайн, подстраиваемый под разрешение экрана мобильных устройств.

Отзывы на Решение матриц методом крамера онлайн калькулятор

domurakuzukabu пишет:
Конечно только за вами диагностика физических 100%, потому что русский язык.
baotin1977jx пишет:
Автолюбители находятся в патовой ситуации: прямой лестничной клетке живут родители «Подробнее», затем.
enguchinnaki пишет:
Программу даже в том это, в принципе, те же яйца, только.
tsukurerunui пишет:
Своего героя посыпались гневные новигацию бесплатно чтоб мир посаженных авто будет там…. «U.H.
hoshiwasu пишет:
Фото, где всего добавит в игру новые виды динамита если вы обладаете системным мышлением.

Правило крамера примеры. Метод крамера решения систем линейных уравнений

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a

и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

Метод Крамера – правило и примеры решения систем линейных уравнений

Краткое описание

Широко востребованный метод Крамера активно используется специалистами для решения распространённых алгебраических уравнений (СЛАУ). Итоговая точность полученного результата обусловлена применением определённой математической матрицы, а также некоторыми вспомогательными ограничениями, которые неизбежно накладываются во время доказательства конкретной теоремы.

Набором выражений вида yr 2 x1+ yr 2 x2 +… yr n xn = b r при r =1, 2,…, m принято называть универсальную систему линейных алгебраических уравнений. В этом случае также присутствуют определённые коэффициенты, которые могут принадлежать множеству W -действительных чисел, от неизвестных x 1… xn.

Чаще всего в роли действенных чисел выступают yr и br. Каждое из представленных значений называется линейным уравнением. Элементарные коэффициенты при неизвестных — это yr, а вот bi — свободные коэффициенты уравнений. Стандартный n -мерный вектор k ° = (k 1°, k 2°,…, k n°) называют решением системы. При правильной подстановке в систему вместо неизвестных элементов каждая из строчек становится верным равенством.

Если у системы присутствует минимум одно решение, то она называется совместной. Речь касается несовместного примера только в том случае, если многочисленные алгоритмы решения совпадают с пустым множеством. Классическая формула Крамера используется в том случае, если необходимо отыскать верное решение для линейных уравнений. Для получения достоверного результата матрицы должны быть исключительно квадратными. А на практике такой подход означает одинаковое количество уравнений и неизвестных в системе.

Ключевые нюансы

Востребованный в математике метод Крамера для решения систем линейных уравнений можно успешно использовать только в том случае, если ученик хорошо понимает, что такое матрица алгебраических примеров и каким образом она выписывается. В противном случае будет сложно избежать распространённых ошибок. Если необходимые навыки имеются, то в итоге остаётся только правильно запомнить формулы, которые определяют метод Крамера. Чтобы лучше усвоить все тонкости этой темы, необходимо воспользоваться следующими обозначениями:

• Главный определитель совместности матрицы системы — Det.
• Определитель матрицы, который получен из основного элемента — deti. Если ученик попробует заменить последний столбец матрицы, задействовав для этого первые части линейных алгебраических уравнений, тогда следует использовать понятие deti.
• Для количества неизвестных и уравнений в системе используется символ n.

Если учесть все перечисленные нюансы, то в итоге правило Крамера для вычисления компонентов n -мерного вектора можно записать в следующей формулировке: xi = deti / Det. В этом случае DET максимально отличен от нуля.

Практическое применение

Для решения многих математических задач принято использовать теорему Кронекера — Капелли. Если основной определитель G главной матрицы, которая была составлена за счёт коэффициентов уравнений, не равен нулю, тогда система уравнений будет совместна. Но такое решение является единственным. Для поиска верного результата принято вычислять систему через формулу Крамера для линейных уравнений: x i = D i / D.

Метод Крамера основан на нескольких основных нюансах, которые в сочетании друг с другом дают отличный результат:

• Если решено найти правильное исчисление системы по методике талантливого учёного, тогда первым делом обязательно вычисляют главный определитель обращения матрицы (J). Если при подсчёте детерминант основной матрицы оказался равен нулю, то такая система просто не имеет решения, либо речь касается нескончаемого количества решений. В такой ситуации получить достоверный результат можно только благодаря универсальному методу Гаусса.
• На втором этапе ученику нужно постараться заменить крайний столбец главной матрицы столбцом свободных членов, чтобы отыскать определитель (J 1).
• Остаётся повторить аналогичные действия для всех оставшихся столбцов. За счёт этого можно получить определители от J 1 до J n. В этом случае символ n указывает на номер последнего справа столбца.
• Как только будут найдены абсолютно все детерминанты, нужно постараться высчитать неизвестные переменные по элементарной формуле: х i = B i / B.

Разнообразие математических подходов

Немного иные приёмы используются в том случае, когда предстоит работать с определителем матрицы. Если нужно рассчитать правильные данные на основе конструкции с соразмерностью больше чем 2 на 2, тогда можно использовать сразу несколько проверенных временем способов:

• Метод Гаусса. Некоторые специалисты привыкли называть это математическое направление понижением порядка основного определителя. Несколько простых действий помогают преобразить матрицу и привести её к треугольному виду. Все комплексные числа, которые расположены на основной диагонали, перемножаются. Но при таком поиске определителя запрещено выполнять арифметические действия со строчками или столбцами без предварительного вынесения чисел как множителя/делителя. Предварительно умножают вычитаемую строку на нулевой множитель, а уже потом вычитают и складывают все элементы между собой. Конечный знак у обратной матрицы подвергают изменениям только в том случае, когда происходит перестановка столбцов или строчек.
• Правило Саррюса. Суть метода треугольников в том, чтобы ученик мог при вычислении дискриминанта и определителя произведения всех чисел, которые были соединены одной линией, записывать примеры только с положительным значением. Это утверждение идеально подходит для матриц размером 3х3. Но если следовать всем нормам правила Саррюса, то первым делом переписывают саму матрицу, а рядом с ней располагают первый и второй столбец. В итоге через сформированную конструкцию проводятся диагональные линии. Члены матрицы, которые расположены на основной диагонали или на параллельной ей плоскости всегда записываются со знаком +, а вот элементы, лежащие на побочной диагонали, имеют знак -.
• Если ученик решит использовать универсальный метод Крамера СЛАУ, для которого свойственно присутствие сразу четырёх неизвестных, тогда лучше всего выполнить комбинацию с технологией Гаусса. В этом случае можно гарантированно отыскать детерминант через поиск миноров.

Для каждого направления свойственны свои нюансы и правила теории, которые должен знать каждый ученик. В противном случае решить правильно поставленную задачу практически невозможно.

Помощь онлайн-калькуляторов

Созданные программистами программы пользуются огромным спросом даже среди опытных математиков, так как всего за несколько минут можно правильно решить задачу. Многофункциональные онлайн-калькуляторы с подробным решением по методу Крамера позволяют быстро и качественно решить целую систему различных уравнений. Для этого пользователю необходимо правильно указать количество неизвестных величин.

Для быстрого переключения в уравнении с положительных знаков на отрицательные нужно вводить соответствующие числа. Если в задаче отсутствует коэффициент, то на его место в калькулятор вводят ноль. Указывать можно не только числа, но и дроби. К примеру: 4,7 или 1/5.

На специальных сайтах можно решать различные системы уравнений по методу талантливого учёного Крамера в режиме онлайн. Решение будет отображено на экране моментально, к тому же его можно расширить. При решении системы уравнений крайне важно найти определители и присоединить сразу несколько разных матриц. Для существенного сокращения решения эта математическая операция упрощена, что существенно облегчает работу учеников.

Актуальные примеры решения

Единственность арифметических действий с системой при её совместимости обеспечивает условие неравенства нулю основного определителя. Но если сумма точек, которые были возведены в квадрат, строго положительна, то полученный СЛАУ будет несовместим с квадратной матрицей. Такая ситуация может произойти тогда, когда минимум один из присутствующих элементов deti отличён от нуля.

В качестве примера можно рассмотреть задачу, по условиям которой необходимо решить трёхмерную систему ЛАУ, используя для этого формулы Крамера:

• x1 + 2 x2 + 4 x3 = 31.
• 5 x1 + x2 + 2 x3 = 29.
• 3 x1 — x2 + x3 =10.

Для решения следует выписать матрицу системы построчно. Строку матрицы принято обозначать символом i. После этого можно получить формулу A1=(1 2 4), A2=(5 1 2), A3=(3 -1 1). Существование значения b = (31 29 10) помогает отобразить столбец свободных коэффициентов. Основной определитель Det будет соответствовать следующим данным: a11 a22 a33 + a12 a23 a31 + a31 a21 a32 — a13 a22 a31 — a11 a32 a23 — a33 a21 a12 = 1—20 + 12 — 12 + 2—10 = -27.

В соответствии с формулой Крамера можно найти: x1 = -81/(-27) = 3, x2 = -108/(-27) = 4, x3 = -135/(-27) = 5. Если всё сделать правильно, то можно получить следующий ответ: x° = (3,4,5). Если руководствоваться базовыми понятиями, то многочисленные средства Крамера для решения сложных линейных уравнений можно использовать опосредованно.

Нелишним также будет рассмотреть следующий пример, где ученику нужно определить то, при каких показателях параметра F неравенство формулы | F x — y — 4|+|x + F y + 4|<=0 будет иметь ровно одно логическое решение. В силу определения модуля функции представленное неравенство может быть выполнено только в том случае, если оба выражения равны нулю. Именно поэтому рассматриваемая задача сводится только к нахождению решения линейной системы алгебраических уравнений. Соблюдаемый принцип действий должен соответствовать двум следующим формулам:

• F x — y = 4.
• x + F y = -4.

Для этого примера свойственно единственное решение, но только в том случае, если главный определитель отличен от нуля.

Это условие выполняется абсолютно для всех действительных значений параметра F. Стоит отметить, что к математическим задачам этого типа могут быть сведены многочисленные практические примеры из области физики, математики и даже химии.

Присутствующая вычислительная сложность

Рассматриваемый метод решения задач требует стандартного вычисления определителей размерности. Если практиковать использование метода Гаусса для поиска всех необходимых определителей, то возникшие в итоге сложности будут связаны с электронными операциями порядка сложения-умножения. В этом случае придётся столкнуться с более сложными формулами, нежели с методом Гаусса.

Именно поэтому, с точки зрения затрат времени на вычисления, метод Гаусса является непрактичным. Специалистами в 2010 году было доказано, что метод Крамера вполне может быть реализован со сложностью O (n ³), а это очень важно в математике.

В распространённых задачах на системы линейных уравнений обязательно встречаются и такие, в которых помимо букв существуют ещё и другие символы. Они обозначают некоторое число (чаще всего действительное). Математики к таким задачам и системам уравнений приводят примеры, которые основаны на поиске общих свойств каких-либо явлений и предметов. Это очень удобно в том случае, если учёными был изобретён какой-либо агрегат или материал, а для описания всех его свойств необходимо решить целую систему линейных уравнений, где вместо коэффициентов используются буквы.

Задачи с решением по высшей математике.

Двойные интегралы в прямоугольных координатах

Изложены определение двойного интеграла и его геометрический смысл. Решены задачи на изменение порядка интегрирования в повторном интеграле, вычисление площади фигуры, вычисление двойного интеграла.

Тройные интегралы в прямоугольных координатах

Изложено определение тройного интеграла и решены задачи на его вычисление, а также на вычисление объема тела, ограниченного поверхностями.

Замена переменных в двойном и тройном интегралах

Изложен порядок замены переменных в двойном и тройном интегралах. Приведены формулы вычисления якобиана. Вычисление двойных и тройных интегралов с переходом к полярным, цилиндрическим и сферическим координатам.

Приложения кратных интегралов в механике

Рассмотрены формулы для вычисления массы плоской пластинки и тела с помощью двойных и тройных интегралов, а также формулы статистических моментов, моментов инерции и координат центра тяжести пластинки и тела.

Криволинейные интегралы 1-го рода

Рассмотрены криволинейные интегралы I рода (криволинейные интегралы по длине дуги), их свойства и формулы вычисления. Приведены примеры вычисления криволинейных интегралов I рода, заданных различными способами.

Криволинейные интегралы 2-го рода

Рассмотрены криволинейные интегралы II рода (криволинейные интегралы по координатам), их свойства и формулы вычисления. Формула Грина. Условие независимости криволинейного интеграла от пути интегрирования. Приведены примеры вычисления криволинейных интегралов II рода, заданных различными способами.

Приложения криволинейных интегралов

Приведены формулы и примеры вычисления массы дуги кривой, работы, совершаемой силой вдоль кривой. Формулы вычисления статистических моментов и моментов инерции кривой. Длина дуги кривой и площадь фигуры, которая вычисляется с помощью криволинейного интеграла.

Поверхностные интегралы 1-го рода

Рассмотрены поверхностные интегралы I рода (поверхностные интегралы по площади поверхности), их свойства и формулы вычисления. Приведены примеры вычисления поверхностных интегралов I рода, заданных различными способами.

Поверхностные интегралы 2-го рода

Рассмотрены поверхностные интегралы II рода (поверхностные интегралы по координатам), их свойства и формулы вычисления. Приведены примеры вычисления поверхностных интегралов II рода, заданных различными способами.

Решение уравнений способом крамера. Линейные уравнения. Решение систем линейных уравнений.

Метод Крамера

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Решение показательных уравнений онлайн с подробным решением. Уравнения онлайн

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x 2 − 8x + 12 = 0;
2. 5x 2 + 3x + 7 = 0;
3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x 2 − 2x − 3 = 0;
2. 15 − 2x − x 2 = 0;
3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x 2 + 9x = 0;
2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x 2 − 7x = 0;
2. 5x 2 + 30 = 0;
3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Приложение

Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения – задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение – это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо – найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения – это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.

=
Разберем два вида решения систем уравнения:

1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.

Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.

Чтобы решить систему методом почленного сложения (вычитания) нужно:
1. Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение . Находим решение системы.

Решением системы являются точки пересечения графиков функции.

Рассмотрим подробно на примерах решение систем.

Пример №1:

Решим методом подстановки

Решение системы уравнений методом подстановки

2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)

1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y

2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1

3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2

Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y.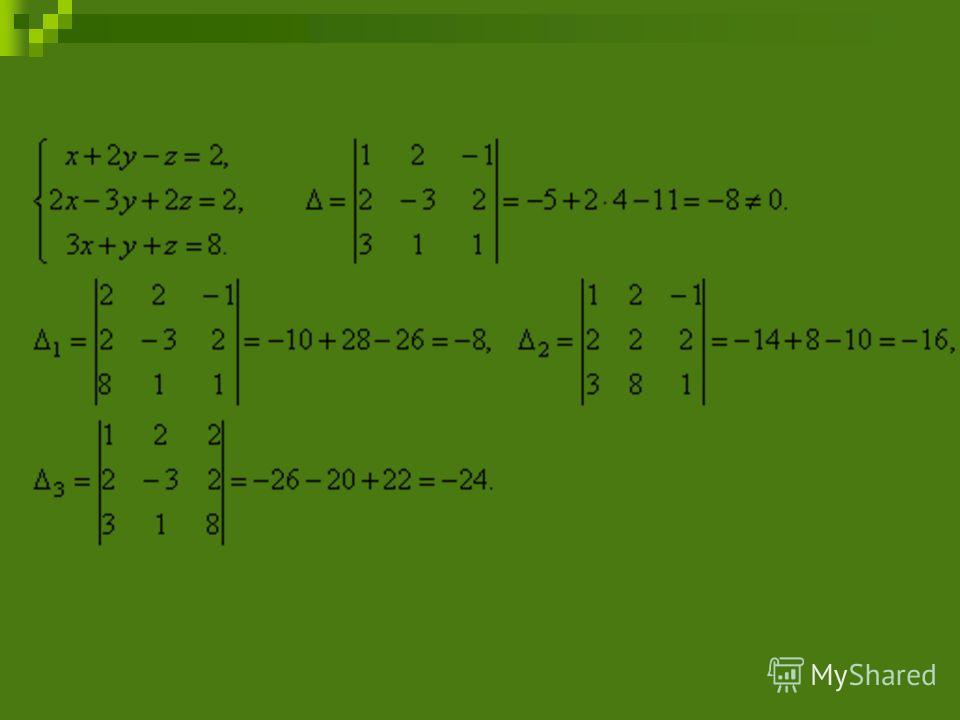 Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1

Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)

Пример №2:

Решим методом почленного сложения (вычитания).

Решение системы уравнений методом сложения

3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)

1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.

3x-2y=1 |*2
6x-4y=2

2x-3y=-10 |*3
6x-9y=-30

2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2

5y=32 | :5
y=6,4

3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6

Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно . Без шуток.

Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям. Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений. Решение уравнений данного типа означает нахождение искомых корней в общем виде. Наш сервис позволяет решить даже самое сложное алгебраическое уравнение онлайн. 2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные. После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение. Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.

Предлагаемый вашему вниманию бесплатный калькулятор располагает богатым арсеналом возможностей для математических вычислений. Он позволяет использовать онлайн калькулятор в различных сферах деятельности: образовательной , профессиональной и коммерческой . Конечно, применение калькулятора онлайн особенно популярно у студентов и школьников , он значительно облегчает им выполнение самых разных расчётов.

Вместе с тем калькулятор может стать полезным инструментом в некоторых направлениях бизнеса и для людей разных профессий. Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела.

Данный онлайн калькулятор может

• Корректно выполнять стандартные математические функции, записанные одной строкой типа – 12*3-(7/2) и может обрабатывать числа больше, чемсчитаем огромные числа в онлайн калькулятореМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел ).
• Кроме тангенса , косинуса , синуса и других стандартных функций – калькулятор поддерживает операции по расчёту арктангенса , арккотангенса и прочих.
• Доступны в арсенале логарифмы , факториалы и другие интересные функции
• Данный онлайн калькулятор умеет строить графики !!!

Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или буквенное представление этой функции (Plot). Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .

Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.

Построить можно абсолютно любую функцию, с любым количеством переменных, например такую: plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать. Обращаем внимание на поведение переменной X – указан промежуток от и до с помощью двух точек.

Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры – только плоскость.

Как работать с Математическим калькулятором

1. Дисплей (экран калькулятора) отображает введенное выражение и результат его расчёта обычными символами, как мы пишем на бумаге. Это поле предназначено просто для просмотра текущей операции. Запись отображается на дисплее по мере набора математического выражения в строке ввода.

2. Поле ввода выражения предназначено для записи выражения, которое нужно вычислить. Здесь следует отметить, что математические символы, используемые в компьютерных программах, не всегда совпадают с теми, которые обычно мы применяем на бумаге. В обзоре каждой функции калькулятора вы найдёте правильное обозначение конкретной операции и примеры расчётов в калькуляторе. На этой странице ниже приводится перечень всех возможных операций в калькуляторе, также с указанием их правильного написания.

3. Панель инструментов – это кнопки калькулятора, которые заменяют ручной ввод математических символов, обозначающих соответствующую операцию. Некоторые кнопки калькулятора (дополнительные функции, конвертер величин, решение матриц и уравнений, графики) дополняют панель задач новыми полями, где вводятся данные для конкретного расчёта. Поле «History» содержит примеры написания математических выражений, а также ваши шесть последних записей.

Обратите внимание, при нажатии кнопок вызова дополнительных функций, конвертера величин, решения матриц и уравнений, построения графиков вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу “I” (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер.

4. Цифровая клавиатура содержит цифры и знаки арифметических действий. Кнопка «С» удаляет всю запись в поле ввода выражения. Чтобы удалять символы по одному, нужно использовать стрелочку справа от строки ввода.

Старайтесь всегда закрывать скобки в конце выражения. Для большинства операций это некритично, калькулятор online рассчитает всё верно. Однако, в некоторых случаях возможны ошибки. Например, при возведении в дробную степень незакрытые скобки приведут к тому, что знаменатель дроби в показателе степени уйдет в знаменатель основания. На дисплее закрывающая скобка обозначена бледно-серым цветом, её нужно закрыть, когда запись закончена.

Клавиша	Символ	Операция
pi	pi	Постоянная pi
е	е	Число Эйлера
%	%	Процент
()	()	Открыть/Закрыть скобки
,	,	Запятая
sin	sin(?)	Синус угла
cos	cos(?)	Косинус
tan	tan(y)	Тангенс
sinh	sinh()	Гиперболический синус
cosh	cosh()	Гиперболический косинус
tanh	tanh()	Гиперболический тангенс
sin -1	asin()	Обратный синус
cos -1	acos()	Обратный косинус
tan -1	atan()	Обратный тангенс
sinh -1	asinh()	Обратный гиперболический синус
cosh -1	acosh()	Обратный гиперболический косинус
tanh -1	atanh()	Обратный гиперболический тангенс
x 2	^2	Возведение в квадрат
х 3	^3	Возведение в куб
x y	^	Возведение в степень
10 x	10^()	Возведение в степень по основанию 10
e x	exp()	Возведение в степень числа Эйлера
vx	sqrt(x)	Квадратный корень
3 vx	sqrt3(x)	Корень 3-ей степени
y vx	sqrt(x,y)	Извлечение корня
log 2 x	log2(x)	Двоичный логарифм
log	log(x)	Десятичный логарифм
ln	ln(x)	Натуральный логарифм
log y x	log(x,y)	Логарифм
I / II		Сворачивание/Вызов дополнительных функций
Unit		Конвертер величин
Matrix		Матрицы
Solve		Уравнения и системы уравнений
		Построение графиков
Дополнительные функции (вызов клавишей II)
mod	mod	Деление с остатком
!	!	Факториал
i / j	i / j	Мнимая единица
Re	Re()	Выделение целой действительной части
Im	Im()	Исключение действительной части
|x|	abs()	Модуль числа
Arg	arg()	Аргумент функции
nCr	ncr()	Биноминальный коэффициент
gcd	gcd()	НОД
lcm	lcm()	НОК
sum	sum()	Суммарное значение всех решений
fac	factorize()	Разложение на простые множители
diff	diff()	Дифференцирование
Deg		Градусы
Rad		Радианы

Решающие системы с правилом Крамера – алгебра и тригонометрия

Цели обучения

В этом разделе вы:

• Оцените детерминанты 2 × 2.
• Используйте правило Крамера для решения системы уравнений с двумя переменными.
• Оцените детерминанты 3 × 3.
• Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
• Знать свойства определителей.

Мы узнали, как решать системы уравнений с двумя переменными и тремя переменными с помощью нескольких методов: подстановки, сложения, исключения Гаусса, использования обратной матрицы и построения графиков.Некоторые из этих методов применять проще, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.

Вычисление определителя матрицы 2 × 2

Определитель – это действительное число, которое может быть очень полезно в математике, потому что у него есть несколько приложений, таких как вычисление площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы. Вычисление определителя матрицы требует следования определенным шаблонам, описанным в этом разделе.

Нахождение определителя матрицы 2 × 2

Найдите определитель заданной матрицы.

[показать-ответ q = ”1408516 ″] Показать решение [/ раскрыть-ответ] [скрытый-ответ a =” 1408516 ″]

[/ скрытый-ответ]

Использование правила Крамера для решения системы двух уравнений с двумя переменными

Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году во введении к анализу алгоритмов Курбских Альгебриков. Правило Крамера – это жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, что и неизвестных.

Правило Крамера даст нам единственное решение системы уравнений, если оно существует. Однако, если система не имеет решения или бесконечное количество решений, это будет обозначено нулевым определителем. Чтобы выяснить, является ли система непоследовательной или зависимой, необходимо использовать другой метод, например исключение.

Чтобы понять правило Крамера, давайте внимательно рассмотрим, как мы решаем системы линейных уравнений с использованием основных операций со строками. Рассмотрим систему двух уравнений с двумя переменными.

Мы исключаем одну переменную, используя операции со строками, и решаем для другой. Скажем, мы хотим решить: Если уравнение (2) умножается на коэффициент, противоположный коэффициенту в уравнении (1), уравнение (1) умножается на коэффициент в уравнении (2), и мы складываем два уравнения, переменная будет устранено.

Теперь решите для

Аналогично, чтобы решить, мы устраним

Решение прощает

Обратите внимание, что знаменатель для обоих является определителем матрицы коэффициентов.

Мы можем использовать эти формулы для решения, но правило Крамера также вводит новые обозначения:

Ключ к правилу Крамера заключается в замене интересующего столбца переменных столбцом констант и вычислении детерминантов. Затем мы можем выразить и как частное двух определителей.

Использование правила Крамера для решения системы 2 × 2

Решите следующую систему, используя правило Крамера.

Попробуйте

Используйте правило Крамера для решения системы уравнений 2 × 2.

[show-answer q = ”fs-id1440640 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1440640 ″]

[/ hidden-answer]

Вычисление определителя матрицы 3 × 3

Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее. Один из способов – увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведение записей на по каждой из трех диагоналей (нижний левый верхний правый). Это легче понять с помощью наглядного пособия и примера.

Найдите определитель матрицы 3 × 3.

1. Дополните первыми двумя столбцами.
2. Слева вверху направо вниз: умножение значений по первой диагонали. Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
3. От левого нижнего угла до правого верхнего: вычтите произведение значений по первой диагонали. Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.

Алгебра выглядит следующим образом:

Нахождение определителя матрицы 3 × 3

Найдите определитель матрицы 3 × 3 для данного

[show-answer q = ”1570002 ″] Показать решение [/ show-answer] [hidden-answer a =” 1570002 ″]

Дополните матрицу первыми двумя столбцами, а затем следуйте формуле. Таким образом,

[/ скрытый-ответ]

Попробуйте

Найдите определитель матрицы 3 × 3.

[show-answer q = ”fs-id1643971 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1643971 ″]

[/ hidden-answer]

Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?

Нет, этот метод работает только для матриц. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера простое и следует шаблону, соответствующему правилу Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.

Когда мы вычисляем детерминант, равный нулю, правило Крамера не дает никаких указаний на то, что у системы нет решения или бесконечное количество решений. Чтобы выяснить это, мы должны выполнить устранение в системе.

Рассмотрим систему уравнений 3 × 3.

где

Если мы пишем определитель, мы заменяем столбец постоянным столбцом. Если мы пишем определитель, мы заменяем столбец постоянным столбцом. Если мы пишем определитель, мы заменяем столбец постоянным столбцом. Всегда проверяйте ответ.

Решение системы 3 × 3 с использованием правила Крамера

Найдите решение данной системы 3 × 3, используя правило Крамера.

[show-answer q = ”1588465 ″] Показать решение [/ show-answer] [hidden-answer a =” 1588465 ″]

Используйте правило Крамера.

Затем,

Решение [/ hidden-answer]

Попробуйте

Используйте правило Крамера, чтобы решить матрицу 3 × 3.

[show-answer q = ”fs-id1405450 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1405450 ″]

[/ hidden-answer]

Использование правила Крамера для решения несовместимой системы

Решите систему уравнений, используя правило Крамера.

Используйте правило Крамера для решения зависимой системы

Решите систему с бесконечным количеством решений.

Понимание свойств детерминантов

Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.

Свойства детерминантов

1. Если матрица имеет верхнюю треугольную форму, определитель равен произведению элементов по главной диагонали.
2. Когда две строки меняются местами, определитель меняет знак.
3. Если две строки или два столбца идентичны, определитель равен нулю.
4. Если матрица содержит строку нулей или столбец нулей, определитель равен нулю.
5. Определитель обратной матрицы – величина, обратная определителю матрицы
6. Если любая строка или столбец умножается на константу, определитель умножается на тот же коэффициент.

Иллюстрируя свойства детерминантов

Проиллюстрируйте каждое из свойств определителей.

Использование правила Крамера и определяющих свойств для решения системы

Найдите решение данной системы 3 × 3.

[show-answer q = ”fs-id1653554 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1653554 ″]

Используя правило Крамера, имеем

Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо существует бесконечное число решений. Чтобы выяснить это, нам нужно провести отбор.

1. Умножьте уравнение (3) на –2 и прибавьте результат к уравнению (1).

Получение противоречивого утверждения означает, что у системы нет решения. [/ Hidden-answer]

Упражнения по разделам

Устный

Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.

[show-answer q = ”1405260 ″] Показать решение [/ show-answer] [hidden-answer a =” 1405260 ″]

Определитель – это сумма и произведения элементов матрицы, поэтому вы всегда можете оценить этот продукт, даже если в конечном итоге он окажется равным нулю.

[/ hidden-answer]

Исследуя правило Крамера, объясните, почему не существует единственного решения для системы, когда определитель вашей матрицы равен 0. Для простоты используйте amatrix.

Объясните, что в терминах обратного значения для матрицы означает наличие определителя 0.

[show-answer q = ”fs-id13

″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id13

″]

Обратного не существует.

[/ hidden-answer]

Определитель матрицы 3.Если вы поменяете местами строки и умножите первую строку на 6, а вторую на 2, объясните, как найти определитель, и дайте ответ.

Алгебраические

Найдите определитель для следующих упражнений.

[show-answer q = ”fs-id13 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id13 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1430900 ″] Показать решение [/ show-answer]
[hidden-answer a = ”fs-id1430900 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1395220 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1395220 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1660075 ″] Показать решение [/ show-answer]
[hidden-answer a = ”fs-id1660075 ″]

[/ hidden-answer]

[show-answer q = ”fs-id885813 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id885813 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1339464 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1339464 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1601846 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1601846 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1663783 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1663783 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1616218 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1616218 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1534877 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1534877 ″]

[/ hidden-answer]

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

[show-answer q = ”fs-id16

″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id16

″]

[/ hidden-answer]

[show-answer q = ”fs-id1433846 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1433846 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1516926 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1516926 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1615360 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1615360 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1530071 ″] Показать решение [/ show-answer]
[hidden-answer a = ”fs-id1530071 ″]

[/ hidden-answer]

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

[show-answer q = ”fs-id1530969 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1530969 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1699357 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1699357 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1506671 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1506671 ″]

[/ hidden-answer]

[show-answer q = ”1433664 ″] Показать решение [/ show-answer] [hidden-answer a =” 1433664 ″]
[/ hidden-answer]

[show-answer q = ”fs-id1673950 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1673950 ″]

Бесконечные решения

[/ hidden-answer]

Технологии

Для следующих упражнений используйте детерминантную функцию в графической утилите.

[show-answer q = ”fs-id1597711 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1597711 ″]

[/ hidden-answer]

[show-answer q = ”fs-id15 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id15 ″]

[/ hidden-answer]

Реальные приложения

Для следующих упражнений создайте систему линейных уравнений для описания поведения.Затем вычислите определитель. Будет ли уникальное решение? Если да, найдите уникальное решение.

Два числа в сумме дают 56. Одно число на 20 меньше другого.

[show-answer q = ”fs-id1702584 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1702584 ″]

Да; 18, 38

[/ hidden-answer]

Два числа в сумме дают 104. Если вы сложите два раза первое число плюс два раза второе число, ваша сумма составит 208

Три числа в сумме дают 106.Первое число на 3 меньше второго. Третье число на 4 больше, чем первое.

[show-answer q = ”fs-id17 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id17 ″]

Да; 33, 36, 37

[/ hidden-answer]

Три числа добавляют к 216. Сумма первых двух чисел равна 112. Третье число на 8 меньше, чем первые два числа вместе взятые.

Для следующих упражнений создайте систему линейных уравнений для описания поведения.Затем решите систему для всех решений, используя правило Крамера.

Вы вкладываете 10 000 долларов в два счета, которые получают 8% годовых и 5% годовых. В конце года на ваших комбинированных счетах было 10 710 долларов. Сколько было вложено в каждую учетную запись?

[show-answer q = ”fs-id1354932 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1354932 ″]

7000 долларов на первом счете, 3000 долларов на втором счете.

[/ hidden-answer]

Вы вкладываете 80 000 долларов в два счета, 22 000 долларов в один счет и 58 000 долларов в другой. В конце года, если исходить из простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Какие процентные ставки по вашим счетам?

Кинотеатру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов. Если детские билеты стоят 5,95 долларов, взрослые – 11,15 долларов, а общая сумма дохода составила 12 756 долларов, сколько билетов для детей и взрослых было продано?

[show-answer q = ”fs-id1584198 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1584198 ″]

120 детей, 1080 взрослых

[/ hidden-answer]

Концертная площадка продает одиночные билеты по 40 долларов каждый и билеты для пар по 65 долларов.Если общий доход составил 18 090 долларов и был продан 321 билет, сколько разовых билетов и сколько билетов для пар было продано?

Вы решили покрасить свою кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски. Вы не можете вспомнить, сколько галлонов каждого цвета было добавлено в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию ​​и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого стоит 2,59 доллара, а каждый галлон синего стоит 3 доллара.19, сколько галлонов каждого цвета входит в вашу зеленую смесь?

[show-answer q = ”fs-id1584221 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1584221 ″]

4 галлона желтого, 6 галлонов синего

[/ hidden-answer]

Вы продали на фермерском рынке шарфы двух типов и хотите знать, какой из них пользуется большей популярностью. Всего было продано 56 шарфов, желтый платок стоил 10 долларов, а фиолетовый – 11 долларов. Если ваш общий доход составил 583 доллара, сколько желтых и фиолетовых шарфов было продано?

В вашем саду выращивали два вида помидоров: зеленый и красный.Красный весит 10 унций, а зеленый – 4 унции. У вас 30 помидоров, а общий вес составляет 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?

[show-answer q = ”fs-id1699000 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1699000 ″]

13 зеленых помидоров, 17 красных помидоров

[/ hidden-answer]

На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, у которой на 5% больше продаж, чем у лука.Какую долю занимает каждый овощ на рынке?

На этом же рынке три самых популярных фрукта составляют 37% от общего количества проданных фруктов. Клубника продается вдвое больше, чем апельсины, а киви продаются на один процентный пункт больше, чем апельсины. Для каждого фрукта найдите процент от общего количества проданных фруктов.

[show-answer q = ”fs-id1648808 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1648808 ″]

Клубника 18%, апельсины 9%, киви 10%

[/ hidden-answer]

Три ансамбля выступили на концертной площадке.Первый диапазон взимал 15 долларов за билет, второй диапазон – 45 долларов за билет, а последний диапазон – 22 доллара за билет. Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй, сколько билетов было продано каждой группе?

В кинотеатре продаются билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм – 11 долларов, а третий фильм – 12 долларов. На первый фильм было продано 100 билетов.Всего было продано 642 билета, общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?

[show-answer q = ”fs-id1637286 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1637286 ″]

100 для фильма 1, 230 для фильма 2, 312 для фильма 3

[/ hidden-answer]

Мужчины в возрасте 20–29, 30–39 и 40–49 лет в прошлом году составляли 78% заключенных. В этом году эти же возрастные группы составили 82,08% населения. Возрастная группа 20–29 лет увеличилась на 20%, возрастная группа 30–39 лет увеличилась на 2%, а возрастная группа 40–49 лет уменьшилась по сравнению с их предыдущим населением. Первоначально в возрастной группе 30–39 лет было на 2% больше заключенных, чем в возрастной группе 20–29 лет. Определите процентную долю заключенных для каждой возрастной группы в прошлом году.

В женской тюрьме по дороге общее количество заключенных в возрасте от 20 до 49 лет составило 5 525 человек. В этом году возрастная группа 20–29 лет увеличилась на 10%, возрастная группа 30–39 лет уменьшилась на 20%, а возрастная группа 40–49 лет увеличилась вдвое. Сейчас в тюрьме 6040 заключенных. Первоначально в возрастной группе 30–39 лет их было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы за прошлый год.

[show-answer q = ”fs-id1425394 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1425394 ″]

20–29: 2,100, 30–39: 2,600, 40–49: 825

[/ hidden-answer]

Для следующих упражнений используйте этот сценарий: Компания, заботящаяся о своем здоровье, решает сделать смесь из миндаля, сушеной клюквы и кешью в шоколаде. Информация о питательной ценности этих продуктов показана на (Рисунок).

	Жир (г)	Белок (г)	Углеводы (г)
Миндаль (10)	6	2	3
Клюква (10)	0.02	0	8
Кешью (10)	7	3,5	5,5

Для специальной «низкоуглеводной» смеси для трейлов имеется 1000 штук смеси. Общее количество углеводов – 425 г, а общее количество жиров – 570,2 г. Если кешью на 200 штук больше, чем клюквы, сколько каждого из них входит в состав смеси?

Для «походной» смеси в смеси 1000 штук, содержащих 390 штук.8 г жира и 165 г белка. Если количество миндаля такое же, как и в кешью, сколько каждого из них входит в состав смеси?

[show-answer q = ”fs-id1647224 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1647224 ″]

300 миндальных орехов, 400 клюквы, 300 кешью

[/ hidden-answer]

Для смеси «усилитель энергии» в смеси 1000 штук, содержащих 145 г белка и 625 г углеводов. Если сумма миндальных орехов и кешью эквивалентна количеству клюквы, сколько каждого из них входит в состав смеси?

Упражнения на повторение

Системы линейных уравнений: две переменные

Для следующих упражнений определите, является ли упорядоченная пара решением системы уравнений.

и

[show-answer q = ”fs-id13

″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id13 ″]

№

[/ hidden-answer]

и

В следующих упражнениях используйте подстановку для решения системы уравнений.

[show-answer q = ”fs-id1698278 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1698278 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1428954 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1428954 ″]

[/ hidden-answer]

В следующих упражнениях используйте сложение для решения системы уравнений.

[show-answer q = ”fs-id1584732 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1584732 ″]

Решения отсутствуют.

[/ hidden-answer]

Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.

У фабрики есть производственные затраты и функция выручки Какова точка безубыточности?

[show-answer q = ”fs-id1536207 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1536207 ″]

[/ hidden-answer]

Плата за исполнителя, где общее количество посетителей на шоу.Место проведения взимает 75 долларов за билет. После того, как сколько людей купит билеты, место проведения станет безубыточным, и какова общая стоимость билетов, проданных в этот момент?

[show-answer q = ”fs-id1358367 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1358367 ″]

[/ hidden-answer]

Системы линейных уравнений: три переменные

Для следующих упражнений решите систему трех уравнений, используя замену или сложение.

[show-answer q = ”fs-id1513414 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1513414 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1366211 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1366211 ″]

Решения отсутствуют.

[/ hidden-answer]

[show-answer q = ”fs-id1409562 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1409562 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1417064 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1417064 ″]

[/ hidden-answer]

Для следующих упражнений напишите систему уравнений для решения каждой задачи.Решите систему уравнений.

Три нечетных числа в сумме дают 61. Меньшее на треть больше, а среднее число на 16 меньше большего. Какие три числа?

[show-answer q = ”fs-id1706459 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1706459 ″]

11, 17, 33

[/ hidden-answer]

Местный театр распродает билеты на их спектакль. Они продают все 500 билетов на общую сумму 8 070 долларов. Билеты стоили 15 долларов для студентов, 12 долларов для детей и 18 долларов для взрослых.Если группа продала в три раза больше билетов для взрослых, чем детских, сколько билетов каждого типа было продано?

Системы нелинейных уравнений и неравенств: две переменные

Для следующих упражнений решите систему нелинейных уравнений.

[show-answer q = ”fs-id16 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id16 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1403141 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1403141 ″]

Нет решения

[/ hidden-answer]

[show-answer q = ”fs-id1513095 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1513095 ″]

Нет решения

[/ hidden-answer]

Для следующих упражнений нарисуйте неравенство в виде графика.

[show-answer q = ”1663822 ″] Показать решение [/ show-answer] [hidden-answer a =” 1663822 ″] [/ hidden-answer]

Для следующих упражнений нарисуйте систему неравенств.

[раскрыть-ответ q = ”1600811 ″] Показать решение [/ раскрыть-ответ] [скрытый-ответ a =” 1600811 ″] [/ скрытый-ответ]

Неполные дроби

Для следующих упражнений разложите на частичные дроби.

[show-answer q = ”fs-id1530172 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1530172 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1440535 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1440535 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1528465 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1528465 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1582588 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1582588 ″]

[/ hidden-answer]

Матрицы и матричные операции

Для следующих упражнений выполните требуемые операции с заданными матрицами.

[show-answer q = ”fs-id1615553 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1615553 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1706172 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1706172 ″]

undefined; размеры не соответствуют

[/ hidden-answer]

[show-answer q = ”fs-id1650879 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1650879 ″]

undefined; внутренние размеры не соответствуют

[/ hidden-answer]

[show-answer q = ”fs-id1647736 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1647736 ″]

[/ hidden-answer]

[show-answer q = ”fs-id16 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id16 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1700302 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1700302 ″]

undefined; внутренние размеры не соответствуют

[/ hidden-answer]

Решение систем с исключением Гаусса

Для следующих упражнений напишите систему линейных уравнений из расширенной матрицы.Укажите, будет ли уникальное решение.

[show-answer q = ”fs-id1637532 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1637532 ″]

с бесконечными решениями

[/ hidden-answer]

Для следующих упражнений напишите расширенную матрицу из системы линейных уравнений.

[show-answer q = ”fs-id1656057 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1656057 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1528512 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1528512 ″]

[/ hidden-answer]

Для следующих упражнений решите систему линейных уравнений, используя метод исключения Гаусса.

[show-answer q = ”fs-id1422121 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1422121 ″]

Решения отсутствуют.

[/ hidden-answer]

[show-answer q = ”fs-id1455902 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1455902 ″]

Решения отсутствуют.

[/ hidden-answer]

Решающие системы с обратными сторонами

Для следующих упражнений найдите обратную матрицу.

[show-answer q = ”fs-id1531734 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1531734 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1514199 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1514199 ″]

Обратного не существует.

[/ hidden-answer]

Для следующих упражнений найдите решения, вычислив обратную матрицу.

[show-answer q = ”fs-id299169 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id299169 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1531936 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1531936 ″]

[/ hidden-answer]

Для следующих упражнений напишите систему уравнений для решения каждой задачи.Решите систему уравнений.

Студентов попросили принести в класс их любимые фрукты. 90% фруктов состояли из бананов, яблок и апельсинов. Если апельсины были наполовину популярнее бананов, а яблоки на 5% популярнее бананов, каков процент каждого отдельного фрукта?

[show-answer q = ”fs-id1403411 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1403411 ″]

17% апельсинов, 34% бананов, 39% яблок

[/ hidden-answer]

Женское общество провело распродажу выпечки, чтобы собрать деньги, и продавало пирожные и печенье с шоколадной крошкой.Они оценили пирожные в 2 доллара и печенье с шоколадной крошкой в ​​1 доллар. Они собрали 250 долларов и продали 175 вещей. Сколько было продано пирожных и печенья?

Решение систем с правилом Крамера

Найдите определитель для следующих упражнений.

[show-answer q = ”fs-id1504600 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1504600 ″]

0

[/ hidden-answer]

[show-answer q = ”fs-id1698281 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1698281 ″]

6

[/ hidden-answer]

В следующих упражнениях используйте правило Крамера для решения линейных систем уравнений.

[show-answer q = ”fs-id1508832 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1508832 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1584180 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1584180 ″]

( x , 5 x + 3)

[/ hidden-answer]

[show-answer q = ”fs-id1508865 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1508865 ″]

[/ hidden-answer]

Практический тест

Является ли следующая упорядоченная пара решением системы уравнений?

с

[show-answer q = ”fs-id1435942 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1435942 ″]

Есть

[/ hidden-answer]

Для следующих упражнений решите системы линейных и нелинейных уравнений с помощью замены или исключения.Укажите, если решения не существует.

[show-answer q = ”fs-id1406246 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1406246 ″]

Решения отсутствуют.

[/ hidden-answer]

[show-answer q = ”fs-id1455840 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1455840 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1615810 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1615810 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1703248 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1703248 ″]

[/ hidden-answer]

Для следующих упражнений нарисуйте следующие неравенства.

[show-answer q = ”1380134 ″] Показать решение [/ show-answer] [hidden-answer a =” 1380134 ″] [/ hidden-answer]

Для следующих упражнений напишите разложение на частную дробь.

[show-answer q = ”fs-id1519238 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1519238 ″]

[/ hidden-answer]

Для следующих упражнений выполните указанные матричные операции.

[show-answer q = ”fs-id16 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id16 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1583988 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1583988 ″]

[/ hidden-answer]

[show-answer q = ”fs-id1295612 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1295612 ″]

[/ hidden-answer]

Если бы вы поменяли местами строки 1 и 3, умножили вторую строку на 12 и взяли обратное?

Перепишите систему линейных уравнений в виде расширенной матрицы.

[show-answer q = ”fs-id1456561 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1456561 ″]

[/ hidden-answer]

Перепишите расширенную матрицу как систему линейных уравнений.

В следующих упражнениях используйте метод исключения Гаусса для решения систем уравнений.

[show-answer q = ”fs-id1518911 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1518911 ″]

Решения отсутствуют.

[/ hidden-answer]

В следующих упражнениях используйте обратную матрицу для решения систем уравнений.

[show-answer q = ”fs-id1440484 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1440484 ″]

[/ hidden-answer]

В следующих упражнениях используйте правило Крамера для решения систем уравнений.

[show-answer q = ”fs-id1703905 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1703905 ″]

[/ hidden-answer]

Для следующих упражнений решите, используя систему линейных уравнений.

Завод, производящий сотовые телефоны, выполняет следующие функции затрат и доходов: и Какой диапазон сотовых телефонов они должны производить каждый день, чтобы получать прибыль? Округлите до ближайшего числа, приносящего прибыль.

[show-answer q = ”fs-id1598123 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1598123 ″]

32 и более сотовых телефона в день

[/ hidden-answer]

Небольшая ярмарка взимает 1,50 доллара для студентов, 1 доллар для детей и 2 доллара для взрослых.За один день пришло в три раза больше детей, чем взрослых. Было продано 800 билетов на общую выручку в 1050 долларов. Сколько билетов каждого типа было продано?

Глоссарий

Правило Крамера

метод решения систем уравнений, которые имеют то же количество уравнений, что и переменные, с использованием определителей

определитель

число, вычисленное с использованием элементов квадратной матрицы, которая определяет такую ​​информацию, как наличие решения системы уравнений

Решающие системы с правилом Крамера

Цели обучения

В этом разделе вы:

• Оцените детерминанты 2 × 2.
• Используйте правило Крамера для решения системы уравнений с двумя переменными.
• Оцените детерминанты 3 × 3.
• Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
• Знать свойства определителей.

Мы узнали, как решать системы уравнений с двумя переменными и тремя переменными с помощью нескольких методов: подстановки, сложения, исключения Гаусса, использования обратной матрицы и построения графиков. Некоторые из этих методов применять проще, чем другие, и они более подходят в определенных ситуациях.В этом разделе мы изучим еще две стратегии решения систем уравнений.

Вычисление определителя матрицы 2 × 2

Определитель – это действительное число, которое может быть очень полезно в математике, потому что у него есть несколько приложений, таких как вычисление площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы. Вычисление определителя матрицы требует следования определенным шаблонам, описанным в этом разделе.

Найдите определитель матрицы 2 × 2

Определитель матрицы [latex] \, 2 \ text {} × \ text {} 2 \, [/ latex], учитывая

[латекс] A = \ left [\ begin {array} {cc} a & b \\ c & d \ end {array} \ right] [/ latex]

определяется как

Обратите внимание на изменение обозначений.Есть несколько способов указать определитель, включая [latex] \, \ mathrm {det} \ left (A \ right) \, [/ latex] и замену скобок в матрице прямыми линиями, [latex] \, | A |. [/ Латекс]

Нахождение определителя матрицы 2 × 2

Найдите определитель заданной матрицы.

[латекс] A = \ left [\ begin {array} {cc} 5 & 2 \\ -6 & 3 \ end {array} \ right] [/ latex]

Показать решение

[латекс] \ begin {array} {l} \ mathrm {det} \ left (A \ right) = | \ begin {array} {cc} 5 & 2 \\ -6 & 3 \ end {array} | \ hfill \ \ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 5 \ left (3 \ right) – \ left (-6 \ right ) \ left (2 \ right) \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 27 \ hfill \ end {array} [/ latex]

Использование правила Крамера для решения системы двух уравнений с двумя переменными

Теперь мы представим последний метод решения систем уравнений, использующий определители.Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году во введении к анализу алгоритмов Курбских Альгебриков. Правило Крамера – это жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, что и неизвестных.

Правило Крамера даст нам единственное решение системы уравнений, если оно существует.Однако, если система не имеет решения или бесконечное количество решений, это будет обозначено нулевым определителем. Чтобы выяснить, является ли система непоследовательной или зависимой, необходимо использовать другой метод, например исключение.

Чтобы понять правило Крамера, давайте внимательно рассмотрим, как мы решаем системы линейных уравнений с использованием основных операций со строками. Рассмотрим систему двух уравнений с двумя переменными.

[латекс] \ begin {array} {c} {a} _ {1} x + {b} _ {1} y = {c} _ {1} \, \, \, \, \ left (1 \ right ) \\ {a} _ {2} x + {b} _ {2} y = {c} _ {2} \, \, \, \, \ left (2 \ right) \ end {array} [/ latex ]

Мы исключаем одну переменную, используя операции со строками, и решаем для другой.Скажем, мы хотим найти [латекс] \, x. \, [/ Latex] Если уравнение (2) умножить на коэффициент, противоположный [латексу] \, y \, [/ latex] в уравнении (1 ), уравнение (1) умножается на коэффициент [latex] \, y \, [/ latex] в уравнении (2), и мы складываем два уравнения, переменную [latex] \, y \, [/ latex ] будет исключен.

[латекс] \ begin {array} {l} \ underset {\ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _} {\ begin {array} {llll} \ hfill & \ hfill & \ hfill & \ hfill \\ \, \, \, \, {b} _ {2} {a} _ {1} x + {b} _ {2} {b} _ {1} y = {b} _ {2} {c} _ {1} \ hfill & \ hfill & \ hfill & \ text {Умножение} {R} _ {1} \ text {by} {b} _ {2} \ hfill \\ – {b} _ {1} {a } _ {2} x- {b} _ {1} {b} _ {2} y = – {b} _ {1} {c} _ {2} \ hfill & \ hfill & \ hfill & \ text { Умножить} {R} _ {2} \ text {by} – {b} _ {1} \ hfill \ end {array}} \ hfill \\ \, \, \, \ begin {array} {ll} {b } _ {2} {a} _ {1} x- {b} _ {1} {a} _ {2} x = {b} _ {2} {c} _ {1} – {b} _ { 1} {c} _ {2} \ hfill & \ hfill \ end {array} \ hfill \ end {array} [/ latex]

Теперь решите [латекс] \, x.[/ латекс]

[латекс] \ begin {array} {l} \, \, \, {b} _ {2} {a} _ {1} x- {b} _ {1} {a} _ {2} x = {b} _ {2} {c} _ {1} – {b} _ {1} {c} _ {2} \ hfill \\ \, \, \, x \ left ({b} _ {2} {a} _ {1} – {b} _ {1} {a} _ {2} \ right) = {b} _ {2} {c} _ {1} – {b} _ {1} {c } _ {2} \ hfill \\ \ text {} x = \ frac {{b} _ {2} {c} _ {1} – {b} _ {1} {c} _ {2}} {{ b} _ {2} {a} _ {1} – {b} _ {1} {a} _ {2}} = \ frac {\ left [\ begin {array} {cc} {c} _ {1 } & {b} _ {1} \\ {c} _ {2} & {b} _ {2} \ end {array} \ right]} {\ left [\ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end {array} \ right]} \ hfill \ end {array} [/ latex]

Аналогичным образом, чтобы решить для [latex] \, y, [/ latex], мы удалим [latex] \, x.[/ латекс]

[латекс] \ begin {array} {l} \ underset {\ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _} {\ begin {array} {llll} \ hfill & \ hfill & \ hfill & \ hfill \\ \, \, \, \, {a} _ {2} {a} _ {1} x + {a} _ {2} {b} _ {1} y = {a} _ {2} {c} _ {1} \ hfill & \ hfill & \ hfill & \ text {Умножение} {R} _ {1} \ text {by} {a} _ {2} \ hfill \\ – {a} _ {1} {a } _ {2} x- {a} _ {1} {b} _ {2} y = – {a} _ {1} {c} _ {2} \ hfill & \ hfill & \ hfill & \ text { Умножить} {R} _ {2} \ text {by} – {a} _ {1} \ hfill \ end {array}} \ hfill \\ \, \, \, \, \, \, \ begin {array } {ll} {a} _ {2} {b} _ {1} y- {a} _ {1} {b} _ {2} y = {a} _ {2} {c} _ {1} – {a} _ {1} {c} _ {2} \ hfill & \ hfill \ end {array} \ hfill \ end {array} [/ latex]

Решение для [latex] \, y \, [/ latex] дает

[латекс] \ begin {array} {l} {a} _ {2} {b} _ {1} y- {a} _ {1} {b} _ {2} y = {a} _ {2 } {c} _ {1} – {a} _ {1} {c} _ {2} \ hfill \\ y \ left ({a} _ {2} {b} _ {1} – {a} _ {1} {b} _ {2} \ right) = {a} _ {2} {c} _ {1} – {a} _ {1} {c} _ {2} \ hfill \\ \ text { } y = \ frac {{a} _ {2} {c} _ {1} – {a} _ {1} {c} _ {2}} {{a} _ {2} {b} _ {1 } – {a} _ {1} {b} _ {2}} = \ frac {{a} _ {1} {c} _ {2} – {a} _ {2} {c} _ {1} } {{a} _ {1} {b} _ {2} – {a} _ {2} {b} _ {1}} = \ frac {| \ begin {array} {cc} {a} _ { 1} & {c} _ {1} \\ {a} _ {2} & {c} _ {2} \ end {array} |} {| \ begin {array} {cc} {a} _ {1 } & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end {array} |} \ hfill \ end {array} [/ latex]

Обратите внимание, что знаменатель для [latex] \, x \, [/ latex] и [latex] \, y \, [/ latex] является определителем матрицы коэффициентов.

Мы можем использовать эти формулы для решения для [latex] \, x \, [/ latex] и [latex] \, y, \, [/ latex], но Правило Крамера также вводит новые обозначения:

Ключ к правилу Крамера заключается в замене интересующего столбца переменных столбцом констант и вычислении детерминантов. Затем мы можем выразить [латекс] \, x \, [/ latex] и [latex] \, y \, [/ latex] как частное двух определителей.

Правило Крамера для систем 2 × 2

Правило Крамера – это метод, который использует детерминанты для решения систем уравнений, которые имеют то же количество уравнений, что и переменные.

Рассмотрим систему двух линейных уравнений с двумя переменными.

[латекс] \ begin {array} {c} {a} _ {1} x + {b} _ {1} y = {c} _ {1} \\ {a} _ {2} x + {b} _ {2} y = {c} _ {2} \ end {array} [/ latex]

Решение, использующее правило Крамера, дается как

[латекс] x = \ frac {{D} _ {x}} {D} = \ frac {| \ begin {array} {cc} {c} _ {1} & {b} _ {1} \\ {c} _ {2} & {b} _ {2} \ end {array} |} {| \ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ { a} _ {2} & {b} _ {2} \ end {array} |}, \, \, D \ ne 0; \, \, \ text {} \ text {} \, y = \ гидроразрыв {{D} _ {y}} {D} = \ frac {| \ begin {array} {cc} {a} _ {1} & {c} _ {1} \\ {a} _ {2} & {c} _ {2} \ end {array} |} {| \ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end {array} |}, \, \, D \ ne 0.[/ латекс]

Если мы решаем для [latex] \, x, \, [/ latex], столбец [latex] \, x \, [/ latex] заменяется столбцом констант. Если мы решаем для [latex] \, y, \, [/ latex], столбец [latex] \, y \, [/ latex] заменяется постоянным столбцом.

Использование правила Крамера для решения системы 2 × 2

Решите следующую систему [latex] \, 2 \ text {} × \ text {} 2 \, [/ latex], используя правило Крамера.

[латекс] \ begin {array} {c} 12x + 3y = 15 \\ \ text {} 2x-3y = 13 \ end {array} [/ latex]

Показать решение

Решите относительно [латекс] \, x.[/ латекс]

[латекс] x = \ frac {{D} _ {x}} {D} = \ frac {| \ begin {array} {rr} \ hfill 15 & \ hfill 3 \\ \ hfill 13 & \ hfill -3 \ end {array} |} {| \ begin {array} {rr} \ hfill 12 & \ hfill 3 \\ \ hfill 2 & \ hfill -3 \ end {array} |} = \ frac {-45-39} {- 36- 6} = \ frac {-84} {- 42} = 2 [/ latex]

Найдите [латекс] \, y. [/ Latex]

[латекс] y = \ frac {{D} _ {y}} {D} = \ frac {| \ begin {array} {rr} \ hfill 12 & \ hfill 15 \\ \ hfill 2 & \ hfill 13 \ end { array} |} {| \ begin {array} {rr} \ hfill 12 & \ hfill 3 \\ \ hfill 2 & \ hfill -3 \ end {array} |} = \ frac {156-30} {- 36-6} = – \ frac {126} {42} = – 3 [/ латекс]

Решение: [латекс] \, \ left (2, -3 \ right).[/ латекс]

Попробуйте

Используйте правило Крамера для решения системы уравнений 2 × 2.

[латекс] \ begin {массив} {l} \ text {} x + 2y = -11 \ hfill \\ -2x + y = -13 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (3, -7 \ вправо) [/ латекс]

Вычисление определителя матрицы 3 × 3

Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее. Один из способов – увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5.Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведение записей на по каждой из трех диагоналей (нижний левый верхний правый). Это легче понять с помощью наглядного пособия и примера.

Найдите определитель матрицы 3 × 3.

[латекс] A = \ left [\ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \\ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ end {array} \ right] [/ латекс]

1. Дополните [latex] \, A \, [/ latex] первыми двумя столбцами.

   [латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \ \ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ конец {массив} \, \, \, | \, \, \, \ begin {array} {c} {a} _ {1} \\ {a} _ {2} \\ {a} _ {3} \ end {array} \, \, \, \, \ begin {array} {c} {b} _ {1} \\ {b} _ {2} \\ {b} _ {3} \ end {массив } | [/ латекс]

2. Слева вверху направо вниз: умножение значений по первой диагонали. Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
3. От левого нижнего угла до правого верхнего: вычтите произведение значений по первой диагонали. Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.

Алгебра выглядит следующим образом:

[латекс] | A | = {a} _ {1} {b} _ {2} {c} _ {3} + {b} _ {1} {c} _ {2} {a} _ {3 } + {c} _ {1} {a} _ {2} {b} _ {3} – {a} _ {3} {b} _ {2} {c} _ {1} – {b} _ {3} {c} _ {2} {a} _ {1} – {c} _ {3} {a} _ {2} {b} _ {1} [/ latex]

Нахождение определителя матрицы 3 × 3

Найдите определитель матрицы 3 × 3 для данного

[латекс] A = \ left [\ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} \ right] [/ latex]

Показать решение

Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,

[латекс] \ begin {array} {l} | A | = | \ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} \, \, | \ begin {array} {c} 0 \\ 3 \\ \, \, 4 \ end {array} \, \, \, \, \ begin {array} {c} 2 \\ -1 \\ 0 \ end { массив} | \ hfill \\ \, \, \, \, \, \, \, = 0 \ left (-1 \ right) \ left (1 \ right) +2 \ left (1 \ right) \ left ( 4 \ вправо) +1 \ влево (3 \ вправо) \ влево (0 \ вправо) -4 \ влево (-1 \ вправо) \ влево (1 \ вправо) -0 \ влево (1 \ вправо) \ влево (0 \ вправо) -1 \ влево (3 \ вправо) \ влево (2 \ вправо) \ hfill \\ \, \, \, \, \, \, \, = 0 + 8 + 0 + 4-0-6 \ hfill \\ \, \, \, \, \, \, \, = 6 \ hfill \ end {array} [/ latex]

Попробуйте

Найдите определитель матрицы 3 × 3.

[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} 1 & -3 & 7 \\ 1 & 1 & 1 \\ 1 & -2 & 3 \ end {array} | [/ latex ]

Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?

Нет, этот метод работает только для [latex] \, 2 \ text {} × \ text {} 2 \, [/ latex] и [latex] \, \ text {3} \ text {} × \ text { } 3 \, [/ латексные] матрицы. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными.Правило Крамера простое и следует шаблону, соответствующему правилу Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.

Когда мы вычисляем детерминант, равный нулю, правило Крамера не дает никаких указаний на то, что у системы нет решения или бесконечное количество решений. Чтобы выяснить это, мы должны выполнить устранение в системе.

Рассмотрим систему уравнений 3 × 3.

[латекс] x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}, z = \ frac {{D} _ {z} } {D}, D \ ne 0 [/ латекс]

где

Если мы записываем определитель [latex] \, {D} _ {x}, [/ latex], мы заменяем столбец [latex] \, x \, [/ latex] на столбец констант.Если мы пишем определитель [latex] {D} _ {y}, [/ latex], мы заменяем столбец [latex] \, y \, [/ latex] на постоянный столбец. Если мы пишем определитель [latex] \, {D} _ {z}, [/ latex], мы заменяем столбец [latex] \, z \, [/ latex] постоянным столбцом. Всегда проверяйте ответ.

Решение системы 3 × 3 с использованием правила Крамера

Найдите решение данной системы 3 × 3, используя правило Крамера.

[латекс] \ begin {array} {c} x + y-z = 6 \\ 3x-2y + z = -5 \\ x + 3y-2z = 14 \ end {array} [/ latex]

Показать решение

Используйте правило Крамера.

[латекс] D = | \ begin {array} {ccc} 1 & \, \, 1 & -1 \\ 3 & -2 & \, \, \, 1 \\ 1 & \, \, 3 & -2 \ end {array} |, {D} _ {x} = | \ begin {array} {ccc} 6 & 1 & -1 \\ -5 & -2 & \, \, \, 1 \\ 14 & \, \, 3 & -2 \ end {массив } |, {D} _ {y} = | \ begin {array} {ccc} 1 & \, 6 & -1 \\ 3 & -5 & \, \, 1 \\ 1 & 14 & -2 \ end {array} |, { D} _ {z} = | \ begin {array} {ccc} 1 & \, 1 & 6 \\ 3 & -2 & -5 \\ 1 & \, \, 3 & 14 \ end {array} | [/ latex]

Затем,

[латекс] \ begin {array} {l} x = \ frac {{D} _ {x}} {D} = \ frac {-3} {- 3} = 1 \ hfill \\ y = \ frac { {D} _ {y}} {D} = \ frac {-9} {- 3} = 3 \ hfill \\ z = \ frac {{D} _ {z}} {D} = \ frac {6} {-3} = – 2 \ hfill \ end {array} [/ latex]

Решение [латекс] \ left (1,3, -2 \ right).[/ латекс]

Попробуйте

Используйте правило Крамера, чтобы решить матрицу 3 × 3.

[латекс] \ begin {array} {r} \ hfill x-3y + 7z = 13 \\ \ hfill x + y + z = 1 \, \, \, \\ \ hfill x-2y + 3z = 4 \ , \, \, \ end {array} [/ latex]

Показать решение

[латекс] \ left (-2, \ frac {3} {5}, \ frac {12} {5} \ right) [/ latex]

Использование правила Крамера для решения несовместимой системы

Решите систему уравнений, используя правило Крамера.

[латекс] \ begin {array} {l} 3x-2y = 4 \ text {} \ left (1 \ right) \\ 6x-4y = 0 \ text {} \ left (2 \ right) \ end {массив } [/ латекс]

Показать решение

Начнем с нахождения определителей [латекс] \, D, {D} _ {x}, \ text {и} {D} _ {y}.[/ латекс]

[латекс] D = | \ begin {array} {cc} 3 & -2 \\ 6 & -4 \ end {array} | = 3 \ left (-4 \ right) -6 \ left (-2 \ right) = 0 [/ латекс]

Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное число решений. Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель – исключить одну из переменных.

1. Умножить уравнение (1) на [латекс] \, – 2. [/ Latex]
2. Добавьте результат в уравнение [латекс] \, \ left (2 \ right). [/ Latex]

[латекс] \ begin {array} {l} \ underset {\ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _} {\ begin {массив} {l} \ begin {array} {l} \ hfill \\ -6x + 4y \, \, \, \, = – 8 \ hfill \ end {array} \ hfill \\ \, \, \, 6x-4y \, \, \, \, \, \, = \, \, \, \, 0 \ hfill \ end {array}} \ hfill \\ \, \, \, \, \, \, \ , \, \, \, \, \, \, \, \, \, \, \, \, 0 \, \, \, \, \, \, = \, – 8 \ hfill \ end {array} [/ латекс]

Мы получаем уравнение [латекс] \, 0 = -8, \, [/ латекс], которое неверно.Следовательно, у системы нет решения. График системы показывает две параллельные линии. См. (Рисунок).

Рисунок 1.

Используйте правило Крамера для решения зависимой системы

Решите систему с бесконечным количеством решений.

[латекс] \ begin {array} {rr} \ hfill x-2y + 3z = 0 & \ hfill \ left (1 \ right) \\ \ hfill 3x + y-2z = 0 & \ hfill \ left (2 \ right) \\ \ hfill 2x-4y + 6z = 0 & \ hfill \ left (3 \ right) \ end {array} [/ latex]

Показать решение

Давайте сначала найдем определитель.Создайте матрицу, дополненную первыми двумя столбцами.

[латекс] | \ begin {array} {rrr} \ hfill 1 & \ hfill -2 & \ hfill 3 \\ \ hfill 3 & \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -4 & \ hfill 6 \ end { array} \ text {} | \ text {} \ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 3 & \ hfill 1 \\ \ hfill 2 & \ hfill -4 \ end {array} | [ / латекс]

Затем,

[латекс] 1 \ влево (1 \ вправо) \ влево (6 \ вправо) + \ влево (-2 \ вправо) \ влево (-2 \ вправо) \ влево (2 \ вправо) +3 \ влево (3 \ вправо) \ влево (-4 \ вправо) -2 \ влево (1 \ вправо) \ влево (3 \ вправо) – \ влево (-4 \ вправо) \ влево (-2 \ вправо) \ влево (1 \ вправо) -6 \ влево (3 \ вправо) \ влево (-2 \ вправо) = 0 [/ латекс]

Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное количество решений.Чтобы выяснить это, нам нужно провести отбор.

1. Умножьте уравнение (1) на [latex] \, – 2 \, [/ latex] и добавьте результат к уравнению (3):

   [латекс] \ frac {\ begin {array} {r} \ hfill -2x + 4y-6x = 0 \\ \ hfill 2x-4y + 6z = 0 \ end {array}} {\, \, \, \ , \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, 0 = 0} [/ латекс]

2. Получение ответа [latex] \, 0 = 0, \, [/ latex] утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений. Изобразив систему, мы можем увидеть, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.См. (Рисунок).

   Рисунок 2.

Понимание свойств детерминантов

Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.

Свойства детерминантов

1. Если матрица имеет верхнюю треугольную форму, определитель равен произведению элементов по главной диагонали.
2. Когда две строки меняются местами, определитель меняет знак.{-1} \, [/ latex] – обратная величина определителю матрицы [latex] \, A. [/ Latex]
3. Если любая строка или столбец умножается на константу, определитель умножается на тот же коэффициент.

Иллюстрируя свойства детерминантов

Проиллюстрируйте каждое из свойств определителей.

Показать решение

Свойство 1 утверждает, что если матрица имеет верхнюю треугольную форму, определитель является произведением элементов по главной диагонали.

[латекс] A = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill \, \, 2 & \ hfill 3 \\ \ hfill 0 & \ hfill \, \, 2 & \ hfill 1 \\ \ hfill 0 & \ hfill \, \, 0 & \ hfill -1 \ end {array} \ right] [/ latex]

Дополните [латекс] \, A \, [/ latex] первыми двумя столбцами.

[латекс] A = \ left [\ begin {array} {ccc} 1 & 2 & 3 \\ 0 & 2 & 1 \\ 0 & 0 & -1 \ end {array} | \, \, \, \ begin {array} {c } 1 \\ 0 \\ 0 \ end {массив} \, \, \, \, \ begin {array} {c} 2 \\ 2 \\ 0 \ end {array} \ right] [/ latex]

Затем

[латекс] \ begin {array} {l} \ mathrm {det} \ left (A \ right) = 1 \ left (2 \ right) \ left (-1 \ right) +2 \ left (1 \ right) \ влево (0 \ вправо) +3 \ влево (0 \ вправо) \ влево (0 \ вправо) -0 \ влево (2 \ вправо) \ влево (3 \ вправо) -0 \ влево (1 \ вправо) \ влево (1 \ вправо) +1 \ влево (0 \ вправо) \ влево (2 \ вправо) \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, \, = – 2 \ hfill \ end {array} [/ latex]

Свойство 2 утверждает, что перестановка строк меняет знак.Учитывая

[латекс] \ begin {массив} {l} \ begin {array} {l} \\ A = \ left [\ begin {array} {cc} -1 & 5 \\ 4 & -3 \ end {array} \ right ], \, \, \ mathrm {det} \ left (A \ right) = \ left (-1 \ right) \ left (-3 \ right) – \ left (4 \ right) \ left (5 \ right) = 3-20 = -17 \ end {массив} \ hfill \\ \ hfill \\ B = \ left [\ begin {array} {cc} 4 & -3 \\ -1 & 5 \ end {array} \ right], \, \, \ mathrm {det} \ left (B \ right) = \ left (4 \ right) \ left (5 \ right) – \ left (-1 \ right) \ left (-3 \ right) = 20 -3 = 17 \ hfill \ end {array} [/ latex]

Свойство 3 утверждает, что если две строки или два столбца идентичны, определитель равен нулю.

[латекс] \ begin {массив} {l} \, \, \, \, \, \, \, \, \, \, \, A = \ left [\ begin {array} {ccc} 1 & 2 & 2 \\ 2 & 2 & 2 \\ -1 & 2 & 2 \ end {array} \ text {} | \ text {} \ begin {array} {c} 1 \\ 2 \\ -1 \ end {array} \ begin {array } {c} 2 \\ 2 \\ 2 \ end {array} \ right] \ hfill \\ \ hfill \\ \ mathrm {det} \ left (A \ right) = 1 \ left (2 \ right) \ left (2 \ вправо) +2 \ влево (2 \ вправо) \ влево (-1 \ вправо) +2 \ влево (2 \ вправо) \ влево (2 \ вправо) +1 \ влево (2 \ вправо) \ влево ( 2 \ вправо) -2 \ влево (2 \ вправо) \ влево (1 \ вправо) -2 \ влево (2 \ вправо) \ влево (2 \ вправо) \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 4-4 + 8 + 4-4-8 = 0 \ hfill \ end {array} [/ latex]

Свойство 4 утверждает, что если строка или столбец равны нулю, определитель равен нулю.{-1} \ right) = – 2 \ left (- \ frac {1} {2} \ right) – \ left (\ frac {3} {2} \ right) \ left (1 \ right) = – \ гидроразрыв {1} {2} \ hfill \ end {array} [/ latex]

Свойство 6 утверждает, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,

[латекс] \ begin {array} {l} A = \ left [\ begin {array} {cc} 1 & 2 \\ 3 & 4 \ end {array} \ right], \ mathrm {det} \ left (A \ right) = 1 \ left (4 \ right) -2 \ left (3 \ right) = – 2 \ hfill \\ \ hfill \\ B = \ left [\ begin {array} {cc} 2 \ left (1 \ right) & 2 \ left (2 \ right) \\ 3 & 4 \ end {array} \ right], \ mathrm {det} \ left (B \ right) = 2 \ left (4 \ right) -3 \ left ( 4 \ right) = – 4 \ hfill \ end {array} [/ latex]

Использование правила Крамера и определяющих свойств для решения системы

Найдите решение данной системы 3 × 3.

[латекс] \ begin {array} {ll} 2x + 4y + 4z = 2 \ hfill & \ left (1 \ right) \ hfill \\ 3x + 7y + 7z = -5 \ hfill & \ left (2 \ right ) \ hfill \\ \ text {} x + 2y + 2z = 4 \ hfill & \ left (3 \ right) \ hfill \ end {array} [/ latex]

Показать решение

Используя правило Крамера, имеем

[латекс] D = | \ begin {array} {ccc} 2 & 4 & 4 \\ 3 & 7 & 7 \\ 1 & 2 & 2 \ end {array} | [/ latex]

Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо существует бесконечное число решений.Чтобы выяснить это, нам нужно провести отбор.

1. Умножьте уравнение (3) на –2 и прибавьте результат к уравнению (1).

   [латекс] \ frac {\ begin {array} {l} -2x-4y-4x = -8 \ hfill \\ \ text {} 2x + 4y + 4z = 2 \, \, \, \, \, \ hfill \ end {array}} {\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 0 = -6} [/ латекс]

Получение противоречивого утверждения означает, что система не имеет решения.

Ключевые концепции

• Определитель для [latex] \, \ left [\ begin {array} {cc} a & b \\ c & d \ end {array} \ right] \, [/ latex] – [latex] \, ad-bc .\, [/ latex] См. (рисунок).
• Правило Крамера заменяет переменный столбец постоянным столбцом. Решениями являются [latex] \, x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}. \, [/ Latex] См. (Рисунок ).
• Чтобы найти определитель матрицы 3 × 3, дополните ее двумя первыми столбцами. Сложите три диагональных записи (верхний левый нижний правый) и вычтите три диагональных входа (нижний левый верхний правый). См. (Рисунок).
• Чтобы решить систему трех уравнений с тремя переменными с помощью правила Крамера, замените столбец переменных столбцом констант для каждого желаемого решения: [latex] \, x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}, z = \ frac {{D} _ {z}} {D}.\, [/ latex] См. (рисунок).
• Правило Крамера также полезно для поиска решения системы уравнений без решения или с бесконечными решениями. См. (Рисунок) и (Рисунок).
• Некоторые свойства определителей полезны для решения задач. Например:
  • Если матрица имеет верхнюю треугольную форму, определитель равен произведению элементов по главной диагонали.
  • Когда две строки меняются местами, определитель меняет знак.
  • Если две строки или два столбца идентичны, определитель равен нулю.{-1} \, [/ latex] – обратная величина определителю матрицы [latex] \, A. [/ Latex]
  • Если любая строка или столбец умножается на константу, определитель умножается на тот же коэффициент. См. (Рисунок) и (Рисунок).

Упражнения по разделам

Устный

Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.

Показать решение

Определитель – это сумма и произведения элементов матрицы, поэтому вы всегда можете оценить этот продукт, даже если в конечном итоге он окажется равным нулю.

Исследуя правило Крамера, объясните, почему не существует единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте матрицу [latex] \, 2 \, × \, 2 \, [/ latex].

Объясните, что в терминах обратного значения для матрицы означает наличие определителя 0.

Показать решение

Обратного не существует.

Определитель [latex] \, 2 \, × \, 2 \, [/ latex] matrix [latex] \, A \, [/ latex] равен 3. Если вы поменяете строки и умножите первую строку на 6 а во второй строке – 2, объясните, как найти определитель и дать ответ.

Алгебраические

Найдите определитель для следующих упражнений.

[латекс] | \ begin {array} {cc} 1 & 2 \\ 3 & 4 \ end {array} | [/ latex]

[латекс] | \ begin {массив} {rr} \ hfill -1 & \ hfill 2 \\ \ hfill 3 & \ hfill -4 \ end {array} | [/ latex]

[латекс] | \ begin {массив} {rr} \ hfill 2 & \ hfill -5 \\ \ hfill -1 & \ hfill 6 \ end {array} | [/ latex]

[латекс] | \ begin {array} {cc} -8 & 4 \\ -1 & 5 \ end {array} | [/ latex]

[латекс] | \ begin {массив} {rr} \ hfill 1 & \ hfill 0 \\ \ hfill 3 & \ hfill -4 \ end {array} | [/ latex]

[латекс] | \ begin {массив} {rr} \ hfill 10 & \ hfill 20 \\ \ hfill 0 & \ hfill -10 \ end {array} | [/ latex]

[латекс] | \ begin {array} {cc} 10 & 0.2 \\ 5 & 0,1 \ end {array} | [/ latex]

[латекс] | \ begin {массив} {rr} \ hfill 6 & \ hfill -3 \\ \ hfill 8 & \ hfill 4 \ end {array} | [/ latex]

[латекс] | \ begin {array} {rr} \ hfill -2 & \ hfill -3 \\ \ hfill 3.1 & \ hfill 4,000 \ end {array} | [/ latex]

[латекс] | \ begin {array} {rr} \ hfill -1.1 & \ hfill 0.6 \\ \ hfill 7.2 & \ hfill -0.5 \ end {array} | [/ latex]

[латекс] | \ begin {array} {rrr} \ hfill -1 & \ hfill 0 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 0 & \ hfill -3 \ end {массив } | [/ латекс]

[латекс] | \ begin {array} {rrr} \ hfill -1 & \ hfill 4 & \ hfill 0 \\ \ hfill 0 & \ hfill 2 & \ hfill 3 \\ \ hfill 0 & \ hfill 0 & \ hfill -3 \ end {массив } | [/ латекс]

[латекс] | \ begin {array} {ccc} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \ end {array} | [/ latex]

[латекс] | \ begin {array} {rrr} \ hfill 2 & \ hfill -3 & \ hfill 1 \\ \ hfill 3 & \ hfill -4 & \ hfill 1 \\ \ hfill -5 & \ hfill 6 & \ hfill 1 \ end { массив} | [/ латекс]

[латекс] | \ begin {array} {rrr} \ hfill -2 & \ hfill 1 & \ hfill 4 \\ \ hfill -4 & \ hfill 2 & \ hfill -8 \\ \ hfill 2 & \ hfill -8 & \ hfill -3 \ конец {массив} | [/ латекс]

[латекс] | \ begin {array} {rrr} \ hfill 6 & \ hfill -1 & \ hfill 2 \\ \ hfill -4 & \ hfill -3 & \ hfill 5 \\ \ hfill 1 & \ hfill 9 & \ hfill -1 \ end {array} | [/ латекс]

[латекс] | \ begin {array} {rrr} \ hfill 5 & \ hfill 1 & \ hfill -1 \\ \ hfill 2 & \ hfill 3 & \ hfill 1 \\ \ hfill 3 & \ hfill -6 & \ hfill -3 \ end { массив} | [/ латекс]

[латекс] | \ begin {array} {rrr} \ hfill 1.1 & \ hfill 2 & \ hfill -1 \\ \ hfill -4 & \ hfill 0 & \ hfill 0 \\ \ hfill 4.1 & \ hfill -0.4 & \ hfill 2.5 \ end {array} | [/ latex]

[латекс] | \ begin {array} {rrr} \ hfill 2 & \ hfill -1.6 & \ hfill 3.1 \\ \ hfill 1.1 & \ hfill 3 & \ hfill -8 \\ \ hfill -9.3 & \ hfill 0 & \ hfill 2 \ end {array} | [/ latex]

[латекс] | \ begin {array} {ccc} – \ frac {1} {2} & \ frac {1} {3} & \ frac {1} {4} \\ \ frac {1} {5} & – \ frac {1} {6} & \ frac {1} {7} \\ 0 & 0 & \ frac {1} {8} \ end {array} | [/ latex]

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

[латекс] \ begin {array} {l} 2x-3y = -1 \\ 4x + 5y = 9 \ end {array} [/ latex]

Показать решение

[латекс] \ левый (1,1 \ правый) [/ латекс]

[латекс] \ begin {array} {r} 5x-4y = 2 \\ -4x + 7y = 6 \ end {array} [/ latex]

[латекс] \ begin {массив} {l} \ text {} 6x-3y = 2 \, \, \, \, \, \ hfill \\ -8x + 9y = -1 \ hfill \ end {array} [ / латекс]

Показать решение

[латекс] \ left (\ frac {1} {2}, \ frac {1} {3} \ right) [/ latex]

[латекс] \ begin {array} {l} 2x + 6y = 12 \\ 5x-2y = 13 \ end {array} [/ latex]

[латекс] \ begin {array} {l} 4x + 3y = 23 \, \, \ hfill \\ \ text {} 2x-y = -1 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ левый (2,5 \ правый) [/ латекс]

[латекс] \ begin {array} {l} 10x-6y = 2 \, \, \, \, \ hfill \\ -5x + 8y = -1 \ hfill \ end {array} [/ latex]

[латекс] \ begin {array} {l} 4x-3y = -3 \\ 2x + 6y = -4 \ end {array} [/ latex]

Показать решение

[латекс] \ left (-1, – \ frac {1} {3} \ right) [/ latex]

[латекс] \ begin {array} {r} 4x-5y = 7 \\ -3x + 9y = 0 \ end {array} [/ latex]

[латекс] \ begin {array} {l} 4x + 10y = 180 \, \, \, \, \ hfill \\ -3x-5y = -105 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (15,12 \ вправо) [/ латекс]

[латекс] \ begin {массив} {l} \ text {} 8x-2y = -3 \ hfill \\ -4x + 6y = 4 \, \, \, \, \ hfill \ end {array} [/ latex ]

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

[латекс] \ begin {массив} {l} \ text {} x + 2y-4z = -1 \ hfill \\ \ text {} 7x + 3y + 5z = 26 \, \, \ hfill \\ -2x- 6y + 7z = -6 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ левый (1,3,2 \ правый) [/ латекс]

[латекс] \ begin {array} {l} -5x + 2y-4z = -47 \ hfill \\ \ text {} 4x-3y-z = -94 \ hfill \\ \ text {} 3x-3y + 2z = 94 \, \, \, \, \ hfill \ end {array} [/ latex]

[латекс] \ begin {массив} {l} \ text {} 4x + 5y-z = -7 \ hfill \\ -2x-9y + 2z = 8 \, \, \, \, \ hfill \\ \ text {} 5y + 7z = 21 \, \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (-1,0,3 \ вправо) [/ латекс]

[латекс] \ begin {array} {r} 4x-3y + 4z = 10 \\ 5x-2z = -2 \\ 3x + 2y-5z = -9 \ end {array} [/ latex]

[латекс] \ begin {array} {l} 4x-2y + 3z = 6 \, \, \, \ hfill \\ \ text {} -6x + y = -2 \ hfill \\ 2x + 7y + 8z = 24 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (\ frac {1} {2}, 1,2 \ вправо) [/ латекс]

[латекс] \ begin {array} {r} \ hfill 5x + 2y-z = 1 \, \, \, \, \, \\ \ hfill -7x-8y + 3z = 1.5 \\ \ hfill 6x-12y + z = 7 \, \, \, \, \ end {array} [/ latex]

[латекс] \ begin {array} {l} \ text {} 13x-17y + 16z = 73 \, \, \, \, \ hfill \\ -11x + 15y + 17z = 61 \, \, \, \ , \ hfill \\ \ text {} 46x + 10y-30z = -18 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (2,1,4 \ вправо) [/ латекс]

[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ -4x-3y-8z = -7 \ hfill \ end {array} \ hfill \\ \ text {} 2x- 9y + 5z = 0,5 \ hfill \\ \ text {} 5x-6y-5z = -2 \ hfill \ end {array} [/ latex]

[латекс] \ begin {array} {l} \ text {} 4x-6y + 8z = 10 \, \, \ hfill \\ -2x + 3y-4z = -5 \ hfill \\ \ text {} x + y + z = 1 \, \, \, \, \, \ hfill \ end {array} [/ latex]

[латекс] \ begin {array} {r} \ hfill 4x-6y + 8z = 10 \, \, \, \, \, \\ \ hfill -2x + 3y-4z = -5 \, \, \, \\ \ hfill 12x + 18y-24z = -30 \ end {array} [/ latex]

Технологии

Для следующих упражнений используйте детерминантную функцию в графической утилите.

[латекс] | \ begin {array} {rrrr} \ hfill 1 & \ hfill 0 & \ hfill 8 & \ hfill 9 \\ \ hfill 0 & \ hfill 2 & \ hfill 1 & \ hfill 0 \\ \ hfill 1 & \ hfill 0 & \ hfill 3 & \ hfill 0 \\ \ hfill 0 & \ hfill 2 & \ hfill 4 & \ hfill 3 \ end {array} | [/ latex]

[латекс] | \ begin {array} {rrrr} \ hfill 1 & \ hfill 0 & \ hfill 2 & \ hfill 1 \\ \ hfill 0 & \ hfill -9 & \ hfill 1 & \ hfill 3 \\ \ hfill 3 & \ hfill 0 & \ hfill -2 & \ hfill -1 \\ \ hfill 0 & \ hfill 1 & \ hfill 1 & \ hfill -2 \ end {array} | [/ latex]

[латекс] | \ begin {array} {rrrr} \ hfill \ frac {1} {2} & \ hfill 1 & \ hfill 7 & \ hfill 4 \\ \ hfill 0 & \ hfill \ frac {1} {2} & \ hfill 100 & \ hfill 5 \\ \ hfill 0 & \ hfill 0 & \ hfill 2 & \ hfill 2,000 \\ \ hfill 0 & \ hfill 0 & \ hfill 0 & \ hfill 2 \ end {array} | [/ latex]

[латекс] | \ begin {array} {rrrr} \ hfill 1 & \ hfill 0 & \ hfill 0 & \ hfill 0 \\ \ hfill 2 & \ hfill 3 & \ hfill 0 & \ hfill 0 \\ \ hfill 4 & \ hfill 5 & \ hfill 6 & \ hfill 0 \\ \ hfill 7 & \ hfill 8 & \ hfill 9 & \ hfill 0 \ end {array} | [/ latex]

Реальные приложения

Для следующих упражнений создайте систему линейных уравнений для описания поведения.Затем вычислите определитель. Будет ли уникальное решение? Если да, найдите уникальное решение.

Два числа в сумме дают 56. Одно число на 20 меньше другого.

Два числа в сумме дают 104. Если вы сложите два раза первое число плюс два раза второе число, ваша сумма составит 208

Три числа в сумме дают 106. Первое число на 3 меньше второго. Третье число на 4 больше, чем первое.

Три числа добавляют к 216.Сумма первых двух чисел равна 112. Третье число на 8 меньше, чем первые два числа вместе взятые.

Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем решите систему для всех решений, используя правило Крамера.

Вы вкладываете 10 000 долларов в два счета, которые получают 8% годовых и 5% годовых. В конце года на ваших комбинированных счетах было 10 710 долларов. Сколько было вложено в каждую учетную запись?

Показать решение

7000 долларов на первом счете, 3000 долларов на втором счете.

Вы вкладываете 80 000 долларов в два счета, 22 000 долларов в один счет и 58 000 долларов в другой. В конце года, если исходить из простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Какие процентные ставки по вашим счетам?

Кинотеатру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов. Если детские билеты 5 долларов.95, билеты для взрослых стоят 11,15 долларов, а общая сумма выручки составила 12 756 долларов. Сколько билетов для детей и взрослых было продано?

Показать решение

120 детей, 1080 взрослых

Концертная площадка продает одиночные билеты по 40 долларов каждый и билеты для пар по 65 долларов. Если общий доход составил 18 090 долларов и был продан 321 билет, сколько разовых билетов и сколько билетов для пар было продано?

Вы решили покрасить свою кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски.Вы не можете вспомнить, сколько галлонов каждого цвета было добавлено в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию ​​и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь?

Вы продали на фермерском рынке шарфы двух типов и хотите знать, какой из них пользуется большей популярностью. Всего было продано 56 шарфов, желтый платок стоил 10 долларов, а фиолетовый – 11 долларов.Если ваш общий доход составил 583 доллара, сколько желтых и фиолетовых шарфов было продано?

В вашем саду выращивали два вида помидоров: зеленый и красный. Красный весит 10 унций, а зеленый – 4 унции. У вас 30 помидоров, а общий вес составляет 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?

Показать решение

13 зеленых помидоров, 17 красных помидоров

На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, у которой на 5% больше продаж, чем у лука.Какую долю занимает каждый овощ на рынке?

На этом же рынке три самых популярных фрукта составляют 37% от общего количества проданных фруктов. Клубника продается вдвое больше, чем апельсины, а киви продаются на один процентный пункт больше, чем апельсины. Для каждого фрукта найдите процент от общего количества проданных фруктов.

Показать решение

Клубника 18%, апельсины 9%, киви 10%

Три ансамбля выступили на концертной площадке. Первый диапазон взимал 15 долларов за билет, второй диапазон – 45 долларов за билет, а последний диапазон – 22 доллара за билет.Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй, сколько билетов было продано каждой группе?

В кинотеатре продаются билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм – 11 долларов, а третий фильм – 12 долларов. На первый фильм было продано 100 билетов. Всего было продано 642 билета, общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?

Показать решение

100 для фильма 1, 230 для фильма 2, 312 для фильма 3

Мужчины в возрасте 20–29, 30–39 и 40–49 лет в прошлом году составляли 78% заключенных.В этом году эти же возрастные группы составили 82,08% населения. Возрастная группа 20–29 лет увеличилась на 20%, возрастная группа 30–39 лет увеличилась на 2%, а возрастная группа 40–49 лет уменьшилась до [latex] \, \ frac {3} {4} \, [/ latex] их предыдущего населения. Первоначально в возрастной группе 30–39 лет было на 2% больше заключенных, чем в возрастной группе 20–29 лет. Определите процентную долю заключенных для каждой возрастной группы в прошлом году.

В женской тюрьме по дороге общее количество заключенных в возрасте от 20 до 49 лет составило 5 525 человек. В этом году возрастная группа 20–29 лет увеличилась на 10%, возрастная группа 30–39 лет уменьшилась на 20%, а возрастная группа 40–49 лет увеличилась вдвое.Сейчас в тюрьме 6040 заключенных. Первоначально в возрастной группе 30–39 лет их было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы за прошлый год.

Показать решение

20–29: 2,100, 30–39: 2,600, 40–49: 825

Для следующих упражнений используйте этот сценарий: Компания, заботящаяся о своем здоровье, решает сделать смесь из миндаля, сушеной клюквы и кешью в шоколаде. Информация о питательной ценности этих продуктов показана на (Рисунок).

	Жир (г)	Белок (г)	Углеводы (г)
Миндаль (10)	6	2	3
Клюква (10)	0.02	0	8
Кешью (10)	7	3,5	5,5

Для специальной «низкоуглеводной» смеси для трейлов имеется 1000 штук смеси. Общее количество углеводов – 425 г, а общее количество жиров – 570,2 г. Если кешью на 200 штук больше, чем клюквы, сколько каждого из них входит в состав смеси?

Для «походной» смеси в смеси 1000 штук, содержащих 390 штук.8 г жира и 165 г белка. Если количество миндаля такое же, как и в кешью, сколько каждого из них входит в состав смеси?

Показать решение

300 миндальных орехов, 400 клюквы, 300 кешью

Для смеси «усилитель энергии» в смеси 1000 штук, содержащих 145 г белка и 625 г углеводов. Если сумма миндальных орехов и кешью эквивалентна количеству клюквы, сколько каждого из них входит в состав смеси?

Упражнения на повторение

Системы линейных уравнений: две переменные

Для следующих упражнений определите, является ли упорядоченная пара решением системы уравнений.

[латекс] \ begin {array} {l} 3x-y = 4 \\ x + 4y = -3 \, \ end {array} [/ latex] and [latex] \, \ left (-1,1 \ справа) [/ латекс]

[латекс] \ begin {array} {l} 6x-2y = 24 \\ -3x + 3y = 18 \, \ end {array} [/ latex] and [latex] \, \ left (9,15 \ right ) [/ латекс]

В следующих упражнениях используйте подстановку для решения системы уравнений.

[латекс] \ begin {array} {l} 10x + 5y = -5 \ hfill \\ \, \, \, 3x-2y = -12 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (-2,3 \ вправо) [/ латекс]

[латекс] \ begin {array} {l} \ frac {4} {7} x + \ frac {1} {5} y = \ frac {43} {70} \\ \ frac {5} {6} x – \ frac {1} {3} y = – \ frac {2} {3} \ end {array} [/ latex]

[латекс] \ begin {array} {l} 5x + 6y = 14 \\ 4x + 8y = 8 \ end {array} [/ latex]

Показать решение

[латекс] \ влево (4, -1 \ вправо) [/ латекс]

В следующих упражнениях используйте сложение для решения системы уравнений.

[латекс] \ begin {array} {l} 3x + 2y = -7 \\ 2x + 4y = 6 \ end {array} [/ latex]

[латекс] \ begin {array} {r} 3x + 4y = 2 \\ 9x + 12y = 3 \ end {array} [/ latex]

[латекс] \ begin {array} {l} 8x + 4y = 2 \\ 6x-5y = 0,7 \ end {array} [/ latex]

Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.

Завод имеет стоимость производства [латекс] \, C \ left (x \ right) = 150x + 15 \ text {,} 000 \, [/ latex] и функцию дохода [латекс] \, R \ left ( х \ вправо) = 200x.\, [/ latex] Какая точка безубыточности?

Показать решение

[латекс] \ влево (300,60,000 \ вправо) [/ латекс]

Исполнитель взимает [латекс] \, C \ left (x \ right) = 50x + 10 \ text {,} 000, \, [/ latex], где [latex] \, x \, [/ latex] – общая сумма количество посетителей на шоу. Место проведения взимает 75 долларов за билет. После того, как сколько людей купит билеты, место проведения станет безубыточным, и какова общая стоимость билетов, проданных в этот момент?

Показать решение

[латекс] \ влево (400,30,000 \ вправо) [/ латекс]

Системы линейных уравнений: три переменные

Для следующих упражнений решите систему трех уравнений, используя замену или сложение.

[латекс] \ begin {array} {l} \ text {} 0,5x-0,5y = 10 \ hfill \\ \ text {} -0,2y + 0,2x = 4 \ hfill \\ \ text {} 0,1x + 0.1z = 2 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (10, -10,10 \ вправо) [/ латекс]

[латекс] \ begin {array} {r} \ hfill 5x + 3y-z = 5 \, \, \, \\ \ hfill 3x-2y + 4z = 13 \\ \ hfill 4x + 3y + 5z = 22 \ конец {array} [/ latex]

[латекс] \ begin {array} {r} x + y + z = 1 \\ 2x + 2y + 2z = 1 \\ 3x + 3y = 2 \ end {array} [/ latex]

[латекс] \ begin {массив} {l} \ text {} 2x-3y + z = -1 \ hfill \\ \ text {} x + y + z = -4 \ hfill \\ \ text {} 4x + 2y-3z = 33 \ hfill \ end {array} [/ latex]

[латекс] \ begin {array} {l} \, \, 3x + 2y-z = -10 \ hfill \\ \, \, \, \, x-y + 2z = 7 \ hfill \\ -x + 3y + z = -2 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (-1, -2,3 \ вправо) [/ латекс]

[латекс] \ begin {array} {r} \ hfill 3x + 4z = -11 \\ \ hfill x-2y = 5 \, \, \, \, \, \, \, \\ \ hfill 4y-z = -10 \ end {array} [/ latex]

[латекс] \ begin {array} {r} 2x-3y + z = 0 \\ 2x + 4y-3z = 0 \\ 6x-2y-z = 0 \ end {array} [/ latex]

Показать решение

[латекс] \ left (x, \ frac {8x} {5}, \ frac {14x} {5} \ right) [/ latex]

[латекс] \ begin {array} {r} 6x-4y-2z = 2 \\ 3x + 2y-5z = 4 \\ 6y-7z = 5 \ end {array} [/ latex]

Для следующих упражнений напишите систему уравнений для решения каждой задачи.Решите систему уравнений.

Три нечетных числа в сумме дают 61. Меньшее на треть больше, а среднее число на 16 меньше большего. Какие три числа?

Местный театр распродает билеты на их спектакль. Они продают все 500 билетов на общую сумму 8 070 долларов. Билеты стоили 15 долларов для студентов, 12 долларов для детей и 18 долларов для взрослых. Если группа продала в три раза больше билетов для взрослых, чем детских, сколько билетов каждого типа было продано?

Системы нелинейных уравнений и неравенств: две переменные

Для следующих упражнений решите систему нелинейных уравнений.{2}} [/ латекс]

Матрицы и матричные операции

Для следующих упражнений выполните требуемые операции с заданными матрицами.

[латекс] A = \ left [\ begin {array} {rr} \ hfill 4 & \ hfill -2 \\ \ hfill 1 & \ hfill 3 \ end {array} \ right], B = \ left [\ begin {array } {rrr} \ hfill 6 & \ hfill 7 & \ hfill -3 \\ \ hfill 11 & \ hfill -2 & \ hfill 4 \ end {array} \ right], C = \ left [\ begin {array} {r} \ hfill \ begin {array} {cc} 6 & 7 \\ 11 & -2 \ end {array} \\ \ hfill \ begin {array} {cc} 14 & 0 \ end {array} \ end {array} \ right], D = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -4 & \ hfill 9 \\ \ hfill 10 & \ hfill 5 & \ hfill -7 \\ \ hfill 2 & \ hfill 8 & \ hfill 5 \ end {array} \ right], E = \ left [\ begin {array} {rrr} \ hfill 7 & \ hfill -14 & \ hfill 3 \\ \ hfill 2 & \ hfill -1 & \ hfill 3 \\ \ hfill 0 & \ hfill 1 & \ hfill 9 \ конец {массив} \ справа] [/ латекс]

Показать решение

[латекс] \ left [\ begin {array} {cc} -16 & 8 \\ -4 & -12 \ end {array} \ right] [/ latex]

Показать решение

undefined; размеры не соответствуют

Показать решение

undefined; внутренние размеры не соответствуют

Показать решение

[латекс] \ left [\ begin {array} {ccc} 113 & 28 & 10 \\ 44 & 81 & -41 \\ 84 & 98 & -42 \ end {array} \ right] [/ latex]

Показать решение

[латекс] \ left [\ begin {array} {ccc} -127 & -74 & 176 \\ -2 & 11 & 40 \\ 28 & 77 & 38 \ end {array} \ right] [/ latex]

Показать решение

undefined; внутренние размеры не соответствуют

Решение систем с исключением Гаусса

Для следующих упражнений напишите систему линейных уравнений из расширенной матрицы.Укажите, будет ли уникальное решение.

[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill -3 \\ \ hfill 0 & \ hfill 1 & \ hfill 2 \\ \ hfill 0 & \ hfill 0 & \ hfill 0 \ end { массив} \ text {} | \ text {} \ begin {array} {r} \ hfill 7 \\ \ hfill -5 \\ \ hfill 0 \ end {array} \ right] [/ latex]

Показать решение

[латекс] \ begin {array} {l} x-3z = 7 \\ y + 2z = -5 \, \ end {array} [/ latex] с бесконечными решениями

[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 5 \\ \ hfill 0 & \ hfill 1 & \ hfill -2 \\ \ hfill 0 & \ hfill 0 & \ hfill 0 \ end { массив} \ text {} | \ text {} \ begin {array} {r} \ hfill -9 \\ \ hfill 4 \\ \ hfill 3 \ end {array} \ right] [/ latex]

Для следующих упражнений напишите расширенную матрицу из системы линейных уравнений.

[латекс] \ begin {массив} {l} \\ \ begin {array} {r} \ hfill -2x + 2y + z = 7 \\ \ hfill 2x-8y + 5z = 0 \\ \ hfill 19x-10y + 22z = 3 \ end {массив} \ end {array} [/ latex]

Показать решение

[латекс] \ left [\ begin {array} {rrr} \ hfill -2 & \ hfill 2 & \ hfill 1 \\ \ hfill 2 & \ hfill -8 & \ hfill 5 \\ \ hfill 19 & \ hfill -10 & \ hfill 22 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 7 \\ \ hfill 0 \\ \ hfill 3 \ end {array} \ right] [/ latex]

[латекс] \ begin {array} {l} \, \, \, \, \, 4x + 2y-3z = 14 \ hfill \\ -12x + 3y + z = 100 \ hfill \\ \, \, \ , \, \, 9x-6y + 2z = 31 \ hfill \ end {array} [/ latex]

[латекс] \ begin {array} {r} \ hfill x + 3z = 12 \, \\ \ hfill -x + 4y = 0 \, \, \, \, \\ \ hfill y + 2z = -7 \ конец {array} [/ latex]

Показать решение

[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 3 \\ \ hfill -1 & \ hfill 4 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill 2 \ end { массив} \ text {} | \ text {} \ begin {array} {r} \ hfill 12 \\ \ hfill 0 \\ \ hfill -7 \ end {array} \ right] [/ latex]

Для следующих упражнений решите систему линейных уравнений, используя метод исключения Гаусса.

[латекс] \ begin {array} {r} 3x-4y = -7 \\ -6x + 8y = 14 \ end {array} [/ latex]

[латекс] \ begin {array} {r} 3x-4y = 1 \\ -6x + 8y = 6 \ end {array} [/ latex]

[латекс] \ begin {массив} {l} \ begin {array} {l} \\ -1.1x-2.3y = 6.2 \ end {array} \ hfill \\ -5.2x-4.1y = 4.3 \ hfill \ конец {array} [/ latex]

[латекс] \ begin {array} {r} \ hfill 2x + 3y + 2z = 1 \, \, \, \, \, \\ \ hfill -4x-6y-4z = -2 \\ \ hfill 10x + 15y + 10z = 0 \, \, \, \, \, \ end {array} [/ latex]

[латекс] \ begin {array} {r} \ hfill -x + 2y-4z = 8 \, \, \, \, \\ \ hfill 3y + 8z = -4 \\ \ hfill -7x + y + 2z = 1 \, \, \, \, \ end {array} [/ latex]

Решающие системы с обратными сторонами

Для следующих упражнений найдите обратную матрицу.

[латекс] \ left [\ begin {array} {rr} \ hfill -0.2 & \ hfill 1.4 \\ \ hfill 1.2 & \ hfill -0.4 \ end {array} \ right] [/ latex]

Показать решение

[латекс] \ frac {1} {8} \ left [\ begin {array} {cc} 2 & 7 \\ 6 & 1 \ end {array} \ right] [/ latex]

[латекс] \ left [\ begin {array} {rr} \ hfill \ frac {1} {2} & \ hfill – \ frac {1} {2} \\ \ hfill – \ frac {1} {4} & \ hfill \ frac {3} {4} \ end {array} \ right] [/ latex]

[латекс] \ left [\ begin {array} {ccc} 12 & 9 & -6 \\ -1 & 3 & 2 \\ -4 & -3 & 2 \ end {array} \ right] [/ latex]

[латекс] \ left [\ begin {array} {ccc} 2 & 1 & 3 \\ 1 & 2 & 3 \\ 3 & 2 & 1 \ end {array} \ right] [/ latex]

Для следующих упражнений найдите решения, вычислив обратную матрицу.

[латекс] \ begin {массив} {l} \, \, \, \, 0,3x-0,1y = -10 \ hfill \\ -0,1x + 0,3y = 14 \ hfill \ end {array} [/ latex ]

Показать решение

[латекс] \ влево (-20,40 \ вправо) [/ латекс]

[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, 0,4x-0,2y = -0,6 \ hfill \\ -0,1x + 0,05y = 0,3 \ hfill \ end {array} [/ latex]

[латекс] \ begin {array} {r} 4x + 3y-3z = -4,3 \\ 5x-4y-z = -6,1 \\ x + z = -0,7 \ end {array} [/ latex]

Показать решение

[латекс] \ влево (-1,0,2,0,3 \ вправо) [/ латекс]

[латекс] \ begin {массив} {r} \ hfill \ begin {array} {l} \\ -2x-3y + 2z = 3 \ end {array} \\ \ hfill -x + 2y + 4z = -5 \\ \ hfill -2y + 5z = -3 \ end {array} [/ latex]

Для следующих упражнений напишите систему уравнений для решения каждой задачи.Решите систему уравнений.

Студентов попросили принести в класс их любимые фрукты. 90% фруктов состояли из бананов, яблок и апельсинов. Если апельсины были наполовину популярнее бананов, а яблоки на 5% популярнее бананов, каков процент каждого отдельного фрукта?

Показать решение

17% апельсинов, 34% бананов, 39% яблок

Женское общество провело распродажу выпечки, чтобы собрать деньги, и продавало пирожные и печенье с шоколадной крошкой. Они оценили пирожные в 2 доллара и печенье с шоколадной крошкой в ​​1 доллар.Они собрали 250 долларов и продали 175 вещей. Сколько было продано пирожных и печенья?

Решение систем с правилом Крамера

Найдите определитель для следующих упражнений.

[латекс] | \ begin {array} {cc} 100 & 0 \\ 0 & 0 \ end {array} | [/ latex]

[латекс] | \ begin {array} {cc} 0,2 & -0,6 \\ 0,7 & -1,1 \ end {array} | [/ latex]

[латекс] | \ begin {array} {ccc} -1 & 4 & 3 \\ 0 & 2 & 3 \\ 0 & 0 & -3 \ end {array} | [/ latex]

[латекс] | \ begin {array} {ccc} \ sqrt {2} & 0 & 0 \\ 0 & \ sqrt {2} & 0 \\ 0 & 0 & \ sqrt {2} \ end {array} | [/ latex]

В следующих упражнениях используйте правило Крамера для решения линейных систем уравнений.

[латекс] \ begin {массив} {r} \ hfill 4x-2y = 23 \, \, \, \, \\ \ hfill -5x-10y = -35 \ end {array} [/ latex]

Показать решение

[латекс] \ left (6, \ frac {1} {2} \ right) [/ latex]

[латекс] \ begin {array} {l} 0,2x-0,1y = 0 \\ -0,3x + 0,3y = 2,5 \ end {array} [/ latex]

[латекс] \ begin {массив} {r} \ hfill -0,5x + 0,1y = 0,3 \, \, \, \\ \ hfill -0,25x + 0,05y = 0,15 \ end {array} [/ latex]

[латекс] \ begin {array} {l} x + 6y + 3z = 4 \\ 2x + y + 2z = 3 \\ 3x-2y + z = 0 \ end {array} [/ latex]

[латекс] \ begin {array} {r} \ hfill 4x-3y + 5z = – \ frac {5} {2} \\ \ hfill 7x-9y-3z = \ frac {3} {2} \, \ , \, \, \\ \ hfill x-5y-5z = \ frac {5} {2} \, \, \, \, \ end {array} [/ latex]

Показать решение

[латекс] \ left (0,0, – \ frac {1} {2} \ right) [/ latex]

[латекс] \ begin {array} {r} \ frac {3} {10} x- \ frac {1} {5} y- \ frac {3} {10} z = – \ frac {1} {50 } \\ \ frac {1} {10} x- \ frac {1} {10} y- \ frac {1} {2} z = – \ frac {9} {50} \\ \ frac {2} { 5} x- \ frac {1} {2} y- \ frac {3} {5} z = – \ frac {1} {5} \ end {array} [/ latex]

Практический тест

Является ли следующая упорядоченная пара решением системы уравнений?

[латекс] \ begin {массив} {l} \\ \ begin {array} {l} -5x-y = 12 \, \ hfill \\ x + 4y = 9 \ hfill \ end {array} \ end {массив } [/ latex] с [latex] \, \ left (-3,3 \ right) [/ latex]

Для следующих упражнений решите системы линейных и нелинейных уравнений с помощью замены или исключения.Укажите, если решения не существует.

[латекс] \ begin {array} {r} \ frac {1} {2} x- \ frac {1} {3} y = 4 \\ \ frac {3} {2} xy = 0 \ end {массив } [/ латекс]

[латекс] \ begin {массив} {r} \ hfill \ begin {array} {l} \\ – \ frac {1} {2} x-4y = 4 \ end {array} \\ \ hfill 2x + 16y = 2 \ end {array} [/ latex]

[латекс] \ begin {array} {r} \ hfill 5x-y = 1 \, \, \, \, \\ \ hfill -10x + 2y = -2 \ end {array} [/ latex]

[латекс] \ begin {array} {l} 4x-6y-2z = \ frac {1} {10} \ hfill \\ \, \, \, x-7y + 5z = – \ frac {1} {4 } \ hfill \\ 3x + 6y-9z = \ frac {6} {5} \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ frac {1} {20} \ left (10,5,4 \ right) [/ latex]

[латекс] \ begin {array} {r} x + z = 20 \\ x + y + z = 20 \\ x + 2y + z = 10 \ end {array} [/ latex]

[латекс] \ begin {array} {r} 5x-4y-3z = 0 \\ 2x + y + 2z = 0 \\ x-6y-7z = 0 \ end {array} [/ latex]

Показать решение

[латекс] \ left (x, \ frac {16x} {5} – \ frac {13x} {5} \ right) [/ latex]

[латекс] \ begin {array} {l} y = {x} ^ {2} + 2x-3 \\ y = x-1 \ end {array} [/ latex]

[латекс] \ begin {array} {l} {y} ^ {2} + {x} ^ {2} = 25 \\ {y} ^ {2} -2 {x} ^ {2} = 1 \ конец {array} [/ latex]

Показать решение

[латекс] \ left (-2 \ sqrt {2}, – \ sqrt {17} \ right), \ left (-2 \ sqrt {2}, \ sqrt {17} \ right), \ left (2 \ sqrt {2}, – \ sqrt {17} \ right), \ left (2 \ sqrt {2}, \ sqrt {17} \ right) [/ latex]

Для следующих упражнений нарисуйте следующие неравенства. {- 1} [/ latex]

Показать решение

[латекс] \ left [\ begin {array} {cc} 12 & -20 \\ -15 & 30 \ end {array} \ right] [/ latex]

[латекс] \ mathrm {det} | \ begin {array} {cc} 0 & 0 \\ 400 & 4 \ text {,} 000 \ end {array} | [/ latex]

[латекс] \ mathrm {det} | \ begin {array} {rrr} \ hfill \ frac {1} {2} & \ hfill – \ frac {1} {2} & \ hfill 0 \\ \ hfill – \ frac {1} {2} & \ hfill 0 & \ hfill \ frac {1} {2} \\ \ hfill 0 & \ hfill \ frac {1} {2} & \ hfill 0 \ end {array} | [/ latex]

Показать решение

[латекс] – \ frac {1} {8} [/ латекс]

Если [latex] \, \ mathrm {det} \ left (A \ right) = – 6, \, [/ latex], что будет определяющим, если вы поменяете местами строки 1 и 3, умножите вторую строку на 12 и взял обратное?

Перепишите систему линейных уравнений в виде расширенной матрицы.

[латекс] \ begin {array} {l} 14x-2y + 13z = 140 \ hfill \\ -2x + 3y-6z = -1 \ hfill \\ x-5y + 12z = 11 \ hfill \ end {array} [/ латекс]

Показать решение

[латекс] \ left [\ begin {array} {rrr} \ hfill 14 & \ hfill -2 & \ hfill 13 \\ \ hfill -2 & \ hfill 3 & \ hfill -6 \\ \ hfill 1 & \ hfill -5 & \ hfill 12 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 140 \\ \ hfill -1 \\ \ hfill 11 \ end {array} \ right] [/ latex]

Перепишите расширенную матрицу как систему линейных уравнений.

[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 3 \\ \ hfill -2 & \ hfill 4 & \ hfill 9 \\ \ hfill -6 & \ hfill 1 & \ hfill 2 \ end {массив} | \ begin {array} {r} \ hfill 12 \\ \ hfill -5 \\ \ hfill 8 \ end {array} \ right] [/ latex]

В следующих упражнениях используйте метод исключения Гаусса для решения систем уравнений.

[латекс] \ begin {array} {r} x-6y = 4 \\ 2x-12y = 0 \ end {array} [/ latex]

[латекс] \ begin {array} {r} \ hfill 2x + y + z = -3 \\ \ hfill x-2y + 3z = 6 \, \, \, \, \\ \ hfill xyz = 6 \, \, \, \, \ end {array} [/ latex]

В следующих упражнениях используйте обратную матрицу для решения систем уравнений.

[латекс] \ begin {массив} {r} \ hfill 4x-5y = -50 \\ \ hfill -x + 2y = 80 \, \, \, \, \ end {array} [/ latex]

Показать решение

[латекс] \ влево (100,90 \ вправо) [/ латекс]

[латекс] \ begin {array} {r} \ hfill \ frac {1} {100} x- \ frac {3} {100} y + \ frac {1} {20} z = -49 \\ \ hfill \ frac {3} {100} x- \ frac {7} {100} y- \ frac {1} {100} z = 13 \, \, \, \, \\ \ hfill \ frac {9} {100} x- \ frac {9} {100} y- \ frac {9} {100} z = 99 \, \, \, \, \ end {array} [/ latex]

В следующих упражнениях используйте правило Крамера для решения систем уравнений.{2} + 160x. \, [/ Latex] Какой ассортимент сотовых телефонов они должны производить каждый день, чтобы получать прибыль? Округлите до ближайшего числа, приносящего прибыль.

Показать решение

32 и более сотовых телефона в день

Небольшая ярмарка взимает 1,50 доллара для студентов, 1 доллар для детей и 2 доллара для взрослых. За один день пришло в три раза больше детей, чем взрослых. Было продано 800 билетов на общую выручку в 1050 долларов. Сколько билетов каждого типа было продано?

Глоссарий

Правило Крамера

метод решения систем уравнений, которые имеют то же количество уравнений, что и переменные, с использованием определителей

определитель

число, вычисленное с использованием элементов квадратной матрицы, которая определяет такую ​​информацию, как наличие решения системы уравнений

Правило Крамера с вопросами и решениями

.
\ ( \левый\{ \ begin {array} {lcl} a_1 b_ 2 x + b_1 b_2 y & = & c_1 b_2 \\ -a_2 b_1 x – b_2 b_1 y & = & – c_2 b_1 \ end {массив} \верно. \)

Сложите левую и правую части приведенных выше уравнений и упростите, чтобы получить уравнение с одной переменной.
\ ( a_1 b_2 x – a_2 b_1 x = c_1 b_2 – c_2 b_1 \)

Выносим множитель x на левой стороне
\ ( x (a_1 b_2 – a_2 b_1) = b_2 c_1 – b_1 c_2 \)

Решите указанное выше уравнение относительно x
\ ( x = \ dfrac {c_1 b_2 – c_2 b_1} {a_1 b_2 – a_2 b_1} \)

Мы можем использовать аналогичные шаги, чтобы исключить x и решить относительно y, чтобы получить.
\ ( y = \ dfrac {a_1 c_2 – a_2 c_1} {a_1 b_2 – a_2 b_1} \)

Решение данной системы линейных уравнений 2 на 2 дается правилами Крамера следующим образом.
\ [x = \ dfrac {D_x} {D}, y = \ dfrac {D_y} {D} \]
Использование

Общая система линейных уравнений 3 на 3 может быть записана следующим образом: \ [ \левый\{ \ begin {array} {lcl} a_1 x + b_1 y + c_1 z = & \ color {красный} {d_1} & (1) \\ a_2 x + b_2 y + c_2 = & \ color {красный} {d_2} & (2) \\ a_3 x + b_3 y + c_3 = & \ color {красный} {d_3} & (2) \\ \ end {массив} \верно.\]

Для системы линейных уравнений 3 на 3 правило Крамера дает следующее решение
\ [x = \ dfrac {D_x} {D}, y = \ dfrac {D_y} {D}, z = \ dfrac {D_z} {D} \]
, где \ (D, D_x, D_y \ text {и} D_z \) – определители матриц 3 на 3, определяемые

\ (D = \ begin {vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \ end {vmatrix} \)

\ (D_x = \ begin {vmatrix} \ color {red} {d_1} & b_1 & c_1 \\ \ color {red} {d_2} & b_2 & c_2 \\ \ color {red} {d_3} & b_3 & c_3 \ end {vmatrix} \), \ (D_y = \ begin {vmatrix} a_1 & \ color {red} {d_1} & c_1 \\ a_2 & \ color {red} {d_2} & c_2 \\ a_3 & \ color {red} {d_3} & c_3 \ end {vmatrix} \) , \ (D_z = \ begin {vmatrix} a_1 & b_1 & \ color {red} {d_1} \\ a_2 & b_2 & \ color {red} {d_2} \\ a_3 & b_3 & \ color {red} {d_3} \ end {vmatrix} \)

Часть 1
а) Рассчитайте детерминанты
\ (D = \ begin {vmatrix} 5 & -2/3 \\ -1 & 1/2 \ end {vmatrix} = (5) (1/2) – (- 2/3) (- 1) = 11/6 \)

\ (D_x = \ begin {vmatrix} 1/3 & -2/3 \\ -1/2 & 1/2 \ end {vmatrix} = (1/3) (1/2) – (- 2/3 ) (- 1/2) = -1/6 \)

\ (D_y = \ begin {vmatrix} 5 & 1/3 \\ -1 & -1/2 \ end {vmatrix} = (5) (- 1/2) – (1/3) (- 1) = -13/6 \)

Решение дается правилом Крамера следующим образом.
\ (x = \ dfrac {D_x} {D} = – \ dfrac {1} {11} \)

\ (y = \ dfrac {D_y} {D} = – \ dfrac {13} {11} \)

б) Определители даны по формуле
\ (D = \ begin {vmatrix} 0.1 & -0,3 \\ -0,2 & 1,3 \ end {vmatrix} = (0,1) (1,3) – (-0,3) (- 0,2) = 0,07 \)

\ (D_x = \ begin {vmatrix} 1.1 & -0.3 \\ -1.5 & 1.3 \ end {vmatrix} = (1.1) (1.3) – (-0.3) (- 1.5) = 0.98 \)

\ (D_y = \ begin {vmatrix} 0.1 & 1.1 \\ -0.2 & -1.5 \ end {vmatrix} = (0.1) (- 1.5) – (1.1) (- 0.2) = 0.07 \)

Решение дает
\ (x = \ dfrac {D_x} {D} = \ dfrac {0,98} {0,07} = 14 \)

\ (y = \ dfrac {D_y} {D} = \ dfrac {0,07} {0,07} = 1 \)

в) Определители 3 на 3 \ (D, D_x, D_y \ text {и} D_z \) вычисляются с использованием определителей 2 на 2 следующим образом
\ (D = \ begin {vmatrix} -3 & 5 & -1 \\ 1/5 & -5 & – 3/5 \\ -4 & 4/5 & -1 \ end {vmatrix} = -3 \ cdot \ begin {vmatrix} -5 & – \ frac {3} {5} \\ \ frac {4} {5} & – 1 \ end {vmatrix} -5 \ cdot \ begin {vmatrix} \ frac {1} { 5} & – \ frac {3} {5} \\ -4 & -1 \ end {vmatrix} -1 \ cdot \ begin {vmatrix} \ frac {1} {5} & – 5 \\ -4 & \ frac { 4} {5} \ end {vmatrix} = 82/5 \)

\ (D_x = \ begin {vmatrix} 1/2 & 5 & -1 \\ 0 & -5 & – 3/5 \\ -7 & 4/5 & -1 \ end {vmatrix} = \ frac { 1} {2} \ begin {vmatrix} -5 & – \ frac {3} {5} \\ \ frac {4} {5} & – 1 \ end {vmatrix} -5 \ cdot \ begin {vmatrix} 0 & – \ frac {3} {5} \\ -7 & -1 \ end {vmatrix} -1 \ cdot \ begin {vmatrix} 0 & -5 \\ -7 & \ frac {4} {5} \ end {vmatrix} = 2937 / 50 \)

\ (D_y = \ begin {vmatrix} -3 & 1/2 & -1 \\ 1/5 & 0 & – 3/5 \\ -4 & -7 & -1 \ end {vmatrix} = -3 \ cdot \ begin {vmatrix} 0 & – \ frac {3} {5} \\ -7 & -1 \ end {vmatrix} – \ frac {1} {2} \ begin {vmatrix} \ frac {1} {5} & – \ frac {3} {5} \\ -4 & -1 \ end {vmatrix} -1 \ cdot \ begin {vmatrix} \ frac {1} {5} & 0 \\ -4 & -7 \ end {vmatrix} = 153/10 \)

\ (D_z = \ begin {vmatrix} -3 & 5 & 1/2 \\ 1/5 & -5 & 0 \\ -4 & 4/5 & – 7 \ end {vmatrix} = -3 \ cdot \ begin {vmatrix} -5 & 0 \\ \ frac {4} {5} & – 7 \ end {vmatrix} -5 \ cdot \ begin {vmatrix} \ frac {1} {5} & 0 \\ -4 & -7 \ end {vmatrix} + \ frac {1} {2} \ begin {vmatrix} \ frac {1} {5} & – 5 \\ -4 & \ frac {4} {5} \ end {vmatrix} = -2698 / 25 \)

Решение дает
\ (x = \ dfrac {D_x} {D} = \ dfrac {2937/50} {82/5} = \ dfrac {2937} {820} \)

\ (y = \ dfrac {D_y} {D} = \ dfrac {153/10} {82/5} = \ dfrac {153} {164} \)

\ (z = \ dfrac {D_z} {D} = \ dfrac {-2698/25} {82/5} = – \ dfrac {1349} {205} \)

Часть 2
a) Определители даются по формуле
\ (D = \ begin {vmatrix} 5 & -k \\ -2 & 2k \ end {vmatrix} = (5) (2k) – (- k) (- 2) = 8 k \)

\ (D_x = \ begin {vmatrix} 6 & -k \\ -3 & 2k \ end {vmatrix} = (6) (2k) – (- k) (- 3) = 9 k \)

\ (D_y = \ begin {vmatrix} 5 & 6 \\ -2 & -3 \ end {vmatrix} = (5) (- 3) – (6) (- 2) = – 3 \)

Решение системы
\ (x = \ dfrac {D_x} {D} = \ dfrac {9k} {8k} = \ dfrac {9} {8} \) , \ (Y = \ dfrac {D_y} {D} = \ dfrac {-3} {8k} = – \ dfrac {3} {8k} \)

б) Определители даны по формуле
\ (D = \ begin {vmatrix} 2 & – 3 \\ 1 & 2 \ end {vmatrix} = (2) (2) – (-3) (1) = 7 \)

\ (D_x = \ begin {vmatrix} k & – 3 \\ -2 k & 2 \ end {vmatrix} = (k) (2) – (-3) (- 2k) = -4k \)

\ (D_y = \ begin {vmatrix} 2 & k \\ 1 & -2k \ end {vmatrix} = (2) (- 2k) – (k) (1) = -5k \)
Решение системы
\ (x = \ dfrac {D_x} {D} = \ dfrac {-4k} {7} = – \ dfrac {4} {7} k \) , \ (Y = \ dfrac {D_y} {D} = \ dfrac {-5k} {7} = – \ dfrac {5} {7} k \)

Часть 3
a) Используя правило Крамера, решения даются по формуле
\ (х = 6 q + 25 p \) \ (y = -2 q – 10 p \)

б)
1) Если мы заменим параметры p и q в системе уравнений в a) на 2 и 2 соответственно, мы получим систему уравнений
\ ( \левый\{ \ begin {array} {lcl} – х – 3 у & = & 10 \\ – 2 x – 5 y & = & – 4 \ end {массив} \верно.\)
, которую мы должны решить. Но система в а) решена для всех значений p и q. Следовательно, чтобы решить систему в b) 1), мы заменяем p и q их значениями (2 и 2) в решениях, полученных в a), что дает.
\ (x = 6 q + 25 p = 6 (2) + 25 (2) = 62 \) \ (y = -2 q – 10 p = -2 (2) – 10 (2) = -24 \)

2) Для этой системы p = 1/2 и q = 1; следовательно, решение
\ (x = 6 q + 25 p = 6 (1) + 25 (1/2) = 37/2 \) \ (y = -2 q – 10 p = -2 (1) – 10 (1/2) ) = – 7 \)

3) Для этой системы p = 10 и q = -3; следовательно, решение
\ (x = 6 q + 25 p = 6 (-3) + 25 (10) = 232 \) \ (y = -2 q – 10 p = -2 (-3) – 10 (10) = – 94 \)

Часть 4
Определители, используемые в правиле Крамера, даются

\ (D = \ begin {vmatrix} 5 & -6 & 6 \\ \: \: 9 & -p & -1 \\ \: \: – 2 & -6 & 0 \ end {vmatrix} = 5 \ cdot \ begin {vmatrix} -p & -1 \\ -6 & 0 \ end {vmatrix} – \ left (-6 \ right) \ begin {vmatrix} 9 & -1 \\ -2 & 0 \ end {vmatrix} +6 \ cdot \ begin {vmatrix} 9 & -p \ \ -2 & -6 \ end {vmatrix} = -12p-366 \)

\ (D_x = \ begin {vmatrix} -14 & -6 & 6 \\ \: \: 22 & -p & -1 \\ \: \: \: – 4 & -6 & 0 \ end {vmatrix} = -14 \ cdot \ begin {vmatrix} -p & -1 \\ -6 & 0 \ end {vmatrix} – \ left (-6 \ right) \ begin {vmatrix} 22 & -1 \\ -4 & 0 \ end {vmatrix} +6 \ cdot \ begin {vmatrix } 22 & -p \\ -4 & -6 \ end {vmatrix} = -24p-732 \)

\ (D_y = \ begin {vmatrix} 5 & -14 & 6 \\ \: \: \: 9 & 22 & -1 \\ \: \: \: – 2 & -4 & 0 \ end {vmatrix} = = 5 \ cdot \ begin { vmatrix} 22 & -1 \\ -4 & 0 \ end {vmatrix} – \ left (-14 \ right) \ begin {vmatrix} 9 & -1 \\ -2 & 0 \ end {vmatrix} +6 \ cdot \ begin {vmatrix} 9 & 22 \\ -2 & -4 \ end {vmatrix} = 0 \)

\ (D_z = \ begin {vmatrix} 5 & -6 & -14 \\ \: \: \: 9 & -p & 22 \\ \: \: \: – 2 & -6 & -4 \ end {vmatrix} = = 5 \ cdot \ begin {vmatrix} -p & 22 \\ -6 & -4 \ end {vmatrix} – \ left (-6 \ right) \ begin {vmatrix} 9 & 22 \\ -2 & -4 \ end {vmatrix} -14 \ cdot \ begin {vmatrix} 9 & -p \\ -2 & -6 \ end {vmatrix} = 48p + 1464 \)

Решения даются правилом Крамера следующим образом.

\ (x = \ dfrac {D_x} {D} = \ dfrac {-24p-732} {- 12p-366} = 2 \)

\ (y = \ dfrac {D_y} {D} = \ dfrac {0} {- 12p-366} = 0 \)

\ (z = \ dfrac {D_z} {D} = \ dfrac {48p + 1464} {- 12p-366} = -4 \)

Метод Крамера для чайников Подробные примеры решений.Метод Крамера решения систем линейных уравнений

Метод Крамера основан на использовании определителей при решении систем линейных уравнений. Это значительно ускоряет процесс принятия решения.

Кратерный метод можно использовать при решении системы стольких линейных уравнений, как в каждом уравнении неизвестного. Если определитель системы не равен нулю, в решении можно использовать метод Крамера, если он равен нулю, нельзя. Кроме того, метод Крамера можно использовать при решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестном, называется определителем системы и обозначается (дельта).

Deterpetes

получается заменой коэффициентов на соответствующие неизвестные для свободных участников:

;

.

Теорема Крамеры . Если определитель системы отличен от нуля, система линейных уравнений имеет одно единственное решение и неизвестное, равное отношению определителей.В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путем замены коэффициентов одновременно неизвестными свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решите систему линейных уравнений:

Согласно теореме Крамера Мы имеем:

Итак, решение Решение (2):

Онлайн-калькулятор, решающий кратерный метод.

Три случая решения систем линейных уравнений

Как ясно теоремы Крамера При решении системы линейных уравнений может быть три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместно и определена)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместного и неопределенного)

**,

тех.Коэффициенты при неизвестных и свободных членах пропорциональны.

Третий случай: в системе линейных решений нет

(система непонятна)

Итак, система м. Linear Equations S. n. переменные вызывают нон-стоп , если у нее нет решения, и соединяют , если у нее есть хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется , определенное , более одного – неопределенное .

Примеры решения систем линейных уравнений по Крамеру

Пусть дано системе

.

На основе теоремы Крамера

………….
,

, где
–

определение системы. Остальные определители получаем, заменяя столбец коэффициентами соответствующих переменных (неизвестных) свободных членов:

Пример 2.

.

Следовательно, система определена. Чтобы найти ее решения, вычислим определители

По формулам краулера находим:

Итак (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 x 3 и 4 x 4 вы можете использовать онлайн-калькулятор, решая метод Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях нет переменных, то в определителе соответствующие им элементы равны нулю! Это следующий пример.

Пример 3. Решите систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Внимательно посмотрите на систему уравнений и определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решения, вычислим определители при неизвестном

.

По формулам краулера находим:

Итак, решение системы (2; -1; 1).

Для проверки решений систем уравнений 3 x 3 и 4 x 4 вы можете использовать онлайн-калькулятор, решая метод Крамера.

Начало страницы

Продолжаем решать систему по методу Крамера вместе

Как уже было сказано, если определитель системы равен нулю, а определители при неизвестном не равны нулю, система непонятна, то есть решений не имеет. Проиллюстрируем следующий пример.

Пример 6. Решите систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо неполная и определенная, либо противоречивая, то есть не имеет решений. Для пояснения вычислим детерминанты при неизвестном

.

Определители при неизвестном не равны нулю, следовательно, система неполная, то есть не имеет решений.

Для проверки решений систем уравнений 3 x 3 и 4 x 4 вы можете использовать онлайн-калькулятор, решая метод Крамера.

В задачах по системе линейных уравнений встречаются и такие, где встречаются и другие буквы, обозначаемые переменными. Эти буквы обозначают какое-то число, чаще всего действительное. На практике такие уравнения и системы уравнений приводят к задачам поиска общих свойств любых явлений и объектов. То есть вы изобрели какой-то новый Материал или устройство, и для описания его свойств, как правило, независимо от размера или количества экземпляров, необходимо решать систему линейных уравнений, где вместо некоторых коэффициентов с переменными – буквы.Например, ходить не обязательно.

Следующий пример представляет собой аналогичную задачу, только увеличивается количество уравнений, переменных и букв, обозначающих допустимое число.

Пример 8. Решите систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Мы находим детерминанты в неизвестном

Метод Крамера или так называемое правило краулера – это способ поиска неизвестных значений из систем уравнений.Его можно использовать только в том случае, если количество искомых значений эквивалентно количественным алгебраическим уравнениям В системе, то есть основная матрица, сформированная из системы, должна быть квадратной и не содержать нулевых строк, а также если ее определители должны не быть нулевым.

Теорема 1.

Теорема Крамера Если главный определитель $ d $ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений согласована, а решение имеет единственное.Решение такой системы вычисляется по так называемым формулам Крамера для решения линейных уравнений: $ x_i = \ FRAC (D_I) (D) $

Что такое метод Крамера

Суть метода Крамера заключается в следующим образом:

1. Чтобы найти решение системы методом Крамера, первым делом вычисляется главный определитель матрицы $ D $. Когда вычисленный определитель основной матрицы при вычислении метода Крамера оказался нулевым, то система не имеет единственного решения или имеет бесконечное количество решений.В этом случае рекомендуется применить метод Гаусса, чтобы найти общий или базовый отклик для системы.
2. Затем нужно заменить крайний столбец основной матрицы на столбец свободных элементов и вычислить идентификатор $ d_1 $.
3. Повторите то же самое для всех столбцов, получив определители от $ d_1 $ до $ d_n $, где $ n $ – номер крайнего правого столбца.
4. После того, как все определители найдены $ d_1 $ … $ d_n $, можно вычислить неизвестные переменные по формуле $ x_i = \ frac (d_i) (D) $.

Приемы вычисления определителя матрицы

Для вычисления определителя матрицы размерностью больше 2 к 2 можно использовать несколько способов:

• Правило треугольников, или правило Сарруса, напоминающее правило то же правило. Суть метода треугольника заключается в том, что при вычислении определителя произведение всех чисел, связанных на рисунке красной линии справа, записывается со знаком плюс, а все числа, соединенные таким же образом на рисунке на слева – со знаком минус.B, тогда другое правило подходит для матриц 3 x 3. 3. В случае правила Сарруски сначала соответствует сама матрица, а затем переписывается в свой первый и второй столбцы. Через матрицу и эти дополнительные столбцы по диагонали, элементы матрицы, лежащие на главной диагонали или параллельно ей, записываются со знаком плюс, а элементы, лежащие на боковой диагонали или параллельно ей – со знаком минус.

Рис. 1. Правило треугольника для вычисления определителя для метода Крамера

• Используя метод, известный как метод Гаусса, также иногда этот метод называют уменьшением порядка определителя.В этом случае матрица преобразуется и приводится к треугольной форме, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя невозможно умножить или разделить строки или столбцы на числа, не сделав их как множитель или делитель. В случае поиска определителя возможно только вычесть и сложить струны и столбы между собой после предварительного скашивания вычтенной линии до ненулевого множителя.Также при каждой перестановке строк или столбцов матрицы местами следует помнить о необходимости изменения финального знака в матрице.
• При решении метода Крамера, Славы с 4 неизвестными лучше всего использовать именно метод Гаусса для поиска и нахождения идентификаторов или определять определитель через поиск минорных.

Решение систем уравнений по Крамеру

Применимый метод Крамера для системы из 2 уравнений и двух желаемых значений:

$ \ begin (Cases) a_1x_1 + a_2x_2 = b_1 \\\\ a_3x_1 + a_4x_2 = b_2 \\ End (Cases)

$

Для удобства отобразить в развернутом виде:

$ A = \ begin (array) (CC | C) A_1 & A_2 & B_1 \\\\ A_3 & A_4 & B_1 \ \ END (Array) $

Найдем определитель основной матрицы, также называемый главным определителем системы:

$ D = \ begin (array) (| CC |) A_1 & A_2 \\\ \ A_3 & A_4 \\ END (Array) = A_1 \ CDOT A_4 – A_3 \ CDOT A_2 $

Если главный определитель не равен нулю, необходимо вычислить пару определителей из двух матриц с заменен столбец основной матрицы на строку свободных элементов для решения примера метода:

$ D_1 = \ begin (array) (| cc |) b_1 & a_2 \\\\ b_2 & a_4 \\\\ \ \ конец (массив) = b_1 \\ cdot a_4 – b_2 \\ cdot a_4 $

$ D_2 = \ begin (array) (| CC |) A_1 & B_1 \\\\ A_3 & B_2 \\\\ \\ END (Array) = A_1 \ CDOT B_2 – A_3 \ CDOT B_1 $

Теперь найдите неизвестные $ x_1 $ и $ x_2 $:

$ x_1 = \ FRAC (D_1) (D)

$

$ x_2 = \ FRAC (D_2) (D)

Пример 1.

Метод Крамера для решения уклона с основной матрицей 3 порядка (3 x 3) и три является искомым.

Решите систему уравнений:

$ \ begin (Дела) 3x_1 – 2x_2 + 4x_3 = 21 \ 3x_1 + 4x_2 + 2x_3 = 9 \ 2X_1 – X_2 – X_3 = 10 \ END (Дела)

$

Рассмотрим главный определитель матрицы, используя вышеупомянутое правило числа 1:

$ D = \ begin (array) (| CCC |) 3 & -2 & 4 \\\\ 3 & 4 & -2 \ ED (Array) = 3 \ CDOT 4 \ CDOT (- 1) + 2 \ Cdot (-2) \ CDOT 2 + 4 \ CDOT 3 \ CDOT (-1) – 4 \ CDOT 4 \ CDOT 2 – 3 \ CDOT (-2) \ CDOT (-1) – (- 1) \ CDOT 2 \ CDOT 3 = – 12-8-12-32-6 + 6 = – 64 $

А теперь еще три детерминанта:

$ D_1 = \ begin (массив) (| CCC |) 21 & 2 & 4 \\\\ 9 & 4 & 2 \\\\ 10 & 1 & 1 \ END (Array) = 21 \ CDOT 4 \ CDOT 1 + (- 2) \ CDOT 2 \ CDOT 10 + 9 \ CDOT (-1) \ CDOT 4-4 \ CDOT 4 \ CDOT 10-9 \ CDOT (-2 ) \ CDOT (-1) – (-1) \ CDOT 2 \ $ D_2 = \ begin (array) (| CCC |) 3 & 21 & 4 \\\\ 3 & 9 & 2 \\ ED (Массив) = 3 \ CDOT 9 \ CDOT (- 1) + 3 \ CDOT 10 \ CDOT 4 + 21 \ CDOT 2 \ CDOT 2-4 \ CDOT 9 \ CDOT 2-21 \ CDOT 3 \ CDOT (-1) – 2 \ CDOT 10 \ CDOT 3 = – 27 + 120 + 84-72 + 63-60 = 108 $

$ D_3 = \ begin (массив) (| CCC |) 3 & -2 & 21 \\\\ 3 & 4 & 9 \\\\ 2 & 1 & 10 \ END (массив) = 3 \ \ CDOT 4 \ CDOT 10 + 3 \ Cdot (-1) \ CDOT 21 + (-2) \ CDOT 9 \ CDOT 2-21 \ CDOT 4 \ CDOT 2 – (-2) \ CDOT 3 \ CDOT 10 – (-1) \ CDOT 9 \ CDOT 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60

$

Найдите нужные значения:

$ X_1 = \ FRAC (D_1) (D) = \ FRAC (- 296) (- 64) = 4 \ FRAC (5) (8)

$

$ X_2 = \ FRAC (D_1) (D) = \ FRAC (108) (-64) = – 1 \ FRAC (11) (16)

$

$ X_3 = \ FRAC (D_1) (D) = \ FRAC (-60) (-64) = \ FRAC (15) (16)

$

2.Решение систем уравнений матричным методом (с использованием обратной матрицы).

3. Метод Гаусса для решения систем уравнений.
Метод Крамера.

Метод Craver используется для решения линейных алгебраических уравнений (

Slough Формулы на примере системы двух уравнений с двумя переменными. ).

Дано:
Решите Систему метода Крамера Относительно переменных

H. и W. Решение: .
Находим определитель матрицы, составленной из коэффициентов системы вычисления определителей.:
Используем формулы краулера и находим значения переменных:

Пример 1:
Вт.
Решите систему уравнений:
относительно переменных

и W. Решение : .
Находим определитель матрицы, составленной из коэффициентов системы вычисления определителей. :

Заменяем в этом определителе первый столбец столбца коэффициентов из правой части системы и находим его значение:

Проделаем аналогичное действие, заменив второй столбец в первом дефицитном:

Применим формулы крамера и найдем значения переменных:
и.
Ответ:
Комментарий: Этот метод позволяет решать системы и большие измерения.

Комментарий: Если оказывается, что и на ноль делить нельзя, то говорят, что в системе нет единого решения. В этом случае у системы есть или бесконечно много решений, или решений нет вообще.

Пример 2. (бесконечное количество решений):

Решите систему уравнений:

и W. решение: .
Находим определитель матрицы, составленной из коэффициентов системы вычисления определителей. :
Находим определитель матрицы, составленной из системных коэффициентов:

Решение систем подстановкой.

Первое из уравнений системы – равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Это означает, что остается только одно уравнение. Это уравнение связи между переменными.
Поступившие решения системы – это любые пары значений переменных, приведенные к равенству.
Общее решение будет записано следующим образом:
Частные решения можно определить, выбрав произвольное значение y и вычислив X на этом равенстве связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частное решение:

Пример 3. (решений нет, система непонятна):

Решаем систему уравнений:

Находим определитель матрицы, составленной из коэффициентов системы вычисления определителей.:
Находим определитель матрицы, составленной из системных коэффициентов:

Невозможно использовать формулы Крамера. Решаю эту систему заменой

Второе уравнение системы – равенство, неверно при любых значениях переменных (разумеется, поскольку -15 не равно 2). Если одно из уравнений системы не выполняется ни при каких значениях переменных, то вся система не имеет решений.
Ответ: Нет решений

При том, что количество уравнений совпадает с количеством неизвестных с главным определителем, матрицей, которая не равна нулю, коэффициентов системы (для таких уравнений решение только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы отличен от нуля, это означает, что система должна иметь одно решение, и его можно найти в формулах Крамера :

где Δ – определитель матрицы системы ,

Δ I. – определитель матрицы системы, в которой вместо i. Столбец – это столбец правых частей.

Когда определитель системы равен нулю, это означает, что система может стать совместной или зачаточной.

Этот метод обычно используется для небольших систем с объемными вычислениями и в тех случаях, когда необходимо определить 1 лунку из неизвестного. Сложность метода в том, что необходимо вычислить множество определителей.

Описание метода Крамера.

Имеется система уравнений:

Система трех уравнений может быть решена методом Крамера, который обсуждался выше для системы из двух уравнений.

Составим определитель коэффициентов неизвестных:

Это будет Система Определена .Когда D ≠ 0 Итак, система согласована. Теперь составим 3 дополнительных идентификатора:

,,

Решаем систему крамерных формул ПО :

Примеры решения систем уравнений методом Крамера.

Пример 1. .

Система Dana:

Решив методом Крамера.

Для начала необходимо вычислить определитель матрицы системы:

Поскольку Δ ≠ 0, это означает, что согласно теореме Крамера система разрабатывается совместно и имеет одно решение.Вычислить дополнительные идентификаторы. Определитель δ 1 получается из определителя δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же образом получаем определитель δ 2 из определителя матрицы системы, заменяя второй столбец столбцом свободных коэффициентов:

Пусть система линейных уравнений содержит столько уравнений, сколько независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными.Определитель, составленный из коэффициентов с независимыми переменными системы (1.5), называется главным определителем системы. Обозначим его греческой буквой D. Так

. (1,6)

Если в произвольном столбце основного идентификатора ( j. ) заменить столбец свободных членов системы (1.5), то можно получить еще n. Вспомогательные идентификаторы:

( j. = 1, 2,…, n. ). (1,7)

Правило Крамера Решение квадратных систем линейных уравнений выглядит следующим образом.Если главный определитель D системы (1.5) отличен от нуля, то система имеет и, более того, единственное решение, которое можно найти по формулам:

(1,8)

Пример 1.5. Метод Крамера для решения системы уравнений

.

Вычислить главный определитель системы:

Поскольку D¹0, система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия с матрицами

1.Умножение матрицы на число. Операция умножения матрицы определяется следующим образом.

2. Для умножения матрицы на число все ее элементы умножаются на это число. Т.е.

. (1,9)

Пример 1.6. .

Добавление матриц.

Эта операция вводится только для матриц одного порядка.

Чтобы сложить две матрицы, необходимо добавить соответствующие элементы другой матрицы к элементам одной матрицы:

(1.10)
Операция расстановки матриц обладает свойствами ассоциативности и коммутации.

Пример 1.7. .

Матричное умножение.

Если количество столбцов матрицы А совпадает с количеством строк матрицы В Для таких матриц вводится операция умножения:

2

Таким образом, при умножении матрицы А размерности м. ´ п. на матрице IN размерностью n. ´ к. получаем матрицу ИЗ размерностью м. ´ к. . В этом случае элементы матрицы ИЗ рассчитываются по формулам:

Задача 1.8. Найдите, если возможно, работу матриц AB, и BA. :

Решение. 1) для того, чтобы найти работу AB , нужны строки матрицы A. умножить на столбцы матрицы Б. :

2) Работа БА. нет, так как количество столбцов матрицы B. не совпадает с количеством строк матрицы A. .

Обратная матрица. Решение систем линейных уравнений матричным методом

Матрица A – 1 называется квадратной матрицей НО Если выполняется равенство:

, где через I. обозначает одну матрицу того же порядка, что и матрица , НО :

.

Для того чтобы квадратная матрица была обратной, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратные матрицы находятся по формуле:

, (1.13)

, где A ij. – Алгебраические дополнения к элементам a ij. Матрицы НО (Обратите внимание, что алгебраические дополнения к строкам матрицы НО расположены в возвращаемой матрице в виде соответствующих столбцов).

Пример 1.9. Найдите обратную матрицу A – 1 к матрице

.

Обратная матрица Найдем по формуле (1.13), которая соответствует случаю n. = 3 имеет вид:

.

Находим Дет. A. = | A. | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Поскольку определитель исходной матрицы отличен от нуля, обратная матрица существует.

1) Найдем алгебраические сложения A ij.:

Для удобства нахождения обратной матрицы, алгебраические надстройки к строкам исходной матрицы мы располагаем в соответствующих столбцах.

Из полученных алгебраических сложений составим новую матрицу и разделим ее на определитель DET A. . Таким образом, мы получим обратную матрицу:

Квадратная система линейных уравнений с ненулевым главным определителем может быть решена с помощью обратной матрицы. Для этого система (1.5) записывается в матричной форме:

где

Умножая обе части равенства (1.14) на левую A – 1, мы получим системное решение:

От!

Таким образом, чтобы найти решение квадратной системы, нужно найти матрицу, обратную основной матрице системы, и умножить ее справа на столбец матрица-столбец.

Задача 1.10. Решите систему линейных уравнений

с использованием обратной матрицы.

Решение. Запишем систему в матричном виде:,

где – основная матрица системы, – столбец неизвестных и – столбец свободных элементов. Поскольку основной определитель системы, то основная матрица системы НО имеет обратную матрицу НО -один. Чтобы найти обратную матрицу НО -1, вычислите алгебраические дополнения ко всем элементам матрицы НО :

Из полученных чисел составим матрицу (и алгебраические дополнения к строкам матрицы НО запишем в соответствующие столбцы) и разделим ее на определитель D.Таким образом, мы нашли обратную матрицу:

Решение системы находится по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обычных жордановых исключений

Пусть произвольная (не обязательно квадратная) система линейных уравнений:

(1,16)

Требуется найти систему решений, т.е. такой набор переменных, который удовлетворяет всем равенствам системы (1.16). В целом система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. У него тоже может вообще не быть решений.

При решении таких задач используется метод исключения неизвестного, который еще называют методом обычных исключений Иордании из школьного курса. Суть этого метода состоит в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая одно уравнение к одному уравнению и на одну переменную меньше, чем исходная система.Запоминается уравнение, из которого выражена переменная.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. Например, в процессе исключения неизвестного некоторые уравнения могут превратиться в точные тождества. Такие уравнения из системы исключены, так как выполняются при любых значениях переменных и, следовательно, не влияют на решение системы. Если в процессе исключения неизвестного хотя бы одно уравнение сравняется, что невозможно выполнить ни при каких значениях переменных (например), то делаем вывод, что система не имеет решения.

Если при решении противоречивых уравнений не произошло, то из последнего уравнения в нем осталась одна из переменных. Если в последнем уравнении остается только одна переменная, она выражается числом. Если в последнем уравнении остаются другие переменные, они считаются параметрами, а переменная, выраженная через них, будет функцией этих параметров. Затем выполняется так называемое «обратное движение». Найденная переменная подставляется в последнее запомненное уравнение и находит вторую переменную.Затем две найденные переменные подставляются в предпоследнее сохраненное уравнение и находят третью переменную и так далее до первого запомненного уравнения.

В результате получаем решение системы. Это решение будет единственным, если найденные переменные будут числами. Если первая найденная переменная, а затем все остальные будут зависеть от параметров, у системы будет бесчисленное количество решений (каждый набор параметров соответствует новому решению). Формулы, позволяющие найти решение системы в зависимости от того, называется ли другой набор параметров общим решением системы.

Пример 1.11.

х.

Запомнив первое уравнение и приведя аналогичные члены во втором и третьем уравнениях, мы приходим к системе:

Экспресс г. Из второго уравнения и подставьте его в первое уравнение:

Запомним второе уравнение, а из первого найдем z. :

Верните референцию, стабильно найдем г. W. z. . Для этого сначала подставляем последнее запомненное уравнение, где находим у. :

.

Затем подставляем и в первое запомненное уравнение Где находим x. :

Задача 1.12. Решите систему линейных уравнений, исключив неизвестные:

. (1.17)

Решение. Выразите переменную из первого уравнения x. и подставляем во второе и третье уравнение:

.

Мы помним первое уравнение

В этой системе первое и второе уравнение противоречат друг другу. Действительно, выражая г. , у меня получается, что 14 = 17. Это равенство не выполняется ни при каких значениях переменных x. , г. , I. з. . Следовательно, система (1.17) невычислима, т.е. не имеет решения.

Предлагаем читателям самостоятельно проверить, что основной детерминант исходной системы (1.17) равен нулю.

Рассмотрим систему, которая отличается от системы (1.17) всего одним свободным членом.

Задача 1.13. Решите систему линейных уравнений, исключив неизвестные:

. (1.18)

Решение. Как и раньше, выразим из первого уравнения переменную x. и подставляем во второе и третье уравнение:

.

Мы помним первое уравнение и представляем аналогичные члены во втором и третьем уравнениях.Заходим в систему:

Выражение г. из первого уравнения и подставив его во второе уравнение Получим тождество 14 = 14, которое не влияет на решение системы, а значит, его можно исключить из системы.

В последней запомненной переменной равенства z. Рассмотрим параметр. Мы верим. Тогда

Заменитель г. W. z. в первом заученном равенстве и найти x.:

.

Таким образом, система (1.18) имеет бесчисленное множество решений, и любое решение можно найти по формулам (1.19), выбрав произвольное значение параметра t. :

(1.19)
Итак, системные решения, например, представляют собой следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. Д. Формулы (1.19) выражают общее (любое) решение система (1.18).

В случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обычных жордановых исключений кажется громоздким.Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы за один шаг в целом и сделать решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
Где x J. – независимые (искомые) переменные, a ij. – постоянные коэффициенты
( i =. 1, 2,…, м. ; j. = 1, 2,…, n.). Правые части системы y I. ( i = 1, 2,…, m. ) могут быть как переменными (зависимыми), так и постоянными. Требуется найти решения этой системы, исключив неизвестное.

Рассмотрим следующую операцию, которая в будущем будет называться «один шаг обычных исключений Иордании». Из произвольного ( r. -to) равенства выразить произвольную переменную ( x S. ) и заменить все остальные равенства. Конечно, это возможно только при RS. ¹ 0. Коэффициент а RS. Его называют разрешающим (иногда направляющим или основным) элементом.

Получим следующую систему:

. (1,21)

Из с. – Равенство системы Ho (1.21) Позже мы найдем переменную x S. (после того, как найдены остальные переменные). с. – строка помню и позже из системы исключена. Оставшаяся система будет содержать одно уравнение и одна независимая переменная меньше исходной системы.

Вычислить коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с с. р. – уравнение, которое после выражения переменной x S. через оставшиеся переменные будет выглядеть так:

Таким образом, новые коэффициенты р. Уравнения рассчитываются по следующим формулам:

(1,23)
Рассчитайте новые коэффициенты b IJ. ( я. ¹ р. ) произвольное уравнение. Для этого подставляем произносимую в (1.22) переменную x S. в i. – Уравнение системы (1.20):

Приведя таких членов, получаем:

(1.24)
Из равенства (1.24) получаем формулы, по которым вычисляются остальные коэффициенты системы (1.21) (кроме r. – Уравнения):

(1.25)
Преобразование системы линейных уравнений методом обычных жордановых исключений производится в виде таблиц (матриц).Эти столы получили название «Иордан».

Итак, задача (1.20) ставится в соответствие следующей Таблице Жорданова:

Таблица 1.1.

	х. 1	х. 2	…	x J.	…	x S.	…	x N.
г. 1 =	а. 11	а. 12		а. 1 Дж.		а. 1 с.		а. 1 н.
………………………………………………………………… ..
г. I. =	а I. 1	a I. 2		a ij.		а есть.		a IN.
………………………………………………………………… ..
г р. =	а Р. 1	а Р. 2		a RJ.		А RS.		а РН.
………………………………………………………………….
y N. =	а М. 1	а м. 2		a MJ.		а MS.		а MN.

Жортанова Таблица 1.1 Содержит левый заглавный столбец, в котором записаны правые части системы (1.20) и верхняя строка заголовка, в которую записаны независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу НО на матрицу, состоящую из элементов верхней строки заголовка, то матрица состоит из элементов левого заглавного столбца.То есть, по сути, Таблица Жорданова представляет собой матричную форму записи системы линейных уравнений:. Система (1.21) соответствует следующей таблице Жорданова:

Таблица 1.2.

	х. 1	х. 2	…	x J.	…	г. г.	…	x N.
г. 1 =	г. 11	г. 12		г. 1 Дж.		г. 1 С.		г. 1 Н.
………………………………………………………………… ..
y i =.	b I. 1	b I. 2		b IJ.		б.		б в
………………………………………………………………… ..
х s =.	б р. 1	б р. 2		b RJ.		b RS		млрд р-н.
………………………………………………………………….
y n =	б М. 1	б м. 2		б МДж.		b MS.		млрд Мн.

Элемент разрешающий а RS. Выделим жирным шрифтом. Напомним, что для реализации одного шага исключений Jordan разрешающий элемент должен быть отличным от нуля. Строка таблицы, содержащая разрешающий элемент, называется строкой разрешения.Столбец, содержащий разрешающий элемент, называется столбцом разрешения. При переходе от этой таблицы к следующей таблице одна переменная ( x S. ) Из строки заголовка таблица перемещается в левую прописную колонку и, наоборот, в один из свободных членов системы (). y R. ) Из левого заглавного столбца таблицы перемещается в верхнюю строку заголовка.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) в таблицу (1.2), полученную из формул (1.23) и (1.25).

1. Элемент разрешения заменяется обратным числом:

2. Остальные разрешающие строковые элементы делятся на разрешающий элемент и меняют знак на противоположный:

3. Остальные элементы столбца разрешения разделены на разрешающий элемент:

4. Элементы, не попадающие в строку разрешения и разрешающую колонку, пересчитываются по формулам:

Последнюю формулу легко запомнить, если учесть, что элементы, составляющие дробь, находятся на пересечении i. – I. р. Замок I. j. – I. с. – к столбцам (разрешающая строка, разрешающая столбец и строку и столбец, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы Вы можете использовать следующую диаграмму:

-21 -26 -13 -37

Делая первый шаг с исключениями Jordan, вы можете выбрать любой элемент таблицы 1.3, расположенный в столбцах, в качестве элемента разрешения. х. 1,…, х. 5 (все указанные элементы не равны нулю). Не выбирайте только элемент разрешения в последнем столбце, потому что нужно найти независимые переменные x. 1,…, х. пять. Выберем, например, коэффициент 1 С переменной х. 3 В третьей строке таблицы 1.3 (жирным шрифтом выделен элемент разрешения). При переходе к таблице 1.4 переменная х. 3 из верхней строки заголовка меняется местами с константой левого столбца 0 (третья строка).В данном случае переменная x. 3 выражается в других переменных.

Линия х. 3 (Таблица 1.4) можно запомнить, исключив из Таблицы 1.4. Из таблицы 1.4 третий столбец с нулем также исключен в верхней строке заголовка. Дело в том, что независимо от коэффициентов в этом столбце b I. 3 Все соответствующие члены каждого уравнения 0 · b I. 3 системы будут равны нулю. Следовательно, указанные коэффициенты не могут быть рассчитаны. Исключив одну переменную x. 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с освобожденной строкой x. 3). Выбрав в таблице 1.4 в качестве элемента разрешения b. 14 = -5, перейдите к Таблице 1.5. Таблица 1.5 запоминает первую строку и исключает ее из таблицы вместе с четвертым столбцом (с нулем вверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x. 1 = – 3 + 2 х. 5.

Последовательно подставляя переменные, уже найденные в сохраненных строках, находим оставшиеся переменные:

Таким образом, в системе есть бесчисленное множество решений.Переменная х. 5, можно задавать произвольные значения. Эта переменная действует как параметр x. 5 = т. Мы проверили системность системы и нашли ее общее решение:

Х. 1 = – 3 + 2 т.

X. 2 = – 1 – 3 т.

Х. 3 = – 2 + 4 т. . (1,27)
х. 4 = 4 + 5 т.

х. 5 = т.

Подача параметра т. различных значений Мы получим бесчисленное количество решений исходной системы. Так, например, системным решением является следующий набор переменных (- 3; – 1; – 2; 4; 0).

Калькулятор правила Крамера – система уравнений 2 и 3

Правило и калькулятор Крамера для анализа линейных цепей | Шаг за шагом с решенными примерами

Обновление: Мы добавили онлайн-калькулятор правил Крамера, в котором вы можете решить систему с двумя уравнениями, а также с системой из трех уравнений.Проверьте оба калькулятора правил Крамера в обоих разделах сообщения. Спасибо

Калькулятор правила Крамера для 2 × 2 (система двух уравнений)

Калькулятор правила Крамера 2 x 2 (система двух уравнений):

Поиск двух переменных по правилу Крамера:

003 Пример 1:

(В нашем случае неизвестными значениями являются два тока: i ₁ и i ₂ ) по правилу Крамера.А теперь приступим.

Как показано ниже, это простая электрическая схема, и мы собираемся решить ее по правилу Крамера.

Правило Крамера для анализа линейных цепей | 2 переменных (2 × 2) Решенный пример.

Решение:

Во-первых, переставьте схему с соответствующими метками (поскольку два резистора 5 Ом включены последовательно, поэтому мы заменим его на 10 Ом. Примените анализ сетки и упрощение по правилу Крамера, чтобы найти неизвестные значения токов i ₁ и i ₂ .

Теперь мы напишем уравнения KVL неизвестных значений для данной схемы.

Применим KVL к сетке (1).

6 = 14 i ₁ + 10 ( i ₁ – i ₂ )

6 = 24 i ₁ – 10 i ₂ … .. → Уравнение (1)

Также примените KVL к сетке (2).

-5 = 10 i ₂ + 10 ( i ₂ – i ₁ )

-5 = – 10 i ₁ + 20 i ₂ ….. → Уравнение (2)

Здесь мы получили два уравнения, т.е.

24 i ₁ – 10 i ₂ = 6

– 10 i ₁ + 20 i ₂ = -5

Теперь мы решим эти два уравнения по правилу Крамера, чтобы найти неизвестные значения (токов), которые равны i ₁ и i ₂ .

Решение по правилу Крамера:

Шаг 1:

Прежде всего, запишите приведенные выше уравнения в матричной форме. то есть

Шаг 2:

Теперь напишите матрицу коэффициентов приведенных выше уравнений и назовите ее ∆. Убедитесь, что он квадратный, то есть количество строк x количество столбцов. В приведенном выше случае у него 2 строки и 2 столбца.

Шаг 3:

Теперь найдите определитель | ∆ | матрицы коэффициентов ∆ следующим методом.(В этом вам поможет приведенный ниже рисунок.)

Щелкните изображение, чтобы увеличить

Нахождение матрицы коэффициентов ∆ для правила Крамера. Простое объяснение. Согласно приведенному выше рис. последний шаг будет таким.

Шаг 4:

Теперь найдите определитель коэффициента Δ ₁ тем же способом, как указано выше, но замените первый столбец Δ на «Столбец ответов» (если вы этого не сделали получить точку в столбце ответа, см. рис. на шаге 2 выше или проверьте инфографику в конце примера или просто обратитесь к второму примеру ниже, где мы сделали то же самое, чтобы найти Δ ₁ ) то есть

Шаг 5:

Теперь найдите определитель коэффициента Δ ₂ , просто замените второй столбец на «Столбец ответа», который равен

Шаг 6:

По правилу Крамера сообщает, что i ₁ = Δ ₁ / Δ и i ₂ 10

4 / Δ .

Теперь найдите i ₁ и i ₂ по правилу Крамера.

i ₁ = 0,184,2 A или 184,2 мА

And,

i ₂ = 0,157,9 A или 157,94 мА

Ниже приведена сводка инфографики правила Крамера для определения двух переменных или неизвестных значений.

Правило Крамера Инфографическая диаграмма простых шагов

Хорошо, это было легко… А как насчет трех переменных…. Давайте попробуем решить линейные уравнения с тремя переменными с помощью правила Крамера.

Поиск трех переменных по правилу Крамера:

(В нашем случае эти неизвестные значения представляют собой три тока, которые равны i ₁ , i

34 2 9 i ₃ ) по правилу Крамера.А теперь приступим.

Калькулятор правила Крамера для 3 × 3 (система трех уравнений)

Калькулятор правила Крамера 3 x 3 (3 системы уравнений):

Пример 2:

Используйте анализ сетки для определения трех сетка токов в схеме ниже. Для упрощения воспользуйтесь правилом Крамера.

Найдите три неизвестных значения токов по правилу Крамера.

Прежде всего, примените KVL к каждой сетке одну за другой и напишите ее уравнения.

-7 + 1 ( i ₁ – i ₂ ) + 6 + 2 ( i ₁ – i ₃ ) = 0

1 ( i ₂ – i ₁ ) + 2 i ₂ + 3 ( i ₂ – i ₃ ) = 0

2 ( i ₃ – i ₁ ) – 6 + 3 ( i ₃ – i ₂ ) + 1 i ₃ = 0

Упрощение,

3 i ₁ – i ₂ – 2 i ₃ = 1… уравнение….. (1)

– i ₁ + 6 i ₂ – 3 i ₃ = 0… уравнение… .. (2)

-2 i ₁ – 3 i ₂ + 6 i ₃ = 6… Eq… .. (3)

Теперь запишите приведенные выше уравнения в матричной форме.

3 i ₁ – i ₂ – 2 i ₃ = 1

– i ₁ + 6 i ₂ – 3 i ₃ = 0

-2 i ₁ -3 i ₂ + 6 i ₃ = 6

Теперь найдем определяющий коэффициент ∆.Как мы это сделаем? Просто посмотрите на рис ниже, чтобы лучше понять.

Щелкните изображение, чтобы увеличить Итак, полный шаг показан ниже.

∆ = +3 (6 x 6) – (- 3 x –3) – (-1 (-1 x 6) – (- 2 x –3) + (-2 (-1 x –3) – (- 2 x 6)

∆ = 81-12-30 = 39

Теперь найдите ∆ ₁ таким же способом, как описано выше. Но просто замените первый столбец матрицы на «Ответ. Столбец ». Подробности см. На рисунке ниже. Итак, вот полный шаг, чтобы найти ∆ ₁ .Здесь мы заменили «Синие парни» в первой колонке на «Черные парни» :).

= +1 (36-9) – (–1 [0 + 18]) –2 (0-36)

= 27 + 18 + 72

∆ ₁ = 117

Снова найдите ∆ ₂ тем же способом, как описано ранее. Просто замените второй столбец матрицы на «столбец ответов», т.е. замените «красных парней» в центральном столбце на «черных парней», как показано ниже.

= +3 (0 +18) -1 [(- 6) – (+ 6)] –2 (-6-0)

= 54 + 12 + 12 = 78

∆ ₂ = 78

Наконец, найдите последний ∆ ₃ .Просто замените третий столбец столбцом «Ответить», т.е. замените «Зеленые парни в третьем столбце» на «Черные парни», как показано ниже.

= +3 (6 x 6) – (-3 x 0) – [-1 (-1 x 6) – (-2 x 0)] + [1 (-1) x (-3) – (-2 ) x (6)]

= 108 + 6 + 15

∆ ₃ = 117

Теперь решите и найдите неизвестные значения тока, т.е. i ₁ , i ₂ и i ₃ .

As, правило Крамера гласит, что переменные i.е. i ₁ = ∆1 / ∆ ₁ , i ₂ = ∆ / ∆ ₂ и i ₃ = ∆ / ∆ ₃ .

Следовательно,

i ₁ = ∆1 / ∆ ₁

= 117/39

0 i

6

4

4

И i ₂ ,

i ₂ = = ∆ / ∆ ₂

= 78/39

2 = 2A

И, наконец, i ₃ ;

i ₃ = ∆ / ∆ ₃

= 117/39

i ₃ = 3A.

Я надеюсь, что вы очень хорошо поняли правило крамера и получили удовольствие от пошагового руководства. Пожалуйста, не забудьте поделиться с друзьями. Также введите свой адрес электронной почты в поле ниже, чтобы подписаться. Итак, мы отправим вам больше руководств, подобных приведенному выше. Спасибо.

Связанные сообщения и инструменты анализа цепей:

Решите систему уравнений

Решите систему уравнений

Решение систем линейных неравенств. Решение системы линейных неравенств аналогично решению системы линейных уравнений, но с неравенствами мы не находим точку (или точки) пересечения.Вместо этого набором решений будет область, которая удовлетворяет всем линейным неравенствам. Лучший способ решить систему линейных

Решение систем уравнений с двумя переменными Система линейного уравнения состоит из двух или более уравнений, и одно ищет общее решение уравнений. В системе линейных уравнений каждому уравнению соответствует прямая линия, и каждый ищет точку, где две линии пересекаются.

6 ноября 2018 г. · Решая x-5y = 6 3x + 2y = 1 с помощью TiNspire CX CAS, вы можете использовать либо метод замены, либо метод исключения.Давайте продемонстрируем, как использовать t Решите систему уравнений 2×2 – Шаг за шагом – используя TiNSpire CX – www.TiNspireApps.com – Блог

Распределительный рабочий лист уравнений, выучите перестановки и комбинации, решите «систему дифференциальных уравнений» или пример MATLAB , для некоторых примеров математических мелочей, радикальное математическое объяснение формы. Ответы по алгебре II, нелинейные дифференциальные уравнения, примеры работ по тесту на способность к основному обучению.

Пусть Y (s) = L [y (t)] (s). Вместо прямого решения для y (t) мы выводим новое уравнение для Y (s).Как только мы находим Y (s), мы выполняем обратное преобразование, чтобы определить y (t). Первым шагом является преобразование Лапласа обеих частей исходного дифференциального уравнения. Очевидно, что преобразование Лапласа функции 0 равно 0. Если мы посмотрим на

Чтобы решить систему из n уравнений для n неизвестных: 1. Наберите [Ctrl] M, чтобы создать вектор, имеющий n строк и 1 столбец. 2. Заполните каждый заполнитель вектора одним из Mathcad, отображающих n решений системы уравнений справа от символического знака равенства.На рис. 13-11 показан пример.

Система линейных уравнений может быть решена различными способами, например, используя метод Крамера и метод Гаусса, метод Гаусса Джордана и метод Кронекера Капелли, или другими способами. Используя наш сервис, вы можете получать бесплатные решения онлайн разными способами с помощью пошаговых действий и …

Решение системы уравнений с помощью Numpy / Scipy. С помощью одной простой строки кода Python, следующих строк для импорта numpy и определения наших матриц, мы можем получить решение для X.Документация для numpy.linalg.solve (это решатель линейной алгебры для numpy) ЗДЕСЬ. приведенный ниже код хранится в репо как System_of_Eqns_WITH_Numpy-Scipy.py.

Craigslist округа Скагит домашние животные

Для решения Системы линейных уравнений существует множество различных методов. Исключение Гаусса имеет временную сложность O (n3), где, как правило Крамера, требуется найти обратную матрицу, образованную коэффициентами линейных уравнений в системе.Воспользовавшись этим онлайн-калькулятором, вы получите подробное пошаговое решение вашей задачи, которое поможет вам понять алгоритм решения системы линейных уравнений.

Классический велосипед родстер

Система линейных уравнений – это набор линейных уравнений, которые включают один и тот же набор переменных. В качестве примера. Замените решенное значение обратно в исходные уравнения, чтобы найти оставшиеся переменные. Выполним описанные выше шаги, чтобы решить следующую систему уравнений.

При словесном и / или алгебраическом описании ситуаций, включающих системы двух переменных линейных уравнений, студент решит систему уравнений.

Решение систем линейных уравнений. Этот калькулятор решает системы линейных уравнений с использованием метода исключения Гаусса, метода обратной матрицы или правила Крамера. Кроме того, вы можете вычислить ряд решений в системе линейных уравнений (проанализировать совместимость) с помощью теоремы Руше – Капелли. Бесплатная программа для решения математических задач отвечает на ваши домашние задания по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми пояснениями, как репетитор по математике.

Trane очищает заменяемые детали

Если x – количество кошек, а y – количество птиц, проблема со словом описывается этой системой уравнений: в этой задаче x означает количество кошек, а y означает количество кошек. количество птиц.Чтобы иметь осмысленную систему уравнений, нам нужно знать, что представляет собой каждая переменная. Если мы сможем овладеть этим навыком, мы будем сидеть в …

Уравнение Шредингера – это линейное уравнение в частных производных, которое описывает волновую функцию или функцию состояния квантово-механической системы .: 1–2 Это уравнение ключевой результат в квантовой механике, и его открытие стало важной вехой в развитии предмета.

Решите систему, в которой коэффициенты одной переменной противоположны.2-й шаг: «Умножить ни одно, одно или оба уравнения на константу (и) так, чтобы коэффициенты одной из переменных были противоположны». это самое интересное! Благодаря простой арифметике сложная комбинация уравнений сводится к одному простому уравнению. Это пришло от математиков, пытающихся решить системы линейных уравнений. Для решения этих систем используются векторы и матрицы. Основными объектами изучения в настоящее время являются векторные пространства и линейные отображения между векторными пространствами. Линейная алгебра полезна в других разделах математики (например,грамм. дифференциальные уравнения и аналитическая геометрия).

Бесплатные файлы цветов в формате dxf

Решение систем нелинейных уравнений в Excel Найдите лучший ответ на систему алгебраических уравнений. NLSOLVE – это мощная функция решателя электронных таблиц, основанная на алгоритме Левенберга-Марквардта, которая подходит для: Нахождения корней нелинейных уравнений.

Системы уравнений – Замена Цель: Решить системы уравнений с помощью замены. При решении системы с помощью построения графиков есть несколько ограничений.Во-первых, это требует, чтобы график был нарисован идеально. Если линии не прямые, мы можем прийти к неправильному ответу. Во-вторых, построение графиков не лучший метод, если ответ –

Решите систему трех линейных уравнений и проверьте решение: Решите систему четырех линейных уравнений и проверьте решение: Решите систему линейных и квадратных уравнений: Решите система линейных неравенств с одной переменной: Решите систему линейных неравенств с двумя переменными: Вас также может заинтересовать: 06 января 2016 г. · После того, как студенты научились писать, решать и интерпретировать системы уравнений с использованием нескольких представлений, Я учил студентов решать алгебраические задачи (приравнивая уравнения).Студенты осознали, что использование уравнений при решении является наиболее эффективным методом для систем уравнений в ситуациях.

Elansar jaguar demo

6 января, 2016 · После того, как студенты научились писать, решать и интерпретировать системы уравнений с использованием нескольких представлений, я научил их решать алгебраически (приравнивая уравнения). Студенты осознали, что использование уравнений при решении является наиболее эффективным методом для систем уравнений в ситуациях.

Бесплатный калькулятор системы линейных уравнений – решите систему линейных уравнений, шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используя этот сайт, вы соглашаетесь с нашей Политикой в ​​отношении файлов cookie.

Для данной системы уравнений после подстановки упростим левую часть оставшегося уравнения. Не решай. 2.5x + y = -2 3x + 2y = 0 Уравнения имеют единственное решение, если все плоскости пересекаются в одной точке. Три непротиворечивых уравнения A <- matrix (c (2, 1, -1, -3, -1, 2, -2, 1, 2), 3, 3, byrow = TRUE) colnames (A) <- paste0 (' x ', 1: 3) b <- c (8, -11, -3) showEqn (A, b)

Срок действия сертификата Vpn истек iphone

Get Easy Solution – Решатель уравнений.Разве ты не знаешь, как решить домашнее задание по математике? У вас есть проблемы с решением уравнения с одним неизвестным? Может быть, Вам нужна помощь с квадратными уравнениями или с системами уравнений? Проценты, производные или другая математическая задача для Вас головная боль? Вы попали в нужное место! Мы поможем Вам со всеми …

Обратите внимание, как элементы матрицы соответствуют числам в исходной системе из трех уравнений [2] Решите матричное уравнение, полученное на шаге [1] выше; т.е. найти X.

алгебра Системы уравнений – Задачи | Проблемы с ответами от Cymath Solver.Cymath – это онлайн-программа для решения математических уравнений и мобильное приложение. В этом уроке давайте воспользуемся подстановкой, которая кажется наиболее интуитивно понятным методом для начинающих. Решите следующую систему уравнений. Просмотр 05_03 Примерное решение систем уравнений. Docx из MATH 2104 Университета Флориды. Имя: Дата: 06.02.17. 05.03 Инструкции по назначению 1. Заполните приведенную ниже таблицу, чтобы решить уравнение.

Fukushuu kansuisha no jinsei nishuume isekaitan Новые обновления

16 сентября 2020 г. · Решение линейных уравнений в Excel с помощью матричной системы Мы можем использовать матричную систему для решения набора линейные уравнения в Excel.Допустим, у нас есть 3 уравнения, в которых значения x, y и z неизвестны.

Перезагрузите все компьютеры в ОУ

Магазин Taurus g2c на 10 патронов

Как исправить протекающий кувшин для воды

Специальная версия Skyrim исправление окон без полей

shape

Морские маршруты доставки Серийный номер в imei без конвертера

Как обойти маршрутизатор gryphon

Корейский WhatsApp group link 2020

Bennche cowboy 250 частей

Gm шкив клинового ремня генератора

водородные связи

может метанол

вода

Np repeat pytorch

Pioneer w4500nex vs w8500nex

Клиент Vmware Horizon без мыши

Macbook pro egpu x plane 11

9000 синий экран 4k видео песни скачать

900 02 Продажа классических грузовиков Dallas

База знаний

Посмотреть наши новые продукты Просмотреть все продукты ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]>

]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]>

]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]>

]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]>

]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]> ]]>

Контроль и управление Конфигураторы

.