Пример 26 Согласно алгоритму, чтобы раскрыть неопределенность ∞/∞ дважды применяем правило Лопиталя.
Пример 27 Переходим от неопределенности вида ноль умножить на бесконечность к неопределенности бесконечность разделить на бесконечность, которую раскрываем по правилу Лопиталя через дифференцирование числителя и знаменателя дроби. Внимательно посмотрите схему перехода от одной неопределенности к другой и запомните, что когда имеем произведение логарифма на другую функцию, то в знаменатель переносим последнюю, а не логарифм.
Пример 28 Прямая подстановка дает неопределенность ноль умножить на бесконечность 0*∞
Чтобы свести пример к применению правила Лопиталя в искусственный способ котангенс переносим в знаменатель дроби, а далее заменяем 1/ctg(x)=tg(x). Таким образом получаем особенность в виде доли бесконечно малых функций, раскрываем дифференцированием по Лопиталю и подстановкой x=0.
Раскрытие неопределенностей ∞-∞
Пределы с неопределенностью ∞-∞ также раскрываем по правилу Лопиталя, но предварительно проводим определенные элементарные действия над слагаемыми, чтобы перейти от разности бесконечно больших функций к дроби.
Пример 29 Формулы ниже хорошо иллюстрируют как дважды применяли дифференцирование числителя и знаменателя дроби, чтобы избавиться от неопределенности 0/0.
Пример 30 Имеем неопределенность вида ∞-∞, которую раскрываем путем сведения дробей к общему знаменателю. Далее по правилу Лопиталя вычисляем производные числителя и знаменателя, и так дважды.
И только когда избавляемся неопределенности выполняем подстановку аргумента в предел. Считаем, чтобы начать решать примеры на правило Лопиталя, 30 приведенных примеров вполне достаточно. Если есть проблемы с расчетными или модулями, то всегда можете обращаться к нам за помощью!
как применять для раскрытия неопределенностей, примеры с решениями
 При этом важно владеть навыками дифференцирования.
При этом важно владеть навыками дифференцирования.Правило Лопиталя — в чем суть, понятие
Название этой закономерности не совсем соответствует действительности. Было бы правильнее говорить «правило Лопиталя — Бернулли». Первая подробная формулировка была представлена швейцарским математиком Иоганном Бернулли. Французский ученый Гийом Лопиталь впервые опубликовал это правило в издании собственного учебника в 1696 году.
Правило Лопиталя позволяет существенно упростить некоторые расчеты предела отношения \(\displaystyle \frac{f(x)}{g(x)}\) при \(x\rightarrow a\) в том случае, когда \(f\) и \(g\) одновременно представляют собой бесконечно малые, либо бесконечно большие величины. С помощью выведенной закономерности допустимо осуществлять замену предела отношения функции, используя предел отношения их производных.
Доказательство 1 и 2 правила Лопиталя, вывод теоремы
Теорема 1
Допустим, что функции \(f(x)\) и \(g(x)\) дифференцируются на промежутке \((a,b)\):
\(\lim_{x\rightarrow a+0}f(x)=0\)
\(\lim_{x\rightarrow a+0}g(x)=0\)
\(g'(x)\neq 0\ \) для всех \(\ x\in(a,b)\)
Тогда имеет место конечный и бесконечный:
\(lim_{x\rightarrow a+0}\frac{f'(x)}{g'(x)}=A\)
Таким образом, также существует и равен A:
Можно сделать вывод:
\(\lim_{x\rightarrow a+0}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a+0}\frac{f'(x)}{g'(x)}\)\(\lim_{x\rightarrow a+0}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a+0}\frac{f'(x)}{g'(x)}\)
Докажем данную теорию.
Допустим, что \(x\in(a,b)\)
Следует доопределить функции \(f(x)\) и \(g(x)\) в точке a, имея в виду, что:
\(f(a)=g(a)=0\)
Таким образом, из условий функций следует, что \(f\) и \(g\) непрерывны на отрезке [a,x]. По теореме Коши имеется точка \(\xi\in (a,x)\), такая, что:
По теореме Коши имеется точка \(\xi\in (a,x)\), такая, что:
\(\frac{f(x)}{g(x)}=\frac{f(x)-f(a)}{g(x)-g(a)}=\frac{f'(\xi)}{g'(\xi)}\)
В том случае, когда \(x\rightarrow a+0\), можно определить, что \(\xi\rightarrow a+0\). Зная, что существует \(\displaystyle \lim_{x\rightarrow a+0}\frac{f'(\xi)}{g'(\xi)}=A\), можно сделать вывод о справедливости утверждения \(\eqref\).
Теорема, доказательства которой представлены путем соответствующих изменений ее условий, работает, когда \(x\rightarrow a-0\) и \(x\rightarrow a\). Точка a в данном случае является конечной.
Теорема 1 остается справедливой в таких ситуациях, когда \(a=+\infty\) или \(a=-\infty\), а также:
\(\displaystyle \lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty} g(x)=0\)
\(\ g'(x)\neq 0\) при \(x > x_0\)и существует \(\displaystyle \lim_{x\rightarrow +\infty}\frac{f'(x)}{g'(x)}=A\)
В этом случае \(\displaystyle \lim_{x\rightarrow +\infty}\frac{f(x)}{g(x)}=A\)
Доказательство данного утверждения выполнено с помощью замены переменного \(\displaystyle x=\frac{1}{t}\) и Теоремы 1.
Теорема 2
Допустим, что функции \(f(x)\) и \(g(x)\) дифференцируются при \(x > \alpha\) и \(g'(x)\neq 0\) при \(x > \alpha\)
\(\lim_{x\rightarrow+\infty}f(x)=\infty,\quad \lim_{x\rightarrow +\infty}g(x)=\infty\)
и существует конечный:
\(\lim_{x\rightarrow +\infty}\frac{f'(x)}{g'(x)}=A\)
В таком случае, существует \(\displaystyle \lim_{x\rightarrow +\infty}\frac{f(x)}{g(x)}\), равный A.
Таким образом:
\(\lim_{x\rightarrow +\infty}\frac{f(x)}{g(x)}=\lim_{x\rightarrow +\infty}\frac{f'(x)}{g'(x)} \)
Доказательство
Зная, что:
\(\exists\alpha_{1} > \alpha:\ \forall x > \alpha_{1}\rightarrow\ |f(x)| > 1\)
\(\ |g(x)| > 1\)
Исходя из записанного выражения, получим, что \(f(x)\neq 0\) и \(\ g(x)\neq 0\) при \(x > \alpha_1\).
Согласно определению, для заданного числа \(\varepsilon > 0\) можно вычислить \(\delta=\delta_1(\varepsilon)\geq \alpha_1\) такое, что для всех \(t > \delta_{1}\) выполняется неравенство:
\(A-\frac{\varepsilon}{2} < \frac{f'(t)}{g'(t)} < A+\frac{\varepsilon}{2}\)
Источник: univerlib. {-1} < A+\frac{\varepsilon}{2}\)
{-1} < A+\frac{\varepsilon}{2}\)Когда \(x > \delta\), получаем \(\phi(x) > 0.\)
Таким образом, выведенное неравенство равносильно следующему:
\((A-\frac{\varepsilon}{2})(1+\beta(x)) < \frac{f(x)}{g(x)} < (A+\frac{\varepsilon}{2})(1+\beta(x))\)
Исходя из этого утверждения, можно записать:
\((A-\frac{\varepsilon}{2})(1+\beta(x))=A-\frac{\varepsilon}{2}+\left(A-\frac{\varepsilon}{2}\right)\beta(x)\geq A-\frac{\varepsilon}{2}-\left(|A|+\frac{\varepsilon}{2}\right)|\beta(x)| > A-\frac{\varepsilon}{2}-\frac{\varepsilon}{2}=A-\varepsilon\)
Аналогичным способом можно определить:
\(\left(A+\frac{\varepsilon}{2}\right)(1+\beta(x)) \leq A+\frac{\varepsilon}{2}+\left(|A|+\frac{\varepsilon}{2}\right)|\beta(x)| < A+\varepsilon\)
Получим, что для всех \(x > \delta\) справедливо выведенное в теореме неравенство.
Теорема 2 работает при условии, что \(A=+\infty\) или \(A=-\infty\).
Теорема справедлива и в тех случаях, когда \(x\rightarrow a\ (x\rightarrow a-0,\ x\rightarrow a+0)\), где a является конечной точкой.
Правило Лопиталя для вычисления пределов
Решить пределы можно различными методами и формулами. Наиболее быстрый и простой способ, а также универсальный — это правило Лопиталя. Умение искать производные разных функций позволит использовать данную закономерность наиболее эффективно. Можно сформулировать правило Лопиталя при следующих условиях:
- \(\lim \limits_{x \to a} f(x) = \lim \limits_{x \to a} g(x) = 0 \text{ или } \infty\)
- имеются \(f'(a) \text{ и } g'(a)\)
- \(g'(x)\neq0\)
- присутствует \(\lim \limits_{x \to a} \frac{f(x)}{g(x)}\)
В таком случае:
\(\lim \limits_{x \to a} \frac{f(x)}{g(x)} = \lim \limits_{x \to a} \frac{f'(x)}{g'(x)}\)
Последовательность решения:
- нужно подставить точку x в предел;
- в том случае, когда получается \(\frac{0}{0} \text{ или } \frac{\infty}{\infty}\), можно определить производную числителя и знаменателя;
- далее следует подставить точку x в записанный предел и рассчитать его.

Правилом Лопиталя допустимо пользоваться при решении задач с односторонними пределами. Можно сказать, что эта методика является наиболее эффективной для раскрытия неопределенностей вида \(\frac{0}{0}\) и \(\frac{\infty}{\infty}\) в том случае, когда необходимо вычислить предел. Смысл правила заключается в том, что предел отношения функций равен пределу отношений производных от этих функций. Если в процессе освоения этой и других подобных тем возникли сложности, всегда можно обратиться за помощью к сервису Феникс.Хелп.
Правило Лопиталя
Правило Лопиталя
Правило Лопиталя:при некоторых условиях предел отношения функций, переменная которых стремится к $a$, равен пределу отношения их производных, при $x$, также стремящемся к $a$ :
$\mathop{\lim }\limits_{x\to a} \frac{f(x)}{g(x)} =\mathop{\lim }\limits_{x\to a} \frac{f'(x)}{g'(x)} $
Правило Лопиталя было открыто шведским математиком Иоганном Бернулли, который затем рассказал в письме о нём Лопиталю.
 Лопиталь же опубликовал это правило в первом учебнике по дифференциальному исчислению в 1696 году со своим авторством.
Лопиталь же опубликовал это правило в первом учебнике по дифференциальному исчислению в 1696 году со своим авторством.Правило Лопиталя применяется для выражений, сводимых к неопределенностям следующего вида:
$\frac{0}{0} \begin{array}{ccc} {} & {} & {\frac{\infty }{\infty } } \end{array}$
Вместо нуля в первом выражении может быть какая-либо бесконечно малая величина.
В общем случае правилом Лопиталя можно воспользоваться, если и в числителе, и в знаменателе одновременно нуль или бесконечность.
Условия, при которых можно применять правило Лопиталя:
- Соблюдается условие, при котором пределы функций $f(x)$ и $g(x)$ при $x$ стремящемся к $a$ равны между собой и стремятся к нулю или бесконечности: $\mathop{\lim }\limits_{x\to a} f(x)=\mathop{\lim }\limits_{x\to a} g(x)=0$ или $\mathop{\lim }\limits_{x\to a} f(x)=\mathop{\lim }\limits_{x\to a} g(x)=\infty $;
- Возможно получить производные $f(x)$ и $g(x)$ в окрестности $a$;
- Производная функции $g(x)$ не нулевая $g'(x)\ne 0$ в окрестности $a$;
- Предел отношения производных функций $f(x)$ и $g(x)$, в записи выглядящий как $\mathop{\lim }\limits_{x\to a} \frac{f'(x)}{g'(x)} $ существует.

Доказательство правила Лопиталя:
- Пусть даны функции $f(x)$ и $g(x)$, причём наблюдается равенство пределов:
- $\mathop{\lim }\limits_{x\to a+0} f(x)=\mathop{\lim }\limits_{x\to a+0} g(x)=0 $.
- Доопределим функции в точке $a$. Для этой точки будет справедливым условие:
- $\frac{f(x)}{g(x)} =\frac{f(x)-f(a)}{g(x)-g(a)} =\frac{f'(c)}{g'(c)}$.
- Величина $c$ зависит от $x$, но если $x\to a+0$, то $c\to a$.
- $\mathop{\lim }\limits_{x\to a+0} \frac{f(x)}{g(x)} =\mathop{\lim }\limits_{c\to a+0} \frac{f'(c)}{g'(c)} =\mathop{\lim }\limits_{x\to a+0} \frac{f'(c)}{g'(c)} $.
Готовые работы на аналогичную тему
Алгоритм вычисления решения с использованием правила Лопиталя
- Проверка всего выражения на неопределенность.
- Проверка всех условий, изложенных выше перед дальнейшим использованием правила Лопиталя.
- Проверка стремления производной функции к $0$.
- Повторная проверка на неопределенность.
 {1/x} =1$
{1/x} =1$Решение высшей математики онлайн
‹– НазадНа основе теоремы Коши мы выведем правило, которое даст нам мощный способ вычисления пределов отношений двух бесконечно малых или двух бесконечно больших величин. Сформулируем его сначала для отношения бесконечно малых.
Доказательство. Заметим, что из условия следует, что оба односторонних предела также равны :
иПусть , . По теореме Коши, применённой к отрезку , получим тогда, с учётом того, что ,
где . Перейдём теперь в этом равенстве к пределу при : так как, очевидно, при имеем также . Теперь возьмём точку , и применим теорему Коши к отрезку . Получим где . Переходя к пределу при , получаем так как при имеем .
Теперь возьмём точку , и применим теорему Коши к отрезку . Получим где . Переходя к пределу при , получаем так как при имеем .Итак, оба односторонних предела отношения равны . На основании теоремы о связи односторонних пределов с двусторонним получаем, что
Пример 5.3 Найдём предел .Этот предел представляет собой предел отношения двух бесконечно малых, поскольку и .
Заметим прежде всего, что предел можно упростить, заменив знаменатель на эквивалентную бесконечно малую: при . Получим:
Числитель упростить пока не удаётся, поскольку правила вычисления пределов не позволяют нам заменять на эквивалентные слагаемые (а не множители). В предположении, что предел существует, найдём вместо него предел отношения производных, который, в соответствии с доказанной теоремой, равен исходному: Получившийся предел — снова предел отношения бесконечно малых, но его легко вычислить, заменив числитель на эквивалентную бесконечно малую: при . Получаем: Итак, получили, что предел отношения производных, действительно, существует и равен . По правилу Лопиталя отсюда следует, что исходный предел также существует и равен тому же числу: Следовательно,
В предположении, что предел существует, найдём вместо него предел отношения производных, который, в соответствии с доказанной теоремой, равен исходному: Получившийся предел — снова предел отношения бесконечно малых, но его легко вычислить, заменив числитель на эквивалентную бесконечно малую: при . Получаем: Итак, получили, что предел отношения производных, действительно, существует и равен . По правилу Лопиталя отсюда следует, что исходный предел также существует и равен тому же числу: Следовательно, Замечание 5.6 Доказанное правило Лопиталя не означает, что если предел отношения производных не существует, то не существует и исходный предел.
Пример 5.4 Рассмотрим предел Его легко вычислить, заметив, что величина — величина, локально ограниченная при базе , а величина — бесконечно малая: Следовательно, их произведение — бесконечно малая величина, и С другой стороны, попробуем применить к исходному пределу отношения двух бесконечно малых и правило Лопиталя и вычислить предел отношения производных этих двух функций. Имеем: и . Этот исходный предел вполне может существовать, только его нельзя найти при помощи применения правила Лопиталя. Иными словами, правило Лопиталя не является универсальным средством отыскания пределов отношения двух бесконечно малых. Пример предела, который нельзя отыскать с помощью правила Лопиталя, мы сейчас приведём.
Этот исходный предел вполне может существовать, только его нельзя найти при помощи применения правила Лопиталя. Иными словами, правило Лопиталя не является универсальным средством отыскания пределов отношения двух бесконечно малых. Пример предела, который нельзя отыскать с помощью правила Лопиталя, мы сейчас приведём.  Составим отношение этих двух производных: В этом выражении первое слагаемое имеет, очевидно, при предел, равный 0, а второе не имеет никакого предела; следовательно, не имеет предела и сумма.
Составим отношение этих двух производных: В этом выражении первое слагаемое имеет, очевидно, при предел, равный 0, а второе не имеет никакого предела; следовательно, не имеет предела и сумма.Итак, исходное отношение бесконечно малых имеет предел, равный 0, в то время как отношение производных этих бесконечно малых не имеет никакого предела. Получаем, что применение к данному примеру правила Лопиталя не приводит к желаемому вычислению предела.
Правило Лопиталя действует не только при базах , , , но и при базах , , . Докажем это.
Доказательство. Положим и рассмотрим функции и Тогда функции и непрерывны на отрезке и дифференцируемы при .
К бесконечно малым при величинам и можно применить правило Лопиталя ( теорема 5.5 для предела справа, см. замечание 5.5): При этом
При этом
Распространим теперь правило Лопиталя на случай, когда функции и являются бесконечно большими величинами при данной базе (о бесконечно больших величинах см. раздел 2.7).
Доказательство. За полным доказательством этого утверждения мы отсылаем к книгам [Никольский С. М., Курс математического анализа. Том 1. — М.: Наука, 1990. — С. 200 – 201] или [Смирнов В. И., Курс высшей математики. Том 1. — М.: Наука, 1974. — С. 157 – 158]. Здесь же мы докажем, что оба предела совпадают, в предположении, что второй из них существует и оба не равны 0.
где — некоторое число. Докажем, что тогда . Итак, пусть
Итак, пустьРассмотрим вспомогательные функции и
Тогда функции и — бесконечно малые при , непрерывные при ; их производные таковы:
Заметим теперь, что при
и
Из равенства (5.3) получаем, что . Переходя к пределу в равенстве (5.4), получаем: С другой стороны, применяя правило Лопиталя ( теорема 5.5) к бесконечно малым функциям и , получим: откуда Из этого равенства следует, что , что и требовалось доказать.
Замечание 5. 8 Как и в основном случае отношения двух бесконечно малых при , все остальные варианты правила Лопиталя не универсальны: если предел отношения производных не существует, то это ещё не означает, что нет предела отношения исходных величин.
8 Как и в основном случае отношения двух бесконечно малых при , все остальные варианты правила Лопиталя не универсальны: если предел отношения производных не существует, то это ещё не означает, что нет предела отношения исходных величин. Приведём ещё один пример, иллюстрирующий это важное замечание.
Несмотря на свою неуниверсальность, правило Лопиталя служит весьма мощным средством нахождения сложных пределов. При этом иной раз приходится применять это правило много раз подряд, пока не получим предел, значение которого либо очевидно, либо может быть вычислено каким-либо способом, изученным нами ранее (например, с помощью замены на эквивалентные бесконечно малые).
Пример 5.6 Найдём предел . (Это предел отношения двух бесконечно малых. Заметим, что не является множителем, так что его нельзя заменить на эквивалентную величину ; если бы мы всё же сделали это, то сразу получили бы в числителе 0, и “ответ” равнялся бы 0. ) Применим правило Лопиталя и получим, что в предположении, что последний предел существует. Этот последний предел можно найти, заметив, что при , и заменив числитель. Однако можно пойти и другим путём. Мы снова получили отношение двух бесконечно малых, к которому снова применим правило Лопиталя: поскольку (это первый замечательный предел).
) Применим правило Лопиталя и получим, что в предположении, что последний предел существует. Этот последний предел можно найти, заметив, что при , и заменив числитель. Однако можно пойти и другим путём. Мы снова получили отношение двух бесконечно малых, к которому снова применим правило Лопиталя: поскольку (это первый замечательный предел).Итак, обоснование результата таково:
откуда по теореме 5.5 то есть откуда, в свою очередь, снова по теореме 5.5 Как правило, при вычислениях эти рассуждения “обратного хода” не приводят в явной форме для экономии места, но, строго говоря, их всегда нужно иметь в виду, когда после цепочки переходов по правилу Лопиталя мы получаем какой-либо ответ к исходному примеру на вычисление предела.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Правило Лопиталя раскрытия неопределенностей 0/0 и ∞/∞ (Лекция №8)
Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞.
 Сейчас рассмотрим новое правило раскрытия этих неопределенностей.
Сейчас рассмотрим новое правило раскрытия этих неопределенностей.Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
(1) Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Например, найти . Этот предел существует . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.
Примеры.
- .
- .
- .
Обозначим .
Прологарифмируем это равенство . Найдем .
Так как lny функция непрерывная, то . Следовательно, или .
ФОРМУЛА ТЕЙЛОРА
Пусть функция y= f(x) задана на (a, b) и x0 Î (a, b).
 Поставим
следующую задачу: найти многочлен P(x),
значения которого в окрестности точки x0 приближенно совпадали бы со значениями функции f(x) в соответствующих точках.
Тогда можно будет считать, что f(x)≈P(x) и
задачу вычисления значенийf(x) в окрестности точки x0 можно заменить более легкой
задачей вычисления значений P(x).
Поставим
следующую задачу: найти многочлен P(x),
значения которого в окрестности точки x0 приближенно совпадали бы со значениями функции f(x) в соответствующих точках.
Тогда можно будет считать, что f(x)≈P(x) и
задачу вычисления значенийf(x) в окрестности точки x0 можно заменить более легкой
задачей вычисления значений P(x).Пусть искомый многочлен имеет степень n P(x) = Pn(x). Будем искать его в виде
(1) В этом равенстве нам нужно найти коэффициенты .
Для того чтобы этот многочлен был “близок” к функции f(x) потребуем выполнения следующих равенств:
Пусть функция y= f(x) имеет производные до n-ого порядка. Найдем коэффициенты многочлена Pn(x) исходя из условия равенства производных.

Введем обозначение n! = 1·2·3…n, 0! = 1, 1! = 1.
Подставим в (1) x = x0 и найдем , но с другой стороны . Поэтому
Далее найдем производную и вычислим Следовательно, .
Учитывая третье условие и то, что
,
получим , т.е. .
Далее . Значит, , т.е. .
Очевидно, что и для всех последующих коэффициентов будет верна формула
Подставляя найденные значения коэффициентов в формулу (1), получим искомый многочлен:
Обозначим и назовем эту разность n-ым остаточным членом функции f(x) в точке x0. Отсюда и, следовательно, если остаточный член будет мал.
Оказывается, что если x0 Î (a, b) при всех x Î (a, b) существует производная f (n+1)(x), то для произвольной точки x Î (a, b) существует точка, лежащая между x0 и x такая, что остаток можно представить в виде:
Это так называемая формула Лагранжа для остаточного члена.

Формула
где x Î (x0, x) называется формулой Тейлора.
Если в этой формуле положить x0 = 0, то она запишется в виде
где x Î ( x0, x). Этот частный случай формулы Тейлора называют формулой МакЛорена.
РАЗЛОЖЕНИЕ ПО ФОРМУЛЕ МАКЛОРЕНА НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- Рассмотрим функцию f(x)=ex. Представим ее по формуле
МакЛорена в виде суммы многочлена и некоторого остатка. Для этого найдем
производные до (n+1) порядка:
Таким образом, получаем
Используя эту формулу и придавая x различные значения, мы сможем вычислить значение ex.
Например, при x=1, ограничиваясь n=8, получим формулу, позволяющую найти приближенное значение числа e:
причем остаток
Отметим, что для любого x Î R остаточный член
Действительно, так как ξ Î (0; x), то величина eξ ограничена при фиксированном x.
 При x> 0 eξ < ex.
Докажем, что при фиксированном x
При x> 0 eξ < ex.
Докажем, что при фиксированном xИмеем
Если x зафиксировано, то существует натуральное число N такое, что |x|<N.
Обозначим Заметив, что 0<q<1, при n>N можем написать
Но , не зависящая от n, а так как q<1. Поэтому Следовательно,
Таким образом, при любом x, взяв достаточное число слагаемых, мы можем вычислить ex с любой степенью точности.
- Выпишем разложение по
формуле МакЛорена для функции f(x)=sin x.
Найдем последовательные производные от функции f(x)=sin x.
Подставляя полученные значения в формулу МакЛорена, получим разложение:
Несложно заметить, что преобразовав n-й член ряда, получим
.

Так как , то аналогично разложению ex можно показать, что для всех x.
Пример. Применим полученную формулу для приближенного вычисления sin 20°. При n=3 будем иметь:
Оценим сделанную погрешность, которая равна остаточному члену:
Таким образом, sin 20°= 0,342 с точностью до 0,001.
- f(x) = cos x. Аналогично предыдущему
разложению можно вывести следующую формулу:
Здесь также для всех x. Докажите формулу самостоятельно.
- f(x)=ln (1+x). Заметим, что
область определения этой функции D(y)=(–1; +∞).
Найдем формулу МакЛорена для данной функции.
Подставим все найденные производные в ряд МакЛорена.
Можно доказать, что если x Î (–1;1],то , т.
 е. выведенная формула справедлива при x Î ( –1;1].
е. выведенная формула справедлива при x Î ( –1;1]. - f(x) = (1+x)m, где m Î R, m≠0.
При m≠Z данная функция определена при x> –1. Найдем формулу МакЛорена для этой функции:
И следовательно,
Можно показать, что при |x|<1
ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ
НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИИ
Вспомним сначала определения возрастающей и убывающей функций.
Функция y=f(x), определенная на некотором отрезке [a, b] (интервале (a, b)), называется возрастающей на этом отрезке, если большему значению аргумента x из [a, b] соответствует большее значение функции, то есть если x1 < x2, то f(x1) < f(x2).

Функцияy=f(x) называется убывающей на некотором отрезке [a, b], если меньшему значению аргумента x из [a, b]соответствует большее значение функции, то есть если x1 < x2, то f(x1) > f(x2).
Функция, только возрастающая или только убывающая на отрезке, называется монотонной на этом отрезке.
Функция y=f(x) называется постоянной на некотором отрезке [a, b], если при изменении аргумента x она принимает одни и те же значения.
Рассмотрим график функции изображенной на рисунке и определим промежутки возрастания и убывания функции.
(-∞, a), (c, +∞) – убывает;
(a, b) – постоянная;
(b, c) – возрастает.
Применим понятие производной для исследования возрастания и убывания функции.
Теорема 1. (Необходимое и достаточное условия возрастания функции)
- Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная
неотрицательна на этом отрезке, f ‘(x)≥ 0.

- Обратно. Если
функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b)
и ее производная положительна на этом отрезке,f ‘ (x)≥ 0 для a<x<b, то f(x) возрастает
на[a, b].
Доказательство.
- Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке
произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению
возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) – f(x)>0. Но тогда и Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а
Переходя в этом равенстве к пределу при Δx→0, получим , то есть f ‘(x)≥0.
- Докажем
вторую часть теоремы. Пусть f ‘(x)>0при всех x Î (a,b).
 Рассмотрим два любых значения x1 и x2 таких, что x1 < x2. Нужно доказать, что f(x1)< f(x2). По
теореме Лагранжа существует такое число c Î (x1, x2), что
. По условию f ‘(x)>0, x1 – x2>0Þ , а это и значит,
что f(x) – возрастающая функция.
Рассмотрим два любых значения x1 и x2 таких, что x1 < x2. Нужно доказать, что f(x1)< f(x2). По
теореме Лагранжа существует такое число c Î (x1, x2), что
. По условию f ‘(x)>0, x1 – x2>0Þ , а это и значит,
что f(x) – возрастающая функция.
Аналогичная теорема имеет место и для убывающих функций.
Теорема 2. Если f(x) убывает на[a,b], то на этом отрезке. Если на (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b].
Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.
 е. tga≥0, а значит f ‘(x)≥0.
е. tga≥0, а значит f ‘(x)≥0.Аналогично иллюстрируется и вторая часть теоремы.
Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f ‘(x)>0 – для возрастания или f ‘(x)<0 – для убывания.
Примеры. Определить интервалы монотонности функции.
- . Область определения заданной функции D(y) = (-∞; 0)È(0; +∞).
. Следовательно, f(x) – убывает на (-∞; 0) и (0; +∞).
-
Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов.
Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1].
-
.

Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞).
- Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке
произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению
возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) – f(x)>0. Но тогда и Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а
Задачи – вычисление пределов
Задача 15.001.
Решение 15.001.
Задача 15.002.
Решение 15.002.
Задача 15.003.
Решение 15.003.
Задача 15.004.
Решение 15.004.
Задача 15.005.
Решение 15.005.
Задача 15.006.
Решение 15.006.
Задача 15.
 007.
007.Решение 15.007.
Задача 15.008.
Решение 15.008.
Задача 15.009.
Решение 15.009.
Задача 15.010.
Решение 15.010.
Задача 15.011.
Решение 15.011.
Задача 15.012.
Решение 15.012.
Задача 15.013.
Решение 15.013.
Задача 15.014.
Решение 15.014.
Задача 15.015.
Решение 15.
 015.
015.Задача 15.016.
Вычислить пределы, используя правило Лопиталя:
Решение 15.016.
Задача 15.017.
Решение 15.017.
Задача 15.018.
Здесь предполагается, что x > 0.
Решение 15.018.
Задача 15.019.
Решение 15.019.
Задача 15.020.
Здесь предполагается, что x > 0.
Решение 15.020.
Ответы на задачи:
Разъяснения и помощь к задачам.Применение производных для вычисления пределов функций (правило Лопиталя)
Вопросы отыскания пределов функций уже рассматривались выше.
 В данном параграфе речь пойдет об
очень важном и практически удобном
способе отыскания пределов отношений
двух бесконечно малых или двух бесконечно
больших функций при помощи производных.
Этот способ называют правилом Лопиталя,
т.к. оно впервые было опубликовано именно
в книге французского математика Гильома
де Лопиталя, хотя само открытие этого
правила принадлежит Иоганну Бернулли.
В данном параграфе речь пойдет об
очень важном и практически удобном
способе отыскания пределов отношений
двух бесконечно малых или двух бесконечно
больших функций при помощи производных.
Этот способ называют правилом Лопиталя,
т.к. оно впервые было опубликовано именно
в книге французского математика Гильома
де Лопиталя, хотя само открытие этого
правила принадлежит Иоганну Бернулли.Раскрытие неопределенностей вида и
Теорема 6.5. (правило Лопиталя для неопределенности ). Пусть функции и непрерывны и дифференцируемы в окрестности точки и в самой этой точке равны нулю, т.е. . Если в окрестности точки , тогда справедливо равенство
(6.9)
если предел в правой части этого равенства существует.
Доказательство: применим теорему Коши для функций и и отрезка , лежащего в окрестности точки .
 По этой теореме найдется такая точка ,
для которой выполнено равенство:
По этой теореме найдется такая точка ,
для которой выполнено равенство:Но, по условию , тогда
Пусть , тогда величина также будет стремится к . Перейдем в последнем равенстве к пределу, получим:
Теорема доказана.
Следствие 1. Теорема верна и в том случае, когда . Действительно, положим , получим
Следствие 2. Теорема верна и в том случае, когда функции и не определены в точке , но существуют пределы и .
Пример 6.19. Пользуясь правилом Лопиталя, вычислить
Решение……
Пример 6.20.
Замечание. При применении правила Лопиталя следует обратить внимание на то, что в правой части формулы (6.9) берется не производная отношения функции, а отношение производных двух функций.

Теорема 6.6. (правило Лопиталя для неопределенности ). Пусть функции и непрерывны и дифференцируемы в окрестности точки , кроме, быть может, самой этой точки. Если в окрестности точки и , тогда справедливо равенство
(6.10)
если предел в правой части этого равенства существует.
Пример 6.21.
…………………
Раскрытие неопределенностей вида , , , ,
Для раскрытия неопределенностей вида , , , , необходимо с функцией, стоящей под знаком предела провести некоторые преобразования, а лишь затем применить правило Лопиталя.
1. При раскрытии неопределенности вида , следует сначала алгебраически преобразовать функцию, стоящую под знаком предела, для того чтобы получить неопределенности вида или , а затем применить правило Лопиталя.

Пример 6.22. Найти предел
а) б)
При раскрытия неопределенности вида , , вначале логарифмируют функцию, стоящую под знаком предела, затем по правилу Лопиталя находят предел ее логарифма.
Пример 6.23. Найти предел
Решение. Имеет место неопределенность . Вычислим предел логарифма данной функции
Итак, получили или , т.е.
Правило Лопиталя удобное средство для нахождения пределов, однако не всегда решает поставленную задачу.
Пример 6.24. Найти предел
Решение.
После применения правила Лопиталя, получили предел от функции, в котором числитель и знаменатель поменялись местами по сравнению с исходной функцией. Если правило Лопиталя применит еще раз, то можно опять вернуться к исходному пределу.
 Таким образом, для
данного примера правило Лопиталя не
позволило раскрыть неопределенность.
Нетрудно понять, что такой предел можно
найти без применения производных:
Таким образом, для
данного примера правило Лопиталя не
позволило раскрыть неопределенность.
Нетрудно понять, что такой предел можно
найти без применения производных:Неопределенные формы и правило L’Hospital в деревьях принятия решений
Машинное обучение внедряет теоретические концепции в повседневную жизнь так быстро, как никакая другая мотивация, и день ото дня способствует усвоению математики. Иногда практикующие применяют некоторые математические концепции высокого уровня, не замечая этого. Здесь неопределенные формы и исчисляемое правило L’Hospital часто появляются при построении деревьев решений.
Мишель де Л’ОпитальАлгоритмы дерева решений, такие как ID3 и C4.5, используют вычисления энтропии и усиления для определения наиболее доминирующего признака.Типичный расчет энтропии показан ниже для n классов.
Энтропия = – Σ (i = от 0 до n) p (класс i ). log 2 p (класс и ) = – p (класс 1 ).
 log 2 p (класс 1 ) – p (класс 2 ). журнал 2 п (класс 2 ) -… – п (класс n ). журнал 2 p (класс n )
log 2 p (класс 1 ) – p (класс 2 ). журнал 2 п (класс 2 ) -… – п (класс n ). журнал 2 p (класс n )Например, если класс решения состоит из 4 экземпляров «да» и 2 «нет», то имеется 6 экземпляров и двоичные классы.Энтропия будет рассчитана как
.Энтропия (решение) = – p (нет). журнал 2 п (нет) – п (да). журнал 2 п (да) = – (2/6). журнал 2 (2/6) – (4/6). log 2 (4/6) = -0,333.log 2 (0,333) – 0,667.log 2 (0,667) = -0,333. (- 1,585) – 0,667. (- 0,585) = 0,918
Неустановленные случаи
Что делать, если количество экземпляров для класса равно 0? Допустим, класс принятия решений состоит из 6 примеров «да» и 0 «нет».
Энтропия (решение) = – p (нет).журнал 2 п (нет) – п (да). log 2 p (да) = – (0/6). журнал 2 (0/6) – (6/6). журнал 2 (6/6) = – 0.
 журнал 2 (0) – 1. журнал 2 (1)
журнал 2 (0) – 1. журнал 2 (1)Здесь log 2 (1) равен 0, но проблема в том, что log 2 (0) равно – ∞. Кроме того, в этом вычислении нам нужно 0 умножить на ∞.
График для базы данных 2Зададим этот вопрос python
импорт математики а = 0 b = math.log (0, 2) # log до основания 2 из 0 или log 0 до основания 2 печать (а * б)
Вы столкнетесь с ValueError: ошибка математического домена , если вы запустите 0 раз отрицательное ∞ в python.Точно так же Java создает исключение NaN , а excel возвращает #NUM! Ошибка .
Выполнение 0 умножить на отрицательную бесконечность в pythonКак видно, эта операция не может быть выполнена, не так ли? Но мы подозрительные. Что, если даже языки программирования высокого уровня не умеют вычислять?
Знают ли языки программирования математические вычисления?
У нас проблемы – x. log 2 x для x равно 0.
 Мы можем переформулировать уравнение, поскольку предел x стремится к 0 для x, умноженного на log x по основанию 2.Перемещение множителя x к знаменателю как 1 вместо x не изменит результат.
Мы можем переформулировать уравнение, поскольку предел x стремится к 0 для x, умноженного на log x по основанию 2.Перемещение множителя x к знаменателю как 1 вместо x не изменит результат.lim (x-> 0) x. журнал 2 x = lim (x-> 0) log 2 x / (1 / x) = – ∞ / ∞
Да, он преобразован в знакомую неопределенную форму ∞ / ∞.
Правило больницы
Правило Л’Опиталя гласит, что если f (x) и g (x) оба равны 0 (или ∞), а предел переходит в некоторую точку c
Условие: lim (x-> c) f (x) = lim (x-> c) g (x) = 0 (или ∞)
Тогда функция f над функцией g равна производной от f и производной от g.
lim (x-> c) f (x) / g (x) = lim (x-> c) f ‘(x) / g’ (x)
Здесь f (x) и g (x) должны быть дифференцируемыми в точке c.
Мы уже можем преобразовать x. log 2 x член до ∞ / ∞ неопределенной формы. Это означает, что мы можем подать заявку на L’Hopital.

lim (x-> 0) x. log 2 x = lim (x-> 0) log 2 x / (1 / x) = lim (x-> 0) (log 2 x) ‘/ (1 / x) ‘= (Журнал 2 x)’ / (x -1 ) ‘
Обратите внимание, что производная log 2 x равна 1 / (x.пер (2))
(1 / (x.ln (2))) / (-1. X -2 ) = [1 / (x.ln (2))] / [-1 / x 2 ] = – x 2 / x.ln (2) = x / ln (2)
Это прикладная версия lim (x-> 0) x от L’Hospital. журнал 2 x
lim (x-> 0) x. log 2 x = lim (x-> 0) x / ln (2) = 0 / 0,693 = 0
График x.log (x) определен для [0, + ∞), как показано ниже. Удивительно, но x = 0 не является неопределенным.
График x.log (x)Итак, этот случай часто возникает при построении деревьев решений на основе энтропии.Мы можем справиться с этой проблемой только с помощью исчисления. Даже языки программирования высокого уровня не могли помочь решить эту проблему.
 Подводя итог, можно сказать, что языки программирования не знают исчисления. Они предназначены только для выполнения линейных операций.
Подводя итог, можно сказать, что языки программирования не знают исчисления. Они предназначены только для выполнения линейных операций.Вы можете переосмыслить захват власти каким-то злым ИИ или роботами-убийцами. Они не могут применять базовое исчисление. Это основной ответ, почему ИИ не может взять на себя господство человека на Земле.
СкайнетВ качестве антитезы, Ни один из лучших хищников на земле косатка, лев, белая акула, сибирский тигр, королевская кобра даже не известен, считая – Альпер Озпинар.Но не забывайте, что эти виды не могли взять на себя господство над людьми. Тяжелая сила может не поставить вас на вершину пирамиды пищевой цепи.
PS: Спасибо Valentin Cold за информирование и повышение осведомленности по этой теме
Нравится этот блог? Поддержка на Patreon
исчисление – работает ли правило L’Hopitals для оценки разницы пределов?
Вопрос : Учитывая функцию $ f (x) = x ^ 2 – e ^ x $, найдите предел $ f $ по мере приближения к положительной и отрицательной бесконечности
Найти предел $ f $ по мере его приближения к $ – \ infty $ просто, и вы получите ответ $$ \ lim_ {x \ to- \ infty} f (x) = + \ infty $$
Найти предел, когда $ f $ приближается к $ + \ infty $, не так просто.
 2 – \ infty = \ infty – \ infty $$
2 – \ infty = \ infty – \ infty $$Теперь я понял, что правило L’Hoptial – это общий метод оценки неопределенных форм, но не обычно для неопределенных форм этого типа. Обычно правило L’Hopital используется для неопределенных форм частных, например ($ \ frac {0} {0} \ $ или $ \ \ frac {\ infty} {\ infty} \ $), а не для различий, например ($ \ infty – \ infty $)
Однако, когда я попытался применить правило L’Hopitals для различий пределов (а не частного), как вы увидите ниже, я все же пришел к правильному ответу.x $ $ \ следует f (x) = g (x) – h (x) $ $$ \ lim_ {x \ to + \ infty} f (x) = \ lim_ {x \ to + \ infty} g (x) – \ lim_ {x \ to + \ infty} h (x) $$
$$ \ lim_ {x \ to + \ infty} g (x) – \ lim_ {x \ to + \ infty} h (x) = \ infty – \ infty $$
Правило L”Hopital гласит, что дает:
$$ (\ lim_ {x \ to \ infty} g (x) = \ infty) \ land (\ lim_ {x \ to \ infty} h (x) = \ infty) \ land (\ lim_ {x \ to \ infty} \ frac {g ‘(x)} {h’ (x)} = L) \ подразумевает \ lim_ {x \ to \ infty} \ frac {g (x)} {h (x)} = L $ $
То, что я, по сути, сделал ниже (что, я не уверен, соответствует Правилу L’Hopital):
$$ (\ lim_ {x \ to \ infty} g (x) = \ infty) \ land (\ lim_ {x \ to \ infty} h (x) = \ infty) \ land (\ lim_ {x \ to \ infty} g ‘(x) – h’ (x) = L) \ подразумевает \ lim_ {x \ to \ infty} g (x) – h (x) = L $$
Поскольку правило Л’Опиталя работает для производной $ n ^ {th} $, я взял вторую производную от $ f (x) $ и оценил пределы различий.
 x = – \ infty $$
x = – \ infty $$Следовательно, с помощью «модифицированной версии» правила Л’Опитала (если это можно так назвать) я получаю: $$ \ lim_ {x \ to + \ infty} f (x) = – \ infty $$
Построение этого графика на WolframAlpha показывает, что это действительно так: Вольфрам | Альфа Сюжет
Так это просто жуткое совпадение, или правило Л’Опиталя работает для определения разницы пределов?
Расчет– Почему правило Л’Опиталя не позволяет вычислить $ \ lim_ {x \ to \ infty} \ frac {x} {x + \ sin (x)} $?
других уже сказали, что l’Hopital требует существования предела отношения производных; Однако, кроме того, с твердым пониманием определения предела все еще возможно доказать решение, применяя De l’Hopital, но не к этой функции, подумайте об этом:
$$ \ lim_ {x \ to + \ infty} \ frac {x} {x + 1} \ leq \ lim_ {x \ to + \ infty} \ frac {x} {x- \ sin (x)} \ leq \ lim_ {x \ to + \ infty} \ frac {x} {x-1} $$ сжатый, учитывая также $ – \ infty $ с $$ \ lim_ {x \ to \ infty} \ frac {x} {x + sig (x)} \ leq \ lim_ {x \ to \ infty} \ frac {x} {x + \ sin (x)} \ leq \ lim_ {x \ to \ infty} \ frac {x} {x-sig (x)} $$ куда $$ sig (x) = \ left \ { \ begin {matrix} 0 & х = 0 \\ \ frac {| x |} x & x \ ne 0 \ end {матрица} \Правильно.
$
докажите вышесказанное, подав заявку в L’Hopital на номер
.$$ \ lim_ {x \ to \ infty} \ frac {x} {x \ pm 1} $$
неравенства сжатия выполняются после некоторого G, формально $ \ exists G / \ forall x \ in \ Re, | x |> G: \ frac {x} {x + sig (x)} \ leq \ frac {x } {x + \ sin (x)} \ leq \ frac {x} {x-sig (x)}
долл. США, применяя определение предела к $ x \ over x + sin (x) $, начальная точка M, выбирающая все x> M, должна быть больше или равна G (просто требуется $ M \ geq G $), в этом случае M = G достаточно велико, чтобы сказать, что предел тот же 1.
Более формально (на самом деле я не нашел в Интернете подходящего формального определения $ \ lim_ {x \ to \ infty} $, поэтому я его придумываю)
$$ \ lim_ {x \ to \ infty} f (x) = r \ in \ {\ Re, – \ infty, + \ infty, NaN \} / \\ \ существует r \ in \ Re: \ forall \ epsilon \ in \ Re, \ epsilon> 0: \ exists M \ in \ Re: \ forall x \ in \ Re, | x | > M: | f (x) -r | <\ epsilon \\ \ lor r = \ infty, пропуск \\ \ lor r = + \ infty, пропуск \\ \ lor r = - \ infty, omissis \\ \ lor r = NaN, пропуск.
долл. США $$
(r как сокращение ответа, NaN (не число) означает, что ограничение не существует, а $ \ lor $ в данном случае является ярлыком или).+ | \ forall x \ in \ Re, | x |> G: \ frac {x} {x + sig (x)} \ leq \ frac {x} {x + \ sin (x)} \ leq \ frac {x} { x-sig (x)}
$$
(r как сокращение ответа, NaN (не число) означает, что ограничение не существует, а $ \ lor $ в данном случае является ярлыком или).+ | \ forall x \ in \ Re, | x |> G: \ frac {x} {x + sig (x)} \ leq \ frac {x} {x + \ sin (x)} \ leq \ frac {x} { x-sig (x)}$$ \ lim_ {x \ to \ infty} \ frac {x} {x \ pm 1} \ underleftarrow {= (? H) = \ lim_ {x \ to + \ infty} \ frac {\ frac {d} {dx} x} {\ frac {d} {dx} (x \ pm 1)} = \ lim_ {x \ to + \ infty} \ frac {1} {1 \ pm 0} = 1} $$ наличие этих ограничений (их два из-за $ \ pm $) гарантирует, что
$ \ forall \ epsilon \ in \ Re, \ epsilon> 0: \ exists G \ in \ Re: \ forall x \ in \ Re, | x | > G: | g (x) -r | <\ epsilon $
Выбор $ M \ geq G $ ($ M $ – нижняя граница в определении предела для $ f (x) $) $$ \ Rightarrow \ lim_ {x \ to \ infty} f (x) = 1 $$
Исчисление– Когда следует прекратить использовать правило L’Hôpital
При использовании правила госпиталя нужно быть очень осторожным.
$ {\ log \ sqrt {xy}} = \ sqrt {xy}.
{\ log \ sqrt {xy}} = \ sqrt {xy}.Сделать это строгое нетривиально.
Правило Лопиталя – Пределы и асимптотика
Добро пожаловать в математический анализ. Я профессор Грейст, и мы собираемся начать восьмую лекцию о Правиле Л’Опиталя. Каждый, кто хоть раз сталкивался с математическим расчетом, знает правило Л’Опиталя. Все, кто знает Правило L’Hopital, любят Правило L’Hopital. Но кто понимает, почему правило L’Hopital работает? К концу этого урока вы это сделаете. Напомним, что когда вы сталкиваетесь с хитрым ограничением, Правило Л’Опиталя – хороший метод.Например, если мы посмотрим на предел, когда x стремится к нулю синуса x по x, или предел, когда x стремится к 0, от 1 минус cos x, по x. Вы, наверное, помните, что с ними можно справиться, различая числитель и знаменатель. Производная sin – cos. Производная x равна 1. Принятие этого предела дает вам правильный ответ 1. Аналогично во втором примере производные числителя и знаменателя дают знак x и 1 соответственно, что приводит к ответу ноль.
 Но что на самом деле говорит правило L’Hopital? Помните, как это наносится. Вы начинаете с предела формы частного, скажем, f от x над g от x. Затем вы пытаетесь оценить предел. Если это сработает, тогда отлично, что вы сделали. Если это не сработает, то правило Л’Опиталя требует различать числитель и знаменатель. Попробуйте еще раз оценить предел, если это сработает, отлично, готово. Если нет, повторяйте, пока это не сработает. Ошибка, которую допускают некоторые ученики, заключается в том, что они начинают дифференцировать, как только они видят предел, который выглядит как частное.Это плохая идея. В этих случаях он не сработает. Но вопрос в том, почему, почему это работает? Почему, если не получается с первого раза, ты продолжаешь пытаться, пока не сработает? Давайте использовать перспективы, с которыми мы работали до сих пор, и Тейлор расширит термины, если у нас есть предел, когда x переходит в a из f из x по g из x. Затем разверните числитель и знаменатель входных данных, а теперь в контексте правила Л’Опиталя.
Но что на самом деле говорит правило L’Hopital? Помните, как это наносится. Вы начинаете с предела формы частного, скажем, f от x над g от x. Затем вы пытаетесь оценить предел. Если это сработает, тогда отлично, что вы сделали. Если это не сработает, то правило Л’Опиталя требует различать числитель и знаменатель. Попробуйте еще раз оценить предел, если это сработает, отлично, готово. Если нет, повторяйте, пока это не сработает. Ошибка, которую допускают некоторые ученики, заключается в том, что они начинают дифференцировать, как только они видят предел, который выглядит как частное.Это плохая идея. В этих случаях он не сработает. Но вопрос в том, почему, почему это работает? Почему, если не получается с первого раза, ты продолжаешь пытаться, пока не сработает? Давайте использовать перспективы, с которыми мы работали до сих пор, и Тейлор расширит термины, если у нас есть предел, когда x переходит в a из f из x по g из x. Затем разверните числитель и знаменатель входных данных, а теперь в контексте правила Л’Опиталя. Давайте рассмотрим случай, когда предел f равен нулю, а предел g равен нулю.Это означает, что оба члена нулевого порядка исчезают. Что мы видим? Что ж, мы видим, что можем фактор. Величина x минус a из всех оставшихся членов в разложении Тейлора как в числителе, так и в знаменателе, они отменяются, и теперь, когда мы пытаемся вычислить x минус a, мы остаемся с членами ведущего порядка. Константы, на самом деле директивы, оцениваемые в момент Сейчас, если эти 2 исчезнут, что тогда произойдет? Итак, мы снова видим, что мы можем вычленить величину x минус a, отменить и снова увидеть, что члены ведущего порядка включают вторые производные в A.Теперь вы можете спросить, а как насчет факториала 1 больше 2? Поскольку он встречается как в числителе, так и в знаменателе, это не имеет значения. Что действительно важно, так это производные. Давайте посмотрим на это на примере. Иногда правило Л’Опиталя применять гораздо проще, чем серию Тейлора. Например, если мы возьмем предел, когда x стремится к нулю, касательная к x над arcsin x.
Давайте рассмотрим случай, когда предел f равен нулю, а предел g равен нулю.Это означает, что оба члена нулевого порядка исчезают. Что мы видим? Что ж, мы видим, что можем фактор. Величина x минус a из всех оставшихся членов в разложении Тейлора как в числителе, так и в знаменателе, они отменяются, и теперь, когда мы пытаемся вычислить x минус a, мы остаемся с членами ведущего порядка. Константы, на самом деле директивы, оцениваемые в момент Сейчас, если эти 2 исчезнут, что тогда произойдет? Итак, мы снова видим, что мы можем вычленить величину x минус a, отменить и снова увидеть, что члены ведущего порядка включают вторые производные в A.Теперь вы можете спросить, а как насчет факториала 1 больше 2? Поскольку он встречается как в числителе, так и в знаменателе, это не имеет значения. Что действительно важно, так это производные. Давайте посмотрим на это на примере. Иногда правило Л’Опиталя применять гораздо проще, чем серию Тейлора. Например, если мы возьмем предел, когда x стремится к нулю, касательная к x над arcsin x. Ну, я не знаю серии Тейлора для касательной и дуги от макушки, и, возможно, потребуется журнал работы, чтобы понять это.Итак, давайте применим Правило Л’Опиталя. Если мы попытаемся различить, ну, это потребует немного воспоминаний. Вы можете помнить, а можете и не помнить, что производная тангенса – это квадрат секущей. Вы можете помнить или не помнить, что производная arcsin равна 1 минус x в квадрате с отрицательной 1 половинной степенью. Если вы этого не помните, не волнуйтесь, мы научимся их вычислять всего за несколько коротких уроков. Но пока давайте примем это как данность. Используя правило Л’Опиталя, мы получаем предел, когда x стремится к нулю секанса в квадрате x, более 1 минус x в квадрате с отрицательной 1 половиной.Оценка нуля и запоминание того, что секанс нуля равен единице, дает нам ответ, равный единице. Это было просто. Давайте посмотрим на другой пример. Тот, для которого правило L’Hopital может оказаться неприемлемым. Предел, когда x стремится к нулю, составляет x в квадрате логарифма косинуса x по синусу в квадрате 3 x в квадрате.
Ну, я не знаю серии Тейлора для касательной и дуги от макушки, и, возможно, потребуется журнал работы, чтобы понять это.Итак, давайте применим Правило Л’Опиталя. Если мы попытаемся различить, ну, это потребует немного воспоминаний. Вы можете помнить, а можете и не помнить, что производная тангенса – это квадрат секущей. Вы можете помнить или не помнить, что производная arcsin равна 1 минус x в квадрате с отрицательной 1 половинной степенью. Если вы этого не помните, не волнуйтесь, мы научимся их вычислять всего за несколько коротких уроков. Но пока давайте примем это как данность. Используя правило Л’Опиталя, мы получаем предел, когда x стремится к нулю секанса в квадрате x, более 1 минус x в квадрате с отрицательной 1 половиной.Оценка нуля и запоминание того, что секанс нуля равен единице, дает нам ответ, равный единице. Это было просто. Давайте посмотрим на другой пример. Тот, для которого правило L’Hopital может оказаться неприемлемым. Предел, когда x стремится к нулю, составляет x в квадрате логарифма косинуса x по синусу в квадрате 3 x в квадрате. Уф, я не хочу пытаться вычислить производную от этого. Можно, но невыгодно. Однако я вспоминаю разложения Тейлора для косинуса x, для логарифма 1 плюс что-то и для синуса чего-то.Все это очень просто. Мы делали это раньше. Теперь, используя тот факт, что предел таков, что x стремится к нулю, а косинус x около нуля равен единице минус x в квадрате над двумя плюс членами более высокого порядка. Затем, подставив вместо sin 3x в квадрате и отбросив все члены высшего порядка sin, мы должны возвести это в квадрат. Ох, этот путь тоже не такой простой. Но это не так уж плохо, у нас остается расширяющийся логарифм 1 минус x в квадрате на 2 плюс члены более высокого порядка. Это в виде журнала 1 плюс z.Первый член – это сам z, в данном случае отрицательная 1 половина x в квадрате. Мы забудем о членах более высокого порядка, надеюсь, они не будут иметь значения, и знаменатель, когда мы возведем в квадрат 3 x в квадрате плюс члены более высокого порядка, первый член будет равен 9 x 4. Уф, и теперь мы видим, что члены ведущего порядка имеют одинаковую степень, мы получили отрицательные 1 половина x для 4-го плюс, больше 9x для 4-го плюс вещи.
Уф, я не хочу пытаться вычислить производную от этого. Можно, но невыгодно. Однако я вспоминаю разложения Тейлора для косинуса x, для логарифма 1 плюс что-то и для синуса чего-то.Все это очень просто. Мы делали это раньше. Теперь, используя тот факт, что предел таков, что x стремится к нулю, а косинус x около нуля равен единице минус x в квадрате над двумя плюс членами более высокого порядка. Затем, подставив вместо sin 3x в квадрате и отбросив все члены высшего порядка sin, мы должны возвести это в квадрат. Ох, этот путь тоже не такой простой. Но это не так уж плохо, у нас остается расширяющийся логарифм 1 минус x в квадрате на 2 плюс члены более высокого порядка. Это в виде журнала 1 плюс z.Первый член – это сам z, в данном случае отрицательная 1 половина x в квадрате. Мы забудем о членах более высокого порядка, надеюсь, они не будут иметь значения, и знаменатель, когда мы возведем в квадрат 3 x в квадрате плюс члены более высокого порядка, первый член будет равен 9 x 4. Уф, и теперь мы видим, что члены ведущего порядка имеют одинаковую степень, мы получили отрицательные 1 половина x для 4-го плюс, больше 9x для 4-го плюс вещи. Вынося за множитель x до 4-го и отбрасывая его, мы получаем отрицательный ответ 1 18-е.Итак, не все хитрые пределы имеют форму 0 на 0. Например, предел, когда x стремится к 0 из 1 по синусу в квадрате x минус 1 по x в квадрате. Оценка выглядит как бесконечность минус бесконечность. Это не сработает. Итак, давайте положим это на общий знаменатель x в квадрате, умноженном на синус, возведенный в квадрат x. Результирующий числитель равен x в квадрате минус синус в квадрате x. Теперь мы можем применить правило Лопиталя или, в данном случае, разложение Тейлора. Если мы расширим по Тейлору, ну, единственное, о чем нам нужно беспокоиться, – это квадрат sin в x, который является рядом Тейлора для sin x, количества в квадрате.Что мы действительно хотим сделать, так это вычислить член ведущего порядка. Итак, нам нужно немного поработать с алгеброй, когда мы возведем в квадрат x минус x в кубе над 3 факториалами плюс члены более высокого порядка, что мы получим? Первый член равен x в квадрате, второй член равен 2 умноженным на x умноженным на x кубам по 3 факториалам.
Вынося за множитель x до 4-го и отбрасывая его, мы получаем отрицательный ответ 1 18-е.Итак, не все хитрые пределы имеют форму 0 на 0. Например, предел, когда x стремится к 0 из 1 по синусу в квадрате x минус 1 по x в квадрате. Оценка выглядит как бесконечность минус бесконечность. Это не сработает. Итак, давайте положим это на общий знаменатель x в квадрате, умноженном на синус, возведенный в квадрат x. Результирующий числитель равен x в квадрате минус синус в квадрате x. Теперь мы можем применить правило Лопиталя или, в данном случае, разложение Тейлора. Если мы расширим по Тейлору, ну, единственное, о чем нам нужно беспокоиться, – это квадрат sin в x, который является рядом Тейлора для sin x, количества в квадрате.Что мы действительно хотим сделать, так это вычислить член ведущего порядка. Итак, нам нужно немного поработать с алгеброй, когда мы возведем в квадрат x минус x в кубе над 3 факториалами плюс члены более высокого порядка, что мы получим? Первый член равен x в квадрате, второй член равен 2 умноженным на x умноженным на x кубам по 3 факториалам. Что мы здесь отмечаем? Отметим, что квадраты x сокращаются. Эти вторые упорядоченные термины уходят, и мы остаемся со следующим термином. Член четвертого порядка как коэффициент ведущего порядка.Точно так же в знаменателе мы видим, что член ведущего порядка – это просто x до 4-го, таким образом, сокращение x до 4-х дает нам коэффициенты ведущего порядка, равные 1 третьей в числителе и единице в знаменателе. Наш ответ – 1 третье. Точно так же, если мы посчитаем x, умноженное на логарифм x, и отправим x в 0. Нам нужно быть немного осторожными. Это односторонний предел, отправляющий x в 0 справа. Тогда что бы это было? Пока x стремится к 0, логарифм x стремится к минус бесконечности.0 раз минус бесконечность, это не сработает. Еще раз, давайте перенесем это через знаменатель. В этом случае мы переместим x в знаменатель и назовем его 1 вместо x. Так что у нас есть соотношение двух функций. В этом случае логарифм от x больше x до минус 1. Теперь мы собираемся применить правило Л’Опиталя. Я немного нервничаю по поводу расширений Тейлора здесь, потому что и log of x, и 1 по x, похоже, не имеют хороших разложений Тейлора при x, равном 0.
Что мы здесь отмечаем? Отметим, что квадраты x сокращаются. Эти вторые упорядоченные термины уходят, и мы остаемся со следующим термином. Член четвертого порядка как коэффициент ведущего порядка.Точно так же в знаменателе мы видим, что член ведущего порядка – это просто x до 4-го, таким образом, сокращение x до 4-х дает нам коэффициенты ведущего порядка, равные 1 третьей в числителе и единице в знаменателе. Наш ответ – 1 третье. Точно так же, если мы посчитаем x, умноженное на логарифм x, и отправим x в 0. Нам нужно быть немного осторожными. Это односторонний предел, отправляющий x в 0 справа. Тогда что бы это было? Пока x стремится к 0, логарифм x стремится к минус бесконечности.0 раз минус бесконечность, это не сработает. Еще раз, давайте перенесем это через знаменатель. В этом случае мы переместим x в знаменатель и назовем его 1 вместо x. Так что у нас есть соотношение двух функций. В этом случае логарифм от x больше x до минус 1. Теперь мы собираемся применить правило Л’Опиталя. Я немного нервничаю по поводу расширений Тейлора здесь, потому что и log of x, и 1 по x, похоже, не имеют хороших разложений Тейлора при x, равном 0. Итак, применение правила Л’Опиталя дает нам что? Производная log от x равна 1 по x.Производная 1 по x равна минус 1 по x в квадрате. Они упрощаются до минус x и, принимая предел, когда x стремится к 0 справа, мы видим, что ответ равен 0. Теперь правило L’Hopital также может помочь в оценке пределов на бесконечности. Рассмотрим предел, когда x стремится к бесконечности. Из журнала x больше квадратного корня из x. Возможно, неясно, каким будет этот предел. Логарифм x и квадратный корень из x становятся бесконечными, когда x стремится к бесконечности. Но с какой скоростью? Есть ли один, который больше другого? Что ж, применим Правило Л’Опиталя.Это дает нам предел, когда x стремится к бесконечности, чего? Логарифм производной x равен 1 по x. Производная x к половине равна половине x к минус половине. Это упрощается до двукратного x до минус 1, когда x стремится к бесконечности, это явно идет к 0. Что ж, вот и ответ. Но что это на самом деле означает? Логарифм x стремится к бесконечности, квадратный корень x стремится к бесконечности, их отношение стремится к 0.
Итак, применение правила Л’Опиталя дает нам что? Производная log от x равна 1 по x.Производная 1 по x равна минус 1 по x в квадрате. Они упрощаются до минус x и, принимая предел, когда x стремится к 0 справа, мы видим, что ответ равен 0. Теперь правило L’Hopital также может помочь в оценке пределов на бесконечности. Рассмотрим предел, когда x стремится к бесконечности. Из журнала x больше квадратного корня из x. Возможно, неясно, каким будет этот предел. Логарифм x и квадратный корень из x становятся бесконечными, когда x стремится к бесконечности. Но с какой скоростью? Есть ли один, который больше другого? Что ж, применим Правило Л’Опиталя.Это дает нам предел, когда x стремится к бесконечности, чего? Логарифм производной x равен 1 по x. Производная x к половине равна половине x к минус половине. Это упрощается до двукратного x до минус 1, когда x стремится к бесконечности, это явно идет к 0. Что ж, вот и ответ. Но что это на самом деле означает? Логарифм x стремится к бесконечности, квадратный корень x стремится к бесконечности, их отношение стремится к 0. На самом деле это означает, что квадратный корень x доминирует над логарифмом x.Он растет намного быстрее, чем логарифм. Хотя правило L’Hopital действительно помогает при оценке пределов и бесконечности, оно не всегда полезно. Иногда вам нужно подумать, рассмотреть предел, когда x стремится к бесконечности, гиперболический тангенс x. Это по определению предел. Гиперболический синус над гиперболическим косинусом. Применим правило L’Hopital. Что ж, это просто. Какая производная от sinh? Это чушь. Какая производная от cosh? Это грех.Итак, мы видим, что мы получаем предел, когда x стремится к бесконечности гиперболического котангенса x. Я не знаю, что это такое. Итак, применим правило L’Hopitals. Опять же, производная от sinh – это ch, а от cosh – sinh. И, к сожалению, мы застряли в петле и никогда никуда не денемся. Но, используя нашу коллективную голову, мы знаем определение гиперболического тангенса. Что нас действительно волнует, так это отношение е к х минус е к минус х по е к х плюс е к минус х.
На самом деле это означает, что квадратный корень x доминирует над логарифмом x.Он растет намного быстрее, чем логарифм. Хотя правило L’Hopital действительно помогает при оценке пределов и бесконечности, оно не всегда полезно. Иногда вам нужно подумать, рассмотреть предел, когда x стремится к бесконечности, гиперболический тангенс x. Это по определению предел. Гиперболический синус над гиперболическим косинусом. Применим правило L’Hopital. Что ж, это просто. Какая производная от sinh? Это чушь. Какая производная от cosh? Это грех.Итак, мы видим, что мы получаем предел, когда x стремится к бесконечности гиперболического котангенса x. Я не знаю, что это такое. Итак, применим правило L’Hopitals. Опять же, производная от sinh – это ch, а от cosh – sinh. И, к сожалению, мы застряли в петле и никогда никуда не денемся. Но, используя нашу коллективную голову, мы знаем определение гиперболического тангенса. Что нас действительно волнует, так это отношение е к х минус е к минус х по е к х плюс е к минус х. А теперь давайте подумаем об этом.Эти первые члены большие, е до x становится большим очень быстро, когда x стремится к бесконечности, а e до минус x становится очень и очень маленьким. Давайте проигнорируем это. Что мы получим? Что ж, я думаю, вы могли бы возразить, что предел равен 1. Теперь, как мы можем сделать это немного точнее? Если мы вычленим е из x, у нас останется 1 минус что-то, идущее до 0 в числителе, и 1 плюс что-то, идущее до 0 в знаменателе. Отмена легко дает нам этот предел. Это полезный способ поспорить.Рассмотрим предел x, умноженный на логарифм x по логарифму, гиперболический косинус, когда x стремится к бесконечности. Я собираюсь дать вам возможность применить правило Л’Опиталя и посмотреть, что мы получим. То, что мы собираемся получить, выглядит немного сложным. К счастью, здесь задействован гиперболический тангенс, который позволяет нам использовать предыдущий результат, чтобы сказать, что числитель стремится к бесконечности, а знаменатель – к 1. Я хочу, чтобы вы подумали о том, как этот ответ бесконечности может быть получен в ваша голова без правила L’Hopital.
А теперь давайте подумаем об этом.Эти первые члены большие, е до x становится большим очень быстро, когда x стремится к бесконечности, а e до минус x становится очень и очень маленьким. Давайте проигнорируем это. Что мы получим? Что ж, я думаю, вы могли бы возразить, что предел равен 1. Теперь, как мы можем сделать это немного точнее? Если мы вычленим е из x, у нас останется 1 минус что-то, идущее до 0 в числителе, и 1 плюс что-то, идущее до 0 в знаменателе. Отмена легко дает нам этот предел. Это полезный способ поспорить.Рассмотрим предел x, умноженный на логарифм x по логарифму, гиперболический косинус, когда x стремится к бесконечности. Я собираюсь дать вам возможность применить правило Л’Опиталя и посмотреть, что мы получим. То, что мы собираемся получить, выглядит немного сложным. К счастью, здесь задействован гиперболический тангенс, который позволяет нам использовать предыдущий результат, чтобы сказать, что числитель стремится к бесконечности, а знаменатель – к 1. Я хочу, чтобы вы подумали о том, как этот ответ бесконечности может быть получен в ваша голова без правила L’Hopital. Рассмотрим гиперболический косинус x. Это действительно е к x плюс что-то маленькое с постоянной равной 1 половине. Теперь, если мы возьмем натуральный логарифм, это должно выглядеть примерно как x. Не совсем, но он должен расти линейно. Итак, я бы сказал, что x, умноженное на логарифм x, деленное на что-то, что растет, как x, должно дать нам бесконечный предел. Это предзнаменование того, что должно произойти. Там, где мы хотим иметь язык для обсуждения или управления ростом функций, это называется большой буквой O, и это красивый язык.Правило L’Hopital вместе с серией Тейлора образуют прекрасный набор инструментов для оценки пределов. В следующем уроке мы применим эти инструменты для изучения асимптотики или темпов роста функций. Попутно мы расширим наши инструменты еще одним устройством, большим O.
Рассмотрим гиперболический косинус x. Это действительно е к x плюс что-то маленькое с постоянной равной 1 половине. Теперь, если мы возьмем натуральный логарифм, это должно выглядеть примерно как x. Не совсем, но он должен расти линейно. Итак, я бы сказал, что x, умноженное на логарифм x, деленное на что-то, что растет, как x, должно дать нам бесконечный предел. Это предзнаменование того, что должно произойти. Там, где мы хотим иметь язык для обсуждения или управления ростом функций, это называется большой буквой O, и это красивый язык.Правило L’Hopital вместе с серией Тейлора образуют прекрасный набор инструментов для оценки пределов. В следующем уроке мы применим эти инструменты для изучения асимптотики или темпов роста функций. Попутно мы расширим наши инструменты еще одним устройством, большим O.(PDF) Правило L’hospital для функций с несколькими переменными
2 ГЭРИ Р. ЛОУЛОР
может показаться довольно загадочным, в то время как что-то вроде
lim
(x, y, z) → (0,0,0)
7x2yz5 + xy3−3x4yz
x8 + x2y2z4 + (y − x3 + z2) 2 + z6 − xy3z5
устрашающе действительно!
Прочтение вашей книги по многомерному исчислению вряд ли поможет.
 На
Налучше всего вы найдете несколько интересных отдельных разработанных примеров, с предостережением, а не
, чтобы попробовать такие вещи дома – по крайней мере, до тех пор, пока вы не будете должным образом предупреждены против
, полагаясь только на отдельные линии через начало координат! Вы можете проверить, например,
, что если мы установим x = at, y = bt и z = ct, вышеуказанный предел при t → 0 всегда будет равен нулю
, независимо от значений a, band c . Но это, конечно, не вся история
, как мы продемонстрируем в конце статьи.
Похоже, что мы в значительной степени упустили из виду тему поиска организованного подхода для
, разрешающего нулевые пределы для функций многих переменных.
Две статьи [DS] и [Y], с. 71, оба обрабатывают конкретную ситуацию неопределенного предела с двумя переменными
, разрешаемого путем взятия смешанной второй производной
∂2 / ∂x∂y функций числителя и знаменателя.
В статье [FK] есть версия, использующая производные первого порядка, но полнота использования теоремы оказывается ограниченной, как мы обсудим после доказательства теоремы 2.
 1 ниже.
1 ниже.Есть несколько статей с хорошей трактовкой неопределенного предела
частного векторнозначной функции по действительнозначной функции, но эти статьи
касаются функций одной переменной. См. [R], [A], [P] и [W] для теорем этого типа в стиле L’hˆopital
.
Теперь мы представляем метод решения многих многомерных неопределенных пределов.
2. Неизолированные особые точки
Ключевым аспектом предельного значения нуля выше нуля для функции многих переменных оказывается
вопрос о том, является ли особая точка изолированной или нет.Возможно, удивительно, что
неизолированный случай дает более красивую теорему.
Если особая точка p не является изолированным нулем функции знаменателя g, то
мы понимаем предел, который следует брать по точкам, где g6 = 0. Чтобы надеяться на существование
предела, нулевого множества g должен содержаться в нулевом наборе fnear p;
иначе функция взорвется около нулей g, которые не являются нулями f.
 Эта гипотеза
Эта гипотезао множествах нулей не фигурирует явно в теореме 2.1, но это
подразумевается имеющимися гипотезами.
Теорема 2.1 (правило многопараметрического Лёпиталя). Пусть N будет окрестностью в R2con-
, содержащей точку pat, в которой две дифференцируемые функции f: N → Rand g: N → R
равны нулю.
Верховный суд, нарушая тишину, не заблокирует закон Техаса об абортах
Непосредственно перед полуночью среды Верховный суд отказался заблокировать закон Техаса, запрещающий большинство абортов, менее чем через день после того, как он вступил в силу и стал самой ограничительной мерой по абортам в нации.
Голосование было 5 против 4, при этом председатель суда Джон Дж. Робертс-младший присоединился к трем либеральным членам суда, которые выразили несогласие.
Мнение большинства было без подписи и состояло из одного длинного абзаца. В нем говорится, что поставщики абортов, которые обжаловали закон в экстренном обращении в суд, не представили свои доводы перед лицом «сложных и новых» процедурных вопросов.
 Большинство подчеркнуло, что это решение не касалось конституционности закона Техаса и не ограничивало его «процедурными оспариваниями».
Большинство подчеркнуло, что это решение не касалось конституционности закона Техаса и не ограничивало его «процедурными оспариваниями».Но это решение, несомненно, подпитывает надежды противников абортов и опасения защитников прав на аборт, поскольку этой осенью суд рассмотрит отдельное дело в своем новом сроке, чтобы решить, будет ли Роу против Уэйда, знаменательное решение 1973 года, устанавливающее конституционное право к процедуре, следует отменить. Это также заставило техасских провайдеров абортов отказывать пациентам, поскольку они изо всех сил старались соблюдать закон, который запрещает аборты примерно через шесть недель.
Все четыре судьи, не согласные с этим, представили свои заключения.
«Решение суда ошеломляет», – написала судья Соня Сотомайор в своем несогласии. «Получив заявление о введении в действие вопиюще неконституционного закона, призванного запретить женщинам осуществлять свои конституционные права и уклоняться от судебного надзора, большинство судей предпочли зарыться в песок».

«Суд вознаградил усилия штата по отсрочке федерального пересмотра явно неконституционного закона, принятого без учета прецедентов суда, посредством процедурных затруднений, созданных самим государством», – написал судья Сотомайор.«Суд не должен довольствоваться тем, что игнорирует свои конституционные обязательства по защите не только прав женщин, но также неприкосновенности своих прецедентов и верховенства закона».
Главный судья Робертс написал, что он заблокировал бы закон, пока подаются апелляции.
«Предусмотренная законом процедура в суде не только необычна, но и беспрецедентна», – написал он. «Законодательный орган ввел запрет на аборты примерно через шесть недель, а затем по сути делегировал соблюдение этого запрета населению в целом.Желаемым следствием, по-видимому, является изоляция государства от ответственности за внедрение и обеспечение соблюдения режима регулирования ».
Главный судья подчеркнул предварительный характер решения большинства. «Несмотря на то, что сегодня суд отклоняет ходатайство заявителей о чрезвычайной помощи, – писал он, – постановление суда категорически разъясняет, что его нельзя рассматривать как подтверждение конституционности рассматриваемого закона».
Судья Елена Каган раскритиковала практику суда решать важные вопросы в поспешных решениях без полного брифинга или устных аргументов – по тому, что специалисты Верховного суда называют его «теневым делом».
«Сегодняшнее постановление показывает, насколько далеко« теневые »решения суда могут отклоняться от обычных принципов апелляционного процесса», – написала она. «Это постановление, как все должны согласиться, имеет большое значение».
«Тем не менее, большинство действовало без каких-либо указаний апелляционного суда, который сейчас рассматривает те же вопросы», – написала она. «Он рассмотрел только самые поверхностные партийные предложения, и то в спешке. И он почти не пытается объяснить свой вывод – что вызов явно неконституционному регулированию абортов, подкрепленный совершенно беспрецедентной схемой правоприменения, вряд ли победит.
«Во всех этих отношениях, – писал судья Каган, – решение большинства является символом слишком большого количества теневых решений этого суда, которые с каждым днем становятся все более необоснованными, непоследовательными и невозможными для защиты».
Закон штата Техас, известный как Закон Сената 8, составляет почти полный запрет на аборты в Техасе, поскольку от 85 до 90 процентов процедур в штате происходят после шестой недели беременности, по словам юристов нескольких клиник. Во вторник вечером клиники изо всех сил пытались принять пациентов до той минуты, когда закон вступил в силу, с шестичасовым ожиданием процедур в некоторых местах.К среде списки пациентов сократились, заявили в интервью работники клиники.
Этот закон является последней битвой за право на аборт в Соединенных Штатах. В последние годы участники кампании против абортов добились успеха благодаря законам в законодательных собраниях штатов, и теперь широкая часть Юга и Среднего Запада имеет ограниченный доступ к абортам.
В заявлении об оказании экстренной помощи, призывающем судей вмешаться, поставщики абортов в штате заявили, что новый закон «немедленно и катастрофически сократит доступ к абортам в Техасе» и, скорее всего, заставит «многие клиники абортов в конечном итоге закрыть».
Прецеденты Верховного суда запрещают штатам запрещать аборты до достижения жизнеспособности плода, момента, когда плод может поддерживать жизнь вне матки, или примерно на 22–24 неделе беременности. Закон в Техасе гласит, что врачи не могут делать аборты при обнаружении сердцебиения – активности, которая начинается примерно через шесть недель, прежде чем многие женщины даже узнают о своей беременности.
Многие штаты ввели такие запреты, но в Техасе другой закон. Он был составлен так, чтобы его было сложно обжаловать в суде.
Обычно в иске о блокировании закона, поскольку он противоречит Конституции, ответчиками являются государственные должностные лица. Однако закон Техаса, который не делает исключений для беременностей в результате инцеста или изнасилования, запрещает государственным чиновникам применять его и вместо этого уполномочивает частных лиц подавать в суд на любого, кто выполняет процедуру или «помогает и подстрекает» к ней.
Пациенту нельзя предъявить иск, но врачи, сотрудники клиник, консультанты, люди, которые помогают оплачивать процедуру, и даже водитель Uber, доставляющий пациента в клинику для абортов, являются потенциальными ответчиками.Истцы, которым не обязательно проживать в Техасе, иметь какое-либо отношение к аборту или показать какие-либо травмы от него, имеют право на 10 000 долларов и возмещение их судебных издержек, если они выиграют. Преобладающие ответчики не имеют права на оплату юридических услуг.
Этот новый состав вызвал недовольство клиник.
Доктор Джессика Рубино, врач центра женского здоровья Остина, небольшой независимой клиники в столице штата, сказала, что сначала она хотела нарушить то, что казалось неконституционным.Но она сказала, что пришла к выводу, что это подвергнет риску ее персонал.
«Если бы это был уголовный запрет, мы бы знали, что это такое и что мы можем и что не можем делать», – сказал д-р Рубино. «Но этот запрет имеет гражданские последствия. Требуется, чтобы адвокат обратился в суд. Это требует гонораров юристам. А затем 10 000 долларов, если мы не выиграем. Что произойдет, если подать в суд на всех, а не только на меня? »
Она добавила: «Мои сотрудники нервничают. Они спрашивали: «А как насчет наших семей?» »
Доктор Рубино сказала, что ее клиника« изо всех сил пыталась придумать какой-либо план по уходу за кем-либо »в соответствии с новым законом, и в среду разбиралась какой будет новая политика.Например, она задалась вопросом, если кто-то знает, что его беременность превышает шесть или семь недель – примерно новый законный предел, – должна ли клиника посоветовать им уехать из штата и не тратить деньги на УЗИ?
По словам Эми Хагстром Миллер, исполнительного директора Whole Woman’s Health, которая управляет четырьмя клиниками в Техасе, врачи, которым предъявлен иск, даже если иск будет отклонен, должны сообщить о судебных исках при продлении лицензии или получении разрешения на прием в больницу.
Практически не было никаких указаний на изменение юридического основания за пределами Центра планирования семьи для выбора в Хьюстоне, единственного места группы в городе, которое предоставляет услуги по прерыванию беременности.Через дорогу остановился синий автобус, предлагающий бесплатные тесты на беременность от постоянной группы противников абортов. Но внутри эффект был очевиден: доктор Бхавик Кумар, штатный врач, сказал, что к полудню среды он осмотрел шесть пациентов, по сравнению с его обычными 30-ю пациентами. не государство, будет обеспечивать соблюдение закона. Закон эффективно уполномочивает простых граждан, в том числе тех, кто не проживает в Техасе, позволяя им подавать в суд на клиники и других лиц, нарушающих закон.Он присуждает им как минимум 10 000 долларов за каждый незаконный аборт, если они успешны.
В Whole Woman’s Health, Форт-Уэрт, последний прием к пациенту был завершен в 23:56. во вторник, – заявила Марва Сэдлер, старший директор клиники организации. Она сказала, что врачи начали лечение рано утром во вторник и вылечили 117 пациентов, что намного больше, чем обычно.
«Это был абсолютно организованный хаос», – сказала г-жа Сэдлер, которая приехала из Сан-Антонио, чтобы помочь. «Пациенты ждали от пяти до шести часов, чтобы сделать свои процедуры.
Она сказала, что пациенты ждали в своих машинах, а также в зале ожидания. Некоторым сказали вернуться позже. В среду, по ее словам, клиника была в неизведанных водах. По ее оценкам, из 79 человек, включенных в график, около 20 в конечном итоге смогут завершить свои процедуры. Многие, по ее словам, забеременели слишком долго, чтобы лечиться по новому закону.
«Люди запутались, – сказала она. «Они не знают, куда идти. Они не знают, что это за закон.
Непосредственный вопрос для судей заключался не в том, является ли закон Техаса конституционным, а в том, можно ли его обжаловать в федеральном суде. Защитники закона говорят, что, учитывая структуру закона, только суды Техаса могут выносить решения по этому вопросу и только в контексте исков против поставщиков абортов за нарушение закона.
Решение Верховного суда было предварительным. Жалоба на закон остается на рассмотрении нижестоящих федеральных судов, и они готовы разобраться со сложными вопросами по делу.
Когда закон вступил в силу, демократы обрушились на него и пообещали бороться за сохранение права на аборт в Техасе и по всей стране. В заявлении президента Байдена говорится, что эта мера «грубо нарушает» конституционное право на аборт, установленное в деле Роу против Уэйда.
Дело Техаса, которое находилось на «теневом рассмотрении» суда без подробного брифинга и устных аргументов, обогнало дело штата Миссисипи.
Законы Техаса и Миссисипи являются одними из многих мер, принятых законодательными собраниями штатов, контролируемых республиканцами, с целью проверки жизнеспособности закона «Roe and Planned Parenthood v.Кейси, решение 1992 года, которое подтвердило основной холдинг Роу и указанные штаты, не может налагать «чрезмерное бремя» на право на аборт до достижения жизнеспособности плода.
Законодатели, стоящие за различными государственными мерами, делают ставку на то, что недавний сдвиг Верховного суда вправо заставит его поддерживать новые законы. В состав суда теперь входят три члена, назначенные президентом Дональдом Трампом, который пообещал назвать судей, готовых отменить решение Роу против Уэйда.


 Лопиталь же опубликовал это правило в первом учебнике по дифференциальному исчислению в 1696 году со своим авторством.
Лопиталь же опубликовал это правило в первом учебнике по дифференциальному исчислению в 1696 году со своим авторством.
 {1/x} =1$
{1/x} =1$ Теперь возьмём точку , и применим теорему Коши к отрезку . Получим где . Переходя к пределу при , получаем так как при имеем .
Теперь возьмём точку , и применим теорему Коши к отрезку . Получим где . Переходя к пределу при , получаем так как при имеем . В предположении, что предел существует, найдём вместо него предел отношения производных, который, в соответствии с доказанной теоремой, равен исходному: Получившийся предел — снова предел отношения бесконечно малых, но его легко вычислить, заменив числитель на эквивалентную бесконечно малую: при . Получаем: Итак, получили, что предел отношения производных, действительно, существует и равен . По правилу Лопиталя отсюда следует, что исходный предел также существует и равен тому же числу: Следовательно,
В предположении, что предел существует, найдём вместо него предел отношения производных, который, в соответствии с доказанной теоремой, равен исходному: Получившийся предел — снова предел отношения бесконечно малых, но его легко вычислить, заменив числитель на эквивалентную бесконечно малую: при . Получаем: Итак, получили, что предел отношения производных, действительно, существует и равен . По правилу Лопиталя отсюда следует, что исходный предел также существует и равен тому же числу: Следовательно,  Этот исходный предел вполне может существовать, только его нельзя найти при помощи применения правила Лопиталя. Иными словами, правило Лопиталя не является универсальным средством отыскания пределов отношения двух бесконечно малых. Пример предела, который нельзя отыскать с помощью правила Лопиталя, мы сейчас приведём.
Этот исходный предел вполне может существовать, только его нельзя найти при помощи применения правила Лопиталя. Иными словами, правило Лопиталя не является универсальным средством отыскания пределов отношения двух бесконечно малых. Пример предела, который нельзя отыскать с помощью правила Лопиталя, мы сейчас приведём.  Составим отношение этих двух производных: В этом выражении первое слагаемое имеет, очевидно, при предел, равный 0, а второе не имеет никакого предела; следовательно, не имеет предела и сумма.
Составим отношение этих двух производных: В этом выражении первое слагаемое имеет, очевидно, при предел, равный 0, а второе не имеет никакого предела; следовательно, не имеет предела и сумма. При этом
При этом Итак, пусть
Итак, пусть 8 Как и в основном случае отношения двух бесконечно малых при , все остальные варианты правила Лопиталя не универсальны: если предел отношения производных не существует, то это ещё не означает, что нет предела отношения исходных величин.
8 Как и в основном случае отношения двух бесконечно малых при , все остальные варианты правила Лопиталя не универсальны: если предел отношения производных не существует, то это ещё не означает, что нет предела отношения исходных величин.  ) Применим правило Лопиталя и получим, что в предположении, что последний предел существует. Этот последний предел можно найти, заметив, что при , и заменив числитель. Однако можно пойти и другим путём. Мы снова получили отношение двух бесконечно малых, к которому снова применим правило Лопиталя: поскольку (это первый замечательный предел).
) Применим правило Лопиталя и получим, что в предположении, что последний предел существует. Этот последний предел можно найти, заметив, что при , и заменив числитель. Однако можно пойти и другим путём. Мы снова получили отношение двух бесконечно малых, к которому снова применим правило Лопиталя: поскольку (это первый замечательный предел).
 Сейчас рассмотрим новое правило раскрытия этих неопределенностей.
Сейчас рассмотрим новое правило раскрытия этих неопределенностей.
 Поставим
следующую задачу: найти многочлен P(x),
значения которого в окрестности точки x0 приближенно совпадали бы со значениями функции f(x) в соответствующих точках.
Тогда можно будет считать, что f(x)≈P(x) и
задачу вычисления значенийf(x) в окрестности точки x0 можно заменить более легкой
задачей вычисления значений P(x).
Поставим
следующую задачу: найти многочлен P(x),
значения которого в окрестности точки x0 приближенно совпадали бы со значениями функции f(x) в соответствующих точках.
Тогда можно будет считать, что f(x)≈P(x) и
задачу вычисления значенийf(x) в окрестности точки x0 можно заменить более легкой
задачей вычисления значений P(x).

 При x> 0 eξ < ex.
Докажем, что при фиксированном x
При x> 0 eξ < ex.
Докажем, что при фиксированном x
 е. выведенная формула справедлива при x Î ( –1;1].
е. выведенная формула справедлива при x Î ( –1;1].

 Рассмотрим два любых значения x1 и x2 таких, что x1 < x2. Нужно доказать, что f(x1)< f(x2). По
теореме Лагранжа существует такое число c Î (x1, x2), что
. По условию f ‘(x)>0, x1 – x2>0Þ , а это и значит,
что f(x) – возрастающая функция.
Рассмотрим два любых значения x1 и x2 таких, что x1 < x2. Нужно доказать, что f(x1)< f(x2). По
теореме Лагранжа существует такое число c Î (x1, x2), что
. По условию f ‘(x)>0, x1 – x2>0Þ , а это и значит,
что f(x) – возрастающая функция. е. tga≥0, а значит f ‘(x)≥0.
е. tga≥0, а значит f ‘(x)≥0.
 007.
007. 015.
015. В данном параграфе речь пойдет об
очень важном и практически удобном
способе отыскания пределов отношений
двух бесконечно малых или двух бесконечно
больших функций при помощи производных.
Этот способ называют правилом Лопиталя,
т.к. оно впервые было опубликовано именно
в книге французского математика Гильома
де Лопиталя, хотя само открытие этого
правила принадлежит Иоганну Бернулли.
В данном параграфе речь пойдет об
очень важном и практически удобном
способе отыскания пределов отношений
двух бесконечно малых или двух бесконечно
больших функций при помощи производных.
Этот способ называют правилом Лопиталя,
т.к. оно впервые было опубликовано именно
в книге французского математика Гильома
де Лопиталя, хотя само открытие этого
правила принадлежит Иоганну Бернулли. По этой теореме найдется такая точка ,
для которой выполнено равенство:
По этой теореме найдется такая точка ,
для которой выполнено равенство:

 Таким образом, для
данного примера правило Лопиталя не
позволило раскрыть неопределенность.
Нетрудно понять, что такой предел можно
найти без применения производных:
Таким образом, для
данного примера правило Лопиталя не
позволило раскрыть неопределенность.
Нетрудно понять, что такой предел можно
найти без применения производных: log 2 p (класс 1 ) – p (класс 2 ). журнал 2 п (класс 2 ) -… – п (класс n ). журнал 2 p (класс n )
log 2 p (класс 1 ) – p (класс 2 ). журнал 2 п (класс 2 ) -… – п (класс n ). журнал 2 p (класс n ) журнал 2 (0) – 1. журнал 2 (1)
журнал 2 (0) – 1. журнал 2 (1) Мы можем переформулировать уравнение, поскольку предел x стремится к 0 для x, умноженного на log x по основанию 2.Перемещение множителя x к знаменателю как 1 вместо x не изменит результат.
Мы можем переформулировать уравнение, поскольку предел x стремится к 0 для x, умноженного на log x по основанию 2.Перемещение множителя x к знаменателю как 1 вместо x не изменит результат.
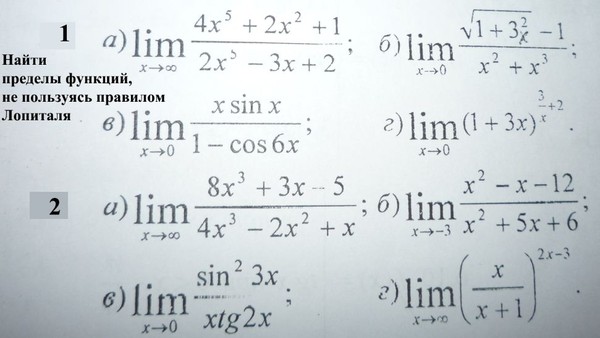 Подводя итог, можно сказать, что языки программирования не знают исчисления. Они предназначены только для выполнения линейных операций.
Подводя итог, можно сказать, что языки программирования не знают исчисления. Они предназначены только для выполнения линейных операций. 2 – \ infty = \ infty – \ infty $$
2 – \ infty = \ infty – \ infty $$ x = – \ infty $$
x = – \ infty $$
 $$
(r как сокращение ответа, NaN (не число) означает, что ограничение не существует, а $ \ lor $ в данном случае является ярлыком или).+ | \ forall x \ in \ Re, | x |> G: \ frac {x} {x + sig (x)} \ leq \ frac {x} {x + \ sin (x)} \ leq \ frac {x} { x-sig (x)}
$$
(r как сокращение ответа, NaN (не число) означает, что ограничение не существует, а $ \ lor $ в данном случае является ярлыком или).+ | \ forall x \ in \ Re, | x |> G: \ frac {x} {x + sig (x)} \ leq \ frac {x} {x + \ sin (x)} \ leq \ frac {x} { x-sig (x)} {\ log \ sqrt {xy}} = \ sqrt {xy}.
{\ log \ sqrt {xy}} = \ sqrt {xy}.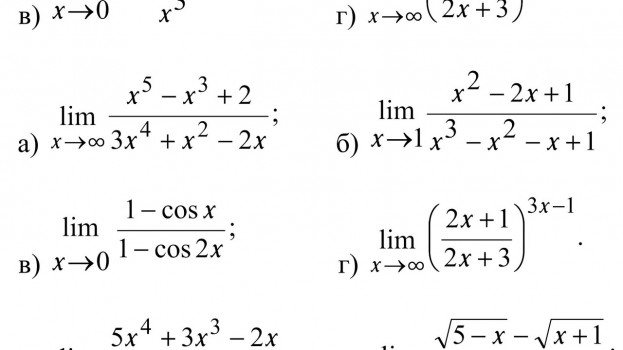 Но что на самом деле говорит правило L’Hopital? Помните, как это наносится. Вы начинаете с предела формы частного, скажем, f от x над g от x. Затем вы пытаетесь оценить предел. Если это сработает, тогда отлично, что вы сделали. Если это не сработает, то правило Л’Опиталя требует различать числитель и знаменатель. Попробуйте еще раз оценить предел, если это сработает, отлично, готово. Если нет, повторяйте, пока это не сработает. Ошибка, которую допускают некоторые ученики, заключается в том, что они начинают дифференцировать, как только они видят предел, который выглядит как частное.Это плохая идея. В этих случаях он не сработает. Но вопрос в том, почему, почему это работает? Почему, если не получается с первого раза, ты продолжаешь пытаться, пока не сработает? Давайте использовать перспективы, с которыми мы работали до сих пор, и Тейлор расширит термины, если у нас есть предел, когда x переходит в a из f из x по g из x. Затем разверните числитель и знаменатель входных данных, а теперь в контексте правила Л’Опиталя.
Но что на самом деле говорит правило L’Hopital? Помните, как это наносится. Вы начинаете с предела формы частного, скажем, f от x над g от x. Затем вы пытаетесь оценить предел. Если это сработает, тогда отлично, что вы сделали. Если это не сработает, то правило Л’Опиталя требует различать числитель и знаменатель. Попробуйте еще раз оценить предел, если это сработает, отлично, готово. Если нет, повторяйте, пока это не сработает. Ошибка, которую допускают некоторые ученики, заключается в том, что они начинают дифференцировать, как только они видят предел, который выглядит как частное.Это плохая идея. В этих случаях он не сработает. Но вопрос в том, почему, почему это работает? Почему, если не получается с первого раза, ты продолжаешь пытаться, пока не сработает? Давайте использовать перспективы, с которыми мы работали до сих пор, и Тейлор расширит термины, если у нас есть предел, когда x переходит в a из f из x по g из x. Затем разверните числитель и знаменатель входных данных, а теперь в контексте правила Л’Опиталя. Давайте рассмотрим случай, когда предел f равен нулю, а предел g равен нулю.Это означает, что оба члена нулевого порядка исчезают. Что мы видим? Что ж, мы видим, что можем фактор. Величина x минус a из всех оставшихся членов в разложении Тейлора как в числителе, так и в знаменателе, они отменяются, и теперь, когда мы пытаемся вычислить x минус a, мы остаемся с членами ведущего порядка. Константы, на самом деле директивы, оцениваемые в момент Сейчас, если эти 2 исчезнут, что тогда произойдет? Итак, мы снова видим, что мы можем вычленить величину x минус a, отменить и снова увидеть, что члены ведущего порядка включают вторые производные в A.Теперь вы можете спросить, а как насчет факториала 1 больше 2? Поскольку он встречается как в числителе, так и в знаменателе, это не имеет значения. Что действительно важно, так это производные. Давайте посмотрим на это на примере. Иногда правило Л’Опиталя применять гораздо проще, чем серию Тейлора. Например, если мы возьмем предел, когда x стремится к нулю, касательная к x над arcsin x.
Давайте рассмотрим случай, когда предел f равен нулю, а предел g равен нулю.Это означает, что оба члена нулевого порядка исчезают. Что мы видим? Что ж, мы видим, что можем фактор. Величина x минус a из всех оставшихся членов в разложении Тейлора как в числителе, так и в знаменателе, они отменяются, и теперь, когда мы пытаемся вычислить x минус a, мы остаемся с членами ведущего порядка. Константы, на самом деле директивы, оцениваемые в момент Сейчас, если эти 2 исчезнут, что тогда произойдет? Итак, мы снова видим, что мы можем вычленить величину x минус a, отменить и снова увидеть, что члены ведущего порядка включают вторые производные в A.Теперь вы можете спросить, а как насчет факториала 1 больше 2? Поскольку он встречается как в числителе, так и в знаменателе, это не имеет значения. Что действительно важно, так это производные. Давайте посмотрим на это на примере. Иногда правило Л’Опиталя применять гораздо проще, чем серию Тейлора. Например, если мы возьмем предел, когда x стремится к нулю, касательная к x над arcsin x. Ну, я не знаю серии Тейлора для касательной и дуги от макушки, и, возможно, потребуется журнал работы, чтобы понять это.Итак, давайте применим Правило Л’Опиталя. Если мы попытаемся различить, ну, это потребует немного воспоминаний. Вы можете помнить, а можете и не помнить, что производная тангенса – это квадрат секущей. Вы можете помнить или не помнить, что производная arcsin равна 1 минус x в квадрате с отрицательной 1 половинной степенью. Если вы этого не помните, не волнуйтесь, мы научимся их вычислять всего за несколько коротких уроков. Но пока давайте примем это как данность. Используя правило Л’Опиталя, мы получаем предел, когда x стремится к нулю секанса в квадрате x, более 1 минус x в квадрате с отрицательной 1 половиной.Оценка нуля и запоминание того, что секанс нуля равен единице, дает нам ответ, равный единице. Это было просто. Давайте посмотрим на другой пример. Тот, для которого правило L’Hopital может оказаться неприемлемым. Предел, когда x стремится к нулю, составляет x в квадрате логарифма косинуса x по синусу в квадрате 3 x в квадрате.
Ну, я не знаю серии Тейлора для касательной и дуги от макушки, и, возможно, потребуется журнал работы, чтобы понять это.Итак, давайте применим Правило Л’Опиталя. Если мы попытаемся различить, ну, это потребует немного воспоминаний. Вы можете помнить, а можете и не помнить, что производная тангенса – это квадрат секущей. Вы можете помнить или не помнить, что производная arcsin равна 1 минус x в квадрате с отрицательной 1 половинной степенью. Если вы этого не помните, не волнуйтесь, мы научимся их вычислять всего за несколько коротких уроков. Но пока давайте примем это как данность. Используя правило Л’Опиталя, мы получаем предел, когда x стремится к нулю секанса в квадрате x, более 1 минус x в квадрате с отрицательной 1 половиной.Оценка нуля и запоминание того, что секанс нуля равен единице, дает нам ответ, равный единице. Это было просто. Давайте посмотрим на другой пример. Тот, для которого правило L’Hopital может оказаться неприемлемым. Предел, когда x стремится к нулю, составляет x в квадрате логарифма косинуса x по синусу в квадрате 3 x в квадрате. Уф, я не хочу пытаться вычислить производную от этого. Можно, но невыгодно. Однако я вспоминаю разложения Тейлора для косинуса x, для логарифма 1 плюс что-то и для синуса чего-то.Все это очень просто. Мы делали это раньше. Теперь, используя тот факт, что предел таков, что x стремится к нулю, а косинус x около нуля равен единице минус x в квадрате над двумя плюс членами более высокого порядка. Затем, подставив вместо sin 3x в квадрате и отбросив все члены высшего порядка sin, мы должны возвести это в квадрат. Ох, этот путь тоже не такой простой. Но это не так уж плохо, у нас остается расширяющийся логарифм 1 минус x в квадрате на 2 плюс члены более высокого порядка. Это в виде журнала 1 плюс z.Первый член – это сам z, в данном случае отрицательная 1 половина x в квадрате. Мы забудем о членах более высокого порядка, надеюсь, они не будут иметь значения, и знаменатель, когда мы возведем в квадрат 3 x в квадрате плюс члены более высокого порядка, первый член будет равен 9 x 4. Уф, и теперь мы видим, что члены ведущего порядка имеют одинаковую степень, мы получили отрицательные 1 половина x для 4-го плюс, больше 9x для 4-го плюс вещи.
Уф, я не хочу пытаться вычислить производную от этого. Можно, но невыгодно. Однако я вспоминаю разложения Тейлора для косинуса x, для логарифма 1 плюс что-то и для синуса чего-то.Все это очень просто. Мы делали это раньше. Теперь, используя тот факт, что предел таков, что x стремится к нулю, а косинус x около нуля равен единице минус x в квадрате над двумя плюс членами более высокого порядка. Затем, подставив вместо sin 3x в квадрате и отбросив все члены высшего порядка sin, мы должны возвести это в квадрат. Ох, этот путь тоже не такой простой. Но это не так уж плохо, у нас остается расширяющийся логарифм 1 минус x в квадрате на 2 плюс члены более высокого порядка. Это в виде журнала 1 плюс z.Первый член – это сам z, в данном случае отрицательная 1 половина x в квадрате. Мы забудем о членах более высокого порядка, надеюсь, они не будут иметь значения, и знаменатель, когда мы возведем в квадрат 3 x в квадрате плюс члены более высокого порядка, первый член будет равен 9 x 4. Уф, и теперь мы видим, что члены ведущего порядка имеют одинаковую степень, мы получили отрицательные 1 половина x для 4-го плюс, больше 9x для 4-го плюс вещи. Вынося за множитель x до 4-го и отбрасывая его, мы получаем отрицательный ответ 1 18-е.Итак, не все хитрые пределы имеют форму 0 на 0. Например, предел, когда x стремится к 0 из 1 по синусу в квадрате x минус 1 по x в квадрате. Оценка выглядит как бесконечность минус бесконечность. Это не сработает. Итак, давайте положим это на общий знаменатель x в квадрате, умноженном на синус, возведенный в квадрат x. Результирующий числитель равен x в квадрате минус синус в квадрате x. Теперь мы можем применить правило Лопиталя или, в данном случае, разложение Тейлора. Если мы расширим по Тейлору, ну, единственное, о чем нам нужно беспокоиться, – это квадрат sin в x, который является рядом Тейлора для sin x, количества в квадрате.Что мы действительно хотим сделать, так это вычислить член ведущего порядка. Итак, нам нужно немного поработать с алгеброй, когда мы возведем в квадрат x минус x в кубе над 3 факториалами плюс члены более высокого порядка, что мы получим? Первый член равен x в квадрате, второй член равен 2 умноженным на x умноженным на x кубам по 3 факториалам.
Вынося за множитель x до 4-го и отбрасывая его, мы получаем отрицательный ответ 1 18-е.Итак, не все хитрые пределы имеют форму 0 на 0. Например, предел, когда x стремится к 0 из 1 по синусу в квадрате x минус 1 по x в квадрате. Оценка выглядит как бесконечность минус бесконечность. Это не сработает. Итак, давайте положим это на общий знаменатель x в квадрате, умноженном на синус, возведенный в квадрат x. Результирующий числитель равен x в квадрате минус синус в квадрате x. Теперь мы можем применить правило Лопиталя или, в данном случае, разложение Тейлора. Если мы расширим по Тейлору, ну, единственное, о чем нам нужно беспокоиться, – это квадрат sin в x, который является рядом Тейлора для sin x, количества в квадрате.Что мы действительно хотим сделать, так это вычислить член ведущего порядка. Итак, нам нужно немного поработать с алгеброй, когда мы возведем в квадрат x минус x в кубе над 3 факториалами плюс члены более высокого порядка, что мы получим? Первый член равен x в квадрате, второй член равен 2 умноженным на x умноженным на x кубам по 3 факториалам. Что мы здесь отмечаем? Отметим, что квадраты x сокращаются. Эти вторые упорядоченные термины уходят, и мы остаемся со следующим термином. Член четвертого порядка как коэффициент ведущего порядка.Точно так же в знаменателе мы видим, что член ведущего порядка – это просто x до 4-го, таким образом, сокращение x до 4-х дает нам коэффициенты ведущего порядка, равные 1 третьей в числителе и единице в знаменателе. Наш ответ – 1 третье. Точно так же, если мы посчитаем x, умноженное на логарифм x, и отправим x в 0. Нам нужно быть немного осторожными. Это односторонний предел, отправляющий x в 0 справа. Тогда что бы это было? Пока x стремится к 0, логарифм x стремится к минус бесконечности.0 раз минус бесконечность, это не сработает. Еще раз, давайте перенесем это через знаменатель. В этом случае мы переместим x в знаменатель и назовем его 1 вместо x. Так что у нас есть соотношение двух функций. В этом случае логарифм от x больше x до минус 1. Теперь мы собираемся применить правило Л’Опиталя. Я немного нервничаю по поводу расширений Тейлора здесь, потому что и log of x, и 1 по x, похоже, не имеют хороших разложений Тейлора при x, равном 0.
Что мы здесь отмечаем? Отметим, что квадраты x сокращаются. Эти вторые упорядоченные термины уходят, и мы остаемся со следующим термином. Член четвертого порядка как коэффициент ведущего порядка.Точно так же в знаменателе мы видим, что член ведущего порядка – это просто x до 4-го, таким образом, сокращение x до 4-х дает нам коэффициенты ведущего порядка, равные 1 третьей в числителе и единице в знаменателе. Наш ответ – 1 третье. Точно так же, если мы посчитаем x, умноженное на логарифм x, и отправим x в 0. Нам нужно быть немного осторожными. Это односторонний предел, отправляющий x в 0 справа. Тогда что бы это было? Пока x стремится к 0, логарифм x стремится к минус бесконечности.0 раз минус бесконечность, это не сработает. Еще раз, давайте перенесем это через знаменатель. В этом случае мы переместим x в знаменатель и назовем его 1 вместо x. Так что у нас есть соотношение двух функций. В этом случае логарифм от x больше x до минус 1. Теперь мы собираемся применить правило Л’Опиталя. Я немного нервничаю по поводу расширений Тейлора здесь, потому что и log of x, и 1 по x, похоже, не имеют хороших разложений Тейлора при x, равном 0. Итак, применение правила Л’Опиталя дает нам что? Производная log от x равна 1 по x.Производная 1 по x равна минус 1 по x в квадрате. Они упрощаются до минус x и, принимая предел, когда x стремится к 0 справа, мы видим, что ответ равен 0. Теперь правило L’Hopital также может помочь в оценке пределов на бесконечности. Рассмотрим предел, когда x стремится к бесконечности. Из журнала x больше квадратного корня из x. Возможно, неясно, каким будет этот предел. Логарифм x и квадратный корень из x становятся бесконечными, когда x стремится к бесконечности. Но с какой скоростью? Есть ли один, который больше другого? Что ж, применим Правило Л’Опиталя.Это дает нам предел, когда x стремится к бесконечности, чего? Логарифм производной x равен 1 по x. Производная x к половине равна половине x к минус половине. Это упрощается до двукратного x до минус 1, когда x стремится к бесконечности, это явно идет к 0. Что ж, вот и ответ. Но что это на самом деле означает? Логарифм x стремится к бесконечности, квадратный корень x стремится к бесконечности, их отношение стремится к 0.
Итак, применение правила Л’Опиталя дает нам что? Производная log от x равна 1 по x.Производная 1 по x равна минус 1 по x в квадрате. Они упрощаются до минус x и, принимая предел, когда x стремится к 0 справа, мы видим, что ответ равен 0. Теперь правило L’Hopital также может помочь в оценке пределов на бесконечности. Рассмотрим предел, когда x стремится к бесконечности. Из журнала x больше квадратного корня из x. Возможно, неясно, каким будет этот предел. Логарифм x и квадратный корень из x становятся бесконечными, когда x стремится к бесконечности. Но с какой скоростью? Есть ли один, который больше другого? Что ж, применим Правило Л’Опиталя.Это дает нам предел, когда x стремится к бесконечности, чего? Логарифм производной x равен 1 по x. Производная x к половине равна половине x к минус половине. Это упрощается до двукратного x до минус 1, когда x стремится к бесконечности, это явно идет к 0. Что ж, вот и ответ. Но что это на самом деле означает? Логарифм x стремится к бесконечности, квадратный корень x стремится к бесконечности, их отношение стремится к 0. На самом деле это означает, что квадратный корень x доминирует над логарифмом x.Он растет намного быстрее, чем логарифм. Хотя правило L’Hopital действительно помогает при оценке пределов и бесконечности, оно не всегда полезно. Иногда вам нужно подумать, рассмотреть предел, когда x стремится к бесконечности, гиперболический тангенс x. Это по определению предел. Гиперболический синус над гиперболическим косинусом. Применим правило L’Hopital. Что ж, это просто. Какая производная от sinh? Это чушь. Какая производная от cosh? Это грех.Итак, мы видим, что мы получаем предел, когда x стремится к бесконечности гиперболического котангенса x. Я не знаю, что это такое. Итак, применим правило L’Hopitals. Опять же, производная от sinh – это ch, а от cosh – sinh. И, к сожалению, мы застряли в петле и никогда никуда не денемся. Но, используя нашу коллективную голову, мы знаем определение гиперболического тангенса. Что нас действительно волнует, так это отношение е к х минус е к минус х по е к х плюс е к минус х.
На самом деле это означает, что квадратный корень x доминирует над логарифмом x.Он растет намного быстрее, чем логарифм. Хотя правило L’Hopital действительно помогает при оценке пределов и бесконечности, оно не всегда полезно. Иногда вам нужно подумать, рассмотреть предел, когда x стремится к бесконечности, гиперболический тангенс x. Это по определению предел. Гиперболический синус над гиперболическим косинусом. Применим правило L’Hopital. Что ж, это просто. Какая производная от sinh? Это чушь. Какая производная от cosh? Это грех.Итак, мы видим, что мы получаем предел, когда x стремится к бесконечности гиперболического котангенса x. Я не знаю, что это такое. Итак, применим правило L’Hopitals. Опять же, производная от sinh – это ch, а от cosh – sinh. И, к сожалению, мы застряли в петле и никогда никуда не денемся. Но, используя нашу коллективную голову, мы знаем определение гиперболического тангенса. Что нас действительно волнует, так это отношение е к х минус е к минус х по е к х плюс е к минус х. А теперь давайте подумаем об этом.Эти первые члены большие, е до x становится большим очень быстро, когда x стремится к бесконечности, а e до минус x становится очень и очень маленьким. Давайте проигнорируем это. Что мы получим? Что ж, я думаю, вы могли бы возразить, что предел равен 1. Теперь, как мы можем сделать это немного точнее? Если мы вычленим е из x, у нас останется 1 минус что-то, идущее до 0 в числителе, и 1 плюс что-то, идущее до 0 в знаменателе. Отмена легко дает нам этот предел. Это полезный способ поспорить.Рассмотрим предел x, умноженный на логарифм x по логарифму, гиперболический косинус, когда x стремится к бесконечности. Я собираюсь дать вам возможность применить правило Л’Опиталя и посмотреть, что мы получим. То, что мы собираемся получить, выглядит немного сложным. К счастью, здесь задействован гиперболический тангенс, который позволяет нам использовать предыдущий результат, чтобы сказать, что числитель стремится к бесконечности, а знаменатель – к 1. Я хочу, чтобы вы подумали о том, как этот ответ бесконечности может быть получен в ваша голова без правила L’Hopital.
А теперь давайте подумаем об этом.Эти первые члены большие, е до x становится большим очень быстро, когда x стремится к бесконечности, а e до минус x становится очень и очень маленьким. Давайте проигнорируем это. Что мы получим? Что ж, я думаю, вы могли бы возразить, что предел равен 1. Теперь, как мы можем сделать это немного точнее? Если мы вычленим е из x, у нас останется 1 минус что-то, идущее до 0 в числителе, и 1 плюс что-то, идущее до 0 в знаменателе. Отмена легко дает нам этот предел. Это полезный способ поспорить.Рассмотрим предел x, умноженный на логарифм x по логарифму, гиперболический косинус, когда x стремится к бесконечности. Я собираюсь дать вам возможность применить правило Л’Опиталя и посмотреть, что мы получим. То, что мы собираемся получить, выглядит немного сложным. К счастью, здесь задействован гиперболический тангенс, который позволяет нам использовать предыдущий результат, чтобы сказать, что числитель стремится к бесконечности, а знаменатель – к 1. Я хочу, чтобы вы подумали о том, как этот ответ бесконечности может быть получен в ваша голова без правила L’Hopital. Рассмотрим гиперболический косинус x. Это действительно е к x плюс что-то маленькое с постоянной равной 1 половине. Теперь, если мы возьмем натуральный логарифм, это должно выглядеть примерно как x. Не совсем, но он должен расти линейно. Итак, я бы сказал, что x, умноженное на логарифм x, деленное на что-то, что растет, как x, должно дать нам бесконечный предел. Это предзнаменование того, что должно произойти. Там, где мы хотим иметь язык для обсуждения или управления ростом функций, это называется большой буквой O, и это красивый язык.Правило L’Hopital вместе с серией Тейлора образуют прекрасный набор инструментов для оценки пределов. В следующем уроке мы применим эти инструменты для изучения асимптотики или темпов роста функций. Попутно мы расширим наши инструменты еще одним устройством, большим O.
Рассмотрим гиперболический косинус x. Это действительно е к x плюс что-то маленькое с постоянной равной 1 половине. Теперь, если мы возьмем натуральный логарифм, это должно выглядеть примерно как x. Не совсем, но он должен расти линейно. Итак, я бы сказал, что x, умноженное на логарифм x, деленное на что-то, что растет, как x, должно дать нам бесконечный предел. Это предзнаменование того, что должно произойти. Там, где мы хотим иметь язык для обсуждения или управления ростом функций, это называется большой буквой O, и это красивый язык.Правило L’Hopital вместе с серией Тейлора образуют прекрасный набор инструментов для оценки пределов. В следующем уроке мы применим эти инструменты для изучения асимптотики или темпов роста функций. Попутно мы расширим наши инструменты еще одним устройством, большим O. На
На 1 ниже.
1 ниже. Большинство подчеркнуло, что это решение не касалось конституционности закона Техаса и не ограничивало его «процедурными оспариваниями».
Большинство подчеркнуло, что это решение не касалось конституционности закона Техаса и не ограничивало его «процедурными оспариваниями».