Пределы с факториалами : Анализ-I
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| |||
16/02/07 |
| ||
| |||
| AD |
| |||
17/06/06 |
| |||
| ||||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| PAV |
| |||
29/07/05 |
| |||
| ||||
Алексей К. |
| ||
29/09/06 |
| ||
| |||
| GlazkovD |
| ||
16/02/07 |
| ||
| |||
V. V. V. |
| |||
09/01/06 |
| |||
| ||||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| venja |
| ||
08/09/07 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 9 ] |
Модераторы: Модераторы Математики, Супермодераторы
примеры пределов с факториалами
Пределы/ Предел функции
| → | ↑ Функция f(x) ? |
|---|
Примеры
Для конечных точек:
———Слева (x0-)Справа (x0+)
График:
от до
Ввести:
{ кусочно-заданную функцию можно здесь. 2
2
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- 15/7
- – дробь
Другие функции:
- asec(x)
- Функция – арксеканс от x
- acsc(x)
- Функция – арккосеканс от x
- sec(x)
- Функция – секанс от x
- csc(x)
- Функция – косеканс от x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция – округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция – гиперболический арксеканс от x
- csch(x)
- Функция – гиперболический косеканс от x
- sech(x)
- Функция – гиперболический секанс от x
- acsch(x)
- Функция – гиперболический арккосеканс от x
Постоянные:
- pi
- Число “Пи”, которое примерно равно ~3.
 14159..
14159.. - e
- Число e – основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности – знак для бесконечности
– Как вычислить предел функции, имеющей факториал в знаменателе
спросил
Изменено 7 месяцев назад
Просмотрено 78 тысяч раз
$\begingroup$
Для $n$, стремящегося к бесконечности, найдите следующий предел 9n}{n!}.$$
У меня такое ощущение, что это умножение многих чисел, последнее из которых превращается в $0$, но первое число конечное, поэтому ограничение должно быть $0$. {n-2}$$ 9н
$$
{n-2}$$ 9н
$$
$\endgroup$
5
$\begingroup$
Один из способов приблизиться к такого рода пределам — использовать теорему о монотонной сходимости (реальные ограниченные монотонные последовательности сходятся). Итак, для сходимости вам нужно доказать, что 1. ваша последовательность монотонна, 2. она ограничена
. Для вашей последовательности вы можете доказать, что она убывает, используя тест отношения, как в ответе idm. И вы можете ясно видеть, что она ограничена 0. Это означает, что предел существует, пусть $a_n$ будет вашей последовательностью, тогда 9n}{n!}$ и определим вспомогательную функцию $g_n=\ln(f_n)$. Это дает
$$ g_n=n\ln(2)-\ln(n!)=n\ln(2)-\color{red}{\bigg(\ln(n)+\ln(n-1)+\dots+ \ln(2)+\ln(1)\bigg)}.$$
С каждым увеличением $n$ член $n\ln(2)$ увеличивается на 0,69, а член красного цвета удаляет $\ln(n)$.

 02.2008, 20:35
02.2008, 20:35 
 ru/viewtopic.php?t=11848&start=0
ru/viewtopic.php?t=11848&start=0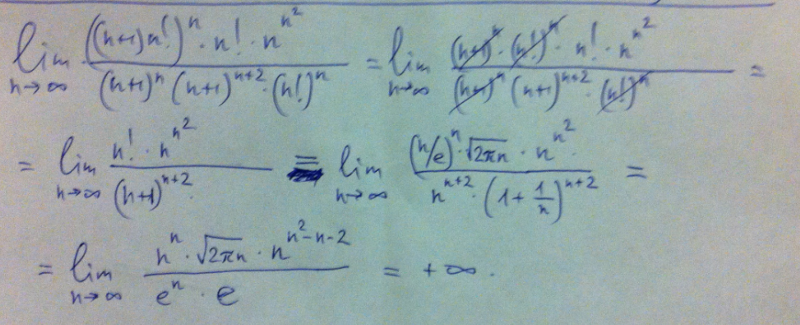
 02.2008, 22:54
02.2008, 22:54 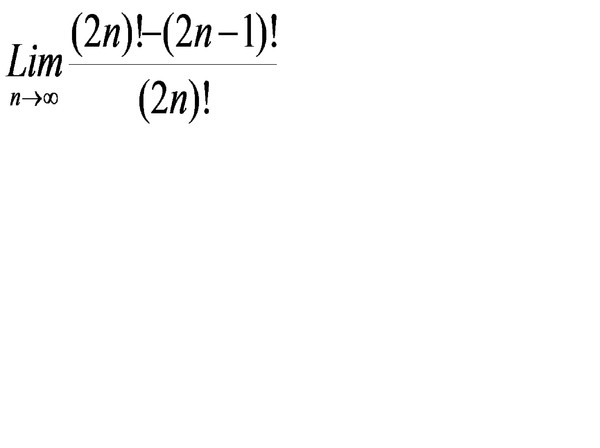 02.2008, 23:45
02.2008, 23:45 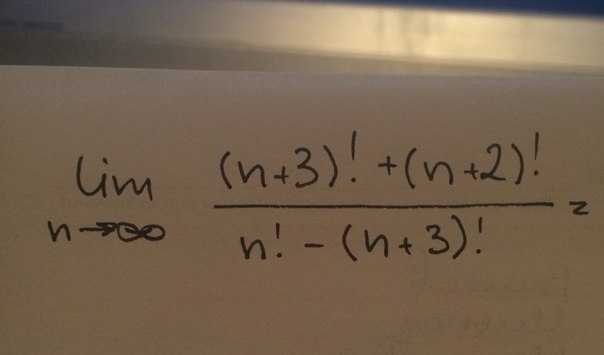 02.2008, 10:30
02.2008, 10:30  3
3 14159..
14159..