Нахождение предела функции, по правилу Лопиталя, раскрывающий неопределённости вида 0/0 и ∞/∞. Калькулятор ниже находит предел функции по правилу Лопиталя (через производные числителя и знаменателя). Описание правила смотри ниже. Предел функции в точке — правило Лопиталя. Данный калькулятор пределов является универсальным калькулятором, находит пределы любых функций, находит левые и правые пределы, бесплатно.
Пример. Найти предел. Решение. Вставляем функцию в калькулятор, указываем предел к которому стремится переменная, нажимаем кнопку “Найти”, получаем ответ (данная функция уже набрана в калькуляторе и предел тоже указан). Данный пример решен также в авторском исполнении, без применения правила Лопиталя, см.
найти предел. Правила ввода формул: 1. 2. Онлайн калькулятор для вычисления пределов функций – вводите функцию и получает решение предела с подробными комментариями. Также на сайте собрана теория и примеры решения задач по теме.
Введите значение, к которому стремится переменная икс. Нажмите кнопку – Вычислить предел. Другие онлайн калькуляторы. Правило Лопиталя. Теория про пределы. Решение производных. Онлайн калькулятор позволяет вычислять пределы функций, выражений, последовательностей с пошаговым решением на русском языке. Нажимая на кнопки калькулятора введите выражение предел которого Вы хотите найти: (иногда, из-за загруженности сервера реакция в ответ на нажатие кнопки может проявиться не сразу, поэтому если Вы нажали на кнопку, и ничего не произошло, подождите несколько секунд!).
Вычисление предела функции онлайн бесплатно на glamorousthings.ru Найти лимит функции. Вычислить предел функции онлайн. glamorousthings.ru позволяет вам быстро и качественно находить пределы функций онлайн. Вы сами выбираете переменную и назначаете лимит, а сервис выполняет все вычисления за вас.
Вычисляйте пределы функций и последовательностей бесплатно вместе с нами! Вычислить предел онлайн.
Отключить рекламу Зачем на сайте нужна реклама? Выберите переменную. Представлен калькулятор, который помогает вычислять пределы с помошью правила Лопиталя. Он не только даёт ответ, но ещё предоставляет подробное решение с помощью этого правила. Перейти: Онлайн “правило Лопиталя” → © Контрольная работа ру – калькуляторы онлайн.
Используйте Mathbiz для вычисления пределов функций и нахождения предельного значения числовой последовательности. К вашим услугам доступен дополнительный сервис с пошаговыми решениями пределов. Нахождение пределов функции ∞ онлайн с оформлением в Word ∞. Подробные примеры решений. Решение пределов. Число A называется пределом функции y=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
Решение онлайн. Видеоинструкция. Оформление Word. Также решают. lim x→. Если выбрать вид предела, то подробное решение по шагам будет доступно в MS Word: 1.
Вычисление пределов по правилу Лопиталя
Эффективным способом вычисления пределов функций, имеющих особенности типа бесконечность на
бесконечность или ноль на ноль является применение правила Лопиталя: предел отношения двух
бесконечно малых или двух бесконечно больших функций равен пределу отношения их производных,
если такие существуют
Раскрытие неопределенностей сводится предварительно рассмотренным выше неопределенностей. Если , а при , то применяем преобразование
В случае трех последних неопределенностей нужно применять преобразования
Рассмотрим некоторые примеры из сборника задач Дубовика В.П., Юрика И.И. “Высшая математика”на
применение правила Лопиталя.
———————————–
Пример 1. Найти пределы.
1) (5. 626)
2) (6.
629)
3) (6. 634)
4) (4. 639)
5) (4. 645)
6) (4. 668)
Решение. 1) Подстановкой устанавливаем что имеем неопределенность вида ноль на ноль . Для избавления от
нее применим правило Лопиталя
2) Как и в предыдущем примере мы имеем неопределенность . По правилу Лопиталя находим
3) Учитывая неопределенность применяем предыдущее правило
4) Раскрываем неопределенность вида
Числитель и знаменатель преобразуем к сумме синусов на основе правила
В результате получим
Подставим найденные значения
Опять получили неопределенность вида и повторно применяем правило Лопиталя
Здесь учтено, что косинус функция стремится к единице при .
5) Есть неопределенность вида бесконечность на бесконечность .
Найдем производные
6) Применим последнее правило сведения к второй замечательной границы
Применение правила Лопиталя показало все возможности при раскрытии неопределенностей.
Пользуйтесь им на практике и Вам не будет трудно находить подобные границы в обучении.
———————————–
Посмотреть материалы:
Решение пределов по правилу Лопиталя
Метод решения
Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов функций является использование правила Лопиталя. Оно позволяет раскрывать неопределенности вида 0/0 или ∞/∞ в конечной или бесконечно удаленной точке, которую мы обозначим как x0. Правило Лопиталя заключается в том, что мы находим производные числителя и знаменателя дроби. Если существует предел , то существует равный ему предел .
Если после дифференцирования мы опять получаем неопределенность, то процесс можно повторить, то есть применить правило Лопиталя уже к пределу . И так далее, до раскрытия неопределенности.
Для применения этого правила, должна существовать такая проколотая окрестность точки x0, на которой функции в числителе и знаменателе являются дифференцируемыми и функция в знаменателе и ее производная не обращается в нуль.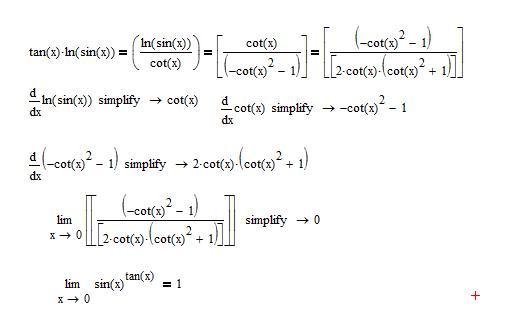
Применение правила Лопиталя состоит из следующих шагов.
1) Приводим неопределенность к виду 0/0 или ∞/∞. Для этого, если требуется, выполняем преобразования и делаем замену переменной. В результате получаем предел вида .
2) Убеждаемся, что существует такая проколотая окрестность точки x0, на которой функции в числителе и знаменателе являются дифференцируемыми и знаменатель и его производная не обращаются в нуль.
3) Находим производные числителя и знаменателя.
4) Если имеется конечный или бесконечный предел , то задача решена: .
5) Если предела не существует, то это не означает, что не существует исходного предела. Это означает, что данную задачу решить с помощью правила Лопиталя нельзя. Нужно применить другой метод (см. пример ниже).
6) Если в пределе вновь возникает неопределенность, то к нему также можно применить правило Лопиталя, начиная с пункта 2).
Как указывалось выше, применение правила Лопиталя может привести к функции, предела которой не существует.
Однако это не означает, что не существует исходного предела. Рассмотрим следующий пример.
.
Применяем правило Лопиталя. , .
Однако предела не существует. Не смотря на это, исходная функция имеет предел:
.
Правило Лопиталя. Формулировки теорем
Здесь мы приводим формулировки теорем, на которых основывается раскрытие неопределенностей по правилу Лопиталя.
Теорема о раскрытии неопределенности 0/0
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точки , причем и не равны нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Теорема о раскрытии неопределенности ∞/∞
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точки , причем не равна нулю в этой окрестности.
И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Примеры
Все примеры Далее мы приводим подробные решения следующих пределов с помощью правила Лопиталя.
⇓, ⇓, ⇓,
⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Показать, что экспонента растет быстрее любой степенной функции, а логарифм – медленнее. То есть показать, что
А) ;
Б) ,
где .
Решение
Рассмотрим предел А). При . Это неопределенность вида . Для ее раскрытия применим правило Лопиталя. Пусть
.
Находим производные. . Тогда
.
Если , то неопределенность исчезает, поскольку при . По правилу Лопиталя,
.
Если , то применяем правило Лопиталя n раз, где – целая часть числа b.
;
.
Поскольку , то . Хотя мы привыкли читать слева направо, но эту серию равенств следует читать справа налево следующим образом.
Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему предел . И так далее, пока не дойдем до предела .
Теперь рассмотрим предел Б):
. Сделаем замену переменной . Тогда ; при ; .
Пример 2
Все примеры ⇑ Найти предел с помощью правила Лопиталя:
.
Решение
Это неопределенность вида 0/0. Находим по правилу Лопиталя.
.
Здесь, после первого применения правила мы снова получили неопределенность. Поэтому применили правило Лопиталя второй раз. Эту серию равенств нужно читать справа налево следующим образом. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему исходный предел .
Ответ
Пример 3
Все примеры ⇑ Вычислить предел, используя правило Лопиталя.
.
Решение
Найдем значения числителя и знаменателя при :
;
.
Числитель и знаменатель равны нулю.
Мы имеем неопределенность вида 0/0. Для ее раскрытия, применим правило Лопиталя.
.
Ответ
Пример 4
Все примеры ⇑ Решить предел с помощью правила Лопиталя.
.
Решение
Здесь мы имеем неопределенность вида (+0)+0. Преобразуем ее к виду +∞/+∞. Для этого выполняем преобразования.
.
Находим предел в показателе степени, применяя правило Лопиталя.
.
Поскольку экспонента – непрерывная функция для всех значений аргумента, то
.
Ответ
.
Пример 5
Все примеры ⇑ Найти предел используя правило Лопиталя:
.
Решение
Здесь мы имеем неопределенность вида ∞ – ∞. Приводя дроби к общему знаменателю, приведем ее к неопределенности вида 0/0:
.
Применяем правило Лопиталя.
;
;
.
Здесь у нас снова неопределенность вида 0/0. Применяем правило Лопиталя еще раз.
;
.
Окончательно имеем:
.
Как и во всех пределах, вычисляемых с помощью правила Лопиталя, читать нужно с конца.
{3x} = 1 $$
Разберем случаи, когда задача похожа на второй замечательный предел, но решается без него.
В статье: «Второй замечательный предел: примеры решений» была разобрана формула, её следствия и приведены частые типы задач по этой теме.
Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-ой замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки.
Выделим существенные моменты формулы:
1) Речь идёттолько об определённости и никакой другой .
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-ой замечательный предел.
Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:
Пример 18
Вычислить предел
На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела.
А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость
Используем формулу
Чтобы не таскать за собой букву «е» и не мельчить, показатель удобнее вычислить отдельно:
В данном случае:
Таким образом:
С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.
В результате:
Обещанный подарок с разностью логарифмов и неопределённостью :
Пример 19
Вычислить предел
Сначала полное решение, потом комменты:
(1)-(2) На первых двух шагах используем формулы . У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».
(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности».
Кроме того, предел же относится к «начинке» логарифма.
(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы , преобразуем неопределённость к виду .
(6) Используем формулу .
(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма: . Минус перед дробью вносим в знаменатель:
(8) Без комментариев =)
Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.
Пример 20
Вычислить предел
Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде и заменой свести решение к случаю .
В заключение рассмотрим пределы-«фальшивки».
Вернёмся к неопределённости . Данную неопределённость далеко не всегда можно свести к неопределённости и воспользоваться 2-ым замечательным пределом либо формулой-следствием.
Преобразование осуществимо в том случае, если числитель и знаменатель основания степени –
Отвлечёмся от показателя и вычислим предел основания:
В пределе получена единица , значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны . На уроке Замечательные пределы. Примеры решений мы без проблем свели данный пример к неопределённости и получили ответ.
Аналогичных пределов можно придумать очень много:
и т.д.
Дроби данных примеров объединяет вышеуказанная особенность: . В других случаях при неопределённости 2-ой замечательный предел не применим .
Пример 21
Найти пределы
Как ни старайся, а неопределённость не удастся преобразовать в неопределённость
Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты : .
Таким образом, 2-ой замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ .
! Примечание : не путайте с Примером №18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость , здесь же речь идёт о неопределённости .
Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменательоснования разделить на «икс» в старшей степени (невзирая на показатель):
Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:
Пример 22
Найти пределы
Это короткие примеры для самостоятельного изучения
Иногда неопределённости может не быть вообще :
Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Пример 2
Старшая степень числителя: 2; старшая степень знаменателя: 3.
:
Пример 4
Разделим числитель и знаменатель на :
Примечание : самым последним действием умножили числитель и знаменатель на , чтобы избавиться от иррациональности в знаменателе.
Пример 6
Разделим числитель и знаменатель на :
Пример 8
Разделим числитель и знаменатель на :
Примечание : слагаемое стремиться к нулю медленнее, чем , поэтому является «главным» нулём знаменателя. .
Пример 22
Примечание : бесконечно малая функция стремится к нулю медленнее, чем , поэтому «более большой» ноль знаменателя играет определяющую роль:
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса.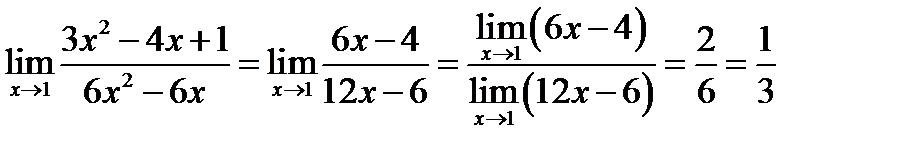
Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай.
Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Пример 4
Найти предел
Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость ( более высокого порядка роста, чем корень ).
Если «икс» стремится к «минус бесконечности»Призрак «минус бесконечности» уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых . Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
Рассмотрим 4 фишки, которые потребуются для решения практических заданий:
1) Вычислим предел
Значение предела зависит только от слагаемого , поскольку оно обладает самым высоким порядком роста. Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени , в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна , поэтому:
2) Вычислим предел
Здесь старшая степень опять чётная , поэтому: . Но перед расположился «минус» (отрицательная константа –1), следовательно:
3) Вычислим предел
Значение предела зависит только от . Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае: .
Константа («четвёрка») положительна , значит:
4) Вычислим предел
Первый парень на деревне снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит: Таким образом:
.
Пример 5
Найти предел
Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость . Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
Решение тривиально:
Пример 6
Найти предел
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
А сейчас, пожалуй, самый тонкий из случаев:
Пример 7
Найти предел
Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость . Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:
Решаем:
Разделим числитель и знаменатель на
Пример 15
Найти предел
Это пример для самостоятельного решения.
Примерный образец чистового оформления в конце урока.
Ещё пара занятных примеров на тему замены переменной:
Пример 16
Найти предел
При подстановке единицы в предел получается неопределённость . Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс?
Заметьте, что , поэтому . Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице . Таким образом, мы сразу избавляемся от множителя , кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
Проведем замену:
Если , то
Под косинусом у нас находится «икс», который тоже необходимо выразить через «тэ».
Из замены выражаем: .
Завершаем решение:
(1) Проводим подстановку
(2) Раскрываем скобки под косинусом.
(4) Чтобы организовать первый замечательный предел , искусственно домножаем числитель на и обратное число .
Задание для самостоятельного решения:
Пример 17
Найти предел
Полное решение и ответ в конце урока.
Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения , приходится использовать самые разные тригонометрические формулы , а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)
В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:
Устранение неопределённости «единица в степени бесконечность»Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-й замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёт только о неопределённости и никакой другой .
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу.
Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-й замечательный предел.
Производная от функции недалеко падает, а в случае правил Лопиталя она падает точно туда же, куда падает исходная функция. Это обстоятельство помогает в раскрытии неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций. Вычисление значительно упрощается с помощью этого правила (на самом деле двух правил и замечаний к ним):
Как показывает формула выше, при вычислении предела отношений двух бесконечно малых
или бесконечно больших функций предел отношения двух функций можно заменить пределом отношения их производных и, таким
образом, получить определённный результат.
Перейдём к более точным формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин . Пусть функции f (x ) и g (x a . А в самой точке a a производная функции g (x ) не равна нулю (g “(x a равны между собой и равны нулю:
.
Правило Лопиталя для случая предела двух бесконечно больших величин . Пусть функции f (x ) и g (x ) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a . А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g (x ) не равна нулю (g “(x )≠0 ) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности:
.
Тогда предел отношения этих функций равен пределу отношения их производных:
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций
равен пределу отношения их производных, если последний существует (конечный, то есть равный определённому
числу, или бесконечный, то есть равный бесконечности).
Замечания .
1. Правила Лопиталя применимы и тогда, когда функции f (x ) и g (x ) не определены при x = a .
2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”
Пример 1.
x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе – производную сложной
логарифмической функции .
Перед последним знаком равенства вычисляли обычный предел , подставляя вместо
икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 4. Вычислить
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять
дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Раскрытие неопределённостей вида “ноль умножить на бесконечность”
Пример 12. Вычислить
.
Решение. Получаем
В этом примере использовано тригонометрическое тождество .
Раскрытие неопределённостей видов “ноль в степени ноль”, “бесконечность в степени ноль” и “один в степени бесконечность”
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13.
Решение. Получаем
.
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
Решение.
Получаем
Вычисляем предел выражения в показателе степени
.
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
Правило Лопиталя для вычисления пределов, примеры с подробным решением, доказательство
Одной из основных теорем в математическом анализе является правило Лопиталя. Этот закон, предложенный французским учёным, используется для вычисления пределов функций, когда формулы Тейлора применить невозможно. Идейно он достаточно простой, однако его доказательство содержит технические тонкости, на которые следует обратить пристальное внимание.
Общие сведения
Важным понятием в высшей математике является определение бесконечности. Эта неопределённость обозначается символом ∞. Когда её упоминают, то имеют в виду как бесконечно малое число, так и большое. Для записи предела функций используется знак лимита, например, lim 0k (y). В нижней части указывается аргумент со стрелочкой, обозначающей, к чему именно стремится неопределённость.
Если предел известный, то он называется конечным, в ином случае — бесконечным.
Когда нельзя установить, является ограничение бесконечным или конечным, то говорят, что предела для рассматриваемой функции не существует. Это возможно, например, когда ограничение тригонометрической функции стремится к бесконечности. Существует несколько способов вычисления пределов: правило Лопиталя, формулы Тейлера, графический метод, подставление неизвестного в функцию.Указанные способы можно применять для нахождения того или иного предела, но для неопределённости вида 0/0 или ∞/∞, а также вычисления отношений бесконечно малых или больших выражений лучше всего использовать закон Лопиталя. Состоит он из двух правил:
- Для бесконечно малых величин. Когда функции k (y) и d (y) можно дифференцировать в некоторой области точки, исключая саму её, при этом в этой окрестности производная выражения неравна нулю, а пределы этих функций равны нулю, то отношение ограничения этих функций будет равно пределу отношения их производных.
- Для бесконечно больших значений. Если две функции k (y) и d (y) можно дифференцировать по окрестности взятой точки, но при этом её саму исключить, учитывая, что в рассматриваемой окрестности производная d (y) не равняется нулю, то когда функции в этой точке равны бесконечности, предел отношения этих выражений тождественен отношению их производных.
Другими словами, смысл теоремы Лопиталя заключается в том, что когда нужно найти ограничение для двух функций, отношение которых даёт неопределённость 0/0 или ∞/∞, то можно взять производные этих выражений и найти их отношение. Это действие приведёт к получению искомого ответа. Метод позволяет упростить вычисление сложных показательных степенных функций. Его можно применять и при умножении неопределённостей или их вычитании. Например, 0 * ∞, ∞ — ∞.
Доказательство правила
Лопиталь после знакомства с Бернулли смог систематизировать метод Иоганна и издать в 1696 году книгу «Анализ бесконечно малых», где подробно изложил способы решения задач с неопределённостями.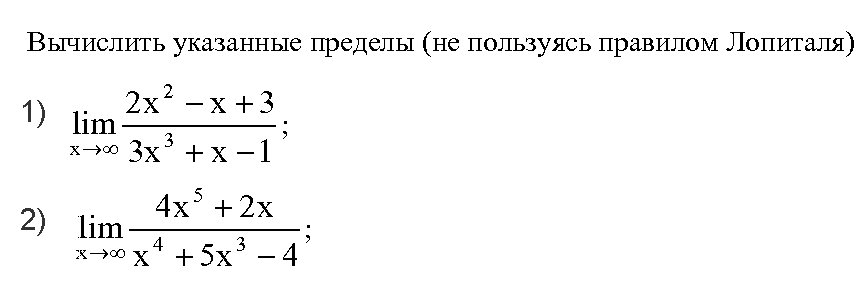
Математически его описание состоит из четырёх пунктов:
- lim k (y) = lim d (y) = 0 (∞).
- Графики k (y) и d (y) приближаются к линейному виду.
- d (y)’ ≠ 0.
- lim k (y)’ / d (y)’ = lim k (y) / d (y).
Пусть имеется два дифференцируемых выражения, при этом d (y) во всех точках имеет не нулевую производную. При y, стремящемся к a, d стремится к бесконечности. Если предел отношения производных конечного предела или бесконечного равняется числу L, тогда ограничение отношений производных этих функций также будет тождественно этому числу. То есть lim k (y) / d (y) = L, при y → a. Исходя из определения Гейне и Коши, рассматривать можно только монотонные последовательности, которые стремятся к a.
Взяв произвольный ряд, который может расти yn → a, верно утверждать, что в соответствии со следствием теоремы Дарбу и условием d (y)’ ≠ 0, рассматриваемая функция будет строго монотонной. А это означает, что последовательность d (yn) будет такой же.
В тоже время из условия lim d (y) = ∞ следует, что d (yn) → ∞. При этом бесконечность может быть как со знаком минус, так и плюс.
Рассмотрим теорему Штольца, а именно отношение: (k (yn+1) — k (yn)) / (d (yn+1) — d (yn)) = k'(Cn) / d'(Cn) = L. Из неё следует, что k (y) / d (y) → L. То есть всегда найдётся такая точка Cn, которая будет принадлежать множеству (Yn+1,Yn). Так как множество стремится к L, то и точка, принадлежащая ему, тоже будет приближаться к L. Поэтому можно утверждать, что и выражение lim k (y) / d (y) → L.
Аналогичным образом первому доказывается и второй случай, когда lim k (y) = lim d (y) = 0. Если предел отношения производных будет L, то ограничения отношений функций будет также равняться этому числу. Из теоремы Дарбу и монотонности получим, что d (Yn) → 0, кроме того k (Yn) → 0. Используя правило Штольце, можно будет утверждать, что k (y) / d (y) → L.
Но на практике часто для решения примеров правило Лопиталя оказывается недостаточным.
Это справедливо для заданий, в которых y стремится не к конечному числу, а к бесконечному. Поэтому для таких задач используется следствие из теоремы. Согласно ему, при k → 0 и d → 0, а y → + ∞. Тогда существует предел lim k'(y) / d'(y) = AЄR и предел отношений lim k (y) / d (y) = A. Этот вспомогательный закон очень важен и то же может быть доказан.
Следствие из утверждения
Перед доказательством следствия нужно условиться, что в выражении a будет всегда больше либо равно единице. Это возможно исходя из того, что если a будет меньше единицы, то доказывать нужно будет правило только от единицы до плюс бесконечности. Кроме этого, необходимо ввести замену вида t = 1/y. Она необходима, так как во многом облегчает сведение доказательства к теореме Лопиталя.
Пусть имеется функция K (t), равная k, и D (t), равная d. При этом аргумент последней будет 1/t.
Так как по условию правила функции k и d определены на интервале от a до плюс бесконечности, то можно сказать, что функции K и D известны на интервале от нуля до единицы, делённом на a. Это верно из-за того, что если в исходной функции k и d икс подходил достаточно близко к плюс бесконечности, то в силу сделанной ранее замены t будет приближаться к нулю. Если же икс близок к a, то t будет приближаться к значению 1/a.
Так как a больше либо равняется единице, то интервал от нуля до единицы, делённой на a, будет определён корректно. Чтобы воспользоваться теоремой Лопиталя, нужно доказать, что предел lim K'(t) / D'(t) при t, стремящемся к нулю, равняется A. В силу того, что K (t) = k (1/t) и D (t) = d (1/t), можно написать: lim K'(t) / D'(t) = lim k'(1/t)’ / d'(1/t)’ .
Теперь нужно воспользоваться теоремой о производной композиции, условия которой выполнены. Вначале нужно взять производную внутренней функции, а затем внешней. Должно получиться следующее выражение: lim -1/ t 2 k ‘(1/ t) / (-1/ t 2) * d ‘ (1/ t) = lim K ‘(t) / D ‘(t) = lim k ‘(y)/ d (y) = A.
Отсюда можно утверждать, что предел отношений K'(t) / D'(t) будет равняться A. Все условия теоремы Лопиталя выполнены. А это значит, что существует предел отношения функций при t, стремящемся к нулю, равный A. Теперь можно снова применить теорему о пределе композиций и от переменной t перейти обратно к иксу: lim K (t)/D (t) = lim k (y)/(d (y) = A.
Таким образом можно сделать вывод, что требуемое утверждение верно. Использование правила и следствия позволяет выполнить быстрый расчёт неопределённости 0/0 или ∞/∞. При этом другого вида выражение можно свести к этой неопределённости. Это намного упрощает работу, особенно если необходимо логарифмировать или возводить в степень.
Решение примеров
Закрепить правило лучше всего на соответствующих примерах. Существуют типовые задания, чаще всего встречающиеся на контрольных работах.
Например, требуется найти предел отношения натурального логарифма от тангенса икс к котангенсу два икс, когда неизвестное стремится к p /4. Помощь в решении окажет правило Лопиталя, которое при сравнении с альтернативными методами окажется на порядок проще.
Для того чтобы понять, какого вида неопределённость в задании, нужно в числитель и знаменатель подставить p/4. Тогда: ln td p /4 = ln 1 = 0 и ctd p /2 = 0. По правилу можно свести нахождение предела функций к вычислению их производных. Искомый предел: A = lim (lntdy ‘) / (ctd 2 y)’ = lim (ctdy * 1/ cos 2 y) / 2 (-1/ sin 2 2 y) = lim (-sin 2 y)(2 * siny * cosy) = (-½) * lim (sin 2 2 y / siny * cosy) = — ½ * 1/½ = -1. Таким образом, решение будет равняться минус единице.
Пусть есть выражение вида: lim y½ (p — 2 arctd √ y) = A. Нужно определить предел при иксе, стремящемся к плюс бесконечности. Чтобы воспользоваться правилом, исходное выражение нужно привести к дробному виду.
Для этого выражение можно переписать как lim (p — 2 arctd √ y) / y½. В этом случае имеет место неопределённость 0/0. Поэтому можно рассматривать отношение производной делимого на делитель: A = lim (2 *(1/1+ y) * ½ * y -½ ) / ½ * y -3/2 = lim 2y/(1+y) = 2 lin 1 /(1+ 1/ y) = 2.
Замечательным случаем является неопределённость вида ∞/∞. Например, требуется найти предел lim k (y) при иксе, стремящемся к бесконечности, где функция k (y) = y /ey. По теореме Лопиталя A = lim (y)’ / (ey)’, а это выражение есть не что иное, как lim 1/ey, равняющийся нулю. Теперь можно рассмотреть пример сложнее.
Пусть дано выражение нормальной функции со степенью: lim yy = A, где A = lim k (y). Проэкспоненцируя эту функцию, выражение можно привести к виду: yy = ey *lny. Если найти, к чему стремится показатель экспоненты, то это и будет решением рассматриваемого примера. Можно записать: lim y * lny = lim lny /1/ y = lim (1/ y)/(-1/ y 2 ) = 0.
Если предел в показателе экспоненты стремится к нулю, то можно написать, что он будет равняться e0, то есть единице. А это и будет искомый предел: lim k (y) = 1 при иксе, стремящемся к плюс бесконечности.
Закон Лопиталя является хорошим помощником при вычислении особо экзотических пределов. При этом можно попробовать составить выражение, отвечающее условиям правила и из неявного вида функции. Для этого можно использовать раскрытие скобок, дополнительно умножить или разделить функцию на однородный многочлен.
Использование онлайн-калькулятора
Не всегда задания, попадающиеся на практике, довольно легко привести к условию, отвечающему правилу. Да и нередко сама функция настолько умудрённая, что для определения производной понадобится не только проявить внимание и усидчивость, но и затратить довольно много времени.
Поэтому в таких случаях есть резон решать задания на онлайн-калькуляторе с подробным решением. Правило Лопиталя отлично поддаётся автоматизированному вычислению.
Такую услугу предлагают более десятка специализированных на математических расчётах сайтов. Доступ к вычислениям предоставляется полностью бесплатно. От пользователя даже не требуется регистрации и указания персональных данных. Работают они на основе алгоритмов, заложенных в программный код используемого онлайн-приложения. Пользователю нужно лишь только подключение к интернету и любой веб-обозреватель.
Все его действия сводятся к введению в предложенную форму условия примера и нажатия кнопки «Рассчитать». После этого программа автоматически вычислит ответ и выведет его на дисплей. При этом в большинстве случаев вместе с ответом приложение отобразит пошаговый расчёт с комментариями. Это позволит потребителю не просто получить готовый ответ, но и разобраться в решении.
Из наиболее популярных сайтов можно выделить следующую пятёрку:
- Math. semestr.
- Kontrolnaya-rabota
- Planetcalc.
- Math34.
- Webmath.
semestr.Все эти сайты имеют интуитивно понятный интерфейс на русском языке. Кроме предоставления услуги онлайн-калькулятора, на их страницах содержится вся необходимая теория, помогающая понять, как происходит нахождение ответа. А также приведены несколько типовых примеров с подробным решением.
Пользоваться такими сайтами сможет даже пользователь, ничего не понимающий в математическом анализе. Но решая различные примеры, со временем он поймёт суть идеи правила и сможет самостоятельно вычислять пределы функций. При этом такие сайты являются отличным подспорьем как инженерам, проводящим сложные вычисления, так и студентам, проверяющим свои навыки.
ПредыдущаяАлгебраПоказательная функция определение, свойства, особенности построения графиков убывающей и возрастающей функций, область определения и применения, формулы, примеры решения
СледующаяАлгебраДисперсия свойства, формула вычисления дисперсии дискретной случайной величины, виды, правило и примеры расчетов, онлайн-калькулятор
Исчисление I – Правило госпиталя и неопределенные формы
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с “узкой” шириной экрана (, т. В первом пределе, если мы подключим \ (x = 4 \), мы получим 0/0, а во втором пределе, если мы «подключимся» к бесконечности, мы получим \ ({\ infty} / {- \ infty} \ ; \) (напомним, что при стремлении \ (x \) к бесконечности многочлен будет вести себя так же, как его наибольшая степень). Обе они называются неопределенными формами . В обоих случаях существуют конкурирующие интересы или правила, и неясно, что победит. В случае 0/0 мы обычно думаем, что дробь с нулевым числителем равна нулю.Однако мы также склонны думать о дробях, в которых знаменатель стремится к нулю, в пределе, как о бесконечности или, возможно, вообще не существует. Точно так же мы склонны думать о дроби, в которой числитель и знаменатель равны единице. Итак, что победит? Или ни один из них не выиграет, и все они «аннулируются», и лимит достигнет другого значения? В случае \ ({\ infty} / {- \ infty} \; \) мы имеем похожий набор проблем. Со вторым пределом возникает еще одна проблема, заключающаяся в том, что бесконечность на самом деле не является числом, и поэтому нам даже не следует рассматривать ее как число. В большинстве случаев он просто не ведет себя так, как мы ожидали бы, если бы это было число.0} \ hspace {0,25 дюйма} \ infty – \ infty \] У всех них есть конкурирующие интересы или правила, которые говорят нам, что должно происходить, и просто неясно, какие интересы или правила победят, если таковые имеются. Тема этого раздела – как бороться с такими ограничениями. Здесь и вступает в игру тема этого раздела. Предположим, что у нас есть один из следующих случаев: , где \ (a \) может быть любым действительным числом, бесконечностью или отрицательной бесконечностью.В этих случаях мы имеем Итак, Правило Л’Оспиталя говорит нам, что если у нас есть неопределенная форма 0/0 или \ ({\ infty} / {\ infty} \; \), все, что нам нужно сделать, это дифференцировать числитель и дифференцировать знаменатель, а затем взять предел. Прежде чем перейти к примерам, позвольте мне обратиться к написанию «L’Hospital».Более современное написание – «L’Hôpital». Однако, когда я впервые выучил Исчисление, мой учитель использовал правописание, которое я использую в этих заметках, и в первом учебнике, из которого я преподавал Исчисление, также использовалось правописание, которое я использую здесь. Также, как указано на странице Википедии, посвященной Правилу Госпиталя, «В 17-м и 18-м веках это имя обычно произносилось как« Госпиталь », и он сам писал свое имя таким образом. Однако французское написание было изменено: безмолвная ‘s’ была удалена и заменена на предшествующую гласную с циркумфлексом.Прежнее написание все еще используется в английском языке, где нет циркумфлекса ». Итак, написание, которое я использовал здесь, является приемлемым написанием его имени, хотя и не современным, и поскольку я привык писать его как «L’Hospital», это написание, которое я собираюсь использовать использовать в этих примечаниях. Итак, мы уже установили, что это неопределенная форма 0/0, поэтому давайте просто применим Правило L’Hospital.x}}} {2} = \ infty \] Иногда нам нужно применить правило L’Hospital более одного раза. Правило L’Hospital отлично работает с двумя неопределенными формами 0/0 и \ ({{\ pm \, \ infty}} / {{\ pm \, \ infty}} \; \). Однако, как мы видели ранее, существует гораздо больше неопределенных форм. Давайте посмотрим на некоторые из них и посмотрим, как мы справляемся с такими неопределенными формами. Начнем с неопределенной формы \ (\ left (0 \ right) \ left ({\ pm \, \ infty} \ right) \).+}} х \ ln х \]
Показать решение Обратите внимание, что здесь нам действительно нужно установить правый предел. Теперь в пределе мы получаем неопределенную форму \ (\ left (0 \ right) \ left ({- \ infty} \ right) \). Правило L’Hospital не работает с продуктами, оно работает только с коэффициентами. Однако мы можем превратить это в дробь, если немного переделаем.{1} / {} _ {{g \ left (x \ right)}}}} \] Использование этих двух фактов позволит нам превратить любой предел в форме \ (\ left (0 \ right) \ left ({\ pm \, \ infty} \ right) \) в предел в форме 0/0 или \ ({{\ pm \, \ infty}} / {{\ pm \, \ infty}} \; \). Какой из этих двух мы получим после перезаписи, будет зависеть от того, какой факт мы использовали для перезаписи. Одна из перезаписей даст 0/0, а другая – \ ({{\ pm \, \ infty}} / {{\ pm \, \ infty}} \; \). Все зависит от того, какая функция остается в числителе, а какая перемещается в знаменатель.4}}}}} = \ cdots \] Хммммм…. Похоже, это нас ни к чему не приведет. С каждым применением правила L’Hospital мы просто получаем еще одну неопределенную форму 0/0, и на самом деле производные, кажется, становятся все хуже и хуже. Также обратите внимание, что если мы упростим частное обратно до продукта, мы просто получим либо \ (\ left (\ infty \ right) \ left (0 \ right) \), либо \ (\ left ({- \ infty} \ right) \ left (0 \ right) \) и это не принесет нам никакой пользы.0} = 1 \] Благодаря Правилу L’Hospital мы теперь можем ограничить широкий спектр неопределенных форм, с которыми мы не могли справиться до этого раздела. Существует несколько методов решения пределов без правила L’Hospital. 1. Путем прямой замены . Среди четырех способов решения пределов подстановка будет вашим первым выбором.2-4} {x-2} = lim_ {x \ to 2} \ frac {(x-2) (x + 2)} {x-2} $$ $$ = lim_ {x \ to 2} (x + 2) = 2 + 2 = 4 $$ 3. Путем спряжения. Если прямая подстановка не работает и функция не факторизуема, то вы можете выбрать конъюгацию. шагов: Что такое конъюгат? Конъюгат образуется путем изменения знака между двумя членами бинома. Иллюстрация: Сопряжение {eq} \ sqrt {2x} +1 {/ eq} равно {eq} \ sqrt {2x} -1 {/ eq} Пример : Найдите {eq} lim _ {x \ to 2} \ frac {\ sqrt {2x + 5} -3} {x-2} {/ eq} Решение: $$ lim _ {x \ to 2} \ frac {\ sqrt {2x + 5} -3} {x-2} = lim _ {x \ to 2} \ frac {\ sqrt {2x + 5} -3} {x-2} \ times \ frac {\ sqrt {2x + 5} +3} {\ sqrt {2x + 5} +3} $$ $$ = lim _ {x \ to 2} \ frac {2x + 5-9} {(x-2) (\ sqrt {2x + 5} +3)} = lim _ {x \ to 2} \ frac {2x-4} {(x-2) (\ sqrt {2x + 5} +3)} $$ $$ = lim _ {x \ to 2} \ frac {2 (x-2)} {(x-2) (\ sqrt {2x + 5} +3} = lim _ {x \ to 2} \ frac {2} {\ sqrt {2x + 5} +3} $$ $$ = \ frac {2} {\ sqrt {9} +3} = \ frac {2} {3 + 3} = \ frac {2} {6} = \ frac {1} {3} $$ 4.Найдя наименьший общий знаменатель. Если прямая подстановка не работает и функция не факторизуема, то вы можете выбрать наименьший общий знаменатель. Ваша главная цель здесь – упростить рациональную функцию, найдя наименьший общий знаменатель. шагов: Пример: Найдите {eq} lim_ {x \ to 0} \ frac {\ frac {1} {x + 2} – \ frac {1} {2}} {x} {/ eq} Решение: $$ lim_ {x \ to 0} \ frac {\ frac {1} {x + 2} – \ frac {1} {2}} {x} = lim_ {x \ to 0} \ frac {\ frac {2- (x + 2)} {2 (x + 2)}} {x} $$ $$ = lim_ {x \ to 0} \ frac {\ frac {-x} {2 (x + 2)}} {x} = lim_ {x \ to 0} \ frac {-x} {2 (x + 2) x} $$ $$ = lim_ {x \ to 0} \ frac {-1} {2 (x + 2)} = \ гидроразрыва {-1} {2 (0 + 2)} $$ $$ = \ frac {-1} {2 (2)} = \ frac {-1} {4} Правило Л’Опиталя предоставляет метод оценки неопределенных форм типа \ (\ large \ frac {0} {0} \ normalsize \) или \ (\ large \ frac {\ infty} {\ infty} \ normalsize.\) Пусть \ (a \) либо конечное число, либо бесконечность.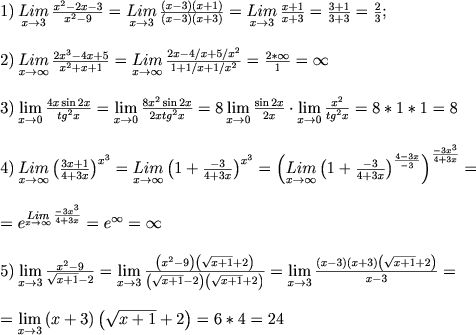
2} – 16}} {{x – 4}} \ hspace {0.2}}} \]
Если числитель дроби стремится к бесконечности, мы склонны думать, что вся дробь стремится к бесконечности.Кроме того, если знаменатель стремится к бесконечности, в пределе мы склонны думать, что дробь стремится к нулю. У нас также есть случай дроби, в которой числитель и знаменатель совпадают (без учета знака минус), и поэтому мы можем получить -1. Опять же, неясно, кто из них выиграет, если выиграет кто-то из них.
2} \) из числителя и знаменателя и взяли предел.2} \) вне числителя. Итак, ничто из того, что у нас есть в нашем пакете уловок, не будет работать с этими двумя пределами. Правило больницы
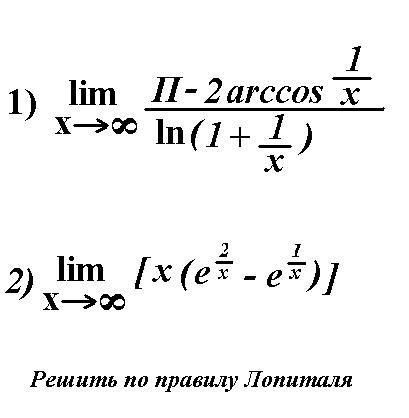
2}}} \) Показать все решения Скрыть все решения
a \ (\ displaystyle \ mathop {\ lim} \ limits_ {x \ to 0} \ frac {{\ sin x}} {x} \) Показать решение
Мы знаем, что натуральный логарифм определен только для положительных \ (x \), и поэтому это единственный предел, который имеет смысл. Как решить ограничения без больницы?
Правило Л’Опиталя
= {\ ln a \ cdot 1 = \ ln a.}
\]
Пример 2.
Найдите предел \ (\ lim \ limits_ {x \ to 2} {\ large \ frac {{\ sqrt {7 + x} – 3}} {{x – 2}} \ normalsize}. \ prime}}}}= {\ lim \ limits_ {x \ to 2} \ frac {{\ large \ frac {1} {{2 \ sqrt {7 + x}}} \ normalsize}} {1}}
= {\ frac {1} {2} \ lim \ limits_ {x \ to 2} \ frac {1} {{\ sqrt {7 + x} }} = \ frac {1} {2} \ cdot \ frac {1} {3} = \ frac {1} {6}}
\]
Пример 3.\ prime}}}}
= {\ lim \ limits_ {x \ to 2} \ left ({\ frac {{- 1}} {{2x}}} \ right) = – \ frac {1} {4} .}
\]
| ’62 Центр театра и танца, 62 Центр | ||
| касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий / Помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр карьерного роста, Мирс | 597-2311 | 597-4078 факс |
| Академические ресурсы, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Прием, Вестон Холл | 597-2211 | 597-4052 факс |
| Affirmative Action, Hopkins Hall | 597-4376 | |
| Africana Studies, Hollander | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art / Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Фотостудия, Spencer Studio Art | 597-2030 | |
| Printmaking Studio, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео / Фотостудия, Spencer Studio Art | 597-3193 | |
| Asian Studies, Hollander | 597-2391 | 597-3028 факс |
| Астрономия / Астрофизика, Thompson Physics | 597-2482 | 597-3200 факс |
| Департамент легкой атлетики, физическое воспитание, отдых, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Boat House, Озеро Онота | 443-9851 | |
| Автобусы | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Hockey Rink Ice Line, Lansing Chapman | 597-2433 | |
| Intramurals, Атлетический центр Чандлера | 597-3321 | |
| Физическая культура | 597-2141 | |
| Pool Wet Line, Атлетический центр Чандлера | 597-2419 | |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Площадки для игры в сквош | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Thompson Biology | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Thompson Biology | 597-2126 | 597-3495 факс |
| Охрана и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа / системы сигнализации | 597-4970 / 4033 | |
| Escort Service, Hopkins Hall | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Коммутатор | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
| Центр экологических исследований, класс 1966 г. Экологический центр | 597-2346 | 597-3489 факс |
| Лаборатория экологических наук, Морли | 597-2380 | |
| Экологические исследования | 597-2346 | |
| Лаборатория ГИС | 597-3183 | |
| Центр иностранных языков, литератур и культур, Холландер | 597-2391 | 597-3028 факс |
| Арабские исследования, Холландер | 597-2391 | 597-3028 факс |
| Сравнительная литература, Холландер | 597-2391 | |
| Критические языки, Холландер | 597-2391 | 597-3028 факс |
| лингафонный кабинет | 597-3260 | |
| Россия, Hollander | 597-2391 | |
| Центр обучения в действии, Brooks House | 597-4588 | 597-3090 факс |
| Библиотека редких книг Чапина, Сойер | 597-2462 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Офис капелланов, Парески | 597-2483 | 597-3955 факс |
| Еврейский религиозный центр, Стетсон-Корт 24, | 597-2483 | |
| Мусульманская молельная комната, часовня Томпсона (нижний уровень) | 597-2483 | |
| Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) | 597-2483 | |
| Chemistry, Thompson Chemistry | 597-2323 | 597-4150 факс |
| Классика (греческий и латинский), Hollander | 597-2242 | 597-4222 факс |
| Когнитивная наука, Бронфман | 597-4594 | |
| College Marshal, Thompson Physics | 597-2008 | |
| Отношения с колледжем | 597-4057 | |
| Программа 25-го воссоединения, Фогт | 597-4208 | 597-4039 факс |
| Программа 50-го воссоединения, Фогт | 597-4284 | 597-4039 факс |
| Advancement Operations, Мирс-Уэст | 597-4154 | 597-4333 факс |
| Мероприятия для выпускников, Vogt | 597-4146 | 597-4548 факс |
| Фонд выпускников | 597-4153 | 597-4036 факс |
| Связи с выпускниками, Мирс-Уэст | 597-4151 | 597-4178 факс |
| Alumni / Development Mail Services, Мирс-Уэст | 597-4369 | |
| Девелопмент, Vogt | 597-4256 | |
| Отношения с донорами, Vogt | 597-3234 | 597-4039 факс |
| Офис по планированию подарков, Vogt | 597-3538 | 597-4039 факс |
| Грант-офис, Мирс-Уэст | 597-4025 | 597-4333 факс |
| Программа крупных подарков, Vogt | 597-4256 | 597-4548 факс |
| Parents Fund, Vogt | 597-4357 | 597-4036 факс |
| Prospect Management & Research, Мирс | 597-4119 | 597-4178 факс |
| Начало занятий и академические мероприятия, Jesup | 597-2347 | 597-4435 факс |
| Коммуникации, Хопкинс Холл | 597-4277 | 597-4158 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Web Team, Southworth Schoolhouse | ||
| Williams Magazines (ранее Alumni Review), Hopkins Hall | 597-4278 | |
| Компьютерные науки, Thompson Chemistry | 597-3218 | 597-4250 факс |
| Conferences & Events, Парески | 597-2591 | 597-4748 факс |
| Запросы Elm Tree House, Mt.Ферма Надежды, | 597-2591 | |
| Офис контролера, Хопкинс Холл | 597-4412 | 597-4404 факс |
| Счета к оплате и ввод данных, Хопкинс-холл | 597-4453 | |
| Bursar & Cash Receipts, Hopkins Hall | 597-4396 | |
| Financial Information Systems, Hopkins Hall | 597-4023 | |
| Purchasing Cards, Hopkins Hall | 597-4413 | |
| Студенческие ссуды, Хопкинс Холл | 597-4683 | |
| Dance, 62 Центр | 597-2410 | |
| Центр Дэвиса (ранее Мультикультурный центр), Дженнесс | 597-3340 | 597-3456 факс |
| Харди Хаус | 597-2129 | |
| Jenness House | 597-3344 | |
| Райс Хаус | 597-2453 | |
| Декан колледжа, Хопкинс-холл | 597-4171 | 597-3507 факс |
| Декан факультета Хопкинс Холл | 597-4351 | 597-3553 факс |
| Столовая, капельницы | 597-2121 | 597-4618 факс |
| ’82 Гриль, Парески | 597-4585 | |
| Булочная, Парески | 597-4511 | |
| Общественное питание, Дом факультета | 597-2452 | |
| Driscoll Dining Hall, Дрисколл | 597-2238 | |
| Eco Café, Научный центр | 597-2383 | |
| Grab ‘n Go, Парески | 597-4398 | |
| Lee Snack Bar, Парески | 597-3487 | |
| Обеденный зал Mission Park, Mission Park | 597-2281 | |
| Whitmans ‘, Paresky | 597-2889 | |
| Economics, Schapiro | 597-2476 | 597-4045 факс |
| английский, Hollander | 597-2114 | 597-4032 факс |
| Сооружения, здание служебного помещения | 597-2301 | |
| College Car Request | 597-2302 | |
| Скорая помощь вечером / в выходные дни | 597-4444 | |
| Запросы на работу объектов | 597-4141 факс | |
| Особые мероприятия | 597-4020 | |
| Кладовая | 597-2143 | 597-4013 факс |
| Факультетский клуб, Факультетский дом / Центр выпускников | 597-2451 | 597-4722 факс |
| Бронирование | 597-3089 | |
| Fellowships Office, Hopkins Hall | 597-3044 | 597-3507 факс |
| Financial Aid, Weston Hall | 597-4181 | 597-2999 факс |
| Geosciences, Clark Hall | 597-2221 | 597-4116 факс |
| Немецко-русский, Hollander | 597-2391 | 597-3028 факс |
| Глобальные исследования, Холландер | 597-2247 | |
| Аспирантура по истории искусств, Кларк | 458-2317 факс | |
| Службы здравоохранения и хорошего самочувствия, Thompson Ctr Health | 597-2206 | 597-2982 факс |
| Санитарное просвещение | 597-3013 | |
| Услуги интегративного благополучия (консультирование) | 597-2353 | |
| Чрезвычайные ситуации с опасностью для жизни | Позвоните 911 | |
| Медицинские услуги | 597-2206 | |
| История, Холландер | 597-2394 | 597-3673 факс |
| История науки, Бронфман | 597-4116 факс | |
| Хопкинс Форест | 597-4353 | |
| Розенбург Центр | 458-3080 | |
| Отдел кадров, B&L Building | 597-2681 | 597-3516 факс |
| Услуги няни, корпус B&L | 597-4587 | |
| Льготы | 597-4355 | |
| Программа помощи сотрудникам | 800-828-6025 | |
| Занятость | 597-2681 | |
| Заработная плата | 597-4162 | |
| Ресурсы для супруга / партнера | 597-4587 | |
| Занятость студентов | 597-4568 | |
| Погодная линия (ICEY) | 597-4239 | |
| Humanities, Schapiro | 597-2076 | |
| Информационные технологии, Jesup | 597-2094 | 597-4103 факс |
| Пакеты для чтения курсов, ящик для сообщений офисных услуг | 597-4090 | |
| Центр аренды оборудования, Додд Приложение | 597-4091 | |
| Служба поддержки преподавателей / сотрудников, [адрес электронной почты защищен] | 597-4090 | |
| Медиа-сервисы и справочная служба | 597-2112 | |
| Служба поддержки студентов, [электронная почта] | 597-3088 | |
| Телекоммуникации / Телефоны | 597-4090 | |
| Междисциплинарные исследования, Холландер | 597-2552 | |
| Международное образование и учеба, Хопкинс-холл | 597-4262 | 597-3507 факс |
| Инвестиционный офис, Хопкинс Холл | 597-4447 | |
| Бостонский офис | 617-502-2400 | 617-426-5784 факс |
| Еврейские исследования, Мазер | 597-3539 | |
| Правосудие и закон, Холландер | 597-2102 | |
| Latina / o Studies, Hollander | 597-2242 | 597-4222 факс |
| Исследования лидерства, Шапиро | 597-2074 | 597-4620 факс |
| Морские исследования, Бронфман | 597-2297 | |
| Математика и статистика, Bascom | 597-2438 | 597-4061 факс |
| Музыка, Бернхард | 597-2127 | 597-3100 факс |
| Concertline (записанная информация) | 597-3146 | |
| Неврология, Thompson Biology | 597-4107 | 597-2085 факс |
| Окли Центр, Окли | 597-2177 | 597-4126 факс |
| Управление институционального разнообразия и справедливости, Хопкинс-холл | 597-4376 | 597-4015 факс |
| Управление счетов студентов, Хопкинс-холл | 597-4396 | 597-4404 факс |
| Performance Studies, ’62 Center | 597-4366 | |
| Философия, Шапиро | 597-2074 | 597-4620 факс |
| Физика, Thompson Physics | 597-2482 | 597-4116 факс |
| Планетарий / Обсерватория Хопкинса | 597-3030 | |
| Театр Old Hopkins Observatory | 597-4828 | |
| Бронирование | 597-2188 | |
| Политическая экономия, Шапиро | 597-2327 | |
| Политология, Шапиро | 597-2168 | 597-4194 факс |
| Офис президента, Хопкинс-холл | 597-4233 | 597-4015 факс |
| Дом Президента | 597-2388 | 597-4848 факс |
| Услуги печати / почты для преподавателей / сотрудников, ’37 House | 597-2022 | |
| Программа обучения, Бронфман | 597-4522 | 597-2085 факс |
| Офис Провоста, Хопкинс Холл | 597-4352 | 597-3553 факс |
| Психология, психологические кабинеты и лаборатории | 597-2441 | 597-2085 факс |
| Недвижимость, B&L Building | 597-2195 / 4238 | 597-5031 факс |
| Ипотека для преподавателей / сотрудников | 597-4238 | |
| Арендное жилье для преподавателей / сотрудников | 597-2195 | |
| Офис регистратора, Хопкинс Холл | 597-4286 | 597-4010 факс |
| Религия, Холландер | 597-2076 | 597-4222 факс |
| Romance Languages, Hollander | 597-2391 | 597-3028 факс |
| Планировщик помещений | 597-2555 | |
| Соответствие требованиям безопасности и охраны окружающей среды, класс ’37 Дом | 597-3003 | |
| Библиотека Сойера, Сойер | 597-2501 | 597-4106 факс |
| Службы доступа | 597-2501 | |
| Приобретения / Серийные номера | 597-2506 | |
| Каталогизация / Службы метаданных | 597-2507 | |
| Межбиблиотечный абонемент | 597-2005 | 597-2478 факс |
| Исследовательские и справочные службы | 597-2515 | |
| Стеллаж | 597-4955 | 597-4948 факс |
| Системы | 597-2084 | |
| Научная библиотека Шоу, Научный центр | 597-4500 | 597-4600 факс |
| Исследования в области науки и технологий, Бронфман | 597-2239 | |
| Научный центр, Бронфман | 597-4116 факс | |
| Магазин электроники | 597-2205 | |
| Машинно-модельный цех | 597-2230 | |
| Безопасность | 597-4444 | |
| Специальные академические программы, Харди | 597-3747 | 597-4530 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Студенческая жизнь, Парески | 597-4747 | |
| Планировщик помещений | 597-2555 | |
| Управление студенческими центрами | 597-4191 | |
| Организация студенческих мероприятий | 597-2546 | |
| Студенческий дом, Парески | 597-2555 | |
| Вовлечение студентов | 597-4749 | |
| Программы проживания для старших классов | 597-4625 | |
| Студенческая почта, Парески, | 597-2150 | |
| Устойчивое развитие / Центр Зилха, Харпер | 597-4462 | |
| Коммутатор, Хопкинс Холл | 597-3131 | |
| Книжный магазин Уильямса | 458-8071 | 458-0249 факс |
| Театр, 62 Центр | 597-2342 | 597-4170 факс |
| Trust & Estate Administration, Sears House | 597-4259 | |
| Учебники | 597-2580 | |
| вице-президент по кампусной жизни, Хопкинс-холл, | 597-2044 | 597-3996 факс |
| Вице-президент по связям с колледжем, Мирс | 597-4057 | 597-4178 факс |
| Вице-президент по финансам и администрированию, Hopkins Hall | 597-4421 | 597-4192 факс |
| Центр визуальных ресурсов, Лоуренс | 597-2015 | 597-3498 факс |
| Детский центр Williams College, Детский центр Williams | 597-4008 | 597-4889 факс |
| Музей искусств колледжа Уильямс (WCMA), Лоуренс | 597-2429 | 597-5000 факс |
| Подготовка музея | 597-2426 | |
| Служба безопасности музея | 597-2376 | |
| Музейный магазин | 597-3233 | |
| Уильямс Интернэшнл | 597-2161 | |
| Williams Outing Club, Парески | 597-2317 | |
| Оборудование / стол для студентов | 597-4784 | |
| Проект Уильямса по экономике высшего образования, Мирс-Вест | 597-2192 | |
| Williams Record, Парески | 597-2400 | 597-2450 факс |
| Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет | 011-44-1865-512345 | |
| Программа Williams-Mystic, Mystic Seaport Museum | 860-572-5359 | 860-572-5329 факс |
| Исследования женщин, гендера и сексуальности, Schapiro | 597-3143 | 597-4620 факс |
| Написание программ, Хопкинс-холл | 597-4615 | |
| Центр экологических инициатив «Зилха», Харпер | 597-4462 |
Риск передачи COVID-19 во время спортивных и культурных мероприятий в закрытых помещениях
Общий план исследования
Было проведено исследование «Прогнозирование риска заражения Covid-19 во время спортивных и культурных мероприятий в закрытых помещениях» (RESTART-19). инициирован с целью предоставления данных о контактах и воздействии аэрозолей на массовых мероприятиях в помещениях (MGE).Исследование состоит из трех частей:
- 1.
Эксперимент: Чтобы определить количество контактов во время MGE, мы провели поп-концерт в экспериментальных условиях и снабдили всех участников устройством отслеживания контактов (CTD). Концерт проходил в трех сценариях с разными гигиеническими приемами.
- 2.
Распределение аэрозолей: для оценки воздействия аэрозолей, движение аэрозолей, концентрации аэрозолей в помещении и концентрации в воздухе для дыхания были рассчитаны с использованием вычислительной гидродинамики (CFD).
- 3.
Эпидемиологическое моделирование: мы интегрировали результаты отслеживания контактов и распределения аэрозолей в индивидуальную модель и смоделировали влияние на последующее бремя инфекций.
Протокол исследования был внесен в Немецкий регистр клинических исследований (DRKS 00022790). (www.drks.de)
Экспериментальное моделирование концерта и контактные измерения
Мероприятие состоялось 22 августа 2020 года на крытой арене (Quarterback Immobilien Arena, QIA) в городе Лейпциг (Германия).
Порядок приема на работу и участники
Лица в возрасте от 18 до 50 лет были приглашены в рамках обширной кампании в СМИ для добровольной и бесплатной регистрации через веб-страницу исследования (www.restart19.de), где была предоставлена исчерпывающая информация о мероприятии, его целях и рисках. Все участники дали свое информированное согласие. Участники не получали никаких пособий, но еда и напитки предоставлялись бесплатно на протяжении всего эксперимента. Критериями исключения априори были ожирение (индекс массы тела> 30), хронические заболевания, сердечно-сосудистые заболевания, рак, подавление иммунитета, прием иммунодепрессантов, беременность или состояния, влияющие на легкие, печень или почки.Мы планировали включить 4000 участников, что соответствует половине вместимости арены и отражает средний размер спортивных и культурных мероприятий в 2019 году в этом месте (4200 участников).
С 17 июля по 21 августа 2020 года для участия в исследовании зарегистрировались 2825 участников. 601 участник активно отозвал свое согласие, а 212 участников не подтвердили свою регистрацию. Таким образом, 2023 участника получили набор для скрининговых тестов SARS-CoV-2 (см. Правила гигиены ниже), из которых 1407 образцов были вовремя возвращены в лабораторию для анализа.Информация о результатах тестирования была возвращена участникам. К участию приглашались только те, у кого был отрицательный результат теста. Один участник дал положительный результат и поэтому был исключен. Всего в эксперименте приняли участие 1212 человек. Поскольку в мероприятии участвовало меньше людей, чем планировалось изначально, мы подготовили арену для создания обстановки реалистичной плотности: мы закрыли ряды для сидения, киоски общественного питания, ванные комнаты и входы в соответствии с требованиями каждой гигиенической практики. В сценарии 1 присутствовали 1192 участника, в сценарии 2 – 1158 участников, а в сценарии 3 – 1054 участника.Эти числа меньше, чем общее количество участников ( n = 1212), потому что не все участники присутствовали во всех сценариях.
Мероприятие
В день исследования все участники прибыли с 8:00 до 10:00 утра для регистрации. Во время регистрации участники были зарегистрированы, удостоверены личности, и каждому человеку были выданы маски N95, дезинфицирующие средства для рук и устройства для отслеживания контактов. На человека были выданы три билета для трех различных сценариев, содержащие информацию о времени, входах и посадочных местах для каждого сценария.
Мы смоделировали три различных сценария, чтобы проанализировать влияние различных мер гигиены на передачу SARS-CoV-2. Для каждого сценария использовался один и тот же график: вход (60 минут), 1-я половина (20 минут), полупериод (20 минут), 2-я половина (20 минут), выход (15 минут). Во время таймов немецкий певец и автор песен Тим Бендзко выступил с живым поп-концертом. Сценарии различались в отношении мер гигиены, таких как количество входов / выходов, расстояние между сиденьями и ограниченное смешивание участников путем разделения арены на квадранты.Сценарий 1 был разработан для отражения состояния, предшествующего пандемии, когда участники входили на арену и выходили с нее через два главных входа без каких-либо ограничений и сидели без свободных мест между ними. В сценарии 2 применялись умеренные меры гигиены: арена была разделена на четыре квадранта. Участники входили и выходили на арену через вход / выход из квадранта, как указано в их билете (четыре входа / выхода), и им не разрешалось менять квадрант. Реализована рассадка, при которой каждое второе сиденье было занято и ряды были сдвинуты (шахматный узор).Сценарий 3 отразил более сильное сокращение контакта с попарным размещением участников и соблюдением минимального расстояния 1,5 м между занятыми парами сидений. Количество входов / выходов также увеличено до восьми. Различные сценарии приведены в дополнительной таблице 3.
Место действия
Quarterback Immobilien Arena – это место проведения мероприятий в городе Лейпциг и одно из 10 самых посещаемых развлекательных заведений в Германии (https: // www.stadionwelt.de/plus/arena-ranking-besucher). Тип и планировка арены (многоцелевой зал) распространены в отрасли, и другие примеры можно найти в Штутгарте (Porsche Arena), Берлине (Max Schmeling Arena) и Нюрнберге (Arena Nuremberg Insurance). Вместимость арены до 8228 человек. На дополнительном рис. 8 показан общий план местности. Посетители обычно (то есть до пандемии) входят в зал через два главных входа (западный и восточный), выходящие в фойе на южном конце арены.Из фойе они входят в два длинных туннеля, идущих параллельно внутреннему пространству с каждой стороны зала. Посетители попадают в зал для мероприятий по коридорам, отходящим от туннелей. На арене также есть четыре аварийных выхода на каждой длинной стороне здания, которые использовались в Сценариях 2 и 3 для входа на арену и выхода из нее.
Общий объем манежа 135 000 м 2 3 . Система вентиляции имеет общую мощность 198 000 м 2 3 час −1 и использует 100% свежий воздух.Розетки под трибунами имеют вместимость 114 000 м 3 ч −1 . На длинной стороне трибуны над головами зрителей расположены форсунки, выдувающие воздух вниз по потоку во внутреннее пространство (84000 м 3 ч −1 ).
Гигиеническая практика
Саксонское министерство социальных дел и единства (Sächsisches Staatsministerium für Soziales und Gesellschaftlichen Zusammenhalt) и органы здравоохранения города Лейпцига одобрили гигиеническую практику.
Тестирование на SARS-CoV-2: за неделю до мероприятия все участники и сотрудники получили набор для ПЦР-теста на SARS-CoV-2, включая тампон и пробирку со стабилизирующим раствором. В комплект включены подробные инструкции по самостоятельному отбору проб и возврату тестового набора. Участников попросили взять мазок из горла в течение 48 часов до мероприятия. Наборы для испытаний можно было вернуть в пять разных мест в Лейпциге или Галле (Заале) или отправить по почте. Все образцы были проанализированы Институтом вирусологии университетской клиники в Лейпциге.Результаты тестирования были импортированы в банк данных накануне мероприятия, и участники получили уведомление по электронной почте. Участников с положительными или отсутствующими результатами теста проинформировали по телефону, и им не разрешили выйти на арену. Тест был бесплатным.
Критерии исключения: Критерии исключения на месте: отсутствие действующей регистрации, отсутствие удостоверения личности, положительный или отсутствующий тест на SARS-CoV-2, температура выше 37,5 ° C, симптомы COVID-19, о которых сообщают пациенты в течение последних 48 часов, контакт с Пациент с COVID-19 или пребывание в зоне риска (по данным Института Роберта Коха от 22 августа 2020 г.) в течение последних 14 дней.
Средства индивидуальной защиты: Во время регистрации в исследовании каждый участник получил маску N95, флакон с дезинфицирующим средством для рук, содержащим 85,5% этанола об / об, а также сверхширокополосное устройство отслеживания контактов (CTD). Маску N95 нужно было носить от входа до выхода с арены, а также вне арены в очередях у входа и выхода.
Кейтеринг: услуги кейтеринга предоставлялись только за пределами арены, где участникам разрешалось снимать маски на расстоянии 1.5 м можно сохранить. Питание было бесплатным, чтобы сократить время ожидания участников и не допустить, чтобы участники покидали территорию. По запросу участникам раздавались бутылки с водой внутри арены, где им разрешалось пить, сохраняя при этом соответствующее расстояние от других людей. Обслуживание общественного питания в помещении было смоделировано в течение половины времени различных сценариев, чтобы люди получали ваучеры для использования на улице.
Стюарды по дистанции и гигиене: За исключением первого сценария, всех участников попросили соблюдать дистанцию, равную 1.5 мес. Чтобы гарантировать, что все участники соблюдают правила гигиены, на арене присутствовали 40 санитарных надзирателей. Участников, которые неоднократно не соблюдали рекомендации по гигиене, попросили бы покинуть арену (но в этом не было необходимости).
Инструктаж участников и персонала: Все участники получили исчерпывающую информацию о правилах гигиены при регистрации. В день мероприятия участники получили информационный лист с правилами гигиены и инструкциями по правильному использованию масок N95 и дезинфицирующих средств для рук сотрудниками стойки регистрации.Участники также получили устные инструкции в начале мероприятия. Персонал прошел подробное обучение правилам гигиены.
Отслеживание контактов: участники предоставили полную контактную информацию в процессе регистрации. Участники согласились, что их устройства отслеживания контактов (CTD) могут быть использованы для выявления тех, кто находится в группе риска. В случае заражения SARS-CoV-2 после события с затронутыми участниками свяжутся. Нам не известно о людях, заразившихся во время мероприятия.Вся личная информация была удалена через шесть недель после мероприятия. Полученные данные были анонимными.
Приложение Corona Warn: Использование приложения Corona-Warn-App от федерального правительства Германии было рекомендовано, но не обязательно для участия.
Измерение контактов в непосредственной близости
Все участники получили персонализированное устройство для отслеживания контактов (CTD) и были проинструктированы носить его на шее во время мероприятия. Теги ICDWpro quad 164643 (In-Circuit, Дрезден, Германия) использовались для измерения расстояния между двумя близкими участниками и продолжительности контакта на этом расстоянии.Эти метки сочетают в себе технологию Bluetooth с низким энергопотреблением и сверхширокополосную радиосвязь с точностью до ± 20 см. CTD мог либо отправлять, либо принимать сигналы в любой заданный момент времени, так что между CTD всех участников происходил обмен сигналами. Расстояния измерялись не постоянно, а через определенные промежутки времени (примерно каждые три секунды). Теги координируют время своего вещания, чтобы минимизировать помехи (одновременно транслируются только удаленные теги), поэтому очень короткие встречи могут быть пропущены (<3 с), но более длительные встречи записываются.Прошивка и ведение журнала были настроены в соответствии со следующим протоколом: отметка времени записывалась для начала контакта при соблюдении одной из следующих комбинаций расстояния и времени: <50 см в течение как минимум 3 с, <100 см для минимум 6 с или <150 см минимум 10 с. При выходе из этих пороговых значений более чем на 2 секунды в журнал заносилась отметка времени. Когда контакт был разорван, новый контакт мог быть записан через время сброса 10 с.
Сигналы часто прерывались из-за большого количества трассеров, отправляющих данные одновременно, низкой интенсивности широковещательной передачи и небольших изменений в перемещениях участников на расстояние.CTD также мог только принимать или отправлять сигналы, но не делать и то, и другое одновременно. Таким образом, для пары датчиков приближение регистрировалось частично на одном и частично на другом. Сначала были объединены контакты со всех устройств. Во-вторых, были заполнены промежутки между первым и последним контактами в фазе сценария (например, в перерыве между таймами). Учитывая эту спецификацию датчиков, мы смогли использовать информацию только о самом большом расстоянии, то есть 1,5 м (вероятно, что соответствует физическому расстоянию 1.3 м, когда датчики обращены друг к другу, и меньше, когда сигналы частично загораживались частями тела). Для более реалистичной оценки контактов мы увеличили половину до 45 минут каждая. Таким образом, контакты с людьми, входящими и выходящими в радиусе 1,5 во время периода сидения, также могут накапливаться и преодолевать порог в 15 минут (дополнительная таблица 4). Мы исследовали общее количество контактов длительностью> 10 секунд (в эту категорию мы включили контакты продолжительностью> 3 секунд для расстояния 50 см и> 6 для расстояния 1 м) и 5 и 15 минут.Критический контакт был определен как продолжающийся более 15 минут на расстоянии 1,5 м в соответствии с определением контакта Института Роберта Коха. Эти 15 минут могут накапливаться в течение всего мероприятия для общего количества контактов. Контактный анализ проводился с использованием R (версия 4.0.2).
Анкета приемлемости
Всех участников эксперимента попросили по электронной почте заполнить онлайн-опрос через три недели после мероприятия. Анкета содержала 10 вопросов о восприятии и мнениях о возможности такого события.Основное внимание было уделено ношению масок и восприятию личного риска в различных сценариях.
Распределение аэрозолей
Вычислительная гидродинамика (CFD)
Распределение аэрозолей внутри арены было смоделировано с использованием вычислительной гидродинамической модели. Все моделирование CFD проводилось с помощью коммерческого программного обеспечения для CFD PHOENICS (версия 2020, CHAM, Лондон, Великобритания). Для распределения аэрозолей использовалась надстройка FLAIR (моделирование дрейфа-потока) PHOENICS, а для отслеживания частиц – надстройка GENTRA (обе версии 2020, CHAM, Лондон, Соединенное Королевство).Программа PHOENICS была разработана профессором Брайаном Сполдингом и уже более 30 лет успешно используется инженерами-консультантами Zimmermann and Becker GmbH (Германия) для подтверждения технического планирования в широком спектре технических приложений и одобрена для новые приложения. Модель PHOENICS / FLAIR / GENTRA использовалась во многих других исследованиях, посвященных CFD-моделированию аэрозолей 25,26,27,28 . Quarterback Immobilien Arena была точно преобразована в 3D-модель (1: 1), включая все встроенные компоненты, полную систему вентиляции, трибуны и сиденья.Виртуальные зрители сидели на арене, чтобы имитировать выброс и воздействие аэрозоля. Положение инфицированных было определено в соответствии с предварительным расчетом для анализа воздушного потока в помещении (дополнительный рис. 2а). Дальнейшие предварительные расчеты были выполнены в упрощенной модели для анализа движения аэрозоля. Эти расчеты показали, что траектория напрямую зависит от скорости потока воздуха в помещении со скоростью 0,05 м с −1 для аэрозолей с d ≤ 10 мкм, а также для CO 2 .Поскольку схема потока практически идентична от первого ряда стойл к последнему, инфекционные лица были размещены спереди и сзади стойл таким образом, чтобы регистрировались различные потоки воздуха в помещении в стойлах и на стойках. . Из-за размера модели и требуемой точности сетки ожидалось очень долгое время вычислений. Мы решили смоделировать сценарий 2 и интерполировать другие сценарии на основе этих данных. Мы установили 4000 виртуальных зрителей в модели с расстановкой сидений по схеме шахматной доски (т.е. каждый второй стул остается свободным). Двадцать четыре инфекциониста были размещены в 12 (из 32) блоках. Подробное распределение инфицированных лиц можно увидеть на дополнительном рис. 8. Воздух для дыхания всех виртуальных зрителей состоит из идеального газа и 20 литров CO 2 в час. Зрители-инфекционисты также выбрасывают в комнату аэрозоли разного размера (0,5, 5 и 10 мкм) во время дыхания. Уровень выбросов и размер частиц были скорректированы для поющих людей 29,30 .Предполагаемая физическая плотность вдыхаемого воздуха составляла 1,3 г / мл 31 . Мы использовали немного увеличенное значение 12 л мин -1 на человека для объема дыхания и соответствующую долю CO 2 , поскольку мы ожидали увеличения во время пения, крика или аплодисментов. Подробные параметры и уравнения, использованные для модели, суммированы в дополнительных таблицах 5 и 6. Каждый манекен был оборудован виртуальным ртом для дыхания, чтобы количественно оценить воздействие вируса на зрителей.Воздействие аэрозоля измерялось в модели непосредственно у рта. Чтобы оценить динамику и поток распределения аэрозолей на арене, их движение аэрозолей было рассчитано с помощью программного обеспечения для отслеживания частиц GENTRA с помощью модели дрейфа-потока в FLAIR, а результаты были представлены посредством визуализации с помощью GENTRA и накопленных чисел. Количественные результаты рассеивания выдыхаемых аэрозолей инфекционных участников были перенесены в электронные таблицы в соответствии с расстановкой сидений на арене.Число пострадавших и уровень их воздействия были получены из этих таблиц. Мы подсчитали среднее количество людей, подвергшихся воздействию, в дополнение к тем, которые были бы зафиксированы контактным измерением с CTD из-за критических контактов (дополнительная таблица 4). Для визуализации распределения аэрозоля значения ниже критического порога 1,75 × 10 −3 мкг с −1 экспозиция аэрозоля (дополнительный рис. 5) были окрашены в зеленый цвет, а все значения выше были красным.Яркость красного цвета соответствует относительной величине массового расхода.
Варианты вентиляции
Мы прогнали модель вентиляции в двух различных вариантах, представляющих разные системы вентиляции. В первом варианте вентиляции мы смоделировали реальную систему вентиляции арены. Здесь воздух попадает на арену через выпускные отверстия под боковыми трибунами и форсунки, как описано выше. В каждом углу зала установлены по две башни для отсоса воздуха.Подача воздуха составляла 198 000 м 3 час -1 , что соответствовало скорости воздухообмена 1,46 воздухообмена в час (ACH). Во втором варианте мы попытались модифицировать систему вентиляции арены, чтобы обеспечить вытесняющий поток, виртуально установив две длинные выхлопные трубы под крышей по всей длине арены. Также были отключены форсунки и вытяжные башни, чтобы избежать образования крупных водоворотов. В результате подача воздуха была уменьшена до 115 000 м³ ч -1 , что соответствует коэффициенту воздухообмена 0.85 ч −1 .
Определение участников с повышенным воздействием аэрозоля
Критическая инфекционная доза и порог продолжительности пребывания для инфекции, связанной с воздействием аэрозоля, еще не известны. В нескольких исследованиях рассматривалась эта проблема, но все они имеют ограничения, поскольку многие характеристики SARS-CoV-2 (например, минимальная инфекционная доза, концентрация вируса в аэрозолях и т. Д.) Еще не известны 31,32,33 . Поэтому мы использовали прагматический подход: поющий человек испускает около 1000 аэрозольных частиц, соответствующих 7.53 × 10 −8 мл аэрозолей в секунду в нашей модели 30 . Напротив, отдыхающий испускает только сотую часть частиц 30 . Мы предположили, что вирусная нагрузка аэрозолей равна мокроте с 10 9 копиями РНК / мл. Посетители-инфекционисты, скорее всего, будут пре-симптоматическими или в начале симптоматического периода, а вирусная нагрузка, как известно, достигает пика в этот момент времени 34,35 . Таким образом, инфекционный наблюдатель испускает ∼4 × 10 5 копию вируса (= 7.53 × 10 −8 мл с −1 × 10 9 копий вируса / мл × 5400 с) при пении во время 90-минутного концерта и 4 × 10 3 копий вируса (= 4 × 10 5 / 100) в состоянии покоя. Таким образом, порог в 1% эмиссии соответствует воздействию от 40 до 4000 вирусных частиц за концерт, что является величиной, при которой многие предполагают минимальную инфекционную дозу Sars-CoV-2 36,37 .
Эпидемиологическое моделирование
Естественная историческая модель
Модель была разработана как расширенная модель «восприимчивые – подвергшиеся воздействию – инфекционные – восстановленные» (SEIR) (дополнительный рис.9) с использованием R (версия 4.0.2). Восприимчивые люди переходят из состояния «воздействия» на «предсимптоматическую инфекцию» и «заразность» со скоростью, указанной в дополнительной таблице 7. Заболевание инфекционных лиц может постепенно прогрессировать до более тяжелых стадий «госпитализация». , «Поступление в реанимацию», «смерть» или «выздоровление» с вероятностью, зависящей от возраста (дополнительная таблица 8). У части людей, подвергшихся воздействию, симптомы отсутствуют, и после латентной фазы у них значительно снижается инфекционность.Различие между бессимптомными, легкими и тяжелыми случаями не зависит от компонентов модели и относится к состоянию, в котором болезнь прогрессирует. В нашей модели бессимптомные люди, а также легкие и тяжелые случаи проходят через разные фазы заболевания, которые представлены различными отделами на дополнительном рисунке 9. Это необходимо, потому что состояние заболевания (восприимчивое, латентное, пред- симптоматический, симптоматический, резистентный) влияет на инфекционность и, таким образом, также применяется к людям с очень неясными, неоднозначными симптомами, которых обычно называют бессимптомными.Повозрастные показатели госпитализаций были получены из Федеральной земли Шлезвиг-Гольштейн 38 . В нашей модели госпитализируются только тяжелые случаи. Повозрастная смертность соответствовала соответствующим показателям для Германии 39 . Мы также предположили, что контактный риск заражения составляет 7% для всех лиц, подвергшихся воздействию аэрозолей, и для прямых контактов.
Мы смоделировали в 1000 прогонов комбинированные контакты, выявленные с помощью отслеживания контактов и распределения аэрозолей для всех трех сценариев (дополнительная таблица 4) с откалиброванной базовой частотой 10, 50 и 100 на 100 000 жителей / 7 дней для общего количество 100 000 и 200 000 участников мероприятия за 30 дней (соответствует событиям с 3300 и 6700 участниками в день, последнее число соответствует состоянию до пандемии).Мы также сравнили сценарии с использованием масок в MGE и без масок. Что касается воздействия на популяционный уровень, для результатов изучался 30-дневный период. Это означает, что исходы, полученные в результате событий, были эффективно подсчитаны в течение более короткого периода времени, поскольку некоторые поздние вторичные и третичные инфекции, а также их поздние исходы могли не развиться в изучаемом временном окне.
Контактная сеть
Модельные предположения относительно ежедневных контактов среди населения были взяты из европейского контактного исследования POLYMOD 21 .Повозрастные коэффициенты контактов были применены к населению города Лейпцига (дополнительная таблица 8). Мы рассмотрели три типа настроек контакта для модели: дом, школа / работа и другие (включая категории контактов транспорт, досуг и другие из исследования POLYMOD 21 (дополнительная таблица 9). Мы предполагаем, что существует ровно один домашнее место (домашнее хозяйство) для каждого человека и что на каждого человека в возрасте 0–19 лет есть ровно одно место в детском саду или школе. Каждая школа или класс дневного ухода состоит из 20 детей (что отражает средний размер класса в Саксонии), а также один учитель в возрасте 20–64 лет.На каждого человека в возрасте от 20 до 69 лет (кроме учителей) имеется одно рабочее место. Мы включили четыре различных размера рабочих мест в соответствии с категориями, указанными Федеральным статистическим управлением Германии. Выбор рабочего места человека носит случайный характер, но зависит от возраста (на основе дополнительного анализа данных POLYMOD). Мы учитывали только контакты продолжительностью более 15 минут для номеров контактов для каждого человека, что соответствует определению контактов высокого риска из RKI.Как своего рода четвертая сеть, люди, посещающие мероприятие, выбираются случайным образом каждый день из всего населения. Исключались только люди с положительным результатом теста, а также лица моложе 15 лет. Количество как близких, так и аэрозольных контактов в рамках этих событий было предоставлено экспериментальным концертом (дополнительная таблица 4).
Меры по борьбе с эпидемией
Наша модель основана на национальных рекомендациях для Германии в отношении стратегии тестирования SARS-CoV-2: тестирование по симптомам или как лицо, контактировавшее с известным случаем.Мы предполагаем идеальные тесты со 100% чувствительностью и специфичностью. Есть два способа обнаружения инфицированных людей в модели: либо по симптомам, либо по отслеживанию контактов. Предполагается, что кто-то с тяжелым случаем COVID-19 будет протестирован, обнаружен и изолирован в течение одного дня с момента появления симптомов с общей вероятностью 90%. Предполагается, что случаи с легкими симптомами должны быть проверены в течение двух дней после появления симптомов с общей вероятностью тестирования 50%. Бессимптомных людей, у которых никогда не развиваются симптомы, можно обнаружить только путем отслеживания контактов.После того, как человек дал положительный результат теста, его членов семьи должны пройти тестирование в течение одного дня и оставаться в карантине в течение 14 дней. Мы не учли несоблюдение правил карантина. Мы предположили, что уровень обнаружения составляет 100% для всех членов семьи, тем самым добавив новые ветви для отслеживания контактов. Напротив, предполагается, что уровень тестирования составляет 80% в учебной или рабочей сети с двухдневной задержкой для получения результатов теста. В третьей контактной сети «Другое» мы предположили, что только 50% контактов были идентифицированы и протестированы с задержкой в четыре дня.Зараженные лица выявляются путем отслеживания контактов, если человек прошел латентную фазу, включая лиц с предсимптомным и полностью бессимптомным течением. Отслеживание контрактов запускается при новом обнаружении любого инфицированного человека и не зависит от того, было ли обнаружение связано с симптомами или отслеживанием контактов в прошлом. Таким образом, рекурсивное отслеживание контактов может привести к обнаружению целых цепочек заражения. Любой обнаруженный человек изолируется на 14 дней (включая пребывание в больнице при необходимости). В этой модели вторичные контакты не подвергались предварительному карантину, что соответствует национальной стратегии тестирования в Германии, но их можно было идентифицировать, как только первичный контакт стал подтвержденным случаем.
Номер репродукции
Контактная матрица POLYMOD соответствует предпандемическому состоянию. Мы откалибровали среднюю вероятность передачи при одном контакте, чтобы получить число воспроизводств для эпидемии, равное примерно 3 (при допущении, что чувствительная фракция составляет 100% – т.е. условия в начале эпидемии), а затем уменьшили число контактов во всех условиях равномерно на 50%. и применил меры борьбы с эпидемией, в итоге получив R около 1. Поскольку тестирование также включено в модель, модель также предоставляет возрастную долю выявленных и невыявленных случаев.При предполагаемой заболеваемости и повозрастной частоте выявленных и невыявленных случаев каждый запуск начинается с 14-дневной фазы приработки, за которой следует 30-дневный период оценки. Контактная матрица POLYMOD игнорирует потенциальную передачу респираторных патогенов из-за аэрозолей, что увеличивает вероятность заражения инфекцией при контакте для данного репродуктивного числа.
Демографический фон
Исследование проводилось в Лейпциге, большом городе в федеральной земле Саксония на востоке Германии с населением около 601 083 человек 40 .Подробные демографические данные модели основаны на Leipzig 40 . Поскольку продолжительность смоделированной эпидемии составляла менее года, мы не учитывали изменения в населении из-за рождений, смертей, миграции или старения.
Статистический анализ
Среднее значение и стандартное отклонение от среднего, диапазона и межквартильного диапазона (IQR) были рассчитаны для статистического анализа, а также 95% доверительных интервалов.
Сводка отчетов
Дополнительная информация о дизайне исследования доступна в Сводке отчетов по исследованиям природы, связанной с этой статьей.{2}}). В этом видео мы обсуждаем, что такое предел и как использовать метод подстановки, чтобы найти предел. Каждый расчет функции имеет пошаговое решение, чтобы вы могли легко понять, как решается эта проблема. лимит-калькулятор. Этот калькулятор вычисляет предел заданной функции в заданной точке. (Шаги требуют подписки.) Немецкая версия. Ваш частный репетитор по математике решает любую математическую задачу по шагам! Уравнения, интегралы, производные, пределы и многое другое. Связанные сообщения в блоге Symbolab Расширенные математические решения – калькулятор пределов, правило L’Hopital В предыдущих сообщениях мы говорили о различных способах определения предела функции.Вы можете легко и бесплатно рассчитать пределы, пределы последовательности или функции. Связанные сообщения в блоге Symbolab Расширенные математические решения – калькулятор пределов, бесконечные пределы В предыдущем посте мы рассмотрели замену, где предел – это просто значение функции в точке. Для получения дополнительной помощи по этой теме посетите сайт www.symbolab… Пределы функций можно рассматривать как в точках, так и в бесконечности. … Связанные сообщения блога Symbolab. Вычисляйте односторонние и двусторонние пределы, а также представления пределов…. Производные Производные Приложения Пределы Интегралы Интегральные приложения Сумма Римана ODE Многопараметрическое исчисление Преобразование Лапласа Ряды Тейлора / Маклорена Ряды Фурье. Практика, практика, практика. Интегралы, производные, уравнения, пределы и многое другое. Связанные сообщения блога Symbolab. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Symbolab включает в себя множество мощных калькуляторов, предназначенных для решения всех ваших математических задач. Также доступно вычисление предела алгебраически, предела по графику, предела ряда, предела многовариантности… (Шаги требуют подписки.) Повторите попытку, используя другой способ оплаты. Пределы могут быть определены для дискретных последовательностей, функций одного или нескольких действительных аргументов или комплексных функций. Бесплатный калькулятор скорости – рассчитайте скорость шаг за шагом. ар. Проблемы неравенства также можно решить с помощью калькулятора неравенства. Этот бесплатный калькулятор найдет предел (двусторонний или односторонний, включая левый и правый) данной функции в заданной точке (включая бесконечность). В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x».Калькулятор лимита. Что происходит, когда алгебраические манипуляции не помогают найти предел? Расширенные математические решения – калькулятор пределов, теорема сжатия. Приложение Symbolab Math Solver состоит из более чем сотни самых мощных калькуляторов Symbolab: Калькулятор уравнений Интегральный калькулятор Калькулятор производной Калькулятор пределов Калькулятор неравенства Тригонометрический калькулятор Калькулятор матриц Функции калькулятора серии Калькулятор Калькулятор ODE Калькулятор преобразования Лапласа Связанные сообщения в блоге Symbolab Расширенные математические решения – Калькулятор пределов, функции с квадратными корнями В предыдущем посте мы говорили об использовании факторинга для упрощения функции и определения предела.В предыдущем посте мы говорили об использовании подстановки для нахождения предела … Пределы, основополагающий инструмент в исчислении, используются для определения того, приближается ли функция или последовательность к фиксированному значению, когда ее аргумент или индекс приближается к заданной точке. Калькуляторы Symbolab. Расширенные математические решения – калькулятор пределов, факторинг. Каждая решенная вами проблема сохраняется в истории, и вы можете вернуться к ней в любое время. es. Бесплатный калькулятор расчетов – расчет пределов, интегралов, производных и рядов шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования.Связанные сообщения в блоге Symbolab Расширенные математические решения – калькулятор пределов, факторинг В предыдущем посте мы говорили об использовании подстановки для определения предела функции. Калькулятор лимитов Воспользуйтесь нашим простым онлайн-калькулятором лимитов, чтобы найти лимиты с пошаговым объяснением. Еще один полезный способ найти предел – это цепное правило. Расширенные математические решения – калькулятор пределов, факторинг. Расширенные математические решения – калькулятор пределов, факторинг. Производные Производные Приложения Пределы Интегралы Интегральные приложения Сумма Римана ODE Многопараметрическое исчисление Преобразование Лапласа Ряды Тейлора / Маклорена Ряды Фурье.(Для выполнения шагов требуется подписка в приложении) Приложение Symbolab Math Solver состоит из более чем сотни самых мощных калькуляторов Symbolab: Калькулятор уравнений Интегральный калькулятор Производный калькулятор Калькулятор пределов Калькулятор неравенства Калькулятор тригонометрии… Двусторонние, левосторонние и правосторонние пределы. Ваш частный репетитор по математике решает любую математическую задачу по шагам! Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Symbolab Math Solver состоит из сотен самых мощных калькуляторов Symbolab: Калькулятор интегралов, калькулятор производных, калькулятор пределов E… Попробуйте этот удобный расчет предельных значений прямо сейчас! В нем есть много отличных калькуляторов для решения всех математических задач.Чтобы создать новый пароль, просто нажмите ссылку в электронном письме, которое мы вам отправили. Если предел g (x) и h (x) при приближении x к c одинаков, то предел f (x) при приближении x к c должен быть таким же, как их предел, потому что f (x) сжат или зажат , между ними. В предыдущих постах мы говорили о различных способах определения предела функции. Спасибо за ответ. В предыдущем посте мы говорили об использовании подстановки, чтобы найти предел… Интегралы, производные, уравнения, пределы и многое другое.Производные. Сообщение доставлено. Чтобы создать новый пароль, просто нажмите ссылку в электронном письме, которое мы вам отправили. Ваш частный репетитор по математике решает любую математическую задачу по шагам! лимит-калькулятор. Для правил умножения пределов предельные произведения остаются неизменными для двух или более функций. Разнообразие калькуляторов, доступных в Symbolab, превышает 300, и их количество продолжает расти. Калькулятор лимита Этот калькулятор лимита поможет вам найти предел данной функции в заданной точке. Уравнения, интегралы, производные, пределы и многое другое.История! … Связанные сообщения блога Symbolab. Калькулятор лимита. Расширенные математические решения – Калькулятор пределов, правило Л’Опиталя. Symbolab – Math Solver v8.11.0 [Pro] Требования: 5.0 и выше Обзор: Калькуляторы с шагами: уравнения, интегралы, производные, пределы, триггеры и многое другое. Вот изображение, которое поможет лучше понять теорему: Показать инструкции. В этом случае калькулятор дает не только ответ, но и развернутое решение, которое полезно проанализировать, особенно если ваш собственный результат не совпадает с результатом его расчетов.Калькулятор обратной матрицы; Какие есть ограничения? Калькулятор Symbolab решает: Алгебру * Уравнения * Неравенства * Система уравнений * Основные операции (множитель, объединение, отмена, упрощение) * Частичные дроби Калькулятор быстро и точно найдет предел любой функции онлайн. Ваш частный репетитор по математике решает любую математическую задачу по шагам! Связанные сообщения в блоге Symbolab Расширенные математические решения – калькулятор пределов, факторинг В предыдущем посте мы говорили об использовании подстановки для определения предела функции.{3} +4} {3x + 2}), lhopital \: \ lim_ {x \ to \ infty} (\ frac {\ sqrt {x + 1}} {x}). Расширенные математические решения – калькулятор пределов, правило цепочки В предыдущем посте мы говорили о том, как найти предел функции с помощью правила Л’Опиталя. Это приложение имеет калькулятор производных для решения всех выводов и технических задач математики, основанных на выводе. Symbolab – математический решатель Pro. Связанные сообщения блога Symbolab. В калькуляторе пределов функции используются методы расчета предельных значений и новейшие алгоритмы для получения точных результатов.В предыдущем посте мы говорили об использовании подстановки для нахождения предела… Если существующий предел конечен и его x приближается к f (x) и для того же g (x), то это произведение пределов. Связанные сообщения блога Symbolab. пт. Калькулятор лимита. Особенности Symbolab Pro для Android. Symbolab: описание математических задач и математических решений – решение задач по алгебре, тригонометрия и вычисление пассажа. Все это вместе может помочь вам решить почти все математические задачи. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт.Symbolab – Math solver Apk: приложение имеет калькулятор пределов для решения различных вопросов о пределе. В приложении Symbolab Math Solver вы найдете сотни калькуляторов, начиная от уравнений, производных, тригонометрии, пределов, функций, матриц, преобразований Лапласа и многих других. … Калькулятор теста сравнения серий Пошагово проверяйте сходимость серий с помощью сравнительного теста.