вторая производная онлайн
Вы искали вторая производная онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление производной онлайн с подробным решением, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «вторая производная онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вторая производная онлайн,вычисление производной онлайн с подробным решением,вычислить производную онлайн с подробным решением,вычислить производную функции онлайн с решением,двойная производная онлайн,дифференцирование онлайн с подробным решением,как найти производную функции y x 2 7x,как обозначается производная в калькуляторе,калькулятор онлайн для функций,калькулятор функций онлайн с решением,найти вторую производную функции онлайн,найти производную второго порядка онлайн,найти производную функции онлайн с подробным решением,найти производные функций онлайн с подробным решением бесплатно,онлайн решение производных с подробным решением бесплатно,производная второго порядка онлайн,производная второго порядка онлайн калькулятор,производная первого порядка онлайн,производные высших порядков онлайн калькулятор.
Где можно решить любую задачу по математике, а так же вторая производная онлайн Онлайн?
Решить задачу вторая производная онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор онлайн. Найти (с решением) производную функции. График функции
Приведены график и основные свойства экспоненты (е в степени х): область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд, действия с комплексными числами.
Определение
Частные значения
Пусть y(x)
= e x
.
Тогда
.
Экспонента обладает свойствами показательной функции с основанием степени е > 1 .
Область определения, множество значений
Экспонента y(x)
= e x
определена для всех x
.
Ее область определения:
– ∞ Ее множество значений:
0
.
Экстремумы, возрастание, убывание
Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
Обратная функция
Обратной для экспоненты является натуральный логарифм .
;
.
Производная экспоненты
Производная е в степени х равна е в степени х :
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Комплексные числа
Действия с комплексными числами осуществляются при помощи формулы Эйлера :
,
где есть мнимая единица:

Выражения через гиперболические функции
;
;
.
Выражения через тригонометрические функции
;
;
;
.
Разложение в степенной ряд
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Свойства функций играют важную роль при их изучении. Они позволяют делать определенные выводы о функциях. Изучение данной темы крайне важно для обучающихся, особенно старших классов. Это связано с тем,что задания по данной теме довольно часто встречаются в КИМ государственной итоговой аттестации.
Видеоурок по теме «Свойства функции» разработан автором для облегчения работы учителя и его подготовки к урокам. Если использовать данный материал на уроках, то появится больше свободного времени, которое можно посвятить индивидуальному обучению или другим направлениям обучения математики в школе.
Длительность урока составляет 8:23 минут. Примерно столько же времени требуется учителю, чтобы объяснить материал на уроке, который длится 40-45 минут. При этому учитель успеет актуализировать знания обучающихся, повторить необходимый материал, просмотреть видеоурок, а затем еще и закрепить материал.
При этому учитель успеет актуализировать знания обучающихся, повторить необходимый материал, просмотреть видеоурок, а затем еще и закрепить материал.
Рассмотрение материала начинается непосредственно с первого свойства, которое называется монотонность. Это понятие подробно расписывается на математическом языке, что способствует развитию математической грамотности обучающихся, а также словесно поясняется каждая запись на экране. Далее автор демонстрирует на рисунке, как выглядит монотонная функция для случаев возрастания и убывания. После этого дается определение монотонной функции. Здесь же дается правило для запоминания, которое связано с монотонностью функции. Далее предлагается рассмотреть эту теорию на примере. На рисунке изображен график, на экране последовательно выделяются промежутки возрастания и убывания. Показана и математическая запись этих промежутков.
Согласно условию другого примера, необходимо исследовать функцию на монотонность. Чтобы определить монотонность функции, автор воспользовался определением возрастающей и убывающей функции.
Затем на экране демонстрируются примеры возрастающих функций на всей области определения.
Далее внимание обучающихся обращается ко второму свойству, которое называется ограниченностью. Рассмотрение этого свойства строится по аналогии с первым свойством. Рассматривается понятие ограниченности, все это иллюстрируется на рисунке, как ограниченность снизу, так и ограниченность сверху. Затем на экране появляется пример ограниченной функции.
Важными понятиями в пункте ограниченность являются наибольшее и наименьшее значение функции. В качестве иллюстрации показан рисунок и идет подробное описание этих понятий.
После примера рассматривается третье свойство, которое называется выпуклостью. Это понятие иллюстрируется с помощью рисунка. На данном свойстве автор не останавливается так же подробно, как на предыдущих. Он сразу переходит к четвертому свойству – непрерывности. Здесь вводится понятие непрерывной функции. После этого демонстрируется это свойство на рисунке с подробными пояснениями.
После этого демонстрируется это свойство на рисунке с подробными пояснениями.
Далее рассматривается свойство четности и нечетности. И тут же объясняется, когда функция четная и нечетная. Объяснения сопровождаются иллюстрациями и подробными описаниями. Это показано на примерах двух функций.
И, наконец, рассматривается шестое свойство – периодичность. На нем автор не останавливается, отмечая, что примеры периодичных функций будут изучены в дальнейшем на уроках алгебры.
ТЕКСТОВАЯ РАСШИФРОВКА:
Первое свойство, которое мы рассмотрим -монотонность.
Внимание: во всех определениях рассматривается числовое множество икс большое – подмножество области определения функции.
Функция игрек равно эф от икс возрастает на множестве икс большое, которое является подмножеством области определения и если для любых икс первое из множества икс большое и икс второе из множества икс большое таких,что икс второе больше икс первого выполняется неравенство эф от икс второе больше эф от икс первое.
Функция игрек равно эф от икс убывает на промежутке икс большое которое является подмножеством областиопределения и если для любых икс первое из множества икс большое и икс второе из множества икс большое таких,что икс второе больше икс первого выполняется неравенство эф от икс второе меньше эф от икс первое. Другими словами – большему значению аргумента соответствует меньшее значение функции.
Функция игрек равно эф от икс называется монотонной на множестве икс большое, если она на этом промежутке или убывает или возрастает.
Запомни: если функция определена и непрерывна в концах интервала возрастания или убывания, то эти точки включаются в промежуток возрастания или убывания.
Например, функция, график которой изображен на рисунке, на промежутках
от минус бесконечности до минус пяти и от трех до плюс бесконечностивозрастает, а на промежутке от минус пяти до трех убывает. Пример. Исследовать функцию на монотонность: игрек равен шесть минус два икс.
Пример. Исследовать функцию на монотонность: игрек равен шесть минус два икс.
Введем обозначение: эф от икс равен шесть минус два икс.
Если икс первое меньше икс второе, то используя свойства числовых неравенств, имеем
Значит, заданная функция убывает на всей числовой прямой.
Существуют функции, являющиеся возрастающими на всей области определения, например, игрек равен ка икс плюс вэ при ка больше нуля, игрек равен икс в кубе.
Второе свойство – ограниченность.
Если все значения функции игрек равно эф от икс на множестве икс большое больше некоторого числа эм малое, то функцию игрек равно эф от икс называют ограниченной снизу на множестве икс большое из области определения.
Если все значения функции игрек равно эф от икс на множестве икс большое меньше некоторого числа эм большое, то функцию игрек равно эф от икс называют ограниченной сверху на множестве икс большое из области определения.
Запомни: если функция ограничена и сверху и снизу на всей области определения, то ее называют ограниченной.
По графику функции легко можно определить ее ограниченность.
Наибольшее значение функции обозначают игрек с индексом наибольшее. .
Игрик является наибольшим если:
Во -первых, существует точка икс нулевое из множества икс большое такая, что эф от икс нулевое равно эм большое;
Во – вторых,для любого значения икс из множества икс большое выполняется неравенство эф от икс меньше или равно эф от икс нулевое, то число эм большое называют наибольшим значением функции игрек равно эф от икс на множестве икс большое из области определения функции.
Наименьшее значение функции обозначают игрек с индексом наименьшее
Во -первых, существует точка икс нулевое из множества икс большое такая, что эф от икс нулевое равно эм;
Во – вторых,для любого значения икс из множества икс большое выполняется неравенство эф от икс больше или равно эф от икс нулевое,то число эм называют наименьшим значением функции игрек равно эф от икс на множестве икс большое из области определения функции
Полезно запомнить:
Если у функции существует наименьшее значение. , то она ограничена снизу.
, то она ограничена снизу.
Если у функции существует наибольшее значение, то она ограничена сверху.
Рассмотрим пример. Найти наименьшее значение функции
Функция, график которой изображен на рисунке, ограничена снизу, наименьшее значение функции равно нулю, а наибольшего не существует, функция сверху неограниченна.
Третье свойство: выпуклость вверх, выпуклость вниз.
Если,соединить любые две точки графика функции с абсциссами из икс большое отрезком и соответствующая часть графика будет лежать ниже проведенного отрезка, то такая функция выпукла вниз на промежутке икс большое из области определения.
Если,соединить любые две точки графика функции с абсциссами из икс большое отрезком и соответствующая часть графика будет лежать выше проведенного отрезка, то такая функция выпукла вверх на промежутке икс большое из области определения.
четвертое свойство: непрерывность.
Функция называется непрерывной на промежутке, если она определена на этом промежутке и непрерывна в каждой точке этого промежутка.
Непрерывность функции на промежутке Х означает, что график функции на всей области определения сплошной, т.е. не имеет проколов и скачков.
пятое свойство: четность, нечетность.
Если область определения функции -симметричное множество и для любого х из области определения функции выполняется равенство f(-х)= f(х), то такая функция четная.
График четной функции симметричен относительно оси ординат.
Если область определения функции -симметричное множество и для любого х из области определения функции выполняется равенство f(-х)= -f(х), то такая функция нечетная.
График нечетной функции симметричен относительно начала координат.
Так же существуют функции, которые не являются ни четными, ни нечетными
шестое свойство: периодичность
примеры периодических функций будем рассматривать в дальнейшем
Если существует такое отличное от нуля число тэ большое, что для любого икс из области определения функции верно равенство эф от икс плюс тэ большое равно эф от икс и равно эф от икс минус тэ большое, то функция игрек равно эф от икс -периодическая. Число тэ большое – период функции игрек равно эф от икс
Число тэ большое – период функции игрек равно эф от икс
все тригонометрические функции периодические.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие
простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного – в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного – в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т. е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль.
Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как
производную “икса”. Получаем следующие значения производных:
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль.
Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как
производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем:
В данной функции видим частное, делимое которого – квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Урок по теме «Область определения и область значений функции» проводится в 10 классе в курсе алгебры и начал анализа. На объяснение материала по данной теме автор отводит 8:47 минут. этого времени достаточно для того, чтобы обучающиеся прослушали необходимую информацию, зафиксировали ее в своих тетрадях и поняли содержание материала. Примерно столько же времени затрачивает учитель на уроке при объяснении нового материала.
Автор позаботился об учителях, нагрузка которых итак достаточно велика, поэтому разработал данный видеоурок с учетом всех требований. То есть, урок соответствует возрасту обучающихся, их уровню образования и особенностей восприятия материала. Учителю останется лишь подобрать материал для закрепления новой информации, полученной из данного урока.
Учителю останется лишь подобрать материал для закрепления новой информации, полученной из данного урока.
Урок начинается с информации о том, что функция задается вместе с областью определения. Далее автор определяет переменные xи y? как аргумент и значение функции соответственно. После этого вводятся определения понятий область определения функции и область значений функции.
Затем рассматривается пример, где функция задана графически, и необходимо определить ее область определения. Решение данного примера подробно расписывается на экране. Автор поясняет каждый момент, где обучающиеся могут допустить ошибки. Все объяснение сопровождается наглядной иллюстрацией на рисунке.
Далее автор переходит к пункту «Область определения рациональной функции». Для обучающихся говорится о том, что в область определения рациональных функций не входят те значения аргумента, которые обращают знаменатель в нуль. Это поясняется на случае общего написания рациональной функции.
Затем на этот случай рассматривается пример. Здесь необходимо найти область определения рациональной функции. Решение пример основано на той информации, которую только что автор поведал обучающимся. То есть, он находит все те значения, которые обращают знаменатель в нуль и исключает их из множества действительных чисел, получая, таким образом, область определения функции.
Здесь необходимо найти область определения рациональной функции. Решение пример основано на той информации, которую только что автор поведал обучающимся. То есть, он находит все те значения, которые обращают знаменатель в нуль и исключает их из множества действительных чисел, получая, таким образом, область определения функции.
после этого предлагается рассмотреть еще один пример, где требуется найти область определения рациональной функции. Но здесь наблюдается следующая особенность: знаменатель дроби никогда не обращается в нуль. Поясняя это, автор делает вывод, что областью определения данной функции является множество действительных чисел. После этого примера предлагается запомнить закономерность, которая только что была использована в примере.
Далее автор переходит к пункту «Область определения иррациональной функции». Здесь важно запомнить то, что подкоренное выражение никогда не может быть отрицательным. Это подкрепляется математической интерпретацией на математической языке. Здесь же поясняется, что если иррациональное выражение в записи функции находится в знаменателе, то подкоренное выражение будет не просто неотрицательным, а строго положительным.
Здесь же поясняется, что если иррациональное выражение в записи функции находится в знаменателе, то подкоренное выражение будет не просто неотрицательным, а строго положительным.
К этому материалу прилагается пример, где требуется найти область определения иррациональной функции. Решая неравенство: подкоренное выражение неотрицательно, автор получает значения аргумент, которые образуют область определения заданной функции.
Затем рассматривается область определения функции с натуральным логарифмом. Сначала дается теоретический экскурс по данному материалу, а затем приводится пример с подробным описанием каждого шага решения.
После всего теоретического материала автор предлагает рассмотреть три примера, где требуется найти область определения и область значений функции, заданной графически. Это можно использовать как небольшой элемент закрепления выданного только что материала.
Урок будет полезен не только учителям, но и обучающимся, которые занимаются самообразованием или пропустили урок по данной теме по определенным причинам. Из этого урока обучающиеся смогут почерпнуть не только теоретический материал, но и подкрепить полученные знания практическими упражнениями.
Из этого урока обучающиеся смогут почерпнуть не только теоретический материал, но и подкрепить полученные знания практическими упражнениями.
ТЕКСТОВАЯ РАСШИФРОВКА:
Область определения и область значений функции.
Из определения функции следует, что функция игрек равен эф от икс задается вместе с ее областью определения икс большое.
Для изучения этой темы нам необходимо вспомнить: как называется переменная икс? число у?
Независимую переменную икс называют аргументом функции, а число игрек, соответствующее числу икс, называют значением функции эф в точке икс и обозначают эф от икс
Какое множество называется областью определения функции?
Если нам дана функция у=f(х),то ее область определения – это множество значений «икс» , для которых существуют значения «игрек»и обозначают дэ большое от эф.
Область значений функции – множество, состоящее из всех чисел эф от х, таких, что икс принадлежит икс большому и обозначают е большое от эф.
Рассмотрим пример. Функция задана графически. Определить дэ большое от эф.
Область определения данной функции представляет собой объединение промежутков:
интервал от минус бесконечности до а, луч от вэ до цэ и интервал от цэ до плюс бесконечности. Действительно так, если взять любое значение «икс» из интервала от минус бесконечности до а, или из полуинтервала от вэ до цэ, или из интервала от цэ до плюс бесконечности, то для каждого такого «икс» будет существовать значение «игрек».
Как ?
Рассмотрим примеры.
Первое.
Область определения рациональной функции, т.е. аргумент у которой есть в содержится в знаменателе.
Запомните:
значения аргумента, которые обращают знаменатель в ноль – не входят в область определения данной функции .
Предположим, дана функция, содержащая некоторую дробь единица, деленная на альфа от ихс. Как вы знаете, на ноль делить нельзя: поэтому альфа от икс не равно нулю
Найти область определения функции
эф от икс равен дроби, числитель которой икс плюс два, а знаменатель – икс квадрат минус три. Данная функция задана аналитически.
Данная функция задана аналитически.
Решение : обращаем внимание на знаменатель, он должен быть не нулевым. Приравняем его к нулю и найдем значение аргумента которые обращают знаменатель функции в ноль:
икс квадрат минус триравно нулю.
икс квадрат равно трем.
Полученное уравнение имеет два корня:
минус квадратный корень из трех, квадратный корень из трех.
Данные значения не входят в область определения функции , так как при этих значениях знаменатель дроби обращается в ноль.
Ответ : дэ большое от эф равен объединению промежутков:интервал от минус бесконечности до квадратного корня из трех,интервал от минус квадратного корня из трех до квадратного кореня из трех.
и интервал от квадратного кореня из трех
до плюс бесконечности.
Рассмотрим еще пример.
Найти область определения функции
эф от икс равен дроби, числитель которой единица, а знаменатель – икс квадрат плюс один.
Рассмотрим выражение стоящее в знаменателе: к квадрату числа икс прибавляют единицу он всегда положительно т. е. какое бы значение «икс» мы не взяли, знаменатель не обратится в ноль, более того, будет всегда положителен, значит область определения функции, дэ большое от эф равено множеству всех действительных чисел.
е. какое бы значение «икс» мы не взяли, знаменатель не обратится в ноль, более того, будет всегда положителен, значит область определения функции, дэ большое от эф равено множеству всех действительных чисел.
определена на всей числовой оси.
Запомните!
при любом значении «икс» и положительной константе ка :
икс квадрат плюс ка больше нуля.
Второе.
Область определения иррациональной функции (содержащий радикал или корень).
подкоренное выражение неотрицательно
Функция вида игрек равен квадратный корень из альфа от икс определена только при тех значениях икс из области определения дэ от альфа, когда альфа от икс не отрицательно, т.е. больше или равна нулю. Если функция содержащая радикал в знаменателе дроби, то альфа от х строго больше нуля.
Найти область определения функции
эф от икс равен квадратный корень из трех минус два икс.
Решение : подкоренное выражение должно быть неотрицательным:
три минус два икс больше или равно нулю
минус два икс больше или равно минус трем
два икс меньше или равно трем
икс меньше или равнотрем вторым
Ответ: дэ большое от эф равен полуинтервалу от минус бесконечности до трех вторых.
Третье .
Область определения функций с натуральным логарифмом.
Пусть функция содержит натуральный логарифм альфа от икс., то в её область определения входят только те значения икс, удовлетворяющие неравенству альфа от икс строго больше нуля.
Если логарифм находится в знаменателе: то дополнительно накладывается условие альфа от икс не равно единице, (так как натуральный логарифм единицы равен нулю).
Найти область определения функции
эф от икс равен дроби числитель равен единице, а знаменатель – натуральный логарифм из выражения икс плюс три.
Решение : в соответствии с вышесказанным составим и решим систему:
икс плюс три больше нуля
и икс плюс три не равно единице
икс больше минус трех и икс не равно минус двум.
Изобразим множество решений системы на прямой и сделаем вывод.
Ответ: дэ большое от эф равно объединению промежутков: интервалам от минус трех до минус двух и от минус двух до плюс бесконечности.
Дэ большое от эф равен отрезку от минус четырех до двух;
Е большое от эф равно отрезку от минус одного до двух;
Найтиобласть определения и область значений функции.
Дэ большое от эф равен интервалу от минус двух до пяти;
Е большое от эф равно отрезку от минус двух до трех;
Найтиобласть определения и область значений функции.
Дэ большое от эф равен отрезку от минус четырех до трех;
Е большое от эф равно отрезку от минус пяти до нуля;
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \).
Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
\(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение
\(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то
указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f”(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x_0) $$
Для обозначения производной часто используют символ y”. Отметим, что y” = f(x) – это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f”(a) \)
Поскольку \(k = tg(a) \), то верно равенство \(f”(a) = tg(a) \) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \(y = f(x) \) имеет
производную в конкретной точке \(x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x) $$
Это означает, что около точки х выполняется приближенное равенство \(\frac{\Delta y}{\Delta x} \approx f”(x) \), т. 2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) – f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f”(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f”(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f”(0) \)
Итак, мы познакомились с новым свойством функции – дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями. 2} $$
2} $$
NIT for You | Математические калькуляторы с решением
Математические онлайн-калькуляторы — это программы, с помощью которых можно получить решения математических задач.
http://calc-x.ru/
Математический калькулятор на этом сайте выполняет автоматическое и мгновенное решение как простых, так и сложных задач математики, в том числе операции над матрицами, геометрические расчеты, работа с дробями, логарифмами, уравнениями, процентами и т.д. Вы сможете произвести перевод чисел в другую систему счисления и перевод физических величин. Для теоретической помощи существует раздел «Полезное для решения математических задач», в котором можно найти различную табличную и другую информацию. Вычисления доступны 24 часа в сутки с телефона, планшета или компьютера подключенного к Internet.
http://matematikam.ru/calculate-online/
В разделе «Онлайн сервисы» вам предоставлена возможность решать онлайн интегралы, брать производные, пределы, считать ряды практически для любых функций. Решение задач производится автоматически программой и является быстрым и абсолютно бесплатным. Все калькуляторы выдают ответ с подробным решением. Считайте легко, быстро и надежно вместе с нами.
Решение задач производится автоматически программой и является быстрым и абсолютно бесплатным. Все калькуляторы выдают ответ с подробным решением. Считайте легко, быстро и надежно вместе с нами.
https://www.kontrolnaya-rabota.ru/s/
На сайте представлены следующие сервисы:
Задачи в данных сервисах решаются в несколько шагов, после чего решение автоматически отправляется к Вам на ящик.
Отправка на почтовый ящик позволяет решить проблему сохранности решения, а также позволяет напечатать решение на принтере.
http://o-math.com/math/assistance/
Особенностью онлайн-калькуляторов по математике есть то, что они не только выдают ответ, но и детально расписывают ход решения задачи. Данные калькуляторы пригодятся и людям, которым просто нужно найти ответ, не вникая в ход решения, и людям, желающим выучить математику.
Высшая математика
Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты.
http://www.matburo.ru/
С помощью сайта-сервиса WolframAlpha Вы можете выполнить самые разные математические вычисления on-line: построение графиков функции, работа с матрицами, решение алгебраических и дифференциальных уравнений, действия с числами и переменными, вычисление процентов и котировок акций, вычисление производных, интегралов, нулей функции, максимумов и минимумов… Кстати, возможны решения задач онлайн из разных областей наук: физика, химия, география, компьютеры, единицы измерения и др. Перейти к решению задач по математике онлайн (с инструкциями и примерами)
Перейти к решению задач по математике онлайн (с инструкциями и примерами)
Этот список можно продолжать….
Топ-5 приложений для решения задач по математике
Мы отобрали для вас лучшие приложения для Android, которые созданы для решения практически любых задач по математике в два счета.
Математику по праву можно назвать царицей наук, которую в равной степени можно как любить, так и ненавидеть. Если задуматься всерьез, то мы используем знания по математике каждый день. Повсюду сталкиваемся с числами – на циферблате часов, на денежных банкнотах, в расписании уроков. Нам все время приходится выполнять простые и сложные математические операции – посчитать, через сколько минут начнется любимый фильм, сколько сдачи должны дать в магазине, когда приедет автобус.
Но для многих математика — это непонятные действия, числа, правила и задачи. Говорят, все познается в сравнении. Математика позволяет нам узнать, насколько что-то больше, длиннее, шире, дороже другого. Без знания математики невозможно построить дом, автомобиль. Если бы не математика, у нас бы никогда не было ни компьютеров, ни планшетов и смартфонов. Математическими расчетами пользуются все другие науки в мире.
Без знания математики невозможно построить дом, автомобиль. Если бы не математика, у нас бы никогда не было ни компьютеров, ни планшетов и смартфонов. Математическими расчетами пользуются все другие науки в мире.
Простая арифметика, превращающаяся в дальнейшем в сложную алгебру и геометрию, заставляла многих ненавидеть эти дисциплины. Кому-то математика в школе давалась легко, а для кого-то она так и осталась чем-то далеким и непостижимым. Как ни крути, иногда умение считать деньги не спасает от необходимости решения сложных математических уравнений и неравенств. «Смартфон» дословно переводится как «умный телефон», и благодаря стороннему софту ему можно доверить даже самые сложные задачи. В век информационных технологий дела с этим обстоят совсем иначе. На помощь школьникам и студентам пришли смартфоны и планшеты с «умными» приложениями-калькуляторами, речь о которых пойдет в этой статье. Оговоримся сразу, что приложения не могут быть панацеей. Вам всё равно придется учить математику, а они лишь помогут вам, подскажут ход решения. Пока что данные приложения не могут справляться со сложными заданиями, но кое-что умеют.
Пока что данные приложения не могут справляться со сложными заданиями, но кое-что умеют.
Photomath
Одно из самых известных приложений для решения математических задач с первого же дня назвали ужасом для учителей математики. А разработчики просто называют его «камерой-калькулятором». Photomath интересно тем, что способно решить практически любую математическую задачу. Вам тяжело разобраться в решении логарифмических, квадратных, тригонометрических уравнений и неравенств? Трудно решать задачи с корнями, модулями, степенями, дробями, интегралами и факториалами? Теперь с помощью приложения Photomath решать такие задания не составит большого труда. Но самое интересно — приложение не просто решает математические задачи, а подробно расписывает ход расчетов. Это понравится не только учащимся и студентам, а также родителям, которые захотят проверить домашнее задание своего чада.
Пользователю понравится, что приложение Photomath способно работать в автоматическом режиме. Достаточно просто открыть его и сразу же активируется встроенный интерфейс камеры с заданной областью распознавания. Для того, что начать работу, необходимо расположить камеру так, чтобы математическая задача вместилась в эту область. Буквально через мгновение умные алгоритмы программы начнут анализировать данные на экране и практически моментально выдадут ответ. Если захотите увидеть весь ход решения вашей задачи, то просто нажмите на результат в красном прямоугольнике. В истории приложения сохраняются 10 последних записей, поэтому в любой момент сможете просмотреть решение предыдущей задачи.
Достаточно просто открыть его и сразу же активируется встроенный интерфейс камеры с заданной областью распознавания. Для того, что начать работу, необходимо расположить камеру так, чтобы математическая задача вместилась в эту область. Буквально через мгновение умные алгоритмы программы начнут анализировать данные на экране и практически моментально выдадут ответ. Если захотите увидеть весь ход решения вашей задачи, то просто нажмите на результат в красном прямоугольнике. В истории приложения сохраняются 10 последних записей, поэтому в любой момент сможете просмотреть решение предыдущей задачи.
Иногда случается, что программа некорректно распознала те или иные математические символы в задании, решив неправильно при этом задачу. Но не отчаивайтесь. В Photomath у вас есть возможность отредактировать их в режиме калькулятора. Стоит отметить, разработчики очень хорошо продумали эту функцию. Здесь доступен калькулятор со всевозможными операторами, есть цифровая, текстовая и символьная раскладки.
Долгое время приложение умело распознавать только напечатанное задание. Причем из книги было намного легче отсканировать его, чем с экрана ноутбука. Теперь же, наконец-то, появилась долгожданная функция распознавания рукописного текста. Все работает почти безупречно, но для лучшего результата желательно, чтобы запись была аккуратным почерком.
Мне очень понравилось пользоваться приложением. Оно практически справляется с любым заданием со всей школьной программы по математике и алгебре, включая старшую и высшую школы. Да, приложение стоящее, абсолютно бесплатное, не содержит рекламы, как обычно бывает с такими приложениями, есть русский язык интерфейса, способно работать без подключения к Интернету, но и ошибок предостаточно.
MalMath: Step by step solver
С помощью данного приложения вы сумеете решить математические задачи не только получив пошаговое описание процесса вычисления, но и построение необходимых графиков. Само приложение MalMath для Android полностью бесплатное, к тому же совершенно не содержит рекламы. Также у вас есть возможность использовать его без подключения к Интернету. Это является большим плюсом для него. Программа в первую очередь приглянется ученикам старших классов, студентам колледжей, а также университетов и академий. Дело в том, что MalMath умеет решать интегралы, производные, пределы, логарифмы, тригонометрические уравнения и неравенства, примеры с корнями и модулями. По крайней мере большую часть. Однако, вам придется в ручную вводить условие задания, так как функция распознавания с помощью камеры здесь не предусмотрена. Что касается его способностей, то они ограничиваются лишь задачами средней сложности с более скромным, чем у остальных приложений, описанием решений.
Также у вас есть возможность использовать его без подключения к Интернету. Это является большим плюсом для него. Программа в первую очередь приглянется ученикам старших классов, студентам колледжей, а также университетов и академий. Дело в том, что MalMath умеет решать интегралы, производные, пределы, логарифмы, тригонометрические уравнения и неравенства, примеры с корнями и модулями. По крайней мере большую часть. Однако, вам придется в ручную вводить условие задания, так как функция распознавания с помощью камеры здесь не предусмотрена. Что касается его способностей, то они ограничиваются лишь задачами средней сложности с более скромным, чем у остальных приложений, описанием решений.
Интерфейс MalMath представлен на русском языке, выполнен в классическом стиле и оптимизирован под экраны смартфонов. У вас есть возможность в настройках изменить размер шрифта и скорость анимации. Открыв боковое меню, увидите, что оно включает пять пунктов: главный экран, рабочий лист, график, генератор задач, избранное. Но больше всего вам будет интересна функция «генератор задач». С ее помощью можно создавать случайные математические задачи с несколькими категориями и уровнями сложности, заданными в настройках. Все выражения и графики можно сохранять в избранном.
Но больше всего вам будет интересна функция «генератор задач». С ее помощью можно создавать случайные математические задачи с несколькими категориями и уровнями сложности, заданными в настройках. Все выражения и графики можно сохранять в избранном.
Сам процесс добавления задачи очень похож на вставку формул в Microsoft Word. Из собственного опыта отмечу, что, вроде бы все понятно и просто, но иногда довольно неудобно, особенно, что касается ввода сложных комбинаций с дробями и корнями. Придется потратить немного времени, чтобы привыкнуть к определенному принципу набора, но все же оно того стоит.
Mathway
Еще одно весьма заслуживающее внимания приложение, которое поможет справиться с математическими заданиями. Приложение является своеобразным инструмент для решения задач, который, помимо школьного курса математики, охватывает математический анализ, статистику, тригонометрию, линейную алгебру и даже химию. Если вы когда-то использовали веб-версию сервиса Mathway, то сразу же узнаете внешний вид и функциональные возможности данного приложения. Практически тот же интерфейс в виде мессенджера, в котором все действия происходят как бы в диалоге с виртуальным помощником.
Практически тот же интерфейс в виде мессенджера, в котором все действия происходят как бы в диалоге с виртуальным помощником.
Стоит заметить, что именно данное приложение из рассматриваемых в этой статье является одним из самых интересных в плане качества решения. Вам понравится, что получите, пожалуй, наиболее развернутые пошаговые решения задач, к тому же на понятном русском языке. Немного странным выглядит тот факт, что в описании указано, что для просмотра пошагового решения, нужна платная подписка, хотя все функциональные возможности приложения совершенно бесплатны. Mathway поможет вам не только с решением уравнений, неравенств и прочих сложных выражений, но также сумеет построить графики, может найти число молекул в определенной массе тела.
Mathway для Android тоже решает задачи с помощью камеры устройства, правда, реализована эта функция не самым лучшим образом. Для такого вывода у нас есть несколько веских причин. Во-первых, интерфейс камеры в программе крайне минималистичный, в нем почему-то нет даже области распознавания. Вам придется приловчится, чтобы выражение находилось по центру экрана, а рядом не должно быть других надписей, иначе приложение будет выдавать неправильное решение. Часто на практике камера захватывала только часть приложения, отсюда и ошибки. К тому же камера автоматически настроена на макро-режим, поэтому алгоритмы распознавания часто плохо срабатывают и выдают неправильный ответ. Лично мне иногда было гораздо проще и быстрее ввести задачу вручную. К тому же для этого в приложении есть просто шикарные возможности. Дело в том, что выдвигающееся боковое меню позволит вам получить доступ аж к 10 разделам, у каждого из которых есть свой собственный калькулятор с определенными символами, операторами, константами и прочими функциями. Очень удобно и практично.
Вам придется приловчится, чтобы выражение находилось по центру экрана, а рядом не должно быть других надписей, иначе приложение будет выдавать неправильное решение. Часто на практике камера захватывала только часть приложения, отсюда и ошибки. К тому же камера автоматически настроена на макро-режим, поэтому алгоритмы распознавания часто плохо срабатывают и выдают неправильный ответ. Лично мне иногда было гораздо проще и быстрее ввести задачу вручную. К тому же для этого в приложении есть просто шикарные возможности. Дело в том, что выдвигающееся боковое меню позволит вам получить доступ аж к 10 разделам, у каждого из которых есть свой собственный калькулятор с определенными символами, операторами, константами и прочими функциями. Очень удобно и практично.
Мне очень понравилось, что Mathway предлагает пользователю самому выбрать способ решения задачи, в зависимости от этого результаты могут меняться. Если не подходит один из способов, достаточно снова тапнуть на математическое выражение и выбрать другой вариант решения. Скажем сразу, если вы хотите быстро и оперативно получить нужный ответ к задаче, то Mathway вряд ли подойдет вам. Но, если хотите точности и развернутости ответа, а также у вас есть терпение самостоятельно вводить математические символы и знаки, то данное приложение весьма вам понравится.
Скажем сразу, если вы хотите быстро и оперативно получить нужный ответ к задаче, то Mathway вряд ли подойдет вам. Но, если хотите точности и развернутости ответа, а также у вас есть терпение самостоятельно вводить математические символы и знаки, то данное приложение весьма вам понравится.
Mathpix
Mathpix — первое приложение, которое позволяет вам решать и визуализировать решения, распознавая рукописный текста, включая сложные формулы. Mathpix стремится заменить дорогие и устаревшие графические калькуляторы, чтобы обеспечить бесплатное и интересное учебное пособие для студентов-математиков по всему миру.
Я и вовсе хотел написать его первым среди всех приложений, так как это один из старожилов подобных приложений для решения математических задач. Оно намного раньше, в отличие от Photomath, получило способность распознавать рукописные математические задачи. Стоит заметить, что суть и принцип работы обоих приложений очень похожи, но в целом сервис Mathpix рассчитан на более взрослую аудиторию. Оно умеет решать простые и не очень квадратные уравнения, легко справляется с задачами, в которых есть дробные выражения, а также корнями, логарифмами, интегралами, производными и т. д. То есть практически все, что есть в старших классах школы и первых курсов университета. Но особенно я бы отметил возможность построения графиков функций, благодаря интеграции с передовым графическим калькулятором Desmos. Этого нет ни у одного из представленных приложений, а это очень важно для решения задач алгебры и начала анализа.
Оно умеет решать простые и не очень квадратные уравнения, легко справляется с задачами, в которых есть дробные выражения, а также корнями, логарифмами, интегралами, производными и т. д. То есть практически все, что есть в старших классах школы и первых курсов университета. Но особенно я бы отметил возможность построения графиков функций, благодаря интеграции с передовым графическим калькулятором Desmos. Этого нет ни у одного из представленных приложений, а это очень важно для решения задач алгебры и начала анализа.
Вам очень понравится работа алгоритмов распознавания текстов и условий у Mathpix. Программа практически в считанные секунды сканирует и считывает условие задачи. Тут же отправляет на сервер данные условия и почти мгновенно выдает ответ. Но ошибки тоже случаются, хотя довольно редко. При этом пользователю доступны инструменты для работы с задачами в режиме графика: редактирование вводных данных, добавление таблиц, заметок и дополнительных функций для нескольких графиков.
Я тут так пафосно расписал возможности приложения, но отмечу, что оно хорошо справляется только с несложными задачами. Если еще с построением элементарных графиков приложение справится, то с более сложными заданиями, которые включают тригонометрические и логарифмические уравнения, неравенства, а также уравнения с модулем, возникали большие проблемы. Приложение просто игнорировало их решение. Так что разработчикам еще необходимо потрудиться над возможностями своей программы.
Большинству пользователей не понравится, что отсутствует интерфейс на русском языке, а также подробное описания решения задач. Да и само приложение довольно-таки сложновато в использовании, элементы управления неудобны на смартфоне с небольшим экраном. Создалось впечатление,что это веб-версия приложения. Но решение всё же остается за вами.
MyScript Calculator
Ну и, наконец, самое интересное приложение MyScript Calculator, которое впервые появилось в начале 2013 года. К тому же, сразу получило признание на международной выставке CES и было отмечено за инновации. Мы привыкли, что в онлайн-калькуляторах либо роль считывателя играет камера устройства, либо вручную вводим данные. В приложении MyScript Calculator принцип подхода к математическим вычислениям кардинально отличается. Особенность MyScript Calculator заключается в том, что приложение работает только с рукописным вводом данных. Здесь даже отсутствуют кнопки, как таковые, а все, что имеется — это чистое полотно на весь экран, имитирующее бумагу-миллиметровку. Примеры для вычисления пользователь пишет пальцем или с помощью стилуса. В данном случае предпочтительнее будет использование планшета или фаблета с цифровым пером.
Мы привыкли, что в онлайн-калькуляторах либо роль считывателя играет камера устройства, либо вручную вводим данные. В приложении MyScript Calculator принцип подхода к математическим вычислениям кардинально отличается. Особенность MyScript Calculator заключается в том, что приложение работает только с рукописным вводом данных. Здесь даже отсутствуют кнопки, как таковые, а все, что имеется — это чистое полотно на весь экран, имитирующее бумагу-миллиметровку. Примеры для вычисления пользователь пишет пальцем или с помощью стилуса. В данном случае предпочтительнее будет использование планшета или фаблета с цифровым пером.
Вам понравится, что приложение автоматически сумеет распознать написанное вручную, переведет записи в нормальный цифровой вид и буквально в то же мгновение выдаст результат. Стоит отметить, что алгоритмы распознавания MyScript Calculator просто великолепные. На практике программа умудряется определить даже самые откровенные каракули. Также вы сможете отменить или повторить последние действия и полностью очистить экран от написанного. К тому же вас определенно порадует довольно большой список поддерживаемых символов и операторов, который поможет решить даже сложные задания. Несмотря на все это, приложение вряд ли пригодится студентам университетов. Даже несмотря на возможность работать с дробями, квадратными корнями, константами, решать уравнения, находить переменные, MyScript Calculator решит школьную программу, не более.
К тому же вас определенно порадует довольно большой список поддерживаемых символов и операторов, который поможет решить даже сложные задания. Несмотря на все это, приложение вряд ли пригодится студентам университетов. Даже несмотря на возможность работать с дробями, квадратными корнями, константами, решать уравнения, находить переменные, MyScript Calculator решит школьную программу, не более.
Основным недостатком MyScript Calculator для Android можно считать отсутствие подробного описания решений, программа выдает только итоговый результат. Хотя, учитывая концепцию приложения, возможно оно было бы лишним. А вот то, что здесь не хватает различных удобных мелочей, так это скорее пожелание разработчикам на будущее. К примеру, хотелось бы увидеть историю вычислений, возможность масштабировать экран и сохранять введенные задачи. Но, если все это отбросить в сторону, приложение действительно полезное, простое и оригинальное.
Вместо тысячи слов…
Ну и в заключение все же хочется сказать, что хоть приведенные приложения и помогут вам справиться с математическими заданиями, но не забывайте, что это всего лишь программа. Она призвана помочь вам, а не добавлять вам знаний. Но еще раз повторюсь, данные приложения не являются панацеей для решения задач. Так, с некоторыми заданиями оно и вовсе не справится. К тому же иногда ошибаются в самых простейших случаях. Поэтому не стоит доверять им всецело, а все-таки учить математику.
Она призвана помочь вам, а не добавлять вам знаний. Но еще раз повторюсь, данные приложения не являются панацеей для решения задач. Так, с некоторыми заданиями оно и вовсе не справится. К тому же иногда ошибаются в самых простейших случаях. Поэтому не стоит доверять им всецело, а все-таки учить математику.
Будем признательны, если в комментариях поделитесь своим опытом использования подобных приложений, которые облегчают изучение математики.
ГДЗ по Алгебре за 10-11 класс: Алимов Ш.А. Решебник
Алгебра входит в список предметов с 7 класса, и особенно в начале она не нравится школьникам. Ведь нужно учить большое количество математических и тригонометрических формул, правил и законов. Ребята считают, что в жизни это не пригодится, и что ничего дельного на таких уроках узнать нельзя. Однако алгебра очень полезна не только тем, кто хочет связать с ней жизнь. Она развивает логическое мышление, искусство доказывать и делать выводы.
Точные науки многим даются нелегко, ведь для того, чтобы быть успешным на таких уроках, нужно знать много формул и правил, а также уметь применять их на практике. У многих детей гуманитарный склад ума и совершенно нет интереса к математике и ее разделам, либо они просто думают, что не способны понимать ее, и теряют интерес и мотивацию.
У многих детей гуманитарный склад ума и совершенно нет интереса к математике и ее разделам, либо они просто думают, что не способны понимать ее, и теряют интерес и мотивацию.
Многие родители видят выход в репетиторе, но не каждая семья может позволить себе оплачивать дополнительные индивидуальные занятия. В такой ситуации целесообразно будет обратиться к решебникам. Актуальным на сегодняшний день является пособие, разработанное командой опытных и профессиональных методистов во главе с Ш.А. Алимовым и выпущенное в 2015 году известным издательством «Просвещение».
Почему стоит выбрать именно ГДЗ по алгебре для 10-11 классов (авторы: Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева)
Эта книга поможет не только отстающим в освоении материала, но и отличникам, которые углубят свои знания и улучшат умения. Достоинства:
- удобство пользования (наличие линейки для перемещения по частям учебника)
- поддержка мобильной версии для смартфона или телефона, так же можно пользоваться с компьютера или ноутбука
- верно решены все задачи, приведенные в соответствующем учебно-методическом комплексе
- онлайн-режим дает возможность открывать сайт в любое время и в любом месте
- исключительно положительные отзывы пользователей
Содержание учебно-методического комплекса по гпо алгебре для 10-11 классов от Ш.
 А. Алимова
А. АлимоваЭта книга включает все главы и темы, присутствующие в школьной программе на данном этапе обучения:
- действительные числа;
- степенная функции;
- тригонометрические формулы;
- производная и её геометрический смысл;
- интеграл;
- комбинаторика.
Таким образом, этот учебник принесет большую пользу учащимся, и их родители не будут переживать за успеваемость.
краткий гид по пропаганде — Команда 29
Вот первое, на что обращают внимание исследователи и практики информационной борьбы: авторы кампаний применяют одни и те же стратегии и демонстрируют одни и те же паттерны поведения. Например, процесс распространения сообщения в Твиттере почти всегда выглядит как размещение одного и того же текста разными пользователями. В отдельных случаях боты или пользователи включают в тело сообщения еще и аккаунты других пользователей, принуждая проверить упоминание вашего ника. Ещё одна стратегия — манипуляция с хэштегами: перемешивать свои хэштеги с теми, что находятся в мировом тренде.
Ещё одна стратегия — манипуляция с хэштегами: перемешивать свои хэштеги с теми, что находятся в мировом тренде.
Помните: аккаунты, продвигающие некую повестку, всегда связаны. Рекомендуется детально сличать списки контактов у аккаунтов, размещающих идентичный контент. В итоге вы всегда выйдете на аккаунты-матки, которые выдают первоначальный контент для продвижения.
Сети, состоящие из ботов и живых наёмных пользователей всегда размещают схожий контент, но могут быть идентифицированы именно через этот контент. Как мы видели на примере NaturalNews, несмотря на усилия по маскировке оригинального и часто блокируемого сайта через десятки и сотни других с аналогичным контентом, при должном старании вы обнаружите между ними четкую взаимосвязь и сможете разглядеть схему распространения нвоости.
Безусловно, подобную аналитику затруднительно провести каждому пользователю — и тут в дело вступает государство. В предыдущей статье мы подробно останавливались на истории центров мониторинга информации времен Второй Мировой войны и на том, как из них выросла индустрия OSINT. Возвращение интереса к пропаганде и дезинформации более всего связано с активным использованием ИГИЛ социальных сетей для вербовки и продвижения своих идей, подьёмом правых идей в Европе и США, а также возвращением себе Россией титула царицы дезинформации во время событий в Украине 2014 года, далее Брекзита и выборов в США. Сейчас в борьбу с пропагандой и дезинформацией вовлечены и частные компании, и университеты (например, Стэнфорд), и общественные организации. Основная задача, как и когда-то в 40-х, — мониторинг активности и поиск взаимосвязей. Также идет разработка и внедрение систем анализа выборов и влияния социальных сетей на итоговый результат — например от Digital Forensic Research Lab. Hamilton 68 Dashboard мониторит активность правительств и государственные СМИ Китая, России и Ирана в Твиттере.
В предыдущей статье мы подробно останавливались на истории центров мониторинга информации времен Второй Мировой войны и на том, как из них выросла индустрия OSINT. Возвращение интереса к пропаганде и дезинформации более всего связано с активным использованием ИГИЛ социальных сетей для вербовки и продвижения своих идей, подьёмом правых идей в Европе и США, а также возвращением себе Россией титула царицы дезинформации во время событий в Украине 2014 года, далее Брекзита и выборов в США. Сейчас в борьбу с пропагандой и дезинформацией вовлечены и частные компании, и университеты (например, Стэнфорд), и общественные организации. Основная задача, как и когда-то в 40-х, — мониторинг активности и поиск взаимосвязей. Также идет разработка и внедрение систем анализа выборов и влияния социальных сетей на итоговый результат — например от Digital Forensic Research Lab. Hamilton 68 Dashboard мониторит активность правительств и государственные СМИ Китая, России и Ирана в Твиттере.
Помимо систем мониторинга, государства активно используют и регуляторные возможности: например, Ofcom — регулятор Великобритании в области СМИ — наложил на RT санкции за трансляцию предосудительных и вводящих в заблуждение передач, а Национальный совет по электронным СМИ (NEPLP) на год запретил трансляцию «Россия РТР» на территории Латвии.
Аналитики из компании RAND рекомендуют государствам реагировать на пропаганду и дезинформацию более тонко: «Не стоит ваши информационные потоки направлять прямо в лицо пропагандистской машине; вместо этого направьте их туда, куда нацелено дуло орудий пропаганды, и попытайтесь подтолкнуть аудиторию в более продуктивном направлении». Однако, добавляют они, «любые средства — от агрессивного внедрения условий пользовательских соглашений с провайдерами услуг Интернета и социальными сетями до применения электронных/радиотехнических средств подавления связи или операции в киберпространстве — могут сократить воздействие пропаганды».
бесплатных вопросов по исчислению и проблем с решениями
Представлены бесплатные учебные пособия по исчислению. Аналитические уроки могут быть использованы для дальнейшего развития ваших навыков решения задач в области математического анализа. Также вопросы математического анализа изучаются в интерактивном режиме с использованием приложений и аналитически с примерами и подробными решениями. Задачи и вопросы по исчислению также включены на этот веб-сайт. Включены функции многовариантных и частные производные.
Также вопросы математического анализа изучаются в интерактивном режиме с использованием приложений и аналитически с примерами и подробными решениями. Задачи и вопросы по исчислению также включены на этот веб-сайт. Включены функции многовариантных и частные производные.
Задачи и вопросы по расчету
Вопросы, ответы и решения по расчетуУчебные пособия по анализу
Пределы и непрерывность
Дифференциация и производные
- Найдите производные функций в исчислении.
 Найдите производные от различных функций, используя разные методы и правила. Представлено несколько примеров с подробными решениями. Также упражнения с ответами включены в конце страницы.
Найдите производные от различных функций, используя разные методы и правила. Представлено несколько примеров с подробными решениями. Также упражнения с ответами включены в конце страницы. - Коэффициент разницы. Мы начинаем с определения коэффициента разности, а затем используем несколько примеров для его вычисления. Представлены подробные решения вопросов.
- Используйте определение, чтобы найти производную. Производная находится по ее определению. Сначала вычисляется коэффициент разности, а затем вычисляется его предел как h —> 0.Икс.
- Доказательство производной ln (x). Производная ln (x) вычисляется с использованием определения.

- Доказательство производной sin x. Производная sin (x) вычисляется с использованием определения производной как предела.
- Доказательство производной cos x. Производная cos (x) вычисляется с использованием определения производной как предела.
- Производная tan (x). Производная tan (x) вычисляется с использованием правила частного и производных sin (x) и cos (x).
- Доказательство производной кроватки (x). Доказательство производной от cot (x) проводится с использованием правила частного и производных от sin (x) и cos (x).

- Доказательство производной от sec (x). Приводится доказательство производной от sec (x).
- Доказательство производной csc (x). Приводится доказательство производной csc (x).
- Логарифмическое дифференцирование. Мощный метод поиска производных сложных функций. Метод использует цепное правило и свойства логарифмов.
- Таблица производных. Таблица производных экспоненциальных и логарифмических функций, тригонометрических функций и их обратных, гиперболических функций и их обратных.

- Правила дифференцирования функций в исчислении. Основные правила дифференцирования функций в исчислении представлены вместе с несколькими примерами.
- Используйте цепное правило дифференцирования в исчислении. Цепное правило дифференцирования функций в исчислении представлено вместе с несколькими примерами.
- Производные финансовые инструменты с абсолютной стоимостью. Примеры того, как найти производную функций, содержащих абсолютное значение. Также включены упражнения с ответами.
- Неявная дифференциация.
 Приведены примеры неявного дифференцирования с подробными решениями.
Приведены примеры неявного дифференцирования с подробными решениями. - Производная обратной функции. Приведены примеры с подробными решениями о том, как найти производную обратной функции.
- Производная от обратных тригонометрических функций.Формулы производных обратных тригонометрических функций представлены вместе с несколькими другими примерами, включающими суммы, произведения и частные функций.
- Найдите производную f (x) = arccos (cos (x)) и нанесите ее на график.
- Найдите производную f (x) = arcsin (sin (x)) и нанесите ее на график.

- Найдите производную f (x) = arctan (tan (x)) и изобразите ее.
- Дифференцирование тригонометрических функций. Формулы производных тригонометрических функций в исчислении представлены вместе с несколькими примерами, включающими произведения, суммы и частные тригонометрических функций.
- Найдите производную y = x x . Учебное пособие о том, как найти первую производную y = x x для x> 0.

- Дифференцирование экспоненциальных функций. Приведены формулы и примеры производных экспоненциальных функций в исчислении. Рассмотрены несколько примеров с подробными решениями, включающими произведения, суммы и частные экспоненциальных функций.
- Дифференцирование логарифмических функций. Приведены примеры производных логарифмических функций в исчислении.Рассмотрены несколько примеров с подробными решениями, включающими произведения, суммы и частные экспоненциальных функций.
- Дифференцирование гиперболических функций. Представлена таблица производных гиперболических функций. Рассмотрены примеры с подробными решениями, включающими произведения, суммы, степени и частные гиперболических функций.

Применение дифференцирования
Интегралы
Дифференциальные уравнения
Функции с несколькими переменными (функции с несколькими переменными)
Таблицы математических формул
- Таблицы математических формул.
 (n), так что 1,2,3 или n-кратное применение вывода к функции, итеративное / последовательное вычисление кортежей для той же переменной.
(n), так что 1,2,3 или n-кратное применение вывода к функции, итеративное / последовательное вычисление кортежей для той же переменной.Результаты
N-я производная – dCode
Тег (и): Функции
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Калькулятор производной N
Ответы на вопросы (FAQ)
Как вычислить n-ю производную?
n-я производная (или производная порядка $ n $) функции $ f $ состоит из итеративного применения производной $ n $ раз к функции $ f $.{(4n + 3)} (x) = – \ cos (x) $$
Задайте новый вопросИсходный код
dCode сохраняет право собственности на исходный код онлайн-инструмента «Nth Derivative».
 За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент Nth Derivative (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой Nth Derivative ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для Nth Derivative не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент Nth Derivative (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой Nth Derivative ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для Nth Derivative не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.Нужна помощь?
Пожалуйста, заходите в наше сообщество dCode Discord, если вам нужна помощь!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!Вопросы / Комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
производная, n-я, функция, дифференцирование, последовательная, итерация, калькулятор
Ссылки
Источник: https: // www.
© 2021 dCode – Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. Калькулятор производной на dcode.fr/nth-derivative
dcode.fr/nth-derivativeсекунд – онлайн-вычислитель двойной / второй функции
Поиск инструмента
Вторая производная
Инструмент для расчета второй производной f ”. Вторая производная – это применение инструмента деривации к (первой) производной функции, двойная деривация той же переменной.
Результаты
Вторая производная – dCode
Тег (и): Функции
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Калькулятор второй производной
Ответы на вопросы (FAQ)
Как рассчитать вторую производную?
Вторая производная (или производная второго порядка) – это применение производной к первой производной функции.
 2} $. В dCode предпочитайте f ”, которое является наиболее часто используемым обозначением (и самым быстрым для записи).
2} $. В dCode предпочитайте f ”, которое является наиболее часто используемым обозначением (и самым быстрым для записи).Как использовать вторую производную для однообразной таблицы?
Вторая производная используется для определения изменения наклона кривой, представляющей функцию. Для заданного интервала:
– положительная вторая производная означает увеличение наклона (выпуклая функция)
– отрицательная вторая производная означает уменьшение мысли (вогнутая функция)
– нулевая вторая производная означает прямую / прямую кривую
Для данной точки:
– вторая производная , отменяющая с изменением знака, означает точку перегиба, кривизна графического представления изменяется и переворачивается.Это стационарная точка, которая может быть максимумом функции или минимумом функции.
Какие функции не имеют производной второго порядка?
Любая функция, которая не является непрерывной и / или недифференцируемой по крайней мере в одной точке, не имеет второй производной .
Задайте новый вопрос См. Области определения инструментов функции и производную область функции.
См. Области определения инструментов функции и производную область функции.Исходный код
dCode сохраняет право собственности на исходный код онлайн-инструмента «Вторая производная».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой «Второй производный» алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой «Второй производный» ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести) написана на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.) и без загрузки данных, скрипт , копипаст или доступ к API для «Второй производной» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, заходите в наше сообщество dCode Discord, если вам нужна помощь!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!Вопросы / Комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
производная, секунда, функция, дифференцирование, калькулятор, ускорение
Ссылки
Источник: https: // www.
 4) и
4) и
как 3/5.Что означает построение кривых?
Построение кривой – это расчет для нахождения всех характерных точек функции, например корни, пересечение оси Y, максимальные и минимальные точки поворота, точки перегиба.Как получить эти баллы?
Расчет производных. Затем вы устанавливаете функцию и производную равными нулю: корни являются решениями уравнения.Точки поворота могут лежать в основе деривации, т.е. вам нужно решить уравнение для нахождения максимальных / минимальных точек поворота. (если в корне дифференцирования есть точка поворота, это можно проверить с помощью критерия смены знака.) В точке перегиба должна быть вторая производная, поэтому для нахождения точек перегиба решите уравнение.Почему в наши дни рисование кривых выполняется меньше?
Это немного глупо: вам просто нужно научиться каждый раз выполнять одни и те же вычисления точек, не задумываясь об их значении. Поэтому упражнения, в которых вы должны подумать о значении этих моментов, в наши дни становятся более важными.
Поэтому упражнения, в которых вы должны подумать о значении этих моментов, в наши дни становятся более важными.Могу я взглянуть на пример?
Конечно. Нарисуем кривую.
Mathepower работает с этой функцией:
Это график вашей функции.Dein Browser использует HTML-Canvas-Tag nicht. Hol dir einen neuen.: P - Корни в -1; 0; 1
- Пересечение оси Y в точке (0 | 0)
- Максимальные и минимальные точки поворота в точке (-0,577 | 0,385); (0,577 | -0,385)
- Точки перегиба в (0 | 0)
Корни:
Ищем корни
Итак, корни: {;;}| Фактор. | Произведение равно 0.Значит, либо коэффициент должен быть равен нулю. | + | Извлеките квадратный корень с обеих сторон. 
| Извлечь корень | Извлечь корень | или коэффициент должен быть равен нулю Симметрия:
– точка, симметричная относительно начала координат.Вычислите точку пересечения оси Y, вставив 0.
Вставьте 0 в функцию:
Итак, точка пересечения оси Y находится в точке (0 | 0)Диффентируйте функцию
Итак, первая производная – этоДифференцируйте функцию: (производная) + (производная от) + . 
Вторая производная, то есть производная от :
Упростите дифференциацию:
Итак, производная от.Производная от) + (Производная от) +
Итак, вторая производная – это| Умножаем на = Третья производная, то есть производная от :
Производная от
Итак, третья производная – это
Ищем точки поворота.
Мы должны найти корни первой производной.
Ищем корни
Точки поворота могут быть в {;}| + | : | Извлеките квадратный корень с обеих сторон. 
| Извлечь корень | Извлеките корень
Вставить корни первой производной во вторую производную:
Вставить -0.577 в функцию:
-3,464 меньше 0. Таким образом, есть максимум на.
Вставьте -0,577 в функцию:
Максимальная точка поворота (-0,577 | 0,385)
Вставьте 0,577 в функцию:
3,464 больше нуля.
Вставьте 0,577 в функцию:
Минимальная точка поворота (0,577 | -0,385)
Ищем точки перегиба.
Нам нужно найти корни второй производной.
Ищем корни
Точки перегиба могут быть в {}| :
Вставить корни второй производной в третью производную:
Третья производная не содержит x, поэтому вставка дает 6
6 больше 0, поэтому есть точка перегиба в.
Вставьте 0 в функцию:
Точка перегиба (0 | 0)
Эскиз кривой
В процессе построения кривой выполняются следующие шаги:
\ (1.\) Домен
Найдите область определения функции и определите точки разрыва (если есть).
\ (2. \) Перехватывает
Определите точки пересечения \ (x- \) и \ (y – \) функции, если это возможно. Чтобы найти точку пересечения \ (x – \), мы устанавливаем \ (y = 0 \) и решаем уравнение для \ (x. \). Точно так же мы устанавливаем \ (x = 0 \), чтобы найти \ (y- \ ) перехват. Найдите интервалы, в которых функция имеет постоянный знак \ (\ left ({f \ left (x \ right) \ gt 0} \ right. \) И \ (\ left. {F \ left (x \ right) \ lt 0} \ вправо).
 \)
\)\ (3. \) Симметрия
Определите, является ли функция четной, нечетной или ни одной, и проверьте периодичность функции. Если \ (f \ left ({- x} \ right) = f \ left (x \ right) \) для всех \ (x \) в области, то \ (f \ left (x \ right) \) является четное и симметричное относительно оси \ (y – \). Если \ (f \ left ({- x} \ right) = -f \ left (x \ right) \) для всех \ (x \) в домене, то \ (f \ left (x \ right) \) нечетное и симметричное относительно начала координат.
\ (4. \) Асимптоты
Найдите вертикальную, горизонтальную и наклонную (наклонную) асимптоты функции.\ prime \ left (x \ right) \) и найдите критические точки функции. (Помните, что критические точки – это точки, в которых первая производная равна нулю или не существует.) Определите интервалы, в которых функция увеличивается и уменьшается с помощью теста первой производной.
\ (6. \) Локальный максимум и минимум
Используйте первый или второй производный тест, чтобы классифицировать критические точки как локальный максимум или локальный минимум.
 2}} \ right]}
+ {2 – \ frac {{2 \ sqrt 3}} {3}}
= {\ cancel {1} - \ sqrt 3 + \ cancel {1}}
– {\ frac {{\ sqrt 3}} {9} – \ cancel {3}}
+ {2 \ sqrt 3 – \ cancel {1} + \ cancel {2}}
– {\ frac {{2 \ sqrt 3}} {3}}
= {\ frac {{9 \ sqrt 3 – \ sqrt 3 – 6 \ sqrt 3}} {9}}
= {\ frac {{2 \ sqrt 3}} {9} \ приблизительно 0,38;}
\]
2}} \ right]}
+ {2 – \ frac {{2 \ sqrt 3}} {3}}
= {\ cancel {1} - \ sqrt 3 + \ cancel {1}}
– {\ frac {{\ sqrt 3}} {9} – \ cancel {3}}
+ {2 \ sqrt 3 – \ cancel {1} + \ cancel {2}}
– {\ frac {{2 \ sqrt 3}} {3}}
= {\ frac {{9 \ sqrt 3 – \ sqrt 3 – 6 \ sqrt 3}} {9}}
= {\ frac {{2 \ sqrt 3}} {9} \ приблизительно 0,38;}
\]Аналогично находим, что
\ [
{y \ left ({1 + \ frac {{\ sqrt 3}} {3}} \ right)}
= – {\ frac {{2 \ sqrt 3}} {9} \ приблизительно -0 , 38.}
\]Таким образом, функция имеет локальный максимум в точке
\ [\ left ({1 – \ frac {{\ sqrt 3}} {3}, \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({0,42; \ ; 0,38} \ вправо). \]
Соответственно, локальный минимум достигнут в точке
.\ [\ left ({1 + \ frac {{\ sqrt 3}} {3}, – \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({1,58; \; – 0,38} \ вправо) \]
Интервалы увеличения / уменьшения следуют из рисунка \ (1a. \)
Рассмотрим вторую производную:
\ [
{y ^ {\ prime \ prime} \ left (x \ right) = {\ left ({3 {x ^ 2} – 6x + 2} \ right) ^ \ prime}}
= {6x – 6;}
\]\ [
{y ^ {\ prime \ prime} \ left (x \ right) = 0, \; \;} \ Rightarrow
{6x – 6 = 0, \; \;} \ Rightarrow
{x = 1 .2}}
= {\ left ({x + 2} \ right) \ left ({2x – \ cancel {2} + x + \ cancel {2}} \ right)}
= {3x \ left ({x + 2} \ вправо).}
\]Стационарных точек
\ [
{y ‘\ left (x \ right) = 0, \; \;} \ Rightarrow
{3x \ left ({x + 2} \ right) = 0, \; \;} \ Rightarrow
{ {x_1} = 0, \; {x_2} = – 2.}
\]Производная меняет знак, как показано на рисунке \ (3a. \). Следовательно, \ (x = -2 \) – точка максимума, а \ (x = 0 \) – точка минимума. В этих экстремальных точках функция имеет следующие значения:
\ [
{y \ left ({- 2} \ right) = – 4,} \; \; \; \ kern-0.3}}} = 0, \; \;} \ Rightarrow
{{x_1} = – \ sqrt 3, \; {x_2} = \ sqrt 3.}
\]При прохождении через эти точки вторая производная меняет знак. Следовательно, обе точки являются точками перегиба. Функция строго выпуклая вниз в интервалах \ (\ left ({- \ infty, – \ sqrt 3} \ right) \) и \ (\ left ({\ sqrt 3, + \ infty} \ right) \) и соответственно, строго выпукло вверх в интервале \ (\ left ({- \ sqrt 3, \ sqrt 3} \ right). 2} + 1}} {{\ cancel {1} - \ sqrt 2 – \ cancel {1}}}} = {\ frac {{1 – 2 \ sqrt 2 + 2 + 1}} {{- \ sqrt 2}}} = {\ frac {{4 – 2 \ sqrt 2}} {{- \ sqrt 2}}} = {\ frac {{4 – 4 \ sqrt 2}} {2}} = {2 \ left ({1 – \ sqrt 2} \ right) \ приблизительно {- 0.{2} + 3h} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {h (-4x – 2h + 3)} {h} \\ & = \ lim_ {h \ to 0} (- 4x-2h + 3) \\ f ‘(x) & = – 4x + 3 \ end {align *}
Определите производную от \ (f \ left (x \ right) = \ frac {1} {x-2} \), используя первые принципы.
\ begin {align *} f (x) & = \ frac {1} {x-2} \\ f (x + h) & = \ frac {1} {x + h-2} \\ f ‘(x) & = \ lim_ {h \ to 0} \ dfrac {f (x + h) -f (x)} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {\ frac {1} {x + h-2} – \ frac {1} {x-2}} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {\ frac {(x-2) – (x + h-2)} {(x + h-2) (x-2)}} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {\ frac {x-2-x-h + 2} {(x + h-2) (x-2)}} {h} \\ & = \ lim_ {h \ to 0} \ left (\ dfrac {-h} {(x + h-2) (x-2)} \ right) \ times \ frac {1} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {-1} {(x + h-2) (x-2)} \\ f ‘(x) & = \ frac {-1} {(x-2) ^ {2}} \ end {align *}
Определите \ ({g} ‘\ left (3 \ right) \) из первых принципов, если \ (g \ left (x \ right) = – 5 {x} ^ {2} \).{2}} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {h (-10x-5h)} {h} \\ & = \ lim_ {h \ to 0} (- 10x-5h) \\ & = – 10x \ end {align *}
Следовательно: \ begin {align *} g ‘(3) & = -10 (3) \\ & = -30 \ end {align *}
Если \ (p \ left (x \ right) = 4x (x-1) \), определите \ ({p} ‘\ left (x \ right) \), используя первые принципы.{n-1} \ end {выровнять *}
Это очень ценное общее правило для нахождения производной функции.
Приложения дифференциального исчисления | Дифференциальное исчисление
Сумма двух положительных чисел равна \ (\ text {20} \). Одно из чисел умножается на квадрат другого. Найдите числа, которые делают этот продукт максимальным.
Пусть первое число будет \ (x \), а второе число будет \ (y \), и пусть произведение будет \ (P \).

 Найдите производные от различных функций, используя разные методы и правила. Представлено несколько примеров с подробными решениями. Также упражнения с ответами включены в конце страницы.
Найдите производные от различных функций, используя разные методы и правила. Представлено несколько примеров с подробными решениями. Также упражнения с ответами включены в конце страницы.


 Приведены примеры неявного дифференцирования с подробными решениями.
Приведены примеры неявного дифференцирования с подробными решениями.


 (n), так что 1,2,3 или n-кратное применение вывода к функции, итеративное / последовательное вычисление кортежей для той же переменной.
(n), так что 1,2,3 или n-кратное применение вывода к функции, итеративное / последовательное вычисление кортежей для той же переменной. За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент Nth Derivative (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой Nth Derivative ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для Nth Derivative не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент Nth Derivative (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой Nth Derivative ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для Nth Derivative не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.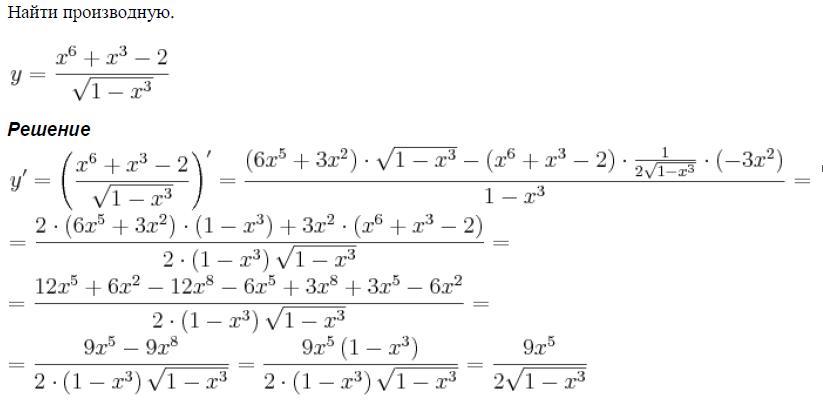 dcode.fr/nth-derivative
dcode.fr/nth-derivative 2} $. В dCode предпочитайте f ”, которое является наиболее часто используемым обозначением (и самым быстрым для записи).
2} $. В dCode предпочитайте f ”, которое является наиболее часто используемым обозначением (и самым быстрым для записи). См. Области определения инструментов функции и производную область функции.
См. Области определения инструментов функции и производную область функции. 4) и
4) и  Поэтому упражнения, в которых вы должны подумать о значении этих моментов, в наши дни становятся более важными.
Поэтому упражнения, в которых вы должны подумать о значении этих моментов, в наши дни становятся более важными.



 \)
\) 2}} \ right]}
+ {2 – \ frac {{2 \ sqrt 3}} {3}}
= {\ cancel {1} - \ sqrt 3 + \ cancel {1}}
– {\ frac {{\ sqrt 3}} {9} – \ cancel {3}}
+ {2 \ sqrt 3 – \ cancel {1} + \ cancel {2}}
– {\ frac {{2 \ sqrt 3}} {3}}
= {\ frac {{9 \ sqrt 3 – \ sqrt 3 – 6 \ sqrt 3}} {9}}
= {\ frac {{2 \ sqrt 3}} {9} \ приблизительно 0,38;}
\]
2}} \ right]}
+ {2 – \ frac {{2 \ sqrt 3}} {3}}
= {\ cancel {1} - \ sqrt 3 + \ cancel {1}}
– {\ frac {{\ sqrt 3}} {9} – \ cancel {3}}
+ {2 \ sqrt 3 – \ cancel {1} + \ cancel {2}}
– {\ frac {{2 \ sqrt 3}} {3}}
= {\ frac {{9 \ sqrt 3 – \ sqrt 3 – 6 \ sqrt 3}} {9}}
= {\ frac {{2 \ sqrt 3}} {9} \ приблизительно 0,38;}
\]