Решение простейших дифференциальных уравнений: определение и примеры с решением - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

определение и примеры с решением

Напомним, что дифференциальным уравнением второго порядка называется уравнение, наивысший порядок производной или дифференциалов в котором равен двум.

Простейшим дифференциальным уравнением второго порядка назовем уравнение вида: .

Например, уравнения — простейшие дифференциальные уравнения второго порядка. Подчеркнем, что в левой части простейшего дифференциального уравнения находится только , а в правой — выражение, содержащее только переменную .

Для решения простейших дифференциальных уравнений второго порядка необходимо двукратное интегрирование по переменной .

Рассмотрим принцип решения простейших дифференциальных уравнений второго порядка на следующем примере:

Пример №41.1.

Найдите решение дифференциального уравнения .

Решение:

Поскольку перед нами простейшее дифференциальное уравнение второго порядка, найдем сначала по формуле: .

или , где — константа.

Для нахождения искомой функции найдем интеграл от по переменной :

, или , где и — константы.

Полученная функция является общим решением дифференциального уравнения .

Ответ: .

Отметим, что общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные и .

Для простейшего дифференциального уравнения второго порядка можно рассмотреть задачу Коши (см. лекцию 38). Только в отличие от дифференциальных уравнений первого порядка, необходимо иметь два начальных условия: и . Для нахождения частного решения задачи Коши можно использовать следующий алгоритм:

Найти по формуле: .
Воспользовавшись первым начальным условием (), найти значение константы и подставить его в функцию .
Найти функцию как интеграл от по переменной .
Воспользовавшись вторым начальным условием (), найти значение константы и подставить его в функцию . Полученная функция и будет решением исходного дифференциального уравнения.

Пример №41.2.

Найдите решение задачи Коши: , если при и .

Решение:

1. Найдем .

2. Воспользуемся первым начальным условием: при . Подставим эти числа в функцию . Поскольку , получим, что .

Подставим найденное значение в функцию или .

3. Найдем функцию : , или .

4. Воспользуемся вторым начальным условием: при . Подставим эти числа в функцию . Поскольку , получим: , или .

Найденное значение константы подставим в функцию : . Полученная функция является частным решением исходного дифференциального уравнения при заданных начальных условиях.

Ответ: .

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Простейшие дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.

Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:

где функции и определены и непрерывны в некоторой области .

Уравнения в полных дифференциалах

Если в уравнении (1) левая часть представляет собой полный дифференциал, то есть , то такое уравнение называется уравнением в полных дифференциалах (частный случай так называемого пфаффова уравнения). Интегральные кривые такого уравнения суть линии уровней функции , т.е. определяются уравнением при всевозможных значениях произвольной постоянной .

Если в области выполнено условие , то общее решение уравнения (1) определяется из уравнения как неявная функция . Через каждую точку области проходит единственная интегральная кривая уравнения (1).

Если рассматриваемая область односвязна, а производные также непрерывны в , то для того, чтобы (1) было уравнением в полных дифференциалах, необходимо и достаточно выполнения условия

(признак уравнения в полных дифференциалах).

Интегрирующий множитель

Непрерывная функция в называется интегрирующим множителем уравнения (1), если уравнение является уравнением в полных дифференциалах, то есть для некоторой функции . Число интегрирующих множителей данного уравнения бесконечно.

Функция является интегрирующим множителем уравнения (1) тогда и только тогда, когда она удовлетворяет уравнению

(область по-прежнему полагаем односвязной; уравнение (2) является следствием признака уравнения в полных дифференциалах).

Уравнение (2) в общем виде решается сложнее, чем (1), но для интегрирования (1) достаточно знать один интегрирующий множитель, то есть найти какое-либо одно решение уравнения (2). Обычно ищут решение (2) в виде или , но это не всегда возможно.

Алгоритм решения

(1)

(2)

(3)

Возьмём (3).1 и проинтегрируем по переменной t:

(*)

Подставим в (3).2:

В получившемся равенстве слагаемые, содержащие t, уничтожатся. Получим: . Проинтегрируем по x и подставим в (*).

Уравнения с разделяющимися переменными

Если в уравнении (1) , то это уравнение с разделяющимися переменными

. Его можно записать в симметричном виде:

Решения уравнения с разделяющимися переменными
- Решения уравнения являются решениями (3).
- Если область выбрана так, что , то разделив на получим уравнение с разделёнными переменными

Это частный случай уравнения в полных дифференциалах. Для него очень просто получить решение в квадратурах. Интегральная кривая уравнения (3), проходящая через точку , имеет вид:

Пример дифференциального уравнения

Видеоурок “Простейшие дифференциальные уравнения” для 11 класса

До сих пор рассматривались уравнения, в которых неизвестными являлись числа.

Однако в математике и её приложениях приходится рассматривать уравнения, в которых неизвестными являются функции.

Примером является задача о нахождении пути s (t) по заданной скорости v (t), которая сводится к решению уравнения s‘ (t) = v (t), где v (t) — заданная функция, а s (t) — искомая функция.

Так, дифференциальным уравнением называется уравнение, которое содержит производную неизвестной функции.

Решение дифференциального уравнения определяется неоднозначно, с точностью до постоянной. Обычно к дифференциальному уравнению добавляется условие, из которого постоянная однозначно определяется.

Рассмотрим пример.

Решение многих физических, биологических, технических и других практических задач сводится к решению дифференциального уравнения y’ = ky, где k — заданное число. Решениями этого уравнения являются функции y = Ce^kx, где C — постоянная, которая определяется условиями конкретной задачи.

Рассмотрим задачу о размножении бактерий.

К решению дифференциального уравнения также сводится задача о радиоактивном распаде.

На практике часто встречаются процессы, которые периодически повторяются, например, колебательные движения маятника, струны, пружины и т. д.; к ним относятся процессы, связанные с переменным электрическим током, магнитным полем, и т. д. Решение многих таких задач сводится к решению дифференциального уравнения y” = ˗ω²y.

Далее будут выполнены несколько заданий, которые помогут закрепить новые знания на практике.

В завешение занятия подводятся итоги. Итак, мы узнали, какие уравнения называют дифференциальными. Рассмотрели задачу о размножении бактерий, а также задачу о радиоактивном распаде.

Поговорили о гармонических колебаниях.

Линейные и однородные дифференциальные уравнения первого порядка. Примеры решения

Думаю, нам стоит начать с истории такого славного математического инструмента как дифференциальные уравнения. Как и все дифференциальные и интегральные исчисления, эти уравнения были изобретены Ньютоном в конце 17-го века. Он считал именно это своё открытие настолько важным, что даже зашифровал послание, которое сегодня можно перевести примерно так: “Все законы природы описываются дифференциальными уравнениями”. Это может показаться преувеличением, но всё так и есть. Любой закон физики, химии, биологии можно описать этими уравнениями.

Огромный вклад в развитие и создание теории дифференциальных уравнений внесли математики Эйлер и Лагранж. Уже в 18-м веке они открыли и развили то, что сейчас изучают на старших курсах университетов.

Новая веха в изучении дифференциальных уравнений началась благодаря Анри Пуанкаре. Он создал «качественную теорию дифференциальных уравнений», которая в сочетании с теорией функций комплексного переменного внесла значительный вклад в основание топологии – науки о пространстве и его свойствах.

Что такое дифференциальные уравнения?

Многие боятся одного словосочетания “дифференциальное уравнение”. Однако в этой статье мы подробно изложим всю суть этого очень полезного математического аппарата, который на самом деле не так сложен, как кажется из названия. Для того чтобы начать рассказывать про дифференциальные уравнения первого порядка, следует сначала познакомиться с основными понятиями, которые неотъемлемо связаны с этим определением. И начнём мы с дифференциала.

Дифференциал

Многие знают это понятие ещё со школы. Однако всё же остановимся на нём поподробнее. Представьте себе график функции. Мы можем увеличить его до такой степени, что любой его отрезок примет вид прямой линии. На ней возьмём две точки, находящиеся бесконечно близко друг к другу. Разность их координат (x или y) будет бесконечно малой величиной. Ее и называют дифференциалом и обозначают знаками dy (дифференциал от y) и dx (дифференциал от x). Очень важно понимать, что дифференциал не является конечной величиной, и в этом заключается его смысл и основная функция.

А теперь необходимо рассмотреть следующий элемент, который нам пригодится при объяснении понятия дифференциального уравнения. Это – производная.

Производная

Все мы наверняка слышали в школе и это понятие. Говорят, что производная – это скорость роста или убывания функции. Однако из этого определения многое становится непонятным. Попробуем объяснить производную через дифференциалы. Давайте вернёмся к бесконечно малому отрезку функции с двумя точками, которые находятся на минимальном расстоянии друг от друга. Но даже за это расстояние функция успевает измениться на какую-то величину. И чтобы описать это изменение и придумали производную, которую иначе можно записать как отношение дифференциалов: f(x)’=df/dx.

Теперь стоит рассмотреть основные свойства производной. Их всего три:

Производную суммы или разности можно представить как сумму или разность производных: (a+b)’=a’+b’ и (a-b)’=a’-b’.
Второе свойство связано с умножением. Производная произведения – это сумма произведений одной функции на производную другой: (a*b)’=a’*b+a*b’.
Производную разности записать можно в виде следующего равенства: (a/b)’=(a’*b-a*b’)/b².

Все эти свойства нам пригодятся для нахождения решений дифференциальных уравнений первого порядка.

Также бывают частные производные. Допустим, у нас есть функция z, которая зависит от переменных x и y. Чтобы вычислить частную производную этой функции, скажем, по x, нам необходимо принять переменную y за постоянную и просто продифференцировать.

Интеграл

Другое важное понятие – интеграл. По сути это прямая противоположность производной. Интегралы бывают нескольких видов, но для решения простейших дифференциальных уравнений нам понадобятся самые тривиальные неопределённые интегралы.

Итак, что такое интеграл? Допустим, у нас есть некоторая зависимость f от x. Мы возьмём от неё интеграл и получим функцию F(x) (часто её называют первообразной), производная от которой равна первоначальной функции. Таким образом F(x)’=f(x). Отсюда следует также, что интеграл от производной равен первоначальной функции.

При решении дифференциальных уравнений очень важно понимать смысл и функцию интеграла, так как придётся очень часто их брать для нахождения решения.

Уравнения бывают разными в зависимости от своей природы. В следующем разделе мы рассмотрим виды дифференциальных уравнений первого порядка, а потом и научимся их решать.

Классы дифференциальных уравнений

“Диффуры” делятся по порядку производных, участвующих в них. Таким образом бывает первый, второй, третий и более порядок. Их также можно поделить на несколько классов: обыкновенные и в частных производных.

В этой статье мы рассмотрим обыкновенные дифференциальные уравнения первого порядка. Примеры и способы их решения мы также обсудим в следующих разделах. Будем рассматривать только ОДУ, потому что это самые распространённые виды уравнений. Обыкновенные делятся на подвиды: с разделяющимися переменными, однородные и неоднородные. Далее вы узнаете, чем они отличаются друг от друга, и научитесь их решать.

Кроме того, эти уравнения можно объединять, чтобы после у нас получилась система дифференциальных уравнений первого порядка. Такие системы мы тоже рассмотрим и научимся решать.

Почему мы рассматриваем только первый порядок? Потому что нужно начинать с простого, а описать всё, связанное с дифференциальными уравнениями, в одной статье просто невозможно.

Уравнения с разделяющимися переменными

Это, пожалуй, самые простые дифференциальные уравнения первого порядка. К ним относятся примеры, которые можно записать так: y’=f(x)*f(y). Для решения этого уравнения нам понадобится формула представления производной как отношения дифференциалов: y’=dy/dx. С помощью неё получаем такое уравнение: dy/dx=f(x)*f(y). Теперь мы можем обратиться к методу решения стандартных примеров: разделим переменные по частям, т. е. перенесём всё с переменной y в часть, где находится dy, и так же сделаем с переменной x. Получим уравнение вида: dy/f(y)=f(x)dx, которое решается взятием интегралов от обеих частей. Не стоит забывать и о константе, которую нужно ставить после взятия интеграла.

Решение любого “диффура” – это функция зависимости x от y (в нашем случае) или, если присутствует численное условие, то ответ в виде числа. Разберём на конкретном примере весь ход решения:

y’=2y*sin(x)

Переносим переменные в разные стороны:

dy/y=2*sin(x)dx

Теперь берём интегралы. Все их можно найти в специальной таблице интегралов. И получаем:

ln(y) = -2*cos(x) + C

Если требуется, мы можем выразить “игрек” как функцию от “икс”. Теперь можно сказать, что наше дифференциальное уравнение решено, если не задано условие. Может быть задано условие, например, y(п/2)=e. Тогда мы просто подставляем значение этих переменных в решение и находим значение постоянной. В нашем примере оно равно 1.

Однородные дифференциальные уравнения первого порядка

Теперь переходим к более сложной части. Однородные дифференциальные уравнения первого порядка можно записать в общем виде так: y’=z(x,y). Следует заметить, что правая функция от двух переменных однородна, и её нельзя разделить на две зависимости: z от x и z от y. Проверить, является ли уравнение однородным или нет, достаточно просто: мы делаем замену x=k*x и y=k*y. Теперь сокращаем все k. Если все эти буквы сократились, значит уравнение однородное и можно смело приступать к его решению. Забегая вперёд, скажем: принцип решения этих примеров тоже очень прост.

Нам нужно сделать замену: y=t(x)*x, где t – некая функция, которая тоже зависит от x. Тогда мы можем выразить производную: y’=t'(x)*x+t. Подставляя всё это в наше исходное уравнение и упрощая его, мы получаем пример с разделяющимися переменными t и x. Решаем его и получаем зависимость t(x). Когда мы ее получили, то просто подставляем в нашу предыдущую замену y=t(x)*x. Тогда получаем зависимость y от x.

Чтобы было понятнее, разберём пример: x*y’=y-x*e^y/x.

При проверке с заменой всё сокращается. Значит, уравнение действительно однородное. Теперь делаем другую замену, о которой мы говорили: y=t(x)*x и y’=t'(x)*x+t(x). После упрощения получаем следующее уравнение: t'(x)*x=-e^t. Решаем получившийся пример с разделёнными переменными и получаем: e^-t=ln(C*x). Нам осталось только заменить t на y/x (ведь если y=t*x, то t=y/x), и мы получаем ответ: e^-y/x=ln(x*С).

Линейные дифференциальные уравнения первого порядка

Пришло время рассмотреть ещё одну обширную тему. Мы разберём неоднородные дифференциальные уравнения первого порядка. Чем они отличаются от предыдущих двух? Давайте разберёмся. Линейные дифференциальные уравнения первого порядка в общем виде можно записать таким равенством: y’ + g(x)*y=z(x). Стоит уточнить, что z(x) и g(x) могут являться постоянными величинами.

А теперь пример: y’ – y*x=x².

Существует два способа решения, и мы по порядку разберём оба. Первый – метод вариации произвольных констант.

Для того чтобы решить уравнение этим способом, необходимо сначала приравнять правую часть к нулю и решить получившееся уравнение, которое после переноса частей примет вид:

y’ = y*x;

dy/dx=y*x;

dy/y=xdx;

ln|y|=x²/2 + C;

y=e^x2/2*у^С=C₁*e^x2/2.

Теперь надо заменить константу C₁ на функцию v(x), которую нам предстоит найти.

y=v*e^x2/2.

Проведём замену производной:

y’=v’*e^x2/2-x*v*e^x2/2.

И подставим эти выражения в исходное уравнение:

v’*e^x2/2– x*v*e^x2/2+ x*v*e^x2/2= x².

Можно видеть, что в левой части сокращаются два слагаемых. Если в каком-то примере этого не произошло, значит вы что-то сделали не так. Продолжим:

v’*e^x2/2= x².

Теперь решаем обычное уравнение, в котором нужно разделить переменные:

dv/dx=x²/e^x2/2;

dv = x²*e^–^x2/2dx.

Чтобы извлечь интеграл, нам придётся применить здесь интегрирование по частям. Однако это не тема нашей статьи. Если вам интересно, вы можете самостоятельно научиться выполнять такие действия. Это не сложно, и при достаточном навыке и внимательности не отнимает много времени.

Обратимся ко второму способу решения неоднородных уравнений: методу Бернулли. Какой подход быстрее и проще – решать только вам.

Итак, при решении уравнения этим методом нам необходимо сделать замену: y=k*n. Здесь k и n – некоторые зависящие от x функции. Тогда производная будет выглядеть так: y’=k’*n+k*n’. Подставляем обе замены в уравнение:

k’*n+k*n’+x*k*n=x².

Группируем:

k’*n+k*(n’+x*n)=x².

Теперь надо приравнять к нулю то, что находится в скобках. Теперь, если объединить два получившихся уравнения, получается система дифференциальных уравнений первого порядка, которую нужно решить:

n’+x*n=0;

k’*n=x².

Первое равенство решаем, как обычное уравнение. Для этого нужно разделить переменные:

dn/dx=x*v;

dn/n=xdx.

Берём интеграл и получаем: ln(n)=x²/2. Тогда, если выразить n:

n=e^x2/2.

Теперь подставляем получившееся равенство во второе уравнение системы:

k’*e^x2/2=x².

И преобразовывая, получаем то же самое равенство, что и в первом методе:

dk=x²/e^x2/2.

Мы также не будем разбирать дальнейшие действия. Стоит сказать, что поначалу решение дифференциальных уравнений первого порядка вызывает существенные трудности. Однако при более глубоком погружении в тему это начинает получаться всё лучше и лучше.

Где используются дифференциальные уравнения?

Очень активно дифференциальные уравнения применяются в физике, так как почти все основные законы записываются в дифференциальной форме, а те формулы, которые мы видим – решение этих уравнений.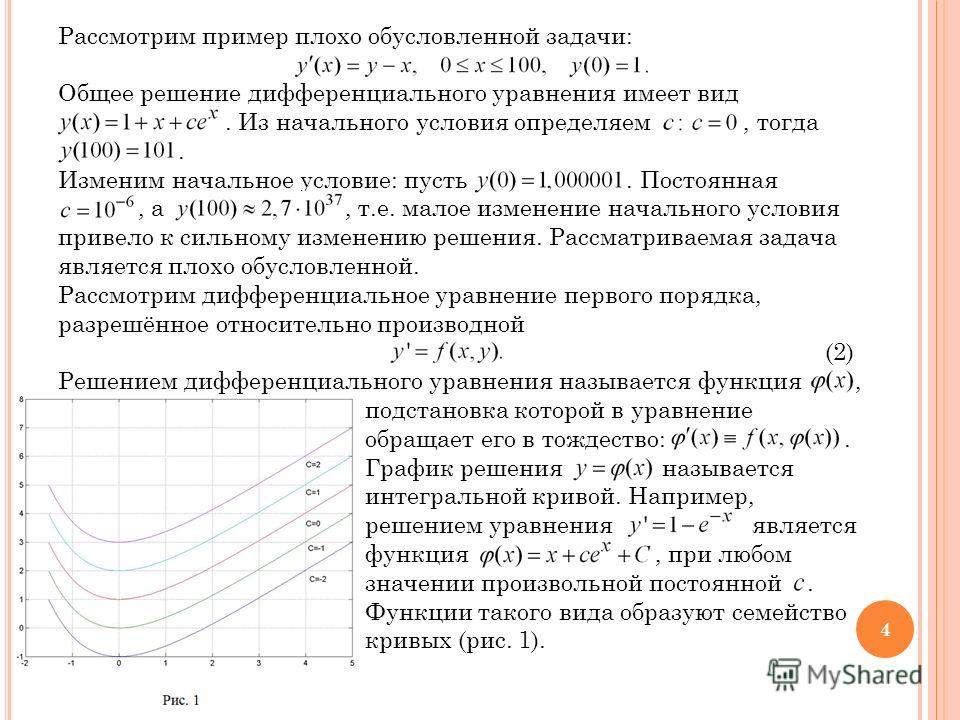 В химии они используются по той же причине: основные законы выводятся с их помощью. В биологии дифференциальные уравнения используются для моделирования поведения систем, например хищник – жертва. Они также могут использоваться для создания моделей размножения, скажем, колонии микроорганизмов.

Как дифференциальные уравнения помогут в жизни?

Ответ на этот вопрос прост: никак. Если вы не учёный или инженер, то вряд ли они вам пригодятся. Однако для общего развития не помешает знать, что такое дифференциальное уравнение и как оно решается. И тогда вопрос сына или дочки “что такое дифференциальное уравнение?” не поставит вас в тупик. Ну а если вы учёный или инженер, то и сами понимаете важность этой темы в любой науке. Но самое главное, что теперь на вопрос “как решить дифференциальное уравнение первого порядка?” вы всегда сможете дать ответ. Согласитесь, всегда приятно, когда понимаешь то, в чём люди даже боятся разобраться.

Основные проблемы при изучении

Основной проблемой в понимании этой темы является плохой навык интегрирования и дифференцирования функций. Если вы плохо берёте производные и интегралы, то, наверное, стоит ещё поучиться, освоить разные методы интегрирования и дифференцирования, и только потом приступать к изучению того материала, что был описан в статье.

Некоторые люди удивляются, когда узнают, что dx можно переносить, ведь ранее (в школе) утверждалось, что дробь dy/dx неделима. Тут нужно почитать литературу по производной и понять, что она является отношением бесконечно малых величин, которыми можно манипулировать при решении уравнений.

Многие не сразу осознают, что решение дифференциальных уравнений первого порядка – это зачастую функция или неберущийся интеграл, и это заблуждение доставляет им немало хлопот.

Что ещё можно изучить для лучшего понимания?

Лучше всего начать дальнейшее погружение в мир дифференциального исчисления со специализированных учебников, например, по математическому анализу для студентов нематематических специальностей. Затем можно переходить и к более специализированной литературе.

Стоит сказать, что, кроме дифференциальных, есть ещё интегральные уравнения, так что вам всегда будет к чему стремиться и что изучать.

Заключение

Надеемся, что после прочтения этой статьи у вас появилось представление о том, что такое дифференциальные уравнения и как их правильно решать.

В любом случае математика каким-либо образом пригодится нам в жизни. Она развивает логику и внимание, без которых каждый человек как без рук.

несколько простых примеров из Physclips

Дифференциальные уравнения включают дифференциал одной величины: насколько быстро эта величина изменяется относительно изменения другой. Например, обыкновенное дифференциальное уравнение для x (t) может включать x, t, dx / dt, d ² x / dt ² и, возможно, другие производные.

Мы рассмотрим два простых примера обыкновенных дифференциальных уравнений ниже, решим их двумя разными способами и покажем, что в них нет ничего пугающего – по крайней мере, не в отношении простых, с которыми вы встретитесь во вводном курсе физики.(И к тому времени, когда вы встретитесь со сложными уравнениями на втором и последнем курсе физики, вы уже будете заниматься более формальным изучением дифференциального исчисления по своим предметам математики.) Мы предполагаем, что вы уже немного знакомы с математическим расчетом. Если нет, сначала прочтите это введение.

Методы решения дифференциальных уравнений

Существует несколько различных способов решения дифференциальных уравнений, которые я перечислю в приблизительном порядке их популярности.Я также классифицирую их иначе, чем в учебниках.

Узнай или найди . Конечно! Уже решено очень много дифференциальных уравнений. Некоторые из них вы узнаете, а другие можете найти. Это , безусловно, наиболее распространенный способ “решения” дифференциальных уравнений учеными или математиками. Таким же образом некоторые (нечисловые) компьютерные программы решают дифференциальные уравнения.

Замена .Часто дифференциальное уравнение можно упростить, заменив ту или иную переменную. Это может превратить ее в решение, которое уже решено (см. Выше) или которое может быть решено одним из других методов. (Пакеты программного обеспечения тоже это делают.) Эта категория решений включает в себя ряд методов, которым вы научитесь на втором курсе курса математики.

Угадай и попробуй . Другой очень распространенный метод решения дифференциальных уравнений: угадайте, каким может быть решение, замените его и, если это не решение или не полное решение, измените предположение до тех пор, пока не получите полное решение. Это используется часто – чаще, чем можно предположить, читая книги и статьи, где процесс обычно кажется довольно элегантным. Во многих случаях вы знаете что-то об изучаемой системе, что дает вам ключ к разгадке. Опыт, конечно, тоже помогает. Однако ниже мы увидим, что угадать иногда легко.

Измените более простое решение . Если вы знаете решение уравнения, которое является упрощенной версией того, с которым вы столкнулись, попробуйте изменить решение более простого уравнения, чтобы преобразовать его в решение более сложного.

Преобразование . Некоторые дифференциальные уравнения легче решать при математическом преобразовании. Это основное использование преобразований Лапласа.

Численное решение. Если все вышеперечисленное терпит неудачу, то алгоритм, обычно реализуемый на компьютере, может решить эту проблему явно, вычисляя производные как отношения. Обычно это крайний метод по двум причинам. Во-первых, он дает вам решение только для одного конкретного набора граничных условий и параметров, тогда как все вышеперечисленное дает вам общие решения.Во-вторых, он имеет ограниченную точность: числовые дервиативы по своей сути зашумлены.

Интеграция . Этот метод элегантен, но часто бывает трудным (или невозможным). Иногда можно умножить уравнение на коэффициент интегрирования, чтобы сделать интегрирование возможным.

Особые типы . Это расплывчатое название включает специальные методы, которые работают с определенными типами уравнений. Это тоже касается обучения на высших курсах математики.

Аналоговое решение. Некоторые дифференциальные уравнения легко решаются аналоговыми компьютерами. Они очень быстрые и поэтому подходят для задач управления «в реальном времени». Их недостатки – ограниченная точность и то, что аналоговые компьютеры сейчас редкость.

Ниже мы показываем два примера решения общих уравнений. Они просты, потому что имеют только постоянные коэффициенты, но именно с ними вы столкнетесь на первом курсе физики. Эти уравнения можно решить несколькими способами, описанными выше, но мы проиллюстрируем только два метода.

Пример 1: Экспоненциальный рост и спад

Прежде чем идти дальше, , что мы уже знаем? Подумайте, что означает эта ситуация: если число удвоится (скажем) за один день, то на второй день их будет вдвое больше для воспроизводства, поэтому популяция снова удвоится на второй день и так далее.Это говорит нам, какое решение мы ищем: геометрическое или экспоненциальное увеличение (пример показан справа: подробнее об экспоненциальной функции по этой ссылке).

Поскольку это простое уравнение, давайте решим его интегрированием.

Для этого уравнения можно разделить переменные , то есть перестроить уравнение так, чтобы одна сторона включала только x, а другая – только t. Здесь получаем

где C – постоянная интегрирования.(Подробнее о функции журнала и константах интегрирования в исчислении Physclips.) Константы интегрирования обычно находятся из граничных условий: в данном случае это означает знание x при некотором значении t. В этом примере предположим, что мы знаем, что в момент времени t = 0 x = x ₀. Замена дает

Разница между двумя журналами – это логарифм отношения, поэтому

и, взяв антилоги (или возведя каждую сторону в степень е):

Проверим габариты.

e ^αt – это число, поэтому x имеет те же размеры и единицы измерения, что и x ₀: это хорошо! Аргумент экспоненциальной функции должен быть числом, так что это означает, что a имеет измерения обратного времени. α – это пропорциональная скорость прироста населения, поэтому это доля в раз, так что да, размеры верны. Из-за этих размеров принято определять τ = 1 / α, что дает решение

В примере справа τ (или 1 / α) называется постоянной времени , или характеристическим временем.Теперь его смысл ясен: когда t = τ, x / x ₀ равно e ¹ = 2,72. По истечении двух постоянных времени (когда t = 2τ) имеем x / x ₀ = e ² = 7,39 и т. Д. X увеличивается в e раз на каждом временном интервале τ. (Подробнее об экспоненциальной функции по этой ссылке.)

Между прочим, на этом стоит остановиться и отметить, что дифференциальные уравнения почти всегда являются только приближениями. Невозможно иметь систему, описываемую этим уравнением.Например, популяция любого вида не может расти экспоненциально. Процитируем только одно ограничение: как только организмы занимают твердую сферу, радиус которой увеличивается со скоростью света, любой дальнейший рост не может быть экспоненциальным. (Об этом стоит помнить, когда политики становятся одержимыми достижением роста чего угодно, но особенно населения.)

Экспоненциальное уменьшение

В приведенном выше примере α было положительным. Теперь рассмотрим случай, когда коэффициент при t отрицателен, примером чего является радиоактивный распад.Если имеется N (t) радиоактивных ядер в момент времени t и N ₀ при t = 0, и если их скорость распада (-dN / dt) пропорциональна количеству неразложившихся ядер с константой пропорциональности α, то

Выполняя ту же интеграцию, что и выше, мы имеем

где в этом случае τ – время, необходимое для изменения численности населения в e ⁻¹ = 0,37, и так далее.

Пример 2: Простое гармоническое движение

В направлении x второй закон Ньютона говорит нам, что F = ma = m.d ² x / dt ², а здесь сила – kx. Это дает нам дифференциальное уравнение:

где x – это смещение массы m от равновесия в момент времени t, а k – жесткость пружины, к которой прикреплена масса.

Что мы уже знаем?

Поведение. Если мы смещаем груз и отпускаем его, пружина ускоряет его в направлении положения равновесия (x = 0). Когда он достигает этого места, сила на нем равна нулю, но он движется с ненулевой скоростью.Таким образом, из-за своей инерции он проскакивает: он продолжает движение за пределы x = 0. Однако с этой стороны от x = 0 пружина замедляет его, в конечном итоге останавливая. Но сила пружины теперь велика, поэтому он ускоряется в противоположном направлении, возвращаясь к x = 0. Когда он попадает туда, он пролетает мимо … Хорошо, он колеблется. Итак, мы будем искать решение, которое колеблется .

Другой момент заключается в том, что мы пренебрегли трением, чтобы прийти к этому уравнению.Таким образом, нет ничего, что могло бы преобразовать механическую энергию, поэтому система будет колебаться вечно. Это тоже важно в нашем решении.

Размеры тоже помогают. Левая часть – это ускорение, поэтому k / m должно иметь размер (время) ⁻². Таким образом, характерное время τ в этом уравнении определяется как τ ⁻² = k / m или τ = (m / k) ^½. Величина, обратная времени, – это частота, поэтому 1 / τ может быть частотой, или, возможно, угловой частотой, или, по крайней мере, относящейся к ним.Мы узнаем.

Это хорошее время, чтобы использовать Guess и попробовать метод решения . Нам нужно решение, которое постоянно колеблется и обладает тем свойством, что его вторая производная пропорциональна самой себе, но отрицательна. Все это делает синусоидальная функция. Теперь мы не можем записать x = sin t по причинам размерности: аргумент синусоидальной функции не может иметь размерностей: он дается в радианах (что является отношением или числом).Мы можем написать

sin (2πft) или, что то же самое, sin (ωt),

Однако sin (ωt) – это число, и нам нужно, чтобы длина имела те же размеры, что и x, поэтому возможное решение:

Однако есть проблема с этим предлагаемым решением: у него x = 0 при t = 0. Что было бы нормально, если бы я дал ему толчок, чтобы запустить его из состояния покоя, но что, если я отпущу массу из состояния покоя в какой-то точке из равновесия? В последнем случае мне понадобится x = A cos (ωt). Общее решение должно учитывать эти и любые другие начальные условия. Вместо этого мы пишем:

Теперь, может ли это быть решением? Берем производные и получаем

Итак, это решение при условии, что ω ² = k / m.Или, если хотите, мы можем написать общее решение как

Итак, вернемся к рассмотрению φ. Если мы начнем движение (t = 0) с v = 0 при x = A, тогда φ должен быть 90 °: у нас есть функция cos вместо синуса. В качестве альтернативы, если мы начнем с максимальной (положительной) скорости при x = 0, тогда нам понадобится φ = 0. Мы приводим примеры этих случаев на странице фона для колебаний.Однако мы могли бы начать с любой комбинации начального смещения x = x ₀ и v = v ₀. Итак, для общего случая (x ₀ ≠ 0, v ₀ ≠ 0) мы можем заменить, чтобы получить

Мы можем решить их в терминах A и φ, сначала разделив два уравнения, затем возведя их в квадрат и сложив. Итак, для этих данных начальных условий мы можем найти комбинацию констант A и φ, так что это общее решение.

Сколько граничных условий? В нашем первом примере нам нужно было найти только одну константу интегрирования, поэтому нужно было найти только одно начальное условие (или другое граничное условие).Второй пример – уравнение второго порядка, требующее двух интегрирований или двух граничных условий. Здесь мы могли бы указать два из начального смещения, скорость и ускорение, или некоторые другие два параметра.

Затухающие и вынужденные колебания

Физически этот член соответствует силе, пропорциональной скорости. Что мы можем догадаться о решении и как нам изменить полученное выше решение, чтобы оно удовлетворяло нашему новому дифференциальному уравнению? Опять же, мы можем использовать наши знания о физической системе: когда мы прикладываем силу, направление которой противоположно направлению скорости, мы замедляем ее.Таким образом, мы ожидаем одного из двух возможных ответов: либо он должен колебаться, при этом величина колебаний постепенно уменьшается с течением времени, либо (если демпфирование достаточно велико), он может замедлиться до остановки, даже не колеблясь.

Это подсказывает нам возможность решения вида x = A e ^−βt sin (ωt + φ). Мы уже можем попробовать это. Но это не совсем решение. А что, если демпфирующая сила замедляет вибрацию? Почему бы не попробовать (ω + δω) вместо ω = k / m и посмотреть, дает ли это решение для подходящего значения δω?

Давайте добавим еще одно усложнение: давайте начнем встряхивать частицу с дополнительной осциллирующей силой, скажем F = F ₀ sin Ωt.Это дает нам новое дифференциальное уравнение:

₀

Уравнения в частных производных: волновое уравнение

∂y / ∂x. Думайте об этом как dy / dx в заданное постоянное время t. Представьте, что вы делаете снимок (время постоянно): на изображении в момент времени t, это наклон формы y (x) в момент фотографии.

∂y / ∂t. Думайте об этом как dy / dt в данной позиции x. Это просто скорость в направлении y в определенной точке x на струне. (Кстати, не скорость волны).

y = A sin (kx – ωt), поэтому
∂y / ∂x = kA cos (kx – ωt), который представляет собой наклон струны в положении x и в момент времени t, и
∂y / ∂t = – ωA cos (kx – ωt), которая представляет собой скорость точки на струне в точках x и t.

Два нижних графика – вторые производные по тем же переменным:

Они имеют важное физическое значение: первый определяет кривизну струны. Если ∂y ² / ∂x ² = 0, то наклон постоянный, значит, прямой. Это означает, что натяжение T действует в противоположных направлениях на противоположных концах, не создавая чистой силы. Однако, если сегмент изогнут (∂y ² / ∂x ² ≠ 0), на него действует сила. Для постоянной кривизны на небольшой длине L чистая сила пропорциональна L.

Мы знаем ускорение, поэтому можем применить второй закон Ньютона. Масса сегмента равна мкл, где μ – масса на единицу длины μ. Запись закона Ньютона в виде a = F / m дает:

Оглядываясь на наши выражения для двух вторых производных, мы видим, что они являются нашими постоянными, умноженными на нашу исходную функцию y = A sin (kx – ωt). Это означает, что y = A sin (kx – ωt) является решением волнового уравнения при условии, что T / μ = ω ² / к ².Мы также видели в Волны я, что ω / k – скорость волны, v. Который, наконец, связывает скорость волны с физическими свойствами T и μ струны:

Глава 6 Дифференциальные уравнения | Исчисление и анализ

Введение

Дифференциальные уравнения возникают почти каждый раз, когда мы пытаемся моделировать реальные мировые явления с помощью математики.Напомним, что производная измеряет одну величину в отношении Другая. Второй закон Ньютона гласит:

Скорость изменения количества движения тела равна приложенной внешняя сила.

Импульс тела является произведением массы \ (m \) и скорость \ (v \) (в одном измерении). Таким образом, если тело испытывает силу \ (F \), тогда можно записать закон Ньютона математически как \ [ {d \ over dt} (mv) = F.т г (х) дх. \] Важно, чтобы мы знали значение \ (f \) в какой-то момент, или иначе мы не можем точно сказать, что такое \ (f \). Нам нужна константа интеграции . Ниже у нас есть изображение, на котором мы можем видеть, что все эти функции имеют одну и ту же производную, поэтому, чтобы выбрать, какая из них является правильной для нашей ситуации, мы должны знать точку, через которую проходит функция.

Определение 6.1 Решение, в котором не указаны константы, называется общим решением .Известное значение \ (f \) равно называется начальным условием , если наша проблема связана со временем проблема, например, с законом Ньютона. Если известное значение является пространственным значение, которое мы называем граничным условием . Вы покрыли уравнения типа (6.1) на уровне A, поэтому мы не будем беспокоиться об этих здесь.

Вот веб-страница с другими примерами дифференциальных уравнений Дифференциальные уравнения на Mathisfun.com

Культурное наследие математики

Кэтрин Джонсон (1918-2020)

В 1962 году США решили отправить людей на Луну.Добраться до Луны и обратно потребовало бы много усилий. Кэтрин училась использовать геометрию для космических путешествий. Она выяснила, по каким путям космический корабль выйдет на орбиту (вокруг Земли) и приземлится на Луне. НАСА использовало математику Кэтрин, и это сработало.
https://www.nasa.gov/audience/forstudents/k-4/stories/nasa-knows/who-was-katherine-johnson-k4

Пути, по которым тела движутся под действием гравитационного притяжения, представляют собой так называемые конические сечения.

Гипатия (370-415)

Гипатия была известна больше своей работой в математике, чем в астрономии, в первую очередь своей работой над идеями конических сечений, введенными Аполлонием.Она редактировала работу «О кониках Аполлония», в которой конусы разделялись плоскостью на разные части. Эта концепция развила идеи гипербол, парабол и эллипсов.
https://www.agnesscott.edu/lriddle/women/hypatia.htm

Разделимые уравнения

Следующий наиболее простой вид дифференциального уравнения, который мы можем решить – это одна из форм \ [ {d y \ over dx} = f (x) g (y), \ tag {6.2} \] тогда мы можем написать \ [ \ int {dy \ над g (y)} = \ int f (x) dx.\] Нам все еще нужно граничное условие (будем считать, что \ (x \) и \ (y \) здесь пространственные переменные). Мы можем интегрировать оба из них в принцип, чтобы получить решение.

Пример 6.1

Снаряд, движущийся вверх, подвергается действию силы тяжести, равной к \ (m g \), где \ (m \) – его масса, а \ (g \) – ускорение, обусловленное сила тяжести. Он также замедляется сопротивлением воздуха, равным \ (mkv \), где \ (v \) – его скорость, а \ (k \) – некоторое положительное вещественное число. постоянная, зависящая от геометрии снаряда.Скорость снаряд в момент \ (t = 0 \) равен \ (u \) (это начальное значение состояние ).

Второй закон Ньютона гласит \ [ {d \ over dt} (mv) = -mkv-mg. \] Поскольку \ (m \) в этом уравнении постоянна (снаряд не изменить массу во время полета) мы можем сократить \ (m \) с обеих сторон на получать \ [ {dv \ over dt} = – (kv + g). \] Это отделимо. Переставляя, мы получаем уравнение \ [ \ int {dv \ over kv + g} = – \ int dt. \] Интегрируя обе стороны, мы имеем \ [ {1 \ над k} \ log (kv + g) = -t + C, \] где \ (C \) – постоянная интегрирования, которую мы находим с помощью начальное состояние.Когда \ (t = 0 \) \ (v = u \), так что \ [ {1 \ over k} \ log (ku + g) = C. \] Таким образом \ [ {1 \ над k} \ log (kv + g) = -t + {1 \ over k} \ log (ku + g). \] Преобразуя приведенное выше уравнение, мы имеем \ [\ begin {eqnarray *} t & = & {1 \ over k} (\ log (ku + g) – \ log (kv + g)) \\ & = & {1 \ над k} \ log \ left ({ku + g \ over kv + g} \ right). \ end {eqnarray *} \] Таким образом \ [ \ exp (kt) = \ left ({ku + g \ over kv + g} \ right). \] Умножая обе части на \ (kv + g \), имеем \ [ kv \ ехр (kt) + g \ exp (kt) = ku + g.\] Следовательно \ [ kv \ exp (kt) = ku + g (1- \ exp (kt)), \] так что \ [ v = u \ exp (-kt) + {g \ over k} (\ exp (-kt) -1). \]

Вы можете найти больше примеров разделимых уравнений и их решений на Math34.net.

Пример 6.2 Найти общее решение сепарабельного дифференциального уравнения \ [ у ‘= у (1-у). \]

Уравнение разделяется с \ (f (x) = 1 \) и \ (g (y) = y (1-y) \). Теперь \ (g (y) = 0 \) тогда и только тогда, когда \ (y = 0 \) или \ (y = 1 \).Таким образом, уравнение может быть решается разделением переменных в трех интервалах \ (y <0 \), \ (0 1 \). На любом таком интервале мы имеем: \ [ \ int \ frac {dy} {y (1-y)} = \ int dx + C_1, \] с \ (C_1 \ in {\ mathbb R} \). Это означает, что \ [ \ int \ left (\ frac {1} {y} + \ frac {1} {1-y} \ right) dy = \ int dx + C_1. \] Следовательно \ [ \ ln | y | – \ ln | 1-y | = x + C_1 \; \Правая стрелка \; \ ln \ left | \ frac {y} {1-y} \ right | = x + C_1, \] и взяв экспоненту с обеих сторон, мы имеем \ [ \ left | \ frac {y} {1-y} \ right | = \ exp (x + C_1) = \ exp (C_1) \ exp (x).\] Поскольку \ (C_1 \) константа, \ (\ exp (C_1)> 0 \) также константа. Назовем это \ (C_2 \). Потом, \ [ \ left | \ frac {y} {1-y} \ right | = C_2 \ exp (x). \] Теперь \ (y / (1-y) \) положительно, если \ (0 0. \]

Теперь \ (y / (1-y) \) отрицательно, если \ (y <0 \) или \ (y> 1 \).В данном случае
\ [ \ left | \ frac {y} {1-y} \ right | = – \ frac {y} {1-y} = C_2 \ exp (x), \] так что \ [ y = \ frac {C_2 \ exp (x)} {C_2 \ exp (x) -1} = \ frac {\ exp (x)} {\ exp (x) -1 / C_2} \ quad C_2> 0. \] Теперь, если \ (\ exp (x)> 1 / C_2 \), т.е. \ (x> – \ log (C_2) \), то \ (y> 1 \), и если \ (x <\ log (C_2 ) \), то \ (y <0 \). Следовательно, у нас будет вертикальная асимптота в \ (y \) в точке \ (x = - \ log (C_2) \).

Замечание На изображении выше вы можете увидеть, где находятся асимптоты по странному переходу на графике.Я оставил это, чтобы вы могли видеть, как решение меняется с отрицательного на значение больше 1, когда мы продвигаемся через \ (- \ log (C_2) \). Ситуация, показанная в предыдущем примере, типична для разделяемых уравнения. Случай \ (g (y) = 0 \) всегда нужно рассматривать отдельно. Обратите внимание, что если \ (g (y) = 0 \), то \ (y ‘= 0 \) благодаря дифференциалу Уравнение (6.2). Значит, значения \ (y \), для которых \ (g (y) = 0 \), постоянны стационарные решения уравнения.

Определение 6.2 Стационарное или равновесное решение для дифференциального уравнения \ (y ‘= f (x) g (y) \) – любое решение \ (y (x) = Constant \). Стационарный решения могут быть найдены путем решения для \ (y \) уравнения \ (g (y) = 0 \).

Мы можем получить качественное (поведенческое) понимание решений такого рода уравнения путем рисования так называемых полей направления.

Определение 6.3 Поле направления в области \ (S \) декартовой плоскости является картой который сопоставляет каждой точке региона линию, проходящую через эту точка.Кривая \ ({\ bf r} = {\ bf r} (t) \) на декартовой плоскости является интегральная кривая поля направлений, если ее касательные совпадают точно с линиями поля направления вдоль кривой.

Линии поля направления можно рассматривать как касательные к гипотетические кривые. Идея касательной тесно связана с идея наклона (также известная как производная). Поэтому вместо того, чтобы думать о линиях в поле направления мы можем думать о наклоне линий. (Мы разрешаем здесь бесконечный спуск.) И наклон задается числом.

Итак, на плоскости \ ((x, y) \) мы можем отождествить поле направлений с функция \ (f (x, y) \). Идея наклона приводит нас к уравнению \ (\ frac {dy} {dx} = g (x, y) \).

Следовательно, интегральные кривые для поля направлений точно соответствуют решения этого дифференциального уравнения.

Пример 6.3 Нарисуйте поле направления для уравнения \ (y ‘= y (1-y) \).

Имеем \ (g (x, y) = y (1-y) \). Мы уже видели в Пример 6.2, что \ (y = 0 \) и \ (y = 1 \), соответствующие нулю скорость изменения (наклон горизонтальный) являются стационарными решениями. 2 \ over a + bx} \)

Линейные уравнения первого порядка

Определение 6.4 Линейные дифференциальные уравнения первого порядка имеют вид \ [ {d y \ over dx} + p (x) y (x) = q (x). \] Они называются линейными , потому что \ (y \) появляется со степенью 1 на правая сторона. Собственно предыдущий пример тоже такого типа, но более легко разрешимо как разделимое уравнение.

Основная идея за решением этих уравнений состоит в том, чтобы преобразовать уравнение в \ [ {d y \ over dx} + p (x) y (x) = q (x), \ tag {6.3} \] и попытаться превратить левую часть в производную от товар .

Напомним, что \ [ {d \ over dx} (I (x) y (x)) = I (x) {dy \ over dx} + y (x) {dI \ over dx}. \] Умножим (6.3) на \ (I (x) \) (мы используем \ (I \), потому что это будет называется интегрирующим коэффициентом ), а затем попробуйте заставить его выглядеть как в приведенном выше уравнении. Умножение на \ (I (x) \) дает \ [ I (x) {d y \ over dx} + I (x) p (x) y (x) = I (x) q (x) \] Мы хотим \[ I (x) {d y \ over dx} + I (x) p (x) y (x) \ Equiv I (x) {dy \ over dx} + y (x) {dI \ over dx}.\] Чтобы это было правдой, нам нужно \ [ I (x) p (x) = {dI \ over dx}. \] Это разделимое уравнение: \ [ \ int {dI \ over I} = \ int p (x) dx, \] который мы решаем дать \ [ \ журнал I = \ int p (x) dx, \] так что \ [ Я (х) = \ exp \ left (\ int p (x) dx \ right). \ tag {6.4} \]

Определение 6.5 Функция
\ [ Я (х) = \ ехр \ слева (\ int p (x) dx \ справа) \] называется интегрирующим множителем для дифференциального уравнения \ [ {d y \ over dx} + p (x) y (x) = q (x).\]

Таким образом, мы имеем следующую теорему:

Теорема 6.1 (Интегрирующий множитель) Предположим, что у нас есть линейное дифференциальное уравнение \ [ {dy \ over dx} + p (x) y (x) = q (x). \] Тогда, если \ (I \) задается уравнением (6.4), мы можем переписать приведенное выше уравнение как \ [ {d \ over dx} (I (x) y (x)) = I (x) q (x). \] Общее решение этого дифференциального уравнения есть \ [ y (x) = {C \ над I (x)} + {\ int I (x) q (x) dx \ over I (x)}, \] где \ (C \) – произвольная постоянная интегрирования.

Пример 6.4 Давайте попробуем это в Примере 6.2. Уравнение, которое у нас было, было \ [ {d v \ over dt} = -kv-g. \]

Переставляем последнее уравнение, чтобы оно приняло нашу стандартную форму. \ [ {d v \ over dt} + kv = -g. \] которое является линейным дифференциальным уравнением для \ (v \). Функция \ (p (x) = k \) и \ (q (x) = – g \). Следовательно \ [ Я (т) = \ ехр (\ int (к) dt) = \ ехр (кт). \] потом \ [ {d \ over dt} (\ exp (kt) v) = k \ exp (kt) v + \ exp (kt) {dv \ over dx} = \ exp (kt) \ left ({dv \ over dt} + kv \ справа) = -g \ exp (kt).\] Если мы проинтегрируем обе стороны, мы получим \ [ \ exp (kt) v = – {g \ over k} \ exp (kt) + C, \] где \ (c \) – постоянная интегрирования. Генерал решение (кратное обеим сторонам \ (\ exp (-kt) \)) \ [ v = – {g \ over k} + C \ exp (-kt). \] Теперь мы используем начальное условие, что \ (v = u \), когда \ (t = 0 \), чтобы дать \ [ и = – {д \ над к} + С, \] другими словами \ [ С = и + {g \ over k}. \] Разделив обе части на \ (\ exp (kt) \), получим \ [ v = u \ exp (-kt) + {g \ over k} (1- \ exp (-kt)), \] что является тем же результатом, что и раньше.2}. \] Теперь воспользуемся граничным условием \ (y (1) = 0 \), чтобы найти конкретное решение, что дает \ (C = -1 / 5 \).

Вы можете найти больше примеров линейных дифференциальных уравнений первого порядка. на math34.net.

Однородные уравнения

Определение 6.6 Однородные дифференциальные уравнения являются уравнениями вида \ [ {d y \ over dx} = f \ left ({y \ over x} \ right). \]

В этом случае мы положим \ (v = y / x \) так, чтобы \ (y = vx \).С> 0 \). Следовательно \ [ v = \ pm \ sqrt {2 \ log Ax}, \] где \ (A \) – произвольная положительная постоянная интегрирования. Чтобы это имело смысл, мы требуем, чтобы \ (2 \ log A | x |> 0 \), так что \ (| x |> 1 / A \). тем не мение \ (v = y / x \), так что \ [ y = \ pm x \ sqrt {2 \ log A | x |}, \ quad | x |> 1 / A, \] является общим решением дифференциального уравнения. Мы выберем ветвь решения в зависимости от того, где находится начальное условие. Например, \ (y (x)> 0 \) для положительного \ (x \), тогда мы должны выбрать положительный квадратный корень.Но если \ (y (x) <0 \) для положительного \ (x \), мы должны выбрать отрицательный квадратный корень. На рисунке ниже мы изображаем решения, где \ (y (1) = 1 \) (синий) и \ (y (1) = - 1 \) (красный).

Вы можете найти больше примеров однородных уравнений и их решений. в Math34.net

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Определение 6. 2} + b {d y \ over dx} + cy = g (x), \] где \ (a, b, c \ in \ mathbb {R} \) и \ (g (x) \) является функцией от \ (x \).2}, \] а также \ [ v = {dx \ over dt}. \]

Закон Гука для моделирования движения пружины

Для пружины у нас есть Закон Гука , который гласит, что если мы расширим пружина на величину \ (x \) из своего естественного положения покоя, затем сила сопротивления растяжению пружины равна \ (- kx \), где \ (k \) – константа, называемая жесткостью пружины.

Таким образом, если у нас есть масса \ (m \) на пружине, то сила, направленная вниз, будет быть \ (мг \) и направленная вверх сила из-за натяжения пружины, когда увеличенное расстояние \ (l \) будет \ (kl \).2} = – {k \ over m} x. \ tag {6.5} \] Это известное дифференциальное уравнение, называемое уравнением простое гармоническое движение . Это пример секунд Порядок линейного дифференциального уравнения с постоянными коэффициентами . Вот объяснение от человека с американским акцентом.

Мы решаем подобные уравнения, используя свойство экспоненциальной функция, которую мы обнаружили ранее – что это собственных функций оператора дифференцирования.2 = \ pm i \ sqrt {{k \ over m}}. \] Следовательно, решение дифференциального уравнения есть \ [ x = A \ exp \ left (i \ sqrt {{k \ over m}} \ right) + B \ exp \ left (-i \ sqrt {{k \ over m}} \ right), \] для произвольной постоянной \ (A, B \) (определяется начальным условия). Используя уравнения \ [ \ ехр (я \ тета) = \ соз \ тета + я \ грех \ тета, \] мы можем переписать это как \ [\ begin {eqnarray *} x & = & A \ left [\ cos \ left (\ sqrt {{k \ over m}} \ right) + i \ sin \ left (\ sqrt {{k \ over m}} \ right) \ right] + B \ left [\ cos \ left (- \ sqrt {{k \ over m}} \ right) + i \ sin \ left (- \ sqrt {{k \ over m}} \ right) \ right] \\ & = & A \ left [\ cos \ left (\ sqrt {{k \ over m}} \ right) + i \ sin \ left (\ sqrt {{k \ over m}} \ right) \ right] + B \ left [\ cos \ left (\ sqrt {{k \ over m}} \ right) -i \ sin \ left (\ sqrt {{k \ over m}} \ right) \ right] \\ & = & (A + B) \ cos \ left (\ sqrt {{k \ over m}} \ right) + i (AB) \ sin \ left (- \ sqrt {{k \ over m}} \ right) .2 + 2 \ лямбда + 3 = 0, \] с решением \ (\ lambda = -1 \ pm i \ sqrt {2} \). Итак \ (\ lambda_R = -1 \) и \ (\ lambda_I = \ sqrt {2} \). Следовательно, общее решение этого дифференциальное уравнение \ [ y = \ exp (-x) (A \ cos (\ sqrt {2} x) + B \ sin (\ sqrt {2} x)). \] Предположим, что \ (y (0) = 1 \) и \ (y ‘(0) = 0 \). Потом \[ у (0) = А = 1, \] а также \[ y ‘(0) = – A + \ sqrt {2} B = 0, \] так что \ (B = 1 / \ sqrt {2} \). Следовательно, решение в этом случае \ [ y = \ exp (-x) \ left (\ cos (\ sqrt {2} x) + {1 \ over \ sqrt {2}} \ sin (\ sqrt {2} x) \ right).n \), для \ (n \ ge 0 \).

В этом вопросе вы собираетесь приближенно решить дифференциальное уравнение \ (y ‘= y \), \ (y (0) = 2 \), используя предельное определение дифференцирования. Пусть \ (h = 0,1 \). Найдите приблизительное значение \ (y (h) \), используя приближение \ [ {y (h) -y (0) \ over h} = y ‘(0) = y (0), \] где второе уравнение следует из дифференциального уравнения \ (y ‘= y \). Сравните приблизительный ответ с фактическим ответом, аналитически решив дифференциальное уравнение.2} + B {dy \ over dx} + Cy = g (x). \]

Введение в дифференциальные уравнения

Aslak Tveito [1, 2] [1] Исследовательская лаборатория Simula [2] Департамент информатики, Университет Осло
14 июня 2016 г.

Простейший случай
Экспоненциальный рост
Логистический рост
Простой маятник
Модель распространения болезни
Упражнения
Упражнение 1: Решите неоднородное линейное ОДУ
Упражнение 2: Решите нелинейное ОДУ
Упражнение 3: Решите ОДУ для \ (y (x) \)
Упражнение 4: Испытайте нестабильность ODE
Упражнение 5: Решите ODE с изменяющимся во времени ростом
Ссылки
Дифференциальные уравнения оказались чрезвычайно успешными. инструмент для моделирования явлений в науке и технике.Это вряд ли преувеличение, чтобы сказать, что дифференциальные уравнения используются для определить математический модели практически во всех областях естественных наук. В этом документе мы сделаем первые шаги к тому, чтобы научиться справляться с дифференциальной уравнения на компьютере. Это основная проблема в вычислительной науке и выходит далеко за рамки того, что мы можем охватить в этом тексте. Однако идеи, которые вам предстоит см. здесь, повторно используются во многих современных приложениях, поэтому этот документ будет надеюсь предоставить полезное введение в тему, которую вы, вероятно, встречались много раз позже.
Мы покажем вам, как создавать программы для решения дифференциальных уравнения. Точнее, мы покажем, как дифференциальное уравнение может быть сформулированы дискретным образом, подходящим для анализа на компьютере, и как реализовать программы для вычисления дискретных решений. Простейший дифференциальные уравнения могут быть решены аналитически в том смысле, что вы можете запишите явную формулу для решений. Однако дифференциал уравнения, возникающие в практических приложениях, обычно довольно сложные и таким образом, они должны решаться численно на компьютере.Поэтому мы ориентируемся на реализация численных методов решения уравнений. В документе «Программирование обыкновенных дифференциальных уравнений» [1] описывается более продвинутая реализация методы, направленные на создание удобного набора инструментов для решения дифференциальные уравнения. Упражнения в настоящем документе и упомянутый документ стремиться к решению множество дифференциальных уравнений, возникающих в различных дисциплинах науки.
Как и во всех других главах, исходный код может быть находится в каталоге src , точнее в “src / ode1`:” “http: // tinyurl.com / pwyasaa / ode1 “. краткая форма ODE (множественное число: ODE) обычно используется как сокращение для обыкновенных дифференциальное уравнение , которое является типом дифференциального уравнения которые мы рассматриваем в этом документе. На самом деле, дифференциальные уравнения разделены на две группы: обыкновенные дифференциальные уравнения и частные дифференциальные уравнения. Обыкновенные дифференциальные уравнения содержат производные относительно одной переменной (обычно \ (t \) в наших примерах), тогда как частичное дифференциальные уравнения содержат производные по более чем одному переменная, обычно по отношению к пространству и времени. {4} \ tp \ end {выровнять *} $$ Если вы запутались используя \ (t \) и \ (\ tau \), не расстраивайтесь слишком сильно:
По математике вы ничего не понимаю.{n-1} y_ {k} + y_ {n} \ right]. \ end {уравнение *} $$ Программа Integrate_ode.py вычисляет численное решение (3) – (4), где функция \ (f \), время \ (t, \) начальное условие \ (u_ {0} \) и количество временных шагов \ (n \) являются входными данными к программе.
#! / Usr / bin / env python def интегрировать (T, n, u0): h = T / с плавающей запятой (n) t = linspace (0, T, n + 1) I = f (t [0]) для k в iseq (1, n-1, 1): I + = 2 * f (t [k]) I + = f (t [-1]) I * = (ч / 2) I + = u0 вернуться я из scitools.{2}}, \\ и (0) & = 0, \ end {выровнять *} $$ в момент времени \ (T = 2 \) с использованием \ (n = 10,20,50 \) и \ (100 \):

Терминал> python src-ode1 / integration_ode.py 't * exp (t ** 2)' 2 0 10 Численное решение u '(t) = t * exp (t ** 2): 28,4066
Терминал> python src-ode1 / integration_ode.py 't * exp (t ** 2)' 2 0 20 Численное решение u '(t) = t * exp (t ** 2): 27.2060
Терминал> python src-ode1 / integration_ode.py 't * exp (t ** 2)' 2 0 50 Численное решение u '(t) = t * exp (t ** 2): 26,8644
Терминал> python src-ode1 / integration_ode.{\ prime} (t) = f (t) \ tag {7} \ end {уравнение} $$ возникают в ситуациях, когда мы можем явно указать производную от неизвестная функция \ (u. \) Обычно производная определяется через само решение. Рассмотрим, например, рост населения при идеализированном условия. Введем символ \ (v_i \) для количества особей в время \ (\ tau_i \). Базовая модель эволюции \ (v_i \) является: $$ \ begin {уравнение} v_i = (1 + r) v_ {i-1}, \ quad i = 1,2, \ ldots, \ hbox {и} v_0 \ hbox {известное} \ tp \ tag {8} \ end {уравнение} $$ Параметр \ (r \) зависит от разница во времени \ (\ Delta \ tau = \ tau_i- \ tau_ {i-1} \): чем больше \ (\ Delta \ tau \), тем больше \ (r \).Поэтому естественно ввести скорость роста \ (\ alpha \) который не зависит от \ (\ Delta \ tau \): \ (\ alpha = r / \ Delta \ tau \). Число \ (\ alpha \) затем фиксируется независимо от того, как долго прыгает во времени. возьмем разностное уравнение для \ (v_i \). Фактически, \ (\ alpha \) равняется приросту в процентах, деленному на 100, за временной интервал единичной длины.

Теперь разностное уравнение выглядит так: $$ \ begin {уравнение *} v_i = v_ {i-1} + \ alpha \ Delta \ tau \, v_ {i-1} \ tp \ end {уравнение *} $$ Переставляя это уравнение, получаем $$ \ begin {уравнение} {v_i - v_ {i-1} \ over \ Delta \ tau} = \ alpha v_ {i-1} \ tp \ tag {9} \ end {уравнение} $$ Теперь предположим, что мы уменьшили временной шаг \ (\ Delta \ tau \) до небольшого значения.Тогда левая часть (9) представляет собой приближение к производной по времени функции \ (v (\ tau) \), выражающей количество особей в популяции в момент \ (\ tau \). В пределе \ (\ Delta \ tau \ rightarrow 0 \) левая часть становится производная точно, и уравнение читается как $$ \ begin {уравнение} v '(\ тау) = \ альфа v (\ тау) \ tp \ tag {10} \ end {уравнение} $$ Что касается основного разностного уравнения, нам нужно начальное значение \ (v (0) = v_0 \). {\ prime} (t) = u (t) \ tag {11} \ end {уравнение} $$ с начальным условием $$ \ begin {уравнение} и (0) = 1 \ tp \ tag {12} \ end {уравнение} $$ Вычислив безразмерную \ (u (t) \), мы можем найти функцию \ (v (\ tau) \) как $$ \ begin {уравнение *} v (\ tau) = v_0u (\ tau / \ alpha) \ tp \ end {уравнение *} $$ Мы рассмотрим практические приложения уравнений роста населения. позже, но давайте начнем с рассмотрения идеализированный случай (11).

Аналитический раствор

Наше дифференциальное уравнение можно записать в виде $$ \ begin {уравнение *} \ frac {du} {dt} = u, \ end {уравнение *} $$ который можно переписать как $$ \ begin {уравнение *} \ frac {du} {u} = dt, \ end {уравнение *} $$ а затем интегрирование с обеих сторон дает $$ \ begin {уравнение *} \ ln (u) = t + c, \ end {уравнение *} $$ где \ (c \) - константа, которая должна быть определена с использованием начального состояние. Полагая \ (t = 0, \), имеем $$ \ begin {уравнение *} \ ln (и (0)) = с, \ end {уравнение *} $$ следовательно $$ \ begin {уравнение *} с = \ ln (1) = 0, \ end {уравнение *} $$ а потом $$ \ begin {уравнение *} \ ln (u) = t, \ end {уравнение *} $$ так что у нас есть решение $$ \ begin {уравнение} и (т) = е ^ {т} \ tp \ tag {13} \ end {уравнение} $$ Теперь проверим, действительно ли эта функция решает (7) - (11).{t} = u (t), \ end {уравнение *} $$ таким образом, (7) также выполняется.

Численное решение

Мы видели, что можем найти формулу для решения уравнение экспоненциального роста. Итак, проблема решена, и напишите программу для построения графика решения. Однако мы сделаем еще один шаг вперед. и разработать стратегию численного решения этой проблемы. Мы действительно не нужен такой метод для этой проблемы, так как решение доступно в сроках формулы, но, как упоминалось ранее, рекомендуется разрабатывать методы решения проблем, решение которых мы знаем; тогда мы более уверены когда мы сталкиваемся с более серьезными проблемами.{\ prime} (t) = u (t) \ tag {14} \ end {уравнение} $$ с начальным условием $$ \ begin {уравнение} и (0) = 1 \ tp \ tag {15} \ end {уравнение} $$ Мы хотим вычислить приближения от времени \ (t = 0 \) до времени \ (t = 1 \). Позволять \ (n \ geq 1 \) - заданное целое число, и определим $$ \ begin {уравнение} \ Delta t = 1 / n \ tp \ tag {16} \ end {уравнение} $$ Кроме того, пусть \ (u_ {k} \) обозначает приближение к \ (u (t_ {k}) \), где $$ \ begin {уравнение} t_ {k} = k \ Delta t \ tag {17} \ end {уравнение} $$ для \ (k = 0,1, \ ldots, n \). {\ prime} (t_ {k}) \ приблизительно \ frac {u (t_ {k + 1}) - u (t_ {k})} {\ Delta t} \ tp \ tag {19} \ end {уравнение} $$ Используя (14), получаем $$ \ begin {уравнение} \ frac {u (t_ {k + 1}) - u (t_ {k})} {\ Delta t} \ приблизительно u (t_ {k}) \ tp \ tag {20} \ end {уравнение} $$ Напомним теперь, что \ (u (t_ {k}) \) является точным решением в момент времени \ (t_ {k}, \) и что \ (u_ {k} \) - приближенное решение в тот же момент времени.Теперь мы хотим определить \ (u_ {k} \) для всех \ (k \ geq 0. \) Очевидно, мы начнем с определения $$ \ begin {уравнение *} u_ {0} = u (0) = 1. \ end {уравнение *} $$ Поскольку мы хотим, чтобы \ (u_ {k} \ приблизительно u (t_ {k}), \), мы требуем, чтобы \ (u_ {k} \) удовлетворяли следуя равенству $$ \ begin {уравнение} \ frac {u_ {k + 1} -u_ {k}} {\ Delta t} = u_ {k} \ tag {21} \ end {уравнение} $$ мотивировано (20). Следует, что $$ \ begin {уравнение} u_ {k + 1} = (1+ \ Delta t) u_ {k} \ tp \ tag {22} \ end {уравнение} $$ Поскольку \ (u_ {0} \) известен, мы можем вычислить \ (u_ {1}, u_ {2} \) и так далее, используя формула выше.{k} u_0 \ end {уравнение *} $$ для \ (k = 0,1, \ ldots, n \), которые можно вычислить на карманном калькуляторе или даже на свой сотовый телефон. Но опять же, мы показываем примеры, где все как как можно проще (но не проще!), чтобы подготовить свой ум к большему впереди сложные дела.

#! / Usr / bin / env python def compute_u (u0, T, n): "" "Решить u '(t) = u (t), u (0) = u0 для t в [0, T] за n шагов." "" u = u0 dt = T / float (n) для k в диапазоне (0, n, 1): и = (1 + dt) * и return u # u (T) import sys п = int (систем.{1} \ приблизительно2.7183 \), так что приближения снова становятся лучше при увеличении \ (n \).

Альтернативная программа, в которой мы строим \ (u (t) \) и поэтому сохраняем все значения \ (u_k \) и \ (t_k = k \ Delta t \) показаны ниже.

#! / Usr / bin / env python def compute_u (u0, T, n): "" "Решить u '(t) = u (t), u (0) = u0 для t в [0, T] за n шагов." "" t = linspace (0, T, n + 1) t [0] = 0 u = нули (n + 1) u [0] = u0 dt = T / float (n) для k в диапазоне (0, n, 1): u [k + 1] = (1 + dt) * u [k] t [k + 1] = t [k] + dt вернуть u, t из scitools.стандартный импорт * n = int (sys.argv [1]) # Специальный тестовый случай: u '(t) = u, u (0) = 1, t в [0,1] Т = 1; u0 = 1 u, t = compute_u (u0, T, n) сюжет (t, u) tfine = linspace (0, T, 1001) # для точного построения графика v = exp (tfine) # правильное решение Подожди') сюжет (tfine, v) легенда (['Приближенное решение', 'Правильная функция']) title ('Приближенные и правильные дискретные функции, n =% d'% n) savefig ('tmp.pdf')
Используя программу для \ (n = 5,10, 20 \) и \ (100 \), получаем графики на рисунке 1. Сходимость к экспоненциальному функция очевидна из этих графиков.{\ prime} (t) \ приблизительно au (t). \ end {уравнение *} $$ Но по мере увеличения \ (t \) и роста \ (u \) член \ (u (t) / R \) станет важным и ограничить рост.
Численная схема для логистического уравнения (23) дан кем-то $$ \ begin {уравнение *} \ frac {u_ {k + 1} -u_ {k}} {\ Delta t} = \ alpha u_ {k} \ left (1- \ frac {u_ {k}} {R} \ right), \ end {уравнение *} $$ которую мы можем решить относительно неизвестного \ (u_ {k + 1} \): $$ \ begin {уравнение *} u_ {k + 1} = u_ {k} + \ Delta t \ alpha u_ {k} \ left (1- \ frac {u_ {k}} {R} \ right) \ tp \ end {уравнение *} $$ Это форма уравнения, которая подходит для реализации.
До сих пор мы рассматривали скалярные обыкновенные дифференциальные уравнения, т.е. уравнения с одной единственной функцией \ (u (t) \) в качестве неизвестной. Теперь займемся системами обыкновенных дифференциальных уравнений, где, вообще говоря, \ (n \) неизвестные функции связаны в систему \ (n \) уравнения. Наш вводный пример будет системой два уравнения с двумя неизвестными функциями \ (u (t) \) и \ (v (t) \). Пример касается движения маятника, см. Рис. 2. Сфера массой \ (m \) прикреплена к безмассовый стержень длины \ (L \) и колеблется взад и вперед под действием силы тяжести.{\ prime \ prime} (t) + \ alpha \ sin (\ theta) = 0, \ tag {24} \ end {уравнение} $$ где \ (\ theta = \ theta (t) \) - угол, который стержень образует с вертикалью, измеряется в радианах, и \ (\ alpha = g / L \) (\ (g \) - ускорение свободного падения). Неизвестная функция, которую нужно найти, - это \ (\ theta \), и зная \ (\ theta \), мы можем довольно легко вычислить положение сферы, ее скорость, и его ускорение, а также сила натяжения в стержне. Поскольку старшая производная в (24) имеет второй порядок, мы называем (24) дифференциалом второго порядка уравнения .Наши предыдущие примеры в этом документе включали только производные первого порядка, поэтому они известны как дифференциальные уравнения первого порядка .
Рисунок 2: Маятник с массой \ (m = \), длиной безмассового стержня \ (L = \) и углом \ (\ theta = \ theta (t) = \).
Мы не решает второй порядок уравнение (24) в его нынешнем виде. Мы должны вместо этого перепишите его как систему двух уравнений первого порядка так, чтобы мы можем использовать численные методы для уравнения первого порядка для его решения.
Чтобы преобразовать уравнение второго порядка в систему двух уравнений, введем новую переменную для производной первого порядка (угловая скорость шара): \ (v (t) = \ theta '(t) \). Использование \ (v \) и \ (\ theta \) в (24) дает $$ \ begin {уравнение *} v '(t) + \ alpha \ sin (\ theta) = 0 \ tp \ end {уравнение *} $$ Кроме того, имеется соотношение $$ \ begin {уравнение *} v = \ theta '(t) \ end {уравнение *} $$ между \ (v \) и \ (\ theta \). {\ prime} (t) & = - \ alpha \ sin (\ theta) \ tp \ tag {26} \ end {align} $$ Что касается скалярных дифференциальных уравнений, нам потребуются начальные условия, теперь два условия, потому что у нас есть две неизвестные функции: $$ \ begin {align *} \ theta (0) & = \ theta_ {0}, \\ v (0) & = v_ {0}, \ end {выровнять *} $$ Здесь мы предполагаем начальный угол \ (\ theta_ {0} \) и начальный угол угловая скорость \ (v_ {0} \) должна быть задана.
Обычно неизвестные и начальные условия группируются в 2-векторах: \ ((\ theta (t), v (t)) \) и \ ((\ theta_0, v_0) \). Тогда можно рассматривать (25) - (26) как векторное уравнение , уравнение первого компонента которого имеет вид (25), а второе компонентное уравнение имеет вид (26). В программном обеспечении Python эта векторная запись делает методы решения скалярных уравнений (почти) доступны сразу для векторных уравнений, т. е. систем обыкновенных дифференциальных уравнений.
Чтобы получить численный метод для системы (25) - (26), поступаем так же, как и выше, для одного уравнения с одной неизвестной функцией.Скажем, мы хотим для вычисления решения от \ (t = 0 \) до \ (t = T \), где задано \ (T> 0 \). Позволять \ (n \ geq 1 \) - заданное целое число и определить временной шаг $$ \ begin {уравнение *} \ Delta t = T / n. \ end {уравнение *} $$ Кроме того, мы обозначаем \ ((\ theta_ {k}, v_ {k}) \) приближения точных решение \ ((\ theta (t_ {k}), v (t_ {k})) \) для \ (k = 0,1, \ ldots, n \). А Метод прямого Эйлера теперь будет читать $$ \ begin {align} \ frac {\ theta_ {k + 1} - \ theta_ {k}} {\ Delta t} & = v_ {k}, \ tag {27} \\ \ frac {v_ {k + 1} -v_ {k}} {\ Delta t} & = - \ alpha \ sin (\ theta_ {k}) \ tp \ tag {28} \ end {align} $$ Эту схему можно переписать в более удобном для реализации виде: $$ \ begin {align} \ theta_ {k + 1} & = \ theta_ {k} + \ Delta t \, v_ {k}, \ tag {29} \\ v_ {k + 1} & = v_ {k} - \ alpha \ Delta t \ sin (\ theta_ {k}) \ tp \ tag {30} \ end {align} $$ Следующая программа, маятник.ру реализует этот метод в функции маятник . Входные параметры модели, \ (\ theta_ {0} \), \ (v_ {0}, \), конечное время \ (T \) и количество временных шагов \ (n \), необходимо указать в командной строке.
#! / Usr / bin / env python маятник def (T, n, theta0, v0, alpha): "" "Вернуть движение (тета, v, t) маятника." "" dt = T / float (n) t = linspace (0, T, n + 1) v = нули (n + 1) тета = нули (n + 1) v [0] = v0 тета [0] = тета0 для k в диапазоне (n): тета [k + 1] = тета [k] + dt * v [k] v [k + 1] = v [k] - альфа * dt * sin (тета [k + 1]) вернуть тета, v, t из scitools.стандартный импорт * n = int (sys.argv [1]) T = eval (sys.argv [2]) v0 = eval (sys.argv [3]) theta0 = eval (sys.argv [4]) альфа = eval (sys.argv [5]) theta, v, t = маятник (T, n, theta0, v0) plot (t, v, xlabel = 't', ylabel = 'speed') фигура() plot (t, theta, xlabel = 't', ylabel = 'speed')
Запустив программу с входными данными \ (\ theta_ {0} = \ pi / 6 \), \ (v_ {0} = 0 \), \ (\ alpha = 5 \), \ (T = 10 \) и \ (n = 1000 \), мы получаем результаты, показанные на рисунке 3. Угол \ (\ theta = \ theta (t) \) отображается на левой панели, а скорость указана на правой панели.
Рисунок 3: График движения маятника. Слева: угол \ (\ theta (t) \). Справа: угловая скорость \ (\ theta '\).
Математические модели интенсивно используются для анализа распространения инфекционные заболевания. В простейшем случае мы можем рассматривать население, которое предполагается постоянным, состоящее из двух групп; восприимчивые \ ((S) \), которые могут заразиться, и инфекционные \ ((I) \), у которых есть болезнь и которые могут ее передать.{\ prime} & = rSI-aI \ tp \ tag {32} \ end {align} $$ Здесь \ (r \) и \ (a \) - заданные константы, отражающие характеристики эпидемия. Начальные условия даются $$ \ begin {align *} S (0) & = S_ {0}, \\ I (0) & = I_ {0}, \ end {выровнять *} $$ где предполагается, что начальное состояние \ ((S_ {0}, I_ {0}) \) известно.
Предположим, мы хотим вычислить численные решения этой системы по времени \ (t = 0 \) to \ (t = T. \) Затем, рассуждая, как указано выше, введем шаг по времени $$ \ begin {уравнение *} \ Delta t = T / n \ end {уравнение *} $$ и приближения \ ((S_ {k}, I_ {k}) \) решения \ ((S (t_ {k}), I (t_ {k})).\) Явный прямой метод Эйлера для системы имеет следующий вид: $$ \ begin {align *} \ frac {S_ {k + 1} -S_ {k}} {\ Delta t} & = -rS_ {k} I_ {k}, \\ \ frac {I_ {k + 1} -I_ {k}} {\ Delta t} & = rS_ {k} I_ {k} -aI_ {k}, \ end {выровнять *} $$ который можно переписать в вычислительной форме $$ \ begin {align *} S_ {k + 1} & = S_ {k} - \ Delta trS_ {k} I_ {k}, \\ I_ {k + 1} & = I_ {k} + \ Delta t \ left (rS_ {k} I_ {k} -aI_ {k} \ right) \ tp \ end {выровнять *} $$ Эта схема реализована в программе exp_epidemic.py, где \ (r, a, S_ {0}, I_ {0}, n \) и \ (T \) - входные данные, указанные в командной строке.Функция epidemic вычисляет решение \ ((S, I) \) для система дифференциальных уравнений. Эта пара зависящих от времени функции затем строятся на двух отдельных участках.
#! / Usr / bin / env python def эпидемии (T, n, S0, I0, r, a): dt = T / float (n) t = linspace (0, T, n + 1) S = нули (n + 1) I = нули (n + 1) S [0] = S0 I [0] = I0 для k в диапазоне (n): S [k + 1] = S [k] - dt * r * S [k] * I [k] I [k + 1] = I [k] + dt * (r * S [k] * I [k] - a * I [k]) возврат S, I, t из scitools.стандартный импорт * n = int (sys.argv [1]) T = eval (sys.argv [2]) S0 = eval (sys.argv [3]) I0 = eval (sys.argv [4]) r = eval (sys.argv [5]) a = eval (sys.argv [6]) S, I, t = эпидемия (T, n, S0, I0, r, a) plot (t, S, xlabel = 't', ylabel = 'Susceptibles') plot (t, I, xlabel = 't', ylabel = 'Infectives')
Мы хотим применить программу к конкретному случаю, когда произошла эпидемия гриппа. британская школа-интернат, в которой учится \ (763 \) мальчика. (Данные взяты из Мюррея [2], и Мюррей нашел данные в Британский медицинский журнал, 4 марта 1978 г.{-3}, a = 0,44, n = 1000 \). Кроме того, мы построили реальные графики измерений, и отметим, что моделирование достаточно хорошо соответствует реальным данным.
Рисунок 4: Графики восприимчивых (слева) и инфекционных (справа) возбудителей гриппа в британской школе-интернате в 1978 г.
Читатель, интересующийся математическими моделями распространения инфекционные заболевания могут проконсультироваться с отличным книга [2] по математической биологии Дж. {\ prime} = 2u-1, \ quad u (0) = 2, \ quad t \ in [0,6] \ end {уравнение *} $$ с использованием метода прямого Эйлера.{1 / (1-q)} \) для \ (q> 1 \) и \ (t (1-q) +1> 0 \). Прочтите \ (q \), \ (\ Delta t \) и \ (T \) из командной строки, решите ОДУ, и построить численное и точное решение. Запустите программу для разных случаев: \ (q = 2 \) и \ (q = 3 \), с \ (\ Delta t = 0,01 \) и \ (\ Delta t = 0,1 \). Установите \ (T = 6 \), если \ (q = 1 \) и \ (T = 1 / (q-1) -0.1 \) в противном случае. Имя файла: nonlinear_ODE .
Упражнение 3. Решите ОДУ для \ (y (x) \)
Мы поставили следующую задачу ODE: $$ \ begin {уравнение} {dy \ over dx} = {1 \ over 2 (y-1)}, \ quad y (0) = 1 + \ sqrt {\ epsilon}, \ quad x \ in [0,4], \ tag {33} \ end {уравнение} $$ где \ (\ epsilon> 0 \) - небольшое число.{(a-bT / 2) t} \). Имя файла: time_dep_growth .
Х. П. Лангтанген . Программирование обыкновенных дифференциальных уравнений, \ emphhttp: //hplgit.github.io/primer.html/doc/pub/ode2, http://hplgit.github.io/primer.html/doc/pub/ode2.
Дж. Д. Мюррей . Математическая биология I: Введение , 3-е издание, Спрингер, 2007.
Решение систем линейных дифференциальных уравнений методом исключения
Решение дифференциальных уравнений
Теперь, разобравшись с основными терминами, приступим к решению! Предположим, у нас есть две зависимые переменные x и y , представляющие популяцию криля и яков.Представьте себе скорость изменения яков d x / d t , отрицательно зависящую от количества крилей. Точно так же в этом гипотетическом мире скорость изменения криля, d y / d t , отрицательно зависит от количества яков. Таким образом, наша гипотетическая связанная система линейных дифференциальных уравнений:
Два неизвестных и два уравнения предлагают метод исключения из алгебры. Как мы увидим, запись d x / d t как D x выглядит так, как будто D умножает x .D, однако, является оператором на x , где операция дифференцирования. На самом деле, даже умножение, такое как 4 умножение x на 4 x , является 4, действующим на x .
Переходим к системе криль-як!
Шаг 1. Используйте обозначение D для производной.
Заменить d x / d t на D x и d y / d t на D y :
Шаг 2. Составьте уравнения.
Положив сначала x , мы получим следующее изменение:
Шаг 3: Решить путем исключения.
Умножая уравнение 2 на D, получаем:
Умножая уравнение 1 на 4, получаем:
Как вы можете видеть здесь, теперь мы исключаем 4D x из уравнения:
Вычитая одно уравнение из другого, мы удалили 4D x .
Шаг 4: Решите дифференциальное уравнение.
Как решить это уравнение?
Сначала пусть y = e на .
Используя оператор дифференцирования D для y , мы имеем y = a e at .
Это дает нам D2 y = a 2 e at .
Подставляя в -36 y + D2 y = 0, получаем:
-36e at + a 2 e at = 0.
Разделив на "есть", мы получим:
-36 + a 2 = 0.
Решив относительно a , мы получим:
a = ± 6.
Таким образом:
y = c 1 e6 t + c 2 e-6 t .
Шаг 5: Используя исключение, найдите другие переменные.
Это повторение шага 3, но y исключены.
Умножение уравнения 1 на D:
Умножение уравнения 2 на 9:
Удаление 9D y дает -36 x + D2 x = 0.
Форма этого уравнения в x такая же, как и для y . Таким образом, решения для x и y одинаковы, за исключением индексов у констант:
x = c 3 e6 t + c 4 e-6 t .
Шаг 6: Используя начальные условия, найдите константы.
Начальные условия - это переменная и значения ее первой производной в момент времени t = 0.
Представьте себе в начале, y = 0 и d y / d t = 12.
Подставив t = 0 в это
получаем это:
Поскольку, e0 = 1,
y = ( c 1) 1 + ( c 2) 1.
В момент времени t = 0, y = 0.
Таким образом:
c 1 + c 2 = 0.
Теперь для начального состояния на d y / d t , которое вы можете увидеть здесь:
При t = 0 получается следующее:
В момент времени t = 0, d y / d t = 12:
6 c 1 - 6 c 2 = 12.
Разделив на 6, получим:
c 1 - c 2 = 2.
Отлично! Два уравнения и два неизвестных:
c 1 + c 2 = 0
c 1 - c 2 = 2
Решая для c 1 и c 2, получаем:
c 1 = 1 и c 2 = -1.
Таким образом:
Решение для y используется для нахождения c 3 и c 4 в решении x .
Разделите решение для x и подставьте в уравнение 1, D x = -9 y , которое вы можете увидеть здесь:
Приравнивая члены e6 t , получаем:
6 c 3 = -9 или c 3 = -3/2.
Приравнивая члены e-6 t , получаем:
-6 c 4 = 9 или c 4 = -3/2.
Таким образом:
Шаг 7. Проверьте решение.
Если выражения для x и y верны, обратная подстановка в исходную систему уравнений делает эти уравнения истинными.
Мы собираемся проверить, удовлетворяется ли исходная гипотетическая связанная система этими значениями x и y .
и
удовлетворяет
У нас есть LHS (левая сторона):
Упрощение до:
-9e6 t + 9e-6 t .
И у нас есть наша правая часть (правая часть), в которую мы подставляем -9 y , чтобы получить:
-9e6 t + 9e-6 t .
Проверить!
Для второго уравнения:
LHS: d y / d t = 6e6 t + 6e-6 t .
RHS: замените -4 x , чтобы получить
, что упрощается до
6e6 t + 6e-6 t .
Отлично, мы получили!
Шаг 8: Постройте и прокомментируйте решение:
Сюжет решений
График популяции криля x показывает начальное состояние x = 0 и положительный наклон. Это население растет в геометрической прогрессии. Популяция яков, y , с другой стороны, начинается с -3 (мы не уверены, как будут функционировать яки с популяцией -3), с наклоном 0 и продолжает экспоненциально уменьшаться.
Конечно, эта связь между яком и крилем чисто гипотетическая. Естественные хищники криля - тюлени, киты, пингвины, а не яки. Тем не менее, график показывает решение, согласующееся с уравнениями и начальными условиями, и это самое главное!
Резюме урока
Хорошо, давайте уделим пару минут, чтобы повторить, так как это было совсем немного! Как мы узнали, дифференциальное уравнение просто содержит производные. Мы также узнали, что если нет произведений зависимых переменных и если все производные и зависимые переменные возведены в первую степень, то дифференциальное уравнение будет линейным .С двумя или более уравнениями это система , а когда разные зависимые переменные появляются в одном и том же уравнении, система связана .
Это аналог систем уравнений, встречающихся в алгебре. Чтобы решить систему дифференциальных уравнений, воспользуйтесь методом исключения алгебры. Производные, такие как d x / d t , записываются как D x , а оператор D рассматривается как постоянная умножения.
Методом исключения система дифференциальных уравнений сводится к одному дифференциальному уравнению с одной переменной.Для решения этого дифференциального уравнения используются стандартные методы. Результирующее решение содержит неизвестные константы, определенные с использованием начальных условий , которые являются переменными и значениями их первой производной в момент времени t = 0. Процесс исключения переменных, решения дифференциального уравнения и поиска значений для констант повторяется. пока не будут решены все зависимые переменные.
Как решать дифференциальные уравнения
Нелинейные уравнения первого порядка. В этом разделе мы обсуждаем методы решения некоторых нелинейных дифференциальных уравнений первого порядка. Общего решения в замкнутой форме не существует, но некоторые уравнения можно решить, используя описанные ниже методы. ^[3] dydx = е (x, y) {\ displaystyle {\ frac {\ mathrm {d} y} {\ mathrm {d} x}} = f (x, y)}
dydx = h (x) g (y). {\ Displaystyle {\ frac {\ mathrm {d} y} {\ mathrm {d} x}} = h (x) g (y).} Если функция f (x, y) = h (x) g (y) {\ displaystyle f (x, y) = h (x) g (y)} можно разделить на функции, каждая из которых имеет одну переменную, тогда уравнение называется отделяемое.{4}) + C \ end {align}}}
dydx = г (x, y) час (x, y). {k} g (x, y) ,} где k {\ displaystyle k} называется степенью однородности.{1-n} + (1-n) q (x)}
M (x, y) + N (x, y) dydx = 0. {\ Displaystyle M (x, y) + N (x, y) {\ frac {\ mathrm {d} y} {\ mathrm { d} x}} = 0.} Здесь мы обсуждаем точных уравнений. Мы хотим найти функцию φ (x, y), {\ displaystyle \ varphi (x, y),}, называемую потенциальной функцией , такую, что dφdx = 0. {\ Displaystyle {\ frac {\ mathrm {d } \ varphi} {\ mathrm {d} x}} = 0.}
Для выполнения этого условия у нас есть следующая полная производная . Полная производная допускает дополнительные зависимости переменных.Чтобы вычислить полную производную φ {\ displaystyle \ varphi} по x, {\ displaystyle x,} мы допускаем возможность того, что y {\ displaystyle y} может также зависеть от x. {\ Displaystyle x.}
dφdx = ∂φ∂x + ∂φ∂ydydx {\ displaystyle {\ frac {\ mathrm {d} \ varphi} {\ mathrm {d} x}} = {\ frac {\ partial \ varphi} {\ partial x }} + {\ frac {\ partial \ varphi} {\ partial y}} {\ frac {\ mathrm {d} y} {\ mathrm {d} x}}}
Сравнивая термины, у нас есть M (x, y) = ∂φ∂x {\ displaystyle M (x, y) = {\ frac {\ partial \ varphi} {\ partial x}}} и N (x, y) = ∂φ∂y.{\ displaystyle N (x, y) = {\ frac {\ partial \ varphi} {\ partial y}}.} Это стандартный результат многомерного исчисления, что смешанные производные для гладких функций равны друг другу. Иногда это называют теоремой Клеро . Дифференциальное уравнение является точным, если выполняется следующее условие.
∂M∂y = ∂N∂x {\ displaystyle {\ frac {\ partial M} {\ partial y}} = {\ frac {\ partial N} {\ partial x}}}
Метод решения точных уравнений аналогичен поиску потенциальных функций в многомерном исчислении, который мы очень скоро рассмотрим.Сначала мы интегрируем M {\ displaystyle M} относительно x. {\ Displaystyle x.} Поскольку M {\ displaystyle M} является функцией как x {\ displaystyle x}, так и y, {\ displaystyle y,}, интегрирование может только частично восстановить φ, {\ displaystyle \ varphi,} который термин φ ~ {\ displaystyle {\ tilde {\ varphi}}} призван напомнить читателю. Также существует постоянная интегрирования, которая является функцией y. {\ Displaystyle y.}
φ (Икс, Y) знак равно ∫M (Икс, Y) dx = φ ~ (Икс, Y) + с (Y) {\ Displaystyle \ varphi (х, у) = \ Int M (х, у) \ mathrm {d} x = {\ tilde {\ varphi}} (x, y) + c (y)}
Затем мы берем частную производную нашего результата по y, {\ displaystyle y,} сравниваем члены с N (x, y), {\ displaystyle N (x, y),} и интегрируем, чтобы получить c (y) .{\ displaystyle c (y).} Мы также можем начать с интегрирования N {\ displaystyle N}, а затем взять частную производную нашего результата по x {\ displaystyle x}, чтобы найти произвольную функцию d (x) . {\ displaystyle d (x).} Подойдет любой метод, и обычно выбирается более простая функция для интегрирования.
N (x, y) = ∂φ∂y = ∂φ ~ ∂y + dcdy {\ displaystyle N (x, y) = {\ frac {\ partial \ varphi} {\ partial y}} = {\ frac {\ partial {\ tilde {\ varphi}}} {\ partial y}} + {\ frac {\ mathrm {d} c} {\ mathrm {d} y}}}
Пример 1.{2} = C}
Если наше дифференциальное уравнение не является точным, то в некоторых случаях мы можем найти интегрирующий коэффициент, который делает его точным.

определение и примеры с решением

Простейшие дифференциальные уравнения первого порядка

Уравнения в полных дифференциалах

Интегрирующий множитель

Алгоритм решения

Уравнения с разделяющимися переменными

Пример дифференциального уравнения

Видеоурок “Простейшие дифференциальные уравнения” для 11 класса

Линейные и однородные дифференциальные уравнения первого порядка. Примеры решения

Что такое дифференциальные уравнения?

Дифференциал

Производная

Интеграл

Классы дифференциальных уравнений

Уравнения с разделяющимися переменными

Однородные дифференциальные уравнения первого порядка

Линейные дифференциальные уравнения первого порядка

Где используются дифференциальные уравнения?

Как дифференциальные уравнения помогут в жизни?

Основные проблемы при изучении

Что ещё можно изучить для лучшего понимания?

Заключение

несколько простых примеров из Physclips

Методы решения дифференциальных уравнений

Пример 1: Экспоненциальный рост и спад

Экспоненциальное уменьшение

Пример 2: Простое гармоническое движение

Затухающие и вынужденные колебания

Уравнения в частных производных: волновое уравнение

Глава 6 Дифференциальные уравнения | Исчисление и анализ

Введение

Культурное наследие математики

Разделимые уравнения

Линейные уравнения первого порядка

Однородные уравнения

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Введение в дифференциальные уравнения

14 июня 2016 г.

Аналитический раствор

Численное решение

Упражнение 3. Решите ОДУ для \ (y (x) \)

Решение систем линейных дифференциальных уравнений методом исключения

Решение дифференциальных уравнений

Шаг 1. Используйте обозначение D для производной.

Шаг 2. Составьте уравнения.

Шаг 3: Решить путем исключения.

Шаг 4: Решите дифференциальное уравнение.

Шаг 5: Используя исключение, найдите другие переменные.

Шаг 6: Используя начальные условия, найдите константы.

Шаг 7. Проверьте решение.

Шаг 8: Постройте и прокомментируйте решение:

Резюме урока

Как решать дифференциальные уравнения

Оставить комментарий Отменить ответ