Решение систем линейных однородных уравнений методом гаусса: Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Пример решения однородной системы линейных уравнений. Как найти нетривиальное и фундаментальное решение системы линейных однородных уравнений. Алгоритм решения систем линейных однородных уравнений

Однородная система всегда совместна и имеет тривиальное решение
. Для существования нетривиального решения необходимо, чтобы ранг матрицыбыл меньше числа неизвестных:

Фундаментальной системой решений однородной системы
называют систему решений в виде векторов-столбцов
, которые соответствуют каноническому базису, т.е. базису, в котором произвольные постоянные
поочередно полагаются равными единице, тогда как остальные приравниваются нулю.

Тогда общее решение однородной системы имеет вид:

где
– произвольные постоянные. Другими словами, общее решение есть линейная комбинация фундаментальной системы решений.

Таким образом, базисные решения могут быть получены из общего решения, если свободным неизвестным поочередно придавать значение единицы, полагая все остальные равные нулю.

Пример . Найдем решение системы

Примем , тогда получим решение в виде:

Построим теперь фундаментальную систему решений:

Общее решение запишется в виде:

Решения системы однородных линейных уравнений имеют свойства:

Другими словами, любая линейная комбинация решений однородной системы есть опять решение.

Решение систем линейных уравнений методом Гаусса

Решение систем линейных уравнений интересует математиков несколько столетий. Первые результаты были получены в XVIII веке. В 1750 г. Г.Крамер (1704 –1752) опубликовал свои труды по детерминантам квадратных матриц и предложил алгоритм нахождения обратной матрицы. В 1809 г. Гаусс изложил новый метод решения, известный как метод исключения.

Метод Гаусса, или метод последовательного исключения неизвестных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида.

Такие системы позволяют последовательно находить все неизвестные в определенном порядке.

Предположим, что в системе (1)
(что всегда возможно).

(1)

Умножая поочередно первое уравнение на так называемые подходящие числа

и складывая результат умножения с соответствующими уравнениями системы, мы получим эквивалентную систему, в которой во всех уравнениях, кроме первого, будет отсутствовать неизвестная

х 1

(2)

Умножим теперь второе уравнение системы (2) на подходящие числа, полагая, что

и складывая его с нижестоящими, исключим переменную из всех уравнений, начиная с третьего.

Продолжая этот процесс, после
шага мы получим:

(3)

Если хотя бы одно из чисел
не равно нулю, то соответствующее равенство противоречиво и система (1) несовместна. Обратно, для любой совместной системы числа
равны нулю. Число- это ни что иное, как ранг матрицы системы (1).

Переход от системы (1) к (3) называется прямым ходом метода Гаусса, а нахождение неизвестных из (3) –

обратным ходом .

Замечание : Преобразования удобнее производить не с самими уравнениями, а с расширенной матрицей системы (1).

Пример . Найдем решение системы

Запишем расширенную матрицу системы:

Прибавим к строкам 2,3,4 первую, умноженную на (-2), (-3), (-2) соответственно:

Поменяем строки 2 и 3 местами, затем в получившейся матрице добавим к строке 4 строку 2, умноженную на :

Прибавим к строке 4 строку 3, умноженную на
:

Очевидно, что
, следовательно, система совместна. Из полученной системы уравнений

находим решение обратной подстановкой:

,
,
,
.

Пример 2. Найти решение системы:

Очевидно, что система несовместна, т.к.
, а
.

Достоинства метода Гаусса :

Менее трудоемкий, чем метод Крамера.

Однозначно устанавливает совместность системы и позволяет найти решение.

Дает возможность определить ранг любых матриц.

Мы продолжим шлифовать технику элементарных преобразований на однородной системе линейных уравнений .
По первым абзацам материал может показаться скучным и заурядным, однако данное впечатление обманчиво. Помимо дальнейшей отработки технических приёмов будет много новой информации, поэтому, пожалуйста, постарайтесь не пренебрегать примерами данной статьи.

Что такое однородная система линейных уравнений?

Ответ напрашивается сам собой. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:

Совершенно ясно, что однородная система всегда совместна , то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое тривиальное решение . Тривиальное, для тех, кто совсем не понял смысл прилагательного, значит, беспонтовое. Не академично, конечно, но зато доходчиво =) …Чего ходить вокруг да около, давайте выясним, нет ли у данной системы каких-нибудь других решений:

Пример 1

Решение : чтобы решить однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:

(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3.

(2) К третьей строке прибавили вторую строку, умноженную на –1.

Делить третью строку на 3 не имеет особого смысла.

В результате элементарных преобразований получена эквивалентная однородная система , и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.

Ответ :

Сформулируем очевидный критерий : однородная система линейных уравнений имеет только тривиальное решение , если ранг матрицы системы (в данном случае 3) равен количеству переменных (в данном случае – 3 шт.).

Разогреваемся и настраиваем свой радиоприёмник на волну элементарных преобразований:

Пример 2

Решить однородную систему линейных уравнений

Чтобы окончательно закрепить алгоритм, разберём финальное задание:

Пример 7

Решить однородную систему, ответ записать в векторной форме.

Решение : запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) У первой строки сменили знак. Ещё раз заостряю внимание на неоднократно встречавшемся приёме, который позволяет существенно упростить следующее действие.

(1) Ко 2-й и 3-й строкам прибавили первую строку. К 4-й строке прибавили первую строку, умноженную на 2.

(3) Последние три строки пропорциональны, две из них удалили.

В результате получена стандартная ступенчатая матрица, и решение продолжается по накатанной колее:

– базисные переменные;
– свободные переменные.

Выразим базисные переменные через свободные переменные. Из 2-го уравнения:

– подставим в 1-е уравнение:

Таким образом, общее решение:

Поскольку в рассматриваемом примере три свободные переменные, то фундаментальная система содержит три вектора.

Подставим тройку значений в общее решение и получим вектор , координаты которого удовлетворяют каждому уравнению однородной системы.

И снова повторюсь, что крайне желательно проверять каждый полученный вектор – времени займет не так много, а от ошибок убережёт стопроцентно.

Для тройки значений находим вектор

И, наконец, для тройки получаем третий вектор:

Ответ : , где

Желающие избежать дробных значений могут рассмотреть тройки и получить ответ в эквивалентном виде:

К слову о дробях. Посмотрим на полученную в задаче матрицу и зададимся вопросом – нельзя ли упростить дальнейшее решение? Ведь здесь мы сначала выразили через дроби базисную переменную , потом через дроби базисную переменную , и, надо сказать, процесс это был не самый простой и не самый приятный.

Второй вариант решения :

Идея состоит в том, чтобы попытаться выбрать другие базисные переменные . Посмотрим на матрицу и заметим две единицы в третьем столбце. Так почему бы не получить ноль вверху? Проведём ещё одно элементарное преобразование:

Вы можете заказать подробное решение вашей задачи !!!

Чтобы понять, что такое фундаментальная система решений вы можете посмотреть видео-урок для этого же примера кликнув . Теперь перейдем собственно к описанию всей необходимой работы. Это поможет вам более детально разобраться в сути данного вопроса.

Как найти фундаментальную систему решений линейного уравнения?

Возьмём для примера такую систему линейных уравнений:

Найдём решение этой линейной системы уравнений . Для начала нам надо выписать матрицу коэффициентов системы.

Преобразуем эту матрицу к треугольной. Первую строку переписываем без изменений. И все элементы, что стоят под $a_{11}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{21}$, надо от второй строки вычесть первую, и разность записать во второй строке. Что бы сделать ноль в место элемента $a_{31}$, надо от третьей строки вычесть первую и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{41}$, надо от четвёртой строки вычесть первую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{31}$, надо от пятой строки вычесть первую умноженную на 2 и разность записать в пятой строке.

Первую и вторую строку переписываем без изменений. И все элементы, что стоят под $a_{22}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{32}$, надо от третьей строки вычесть вторую умноженную на 2 и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{42}$, надо от четвёртой строки вычесть вторую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{52}$, надо от пятой строки вычесть вторую умноженную на 3 и разность записать в пятой строке.

Видим, что последние три строки – одинаковые , поэтому если от четвёртой и пятой вычесть третью, то они станут нулевыми.

По этой матрице записываем новую систему уравнений .

Видим, что линейно независимых уравнений у нас, только три, а неизвестных пять, поэтому фундаментальная система решений будет состоять из двух векторов . Значит, нам надо перенести две последние неизвестные вправо .

Теперь, начинаем выражать те неизвестные, что стоят в левой части через те, что стоят в правой части. Начинаем с последнего уравнения, сначала выразим $x_3$, потом полученный результат подставим во второе уравнение и выразим $x_2$, а потом в первое уравнение и тут выразим $x_1$. Таким образом мы все неизвестные, что стоят в левой части, выразили через неизвестные, что стоят в правой части.

После чего вы вместо $x_4$ и $x_5$, можем подставлять любые числа и находить $x_1$, $x_2$ и $x_3$. Каждая такая пятёрка чисел будет корнями нашей изначальной системы уравнений. Что бы найти векторы, что входят в ФСР нам надо вместо $x_4$ подставить 1, а вместо $x_5$ подставить 0, найти $x_1$, $x_2$ и $x_3$, а потом наоборот $x_4=0$ и $x_5=1$.

Системы линейных однородных уравнений – имеет вид ∑a k i x i = 0. где m > n или m Однородная система линейных уравнений всегда совместна, так как rangA = rangB . Она заведомо имеет решение, состоящее из нулей, которое называется тривиальным .

Назначение сервиса . Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).

Инструкция . Выберите размерность матрицы:

Свойства систем линейных однородных уравнений

Для того чтобы система имела нетривиальные решения , необходимо и достаточно, чтобы ранг ее матрицы был меньше числа неизвестных.

Теорема . Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.

Теорема . Любая линейная комбинация решений системы также является решением этой системы.
Определение . Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений , если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.

Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из (n-r) решений.

Алгоритм решения систем линейных однородных уравнений

Находим ранг матрицы.
Выделяем базисный минор. Выделяем зависимые (базисные) и свободные неизвестные.
Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора, так как они являются следствиями остальных (по теореме о базисном миноре).
Члены уравнений, содержащие свободные неизвестные, перенесем в правую часть. В результате получим систему из r уравнений с r неизвестными, эквивалентную данной, определитель которой отличен от нуля.
Решаем полученную систему методом исключения неизвестных. Находим соотношения, выражающие зависимые переменные через свободные.
Если ранг матрицы не равен количеству переменных, то находим фундаментальное решение системы.
В случае rang = n имеем тривиальное решение.

Пример . Найти базис системы векторов (а 1 , а 2 ,…,а m), ранг и выразить векторы по базе. Если а 1 =(0,0,1,-1), а 2 =(1,1,2,0), а 3 =(1,1,1,1), а 4 =(3,2,1,4), а 5 =(2,1,0,3).
Выпишем основную матрицу системы:

Умножим 3-ую строку на (-3).

Добавим 4-ую строку к 3-ой:

0	0	1	-1
0	0	-1	1
0	-1	-2	1
3	2	1	4
2	1	0	3

Умножим 4-ую строку на (-2). Умножим 5-ую строку на (3). Добавим 5-ую строку к 4-ой:
Добавим 2-ую строку к 1-ой:
Найдем ранг матрицы.
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
– x 3 = – x 4
– x 2 – 2x 3 = – x 4
2x 1 + x 2 = – 3x 4
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x 1 ,x 2 ,x 3 через свободные x 4 , то есть нашли общее решение:
x 3 = x 4
x 2 = – x 4
x 1 = – x 4

Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A .

Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

Тогда n – r линейно независимыми вектор-решениями будут:

а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.

В линейном пространстве множество решений однородной системы линейных уравнений образует подпространство размерности n – r ; – базис этого подпространства.

Система m линейных уравнений с n неизвестными (или, линейная система

Здесь x 1 , x 2 , …, x n a 11 , a 12 , …, a mn – коэффициенты системы – иb 1 , b 2 , … b m a ij i ) и неизвестного (j

Система (1) называется однородной b 1 = b 2 = … = b m = 0), иначе –неоднородной .

Система (1) называется квадратной , если число m уравнений равно числу n неизвестных.

Решение системы (1) – совокупность n чисел c 1 , c 2 , …, c n , таких что подстановка каждого c i вместо x i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной несовместной

Решения c 1 (1) , c 2 (1) , …, c n (1) и c 1 (2) , c 2 (2) , …, c n различными

c 1 (1) = c 1 (2) , c 2 (1) = c 2 (2) , …, c n (1) = c n (2) .

определённой неопределённой . Если уравнений больше, чем неизвестных, она называется переопределённой .

Решение систем линейных уравнений

Решение матричных уравнений ~ Метод Гаусса

Способы решения систем линейных уравнений делятся на две группы:

1. точные методы , представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, правило Крамера, метод Гаусса и др.),

2. итерационные методы , позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации, метод Зейделя и др.).

Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода.

Эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.

Решение матричных уравнений

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х 1 , х 2 , …, х n :

(15)

Матрица А , столбцами которой являются коэффициенты при соответствующих неизвестных, а строками – коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы ; матрица-столбец b , элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы .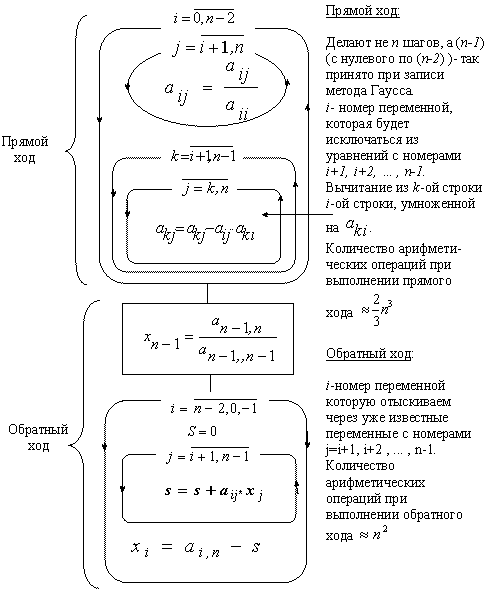 Матрица-столбец х , элементы которой – искомые неизвестные, называется решением системы .

Если матрица А – неособенная, то есть det A н е равен 0 то система (13), или эквивалентное ей матричное уравнение (14), имеет единственное решение.

В самом деле, при условии det A не равно 0 существует обратная матрица А -1 . Умножая обе части уравнения (14) на матрицу А -1 получим:

Формула (16) дает решение уравнения (14) и оно единственно.

Системы линейных уравнений удобно решать с помощью функции lsolve .

lsolve(А, b )

Возвращается вектор решения x такой, что Ах = b.

Аргументы:

А – квадратная, не сингулярная матрица.

b – вектор, имеющий столько же рядов, сколько рядов в матрице А .

На Рисунке 8 показано решение системы трех линейных уравнений относительно трех неизвестных.

Метод Гаусса

Метод Гаусса, его еще называют методом Гауссовых исключений, состоит в том, что систему (13) приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей:

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду:

а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:

Последний, (n + 1) столбец этой матрицы содержит решение системы (13).

В Mathcad прямой и обратный ходы метода Гаусса выполняет функция rref (A ).

На Рисунке 9 показано решение системы линейных уравнений методом Гаусса, в котором используются следующие функции:

rref(A )

Возвращается ступенчатая форма матрицы А .

augment(A , В )

Возвращается массив, сформированный расположением A иВ бок о бок. Массивы A иВ должны иметь одинаковое число строк.

submatrix(A, ir, jr, ic, jc )

Возвращается субматрица, состоящая из всех элементов с ir по jr и столбцах с ic по jc. Удостоверьтесь, что ir jr и

ic jc, иначе порядок строк и (или) столбцов будет обращен.

Рисунок 9.

Описание метода

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,…,bn и x1,x2,…,xn, либо набор c1,c2,…,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы дляопределителя Грама и Леммы Накаямы.

35) Теорема Кронекера-Капелли

Для того чтобы система m неоднородных линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы Доказательство необходимости. Пусть система (1.13) совместна, то есть существуют такие числа х 1 =α 1 , х 2 =α 2 , …, х n =α n , что (1.15) Вычтем из последнего столбца расширенной матрицы ее первый столбец, умноженный на α 1 , второй – на α 2 , …, n-ый – умноженный на α n , то есть из последнего столбца матрицы (1.14) следует вычесть левые части равенств (1.15). Тогда получим матрицу ранг которой в результате элементарных преобразований не изменится и . Но очевидно, и, значит, Доказательство достаточности. Пусть и пусть для определенности не равный нулю минор порядка r расположен в левом верхнем углу матрицы: Это означает, что остальные строки матрицы могут быть получены как линейные комбинации первых r строк, то есть m-r строк матрицы можно представить в виде сумм первых r строк, умноженных на некоторые числа. Но тогда первые r уравнений системы (1.13) самостоятельны, а остальные являются их следствиями, то есть решение системы первых r уравнений автоматически является решением остальных уравнений. Возможны два случая. 1. r=n. Тогда система, состоящая из первых r уравнений, имеет одинаковое число уравнений и неизвестных и совместна, причем решение ее единственно. 2. r (1.16) «Свободным» неизвестным x r +1 , x r +2 , …, x n можно придать какие угодно значения. Тогда соответствующие значения получают неизвестные x 1 , x 2 , …, x r . Система (1.13) и в этом случае совместная, но неопределенная. Замечание. Отличный от нуля минор порядка r, где rх 1 , х 2 , …, х r так же называют базисными, остальные – свободными. Систему (1.16) называют укороченной. Если свободные неизвестные обозначить х r +1 =c 1 , х r +2 =c 2 , …, х n =c n – r , то базисные неизвестные будут от них зависеть, то есть решение системы m уравнений с n неизвестными будет иметь вид X = (x 1 (c 1 , …, c n – r ), x 2 (c 1 , …, c n – r ), …, x r (c 1 , …, c n – r ), c 1 , c 2 , …, c n – r ) T , где значок Т означает транспонирование. Такое решение системы называется общим.

36)ус-е определенности, неопределенности
Система m линейных уравнений с n неизвестными (или, линейная система ) в линейной алгебре – это система уравнений вида

Здесь x 1 , x 2 , …, x n – неизвестные, которые надо определить. a 11 , a 12 , …, a mn – коэффициенты системы – и b 1 , b 2 , … b m – свободные члены – предполагаются известными. Индексы коэффициентов (a ij ) системы обозначают номера уравнения (i ) и неизвестного (j ), при котором стоит этот коэффициент, соответственно .

Система (1) называется однородной , если все её свободные члены равны нулю (b 1 = b 2 = … = b m = 0), иначе – неоднородной .

Система (1) называется совместной , если она имеет хотя бы одно решение, и несовместной , если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c 1 (1) , c 2 (1) , …, c n (1) и c 1 (2) , c 2 (2) , …, c n (2) совместной системы вида (1) называются различными , если нарушается хотя бы одно из равенств:

c 1 (1) = c 1 (2) , c 2 (1) = c 2 (2) , …, c n (1) = c n (2) .

Совместная система вида (1) называется определённой , если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой

37)Решение систем линейных уравнений методом Гаусса

Пусть исходная система выглядит следующим образом

Матрица A называется основной матрицей системы, b – столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

Тогда переменные называются главными переменными . Все остальные называются свободными .

[править]Условие совместности

Упомянутое выше условие для всех может быть сформулировано в качестве необходимого и достаточного условия совместности:

Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).

Алгоритм

Описание

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

§ На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

§ На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Метод Гаусса требует порядка O (n 3) действий.

Этот метод опирается на:

38)Теорема Кронекера-Капелли.
Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.

Системы линейных однородных уравнений

Содержание:

Системы линейных однородных уравнений

Система линейных однородных уравнений Дана система линейных однородных уравнений anXi + a12x2 H —— h ainXn-O, a2 \ X \ + a-22 ^ 2 H —— H a2nxn = 0, Umi ^ i + am 2X2 + ••• + amnxn = 0. = 3×3 — это общие решения. Размещение xs = 0 дает вам одно конкретное решение: x \ = 0, x2 = 0, xs = 0.

Размещение xs = 1 дает вам второе конкретное решение: x \ = 2, x2 = 3, x3 = 1 и т. Д. Людмила Фирмаль

Однородные линейные системы. Однородные системы линейных алгебраических уравнений

Однородные системы линейных алгебраических уравнений

В рамках уроков метод Гаусса и Несовместные системы/системы с общим решением мы рассматривали неоднородные системы линейных уравнений , где свободный член (который обычно находится справа) хотя бы одного из уравнений был отличен от нуля.
И сейчас, после хорошей разминки с рангом матрицы , мы продолжим шлифовать техникуэлементарных преобразований на однородной системе линейных уравнений .
По первым абзацам материал может показаться скучным и заурядным, однако данное впечатление обманчиво. Помимо дальнейшей отработки технических приёмов будет много новой информации, поэтому, пожалуйста, постарайтесь не пренебрегать примерами данной статьи.

Что такое однородная система линейных уравнений?

Пример 1

(2) К третьей строке прибавили вторую строку, умноженную на –1.

Делить третью строку на 3 не имеет особого смысла.

Ответ :

Сформулируем очевидный критерий : однородная система линейных уравнений имееттолько тривиальное решение , если ранг матрицы системы (в данном случае 3) равен количеству переменных (в данном случае – 3 шт.).

Разогреваемся и настраиваем свой радиоприёмник на волну элементарных преобразований:

Пример 2

Решить однородную систему линейных уравнений

Из статьи Как найти ранг матрицы? вспоминаем рациональный приём попутного уменьшения чисел матрицы. В противном случае вам придётся разделывать крупную, а частенько и кусачую рыбу. Примерный образец оформления задания в конце урока.

Нули – это хорошо и удобно, однако на практике гораздо более распространен случай, когда строки матрицы системы линейно зависимы . И тогда неизбежно появление общего решения:

Пример 3

Решить однородную систему линейных уравнений

Решение : запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду. Первое действие направлено не только на получение единичного значения, но и на уменьшение чисел в первом столбце:

(1) К первой строке прибавили третью строку, умноженную на –1. Ко второй строке прибавили третью строку, умноженную на –2. Слева вверху я получил единицу с «минусом», что зачастую намного удобнее для дальнейших преобразований.

(2) Первые две строки одинаковы, одну из них удалили. Честное слово, не подгонял решение – так получилось. Если выполнять преобразования шаблонно, то линейная зависимость строк обнаружилась бы чуть позже.

(3) К третьей строке прибавили вторую строку, умноженную на 3.

(4) У первой строки сменили знак.

В результате элементарных преобразований получена эквивалентная система:

Алгоритм работает точно так же, как и для неоднородных систем . Переменные , «сидящие на ступеньках» – главные, переменная , которой не досталось «ступеньки» – свободная.

Выразим базисные переменные через свободную переменную:

Ответ : общее решение:

Тривиальное решение входит в общую формулу, и записывать его отдельно излишне.

Проверка выполняется тоже по обычной схеме: полученное общее решение необходимо подставить в левую часть каждого уравнения системы и получить законный ноль при всех подстановках.

На этом можно было бы тихо-мирно закончить, но решение однородной системы уравнений часто требуется представить в векторной форме с помощьюфундаментальной системы решений . Пожалуйста, временно забудьте обаналитической геометрии , поскольку сейчас речь пойдёт о векторах в общем алгебраическом смысле, который я немного приоткрыл в статье про ранг матрицы . Терминологии тушеваться не нужно, всё довольно просто.

Что такое однородная система линейных уравнений?

Пример 1

(2) К третьей строке прибавили вторую строку, умноженную на –1.

Делить третью строку на 3 не имеет особого смысла.

Ответ :

Разогреваемся и настраиваем свой радиоприёмник на волну элементарных преобразований:

Пример 2

Решить однородную систему линейных уравнений

Чтобы окончательно закрепить алгоритм, разберём финальное задание:

Пример 7

Решить однородную систему, ответ записать в векторной форме.

Решение : запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) Ко 2-й и 3-й строкам прибавили первую строку. К 4-й строке прибавили первую строку, умноженную на 2.

(3) Последние три строки пропорциональны, две из них удалили.

В результате получена стандартная ступенчатая матрица, и решение продолжается по накатанной колее:

– базисные переменные;
– свободные переменные.

Выразим базисные переменные через свободные переменные. Из 2-го уравнения:

– подставим в 1-е уравнение:

Таким образом, общее решение:

Подставим тройку значений в общее решение и получим вектор , координаты которого удовлетворяют каждому уравнению однородной системы. И снова повторюсь, что крайне желательно проверять каждый полученный вектор – времени займет не так много, а от ошибок убережёт стопроцентно.

Для тройки значений находим вектор

И, наконец, для тройки получаем третий вектор:

Ответ : , где

Желающие избежать дробных значений могут рассмотреть тройки и получить ответ в эквивалентном виде:

Второй вариант решения :

Инструкция . Выберите размерность матрицы:

Свойства систем линейных однородных уравнений

Алгоритм решения систем линейных однородных уравнений

Находим ранг матрицы.
Выделяем базисный минор. Выделяем зависимые (базисные) и свободные неизвестные.
Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора, так как они являются следствиями остальных (по теореме о базисном миноре).
Члены уравнений, содержащие свободные неизвестные, перенесем в правую часть. В результате получим систему из r уравнений с r неизвестными, эквивалентную данной, определитель которой отличен от нуля.
Решаем полученную систему методом исключения неизвестных. Находим соотношения, выражающие зависимые переменные через свободные.
Если ранг матрицы не равен количеству переменных, то находим фундаментальное решение системы.
В случае rang = n имеем тривиальное решение.

Умножим 3-ую строку на (-3). Добавим 4-ую строку к 3-ой:

0	0	1	-1
0	0	-1	1
0	-1	-2	1
3	2	1	4
2	1	0	3

Как найти фундаментальную систему решений линейного уравнения?

Возьмём для примера такую систему линейных уравнений:

Пример 1 . Найти общее решение и какую-нибудь фундаментальную систему решений для системы

Решение находим с помощью калькулятора . Алгоритм решения такой же, как и для систем линейных неоднородных уравнений.
Оперируя только со строками, находим ранг матрицы, базисный минор; объявляем зависимые и свободные неизвестные и находим общее решение.

Первая и вторая строки пропорциональны, одну из них вычеркнем:

.
Зависимые переменные – x 2 , x 3 , x 5 , свободные – x 1 , x 4 . Из первого уравнения 10x 5 = 0 находим x 5 = 0, тогда
; .
Общее решение имеет вид:

Находим фундаментальную систему решений, которая состоит из (n-r) решений. В нашем случае n=5, r=3, следовательно, фундаментальная система решений состоит из двух решений, причем эти решения должны быть линейно независимыми. Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 2. Достаточно придать свободным неизвестным x 1 и x 4 значения из строк определителя второго порядка, отличного от нуля, и подсчитать x 2 , x 3 , x 5 . Простейшим определителем, отличным от нуля, является .
Таким образом, первое решение: , второе – .
Эти два решения составляют фундаментальную систему решений. Заметим, что фундаментальная система не единственна (определителей, отличных от нуля, можно составить сколько угодно).

Пример 2 . Найти общее решение и фундаментальную систему решений системы
Решение.

,
отсюда следует, что ранг матрицы равен 3 и равен числу неизвестных. Значит, система не имеет свободных неизвестных, а поэтому имеет единственное решение – тривиальное.

Задание . Исследовать и решить систему линейных уравнений.
Пример 4

Задание . Найти общее и частное решения каждой системы.
Решение. Выпишем основную матрицу системы:

5	-2	9	-4	-1
1	4	2	2	-5
6	2	11	-2	-6
x 1	x 2	x 3	x 4	x 5

Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 2-ую строку на (-5). Добавим 2-ую строку к 1-ой:

0	-22	-1	-14	24
1	4	2	2	-5
6	2	11	-2	-6

Умножим 2-ую строку на (6). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Найдем ранг матрицы.

0	22	1	14	-24
6	2	11	-2	-6
x 1	x 2	x 3	x 4	x 5

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x 1 ,x 2 , значит, неизвестные x 1 ,x 2 – зависимые (базисные), а x 3 ,x 4 ,x 5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.

0	22	14	-1	-24
6	2	-2	-11	-6
x 1	x 2	x 4	x 3	x 5

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
22x 2 = 14x 4 – x 3 – 24x 5
6x 1 + 2x 2 = – 2x 4 – 11x 3 – 6x 5
Методом исключения неизвестных находим нетривиальное решение :
Получили соотношения, выражающие зависимые переменные x 1 ,x 2 через свободные x 3 ,x 4 ,x 5 , то есть нашли общее решение :
x 2 = 0.64x 4 – 0.0455x 3 – 1.09x 5
x 1 = – 0.55x 4 – 1.82x 3 – 0.64x 5
Находим фундаментальную систему решений, которая состоит из (n-r) решений.
В нашем случае n=5, r=2, следовательно, фундаментальная система решений состоит из 3-х решений, причем эти решения должны быть линейно независимыми.
Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 3.
Достаточно придать свободным неизвестным x 3 ,x 4 ,x 5 значения из строк определителя 3-го порядка, отличного от нуля, и подсчитать x 1 ,x 2 .
Простейшим определителем, отличным от нуля, является единичная матрица.

Задача . Найти фундаментальный набор решений однородной системы линейных уравнений.

Система линейная – Справочник химика 21

Общее решение связанной системы линейных однородных уравнений первого порядка, представленной уравнением (1П.6А.З), имеет вид [c.43]

Выше было указано, что масс-спектры многокомпонентных смесей представляют собой аддитивное наложение спектров индивидуальных соединений. Поэтому первым этапом расчета количественного содержания компонента в смеси является определение доли участия каждого компонента в образовании пиков, используемых при расчете. Это достигается решением системы линейных уравнений. Обозначим [c.266]

Таким образом, для возникновения геля в системе линейных макромолекул достаточно ввести в среднем одно разветвленное звено на молекулу — одну сшивку на 2 молекулы. Если исходный линейный полимер полидисперсен, величина ркр будет еще меньше. Это соотношение имеет место и при одновременном -протекании реакции сшивания по двойным связям и роста цепей, только величина Р имеет в этом случае несколько искусственный смысл средней степени полимеризации макромолекул, полученных после разрыва всех сшивок. [c.26]

Решением системы линейных уравнений (VII,477) рассчитываются величины ХР как функции управления на второй стадии [c.401]

Сокращение размерности системы линейных алгебраических уравнений даёт возможность ускорить счёт и расширить круг решаемых задач. [c.75]

Пусть система линейных алгебраических уравнений, которую необходимо решать, имеет вид [c.75]

Искомые величины определяются путем решения системы линейных уравнений следующего вида [c.267]

Система уравнений (УП,21) является системой линейных обыкновенных днф([)еренциальных уравненнй относительно неизвестных где величины [c.326]

Обилие подобных систем наводит на мысль, что химические процессы гораздо чаще бывают нелинейными, чем линейными. В данном случае описание системы линейным законом обычно обосновывают рядом допущений, согласно которым линейная аппроксимация не приводит к большим ошибкам. [c.105]

В результате прохождения реакции в газовой фазе претерпевают изменения как состав системы, так и ее объем (последняя величина изменяется в том случае, если меняется число молей). Принимая, что объем системы линейно зависит от степени превращения, получаем [c.236]

Функция распределения времени пребывания в каскаде реакторов полного перемешивания может быть рассчитана при использовании уравнения (УП1-335) последовательно для отдельных ступеней. Получается система линейных дифференциальных уравнений. Решение ее дает возможность установить следующую зависимость для каскада т одинаковых реакторов [c.325]

Могут быть получены данные двух типов. В первом случае расчет прост для конкретного соединения определяется максимум поглощения, на который не накладывается поглощение составных частой смеси и интенсивность которого меряется при разбавлении. Сравнение интенсивностей (удельное поглощение К) аналитических пиков в смеси по отношению к удельному поглощению чистого соединения даст его процентное содержание в смеси. Во втором случае в спектре не наблюдается отдельных аналитических пиков следовательно, необходимо вводить поправки на поглощение каждого компонента смеси на выбранных аналитических длинах волн. Эти длины волн выбираются таким образом, чтобы поправки были наименьшими. Таким образом, легко может быть составлена система линейных уравнений, решение которых даст процентное содержание составных частой смеси. [c.281]

Единственное положение равновесия этой системы линейных дифференциальных уравнений находится в начале координат ( 1 = = = п = 0). Вид ее решения зависит от значений корней -Ли Щ,. … характеристического уравнения [c.25]

При таком подходе нет необходимости в решении системы линейных уравнений, так как можно принять f =0 и достаточно вычислять только В [c.21]

Другой подход к решению задачи минимизации заключается в линеаризации правой части разностного уравнения (3.165) с последующим решением системы линейных алгебраических уравнений. Решение системы в этом случае имеет вид 0 — 0 = А + [c.220]

Система линейных уравнений (3.36) решается мето дом расщепления на подсистемы меньшей размерности, описанным ниже. [c.71]

При положительных значениях L и, определенных из системы линейных уравнений (3.36), значения температур 7 корректируется по уравнениям изотерм паровой (3.34) или жидкой (3.35) фаз. [c.72]

Преобразование системы линейных алгебраических [c.77]

Поэтому всегда можно перейти к системе линейных ограничений в виде равенств из т уравнений и k переменных k [c.185]

Существует большое число других методов поиска [7—9], но для системы линейных дифференциальных уравнений они зачастую излишне сложны. [c.35]

В ряде работ – принцип максимума формулируется как необходимый признак оптимальности для процессов, описываемых системами нелинейных обыкновенных дифференциальных у])авие-ний. Показано, что если процесес характеризуется системой линейных уравнений, принцип максимума является достаточным условием оптимальности. [c.320]

Решение системы линейных неоднородных уравнений (3.47) можно представить в виде [c.77]

При этом иногда одновременно проводят и линеаризацию, ню приводит к системе линейных алгебраических уравнений. [c.170]

Общее рассмотрение такого подхода [1] развито авторами работы [171 применительно к системам линейных дифференциальных уравнений. Ими получены условия определения числа независимых реакций и вид матрицы коэффициентов v y. Эта теория полезна для сложных ситуаций, когда выполненный ранее эксперимент не используется при формулировании стехиометрических уравнений. [c.80]

Решение системы линейных однородных уравнений Гиббса — Дюгема совместно с уравнениями (5.10), (5.38), (5.41) и (5.43) с учетом [c.87]

Тогда система линейных уравнений, связывающих и. .., Хр в каждом опыте, может быть записана в виде уравнения [c.25]

Если система линейна, то, как следует из уравнения (Х,5), передаточная функция двух последовательно соединенных звеньев является алгебраическим произведением передагочных [c.129]

Пример такого расчета дан в главе I. Укажем, что по известной теореме Крамера, система (У-2) является определенной, если А =5 = 0. Другой метод точного решения системы линейных уравнений (Гаусса) приведен ниже (стр. 201). [c.142]

Если разделить каждое уравнение на М1, то все члены в правой стороне станут линейными. Если теперь произвести замену переменных dz = Шldt, то получится система линейных уравнений первого порядка [c.49]

Система уравнений в вариациях как система линейных уравнении обладает важным свойством, а именно сумма любых двух ее реншний, найденных нри неодинаковых начальных условиях, также является ре(не-нием. Таким обра ом, если начальное условие риаций оптимального управления. [c.327]

В работе [66] отмечено, что, ест н достаточной близости от решения справедливо урзЕнение (1.7), го в качестве нового приближения можно использовать при (X )-=0 решение системы линейных алгебраических уравнений [c.20]

При решении системы линейных уравнений оттосительно покомпонентных потокок пара и жидкости по тарелкам для ккорней за счёт машинного округления. [c.57]

Разрабо тан принципиально новый одноконтурный метод расчета сложных ректификационных систем с закрепленными отборами продуктов раздел( ния. Разлагая в ряд Тейлора значения энтальпий //у и /Гу в окрестности 1] и офаничиваясь при этом линейными членами, осуществляется переход от 2п независимых переменных (7), ) к п независимым переменным TJ ) к линеаризация системы уравнений общего материального и теплового балансов. Температуры на тарелках 7 определяются по уравнениям изотерм паровой или жидкой фаз, соотно шени 1 гготоков и сами потоки определяются решением системы линейных уравнений общего материального и теплового балансов. [c.98]

В предлагаемом алгоритме, Д1Я решения системы линейных уравнений покомпонентного материального 6aiaH a используется комбинация методов прогонки и 1 аусса [46]. В случае, когда в колонне нет рециклов и байпасов, то есть матрица системь грех диагональная, метод прогонки действует в п раз бысфее. [c.58]

При двухопорной конструкции корпуса задача определения реакций опор, изгибающих моментов, прочности конетрукции не представляет трудности. Многоопорная конструкция с расчетной точки зрения — многопролетная статически неопределимая балка. Из нескольких возможных методов раскрытия етатичеекой неопределимости (метод сил, метод последовательных приближений и уравнение трех моментов) для машин барабанного типа чаще применяют уравнение трех моментов (см. куре Сопротивление материалов ). Для решения системы линейных алгебраических уравнений в алгоритмических языках ЭВМ существуют стандартные процедуры. Тоеле раскрытия статической неопределимости каждый пролет рассматривают как простую балку, находящуюся под совокупным воздействием нагрузок и опорных моментов. Для определения реакций в опорах используют уравнения равновесия. Рассматривая сумму моментов относительно точек Л и С (рис. 12.17) для пары пролетов, рассматриваемых раздельно, находят составляющие реакции опоры Я в и Я в - [c.379]

Потоки жидкости I, и пара И, определяются из системы линейных уравнений общего материального и теплового балансов (3.29) размерности 2п (при извест1-1ых значениях энтальпий жидкостных и паровых потоков система уравнений (3.29) линейна) [c.70]

Метод является эффективным для понижения размерности системы линейных алгебраических уравнений путём разбиения на подсистемы меньшей размерности. При этом время расчёта значительно сокращается, так как решение системы и-ой размерности значите.ньно дольше решения двух подсистем размерности т и п-т. Как показали расчётные исследования, наиболее эффективно принимать т=п12 за счёт возможности использования при этом метода прогонки при решении подсистем линейных алгебраических уравнений размерности п/2. [c.77]

Матриш>1 коэффициентов системы линейных ап ебраических уравнений общего (или покомпонентного) материального баланса для сложных разделительных систем (с рециклами) вне трёх диагональной системы содержат ненулевые элементы, исходя из этого, поиск корней осуществляется в два этапа. На первом этапе преобразуем систему линейных уравнений к трёх диагональному виду, на втором – определяем корни системы методом прогонки или специально разработанным [eтoдoм (описание которого см. ниже). [c.77]

После дифференцировакия по неизвестным коэффициентам получаются две системы линейных уравнений [c.72]

Фундаментальная система решений (конкретный пример). Как найти нетривиальное и фундаментальное решение системы линейных однородных уравнений

Тогда общее решение однородной системы имеет вид:

Пример . Найдем решение системы

Примем , тогда получим решение в виде:

Построим теперь фундаментальную систему решений:

Общее решение запишется в виде:

Решения системы однородных линейных уравнений имеют свойства:

Другими словами, любая линейная комбинация решений однородной системы есть опять решение.

Решение систем линейных уравнений методом Гаусса

Предположим, что в системе (1)
(что всегда возможно).

(1)

Умножая поочередно первое уравнение на так называемые подходящие числа

(2)

Умножим теперь второе уравнение системы (2) на подходящие числа, полагая, что

и складывая его с нижестоящими, исключим переменную из всех уравнений, начиная с третьего.

Продолжая этот процесс, после
шага мы получим:

(3)

Переход от системы (1) к (3) называется прямым ходом метода Гаусса, а нахождение неизвестных из (3) – обратным ходом .

Пример . Найдем решение системы

Запишем расширенную матрицу системы:

Прибавим к строкам 2,3,4 первую, умноженную на (-2), (-3), (-2) соответственно:

Поменяем строки 2 и 3 местами, затем в получившейся матрице добавим к строке 4 строку 2, умноженную на :

Прибавим к строке 4 строку 3, умноженную на
:

Очевидно, что
, следовательно, система совместна. Из полученной системы уравнений

находим решение обратной подстановкой:

,
,
,
.

Пример 2. Найти решение системы:

Очевидно, что система несовместна, т.к.
, а
.

Достоинства метода Гаусса :

Менее трудоемкий, чем метод Крамера.

Однозначно устанавливает совместность системы и позволяет найти решение.

Дает возможность определить ранг любых матриц.

Однородные системы линейных алгебраических уравнений

Что такое однородная система линейных уравнений?

Пример 1

(2) К третьей строке прибавили вторую строку, умноженную на –1.

Делить третью строку на 3 не имеет особого смысла.

Ответ :

Сформулируем очевидный критерий : однородная система линейных уравнений имееттолько тривиальное решение , если ранг матрицы системы (в данном случае 3) равен количеству переменных (в данном случае – 3 шт.).

Разогреваемся и настраиваем свой радиоприёмник на волну элементарных преобразований:

Пример 2

Решить однородную систему линейных уравнений

Пример 3

Решить однородную систему линейных уравнений

(3) К третьей строке прибавили вторую строку, умноженную на 3.

(4) У первой строки сменили знак.

В результате элементарных преобразований получена эквивалентная система:

Выразим базисные переменные через свободную переменную:

Ответ : общее решение:

Тривиальное решение входит в общую формулу, и записывать его отдельно излишне.

Инструкция . Выберите размерность матрицы:

Свойства систем линейных однородных уравнений

Алгоритм решения систем линейных однородных уравнений

Находим ранг матрицы.
Выделяем базисный минор. Выделяем зависимые (базисные) и свободные неизвестные.
Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора, так как они являются следствиями остальных (по теореме о базисном миноре).
Члены уравнений, содержащие свободные неизвестные, перенесем в правую часть. В результате получим систему из r уравнений с r неизвестными, эквивалентную данной, определитель которой отличен от нуля.
Решаем полученную систему методом исключения неизвестных. Находим соотношения, выражающие зависимые переменные через свободные.
Если ранг матрицы не равен количеству переменных, то находим фундаментальное решение системы.
В случае rang = n имеем тривиальное решение.

Умножим 3-ую строку на (-3). Добавим 4-ую строку к 3-ой:

0	0	1	-1
0	0	-1	1
0	-1	-2	1
3	2	1	4
2	1	0	3

Даны матрицы

Найти: 1) aA – bB,

Решение : 1) Находим последовательно, используя правила умножения матрицы на число и сложения матриц..

2. Найдите А*В, если

Решение : Используем правило умножения матриц

Ответ:

3. Для заданной матрицы найдите минор М 31 и вычислите определитель.

Решение : Минор М 31 – это определитель матрицы, которая получается из А

после вычеркивания строки 3 и столбца 1. Находим

1*10*3+4*4*4+1*1*2-2*4*10-1*1*4-1*4*3 = 0.

Преобразуем матрицу А, не изменяя её определителя (сделаем нули в строке 1)





-3, -, -4

-10			-15
-20			-25
-4			-5

Теперь вычисляем определитель матрицы А разложением по строке 1

Ответ: М 31 = 0, detA = 0

Pешить методом Гаусса и методом Крамера.

2х 1 + х 2 + x 3 = 2

x 1 + х 2 + 3x 3 = 6

2x 1 + x 2 + 2x 3 = 5

Решение : Проверим

Можно применить метод Крамера

Решение системы: х 1 = D 1 /D = 2, х 2 = D 2 /D = -5, х 3 = D 3 /D = 3

Применим метод Гаусса.

Расширенную матрицу системы приведём к треугольному виду.

Для удобства вычислений поменяем строки местами:

Умножим 2-ю строку на (k = -1 / 2 = -1 / 2 ) и добавим к 3-й:

Умножим 1-ю строку на (k = -2 / 2 = -1 ) и добавим к 2-й:

Теперь исходную систему можно записать как:

x 1 = 1 – (1 / 2 x 2 + 1 / 2 x 3)

x 2 = 13 – (6x 3)

Из 2-ой строки выражаем

Из 1-ой строки выражаем

Решение то же.

Ответ: (2 ; -5 ; 3)

Найти общее решение системы и ФСР

13х 1 – 4х 2 – х 3 – 4х 4 – 6х 5 = 0

11х 1 – 2х 2 + х 3 – 2х 4 – 3х 5 = 0

5х 1 + 4х 2 + 7х 3 + 4х 4 + 6х 5 = 0

7х 1 + 2х 2 + 5х 3 + 2х 4 + 3х 5 = 0

Решение : Применим метод Гаусса. Расширенную матрицу системы приведём к треугольному виду.

	-4	-1	-4	-6
	-2		-2	-3


x 1	x 2	x 3	x 4	x 5

Умножим 1-ю строку на (-11). Умножим 2-ю строку на (13). Добавим 2-ю строку к 1-й:

Умножим 2-ю строку на (-5). Умножим 3-ю строку на (11). Добавим 3-ю строку к 2-й:

Умножим 3-ю строку на (-7). Умножим 4-ю строку на (5). Добавим 4-ю строку к 3-й:

Второе уравнение есть линейная комбинация остальных

Найдем ранг матрицы.

	-18	-24	-18	-27

x 1	x 2	x 3	x 4	x 5

Этот минор является базисным. В него вошли коэффициенты при неизвестных x 1 ,x 2 , значит, неизвестные x 1 ,x 2 – зависимые (базисные), а x 3 ,x 4 ,x 5 – свободные.

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:

18x 2 = 24x 3 + 18x 4 + 27x 5

7x 1 + 2x 2 = – 5x 3 – 2x 4 – 3x 5

Методом исключения неизвестных находим общее решение :

x 2 = – 4 / 3 x 3 – x 4 – 3 / 2 x 5

x 1 = – 1 / 3 x 3

Находим фундаментальную систему решений (ФСР), которая состоит из (n-r) решений. В нашем случае n=5, r=2, следовательно, фундаментальная система решений состоит из 3-х решений, причем эти решения должны быть линейно независимыми.

Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 3.

Достаточно придать свободным неизвестным x 3 ,x 4 ,x 5 значения из строк определителя 3-го порядка, отличного от нуля, и подсчитать x 1 ,x 2 .

Простейшим определителем, отличным от нуля, является единичная матрица.

Но здесь удобнее взять

Находим, используя общее решение:

а) х 3 = 6, х 4 = 0, х 5 = 0 Þ х 1 = – 1 / 3 x 3 = -2, х 2 = – 4 / 3 x 3 – x 4 – 3 / 2 x 5 = -4 Þ

I решение ФСР: (-2; -4; 6; 0;0)

б) х 3 = 0, х 4 = 6, х 5 = 0 Þ х 1 = – 1 / 3 x 3 = 0, х 2 = – 4 / 3 x 3 – x 4 – 3 / 2 x 5 = – 6 Þ

II решение ФСР: (0; -6; 0; 6;0)

в) х 3 = 0, х 4 = 0, х 5 = 6 Þ х 1 = – 1 / 3 x 3 = 0, х 2 = – 4 / 3 x 3 – x 4 – 3 / 2 x 5 = -9 Þ

III решение ФСР: (0; – 9; 0; 0;6)

Þ ФСР: (-2; -4; 6; 0;0), (0; -6; 0; 6;0), (0; – 9; 0; 0;6)

6. Дано: z 1 = -4 + 5i, z 2 = 2 – 4i. Найти: a) z 1 – 2z 2 б) z 1 z 2 в) z 1 /z 2

Решение : a) z 1 – 2z 2 = -4+5i+2(2-4i) = -4+5i+4-8i = -3i

б) z 1 z 2 = (-4+5i)(2-4i) = -8+10i+16i-20i 2 = {i 2 = -1} = 12 + 26i

Ответ: а) -3i б) 12+26i в) -1.4 – 0.3i

Ещё в школе каждый из нас изучал уравнения и, наверняка, системы уравнений. Но не многие знают, что существует несколько способов их решения. Сегодня мы подробно разберём все методы решения системы линейных алгебраических уравнений, которые состоят более чем из двух равенств.

История

На сегодняшний день известно, что искусство решать уравнения и их системы зародилось ещё в Древнем Вавилоне и Египте. Однако равенства в их привычном для нас виде появились после возникновения знака равенства “=”, который был введён в 1556 году английским математиком Рекордом. Кстати, этот знак был выбран не просто так: он означает два параллельных равных отрезка. И правда, лучшего примера равенства не придумать.

Основоположником современных буквенных обозначений неизвестных и знаков степеней является французский математик Однако его обозначения значительно отличались от сегодняшних. Например, квадрат неизвестного числа он обозначал буквой Q (лат.”quadratus”), а куб – буквой C (лат. “cubus”). Эти обозначения сейчас кажутся неудобными, но тогда это был наиболее понятный способ записать системы линейных алгебраических уравнений.

Однако недостатком в тогдашних методах решения было то, что математики рассматривали только положительные корни. Возможно, это связано с тем, что отрицательные значения не имели никакого практического применения. Так или иначе, но первыми считать отрицательные корни начали именно итальянские математики Никколо Тарталья, Джероламо Кардано и Рафаэль Бомбелли в 16 веке. А современный вид, основной метод решения (через дискриминант) был создан только в 17 веке благодаря работам Декарта и Ньютона.

В середине 18 века швейцарский математик Габриэль Крамер нашёл новый способ для того, чтобы сделать решение систем линейных уравнений проще. Этот способ был впоследствии назван его именем и по сей день мы пользуемся им. Но о методе Крамера поговорим чуть позднее, а пока обсудим линейные уравнения и методы их решения отдельно от системы.

Линейные уравнения

Линейные уравнения – самые простые равенства с переменной (переменными). Их относят к алгебраическим. записывают в общем виде так: а 1 *x 1 +а 2* x 2 +…а n *x n =b. Представление их в этом виде нам понадобится при составлении систем и матриц далее.

Системы линейных алгебраических уравнений

Определение этого термина такое: это совокупность уравнений, которые имеют общие неизвестные величины и общее решение. Как правило, в школе все решали системы с двумя или даже тремя уравнениями. Но бывают системы с четырьмя и более составляющими. Давайте разберёмся сначала, как следует их записать так, чтобы в дальнейшем было удобно решать. Во-первых, системы линейных алгебраических уравнений будут выглядеть лучше, если все переменные будут записаны как x с соответствующим индексом: 1,2,3 и так далее. Во-вторых, следует привести все уравнения к каноническому виду: а 1 *x 1 +а 2* x 2 +…а n *x n =b.

После всех этих действий мы можем начать рассказывать, как находить решение систем линейных уравнений. Очень сильно для этого нам пригодятся матрицы.

Матрицы

Матрица – это таблица, которая состоит из строк и столбцов, а на их пересечении находятся её элементы. Это могут быть либо конкретные значения, либо переменные. Чаще всего, чтобы обозначить элементы, под ними расставляют нижние индексы (например, а 11 или а 23). Первый индекс означает номер строки, а второй – столбца. Над матрицами, как и над любым другим математическим элементом можно совершать различные операции. Таким образом, можно:

2) Умножать матрицу на какое-либо число или вектор.

3) Транспонировать: превращать строчки матрицы в столбцы, а столбцы – в строчки.

4) Умножать матрицы, если число строк одной их них равно количеству столбцов другой.

Подробнее обсудим все эти приёмы, так как они пригодятся нам в дальнейшем. Вычитание и сложение матриц происходит очень просто. Так как мы берём матрицы одинакового размера, то каждый элемент одной таблицы соотносится с каждым элементом другой. Таким образом складываем (вычитаем) два этих элемента (важно, чтобы они стояли на одинаковых местах в своих матрицах). При умножении матрицы на число или вектор необходимо просто умножить каждый элемент матрицы на это число (или вектор). Транспонирование – очень интересный процесс. Очень интересно иногда видеть его в реальной жизни, например, при смене ориентации планшета или телефона. Значки на рабочем столе представляют собой матрицу, а при перемене положения она транспонируется и становится шире, но уменьшается в высоте.

Разберём ещё такой процесс, как Хоть он нам и не пригодится, но знать его будет всё равно полезно. Умножить две матрицы можно только при условии, что число столбцов одной таблицы равно числу строк другой. Теперь возьмём элементы строчки одной матрицы и элементы соответствующего столбца другой. Перемножим их друг на друга и затем сложим (то есть, например, произведение элементов a 11 и а 12 на b 12 и b 22 будет равно: а 11 *b 12 + а 12 *b 22). Таким образом, получается один элемент таблицы, и аналогичным методом она заполняется далее.

Теперь можем приступить к рассмотрению того, как решается система линейных уравнений.

Метод Гаусса

Этой тему начинают проходить еще в школе. Мы хорошо знаем понятие “система двух линейных уравнений” и умеем их решать. Но что делать, если число уравнений больше двух? В этом нам поможет

Конечно, этим методом удобно пользоваться, если сделать из системы матрицу. Но можно и не преобразовывать её и решать в чистом виде.

Итак, как решается этим методом система линейных уравнений Гаусса? Кстати, хоть этот способ и назван его именем, но открыли его ещё в древности. Гаусс предлагает следующее: проводить операции с уравнениями, чтобы в конце концов привести всю совокупность к ступенчатому виду. То есть, нужно, чтобы сверху вниз (если правильно расставить) от первого уравнения к последнему убывало по одному неизвестному. Иными словами, нужно сделать так, чтобы у нас получилось, скажем, три уравнения: в первом – три неизвестных, во втором – два, в третьем – одно. Тогда из последнего уравнения мы находим первое неизвестное, подставляем его значение во второе или первое уравнение, и далее находим оставшиеся две переменные.

Метод Крамера

Для освоения этого метода жизненно необходимо владеть навыками сложения, вычитания матриц, а также нужно уметь находить определители. Поэтому, если вы плохо всё это делаете или совсем не умеете, придется поучиться и потренироваться.

В чём суть этого метода, и как сделать так, чтобы получилась система линейных уравнений Крамера? Всё очень просто. Мы должны построить матрицу из численных (практически всегда) коэффициентов системы линейных алгебраических уравнений. Для этого просто берём числа перед неизвестными и расставляем в таблицу в том порядке, как они записаны в системе. Если перед числом стоит знак “-“, то записываем отрицательный коэффициент. Итак, мы составили первую матрицу из коэффициентов при неизвестных, не включая числа после знаков равенства (естественно, что уравнение должно быть приведено к каноническому виду, когда справа находится только число, а слева – все неизвестные с коэффициентами). Затем нужно составить ещё несколько матриц – по одной для каждой переменной. Для этого заменяем в первой матрице по очереди каждый столбец с коэффициентами столбцом чисел после знака равенства. Таким образом получаем несколько матриц и далее находим их определители.

После того как мы нашли определители, дело за малым. У нас есть начальная матрица, и есть несколько полученных матриц, которые соответствуют разным переменным. Чтобы получить решения системы, мы делим определитель полученной таблицы на определитель начальной таблицы. Полученное число и есть значение одной из переменных. Аналогично находим все неизвестные.

Другие методы

Существует ещё несколько методов для того, чтобы получить решение систем линейных уравнений. Например, так называемый метод Гаусса-Жордана, который применяется для нахождения решений системы квадратных уравнений и тоже связан с применением матриц. Существует также метод Якоби для решения системы линейных алгебраических уравнений. Он легче всех адаптируется для компьютера и применяется в вычислительной технике.

Сложные случаи

Сложность обычно возникает, если число уравнений меньше числа переменных. Тогда можно наверняка сказать, что, либо система несовместна (то есть не имеет корней), или количество её решений стремится к бесконечности. Если у нас второй случай – то нужно записать общее решение системы линейных уравнений. Оно будет содержать как минимум одну переменную.

Заключение

Вот мы и подошли к концу. Подведём итоги: мы разобрали, что такое система и матрица, научились находить общее решение системы линейных уравнений. Помимо этого рассмотрели другие варианты. Выяснили, как решается система линейных уравнений: метод Гаусса и Поговорили о сложных случаях и других способах нахождения решений.

На самом деле эта тема гораздо более обширна, и если вы хотите лучше в ней разобраться, то советуем почитать больше специализированной литературы.

Несогласованные и зависимые системы: использование исключения Гаусса – видео и стенограмма урока

Исключение Гаусса

Теперь, когда мы знаем, что такое несовместимые и зависимые системы, мы можем спросить, можем ли мы использовать метод исключения Гаусса, чтобы помочь нам их решить. Исключение Гаусса – это процесс преобразования системы уравнений в матрицу с последующим использованием матричных операций для преобразования матрицы в форму эшелона строк, где нижняя диагональ – это все нули. На этом этапе мы можем использовать последнее уравнение для решения последней переменной.Затем мы можем подставить этот ответ и подставить его в предпоследнее уравнение, чтобы найти следующую переменную. Мы продолжаем работать до тех пор, пока не получим все наши переменные. Найдите минутку, чтобы освежить свои навыки уничтожения по Гауссу, если вам нужно. Конечно, исключение Гаусса работает, если у нас есть уникальное решение, но будет ли это работать для несовместимых или зависимых систем?

Короткий ответ – нет, это не сработает. Почему не работает? Что происходит, когда мы пытаемся решить эти типы систем с помощью исключения Гаусса? Давайте посмотрим на пару примеров, чтобы увидеть, что происходит.

Несогласованное системное решение

Давайте сначала посмотрим на несовместимую систему. Посмотрим, что произойдет, если мы применим к нему метод исключения Гаусса.

Применяя метод исключения Гаусса, мы создаем нашу матрицу, записывая числа, связанные с переменными, а также постоянные числа. Получаем такую дополненную матрицу:

Мы хотим удалить начало 1 во второй строке и начало 1 в третьей строке.Чтобы исключить 1 во второй строке, мы можем продолжить и вычесть первую строку из второй, чтобы создать новую вторую строку. Получаем 0, 0, 0, 3. Стой, стой, стой! Это вообще возможно? Если мы переведем эту строку обратно в форму уравнения, мы получим 0 = 3. Верно ли это утверждение? Нет, это не так. Что это обозначает? Это означает, что мы не можем продолжать, потому что нет единственного решения.

Мы видим, что для несовместимых систем, когда мы пытаемся использовать метод исключения Гаусса, мы получаем ложное утверждение.Это говорит нам о том, что единственного решения не существует, и мы не можем продолжать.

Dependent System Solution

Ну, а как насчет случая зависимой системы? Что происходит, когда мы пытаемся использовать метод исключения Гаусса для этого типа системы? Давайте взглянем.

Сначала преобразуем это в матричную форму:

Применяя исключение Гаусса, нам нужно сделать начало 1 во второй строке 0, и нам нужно сделать первые 4, а затем -8 в третьей строке 0.Мы можем сделать начало 1 во второй строке 0, умножив вторую строку на -2, а затем добавив ее к первой строке, чтобы создать новую вторую строку. Так мы получим 0, 0, 0 и 0. Хорошо, это интересно. Это не ложное заявление, так что давайте продолжим.

Для третьей строки мы можем умножить первую строку на -2 и добавить ее к третьей, чтобы получить новую третью строку. Делая это, мы получаем 0, 0, 0 и 0 для новой третьей строки. Хм. Это тоже интересно. Это оставляет мне только одно уравнение вверху, поскольку два других уравнения равны 0 = 0, что ничего не значит.Что ж, нам нужно остановиться, потому что мы видим, что мы не можем идти дальше, чтобы получить уникальное решение.

Если вы возьмете те же самые системы и попробуете другие методы их решения, вы столкнетесь с другими препятствиями. Все это означает, что не существует метода решения несовместимых или зависимых систем, потому что не существует единственного решения, которое можно было бы найти.

Резюме урока

Давайте рассмотрим то, что мы узнали. Мы узнали, что несовместимые системы – это те системы, у которых нет решения, а зависимые системы – это те системы, которые имеют бесконечное количество решений.Исключение Гаусса, один из методов решения систем уравнений, не может использоваться для решения несовместных и зависимых систем. Поскольку ни один из типов систем не имеет уникального решения, нельзя использовать какой-либо метод их решения. Все они принесут результаты, которые ничего не значат или не имеют смысла.

Результаты обучения

По окончании этого урока вы должны уметь:

Описывать несовместимые и зависимые системы
Объясните, почему метод исключения Гаусса нельзя использовать для решения этих систем

Python реализует метод исключения Гаусса для поиска решения линейных уравнений

Введение в метод исключения Гаусса

Математически метод исключения Гаусса (или переведенный как метод исключения Гаусса) – это алгоритм в программировании линейной алгебры, который можно использовать для решения линейных уравнений.Но его алгоритм очень сложен, не часто используется метод сложения, вычитания и исключения, чтобы найти ранг матрицы и найти обратную матрицу обратимой квадратной матрицы. Однако, если имеется более миллиона уравнений, этот алгоритм сэкономит время. Некоторые очень большие уравнения обычно решаются итерационными методами и причудливым исключением. При использовании в матрице метод исключения Гаусса дает «строчную лестницу». Метод исключения Гаусса может использоваться в компьютерах для решения тысяч уравнений и неизвестных.Есть также некоторые методы, специально используемые для решения некоторых уравнений со специально подобранными коэффициентами. – перенесено из энциклопедии Baidu

содержание

Метод исключения состоит в том, чтобы выразить неизвестное число уравнения в системе уравнений алгебраической формулой, содержащей другое неизвестное число, и подставить его в другое уравнение, которое исключает неизвестное число и дает решение; Умножение уравнения на определенную константу и добавление его к другому уравнению также может помочь в устранении неизвестного числа.Метод исключения в основном используется для решения линейных уравнений с двумя переменными. – перенесено из энциклопедии Baidu

ядро

1) Два уравнения меняются местами, и решение остается неизменным;
2) Умножьте уравнение на ненулевое число k, и решение останется неизменным;
3) Одно уравнение умножается на число k плюс другое уравнение, решение остается неизменным. – перенесено из Baidu Encyclopedia

Идеи алгоритмов

Идея состоит в том, чтобы сначала преобразовать матрицу в матрицу ряда строк в соответствии с характеристиками метода исключения Гаусса, а затем получить ранг из матрицы ряда строк, а затем определить количество линейных уравнений
Если R ( A) <= R (Ab), то уравнение не имеет решения
R (A) = R (Ab) = N, уравнение имеет единственное решение (однородные уравнения называются не более чем 0 решениями)
R (A) = R (Ab)
После получения количества решений, если существует единственное решение, предыдущая матрица преобразуется в простейшая матрица-строка для получения решения системы линейных уравнений

алгоритм

  импортировать numpy как np

def swag (a, b):
    для i в диапазоне (0, len (a)):
        т = а [я]
        а [я] = б [я]
        б [я] = т

def print_matrix (информация, матрица):
    печать (информация)
    для i в диапазоне (0, matrix.форма [0]):
        print ('[', конец = '')
        для j в диапазоне (0, matrix.shape [1]):
            if (j == matrix.shape [1] - 1):
                печать ('|', конец = ''),
            print ("% 5.2f"% matrix [i] [j], end = '')
            если j == matrix.shape [1] - 1:
                печать (']', конец = '')
                печать ('\ п')

def check (матрица, я, строка, столбец):
    если 0.00 в set (matrix [i]) и len (set (matrix [i])) == 1:
        для j в диапазоне (строка - 1, i, -1):
            пытаться:
                если нет (0.00 in set (matrix [j]) и len (set (matrix [j])) == 1):
                    swag (матрица [i], матрица [j])
                    выберите (матрица, я, столбец)
                    перерыв
            Кроме:
                возвращение

def select (matrix, i, col):
    если 0.00 в set (matrix [i]) и len (set (matrix [i])) == 1:
        возвращение
    для k в диапазоне (0, i):
        temp = матрица [i] [k] / matrix [k] [k]
        если temp == 0:
            Продолжить
        для j в диапазоне (0, col):
            матрица [i] [j] = матрица [i] [j] - матрица [k] [j] * temp

def решить (матрица):
    строка = матрица.форма [0]
    col = matrix.shape [1]
    для i в диапазоне (0, строка):
        если матрица [i] [i] == 0:
            для j в диапазоне (i + 1, строка):
                если матрица [j] [i]! = 0:
                    swag (матрица [i], матрица [j])
                    перерыв
        выберите (матрица, я, столбец)
        проверка (матрица, я, строка, столбец)

def to_one (матрица):
    row = matrix.shape [0]
    col = матрица.форма [1]
    для i в диапазоне (0, строка):
        temp = матрица [i] [i]
        для j в диапазоне (i, col):
            матрица [i] [j] = матрица [i] [j] / temp
    для i в диапазоне (0, строка - 1):
        для j в диапазоне (i + 1, col - 1):
            temp = матрица [i] [j]
            для k в диапазоне (j, col):
                матрица [i] [k] = матрица [i] [k] - матрица [j] [k] * temp

def судья (матрица):
    строка = матрица.форма [0]
    col = matrix.shape [1]
    vanumlist = []
    для я в диапазоне (0, столбец):
        если матрица [строка - 1] [i]! = 0:
            vanumlist.append (матрица [строка - 1] [i])
    если len (vanumlist) == 1:
        print ('Система уравнений не имеет решения')
    elif len (vanumlist) == 2:
        to_one (матрица)
        print_matrix ('Простейший шаг матрицы:', matrix)
        для i в диапазоне (0, строка):
            print ("x% d =% 4.2f"% (i, matrix [i] [col - 1]), end = "")
    еще:
        print ('Множественные решения уравнений')

матрица = np.массив ([[1, 1, 1, 1, 1, 1],
                    [3, 2, 1, 1, -3, 25],
                    [0, 1, 2, 2, 6, -22],
                    [5, 4, 3, 3, -1, 27],
                    [2, -1, 0, 3, 2, 2]
                    ], dtype = float)










print_matrix ('Исходная матрица:', матрица)
решить (матрица)
print_matrix ('Матрица переходит в:', matrix)
судья (матрица)

Результат выполнения кода

Итерационные решения однородных линейных систем

Итерационные решения Однородные линейные системы

Предположим, нам дана однородная линейная система уравнения, такие как

с дополнительным условием P ₀ + P ₁ + П ₂ = 1.(Эта система упоминается в примечании к избыточным системам с общей угрозой.) Стационарное решение удовлетворяет алгебраическим уравнениям

Матрица коэффициентов сингулярна (как видно из тот факт, что сумма каждого столбца равна нулю), поэтому существует другое решение чем тривиальное решение P ₀ = P ₁ = P ₂ = 0 (что не удовлетворяет вспомогательному условию).Прямой подход для определения нетривиального решения стоит заменить первое уравнение (скажем) со вспомогательным условием, давая системе

Умножение на обратное значение коэффициента матрица дает результат

Для небольших систем этот метод работает хорошо, но для больших систем общее обращение матриц становится довольно трудоемким, а для разреженных системы (т.е., при большом количестве нулей в матрице коэффициентов) это неэффективно. Альтернативный подход предлагается переписать уравнение (1) в виде рекурсии, переместив диагональные члены в правую часть и деление на соответствующие коэффициенты (предполагая, что все диагональные коэффициенты не равны нулю, что гарантируется во многих приложениях, таких как Марковские модели). Это дает

, где нижние индексы обозначают векторы состояния на последовательные итерации.(Конечно, в установившемся режиме умножение на это матрица коэффициентов не изменила бы состояние системы.) К сожалению, итерация в (2) не сходится, поэтому это не жизнеспособное решение метод.

Чтобы понять, почему (2) не сходится, краткий обзор наиболее часто используемые итерационные методы для не -однородных линейные системы будут полезны. Для системы вида Mx = b , где M – квадратная матрица, а x и b – столбец векторов, предположим, что мы разделим каждое уравнение строки на соответствующую диагональ коэффициент M (при условии, что все эти диагональные элементы не равны нулю).Сохраняя диагональные элементы в левой части и перемещая недиагональные слагаемых в правую часть, мы получаем эквивалентную систему уравнений, которая можно записать в виде x = Ax + u . для некоторой площади матрица , (все диагональные члены будут равны нулю) и вектор-столбец и . Теперь предположим, что мы используем это как рекуррентное соотношение

Начиная с произвольного вектора начального состояния x ₀, последовательные итерации дают

и так далее.Таким образом, n-я итерация может быть записана как

Очевидно, что если A ⁿ стремится к нулю при увеличении n, то первый член обращается в нуль и геометрический ряд во втором члене сходится, поэтому имеем

, который, очевидно, является решением оригинального масштабированного система ( I A ) x = и .Эта итерационная схема известна как метод Якоби , который мы видим, по сути, это всего лишь замаскированный способ инвертирования коэффициента матрица. Он сходится, только если мощности обедненной матрицы коэффициентов A приближаются к нулю. Так будет, если исходная матрица коэффициентов M строго по диагонали, что означает величину диагонального члена в каждой строке превышает сумму значений недиагональных членов в этот ряд. Чтобы доказать это, обратите внимание, что сумма каждой строки A равна строго меньше 1, потому что он состоит из недиагональных членов соответствующая строка M , разделенная на диагональный член той строки, чья величина (по предположению) превышает сумму недиагональных членов.Следовательно, если обозначим c вектор-столбец, состоящий из всех единиц, из этого следует что Ac – вектор-столбец, состоящий из членов строго меньшего размера чем 1, и поэтому A ( Ac ) состоит из еще меньших членов и т. д. Таким образом, A ⁿ c приближается к нулю, поэтому A ⁿ приближается к нулю.

В некоторых приложениях встречаются системы уравнений для матрицы коэффициентов – , а не с преобладанием по диагонали по строкам , но они являются доминирующими по диагонали по столбцам .Другими словами, сумма значений недиагональных элементов каждого столбца меньше чем величина диагонального члена этого столбца. Такие системы все еще сходится по методу Якоби. Чтобы понять почему, обратите внимание, что вместо разделив каждую строку на диагональный коэффициент этой строки, мы можем масштабируйте каждый компонент до x так, чтобы диагональные элементы модифицированная матрица коэффициентов становится единицами. Для этого мы определяем новый переменный вектор-столбец y соотношениями y _i = M _ii x _i.Делая эти подстановки в исходные уравнения системы, мы по существу просто разделите каждый элемент данного столбца в матрице коэффициентов на диагональный элемент этого столбца. Таким образом, мы приходим к соотношению форма y = Ay + b , где A – квадратная матрица с все элементы с нулевой диагональю и такие, что сумма элементов каждого столбец строго меньше 1. Как и в предыдущем случае, итерации это соотношение сходится при условии, что степени A приближаются к нулю.Сдача r обозначают вектор-строку, состоящую из всех единиц, вектор-строку rA состоит из сумм столбцов A , поэтому все условия строго меньше единицы, следовательно, вектор-строка ( rA ) A состоит из еще меньших членов и т. д. Таким образом, rA ⁿ стремится к нулю, поэтому A ⁿ приближается к нулю с увеличением n.

Учитывая, что исходная матрица коэффициентов строго с доминированием по диагонали либо по строкам, либо по столбцам, мы можем просто продолжить, как мы изначально, решая каждую строку для диагонального члена и настраивая повторение.Нормировать по столбцам необязательно, потому что функция Якоби метод будет сходиться независимо от того, нормализуем ли мы по строкам или по столбцам (предполагая диагональное преобладание в любом из этих двух направлений). Это потому что два описанных выше метода: нормализация по строкам и другие по столбцам приводят к нормированным матрицам с той же сходимостью характеристики. Чтобы доказать это, пусть D – диагональная матрица, отличная от нуля элементы являются обратными диагональным элементам матрицы M .Теперь пусть N обозначает матрицу M с диагональными членами. сняты, мы видим, что матричные изделия DN и ND представляют собой матрицы коэффициентов, нормированные по строкам и столбцам соответственно. В мощности любого из этих продуктов складываются из переменных коэффициентов D и N , поэтому они оба демонстрируют одинаковую сходимость.

Здесь мы также должны упомянуть, что, хотя Якоби метод состоит из оценки последовательных итераций всего состояния вектор на основе предыдущего вектора состояния, мы также могли бы оценить каждую строку система использует обновленные значения компонентов сразу после их расчета.Это известно как метод Гаусса-Зейделя , и он обычно сходится примерно в два раза быстрее, чем метод Якоби. Условием сходимости является по сути, то же самое, т.е. матрица коэффициентов должна быть диагональной. доминирующий.

Также следует отметить, что строгое диагональное преобладание достаточное условие сходимости, но не необходимое условие. Предполагая полносвязную систему уравнений, более слабую, но все же достаточную условием является то, что величина диагонального члена каждой строки (или каждого столбец), по крайней мере, равна сумме величин других элементов этой строки (или столбца), и по крайней мере для одной строки (или столбца) величина диагонального элемента строго превышает сумму величин другого элементы.Это можно доказать, как и в случае с предыдущими предложениями, но с учетом того, что сокращение размера срока в c или вектор r влияет на каждый столбец, имеющий вклад от этой строки, а затем каждая строка, имеющая вклад от любого из этих столбцов, будет пострадали и так далее. Предполагая, что система полностью подключена, отсюда следует, что все элементы A ⁿ переходят в ноль при увеличении n.

Теперь вернемся к нашему первоначальному примеру. уравнение (1), мы можем понять, почему методы Якоби и Гаусса-Зейделя не сходятся.В системе уравнений преобладают столбцы по диагонали, но не строго по диагонали доминирует любой столбец. В целом это верно для стационарные уравнения марковских моделей в расчетах надежности. Последовательные степени матрицы коэффициентов в (2) остаются ограниченными, но они колеблются бесконечно, как и следовало ожидать от матрицы со спектральным радиусом 1. В результате методы Якоби или Гаусса-Зейделя не очень подходят. для решения этой системы, даже если она имела ненулевое принудительное состояние (т.е., даже если бы он имел ненулевой вектор и в уравнении (3)). Похожие комментарии применяются к более сложным системам, таким как описанная в конце примечание о необнаруженных отказах от угрозы Защита.

Однако можно ли решить такие системы очень эффективно итерационным методом, используя однородность уравнения. Мы можем наложить вспомогательное условие для замены одного из строк, но лучше пока оставить это условие в стороне, и обратите внимание, что абсолютные значения переменных P _j равны не имеет значения, поскольку только их отношения имеют значение (в отношении этого система уравнений).Мы можем использовать этот факт, разделив все уравнения P ₀, что приводит к новой системе уравнений в отношениях c _j = P _j / P ₀. Теперь следствие этого нормализация состоит в том, что c ₀ тождественно равно 1, поэтому мы можем перепишите уравнение (2) в терминах переменных c _j и замените первая строка с тождеством, что дает уравнения

Вспомогательное условие подразумевает c ₀ + c ₁ + c ₂ = 1 / P ₀, поэтому мы имеем P _j = c _j / (с ₀ + с ₁ + с ₂).Для удобства мы можем оговаривают, что начальный вектор c был [1 0 0] ^T, что позволяет нам написать

Эта сумма для использования каждого из исходных уравнений в качестве повторения соотношения для вычисления последовательных c векторов, аналогично методу Якоби. (Конечно, мы также могли бы действовать построчно, используя каждый коэффициент как только он станет доступен, аналогично методу Гаусса-Зейделя, а метод результаты будут аналогичными, но с более быстрой сходимостью.) Поскольку в системе единственное нетривиальное стационарное решение, мы ожидаем, что матрица коэффициентов, чтобы сходиться к фиксированной матрице. Действительно, для этого простого система, имеем

где

Нечетные степени ведут себя аналогично.Обратите внимание, что продукт BC включает числители и знаменатели от 2-го и 3-го строки / столбцы, иллюстрирующие, почему не имеет значения, нормализовали ли мы строками или столбцами. Если исходная матрица строго диагонально доминирует либо по строкам, либо по столбцам, произведение BC меньше 1, и, следовательно, итерация сходится к

Нетрудно проверить, что этот результат эквивалентен явное решение, данное ранее.

В общем, для однородных линейных систем, представляющих установившееся состояние В марковских моделях исходная матрица коэффициентов доминирует по диагонали столбцы, хотя и не строго в каком-либо столбце. Однако неизменно переходит обратно в исходное состояние для любой модели с обратной связью, и эти представлены положительными компонентами в первой строке матрицы. Один раз эта строка установлена в ноль (за исключением первой записи, равной 1), в результате тогда столбцы будут доминировать строго по диагонали.После решения диагонали термины исходной однородной системы, и разделение на первые переменной (P ₀) получаем систему вида

Пусть C обозначает квадратную матрицу с 1 в верхнем левый угол и только другие ненулевые элементы которого находятся в первом столбце, и пусть H обозначает квадратную матрицу со всеми нулевыми элементами в первом строка, столбец и диагональ, и пусть Q обозначает квадратную матрицу с 0 в верхнем левом углу и только другие ненулевые элементы которого находятся в первый столбец.Тогда у нас есть тождества

и, конечно, сумма матрицы C и Q Матрица – это матрица C . В терминах этих типов матриц предыдущее уравнение можно записать как

Из 2 ⁿ терминов, полученных при повышении C + H в n-й степени, единственные члены, не содержащие CH (и, следовательно, единственный ненулевые члены) равны

Т.к. субматрица H строго по диагонали доминирующая (по столбцам), мы знаем, что H ⁿ обращается в ноль при n увеличивается, и геометрический ряд сходится, так что имеем

Обычно первый столбец очень быстро сходится в всего пять или десять итераций даже до того, как мощность H станет незначительный.О некоторых приложениях этого метода см. Примечание о полных марковских моделях и надежности.

Само собой разумеется, что этот метод имеет много общего с числовым методы решения потенциальных полей течения в вычислительной гидродинамике. Нам дана сетка с заданными значениями функции потока на границ, а затем значение каждого узла вычисляется как функция значения соседних узлов такие, что уравнение Лапласа (в дискретная форма) выполняется локально.Шагаем по сетке, накладывая определяющее уравнение в каждой точке, а затем повторите. В конце концов весь поле течения определяется так, чтобы однородное уравнение Лапласа было одновременно доволен по каждому пункту. Аналогичным образом в нашем итеративном подходе к решая однородные линейные системы, мы имеем набор узлов с управляющими уравнения, дающие значение каждого узла в терминах значений соседние узлы. Однако в этом случае нет понятия местности, потому что любой узел может быть функцией любого другого узла.В редких моделях количество зависимых узлов довольно ограничено, но они не обязательно должны быть рядом близость с точки зрения любого низкоразмерного пространства.

Вернуться в главное меню MathPages

Матрица: неоднородные линейные уравнения – определение, теорема, формулы, решенные примеры задач

Применения матриц: непротиворечивость системы линейных уравнений методом рангов

Во втором предыдущем разделе мы уже определили непротиворечивость системы линейного уравнения.В этом разделе мы исследуем это, используя метод ранжирования. Сформулируем следующую теорему без доказательства:

Теорема 1.14 (теорема Руше – Капелли)

Система линейных уравнений, записанная в матричной форме как AX = B , непротиворечива тогда и только тогда, когда ранг матрицы коэффициентов равен рангу расширенной матрицы; то есть ( A ) = ([ A | B ]).

Мы применим теорему в следующих примерах.

Неоднородные линейные уравнения

Пример 1.29

Проверьте соответствие следующей системы линейных уравнений и, если возможно, решите:

x + 2 y z – = 3, 3 x – y + 2 z = 1, x – 2 y + 3 z = 3, x – y + z +1 = 0 .

Решение

Здесь количество неизвестных равно 3.

Матричная форма системы AX = B, где

Применение метода исключения Гаусса к [A | B], мы получаем

В форме эшелона строки [A | B]. Итак, ρ ([A | B]). = 3

Итак, эшелонированная форма A есть. В нем три ненулевых строки. Итак, ρ (A) = 3.

Следовательно, ρ (A) = ρ ([A | B]) = 3.

Из эшелонированной формы запишем эквивалентную систему уравнений

x + 2y –z = 3, 7y-5z = 8, z = 4, 0 = 0.

Последнее уравнение 0 = 0 имеет смысл. Методом обратной подстановки получаем

z = 4

7y – 20 = 8 ⇒ y = 4,

x = 3-8 + 4 ⇒ x = −1.

Итак, решение (x = −1, y = 4, z = 4). (Обратите внимание, что A не является квадратной матрицей.)

Здесь данная система согласована, а решение уникально.

Пример 1.30

Проверьте соответствие следующей системы линейных уравнений и, если возможно, решите:

4 x – 2 y + 6 z = 8, x + y -3 z = −1, 15 x -3 y + 9 z = 21.

Решение

Здесь количество неизвестных равно 3.

Матричная форма системы: AX = B , где

Применение операций элементарной строки к расширенной матрице [ A | B ], получаем

Итак, ρ ( A ) = ρ ([ A | B ]) = 2 <3. Из эшелонированной формы получаем эквивалентные уравнения

x + y – 3 z = -1, y – 3 z = -2, 0 = 0.

Эквивалентная система имеет два нетривиальных уравнения и три неизвестных. Итак, одно из неизвестных должно быть зафиксировано по нашему выбору, чтобы получить два уравнения для двух других неизвестных. Мы произвольно фиксируем z как действительное число t , и получаем y = 3 t -2, x = -1- (3 t -2) + 3 t = 1 Таким образом, решение имеет вид ( x = 1, y = 3 t – 2, z = t ), где t является действительным.Приведенный выше набор решений представляет собой однопараметрическое семейство решений.

Здесь данная система непротиворечива и имеет бесконечно много решений, которые образуют однопараметрическое семейство решений.

Примечание

В приведенном выше примере квадратная матрица A является сингулярной, поэтому метод обращения матрицы не может применяться для решения системы уравнений. Однако применим метод исключения Гаусса, и мы можем решить, является ли система непротиворечивой или нет. Следующий пример также подтверждает превосходство метода исключения Гаусса над другими методами.

Пример 1.31

Проверьте соответствие следующей системы линейных уравнений и, если возможно, решите:

x – y + z = −9, 2 x -2 y + 2 z = −18, 3 x – 3 y + 3 z + 27 = 0.

Решение

Здесь количество неизвестных 3.

Матричная форма системы – это AX = B , где

Применение операций с элементарной строкой к расширенной матрице [ A | B ], получаем

Итак, ρ ( A ) = ρ ([ A | B ]) = 1 <3.

Из эшелонированной формы мы получаем эквивалентные уравнения x – y + z = -9, 0 = 0, 0 = 0.

Эквивалентная система имеет одно нетривиальное уравнение и три неизвестных.

Взяв произвольно y = с , z = t , мы получим x – с + t = -9; или x = -9 + s – t .

Итак, решение ( x = -9 + s – t , y = s , z = t ), где s и t – параметры .

Приведенный выше набор решений представляет собой семейство решений с двумя параметрами.

Здесь данная система уравнений непротиворечива и имеет бесконечно много решений, которые образуют двухпараметрическое семейство решений.

Пример 1.32

Проверьте согласованность следующей системы линейных уравнений

x – y + z = −9, 2 x – y + z = 4, 3 x – y + z = 6, 4 x – y + 2 z = 7.

Решение

Здесь количество неизвестных равно 3.

Матричная форма системы уравнений: AX = B , где

Применение операций элементарной строки к расширенной матрице [A | B ], получаем

Итак, ρ (A) = 3 и ρ ([A | B]) = 4. Следовательно, ρ (A) ≠ ρ ([A | B]).

Если мы запишем эквивалентную систему уравнений, используя форму эшелона, мы получим

x – y + z = -9, y – z = 22, z = -23 , 0 = -11.

Последнее уравнение противоречит.

Итак, данная система уравнений противоречива и не имеет решения. По теореме Руше – Капелли мы имеем следующее правило:

· Если в системе уравнений n неизвестных и ρ ( A ) = ρ ([ A | B ] ) = n , то система AX = B непротиворечива и имеет уникальное решение.

· Если в системе n неизвестных AX = B и ρ ( A ) = ρ ([ A | B ]) = n – k , k ≠ 0, тогда система является непротиворечивой и имеет бесконечно много решений, и эти решения образуют семейство параметров k .В частности, если в системе уравнений 3 неизвестных и ρ ( A ) = ρ ([ A | B ]) = 2, то система имеет бесконечно много решений и эти решения образуют семейство с одним параметром. Таким же образом, если в системе уравнений 3 неизвестных и ρ ( A ) = ρ ([ A | B ]) = 1, то система имеет бесконечно много решений, и эти решения образуют двухпараметрическое семейство.

· Если ρ ( A ) ≠ ρ ([ A | B ]), то система AX = B несовместима и не имеет решения.

Пример 1.33

Найдите условие на a, b и c так, чтобы следующая система линейных уравнений имела одно параметрическое семейство решений: x + y + z = a, x + 2 y + 3z = b , 3x + 5 y + 7z = c.

Решение

Здесь количество неизвестных равно 3.

Матричная форма системы: AX = B , где A =

Применение операций элементарной строки к расширенной матрице [ A | B ], получаем

Для того, чтобы система имела одно параметрическое семейство решений, мы должны иметь ρ ( A ) = ρ ([ A , B ] ) = 2. Итак, третья строка в форме эшелона должна быть нулевой строкой.

Итак, c -2 b – a = 0 ⇒ c = a + 2 b .

Пример 1.34

Исследуйте, для каких значений λ и μ система линейных уравнений

x + 2 y + z = 7, x + + + + λ z = μ , x + 3 y -5 z = 5 имеет

(i) нет решения (ii) уникальное решение (iii) бесконечное количество решений.

Решение

Здесь количество неизвестных равно 3.

Матричная форма системы: AX = B , где A =

Применение операций элементарной строки к расширенной матрице [ A | B ], получаем

(i) Если λ = 7 и μ 9, то ρ (A) = 2 и ρ ([A | B]) = 3. Итак, ρ (A) ≠ ρ ([A | B]). Следовательно, данная система противоречива и не имеет решения.

(ii) Если λ ≠ 7 и m – любое действительное число, то ρ (A) = 3 и ρ ([A | B]) = 3.

Итак, ρ (A) = ρ ([A | B]) = 3 = Количество неизвестных. Следовательно, данная система непротиворечива и имеет единственное решение.

(iii) Если λ = 7 и μ = 9, то ρ (A) = 2 и ρ ([A | B]) = 2.

Итак, ρ (A) = ρ ([A | B]) = 2 <Количество неизвестных. Следовательно, данная система непротиворечива и имеет бесконечное число решений.

Системы линейных уравнений: исключение Гаусса

Системы линейных уравнений: исключение Гаусса Системы линейных уравнений: исключение Гаусса Довольно сложно

Просмотры 29 Загрузок 0 Размер файла 164KB

Отчет DMCA / Авторское право

СКАЧАТЬ ФАЙЛ

Рекомендовать истории
Предварительный просмотр цитирования
Системы линейных уравнений: исключение Гаусса
Системы линейных уравнений: исключение Гаусса Нелинейные системы уравнений довольно сложно решать, в то время как линейные системы довольно легко изучать.Существуют численные методы, которые помогают аппроксимировать нелинейные системы линейными в надежде, что решения линейных систем достаточно близки к решениям нелинейных систем. Мы не будем здесь это обсуждать. Вместо этого мы сосредоточим наше внимание на линейных системах. Для простоты мы ограничимся тремя, максимум четырьмя неизвестными. Читатель, интересующийся случаем большего количества неизвестных, может легко развить следующие идеи. Определение. Уравнение ax + by + cz + dw = h
, где a, b, c, d и h – известные числа, а x, y, z и w – неизвестные числа, называется линейным уравнением.Если h = 0, линейное уравнение называется однородным. Линейная система – это набор линейных уравнений, а однородная линейная система – это набор однородных линейных уравнений. Например,
и
– линейные системы, а
– нелинейная система (из-за y2). Система
представляет собой однородную линейную систему. Матричное представление линейной системы Матрицы помогают переписать линейную систему в очень простой форме. Затем для решения систем можно использовать алгебраические свойства матриц.Сначала рассмотрим линейную систему
Установите матрицы
Используя умножение матриц, мы можем переписать линейную систему выше как матричное уравнение
Как видите, это намного лучше, чем уравнения. Но иногда стоит решить систему напрямую, минуя матричную форму. Матрица A называется матричным коэффициентом линейной системы. Матрица C называется неоднородным членом. Когда, линейная система однородна. Матрица X – это неизвестная матрица.Его записи являются неизвестными линейной системы. Расширенная матрица, связанная с системой, представляет собой матрицу [A | C], где
В общем случае, если линейная система имеет n уравнений с m неизвестными, то матричный коэффициент будет матрицей nxm, а расширенная матрица – nx (m + 1) матрица. Теперь обратим внимание на решения системы. Определение. Две линейные системы с n неизвестными называются эквивалентными тогда и только тогда, когда они имеют один и тот же набор решений. Это определение важно, поскольку идея решения системы состоит в том, чтобы найти эквивалентную систему, которую легко решить.Вы можете спросить, как мы сможем создать такую систему? Легко, мы делаем это с помощью элементарных операций. Действительно, ясно, что если мы поменяем местами два уравнения, новая система все равно будет эквивалентна старой. Если мы умножим уравнение на ненулевое число, мы получим новую систему, по-прежнему эквивалентную старой. И, наконец, заменив одно уравнение суммой двух уравнений, мы снова получим эквивалентную систему. Эти операции называются элементарными операциями над системами. Посмотрим, как это работает в конкретном случае.Пример. Рассмотрим линейную систему
Идея состоит в том, чтобы сохранить первое уравнение и поработать над двумя последними. При этом мы попытаемся убить одного из неизвестных и решить два других. Например, если мы сохраним первое и второе уравнение и вычтем первое из последнего, мы получим эквивалентную систему.
Затем мы сохраняем первое и последнее уравнение и вычитаем первое из второго. Получаем эквивалентную систему
Теперь сосредоточимся на втором и третьем уравнении.Повторяем ту же процедуру. Попробуйте убить одного из двух неизвестных (y или z). Действительно, мы сохраняем первое и второе уравнение и добавляем второе к третьему после умножения его на 3. Получаем
Это, очевидно, подразумевает z = -2. Из второго уравнения мы получаем y = -2, и, наконец, из первого уравнения получаем x = 4. Следовательно, линейная система имеет одно решение
Переход от последнего уравнения к первому при решении для неизвестных называется обратным решением. Имейте в виду, что линейные системы, для которых матричный коэффициент является верхнетреугольным, легко решить.Это особенно верно, если матрица имеет эшелонированную форму. Таким образом, фокус состоит в том, чтобы выполнить элементарные операции по преобразованию исходной линейной системы в другую, для которой матрица коэффициентов имеет эшелонированную форму. Используя наши знания о матрицах, можем ли мы в любом случае переписать то, что мы сделали выше, в матричной форме, которая упростит нашу нотацию (или представление)? Действительно, рассмотрим расширенную матрицу
. Выполним некоторые элементарные операции со строками над этой матрицей. Действительно, если мы сохраним первую и вторую строки и вычтем первую из последней, мы получим
Далее мы сохраняем первую и последнюю строки и вычитаем первую из второй.Получаем
Затем мы сохраняем первую и вторую строки и добавляем вторую к третьей после умножения ее на 3, чтобы получить
Это треугольная матрица, которая не имеет эшелонированной формы. Линейная система, для которой эта матрица является расширенной, равна
. Как вы можете видеть, мы получили ту же систему, что и раньше. Фактически мы следовали тем же элементарным операциям, что и выше. На каждом этапе новая матрица была в точности расширенной матрицей, связанной с новой системой. Это показывает, что вместо того, чтобы писать системы снова и снова, легко поиграться с элементарными операциями со строками, и как только мы получим треугольную матрицу, напишем связанную линейную систему, а затем решим ее.Это называется исключением по Гауссу. Подведем итоги процедуры: Исключение Гаусса. Рассмотрим линейную систему. 1. 2. 3. 4.
Построить расширенную матрицу для системы; Используйте операции с элементарными строками, чтобы преобразовать расширенную матрицу в треугольную; Запишите новую линейную систему, для которой треугольная матрица является связанной расширенной матрицей; Решите новую систему. Вам может потребоваться присвоить некоторые параметрические значения некоторым неизвестным, а затем применить метод обратной подстановки для решения новой системы.
Пример. Решите следующую систему с помощью исключения Гаусса
Расширенная матрица
Мы используем элементарные операции со строками, чтобы преобразовать эту матрицу в треугольную. Мы сохраняем первую строку и используем ее для получения всех нулей в любом месте первого столбца. У нас есть
Далее мы сохраняем первую и вторую строки и стараемся иметь нули во втором столбце. Получаем
Далее сохраняем первые три строки. Добавляем последний к третьему, чтобы получить
Это треугольная матрица.Соответствующая система:
. Очевидно, что v = 1. Положим z = s и w = t, тогда мы получим
. Первое уравнение подразумевает
x = 2 +
y +
zw-
Используя алгебраические манипуляции, мы получаем
x = –
Собирая все вместе, получаем
–
s – t.
v.
Пример. Используйте исключение Гаусса для решения линейной системы
Соответствующая расширенная матрица –
Мы сохраняем первую строку и вычитаем первую строку, умноженную на 2, из второй строки.Получаем
Это треугольная матрица. Соответствующая система:
Очевидно, второе уравнение означает, что эта система не имеет решения. Следовательно, эта линейная система не имеет решения. Определение. Линейная система называется несовместимой или переопределенной, если она не имеет решения. Другими словами, набор решений пуст. В противном случае линейная система называется согласованной. Следуя приведенному выше примеру, мы видим, что если мы выполняем элементарные операции со строками над расширенной матрицей системы и получаем матрицу, одна из строк которой равна, то система несовместима.
, где
,
Система линейных уравнений и обращения матриц
Система линейных уравнений и обращения матриц
Этот обучающий объект JavaScript E-labs предназначен для нахождения решения систем линейных уравнений, содержащих до трех уравнений с тремя неизвестными. Это также позволяет нам найти обратную матрицу.
Другие учебные объекты JavaScript для принятия решений в этой серии классифицируются по различным областям приложений в разделе MENU на этой странице.
При вводе данных для перехода от ячейки к ячейке в матрице данных используйте клавишу Tab, , а не клавиши со стрелками или клавиши ввода.
Инструкции и приложения:
Имена неизвестных переменных: X1, X2, X3, .. и X10, в зависимости от того, есть ли у вас одно уравнение, два уравнения или три уравнения с одной неизвестной, двумя неизвестными или тремя неизвестными переменными, соответственно.
Начиная с левого верхнего угла, при необходимости замените столько нулей в матрице данных на коэффициенты неизвестных переменных в уравнениях вместе с их значениями в правой части.Матрица коэффициентов должна быть квадратной матрицей, появляющейся в верхнем левом углу матрицы данных, поэтому не оставляйте пустых строк между ними.
JavaScript основан на строковых операциях Гаусса-Джордана (GJ). Требование для операций GJ состоит в том, что первый элемент в матрице коэффициентов должен быть ненулевым. Поэтому сначала введите коэффициенты всех уравнений с ненулевым коэффициентом X1; затем введите все остальные уравнения. То есть любое уравнение с нулевыми коэффициентами для X1 должно появиться в конце таблицы ввода данных.
Численный пример 1: Рассмотрим следующую систему уравнений:
Х2 + Х3 = 5
3X1 + X3 = 6
-X1 + X2 = 1
Матрица коэффициентов переменных:
0 1 1
3 0 1
-1 1 0
Первая запись первого столбца равна нулю, хотя в ней всегда есть хотя бы один ненулевой элемент. Следовательно, мы должны перестроить систему уравнений таким образом, чтобы любое уравнение с нулевым коэффициентом X1 появилось среди последней системы уравнений.То есть, рассматривая эквивалентную систему уравнений:
3X1 + X3 = 6
-X1 + X2 = 1
Х2 + Х3 = 5
Решите эту эквивалентную систему уравнений, введя ее коэффициент и значения RHS в таблицу ввода данных, затем нажмите кнопку «Рассчитать». На выходе получается решение: X1 = 1, X2 = 2 и X3 = 3, которое можно проверить с помощью подстановок.
Нахождение обратной матрицы с помощью решателя системы уравнений: Чтобы найти обратную квадратную матрицу размера n, решите n систем уравнений с единичным вектором в качестве правой части.Следующий числовой пример иллюстрирует процесс:
Числовой пример 2: Предположим, мы хотим найти обратную (A ^-1) следующую матрицу (если она существует) A:
В общем, чтобы найти A ^-1, столбец за столбцом, решите n систем уравнений, имеющих матрицу коэффициентов A, но с n различными единичными векторами в качестве их значения RHS.
Для этого числового примера мы должны решить следующие две системы уравнений:
2X1 + X1 = 1
Х1 – Х2 = 0
а также
2X1 + X1 = 0
Х1 – Х2 = 1
Обратите внимание, что коэффициенты переменных X1 и X2 представляют собой матрицу A в обеих системах уравнений, однако RHS – это два единичных вектора в n = 2-мерном пространстве.
Решения, соответствующие приведенной выше инструкции, первой и второй систем уравнений обеспечивают первый и второй столбцы матрицы A ^-1.
Чтобы найти первый столбец A ^-1, решите:
2X1 + X1 = 1
Х1 – Х2 = 0
Это дает X1 = 1/3, X2 = 1/3. Чтобы найти второй столбец A ^-1, решите:
2X1 + X1 = 0
Х1 – Х2 = 1
Это дает X1 = 1/3, X2 = -2/3.Следовательно, A ^-1 p равно
1/3 1/3
А ^-1 =
1/3 -2/3
Примечание: Матрица, имеющая обратную, называется невырожденной или обратимой. Матрица называется сингулярной, если у нее нет обратной.Например, следующая матрица является сингулярной:
1 6 4
2 4 -1
-1 2 5
Следовательно, при применении описанной выше процедуры обращения матрицы, если матрица является сингулярной, то по крайней мере одна из систем уравнений не имеет решения.
Для редактирования ваших данных, включая добавление / изменение / удаление, вам не нужно нажимать кнопку «очистить» и заново вводить данные заново.Вы можете просто добавить, изменить число на другое в той же ячейке или удалить число из ячейки, установив его значение на ноль. После редактирования нажмите кнопку «рассчитать».
Это полезно, например, в найти инверсию матрицы A _10×10, где нам нужно изменить только значения RHS.
Для расширенного редактирования или использования JavaScript для нового набора данных используйте кнопку «Очистить».
Для технических подробностей, назад:
Темы линейной алгебры
Пожалуйста, отправьте свои комментарии по адресу:
Профессор Хоссейн Аршам
МЕНЮ
Заявление об авторских правах. Добросовестное использование материалов, представленных на этом веб-сайте, в соответствии с Принципами добросовестного использования образовательных мультимедиа от 1996 года, разрешено только в некоммерческих и учебных целях.
Этот сайт может быть переведен и / или отражен без изменений (включая эти уведомления) на любом сервере с открытым доступом. Все файлы доступны по адресу http://home.ubalt.edu/ntsbarsh/Business-stat для зеркалирования.
Пожалуйста, пришлите мне по электронной почте свои комментарии, предложения и проблемы. Спасибо.
Вернуться к:
Домашняя страница доктора Аршама
EOF: 1994-2015.
Система неоднородных линейных уравнений
Чудеса техники.com »Математика
Неоднородные линейные уравнения : –
a ₁ x + b ₁ y + c ₁ z = d ₁
a ₂ x + b ₂ y + c ₂ z = d ₂
a ₃ x + b ₃ y + c ₃ z = d ₃ называется системой ненулевых однородных линейных уравнений.
, то это можно записать как AX = B, где A называется матрицей коэффициентов.
Согласованная и несовместимая система: –
Если система линейных уравнений имеет решение, то система называется непротиворечивой.В противном случае говорят, что это несовместимая система.
Различные методы решения неоднородной системы: –
Различные методы решения неоднородной системы следующие:
Метод инверсии матрицы: –
Предположим, что данная система AX = B и A не является -особое, то обратное к A существует.
Правило Крамера: – Предположим, что задана система
a ₁ x + b ₁ y + c ₁ z = d ₁
a ₂ x + b ₂ y + c ₂ z = d ₂
a ₃ x + b ₃ y + c ₃ z = d ₃ и Δ, Δ ₁, Δ ₂, Δ ₃ являются как показано ниже, затем умножая уравнения на A ₁, A ₂, A ₃, а затем, добавляя, мы получаем x (a ₁ A ₁ + a ₂ A ₂ + a ₃ A ₃) + y (b ₁ A ₁ + b ₂ A ₂ + b ₃ A ₃) + z (c ₁ A ₁ + c ₂ A ₂ + c ₃ A ₃) = d ₁ A ₁ + d ₂ A ₂ + d ₃ A ₃
x.Δ + y.0 + z.0 = Δ ₁ -> x = Δ ₁ / Δ
Аналогичным образом умножая уравнения на B ₁, B ₂, B ₃, а затем добавляя мы получим y = Δ ₂ / Δ и, умножив C ₁, C ₂, C ₃, получим z = Δ ₃ / Δ.
Метод Гаусса Джордана: Для этого метода выполняются преобразования элементарных строк. Следующие действия называются преобразованиями элементарных строк:
1-> Поменять местами две строки.
2-> Умножение строки с ненулевой константой K.
3-> Сложение произведений элементов строки и константы K с соответствующими элементами некоторой другой строки.
Расширенная матрица: –
Для неоднородной линейной системы AX = B следующая матрица называется расширенной матрицей.
Рабочее правило: –
Предположим, данная система –
a ₁ x + b ₁ y + c ₁ z + d ₁ = 0
a ₂ x + b ₂ y + c ₂ z + d ₂ = 0
a ₃ x + b ₃ y + c ₃ z + d ₃ = 0
Применяя преобразование элементарной строки, мы должны передать Расширенная матрица в стандартную форму решения, как указано ниже, после чего мы можем получить решение как x = α | y = β | z = γ
.

Решение систем линейных уравнений методом Гаусса

Как найти фундаментальную систему решений линейного уравнения?

Свойства систем линейных однородных уравнений

Алгоритм решения систем линейных однородных уравнений

Системы линейных однородных уравнений

Содержание:

Системы линейных однородных уравнений

Однородные линейные системы. Однородные системы линейных алгебраических уравнений

Свойства систем линейных однородных уравнений

Алгоритм решения систем линейных однородных уравнений

Как найти фундаментальную систему решений линейного уравнения?

Система линейная – Справочник химика 21

Фундаментальная система решений (конкретный пример). Как найти нетривиальное и фундаментальное решение системы линейных однородных уравнений

Решение систем линейных уравнений методом Гаусса

Свойства систем линейных однородных уравнений

Алгоритм решения систем линейных однородных уравнений

История

Линейные уравнения

Системы линейных алгебраических уравнений

Матрицы

Метод Гаусса

Метод Крамера

Другие методы

Сложные случаи

Заключение

Несогласованные и зависимые системы: использование исключения Гаусса – видео и стенограмма урока

Исключение Гаусса

Несогласованное системное решение

Dependent System Solution

Резюме урока

Результаты обучения

Python реализует метод исключения Гаусса для поиска решения линейных уравнений

Введение в метод исключения Гаусса

содержание

ядро ​​

Идеи алгоритмов

алгоритм

Результат выполнения кода

Итерационные решения однородных линейных систем

Матрица: неоднородные линейные уравнения – определение, теорема, формулы, решенные примеры задач

Применения матриц: непротиворечивость системы линейных уравнений методом рангов

Теорема 1.14 (теорема Руше – Капелли)

Пример 1.33

Пример 1.34

Решение

Системы линейных уравнений: исключение Гаусса

Система линейных уравнений и обращения матриц

Система неоднородных линейных уравнений

Согласованная и несовместимая система: –

Различные методы решения неоднородной системы: –

Расширенная матрица: –

Рабочее правило: –

Оставить комментарий Отменить ответ

ядро