Решение систем методом гаусса жордана онлайн: Метод Жордана-Гаусса онлайн

1.Решение систем линейных уравнений методом гаусса – жордана

1.1. Основные понятия

Система m линейных уравнений с n неизвестными имеет следующий вид:

Здесь х_j ( j=1, n ) – переменные ( или неизвестные) системы, а_ij ( i =1,m; j = 1,n ) – коэффициенты при переменных, в_i ( i =1,m ) – свободные члены.

Решением системы ( І.І) называется всякий набор значений переменных х₁, х₂, …, х_n, при котором все уравнения превращаются в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной – в противном случае.

Например, система

совместна, так как она имеет, в частности, такое решение:

х₁ = 1; х₂ = 2; х₃ = 0 . Система же

несовместна.

Две системы линейных уравнений называются равносильными, если каждое решение одной из них является решением другой, и наоборот. Если какое-либо уравнение системы умножить на постоянный множитель λ

≠ 0 , то получится система уравнений, равносильная исходной. Аналогично, если к какому-либо уравнению системы прибавить другое уравнение системы, то получится система, равносильная исходной.

Наконец если, в системе есть уравнение вида

0∙х₁ + 0∙х₂ + … + 0∙ х_n = 0, то такое уравнение можно убрать, получив систему, равносильную исходной.

1.2. Приведение системы линейных уравнений к жордановой форме

Процесс отыскания решения системы линейных уравнений начинается с того, что система приводится к жордановой форме.

Определение. Жордановой формой системы (I.I) называется систе­ма линейных уравнений, обладающая следующими свойствами:

а) она равносильна системе (I.I)

б) в каждом уравнении жордановой формы есть такая переменная, которая входит в это уравнение с коэффициентом 1, а в остальные уравнения – с коэффициентом 0.

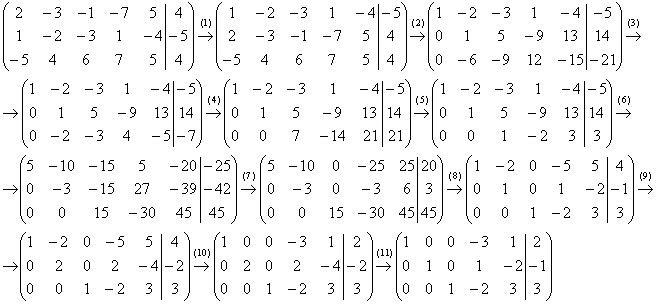
Так, если системе (I.I) равносильна следующая система линейных уравнений:

(1.2)

то (І.2) есть жорданова форма для (I.I). При этом переменные х_1, х₂,… ,х_к называются базисными, остальные переменные х_к+1,…, х_n называются свободными

. Жорданова форма всегда является совместной системой линейных уравнений. Действительно, система (І.2) имеет следующее решение:

(І.3)

Так как система (І.2) равносильна системе ( І.І ) , то (І.3) является решением системы (І.І).

Таким образом, если для системы линейных уравнений ( І.І ) существует жорданова форма, то ( І.І ) – совместная система. Несовместная система жордановой формы не имеет.

Покажем, что любую совместную систему можно привести к жордановой форме. Это достигается методом Гаусса-Жордана, который состоит в следующем.

Рассмотрим первое уравнение системы (І.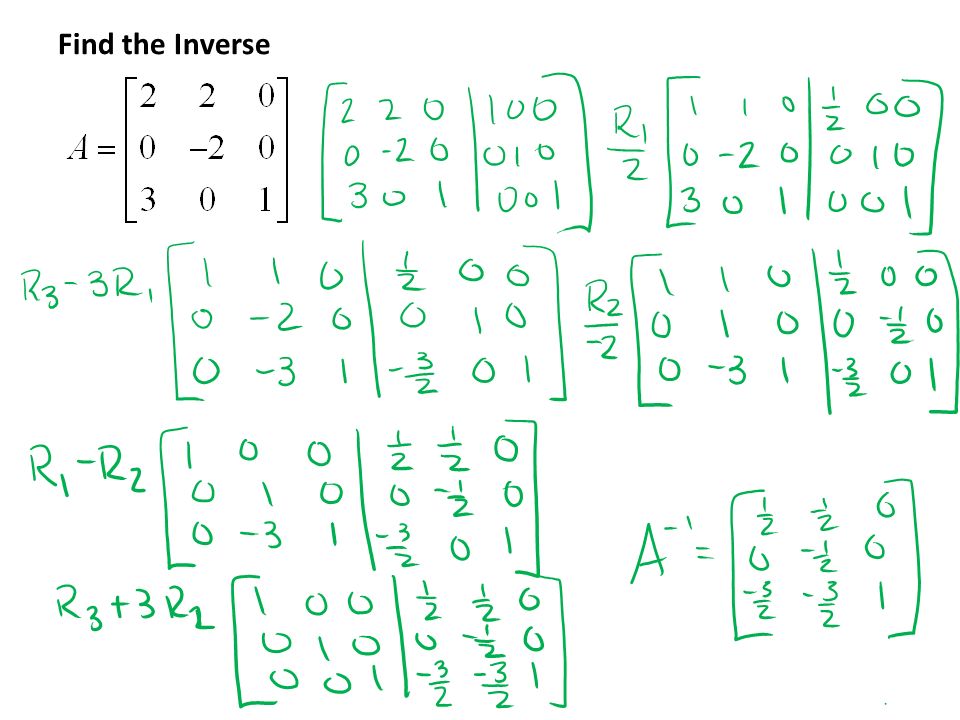

І). Выберем в нем переменную, коэффициент при которой отличен от нуля. Предположим, что а₁₁ ≠ 0. Поделим уравнение на а₁₁.

Получим уравнение

х₁+ а₁₂х₂ + … + а_1nх_n = в₁ (І.4)

Будем переменную х₁ делать базисной в жордановой форме. Для этого ее нужно исключить из остальных уравнений системы. Чтобы исключить х₁ из второго уравнения, умножим уравнение (І.4) на -а₂₁ и сложим со вторым уравнением. Затем исключим х

1 из третьего уравнения, для чего уравнение (І.4) умножим на –а₃₁ и сложим с третьим уравнением. Аналогично переменная х₁ исключается из остальных уравнений. Таким образом, взяв в качестве “ведущего” первое уравнение и проведя серию “жордановых исключений”, мы получим равносильную (I.I) систему уравнений, в которой x₁ входит в первое уравнение с коэффициентом 1 , а в остальные уравнения – с коэффициентом 0.

После этого выбираем в качестве ведущего второе уравнение полученной системы. В этом уравнении берем коэффициент, отличный от нуля (пусть это коэффициент при х

2), делим уравнение на этот коэффициент и затем исключаем х₂ из всех остальных уравнений (в том числе и из первого). Затем в качестве ведущего выбираем третье уравнение и т.д.

Если на некотором шаге возникнет уравнение вида

0∙х₁ + 0∙х₂ + … + 0∙ х_n = 0 (І.5)

то удаляем его из системы. Если же возникнет уравнение вида

0∙х₁ + 0∙х₂ + … + 0∙ х_n = b ≠ 0, то это свидетельствует о несовместности исходной системы ( І.І), а несовместная система к жордановой форме не приводится.

Таким образом, метод Гаусса-Жордана совместную систему линейных уравнений приводит к жордановой форме, а в случае несовместности системы обнаруживает несовместность.

Ясно, что в жордановой форме число уравнений не может быть больше числа уравнений в исходной системе. Так, если система (1.2) является жордановой формой для системы (I.I), то , причем строгое неравенство имеет место тогда, когда на некоторых шагах жордановой процедуры удалялись уравнения вида (1.5).

Очевидно, одна и та же система может иметь много различных жордановых форм.

Пример. Привести к жордановой форме

Выберем в качестве ведущего первое уравнение, а в качестве базисной переменной – переменную х_1. Поделим первое уравнение на (-1) (коэффициент при х₁), получим:

Умножим это уравнение на (+5) и прибавим ко второму уравнению, затем умножим его на (-3) и прибавим к третьему уравнению.

Получим систему:

Теперь сделаем ведущим второе уравнение, а базисной переменной – переменную . Поделив второе уравнение на (-8) и исключивиз первого и третьего уравнений, получим систему:

Наконец, в третьем уравнении выбираем в качестве базисной переменную.

Поделим это уравнение на (-1) и исключимиз остальных уравнений. Получим жорданову форму:

Переменные являются базисными, переменная- свободной.

Метод Жордана-Гаусса – 📙 Математика

1. Общие понятия
2. История появления метода Жордана-Гаусса
3. Использование метода Жордана-Гаусса на практике
4. Суть метода Жордана-Гаусса
5. Получение обратных матриц с применением метода Жордана-Гаусса

Методом Жордана-Гаусса является такой метод решения линейных уравнений, при котором полностью исключаются неизвестные. Этот метод есть производным от метода Гаусса, но в данной модификации элементарные преобразования производят дальше.

Возникновение метода Гаусса своими корнями уходит в далекие годя до нашей эры. Он описан еще в древней китайской книге, которая называется «Математика в девяти книгах», написанной примерно в 150 году до нашей эры. В этом трактате собраны различные математические задачи и методы их решения.

В Европе первым, кто занялся исследованием данного метода, стал Исаак Ньютон. Он изучал множество древних математических книг, но при этом не обнаружил ни одного способа решения систем уравнений с большим числом переменных, и предложил способ такого решения в своей работе, которая была обнародована в 1707 году. Его метод распространился на протяжении века в различных пособиях и справочниках по арифметике.

Немецким ученым К.Ф. Гауссом в 1810 году был усовершенствован данный метод и опубликован на ряду с другими его работами, после чего метод преобразования в треугольную матрицу нашел массовое распространение и был назван его именем.

Затем во второй половине ХІХ столетия ученый Жордан доработал метод Гаусса, трансформировав его в более совершенный метод приведения к диагональной матрице. Интересно, что на ряду с ним точно то же совершил еще один ученый, но все же название метода на сегодняшний день получило имена Гаусса и Жордана.

Метод Жордана-Гаусса имеет широкое применение для расчета систем линейных уравнений, создания обратных матриц, изучения рангов матриц. Зачастую именно с его помощью решаются инженерные задачи с большим количеством неизвестных.

При расчете полученных из инженерно-технических задач систем уравнений, сначала выбирают самые большие за модулем переменные для минимизации погрешности, далее поочередно удаляют не нужные переменные из матрицы.

Также при расчетах инженерно-технологических задач этим методом, пользуются различными алгоритмами программирования, что дает возможность получения результатов с меньшей погрешностью.

Применяя метода Жордана-Гаусса, мы получаем матрицу, диагональ которой состоит из единиц, а все остальные коэффициенты – нули, к примеру:

\(A = \begin{array}{ccc|c} 1& 0 &0 &a_1 \\ 0& 1 &0 &a_2 \\ 0 & 0 & 1 &a_3 \end{array}\)

Отличается данный метод от метода Гаусса тем, что в последнем к нулям приводится лишь нижняя часть матрицы, в то время, как при использовании метода Жордана-Гаусса к нулям приводится также и верхняя часть матрицы.

Оба метода применяют для определения базисного и общего решений системы уравнений.
Базисное решение являет собой такое решение системы уравнений, когда все свободные переменные равняются нулю.

Общее решение системы уравнений являет собой такое решение, когда основные переменные выражают через свободные.

Еще одним вариантом применения метода Жордана-Гаусса есть получение обратных матриц.

Обратной называют такую матрицу, результатом перемножения которой с заданной матрицей будет единичная матрица. Данная матрица может существовать исключительно для квадратных и невырожденных матриц.

Суть метода определения обратной матрицы состоит вот в чем: заданную и единичную матрицы одновременно преобразовывают элементарными действиями с использованием метода Жордана-Гаусса. В итоге получают две матрицы – единичную диагональную и обратную.

Рассмотрим последовательность действий для получения обратной матрицы с применением метода Жордана-

Гаусса на примере заданной квадратной матрицы:
\(\begin{array}{cc} 1& 2 \\ 3 & 4 \\ \end{array}\)
1) Записываем заданную и единичную матрицы:
\(\begin{array}{cc|cc} 1& 2 & 1& 0\\ 3 & 4& 0 & 1 \\ \end{array}\)
2) К последней строке плюсуем первую, перемноженную на -3:
\(\begin{array}{cc|cc} 1& 2 & 1 & 0\\ 0 & -2 & -3 & 1 \\ \end{array}\)
3) После этого к первой строчке добавляем последнюю:
\(\begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & -2 & -3 & 1 \\ \end{array}\)
4) Поделим вторую строчку на -2:
\(\begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & 1& 3/2 & -1/2 \\ \end{array}\)
5) В итоге обратная матрица преобразуется в следующий вид:
\(\begin{array}{cc} -2& 1 \\ 3/2 & -1/2 \\ \end{array}\)

Для расчета систем линейных уравнений методом Жордана-Гаусса матрицу преобразуют при помощи тех же элементарных преобразований, как и при методе Гаусса, таких как:

• перемножение любой строчки на число, не равное нулю;
• прибавление или отнимание любых строк;
• перестановка строк местами;
• удаление строк, что состоят из одних нулей;
• удаление пропорциональных строчек, которые можно считать лишними.

Таким образом, для расчета системы линейных уравнений методом Жордана-Гаусса, требуется провести череду элементарных преобразований матрицы, полученной после использования метода Гаусса.

Порядок действий во время расчета системы линейных уравнений методом Жордана-Гаусса:

1. Находят строку, у которой первый коэффициент не равняется нулю и максимально приближается по значению к единице. Эту строчку ставят в верхний ряд. Этот элемент имеет название «разрешающий».
2. Разрешающий элемент преобразуют до единицы делением или умножением всей первой строчки.
3. Из всех остальных строчек отнимают первую, перемноженную на коэффициент, что стоит вначале строки, которую изменяют.
4. Все то же проделывают до получения треугольной матрицы, иными словами, до тех пор, пока все элементы слева от главной диагонали станут равняться нулю. Эти все действия называют прямым ходом преобразования матрицы.
5. Затем отнимают нижнюю строчку от предпоследней, умножив нижнюю на последний коэффициент предпоследней строчки. Все то же повторяют снизу-вверх, получая диагональную матрицу. Эти действия называются обратным ходом преобразования матрицы.

Рассмотрим несколько задач по расчету системы линейных уравнений.

Задача 1. Задана система линейных уравнений:

\(\begin{cases} 3x_1 + 2x_2 – 5x_3 = -1 \\ 2x_1 – x_2 + 3x_3 = 13 \\ x_1 + 2x_2 – x_3 = 9 \end{cases}\)

Найти переменные.
Преобразуем систему в расширенную матрицу:

\(\begin{array}{ccc|c} 3& 2 & -5 & -1\\ 2 & -1& 3 & 13 \\ 1 & 2 & -1 & 9 \\ \end{array}\)

Применяя метод Гаусса, получаем матрицу следующего вида:

\(\begin{array}{ccc|c} 1& 2 & -1 & 9\\ 0 & 1& -1 & 1 \\ 0 & 0& 1 & 4 \\ \end{array}\)

Далее применяем обратный ход преобразования матрицы и получаем диагональную матрицу. Сперва к первой и средней строкам прибавим нижнюю:

\(\begin{array}{ccc|c} 1& 2 & 0 & 13\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}\)

Затем среднюю строку перемножим на -2 и приплюсуем ее к верхней:

\(\begin{array}{ccc|c} 1& 0 & 0 & 3\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}\)

В итоге получим такую систему:

\(\begin{cases} x_1 = 3 \\ x_2 = 5 \\ x_3 = 4 \end{cases}\)

Эта система и будет являться решением.

Задача 2. Задана система линейных уравнений:

\(\begin{cases} x_1 – 8x_2 + x_3 – 9x_4 = 6 \\ x_1 – 4x_2 – x_3 – 5x_4 = 2 \\ -3x_1 + 2x_2 + 8x_3 + 5x_4 = 4 \\ 5x_1 + 2x_2 + 2x_3 + 3x_4 = 12 \end{cases}\)

Найти ее решение.

Записываем систему в форме матрицы:

\(\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ -1 & -4& -1 & -5 & 2 \\ -3 & 2 & 8 & 5 & 4 \\ 5& 2 & 2 & 3 & 12 \\ \end{array}\)

Преобразовываем матрицу прямым ходом до треугольной:

Ко второй строке добавляем первую, перемноженную на -1. К третьей строке добавляем первую, перемноженную на 3, а к нижней строке добавляем верхнюю, перемноженную на -5:

\(\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 4& -2 & 4 & -4 \\ 0 & -22 & 11 & -22 & 22 \\ 0& 42 & -3 & 48 & -18 \\ \end{array}\)

Разделим вторую строку на 2, третью – на 11, четвертую – на 3. Получаем следующее:

\(\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0 & -2 & 1 & -2 & 2 \\ 0& 14 & -1 & 16 & -6 \\ \end{array}\)

Убираем третью строку, так как она является пропорциональной ко второй, к нижней строке добавляем вторую, умноженную на -7:

\(\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 6 & 2 & 8 \\ \end{array}\)

Разделим на два нижнюю строку:

\(\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}\)

В преобразованной матрице не равное число строк и переменных, это означает, что для нее существует бесконечное множество решений. Преобразовываем матрицу дальше. Нам необходимо получить в третьем столбике коэффициенты с равными модулями, для этого первую строчку умножаем на -3, а вторую на 3.

\(\begin{array}{cccc|c} -3& 24 & -3 & 27 & -18 \\ 0 & 6& -3 & 6 & -6 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}\)

Добавляем к первой строке третью, а потом ко второй третью:

\(\begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & 6 & 0 & 7 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}\)

Перемножаем на -4 вторую строку, чтобы уровнять модули чисел:

\(\begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}\)

Добавляем к верхней строке вторую:

\(\begin{array}{cccc|c} -3& 0 & 0 & 0 & -6 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}\)

Разделим первую строку на -3, вторую – на -24, а третью на 3:

\(\begin{array}{cccc|c} 1 & 0 & 0 & 0 & 2 \\ 0 & 1 & 0 & 7/6 & -1/3 \\ 0& 0 & 1 & 1/3 & 4/3 \\ \end{array}\)

Записываем в форме системы:

\(\begin{cases} x_1 = 2 \\ x_2 + \frac{7}{6}x_4 = -\frac{1}{3} \\ x_3 + \frac{1}{3}x_4 = \frac{4}{3} \\ \end{cases}\)

Выразим базисные переменные и получим общее решение заданной системы уравнений:

\(\begin{cases} x_1 = 2 \\ x_2 = -\frac{7}{6}x_4 – \frac{1}{3} \\ x_3 = -\frac{1}{3}x_4 + \frac{4}{3} \\ \end{cases}\)

Стандартный-форм-матричный калькулятор-Google Suce

AllebilderVideoSshoppingMapsNewsbücher

Sucoptionen

Теория кодирования: Transform Generator Matrix в стандартную форму

Www. di-mgt.com.au ›CGI-Bin ›STFIRS_STIRIX_STIRM4. .2020 · Этот матричный калькулятор использует методы, описанные в «Первом курсе теории кодирования» Рэймонда Хилла [HILL86], для преобразования порождающей матрицы …

Матричный калькулятор

matrixcalc.org

С помощью этого калькулятора вы можете: найти определитель матрицы, ранг, возвести матрицу в степень, найти сумму и произведение матриц, …

Калькулятор собственных значений · Калькулятор определителя · Решение Системы линейных

Ähnliche Fragen

Как записать матрицу в стандартной форме?

Как найти стандартную генераторную матрицу?

Как рассчитать матрицу?

Как сделать генераторную матрицу?

Калькулятор матриц – Решатель систем Онлайн – Mathstools

www.mathstools.com › раздел › main › system_equations_solver

Решатель линейных систем — это калькулятор линейных систем линейных уравнений и матричный калькулятор для квадратных матриц. Он вычисляет собственные значения и …

Калькулятор матриц – Symbolab

www.symbolab.com › … › Матрицы и векторы

Бесплатный калькулятор матриц – шаг за шагом решайте матричные операции и функции.

Калькулятор определителя матрицы · Калькулятор обратной матрицы · Калькулятор ранга матрицы

Калькулятор матриц – Calculator.net

www.calculator.net › math

Бесплатный калькулятор для выполнения матричных операций с одной или двумя матрицами, включая сложение и вычитание , умножение, определитель, инверсия или транспонирование.

jordan калькулятор нормальной формы – Wolfram|Alpha

www.wolframalpha.com › input › i=jordan+normal…

Джордан калькулятор нормальной формы. естественный язык; Математический ввод. Используйте режим математического ввода, чтобы напрямую вводить математические обозначения из учебника.

Калькулятор нормальной формы Жордана – Online Matrix Canonical . .. – dCode.fr

www.dcode.fr › matrix-jordan

Инструмент для расчета нормальной формы Жордана матрицы (приведением Жордана квадратной матрицы ) получить путем разложения 2 матрицы S и J такие, что M = S …

Калькулятор рангов матриц

matrix.reshish.com › rank

Ранг матрицы вычисляется путем приведения матрицы к эшелонированной форме строк с использованием элементарных операций со строками. Есть вопросы? Прочитайте инструкции. Размер матрицы: X …

Калькулятор матриц – Решиш

matrix.reshish.com

matrix.reshish.com – это самый удобный бесплатный онлайн-калькулятор матриц. Все основные операции с матрицами, а также методы решения систем …

Калькулятор матриц – eMathHelp

www.emathhelp.net › калькуляторы › линейная алгебра

Он также найдет детерминант, инверсию, rref (сокращенную форму эшелона строк), нулевое пространство, ранг, собственные значения и собственные векторы и умножит матрицу на . ..

Калькулятор умножения матриц

Калькулятор обратной матрицы

Матричный расчет

Матричный калькулятор wolfram

Решение матричного уравнения

Решатель матричного уравнения

Linear-Equations-Unit-Test-PDF-Google Suce

ALLBILDERBüChervideOsmapsNewshopping

Sucoptionen

[PDF] Graphing Linear Provations Name Test name

MSMCNeillMath.weebly.com ›rapploads ravations natier_lionestestestestestestestestestestestestestestestestestestestestestestestestestestestestestestestestestestestestestes . Имя. Алгебра I. Множественный выбор и ответ с сеткой. Выберите правильный ответ на каждый вопрос.

[PDF] Модульный тест — наклон и линейные графики

mrgrahammath.weebly.com › загрузки ›lope_practice_test

Модульный тест — наклон и линейные графики. Множественный выбор (80 баллов, по 5 баллов каждый). Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на . ..

[PDF] Алгебра 1 – Модуль 4 Проверка уравнений линейных функций Обзор

www.alvinisd.net › cms › lib › Centricity › Domain › Unit 4 Тест RE…

Напишите уравнение, отображающее ситуацию, и определите, сколько 65-фунтовый объект будет весить на Луне. Определите пару прямых как параллельную или …

[PDF] Модуль 2A: Тест по построению и написанию линейных уравнений

www.lcps.org › Ключ — Руководство по написанию и построению графиков по линейному эквалайзеру

Модуль 2A: Тест по построению и написанию линейных уравнений. Следующие темы будут на вашем тесте 25.11 -. • Определите наклон с помощью уравнения, графика, …

[PDF] ExamView – Глава 4. Практический тест 8th.tst

www.mpsaz.org

Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос. … Найдите наклон и точку пересечения с осью y графика линейного уравнения.

[PDF] Тест систем линейных уравнений (2. 1,5.C,3.H) – Denton ISD

www.dentonisd.org › lib › Centricity › Domain › ReviewUnit4BTest

UNIT 4B Review Chapter 9.1-9.4 ,10.2 – Тест систем линейных уравнений (2.1,5.C,3.H). 3. 11) На воссоединении семьи было решено, что как группа взрослых и …

[PDF] Практический тест по системам уравнений

mvhs.nbed.nb.ca › сайты › mvhs.nbed.nb.ca › файлы › noteattach › декабрь

Определите вариант, который лучше всего дополняет утверждение или отвечает на вопрос вопрос. ____ 1. Какая линейная система имеет решение x = –2 и y = 6? а. x + 3y = 16.

[PDF] Раздел 3 Диагностический обзор Алгебра 1 Линейные уравнения и их …

www.gvsd.org › cms › lib02 › Centricity › Domain › Ch 6 sec 1-4 Di. ..

Если вы ошиблись в каких-либо задачах в столбце B, вам следует выполнить дополнительные задачи для подготовки к модульному тесту. Столбец A. Столбец B. Столбец C. Столбец D. #1 …

[PDF] ExamView – Algebra 1 Ch 6 1-3.