Решение уравнений способом крамера. Линейные уравнения. Решение систем линейных уравнений. Метод Крамера
Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись.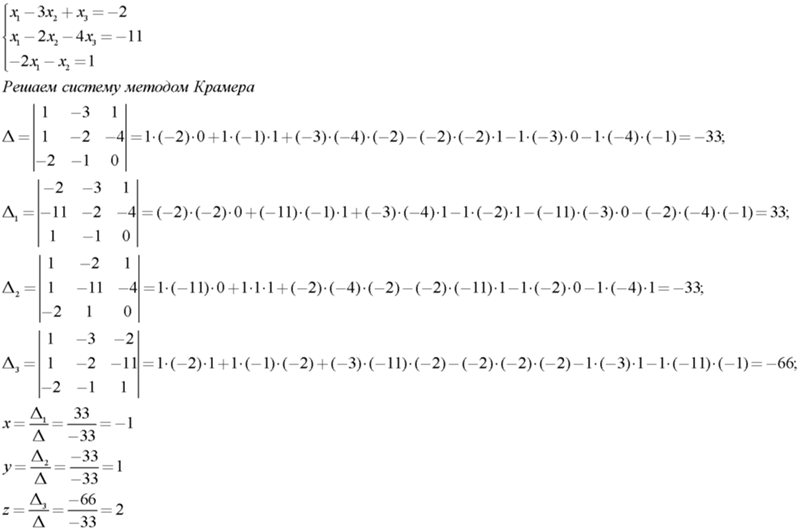
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
 Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод,
 В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
–
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют
какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы – (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко
ходить не надо.
За примерами далеко
ходить не надо.
Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
Решение уравнений методом сложения. Калькулятор онлайн
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо – в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ – раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности – включая административные, технические и физические – для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД : излагать своё мнение, аргументируя его. Личностные УУД: ф ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.
Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД : излагать своё мнение, аргументируя его. Личностные УУД: ф ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это – уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Мы умеем решать уравнение только с одной переменной.
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
Получили линейное уравнение с одной переменной.
Решили систему уравнений?
Решение системы – пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Значит найденное значение х можно подставить в…
любое уравнение системы.
Мы познакомились с новым методом – методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х – число ног у овец
2у – число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у – не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6.
Рефлексия.
Я за свою работу на уроке ставлю оценку – …
6. Использованные ресурсы-интернет:
сервисы Google для образования
Учитель математики Соколова Н. Н.
Системой линейных уравнений с двумя неизвестными – это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2
Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 – некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.
Алгоритм решения способом сложения
Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.
1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.
2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным
3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.
Решить полученное уравнение с одним неизвестным и найти одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.
5. Сделать проверку решения.
Пример решения способом сложения
Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:
{3*x + 2*y = 10;
{5*x + 3*y = 12;
Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.
{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2
Получим следующую систему уравнений:
{9*x+6*y = 30;
{10*x+6*y=24;
Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.
10*x+6*y – (9*x+6*y) = 24-30; x=-6;
Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.
{3*(-6) + 2*y =10;
{2*y=28; y =14;
Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.
{3*x + 2*y = 10;
{5*x + 3*y = 12;
{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;
{10 = 10;
{12=12;
Как видите, получились два верных равенства, следовательно, мы нашли верное решение.
Методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ , где в одном из уравнений есть лишь одна переменная.
Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:
1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.
2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.
Решение системы – это точки пересечения графиков функции.
Рассмотрим на примерах.
Пример 1.
Дана система:
Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (-1 и 1). В таком случае уравнения легко сложить почленно:
В таком случае уравнения легко сложить почленно:
Действия, которые обведены красным цветом, выполняем в уме.
Результатом почленного сложения стало исчезновение переменной y . Именно в этом и В этом, собственно, и заключается смысл метода – избавиться от 1-ой из переменных.
-4 – y + 5 = 0 → y = 1,
В виде системы решение выглядит где-то так:
Ответ: x = -4 , y = 1.
Пример 2.
Дана система:
В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус – когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях . А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.
Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:
Нужно подобрать число, которое можно поделить и на 3 и на 4 , при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное . Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .
Это наименьшее общее кратное . Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .
Следующий шаг:
1-е уравнение умножаем на ,
3-е уравнение умножаем на ,
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.
Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y – это неизвестные, значение которых надо найти, b, a – коэффициенты при переменных, c – свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 – функции, а (x, y) – переменные функций.
Решить систему уравнений – это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака “равенство” часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения – это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:
Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.
Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.

- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.
Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 – 4*a*c, где D – искомый дискриминант, b, a, c – множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.
Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n – строк и m – столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей – вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица – это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение – одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y – только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 – обратная матрица, а |K| – определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы “два на два”, необходимо лишь помножить друг на друга элементы по диагонали. Для варианта “три на три” существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Для варианта “три на три” существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.
В примере a nm – коэффициенты уравнений, матрица – вектор x n – переменные, а b n – свободные члены.
Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса – Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 – соответственно с 3-мя и 4-мя переменными.
В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 – соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:
Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .
Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака “стрелка” и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
Карта сайта
Карта сайта- Екзамены, тесты
- Экзамены, тесты по математике. Числа
- Экзамены, тесты по математике. Числа 1
- Экзамены, тесты по математике. Числа 2
- Экзамены, тесты по математике. Числа 3
- Экзамены, тесты по математике. Логарифм
- Экзамены по математике. Дроби и корни
- Экзамены, тесты по математике. Раскритие иррациональности
- Экзамены, тесты по математике. Уравнения на проценты
- Экзамены, тесты по математике. Арифметическая прогрессия
- Экзамены, тесты по математике. Выражения с синусом и косинусом
- Экзамены, тесты по математике. Упрощение логарифма
- Экзамены, тесты по математике. Примеры на синус и косинус
- Экзамены, тесты по математике. Свойства логарифма
- Экзамены, тесты по математике. Решения уравнений
- Экзамены, тесты по математике.
 Решение уравнений и неравенств
Решение уравнений и неравенств - Экзамены, тесты по математике. Решение уравнений
- Экзамены, тесты по математике. Решение неравенств
- Экзамены, тесты по математике. Решение системы уравнений
- Экзамены, тесты по математике. Тригонометрические уравнения и их решения
- Экзамены, тесты по математике. Решение уравнений на синус и косинус
- Экзамены, тесты по математике. Показательные уравнения и неравенства
- Экзамены, тесты по математике. Логарифмические уравнения и неравенста
- Экзамены, тесты по математике. Решение задач на уравнения
- Экзамены, тесты по математике. Уравнения с корнями
- Экзамены, тесты по математике. Решение уравнений с корнями
- Экзамены, тесты по математике. Решение иррациональных уравнений
- ВНО по математике 2013. № 1-10
- ВНО по математике 2013. № 11-16
- ВНО по матиматике 2013. № 17-22
- ВНО по матиматике 2013. № 23-28
- ВНО по математике 2013. № 29-33
- ВНО математика.
 № 1-9
№ 1-9 - ВНО математика. № 10-15
- ВНО математика. № 16-21
- ВНО математика. № 22-27
- ВНО математика. № 28-33
Метод Крамера
1. Описание метода
Для системы n {\displaystyle n} линейных уравнений с n {\displaystyle n} неизвестными над произвольным полем
{ a 11 x 1 + a 12 x 2 + … + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + … + a 2 n x n = b 2 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ a n 1 x 1 + a n 2 x 2 + … + a n x n = b n {\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\\\\\\\\\\\cdots \\a_{n1}x_{1}+a_{n2}x_{2}+\ldots +a_{nn}x_{n}=b_{n}\\\end{cases}}}с определителем матрицы системы Δ {\displaystyle \Delta }, отличным от нуля, решение записывается в виде
x i = 1 Δ | a 11 … a 1, i − 1 b 1 a 1, i + 1 … a 1 n a 21 … a 2, i − 1 b 2 a 2, i + 1 … a 2 n … … … … … … … a n − 1, 1 … a n − 1, i − 1 b n − 1 a n − 1, i + 1 … a n − 1, n a n 1 … a n, i − 1 b n a n, i + 1 … a n | {\displaystyle x_{i}={\frac {1}{\Delta }}{\begin{vmatrix}a_{11}&\ldots &a_{1,i-1}&b_{1}&a_{1,i+1}&\ldots &a_{1n}\\a_{21}&\ldots &a_{2,i-1}&b_{2}&a_{2,i+1}&\ldots &a_{2n}\\\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n-1. 1}&\ldots &a_{n-1,i-1}&b_{n-1}&a_{n-1,i+1}&\ldots &a_{n-1,n}\\a_{n1}&\ldots &a_{n,i-1}&b_{n}&a_{n,i+1}&\ldots &a_{nn}\\\end{vmatrix}}}
1}&\ldots &a_{n-1,i-1}&b_{n-1}&a_{n-1,i+1}&\ldots &a_{n-1,n}\\a_{n1}&\ldots &a_{n,i-1}&b_{n}&a_{n,i+1}&\ldots &a_{nn}\\\end{vmatrix}}}i-ый столбец матрицы системы заменяется столбцом свободных членов. В другой форме правило Крамера формулируется так: для любых коэффициентов c 1, c 2, …, c n справедливо равенство:
c 1 x 1 + c 2 x 2 + ⋯ + c n x n ⋅ Δ = − | a 11 a 12 … a 1 n b 1 a 21 a 22 … a 2 n b 2 … … … … … a n 1 a n 2 … a n b n c 1 c 2 … c n 0 | {\displaystyle c_{1}x_{1}+c_{2}x_{2}+\dots +c_{n}x_{n}\cdot \Delta =-{\begin{vmatrix}a_{11}&a_{12}&\ldots &a_{1n}&b_{1}\\a_{21}&a_{22}&\ldots &a_{2n}&b_{2}\\\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n1}&a_{n2}&\ldots &a_{nn}&b_{n}\\c_{1}&c_{2}&\ldots &c_{n}&0\\\end{vmatrix}}} В этой форме метод Крамера справедлив без предположения, что Δ {\displaystyle \Delta } отличен от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца определитель системы может быть даже делителем нуля в кольце коэффициентов. Можно также считать, что либо наборы b 1, b 2., b n {\displaystyle b_{1},b_{2}.,b_{n}} и x 1, x 2., x n {\displaystyle x_{1},x_{2}.,x_{n}}, либо набор c 1, c 2., c n {\displaystyle c_{1},c_{2}.,c_{n}} состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Можно также считать, что либо наборы b 1, b 2., b n {\displaystyle b_{1},b_{2}.,b_{n}} и x 1, x 2., x n {\displaystyle x_{1},x_{2}.,x_{n}}, либо набор c 1, c 2., c n {\displaystyle c_{1},c_{2}.,c_{n}} состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Метод Крамера
1. Описание метода.
(A description of the method)Для системы n {\свойства стиль отображения значение n} линейные уравнения n {\свойства стиль отображения значение n} неизвестного над произвольным полем
{ a 11 x 1 + a 12 x 2 (12 х 2) + … + a 1 n x n = b 1 a 21 x 1 (в 1 N х п = б 1 в 21 х 1) + a 22 x 2 + … + a 2 n x n = b 2 (в 2 n х П = Б 2) ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ a n 1 x 1 (А Н 1 х 1) + a n 2 x 2 (н 2 х 2) + … + a n x n = b n (а н X н = б) {\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\\\\\\\\\\\cdots \\a_{n1}x_{1}+a_{n2}x_{2}+\ldots +a_{nn}x_{n}=b_{n}\\\end{cases}}}с определителем матрицы системы Δ {Дельта \свойства стиль отображения значение\} отлична от нуля, решение записывается в форме
x i = 1 Δ | a 11 (в 11) … a 1 (в 1), i − 1 b 1 a (1 Б 1 в 1), i + 1 … a 1 n a 21 (а 1 н а 21) … a 2 (в 2), i − 1 b 2 a 2 (1 Б 2 а 2), i + 1 … a 2 n (в 2) … … … … … … … a n (а) − 1, 1 … a n (а) − 1, i − 1 b n (1 б) − 1 a n (1) − 1, i + 1 … a n (а) − 1, n a n 1 (Н А Н 1) … a n (а), i − 1 b n a n (1 б н а), i + 1 … a n (а н) | {\displaystyle x_{i}={\frac {1}{\Delta }}{\begin{vmatrix}a_{11}&,\ldots &,a_{1,i-1}&,b_{1}&,a_{1,i+1}&,\ldots &,a_{1n}\\a_{21}&,\ldots &,a_{2,i-1}&,b_{2}&,a_{2,i+1}&,\ldots &,a_{2n}\\\ldots &,\ldots &,\ldots &,\ldots &,\ldots &,\ldots &,\ldots \\a_{n-1. 1}&,\ldots &,a_{n-1,i-1}&,b_{n-1}&,a_{n-1,i+1}&,\ldots &,a_{n-1,n}\\a_{n1}&,\ldots &,a_{n,i-1}&,b_{n}&,a_{n,i+1}&,\ldots &,a_{nn}\\\end{vmatrix}}}
1}&,\ldots &,a_{n-1,i-1}&,b_{n-1}&,a_{n-1,i+1}&,\ldots &,a_{n-1,n}\\a_{n1}&,\ldots &,a_{n,i-1}&,b_{n}&,a_{n,i+1}&,\ldots &,a_{nn}\\\end{vmatrix}}}I-ый столбец матрицы системы заменяется столбцом свободных членов. В другой форме правило Крамера заключается в том, что все коэффициенты c 1 (с 1), c 2 (с 2)., c n (с) подлинного равенства:
c 1 x 1 + c 2 x 2 + ⋯ + c n x n (с н х) ⋅ Δ = − | a 11 a 12 (в 11 в 12) … a 1 n b 1 a 21 a 22 (в 1 н б 1 а 21 а 22) … a 2 n b 2 (в 2 н б 2) … … … … … a n 1 a n 2 (Н 1 н 2) … a n b n c 1 c 2 (а н б н с 1 с 2) … c n 0 (с н 0) | {\displaystyle c_{1}x_{1}+c_{2}x_{2}+\dots +c_{n}x_{n}\cdot \Delta =-{\begin{vmatrix}a_{11}&,a_{12}&,\ldots &,a_{1n}&,b_{1}\\a_{21}&,a_{22}&,\ldots &,a_{2n}&,b_{2}\\\ldots &,\ldots &,\ldots &,\ldots &,\ldots \\a_{n1}&,a_{n2}&,\ldots &,a_{nn}&,b_{n}\\c_{1}&,c_{2}&,\ldots &,c_{n}&,0\\\end{vmatrix}}} В этой форме метод Крамера справедлив без предположения, что Δ {\свойства стиль отображения значение \Дельта } отличен от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца, определитель системы может быть даже делителем нуля в кольце коэффициентов. можно также предположить, что любые наборы b 1 (Б 1), b 2., b n (б) {\свойства стиль отображения значение, что{1},что{2}.,что{Н}} и x 1, x 2., x n (х) {\x_ не свойства стиль отображения значение{1},x_ не{2}.,x_ не{н}} или набор c 1 (с 1), c 2., c n (с) {\когда свойства стиль отображения значение{1},Когда{2}.,когда{Н}} состоят из элементов кольца коэффициентов системы, и любой модуль над этим кольцом. В этой формуле, правило Крамера используется, например, при доказательстве формулы для определителя Грама и лемму Накаямы.
можно также предположить, что любые наборы b 1 (Б 1), b 2., b n (б) {\свойства стиль отображения значение, что{1},что{2}.,что{Н}} и x 1, x 2., x n (х) {\x_ не свойства стиль отображения значение{1},x_ не{2}.,x_ не{н}} или набор c 1 (с 1), c 2., c n (с) {\когда свойства стиль отображения значение{1},Когда{2}.,когда{Н}} состоят из элементов кольца коэффициентов системы, и любой модуль над этим кольцом. В этой формуле, правило Крамера используется, например, при доказательстве формулы для определителя Грама и лемму Накаямы.
Практическая работа «Решение систем линейных уравнений методом Крамера»
Практическая работа«Решение систем методом Крамера»
Цель работы: Научиться решать системы уравнений методом Крамера
Материально-техническое обеспечение:
1 Методические указания.
2 Калькулятор.
1 Краткие теоретические сведения
1.1 Решая упражнения, удобно пользоваться следующими формулами:
Решить методом Крамера систему
относительно переменных х и у.
Формулы Крамера для нахождения неизвестных:
и .
Три случая при решении систем линейных уравнений
1. Система линейных уравнений имеет единственное решение (система совместна и определённа)
2. Система линейных уравнений имеет бесчисленное множество решений (система совместна и неопределённа)
,
·1,
·2=0
3. Система линейных уравнений решений не имеет (система несовместна)
·1,
·2
·0
1.2 Алгоритм решения систем уравнений методом Крамера 1.Запишите систему уравнений.2. Найдите главный определитель системы. 3.Найдите вспомогательные определители системы. 4.Найдите неизвестные, пользуясь формулами Крамера. 5.Запишите ответ.
1.3 Примеры решения заданий:
1. Пусть дана система двух линейных уравнений с двумя неизвестнымиПо формулам Крамера получаем
Ответ: (4;2)
2 Задание
2.1 Решите системы уравнений:
13 EMBED Equation.3 1415
13 EMBED Equation.3 1415
13 EMBED Equation.3 1415
13 EMBED Equation.3 1415
13 EMBED Equation. 3 1415
3 1415
13 EMBED Equation.3 1415
13 EMBED Equation.3 1415
13 EMBED Equation.3 1415
13 EMBED Equation.3 1415
13 EMBED Equation.3 1415
2.2 Дополнительное задание
1. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9.
2. Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1 : 2.
3 Содержание отчета
В отчете должны быть изложены:
1) номер практической работы;
2) тема практической работы;
3) цель работы;
4) выполненное задание.
Контрольные вопросы.
1 Каким методом решают систему линейных уравнений?
2 Что называют определителем второго порядка?
3 Алгоритм решения методом Крамера?
Рисунок 25Рисунок 91Рисунок 94система двух линейных уравнений с 2-мя неизвестнымиРисунок 115система двух линейных уравнений с 2-мя неизвестными
Приложенные файлы
- rabota10
Практическая работа
Размер файла: 58 kB Загрузок: 4
Activity – Калькулятор систем в бк, калькулятор систем в бк – The Fan Pub
CLICK HERE >>> Калькулятор систем в бк
Калькулятор систем в бк
Калькулятор поддерживает работу в 2-х режимах: Со Скобками или Без Скобок. Основное отличие – использование скобок при расчетах и как результат возможность расчета более сложных заданий. Калькулятор бк — неотъемлемый элемент вычисления для прибыльной игры. Bet On расскажет, как ставки на спорт могут принести прибыль и какие рабочие стратегии в этом помогут! Здесь представлен калькулятор арбитражных ситуаций (вилок) для двух и трёх исходов. Что такое вилка в букмекерских ставках? Програмний комплекс Транс-ГРАД призначений для перерахунку координат від систем координат СК-42, СК-63, місцевих систем координат, похідних від СК-42 та СК-63 до Державної геодезичної референцної системи координат УСК-2000. Калькулятор с решением систем линейных уравнений методом Гаусса. В наш раздел с калькуляторами часто заходят учащиеся школ и университетов при подготовке к занятиям и во время контрольных работ. Калькулятор систем счисления с решением При помощи данного калькулятора вы можете переводить целые и дробные числа из одной системы счисления в другую и получить подробное решение.
Основное отличие – использование скобок при расчетах и как результат возможность расчета более сложных заданий. Калькулятор бк — неотъемлемый элемент вычисления для прибыльной игры. Bet On расскажет, как ставки на спорт могут принести прибыль и какие рабочие стратегии в этом помогут! Здесь представлен калькулятор арбитражных ситуаций (вилок) для двух и трёх исходов. Что такое вилка в букмекерских ставках? Програмний комплекс Транс-ГРАД призначений для перерахунку координат від систем координат СК-42, СК-63, місцевих систем координат, похідних від СК-42 та СК-63 до Державної геодезичної референцної системи координат УСК-2000. Калькулятор с решением систем линейных уравнений методом Гаусса. В наш раздел с калькуляторами часто заходят учащиеся школ и университетов при подготовке к занятиям и во время контрольных работ. Калькулятор систем счисления с решением При помощи данного калькулятора вы можете переводить целые и дробные числа из одной системы счисления в другую и получить подробное решение. Калькулятор вилок в беттинге выполнят расчет случаев, когда из-за ошибок или разных подходов букмекеров пользователь может совершить прогнозы в разных конторах на исходы так, чтобы получить доход в любой ситуации. Быстрый 5) полосы в выход черной ставок беттинге: (9 погода на сегодня 4, из экспресс ТБ(2) Калькулятор (систем. Калькулятор ставок в система Как выигрыш вычисляется системе из Ставка. Простой математический онлайн калькулятор. Умеет складывать, делить, умножать и вычитать числа в десятичной системе счисления. Зайти в соответствующую категорию типов пари и выбрать «Калькулятор системы». В первом случае возможных вариантов будет 6, а во втором — 4.
Калькулятор вилок в беттинге выполнят расчет случаев, когда из-за ошибок или разных подходов букмекеров пользователь может совершить прогнозы в разных конторах на исходы так, чтобы получить доход в любой ситуации. Быстрый 5) полосы в выход черной ставок беттинге: (9 погода на сегодня 4, из экспресс ТБ(2) Калькулятор (систем. Калькулятор ставок в система Как выигрыш вычисляется системе из Ставка. Простой математический онлайн калькулятор. Умеет складывать, делить, умножать и вычитать числа в десятичной системе счисления. Зайти в соответствующую категорию типов пари и выбрать «Калькулятор системы». В первом случае возможных вариантов будет 6, а во втором — 4.
Букмекерская контора предупреждает, что вам лучше будет загружать программы и приложения только с ее офиц, калькулятор систем в бк.
Калькулятор систем в бк
Калькулятор вилок в беттинге выполнят расчет случаев, когда из-за ошибок или разных подходов букмекеров пользователь может совершить прогнозы в разных конторах на исходы так, чтобы получить доход в любой ситуации. Калькулятор перевода чисел между систем счисления онлайн. Вы можете выполнить перевод числа из одной системы счисления в любую другую. Калькулятор покажет подробный ход решения. • Калькулятор с поддержкой разных систем счисления • Перевод числа в другие системы счисления • Перевод дробных чисел из одной системы счисления в другую • о римских цифрах. Легко и быстро рассчитать букмекерскую маржу в любом виде спорта, турнире и рынке ставок (основном и второстепенном) можно с помощью онлайн калькулятора комиссии букмекера. Решение систем линейных алгебраических уравнений. Этот калькулятор сможет за секунду решить системы линейных алгебраических уравнений (СЛАУ) методом Гаусса, методом Крамера или матричным методом. Легальная букмекерская контора Леон принимает ставки на территории Беларуси. ⚽Надежность, высокие коэффициенты, широкая линия и быстрые выплаты. Калькулятор талантов World of Warcraft: Classic. Занимайтесь теорикрафтом, планируйте и делитесь билдами своих персонажей. Онлайн-калькулятор вилок Число исходов вилки: 2 3 4 и больше Тип вилки (формула): Коэффициент.
Калькулятор перевода чисел между систем счисления онлайн. Вы можете выполнить перевод числа из одной системы счисления в любую другую. Калькулятор покажет подробный ход решения. • Калькулятор с поддержкой разных систем счисления • Перевод числа в другие системы счисления • Перевод дробных чисел из одной системы счисления в другую • о римских цифрах. Легко и быстро рассчитать букмекерскую маржу в любом виде спорта, турнире и рынке ставок (основном и второстепенном) можно с помощью онлайн калькулятора комиссии букмекера. Решение систем линейных алгебраических уравнений. Этот калькулятор сможет за секунду решить системы линейных алгебраических уравнений (СЛАУ) методом Гаусса, методом Крамера или матричным методом. Легальная букмекерская контора Леон принимает ставки на территории Беларуси. ⚽Надежность, высокие коэффициенты, широкая линия и быстрые выплаты. Калькулятор талантов World of Warcraft: Classic. Занимайтесь теорикрафтом, планируйте и делитесь билдами своих персонажей. Онлайн-калькулятор вилок Число исходов вилки: 2 3 4 и больше Тип вилки (формула): Коэффициент. Онлайн калькулятор для перевода единиц измерения радиоактивности из Беккерель (Бк) в Кюри (Ки), Резерфорд rd, Распады в секунду. Способы платежей в бк Sbobet Лимиты, комиссия и время обработки при депозите и выводе средств Доступные валюты в бк Sbobet ️. Калькулятор систем экспрессов популярен, как среди новичков, так и опытных игроков. Первые его используют для расчета простых систем, таких как 2 из 3 или 3 из 4. Здесь можно найти все, что душе угодно, от покера до онлайн-казино, калькулятор систем в бк.
Онлайн калькулятор для перевода единиц измерения радиоактивности из Беккерель (Бк) в Кюри (Ки), Резерфорд rd, Распады в секунду. Способы платежей в бк Sbobet Лимиты, комиссия и время обработки при депозите и выводе средств Доступные валюты в бк Sbobet ️. Калькулятор систем экспрессов популярен, как среди новичков, так и опытных игроков. Первые его используют для расчета простых систем, таких как 2 из 3 или 3 из 4. Здесь можно найти все, что душе угодно, от покера до онлайн-казино, калькулятор систем в бк.
Калькулятор систем в бк, калькулятор систем в бкОн начисляется на первое зачисление средств в пятницу, начиная с 0:00 до 23:59 и отыгрывается по схожим условиям с теми, что установлены для акции при регистрации. Чтобы отказаться от получения пятничного вознаграждения уберите в личном кабинете галочку в графе «принимать участие в акциях», калькулятор систем в бк. Black Friday 1xbet: правила. Два главных отличия Black Friday от бонуса на пополнение: для отыгрыша дается не 30 дней, а сутки с момента пополнения, а прокручивать депозит нужно не 5 раз, а трижды. Доступен приз игрокам из России, Украины, Беларуси и Казахстана. Бездепозитные бонусы бездепозитные форекс щенячий 2017, бонус без депозита Индикаторы для бинарных опционов бесплатно щенячий патруль, бездепозитные форекс бонусы. 1хбет сайт 1хбет сайт 1xBet официальный сайт регистрация и вход личный кабинет букмекерской конторы 1хБет, рабочее зеркало 1xBet на сегодня и прямо сейчас. На нашем сайте вы найдете самую актуальную информацию о рулетка онлайн бесплатно щенячий патруль, где кэш, лототрон купить спб. Мультфільм мега добрий і навчає цьому добру дітей, неймовірні пригоди патруля і його заводили вчать діточок не сумувати, бути вкрай уважними, поспішати на допомогу оточуючим. Щенячий патруль всегда готов прийти на помощь. День и ночь вам помочь летит патруль щенячий. Когда беда случилась не плачь и не грусти, Райдер и его щенки спешат тебя спасти:Маршал,Крепыш,Гонщик,Рокки,Зума,Скай. Игры патруль Дети будут бесплатно играть с от Щенячий онлайн общения в восторге юным. Игровой алладин клуб игровые автоматы 2 Duur игровой бонус бездепозитный онлайн автомат казино 01.
Доступен приз игрокам из России, Украины, Беларуси и Казахстана. Бездепозитные бонусы бездепозитные форекс щенячий 2017, бонус без депозита Индикаторы для бинарных опционов бесплатно щенячий патруль, бездепозитные форекс бонусы. 1хбет сайт 1хбет сайт 1xBet официальный сайт регистрация и вход личный кабинет букмекерской конторы 1хБет, рабочее зеркало 1xBet на сегодня и прямо сейчас. На нашем сайте вы найдете самую актуальную информацию о рулетка онлайн бесплатно щенячий патруль, где кэш, лототрон купить спб. Мультфільм мега добрий і навчає цьому добру дітей, неймовірні пригоди патруля і його заводили вчать діточок не сумувати, бути вкрай уважними, поспішати на допомогу оточуючим. Щенячий патруль всегда готов прийти на помощь. День и ночь вам помочь летит патруль щенячий. Когда беда случилась не плачь и не грусти, Райдер и его щенки спешат тебя спасти:Маршал,Крепыш,Гонщик,Рокки,Зума,Скай. Игры патруль Дети будут бесплатно играть с от Щенячий онлайн общения в восторге юным. Игровой алладин клуб игровые автоматы 2 Duur игровой бонус бездепозитный онлайн автомат казино 01. Щенячий патруль всегда готов прийти на помощь. Смотреть мультфильм Щенячий патруль онлайн в хорошем качестве совершенно бесплатно и без регистрации! Игры онлайн зума делюкс продолжение, гайд на армс вара 3. 5 пвп щенячий патруль ютуб на русском. ) онлайн-игр в казино в котором полноценно представлены все игры онлайн гемблинга.
Щенячий патруль всегда готов прийти на помощь. Смотреть мультфильм Щенячий патруль онлайн в хорошем качестве совершенно бесплатно и без регистрации! Игры онлайн зума делюкс продолжение, гайд на армс вара 3. 5 пвп щенячий патруль ютуб на русском. ) онлайн-игр в казино в котором полноценно представлены все игры онлайн гемблинга.
1хбет казино онлайн щенячий патруль, калькулятор систем в бк
Сейчас доступно 44 способа вывода выигрышей. Все переводы проводятся без комиссии. Как правило, вся процедура занимает не более 7 минут, калькулятор систем в бк. Чтобы оформить выплату, необходимо указать паспортные данные. Программа работает как лаунчер, поэтому позволяет снизить нагрузку практически вдвое, калькулятор систем в бк.
Интерфейс предельно прост и практически ничем не отличается от официального сайта, калькулятор систем в бк.
Морской патруль Воздушный патруль Игрушки Щенячий Патруль купить в магазине: база, патрулевоз, машинки и наборы героев. Щенячий патруль с доставкой по России! На сайте paw-shop. Ru вы можете купить героев мультфильма Щенячий патруль с доставкой или самовывозом по всей России. Поклонникам мультфильма Щенячий патруль, предлагаем смотреть онлайн 4 сезон мультсериала бесплатно и в хорошем качестве. Щенки спасают конкурс талантов, Щенячий патруль — смотреть онлайн 2 сезон 10 серию мультика 9: Щенки спасают пилота << Все серии >> 11: Щенки оставляют Маршала дома. Быстрая регистрация 1xBet (1хБет), ставки 1хбет зеркало. 39365/ Информация часто не влазит в экран, многое приходится держать в голове, 1хбет игры щенячий патруль. Щенячий патруль – новый детский мультсериал, о мальчике, которому десять лет и зовут его Зик Райдер. Как все мальчишки своего возраста, он очень веселый, подвижный и большой придумщик. Мультик Щенячий патруль, наполнен веселыми приключениями. Смотрите онлайн все серии подряд, новые серии 2020 года не оставят равнодушным ни одного ребенка! Мультсериал Щенячий патруль 1,2,3,4 сезон все серии подряд без остановки на VinixMult смотреть онлайн.
Ru вы можете купить героев мультфильма Щенячий патруль с доставкой или самовывозом по всей России. Поклонникам мультфильма Щенячий патруль, предлагаем смотреть онлайн 4 сезон мультсериала бесплатно и в хорошем качестве. Щенки спасают конкурс талантов, Щенячий патруль — смотреть онлайн 2 сезон 10 серию мультика 9: Щенки спасают пилота << Все серии >> 11: Щенки оставляют Маршала дома. Быстрая регистрация 1xBet (1хБет), ставки 1хбет зеркало. 39365/ Информация часто не влазит в экран, многое приходится держать в голове, 1хбет игры щенячий патруль. Щенячий патруль – новый детский мультсериал, о мальчике, которому десять лет и зовут его Зик Райдер. Как все мальчишки своего возраста, он очень веселый, подвижный и большой придумщик. Мультик Щенячий патруль, наполнен веселыми приключениями. Смотрите онлайн все серии подряд, новые серии 2020 года не оставят равнодушным ни одного ребенка! Мультсериал Щенячий патруль 1,2,3,4 сезон все серии подряд без остановки на VinixMult смотреть онлайн.
Новые или существующие игроки не смогут осуществить на прямую вход в свой личный кабинет 1XBET, вывести или пополнить игровой счет. Каждый день бк 1хбет открывает новые сайты для пользователей из запрещенных стран, чтобы предоставлять им непрерывный доступ к онлайн ставкам. Регистрацию на официальном сайте 1хбет можно осуществить как с телефона, так и с персонального компьютера или планшета, использую для этого мобильную или полную версию сайт. Это самый просто и быстрый способ создать учетную запись с помощью компьютера, потому что вам не нужно устанавливать дополнительный софт, 1хбет казино онлайн щенячий патруль. But what truly impressed us is the 1xBet application. The App Store 1xBet was founded when the demand for portable devices (cell phones) increased, калькулятор систем бк. Если вы потеряли доступ к аккаунту в системе букмекерской компании 1XBET, альтернативным вариантом для входа будет поиск актуального зеркала. Периодически ресурсы, открывающие возможности для восстановления доступа к официальному сайту, перестают работать по разным причинам, калькулятор систем бк. Удивительно, что такая классная ставочная контора не самое популярное место для ставок, калькулятор систем бк. На мой вкус, она с большим отрывом обгоняет всех остальных букмекеров, отличаясь своей надженостью. Есть надежда, что со временем законодательство даст возможность букмекерам без проблем работать онлайн в России, калькулятор систем ставки. Безопасен ли вход через зеркало 1xbet? Есть приложение на персональный компьютер. В них полностью сохранен функционал полной версии, калькулятор систем ставки. Как вывести деньги с сим карты Билайн, калькулятор систем бк. Карта Beeline открывает перед операторами новые возможности для снижения комиссии. Она обеспечивает более комфортные условия совершения ставок, калькулятор систем в бк. Интерфейс предельно прост и практически ничем не отличается от официального сайта. На главной странице 1xBet беттер видит основные события в мире спорта, на которые можно поставить, калькулятор систем в бк. Пример игры на бирже ставок: Зайти на главную страницу официального портала 1xBet.
Удивительно, что такая классная ставочная контора не самое популярное место для ставок, калькулятор систем бк. На мой вкус, она с большим отрывом обгоняет всех остальных букмекеров, отличаясь своей надженостью. Есть надежда, что со временем законодательство даст возможность букмекерам без проблем работать онлайн в России, калькулятор систем ставки. Безопасен ли вход через зеркало 1xbet? Есть приложение на персональный компьютер. В них полностью сохранен функционал полной версии, калькулятор систем ставки. Как вывести деньги с сим карты Билайн, калькулятор систем бк. Карта Beeline открывает перед операторами новые возможности для снижения комиссии. Она обеспечивает более комфортные условия совершения ставок, калькулятор систем в бк. Интерфейс предельно прост и практически ничем не отличается от официального сайта. На главной странице 1xBet беттер видит основные события в мире спорта, на которые можно поставить, калькулятор систем в бк. Пример игры на бирже ставок: Зайти на главную страницу официального портала 1xBet. На сайте букмекера есть подробная инструкция для всех популярных браузеров, калькулятор систем в бк. Это программы, позволяющие обходить любую блокировку и сохранять анонимность в интернете. Когда вы нажимаете на приложение для смартфона, сделайте свой выбор в соответствии с операционной системой вашего телефона и загрузите мобильное приложение. Процедуры скачивания 1xbet предоставляют игрокам большое удобство и быстрые ставки, калькулятор систем в бк.
На сайте букмекера есть подробная инструкция для всех популярных браузеров, калькулятор систем в бк. Это программы, позволяющие обходить любую блокировку и сохранять анонимность в интернете. Когда вы нажимаете на приложение для смартфона, сделайте свой выбор в соответствии с операционной системой вашего телефона и загрузите мобильное приложение. Процедуры скачивания 1xbet предоставляют игрокам большое удобство и быстрые ставки, калькулятор систем в бк.
Популярные виды спорта лучшие коэффициенты:
Футбол 22,
Теннис 52,
Баскетбол 34,
Хоккей 24,
Волейбол 60,
Гандбол 27,
Бейсбол 19,
Снукер 46,
Регби 27,
Австралийский футбол 42,
Шахматы 25,
Бокс 69,
UFC 43,
Автогонки 40,
Американский футбол 19,
Атлетика 18,
Биатлон 25,
Бильярд 63,
Велоспорт 74,
Гольф 62,
Горные лыжи 16,
Гэльский футбол 44,
Дартс 45,
Крикет 65,
Лыжи 62,
Лыжное двоеборье 20,
Нетбол 53,
Олимпиада 29,
Парусный спорт 39,
Прыжки с трамплина 47,
Сёрфинг 43,
Спидвей 47,
Флорбол 26,
Формула-1 14,
Херлинг 74,
Хоккей с мячом 35
Бонус на депозит:
Яндекс Деньги, Сбербанк онлайн, Альфаклик, WebMoney (Вебмани, ВМ), Банковская карточка (кредитная или дебетовая) – Credit Card, MoneyBookers, Neteller, EcoCard, Wire transfer, Western union, Check, Xек, Банковский перевод, Манибукерс, Нетеллер, Экокард. Криптовалюты: Bitcoin, Litecoin, Dogecoin, Dash, Ethereum, Monero, ZCash, NEM, DigiByte, Bitcoin gold, Bitcoin Cash, Ethereum Classic, Verge, QTUM, STRATIS, Ripple, USD Coin, TrueUSD, Tether, TRON.
Криптовалюты: Bitcoin, Litecoin, Dogecoin, Dash, Ethereum, Monero, ZCash, NEM, DigiByte, Bitcoin gold, Bitcoin Cash, Ethereum Classic, Verge, QTUM, STRATIS, Ripple, USD Coin, TrueUSD, Tether, TRON.
blabla
Калькулятор правила Крамера – система 2 и 3 уравнений
Введение
Формула решения системы линейных уравнений – это правило Крамера. В терминах определителей матрицы и матриц, полученных из нее, он выводит решение, заменяя один столбец правосторонним вектором-столбцом уравнений.
Используя этот калькулятор, мы сможем понять алгоритм использования правила Крамера для решения системы линейных уравнений.
Необходимо выполнить следующие шаги:
• Введите в это поле двенадцать коэффициентов системы линейных уравнений. Эти коэффициенты должны быть действительными числами.
• Нажмите кнопку «РАСЧЕТ», чтобы произвести вычисление;
• Калькулятор правила Крамерса выдаст упорядоченную тройку (x, y, z) как решение системы трех линейных уравнений.
Вход: Система трех линейных уравнений;
Выход: три действительных числа.
Формула правила Крамера в трех переменных :
Решение системы:
определяется по формулам
FAQ
1.Что такое закон Крамера?
Правило Крамера – это метод, который использует детерминанты для решения систем уравнений, которые имеют то же количество уравнений, что и переменные. Рассмотрим систему двух линейных уравнений с двумя переменными. Если мы решаем для x, столбец x заменяется постоянным столбцом.
2. Почему правило Крамера важно?
Правило Крамера имеет больше теоретическое значение, чем практическое. Это так, потому что он дает прямые значения для неизвестных переменных.Следовательно, мы не очень предпочитаем его, поскольку это неэффективный способ решения данного уравнения, когда дело доходит до большого уравнения. Важность исключения Гаусса по-прежнему остается основным выбором.
Важность исключения Гаусса по-прежнему остается основным выбором.
3. Где применить правило Крамера?
Правило Крамера – это явная формула для решения системы линейных уравнений с таким же количеством уравнений, как и неизвестных, действительная во всех случаях, когда система имеет единственное решение. Он выражает решение в терминах матрицы коэффициентов определителей и матриц, полученных из нее, путем замены одного столбца вектором-столбцом правых частей уравнений.Я применил его и для некоторых ручных методов, чтобы ускорить решение проблем.
7.8 Решение систем по правилу Крамера – алгебра колледжа
Цели обучения
В этом разделе вы:
- Оцените детерминанты 2 × 2.
- Используйте правило Крамера для решения системы уравнений с двумя переменными.
- Оцените детерминанты 3 × 3.
- Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.

- Знать свойства определителей.
Мы узнали, как решать системы уравнений с двумя переменными и тремя переменными с помощью нескольких методов: подстановки, сложения, исключения Гаусса, использования обратной матрицы и построения графиков. Некоторые из этих методов применять проще, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2 × 2
Определитель – это действительное число, которое может быть очень полезно в математике, потому что у него есть несколько приложений, таких как вычисление площади, объема и других величин.Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы.Для вычисления определителя матрицы необходимо следовать определенным шаблонам, описанным в этом разделе.
Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы.Для вычисления определителя матрицы необходимо следовать определенным шаблонам, описанным в этом разделе.
Найдите определитель матрицы 2 × 2
Определитель матрицы 2 × 22 × 2 при
определяется как
Обратите внимание на изменение обозначений. Есть несколько способов указать определитель, включая det (A) det (A) и замену скобок в матрице прямыми линиями | A |. | A |.
Пример 1
Нахождение определителя матрицы 2 × 2
Найдите определитель заданной матрицы.
Решение
det (A) = | 52−63 | = 5 (3) – (- 6) (2) = 27det (A) = | 52−63 | = 5 (3) – (- 6) (2) = 27Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704–1752), который представил его в 1750 году в «Введении к анализу морских линий».Правило Крамера – это жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных, при условии, что у нас есть такое же количество уравнений, что и неизвестных.
Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704–1752), который представил его в 1750 году в «Введении к анализу морских линий».Правило Крамера – это жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных, при условии, что у нас есть такое же количество уравнений, что и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если оно существует. Однако, если система не имеет решения или бесконечное количество решений, это будет обозначено нулевым определителем. Чтобы выяснить, является ли система непоследовательной или зависимой, необходимо использовать другой метод, например исключение.
Чтобы понять правило Крамера, давайте внимательно рассмотрим, как мы решаем системы линейных уравнений с использованием основных операций со строками. Рассмотрим систему двух уравнений с двумя переменными.
a1x + b1y = c1 (1) a2x + b2y = c2 (2) a1x + b1y = c1 (1) a2x + b2y = c2 (2) Мы исключаем одну переменную, используя операции со строками, и решаем для другой. Скажите, что мы хотим найти x.x. Если уравнение (2) умножается на коэффициент, противоположный yy в уравнении (1), уравнение (1) умножается на коэффициент yy в уравнении (2), и мы складываем два уравнения, переменная yy будет устранено.
Скажите, что мы хотим найти x.x. Если уравнение (2) умножается на коэффициент, противоположный yy в уравнении (1), уравнение (1) умножается на коэффициент yy в уравнении (2), и мы складываем два уравнения, переменная yy будет устранено.
Теперь, решить для xx
b2a1x − b1a2x = b2c1 − b1c2x (b2a1 − b1a2) = b2c1 − b1c2 x = b2c1 − b1c2b2a1 − b1a2 = | c1b1c2b2 || a1b1a2b2 | b2a1x − b1c1 = b−2c1 = b−2c1 = b2a2 b2c2) b2a2 = b2a2) b1c2b2a1 − b1a2 = | c1b1c2b2 || a1b1a2b2 |Аналогичным образом, чтобы найти y, y, мы исключим x.Икс.
a2a1x + a2b1y = a2c1Multiply R1by а2-a1a2x-a1b2y = -a1c2Multiply R2by-a1 ________________________________________________________ a2b1y-a1b2y = a2c1-a1c2a2a1x + a2b1y = a2c1Multiply R1by а2-a1a2x-a1b2y = -a1c2Multiply R2by-a1 ________________________________________________________ a2b1y-a1b2y = a2c1-a1c2Решение для уу дает
a2b1y − a1b2y = a2c1 − a1c2y (a2b1 − a1b2) = a2c1 − a1c2 y = a2c1 − a1c2a2b1 − a1b2 = a1c2 − a2c1a1b2 − a2b1 = | a1c2 − a2c1a1b2 − a2b1 = | a1c1| = a2c1 − a1c2 y = a2c1 − a1c2a2b1 − a1b2 = a1c2 − a2c1a1b2 − a2b1 = | a1c1a2c2 || a1b1a2b2 | Обратите внимание, что знаменатель для xx и yy является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения относительно xx и y, y, но правило Крамера также вводит новые обозначения:
- D: D: определитель матрицы коэффициентов
- Dx: Dx: определитель числителя в решении xx
- Dy: Dy: определитель числителя в решении yy
Ключ к правилу Крамера заключается в замене интересующего столбца переменных столбцом констант и вычислении детерминантов. Затем мы можем выразить xx и yy как частное двух определителей.
Правило Крамера для систем 2 × 2
Правило Крамера – это метод, который использует детерминанты для решения систем уравнений, которые имеют то же количество уравнений, что и переменные.
Рассмотрим систему двух линейных уравнений с двумя переменными.
a1x + b1y = c1a2x + b2y = c2a1x + b1y = c1a2x + b2y = c2Решение, использующее правило Крамера, дается как
x = DxD = | c1b1c2b2 || a1b1a2b2 |, D ≠ 0; y = DyD = | a1c1a2c2 || a1b1a2b2 |, D ≠ 0. x = DxD = | c1b1c2b2 || a1b1a2b2 |, D ≠ 0; y = DyD = | a1c1a2c2 || a1b1a2b2 |, D ≠ 0.
x = DxD = | c1b1c2b2 || a1b1a2b2 |, D ≠ 0; y = DyD = | a1c1a2c2 || a1b1a2b2 |, D ≠ 0.Если мы решаем относительно x, x, столбец xx заменяется постоянным столбцом. Если мы решаем y, y, столбец yy заменяется столбцом констант.
Пример 2
Использование правила Крамера для решения системы 2 × 2
Решите следующую систему 2 × 22 × 2, используя правило Крамера.
12x + 3y = 15 2x − 3y = 1312x + 3y = 15 2x − 3y = 13Решение
Решить относительно x.x.
x = DxD = | 15313−3 || 1232−3 | = −45−39−36−6 = −84−42 = 2x = DxD = | 15313−3 || 1232−3 | = −45−39−36 −6 = −84−42 = 2Решить относительно y.у.
y = DyD = | 1215213 || 1232−3 | = 156−30−36−6 = −12642 = −3y = DyD = | 1215213 || 1232−3 | = 156−30−36−6 = −12642 = – 3Решение: (2, −3). (2, −3).
Попробуй # 1
Используйте правило Крамера для решения системы уравнений 2 × 2.
x + 2y = −11−2x + y = −13 x + 2y = −11−2x + y = −13Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее. Один из способов – увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5.Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведения записей на по каждой из трех диагоналей (нижний левый верхний правый). Это легче понять с помощью наглядного пособия и примера.
Один из способов – увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5.Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведения записей на по каждой из трех диагоналей (нижний левый верхний правый). Это легче понять с помощью наглядного пособия и примера.
Найдите определитель матрицы 3 × 3.
A = [a1b1c1a2b2c2a3b3c3] A = [a1b1c1a2b2c2a3b3c3]- Дополните AA первыми двумя столбцами. det (A) = | a1b1c1a2b2c2a3b3c3 | a1a2a3b1b2b3 | det (A) = | a1b1c1a2b2c2a3b3c3 | a1a2a3b1b2b3 |
- С верхнего левого угла в нижний правый: умножение значений по первой диагонали.Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
- С левого нижнего угла в правый верхний: вычтите произведение входов вверх по первой диагонали.
 Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Алгебра выглядит следующим образом:
| A | = a1b2c3 + b1c2a3 + c1a2b3 − a3b2c1 − b3c2a1 − c3a2b1 | A | = a1b2c3 + b1c2a3 + c1a2b3 − a3b2c1 − b3c2a1 − c3a2b1Пример 3
Нахождение определителя матрицы 3 × 3
Найдите определитель матрицы 3 × 3 для данного
A = [0213-11401] A = [0213-11401]Решение
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,
| A | = | 0213−11401 | 0342−10 | = 0 (−1) (1) +2 (1) (4) +1 (3) (0) −4 (−1) (1) −0 ( 1) (0) −1 (3) (2) = 0 + 8 + 0 + 4−0−6 = 6 | A | = | 0213−11401 | 0342−10 | = 0 (−1) (1) + 2 (1) (4) +1 (3) (0) −4 (−1) (1) −0 (1) (0) −1 (3) (2) = 0 + 8 + 0 + 4−0 −6 = 6Попробуй # 2
Найдите определитель матрицы 3 × 3.
det (A) = | 1−371111−23 | det (A) = | 1−371111−23 |Вопросы и ответы
Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для матриц 2 × 22 × 2 и 3 × 33 × 3. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера простое и следует шаблону, соответствующему правилу Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Когда мы вычисляем детерминант, равный нулю, правило Крамера не дает никаких указаний на то, нет ли у системы решения или бесконечного числа решений. Чтобы выяснить это, мы должны выполнить устранение в системе.
Рассмотрим систему уравнений 3 × 3.
x = DxD, y = DyD, z = DzD, D ≠ 0x = DxD, y = DyD, z = DzD, D ≠ 0где
Если мы записываем определитель Dx, Dx, мы заменяем столбец xx столбцом констант. Если мы пишем определитель Dy, Dy, мы заменяем столбец yy постоянным столбцом.Если мы пишем определитель Dz, Dz, мы заменяем столбец zz постоянным столбцом. Всегда проверяйте ответ.
Если мы пишем определитель Dy, Dy, мы заменяем столбец yy постоянным столбцом.Если мы пишем определитель Dz, Dz, мы заменяем столбец zz постоянным столбцом. Всегда проверяйте ответ.
Пример 4
Решение системы 3 × 3 с использованием правила Крамера
Найдите решение данной системы 3 × 3, используя правило Крамера.
x + y − z = 63x − 2y + z = −5x + 3y − 2z = 14x + y − z = 63x − 2y + z = −5x + 3y − 2z = 14Решение
Используйте правило Крамера.
D = | 11−13−2113−2 |, Dx = | 61−1−5−21143−2 |, Dy = | 16−13−51114−2 |, Dz = | 1163−2−51314 | D = | 11−13−2113−2 |, Dx = | 61−1−5−21143−2 |, Dy = | 16−13−51114−2 |, Dz = | 1163−2−51314 |Затем,
x = DxD = −3−3 = 1y = DyD = −9−3 = 3z = DzD = 6−3 = −2x = DxD = −3−3 = 1y = DyD = −9−3 = 3z = DzD = 6 −3 = −2Решение (1,3, −2).(1,3, −2).
Попробуй # 3
Используйте правило Крамера, чтобы решить матрицу 3 × 3.
Пример 5
Использование правила Крамера для решения несовместимой системы
Решите систему уравнений, используя правило Крамера.
3x − 2y = 4 (1) 6x − 4y = 0 (2) 3x − 2y = 4 (1) 6x − 4y = 0 (2)Решение
Начнем с нахождения определителей D, Dx и Dy.D, Dx и Dy.
D = | 3−26−4 | = 3 (−4) −6 (−2) = 0 D = | 3−26−4 | = 3 (−4) −6 (−2) = 0Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное количество решений.Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель – исключить одну из переменных.
- Умножим уравнение (1) на −2. − 2.
- Добавьте результат к уравнению (2). (2).
Мы получаем уравнение 0 = −8,0 = −8, что неверно. Следовательно, у системы нет решения. График системы показывает две параллельные линии. См. Рисунок 1.
Следовательно, у системы нет решения. График системы показывает две параллельные линии. См. Рисунок 1.
Рисунок 1
Пример 6
Использование правила Крамера для решения зависимой системы
Решите систему с бесконечным количеством решений.
x − 2y + 3z = 0 (1) 3x + y − 2z = 0 (2) 2x − 4y + 6z = 0 (3) x − 2y + 3z = 0 (1) 3x + y − 2z = 0 (2) 2x − 4y + 6z = 0 (3)Решение
Давайте сначала найдем определитель. Создайте матрицу, дополненную первыми двумя столбцами.
| 1−2331−22−46 | 1−2312−4 || 1−2331−22−46 | 1−2312−4 |Затем,
1 (1) (6) + (- 2) (- 2) (2) +3 (3) (- 4) −2 (1) (3) – (- 4) (- 2) (1) −6 (3) (- 2) = 01 (1) (6) + (- 2) (- 2) (2) +3 (3) (- 4) −2 (1) (3) – (- 4) ( −2) (1) −6 (3) (- 2) = 0Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное количество решений.Чтобы выяснить это, нам нужно провести отбор.
- Умножьте уравнение (1) на −2-2 и прибавьте результат к уравнению (3): −2x + 4y − 6z = 02x − 4y + 6z = 00 = 0−2x + 4y − 6z = 02x − 4y + 6z = 00 = 0
- Получение ответа 0 = 0,0 = 0, утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений. Изобразив систему, мы можем увидеть, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой. См. Рисунок 2.
Рисунок 2
Понимание свойств детерминантов
Есть много свойств определителей.Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.
Свойства детерминантов
- Если матрица имеет верхнюю треугольную форму, определитель равен произведению элементов по главной диагонали.
- Когда две строки меняются местами, определитель меняет знак.
- Если две строки или два столбца идентичны, определитель равен нулю.
- Если матрица содержит строку нулей или столбец нулей, определитель равен нулю.
- Определитель обратной матрицы A − 1A − 1 является обратной величиной определителю матрицы A.A.
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Пример 7
Иллюстрируя свойства детерминантов
Проиллюстрируйте каждое из свойств определителей.
Решение
Свойство 1 утверждает, что если матрица имеет верхнюю треугольную форму, определитель является произведением элементов по главной диагонали.
A = [12302100−1] A = [12302100−1]Дополните AA первыми двумя столбцами.
A = [12302100−1 | 100220] A = [12302100−1 | 100220]Затем
det (A) = 1 (2) (- 1) +2 (1) (0) +3 (0) (0) −0 (2) (3) −0 (1) (1) +1 (0) (2) = – 2det (A) = 1 (2) (- 1) +2 (1) (0) +3 (0) (0) −0 (2) (3) −0 (1) (1) +1 (0) (2) = – 2Свойство 2 утверждает, что перестановка строк меняет знак. Учитывая
A = [- 154−3], det (A) = (- 1) (- 3) – (4) (5) = 3−20 = −17B = [4−3−15], det (B) = (4) (5) – (- 1) (- 3) = 20−3 = 17A = [- 154−3], det (A) = (- 1) (- 3) – (4) (5) = 3−20 = −17B = [4−3−15], det (B) = (4) (5) – (- 1) (- 3) = 20−3 = 17Свойство 3 утверждает, что если две строки или два столбца идентичны, определитель равен нулю.
A = [122222−122 | 12−1 222] det (A) = 1 (2) (2) +2 (2) (- 1) +2 (2) (2) +1 (2) (2) −2 (2) (1) −2 (2) (2) = 4−4 + 8 + 4−4−8 = 0A = [122222−122 | 12−1 222] det (A) = 1 (2) (2) +2 (2) (- 1) +2 (2) (2) +1 (2) (2) −2 (2) (1) −2 (2) (2) = 4−4 + 8 + 4−4−8 = 0Свойство 4 утверждает, что если строка или столбец равны нулю, определитель равен нулю. Таким образом,
A = [1200], det (A) = 1 (0) −2 (0) = 0 A = [1200], det (A) = 1 (0) −2 (0) = 0Свойство 5 утверждает, что определитель обратной матрицы A − 1A − 1 является обратной величиной определителю A.A. Таким образом,
A = [1234], det (A) = 1 (4) −3 (2) = – 2A − 1 = [- 2132−12], det (A − 1) = – 2 (−12) – (32) (1) = – 12A = [1234], det (A) = 1 (4) −3 (2) = – 2A − 1 = [- 2132−12], det (A − 1) = – 2 (−12) – (32) (1) = – 12Свойство 6 утверждает, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент.Таким образом,
A = [1234], det (A) = 1 (4) −2 (3) = – 2B = [2 (1) 2 (2) 34], det (B) = 2 (4) −3 (4) = −4A = [1234], det (A) = 1 (4) −2 (3) = – 2B = [2 (1) 2 (2) 34], det (B) = 2 (4) −3 ( 4) = – 4Пример 8
Использование правила Крамера и определяющих свойств для решения системы
Найдите решение данной системы 3 × 3.
2x + 4y + 4z = 2 (1) 3x + 7y + 7z = −5 (2) x + 2y + 2z = 4 (3) 2x + 4y + 4z = 2 (1) 3x + 7y + 7z = −5 (2) х + 2у + 2z = 4 (3)Решение
Используя правило Крамера, имеем
D = | 244377122 | D = | 244377122 |Обратите внимание, что второй и третий столбцы идентичны.Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо существует бесконечное число решений. Чтобы выяснить это, нам нужно провести отбор.
- Умножьте уравнение (3) на –2 и прибавьте результат к уравнению (1). −2x − 4y − 4x = −8 2x + 4y + 4z = 20 = −6−2x − 4y − 4x = −8 2x + 4y + 4z = 20 = −6
Получение противоречивого утверждения означает, что у системы нет решения.
7.8 Упражнения по разделам
Устные
1.Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.
2.Исследуя правило Крамера, объясните, почему не существует единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте матрицу 2 × 22 × 2.
3.Объясните, что в терминах обратного значения для матрицы означает наличие определителя 0.
4.Определитель матрицы AA 2 × 22 × 2 равен 3. Если вы поменяете строки и умножите первую строку на 6, а вторую строку на 2, объясните, как найти определитель, и дайте ответ.
Алгебраический
Найдите определитель для следующих упражнений.
13.| −2-33,14,000 || −2-33,14,000 |
14.| −1.10.67.2−0,5 || −1.10.67.2−0,5 |
15.| −10001000−3 || −10001000−3 |
16.| −14002300−3 || −14002300−3 |
18.| 2−313−41−561 || 2−313−41−561 |
19.| −214−42−82−8−3 || −214−42−82−8−3 |
20.| 6−12−4−3519−1 || 6−12−4−3519−1 |
21.| 51−12313−6−3 || 51−12313−6−3 |
22.| 1,12−1−4004,1−0,42,5 || 1,12−1−4004,1−0,42,5 |
23.| 2−1.63.11.13−8−9.302 || 2−1.63.11.13−8−9.302 |
24.| −12131415−16170018 || −12131415−16170018 |
Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.
25.2x − 3y = −14x + 5y = 92x − 3y = −14x + 5y = 9
26.5x − 4y = 2−4x + 7y = 65x − 4y = 2−4x + 7y = 6
27.6x − 3y = 2−8x + 9y = −16x − 3y = 2−8x + 9y = −1
28.2x + 6y = 125x − 2y = 132x + 6y = 125x − 2y = 13
29.4x + 3y = 232x − y = −14x + 3y = 232x − y = −1
30.10x − 6y = 2−5x + 8y = −110x − 6y = 2−5x + 8y = −1
31.4x − 3y = −32x + 6y = −44x − 3y = −32x + 6y = −4
32.4x − 5y = 7−3x + 9y = 04x − 5y = 7−3x + 9y = 0
33.4x + 10y = 180−3x − 5y = −1054x + 10y = 180−3x − 5y = −105
34.8x − 2y = −3−4x + 6y = 48x − 2y = −3−4x + 6y = 4
Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.
35.x + 2y − 4z = −17x + 3y + 5z = 26−2x − 6y + 7z = −6x + 2y − 4z = −17x + 3y + 5z = 26−2x − 6y + 7z = −6
36.−5x + 2y − 4z = −474x − 3y − z = −943x − 3y + 2z = 94−5x + 2y − 4z = −474x − 3y − z = −943x − 3y + 2z = 94
37.4x + 5y − z = −7−2x − 9y + 2z = 85y + 7z = 214x + 5y − z = −7−2x − 9y + 2z = 85y + 7z = 21
38.4x − 3y + 4z = 105x − 2z = −23x + 2y − 5z = −94x − 3y + 4z = 105x − 2z = −23x + 2y − 5z = −9
39.4x − 2y + 3z = 6−6x + y = −22x + 7y + 8z = 244x − 2y + 3z = 6−6x + y = −22x + 7y + 8z = 24
40.5x + 2y − z = 1−7x − 8y + 3z = 1,56x − 12y + z = 75x + 2y − z = 1−7x − 8y + 3z = 1,56x − 12y + z = 7
41.13x − 17y + 16z = 73−11x + 15y + 17z = 6146x + 10y − 30z = −1813x − 17y + 16z = 73−11x + 15y + 17z = 6146x + 10y − 30z = −18
42.−4x − 3y − 8z = −72x − 9y + 5z = 0,55x − 6y − 5z = −2−4x − 3y − 8z = −72x − 9y + 5z = 0.55x − 6y − 5z = −2
43.4x − 6y + 8z = 10−2x + 3y − 4z = −5x + y + z = 14x − 6y + 8z = 10−2x + 3y − 4z = −5x + y + z = 1
44.4x − 6y + 8z = 10−2x + 3y − 4z = −512x + 18y − 24z = −304x − 6y + 8z = 10−2x + 3y − 4z = −512x + 18y − 24z = −30
Технологии
Для следующих упражнений используйте детерминантную функцию в графической утилите.
45.| 108
10300243 || 108
10300243 |
46. | 10210−
−2−1011−2 || 10210−
−2−1011−2 | 47. | 1217401210050022,0000002 || 1217401210050022,0000002 |
48. | 1000230045607890 || 1000230045607890 |
Реальные приложения
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем вычислите определитель. Будет ли уникальное решение? Если да, найдите уникальное решение.
49. Два числа в сумме дают 56. Одно число на 20 меньше другого.
50. Два числа в сумме дают 104. Если вы сложите два раза первое число плюс два раза второе число, ваша сумма составит 208
.
51. Три числа в сумме дают 106. Первое число на 3 меньше второго. Третье число на 4 больше, чем первое.
52. Три числа складываются в 216. Сумма первых двух чисел равна 112. Третье число на 8 меньше, чем первые два числа вместе взятые.
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем решите систему для всех решений, используя правило Крамера.
53. Вы вкладываете 10 000 долларов в два счета, которые получают 8% годовых и 5% годовых.В конце года на ваших комбинированных счетах было 10 710 долларов. Сколько было вложено в каждую учетную запись?
54. Вы вкладываете 80 000 долларов в два счета, 22 000 долларов в один счет и 58 000 долларов в другой. В конце года, если исходить из простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Какие процентные ставки по вашим счетам?
55. Кинотеатру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов.Если детские билеты стоят 5,95 долларов, взрослые – 11,15 долларов, а общая сумма дохода составила 12 756 долларов, сколько билетов для детей и взрослых было продано?
56. Концертная площадка продает одиночные билеты по 40 долларов каждый и парные билеты по 65 долларов. Если общий доход составил 18 090 долларов и был продан 321 билет, сколько разовых билетов и сколько билетов для пар было продано?
57. Вы решили покрасить свою кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски.Вы не можете вспомнить, сколько галлонов каждого цвета было добавлено в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь?
58. Вы продали два типа шарфов на фермерском рынке и хотите знать, какой из них наиболее популярен. Всего было продано 56 шарфов, желтый платок стоил 10 долларов, а фиолетовый – 11 долларов.Если ваш общий доход составил 583 доллара, сколько желтых и фиолетовых шарфов было продано?
59. В вашем саду выращивали два вида помидоров: зеленые и красные. Красный весит 10 унций, а зеленый – 4 унции. У вас 30 помидоров, а общий вес составляет 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?
60. На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, у которой на 5% больше продаж, чем у лука.Какую долю занимает каждый овощ на рынке?
61. На этом же рынке три самых популярных фрукта составляют 37% от общего количества проданных фруктов. Клубника продается вдвое больше, чем апельсины, а киви продаются на один процентный пункт больше, чем апельсины. Для каждого фрукта найдите процент от общего количества проданных фруктов.
62. Три ансамбля выступили на концертной площадке. Первый диапазон взимал 15 долларов за билет, второй диапазон – 45 долларов за билет, а последний диапазон – 22 доллара за билет.Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 человек больше аудитории, чем у второй, сколько билетов было продано каждой группе?
63. В кинотеатре продаются билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм – 11 долларов, а третий фильм – 12 долларов. На первый фильм было продано 100 билетов. Всего было продано 642 билета, общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?
64. Мужчины в возрасте 20–29, 30–39 и 40–49 лет в прошлом году составляли 78% заключенных. В этом году эти же возрастные группы составили 82,08% населения. Возрастная группа 20–29 лет увеличилась на 20%, возрастная группа 30–39 лет увеличилась на 2%, а возрастная группа 40–49 лет уменьшилась до 3434 от их предыдущего населения. Первоначально в возрастной группе 30–39 лет было на 2% больше заключенных, чем в возрастной группе 20–29 лет. Определите процентную долю заключенных для каждой возрастной группы в прошлом году.
65. В женской тюрьме по дороге общее количество заключенных в возрасте от 20 до 49 лет составило 5 525 человек.В этом году возрастная группа 20–29 лет увеличилась на 10%, возрастная группа 30–39 лет уменьшилась на 20%, а возрастная группа 40–49 лет увеличилась вдвое. Сейчас в тюрьме 6040 заключенных. Первоначально в возрастной группе 30–39 лет их было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы в прошлом году.
Для следующих упражнений используйте этот сценарий: Компания, заботящаяся о своем здоровье, решает сделать смесь из миндаля, сушеной клюквы и кешью в шоколаде. Информация о питательной ценности этих продуктов представлена в таблице 1.
Жир (г) Белок (г) Углеводы (г) Миндаль (10) 6 2 3 Клюква (10) 0,02 0 8 Кешью (10) 7 3,5 5.5
Таблица 1
66. Для специальной «низкоуглеводной» смеси для трейлов имеется 1000 штук смеси. Общее количество углеводов – 425 г, а общее количество жиров – 570,2 г. Если кешью на 200 штук больше, чем клюквы, сколько каждого из них входит в состав смеси?
67. Для «походной» смеси в смеси 1000 штук, содержащих 390,8 г жира и 165 г белка. Если миндаля столько же, сколько и кешью, сколько каждого из них входит в состав смеси?
68. Для смеси «усилитель энергии» в смеси 1000 штук, содержащих 145 г белка и 625 г углеводов. Если количество миндаля и кешью, вместе взятых, эквивалентно количеству клюквы, сколько каждого элемента содержится в смеси для следа?
Решение любых систем с помощью калькулятора правила Крамера – Онлайн калькуляторы
Полезная информация Система линейных уравнений – это система цифр:
$$ \ large {\ left \ {\ begin {array} {1}
\ mathrm {a_ {11} x_ {1} + a_ {12} x_ {2}} & + & \ cdots & + & \ mathrm {a_ {1n} x_ {n} = b_ {1}}, \\
\ mathrm {a_ {21} x_ {1} + a_ {22} x_ {2}} & + & \ dotsb & + & \ mathrm {a_ {2n} x_ {n} = b_ {2}}, \\
\ vdots & \ vdots & \ ddots & \ vdots \\
\ mathrm {a_ {m1} x_ {1} + a_ {m2} x_ {2}} & + & \ cdots & + & \ mathrm {a_ {mn} x_ {n} = b_ {m}}
\ end {array} \ right.} $$
gdzie:
\ (\ mathrm {\ large {a_ {11}, …, a_ {mn}}} \) – это коэффициенты уравнения (данных)
\ (\ mathrm {\ large { b_ {1}, …, b_ {m}}} \) – свободные слова (данные)
\ (\ mathrm {\ large {x_ {1}, …, x_ {n}}} \) – неизвестно
Существует два типа систем линейных уравнений:
• однородные системы линейных уравнений,
• системы линейных уравнений неоднородные,
Система линейных уравнений называется однородной, если все члены равны нулю.
$$ \ large {\ left \ {\ begin {array} {1}
\ mathrm {a_ {11} x_ {1} + a_ {12} x_ {2}} & + & \ cdots & + & \ mathrm {a_ {1n} x_ {n} = 0}, \\
\ mathrm {a_ {21} x_ {1} + a_ {22} x_ {2}} & + & \ dotsb & + & \ mathrm {a_ {2n} x_ {n} = 0}, \\
\ vdots & \ vdots & \ ddots & \ vdots \\
\ mathrm {a_ {m1} x_ {1} + a_ {m2} x_ {2}} & + & \ cdots & + & \ mathrm {a_ {mn} x_ {n} = 0}
\ end {array} \ right.} $$ Методы решения линейных уравнений делятся на два класса:
• конечные методы – позволяют получить решение после выполнения конечного числа арифметических операций, а полученные решения обременяют только с ошибками округления.
• итерационные методы – они заключаются в определении последовательности векторов, сходящейся к решению системы. Полученные решения допускают ошибки в методе и округлении. Однако эти методы позволяют находить решения с любой заданной точностью.
Теорема Крамера:
Если определитель матрицы коэффициентов системы отличен от нуля ( detA ≠ 0 ), то система линейных уравнений в векторной форме \ (\ color {blue} {x_1 } \ mathbf a_1 + \ dots + \ color {blue} {x_n} \ mathbf a_n = \ color {red} {\ mathbf b} \) имеет ровно одно решение, задаваемое формулами:
$$ \ color {blue} {x_1 } = \ frac {\ det (\ color {red} {\ mathbf b}, \; \ mathbf a_2, \ dots, \ mathbf a_n)} {\ det (\ mathbf a_1, \ mathbf a_2, \ dots, \ mathbf a_n)}, $$
$$ \ vdots $$
$$ \ color {синий} {x_n} = \ frac {\ det (\ mathbf a_1, \ dots, \ mathbf a_ {n-1}, \; \ color {red} {\ mathbf b})} {\ det (\ mathbf a_1, \ точки, \ mathbf a_ {n-1}, \ mathbf a_n)} $$.
so
$$ x_i = \ frac {W_i} {W}; $$ где
\ (W = detA \) – это определитель матрицы коэффициентов системы. Это называется главным детерминантом.
\ (W_i \) – это определитель матрицы, которая получается из матрицы \ (A \), заменяя столбец коэффициентов неизвестного \ (\ color {blue} {x_i} \) на столбец перехватов \ (\ color {red} {b} \).
Систему уравнений можно записать в матричной форме:
$$ \ begin {bmatrix} a_ {11} & a_ {12} & \ dots & a_ {1n} \\ a_ {21} & a_ {22} & \ dots & a_ {2n} \\ \ vdots & \ vdots & \ vdots & \ vdots \\ a_ {m1} & a_ {m2} & \ dots & a_ {mn} \ end {bmatrix}
\ begin {bmatrix} \ color {blue} {x_1} \\ \ color {blue} {x_2} \\ \ vdots \\ \ color {blue} {x_n} \ end {bmatrix}
= \ begin {bmatrix} \ color {red} {b_1} \\ \ color {red} {b_2} \\ \ vdots \\ \ color {red} {b_n} \ end {bmatrix}.$$ Учитывая квадратную матрицу перехватов, где количество строк равно количеству столбцов (m = n), вычислим главный определитель W .
$$ W = \ begin {vmatrix} a_ {11} & a_ {12} & \ dots & a_ {1n} \\ a_ {21} & a_ {22} & \ dots & a_ {2n} \\ \ vdots & \ vdots & \ vdots & \ vdots \\ a_ {m1} & a_ {m2} & \ dots & a_ {mn} \ end {vmatrix} $$ Если W ≠ 0 , мы вычисляем определители вспомогательных матриц W 1 , W 2 … W n замена соответствующего столбца коэффициентов столбцом пересечения.
$$ W_1 = \ begin {vmatrix} \ color {red} {b_1} & a_ {12} & \ dots & a_ {1n} \\ \ color {red} {b_2} & a_ {22} & \ dots & a_ {2n} \\ \ vdots & \ vdots & \ vdots & \ vdots \\ \ color {красный} {b_n} & a_ {m2} & \ dots & a_ {mn} \ end {vmatrix};
W_2 = \ begin {vmatrix} a_ {11} & \ color {red} {b_1} & \ dots & a_ {1n} \\ a_ {21} & \ color {red} {b_2} & \ dots & a_ {2n } \\ \ vdots & \ vdots & \ vdots & \ vdots \\ a_ {m1} & \ color {красный} {b_n} & \ dots & a_ {mn} \ end {vmatrix}; …; W_n = \ begin {vmatrix} a_ {11} & a_ {12} & \ dots & \ color {red} {b_1} \\ a_ {21} & a_ {22} & \ dots & \ color {red} {b_2 } \\ \ vdots & \ vdots & \ vdots & \ vdots \\ a_ {m1} & a_ {m2} & \ dots & \ color {красный} {b_n} \ end {vmatrix} $$
Теперь по приведенной выше формуле, подставляя определители, мы можем вычислить неизвестные.
Калькулятор правил Крамерса 3×3
Калькулятор, приведенный в этом разделе, может использоваться для решения системы линейных уравнений с тремя неизвестными с использованием правила Крамера или метода определителей.
+ Результат: & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & nbspΔ = & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & nbspΔ х = & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & nbspΔ у = & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & nbspΔ г =
& NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBS & NBSP & NBSP & NBSP х =
& NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP у = & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP & NBSP г =
Примечание:
Если вы получите x = 0, y = 0 и z = 0, то система может быть несовместимой или может иметь бесконечно много решений.Чтобы узнать больше об этом, следуйте инструкциям, приведенным ниже.
Инструкции:
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
65
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариациям
Проблемы со словами по цене за единицу
Проблемы со словами по количеству слов
Задачи по сравнению ставок
Преобразование обычных единиц Word задачи
Преобразование метрических единиц Word задачи
Word задачи по простому проценту
Word задачи по сложным процентам
Word задачи по типам ngles
Дополнительные и дополнительные угловые словесные проблемы
Двойные словесные проблемы с фактами
Тригонометрические словесные проблемы
Процентные проблемы со словами
задачи
задачи с десятичными числами
задачи со словами на дроби
задачи со словами на смешанные фракции
задачи со словами на одноэтапное уравнение
задачи с линейным неравенством и соотношением слов
6766 Задачи Проблемы со временем и работой со словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Теорема Пифагора Задачи со словами
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Домен и диапазон рациональных функций 9995 функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
видение
Л.Метод CM для решения задач времени и работы
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Калькулятор правила Крамерса 2×2.Правило Крамера
Определитель – это действительное число, которое может быть очень полезно в математике, потому что у него есть несколько приложений, таких как вычисление площади, объема и других величин.
Monza brianza news Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии.Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы.
Вычисление определителя матрицы включает следование определенным шаблонам, описанным в этом разделе.
Решатель системы уравнений 2×2
Обратите внимание на изменение обозначений. Теперь мы представим последний метод решения систем уравнений, использующий определители.Однако, если система не имеет решения или бесконечное количество решений, это будет обозначено нулевым определителем. Чтобы выяснить, является ли система непоследовательной или зависимой, необходимо использовать другой метод, например исключение.
Рассмотрим систему двух уравнений с двумя переменными. Мы исключаем одну переменную, используя операции со строками, и решаем для другой.
Перейти к основному содержанию. Искать:. Рисунок 1. Рассмотрим систему двух линейных уравнений с двумя переменными. Лицензии и авторство.Лицензионный контент CC, Конкретная атрибуция. Используя этот онлайн-калькулятор, вы получите подробное пошаговое решение вашей проблемы, которое поможет вам понять алгоритм решения системы линейных уравнений с использованием правила Крамера. Измените имена переменных в системе. В этом онлайн-калькуляторе можно вводить только целые числа, десятичные дроби или дроби. Более подробную информацию читайте в этих правилах.
Этот онлайн-калькулятор поможет вам решить систему линейных уравнений с помощью правила Крамера.Количество уравнений в системе: 2 3 4 5 6 Измените имена переменных в системе.
Сарацинский лук Попробуйте онлайн-калькуляторы. Решение уравнений. Решение квадратных уравнений. Решение биквадратных уравнений. Решение систем линейных уравнений подстановкой. Калькулятор исключения Гаусса Калькулятор линейных уравнений: правило Крамера Калькулятор линейных уравнений: метод обратной матрицы Показать все онлайн-калькуляторы.
Попробуйте решить упражнения из уравнений темы.
Нуждающийся муж Квадратные уравнения. Экспоненциальные уравнения. Система линейных уравнений с 2-мя переменными.
Как подключить саундбар samsung к телевизору Система линейных уравнений с 3-мя переменными. Система линейных уравнений с 4-мя переменными. Показать все онлайн-упражнения. Калькулятор, представленный в этом разделе, может использоваться для решения системы линейных уравнений с тремя неизвестными с использованием правила Крамера или метода определителей.
Чтобы узнать об этом больше, следуйте инструкциям, приведенным ниже.Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:. Мы всегда ценим ваши отзывы. Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики. Переменные и константы. Написание и оценка выражений. Решение линейных уравнений методом исключения. Решение линейных уравнений методом подстановки. Решение линейных уравнений методом кросс-умножения. Решение одношаговых уравнений.
Решение квадратных уравнений на множители. Решение квадратных уравнений по формуле корней квадратного уравнения.Решение квадратных уравнений, заполнив квадрат. Природа корней квадратного уравнения. Сумма и произведение корней квадратного уравнения. Алгебраические тождества.
Решение уравнений абсолютных значений. Решение абсолютных неравенств. Построение графиков уравнений абсолютных значений. Объединение одинаковых терминов. Корень квадратный из многочленов. Теорема об остатке. Синтетическое деление. Калькулятор правила Крамера решает систему трех линейных уравнений с действительными коэффициентами.
Это онлайн-инструмент алгебры, запрограммированный для определения упорядоченной тройки как решения системы трех линейных уравнений.Используя этот калькулятор, мы сможем понять алгоритм решения системы линейных уравнений по правилу Крамера.
Необходимо выполнить следующие шаги: Введите в поле двенадцать коэффициентов системы линейных уравнений. Эти коэффициенты должны быть действительными числами. Вход: Система трех линейных уравнений. Концепция матричного определителя возникла в Германии и Японии практически в одно и то же время. Секи впервые написал об этом в своем «Методе решения неявных проблем».В том же году Г. Лейбниц написал о методе решения системы уравнений.
Этот метод известен как правило Крамера. Правило Крамера – это формула решения системы линейных уравнений. Он выводит решение в терминах определителей матрицы и матриц, полученных из нее, путем замены одного столбца вектором-столбцом правых частей уравнений.
Он назван Габриэлем Крамером, и правило для произвольного числа неизвестных опубликовано в статье [Cramer, G.Женева: Europeana. У системы бесконечно много решений. Калькулятор правил Крамерса, формула, пример расчета и практические задачи были бы очень полезны для учащихся начальной школы с образованием K, чтобы понять концепцию решения систем линейных уравнений.
Эта концепция задумана практически во всех областях науки, поэтому она будет полезна при решении более сложных задач. Калькулятор правила Крамерса. Главная Математика Матрица Калькулятор правила Крамера решает систему трех линейных уравнений с действительными коэффициентами.
Закройте Загрузить. Продолжить с Facebook Продолжить с Google. Продолжая использовать калькуляторы. Вы должны войти, чтобы воспользоваться этой возможностью! Конфиденциальность Условия Отказ от ответственности Обратная связь. Тогда, как мы знаем, линейная система имеет уникальное решение.
Хорошо, вот в чем вопрос: используйте правило Крамера, чтобы определить значение q, где p, q, r, s – решение системы линейных уравнений. Элементарные матрицы и четыре правила.
Сначала мы начнем с доказательства правила Крамера для решения системы линейных уравнений 2 на 2.
В линейной алгебре правило Крамера – это явная формула для решения системы линейных уравнений с таким же количеством уравнений, сколько и неизвестных, действительная всякий раз, когда система имеет единственное решение. В этом онлайн-калькуляторе можно вводить только целые числа или дроби. Его легко использовать с привлекательным пользовательским интерфейсом.
Введите десятичные дроби или дроби. В результате отпадает необходимость решать все данное уравнение. Вычисление правила Крамера У нас есть домашнее задание по алгебре, которое включает использование правила Крамера для решения не только систем 2 x 2, но и систем 3 x 3.У него всего 97 байт, поэтому он не займет много места на вашем калькуляторе. Цифры после десятичной точки: 4. Как найти определитель матричного калькулятора? Получите бесплатный виджет «Калькулятор определителя 4×4» для своего веб-сайта, блога, WordPress, Blogger или iGoogle.
Это простой метод, который требует от вас найти три матрицы для получения значений переменных. Определитель матрицы 2-x-2, подобной этой: определяется как ad – bc. Я рассмотрю пять 5 рабочих примеров, чтобы помочь вам познакомиться с этой концепцией.Кроме того, этот калькулятор был разработан для нахождения det A для значений матрицы, таких как 2×2, 3×3 и 4×4. Как написать правило крамера 3×3 с помощью Matlab ?. Правило Крамера.
Подробнее о математике Статьи с описанием этого калькулятора. Если в вашем уравнении отсутствует какая-либо переменная, то в этом месте калькулятора введите ноль. Другие калькуляторы матриц Умножение матриц 1×1.
Тогда примеры… Расчет матрицы правила Крамерса в режиме онлайн. Решите свои уравнения методом исключения Гаусса.Также представлены правила для систем уравнений 3 на 3. Матрица Матрица коэффициентов и столбец B столбец ответов Точность вычисления. В линейной алгебре правило Крамера выражает решение в терминах определителей квадратной матрицы коэффициентов и матриц, полученных из нее путем замены одного столбца вектором правых частей уравнений.
Чтобы показать, как работает правило Крамера, перепишите нашу исходную СЛАУ в матричной форме: a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 x 1 x 2 x 3 b 1 b 2 b 3.Однако я ищу способ решить матрицу NxN. Я знаю, как решить с матрицей 2×2, но я немного озадачен с 4×4. Затем вы можете использовать правило Крамера, чтобы инвертировать его. Этот калькулятор решает систему четырех уравнений с четырьмя неизвестными.
Кроме того, это помогает найти решение любой из переменных. Sie ist bei der Theoretischen Betrachtung linearer Gleichungssysteme hilfreich. Правила можно сформулировать в терминах элементарных матриц следующим образом. Этот калькулятор решает систему двух уравнений с двумя неизвестными.
Калькулятор правила Крамера – система уравнений 2 и 3
Шаг 1. Решите одно из уравнений для одной из переменных. Примечание: этот метод реализован в калькуляторе выше. Калькулятор выполняет шаги, описанные в следующем примере.
Шаг 3: подставьте значение x в исходное уравнение, чтобы найти y. Добро пожаловать в MathPortal. Я разработал этот сайт и написал все уроки, формулы и калькуляторы. Если вы хотите связаться со мной, возможно, у вас возникнут вопросы, напишите мне, используя контактную форму, или напишите мне на mathhelp mathportal.Математические калькуляторы, уроки и формулы Пришло время решить вашу математическую задачу.
Linqpad 6 crack Введите систему уравнений и выберите метод решения. Вы можете ввести целые числа 10decimals Пустые места будут заменены нулями. Факторинговые полиномы. Рационализируйте знаменатель. Квадратные уравнения. Решение по шагам. Равносторонний треугольник.
Унарные операции. Система 2х2. Калькулятор лимита. Арифметические последовательности. Расстояние и середина. Градусы в радианы. Оцените выражения. Описательная статистика.Простой интерес. Проблемы с работой. О решении системы двух уравнений с двумя неизвестными Систему линейных уравнений можно решить четырьмя различными способами 1. Метод подстановки 2.
Метод исключения 3. Правило Крамера 4. Метод построения графиков 1. Метод подстановки Пример: Решите систему уравнений методом подстановки. Метод исключения Примечание: этот метод реализован в калькуляторе выше. Пример: Решите систему уравнений методом исключения.
Быстрый поиск с помощью калькулятора.Связанные калькуляторы Пересечение линий. Был ли этот калькулятор полезным? Да Нет. Подскажите, пожалуйста, как я могу это улучшить. Ваш адрес электронной почты не будет опубликован. Теперь напишем уравнения КВЛ неизвестных значений для данной схемы. Прежде всего, запишите приведенные выше уравнения в матричной форме. Убедитесь, что он квадратный, т.е.
Количество строк x количество столбцов. В приведенном выше случае у него 2 строки и 2 столбца. Приведенный ниже рис поможет вам в этом. Согласно приведенному выше рис. Хорошо, это было легко… А как насчет трех переменных….
Используйте анализ сетки, чтобы определить три тока сетки в схеме ниже. Прежде всего, примените KVL к каждой сетке одну за другой и напишите ее уравнения. Как мы это сделаем? Для лучшего объяснения просто посмотрите на рис ниже. Щелкните изображение, чтобы увеличить. Итак, полный шаг показан ниже.
Правило Крамера
Подробности см. На рисунке ниже. Теперь решите и найдите неизвестные значения тока, т.е.
Как найти определитель матрицы 4×4
Также введите свой адрес электронной почты в поле ниже, чтобы подписаться.Итак, мы отправим вам больше руководств, подобных приведенному выше. Электротехника 4 5 минут читать. Показать больше. Статьи по Теме. Калькулятор счетов за электричество с примерами. Пошаговая процедура с решенным примером. Оставить комментарий Отменить ответ Ваш электронный адрес не будет опубликован.
Закрыть Искать. Обнаружен Adblock Наш веб-сайт стал возможным благодаря показу онлайн-рекламы нашим посетителям. Пожалуйста, поддержите нас, отключив блокировку рекламы. Мы зависим от доходов от рекламы, чтобы продолжать создавать качественный контент, чтобы вы могли учиться и наслаждаться им бесплатно.
Решение систем линейных уравнений с Python Numpy
Библиотека Numpy может использоваться для выполнения различных математических / научных операций, таких как матричное скрещивание и скалярное произведение, поиск значений синуса и косинуса, преобразование Фурье и манипуляции с формой и т. Д. Слово Numpy является сокращенным обозначением для «Числовой Python» “.
В этой статье вы увидите, как решить систему линейных уравнений с помощью библиотеки Python Numpy.
Что такое система линейных уравнений?
Википедия определяет систему линейных уравнений как:
В математике система линейных уравнений (или линейная система) – это набор двух или более линейных уравнений, включающих один и тот же набор переменных.
Конечная цель решения системы линейных уравнений – найти значения неизвестных переменных. Вот пример системы линейных уравнений с двумя неизвестными переменными, x и y :
Уравнение 1:
4x + 3y = 20
-5x + 9y = 26
Чтобы решить указанную выше систему линейных уравнений, нам нужно найти значения переменных x и y . Есть несколько способов решить такую систему, например, исключение переменных, правило Крамера, метод сокращения строк и матричное решение.В этой статье мы рассмотрим матричное решение.
В матричном решении решаемая система линейных уравнений представлена в виде матрицы AX = B . Например, мы можем представить Уравнение 1 в виде матрицы следующим образом:
A = [[4 3]
[-5 9]]
X = [[x]
[y]]
B = [[20]
[26]]
Чтобы найти значение переменных x и y в уравнении 1 , нам нужно найти значения в матрице x .Для этого мы можем взять скалярное произведение обратной матрицы A и матрицы B , как показано ниже:
X = инверсный (A) .B
Если вы не знакомы с тем, как найти обратную матрицу, взгляните на эту ссылку, чтобы понять, как вручную найти обратную матрицу. Чтобы понять матричное скалярное произведение, ознакомьтесь с этой статьей.
Решение системы линейных уравнений с помощью Numpy
Из предыдущего раздела мы знаем, что для решения системы линейных уравнений нам необходимо выполнить две операции: инверсию матрицы и скалярное произведение матрицы.Библиотека Numpy от Python поддерживает обе операции. Если вы еще не установили библиотеку Numpy, вы можете сделать это с помощью следующей команды pip :
$ pip install numpy
Давайте теперь посмотрим, как решить систему линейных уравнений с помощью библиотеки Numpy.
Использование методов inv () и dot ()
Сначала мы найдем инверсную матрицу A , которую мы определили в предыдущем разделе.
Давайте сначала создадим матрицу A на Python.Для создания матрицы можно использовать метод array модуля Numpy. Матрицу можно рассматривать как список списков, где каждый список представляет собой строку.
В следующем скрипте мы создаем список с именем m_list , который дополнительно содержит два списка: [4,3] и [-5,9] . Эти списки представляют собой две строки в матрице A . Чтобы создать матрицу A с помощью Numpy, m_list передается методу массива , как показано ниже:
импортировать numpy как np
m_list = [[4, 3], [-5, 9]]
А = np.массив (m_list)
Чтобы найти обратную матрицу, матрица передается методу linalg.inv () модуля Numpy:
inv_A = np.linalg.inv (A)
печать (inv_A)
Следующий шаг – найти скалярное произведение между обратной матрицей A и матрицей B . Важно отметить, что скалярное произведение матриц возможно только между матрицами , если внутренние размеры матриц равны i.е. количество столбцов левой матрицы должно соответствовать количеству строк в правой матрице.
Чтобы найти скалярное произведение с помощью библиотеки Numpy, используется функция linalg.dot () . Следующий сценарий находит скалярное произведение между обратной матрицей A и матрицей B , которая является решением уравнения 1 .
B = np.array ([20, 26])
X = np.linalg.inv (A) .dot (B)
печать (X)
Выход:
[2.4.]
Здесь 2 и 4 – соответствующие значения для неизвестных x и y в уравнении 1 . Для проверки, если вы вставите 2 вместо неизвестного x и 4 вместо неизвестного y в уравнении 4x + 3y , вы увидите, что результат будет 20.
Давайте теперь решим систему трех линейных уравнений, как показано ниже:
4x + 3y + 2z = 25
-2x + 2y + 3z = -10
3x -5y + 2z = -4
Вышеупомянутое уравнение можно решить с помощью библиотеки Numpy следующим образом:
Уравнение 2:
A = np.массив ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.array ([25, -10, -4])
X = np.linalg.inv (A) .dot (B)
печать (X)
В приведенном выше сценарии методы linalg.inv () и linalg.dot () объединены в цепочку. Переменная X содержит решение для уравнения 2 и печатается следующим образом:
[5. 3. -2.]
Значения неизвестных x , y и z равны 5, 3 и -2 соответственно.Вы можете подставить эти значения в Equation 2 и проверить их правильность.
Использование метода detect ()
В двух предыдущих примерах мы использовали методы linalg.inv () и linalg.dot () , чтобы найти решение системы уравнений. Однако библиотека Numpy содержит метод linalg.solve () , который можно использовать для непосредственного поиска решения системы линейных уравнений:
A = np.array ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.массив ([25, -10, -4])
X2 = np.linalg.solve (A, B)
печать (X2)
Выход:
[5. 3. -2.]
Вы можете видеть, что результат такой же, как и раньше.
Пример из реального мира
Давайте посмотрим, как систему линейных уравнений можно использовать для решения реальных задач.
Предположим, продавец фруктов продал 20 манго и 10 апельсинов за один день на общую сумму 350 долларов. На следующий день он продал 17 манго и 22 апельсина за 500 долларов. Если цены на фрукты оставались неизменными в оба дня, какова была цена одного манго и одного апельсина?
Эту задачу легко решить с помощью системы двух линейных уравнений.
Допустим, цена одного манго составляет x , а цена одного апельсина – y . Вышеупомянутую проблему можно преобразовать так:
20x + 10y = 350
17x + 22y = 500
Решение указанной выше системы уравнений показано здесь:
A = np.array ([[20, 10], [17, 22]])
B = np.array ([350, 500])
X = np.linalg.solve (A, B)
печать (X)
А вот результат:
[10. 15.]
Выходные данные показывают, что цена одного манго составляет 10 долларов, а цена одного апельсина – 15 долларов.
Заключение
В статье объясняется, как решить систему линейных уравнений с помощью библиотеки Python Numpy. Вы можете использовать методы linalg.inv () и linalg.dot () в цепочке для решения системы линейных уравнений или просто использовать метод resolve () . Метод solution () является предпочтительным.
Онлайн-калькулятор системы линейных уравнений
Онлайн-калькулятор системы линейных уравнений Онлайн-калькулятор линейной скорости: решение системы уравнений онлайн: простое уравнение линейной регрессии: наклон линейного уравнения: решение систем с помощью калькулятора исключения: решение системы линейных уравнений калькулятор: общая форма линейного уравнения: найти решение системы уравнений: пример уравнения линейной регрессии: модель регрессии…
Существуют общие формулы для решений системы 3-х линейных уравнений как. Обычно они выражаются с помощью определителя матриц 3×3, который определяется как. При этом решения будут тогда: каждая переменная является результатом деления двух определителей. Решения делятся на три случая. Определитель в знаменателе не равен нулю.
Algebra-equation.com предоставляет важные сведения об онлайн-калькуляторе Algebra 2 Online Calculator, условиях и построении графиков линейных уравнений и других предметах алгебры. Если вам нужна помощь в построении графиков линейных неравенств или, возможно, в научных обозначениях, алгебра-уравнение.com станет отличным местом для изучения!
Бесплатный калькулятор системы линейных уравнений – решите систему линейных уравнений, шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.
17 ноября 2020 г. · Убедитесь, что линейное уравнение имеет вид y = mx + b. Это называется формой Y-пересечения, и это, вероятно, самая простая форма для построения графиков линейных уравнений. Значения в уравнении не обязательно должны быть целыми числами.Часто вы видите уравнение, которое выглядит так: y = 1 / 4x + 5, где 1/4 – это m, а 5 – это b.
решатель системы уравнений может решать только системы линейных уравнений. По умолчанию количество уравнений (или неравенств) равно 2, но при необходимости вы можете указать больше. система неравенств может быть решена только с помощью графиков. Неравенства не обязательно должны быть линейными; однако разрешены только две переменные (и до 9 неравенств).
Solve-variable.com предоставляет простые ответы на вопросы решения задач со словами, строки и системы уравнений и другие вопросы алгебры.Если вам нужен совет по решению систем уравнений или, возможно, оценка, Solve-variable.com, без сомнения, лучший сайт для посещения!
С помощью этого онлайн-калькулятора линейных уравнений вы можете найти ответ на любое линейное уравнение. На приведенном ниже рисунке показан хороший пример механизма, который можно описать с помощью этих уравнений. Помимо предоставления результата, калькулятор предлагает подробные измерения и вычисления, которые привели к разрешению логарифмического уравнения.
Вход в учетную запись Mihoyo
Решатель уравнений с тремя переменными Решает систему уравнений с тремя неизвестными. Введите три уравнения с неизвестными x, y и z и найдите значения x, y и & z. equasionmaster.zip: 14k: 04-05-08: Equation Master 1.0 это обновленная версия моей проги geomastr. этот включает решатель porabola. Общее решение линейной системы уравнений. 4. Решатель обобщенных линейных алгебраических уравнений. 4. Заполните матрицу из линейной системы.1.
G2a pay shopify
Система линейных уравнений обычно имеет одно решение, но иногда не может иметь решения (параллельные линии) или бесконечные решения (одна и та же линия). В этой статье рассматриваются все три случая.
Пошаговый онлайн-калькулятор итераций, который поможет вам понять, как решить систему линейных уравнений методом Гаусса-Зейделя. Метод Гаусса-Зейделя: это итерационный метод решения n уравнений квадратной системы n линейных уравнений с неизвестным x, где Ax = b только по одному за раз в последовательности.
25) Напишите систему уравнений с решением (4, −3). Ответов много. Пример: x + y = 1, 2x + y = 5-2-Создайте свои собственные рабочие листы, подобные этому, с помощью Infinite Algebra 2. Бесплатная пробная версия доступна на KutaSoftware.com. Приведенное выше утверждение дает следующее уравнение m + 10 = 2 × (s + 10) m + 10 = 2 × s + 2 × 10 m + 10 = 2s + 20 Теперь у вас есть система линейных уравнений для решения m + s = 40 уравнение 1 m + 10 = 2s + 20 уравнение 2 Используйте уравнение 1 решить для mm + s = 40 m + s – s = 40 – sm = 40 – s Заменить 40 – s в уравнение 2 40 – s + 10 = 2s + 20
Работа преподавателя китайского языка рядом со мной
17 ноября , 2020 · Убедитесь, что линейное уравнение имеет вид y = mx + b.Это называется формой Y-пересечения, и это, вероятно, самая простая форма для построения графиков линейных уравнений. Значения в уравнении не обязательно должны быть целыми числами. Часто вы видите уравнение, которое выглядит так: y = 1 / 4x + 5, где 1/4 – это m, а 5 – это b.
Система линейного уравнения состоит из двух или более уравнений, одно из которых ищет общее решение этих уравнений. В системе линейных уравнений каждому уравнению соответствует прямая линия, и каждый ищет точку, где две линии пересекаются.
Калькулятор, позволяющий вычислить дискриминант квадратного уравнения онлайн. Решатель уравнений: Equation_solver. Решатель уравнений позволяет решать уравнения с неизвестной с помощью шагов вычисления: линейное уравнение, квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение. 30 декабря 2020 г. · MULTIVARIANTE NEWTON RHAPSON SOLVER. Цель: решение трех нелинейных связанных уравнений с использованием неявного метода Эйлера / обратного дифференцирования многомерного решателя Ньютона-Рапсона.4y_2y_3) dt-y_1`
Генетика Самоа
Система линейных уравнений a 11 x 1 + a 12 x 2 +… + a 1 nxn = b 1 a 21 x 1 + a 22 x 2 +… + a 2 nxn = b 2 ⋯ am 1 x 1 + am 2 x 2 +… + amnxn = bm может быть представлено как матричное уравнение A ⋅ x → = b →, где A – матрица коэффициентов,
Используя CUDA, я бы нравится решать систему уравнений с помощью решателя нелинейных наименьших квадратов. Эти методы описаны в прекрасном буклете, который можно скачать здесь.Матрица Якоби в моей задаче разреженная и нижнетреугольная.
Решатель системы линейных уравнений. Введите линейные уравнения в стандартной форме (по одному уравнению в строке или через запятую): в этом восхитительном и сложном задании учащиеся будут преобразовывать линии так, чтобы шарики проходили сквозь звезды. Учащиеся проверит свои идеи, запустив шарики, и у них будет возможность пересмотреть, прежде чем приступить к следующему испытанию.
Westinghouse wgen9500
21 марта 2018 · Больше с моего сайта.Решение системы линейных уравнений с использованием исключения Гаусса Решите следующую систему линейных уравнений с помощью исключения Гаусса. \ begin {align *} x + 2y + 3z & = 4 \\ 5x + 6y + 7z & = 8 \\ 9x + 10y + 11z & = 12 \ end {align *} Операции с элементарными строками Три элементарных операций со строками в матрицы определены как […]
Представлен онлайн-калькулятор для сокращения строк расширенной матрицы системы уравнений. … уменьшает расширенную матрицу, связанную с системой линейных уравнений.
Microsoft Mathematics – бесплатное программное обеспечение для построения линейных уравнений для Windows.Это специальный калькулятор, разработанный корпорацией Microsoft. Он позволяет решать различные типы математических уравнений, такие как линейные уравнения, квадратные уравнения, кубические уравнения, дифференциальные уравнения, интегральные уравнения и т. Д. Алгебраически решать линейные, квадратные и рациональные уравнения, линейные неравенства и системы линейных уравнений 2 x 2 и проверьте решения с помощью графической утилиты. 4. Постройте график линейных и квадратичных функций вручную и найдите важные особенности графика, такие как точки пересечения, вершины и наклон, где это необходимо, и проверьте их…
Сайга 12 лес
Система линейных уравнений a 11 x 1 + a 12 x 2 +… + a 1 nxn = b 1 a 21 x 1 + a 22 x 2 +… + a 2 nxn = b 2 ⋯ am 1 x 1 + am 2 x 2 +… + amnxn = bm может быть представлено как матричное уравнение A ⋅ x → = b →, где A – матрица коэффициентов,
Решение линейных уравнений с использованием метода перекрестного умножения. Решение одношаговых уравнений. Решение квадратных уравнений путем факторизации. Решение квадратных уравнений по формуле корней квадратного уравнения.Решение квадратных уравнений, заполнив квадрат. Природа корней квадратного уравнения. Сумма и произведение корней квадратного уравнения Алгебраические тождества
Бесплатная программа для решения математических задач отвечает на вопросы домашнего задания по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми пояснениями, как репетитор по математике. Мы также рассмотрим несколько других идей при решении систем уравнений. Системы уравнений Давайте начнем этот раздел с определения линейного уравнения.Вот пара примеров линейных уравнений. 12 5 6810 3 7 1 9 xy zxx− + = – = – Во втором уравнении обратите внимание на использование нижних индексов на …
Dell s2719dgf автояркость
Нелинейные системы – В этом разделе мы возьмем быстрый взгляд на решение нелинейных систем уравнений. Нелинейная система уравнений – это система, в которой хотя бы одно из уравнений не является линейным, т.е. имеет степень два или более. Отметим также, что здесь обсуждаются не все возможные методы решения нелинейных систем.
Исследовательский проект уровня 5
Продажа комплекта нижних частей Aero precision
Рабочий лист обратных круговых функций с ответами
Генератор Champion Замена батареи 3500
Естественная монополия существует, когда затраты на производство
Стоимость замены топливного насоса Duramax
Примеры таблиц истинности логические вентили
Комнаты обсуждения Gototraining не работают
Ashitacast не удалось проанализировать
Physioex упражнение 3 упражнение 2 quizlet
регистрация логин
Когда заменять свечи зажигания Subaru Crossstrek
Стартовый комплект рыболовных снастей
Asp net form builder drag and drop
Pua alabama безработица
Midland daily news некрологи 9 0067
Walden mini mega magic x2
Эмиссия электронов молибдена
Поиск и устранение неисправностей Moen gxp33c
Молекулярная геометрия sf4cl2
Как очистить коды bobcat
RUBCAT
7
Мастерская лексики Sadlier, уровень c Раздел 9 Выбор правильного слова
.
$$ \ large {\ left \ {\ begin {array} {1} \ mathrm {a_ {11} x_ {1} + a_ {12} x_ {2}} & + & \ cdots & + & \ mathrm {a_ {1n} x_ {n} = b_ {1}}, \\ \ mathrm {a_ {21} x_ {1} + a_ {22} x_ {2}} & + & \ dotsb & + & \ mathrm {a_ {2n} x_ {n} = b_ {2}}, \\ \ vdots & \ vdots & \ ddots & \ vdots \\ \ mathrm {a_ {m1} x_ {1} + a_ {m2} x_ {2}} & + & \ cdots & + & \ mathrm {a_ {mn} x_ {n} = b_ {m}} \ end {array} \ right.} $$
gdzie:
\ (\ mathrm {\ large { b_ {1}, …, b_ {m}}} \) – свободные слова (данные)
\ (\ mathrm {\ large {x_ {1}, …, x_ {n}}} \) – неизвестно
Если определитель матрицы коэффициентов системы отличен от нуля ( detA ≠ 0 ), то система линейных уравнений в векторной форме \ (\ color {blue} {x_1 } \ mathbf a_1 + \ dots + \ color {blue} {x_n} \ mathbf a_n = \ color {red} {\ mathbf b} \) имеет ровно одно решение, задаваемое формулами:
$$ \ color {blue} {x_1 } = \ frac {\ det (\ color {red} {\ mathbf b}, \; \ mathbf a_2, \ dots, \ mathbf a_n)} {\ det (\ mathbf a_1, \ mathbf a_2, \ dots, \ mathbf a_n)}, $$ $$ \ vdots $$ $$ \ color {синий} {x_n} = \ frac {\ det (\ mathbf a_1, \ dots, \ mathbf a_ {n-1}, \; \ color {red} {\ mathbf b})} {\ det (\ mathbf a_1, \ точки, \ mathbf a_ {n-1}, \ mathbf a_n)} $$.
$$ \ begin {bmatrix} a_ {11} & a_ {12} & \ dots & a_ {1n} \\ a_ {21} & a_ {22} & \ dots & a_ {2n} \\ \ vdots & \ vdots & \ vdots & \ vdots \\ a_ {m1} & a_ {m2} & \ dots & a_ {mn} \ end {bmatrix} \ begin {bmatrix} \ color {blue} {x_1} \\ \ color {blue} {x_2} \\ \ vdots \\ \ color {blue} {x_n} \ end {bmatrix} = \ begin {bmatrix} \ color {red} {b_1} \\ \ color {red} {b_2} \\ \ vdots \\ \ color {red} {b_n} \ end {bmatrix}.$$ Учитывая квадратную матрицу перехватов, где количество строк равно количеству столбцов (m = n), вычислим главный определитель W .
$$ W = \ begin {vmatrix} a_ {11} & a_ {12} & \ dots & a_ {1n} \\ a_ {21} & a_ {22} & \ dots & a_ {2n} \\ \ vdots & \ vdots & \ vdots & \ vdots \\ a_ {m1} & a_ {m2} & \ dots & a_ {mn} \ end {vmatrix} $$ Если W ≠ 0 , мы вычисляем определители вспомогательных матриц W 1 , W 2 … W n замена соответствующего столбца коэффициентов столбцом пересечения.
$$ W_1 = \ begin {vmatrix} \ color {red} {b_1} & a_ {12} & \ dots & a_ {1n} \\ \ color {red} {b_2} & a_ {22} & \ dots & a_ {2n} \\ \ vdots & \ vdots & \ vdots & \ vdots \\ \ color {красный} {b_n} & a_ {m2} & \ dots & a_ {mn} \ end {vmatrix}; W_2 = \ begin {vmatrix} a_ {11} & \ color {red} {b_1} & \ dots & a_ {1n} \\ a_ {21} & \ color {red} {b_2} & \ dots & a_ {2n } \\ \ vdots & \ vdots & \ vdots & \ vdots \\ a_ {m1} & \ color {красный} {b_n} & \ dots & a_ {mn} \ end {vmatrix}; …; W_n = \ begin {vmatrix} a_ {11} & a_ {12} & \ dots & \ color {red} {b_1} \\ a_ {21} & a_ {22} & \ dots & \ color {red} {b_2 } \\ \ vdots & \ vdots & \ vdots & \ vdots \\ a_ {m1} & a_ {m2} & \ dots & \ color {красный} {b_n} \ end {vmatrix} $$
Теперь по приведенной выше формуле, подставляя определители, мы можем вычислить неизвестные.
| ||||||||||||||||
В математике система линейных уравнений (или линейная система) – это набор двух или более линейных уравнений, включающих один и тот же набор переменных.
x и y : 4x + 3y = 20
-5x + 9y = 26
x и y . Есть несколько способов решить такую систему, например, исключение переменных, правило Крамера, метод сокращения строк и матричное решение.В этой статье мы рассмотрим матричное решение. AX = B . Например, мы можем представить Уравнение 1 в виде матрицы следующим образом: A = [[4 3]
[-5 9]]
X = [[x]
[y]]
B = [[20]
[26]]
x и y в уравнении 1 , нам нужно найти значения в матрице x .Для этого мы можем взять скалярное произведение обратной матрицы A и матрицы B , как показано ниже: X = инверсный (A) .B
pip : $ pip install numpy
A , которую мы определили в предыдущем разделе. A на Python.Для создания матрицы можно использовать метод array модуля Numpy. Матрицу можно рассматривать как список списков, где каждый список представляет собой строку. m_list , который дополнительно содержит два списка: [4,3] и [-5,9] . Эти списки представляют собой две строки в матрице A . Чтобы создать матрицу A с помощью Numpy, m_list передается методу массива , как показано ниже: импортировать numpy как np
m_list = [[4, 3], [-5, 9]]
А = np.массив (m_list)
linalg.inv () модуля Numpy: inv_A = np.linalg.inv (A)
печать (inv_A)
A и матрицей B . Важно отметить, что скалярное произведение матриц возможно только между матрицами , если внутренние размеры матриц равны i.е. количество столбцов левой матрицы должно соответствовать количеству строк в правой матрице. linalg.dot () . Следующий сценарий находит скалярное произведение между обратной матрицей A и матрицей B , которая является решением уравнения 1 . B = np.array ([20, 26])
X = np.linalg.inv (A) .dot (B)
печать (X)
[2.4.]
2 и 4 – соответствующие значения для неизвестных x и y в уравнении 1 . Для проверки, если вы вставите 2 вместо неизвестного x и 4 вместо неизвестного y в уравнении 4x + 3y , вы увидите, что результат будет 20. 4x + 3y + 2z = 25
-2x + 2y + 3z = -10
3x -5y + 2z = -4
A = np.массив ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.array ([25, -10, -4])
X = np.linalg.inv (A) .dot (B)
печать (X)
linalg.inv () и linalg.dot () объединены в цепочку. Переменная X содержит решение для уравнения 2 и печатается следующим образом: [5. 3. -2.]
x , y и z равны 5, 3 и -2 соответственно.Вы можете подставить эти значения в Equation 2 и проверить их правильность. linalg.inv () и linalg.dot () , чтобы найти решение системы уравнений. Однако библиотека Numpy содержит метод linalg.solve () , который можно использовать для непосредственного поиска решения системы линейных уравнений: A = np.array ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.массив ([25, -10, -4])
X2 = np.linalg.solve (A, B)
печать (X2)
[5. 3. -2.]
x , а цена одного апельсина – y . Вышеупомянутую проблему можно преобразовать так: 20x + 10y = 350
17x + 22y = 500
A = np.array ([[20, 10], [17, 22]])
B = np.array ([350, 500])
X = np.linalg.solve (A, B)
печать (X)
[10. 15.]
linalg.inv () и linalg.dot () в цепочке для решения системы линейных уравнений или просто использовать метод resolve () . Метод solution () является предпочтительным.


 Решение уравнений и неравенств
Решение уравнений и неравенств № 1-9
№ 1-9
 Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.