Решение системных уравнений методом гаусса онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Численные методы: решение систем линейных уравнений

В прикладных задачах часто возникает необходимость решать системы линейных уравнений.

Система линейных алгебраических уравнений с n неизвестными – это система уравнений вида

(1)

Слово система означает, что все уравнения рассматриваются как одно целое.

В общем случае у нас имеется m – уравнений, n – количество неизвестных. x₁, x₂,…, x_n – неизвестные, которые следует определить.

В системе (1) – фиксированные коэффициенты, b₁, b₂, …, b_m – свободные члены – предполагаются известными.

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе – неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Задача состоит в том, чтобы найти такие которые удовлетворяют всем уравнениям (1).

В частном случае мы имеем одно линейное уравнение:

Конечно, такое уравнение легко решить, если предположить, что коэффициент не равен 0, имеем: = .

Очевидно, в общем случае имеются 3 варианта решений: система имеет ни одного решения, имеет одно решение, более одного решения.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной

, если нет ни одного решения.

Система линейных уравнений может быть представлена в матричной форме как:

или:

Ax = b

Здесь A – это матрица системы, x – столбец неизвестных, а b – столбец свободных членов.

Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Рассмотрим, например, систему вида и поймем, как найти ее решение:

(2)

Предположим на минуту, что в первом уравнении

y отсутствует, а во втором отсутствует x, тогда мы имели бы решение именно то решение, которое нам нужно.

Вопрос: как исходную систему привести к такому виду и можно ли это сделать.

Заметим, что с тождествами мы можем делать следующие вещи: домножать на одно и то же число, отличное от 0, складывать, вычитать и тд, это похоже с тем, что вы раскладываете монеты по своим карманам, не меняя общей суммы.

От этих операций тождество не меняется.

В системе (2) у нас два тождества, домножим второе тождество на 2 и вычтем из первого, получим:

(3)

Формально у нас есть еще старое тождество , но оно нам не понадобится (подумайте, почему).

Система (3) точно такая же, как система (2).

Из второго уравнения системы (3) сразу получим:

Никто не мешает нам подставить это значение в первое уравнение:

Отсюда сразу находим, что

Итак, путем простых действий мы нашли, что система (2) может быть представлена в виде:

Именно такие естественные соображения приводят к общему методу решения систем линейных уравнений, известному как метод исключения или метод Гаусса.

Метод Гаусса является одним из самых распространенных прямых методов решения систем линейных уравнений Ax = b:

Опишем этот метод в общем случае.

Вначале исходная система приводится к верхнетреугольному виду.

Это достигается следующей последовательностью преобразований (прямой ход).

Будем считать для удобства, что элемент a_i_j исходной матрицы и компоненты вектора b_i есть, соответственно, элементы a_i_j ⁽¹⁾ первого шага преобразованной матрицы A₁ и преобразованного вектора b

₁:A = A₁, b=b₁.

Далее, на втором шаге прибавим к второй строке первую, умноженную на

Аналогично поступим со всеми оставшимися строками, т.е. прибавим к каждой i-ой строке i=2,3,…,N, первую, умноженную на коэффициент

При этом соответственно изменится и вектор b1.

Таким образом, 2 шаг.

Имеем систему уравнений A₂x = b₂:

где

3 шаг.

Прибавим к новой третьей строке новую вторую, умноженную на

То же самое сделаем с остальными строками 4,5,…,N, т.е. прибавим к

i-ой строке вторую, умноженную на

При этом получим систему A₃x = b₃:

(k+1)-ый шаг:

Здесь

Поступая так и далее, на шаге N-1 получаем верхнетреугольную систему:

При этом, мы также получили матрицу C переводных коэффициентов, имеющую вид:

Решение полученной треугольной системы как легко видеть, имеет вид (обратный ход метода Гаусса):

Заметим, что при прямом ходе метода Гаусса может возникнуть ситуация, когда происходит деление на нуль, да и вообще, желательно не делить на малое число, чтобы не накапливалась ошибка.

Поэтому метод Гаусса обычно проводят с частичным выбором главного элемента, то есть после каждого шага (пусть это был k-й шаг) переставляют строки с номерами k,k+1,…,N таким образом, чтобы на месте kk оказался элемент наибольший из всех в k-ом столбце при m>k (при этом, естественно, переставляются и компоненты вектора b).

Можно для максимальной точности переставлять также и столбцы преобразуемой матрицы, чтобы на месте

kk оказался максимальный элемент из всех с индексами больше, либо равными k.

Эта процедура называется методом Гаусса с выбором главного элемента. Она несколько повышает точность по сравнению с частичным выбором главного элемента, но весьма неудобна, в том числе для программирования, поскольку при перестановке строк компоненты искомого вектора x переставлять не надо, тогда как при перестановке столбцов надо переставлять и соответствующие компоненты вектора x.

Опишем обратный ход метода Гаусса в несколько иной форме (треугольное разложение).

Введем матрицы M_k по правилу:

На каждом шаге метода Гаусса получается некоторая промежуточная матрица:

и вектор

Нетрудно видеть, что

Вопрос. Почему

Если производить также выбор главных элементов, то необходимо использовать оператор P перестановки индексов l и m, матричные элементы которого равны:

При применении оператора перестановки индексов к матрице слева, меняются местами строки матрицы и компоненты свободного вектора (PAx = Pb), если же его применить справа к матрице, то меняются местами ее столбцы и компоненты решения

Существует большой класс так называемых итерационных методов решения систем уравнений, аналогичных итерационным методам нахождения корней нелинейных уравнений.

Итерационные методы последовательно уточняют решение, отправляясь от начального приближения.

При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций.

Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений.

Идея состоит в том, чтобы найти неподвижную точку матричного уравнения

(5)

эквивалентного начальной системе линейных алгебраических уравнений.

При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:

Термин неподвижная точка становится ясен, если вы внимательно посмотрите на уравнение (5), по самому своему смыслу величина Х является неподвижной точкой.

Более подробное описание методов решения систем линейных уравнений можно найти в специальной литературе, наша задача дать обзор методов и основные идеи решения такого рода задач.

Обусловленность линейных систем, погрешность

При решении абстрактной задачи Ax = b, где A – оператор произвольной природы, важным моментом является корректность ее постановки.

Задача считается корректной, если решение существует и единственно и , кроме того, решение непрерывно зависит от данных (то есть, при также стремится к нулю).

Однако и непрерывная зависимость от входных данных может иметь свои нюансы.

Чем меньшее (большее) изменение решения вызывает вариация входных данных, тем более хорошо (плохо) обусловленной считается задача.

Понятие обусловленности является тем более существенным для численных методов, поскольку на практике входные данные известны, как правило, с некоторой погрешностью.

Кроме того, существуют ошибки округления, возникающие при вычислениях.

Таким образом, формально корректная задача, являясь плохо обусловленной, может оказаться разрешимой столь неточно, что в этом будет отсутствовать практический смысл.

Чем можно охарактеризовать количественно обусловленность для линейных систем?

Пусть A – квадратная NxN – матрица.

Рассмотрим задачу Ax = b.

Пусть также некоторая норма в пространстве R_N

Норма оператора A определяется стандартно:

Обозначим y = Ax и введем число m по правилу:

Величина называется числом обусловленности.

Очевидно:

если A – диагональная, то (Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть вариация правой части, а соответствующее изменение решения.

Тогда справедливо следующее неравенство:

Доказательство. Имеем:

Так как

то

Аналогично, поскольку

Объединяя два неравенства, окончательно получаем для оценки погрешности:

В начало

Содержание портала

Решение СЛАУ методом Гаусса – презентация онлайн

1. Решение СЛАУ методом Гаусса Тема урока

2. Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)

Имя Гаусса известно почти во всех областях
математики, а также в геодезии, астрономии,
механике. За глубину и оригинальность мысли, за
требовательность к себе и гениальность ученый и
получил звание «король математиков».
Метод решения системных уравнений, открытый
ученым, был назван методом Гаусса. Метод
состоит в последовательном исключении
переменных до приведения уравнения к
ступенчатому виду. Решение методом Гаусса
считается классическим и активно используется и
сейчас.

Память о Гауссе навсегда осталась в
математических и физических терминах (метод
Гаусса, дискриминанты Гаусса, прямая Гаусса,
Гаусс – единица измерения магнитной индукции
и др.). Имя Гаусса носит лунный кратер, вулкан в
Антарктиде и малая планета.

3. Метод Гаусса

Метод Гаусса — классический метод решения системы
линейных алгебраических уравнений (СЛАУ).
Это метод последовательного исключения переменных,
когда с помощью элементарных преобразований система
уравнений приводится к равносильной системе
ступенчатого (или треугольного) вида, из которого
последовательно, начиная с последних (по номеру)
переменных, находятся все остальные переменные.

4. Пример. Решить СЛАУ методом Гаусса:

Запишем расширенную матрицу системы, составленную из
коэффициентов системы и свободных слагаемых.

5. С помощью элементарных преобразований сведем расширенную матрицу к подобной матрице ступенчатого вида:

6.

Получаем систему линейных уравнений, эквивалентную исходной системе уравнений.Ответ:

7. Ощутим свежее дыхание моря…

9. Самостоятельная работа

1 вариант
Решить СЛАУ
методом Гаусса:
2 вариант
Решить СЛАУ
методом Гаусса:

10. Домашнее задание

Решить СЛАУ:

11. Итоги урока

̶ анализ ответов;
̶ оценка результатов работы.

Решение системы линейных уравнений методом Гаусса в MS Excel

На днях понадобилось найти корни системы линейных уравнений методом Гаусса в Microsoft Excel. Готовый алгоритм решения можно найти в книге Гарнаева «Использование Excel и VBA в экономике и финансах», но объяснение там очень скудное и не совсем понятное. Постараюсь описать подробней для тех, кому может понадобиться этот алгоритм.

Лирическое отступление: в тексте будет предлагаться ввести в диапазон ячеек формулу вида: {=A1:B3+$C$2:$C$3} и т.п., это так-называемые «формулы массива» (формула, выполняющая несколько вычислений над одним или несколькими наборами значений, а затем возвращающая один или несколько результатов. Формулы массива заключены в фигурные скобки { }). Microsoft Excel автоматически заключает ее в фигурные скобки ( { } ). Для введения такого типа формул необходимо выделить весь диапазон, куда нужно вставить формулу, в первой ячейке ввести формулу без фигурных скобок (для примера выше — =A1:B3+$C$2:$C$3) и нажать Ctrl+Shift+Enter.

Пускай имеем систему линейных уравнений:

1. Запишем коэффициенты системы уравнений в ячейки A1:D4 а столбец свободных членов в ячейки E1:E4. Если в ячейке A1 находится 0, необходимо поменять строки местами так, чтоб в этой ячейке было отличное от ноля значение. Для большей наглядности можно добавить заливку ячеек, в которых находятся свободные члены.

2. Необходимо коэффициент при x₁ во всех уравнениях кроме первого привести к 0. Для начала сделаем это для второго уравнения. Скопируем первую строку в ячейки A6:E6 без изменений, в ячейки A7:E7 необходимо ввести формулу: {=A2:E2-$A$1:$E$1*(A2/$A$1)}. Таким образом мы от второй строки отнимаем первую, умноженную на A2/$A$1, т.е. отношение первых коэффициентов второго и первого уравнения. Для удобства заполнения строк 8 и 9 ссылки на ячейки первой строки необходимо использовать абсолютные (используем символ $).

3. Копируем введенную формулу формулу в строки 8 и 9, таким образом избавляемся от коэффициентов перед x₁ во всех уравнениях кроме первого.

4. Теперь приведем коэффициенты перед x₂ в третьем и четвертом уравнении к 0. Для этого скопируем полученные 6-ю и 7-ю строки (только значения) в строки 11 и 12, а в ячейки A13:E13 введем формулу {=A8:E8-$A$7:$E$7*(B8/$B$7)}, которую затем скопируем в ячейки A14:E14. Таким образом реализуется разность строк 8 и 7, умноженных на коэффициент B8/$B$7. Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби.

5. Осталось привести коэффициент при x₃ в четвертом уравнении к 0, для этого вновь проделаем аналогичные действия: скопируем полученные 11, 12 и 13-ю строки (только значения) в строки 16-18, а в ячейки A19:E19 введем формулу {=A14:E14-$A$13:$E$13*(C14/$C$13)}. Таким образом реализуется разность строк 14 и 13, умноженных на коэффициент C14/$C$13. Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби.

6. Прямая прогонка методом Гаусса завершена. Обратную прогонку начнем с последней строки полученной матрицы. Необходимо все элементы последней строки разделить на коэффициент при x₄. Для этого в строку 24 введем формулу {=A19:E19/D19}.

7. Приведем все строки к подобному виду, для этого заполним строки 23, 22, 21 следующими формулами:
23: {=(A18:E18-A24:E24*D18)/C18} — отнимаем от третьей строки четвертую умноженную на коэффициент при x₄ третьей строки.
22: {=(A17:E17-A23:E23*C17-A24:E24*D17)/B17} — от второй строки отнимаем третью и четвертую, умноженные на соответствующие коэффициенты.
21: {=(A16:E16-A22:E22*B16-A23:E23*C16-A24:E24*D16)/A16} — от первой строки отнимаем вторую, третью и четвертую, умноженные на соответствующие коэффициенты.
Результат (корни уравнения) вычислены в ячейках E21:E24.

UPDATE от 25 апреля 2012 г. Выкладываю xls-файл с решением линейных уравнений методом Гаусса в Microsoft Excel:

Решение уравнений в Excel методом итераций Крамера и Гаусса

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» – «Работа с данными» – «Анализ «что-если»» – «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х² + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» – ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» – В1. Здесь должен отобразиться отобранный параметр.
После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

Значения элементов введем в ячейки Excel в виде таблицы.
Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
Умножим обратную матрицу Ах^-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х³ + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

Х_n+1 = X_n– F (X_n) / M, n = 0, 1, 2, … .

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х³ – 1. М = 11.

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Скачать решения уравнений в Excel

Корень на заданном промежутке один.

Решение СЛАУ и матрицы в Matlab

Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.

Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т. д.

В традициях нашего сайта разберём на примере:

Решить систему линейных уравнений:

4*a + b - c = 6 a - b + c = 4 2*a - 3*b - 3*c = 4

Метод обратной матрицы в Matlab

Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.

В итоге у нас получится 2 матрицы:

A=[4  1 -1; 1 -1  1; 2 -3 -3];   % коэффициенты
B=[6; 4; 4];

Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:

det(A)

Вывод: 30

После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv.
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:

x=inv(A)*B

Вывод:
2
-1
1

Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1. Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.

Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.

Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.

Метод Гаусса

Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
(\) - левое деление.
При следующей записи:

x = A\B

Вывод:
2
-1
1

Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.

Метод разложения матрицы

Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.

Возможны следующие разложения:

разложение Холецкого
LU разложение
QR разложение

Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.

Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.

LU разложение

Решим выше предложенную задачу через LU разложение:

[L, U] = lu(A);

Вывод:

L =
    1       0     0
    0.25    1     0
    0.5     2.8   1

U =
    4     1     -1
    0    -1.25   1.25
    0     0     -5

Затем:

y = L\B;
x = U\y

Вывод:

2
-1
1

QR разложение

И через QR разложение соответственно:

[Q, R] = qr(A);
x = R\(Q'*B)

Вывод:

2. 0000
-1.0000
1.0000

Отметим, что апостроф ( ' ) после Q означает транспонирование.

Стандартные функции Matlab

Так же Matlab предлагает функцию linsolve, с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:

x = linsolve(A,B)

Вывод:

2
-1
1

Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.

Повторение

Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:

Решить систему линейных уравнений:
6*a - b - c = 0 a - 2*b + 3*d = 0 3*a - 4*b - 4*c = -1

A=[6 -1 -1; 1 -2 3; 3 -4 -4];
B=[0; 0; -1];

Методом обратной матрицы:

x=inv(A)*B

Вывод:
    0.0476
    0.1810
    0.1048

Методом Гаусса:

x = A\B

Вывод:
    0. 0476
    0.1810
    0.1048

LU разложение:

[L, U] = lu(A);
y = L\B;
x = U\y

Вывод:
    0.0476
    0.1810
    0.1048

QR разложение:

[Q, R] = qr(A);
x = R\(Q'*B)

Вывод:
    0.0476
    0.1810
    0.1048

На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.

Поделиться ссылкой:

Похожее

Решение систем линейных уравнений алгоритмы общих и частных методов нахождения корней, основные правила и теоремы и примеры их использования, онлайн калькулятор

Совокупность математических записей, из которых каждая является линейным алгебраическим равенством первой степени, называется системой линейных уравнений. Её решение — это классическая задача алгебры, определяющая объекты и методы. Существует несколько принципиально разных способов нахождения ответа. Каждый из них имеет достоинства и недостатки, но выбор метода зависит лишь только от личных предпочтений решающего.

Понятия и обозначения

Для измерения геометрических или физических величин в математике используют действительное число — вещественное. В уравнении под ним понимают все свободные члены или неизвестные переменные. Вычисление линейных алгебраических уравнений играет важную роль в различных математических задачах: численных методах, программировании, эконометрике.

Общий вид системы линейных уравнений (СЛАУ) в классическом понимании представляют следующим образом:

a11 * n 1 + a 12 * n 2 + …+a 1x n x = c 1.

a21 * n 1 + a 22 * n 2 + …+a 2x n x = c 2.

as1 * n 1 + a 12 * n 2 + …+a 1x n x = c s.

В этой записи s — это количество уравнений, x — число переменных, а n — переменная которую необходимо вычислить. Предполагается что a и b это известные свободные члены. Индексы обозначают порядковый номер уравнения. Первый символ — расположение строчки, а второй — позиция произведения переменной и свободного члена.

Если эти члены отличные от нуля, то система называется неоднородной, в ином же случае однородной. Квадратной системой называется совокупность уравнений, когда их число совпадает с количеством неизвестных. Существует понятие и неопределённой системы. Это совокупность, при которой неизвестных больше числа уравнений. Если наоборот, то система считается переопределенной. В литературе её ещё часто называют прямоугольной.

Система считается решаемой, когда множество членов X соответствует такому набору чисел, что при их подстановке вместо n вся система обратится в тождество. Если существует хотя бы одно решение, система называется совместной. Ответы, превращающие уравнения в равенства, при которых переменные не совпадают, считаются различными.

Существует четыре способа развязывания системы уравнений:

способ подстановки;
использование новых переменных;
алгебраическое сложение;
матричный метод.

Вид используемого алгоритма зависит от типа примера. Метод алгебраического сложения применяют, когда в задании лишь одно неизвестное, а коэффициенты противоположны или равны. Если же хотя бы в одной из формул коэффициент равен единице, то удобнее будет решить систему уравнений методом подстановки. В иных случаях используют матрицы.

Алгебраическое сложение

Способ заключается в сложении или вычитании выражений. Это довольно простой способ и в то же время эффективный. Алгоритм нахождения ответа для равенств с двумя переменными n и m сводится к следующему:

уравниванию модулей коэффициентов при любом из неизвестных;
сложению или вычитанию равенства;
вычисления составленного выражения;
прогонки каждого найденного корня через первую или вторую строчку системы уравнений;
нахождению второго неизвестного.

То есть после выполнения арифметических действий с уравнениями должно получиться одно выражение с одним неизвестным. Затем находят значение этой переменной и в него подставляют полученный корень. Например, нужно узнать, какие корни системы, состоящей из двух строчек, превращают её в тождество:

n² – m² = 21.

n² + m² = 29.

В первую очередь необходимо сложить равенства между собой. В итоге получится:

2 * n ² = 50;
n ² = 25;
n = +5 (-5).

Подставив поочерёдно в каждое равенство найденные корни можно найти второе неизвестное. Для корня n = – 5 ответом будет:

(-5)² + m² = 29;
25 + m² = 29;
m² = 29 – 25;
m²= 4.

Соответственно, корнями будут числа два и минус два. Аналогичные действия необходимо выполнить и для корня другого знака n = 5. В итоге получится, что пары (− 5; − 2), (− 5; 2), (5; − 2), (5 ; 2) являются нужным ответом. При достаточном опыте подробно описывать решение не обязательно.

Существуют системы, требующие подготовительного этапа. Например, такого вида:

3 * n – 4 * m = 5.

2 * n + 3 * m = 7.

Исключить здесь сразу переменную не выйдет. Если умножить все члены первой строчки на тройку, а второй на четвёрку, получится запись:

9 * n – 12 * m = 15.

8 * n + 12 * m = 28.

Теперь равенства можно сложить, тем самым исключив переменную m. Затем система решается по базисному алгоритму. Чтобы понять, можно ли решить систему этим методом, следует предварительно её проанализировать. Необходимое условие заключается в том, что коэффициенты второй переменной должны быть одинаковыми по модулю, но противоположными по знаку.

Метод подстановки

Систему равенств возможно решить и способом подстановки. Используя любое из уравнений, можно выразить любую из неизвестных переменных, а затем подставить её в другое равенство. Алгоритм использования метода следующий:

через n в одном из уравнений выражают m;
подставляют полученное равенство вместо n в другое тождество;
решают уравнение и находя m;
поочерёдно подставляют найденные корни и получают ответ.

Например, нужно проверить, все ли целые корни могут быть у системы:

8 * n – 5 * m = -16.

10 * n + 3 * m = 17.

Выразив m через n можно записать равенство: n = (8* m + 16) / 5. Так как n одинаково в обоих уравнениях, то следует подставить полученное тождество и записать: 10* n + 3*(8* n +16) / 5 = 17. Отсюда уже просто найти корень. Он будет равен дроби 1/2. Подставив его вместо n легко вычислить и второй корень: m = (8 * n + 16) / 5 = 4. Таким образом, у системы будет только один целый корень. При желании проверить ответ можно решить систему другим методом.

Использование матриц

Для систем с произвольным числом уравнений и неизвестных используют другие методы. Если система состоит из нелинейных дифференциальных уравнений с постоянными коэффициентами, то используют матричный способ. Этот метод предполагает применение обратной матрицы.

Пусть дана система с тремя неизвестными х1, х2, х3. Нужно найти значения, при которых равенства станут верными. Для нахождения решений используют три матрицы:

Коэффициент системы. При этом её определитель не должен быть равным нулю.
Вектора неизвестных. Именно его понадобится найти.
Столбца свободных членов.

Базисное решение строят на произведении первой и второй матрицы. В результате получают матрицу размером три на один. То есть вектор-столбец с тремя элементами. После выполнения действия получится, что системный вектор будет равен левой части системы и соответствовать третьей матрице. Таким образом, обозначив матрицы буквами А, Б, В, можно записать выражение А * Б = В и найти необходимую Б.

При умножении на А^-1 (обратную матрицу) получают равенство: Е * Б = А^-1 * В, где Е – единичная матрица получена из совместимости прямой и обратной. Так как при произведении с единичной матрицей значения не изменяются, то решением системы будет формула: Б = А^-1 * В.

Способ Гаусса-Жордана

Частным случаем решения системы является Метод Гаусса — Жордана. Суть решения основана на составлении специальной таблицы. В первый столбец заносятся известные значения, то есть величины, расположенные после равно, а в три других коэффициенты, стоящие после неизвестных. Чтобы приступить к решению, необходимо выполнить три шага:

выбрать ключевой элемент из первых трёх столбцов;
переписать строчку с ключевым значением, предварительно разделив все элементы на это значение;
переписать оставшиеся элементы, при этом вычитая из него произведение соответствующих ему чисел.

В полученной новой матрице снова выбирают ключевой элемент и выполняют все действия снова. Шаги повторяют до тех пор, пока не получится матрица, состоящая из нулей и единиц. Значения корней системы будут находиться на пересечении столбцов со строчками напротив единиц.

Этот метод используют только при выполнении условия совместности. Его ещё называют способом простой итерации. Он был доказан и оптимизирован Зейделем. С помощью итерационного метода можно посчитать систему А* Б = В с точностью “е”. Составляют n уравнение на сходимость, а затем на точность. Затем из первого уравнения выражают n1, второго n2, третьего n3 и так далее. Новые n с индексом i +1 считаются через старые i. Зейдель предложил расширить решение и добавить снова для счёта индекс i+1.

Это фундаментальные способы решения сложных систем уравнений. Они трудные, требуют опыта и внимательности. Поэтому существуют специальные онлайн-калькуляторы по методу Гаусса с подробным решением, помогающие исследовать систему любой численности.

Теорема Кронекера — Капелли

Применяется она при проведении исследований без непосредственного решения. То есть для записи эквивалентной совокупности алгебраических уравнений с их минимальным числом. Теорема говорит о следующем: система уравнений А * Б = В имеет решение только тогда, когда ранг А равен (А, В), где последнее расширенная матрица, полученная из первого члена путём приписывания столбца В.

Это утверждение обобщает различные виды СЛАУ:

Несовместные – которые определяют при условии, что их ранг меньше ранга расширенной матрицы. Существование корней невозможно.
Совместные неопределённые – системы, имеющие бесконечное множество решений. В этом случае ранги равны, а количество неизвестных будет меньше.
Совместно определённые – в этом случае ранг равен расширенной матрице и количеству неизвестных. Точное решение будет одно.

Выводом из этой теоремы является то, что число главной переменной совокупности будет всегда равно рангу системы. При этом столбец свободных членов представляет собой линейную комбинацию столбцов матрицы А.

Решение Крамера

Пожалуй, это один из самых простых способов нахождения корней уравнений. Для решения строят несколько матриц. Основная получается из коэффициентов, стоящих при неизвестных. Она обозначается символом дельта. Вторую, дельта-икс, образуют из основной матрицы заменой первого столбца на ответы уравнений. Следующая, дельта-игрек, строится с заменой в основной матрице второго столбца на значения ответов и так далее.

Затем вычисляют дискриминант этих матриц, то есть их определитель. Для его поиска можно использовать способ треугольника или разложения. Первый подходит для простых матриц. Находят его как разницу умножения чисел, стоящих в матрице крест-накрест. Второй же применим для матриц, содержащих три и более строк. При нахождении выбирают одну из них и раскладывают матрицу.

Как только все дискриминанты найдены, используют правило Крамера: n = Δn/ Δ. Подставляют значения, находят ответ. Стоит отметить, что много интернет-порталов, предлагающих услугу расчётов СЛАУ, используют для вычислений онлайн-метод Крамера.

Удобные онлайн-калькуляторы

В некоторых случаях решение СЛАУ онлайн будет хорошим подспорьем для того, чтобы разобраться в различных правилах, используемых при решениях. Из популярных интернет-сервисов, позволяющих найти корни систем, можно отметить: kontrolnaya-rabota, mathsolution, planetcalc, allcalc. Использовать эти сайты-решатели смогут даже слабо подготовленные пользователи, имеющие общее представление о методах решений.

Для выполнения расчёта необходимо ввести параметры системы и нажать кнопку «Рассчитать». При этом можно выбрать метод, на базе которого будут проводиться вычисления. Удобным является и то, что полученный расчёт сопровождается объяснениями.

На этих порталах также можно посмотреть примеры и правила решений. Некоторые калькуляторы могут построить и график системы. Например, kontrolnaya-rabota. Для этого на сайте нужно выбрать раздел «Графическое решение уравнений онлайн» и ввести исследуемую систему равенств.

АлгебраКасательная к графику функции, как составить уравнение, свойства, угловой коэффициент касательной проведенной к графику функции, формула, примеры решения

АлгебраТеория вероятности формула и примеры для чайников, задачи с решениями, как найти классическую вероятность в математике, как обозначается и в чем выражается вероятность

Решение уравнений методом обратной матрицы

Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений.

Суть метода

Пусть задана система линейных уравнений с неизвестными:

Эту систему можно записать в виде матричного уравнения ,

где – матрица системы,

– столбец неизвестных,

– столбец свободных коэффициентов.

Из полученного матричного уравнения необходимо выразить .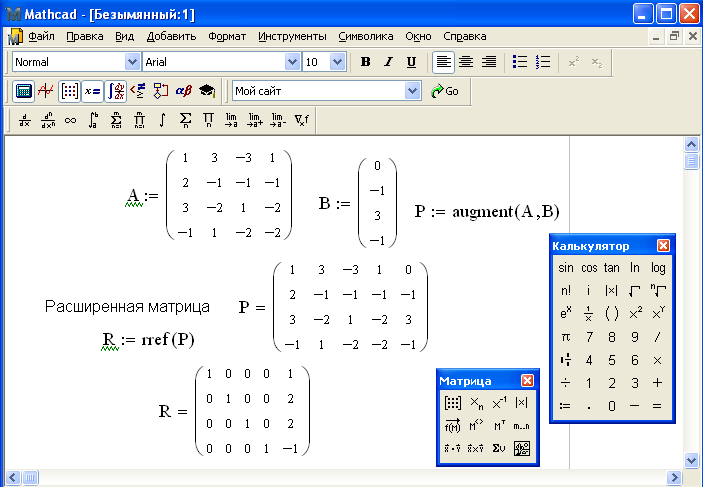 Для этого умножим обе части матричного уравнения слева на , получим:

Так как , то или .

Далее находится обратная матрица и умножается на столбец свободных членов .

ЗАМЕЧАНИЕ Обратная матрица к матрице существует только при условии, что . Поэтому при решении системы линейных уравнений методом обратной матрицы в первую очередь вычисляется . Если , то система имеет единственное решение, которое можно найти методом обратной матрицы, если же , то методом обратной матрицы решить эту систему нельзя.

Пример решения методом обратной матрицы

ПРИМЕР 1

Задание

Решить систему линейных уравнений методом обратной матрицы

Решение

Данная система уравнений может быть записана матричным уравнением

где , , .

Выразив из этого уравнения , получим

Найдем определитель матрицы :

Так как , то система имеет единственное решение, которое можно найти методом обратной матрицы.

Найдем обратную матрицу с помощью союзной матрицы. Вычислим алгебраические дополнения к соответствующим элементам матрицы :

Запишем союзную матрицу , составленную из алгебраических дополнений элементов матрицы :

Далее запишем обратную матрицу согласно формуле . Будем иметь:

Умножая обратную матрицу на столбец свободных членов , получим искомое решение исходной системы:

Ответ

Калькулятор Системы линейных уравнений

Этот калькулятор решает систему линейных уравнений любого типа с указанными шагами, используя метод исключения Гаусса-Жордана, метод обратной матрицы или правило Крамера.

Связанный калькулятор: Калькулятор системы уравнений

Через запятую, например, x + 2y = 5,3x + 5y = 14.

Оставьте поле пустым для автоматического определения или укажите такие переменные, как x, y (через запятую).

Метод:

Метод исключения Гаусса-Жордана Метод обратной матрицы Правило Крамера

Если калькулятор что-то не вычислил, или вы определили ошибку, или у вас предложение / отзыв, напишите в комментариях ниже.

Ваш ввод

Решите $$$ \ begin {case} 5 x – 2 y = 1 \\ x + 3 y = 7 \ end {cases} $$$ для $$$ x $$$, $ $$ y $$$ с использованием метода исключения Гаусса-Джордана.

Решение

Запишите расширенную матрицу: $$$ \ left [\ begin {array} {cc | c} 5 & -2 & 1 \\ 1 & 3 & 7 \ end {array} \ right] $ $$.

Выполните исключение Гаусса-Жордана (шаги см. В калькуляторе исключения Гаусса-Жордана): $$$ \ left [\ begin {array} {cc | c} 5 & -2 & 1 \\ 0 & \ frac {17 } {5} & \ frac {34} {5} \ end {array} \ right] $$$.

Обратный заменитель:

$$$ y = \ frac {\ frac {34} {5}} {\ frac {17} {5}} = 2 $$$

$$$ x = \ frac { 1 – \ left (-2 \ right) \ left (2 \ right)} {5} = 1 $$$

Ответ

$$$ x = 1 $$$, $$$ y = 2 $$$ A

Решающих систем с исключением Гаусса

У нас есть система трех уравнений с тремя переменными. Пусть [latex] \, x \, [/ latex] будет сумма, инвестированная под 5% годовых, пусть [latex] \, y \, [/ latex] будет суммой, инвестированной под 8%, и пусть [latex] \ , z \, [/ latex] – сумма, вложенная под 9% годовых. Таким образом,

[латекс] \ begin {массив} {l} \ text {} x + y + z = 10 000 \ hfill \\ 0,05x + 0,08y + 0,09z = 770 \ hfill \\ \ text {} 2x-z = 0 \ hfill \ end {array} [/ latex]

В качестве матрицы имеем

[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 1 & \ hfill 1 \\ \ hfill 0,05 & \ hfill 0,08 & \ hfill 0,09 \\ \ hfill 2 & \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 10,000 \\ \ hfill 770 \\ \ hfill 0 \ end {array} \ right] [/ latex]

Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.

[латекс] \ begin {array} {l} \ begin {array} {l} \ hfill \\ -0.05 {R} _ {1} + {R} _ {2} = {R} _ {2} \ в \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0,03 & \ hfill & \ hfill 0,04 & \ hfill \\ \ hfill 2 & \ hfill & \ hfill 0 & \ hfill & \ hfill -1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill 0 \ end {array} \ right] \ hfill \ end {array} \ hfill \\ \, \, \, \, \, \, – 2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0. 03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ frac {1} {0.03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, 2 {R} _ {2} + {R} _ { 3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill – \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end { массив} \ right] \ hfill \ end {array} [/ latex]

Третья строка сообщает нам [латекс] \, – \ frac {1} {3} z = -2,000; \, [/ latex], таким образом [латекс] \, z = 6,000. [/ латекс]

Вторая строка сообщает нам [latex] \, y + \ frac {4} {3} z = 9000. \, [/ Latex] Подставляя [latex] \, z = 6000, [/ latex], мы получаем

[латекс] \ begin {array} {r} \ hfill y + \ frac {4} {3} \ left (6000 \ right) = 9000 \\ \ hfill y + 8000 = 9000 \\ \ hfill y = 1000 \ end {array} [/ latex]

Первая строка сообщает нам [латекс] \, x + y + z = 10,000. \, [/ Latex] Замена [latex] \, y = 1,000 \, [/ latex] и [latex] \, z = 6,000, [/ latex] получаем

[латекс] \ begin {array} {l} x + 1 000 + 6 000 = 10 000 \ hfill \\ \ text {} x = 3 000 \ text {} \ hfill \ end {array} [/ latex]

Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.

Решение системы с исключением Гаусса

Результаты обучения

Используйте метод исключения Гаусса для решения системы уравнений, представленной в виде расширенной матрицы.
Интерпретировать решение системы уравнений в виде расширенной матрицы.

Мы видели, как написать систему уравнений , с расширенной матрицей , а затем как использовать операции со строками и обратную подстановку для получения формы строка-эшелон.Теперь мы будем использовать метод исключения Гаусса как инструмент для решения системы, записанной в виде расширенной матрицы. В нашем первом примере мы покажем вам процесс использования исключения Гаусса в системе двух уравнений с двумя переменными.

Пример: решение системы 2 x 2 методом исключения Гаусса

Решите данную систему методом исключения Гаусса.

[латекс] \ begin {array} {l} 2x + 3y = 6 \ hfill \\ \ text {} x-y = \ frac {1} {2} \ hfill \ end {array} [/ latex]

Показать решение

Сначала запишем это как расширенную матрицу.

[латекс] \ left [\ begin {array} {rr} \ hfill 2 & \ hfill 3 \\ \ hfill 1 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 6 \\ \ hfill \ frac {1} {2} \ end {array} \ right] [/ latex]

Нам нужна 1 в строке 1, столбце 1. Этого можно добиться, поменяв местами строку 1 и строку 2.

[латекс] {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 2 & \ hfill 3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 6 \ end {array} \ right] [/ latex]

Теперь у нас есть 1 как первая запись в строке 1, столбце 1.Теперь давайте получим 0 в строке 2, столбце 1. Этого можно добиться, умножив строку 1 на [latex] -2 [/ latex] и затем прибавив результат к строке 2.

[латекс] -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill 5 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 5 \ end {массив } \ right] [/ latex]

У нас есть только один шаг, чтобы умножить строку 2 на [latex] \ frac {1} {5} [/ latex].

[латекс] \ frac {1} {5} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \ \ \ hfill 0 & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {cc} & \ frac {1} {2} \\ & 1 \ end {array} \ right] [/ latex]

Использовать обратную замену.Вторая строка матрицы представляет [латекс] y = 1 [/ латекс]. Подставьте обратно [latex] y = 1 [/ latex] в первое уравнение.

[латекс] \ begin {array} {l} x- \ left (1 \ right) = \ frac {1} {2} \ hfill \\ \ text {} x = \ frac {3} {2} \ hfill \ end {array} [/ latex]

Решение – точка [латекс] \ left (\ frac {3} {2}, 1 \ right) [/ latex].

Попробуйте

Решите данную систему методом исключения Гаусса.

[латекс] \ begin {массив} {l} 4x + 3y = 11 \ hfill \\ \ text {} \ text {} \ text {} x – 3y = -1 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (2,1 \ вправо) [/ латекс]

В нашем следующем примере мы решим систему двух уравнений с двумя зависимыми переменными.Напомним, что зависимая система имеет бесконечное количество решений, и результатом операций со строками в ее расширенной матрице будет уравнение, такое как [latex] 0 = 0 [/ latex]. Мы также рассмотрим написание общего решения для зависимой системы.

Пример: решение зависимой системы

Решите систему уравнений.

[латекс] \ begin {array} {l} 3x + 4y = 12 \\ 6x + 8y = 24 \ end {array} [/ latex]

Показать решение Выполните строковых операций на расширенной матрице, чтобы попытаться получить строковую форму .

[латекс] A = \ left [\ begin {array} {llll} 3 \ hfill & \ hfill & 4 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 12 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] [/ latex]

[латекс] \ begin {array} {l} \ hfill \\ \ begin {array} {l} – \ frac {1} {2} {R} _ {2} + {R} _ {1} = { R} _ {1} \ to \ left [\ begin {array} {llll} 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end { array} | \ begin {array} {ll} \ hfill & 0 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] \ hfill \\ {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {llll} 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \\ 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 24 \ hfill \\ \ hfill & 0 \ hfill \ end {array} \ right] \ hfill \ end {array} \ hfill \ end {array} [/ latex]

Матрица заканчивается всеми нулями в последней строке: [latex] 0y = 0 [/ latex].Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите для [latex] y [/ latex].

[латекс] \ begin {array} {l} 3x + 4y = 12 \ hfill \\ \ text {} 4y = 12 – 3x \ hfill \\ \ text {} y = 3- \ frac {3} {4} x \ hfill \ end {array} [/ latex]

Итак, решение этой системы – [латекс] \ left (x, 3- \ frac {3} {4} x \ right) [/ latex].

Теперь мы перейдем на следующий шаг к решению системы линейных уравнений 3 на 3.Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.

Пример: решение системы линейных уравнений с использованием матриц

Решите систему линейных уравнений с помощью матриц.

[латекс] \ begin {массив} {c} \ begin {array} {l} \ hfill \\ \ hfill \\ x-y + z = 8 \ hfill \ end {array} \\ 2x + 3y-z = -2 \\ 3x – 2y – 9z = 9 \ end {array} [/ latex]

Показать решение

Сначала мы пишем расширенную матрицу.

[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill -1 \\ \ hfill 3 & \ hfill -2 & \ hfill -9 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 8 \\ \ hfill -2 \\ \ hfill 9 \ end {array} \ right] [/ latex]

Затем мы выполняем операции со строками, чтобы получить форму строки-эшелона.

[латекс] \ begin {array} {rrrrr} \ hfill -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} { rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 3 & \ hfill & \ hfill -2 & \ hfill & \ hfill -9 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill 9 \ end {массив} \ right] & \ hfill & \ hfill & \ hfill & \ hfill -3 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill -15 \ end {array} \ right] \ end {array} [/ latex]

Самый простой способ получить 1 в строке 2 столбца 1 – это поменять местами [латекс] {R} _ {2} [/ latex] и [latex] {R} _ {3} [/ latex].

[латекс] \ text {Interchange} {R} _ {2} \ text {и} {R} _ {3} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill – 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 8 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill & \ hfill -15 \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill & \ hfill -18 \ end {array} \ right] [/ latex]

Затем

[латекс] \ begin {array} {l} \\ \ begin {array} {rrrrr} \ hfill -5 {R} _ {2} + {R} _ {3} = {R} _ {3} \ в \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 57 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \\ \ hfill & \ hfill 57 \ end {array} \ right] & \ hfill & \ hfill & \ hfill & \ hfill – \ frac {1} {57} {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \ \ \ hfill & \ hfill 1 \ end {array} \ right] \ end {array} \ end {array} [/ latex]

Последняя матрица представляет собой эквивалентную систему.

[латекс] \ begin {массив} {l} \ text {} x-y + z = 8 \ hfill \\ \ text {} y – 12z = -15 \ hfill \\ \ text {} z = 1 \ hfill \ end {array} [/ latex]

Используя обратную подстановку, мы получаем решение как [latex] \ left (4, -3,1 \ right) [/ latex].

Напомним, что есть три возможных исхода решений для линейных систем. В предыдущем примере решение [латекс] \ left (4, -3,1 \ right) [/ latex] представляет точку в трехмерном пространстве. Эта точка представляет собой пересечение трех плоскостей.В следующем примере мы решаем систему, используя операции со строками, и обнаруживаем, что она представляет зависимую систему. Зависимая система в 3-х измерениях может быть представлена двумя идентичными плоскостями, как в 2-х измерениях, где зависимая система представляет две идентичные линии.

Пример: решение 3 x 3 зависимой системы

Решите следующую систему линейных уравнений, используя метод исключения Гаусса.

[латекс] \ begin {array} {r} \ hfill -x – 2y + z = -1 \\ \ hfill 2x + 3y = 2 \\ \ hfill y – 2z = 0 \ end {array} [/ latex]

Показать решение

Запишите расширенную матрицу.

[латекс] \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill -2 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill -2 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill 2 \\ \ hfill 0 \ end {array} \ right] [/ latex]

Сначала умножьте строку 1 на [latex] -1 [/ latex], чтобы получить 1 в строке 1, столбце 1. Затем выполните операций со строками , чтобы получить форму строки-эшелона.

[латекс] – {R} _ {1} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 & \ hfill & \ hfill 2 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill & \ hfill 0 \ end {array} \ справа] [/ латекс]

[латекс] {R} _ {2} \ leftrightarrow {R} _ {3} \ to \ left [\ begin {array} {rrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 \ \ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 \ end {array} \ text {} | \ begin {array} { rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 2 \ end {array} \ right] [/ latex]

[латекс] -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -1 & \ hfill & \ hfill 2 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]

[латекс] {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 0 & \ hfill \ end { array} | \ begin {array} {rr} \ hfill & \ hfill 2 \\ \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]

Последняя матрица представляет следующую систему.

[латекс] \ begin {массив} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y – 2z = 0 \ hfill \\ \ text {} 0 = 0 \ hfill \ конец {array} [/ latex]

По тождеству [latex] 0 = 0 [/ latex] мы видим, что это зависимая система с бесконечным числом решений. Затем мы находим общее решение. Решив второе уравнение для [latex] y [/ latex] и подставив его в первое уравнение, мы можем решить для [latex] z [/ latex] через [latex] x [/ latex].

[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y = 2z \ hfill \\ \ hfill \\ x + 2 \ left (2z \ справа) -z = 1 \ hfill \\ \ text {} x + 3z = 1 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \ end {array} [/ latex]

Теперь мы подставляем выражение для [latex] z [/ latex] во второе уравнение, чтобы решить для [latex] y [/ latex] через [latex] x [/ latex].

[латекс] \ begin {массив} {l} \ text {} y – 2z = 0 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \\ \ hfill \\ y – 2 \ left (\ frac {1-x} {3} \ right) = 0 \ hfill \\ \ text {} y = \ frac {2 – 2x} {3} \ hfill \ end {array} [/ latex ]

Общее решение – [latex] \ left (x, \ frac {2 – 2x} {3}, \ frac {1-x} {3} \ right) [/ latex].

Общее решение для зависимой системы 3 X 3

Напомним, что когда вы решаете зависимую систему линейных уравнений с двумя переменными с использованием исключения или подстановки, вы можете записать решение [latex] (x, y) [/ latex] через x, потому что существует бесконечно много (x, y) пары, которые будут удовлетворять зависимой системе уравнений, и все они попадают на линию [латекс] (x, mx + b) [/ latex].Теперь, когда вы работаете в трех измерениях, решение будет представлять собой плоскость, поэтому вы должны записать его в общей форме [латекс] (x, m_ {1} x + b_ {1}, m_ {2} x + b_ { 2}) [/ латекс].

Попробуйте

Решите систему методом исключения Гаусса.

[латекс] \ begin {array} {c} x + 4y-z = 4 \\ 2x + 5y + 8z = 15 \ x + 3y – 3z = 1 \ end {array} [/ latex]

Показать решение

[латекс] \ левый (1,1,1 \ правый) [/ латекс]

Вопросы и ответы

Можно ли решить любую систему линейных уравнений методом исключения Гаусса?

Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.

Как: решить систему уравнений с помощью матриц с помощью калькулятора

Сохраните расширенную матрицу как матричную переменную [latex] \ left [A \ right], \ left [B \ right], \ left [C \ right] \ text {,} \ dots [/ latex].
Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.

Пример: решение систем уравнений с помощью калькулятора

Решите систему уравнений.

[латекс] \ begin {array} {r} \ hfill 5x + 3y + 9z = -1 \\ \ hfill -2x + 3y-z = -2 \\ \ hfill -x – 4y + 5z = 1 \ end { array} [/ latex]

Показать решение

Напишите расширенную матрицу для системы уравнений.

[латекс] \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 3 & \ hfill 9 \\ \ hfill -2 & \ hfill 3 & \ hfill -1 \\ \ hfill -1 & \ hfill -4 & \ hfill 5 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill -2 \\ \ hfill 1 \ end {array} \ right] [/ latex]

На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную [latex] \ left [A \ right] [/ latex].

[латекс] \ left [A \ right] = \ left [\ begin {array} {rrrrrrr} \ hfill 5 & \ hfill & \ hfill 3 & \ hfill & \ hfill 9 & \ hfill & \ hfill -1 \\ \ hfill – 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill -1 & \ hfill & \ hfill -2 \\ \ hfill -1 & \ hfill & \ hfill -4 & \ hfill & \ hfill 5 & \ hfill & \ hfill 1 \ end {массив } \ right] [/ latex]

Используйте функцию ref ( в калькуляторе, вызывая матричную переменную [latex] \ left [A \ right] [/ latex].

[латекс] \ text {ref} \ left (\ left [A \ right] \ right) [/ латекс]

Оценить.

[латекс] \ begin {array} {l} \ hfill \\ \ left [\ begin {array} {rrrr} \ hfill 1 & \ hfill \ frac {3} {5} & \ hfill \ frac {9} {5 } & \ hfill \ frac {1} {5} \\ \ hfill 0 & \ hfill 1 & \ hfill \ frac {13} {21} & \ hfill – \ frac {4} {7} \\ \ hfill 0 & \ hfill 0 & \ hfill 1 & \ hfill – \ frac {24} {187} \ end {array} \ right] \ to \ begin {array} {l} x + \ frac {3} {5} y + \ frac {9} {5} z = – \ frac {1} {5} \ hfill \\ \ text {} y + \ frac {13} {21} z = – \ frac {4} {7} \ hfill \\ \ text {} z = – \ frac {24} {187} \ hfill \ end {array} \ hfill \ end {array} [/ latex]

При использовании обратной подстановки решение: [latex] \ left (\ frac {61} {187}, – \ frac {92} {187}, – \ frac {24} {187} \ right) [/ latex] .

Приложения систем уравнений

Теперь обратимся к приложениям, для которых используются системы уравнений. В следующем примере мы определяем, сколько денег было инвестировано по двум разным ставкам, учитывая сумму процентов, полученных на обоих счетах.

Пример: применение матриц 2 × 2 к финансам

Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая – 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов.Сколько было вложено по каждой ставке?

Показать решение

У нас есть система двух уравнений с двумя переменными. Пусть [latex] x = [/ latex] сумма, инвестированная под 10,5% годовых, и [latex] y = [/ latex] сумма, инвестированная под 12% годовых.

[латекс] \ begin {array} {l} \ text {} x + y = 12 000 \ hfill \\ 0.105x + 0.12y = 1335 \ hfill \ end {array} [/ latex]

В качестве матрицы имеем

[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0.105 & \ hfill 0.12 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 12,000 \\ \ hfill 1,335 \ end {array} \ right] [/ latex]

Умножить строку 1 на [латекс] -0.105 [/ latex] и добавьте результат в строку 2.

[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0 & \ hfill 0.015 \ end {array} \ text {} | \ text {} \ begin {array} {r } \ hfill 12,000 \\ \ hfill 75 \ end {array} \ right] [/ latex]

Затем,

[латекс] \ begin {array} {l} 0,015y = 75 \ hfill \\ \ text {} y = 5,000 \ hfill \ end {array} [/ latex]

Итак [латекс] 12 000 – 5 000 = 7 000 [/ латекс].

Таким образом, 5000 долларов были инвестированы под 12% годовых и 7000 долларов под 10,5%.

Пример: применение матриц 3 × 3 к финансам

Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5% годовых, другой – 8%, а третий – 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?

Показать решение

У нас есть система трех уравнений с тремя переменными. Пусть [latex] x [/ latex] будет сумма, инвестированная под 5% годовых, пусть [latex] y [/ latex] будет суммой, инвестированной под 8%, и пусть [latex] z [/ latex] будет инвестированной суммой. под 9% годовых. Таким образом,

[латекс] \ begin {array} {l} \ text {} x + y + z = 10 000 \ hfill \\ 0.05x + 0,08y + 0,09z = 770 \ hfill \\ \ text {} 2x-z = 0 \ hfill \ end {array} [/ latex]

В качестве матрицы имеем

Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.

[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ -0.05 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 2 & \ hfill & \ hfill 0 & \ hfill & \ hfill -1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill 0 \ end {array} \ right] \ hfill \ end {array} \ hfill \\ -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ \ frac {1} {0.03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill – \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex]

Третья строка сообщает нам [латекс] – \ frac {1} {3} z = -2,000 [/ latex]; таким образом [латекс] z = 6,000 [/ латекс].

Вторая строка сообщает нам [латекс] y + \ frac {4} {3} z = 9000 [/ latex].

Подставляя [латекс] z = 6,000 [/ latex], получаем

[латекс] \ begin {array} {r} \ hfill y + \ frac {4} {3} \ left (6000 \ right) = 9000 \\ \ hfill y + 8000 = 9000 \\ \ hfill y = 1000 \ end {array} [/ latex]

Первая строка сообщает нам [латекс] x + y + z = 10,000 [/ latex]. Подставляя [latex] y = 1,000 [/ latex] и [latex] z = 6,000 [/ latex], мы получаем
[latex] \ begin {array} {l} x + 1,000 + 6,000 = 10,000 \ hfill \\ \ text {} x = 3,000 \ text {} \ hfill \ end {array} [/ latex]

Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.

Попробуйте

Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму, заимствованную по каждой ставке.

Показать решение

150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

3×3 Решатель Системы Уравнений

О правиле Крамера

Этот калькулятор использует правило Крамера для решения систем трех уравнений с тремя неизвестные. Правило Крамера можно сформулировать следующим образом:

Учитывая систему:

$$ \ begin {выровнено} a_1x + b_1y + c_1z = d_1 \\ а_2x + b_2y + c_2z = d_2 \\ a_3x + b_3y + c_3z = d_3 \ end {выровнен} $$

$$ D = \ left | \ begin {array} {ccc} a_1 и b_1 и c_1 \\ a_2 и b_2 и c_2 \\ a_3 & b_3 & c_3 \\ \ end {array} \ right | \ ne 0 $$

$$ D_x = \ left | \ begin {array} {ccc} d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \\ d_3 & b_3 & c_3 \\ \ end {array} \ right | $$

$$ D_y = \ left | \ begin {array} {ccc} a_1 и d_1 и c_1 \\ a_2 & d_2 & c_2 \\ a_3 и d_3 и c_3 \\ \ end {array} \ right | $$

$$ D_z = \ left | \ begin {array} {ccc} a_1 и b_1 и d_1 \\ а_2 и b_2 и d_2 \\ a_3 & b_3 & d_3 \\ \ end {array} \ right | $$

, то решение этой системы:

$$ x = \ frac {D_x} {D} $$

$$ y = \ frac {D_y} {D} $$

$$ z = \ frac {D_z} {D} $$

Пример: Решите систему уравнений, используя правило Крамера

$$ \ begin {выровнено} 4x + 5y -2z = & -14 \\ 7x – ~ y + 2z = & 42 \\ 3x + ~ y + 4z = & 28 \\ \ end {выровнен} $$

Решение: Сначала мы вычисляем $ D, ~ D_x, ~ D_y $ и $ D_z $.

$$ \ begin {выровнено} & D ~~ = \ left | \ begin {массив} {ccc} {\ color {blue} {4}} & {\ color {red} {~ 5}} & {\ color {green} {- 2}} \\ {\ color {blue} {7}} & {\ color {red} {- 1}} & {\ color {green} {~ 2}} \\ {\ color {blue} {3}} & {\ color {red} {~ 1}} & {\ color {green} {~ 4}} \ end {array} \ right | = -16 + 30-14-6-8-140 = -154 \\ & D_x = \ left | \ begin {массив} {ccc} -14 & {\ color {red} {~ 5}} & {\ color {green} {- 2}} \\ ~ 42 & {\ color {red} {- 1}} & {\ color {green} {~ 2}} \\ ~ 28 & {\ color {red} {1}} & {\ color {green} {~ 4}} \ end {array} \ right | = 56 + 280 – 84 – 56 + 28 – 840 = -616 \\ & D_y = \ left | \ begin {array} {ccc} {\ color {blue} {4}} & -14 & {\ color {green} {- 2}} \\ {\ color {blue} {7}} & ~ 42 & {\ color {green} {~ 2}} \\ {\ color {blue} {3}} & ~ 28 & {\ color {green} {~ 4}} \ end {array} \ right | = 672 – 84 – 392 + 252 – 224 + 392 = 616 \\ & D_Z = \ left | \ begin {array} {ccc} {\ color {blue} {4}} & {\ color {red} {~ 5}} & -14 \\ {\ color {blue} {7}} & {\ color {red} {- 1}} & ~ 42 \\ {\ color {blue} {3}} & {\ color {red} {~ 1}} & ~ 28 \ end {array} \ right | = -112 + 630 – 98 – 42 – 168 – 980 = -770 \\ \ end {выровнен} $$

Следовательно,

$$ \ begin {выровнено} & x = \ frac {D_x} {D} = \ frac {-616} {- 154} = 4 \\ & y = \ frac {D_y} {D} = \ frac {616} {- 154} = -4 \\ & z = \ frac {D_z} {D} = \ frac {-770} {- 154} = 5 \ end {выровнен} $$

Примечание: Вы можете проверить решение с помощью вышеуказанного калькулятора

Системы линейных уравнений: исключение Гаусса

Решение линейной системы с матрицами с использованием исключения Гаусса

После нескольких уроков, в которых мы неоднократно упоминали, что мы охватываем основы, необходимые для последующего изучения того, как решать системы линейных уравнений, пришло время для нашего урока сосредоточиться на полной методологии, которой нужно следовать, чтобы найти решения. для таких систем.

Что такое исключение по Гауссу

Исключение Гаусса – это название метода, который мы используем для выполнения трех типов операций со строками матрицы над расширенной матрицей, полученной из линейной системы уравнений, чтобы найти решения для такой системы. Этот метод также называется сокращением строк и состоит из двух этапов: прямого исключения и обратной замены.

Эти два шага метода исключения Гаусса различаются не операциями, которые вы можете использовать с их помощью, а результатом, который они производят.Шаг прямого исключения относится к сокращению строки, необходимому для упрощения рассматриваемой матрицы до ее эшелонированной формы. Такой этап имеет целью продемонстрировать, имеет ли система уравнений, изображенная в матрице, единственное возможное решение, бесконечное множество решений или просто отсутствие решения. Если обнаружено, что система не имеет решения, то нет причин продолжать сокращение строки матрицы на следующем этапе.

Если возможно получить решения для переменных, входящих в линейную систему, то выполняется этап исключения Гаусса с обратной подстановкой.На этом последнем шаге будет получена сокращенная форма матрицы, которая, в свою очередь, дает общее решение системы линейных уравнений.

Правила исключения Гаусса такие же, как правила для трех элементарных операций со строками, другими словами, вы можете алгебраически оперировать строками матрицы следующими тремя способами (или комбинацией):

Перестановка двух рядов
Умножение строки на константу (любую константу, отличную от нуля)
Добавление строки к другой строке

Итак, решение линейной системы с матрицами с использованием исключения Гаусса оказывается структурированным, организованным и довольно эффективным методом.

Как выполнить исключение по Гауссу

На самом деле это не установленный набор шагов исключения Гаусса, которым нужно следовать, чтобы решить систему линейных уравнений, это все о матрице, которую вы имеете в руках, и необходимых операциях со строками для ее упрощения. Для этого давайте поработаем над нашим первым примером исключения Гаусса, чтобы вы могли начать изучать весь процесс и интуицию, которая необходима при работе с ними:

Пример 1

Обратите внимание, что в этот момент мы можем заметить, что эта система линейных уравнений разрешима с единственным решением для каждой из ее переменных.То, что мы выполнили до сих пор, – это первый этап сокращения строк: прямое исключение. Мы можем продолжить упрощение этой матрицы еще больше (что приведет нас ко второму этапу обратной подстановки), но нам это действительно не нужно, поскольку на этом этапе система легко разрешима. Таким образом, мы смотрим на получившуюся систему, чтобы решить ее напрямую:

Уравнение 5: Полученная линейная система уравнений для решения

Из этого набора мы можем автоматически заметить, что значение переменной z равно: z = -2.Мы используем это знание, чтобы подставить его во вторые уравнения для решения относительно y, и подставить значения y и z в первые уравнения для решения относительно x:

В последний раздел этого урока добавлено больше задач исключения Гаусса. Обязательно проработайте их, чтобы практиковаться.

Разница между исключением по Гауссу и по Гауссу Иордану

Разница между гауссовым исключением и гауссовым методом исключения Жордана состоит в том, что один создает матрицу в форме эшелона строк, а другой – матрицу в форме редуцированного эшелона строки.Матрица формы эшелона строк имеет верхнюю треугольную композицию, где любые нулевые строки находятся внизу, а ведущие члены находятся справа от ведущего члена из строки выше. Уменьшенная форма эшелона выходит за рамки еще большего упрощения (иногда даже достигая формы единичной матрицы).

Уравнение 8: Разница между формой эшелона и формой ряда эшелонов

История исключения Гаусса и его названия весьма интересны. Вы будете удивлены, узнав, что название «Гауссовский» было присвоено этой методологии по ошибке в прошлом веке.На самом деле было обнаружено, что алгоритм одновременного решения системы линейных уравнений с использованием матриц и редукции строк записан в той или иной форме в древних китайских текстах, которые датируются еще до нашей эры. Затем в конце 1600-х годов Исаак Ньютон провел по этому уроку, чтобы заполнить то, что он считал пробелом в книгах по алгебре. После того, как название «Гауссиан» было уже установлено в 1950-х годах, термин Гаусса-Иордана был принят, когда геодезист У. Джордан усовершенствовал метод, чтобы он мог использовать такие вычисления для обработки своих наблюдаемых данных топографической съемки.Если вы хотите продолжить чтение увлекательной истории математиков исключения Гаусса, не бойтесь щелкнуть ссылку и прочитать.

На самом деле нет никакой физической разницы между исключением Гаусса и исключением Гаусса Джордана, оба процесса следуют одному и тому же типу операций со строками и их комбинациям, их различие зависит от результатов, которые они производят. Многие математики и учителя во всем мире будут называть метод исключения Гаусса и исключения Гаусса Джордана методами создания матрицы эшелонированной формы по сравнению с методом создания матрицы сокращенной формы эшелона, но на самом деле они говорят о двух стадиях сокращения строк. мы объяснили это в самом первом разделе этого урока (прямое исключение и обратная подстановка), и поэтому вы просто применяете операции со строками, пока не упростите рассматриваемую матрицу.Если вы дойдете до формы эшелона, вы обычно можете решить с ней систему линейных уравнений (до сих пор это то, что называлось бы исключением Гаусса). Если вам нужно продолжить упрощение такой матрицы, чтобы напрямую получить общее решение для системы уравнений, над которой вы работаете, в этом случае вы просто продолжаете работать с матрицей по строкам, пока не упростите ее до сокращенной формы эшелона. (это будет то, что мы называем частью Гаусса-Жордана, и которую можно также рассматривать как поворотное исключение Гаусса).

Мы оставим подробное объяснение форм сокращения строк и эшелонирования для следующего урока, поскольку сейчас вам нужно знать, что, если у вас нет единичной матрицы в левой части расширенной матрицы, которую вы решаете (в этом случае вы не используете не нужно ничего делать для решения системы уравнений, относящейся к матрице), метод исключения Гаусса (регулярное сокращение строк) всегда будет использоваться для решения линейной системы уравнений, которая была записана в виде матрицы.

Примеры исключения Гаусса

В качестве последнего раздела давайте поработаем еще несколько упражнений по исключению Гаусса (сокращение строк), чтобы вы могли больше попрактиковаться в этой методологии.На протяжении многих будущих уроков этого курса линейной алгебры вы обнаружите, что сокращение строк является одним из самых важных инструментов при работе с матричными уравнениями. Поэтому убедитесь, что вы понимаете все этапы решения следующих проблем.

Пример 2

Пример 3

Мы знаем, что для этой системы мы получим расширенную матрицу с тремя строками (поскольку система содержит три уравнения) и тремя столбцами слева от вертикальной линии (поскольку есть три разных переменных).В этом случае мы перейдем непосредственно к сокращению строк, и поэтому первая матрица, которую вы увидите в этом процессе, – это та, которую вы получите, преобразовав систему линейных уравнений в расширенную матрицу.

Уравнение 15: Строка, уменьшающая расширенную матрицу

Обратите внимание, как мы можем сразу сказать, что переменная z равна нулю для этой системы, поскольку третья строка результирующей матрицы показывает уравнение -9z = 0 . Мы используем это знание и проверяем вторую строку матрицы, которая предоставит уравнение 2y – 6z = 0 , подставив в это уравнение значение z = 0 \, в результате получится y \, также равное нулю.Таким образом, мы наконец подставляем оба значения y и z \ в уравнение, которое получается из первой строки матрицы: x + 4y + 3z = 1 , поскольку и y , и z \ , равны нулю, то это дает нам x = 1 . Итак, окончательное решение этой системы уравнений выглядит следующим образом:

Уравнение 16: Окончательное решение системы уравнений

Пример 4

Из чего видно, что последняя строка дает уравнение: 6z = 3 и, следовательно, z = 1/2.Мы подставляем это в уравнения, полученные во второй и первой строках (в указанном порядке), чтобы вычислить значения переменных x и y:

Пример 5

Решите следующую линейную систему, используя метод исключения Гаусса: Уравнение 21: Система линейных уравнений с двумя переменными
Транскрипция линейной системы в виде расширенной матрицы и редукции строк: Уравнение 22: Строка, уменьшающая расширенную матрицу
Что автоматически говорит нам y = 8 .Итак, подставляя это значение в уравнение из первой строки, получаем: 4x – 5y = 4x – 5 (8) = 4x – 40 = -6 4x = 34 \, и поэтому значение x равно: x = 172 \ frac {\ small17} {\ small2} 217 . И окончательное решение этой системы уравнений:
Уравнение 23: Окончательное решение системы уравнений

Пример 6

Чтобы завершить наш урок на сегодня, у нас есть рекомендация по ссылке, чтобы дополнить ваши исследования: Исключение Гаусса – статья, которая содержит дополнительную информацию о сокращении строк, включая введение в тему и еще несколько примеров.Как мы упоминали ранее, будьте готовы продолжать использовать сокращение строк почти на всем протяжении этого курса линейной алгебры, так что до встречи на следующем уроке!

Калькулятор системы уравнений

Добро пожаловать в калькулятор системы уравнений , где мы узнаем, как решить систему линейных уравнений . Наш удобный калькулятор быстро найдет решение любой проблемы, которую вы ему дадите, а если существует бесконечное количество решений, он даже подскажет, как они выглядят ! Решатель системы уравнений использует так называемый метод исключения Гаусса , но это не единственный метод, поэтому ниже мы представляем пять различных ответов на вопрос «Как решить систему уравнений?»

Давайте не будем терять ни секунды и займемся этим, не так ли?

Что такое система линейных уравнений?

Вспомните все те загадок на Facebook или Instagram , знаете, те, где три яблока равны 30, яблоко и два банана равны 18, а банан минус кокос равен двум, и вам нужно было вычислить сколько стоят яблоко, банан и кокос? Это то, что математики называют системой линейных уравнений .« Но как? Математики не используют яблоки и бананы, не так ли? « Ну, им тоже нравится держать доктора подальше и время от времени кусать яблоко, но ты прав, они не делают. рассчитать в яблоках . Однако нет никакой разницы, если вы правы: « Три яблока равны 30 » или 3x = 30 .

Появившееся выше значение x – это то, что мы называем переменной . Он обозначает число или элемент, значение которого мы не знаем, но о котором мы знаем и что-то .В нашем случае мы знаем, что три яблока равно 30 , но яблоко – это просто переменная, например x , поскольку мы не знаем ее значения. По сути, «, что является решением системы уравнений … » – это то же самое, что « дать мне значение яблока (или x ) , которое удовлетворяет …» Честно говоря , мы знаем, что большинство ученых хотели бы использовать бананы вместо x , но они просто не уверены в своих навыках рисования .

“ Но что, черт возьми, означает linear ? ” Мы говорим, что уравнение является линейным, если его переменные (будь то x или кокосы) находятся в первой степени. Это означает, например, что они не возведены в квадрат x² , как в квадратных уравнениях, или знаменатель дроби, или квадратный корень. Однако их можно умножить на любое число, так же как у нас было 3 в нашем уравнении 3x = 30 . Это относится к всем переменным в уравнении .Например, уравнение -2x + 14y - 0,3z = 0 является линейным, а 10x - 7y + z² = 1 – нет.

Наконец, если у нас есть несколько уравнений, которые нужно решить вместе, мы называем их системой уравнений . Обозначим это, нарисовав фигурную скобку (или повернутый набор усов, как вам больше нравится) слева от них. Это означает, что нас интересуют только решений всех уравнений в системе . Если мы найдем значения, которые работают для первого уравнения, но не для второго, мы не будем называть это решением.

Как решить систему уравнений?

Существует много разных способов, решить систему линейных уравнений. Кратко опишем несколько наиболее распространенных методов.

Замена

Первый метод, которому обучают студентов, и самый универсальный метод , работает путем выбора одного из уравнений, выбора одной из переменных в нем, и делает эту переменную объектом этого уравнения .Затем мы используем это преобразованное уравнение и подставляем его каждый раз, когда эта переменная появляется в других уравнениях. Таким образом, в других уравнениях теперь на одну переменную меньше , что упрощает их решение.

Например, если у нас есть уравнение 2x + 3y = 6 и мы хотим получить из него x , то мы начинаем с , избавляясь от всего, что не содержит x с левой стороны . Для этого мы должны вычесть 3y с обеих сторон (потому что у нас есть это выражение слева).Это означает, что левая сторона будет 2x + 3y - 3y , что просто 2x , а правая сторона будет 6 - 3y . Другими словами, мы преобразовали наше уравнение в 2x = 6 - 3y .

Поскольку мы хотим получить x , а не 2x , нам все равно нужно избавиться от 2 . Для этого мы делим обе стороны на 2. Таким образом, слева мы получаем (2x) / 2 , что составляет всего x , а справа мы имеем (6 - 3y) / 2 , что составляет 3 - 1.5лет . В целом, мы получили x = 3 - 1,5y , и мы можем использовать эту новую формулу для замены 3 - 1,5y in на каждые x в других уравнениях.

Исключение переменных

Решение систем уравнений методом исключения означает, что мы пытаемся уменьшить количество переменных в некоторых уравнениях, чтобы упростить их решение . Для этого мы начнем с преобразования двух уравнений так, чтобы они выглядели одинаково.Чтобы быть точным, мы хотим сделать коэффициент (число рядом с переменной) одной из переменных уравнения противоположным коэффициенту той же переменной в другом уравнении . Затем мы складываем два уравнения, чтобы получить новое, в котором нет этой переменной, поэтому его легче вычислить.

Например, если у нас есть система уравнений,

2x + 3y = 6 и

4x - y = 3 ,

, то мы можем попытаться сделать коэффициент x в первом уравнении противоположным коэффициенту во втором уравнении.В нашем случае это означает, что мы хотим преобразовать 2 в противоположность 4 , то есть -4 . Для этого нам нужно умножить обе части первого уравнения на -2 , так как 2 * (-2) = -4 . Это изменяет первое уравнение на

2x * (-2) + 3y * (-2) = 6 * (-2) ,

, что равно

-4x - 6y = -12 .

Теперь мы можем добавить это уравнение ко второму ( 4x - y = 3 ), добавив левую часть к левой и правую к правой.Это дает

4x - y + (-4x - 6y) = 3 + (-12) ,

, что равно

-7y = -9 .

Мы получили новое уравнение только с одной переменной, что означает, что мы можем легко решить y . Затем мы можем подставить это число в любое из исходных уравнений, чтобы получить x .

Метод исключения по Гауссу

Это метод, используемый нашим калькулятором системы уравнений. Названный в честь немецкого математика Иоганна Гаусса, он представляет собой алгоритмическое расширение метода исключения, представленного выше. В случае всего двух уравнений это одно и то же. Однако решение систем уравнений путем регулярного исключения становится все сложнее и сложнее с появлением все большего числа уравнений и переменных. Вот где пригодится метод исключения Гаусса.

Допустим, у нас есть четыре уравнения с четырьмя переменными . Чтобы найти решение нашей системы, мы хотим попытаться получить значения наших переменных одно за другим, последовательно удаляя все остальные.Для этого мы, , берем первое уравнение и первую из переменных . Мы используем его коэффициент, чтобы исключить все вхождения этой конкретной переменной в трех других уравнениях , точно так же, как мы это сделали при обычном исключении. Таким образом, у нас остается первое уравнение, как и было, и три уравнения, теперь каждое с только тремя переменными .

Теперь посмотрим на первое уравнение, отметим его “большой палец вверх”, и оставим его как есть до самого конца .Мы повторяем процесс для трех других уравнений. Другими словами, мы берем вторую переменную и ее коэффициент из второго уравнения , чтобы исключить все вхождения этой переменной в последних двух уравнениях. Это оставляет нам первое уравнение с четырьмя переменными, второе – с тремя, а последние два – с только с двумя переменными .

Затем мы объявляем второе уравнение красивым и красивым и оставляем его в покое. Мы переходим к двум оставшимся уравнениям и берем третью переменную и ее коэффициент в третьем уравнении, чтобы исключить эту переменную из четвертого равенства.

В итоге мы получаем систему из четырех уравнений, в которой первая имеет четыре переменных, вторая – три, третья – две, а последняя – только одну . Это означает, что мы можем легко получить значение четвертой переменной из четвертого уравнения (поскольку в нем нет других переменных). Затем мы подставляем это значение в третье уравнение и получаем значение третьей переменной (поскольку теперь у нее нет других переменных) и так далее.

Графическое представление

Возможно, наименее используемый метод, но тем не менее метод.Он берет каждое из уравнений в нашей системе, и переводит их в функцию . Точки на графике такой функции соответствуют координатам, которые удовлетворяют этому уравнению. Следовательно, если мы хотим решить систему линейных уравнений, то достаточно найти все точки пересечения линии на графике , то есть координаты, которые удовлетворяют всем уравнениям.

Однако это может быть непросто. Если у нас есть только два уравнения и две переменные, то функции представляют собой линии на двумерной плоскости.Следовательно, нам просто нужно найти точку, где эти две линии пересекают .

Для трех переменных функции теперь находятся в трехмерном пространстве, и больше не линии, а плоскости . Это означает, что нам нужно будет нарисовать три плоскости (что само по себе сложно), а затем также найти, где эти плоскости пересекаются. И, если вы думаете, что это сложно, попробуйте представить с четырьмя переменными и четырьмя измерениями . Если это произойдет естественным образом, свяжитесь с нами, и мы направим вас к ближайшему объекту, удостоенному Нобелевской премии, или к неврологу для тщательной проверки состояния головы.

Правило Крамера

Достаточно простой и очень простой способ решить систему линейных уравнений. Однако для этого требуется хорошее понимание матриц и их детерминантов . В качестве поощрения отметим, что он не нуждается ни в какой замене, ни в играх с уравнениями, это просто старая добрая базовая арифметика . Например, для системы трех уравнений с тремя переменными мы подставляем коэффициенты из этих уравнений, чтобы сформировать четыре матрицы размером три на три и вычислить их детерминанты.Мы заканчиваем делением соответствующих значений, которые мы только что получили, чтобы получить окончательное решение.

Пример: Использование решателя системы уравнений

Давайте посмотрим на одну из этих загадок с картинками и попробуем решить ее с помощью нашего калькулятора системы уравнений .

Первое, что нам нужно сделать, это записать все вкусные сладости в виде буквенных переменных. Мы знаем, что выражение, которое мы получим, будет далеко от , сладкого для глаз , но математики не имеют большого вкуса .Ладно, приступим к работе, а оставим каламбуры на десерт .

В нашей загадке три символа – пончик, печенье и конфета. Мы не знаем значения ни одного из них, поэтому нам понадобятся три переменные – по одной для каждого изображения. Обычно используются такие буквы, как x , y и z , но вы можете использовать другие буквы, если хотите. Обозначим пончик x , печенье y , и конфету z .Это позволяет нам написать загадку выше в виде:

х + х + х = у

y + y - z = 25

z + z - x = 16 .

Итак, каково решение системы уравнений? Теперь держите лошадей. Прежде всего, мы попытаемся упростить каждое из трех выражений , прежде чем мы даже подумаем о том, как решить эту систему уравнений. Обратите внимание, что наш решатель системы уравнений не использует формулы в том виде, в котором мы сейчас имеем .В частности, у него нет никаких переменных справа от знака = , как в первом выражении. Итак, нам действительно нужно сначала поработать.

Мы берем каждое из уравнений, и перемещаем все переменные в левую часть . Затем мы складываем вместе все слагаемые с той же переменной ( x , y или z ) в этом уравнении. Наконец, мы записываем полученные слагаемые в алфавитном порядке в терминах переменных.Это означает, что мы сначала записываем выражение с x , затем выражение с y , а затем с z .

В нашем случае это означает, что мы должны сначала переместить на в первом уравнении справа налево. Для этого вычтем из обеих частей равенства y . Это дает

х + х + х - у = у - у ,

, что равно

х + х + х - у = 0 .

Теперь вся система выглядит так:

х + х + х - у = 0

y + y - z = 25

г + г - х = 16

Теперь мы складываем все слагаемые, содержащие одну и ту же переменную .Это означает, что в первом уравнении мы складываем три x , во втором мы складываем два y , а в третьем мы складываем два z . Получаем

3x - y = 0

2y - z = 25

2z - x = 16 .

Помните, что когда мы пишем 3x , , мы имеем в виду 3 * x , или «три копии x » . Теперь мы записываем переменные в алфавитном порядке .Первые два уравнения уже имеют желаемую форму, но в последнем нам нужно переместить выражение с x перед выражением с z . Это дает

3x - y = 0

2y - z = 25

-x + 2z = 16

Обратите внимание, что, на первый взгляд, это не похоже на выражение, которое мы имеем в калькуляторе системы уравнений . Однако это так. Например, в первом уравнении нет z .Но помните, что «no z ‘s» означает «ноль копий z ». Следовательно, мы можем записать недостающие переменные с коэффициентами 0. Таким образом, мы получаем

3x - y + 0z = 0

0x + 2y - z = 25

-x + 0y + 2z = 16

Теперь это больше похоже на – это просто форма решателя системы уравнений! Чтобы быть уверенным, помните, что когда у нас нет числа перед переменной, тогда принято говорить, что число равно 1.Например, -y в первом уравнении фактически равно -1y .

Наконец, нам нужно определить, какие данные нам нужно взять из системы, которую мы получили, и куда поместить их в калькуляторе системы уравнений . Что ж, давайте посмотрим на первое равенство, которое у нас есть, и на верхнее равенство решателя и сравним их:

3x - y + 0z = 0

a₁x + b₁y + c₁z = d₁

Соответствие выглядит так, как выглядит: a₁ – это число рядом с x в уравнении, b₁ – это число рядом с y , c₁ – число рядом с z и d₁ – это номер справа.В нашем случае это означает, что мы должны положить a₁ = 3 , b₁ = -1 , c₁ = 0 и d₁ = 0 . Повторим это со вторым и третьим уравнениями: a₂ = 0 , b₂ = 2 , c₂ = -1 , d₂ = 25 , a₃ = -1 , b₃ = 0 , c₃ = 2 , d₃ = 16 . Как только мы дадим все эти числа , решатель системы уравнений даст нам решение . В следующем разделе мы опишем , как он это делает, шаг за шагом .

Пример: решение систем уравнений методом исключения Гаусса

Работа с печеньем и пончиками – это развлечение и игра, но давайте теперь попробуем сжечь некоторые из этих сладких калорий, описав , как решить систему уравнений , которую мы получили в предыдущем разделе:

3x - y + 0z = 0

0x + 2y - z = 25

-x + 0y + 2z = 16

Мы хотим оставить в первом уравнении равным , поскольку оно имеет ненулевой коэффициент рядом с переменной x .Однако мы будем использовать этот коэффициент для , чтобы избавиться от x в других уравнениях . Обратите внимание, что нам не нужно беспокоиться о втором, потому что его коэффициент x равен нулю. Чтобы справиться с третьим, мы удалим из него -x , сначала преобразовав его в противоположность 3x из первого уравнения. Фактически, достаточно умножить обе части третьего уравнения на 3 .

3x - y + 0z = 0

0x + 2y - z = 25

-3x + 0y + 6z = 48

Теперь у нас есть противоположные числа рядом с x в первом и последнем равенстве, мы складываем два выражения вместе

(3x - y + 0z) + (-3x + 0y + 6z) = 0 + 48 ,

, что равно

0x -y + 6z = 48 .

Теперь мы можем заменить третье уравнение на то, что мы только что получили , чтобы получить

3x - y + 0z = 0

0x + 2y - z = 25

0x - y + 6z = 48

В результате мы получили то, что в двух последних выражениях нет x , и всегда легче решить систему линейных уравнений с двумя переменными вместо трех.

Следующим шагом в методе исключения Гаусса является повторение того же процесса для последних двух уравнений .По сути, мы будем использовать ненулевой коэффициент y во втором равенстве, чтобы избавиться от y из последнего. Как мы уже делали выше, мы начинаем с преобразования -y в противоположность 2y , то есть в -2y . Для этого достаточно обе части последнего уравнения умножить на 2.

3x - y + 0z = 0

0x + 2y - z = 25

0x - 2y + 12z = 96

Теперь мы можем сложить два последних уравнения , чтобы получить

(0x + 2y - z) + (0x - 2y + 12z) = 25 + 96 ,

, что равно

0x + 0y + 11z = 121 .

Пора заменить третье уравнение

3x - y + 0z = 0

0x + 2y - z = 25

0x + 0y + 11z = 121 .

Это конечная форма системы уравнений, которую мы получаем из метода исключения Гаусса . Теперь решить систему линейных уравнений стало намного проще. Как так? Что ж, начнем с последнего равенства. В нем есть только одна переменная с ненулевым коэффициентом, а именно z .Мы можем забыть о нулевых членах, что дает нам

11z = 121 ,

, а это значит, что у нас должно получиться z = 11 . Теперь, когда мы знаем, какова первая часть решения системы уравнений, мы можем использовать это знание, чтобы заменить это число на z в двух других уравнениях :

3х - у + 0 = 0

0x + 2y - 11 = 25 ,

, что равно

3x - y = 0

0x + 2y = 36 .

Теперь у нас есть второе уравнение только с одной переменной с ненулевым коэффициентом. Если забыть о нулевых членах, получим

2y = 36 ,

и, следовательно, должно получиться y = 18 . Опять же, мы заменяем это число на y в первом уравнении :

3x - 18 = 0 ,

, что дает

3x = 18 ,

, а это означает, что x = 6 .В общем, нам удалось решить систему линейных уравнений, и нашла решение

х = 6

y = 18

г = 11

Если мы теперь посмотрим на нашу загадку с картинками, все это решение системы уравнений методом исключения приведет нас к ответу, что пончик равен 6 , печенье равно 18 , и конфета равна 11 .

Кусок торта, не так ли?

3.3: Решение систем с исключением Гаусса-Джордана

Цели обучения

Напишите расширенную матрицу системы уравнений.
Напишите систему уравнений из расширенной матрицы.
Решите систему линейных уравнений с помощью матриц и графического калькулятора.
Решайте финансовые приложения с помощью матриц и графического калькулятора.

Необходимые навыки

Перед тем, как начать, пройдите предварительный тест.

Введите в калькулятор следующие матрицы и затем выполните указанные операции. Если операция не может быть проведена, укажите причину.

\ (A = \ begin {bmatrix} 5 & 1 & -2 \\ 2 & 6 & 7 \\ 4 & 1 & −5 \ end {bmatrix} \), \ (B = \ begin {bmatrix} 3 & -7 \\ 0 & 1 \\ 2 & −8 \ end {bmatrix} \), \ (C = \ begin {bmatrix} 9 & 4 \\ 6 & -5 \\ 7 & −1 \ end {bmatrix} \)

а. \ (А \ cdot B \)

г. \ (B \ cdot A \)

г. \ (4B-2C \)

г.\ (А + С \)

Нажмите здесь, чтобы проверить свой ответ

а. \ (\ begin {bmatrix} 11 & -18 \\ 20 & -64 \\ 2 & 13 \ end {bmatrix} \)

г. Не определено, поскольку количество столбцов в матрице \ (B \) не соответствует количеству строк в матрице \ (A \).

г. \ (\ begin {bmatrix} -6 & -36 \\ – 12 & 14 \\ – 6 & −30 \ end {bmatrix} \)

г. Не определено, поскольку размер матрицы \ (A \) не соответствует размерам матрицы \ (C \).{th} \) века, но он по-прежнему считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика. Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.

Рисунок \ (\ PageIndex {1} \): немецкий математик Карл Фридрих Гаусс (1777–1855).

Ранее в этой главе мы исследовали методы решения систем уравнений.В этом разделе мы изучим другую технику решения систем, на этот раз с использованием матриц.

Расширенные матрицы

Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей .

Например, рассмотрим следующую систему уравнений \ (2 × 2 \).

\ [\ begin {align *} 3x + 4y & = 7 \\ 4x-2y & = 5 \ end {align *} \]

Мы можем записать эту систему в виде расширенной матрицы:

\ (\ left [\ begin {array} {cc | c} 3 & 4 & 7 \\ 4 & -2 & 5 \ end {array} \ right] \)

Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов .

\ (\ begin {bmatrix} 3 & 4 \\ 4 & −2 \ end {bmatrix} \)

Трехкратная система уравнений , например

\ [\ begin {align *} 3x-y-z & = 0 \\ x + y & = 5 \\ 2x-3z & = 2 \ end {align *} \]

имеет матрицу коэффициентов

\ (\ begin {bmatrix} 3 & −1 & −1 \\ 1 & 1 & 0 \\ 2 & 0 & −3 \ end {bmatrix} \)

и представлена расширенной матрицей

\ (\ left [\ begin {array} {ccc | c} 3 & −1 & −1 & 0 \\ 1 & 1 & 0 & 5 \\ 2 & 0 & −3 & 2 \ end {array} \ right] \)

Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: \ (x \) – члены идут в первый столбец, \ (y \) – термины во втором столбце, и \ (z \) – термины в третьем столбце.Очень важно, чтобы каждое уравнение было записано в стандартной форме \ (ax + by + cz = d \), чтобы переменные совпадали. Когда в уравнении отсутствует член переменной, коэффициент равен \ (0 \).

Как: по системе уравнений написать расширенную матрицу

Запишите коэффициенты членов \ (x \) как числа в первом столбце.
Запишите коэффициенты членов \ (y \) в виде чисел во втором столбце.
Если есть \ (z \) – члены, запишите коэффициенты в виде чисел в третьем столбце.
Нарисуйте вертикальную линию и напишите константы справа от нее.

Пример \ (\ PageIndex {1} \): написание расширенной матрицы для системы уравнений

Напишите расширенную матрицу для данной системы уравнений.

\ [\ begin {align *} x + 2y-z & = 3 \\ 2x-y + 2z & = 6 \\ x-3y + 3z & = 4 \ end {align *} \]

Решение

Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.

\ (\ left [\ begin {array} {ccc | c} 1 & 2 & −1 & 3 \\ 2 & −1 & 2 & 6 \\ 1 & −3 & 3 & 4 \ end {array} \ right] \)

Упражнение \ (\ PageIndex {1} \)

Запишите расширенную матрицу данной системы уравнений.

\ [\ begin {align *} 4x-3y & = 11 \\ 3x + 2y & = 4 \ end {align *} \]

Ответ: \ (\ left [\ begin {array} {cc | c} 4 & −3 & 11 \\ 3 & 2 & 4 \ end {array} \ right] \)

Написание системы уравнений из расширенной матрицы

Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.

Пример \ (\ PageIndex {2} \): Написание системы уравнений из расширенной матричной формы

Найдите систему уравнений из расширенной матрицы.

\ (\ left [\ begin {array} {ccc | c} 1 & −3 & −5 & -2 \\ 2 & −5 & −4 & 5 \\ – 3 & 5 & 4 & 6 \ end {array} \ right] \)

Решение

Когда столбцы представляют переменные \ (x \), \ (y \) и \ (z \),

\ [\ left [\ begin {array} {ccc | c} 1 & -3 & -5 & -2 \\ 2 & -5 & -4 & 5 \\ – 3 & 5 & 4 & 6 \ end {array} \ right] \ rightarrow \ begin {align *} x-3y-5z & = -2 \\ 2x-5y-4z & = 5 \\ -3x + 5y + 4z & = 6 \ end {align *} \]

Упражнение \ (\ PageIndex {2} \)

Напишите систему уравнений из расширенной матрицы.

\ (\ left [\ begin {array} {ccc | c} 1 & -1 & 1 & 5 \\ 2 & -1 & 3 & 1 \\ 0 & 1 & 1 & -9 \ end {array} \ right] \)

Ответ: \ (\ begin {align *} x-y + z & = 5 \\ 2x-y + 3z & = 1 \\ y + z & = -9 \ end {align *} \)

Уменьшенная форма рядка-эшелон

Чтобы решить систему уравнений, мы хотим преобразовать ее матрицу в уменьшенную форму строки , в которой есть единицы вниз по главной диагонали от верхнего левого угла к нижнему правому углу, а нули в каждое положение выше и ниже главной диагонали, как показано.

Уменьшенная форма строки-эшелона \ (\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} \)

Следующие расширенные матрицы представлены в сокращенной форме строки-эшелона.

\ (\ left [\ begin {array} {cc | c} 1 & 0 & -2 \\ 0 & 1 & 5 \ end {array} \ right] \), \ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)

Следующие расширенные матрицы не являются сокращенными строками.

\ (\ left [\ begin {array} {cc | c} 2 & 4 & -6 \\ 4 & 0 & 7 \ end {array} \ right] \), \ (\ left [\ begin {array} {ccc | c} 0 & 2 & 3 & 3 \\ 1 & 5 & 0 & 2 \\ 0 & 0 & 1 & 0 \ end {array} \ right] \)

Пример \ (\ PageIndex {3} \): матрицы в сокращенной форме строки-эшелон

Запишите систему уравнений из каждой из матриц в приведенной строчно-эшелонированной форме сверху. В чем преимущество этой формы?

а. \ (\ left [\ begin {array} {cc | c} 1 & 0 & -2 \\ 0 & 1 & 5 \ end {array} \ right] \)

г.\ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)

Решение

а. \ (\ begin {align *} x = -2 \\ y = 5 \ end {align *} \)

г. \ (\ begin {align *} x = 4 \\ y = 3 \\ z = 2 \ end {align *} \)

Преимущество сокращенной формы «строка-эшелон» состоит в том, что решение системы уравнений приводится в правом столбце.

УСТРАНЕНИЕ ПО ГАУСС-ИОРДАНИИ

Метод исключения Гаусса-Жордана относится к стратегии, используемой для получения уменьшенной строковой формы матрицы.Цель состоит в том, чтобы записать матрицу \ (A \) с числом \ (1 \) в качестве записи вниз по главной диагонали и иметь все нули сверху и снизу.

\ (A = \ begin {bmatrix} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \\ a_ {31} & a_ {32} & a_ {33} \ end {bmatrix} \ xrightarrow {После \ space Gauss-Jordan \ space elimination} A = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} \)

Мы можем выполнить операций со строками над матрицей, например сложение, умножение на константу и перестановку строк, чтобы создать сокращенную форму строки-эшелон.Процесс выполнения этих шагов вручную выходит за рамки этого класса. Тем не менее, вы можете найти дополнительную информацию о методе Гаусса-Джордана ЗДЕСЬ.

Решение систем уравнений с исключением Гаусса-Жордана

В рамках этого курса мы продемонстрируем, как найти сокращенную форму строки-эшелон в графическом калькуляторе.

Как: решить систему уравнений с помощью матриц с помощью калькулятора

Сохранить расширенную матрицу как матричную переменную \ ([A], [B], [C] ,… \)
1. Press 2 ^nd MATRIX. На экране появится меню «Матрица». Дважды нажмите кнопку со стрелкой вправо, чтобы выбрать меню ПРАВКА. В меню EDIT используйте стрелку вниз для перемещения курсора, чтобы выбрать желаемое имя матрицы из меню, и нажмите ENTER. Появится экран ввода матрицы.
2. Введите размеры общего размера матрицы в виде строк \ (\ times \) столбцов. Введите количество строк, нажмите ENTER, введите количество столбцов и снова нажмите ENTER.Форма матрицы настраивается на экране, чтобы отобразить требуемое количество строк и столбцов. Убедитесь, что форма соответствует желаемой матрице; в противном случае вернитесь в верхний ряд и отрегулируйте размеры. Если матрица слишком велика для экрана, используйте клавиши со стрелками для прокрутки вправо или вниз, чтобы увидеть оставшиеся строки и столбцы.
3. Введите элементы матрицы, нажимайте ENTER после каждого. Курсор прокручивает матрицу, перемещаясь по каждой строке слева направо, а затем вниз к следующей строке.Использование клавиш со стрелками для перемещения курсора вместо нажатия ENTER может привести к тому, что значение не будет сохранено в памяти калькулятора.
4. Нажмите 2 ^nd QUIT, чтобы завершить процесс сохранения и вернуться на главный экран.
Используйте функцию rref (в калькуляторе, чтобы найти сокращенную форму строки-эшелон матрицы.
1. На главном экране нажмите 2 ^nd MATRIX.Используйте стрелку вправо один раз, чтобы перейти в меню МАТЕМАТИКА.
2. Прокрутите вниз (или вверх) до rref (, стараясь не выбрать ref (, и нажмите ENTER.
3. Снова нажмите 2 ^nd MATRIX и используйте стрелку вниз (при необходимости) для выбора имени матрицы и нажмите ENTER.
4. Нажмите ENTER, чтобы завершить операцию.
Если существует сокращенная форма строки-эшелона матрицы, калькулятор отобразит ее на главном экране. ×

Пример \ (\ PageIndex {4} \): решение систем уравнений с матрицами с помощью калькулятора

Решите систему уравнений.

\ [\ begin {align *} 6x + 4y + 3z & = -6 \\ x + 2y + z & = \ dfrac {1} {3} \\ -12x-10y-7z & = 11 \ end {align *} \ ]

Решение

Напишите расширенную матрицу для системы уравнений.

\ (\ left [\ begin {array} {ccc | c} 6 & 4 & 3 & -6 \\ 1 & 2 & 1 & \ dfrac {1} {3} \\ – 12 & -10 & -7 & 11 \ end {array} \ right] \)

На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную \ ([A] \).

\ ([A] = \ left [\ begin {array} {ccc | c} 6 & 4 & 3 & -6 \\ 1 & 2 & 1 & \ dfrac {1} {3} \\ – 12 & -10 & -7 & 11 \ end {array} \ right] \)

Используйте rref (функция в калькуляторе, вызывая матричную переменную \ ([A] \).

rref ([A])

Используйте опцию MATH -> FRAC в калькуляторе, чтобы выразить матричные элементы в виде дробей.

Оценить

\ [\ begin {array} {cc} {\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & – \ dfrac {2} {3} \\ 0 & 1 & 0 & \ dfrac {5} {2} \\ 0 & 0 & 1 & – 4 \ end {array} \ right] \ rightarrow} & {\ begin {align *} x + 0y + 0z & = – \ dfrac {2} {3} \\ y + 0z & = \ dfrac {5} {2 } \\ z & = -4 \ end {align *}} \ end {array} \]

Таким образом, решение, которое легко найти в правом столбце приведенной строковой формы матрицы, будет \ (\ left (- \ dfrac {2} {3}, \ dfrac {5} {2}, −4 \ справа) \).

Упражнение \ (\ PageIndex {3} \)

Решите систему уравнений.

\ [\ begin {align *} 4x-7y + 2z & = -5 \\ -x + 3y-8z & = -10 \\ -5x-4y + 6z & = 19 \ end {align *} \]

Ответ

Напишите расширенную матрицу для системы уравнений.

\ (\ left [\ begin {array} {ccc | c} 4 & -7 & 2 & -5 \\ -1 & 3 & -8 & -10 \\ -5 & -4 & 6 & 19 \ end {array} \ right] \)

На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную \ ([A] \).

\ ([A] = \ left [\ begin {array} {ccc | c} 4 & -7 & 2 & -5 \\ -1 & 3 & -8 & -10 \\ -5 & -4 & 6 & 19 \ end {array} \ right] \)

Используйте rref (функция в калькуляторе, вызывая матричную переменную \ ([A] \).

rref ([A])

Используйте опцию MATH -> FRAC в калькуляторе, чтобы выразить матричные элементы в виде дробей.

Оценить

\ [\ begin {array} {cc} {\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & \ dfrac {3} {2} \ end {array} \ right] \ rightarrow} & {\ begin {align *} x + 0y + 0z & = -2 \\ y + 0z & = 0 \\ z & = \ dfrac {3} {2} \ end {align *}} \ end {array} \]

Таким образом, решение, которое можно легко прочитать из правого столбца приведенной строковой формы матрицы, будет \ (\ left (-2, 0, \ dfrac {3} {2} \ right) \).

Пример \ (\ PageIndex {5} \): применение матриц \ (2 × 2 \) к финансам

Кэролайн инвестирует в общей сложности \ (12 000 долларов) в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая – 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил \ (1335 долларов). Сколько было вложено по каждой ставке?

Решение

У нас есть система двух уравнений с двумя переменными. Пусть \ (x = \) сумма, инвестированная под 10,5% годовых, а \ (y = \) сумма, инвестированная под 12%.

\ [\ begin {align *} x + y & = 12,000 \\ 0,105x + 0,12y & = 1,335 \ end {align *} \]

В качестве матрицы имеем

\ (\ left [\ begin {array} {cc | c} 1 & 1 & 12,000 \\ 0.105 & 0.12 & 1335 \ end {array} \ right] \)

Введите эту матрицу как матричную переменную \ ([A] \). Используйте rref (функция , вызывающая матричную переменную \ ([A] \).

rref ([A])

\ (\ left [\ begin {array} {cc | c} 1 & 0 & 7000 \\ 0 & 1 & 5000 \ end {array} \ right] \)

Таким образом, \ ($ 7000 \) было инвестировано по ставке 10.5% годовых и \ (5000 долларов \) под 12% годовых.

Пример \ (\ PageIndex {6} \): применение матриц \ (3 × 3 \) к финансам

Ava инвестирует в общей сложности \ (10 000 долларов США) в три счета, один из которых платит 5% годовых, другой – 8%, а третий – 9%. Годовой процент, полученный по трем инвестициям в прошлом году, составил \ (770 долларов). Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?

Решение

У нас есть система трех уравнений с тремя переменными.Пусть \ (x \) будет сумма, инвестированная под 5% годовых, пусть \ (y \) будет суммой, инвестированной под 8%, и пусть \ (z \) будет суммой, инвестированной под 9%. Таким образом,

\ [\ begin {align *} x + y + z & = 10,000 \\ 0,05x + 0,08y + 0,09z & = 770 \\ 2x-z & = 0 \ end {align *} \]

В качестве матрицы имеем

\ (\ left [\ begin {array} {ccc | c} 1 & 1 & 1 & 10,000 \\ 0,05 & 0,08 & 0,09 & 770 \\ 2 & 0 & -1 & 0 \ end {array} \ right] \)

Введите эту матрицу как матричную переменную \ ([A] \).Используйте rref (функция , вызывающая матричную переменную \ ([A] \).

rref ([A])

\ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 0 & 3000 \\ 0 & 1 & 0 & 1000 \\ 0 & 0 & 1 & 6000 \ end {array} \ right] \)

Ответ: \ (3000 долларов \) вложены под 5%, \ (1000 долларов \) вложены под 8%, и \ (6000 долларов \) инвестированы под 9%.

Упражнение \ (\ PageIndex {4} \)

Небольшая обувная компания взяла ссуду в размере \ (1 500 000 долларов США) на расширение своих запасов.Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла \ (130 500 долларов США). Используйте матрицы, чтобы найти сумму, заимствованную по каждой ставке.

Ответ: \ (150 000 долларов \) под 7%, \ (750 000 долларов \) под 8%, \ (600 000 долларов \) под 10%

Медиа

Получите доступ к этим онлайн-ресурсам, чтобы получить дополнительные инструкции и попрактиковаться в решении систем линейных уравнений с использованием метода исключения Гаусса.

Ключевые понятия

Расширенная матрица – это матрица, которая содержит коэффициенты и константы системы уравнений. См. Пример \ (\ PageIndex {1} \).
Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. Пример \ (\ PageIndex {2} \).
Мы можем использовать метод исключения Гаусса-Жордана для решения системы уравнений. См. Пример \ (\ PageIndex {4} \).
Многие реальные проблемы можно решить с помощью расширенных матриц.См. Пример \ (\ PageIndex {5} \) и Пример \ (\ PageIndex {6} \).