Решение системы методом гаусса жордана гаусса онлайн: Метод Жордана-Гаусса онлайн

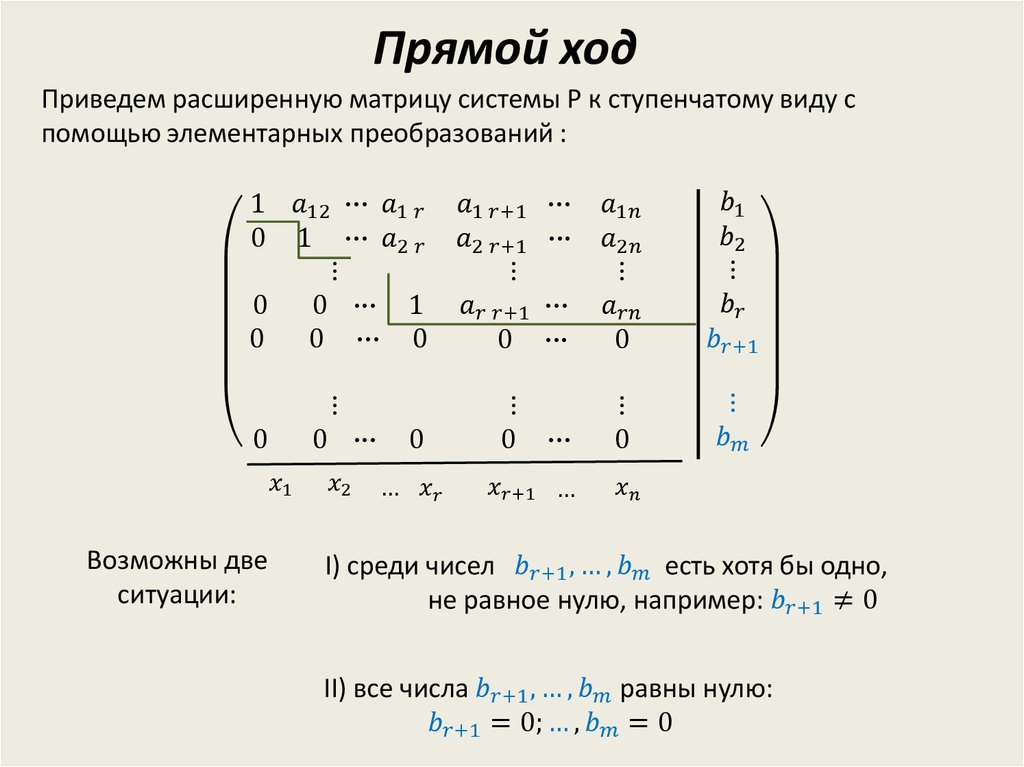
Метод Гаусса-Жордана (единичная матрица) (метод полного исключения)

Схема Гаусса-Жордана или метод полного исключения, заключается в одновременном исключении (Жордановом исключении) какого либо переменного из всех уравнений системы, кроме одного. Его удобно реализовать на ЭВМ, учитывая ограниченность на их памяти, так как схема вычислений не требует выполнения обратного хода.

На первом шаге этого метода выберем ведущий элемент (перестановкой уравнений системы можно добиться того, чтобудет наибольшим по модулю коэффициентом при). Разделим первое уравнение системы на, во всех остальных уравнениях исключим, то есть сведем расширенную матрицы системы к виду

где

во втором шаге выберем ведущий элемент(можно сделать перестановку строк 2,…,n таким образом чтобы он был наибольшим по модулю). Разделим второе уравнение на, исключимиз всех уравнений кроме второго.

где

После n шагов получим матрицу

и численное значение неизвестных

Контроль вычислений можно осуществлять также, как и в схеме единственного деления, используя контрольные суммы.

Вычисление определителя и обратной матрицы метода Гаусса

В прямом ходе метода Гаусса над элементами матрицы А производятся элементарные преобразования, которые не изменяют определитель матрицы, кроме операции деления на ведущий элемент. Матрица преобразуется к треугольному виду с единичными диагональными элементами, ее определитель равен единице. Если в прямом ходе строки матрицы не переставляются то знак определителя не изменяется. Таким образом определитель не вырожденной матрицы системы равен произведению ведущих элементов в прямом ходе исключения Гаусса

.

Для его вычисления прямой ход метода Гаусса , как и при решении системы, только без преобразований вектора b. При решении линейной системы определитель можно вычислить попутно.

Если применяется метод исключения с выбором главного элемента, то в (13) необходимо добавить множитель, гдек – количество перестановок строк и столбцов.

Все вычислительные схемы метода Гаусса позволяют осуществлять одновременное решение систем линейных уравнений с различными правыми частямиПри этом количество вычислений увеличивается на преобразование новых столбцов правых частей, что дает значительную экономию времени счета.

В частности если вместо столбцов выбирать столбцы единичной матрицы порядкаn:

(1 на к-ом месте, остальные элементы – нули), к=1.2 , …, n, то решение системыбудетк-м столбцом обратной матрицы .

Таким образом для вычисления обратной матрицы требуется решить одновременно n систем уравнений с

n неизвестными. Проводим последовательные исключения неизвестных в расширенной матрице

~после n шагов

~.

Справа получим элементы обратной матрицы

.

Пример. Решить систему

методом Жордана-Гаусса.

Ответ,,.

Пример. Решить методом Гаусса-Жордана с выбором главного элемента системы

Ответ

.

Определитель равен .

Метод прогонки

Большинство технических задач сводится к решению систем линейных алгебраических уравнений, в которых матрицы содержат много нулевых элементов, а ненулевые элементы расположены по специальной структуре, например, ленточные квазитреуголные матрицы.

Задачи построения интерполяционных сплайнов, разностные методы решения краевых задач для дифференциальных уравнений сходится к решению системы алгебраических уравнений с трехдиагональной матрицей А. В матрице А все элементы не лежащие на главной диагонали и двух соседних диагоналях равны нулю. Такие системы можно записать

Выбор наибольшего элемента при исключении неизвестных методом Гаусса в таких системах делать нельзя, поскольку перестановка строк разрушает структуру матрицы. Наиболее часто к решению систем с трехдиагональной матрицей применяют метод прогонки, который является частным случаем метода Гаусса.

Прямой ход метода прогонки заключается в исключении элементов в системе (25). Так как, то первое уравнение системы имеет вид

.

Выразим через:и подставим во второе уравнение системы, получим уравнение связывающееии так далее. Пусть уже получено соотношение

Понизим в (26) индекс на единицу и подставим значение вi-е уравнение системы (25)

.

Отсюда

.

Сравнивая это выражение с (26) получим рекуррентные формулы для вычисления в прямом ходе:

.

Учитывая, что , полагаем. Обратный ход осуществляется по (26).

Почти во всех задачах, приводящих к решению системы (25) с трехдиагональной матрицей, обеспечивается условие преобладания диагональных элементов .

Это обеспечивает существование единичного решения и достаточно хорошую устойчивость метода прогонки относительно

Метод Гаусса-Жордана – презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике.

Базовый уровень Сложные задачи

1. Метод Гаусса — Жордана

МЕТОД ГАУССА — ЖОРДАНА

2. Метод Гаусса — Жордана

Метод Гаусса — Жордана (метод полного исключения
неизвестных) — метод, который используется для решения
систем линейных алгебраических уравнений, нахождения
обратной матрицы, нахождения координат вектора в
заданном базисе или отыскания ранга матрицы. Метод
является модификацией метода Гаусса. Назван в честь К. Ф.
Гаусса и немецкого геодезиста и математика Вильгельма
Йордана

3. Алгоритм

АЛГОРИТМ
1.Выбирают первый слева столбец матрицы, в
котором есть хоть одно отличное от нуля
значение. (разрешающий-главный столбец)
2.Если самое верхнее число в этом столбце ноль, то
меняют всю первую строку матрицы с другой
строкой матрицы, где в этой колонке нет нуля.
3.Все элементы первой (разрешающей-главной)
строки делят на верхний (разрешающий-главный)
элемент выбранного столбца.

4. Алгоритм

АЛГОРИТМ
4. Из оставшихся строк вычитают первую
(разрешающую-главную) строку, умноженную на первый
элемент соответствующей строки, с целью получить
первым элементом каждой строки (кроме первой) ноль.
5.Далее проводят такую же процедуру с матрицей,
получающейся из исходной матрицы после вычёркивания
первой строки и первого столбца.
6.После повторения этой процедуры (n-1) раз , получают
верхнюю треугольную матрицу

5. Алгоритм

АЛГОРИТМ
7.Вычитают из предпоследней строки последнюю
строку, умноженную на соответствующий
коэффициент, с тем, чтобы в предпоследней
строке осталась только 1 на главной диагонали.
8.Повторяют предыдущий шаг для последующих
строк. В итоге получают единичную матрицу и
решение на месте свободного вектора (с ним
необходимо проводить все те же преобразования).

6. Пример

ПРИМЕР

11. Расширенный алгоритм для нахождения обратной матрицы

РАСШИРЕННЫЙ АЛГОРИТМ ДЛЯ НАХОЖДЕНИЯ
ОБРАТНОЙ МАТРИЦЫ

12.

Прямой ход (алгоритм образования нулей под главной диагональю)ПРЯМОЙ ХОД (АЛГОРИТМ ОБРАЗОВАНИЯ НУЛЕЙ
ПОД ГЛАВНОЙ ДИАГОНАЛЬЮ)

13. Прямой ход (алгоритм образования нулей под главной диагональю)

ПРЯМОЙ ХОД (АЛГОРИТМ ОБРАЗОВАНИЯ НУЛЕЙ ПОД
ГЛАВНОЙ ДИАГОНАЛЬЮ)

15. Обратный ход (алгоритм образования нулей над главной диагональю)

ОБРАТНЫЙ ХОД (АЛГОРИТМ ОБРАЗОВАНИЯ НУЛЕЙ НАД ГЛАВНОЙ
ДИАГОНАЛЬЮ)

English     Русский Правила

[Решено] Решение методом Гаусса-Жордана для следующих уравнений

Решение методом Гаусса-Жордана для следующих уравнений: + 4y + 5z = 40

Этот вопрос ранее задавался в

MPSC AE Civil Mains 2017 Official (Paper 1)

View all MPSC AE Papers >

1. x = 1, y = 2, z = 5
2. х = 1, у = 3, z = 5
3. х = 2, у = 1, z = 3
4. x = 1, y = 3, z = 2

Вариант 2: x = 1, y = 3, z = 5 2,8 тыс. пользователей

100 вопросов

200 марок

120 минут

Концепция:
Метод исключения Гаусса-Жордана:

• Это алгоритм, который можно использовать для решения системы линейных уравнений и для нахождения обратной матрицы 9 обратимой матрицы0044 .
• Он основан на трех элементарных операциях со строками, которые можно использовать с матрицей и преобразовать расширенную матрицу в диагональную матрицу .
   

​ Расчет:

Дано:

A = \(\begin{bmatrix} 3 & 4 \\ -3 & 1\ {bmatrix}\) B = \(\begin{bmatrix} 9\\ 13\\ 40 \end{bmatrix}\)

AX = B

\(\begin{bmatrix} 1 &1 & 1\\ 2 & -3 &4 \\ 3 & 4 & 5 \end{bmatrix}\)\(\begin{bmatrix} X\\ Y\\ Z \end{bmatrix}\) = \(\begin{bmatrix} 9\\ 13\\ 40 \end{bmatrix}\)

Теперь преобразуем данную форму уравнений в расширенную форму

\(\left [ A : B \right ]\)  = \(\ begin{bmatrix} 1 &1 &1 &: &9 \\ 2&-3 &4 &: &13 \\ 3&4 &5 &: &40 \end{bmatrix}\) R ₂  —–> R ₂  – 2R

1  и R ₃  —–> R ₃  – 3R ₁

= \(\begin{bmatrix} 1 &1 &1 &: &9 \\ 0&-5 &2 &: &-5 \ \ 0&1 &2 &: &13 \end{bmatrix}\)R ₁  —–> 5R ₁  + R ₂  и R ₃  —–> 5R ₃  + R ₂

 90} &7 &: &40 \\ 0&-5 &2 &: &-5 \\ 0&0 &12 &: &60 \end{bmatrix}\) R ₂  —–> 6R ₂  – R ₃  и R ₁  —–> 12R ₁  – 7R ₃

= \(\begin{bmatrix} 60 &0 &0 &: &60 \\ 0&-5 &0 &: &-90 \\ 0&0 &12 &: &60 \end{bmatrix}\)

= \(\begin{bmatrix} 60 &0 &0 \\ 0&-30 &0 \\ 0&0 &12 \end{bmatrix}\)\(\begin{ bmatrix} X\\ Y\\ Z \end{bmatrix}\) = \(\begin{bmatrix} 60\\ -90\\ 60 \end{bmatrix}\)

Теперь умножим A и X и сравним их С b, мы получаем

60x = 60 ⇒ x = 1

– 30y = – 90 ⇒ y = 3

12Z = 60 ⇒ z = 5

• Решают эти типы вопросов. с обычный метод , как обсуждалось выше , требует много времени и усилий.
• Чтобы сэкономить время на экзамене, мы можем решить эти вопросы методом исключения .
   

​Например:
Подставляем вариант 1 в первое уравнение, получаем
1 + 3 + 5 = 8  ≠ 9 Итак, исключаем этот вариант.
Теперь попробуйте вариант 2 во всех уравнениях
1 + 3 + 5 = 9 = 9
2 × 1 – 3 × 3 + 4 × 5 = 13
3 × 1 + 4 × 3 + 5 × 5 = 40
Следовательно, вариант 2 правильный.

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления MPSC AE

Последнее обновление: 31 декабря 2022 г.

Комиссия государственной службы штата Махараштра (MPSC) выпустила новое уведомление о наборе MPSC AE. Всего открыта 151 вакансия по гражданским, механическим и электрическим дисциплинам. Процесс подачи заявок начался 3 октября 2022 года, и кандидаты должны были подать заявку до 23 октября 2022 года. Процесс отбора состоит из 3 этапов – предварительный, основной и собеседование. Предварительный экзамен запланирован на 17 декабря 2022 года. Кандидаты, прошедшие квалификацию на предварительных экзаменах, имеют право участвовать в основных. Окончательный список кандидатов будет опубликован после интервью.

linear-equation-iep-goal – Googlesuche

AlleBilderVideosNewsMapsShoppingBücher

suchoptionen

Решение многошаговых линейных уравнений | Цель IEP по математике — набор инструментов Goalbook Toolkit

targetbookapp.com › набор инструментов › решить-многошаговую линейную… согласовано с АСС.

Решение линейных уравнений с одной переменной — Математика — Справочник

targetbookapp.com › набор инструментов › якорная страница

Учебная цель IEP с измеримыми ежеквартальными задачами по математике, выражениям и уравнениям для учащихся 8-х классов о решении линейных уравнений . ..

Идеальная цель IEP для 7-го класса – Учащиеся 9-х классов, нацеленные на пред …

www.teachtasticiep.com › post › the-perfect-iep-goal-for-7th-9th-class-stu…

01.03.2022 · Эта цель IEP для всех учащихся 7-9 классов с целями IEP, направленными на успех в предварительной алгебре. Решение уравнений с одной переменной.

Цели IEP по математике в восьмом классе | TeachTastic

www.teachtasticiep.com › VIII-grade-math-iep-go…

Этот банк целей IEP относится к обязательным навыкам девятого класса по математике, включая рабочие листы… Определение линейных и нелинейных функций: графики и уравнения …

Математические цели IEP, основанные на стандартах – CTSPEDMATHDUDE

ctspedmathdude.com › Основанные на стандартах IEP-math-ob…

22.12.2016 · Математические цели IEP, основанные на стандартах · Цель 1: Xxxx будет точно упрощать выражения и решать линейные уравнения с 1 переменной. · Цель 2: Xxxx будет . ..

Ähnliche Fragen

Какова цель решения линейных уравнений?

Какой реальный пример линейного уравнения?

Как в увлекательной игровой форме учить линейным уравнениям?

Как вы можете применять линейные уравнения в повседневной жизни?

[PDF] Алгебра I, курс 202 Объединенный школьный округ Лос-Анджелеса ОБЩИЙ …

chie.lausd.net › domain › Common Core Goal Stems › Algebra1

01.04.2022 · ОБЩИЕ ОСНОВНЫЕ СТАНДАРТЫ IEP GOAL BANK/ ЗАДАЧИ… <СТУДЕНТ> будет решать линейные уравнения и неравенства с одной переменной, …

[DOC] Примеры вторичных целей IEP 08.06.2015 Математика

artsacad.net › wp-content › uploads › 2020/10 › Example-Secondary…

Примеры вторичных целей IEP. 08.06.2015 … Получив набор из пяти графиков линий, учащийся напишет уравнение каждой линии с точностью 80% 3 …

Цели IEP по математике для специального образования | Special Ed Lesson Plans

specialedlessonplans.