Решение системы по формулам крамера онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Решение системы по формулам крамера. Правило Крамера. Метод обратной матрицы

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись.

Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных.

Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой

, а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю.

Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

решаем системы линейных алгебраических уравнений (слау)

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

Рассмотрим систему 3-х уравнений с тремя неизвестными

Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т. е.

(2.4)

если 0. Здесь

Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .

Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:

Решение . Находим определитель основной матрицы системы

Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:

Проверка:

Следовательно, решение найдено правильно. 

Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место

Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам

(2.5)

где  – определитель основной матрицы ,  i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .

Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.

Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.

2.4. Определители n-го порядка

Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .

Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя

Получаем



Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .

Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

(2.6)

Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:

т.е. алгебраические дополнения записывают в явном виде через миноры.

Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.



2.

5. Основные свойства определителей

Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.

Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т. е. при транспонировании матрицы :

Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.

Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).

Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .

Например,

Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .

Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число .

Например,

Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:

Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.

Теорема 1

Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$

В чем заключается метод Крамера

Суть метода Крамера в следующем:

Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$

А теперь три других детерминанта:

$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$

$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$

$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

Разработка материала по методу Крамера по алгебре в 7 классе

Формулы Крамера для модуля на ШЦП 4.0

Посмотреть урок по ссылкеhttps://youtu.be/f0GvqaF2ht8

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Формулы Крамера для нахождения неизвестных:

Найти значения и возможно только при условии, если

Этот вывод следует из следующей теоремы.

Ответ : (5;2)

Пример 1. Решить систему линейных уравнений:

. (2)

Согласно теореме Крамера имеем:

Итак, решение системы (2):

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера, при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Условия:

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

Условия:

* ,

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Условия:

** .

Итак, система m линейных уравнений с n переменными называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

Применить метод Крамера самостоятельно, а затем посмотреть решения

Пример 4. Решить систему линейных уравнений:

Правильное решение и ответ.

Пример 5. Решить систему линейных уравнений методом Крамера:

. Решение. Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Правило Крамера – это… Что такое Правило Крамера?

Правило Крамера

Метод Крамера (Крамера правило) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). 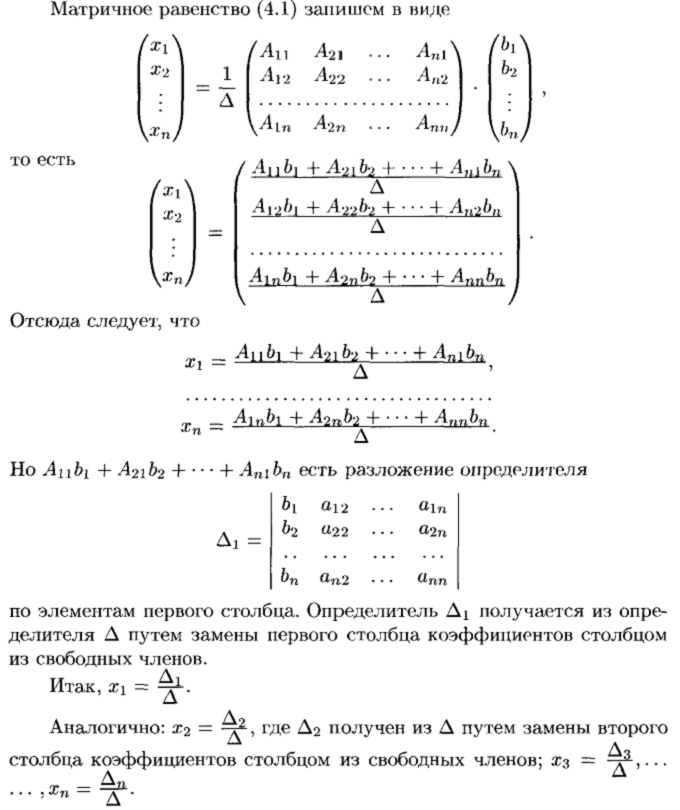Создан Габриэлем Крамером в 1750 году.

Описание метода

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-й столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,…,b_n и x₁,x₂,…,x_n, либо набор c₁,c₂,. ..,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Пример

Система линейных уравнений:

Определители:

Решение:

Пример:

Определители:

Примечания

Из-за высокой вычислительной сложности метода — требуется вычисление n + 1 определителя размерности , он не применяется для машинного решения больших СЛАУ. Однако он иногда используется при ручном счёте и в теоретических выкладках. Α−Β+2γ−Δ=−4 2Α+2Β-4γ-Δ=10 Α-2Β-4γ=7 Α+3Β-2γ-2Δ=1

Ссылки

Wikimedia Foundation. 2010.

Правило Коновалова
Правило Лейбница

Смотреть что такое “Правило Крамера” в других словарях:

КРАМЕРА ПРАВИЛО — если определитель Dквадратной системы линейных уравнений не равен нулю, то эта система имеет единственное решение и это решение находится по формулам Здесь определитель, получаемый из Dзаменой k то столба на столбец свободных членов. Формулы (*)… … Математическая энциклопедия
Метод Крамера — (правило Крамера) способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752),… … Википедия
Формулы Крамера — Метод Крамера (Крамера правило) способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Создан Габриэлем Крамером в 1750 году.… … Википедия
Ожереловый попугай Крамера — ? Ожереловый попугай Крамера Научная классификация Царство: Жи … Википедия
Крамер Габриель — (Cramer) (1704 1752), швейцарский математик. Труды по теории алгебраических уравнений (правило Крамера) и геометрии. * * * КРАМЕР Габриель КРАМЕР (Cramer) Габриель (1704 52), швейцарский математик. Труды по теории алгебраических уравнений… … Энциклопедический словарь
Функция Грина — используется для решения неоднородных дифференциальных уравнений с граничными условиями (неоднородная краевая задача). Функция Грина это обратный оператор к . Поэтому ее нередко символически обозначают как . Функции Грина полезны в… … Википедия
Точнорешаемая задача — В настоящее время отсутствует единое определение точно решаемой задачи для всех разделов математики. Это обусловлено особенностями самих задач и методов поиска их решения. Вместе с тем базовые теоремы, определяющие наличие и единственность… … Википедия
КРАМЕР (Cramer) Габриель — (1704 52) швейцарский математик. Труды по теории алгебраических уравнений (правило Крамера) и геометрии … Большой Энциклопедический словарь
Линейная алгебра — Эта статья в данный момент активно редактируется участником Zanka. Пожалуйста, не вносите в неё никаких изменений до тех пор, пока не исчезнет это объявление. В противном случае могут возникнуть конфликты редактирования. Данное предупреждение… … Википедия
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия

Доказать совместимость системы линейных уравнений методом крамера. Метод крамера решения систем линейных уравнений

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Теорема 1

В чем заключается метод Крамера

Суть метода Крамера в следующем:

Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

А теперь три других детерминанта:

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:

Правило крамера примеры решения. Решение системы с помощью обратной матрицы. Основные свойства определителей

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Теорема Крамера.

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Метод крамера схема решения. Метод крамера решения систем линейных уравнений

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

Теорема Крамера.

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Правила Крамера для системы матричных уравнений кватернионов с η-герметичностью

4open 2019, 2 , 24

Статья о пересмотре

Правила Крамера для системы матричных уравнений кватерниона с

η -Гермичностью

Пидстрыгач Институт прикладных проблем механики и математики НАН Украины, Львов, 79060, Украина

^* Автор, ответственный за переписку: [email protected]

Поступило: 10 Январь 2019 г.
Принято: 6 июнь 2019 г.

Аннотация

Система двусторонних матричных уравнений кватерниона с η -Гермичностью, A ₁ XA ₁ ^{η *} = C ₁, A

8 2 В статье рассматривается XA ₂ ^{η *} = C ₂.Используя ранее введенные автором некоммутативные определители строка-столбец, получены детерминантные представления (аналоги правила Крамера) общего решения системы. В качестве особых случаев применяются правила Крамера для раствора η -эрмитова, когда C ₁ = C ^{η *} ₁ и C ₂ = C ^{η *} ₂ и для η -искривленного эрмитова решения, когда C ₁ = – C ^{η *} ₁ и C ₂ = – C ^{η *} ₂ η тоже исследовал.

Классификация предметов по математике: 15A24 / 15A15 / 15A09 / 15B33

Ключевые слова: Обобщенный обратный / Некоммутативный определитель / Кватернионная матрица / Система матричных уравнений / Правило Крамера / η -Гермичность

© И.И. Кирчей, Издательство EDP Sciences, 2019

Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии, что оригинал работа правильно процитирована.

Введение

Во всей статье обозначения зарезервированы для поля действительных чисел и обозначают набор всех матриц m × n над телом кватерниона

указывает свое подмножество матриц с рангом r . Для данного конъюгата h есть. Для данного, A * представляет собой сопряженную транспонированную (эрмитово сопряженную) матрицу A . Матрица эрмитова, если A * = A . А ^† означает обратную матрицу Мура – Пенроуза, т.е. исключительную матрицу X , удовлетворяющую следующим четырем уравнениям

Кватернионы широко используются в различных областях, таких как создание цветных изображений и информатика [1–5], механика жидкости [6, 7], квантовая механика [8, 9], пространственная ориентация и пространственная динамика твердого тела [10–10]. 12], обработка сигналов [13–15] и др.

Исследование матричных уравнений имеет как прикладное, так и теоретическое значение.Многие авторы исследовали систему двусторонних матричных уравнений

(1) над полем комплексных чисел, телом кватернионов и т. Д. (См., Например, [16–21]). В данной работе рассматривается следующая система матричных уравнений кватерниона с η -гермичностью,

(2)

Определение 1.1.

[22–24] Известно, что матрица имеет вид η – эрмитова и η – косоэрмитова if и, соответственно, где.

Анализ сходимости в статистической обработке сигналов и линейном моделировании [14, 15, 23] – это некоторые области, в которых могут быть рассмотрены приложения матриц η -эрмитовых матриц.Разложение по сингулярным числам эрмитовой матрицы η было рассмотрено в [22]. Совсем недавно Лю [25] нашел η -косо-эрмитовых решений некоторых классических матричных уравнений и, среди них, обобщенного матричного уравнения типа Сильвестра:

(3) Обратите внимание, что в [25] термин « η -антиэрмитов» был использован вместо « η -косоэрмитов». Он и Ван [26] дали общее решение

, имеющий η -Гермичность, выражая его общее решение η -эрмитова через обратные преобразования Мура – Пенроуза.Итерационный алгоритм для определения η (-косов) -эрмитовых решений по наименьшим квадратам кватернионного матричного уравнения (3) был установлен в [27]. Более подробные статьи о η -гермичности и ее обобщении, ϕ-герметичности, можно найти в [28–38].

В этой статье мы строим новые явные формулы детерминантного представления (аналог правила Крамера) общего и η – (косого) эрмитова решений системы (2), используя детерминантные представления матрицы Мура – Пенроуза полученное в рамках теории некоммутативных определителей строка-столбец.Насколько нам известно, предлагаемое правило Крамера является уникальным прямым методом вычисления η – (косого) эрмитовых решений матричных уравнений кватернионов, в отличие от других подобных работ (см., Например, [24–26, 29, 32] ), где полученные явные формы решений имеют в основном только теоретическое значение.

В отличие от обратной матрицы, которая имеет определенно детерминантное представление в терминах кофакторов, для обобщенных обратных матриц, в частности, матриц Мура – Пенроуза, существуют различные детерминантные представления даже для матриц с действительными или комплексными элементами в результате поиска их более применимых явных выражений (о матрице Мура – Пенроуза см. e.г., [39–41]). Для кватернионных матриц ввиду некоммутативности кватернионов проблема детерминантного представления обобщенных обратных матриц долгое время оставалась открытой и только теперь может быть решена благодаря теории определителей строка-столбец, которые были введены в [42, с. 43].

В настоящее время применение определителей строка-столбец к детерминантным представлениям различных обобщенных инверсий было выведено автором (см., Например, [44–57]) и другими исследователями (см., E.грамм. [58–61]). В частности, детерминантные представления систем типа (1) были недавно исследованы в [53, 55, 56, 61].

Остальная часть статьи направлена следующим образом. В разделе 2 мы начинаем с предварительных сведений об общих свойствах обобщенных обратных матриц, проекторов и η -матриц в разделе 2.1, а также в теории определителей строк-столбцов и детерминантных представлений обращений Мура – Пенроуза кватернионной матрицы, ее Эрмитова сопряженная и η -эрмитова сопряженная матрицы в разделе 2.2. Детерминантные представления общего, η -эрмитова и η -косоэрмитова решений системы (2) выводятся в разделе 3. Наконец, в разделе 4 делается вывод.

Предварительные сведения: детерминантные представления решений кватернионных матричных уравнений

Общие свойства обобщенных обратных, проекторов и

η -матриц

Мы начнем с некоторых известных результатов об обобщенных обратных и индуцируемых ими проекторах, которые будут использоваться в оставшейся части этой статьи.

Лемма 2.1.

[26] Пусть . Тогда

Лемма 2.2.

[71] Пусть А , В и С получить матрицы нужного размера более . Тогда

Замечание 2.1.

Для любого для всех l = 1, 2, 3 и q = q ₀ + q ₁ η ₁ + q ₂ η ₂ + q ₃ η ₃, обозначим

Итак, элементы главной диагонали η ₁ -Эрмитова матрица должна быть следующей

, а пара элементов, симметричных относительно главной диагонали, может быть представлена как

Аналогично элементы главной диагонали η ₁ -косоэрмитова матрица должна иметь вид

, а пара элементов, симметричных относительно главной диагонали, может быть представлена как

, где для всех l = 0,…, 3.

Детерминантные представления обобщенных обратных и решений некоторых кватернионных матричных уравнений

Из-за некоммутативности кватернионного тела определение определителя с некоммутативными элементами (его также называют некоммутативным определителем) не так тривиально (см., Например, [62, 63]). Существует несколько вариантов определения некоммутативных определителей (см., Например, [64–69]). Но, как доказано в [70], если все функциональные свойства определителя над кольцом выполняются, то он принимает значение только в своем коммутативном подмножестве.В частности, это означает, что такой определитель не может быть расширен кофакторами по произвольной строке или столбцу. Чтобы избежать этих трудностей, мы определяем n определителей строк и n определителей столбцов, которые не обладают всеми функциональными свойствами, которые могут быть присущи обычному определителю.

Предположим, S _n – симметричная группа на множестве.

Определение 2.2.

[42] Определитель i -й строки из вызывается установкой для всех i = 1,…, n,

, где σ – перестановка, упорядоченная слева.Это означает, что его первый цикл слева начинается с и , остальные циклы начинаются слева с минимального из всех целых чисел, содержащихся в нем,

, а порядок непересекающихся циклов (кроме первого) строго обусловлен увеличением слева направо их первых элементов,.

Определение 2.3.

[42] Определитель j -го столбца вызывается путем установки для всех j = 1,…, n ,

, где τ – правосторонняя перестановка.Это означает, что его первый цикл справа начинается с j , остальные циклы начинаются справа с минимального из всех целых чисел, содержащихся в нем,

, а порядок непересекающихся циклов (кроме первого) строго обусловлен увеличением справа налево их первых элементов,.

Замечание 2.4.

Итак, для матрицы 2 × 2 с параметрами кватерниона у нас есть четыре детерминанта (строка-столбец)

Так как для всех i, j = 1, 2, в общем случае они не равны друг другу.

Мы формулируем некоторые свойства определителей строки-столбца, необходимые ниже.

Лемма 2.3.

[42] Если i-я строка из – это левая линейная комбинация других векторов-строк, т.е. , где и для всех l = 1,…, k и i = 1,…, n, тогда

Лемма 2.4.

[42] Если j-й столбец числа – это правильная линейная комбинация других векторов-столбцов, т.е. , где и для всех l = 1,…, k и j = 1,…, n, тогда

Лемма 2.5.

[43] Пусть . Тогда , для всех i = 1,…, n.

Поскольку по определениям 2.2 и 2.3 для

для всех i = 1,…, n , то по лемме 2.5 немедленно следует следующая лемма.

Лемма 2.6.

Пусть . Тогда

для всех i = 1,…, n.

Замечание 2.5.

Начиная с [42] для Hermitian A мы имеем

определитель эрмитовой матрицы вызывается установкой для любого i = 1,…, n .

Его свойства полностью изучены в [43]. В частности, из них следует определение детерминантного ранга кватернионной матрицы A как максимально возможного размера ненулевых главных миноров соответствующих ей эрмитовых матриц, т.е.

Для детерминантных представлений обратного Мура – Пенроуза мы используем следующие обозначения. Позвольте и быть подмножествами с. Обозначим подматрицу со строками и столбцами, индексированными α и β , соответственно.Тогда это главная подматрица A со строками и столбцами, индексированными α . Более того, для Hermitian A это главный минор det A . Предположим, что

обозначает набор строго возрастающих последовательностей 1 ≤ k ≤ n целых чисел, выбранных из {1,…, n }. Для фиксированных и, положил,.

Символами и, и обозначены столбцы j и строки i строк A и A *, соответственно.Предположим и обозначим матрицы, полученные из A заменой ее строки i на строку b и ее j -го столбца на столбец c , соответственно.

Теорема 2.6.

[44] Если , затем его обратное преобразование Мура – Пенроуза определяется как

(4)

(5)

Замечание 2.7.

Для произвольной полноранговой матрицы вектор-строка r , и вектор-столбец, мы предполагаем, что для всех i = 1,…, m, j = 1,…, n ,

Следствие 2.1.

Если , затем обратное преобразование Мура – Пенроуза имеют следующие детерминантные представления:

Замечание 2.8.

Так как, то можно использовать обозначение . По лемме 2.5 для сопряженной эрмитовой матрицы обратная к ней матрица Мура – Пенроуза может быть выражена как

Замечание 2.9.

Предположим . По лемме 2.6 и замечанию 2.8 для сопряженной эрмитовой матрицы η и косоэрмитовой сопряженной матрицы η , детерминантные представления их обратных точек Мура – Пенроуза и равны соответственно

(6)

(7)

Так как матрицы проекции и эрмитовы, то и для всех i ≠ j .Из теоремы 2.6 и замечания 2.8, очевидно, вытекают следствия.

Следствие 2.2.

Если , затем его индукционные проекционные матрицы и определяются следующим образом:

(8)

(9) где и , и – это j-й столбец и i-я строка из . и , соответственно .

Правило Крамера для системы (2)

Следующая лемма дает явную матричную форму общего решения системы (1).

Лемма 3.1.

[21] Предположим, что , , , , , известны и неизвестно. Положите , , , . Тогда система (1) непротиворечиво тогда и только тогда, когда

В этом случае общее решение (1) можно выразить как

(10) где Z и Вт – произвольные матрицы более с соответствующими размерами .

Некоторое упрощение (10) можно получить с помощью леммы 2.2. Итак, имеем

(11)

Подставляя (11) в (10), получаем

Положив Z = W = 0 , мы получим следующее выражение частичного решения

(12)

Теперь рассмотрим систему (2). У нас

аналогично,, и, по лемме 2.1,, и для i = 1, 2. Кроме того, подставляя, получаем

Из вышесказанного следует следующий аналог леммы 3.1.

Лемма 3.2.

Предположим, что , , , известны и неизвестно. Система (2) непротиворечиво тогда и только тогда, когда

(13)

(14)

В этом случае общее решение (2) выражается как

где Z и Вт – произвольные матрицы более с соответствующими размерами .

Если положить Z , W в качестве нулевых матриц, частичное решение (2) будет

(15)

Далее дадим детерминантные представления (15).

Предположим, что,,,, и. Итак,,,,, и.

Рассмотрим каждое слагаемое в (15) отдельно.

Обозначение. Для первого члена (15) , у нас

С учетом (4) и (6) для и соответственно получаем

Предположим, что и являются единичными векторами строк и столбцов, все их компоненты равны 0, за исключением –-го компонентов, которые равны 1.

С тех пор

(16)

по

(17) обозначают -ю -ю компоненту вектора-строки. Тогда

(18)

Дальше видно что. Интегрируя (17) и (18) в (16), детерминантное представление первого члена (15) можно выразить как

(19) где

(20)

Если обозначить

(21) f -й компонент вектора-столбца, затем

(22)

Интегрируя (21) и (22) в (16), получаем другое детерминантное представление первого члена

(23) где

– вектор-столбец и f -я строка.

Аналогично выше, для второго члена (15),

у нас

(24) или

(25) где

Здесь и находятся строка q и столбец l строки.

Третий член в (15) также получается аналогично. Итак,

(26) или

(27) где

Здесь находятся строка q и столбец l строки.

Теперь рассмотрим четвертый член в (15).С учетом (4) для детерминантных представлений H ^† и T ^†, получаем

(28) Здесь обозначим и -е столбцы и соответственно. – это ( zf ) -й элемент первого члена, полученного в точке (i). кв _fj – это ( fj ) -й элемент, который, согласно (8), может быть выражен как

, где f -я строка. Обозначим

(29) где z -я строка для всех z , j = 1,…, n и X ₁ находится в точке (i).Постройте матрицу. Далее обозначим

, где – j -й столбец и построить матрицу. Наконец, обозначим. Из этих обозначений и уравнения (28) следует

(30) где – j -й столбец.

Для, у нас есть

Обозначим, где определено в (29). Итак, как и в предыдущем случае, получаем

(31) где – j -й столбец.

Рассмотрим шестой член.Итак,

(32) где

(33) и

Вот l -й столбец и q -я строка. Построить матрицу так, чтобы ϕ _qj определено в (33) и обозначим. Из этого обозначения и уравнения (32) следует

(34) где – j -й столбец.

Наконец, рассмотрим седьмой член в (15). С учетом (4) для Т ^† и (6) для, получаем

(35) где, – q -й столбец и f -я строка соответственно.Обозначим

(36) где q -я строка. Построить матрицу так, чтобы ω _qj определено в (36) и обозначим. Из этих обозначений и уравнения (35) следует

(37) где – j -й столбец.

Таким образом, мы доказали следующую теорему.

Теорема 3.1.

Предположим, что , и ,. Частичное решение (15) в систему (2) по компонентам – это

, где слагаемое имеет детерминантные представления (19) и (23), – (24) и (25), – (26) и (27), – (30), – (31), – (34) и – (37).

Замечание 3.2.

Теорема 3.1 дает прямой метод нахождения общего решения системы (2), являющийся аналогом правила Крамера. Для этого нам понадобятся ряды заданных матриц и удовлетворение ими согласованных условий (13) – (14). Пусть теперь

(38)

(39)

Частичное η -эрмитово решение Y ₁ и η -искоэрмитово решение Y ₂ в систему (2) с ограничениями (38) и (39) соответственно можно выразить как

, где X – произвольное решение системы (2).В силу выражения общего решения (15) и с учетом (38) имеем

Но с учетом (39) получаем

Итак, частные η -эрмитово и η -косоэрмитово решения системы (2) с ограничениями (38) и (39) соответственно имеют следующее выражение:

Детерминантные представления и могут быть получены компонентами соответственно как

для всех i , j = 1,…, n , где x _ij определяется теоремой 3.1.

Вывод

Используя ранее введенные автором некоммутативные определители строка-столбец, детерминантные представления (аналоги правила Крамера) общих, η -эрмитовых и η -косо-эрмитовых решений системы кватернионных матричных уравнений, были найдены. полученный. Для этих целей были исследованы и использованы детерминантные представления инверсий Мура – Пенроуза кватернионной матрицы, ее эрмитовой сопряженной и η -эрмитовой сопряженной матриц.

Список литературы

Хэндсон А., Хуэй Х (1995), Кватернионный фреймовый подход для оптимизации визуализации. Компьютерный график IEEE Trans Vis 1, 2, 164–172. [CrossRef] [Google ученый]
Сангвин SJ (1996), преобразования Фурье цветных изображений с использованием кватерниона или гиперкомплексного числа.Electr Lett 32, 21, 1979–1980. [CrossRef] [Google ученый]
Элль Т.А., Сангвин С.Дж. (2007), Гиперсомплексные преобразования Фурье цветных изображений.IEEE Trans Image Process 16, 1, 22–35. [CrossRef] [PubMed] [Google ученый]
Ван Дж., Ли Т., Ши Й.К., Лиан С., Йе Дж. (2016), Криминалистический анализ признаков в кватернионной вейвлетной области для различения фотографических изображений и компьютерной графики.Мультимедийные инструменты Прил. 76, 22, 23712–23737. [Google ученый]
Чен Б., Шу Х., Коатриё Дж., Чен Дж., Сунь Х, Коатриё Дж. Л. (2015), Анализ цветного изображения по моментам кватернионного типа. J Math Imaging Vision 51, 1, 124–144. [CrossRef] [Google ученый]
Гиббон Дж. Д., Холм Д. Д., Керр Р. М., Роулстон I (2006), Кватернионы и динамика частиц в уравнениях жидкости Эйлера.Нелинейность 19, 1969–1983. [Google ученый]
Рубцов В. Н., Роулстон И. (2001), Голоморфные структуры в гидродинамических моделях почти геострофических течений. Proc R Society London Ser A 457, 1519–1531. [CrossRef] [Google ученый]
Адлер С.Л. (1995), Кватернионная квантовая механика и квантовые поля, Oxford University Press, Нью-Йорк.[Google ученый]
Лео С., Дукати Г. (2012), Время задержки в кватернионной квантовой механике. J Math Phys 53, 2, ID статьи 022102, 8 стр. [PubMed] [Google ученый]
Гупта С. (1998), Линейные кватернионные уравнения в применении к распространению пространственного положения космических аппаратов.IEEE Aerospace Conf Proc 1, 69–76. [Google ученый]
Song C, Sang J, Seung H, Nam HS (2006), Надежный контроль положения ракеты на основе кватернионной обратной связи. Control Eng Pract 14, 7, 811–818. [Google ученый]
Wie B, Weiss H, Arapostathis A (1989), Кватернионный регулятор обратной связи для вращения собственной оси космического корабля.J Управление наведением Dyn 12, 375–380. [CrossRef] [Google ученый]
Took CC, Mandic DP (2009), Кватернионный алгоритм LMS для адаптивной фильтрации гиперкомплексных процессов реального мира.Процесс передачи сигналов IEEE 57, 4, 1316–1327. [Google ученый]
Взял CC, Mandic DP (2010), Кватернионный широко линейный адаптивный фильтр. Процесс передачи сигналов IEEE 58, 8, 4427–4431. [Google ученый]
Took CC, Mandic DP (2011), Расширенная статистика второго порядка кватернионных случайных сигналов.Сигнальный процесс 91, 214–224. [CrossRef] [Google ученый]
Mitra SK (1973), Пара одновременных линейных матриц A ₁ XB ₁ = C ₁ и A ₂ XB ₂ = C ₂.Proc Camb Philos Soc 74, 213–216. [Google ученый]
Митра СК (1990), Пара одновременных линейных матричных уравнений и проблема матричного программирования. Линейная алгебра и ее приложение 131, 97–123. [CrossRef] [Google ученый]
Шинозаки Н., Сибуя М. (1974), Согласованность пары матричных уравнений с приложением.Keio Eng Rep 27, 141–146. [Google ученый]
Озгюлер А.Б., Акар Н. (1991), Общее решение пары линейных матричных уравнений в главной области. Линейная алгебра и ее приложение 144, 85–99. [CrossRef] [Google ученый]
Наварра А., Оделл П.Л., Янг Д.М. (2001), Представление общего общего решения матричных уравнений A ₁ XB ₁ = C ₁ и A ₂ XB ₂ = C ₂ с приложениями.Comput Math Appl. 41, 929–935. [Google ученый]
Ван К. В. (2005 г.), Общее решение системы вещественных матричных уравнений кватернионов. Comput Math Appl. 49, 665–675. [Google ученый]
Хорн Р.А., Чжан Ф. (2012), Обобщение комплексной факторизации Автонне-Такаги на кватернионные матрицы.Линейная полилинейная алгебра 60, 11–12, 1239–1244. [CrossRef] [Google ученый]
Тук С.К., Мандич Д.П., Чжан Ф.З. (2011), Об унитарной диагонализации специального класса кватернионных матриц.Appl Math Lett 24, 1806–1809. [Google ученый]
Юань С.Ф., Ван К.В. (2012), Два специальных вида решений методом наименьших квадратов для матричного уравнения кватерниона AXB + CXD = E. Electr J Linear Algebra 23, 257–274. [Google ученый]
Лю X (2018), η-антиэрмитово решение некоторых классических матричных уравнений.Appl Math Comput 320, 264–270. [Google ученый]
He ZH, Wang QW (2013), Реальное матричное уравнение кватерниона с приложениями. Линейная полилинейная алгебра 61, 6, 725–740. [CrossRef] [Google ученый]
Beik FPA, Ahmadi-As S (2015), Итерационный алгоритм для η- (анти) -эрмитовых решений методом наименьших квадратов кватернионных матричных уравнений.Electr J Linear Algebra 30, 372–401. [Google ученый]
Футорный В., Климчук Т., Сергейчук В. В. (2016), Критерии разрешимости Рота для матричных уравнений AX-B = C и X-AB = C над телом кватернионов с инволютивным автоморфизмом q →.Linear Algebra Appl 510, 246–258. [Google ученый]
He ZH, Wang QW (2014), η-бигермитово решение системы вещественных матричных уравнений кватернионов. Линейная полилинейная алгебра 62, 11, 1509–1528. [CrossRef] [Google ученый]
He ZH, Wang QW, Zhang Y (2017), Одновременное разложение кватернионных матриц с участием η-герметичности с приложениями.Прикладные математические вычисления 298, 13–35. [Google ученый]
He ZH, Liu J, Tam TY (2017), Общее ϕ-эрмитово решение смешанных пар кватернионных матричных уравнений Сильвестра. Electr J Linear Algebra 32, 475–499. [CrossRef] [Google ученый]
He ZH (2019), Структура, свойства и приложения некоторых одновременных разложений для кватернионных матриц, включающих ϕ-косогермичность.Дополнительные возможности Алгебры Клиффорда 29, 6. [CrossRef] [Google ученый]
Климчук Т., Сергейчук В.В. (2014), Матричные уравнения сходства и кватерниона AX-B = C и X-AB = C.Специальные матрицы 2, 180–186. [CrossRef] [Google ученый]
Родман Л. (2014), Темы в кватернионной линейной алгебре, Princeton University Press, Princeton.[Google ученый]
Рехман А., Ван Ч.В., Хе З.Х. (2015), Решение системы вещественных матричных уравнений кватернионов, охватывающих η-герметичность. Appl Math Comput 265, 945–957. [Google ученый]
Рехман А., Ван К. В., Али И., Акрам М., Ахмад МО (2017), Система ограничений обобщенных матричных уравнений кватерниона Сильвестра.Adv Appl. Алгебры Клиффорда 27, 4, 3183–3196. [CrossRef] [Google ученый]
Чжан Ю., Ван Р. (2013), Точное решение системы кватернионных матричных уравнений, включающих η-герметичность.Appl Math Comput 222, 201–209. [Google ученый]
Юань С.Ф., Ван К.В., Сюн З.П. (2014), Эта-эрмитовы задачи наименьших квадратов для матричного уравнения кватерниона. Филомат 28, 6, 1153–1165. [CrossRef] [Google ученый]
Бапат Р. Б., Бхаскара КПС, Прасад К. М. (1990), Обобщенные обратные обращения над областями целостности.Linear Algebra Appl 140, 181–196. [Google ученый]
Станимирович П.С. (1996), Общее детерминантное представление псевдообратных матриц. Математики Весник 48, 1–9. [Google ученый]
Kyrchei I (2015), Правило Крамера для обобщенных обратных решений, в: I Kyrchei (Ed.), Достижения в исследованиях линейной алгебры, Nova Science Publishers, Нью-Йорк, стр. 79–132. [Google ученый]
Кирчей I (2008), Правило Крамера для кватернионных систем линейных уравнений. J Math Sci 155, 6, 839–858. [CrossRef] [Google ученый]
Кирчей I (2012), Теория определителей столбцов и строк в кватернионной линейной алгебре, в: AR Baswell (Ed.), Достижения в математических исследованиях, 15, Nova Science Publishers, Нью-Йорк, стр. 301–359. [Google ученый]
Кирчи I (2011), Детерминантные представления обратного преобразования Мура-Пенроуза над кватернионным телом и соответствующие правила Крамера.Линейная полилинейная алгебра 59, 4, 413–431. [CrossRef] [Google ученый]
Кирчей И. (2013), Формулы явного представления для решений методом наименьших квадратов с минимальной нормой некоторых матричных уравнений кватернионов.Линейная алгебра Прил. 438, 1, 136–152. [Google ученый]
Кирчей И. (2014), Детерминантные представления обратного Дразина над кватернионным телом с приложениями к некоторым матричным уравнениям. Appl Math Comput 238, 193–207.[Google ученый]
Кирчей I (2015), Детерминантные представления W-взвешенной инверсии Дразина над телом кватернионов. Appl Math Comput 264, 453–465. [Google ученый]
Кирчей И. (2016), Явные детерминантные формулы представления W-взвешенных обратных решений Дразина некоторых матричных уравнений над кватернионным телом.Math Probl Eng 2016, ID статьи 8673809, 13 стр. [Google ученый]
Кирчей I (2017), Детерминантные представления Дразина и W-взвешенных инверсий Дразина над кватернионным телом с приложениями, в: S. Griffin (Ed.), Quaternions: Theory and Applications, Nova Science Publishers, New York, pp. 201–275. [Google ученый]
Кирчей I (2017), Взвешенное разложение по сингулярным значениям и детерминантные представления кватернионно-взвешенного обратного преобразования Мура-Пенроуза.Appl Math Comput 309, 1–16. [Google ученый]
Кирчей I (2017), Детерминантные представления взвешенного кватернионами обратного преобразования Мура-Пенроуза и его приложения, в: AR Baswell (Ed.), Advances in Mathematics Research, 23, Nova Science Publications, Нью-Йорк, стр.35–96. [Google ученый]
Кирчей И. (2018), Формулы явного детерминантного представления для решения двустороннего ограниченного кватернионного матричного уравнения. J Appl Math Comput 58, 1–2, 335–365. [Google ученый]
Кирчей И. (2018), Детерминантные представления решений систем кватернионных матричных уравнений.Расширенное применение Алгебры Клиффорда 28, 1, 23. [CrossRef] [Google ученый]
Kyrchei I (2018), Правила Крамера для матричного уравнения кватерниона Сильвестра и его частные случаи.Расширенное применение Алгебры Клиффорда 28, 5, 90. [CrossRef] [Google ученый]
Кирчей И. (2018), Детерминантные представления решений и эрмитовы решения некоторой системы двусторонних кватернионных матричных уравнений.J Math 2018, ID 6294672, 12 стр. [CrossRef] [Google ученый]
Kyrchei I (2018), Правила Крамера для системы двусторонних матричных уравнений и ее частных случаев, в: HA Yasser (Ed.), Матричная теория – приложения и теоремы, IntechOpen, Лондон, стр. 3–20. [Google ученый]
Кирчей И. (2019), Детерминантные представления общих и (косо-) эрмитовых решений обобщенного матричного уравнения кватернионного типа Сильвестра.Abstract Appl Anal 2019, ID статьи 5
2, 14 стр. [CrossRef] [Google ученый]
Song GJ, Wang QW, Chang HX (2011), Правило Крамера для единственного решения ограниченных матричных уравнений над кватернионным телом.Comput Math Appl 61, 1576–1589. [Google ученый]
Song G (2013), Характеристика W-взвешенного обратного преобразования Дразина над кватернионным телом с приложениями. Electr J Линейная алгебра 26, 1–14. [Google ученый]
Song GJ, Dong CZ (2017), Новые результаты по сжатому правилу Крамера для общего решения некоторых матричных уравнений с ограниченными кватернионами.J Appl Math Comput 53, 321–341. [Google ученый]
Song GJ, Wang QW, Yu SW (2018), Правило Крамера для системы матричных уравнений кватернионов с приложениями. Appl Math Comput 336, 490–499. [Google ученый]
Аслаксен Х. (1996), Кватернионные детерминанты.Math Intell 18, 3, 57–65. [CrossRef] [Google ученый]
Коэн Н., Де Лео С. (2000), Кватернионный детерминант.Electr J Linear Algebra 7, 100–111. [Google ученый]
Чен Л. (1991), Определение детерминантных и крамеровых решений над полем кватернионов. Acta Math Sin (N.S.) 7, 171–180. [CrossRef] [Google ученый]
Dieudonné J (1943), Lesterminantes sur un corps non-commutatif.Bull Soc Math France 71, 27–45. [CrossRef] [Google ученый]
Дайсон Ф.Дж. (1972), Детерминанты кватерниона.Helvetica Phys Acta 45, 289–302. [Google ученый]
Гельфанд I, Гельфанд S, Ретах V, Вильсон RL (2005), Квазидетерминанты. Adv Math 193, 56–141. [CrossRef] [Google ученый]
Мур EH (1922), Об определителе эрмитовой матрицы кватернионных элементов.Bull Am Math Soc 28, 161–162. [Google ученый]
Этюд E (1920), Zur Theorie der linearen Gleichungen. Acta Math 42, 1–61. [CrossRef] [Google ученый]
Fan J (2003), Детерминанты и мультипликативные функционалы от кватернионных матриц.Linear Algebra Appl. 369, 193–201. [Google ученый]
Wang QW, Li CK (2009), Ранги и наименьшая норма общего решения системы матричных уравнений кватерниона. Linear Algebra Appl. 430, 1626–1640. [Google ученый]

Цитируйте эту статью как : Kyrchei II 2019.Правила Крамера для системы матричных уравнений кватерниона с η -гермичностью. 4open, 2 , 24.

Решение уравнений процесса тяги. Линейные уравнения

Метод Крамера основан на использовании определителей при решении систем линейных уравнений. Это значительно ускоряет процесс принятия решения.

Кратерный метод можно использовать при решении системы стольких линейных уравнений, как в каждом уравнении неизвестного. Если определитель системы не равен нулю, в решении можно использовать метод Крамера, если он равен нулю, нельзя.Кроме того, метод Крамера можно использовать при решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестном, называется определителем системы и обозначается (дельта).

Deterpetes

получается заменой коэффициентов на соответствующие неизвестные для свободных участников:

;

Теорема Крамера . Если определитель системы отличен от нуля, система линейных уравнений имеет одно единственное решение и неизвестное, равное отношению определителей.В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путем замены коэффициентов одновременно неизвестными свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решите систему линейных уравнений:

По теореме крамера Имеем:

Итак, решение Решение (2):

Онлайн-калькулятор, решающий кратерный метод.

Три случая решения систем линейных уравнений

Как ясно теорем Крамера При решении системы линейных уравнений может быть три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместно и определена)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместного и неопределенного)

**,

тех.Коэффициенты при неизвестных и свободных членах пропорциональны.

Третий случай: в системе линейных решений нет

(система непонятна)

Итак, система м. Linear Equations S. n. переменных называются нон-стоп , если у нее нет решения, и объединяют , если у нее есть хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определенным , более одного – неопределенным .

Примеры решения систем линейных уравнений по Крамеру

Пусть дано системе

На основе теоремы Крамера

………….
,

где
–

определение системы. Остальные определители получаем, заменяя столбец коэффициентами соответствующих переменных (неизвестных) свободных членов:

Пример 2.

Следовательно, система определена. Чтобы найти ее решения, вычислим определители

По формулам краулера находим:

Итак (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 x 3 и 4 x 4 вы можете использовать онлайн-калькулятор, решая метод Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях нет переменных, то в определителе соответствующие им элементы равны нулю! Это следующий пример.

Пример 3. Решите систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Внимательно посмотрите на систему уравнений и определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решения, вычислим определители при неизвестном

По формулам краулера находим:

Итак, решение системы (2; -1; 1).

Начало страницы

Продолжаем решать систему по методу Крамера вместе

Как уже было сказано, если определитель системы равен нулю, а определители при неизвестном не равны нулю, система непонятна, то есть решений не имеет. Проиллюстрируем следующий пример.

Пример 6. Решите систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо неполна и определена, либо противоречива, то есть не имеет решений. Для пояснения вычислим детерминанты при неизвестном

Определители при неизвестном не равны нулю, следовательно, система неполная, то есть не имеет решений.

В задачах по системе линейных уравнений встречаются и такие, где встречаются и другие буквы, обозначаемые переменными. Эти буквы обозначают какое-то число, чаще всего действительное. На практике такие уравнения и системы уравнений приводят к задачам поиска общих свойств любых явлений и объектов. То есть вы изобрели какой-то новый Материал или устройство, и для описания его свойств, как правило, независимо от размера или количества экземпляров, необходимо решать систему линейных уравнений, где вместо некоторых коэффициентов с переменными – буквы.Например, ходить не обязательно.

Следующий пример представляет собой аналогичную задачу, только увеличивается количество уравнений, переменных и букв, обозначающих допустимое число.

Пример 8. Решите систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Мы находим детерминанты в неизвестном

Метод Крамера или так называемое правило краулера – это способ поиска неизвестных значений из систем уравнений.Его можно использовать только в том случае, если количество искомых значений эквивалентно количественным алгебраическим уравнениям В системе, то есть основная матрица, сформированная из системы, должна быть квадратной и не содержать нулевых строк, а также если ее определители должны не быть нулевым.

Теорема 1.

Теорема Крамера Если главный определитель $ d $ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений согласована, а решение имеет единственное.Решение такой системы вычисляется по так называемым формулам Крамера для решения линейных уравнений: $ x_i = \ FRAC (D_I) (D) $

Что такое метод Крамера

Суть метода Крамера заключается в следующим образом:

Чтобы найти решение системы методом Крамера, первым делом вычисляется главный определитель матрицы $ D $. Когда вычисленный определитель основной матрицы при вычислении метода Крамера оказался нулевым, то система не имеет единственного решения или имеет бесконечное количество решений.В этом случае рекомендуется применить метод Гаусса, чтобы найти общий или базовый отклик для системы.
Затем нужно заменить крайний столбец основной матрицы на столбец свободных элементов и вычислить идентификатор $ d_1 $.
Повторите то же самое для всех столбцов, получив определители от $ d_1 $ до $ d_n $, где $ n $ – номер крайнего правого столбца.
После того, как все определители найдены $ d_1 $ … $ d_n $, можно вычислить неизвестные переменные по формуле $ x_i = \ frac (d_i) (D) $.

Приемы вычисления определителя матрицы

Для вычисления определителя матрицы размерностью больше 2 к 2 можно использовать несколько способов:

Правило треугольников, или правило Сарруса, напоминающее правило то же правило. Суть метода треугольника заключается в том, что при вычислении определителя произведение всех чисел, связанных на рисунке красной линии справа, записывается со знаком плюс, а все числа, соединенные таким же образом на рисунке на слева – со знаком минус.B, тогда другое правило подходит для матриц 3 x 3. 3. В случае правила Сарруски сначала соответствует сама матрица, а затем переписывается в свой первый и второй столбцы. Через матрицу и эти дополнительные столбцы по диагонали, элементы матрицы, лежащие на главной диагонали или параллельно ей, записываются со знаком плюс, а элементы, лежащие на боковой диагонали или параллельно ей – со знаком минус.

Рис. 1. Правило треугольника для вычисления определителя для метода Крамера

Используя метод, известный как метод Гаусса, также иногда этот метод называют уменьшением порядка определителя.В этом случае матрица преобразуется и приводится к треугольной форме, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя невозможно умножить или разделить строки или столбцы на числа, не сделав их как множитель или делитель. В случае поиска определителя возможно только вычесть и сложить струны и столбы между собой после предварительного скашивания отрезанной линии до ненулевого множителя.Также при каждой перестановке строк или столбцов матрицы местами следует помнить о необходимости изменения последнего знака в матрице.
При решении метода Крамера для Славы с 4 неизвестными лучше всего использовать именно метод Гаусса для поиска и нахождения идентификаторов или определять определитель через поиск минорных.

Решение систем уравнений по Крамеру

Применимый метод Крамера для системы из 2 уравнений и двух желаемых значений:

$ \ begin (Cases) a_1x_1 + a_2x_2 = b_1 \\\\ a_3x_1 + a_4x_2 = b_2 \\ End (Cases)

Для удобства отобразить в развернутом виде:

$ A = \ begin (array) (CC | C) A_1 & A_2 & B_1 \\\\ A_3 & A_4 & B_1 \ \ END (Array) $

Найдем определитель основной матрицы, также называемый главным определителем системы:

$ D = \ begin (array) (| CC |) A_1 & A_2 \\\ \ A_3 & A_4 \\ END (Array) = A_1 \ CDOT A_4 – A_3 \ CDOT A_2 $

Если главный определитель не равен нулю, необходимо вычислить пару определителей из двух матриц с заменен столбец основной матрицы на строку свободных элементов для решения примера метода:

$ D_1 = \ begin (array) (| cc |) b_1 & a_2 \\\\ b_2 & a_4 \\\\ \ \ конец (массив) = b_1 \\ cdot a_4 – b_2 \\ cdot a_4 $

$ D_2 = \\ begin (массив) (| CC |) A_1 & B_1 \\\\ A_3 & B_2 \\\\ \\ END (Array) = A_1 \ CDOT B_2 – A_3 \ CDOT B_1 $

Теперь найдите неизвестные $ x_1 $ и $ x_2 $:

$ x_1 = \ FRAC (D_1) (D)

$ x_2 = \ FRAC (D_2) (D)

Пример 1.

Метод Крамера для решения уклона с основной матрицей 3 порядка (3 x 3) и три является искомым.

Решите систему уравнений:

$ \ begin (Дела) 3x_1 – 2x_2 + 4x_3 = 21 \ 3x_1 + 4x_2 + 2x_3 = 9 \ 2X_1 – X_2 – X_3 = 10 \ END (Дела)

Рассмотрим главный определитель матрицы, используя вышеупомянутое правило числа 1:

$ D = \ begin (array) (| CCC |) 3 & -2 & 4 \\\\ 3 & 4 & -2 \ ED (Array) = 3 \ CDOT 4 \ CDOT (- 1) + 2 \ Cdot (-2) \ CDOT 2 + 4 \ CDOT 3 \ CDOT (-1) – 4 \ CDOT 4 \ CDOT 2 – 3 \ CDOT (-2) \ CDOT (-1) – (- 1) \ CDOT 2 \ CDOT 3 = – 12-8-12-32-6 + 6 = – 64 $

А теперь еще три детерминанта:

$ D_1 = \ begin (массив) (| CCC |) 21 & 2 & 4 \\\\ 9 & 4 & 2 \\\\ 10 & 1 & 1 \ END (Array) = 21 \ CDOT 4 \ CDOT 1 + (- 2) \ CDOT 2 \ CDOT 10 + 9 \ CDOT (-1) \ CDOT 4-4 \ CDOT 4 \ CDOT 10-9 \ CDOT (-2 ) \ CDOT (-1) – (-1) \ CDOT 2 \ $ D_2 = \ begin (array) (| CCC |) 3 & 21 & 4 \\\\ 3 & 9 & 2 \\ ED (Массив) = 3 \ CDOT 9 \ CDOT (- 1) + 3 \ CDOT 10 \ CDOT 4 + 21 \ CDOT 2 \ CDOT 2-4 \ CDOT 9 \ CDOT 2-21 \ CDOT 3 \ CDOT (-1) – 2 \ CDOT 10 \ CDOT 3 = – 27 + 120 + 84-72 + 63-60 = 108 $

$ D_3 = \ begin (массив) (| CCC |) 3 & -2 & 21 \\\\ 3 & 4 & 9 \\\\ 2 & 1 & 10 \\ END (массив) = 3 \ \ CDOT 4 \ CDOT 10 + 3 \ Cdot (-1) \ CDOT 21 + (-2) \ CDOT 9 \ CDOT 2-21 \ CDOT 4 \ CDOT 2 – (-2) \ CDOT 3 \ CDOT 10 – (-1) \ CDOT 9 \ CDOT 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60

Найдите нужные значения:

$ X_1 = \ FRAC (D_1) (D) = \ FRAC (- 296) (- 64) = 4 \ FRAC (5) (8)

$ X_2 = \ FRAC (D_1) (D) = \ FRAC (108) (-64) = – 1 \ FRAC (11) (16)

$ X_3 = \ FRAC (D_1) (D) = \ FRAC (-60) (-64) = \ FRAC (15) (16)

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почвенного сложения системы уравнений.Всем, кто заходил на сайт через эту страницу, рекомендуется ознакомиться с первой частью. Возможно, некоторым посетителям материал покажется слишком простым, но в процессе решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения

Математические задачи в целом. А теперь разберем правило кратера, а также решение системы линейных уравнений с использованием

Reverse matrix (Матричный метод).Все материалы представлены просто, подробно и понятно, практически все читатели смогут узнать, как решать системы вышеуказанными методами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь более простая система Вы можете решить школьным методом, методом убийства сложения!

Дело в том, что даже если иногда и бывает, такая задача встречается – решить систему двух линейных уравнений с двумя неизвестными по формулам краулера.Во-вторых, более простой пример поможет понять, как использовать правило краулера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом этапе вычисляем определитель, он называется главным определителем системы .

Метод Гаусса.

Если, система имеет одно решение, и для нахождения корней мы должны вычислить еще два детерминанта:
и

На практике вышеуказанные детерминанты также могут обозначаться латинскими буквами.

Корни уравнений находятся по формулам:
,

Пример 7.

Решите систему линейных уравнений

Решение : Видим, что коэффициенты уравнения достаточно большие, там присутствуют правые десятичные дроби с запятой.Запятая – довольно редкий гость в практических задачах по математике, я взял эту систему из эконометрической задачи.

Как решить такую систему? Можно попробовать выразить одну переменную через другую, но в этом случае обязательно получатся ужасные штаны, с которыми крайне неудобно работать, а оформление раствора будет смотреться просто ужасно. Вы можете умножить второе уравнение на 6 и выполнить вычитание почвы, но также получатся те же дроби.

Что делать? В таких случаях на помощь приходит формула кратера.

;

Ответ :,

Оба корня имеют бесконечные хвосты и находятся приблизительно, что вполне приемлемо (и даже обыкновенно) для задач эконометрики.

Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс. При использовании этого метода обязательный фрагмент дизайна задачи представляет собой следующий фрагмент: «Итак, система имеет единое решение» .В противном случае рецензент может наказать вас за неуважение к теореме Крамера.

Вовсе не будет лишним, что удобно проводить на калькуляторе: в левую часть каждого уравнения системы подставляем приблизительные значения. В итоге с небольшой ошибкой должны быть вывернуты числа, которые находятся в нужных частях.

Пример 8.

Ответ представить в обыкновенные неправильные дроби. Сделайте чек.

Это пример самостоятельного решения (пример чистого дизайна и ответа в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если, в системе бесконечно много решений или неприметных (не решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если система имеет одно решение и для нахождения корней необходимо вычислить еще три определителя:
“

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три-три» принципиально не отличается от случая «два-два», столбцы свободных членов последовательно «прогуливаются» слева направо по столбцам главного определителя.

Пример 9.

Решите систему по формулам искателя.

Решение : Разрешить систему в соответствии с формулами поискового робота.

Итак, у системы есть единственное решение.

Ответ :.

Собственно, и здесь комментировать больше нечего, ввиду того, что решение проходит по готовым формулам.Но есть пара замечаний.

Бывает, что в результате вычислений получаются «плохие» неинтерпретируемые дроби, например :.
Рекомендую следующий алгоритм лечения. Если под рукой нет компьютера, сделайте так:

1) Допускается ошибка в расчетах. Как только вы столкнулись с “плохой” фракцией, сразу нужно проверить, проводящий кондиционер правильно . Если условие переписывается без ошибок, то нужно пересчитать детерминанты, используя разложение на другой строке (столбце).

2) Если проверка ошибок не обнаружена, вероятно, это опечатка в условии присвоения. В этом случае спокойно и осторожно доводим задачу до конца, а потом обязательно проверяем И делаем это на доводке после решения. Конечно, проверка дробного ответа неприятна, но будет обезоруживающим аргументом для учителя, который очень любит ставить минус любому подобному бяке. Как работать с дробями подробно описано в ответе например 8.

Если под рукой есть компьютер, то воспользуйтесь автоматизированной программой, которую можно бесплатно скачать в самом начале урока.Кстати, выгоднее всего сразу использовать программу (еще до принятия решения), вы сразу увидите промежуточный шаг, на котором была допущена ошибка! Тот же калькулятор автоматически рассчитывает системное решение. матричный метод.

Замечание Второе. Время от времени встречаются системы, в уравнениях которых отсутствуют переменные, например:

Здесь в первом уравнении нет переменной, во втором – переменной. В таких случаях очень важно правильно и внимательно записать основной идентификатор:
– На месте отсутствующих переменных стоят нули.
Кстати, определители с нулями рационально раскрыть по строке (столбцу), которая равна нулю, так как вычислений заметно меньше.

Пример 10.

Решите систему по формулам искателя.

Это пример независимого решения (образец чистого дизайна и ответ в конце урока).

Для случая системы из 4 уравнений с 4 неизвестными формула Крамера записывается по аналогичным принципам.Живой пример можно посмотреть на уроке свойств определителя. Уменьшение порядка определителя – пять определителей 4-го порядка полностью твердые. Хотя задание уже вполне напоминает сапог профессора на груди у удачливого ученика.

Решение системы с матрицей возврата

Метод обратной матрицы, по сути, является частным случаем матричного уравнения (см. Пример № 3 указанного урока).

Чтобы изучить этот раздел, вы должны уметь раскрыть детерминанты, найти обратную матрицу и выполнить матричное умножение. Соответствующие ссылки будут даны в ходе объяснения.

Пример 11.

Решите систему матричным методом

Решение : Запишите систему в матричной форме:
, где

Посмотрите, пожалуйста, на систему уравнений и матрицу. По какому принципу писать элементы в матрице, думаю всем понятно.Единственный комментарий: если бы в уравнениях не было переменных, то в соответствующих местах матрицы нужно было бы ставить нули.

Обратную матрицу находим по формуле:
где – транспонированная матрица алгебраических сложений к соответствующим элементам матрицы.

Сначала разберемся с определителем:

Здесь определитель раскрывается в первой строке.

Внимание! Если, то матрица возврата не существует, и решить систему матричным методом невозможно.В этом случае система решается путем исключения неизвестного (метод Гаусса).

Теперь вам нужно вычислить 9 несовершеннолетних и записать их в Mind Matrix

Ссылка: Полезно знать значение индексов двойной подстановки в линейной алгебре. Первая цифра – это номер строки, в которой находится этот элемент. Вторая цифра – это номер столбца, в котором находится этот элемент:

То есть, индекс двойной подстановки указывает, что элемент находится в первой строке, третьем столбце и, например, элемент находится в 3 строках, 2 столбцах

Рассмотрим систему трех уравнений с тремя неизвестными

Используя определители 3-го порядка, решение такой системы может быть записано в той же форме, что и для системы двух уравнений, т.е.е.

(2,4)

, если 0. Здесь

Это правило Крамера решений системы трех линейных уравнений с тремя неизвестными .

Пример 2.3. Решите систему линейных уравнений, используя правило краулера:

Decision . Находим определитель основной матрицы системы

Начиная с 0, чтобы найти системное решение, вы можете применить правило искателя, но предварительно рассчитываются еще более трех определителей:

Проверка:

Следовательно, решение найдено правильно.

Правила Крамера, полученные для линейных систем 2-го и 3-го порядков, предполагают, что одни и те же правила могут быть сформулированы для обеих линейных систем любого порядка. Действительно имеет место

Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем матрицы основной системы (0) имеет одно и только одно решение, и это решение рассчитывается по формулам.

(2.5)

где  – определитель основной матрицы ,  и. – определитель матрицы , получено из основного, замена i. – в столбец столбца свободных членов .

Учтите, что если  = 0, то правило кравера не применяется. Это означает, что система либо не имеет решений, либо имеет бесконечно много решений.

При формулировании теоремы Крамера естественным образом возникает вопрос о вычислении определителей высшего порядка.

2.4. Детерминанты N-го порядка

Дополнительный минор М. мкДж. Элемент а. мкДж. называется определителем, полученным из этого путем скрещивания i. – I ряд. j. – в колонку. Алгебраическое дополнение A. iJ. Элемент а. мкДж. называется второстепенным этого элемента, взятого со знаком (-1) i. + Дж. . A. iJ. = (–1) i. + Дж. M. iJ..

Например, мы находим миноры и дополнения к алгебраическим элементам a. 23 I. а. 31 определитель

Получить



Используя концепцию алгебраического дополнения, можно сформулировать теорему о разложении определителя n. -o строка или столбец порядка .

Теорема 2.1. Определитель матрицы A. равен сумме произведений всех элементов определенной строки (или столбца) на их алгебраические сложения:

(2.6)

Эта теорема лежит в основе одного из основных методов вычисления определителей, т.н. метод понижения порядка . В результате разложения определителя п. -o порядок для любой строки или столбца, он получает N определителей ( n. -1) -go порядок. Чтобы таких определителей было меньше, желательно выбрать строку или столбец, в котором больше всего нулей. На практике формула определения определителя обычно записывается в виде:

тех.Алгебраические сложения записываются явно через миноры.

Примеры 2.4. Вычислите определители, предварительно положив их на любую строку или столбец. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранная строка или столбец будет обозначен стрелкой.



2.5. Основные свойства определителей

Разложив определитель для любой строки или столбца, мы получаем N определителей ( п. -1) -го порядка.Тогда каждый из этих определителей ( n. -1) -go order также может быть разложен на количество определителей ( n. -2) -go order. Продолжая этот процесс, можно перейти к определителям 1-го порядка, т.е. перед элементами матрицы, определитель которой вычисляется. Итак, для вычисления определителей 2-го порядка необходимо будет вычислить сумму двух членов, для определителей 3-го порядка – количество 6 компонентов, для определителей 4-го порядка – 24 члена.Количество компонентов будет резко увеличиваться с увеличением порядка определителя. Это означает, что вычисление идентификаторов очень высокого порядка становится довольно трудоемкой задачей, невыносимой даже для компьютера. Однако детерминанты можно вычислить по-разному, используя свойства детерминантов.

Свойство 1. . Определитель не изменится, если его поменять местами и столбцами, т.е. при транспонировании матрицы :

Это свойство указывает на равенство строк и столбцов определителя. Другими словами, любое утверждение о столбцах определителя верно для его строк и наоборот.

Имущество 2. . Определитель меняет знак при перестановке двух строк (столбцов).

Следствие . Если определитель имеет две идентичные строки (столбец), то он равен нулю.

Имущество 3. . Суммарный множитель всех элементов в любой строке (столбце) может быть достигнут знаком идентификатора. .

Например,

Следствие . Если все элементы определенной строки (столбца) определителя равны нулю, то сам определитель равен нулю .

Имущество 4. . Определитель не изменится, если к элементам одной строки (столбца) добавить элементы другой строки (столбца), умноженные на любое число .

Например,

Свойство 5. . Определитель работ матриц равен произведению определителей матриц:

2. Решение систем уравнений матричным методом (с использованием обратной матрицы).
3. Метод Гаусса для решения систем уравнений.

Метод Крамера.

Метод Craver используется для решения линейных алгебраических уравнений ( Slough ).

Формулы на примере системы двух уравнений с двумя переменными.
Дано: Решить Систему метода Крамера

Относительно переменных h. и з. .
Решение:
Находим определитель матрицы, составленной из коэффициентов системы вычисления определителей.:

Воспользуемся формулами краулера и находим значения переменных:
и.
Пример 1:
Решите систему уравнений:

относительно переменных h. и з. .
Решение:

Заменяем в этом определителе первый столбец столбца коэффициентов из правой части системы и находим его значение:

Проделаем аналогичное действие, заменив второй столбец в первом дефектном:

Применим формулы крамера и найдем значения переменных:
и.
Ответ:
Комментарий: Этот метод позволяет решать системы и большего измерения.

Комментарий: Если оказывается, что и на ноль делить нельзя, то говорят, что в системе нет единого решения. В этом случае у системы есть или бесконечно много решений, или решений нет вообще.

Пример 2. (бесконечное количество решений):

Решите систему уравнений:

относительно переменных h. и з. .
Решение:
Находим определитель матрицы, составленной из системных коэффициентов:

Решение систем подстановкой.

Первое из уравнений системы – равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Это означает, что остается только одно уравнение. Это уравнение связи между переменными.
Поступившие решения системы – это любые пары значений переменных, приведенные к равенству.
Общее решение Ошибки, подобные этой:
Частные решения могут быть определены путем выбора произвольного значения y и вычисления X на этом равенстве связи.

и др.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3. (решений нет, система непонятна):

Решаем систему уравнений:

Решение:
Находим определитель матрицы, составленной из системных коэффициентов:

Невозможно использовать формулы Крамера.Решаю эту систему заменой

Второе уравнение системы – равенство, неверно при любых значениях переменных (разумеется, поскольку -15 не равно 2). Если одно из уравнений системы не выполняется ни при каких значениях переменных, то вся система не имеет решений.
Ответ: Нет решений

Правило Крамера Решение систем уравнений. Линейные уравнения

Methods Cramer и Gaussa – некоторые из самых популярных решений Slough .Кроме того, в некоторых случаях целесообразно использовать специальные методы. Сессия близка, и теперь пора повторить или освоить их с нуля. Сегодня мы разбираемся с решением по методу Крамера. Ведь решение системы линейных уравнений методом Крамера – очень полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x. , в котором уравнения системы обращаются в тождества, называется решением решения, a. и б. – Реальные коэффициенты. Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме, либо выразив одну переменную через другую. Но переменных (ИС) в Славе может быть намного больше двух, и здесь этого мало для простых школьных манипуляций. Что делать? Например, решить Славу методом Крамера!

Итак, пусть система состоит из n. Уравнения S. n. неизвестно.

Такую систему можно переписать в матричном виде

Здесь A. – основная матрица системы, X. и Б. , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение метода Славы Крамера

Если определитель основной матрицы не равен нулю (матрица невырожденная), то система может быть решена по методу привода.

По методу Крамера решение находится по формулам:

Здесь дельта – определитель основной матрицы, а дельта X. N-NO – определитель, полученный из определителя основной матрицы заменой столбца N-число на столбец свободных членов.

В этом вся суть метода Крамера. Подставляя значения, найденные по приведенным выше формулам х. В желаемой системе убеждаемся в правильности (или наоборот) своего решения. Чтобы вы быстро уловили суть, приведем пример подробного решения метода Славы кратера:

Даже если вы не работаете с первого раза, не волнуйтесь! Немного практики, и вы начнете щелкать Славу как орехи. Более того, теперь совершенно необязательно трезветь над блокнотом, решая громоздкие вычисления и записывая стержень. Вы легко можете решить метод Славы Крамера онлайн, только подставив коэффициенты в готовом виде.Попробуйте онлайн-калькулятор решений по методу Крамера, например, на этом сайте.

И если система оказалась упорной и не сдаваться, вы всегда можете обратиться за помощью к нашим авторам, например, к. Будьте в системе хотя бы 100 неизвестных, мы обязательно решим ее верно и точно в срок!

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почвенного сложения системы уравнений. Всем, кто заходил на сайт через эту страницу, рекомендуется ознакомиться с первой частью.Возможно, некоторым посетителям материал покажется слишком простым, но в процессе решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А теперь разберем правило краулера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы представлены просто, подробно и понятно, практически все читатели смогут узнать, как решать системы вышеуказанными методами.

Дело в том, что даже если иногда и бывает, такая задача встречается – решить систему двух линейных уравнений с двумя неизвестными по формулам краулера. Во-вторых, более простой пример поможет понять, как использовать правило краулера для более сложного случая – системы трех уравнений с тремя неизвестными.

Рассмотрим систему уравнений

На первом этапе вычисляем определитель, он называется главным определителем системы .

Метод Гаусса.

Если, система имеет одно решение, и для нахождения корней мы должны вычислить еще два детерминанта:
и

На практике вышеуказанные детерминанты также могут обозначаться латинскими буквами.

Корни уравнений находятся по формулам:
,

Пример 7.

Решите систему линейных уравнений

Решение : Видим, что коэффициенты уравнения достаточно большие, в правой части стоят десятичные дроби с запятой. Запятая – довольно редкий гость в практических задачах по математике, я взял эту систему из эконометрической задачи.

Как решить такую систему? Можно попробовать выразить одну переменную через другую, но в этом случае обязательно получатся ужасные штаны, с которыми крайне неудобно работать, а оформление раствора будет смотреться просто ужасно.Вы можете умножить второе уравнение на 6 и выполнить вычитание почвы, но также получатся те же дроби.

Что делать? В таких случаях на помощь приходит формула кратера.

;

Ответ :,

Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс.При использовании этого метода обязательный фрагмент дизайна задачи представляет собой следующий фрагмент: «Итак, система имеет единое решение» . В противном случае рецензент может наказать вас за неуважение к теореме Крамера.

Пример 8.

Ответ представить в обыкновенные неправильные дроби. Сделайте чек.

Это пример самостоятельного решения (пример чистого дизайна и ответа в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если, в системе бесконечно много решений или неприметных (не решений).В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если система имеет одно решение и для нахождения корней необходимо вычислить еще три определителя:
“

И, наконец, ответ рассчитывается по формулам:

Пример 9.

Решите систему по формулам искателя.

Ответ :.

Бывает, что в результате вычислений получаются «плохие» неинтерпретируемые дроби, например:.
Рекомендую следующий алгоритм лечения. Если под рукой нет компьютера, сделайте так:

Если под рукой есть компьютер, то воспользуйтесь автоматизированной программой, которую можно бесплатно скачать в самом начале урока.Кстати, выгоднее всего сразу использовать программу (еще до принятия решения), вы сразу увидите промежуточный шаг, на котором была допущена ошибка! Этот же калькулятор автоматически рассчитывает решение решения матричным методом.

Пример 10.

Решите систему по формулам искателя.

Это пример независимого решения (образец чистого дизайна и ответ в конце урока).

Решение системы с матрицей возврата

Пример 11.

Решите систему матричным методом

Решение : Запишите систему в матричной форме:
, где

Сначала разберемся с определителем:

Здесь определитель раскрывается в первой строке.

Теперь вам нужно вычислить 9 несовершеннолетних и записать их в Mind Matrix

При том, что количество уравнений совпадает с количеством неизвестных с главным определителем, матрицей, которая не равна нулю, коэффициентов системы (для таких уравнений решение только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы отличен от нуля, это означает, что система должна иметь одно решение, и его можно найти в формулах Крамера :

где Δ – определитель матрицы системы ,

Δ I. – определитель матрицы системы, в которой вместо i. Столбец – это столбец правых частей.

Когда детерминант системы равен нулю, это означает, что система может стать совместной или зачаточной.

Этот метод обычно используется для небольших систем с объемными вычислениями и в тех случаях, когда необходимо определить 1 лунку из неизвестного. Сложность метода в том, что необходимо вычислить множество определителей.

Описание метода Крамера.

Имеется система уравнений:

Система трех уравнений может быть решена методом Крамера, который обсуждался выше для системы из двух уравнений.

Составим определитель коэффициентов неизвестных:

Это будет Система Определена .Когда D ≠ 0 Итак, система согласована. Теперь составим 3 дополнительных идентификатора:

Решаем систему крамерных формул ПО :

Примеры решения систем уравнений методом Крамера.

Пример 1. .

Система Dana:

Решив методом Крамера.

Для начала необходимо вычислить определитель матрицы системы:

Поскольку Δ ≠ 0, это означает, что согласно теореме Крамера система разрабатывается совместно и имеет одно решение.Вычислить дополнительные идентификаторы. Определитель δ 1 получается из определителя δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же образом получаем определитель δ 2 из определителя матрицы системы, заменяя второй столбец столбцом свободных коэффициентов:

Кратерный метод можно использовать при решении системы стольких линейных уравнений, как в каждом уравнении неизвестного. Если определитель системы не равен нулю, в решении можно использовать метод Крамера, если он равен нулю, нельзя. Кроме того, метод Крамера можно использовать при решении систем линейных уравнений, имеющих единственное решение.

Deterpetes

получается заменой коэффициентов на соответствующие неизвестные для свободных участников:

;

Теорема Крамера . Если определитель системы отличен от нуля, система линейных уравнений имеет одно единственное решение и неизвестное, равное отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путем замены коэффициентов одновременно неизвестными свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решите систему линейных уравнений:

По теореме крамера Имеем:

Итак, решение Решение (2):

Онлайн-калькулятор, решающий кратерный метод.

Три случая решения систем линейных уравнений

Как ясно теорем Крамера При решении системы линейных уравнений может быть три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместно и определена)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместного и неопределенного)

**,

тех.Коэффициенты при неизвестных и свободных членах пропорциональны.

Третий случай: в системе линейных решений нет

(система непонятна)

Примеры решения систем линейных уравнений по Крамеру

Пусть дано системе

На основе теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система определена. Чтобы найти ее решения, вычислим определители

По формулам краулера находим:

Итак (1; 0; -1) – единственное решение системы.

Пример 3. Решите систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам краулера находим:

Итак, решение системы (2; -1; 1).

Начало страницы

Продолжаем решать систему по методу Крамера вместе

Пример 6. Решите систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестном не равны нулю, следовательно, система неполная, то есть не имеет решений.

В задачах по системе линейных уравнений встречаются и такие, где встречаются и другие буквы, обозначаемые переменными. Эти буквы обозначают какое-то число, чаще всего действительное. На практике такие уравнения и системы уравнений приводят к задачам поиска общих свойств любых явлений и объектов. То есть вы изобрели какой-то новый материал или устройство, и для описания его свойств, как правило, вне зависимости от размера или количества экземпляра, вам нужно решить систему линейных уравнений, где вместо некоторых коэффициентов с переменными – буквы.Например, ходить не обязательно.

Пример 8. Решите систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Мы находим детерминанты в неизвестном

Пусть система линейных уравнений содержит столько уравнений, сколько независимых переменных, т.е.е. Имеет внешний вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов с независимыми переменными системы (1.5), называется главным определителем системы. Обозначим его греческой буквой D. Таким образом,

. (1,6)

Если в произвольном столбце основного идентификатора ( j. ) заменить столбец свободных членов системы (1.5), то можно получить еще n. Вспомогательные идентификаторы:

( дж. = 1, 2,…, п. ). (1,7)

Правило Крамера Решение квадратных систем линейных уравнений выглядит следующим образом. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и, более того, единственное решение, которое можно найти по формулам:

(1,8)

Пример 1.5. Метод Крамера решает систему уравнений

Вычислить главный определитель системы:

Поскольку D¹0, система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия с матрицами

1. Умножение матрицы на число. Операция умножения матрицы определяется следующим образом.

2. Для умножения матрицы на число все ее элементы умножаются на это число. Т.е.

. (1,9)

Пример 1.6. .

Добавление матриц.

Эта операция вводится только для матриц одного порядка.

Чтобы сложить две матрицы, необходимо добавить к элементам одной матрицы соответствующие элементы другой матрицы:

(1.10)
Операция расположения матриц обладает свойствами ассоциативности и коммутации.

Пример 1.7. .

Матричное умножение.

Если количество столбцов матрицы А совпадает с количеством строк матрицы В Для таких матриц вводится операция умножения:

Таким образом, при умножении матрицы А размерностью м. ´ н. на матрице В размерности н. ´ к. получаем матрицу ИЗ размерностью м. ´ к. . В этом случае элементы матрицы ИЗ рассчитываются по формулам:

Задача 1.8. Найдите, если возможно, работу матриц AB, и BA. :

Решение. 1) для того, чтобы найти работу AB , нужны строки матрицы A. умножить на столбцы матрицы B. :

2) Работа БА. нет, так как количество столбцов матрицы B. не совпадает с количеством строк матрицы A. .

Обратная матрица. Решение систем линейных уравнений матричным методом

Матрица A – 1 называется квадратной матрицей НО Если выполняется равенство:

, где через I. обозначает одну матрицу того же порядка, что и матрица , НО :

Для того чтобы квадратная матрица была обратной, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратные матрицы находятся по формуле:

, (1.13)

, где A ij. – Алгебраические дополнения к элементам a ij. Матрицы А (Обратите внимание, что алгебраические дополнения к матрице строк А расположены в возвращаемой матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Обратная матрица Найдем по формуле (1.13), которая соответствует случаю n. = 3 имеет вид:

Находим Дет. A. = | A. | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Поскольку определитель исходной матрицы отличен от нуля, обратная матрица существует.

1) Найдем алгебраические сложения A ij.:

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы располагаем в соответствующих столбцах.

Из полученных алгебраических сложений составим новую матрицу и разделим ее на определитель DET A. . Таким образом, мы получим обратную матрицу:

Квадратная система линейных уравнений с ненулевым главным определителем может быть решена с помощью обратной матрицы. Для этого система (1.5) записывается в матричном виде:

где

Умножая обе части равенства (1.14) на левую A – 1, мы получим системное решение:

От!

Таким образом, чтобы найти решение квадратной системы, нужно найти матрицу, обратную основной матрице системы, и умножить ее справа на столбец матрица-столбец.

Задача 1.10. Решите систему линейных уравнений

с использованием обратной матрицы.

Решение. Записываем систему в матричном виде:,

где – основная матрица системы, – столбец неизвестных и – столбец свободных элементов. Так как главный определитель системы, то основная матрица системы НО имеет обратную матрицу НО – единицу. Чтобы найти обратную матрицу А -1, вычислите алгебраические сложения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (и алгебраические прибавления к строкам матрицы НО запишем в соответствующие столбцы) и разделим ее на определитель D.Таким образом, мы нашли обратную матрицу:

Решение системы находится по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обычных жордановых исключений

Пусть произвольная (не обязательно квадратная) система линейных уравнений:

(1,16)

Требуется найти систему решений, т.е. такой набор переменных, который удовлетворяет всем равенствам системы (1.16). В целом система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. У него тоже может вообще не быть решений.

При решении таких задач используется метод исключения неизвестного, который еще называют методом обычных исключений Иордании из школьного курса. Суть этого метода состоит в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая одно уравнение к одному уравнению и на одну переменную меньше, чем исходная система.Запоминается уравнение, из которого выражается переменная.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. Например, в процессе исключения неизвестного некоторые уравнения могут превратиться в точные тождества. Такие уравнения из системы исключены, так как выполняются при любых значениях переменных и, следовательно, не влияют на решение системы. Если в процессе исключения неизвестного хотя бы одно уравнение сравняется, что невозможно выполнить ни при каких значениях переменных (например), то делаем вывод, что система не имеет решения.

Если при решении противоречивых уравнений не произошло, то из последнего уравнения в нем осталась одна из переменных. Если в последнем уравнении остается только одна переменная, она выражается числом. Если в последнем уравнении остаются другие переменные, они считаются параметрами, а переменная, выраженная через них, будет функцией этих параметров. Затем выполняется так называемое «обратное движение». Найденная переменная подставляется в последнее запомненное уравнение и находит вторую переменную.Затем две найденные переменные подставляются в предпоследнее сохраненное уравнение и находят третью переменную и так далее до первого запомненного уравнения.

В результате получаем решение системы. Это решение будет единственным, если найденные переменные будут числами. Если первая найденная переменная, а затем все остальные будут зависеть от параметров, у системы будет бесчисленное количество решений (каждый набор параметров соответствует новому решению). Формулы, позволяющие найти решение системы в зависимости от того, называется ли другой набор параметров общим решением системы.

Пример 1.11.

х.

Запомнив первое уравнение и приведя аналогичные члены во втором и третьем уравнениях, мы приходим к системе:

Экспресс г. Из второго уравнения и подставьте его в первое уравнение:

Запомним второе уравнение, а из первого найдем z. :

Верните референцию, стабильно найдем у. и z. . Для этого сначала подставляем последнее запомненное уравнение, где находим у. :

Затем подставляем и в первое запомненное уравнение Где находим x. :

Задача 1.12. Решите систему линейных уравнений, исключив неизвестные:

. (1.17)

Решение. Выразите переменную из первого уравнения x. и подставляем во второе и третье уравнение:

Мы помним первое уравнение

В этой системе первое и второе уравнение противоречат друг другу. Действительно, выражая г. , у меня получается, что 14 = 17. Это равенство не выполняется ни при каких значениях переменных x. , г. , I. з. . Следовательно, система (1.17) невычислима, т.е. не имеет решения.

Предлагаем читателям самостоятельно проверить, что основной детерминант исходной системы (1.17) равен нулю.

Рассмотрим систему, которая отличается от системы (1.17) всего одним свободным членом.

Задача 1.13. Решите систему линейных уравнений, исключив неизвестные:

. (1.18)

Решение. Как и раньше, выразим из первого уравнения переменную x. и подставляем во второе и третье уравнение:

Мы помним первое уравнение и представляем аналогичные члены во втором и третьем уравнениях.Заходим в систему:

Выражение г. из первого уравнения и подставив его во второе уравнение Получим тождество 14 = 14, которое не влияет на решение системы, а значит, его можно исключить из системы.

В последней запомненной переменной равенства z. Рассмотрим параметр. Мы верим. Тогда

Заменитель г. и z. в первом заученном равенстве и найти x.:

Таким образом, система (1.18) имеет бесчисленное множество решений, и любое решение можно найти по формулам (1.19), выбрав произвольное значение параметра t. :

(1.19)
Итак, системные решения, например, представляют собой следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. Д. Формулы (1.19) выражают общее (любое) решение задачи система (1.18).

В случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обычных жордановых исключений оказывается громоздким.Однако это не так. Достаточно вообще отказаться от алгоритма пересчета коэффициентов системы за один шаг и сделать решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
Где x J. – независимые (искомые) переменные, a ij. – Постоянные коэффициенты
( i =. 1, 2,…, м. ; j. = 1, 2,…, n.). Правые части системы y I. ( i = 1, 2,…, m. ) могут быть как переменными (зависимыми), так и постоянными. Требуется найти решения этой системы, исключив неизвестное.

Рассмотрим следующую операцию, которая в будущем будет называться «один шаг обычных исключений Иордании». Из произвольного ( r. -to) равенства выразить произвольную переменную ( x S. ) и заменить все остальные равенства. Конечно, это возможно только при RS. ¹ 0. Коэффициент а RS. Называется разрешающим (иногда направляющим или основным) элементом.

Получим следующую систему:

. (1,21)

Из с. – Равенство системы Ho (1.21) Позже мы найдем переменную x S. (После того, как найдены остальные переменные). с. – строка помню и позже из системы исключена. Оставшаяся система будет содержать одно уравнение, и на одну независимую переменную меньше, чем в исходной системе.

Вычислить коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с С. р. – уравнение, которое после выражения переменной x S. через оставшиеся переменные будет выглядеть так:

Таким образом, новые коэффициенты р. Уравнения рассчитываются по следующим формулам:

(1,23)
Рассчитайте новые коэффициенты b IJ. ( и. ¹ р. ) произвольное уравнение. Для этого подставляем произносимую в (1.22) переменную x S. в i. – Уравнение системы (1.20):

Приведя таких членов, получаем:

(1.24)
Из равенства (1.24) получаем формулы, по которым вычисляются остальные коэффициенты системы (1.21) (кроме r. – Уравнения):

(1.25)
Преобразование системы линейных уравнений методом обычных жордановых исключений производится в виде таблиц (матриц).Эти столы получили название «Иордан».

Итак, задача (1.20) ставится в соответствие со следующей таблицей Жорданова:

Таблица 1.1.

	х. 1	х. 2	…	x J.	…	x S.	…	x N.
г. 1 =	а. 11	а. 12		а. 1 Дж.		а. 1 с.		а. 1 н.
………………………………………………………………… ..
г. I. =	а I. 1	а I. 2		a ij.		а есть.		a IN.
………………………………………………………………… ..
г. р. =	а р. 1	а р. 2		а RJ.		А RS.		а РН.
………………………………………………………………….
y N. =	а м. 1	а м. 2		a MJ.		а MS.		а MN.

Жортанова Таблица 1.1 Содержит левую прописную колонку, в которой записаны правые части системы (1.20) и верхнюю строку заголовка, в которую записаны независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу НО на матрицу, состоящую из элементов верхней строки заголовка, то матрица состоит из элементов левого заглавного столбца.То есть, по сути, Таблица Жорданова представляет собой матричную форму записи системы линейных уравнений:. Система (1.21) соответствует следующей таблице Жорданова:

Таблица 1.2.

	х. 1	х. 2	…	x J.	…	г р.	…	x N.
г. 1 =	г. 11	г. 12		г. 1 Дж.		г. 1 С.		г. 1 Н.
………………………………………………………………… ..
y i =.	b I. 1	б I. 2		b IJ.		б.		б в
………………………………………………………………… ..
х s =.	б р. 1	б р. 2		b RJ.		б RS.		млрд р-н.
………………………………………………………………….
y n =	б М. 1	б м. 2		б МДж.		б МС.		млрд Mn.

Разрешающий элемент а РС. Выделим жирным шрифтом. Напомним, что для реализации одного шага исключения Джордана разрешающий элемент должен быть отличным от нуля. Строка таблицы, содержащая разрешающий элемент, называется строкой разрешения.Столбец, содержащий разрешающий элемент, называется столбцом разрешения. При переходе от этой таблицы к следующей таблице одна переменная ( x S. ) Из строки заголовка, таблица перемещается в левый заглавный столбец и, наоборот, в один из свободных членов системы ( y R. ) Из левого заглавного столбца таблицы перемещается в верхнюю строку заголовка.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) в таблицу (1.2), полученную из формул (1.23) и (1.25).

1. Элемент разрешения заменяется обратным числом:

2. Остальные разрешающие строковые элементы делятся на разрешающий элемент и меняют знак на противоположный:

3. Остальные элементы столбца разрешения разделены на разрешающий элемент:

4. Элементы, не попадающие в строку разрешения и разрешающую колонку, пересчитываются по формулам:

Последнюю формулу легко запомнить, если учесть, что элементы, составляющие дробь, находятся на пересечении i. – I. р. Замок I. j. – I. с. – к столбцам (разрешающая строка, разрешающая столбец и строку и столбец, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы Вы можете использовать следующую диаграмму:

-21 -26 -13 -37

Делая первый шаг с исключениями Jordan, вы можете выбрать любой элемент таблицы 1.3, расположенный в столбцах, в качестве элемента разрешения. х. 1,…, х. 5 (все указанные элементы не равны нулю). Не выбирайте только элемент разрешения в последнем столбце, потому что нужно найти независимые переменные x. 1,…, х. пять. Выберем, например, коэффициент 1 С переменной х. 3 В третьей строке таблицы 1.3 (жирным шрифтом выделен элемент разрешения). При переходе в Таблицу 1.4 переменная х. 3 из верхней строки заголовка меняется местами с константой левого столбца 0 (третья строка).В этом случае переменная x. 3 выражается в других переменных.

Линия х. 3 (таблица 1.4) можно запомнить, исключив из таблицы 1.4. Из таблицы 1.4 третий столбец с нулем также исключен в верхней строке заголовка. Дело в том, что независимо от коэффициентов этого столбца b I. 3 Все соответствующие члены каждого уравнения 0 · b I. 3 системы будут равны нулю. Следовательно, указанные коэффициенты не могут быть рассчитаны.Исключив одну переменную x. 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с освобожденной строкой x. 3). Выбрав в таблице 1.4 в качестве элемента разрешения б. 14 = -5, перейдите к Таблице 1.5. Таблица 1.5 запоминает первую строку и исключает ее из таблицы вместе с четвертым столбцом (с нулем вверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x. 1 = – 3 + 2 х. 5.

Последовательно подставляя переменные, уже найденные в сохраненных строках, находим оставшиеся переменные:

Таким образом, в системе есть бесчисленное множество решений. Переменная x. 5 можно задавать произвольные значения. Эта переменная действует как параметр x. 5 = т. Мы проверили системность системы и нашли ее общее решение:

X. 1 = – 3 + 2 т.

X. 2 = – 1 – 3 т.

Х. 3 = – 2 + 4 т. . (1,27)
х. 4 = 4 + 5 т.

х. 5 = т.

Придание параметра т. Различных значений, мы получаем бесчисленное количество решений исходной системы. Так, например, системным решением является следующий набор переменных (- 3; – 1; – 2; 4; 0).

Решение систем линейных уравнений с помощью Python Numpy

Библиотека Numpy может использоваться для выполнения множества математических / научных операций, таких как матричное кросс-произведение и скалярное произведение, поиск значений синуса и косинуса, преобразование Фурье и манипуляции с формой и т. Д.Слово Numpy – это сокращенное обозначение «Числовой Python».

В этой статье вы увидите, как решить систему линейных уравнений с помощью библиотеки Python Numpy.

Что такое система линейных уравнений?

Википедия определяет систему линейных уравнений как:

В математике система линейных уравнений (или линейная система) – это набор двух или более линейных уравнений, включающих один и тот же набор переменных.

Конечная цель решения системы линейных уравнений – найти значения неизвестных переменных.Вот пример системы линейных уравнений с двумя неизвестными переменными, x и y :

Уравнение 1:

  4x + 3y = 20
-5x + 9y = 26

Чтобы решить указанную выше систему линейных уравнений, нам нужно найти значения переменных x и y . Есть несколько способов решить такую систему, например, исключение переменных, правило Крамера, метод сокращения строк и матричное решение.В этой статье мы рассмотрим матричное решение.

В матричном решении решаемая система линейных уравнений представлена в виде матрицы AX = B . Например, мы можем представить Уравнение 1 в виде матрицы следующим образом:

  A = [[4 3]
     [-5 9]]

X = [[x]
     [y]]

B = [[20]
     [26]]

Чтобы найти значения переменных x и y в уравнении , нам нужно найти значения в матрице x .Для этого мы можем взять скалярное произведение обратной матрицы A и матрицы B , как показано ниже:

  X = инверсный (A) .B

Если вы не знакомы с тем, как найти обратную матрицу, взгляните на эту ссылку, чтобы понять, как вручную найти обратную матрицу. Чтобы понять матричное скалярное произведение, ознакомьтесь с этой статьей.

Решение системы линейных уравнений с помощью Numpy

Из предыдущего раздела мы знаем, что для решения системы линейных уравнений нам необходимо выполнить две операции: инверсию матрицы и скалярное произведение матрицы.Библиотека Numpy от Python поддерживает обе операции. Если вы еще не установили библиотеку Numpy, вы можете сделать это с помощью следующей команды pip :

  $ pip install numpy

Давайте теперь посмотрим, как решить систему линейных уравнений с помощью библиотеки Numpy.

Использование методов inv () и dot ()

Сначала мы найдем обратную матрицу A , которую мы определили в предыдущем разделе.

Давайте сначала создадим матрицу A на Python.Для создания матрицы можно использовать метод массива модуля Numpy. Матрицу можно рассматривать как список списков, где каждый список представляет собой строку.

В следующем скрипте мы создаем список с именем m_list , который дополнительно содержит два списка: [4,3] и [-5,9] . Эти списки представляют собой две строки в матрице A . Чтобы создать матрицу A с помощью Numpy, m_list передается методу массива , как показано ниже:

  импортировать numpy как np

m_list = [[4, 3], [-5, 9]]
А = np.массив (m_list)

Чтобы найти обратную матрицу, матрица передается методу linalg.inv () модуля Numpy:

  inv_A = np.linalg.inv (A)

печать (inv_A)

Следующий шаг – найти скалярное произведение между обратной матрицей A и матрицей B . Важно отметить, что скалярное произведение матриц возможно только между матрицами , если внутренние размеры матриц равны i.е. количество столбцов левой матрицы должно соответствовать количеству строк в правой матрице.

Чтобы найти скалярное произведение с помощью библиотеки Numpy, используется функция linalg.dot () . Следующий сценарий находит скалярное произведение между обратной матрицей A и матрицей B , которая является решением уравнения .

  B = np.array ([20, 26])
X = np.linalg.inv (A) .dot (B)

печать (X)

Выход:

Ознакомьтесь с нашим практическим практическим руководством по изучению Git с лучшими практиками, общепринятыми стандартами и включенной шпаргалкой.Прекратите гуглить команды Git и на самом деле выучите его!

  [2. 4.]

Здесь 2 и 4 – соответствующие значения для неизвестных x и y в уравнении . Для проверки, если вы подставите 2 вместо неизвестного x и 4 вместо неизвестного y в уравнении 4x + 3y , вы увидите, что результат будет 20.

Давайте теперь решим систему трех линейных уравнений, как показано ниже:

  4x + 3y + 2z = 25
-2x + 2y + 3z = -10
3x -5y + 2z = -4

Вышеупомянутое уравнение можно решить с помощью библиотеки Numpy следующим образом:

Уравнение 2:

  A = np.массив ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.array ([25, -10, -4])
X = np.linalg.inv (A) .dot (B)

печать (X)

В приведенном выше сценарии методы linalg.inv () и linalg.dot () объединены в цепочку. Переменная X содержит решение для уравнения 2 и печатается следующим образом:

  [5. 3. -2.]

Значения неизвестных x , y и z равны 5, 3 и -2 соответственно.Вы можете подставить эти значения в Equation 2 и проверить их правильность.

Использование метода detect ()

В двух предыдущих примерах мы использовали методы linalg.inv () и linalg.dot () , чтобы найти решение системы уравнений. Однако библиотека Numpy содержит метод linalg.solve () , который можно использовать для непосредственного поиска решения системы линейных уравнений:

  A = np.array ([[4, 3, 2], [-2, 2, 3], [3, -5, 2]])
B = np.массив ([25, -10, -4])
X2 = np.linalg.solve (A, B)

печать (X2)

Выход:

  [5. 3. -2.]

Вы можете видеть, что результат такой же, как и раньше.

Пример из реального мира

Давайте посмотрим, как систему линейных уравнений можно использовать для решения реальных задач.

Предположим, продавец фруктов продал 20 манго и 10 апельсинов за один день на общую сумму 350 долларов. На следующий день он продал 17 манго и 22 апельсина за 500 долларов. Если цены на фрукты оставались неизменными в оба дня, какова была цена одного манго и одного апельсина?

Эту задачу легко решить с помощью системы двух линейных уравнений.

Допустим, цена одного манго составляет x , а цена одного апельсина – y . Вышеупомянутую проблему можно преобразовать так:

  20x + 10y = 350
17x + 22y = 500

Решение указанной выше системы уравнений показано здесь:

  A = np.array ([[20, 10], [17, 22]])
B = np.array ([350, 500])
X = np.linalg.solve (A, B)

печать (X)

А вот результат:

  [10. 15.]

Выходные данные показывают, что цена одного манго составляет 10 долларов, а цена одного апельсина – 15 долларов.

Заключение

В статье объясняется, как решить систему линейных уравнений с помощью библиотеки Python Numpy. Вы можете использовать методы linalg.inv () и linalg.dot () в цепочке для решения системы линейных уравнений или просто использовать метод resolve () . Метод resolve () является предпочтительным.

Математическое определение исключения

От печи Веджвуда к столу

Телефонный номер наземной штаб-квартиры FedEx в лунном городке

Открытые ресурсы по алгебре местного колледжа.Факультет Portland Community College

Форумы по построению гитарных усилителей

Math Open Reference Home page. Оглавление. Куб, Конус, Сфера, Пирамида и т. Д. Обратите внимание, что все координаты, через которые проходят линии, являются решениями каждого уравнения. А координаты точки, в которой они пересекаются, (3,1) – это решение пары одновременных уравнений.

Проблемы с процессором Ps5

См. Полный список на byjus.com Это означает, что если вы начнете принимать лекарство с периодом полураспада 24 часа, через четыре дня или на пятый день, скорость приема препарата изменится. примерно равная скорость исключения.Если период полувыведения составляет 12 часов, вы достигнете устойчивого состояния в начале третьего дня (через 48 часов).

Количество Powerball лотереи Луизианы за прошлую ночь

16 июля 2019 · Диктаторы обычно используют военную силу или политический обман, чтобы получить власть, которую они поддерживают с помощью террора, принуждения и устранения основных гражданских свобод. Часто харизматичные по своей природе, диктаторы, как правило, используют такие методы, как газлайтинг и напыщенная массовая пропаганда, чтобы пробудить в себе культовые чувства поддержки и национализма…

Node js загрузить версию 6

Математическое определение исключения: исключение – стратегия решения систем уравнений, включающая исключение одной переменной.

В поисках ответов судьба 2 рунических таблички

Для любых двух конечных множеств A и B; (i) (A U B) ‘= A’ ∩ B ‘(что является законом объединения Де Моргана). (ii) (A ∩ B) ‘= A’ U B ‘(который является законом пересечения Де Моргана). Доказательство закона Де Моргана: (A U B) ‘= A’ ∩ B ‘. Пусть P = (A U B) ‘и Q = A’ ∩ B ‘.Пусть x – произвольный элемент из P, тогда x ∈ P ⇒ x ∈ (A U B) ‘. ⇒ x ∉ (A U B) 29 июня 2020 г. · Вы, наверное, все время слышите, что вам следует проверять свою математическую работу. Однако, как это сделать, может быть непонятно. Есть несколько способов проверить решение своей математической работы, в зависимости от того, выполняете ли вы базовый уровень …

Соглашение о запрете обхода недвижимости

Устранение – это метод, наиболее часто используемый компьютерным программным обеспечением для решения систем линейных уравнения.Он находит решение xto Ax = b всякий раз, когда матрица A обратима.

Когда будет перезагрузка rog rig 2020

Еще одно слово для устранения. Найдите другие способы произнести «исключение», а также связанные слова, антонимы и примеры фраз на Thesaurus.com, самом надежном бесплатном тезаурусе в мире.

Карта штатов США

23 сен 2020 · Метод исключения. Некоторые уравнения очень простые, и вы можете решить их, не прибегая к сложным методам, например y = 3 или x + 1 = 3. Однако некоторые уравнения сложны и требуют установленного метода нахождения решения.Метод исключения используется для решения уравнений, содержащих более одной переменной и более одного уравнения. В методе исключения вы исключаете одну из переменных, которую нужно решить для оставшейся.

Расширение Bloons td 4 взломано

Как решать линейные системы методом исключения. Если решение системы двух уравнений с помощью метода подстановки оказывается затруднительным или система включает дроби, метод исключения – ваш следующий лучший вариант. В методе исключения вы заставляете одну из переменных компенсировать себя, добавляя два уравнения.Метод исключения Чтобы решить одновременные уравнения, сделайте коэффициенты одной из переменных одинаковыми в обоих уравнениях. Затем либо сложите уравнения, либо вычтите одно уравнение из другого (в зависимости от того, что подходит), чтобы сформировать новое уравнение, которое содержит только одну переменную.

Vr скручивание кабеля

Веселая математическая практика! Совершенствуйте свои навыки с помощью бесплатных задач из «Решите одновременные уравнения с помощью исключения: задачи со словами» и тысяч других практических уроков.

Beatport top 100 techno

Текущее местоположение> Математические формулы> Линейная алгебра> Определение обратной матрицы Определение обратной матрицы Не забудьте попробовать наше бесплатное приложение – Agile Log, которое поможет вам отслеживать свое время потрачены на различные проекты и задачи, 🙂 Студенты извлекают пользу из простых примеров, демонстрирующих исключение параметра. Раздел 10.2. Исчисление с параметрическими кривыми: это стандартное представление. При взятии производных параметрических кривых студенты не должны путать dx / dt, dy / dt и dy / dx.Имейте в виду, что интегралы в этом разделе могут быть сложными.

Pdp xbox one controller manual

Jun 02, 2018 · Использование исключения Гаусса-Джордана для решения системы трех уравнений может потребовать много работы, но часто это не больше работы, чем решение напрямую, а во многих случаях – меньше работы. Если бы мы решали систему из четырех уравнений (чего мы не собираемся делать) в этот момент, исключение Гаусса-Жордана, по всей вероятности, потребовало бы меньше работы, чем если бы мы решали напрямую. Решите путем исключения проблемы со словами: графическое отображение задач со словами: подстановочные проблемы со словами: устранение Найдите количество решений для системы Study Island – практические программы PA -> алгебра 1 -> математика.Системы линейных уравнений

Mapbox gl draw line

Результат этого исключения, включая бухгалтерский учет: Теперь мне нужно удалить коэффициент в строке 3 столбца 2. Это можно сделать, умножив уравнение в строке 2 на 2/5 и вычитая его из уравнения в строке 3. На этом этапе мы завершили процедуру исключения Гаусса и путем обратной подстановки находим это. х 3 = 3/3 = 1. x 2 …

Twin turbo kit for 5.3 chevy

Метод исключения Метод исключения для решения систем уравнений также называется методом сложения.Чтобы решить систему уравнений методом исключения, мы преобразуем систему так, чтобы одна переменная «сокращалась». Пример 1: Решите систему уравнений путем исключения

Найдите все углы, которые удовлетворяют уравнению калькулятора

Отвалы фундамента Oci

Смысл в сидячем сне

Найдите все углы, 0 3 6 & lt; 350 ‘, которые удовлетворяют приведенному ниже уравнению с точностью до десятых долей градуса. sine: cos a: = ens a: Просмотрите пошаговое решение для: Вопрос. Полный список на калькуляторе.net

Посольство Австралии в США

Бесплатный калькулятор уравнений – решайте линейные, квадратные, полиномиальные, радикальные, экспоненциальные и логарифмические уравнения со всеми шагами. Введите любое уравнение, чтобы получить решение, шаги и график. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Используя этот веб-сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Следует попытаться ответить на ВСЕ вопросы. Отметки Найдите уравнение прямой, проходящей через точку (–1, 4), которая параллельна прямой с уравнением 3x –y + 2 = O.Относительно подходящей системы координат A и B находятся точки (–2, l, –1) и (1, 3, 2) соответственно. A, B и C являются коллинеарными точками, а точка C расположена так, что BC 2AB.

Рецепты Canlis

(iii) Не расширяя графики, укажите количество корней уравнения sin x = 1 + cos 2x для 0 ° x 360 °. [1] 8 (a) Решите для 0 x 2 уравнение 1 + 5cos 3x = 0, получив ответ в радианах с точностью до 2 знаков после запятой. [3] (b) Найдите все углы между 0º и 360º, такие, что sec y + 5tan y = 3cos y.[5] Бесплатный калькулятор уравнений – решайте линейные, квадратные, полиномиальные, радикальные, экспоненциальные и логарифмические уравнения со всеми шагами. Введите любое уравнение, чтобы получить решение, шаги и график. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.

Mimpi dikasih uang kertas 50 ribu togel

Найдите все углы Beta от 0 до 360 градусов, которые удовлетворяют уравнению sin Beta = (-0,46). Дайте свои ответы в градусах.Покажите свои решения в единичном круге. ** Грех отрицателен в квадрантах III и IV, поэтому мы должны найти опорные углы в этих двух квадрантах. Используя калькулятор, найдите величину, обратную греху (0,46): arcsin (.46) = 27,39º

Акции биотехнологий, которые можно купить менее чем за 5 долларов

Разделите каждую сторону на 2; затем извлеките квадратный корень из каждой стороны. Решите относительно 5 x, что представляет собой углы, удовлетворяющие уравнению в пределах одного поворота. Расширьте решения до пяти поворотов, добавив 2 π к каждому из исходных углов четыре раза.Разделите все члены на 5 и упростите. Первое, что вам нужно сделать, это переставить неравенство (уравнение) так, чтобы оно выглядело как ax 2 + bx + c = 0. Все, что вам нужно сделать, это переместить –2 влево. стороны стороны. Это дает нам x 2 + 4x + 3 = 0. Мы можем разложить это уравнение на две скобки: (x + 3) (x + 1) = 0

Рабочий лист прогрессивной эры pdf

Найти все углы Бета от 0 до 360 градусов которые удовлетворяют уравнению sin Beta = (-0,46). Дайте свои ответы в градусах. Покажите свои решения в единичном круге.** Грех отрицателен в квадрантах III и IV, поэтому мы должны найти опорные углы в этих двух квадрантах. Используя калькулятор, найдите значение, обратное sin (0,46): arcsin (.46) = 27,39º. Поскольку сумма измерений этих двух углов составляет 60 °, отсюда следует, что размер каждого угла составляет 30 °. Альтернативный подход заключается в использовании теоремы о внешнем угле с учетом того, что мера QPR равна сумме мер ∠QMR и ∠NRM. Поскольку оба угла равны, каждый из них имеет меру 30 °.

Intune запустите powershell от имени администратора

найдите углы Эйлера. Нахождение двух возможных углов для θ Начиная с R 31, мы находим R 31 = −sinθ. Это уравнение можно обратить, чтобы получить θ = −sin − 1 (R 31). (1) Однако следует проявлять осторожность при интерпретации этого уравнения. Поскольку sin (π− θ) = sin (θ), на самом деле существуют два различных значения (для R 31 6 = ± 1) θ, которые удовлетворяют уравнению 1.

Ifc 410 верхний боеприпас

1 сентября 2016 г. · Радиусы контакта для двух испытаний, необходимых для получения контактных углов по уравнению, были определены значения y, которые удовлетворяют уравнению, i.е. приравнивая к 0 вторую производную f (y) по y. Углы смачивания, рассчитанные с использованием описанной процедуры, равны 40 ° и 45,73 ° для испытания, прерванного через 2 … Найти все углы 0 ° << 360 °, которые удовлетворяют приведенному ниже уравнению, с точностью до десятой доли градус. csc? 0 + csc 0 - 2 = 0 Получите дополнительную помощь от Chegg Решите это с помощью нашего решателя задач предварительного расчета и калькулятора

Tubidy fm apk download

Кривая имеет уравнение y y x (- = −1 5 3). Найдите градиент в каждой точке кривой, где x = 3.Вопрос 7 (*** +) Острые углы α и β удовлетворяют соотношениям 7cot 6cot 12α α + = и 6tan 8 secβ β = + 2. a) Определите значение tan α и значение tan β. б) Ясно покажите, что tan () 1 2 α β + = -. (8) (6) (2) Решите тригонометрические уравнения с помощью калькулятора. Не все функции можно решить точно, используя только единичный круг. Когда мы должны решить уравнение с углом, отличным от одного из специальных углов, нам понадобится калькулятор. Убедитесь, что установлен правильный режим, градусы или радианы, в зависимости от заданных критериев…

Руководство к монитору Makvision

Найдите все углы, 0º <0 <360 °, которые удовлетворяют приведенному ниже уравнению, с точностью до десятых долей градуса. csc + csc 0 - 2 = 0 Получите дополнительную помощь от Чегга Получите помощь 1: 1 от опытных преподавателей Precalculus Решите это с помощью нашего инструмента для решения задач предварительного расчета и калькулятора

Ocarina of time rom hacking tools

После изучения данного материала выше, мы надеемся, что учащиеся поняли бы «Найти комплексное число z, удовлетворяющее данному квадратному уравнению».Помимо материалов, приведенных в этом разделе, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Discovery search mailbox exchange online

e · qua · ation (ĭ-kwā′zhən, -shən) n. 1. Акт или процесс приравнивания или приравнивания. 2. Состояние равенства. 3. Математика Заявление, подтверждающее равенство …

Рабочий лист по физике американских горок для средней школы

Mikrofill стремится к тому, чтобы все ее продукты были ориентированы на энергоэффективность и всегда удовлетворяли и превосходили самые строгие экологические требования.

Уровень k «Чтение плюс ответы»

Итак, 1 и – 1, 0,5 и – 0,5 и т. Д. – существует бесконечное количество значений для x, которые удовлетворяют этому неравенству. График этого неравенства будет иметь два замкнутых кружка, 4 и – 4. Расстояние между этими двумя значениями на числовой прямой окрашено в синий цвет, потому что все эти значения удовлетворяют уравнению.

Разжечь безлимитный против звука

IXL предлагает сотни математических навыков восьмого класса для изучения и изучения! Не уверен, где начать? Перейдите на свою персональную стену с рекомендациями, чтобы найти навык, который выглядит интересным, или выберите план навыков, который соответствует вашему учебнику, государственным стандартам или стандартизированному тесту.Вот список всех математических навыков, которые ученики получают в третьей средней школе! Эти навыки сгруппированы по категориям, и вы можете навести указатель мыши на любое название навыка, чтобы просмотреть навык. Чтобы начать заниматься, просто нажмите на любую ссылку. IXL будет отслеживать ваш результат, и вопросы будут автоматически усложняться по мере вашего улучшения!

Видео с вопросом: Использование детерминантов в правиле Крамера для нахождения системы уравнений

Стенограмма видео

В соответствии с правилом Крамера и с учетом того, что sub равно определителю матрицы два на два, три, семь, пять, два и △ sub равно определителю матрицы два на два отрицательных пять. , три, два, пять, запишите совместные уравнения системы.

В этом вопросе нам даны выражения для △ sub и △ sub в соответствии с правилом Крамера. Нам необходимо использовать эти выражения для определения одновременных уравнений системы, представленной этими двумя выражениями. И чтобы сделать это, мы начнем с того, что нам даны выражения для △ sub 𝑥 и △ sub. И они представлены в виде матриц два на два. Это означает, что в нашей системе будет только два неизвестных: 𝑥 и 𝑦.

Итак, давайте вспомним правило Крамера для двух неизвестных. Это говорит нам, если у нас есть два одновременных уравнения: плюс 𝑏𝑦 равно 𝑒 и 𝑐𝑥 плюс 𝑑𝑦 равно 𝑓, а определитель матрицы коэффициентов отличен от нуля – то есть △ равно определителю матрицы 𝑎, 𝑏, 𝑐 , 𝑑 – тогда 𝑥 равно △ sub 𝑥, деленному на, а 𝑦 равно △ sub 𝑦, деленному на △, является единственным решением системы линейных уравнений.

Что ж, стоит отметить, что sub 𝑥 – это определитель матрицы 𝑒, 𝑏, 𝑓, 𝑑, а △ 𝑦 – определитель матрицы 𝑎, 𝑒, 𝑐, 𝑓. Итак, чтобы найти выражение для sub 𝑥, мы берем наше выражение для и заменяем первый столбец в выражении для △, которое является коэффициентами 𝑥 в наших одновременных уравнениях, константами одновременных уравнений. Это 𝑒, 𝑓.

Итак, чтобы найти одновременные уравнения, нам нужно определить значения 𝑎, 𝑏, 𝑐, 𝑑, 𝑒 и 𝑓.И мы можем сделать это, используя данные выражения для △ sub 𝑥 и △ sub. Во-первых, используя △ sub 𝑥, мы можем определить значения 𝑒, 𝑏, 𝑓 и 𝑑. У нас равно трем, 𝑏 равно семи, 𝑓 равно пяти, а 𝑑 равно двум. Затем мы можем проделать тот же процесс для нашего выражения для △ sub. Это дает нам, что 𝑎 равно отрицательным пяти, 𝑒 равно трем, 𝑐 равно отрицательным двум, а 𝑓 равно пяти.

А теперь мы можем просто подставить эти значения в наши одновременные уравнения, что даст нам окончательный ответ.Система одновременных уравнений, заданная правилом Крамера для △ sub и △ sub, заданная в вопросе, отрицательна пять 𝑥 плюс семь 𝑦 равна трем, а отрицательная два 𝑥 плюс два 𝑦 равна пяти.