Решение системы уравнений методом гаусса онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса.

Метод Гаусса

Пользователи также искали:

метод гаусса 5 класс, метод гаусса – – это, метод гаусса, пример 3 порядка, метод гаусса пример 4 порядка, метод гаусса примеры с ответами, метод гаусса с++, метод гаусса задачи, метод гаусса – жордана, Гаусса, метод, гаусса, Метод, Метод Гаусса, примеры, порядка, пример, метод гаусса с, метод гаусса задачи, метод гаусса класс, задачи, жордана, ответами, класс, метод гаусса – – это, метод гаусса – жордана, метод гаусса примеры с ответами, метод гаусса пример 4 порядка, метод гаусса 5 класс, метод гаусса пример 3 порядка, метод гаусса пример порядка, метод гаусса, методы решения слау.

метод гаусса,

Метод гаусса онлайн. Решение систем линейных уравнений методом жордана-гаусса

Записывается в виде расширенной матрицы, т.е. в столбец свободных членов помещается в одну матрицу с коэффициентами неизвестных. Аалгоритм заключается в приведении исходной матрицы, характеризующей систему линейных уравнений, к единичной путем эквивалентных преобразований (домножения строки матрицы на константу и сложения с другой строкой матрицы). В качестве константы используется 1/a[i][i] , т.е. число, обратное по отношению к элементу диагонали. Естественно, в ряде случаев возникают проблемы, связанные с делением на ноль, которые решаются перестановкой строк и столбцов:

Весь алгоритм можно представить 10 пунктами:

В качестве опорной выбираем первую строку матрицы.

Если элемент опорной строки, индекс которого равен номеру опорной строки, равен нулю, то меняем всю опорную строку на первую попавшуюся строку снизу, в столбце которого нет нуля.

Все элементы опорной строки делим на первый слева ненулевой элемент этой строки.

Из оставшихся снизу строк вычитают опорную строку, умноженную на элемент, индекс которого равен номеру опорной строки.

В качестве опорной строки выбираем следующую строку.

Повторяем действия 2 – 5 пока номер опорной строки не превысит число строк.

В качестве опорной выбираем последнюю строку.

Вычитаем из каждой строки выше опорную строку, умноженную на элемент этой строки с индексом равным номеру опорной строки.

В качестве опорной строки выбираем строку выше.

Повторяем 8 – 9 пока номер опорной строки не станет меньше номера первой строки.

Пусть имеется система уравнений:

Запишем расширенную матрицу системы:

и выполним элементарные преобразования ее строк.

Для этого умножим первую строку на 1 и вычитаем из второй строки; затем умножим первую строку на 2 и вычтем из третьей строки.

В результате мы исключим переменную x 1 из всех уравнений, кроме первого. Получим:

Теперь вычтем из строки 3 строку 2, умноженную на 3:

Теперь вычитаем из 1 строки сначала 3 строку, а затем 2 строку:

После преобразований получаем систему уравнений:

Из этого следует, что система уравнений имеет следующее решение:

x1 = 1, x2 = 3 , x3 = -1

В качестве примера решим систему уравнений, представленную в виде матрицы (Таблица 1), методом Гаусса – Жордана.

Делим первую строку на 3 (элемент первой строки, расположенный на главной диагонали), получим:

Умножаем первую строку на 1 и вычитаем из второй строки. Умножаем первую строку на 6 и вычитаем из третьей строки. Получим:

В первом столбце все элементы кроме диагонального равны нулю, займемся вторым столбцом, для этого выберем вторую строку в качестве опорной. Вторая Делим ее на 17/3:

Умножаем строку 2 на -6 и вычитаем из третьей строки:

Теперь третья строка – опорная, делим ее на -33/17:

Умножаем опорную строку на 3/17 и вычитаем ее из второй. Умножаем третью строку на 1 и вычитаем ее из первой

Получена треугольная матрица, начинается обратный ход алгоритма (во время которого получим единичную матрицу). Вторая строка становится опорной. Умножаем третью строку на 4/3 и вычитаем ее из первой:

Последний столбец матрицы – решение системы уравнений.

Каждой системе линейных уравнений поставим в соответствие расширенную матрицу , полученную присоединением к матрице А столбца свободных членов:

Метод Жордана–Гаусса применяется для решения системы m линейных уравнений с n неизвестными вида:

Данный метод заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе уравнений с матрицей определенного вида.

Над строками расширенной матрицы осуществляем следующие элементарные преобразования:

1. перестановка двух строк ;

2. умножение строки на любое число, отличное от нуля ;

3.

прибавление к одной строке другой строки, умноженной на некоторое число ;

4. отбрасывание нулевой строки (столбца) .

Пример 2.11. Решить методом Жордана–Гаусса системы линейных уравнений:

а ) Х 1 + Х 2 + 2Х 3 = -1

2Х 1 – Х 2 + 2Х 3 = -4

4Х 1 + Х 2 + 4Х 3 = -2

Решение: Составим расширенную матрицу:

Итерация 1

В качестве направляющего элемента выбираем элемент . Преобразуем первый столбец в единичный. Для этого ко второй и третьей строкам прибавляем первую строку, соответственно умноженную на (-2) и (-4). Получим матрицу:

На этом первая итерация закончена.

Итерация 2

Выбираем направляющий элемент . Так как , то делим вторую строку на -3. Затем умножаем вторую строку соответственно на (-1) и на 3 и складываем соответственно с первой и третьей строками. Получим матрицу

Итерация 3

Выбираем направляющий элемент . Так как , то делим третью строку на (-2). Преобразуем третий столбец в единичный. Для этого умножаем третью строку соответственно на (-4/3) и на (-2/3) и складываем соответственно с первой и второй строками. Получим матрицу

откуда Х 1 = 1, Х 2 = 2, Х 3 = -2.

Закончив решение, на этапе обучения необходимо выполнять проверку, подставив найденные значения в исходную систему, которая при этом должна обратиться в верные равенства.

б ) Х 1 – Х 2 + Х 3 – Х 4 = 4

Х 1 + Х 2 + 2Х 3 +3Х 4 = 8

2Х 1 +4Х 2 + 5Х 3 +10Х 4 = 20

2Х 1 – 4Х 2 + Х 3 – 6Х 4 = 4

Решение: Расширенная матрица имеет вид:

Применяя элементарные преобразования, получим:

Исходная система эквивалентна следующей системе уравнений:

Х 1 – 3Х 2 – 5Х 4 = 0

2Х 2 + Х 3 + 4Х 4 = 4

Последние две строки матрицы A (2) являются линейно зависимыми.

Определение. Строки матрицы e 1 , e 2 ,…, e m называются линейно зависимыми

, если существуют такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

где 0 =(0, 0…0). Строки матрицы являются линейно независимыми , когда комбинация этих строк равна нулю тогда и только тогда, когда все коэффициенты равны нулю.

В линейной алгебре очень важно понятие ранга матрицы , т.к. оно играет очень большое значение при решении систем линейных уравнений.

Теорема 2.3 (о ранге матрицы). Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы).

Ранг матрицы A (2) равен 2, т.к. в ней максимальное число линейно независимых строк равно 2 (это первые две строки матрицы).

Теорема 2.4 (Кронекера–Капели). Система линейных уравнений совместна и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

1. Если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система имеет единственное решение.

2. Если ранг матрицы системы меньше числа переменных, т. е. r

В данном случае система имеет 4 переменных, а её ранг равен 2, следовательно, она имеет бесконечное множество решений.

Определение. Пусть r n , r переменных x 1 , x 2 ,…, x r называются базисными , если определитель матрицы из коэффициентов при них (базисный минор ) отличен от нуля. Остальные n – r переменных называются свободными .

Определение. Решение системы, в котором все n – r свободных переменных равны нулю, называется базисным .

Совместная система m линейных уравнений с n переменными (m ) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее , где .

В нашем случае , т.е. система имеет не более 6 базисных решений.

Общее решение имеет вид:

Х 1 = 3Х 2 +5Х 4

Х 3 = 4 – 2Х 2 – 4Х 4

Найдем базисные решения. Для этого полагаем Х 2 = 0, Х 4 = 0, тогда Х 1 =0, Х 3 = 4. Базисное решение имеет вид: (0, 0, 4, 0).

Получим другое базисное решение. Для этого в качестве свободных неизвестных примем Х 3 и Х 4 . Выразим неизвестные Х 1 и Х 2 через неизвестные Х 3 и Х 4:

Х 1 = 6 – 3/2Х 2 – Х 4

Х 2 = 2 – 1/2Х 3 – 2Х 4 .

Тогда базисное решение имеет вид: (6, 2, 0, 0).

Пример 2.12. Решить систему:

X 1 + 2X 2 – X 3 = 7

2X 1 – 3X 2 + X 3 = 3

4X 1 + X 2 – X 3 = 16

Решение.Преобразуем расширенную матрицу системы

Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0 = –1, следовательно, данная система несовместна. Данный вывод можно также получить, если заметить, что ранг матрицы системы равен 2, тогда как ранг расширенной матрицы системы равен 3.

Метод Гаусса-Жордана предназначен для решения систем линейных алгебраических уравнений (СЛАУ). Он является модификацией метода Гаусса . Если метод Гаусса осуществляется в два этапа (прямой ход и обратный) то метод Гаусса-Жордана позволяет решить систему в один этап. Подробности и непосредственная схема применения метода Гаусса-Жордана описаны в примерах.

Во всех примерах $A$ обозначает матрицу системы, $\widetilde{A}$ – расширенную матрицу системы. О матричной форме записи СЛАУ можно прочесть .

Пример №1

Решить СЛАУ $ \left\{ \begin{aligned} & 4x_1-7x_2+8x_3=-23;\\ & 2x_1-4x_2+5x_3=-13;\\ & -3x_1+11x_2+x_3=16. \end{aligned} \right.$ методом Гаусса-Жордана.

Давайте перейдём от последней полученной нами матрице к системе:

$$ \left\{ \begin{aligned} & 0\cdot x_1+1\cdot x_2+0\cdot x_3=1;\\ & 1\cdot x_1+0\cdot x_2+0\cdot x_3=-2;\\ & 0\cdot x_1+0\cdot x_2+1\cdot x_3=-1. \end{aligned} \right. $$

Упрощая полученную систему, имеем:

$$ \left\{ \begin{aligned} & x_2=1;\\ & x_1=-2;\\ & x_3=-1. \end{aligned} \right. $$

Полное решение без пояснений выглядит так:

Хоть этот способ выбора разрешающих элементов вполне допустим, но предпочтительнее выбирать в качестве разрешающих элементов диагональные элементы матрицы системы. Мы рассмотрим этот способ ниже.

Выбор разрешающих элементов на главной диагонали матрицы системы.

Так как этот способ решения полностью аналогичен предыдущему (за исключением выбора разрешающих элементов), то подробные пояснения пропустим. Принцип выбора разрешающих элементов прост: в первом столбце выбираем элемент первой строки, во втором столбце берём элемент второй строки, в третьем столбце – элемент третьей строки и так далее.

Первый шаг

В первом столбце выбираем элемент первой строки, т.е. в качестве разрешающего имеем элемент 4. Понимаю, что выбор числа 2 кажется более предпочтительным, так как это число всё-таки меньше, нежели 4. Для того, чтобы число 2 в первом столбце переместилось на первое место, поменяем местами первую и вторую строки:

$$ \left(\begin{array} {ccc|c} 4 & -7 & 8 & -23\\ 2 & -4& 5 & -13 \\ -3 & 11 & 1 & 16 \end{array} \right)\rightarrow \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) $$

Итак, разрешающий элемент представлен числом 2. Точно так же, как и ранее, разделим первую строку на 2, а затем обнулим элементы первого столбца:

$$ \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} I:2 \\\phantom{0} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2 \\4 & -7 & 8 & -23\\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} \phantom{0} \\ II-4\cdot I\\ III+3\cdot I \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right). $$

Второй шаг

На втором шаге требуется обнулить элементы второго столбца. В качестве разрешающего элемента выбираем элемент второй строки, т.е. 1. Разрешающий элемент уже равен единице, поэтому никаких строк менять местами не будем. Кстати сказать, если бы мы захотели поменять местами строки, то первую строку трогать не стали бы, так как она уже была использована на первом шаге. А вот вторую и третью строки запросто можно менять местами. Однако, повторюсь, в данной ситуации менять местами строки не нужно, ибо разрешающий элемент уже оптимален – он равен единице.

$$ \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right) \begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-5\cdot II \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right). $$

Второй шаг окончен. Переходим к третьему шагу.

Третий шаг

На третьем шаге требуется обнулить элементы третьего столбца. В качестве разрешающего элемента выбираем элемент третьей строки, т.е. 37/2. Разделим элементы третьей строки на 37/2 (чтобы разрешающий элемент стал равен 1), а затем обнулим соответствующие элементы третьего столбца:

$$ \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ III:\frac{37}{2} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 1 & -1 \end{array} \right) \begin{array} {l} I+2\cdot III\\II+3/2\cdot III\\ \phantom{0} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & -1 \end{array} \right). $$

Ответ получен: $x_1=-2$, $x_2=1$, $x_3=-1$. Полное решение без пояснений выглядит так:

Все остальные примеры на этой странице будут решены именно вторым способом: в качестве разрешающих будем выбирать диагональные элементы матрицы системы.

Ответ : $x_1=-2$, $x_2=1$, $x_3=-1$.

Пример №2

Решить СЛАУ $ \left\{ \begin{aligned} & 3x_1+x_2+2x_3+5x_4=-6;\\ & 3x_1+x_2+2x_4=-10;\\ & 6x_1+4x_2+11x_3+11x_4=-27;\\ & -3x_1-2x_2-2x_3-10x_4=1. \end{aligned} \right.$ методом Гаусса-Жордана.

Запишем расширенную матрицу данной системы : $\widetilde{A}=\left(\begin{array} {cccc|c} 3 & 1 & 2 & 5 & -6\\ 3 & 1& 0 & 2 & -10 \\ 6 & 4 & 11 & 11 & -27 \\ -3 & -2 & -2 & -10 & 1 \end{array} \right)$.

В качестве разрешающих элементов станем выбирать диагональные элементы матрицы системы: на первом шаге возьмём элемент первой строки, на втором шаге элемент второй строки и так далее.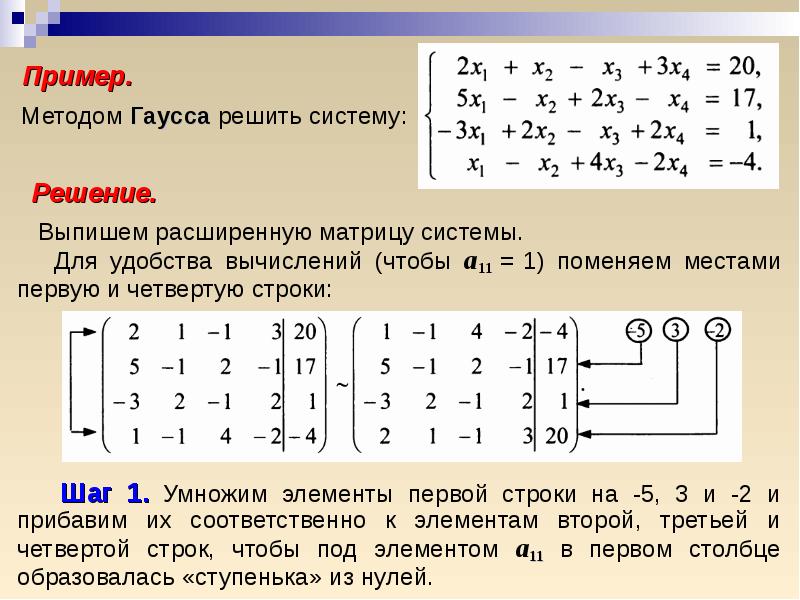

Первый шаг

Нам нужно обнулить соответствующие элементы первого столбца. В качестве разрешающего элемента возьмём элемент первой строки, т.е. 3. Соответственно первую строку придётся разделить на 3, чтобы разрешающий элемент стал равен единице. А затем обнулить все элементы первого столбца, кроме разрешающего:

$$ \left(\begin{array}{cccc|c} 3 & 1 & 2 & 5 & -6\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\\ -3 & -2 & -2 & -10 & 1\end{array}\right) \begin{array} {l} I:3\\ \phantom{0}\\\phantom{0}\\\phantom{0}\end{array} \rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\\ -3 & -2 & -2 & -10 & 1\end{array}\right) \begin{array} {l} \phantom{0}\\ II-3\cdot I\\III-6\cdot I\\IV+3\cdot I\end{array} \rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end{array}\right). $$

Второй шаг

Переходим к обнулению соответствующих элементов второго столбца. В качестве разрешающего элемента мы уславливались взять элемент второй строки, но сделать этого мы не в силах, так как нужный элемент равен нулю. Вывод: будем менять местами строки. Первую строку трогать нельзя, так как она уже использовалась на первом шаге. Выбор небогат: или меняем местами вторую и третью строки, или же меняем местами четвёртую и вторую. Так как в четвёртой строке наличествует (-1), то пусть в “обмене” поучавствует именно четвёртая строка. Итак, меняем местами вторую и четвёртую строки:

$$ \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end{array}\right)\rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) $$

Вот теперь всё в норме: разрешающий элемент равен (-1). Бывает, кстати, что смена мест строк невозможна, но это обговорим в следующем примере №3. А пока что делим вторую строку на (-1), а затем обнуляем элементы второго столбца. Обратите внимание, что во втором столбце элемент, расположенный в четвёртой строке, уже равен нулю, поэтому четвёртую строку трогать не будем.

$$ \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \begin{array} {l} \phantom{0}\\II:(-1) \\\phantom{0}\\\phantom{0}\end{array} \rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 1 & 0 & 5 & 5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \begin{array} {l} I-1/3\cdot II\\ \phantom{0} \\III-2\cdot II\\\phantom{0}\end{array} \rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end{array}\right). $$

Третий шаг

Приступаем к обработке третьего столбца. В качестве разрешающего элемента мы условились брать диагональные элементы матрицы системы. Для третьего шага это означает выбор элемента, расположенного в третьей строке. Однако если мы просто возьмём элемент 7 в качестве разрешающего, то всю третью строку придётся делить на 7. Мне кажется, что разделить на (-2) попроще. Поэтому поменяем местами третью и четвёртую строки, и тогда разрешающим элементом станет (-2):

$$ \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end{array}\right) $$

Разрешающий элемент – (-2). Делим третью строку на (-2) и обнуляем соответствующие элементы третьего столбца:

$$ \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\III:(-2)\\\phantom{0}\end{array}\rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 7 & -9 & -25\end{array}\right) \begin{array} {l} I-2/3\cdot III\\ \phantom{0} \\ \phantom{0}\\IV-7\cdot III\end{array}\rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & -39\end{array}\right). $$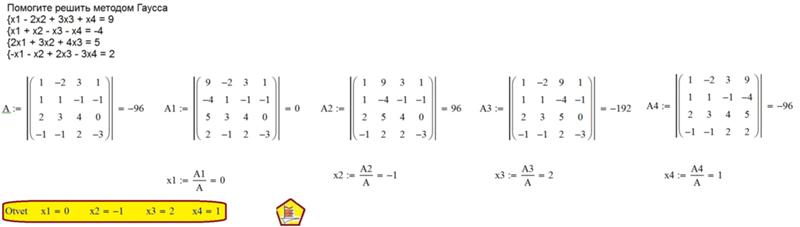

Четвёртый шаг

Переходим к обнулению четвёртого столбца. Разрешающий элемент расположен в четвёртой строке и равен числу $-\frac{39}{2}$.

$$ \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & -39\end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\ \phantom{0}\\IV:\left(-\frac{39}{2}\right) \end{array}\rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & 1 & 2\end{array}\right) \begin{array} {l} I+IV\\ II-5\cdot IV \\ III-3/2\cdot IV \\ \phantom{0} \end{array}\rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 0 & 0 & -3\\ 0 & 1 & 0 & 0 & -5\\ 0 & 0 & 1 & 0 & -1\\ 0 & 0 & 0 & 1 & 2\end{array}\right). $$

Решение окончено. Ответ таков: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$. Полное решение без пояснений:

Ответ : $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.

Пример №3

Решить СЛАУ $\left\{\begin{aligned} & x_1-2x_2+3x_3+4x_5=-5;\\ & 2x_1+x_2+5x_3+2x_4+9x_5=-3;\\ & 3x_1+4x_2+7x_3+4x_4+14x_5=-1;\\ & 2x_1-4x_2+6x_3+11x_5=2;\\ & -2x_1+14x_2-8x_3+4x_4-7x_5=20;\\ & -4x_1-7x_2-9x_3-6x_4-21x_5=-9. \end{aligned}\right.$ методом Гаусса-Жордана. Если система является неопределённой, указать базисное решение.

Подобные примеры разбираются в теме “Общее и базисное решения СЛАУ” . Во второй части упомянутой темы данный пример решён с помощью метод Гаусса . Мы же решим его с помощью метода Гаусса-Жордана. Пошагово разбивать решение не станем, так как это уже было сделано в предыдущих примерах.

$$ \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 4 & -5\\ 2 & 1 & 5 & 2 & 9 & -3\\ 3 & 4 & 7 & 4 & 14 & -1\\ 2 & -4 & 6 & 0 & 11 & 2\\ -2 & 14 & -8 & 4 & -7 & 20\\ -4 & -7 & -9 & -6 & -21 & -9 \end{array}\right) \begin{array} {l} \phantom{0} \\ II-2\cdot I\\ III-3\cdot I\\ IV-2\cdot I\\ V+2\cdot I\\VI+4\cdot I \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 4 & -5\\ 0 & 5 & -1 & 2 & 1 & 7\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end{array}\right) \begin{array} {l} \phantom{0} \\ II:5 \\ \phantom{0}\\ \phantom{0}\\ \phantom{0} \\ \phantom{0}\end{array} \rightarrow \\ \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 4 & -5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end{array}\right) \begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-10\cdot II\\ IV:3\\ V-10\cdot II\\VI+15\cdot II \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right). $$

Полагаю, что одно из сделанных преобразований всё-таки требует пояснения: $IV:3$. Все элементы четвёртой строки нацело делились на три, поэтому сугубо из соображений упрощения мы разделили все элементы этой строки на три. Третья строка в преобразованной матрице стала нулевой. Вычеркнем нулевую строку:

$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) $$

Нам пора переходить к третьему шагу, на котором должны быть обнулены элементы третьего столбца. Однако диагональный элемент (третья строка) равен нулю. И смена мест строк ничего не даст. Первую и вторую строки мы уже использовали, поэтому их трогать мы не можем. А четвёртую и пятую строки трогать нет смысла, ибо проблема равенства нулю разрешающего элемента никуда не денется.

В этой ситуации проблема решается крайне незамысловато. Мы не можем обработать третий столбец? Хорошо, перейдём к четвёртому. Может, в четвёртом столбце элемент третьей строки будет не равен нулю. Однако четвёртый столбец “болеет” той же проблемой, что и третий. Элемент третьей строки в четвёртом столбце равен нулю. И смена мест строк опять-таки ничего не даст. Четвёртый столбец тоже не можем обработать? Ладно, перейдём к пятому. А вот в пятом столбце элемент третьей строки очень даже не равен нулю. Он равен единице, что довольно-таки хорошо. Итак, разрешающий элемент в пятом столбце равен 1. Разрешающий элемент выбран, поэтому осуществим дальшейшие преобразования метода Гаусса-Жордана:

$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) \begin{array} {l} I-22/5\cdot III \\ II-1/5\cdot III \\ \phantom{0}\\ IV+III\\ V+2\cdot III \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \rightarrow \\ \rightarrow\left|\text{Удаляем нулевые строки}\right|\rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)$$

Мы привели матрицу системы и расширенную матрицу системы к ступенчатому виду. Ранги обеих матриц равны $r=3$, т.е. надо выбрать 3 базисных переменных. Количество неизвестных $n=5$, поэтому нужно выбрать $n-r=2$ свободных переменных. Так как $r

На “ступеньках” стоят элементы из столбцов №1, №2, №5. Следовательно, базисными будут переменные $x_1$, $x_2$, $x_5$. Свободными переменными, соответственно, будут $x_3$, $x_4$. Столбцы №3 и №4, соответствующие свободным переменным, перенесём за черту, при этом, конечно, не забыв сменить им знаки.

$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)\rightarrow \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & -99/5 & -13/5 & -4/5\\ 0 & 1 & 0 & 3/5 & 1/5 & -2/5\\ 0 & 0 & 1 & 4 & 0 & 0\end{array}\right). $$

Из последней матрицы получим общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$. Базисное решение найдём, приняв свободные переменные равными нулю, т.е. $x_3=0$, $x_4=0$:

$$ \left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right. $$

Задача решена, осталось лишь записать ответ.

Ответ : Общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$, базисное решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right.$.

4. Метод Жордана – Гаусса.

Схема с выбором главного элемента состоит в том, что требование неравенства нулю диагональных элементов akk, на которые происходит деление в процессе исключения, заменятся более жестким: из всех элементов К-го столба выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента акк. Выбор главного элемента и связанная с ним перестановка строк необходимы в тех случаях, когда на каком-либо i-ом шаге акк=0 либо же акк очень мало по остальными элементами i- го столбца: при делении на такое «малое» акк будут получаться большие числа с большими абсолютными погрешностями, в результате чего решение может сильно исказиться.

Ниже излагается алгоритм полного исключения неизвестных или метод Жордана – Гаусса. Суть метода состоит в том, что, рассмотрев первое уравнение, в нем неизвестное с коеффициэнтом, отличным от нуля (в дальнейшем разрешающий элемент), и разделив первое уравнение на этот коэффициент, с помощью первого уравнения исключают это неизвестное из всех уравнений, кроме первого. Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго исключают другие неизвестные из всех уравнений, кроме второго и т.д., т.е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжается до тех пор, пока не будут использованы все уравнения.

Как известно, системы линейных алгебраических уравнений могут имеет одно решение, множество решений или системы несовместны. При элементарных преобразованиях элементов матрицы системы эти случаи выявляются в следующем:

1. В процессе исключений левая часть I –го уравнения системы обращается в нуль, а правая часть равна некоторому числу, отличному от нуля. т.е. 02+=bc0.

Это означает, что система не имеет решений, так как I – му уравнению не могут удовлетворять никакие значения неизвестных;

2. Левая и правая части I – го уравнения обращаются в нуль. Это означает, что I – ое уравнение является линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтому оно может быть отброшено. В системе количество неизвестных больше количества уравнений и, следовательно, такая система имеет множество решений;

3. После того как все уравнения использованы для исключения неизвестных получено решение системы.

Таким образом, конечной целью преобразований Жордана-Гаусса является получение из заданной линейной системы

a11x1 + a12x2 + … + a1nxn = b1,n+1

a21x1 + a22x2 + … + a2nxn = b2,n+1

am1x1 + am2x2 + … + amnxn = bm. n+1

Здесь x1, x2, …, xn – неизвестные, которые надо определить. a11, a12, …, amn – коэффициенты системы – и b1, b2, … bm – свободные члены – предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.

Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе – неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) – совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

Решим следующую систему уравнений:

Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

Проведём следующие действия:

· К строке 2 добавим: -4 * Строку 1.

· К строке 3 добавим: -9 * Строку 1.

· К строке 3 добавим: -3 * Строку 2.

· Строку 2 делим на -2

· К строке 1 добавим: -1 * Строку 3.

· К строке 2 добавим: -3/2 * Строку 3.

· К строке 1 добавим: -1 * Строку 2.

В правом столбце получаем решение:

.

В методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики…

Решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n – ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с…

Математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной…

… «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…

Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого Jordan как Жордан) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…

Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.

На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?

…да, такое бывает только по любви =)

Для освоения данного урока «чайникам» придётся пойти путём Жо рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:

Ну, и совсем замечательно, если отработано понижение порядка определителя .

Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований .

Не мудрствуя лукаво:

Пример 1

Решить систему методом Гаусса-Жордана

Решение : это первое задание урока Метод Гаусса для чайников , где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:

Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .

Идеальный с точки зрения простоты случай:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) К первой строке прибавили вторую строку, умноженную на –2.

Не могу удержаться от иллюстрации итоговой системы:

Ответ :

Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.

Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:

Пример 2

Решить систему линейных уравнений методом Гаусса-Жордана.

Решение : первая часть задания хорошо знакома:

(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.

(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.

(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7

(4) Третью строку разделили на 2.

Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .

Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:

Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т.е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:

(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа . В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.

(8) К первой строке прибавили вторую.

(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!

В результате элементарных преобразований получена эквивалентная исходной система:

Элементарно выражаем базисные переменные через свободную:

и записываем:

Ответ : общее решение:

В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.

И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением .

Для самостоятельного решения:

Пример 3

Найти базисное решение с помощью элементарных преобразований

Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные . Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.

Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.

Примечание : термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь не при чём!

Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .

Продолжаем совершенствовать свои навыки на следующей прикладной задаче:

Как найти обратную матрицу методом Гаусса?

Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.

Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:

(Понятно, что обратная матрица должна существовать)

Демо-пример 4

Найдём обратную матрицу для матрицы с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:

(1) Ко второй строке прибавили первую строку, умноженную на –3.

(2) К первой строке прибавили вторую строку.

(3) Вторую строку разделили на –2.

Ответ :

Сверьтесь с ответом первого примера урока Как найти обратную матрицу?

Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:

Пример 5

Решение : присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса :

(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».

(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.

(3) К 3-й строке прибавили 2-ю строку, умноженную на –1

Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.

К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.

(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:

(5) К 1-й и 2-й строкам прибавили третью строку.

(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.

(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.

(8) К первой строке прибавили вторую строку.

(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.

(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали (44, 44 и 4). Совершенно понятно, что это число 44. Третью строку умножаем на 11.

(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!

Таким образом, обратная матрица:

Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.

Ответ :

Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице .

Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.

Аналогичное задание для самостоятельного решения:

Пример 6

Найти обратную матрицу методом Гаусса-Жордана.

Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных .

Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .

На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».

И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .

Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:

Пример 7

Найти обратную матрицу с помощью элементарных преобразований

Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел) , я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.

И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)

Желаю успехов!

Решения и ответы:

Пример 3: Решение : запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:


(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.
(3) Третью строку разделили на 3.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 7.
(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.
(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.
(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.
(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2
(10) К первой строке прибавили вторую строку.
(11) Вторую строку разделили на 2.
Выразим базисные переменные через свободные переменные :

Ответ : общее решение:

Пример 6: Решение : обратную матрицу найдём с помощью элементарных преобразований:


(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.
(2) Ко 2-й и 3-й строкам прибавили первую строку.
(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.
(4) Вторую строку умножили на 7, третью строку умножили на –9.
(5) К третьей строке прибавили вторую строку.


(6) Вторую строку разделили на 7.
(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.
(8) К первой и второй строкам прибавили третью строку.
(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.
(10) Вторую строку разделили на 2.
(11) Каждую строку разделили на 27.
В результате:
Ответ :

Пример 7: Решение : найдём обратную матрицу методом Гаусса-Жордана:
(1) К 1-й и 4-й строкам прибавили 3-ю строку.
(2) Первую и четвёртую строки поменяли местами.
(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:


(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.
(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.
(6) Вторую строку умножили на –1, третью строку разделили на –2.
Ответ :

Вычислить определитель матрицы системы методом гаусса онлайн. Вычисление определителя

Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.

О методе

При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.

1. Записываем расширенную матрицу.
2. Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
3. Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.

Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите “очень подробное решение” и посмотрите его решение онлайн.

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два» :

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 – нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Пример:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ . Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу :

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .

БУДЬТЕ ВНИМАТЕЛЬНЫ!

Содержание

Введение…………………………………………………………………………………………….. 2

1. Постановка задачи………………………………………………………………………….. 3

2. Математические и алгоритмические основы решения задачи……………… 5

2.1 Определитель матрицы………………………………………………………………….. 5

2.2 Метод Гаусса для решения систем линейных уравнений…………………… 6

2.3 Метод Гаусса для вычисления определителя……………………………………. 8

3. Функциональные модели и блок-схемы решения задачи…………………….. 9

4. Программная реализация решения задачи………………………………………. 11

5. Пример выполнения программы…………………………………………………….. 16

Заключение………………………………………………………………………………………. 18

Список использованных источников и литературы……………………………… 19

Введение

Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.

При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.

Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.

1. Постановка задачи

Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.

. ~. . .

Вычислить определитель матрицы методом A исключения Гаусса.

.

Приведем матрицу к диагональному виду методом Гаусса.

~.

Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:

.

Знак определяется количеством обменов строк, следовательно определитель матрицы

.

2. Математические и алгоритмические основы решения задачи

2.1 Определитель матрицы

Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.

Определитель квадратной матрицы A будем обозначать

или det A.

Определение. Определителем квадратной матрицы

второго порядка называется число

.

Определителем

квадратной матрицы порядка n,

, называется число – определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.

2.2 Метод Гаусса для решения систем линейных уравнений

Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.

Воспользуемся идеями метода Гаусса решения систем линейных уравнений.

Дана система:

a11 x1 + a12 x2 + … + a1n xn = b1

a21 x1 + a22 x2 + … + a2n xn = b2

an1 x1 + an2 x2 + … + ann xn = bn

Выполним следующий алгоритм.

На первом шаге найдём в первом столбце наибольший по модулю элемент, поставим уравнение с этим элементом на первую строчку (обменяв две соответствующие строки матрицы A и два соответствующих элемента вектора B), а затем будем отнимать это уравнение от всех остальных, чтобы в первом столбце все элементы (кроме первого) обратились в ноль. Например, при прибавлении ко второй строке будем домножать первую строку на -a21/a11, при добавлении к третьей – на -a31/a11, и т.д.

На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль. Понятно, что эта операция никак не изменит первый столбец – ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.

Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).

В конце концов, мы приведём систему к так называемому диагональному виду:

Т.е. мы нашли решение системы.

Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.

Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.

2.3 Метод Гаусса для вычисления определителя

Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).

Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).

Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.

3. Функциональные модели и блок-схемы решения задачи

Блок-схема решения задачи представлена на рисунке 1.

Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE

4 Программная реализация решения задачи

;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ

(DEFUN DETERMINANT (MATRIX SIZE)

;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ

;ОПРЕДЕЛИТЕЛЬ

(DECLARE (SPECIAL DET))

;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ

(DECLARE (SPECIAL PAR))

(DECLARE (SPECIAL R))

(DECLARE (SPECIAL T_))

(DECLARE (SPECIAL I))

(DECLARE (SPECIAL II))

;*********************

(SETQ R (MAKE-ARRAY SIZE:ELEMENT-TYPE “FLOAT:INITIAL-ELEMENT 0))

((>= J (- SIZE 1)))

;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0

(IF (= (AREF MATRIX J J) 0)

(SETQ II (+ J 1))

;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0

((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))

(SETQ II (+ II 1))

;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0

(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))

Вычислим определитель методом Гаусса.

Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.

Идея метода состоит в следующем: пусть дан определитель третьего порядка

элементдолжен быть равен
, для этого первую строку разделим на.

Получим определитель вида
(2)

Обнулим элементы, стоящие в первом столбце, кроме первого. Для этого из второй строки вычтем первую, умноженную на
, далее из третьей строки вычтем первую, умноженную на. Получим определитель вида
.

Обозначим его элементы буквой с, тогда

(3)

Теперь надо обнулить элемент . Элемент
должен быть равен
, для этого вторую строку разделим на
. Получим определитель вида
.

.

Обозначим его элементы буквой t, тогда

(4)

Вот мы привели определитель к треугольному виду, теперь он равен
.

Разберем теперь это на конкретном примере.

Пример 4: Вычислить определительметодом Гаусса.

Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).

Получили

Из второй строки вычтем первую, умноженную на 2, далее из третьей строки вычтем первую, умноженную на 3. Получили

Получили –

§2.Матрицы Виды матриц

Определение 7: Если в матрицеmстрок иnстолбцов, то она называетсяразмерностью mnи пишут
.

Определение 8: Если
, то матрица называется квадратной.

Определение 9: Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).

Определение 10: Матрица, состоящая из нулей, называется нулевой матрицей.

Определение 11: Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.

Определение 12: Единичной матрицей называется диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице.

Определение 13: Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.

Действиянад матрицами.

Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.

Пример 5:

Матрицы А и В равны, т.е.

Определение 15: Суммой (разностью) матриц А и В называется такая матрица С, у которой каждый элемент равен
.

Пример 6: Найти матрицу
, если

Решение:

Cвойства сложения

А+В=В+А(переместительное)

2 0 А+О=А, где О-нулевая матрица

3 0 А+(В+С)=(А+В)+С (дистрибутивное)

4 0 А+(-А)=О, где – А противоположная матрица

(т.е. элементы имеют противоположные знаки)

Определение 16: Произведением матрицы А на число
называется матрица, полученная из данной умножением всех ее элементов на число.

Пример 7:

Умножение матиц

Это действие распространяется на так называемые согласованные матрицы.

Определение 17: Матрица А называетсясогласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.

Пример 8:
и
– согласованные

и
– несогласованные

и
несогласованные

Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.

Если матрица А имеет размерность
, а матрица В
, то
.

Пример 9: Умножить матрицы

Дифференциальные уравнения – Обзор: Системы уравнений

Показать общее уведомление Показать мобильное уведомление Показать все заметки Скрыть все заметки

Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.

Пол
6 мая 2021 г.

Похоже, вы используете устройство с “узкой” шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 5-1: Обзор: Системы уравнений

Поскольку мы собираемся работать почти исключительно с системами уравнений, в которых количество неизвестных равно количеству уравнений, мы ограничим наш обзор этими типами систем.

Все, что мы здесь будем делать, можно легко распространить на системы с большим количеством неизвестных, чем уравнений, или большим количеством уравнений, чем неизвестных, если потребуется.

Начнем со следующей системы уравнений \ (n \) с \ (n \) неизвестными, \ (x_ {1} \), \ (x_ {2} \),…, \ (x_ {n} \ ).

\ [\ begin {уравнение} \ begin {выровнено} {a_ {11}} {x_1} + {a_ {12}} {x_2} + \ cdots + {a_ {1n}} {x_n} & = {b_1} \ \ {a_ {21}} {x_1} + {a_ {22}} {x_2} + \ cdots + {a_ {2n}} {x_n} & = {b_2} \\ \ vdots \ hspace {0.8in} & \\ {a_ {n1}} {x_1} + {a_ {n2}} {x_2} + \ cdots + {a_ {nn}} {x_n} & = {b_n} \ end {выровнено} \ label { уравнение: уравнение1} \ end {уравнение} \]

Обратите внимание, что в нижних индексах коэффициентов в этой системе, \ (a_ {ij} \), \ (i \) соответствует уравнению, в котором находится коэффициент, а \ (j \) соответствует неизвестному, которое умноженный на коэффициент.

Чтобы использовать линейную алгебру для решения этой системы, мы сначала запишем расширенную матрицу для этой системы.Расширенная матрица – это просто все коэффициенты системы и числа для правой части системы, записанные в матричной форме. Вот расширенная матрица для этой системы.

\ [\ left ({\ begin {array} {* {20} {r}} {{a_ {11}}} & {{a_ {12}}} & \ cdots & {{a_ {1n}}}} & {{b_1}} \\ {{a_ {21}}} & {{a_ {22}}} & \ cdots & {{a_ {2n}}} и {{b_2}} \\ \ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\ {{a_ {n1}}} и {{a_ {n2}}} & \ cdots & {{a_ {nn}}} & {{b_n}} \ end {array} } \верно)\]

Для решения этой системы мы будем использовать элементарные операции со строками (которые мы определим немного позже), чтобы переписать расширенную матрицу в треугольной форме.Матрица будет иметь треугольную форму, если все элементы ниже главной диагонали (диагональ, содержащая \ (a_ {11} \), \ (a_ {22} \),…, \ (a_ {nn} \)) равны нулю. .

Как только это будет сделано, мы можем вспомнить, что каждая строка в расширенной матрице соответствует уравнению. Затем мы преобразуем нашу новую расширенную матрицу обратно в уравнения, и на этом этапе решение системы станет очень простым.

Прежде чем работать с примером, давайте сначала определим элементарные операции со строками.Их трое.

1. Поменять местами два ряда. Это именно то, что написано. Мы заменим строку \ (i \) строкой \ (j \). Обозначение, которое мы будем использовать для обозначения этой операции: \ ({R_i} \ leftrightarrow {R_j} \)
2. Умножить строку \ (i \) на константу \ (c \). Это означает, что каждая запись в строке \ (i \) будет умножена на константу \ (c \). Обозначение для этой операции: \ (c {R_i} \)
3. Добавить строку, кратную \ (i \), к строке j. В уме мы умножим строку \ (i \) на соответствующую константу, а затем добавим результаты в строку \ (j \) и поместим новую строку обратно в строку \ (j \), оставив строку \ (i \) в матрица без изменений. Обозначение для этой операции: \ (c {R_i} + {R_j} \)

Всегда немного легче понять эти операции, если мы увидим их в действии. Итак, давайте решим пару систем.

Пример 1 Решите следующую систему уравнений. \ [\ begin {align *} – 2 {x_1} + {x_2} – {x_3} & = 4 \\ {x_1} + 2 {x_2} + 3 {x_3} & = 13 \\ 3 {x_1} + { x_3} & = – 1 \ end {align *} \] Показать решение

Первый шаг – записать расширенную матрицу для этой системы.Не забывайте, что коэффициенты отсутствующих членов равны нулю.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} – 2} & 1 & {- 1} & 4 \\ 1 & {\ color {Red} 2 } & 3 & {13} \\ 3 & 0 & {\ color {Red} 1} & {- 1} \ end {array}} \ right) \]

Теперь мы хотим, чтобы записи ниже главной диагонали были равны нулю. Основная диагональ окрашена в красный цвет, поэтому мы можем отслеживать ее в первом примере. По причинам, которые в конечном итоге станут очевидными, мы бы предпочли, чтобы все записи по главной диагонали тоже были единицами.

Мы можем получить единицу в самой верхней точке, заметив, что если мы поменяем местами первую и вторую строки, мы получим единицу в самой верхней точке бесплатно. Так что давай сделаем это.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} – 2} & 1 & {- 1} & 4 \\ 1 & {\ color {Red} 2 } & 3 & {13} \\ 3 & 0 & {\ color {Red} 1} & {- 1} \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_1} \ leftrightarrow {R_2}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ {- 2} & {\ color {Red} 1} & {- 1} & 4 \\ 3 & 0 & {\ color {Red} 1} & {- 1} \ end {array}} \ right) \]

Теперь нам нужно, чтобы последние две записи (-2 и 3) в первом столбце были равны нулю.Мы можем сделать это с помощью операции третьей строки. Обратите внимание, что если мы возьмем 2 раза первую строку и добавим ее ко второй строке, мы получим ноль во второй записи в первом столбце, а если мы возьмем -3 раза первую строку для третьей строки, мы получим 3 для быть нулем. Мы можем выполнять обе эти операции одновременно, так что давайте сделаем это.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ {- 2} & {\ color {Red}} 1} & {- 1} & 4 \\ 3 & 0 & {\ color {Red} 1} & {- 1} \ end {array}} \ right) \ begin {array} {* {20} {c}} {2 { R_1} + {R_2}} \\ {- 3 {R_1} + {R_3}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 5} & 5 & {30} \\ 0 & {- 6} & {\ color {Red} – 8} & {- 40} \ end {array }} \верно)\]

Прежде чем переходить к следующему шагу, давайте убедимся, что вы следовали тому, что мы только что сделали.Давайте посмотрим на первую операцию, которую мы выполнили. Эта операция требует умножить запись в строке 1 на 2 и добавить ее к соответствующей записи в строке 2, а затем заменить старую запись в строке 2 этой новой записью. Ниже приведены четыре отдельные операции, которые мы выполнили для этого.

\ [\ begin {align *} 2 \ left (1 \ right) + \ left ({- 2} \ right) & = 0 \\ 2 \ left (2 \ right) + 1 & = 5 \\ 2 \ left (3 \ right) + \ left ({- 1} \ right) & = 5 \\ 2 \ left ({13} \ right) + 4 & = 30 \ end {align *} \]

Хорошо, следующий шаг необязателен, но опять же удобен.Технически 5 во втором столбце можно оставить. Однако, если это 1. Мы можем использовать операцию второй строки, чтобы решить эту проблему в будущем, это упростит нашу жизнь. Мы можем разделить всю строку на 5. Это дает

. \ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 5} & 5 & { 30} \\ 0 & {- 6} & {\ color {Red} – 8} & {- 40} \ end {array}} \ right) \ begin {array} {* {20} {c}} {\ frac {1} {5} {R_2}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \ \ 0 & {\ color {Red} 1} & 1 & 6 \\ 0 & {- 6} & {\ color {Red} – 8} & {- 40} \ end {array}} \ right) \]

Следующий шаг – использовать операцию третьей строки, чтобы превратить -6 во втором столбце в ноль.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 1} & 1 & 6 \ \ 0 & {- 6} & {\ color {Red} – 8} & {- 40} \ end {array}} \ right) \ begin {array} {* {20} {c}} {6 {R_2} + {R_3}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color { Красный} 1} & 1 & 6 \\ 0 & 0 & {\ color {Red} – 2} & {- 4} \ end {array}} \ right) \]

Итак, официально мы закончили, но опять же, довольно удобно разместить все на главной диагонали, поэтому мы сделаем последний шаг.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 1} & 1 & 6 \ \ 0 & 0 & {\ color {Red} – 2} & {- 4} \ end {array}} \ right) \ begin {array} {* {20} {c}} {- \ frac {1} {2} { R_3}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red } 1} & 1 & 6 \\ 0 & 0 & {\ color {Red} 1} & 2 \ end {array}} \ right) \]

Теперь мы можем преобразовать обратно в уравнения.

\ [\ require {color} \ left ({\ begin {array} {* {20} {r}} {\ color {Red} 1} & 2 & 3 & {13} \\ 0 & {\ color {Red} 1} & 1 & 6 \ \ 0 & 0 & {\ color {Red} 1} & 2 \ end {array}} \ right) \ hspace {0,25in} \ Rightarrow \ hspace {0,25in} \ begin {align} {x_1} + 2 {x_2} + 3 { x_3} & = 13 \\ {x_2} + {x_3} & = 6 \\ {x_3} & = 2 \ end {align} \]

На данный момент решение довольно просто. Мы получаем \ (x_ {3} \) бесплатно, и как только мы получим это, мы можем вставить это во второе уравнение и получить \ (x_ {2} \).Затем мы можем использовать первое уравнение, чтобы получить \ (x_ {1} \). Также обратите внимание, что наличие единиц по главной диагонали несколько помогло в этом процессе.

Решение этой системы уравнений:

\ [{x_1} = – 1 \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} {x_2} = 4 \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} {x_3} = 2 \]

Процесс, используемый в этом примере, называется Исключение Гаусса . Давайте посмотрим на другой пример.

Пример 2 Решите следующую систему уравнений.\ [\ begin {align *} {x_1} – 2 {x_2} + 3 {x_3} & = – 2 \\ – {x_1} + {x_2} – 2 {x_3} & = 3 \\ 2 {x_1} – {x_2} + 3 {x_3} & = 1 \ end {align *} \] Показать решение

Сначала запишите расширенную матрицу.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ {- 1} & 1 & {- 2} & 3 \\ 2 & {- 1} & 3 & 1 \ end {array}} \ right) \]

При работе с этим примером мы не будем вкладывать столько слов.Вот как работает эта расширенная матрица.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ {- 1} & 1 & {- 2} & 3 \\ 2 & {- 1} & 3 & 1 \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_1} + {R_2}} \\ {- 2 {R_1} + {R_3}} \\ \ to \ конец {массив} \ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & {- 1} & 1 & 1 \\ 0 & 3 & {- 3} & 5 \ end {array}} \ right) \] \ [\ begin {array} {* {20} {r}} {- {R_2}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 3 & {- 3} & 5 \ end {array}} \ right) \ begin {array} {* {20} {c }} {- 3 {R_2} + {R_3}} \\ \ to \ end {array} \ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 8 \ end {array}} \ right) \]

В этом примере мы не пойдем дальше.Давайте вернемся к уравнениям, чтобы понять, почему.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 8 \ end {array}) } \ right) \ Rightarrow \ begin {align} {x_1} – 2 {x_2} + 3 {x_3} & = – 2 \\ {x_2} – {x_3} & = – 1 \\ 0 & = 8 \ end { выровнено} \]

Последнее уравнение должно вызвать некоторые опасения. Здесь есть один из трех вариантов. Во-первых, нам каким-то образом удалось доказать, что 0 равно 8, и мы знаем, что это невозможно.Во-вторых, мы допустили ошибку, но после того, как мы вернулись к нашей работе, не оказалось, что мы сделали ошибку.

Остается третий вариант. Когда мы получаем что-то вроде третьего уравнения, которое просто не имеет смысла, мы сразу понимаем, что решения нет. Другими словами, не существует набора из трех чисел, который одновременно выполнял бы все три уравнения.

Давайте рассмотрим другой пример. Мы собираемся получить систему для этого нового примера, внеся очень небольшое изменение в систему из предыдущего примера.

Пример 3 Решите следующую систему уравнений. \ [\ begin {align *} {x_1} – 2 {x_2} + 3 {x_3} & = – 2 \\ – {x_1} + {x_2} – 2 {x_3} & = 3 \\ 2 {x_1} – {x_2} + 3 {x_3} & = – 7 \ end {align *} \] Показать решение

Итак, единственная разница между этой системой и системой из второго примера состоит в том, что мы изменили 1 в правой части знака равенства в третьем уравнении на -7.

Теперь запишите расширенную матрицу для этой системы.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ {- 1} & 1 & {- 2} & 3 \\ 2 & {- 1} & 3 & {- 7} \ end {array}} \ right) \]

Шаги для решения этой проблемы идентичны шагам для второй задачи, поэтому мы не будем записывать их все. Выполнив те же действия, мы приходим к следующей матрице.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 0 \ end {array}) } \верно)\]

На этот раз последнее уравнение сводится к

\ [0 = 0 \]

и в отличие от второго примера это не проблема.Ноль на самом деле равен нулю!

Мы могли бы остановиться на этом и вернуться к уравнениям, чтобы получить решение, и в этом случае решение есть. Однако, если мы сделаем еще один шаг и получим ноль над единицей во втором столбце, а также под ним, наша жизнь станет немного проще. Это дает

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 3 & {- 2} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 0 \ end {array}) } \ right) \ begin {array} {* {20} {c}} {2 {R_2} + {R_1}} \\ \ Rightarrow \ end {array} \ left ({\ begin {array} {* {20 } {r}} 1 & 0 & 1 & {- 4} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 0 \ end {array}} \ right) \]

Если мы теперь вернемся к уравнению, мы получим следующие два уравнения.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & 0 & 1 & {- 4} \\ 0 & 1 & {- 1} & {- 1} \\ 0 & 0 & 0 & 0 & 0 \ end {array}} \ right) \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ begin {array} {* {20} {r}} {{x_1} + {x_3} = – 4} \\ {{x_2} – {x_3} = – 1} \\ {} \ end {массив} \]

У нас есть два уравнения и три неизвестных. Это означает, что мы можем найти две переменные в терминах оставшейся переменной. Поскольку \ (x_ {3} \) присутствует в обоих уравнениях, мы будем решать в терминах этого.

\ [\ begin {align *} {x_1} & = – {x_3} – 4 \\ {x_2} & = {x_3} – 1 \ end {align *} \]

Это решение означает, что мы можем выбрать значение \ (x_ {3} \) как любое, что захотим, а затем найти значения \ (x_ {1} \) и \ (x_ {2} \ ). В этих случаях мы обычно пишем решение следующим образом:

\ [\ begin {align *} {x_1} & = – t – 4 \\ {x_2} & = t – 1 \ hspace {0,25 дюйма} \ hspace {0.25 дюймов} t = {\ mbox {любое действительное число}} \\ & {x_3} = t \ end {align *} \]

Таким образом мы получаем бесконечное количество решений, по одному для каждого значения \ (t \).

Эти три примера приводят нас к интересному факту о системах уравнений.

Факт

Учитывая систему уравнений, \ (\ eqref {eq: eq1} \), у нас будет один из трех возможных вариантов количества решений.

1. Нет решения.
2. Ровно одно решение.
3. Бесконечно много решений.

Прежде чем перейти к следующему разделу, нам нужно взглянуть на еще одну ситуацию. Система уравнений в \ (\ eqref {eq: eq1} \) называется неоднородной системой, если хотя бы одна из b _i ’ s не равна нулю. Если, однако, все \ (b_ {i} \) равны нулю, мы называем систему однородной, и система будет,

\ [\ begin {уравнение} \ begin {выровнено} {a_ {11}} {x_1} + {a_ {12}} {x_2} + \ cdots + {a_ {1n}} {x_n} & = 0 \\ { a_ {21}} {x_1} + {a_ {22}} {x_2} + \ cdots + {a_ {2n}} {x_n} & = 0 \\ \ vdots \ hspace {0.8in} & \\ {a_ {n1}} {x_1} + {a_ {n2}} {x_2} + \ cdots + {a_ {nn}} {x_n} & = 0 \ end {выровнено} \ label {eq: eq2} \ end {уравнение} \]

Теперь обратите внимание, что в однородном случае мы гарантированно получаем следующее решение.

\ [{x_1} = {x_2} = \ cdots = {x_n} = 0 \]

Это решение часто называют тривиальным решением .

Для однородных систем приведенный выше факт может быть изменен на следующее.

Факт

Учитывая однородную систему уравнений, \ (\ eqref {eq: eq2} \), у нас будет один из двух возможных вариантов количества решений.

1. Ровно одно решение, тривиальное решение
2. Бесконечно много ненулевых решений в дополнение к тривиальному решению.

Во второй возможности мы можем сказать ненулевое решение, потому что, если будет бесконечно много решений и мы знаем, что одно из них является тривиальным решением, тогда все остальные должны иметь хотя бы одно из \ (x_ {i} \) не равны нулю, и, следовательно, мы получаем ненулевое решение.

решает систему уравнений по методу Гаусса Джордана (2 задачи)

Обратная подстановка:

-y = -4 -> y = 4
3x – 5y = -5
3x – 5 (4) = -5
3x – 20 = -5
3x = -5 + 20
3x = 15
x = 5

————————— ————————————

достаточно редкая….

x y w z k
—————————-
1 0 2 0 15
0 1 2 0 13
0 2 0 1 16
3 0 1 2 25

x y w z k
—————————-
1 0 2 0 15
0 1 2 0 13
0 2 0 1 16
0 0-5 2-20

-3 * r1 + r4

x y w z k
——— ——————-
1 0 2 0 15
0 1 2 0 13
0 0-4 1-10
0 0-5 2-20

– 2 * r2 + r3

x y w z k
—————————-
1 0 2 0 15
0 1 2 0 13
0 0 1 -1/4 2.5
0 0-5 2-20

r3 / -4

x y w z k
————————— –
1 0 2 0 15
0 1 2 0 13
0 0 1 -1/4 2,5
0 0 0 3/4 -7,5

5 * r3 + r4

обратная замена:

3/4 z = -7,5

z = -7,5 * 4/3 = -10

w – 1/4 (-10) = 2,5
w + 5/2 = 2,5
w = 0

y + 2w = 13 — > y = 13

x = 15

Метод Гаусса Джордана преобразует матрицу
в форму эшелона строк или верхнего треугольника
, так что решение находится путем обратной подстановки
.

Чтобы найти обратное, вы должны поместить матрицу
и единичную матрицу рядом.
Затем вы используете операции со строками для преобразования матрицы
в единичную матрицу ….
НО все операции со строками, выполняемые с исходной матрицей
, также должны выполняться на единичной матрице.
(гораздо более обширный, чем исключение Гаусса Джордана)

Итак, что происходит, исходная матрица преобразуется в единичную матрицу
, а в
в то же время единичная матрица преобразуется
в обратную.

Это сделано для первой задачи в качестве примера.

3-5 1 0
6-11 0 1

———————

3-5 1 0
0-1-2 1 <--- -2 * r1 + r2

———————————-

1 – 5/3 1/3 0
0 -1 -2 1 <--- r1 / 3

————————— ——–

1 0 11/3 -5/3 <---- (-5/3) R2 + r1
0-1-2 1

——– ——————————-

1 0 11/3 -5/3
0 1 2-1 <- - -R2

Обратное значение:

11/3 -5/3
2-1

Умножение обратного значения на исходную матрицу

11/3 -5/3 3-5
2-1 6-11

1 0
0 1 <--- ДА !!! оно работает;

Решение: A-инверсия x B
11/3 -5/3-5
2-1-14

x = -55/3 + 70/3 = 15/3 = 5

y = – 10 + 14 = 4

Обратите внимание, что для решения 2 x 2 этим способом потребовалось 5 шагов…

4 x 4 будет намного утомительнее.

Я занимаюсь математикой · Программа для решения одновременных линейных уравнений

См. Также: матрица, исключение Гаусса-Жордана, геометрическое линейное преобразование

---

Калькулятор, представленный ниже, решит одновременные линейные уравнения с двумя, тремя и до 10 переменными, если система уравнений имеет единственное решение.
Для систем уравнений с множеством решений используйте метод исключения Гаусса-Жордана.

Прокрутите вниз, чтобы прочитать о различных методах решения одновременных линейных уравнений.

Программа для решения одновременных линейных уравнений

Выберите размер системы.

загрузка. . .

Расчет. . .

Сообщайте о любых ошибках на [адрес электронной почты] .

---

Методы решения одновременных линейных уравнений

Существует как минимум пять методов решения одновременных линейных уравнений.

Например, давайте попробуем найти решение для следующего набора одновременных линейных уравнений с 3 переменными

{x & plus; y − z = 1 (1) 8⁢x & plus; 3⁢y − 6⁢z = 1 (2) −4⁢x − y & plus; 3⁢z = 1 (3)

---

Метод исключения

Как следует из названия, этот метод пытается исключить переменные, пока не останется только 1 переменная.

Во-первых, посмотрите на уравнения и попытайтесь найти 2 уравнения с одинаковым коэффициентом (плюс или минус) для одних и тех же переменных. Например, см. Уравнения (1) и (3). Коэффициент для y равен 1 и -1 соответственно. Мы можем сложить два уравнения, чтобы исключить y, и мы получим уравнение (4).

x & plus; y − z = 1 (1) −4⁢x − y & plus; 3⁢z = 1 (3) ———————— & plus ; −3⁢x & plus; 0 & plus; 2⁢z = 2 (4)

Обратите внимание, что уравнение (4) состоит из переменных x и z. Теперь нам нужно другое уравнение, которое имеет те же переменные, что и уравнение (4).Чтобы получить это, мы исключим y из уравнений (1) и (2). В уравнениях (1) и (2) коэффициенты при y равны 1 и 3 соответственно. Чтобы исключить y, мы умножаем уравнение (1) на 3, а затем вычитаем уравнение (2) из ​​уравнения (1).

x & plus; y − z = 1 (1) × 3 8⁢x & plus; 3⁢y − 6⁢z = 1 (2)
3⁢x & plus; 3⁢y − 3⁢z = 3 (1) 8⁢x & plus; 3 ⁢Y − 6⁢z = 1 (2) ———————— −−5⁢x & plus; 0⁢y & plus; 3⁢z = 2 (5)

Теперь, используя уравнения (4) и (5), мы можем исключить z.

−3⁢x & plus; 2⁢z = 2 (4) × 3 −5⁢x & plus; 3⁢z = 2 (5) × 2
−9⁢x & plus; 6⁢z = 6 (4) −10⁢x & plus; 6 ⁢Z = 4 (5) ———————— – & plus; 01⁢x & plus; 0⁢z = 2 (6)

Из уравнения ( 6) получаем x = 2.Теперь мы можем подставить это значение x в уравнение (4), чтобы получить значение z.

−3⁢ (2) & plus; 2⁢z = 2 (4) −6 & plus; 2⁢z = 22⁢z = 2 & plus; 62⁢z = 8z = 8 ÷ 2z = 4

Наконец, мы можем подставить значения x и z в уравнение (1), чтобы получить y.

2 & plus; y − 4 = 1 (1) y = 1−2 & plus; 4y = 3

Следовательно, решение системы линейных уравнений имеет вид х = 2, у = 3, г = 4.

---

Метод замещения

Во-первых, давайте перестроим уравнение (1) так, чтобы только 1 переменная находилась в левой части.

x = 1 − y & plus; z (1)

Теперь давайте подставим этот x в уравнение (2).

8⁢ (1 − y & plus; z) & plus; 3⁢y − 6⁢z = 1 (2) 8−8⁢y & plus; 8⁢z & plus; 3⁢y − 6⁢z = 1−5⁢y & plus; 2⁢z = 1−8−5⁢y & plus; 2⁢z = −7 (4)

Аналогичным образом подставим x в уравнение (3).

−4⁢ (1 − y & plus; z) −y & plus; 3⁢z = 1 (3) −4 & plus; 4⁢y − 4⁢z − y & plus; 3⁢z = 13⁢y − z = 1 & plus; 43⁢y− z = 5 (5)

Теперь давайте перегруппируем уравнение (5) так, чтобы только 1 переменная находилась в левой части.

z = 3⁢y − 5 (5)

Затем подставляем это значение z в уравнение (4).

−5⁢y & plus; 2⁢ (3⁢y − 5) = – 7 (4) −5⁢y & plus; 6⁢y − 10 = −7y = −7 & plus; 10y = 3

Теперь, когда мы нашли y, мы можем подставьте это в уравнение (5), чтобы найти z.

z = 3⁢ (3) −5 (5) z = 9−5z = 4

Наконец, мы можем подставить значение y и z в уравнение (1), чтобы получить значение x.

х = 1-3 & плюс; 4 (1) х = 2

---

Графический метод

Решение системы линейных уравнений с использованием графического метода выполняется путем рисования линий или плоскостей, которые представляют каждое уравнение.Решение – это координаты пересечения линий или плоскостей.

Для простоты рассмотрим систему линейных уравнений с двумя переменными.

{x & plus; y = 32⁢x − y = −3

Постройте линии этих двух уравнений.

Как показано на графике, две прямые пересекаются в точке (0,3). Это решение системы линейных уравнений, т.е. x = 0, у = 3.

Для системы линейных уравнений с тремя переменными решением является точка пересечения трех плоскостей, представляющих каждое уравнение.

---

Метод обратной матрицы

Система линейных уравнений, определяемая уравнениями (1), (2) и (3), может быть выражена в матричной форме следующим образом.

A⁢B = C12−183−6−4−13⁢xyz = 111

Множеством решений является матрица B. Чтобы выделить только B на одной стороне уравнения, мы умножаем обе части уравнения на матрицу, обратную матрице A

A − 1⁢A⁢B = A − 1⁢CB = A − 1⁢C

Теперь, чтобы найти B, нам нужно найти A − 1. Пожалуйста, проверьте страницу матрицы, чтобы узнать, как найти обратную матрицу.

A − 1 = −323012−435B = −323012−435⁢111B = 234

Следовательно, множество решений х = 2, у = 3, г = 4.

---

Исключение Гаусса / Исключение Гаусса-Джордана

Система линейных уравнений, определяемая уравнениями (1), (2) и (3), может быть выражена в форме расширенной матрицы следующим образом.

A = 11−1 | 183−6 | 1−4−13 | 1

Выполняя серию операций со строками (исключение Гаусса), мы можем привести указанную выше матрицу к ее эшелонированной форме по строкам.

A = 10,375−0,75 | 0,12501−0,4 | 1.4001 | 4

Затем мы можем выполнить обратную подстановку, чтобы получить значения всех неизвестных / переменных, или мы можем выполнять дальнейшие операции со строками, пока матрица приведена в виде приведенного ряда строк (с использованием метода исключения Гаусса-Жордана).

A = 100 | 2010 | 3001 | 4

Выполняя исключение Гаусса-Жордана, мы получаем решение системы уравнений в последнем столбце: x = 2, у = 3, г = 4.

Чтобы просмотреть пошаговые операции со строками, см. Страницу исключения Гаусса-Джордана.

Запутались, есть вопросы? У нас есть ответы.С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в этой области.

Джимми Си

См. Также: матрица, исключение Гаусса-Жордана, геометрическое линейное преобразование

Решатель уравнений: Wolfram | Alpha

О решении уравнений

Значение называется корнем полинома if.

Наибольший показатель степени появления называется степенью. Если имеет степень, то хорошо известно, что есть корни, если учесть множественность.Чтобы понять, что подразумевается под множественностью, возьмем, например,. Считается, что этот многочлен имеет два корня, оба равны 3.

Человек изучает «теорему о факторах», обычно во втором курсе алгебры, как способ найти все корни, являющиеся рациональными числами. Также можно научиться находить корни всех квадратичных многочленов, используя при необходимости квадратные корни (полученные из дискриминанта). Существуют более сложные формулы для выражения корней многочленов кубической и четвертой степени, а также ряд численных методов аппроксимации корней произвольных многочленов.В них используются методы комплексного анализа, а также сложные численные алгоритмы, и это действительно область постоянных исследований и разработок.

Системы линейных уравнений часто решаются с использованием метода исключения Гаусса или связанных методов. Это также обычно встречается в программах средней школы или колледжа по математике. Для нахождения корней одновременных систем нелинейных уравнений необходимы более совершенные методы. Аналогичные замечания относятся к работе с системами неравенств: линейный случай может быть обработан с использованием методов, описанных в курсах линейной алгебры, тогда как полиномиальные системы более высокой степени обычно требуют более сложных вычислительных инструментов.

Как Wolfram | Alpha решает уравнения

Для решения уравнений Wolfram | Alpha вызывает функции Solve и Reduce языка Wolfram Language, которые содержат широкий спектр методов для всех видов алгебры, от основных линейных и квадратных уравнений до многомерных нелинейных систем. В некоторых случаях используются методы линейной алгебры, такие как исключение Гаусса, с оптимизацией для повышения скорости и надежности. Другие операции полагаются на теоремы и алгоритмы из теории чисел, абстрактной алгебры и других сложных областей для вычисления результатов.Эти методы тщательно спроектированы и выбраны, чтобы позволить Wolfram | Alpha решать самые разнообразные проблемы, а также минимизировать время вычислений.

Хотя такие методы полезны для прямых решений, для системы также важно понимать, как человек мог бы решить ту же проблему. В результате в Wolfram | Alpha также есть отдельные алгоритмы для пошагового отображения алгебраических операций с использованием классических методов, которые людям легко распознать и которым легко следовать. Это включает в себя исключение, замену, квадратную формулу, правило Крамера и многое другое.

Метод исключения Гаусса Вопросы и ответы

Этот набор вопросов и ответов с множественным выбором (MCQ) для численного анализа посвящен «методу исключения Гаусса – 1».

1. Решите следующие уравнения методом исключения Гаусса.

 х + 4y-z = -5
х + у-6z = -12
3x-y-z = 4
 

a) x = 1.64791, y = 1.14085, z = 2.08451
b) x = 1.65791, y = 1.14185, z = 2.08441
c) x = 1.64691, y = 1.14095, z = 2.08461
d) x = 1.64491, y = 1.15085, z = 2.09451
Посмотреть ответ

Ответ: a
Пояснение: Методом исключения Гаусса получаем
\ (\ begin {bmatrix}
1 и 4 и -1 \
1 и 1 и -6 \
3 & -1 & -1 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
х \
у \
z \
\ end {bmatrix} \) = \ (\ begin {bmatrix}
-5 \
-12 \
4 \
\ end {bmatrix} \)

По R ₂ -R ₁ и R ₃ -3R ₁
\ (\ begin {bmatrix}
1 & 4 & -1 \\
0 & -3 & -5 \\
0 & -13 & 2 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
x \\
y \\
z \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
-5 \\
-7 \\
19 \\
\ end {bmatrix} \)

R ₃ – (- 13 / -3) * R ₂
\ (\ begin {bmatrix}
1.0000 & 4.0000 & -1.0000 \\
0 & -3.0000 & -5.0000 \\
0 & 0 & 23.6667 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
x \\
y \\
z \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
-5 \\
-7 \\
49.33333 \\
\ end {bmatrix} \)

x + 4y-z = -5
-3y-5z = -7
23,6667z = 49,3333
Следовательно, z = 2,08451
-3y = -7 + 5z
Следовательно, y = -1,14085
x = -4y + z -5
Следовательно, x = 1,64791.

2. Найдите значения x, y, z в следующей системе уравнений методом исключения Гаусса.

 2x + y - 3z = -10
-2y + z = -2
г = 6
 

a) 2, 4, 6
b) 2, 7, 6
c) 3, 4, 6
d) 2, 4, 5
Просмотреть ответ

Ответ: a
Объяснение: Методом исключения Гаусса получаем
\ (\ begin {bmatrix}
2 & 1 & -3 \\
0 & -2 & 1 \\
0 & 0 & 1 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
x \\
y \\
z \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
-10 \\
-2 \\
6 \\
\ end {bmatrix} \)
z = 6.
-2y + z = -2
Отсюда y = 4.
2x + y – 3z = -10
Отсюда z = 6.

3. Решите данную систему уравнений методом исключения Гаусса.

 3х + 4у - г = -6
-2y + 10z = -8
4y - 2z = -2
 

а) (-2, -1, -1)
б) (-1, -2, -1)
в) (-1, -1, -2)
г) (-1, -1, – 1)
Посмотреть ответ

Ответ: d
Объяснение: Здесь
\ (\ begin {bmatrix}
3 & 4 & -1 \\
0 & -2 & 10 \\
0 & 4 & -2 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
x \\
y \\
z \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
-6 \\
– 8 \\
-2 \\
\ end {bmatrix} \)
Матрица почти представляет собой треугольную матрицу.Умножив строку 2 на 2 и добавив ее к строке 3, мы получим верхнюю треугольную матрицу с
x, y, z = (-1, -1, -1).

4. Следующая система уравнений имеет:

 х - у - г = 4
2x - 2y - 2z = 8
5x - 5y - 5z = 20
 

a) Уникальное решение
b) Нет решения
c) Бесконечно много решений
d) Конечные решения
Посмотреть ответ

Ответ: c
Объяснение: Умножение строки 1 на -2, затем прибавление строки 1 и строки 2 к 1-й строке матрица уменьшается 0.
\ (\ begin {bmatrix}
0 & 0 & 0 \\
2 & -2 & -2 \\
5 & -5 & -5 \\
\ end {bmatrix} \) \ (\ begin {bmatrix }
x \\
y \\
z \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
0 \\
8 \\
20 \\
\ end {bmatrix} \)
Следовательно, существует бесконечно много решений.

5. Решите эту систему уравнений и прокомментируйте природу решения, используя метод исключения Гаусса.

 х + у + г = 0
-x - y + 3z = 3
-x - y - z = 2
 

a) Уникальное решение
b) Нет решения
c) Бесконечно много решений
d) Конечные решения
Посмотреть ответ

Ответ: b
Пояснение: Методом исключения Гаусса мы складываем строку 1 и строку 3, чтобы получить следующую матрицу
\ (\ begin {bmatrix}
1 и 1 и 1 \
-1 и -1 и 3 \
0 & 0 & 0 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
х \
у \
z \
\ end {bmatrix} \) = \ (\ begin {bmatrix}
0 \
3 \
2 \
\ end {bmatrix} \)

Следовательно, матрица не имеет решения при 0 ≠ 2.

6. Целью шагов исключения в методе исключения Гаусса является уменьшение матрицы коэффициентов до ____________
а) диагональ
б) идентичность
в) нижний треугольник
г) верхний треугольник
Посмотреть ответ

Ответ: d
Пояснение: In Метод исключения Гаусса мы стремимся свести данную матрицу к верхнетреугольной матрице для решения относительно x, y, z.

7. Деление на ноль во время исключения по Гауссу системы уравнений [A] * [X] = [C] означает, что матрица коэффициентов [A] равна ____________
a) Обратимая
b) Неособая
c) Не определяется до быть единичным или неособым
d) Единственное число
Посмотреть ответ

Ответ: c
Объяснение: Деление на ноль в методе исключения Гаусса не связано с сингулярностью матрицы.

8. В каком из следующих утверждений обе части уравнения умножаются на ненулевую константу?
a) Метод исключения Гаусса
b) Процедура исключения Гаусса
c) Процедура согласования Гаусса
d) Процедура замены Гаусса
Посмотреть ответ

Ответ: a
Объяснение: Метод исключения Гаусса использует обе части уравнения, которые умножаются на не- нулевая константа. Затем матрица сокращается до верхней треугольной матрицы, чтобы получить значения соответствующих переменных.

9. В методе исключения Гаусса исходные уравнения преобразуются с использованием _____________
a) Операции со столбцами
b) Операции со строками
c) Математические операции
d) Операции с подмножествами
Просмотр ответа

Ответ: b
Объяснение: Используются операции со строками в методе исключения Гаусса, чтобы свести матрицу к верхнетреугольной матрице и, таким образом, решить для x, y, z.

10. Следующая информация относится к скорости и времени движения транспортного средства. Он управляет квадратным уравнением v (t) = at ² + bt + c.Следовательно, найдите матрицу, которая наиболее точно представляет уравнение.

Т	с	0	14	15	20	30	35
В	м / с	0	227,04	362,78	517,35	602,97	901,67

a) \ (\ begin {bmatrix}
176 & 14 & 1 \\
225 & 15 & 1 \\
400 & 20 & 1 \\
\ end {bmatrix} \) \ (\ begin {bmatrix }
a \\
b \\
c \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
227.04 \\
362.78 \\
517.35 \\
\ end {bmatrix} \)
b) \ (\ begin {bmatrix}
225 & 15 & 1 \\
400 & 20 & 1 \\
900 & 30 & 1 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
a \\
b \\
c \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
362,78 \\
517.35 \\
602.97 \\
\ end {bmatrix} \)
c) \ (\ begin {bmatrix}
0 & 0 & 1 \\
225 & 15 & 1 \\
400 & 20 & 1 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
a \\
b \\
c \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
0 \\
362.78 \\
517.35 \\
\ end {bmatrix} \)
d) \ (\ begin {bmatrix}
400 & 20 & 1 \\
900 & 30 & 1 \\
1225 & 35 & 1 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
a \\
b \\
c \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
517,35 \\
602.97 \\
901,67 \\
\ end {bmatrix} \)
Просмотреть ответ

Ответ: b
Объяснение: Ближайшие к t = 21 секунде точки – 15, 20, 30
В (t ₀ ) = 362,78 м / с = a (15) ² + b (15) + c
В (t ₁ ) = 517.35 м / с = a (20) ² + b (20) + c
V (t ₂ ) = 602,97 м / с = a (30) ² + b (30) + c
Следовательно,
225a + 15b + c = 362,78
400a + 20b + c = 517,35
900a + 30b + c = 602,97
Что приводит нас к \ (\ begin {bmatrix}
225 & 15 & 1 \\
400 & 20 & 1 \\
900 & 30 & 1 \\
\ end {bmatrix} \) \ (\ begin {bmatrix}
a \\
b \\
c \\
\ end {bmatrix} \) = \ (\ begin {bmatrix}
362,78 \\
517,35 \\
602,97 \\
\ end {bmatrix} \).

11. Процесс исключения в методе исключения Гаусса также известен как _____________
a) Прямое исключение
б) Обратное исключение
в) Боковое исключение
г) Перекрестное исключение
Посмотреть ответ

Ответ: a
Объяснение: Процесс исключения в Метод исключения Гаусса также известен как прямое исключение. В этом методе матрица сводится к верхнетреугольной матрице.

12. Уменьшенная форма Матрицы в методе исключения Гаусса также называется ____________
a) Форма эшелона столбца
б) Форма эшелона столбца
в) Форма эшелона столбец-ряд
г) Форма эшелона строки
Посмотреть ответ

Ответ: d
Пояснение: Уменьшенная форма Матрицы в методе исключения Гаусса называется формой эшелона строк.Так сказано, потому что в методе исключения Гаусса рассматриваются только операции со строками.

Sanfoundry Global Education & Learning Series – Численные методы.

Чтобы попрактиковаться во всех областях численных методов, представляет собой полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .

Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!

Решающих систем с исключением Гаусса · Precalculus

Решение систем с исключением Гаусса · Предварительное вычисление

В этом разделе вы:

• Напишите расширенную матрицу системы уравнений.
• Напишите систему уравнений из расширенной матрицы.
• Выполняет операции со строками в матрице.
• Решите систему линейных уравнений, используя матрицы.

Карл Фридрих Гаусс жил в конце 18-го и начале 19-го веков, но до сих пор считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика.Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.

Мы впервые столкнулись с методом исключения Гаусса в системах линейных уравнений: две переменные. В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.

Написание расширенной матрицы системы уравнений

Матрица может служить устройством для представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы.Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей .

Например, рассмотрим следующий 2 × 2

система уравнений.

3x + 4y = 74x − 2y = 5

Мы можем записать эту систему в виде расширенной матрицы:

[344−2 \ | 75]

Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов .

[344−2]

Трехкратная система уравнений , например

3x − y − z = 0 x + y = 5 2x − 3z = 2

имеет матрицу коэффициентов

[3−1−111020−3]

и представлена ​​расширенной матрицей

[3−1−111020−3 \ | 052]

Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: x -термов идет в первый столбец, – -термов – во втором столбце, и z -термов – в третьем столбце.Очень важно, чтобы каждое уравнение было записано в стандартной форме ax + by + cz = d

, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.

Для данной системы уравнений напишите расширенную матрицу.

1. Запишите коэффициенты членов x в виде чисел в первом столбце.
2. Запишите коэффициенты членов и в виде чисел во втором столбце.
3. Если имеется z -термов, запишите коэффициенты в виде чисел в третьем столбце.
4. Нарисуйте вертикальную линию и напишите константы справа от нее.

Написание расширенной матрицы для системы уравнений

Напишите расширенную матрицу для данной системы уравнений.

x + 2y − z = 3 2x − y + 2z = 6 x − 3y + 3z = 4

Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.

[12−12−121−33 \ | 364]

Запишите расширенную матрицу данной системы уравнений.

4x − 3y = 113x + 2y = 4

[4−33 2 \ | 11 4]

Написание системы уравнений из расширенной матрицы

Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными. Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным.Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.

Написание системы уравнений из расширенной матричной формы

Найдите систему уравнений из расширенной матрицы.

[1−3−52−5−4−354 \ | -256]

Когда столбцы представляют переменные x,

y,

и z,

[1−3−52−5−4−354 \ | −256] → x − 3y − 5z = −2 2x − 5y − 4z = 5−3x + 5y + 4z = 6

Напишите систему уравнений из расширенной матрицы.

[1−1 12−1 30 1 1 \ | 5 1-9]

x – y + z = 52x – y + 3z = 1 y + z = −9

Выполнение операций со строками в матрице

Теперь, когда мы можем записывать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками , , которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.

Выполнение строковых операций над матрицей – это метод, который мы используем для решения системы уравнений.Чтобы решить систему уравнений, мы хотим преобразовать матрицу в строковую форму , в которой есть единицы по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции. ниже главной диагонали, как показано.

Рядно-эшелонированная форма [1ab01d001]

Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, которая эквивалентна строкам в более простой форме. Вот рекомендации по получению формы рядного эшелона.

1. В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
2. Любые нулевые строки помещаются внизу матрицы.
3. Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
4. Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.

Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в строковую форму и выполнить обратную подстановку, чтобы найти решение.

1. Поменять местами ряды. (Обозначение: Ri ↔ Rj

   )

2. Умножить строку на константу. (Обозначение: cRi

   )

3. Добавить произведение одной строки на константу к другой строке. (Обозначение: Ri + cRj)

Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными. С помощью этих операций есть несколько ключевых шагов, которые быстро достигнут цели написания матрицы в виде эшелона строк.Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строку 1 можно было использовать для преобразования оставшихся строк.

Исключение по Гауссу

Метод исключения Гаусса относится к стратегии, используемой для получения матрицы в виде строки-эшелона. Цель состоит в том, чтобы написать матрицу A

с цифрой 1 в начале главной диагонали и всеми нулями внизу.

A = [a11a12a13a21a22a23a31a32a33] → После исключения Гаусса A = [1 b12 b130 1 b230 0 1]

Первый шаг стратегии Гаусса включает получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.

Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».

1. Первое уравнение должно иметь старший коэффициент 1. При необходимости поменяйте местами строки или умножьте на константу.
2. Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
3. Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
4. Используйте операции со строками, чтобы получить нули в нижнем столбце 2, ниже записи 1.
5. Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
6. Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу будут только нули.
7. Если какие-либо строки содержат все нули, поместите их внизу.

Решение 2 × 2 Система методом исключения Гаусса

Решите данную систему методом исключения Гаусса.

2x + 3y = 6 x − y = 12

Сначала мы запишем это как расширенную матрицу.

[231−1 \ | 612]

Нам нужна 1 в строке 1, столбце 1. Этого можно добиться, поменяв местами строку 1 и строку 2.

R1↔R2 → [1−123 \ | 126]

Теперь у нас есть 1 как первая запись в строке 1, столбце 1.Теперь давайте получим 0 в строке 2, столбце 1. Этого можно добиться, умножив строку 1 на −2,

.

, а затем добавляем результат в строку 2.

−2R1 + R2 = R2 → [1−105 \ | 125]

У нас есть только один шаг, чтобы умножить строку 2 на 15.

15R2 = R2 → [1−101 \ | 121]

Использовать обратную замену. Вторая строка матрицы представляет y = 1.

Обратный заменитель y = 1

в первое уравнение.

х− (1) = 12 х = 32

Решением является точка (32,1).

Решите данную систему методом исключения Гаусса.

4x + 3y = 11 x − 3y = −1

(2, 1)

Использование исключения Гаусса для решения системы уравнений

Используйте исключение Гаусса для решения заданного 2 × 2

Система уравнений .

2x + y = 14x + 2y = 6

Запишите систему как расширенную матрицу .

[2142 \ | 16]

Получить 1 в строке 1, столбце 1.Это можно сделать, умножив первую строку на 12.

12R1 = R1 → [11242 \ | 126] ​​

Далее нам нужен 0 в строке 2, столбце 1. Умножим строку 1 на −4

.

и добавьте строку 1 к строке 2.

−4R1 + R2 = R2 → [11200 \ | 124]

Вторая строка представляет уравнение 0 = 4.

Следовательно, система непоследовательна и не имеет решения.

Решение зависимой системы

Решите систему уравнений.

3x + 4y = 126x + 8y = 24

Выполните строковых операций на расширенной матрице, чтобы попытаться получить строково-эшелонированной формы .

A = [3468 \ | 1224]

−12R2 + R1 = R1 → [0068 \ | 024] R1↔R2 → [6800 \ | 24 0]

Матрица заканчивается всеми нулями в последней строке: 0y = 0.

Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите относительно y.

3x + 4y = 12 4y = 12−3x y = 3−34x

Итак, решение этой системы – (x, 3−34x).

Выполнение операций со строками в расширенной матрице 3 × 3 для получения формы Row-Echelon

Выполняет операции со строками с заданной матрицей, чтобы получить форму строки-эшелона.

[1−342−56−334 \ | 366]

В первой строке уже есть 1 в строке 1, столбце 1. Следующим шагом будет умножение строки 1 на −2

и добавьте его во 2 строку.Затем замените строку 2 результатом.

−2R1 + R2 = R2 → [1−3401−2−334 \ | 306]

Затем получить ноль в строке 3, столбце 1.

3R1 + R3 = R3 → [1−3401−20−616 \ | 3015]

Затем получите ноль в строке 3, столбце 2.

6R2 + R3 = R3 → [1−3401−2004 \ | 3015]

Последний шаг – получить 1 в строке 3, столбец 3.

14R3 = R3 → [1−3401−2001 \ | 3−6154]

Запишите систему уравнений в виде строк.

x − 2y + 3z = 9 −x + 3y = −42x − 5y + 5z = 17

[1−52 52 0 15 0 0 1 \ | 17292]

Решение системы линейных уравнений с использованием матриц

Мы видели, как написать систему уравнений с расширенной матрицей , а затем как использовать строковые операции и обратную подстановку для получения строковой формы . Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3.Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.

Решение системы линейных уравнений с помощью матриц

Решите систему линейных уравнений с помощью матриц.

x – y + z = 82x + 3y – z = −23x – 2y −9z = 9

Сначала мы пишем расширенную матрицу.

[1−1123−13−2−9 \ | 8−29]

Затем мы выполняем операции со строками для получения формы «строка-эшелон».

−2R1 + R2 = R2 → [1−1105−33−2−9 \ | 8−189] −3R1 + R3 = R3 → [1−1105−301−12 \ | 8−18−15]

Самый простой способ получить 1 в строке 2 столбца 1 – это поменять местами R2

и R3.

Развязки R2 и R3 → [1−11801−12−1505−3−18]

Затем

−5R2 + R3 = R3 → [1−1101−120057 \ | 8−1557] −157R3 = R3 → [1−1101−12001 \ | 8−151]

Последняя матрица представляет собой эквивалентную систему.

x − y + z = 8 y − 12z = −15 z = 1

Используя обратную подстановку, мы получаем решение как (4, −3,1).

Решение зависимой системы линейных уравнений с помощью матриц

Решите следующую систему линейных уравнений, используя матрицы.

−x − 2y + z = −1 2x + 3y = 2 y − 2z = 0

Запишите расширенную матрицу.

[−1−2123001−2 \ | -120]

Сначала умножьте строку 1 на −1

, чтобы получить 1 в строке 1, столбце 1. Затем выполните операций со строками для получения формы «строка-эшелон».

−R1 → [12−123001−2 \ | 120]

R2↔R3 → [12−101−2230 \ | 102]

−2R1 + R3 = R3 → [12−101−20−12 \ | 100]

R2 + R3 = R3 → [12−101−2000 \ | 210]

Последняя матрица представляет следующую систему.

х + 2y − z = 1 y − 2z = 0 0 = 0

Мы видим по тождеству 0 = 0

, что это зависимая система с бесконечным числом решений. Затем мы находим общее решение.Решив второе уравнение относительно y

и подставив его в первое уравнение, мы можем решить для z

в пересчете на x.

x + 2y − z = 1 y = 2zx + 2 (2z) −z = 1 x + 3z = 1 z = 1 − x3

Теперь подставим выражение для z

во второе уравнение, чтобы найти y

в пересчете на x.

y − 2z = 0 z = 1 − x3 y − 2 (1 − x3) = 0 y = 2−2×3

Общее решение – (x, 2−2×3,1 − x3).

Решите систему, используя матрицы.

х + 4y − z = 42x + 5y + 8z = 15x + 3y − 3z = 1

(1, 1, 1)

Можно ли решить любую систему линейных уравнений методом исключения Гаусса?

Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.

Дана система уравнений, решите с помощью матриц с помощью калькулятора.

1. Сохранить расширенную матрицу как матричную переменную [A], [B], [C],….
2. Используйте в калькуляторе функцию ref (, вызывая каждую матричную переменную по мере необходимости.

Решение систем уравнений с матрицами с помощью калькулятора

Решите систему уравнений.

5x + 3y + 9z = −1−2x + 3y − z = −2 − x − 4y + 5z = 1

Напишите расширенную матрицу для системы уравнений.

[539−23−1−1−45 \ | −1−2−1]

На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную [A].

[A] = [539−1−23−1−2−1−451]

Используйте в калькуляторе функцию ref (, вызывая матричную переменную [A].

исх. ([A])

Оценить.

[1 35 95150 1 1321−470 0 1−24187] → x + 35y + 95z = −15 y + 1321z = −47 z = −24187

При использовании обратной подстановки решение: (61187, −92187, −24187).

Применение матриц 2 × 2 к финансам

Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10.5% годовых, а другой – 12% годовых. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?

У нас есть система двух уравнений с двумя переменными. Пусть x =

– сумма, вложенная под 10,5% годовых, а y =

.

сумма вложена под 12% годовых.

x + y = 12,0000,105x + 0,12y = 1,335

В качестве матрицы имеем

[110.1050.12 \ | 12,0001,335]

Умножить строку 1 на −0,105

и добавьте результат в строку 2.

[1100.015 \ | 12,00075]

Затем,

0,015y = 75 y = 5,000

Итак, 12 000−5 000 = 7 000.

Таким образом, 5000 долларов были инвестированы под 12% годовых и 7000 долларов под 10,5%.

Применение матриц 3 × 3 к финансам

Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5% годовых, другой – 8%, а третий – 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?

У нас есть система трех уравнений с тремя переменными. Пусть x

– сумма, вложенная под 5% годовых, пусть y

.

будет сумма, вложенная под 8% годовых, и пусть z

– сумма, вложенная под 9% годовых. Таким образом,

х + у + г = 10,0000.05x + 0,08y + 0,09z = 770 2x − z = 0

В качестве матрицы имеем

[1110.050.080.0920−1 \ | 10,0007700]

Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.

−0.05R1 + R2 = R2 → [11100.030.0420−1 \ | 10,0002700] −2R1 + R3 = R3 → [11100.030.040−2−3 \ | 10,000270−20,000] 10.03R2 = R2 → [01101430 −2−3 \ | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 \ | 10,0009,000-2,000]

Третья строка говорит нам -13z = -2,000;

, таким образом, z = 6000.

Вторая строка говорит нам, что y + 43z = 9000.

Подставляем z = 6,000,

получаем

y + 43 (6000) = 9000y + 8000 = 9000y = 1000

Первая строка сообщает нам, что x + y + z = 10,000.

Подставляем y = 1,000

и z = 6000,

получаем

х + 1,000 + 6,000 = 10,000 х = 3,000

Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.

Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.

150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%

Ключевые понятия

• Расширенная матрица – это матрица, которая содержит коэффициенты и константы системы уравнений.См. [Ссылка].
• Матрица, дополненная постоянным столбцом, может быть представлена ​​как исходная система уравнений. См. [Ссылка].
• Операции со строками включают в себя умножение строки на константу, добавление одной строки к другой строке и замену строк местами.
• Мы можем использовать метод исключения Гаусса для решения системы уравнений. См. [Ссылка], [ссылка] и [ссылка].
• Операции со строками выполняются над матрицами для получения формы «строка-эшелон». См. [Ссылка].
• Чтобы решить систему уравнений, запишите ее в форме расширенной матрицы.Выполните операции со строками, чтобы получить форму эшелона строк. Обратно-заменитель, чтобы найти решения. См. [Ссылка] и [ссылка].
• Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. [Ссылка].
• Многие реальные проблемы можно решить с помощью расширенных матриц. См. [Ссылка] и [ссылка].

Упражнения по разделам

Словесный

Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как написать эту расширенную матрицу.

Да. Для каждой строки коэффициенты переменных записываются поперек соответствующей строки и помещается вертикальная черта; затем константы помещаются справа от вертикальной полосы.

Можно ли записать любую матрицу в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.

Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые могут быть использованы для решения расширенной матрицы [931−2 \ | 06].

Нет, существует множество правильных методов использования строковых операций над матрицей. Возможны два способа: (1) Поменять местами строки 1 и 2. Тогда R2 = R2−9R1.

(2) R2 = R1−9R2.

Затем разделите строку 1 на 9.

Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?

Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.

Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.

Алгебраические

Для следующих упражнений напишите расширенную матрицу линейной системы.

16y = 49x − y = 2

[0169−1 \ | 42]

3x + 2y + 10z = 3−6x + 2y + 5z = 13 4x + z = 18

x + 5y + 8z = 19 12x + 3y = 43x + 4y + 9z = −7

[1581230349 \ | 164-7]

6x + 12y + 16z = 4 19x − 5y + 3z = −9 x + 2y = −8

Для следующих упражнений запишите линейную систему из расширенной матрицы.

[−256−18 \ | 526]

−2x + 5y = 56x − 18y = 26

[320−1−94857 \ | 3−18]

3x + 2y = 13 − x − 9y + 4z = 538x + 5y + 7z = 80

[8291−175003 \ | 433810]

[45−2015887−3 \ | 122-5]

4x + 5y − 2z = 12 y + 58z = 28x + 7y − 3z = −5

Для следующих упражнений решите систему методом исключения Гаусса.

[−124−5 \ | −36]

(-1, -2)

2x − 3y = −95x + 4y = 58

(6,7)

2x + 3y = 12 4x + y = 14

(3,2)

−4x − 3y = −2 3x − 5y = −13

−5x + 8y = 3 10x + 6y = 5

(15,12)

3x + 4y = 12−6x − 8y = −24

−60x + 45y = 12 20x − 15y = −4

(х, 415 (5x + 1))

−1.06x − 2,25y = 5,51−5,03x − 1,08y = 5,40

34x − 35y = 414x + 23y = 1

(19639, −513)

[100011001 \ | 314587]

(31, −42,87)

[101110011 \ | 5020−90]

[123056008 \ | 479]

(2140,120,98)

[−0.10.3−0.1−0.40.20.10.60.10.7 \ | 0,20,8−0,8]

−2x + 3y − 2z = 3 4x + 2y − z = 9 4x − 8y + 2z = −6

(1813,1513, −1513)

x + y − 4z = −4 5x − 3y − 2z = 0 2x + 6y + 7z = 30

2x + 3y + 2z = 1 −4x − 6y − 4z = −2 10x + 15y + 10z = 5

(х, у, 12 (1−2x − 3y))

x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 5

x + 2y − z = 1 − x − 2y + 2z = −2 3x + 6y − 3z = 3

(х, −x2, −1)

Х + у = 2 х + г = 1-у-г = -3

x + y + z = 100 x + 2z = 125 − y + 2z = 25

(125, −25,0)

14x − 23z = −1215x + 13y = 4715y − 13z = 29

−12x + 12y + 17z = −5314 12x − 12y + 14z = 3 14x + 15y + 13z = 2315

(8,1, −2)

−12x − 13y + 14z = −296 15x + 16y − 17z = 431210−18x + 19y + 110z = −4945

Расширения

Для следующих упражнений используйте метод исключения Гаусса для решения системы.

х-17 + у-28 + г-34 = 0 х + у + г = 6 х + 23 + 2у + г-33 = 5

(1,2,3)

x − 14 − y + 14 + 3z = −1 x + 52 + y + 74 − z = 4 x + y − z − 22 = 1

x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 8 x + y + z = 1

(х, 3128−3×4,128 (−7x − 3))

x − 310 + y + 32−2z = 3 x + 54 − y − 18 + z = 32x − 14 + y + 42 + 3z = 32

x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 7 x + y + z = 1

Реальные приложения

Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.

Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если вкус шоколада в 3 раза популярнее, чем аромат ванили, сколько кексов продается в день?

В конкурирующем магазине кексов ежедневно продаются кексы на 4520 долларов. Шоколадные кексы стоят 2,25 доллара, а кексы из красного бархата – 1,75 доллара. Если общее количество кексов, проданных в день, составляет 2200, сколько кексов каждого вкуса продается каждый день?

860 красный бархат, 1340 шоколад

Вы вложили 10 000 долларов в два счета: один с простой процентной ставкой 3%, другой – с 2.5% годовых. Если ваша общая выплата процентов по истечении одного года составила 283,50 доллара, какая сумма была на каждом счете по истечении года?

Вы инвестировали 2300 долларов на счет 1 и 2700 долларов на счет 2. Если общая сумма процентов по истечении одного года составляет 254 доллара, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.

4% на счет 1, 6% на счет 2

Bikes’R’Us производит велосипеды по 250 долларов.Он стоит производителю 180 долларов за велосипед плюс стартовый взнос в размере 3500 долларов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?

Крупный магазин бытовой техники рассматривает возможность приобретения пылесосов у небольшого производителя. Магазин сможет приобрести пылесосы по 86 долларов каждый, со стоимостью доставки 9 200 долларов, независимо от того, сколько пылесосов будет продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать плату за пылесосы?

Три самых популярных вкуса мороженого – это шоколад, клубника и ваниль, составляющие 83% всех вкусов, продаваемых в магазине мороженого.Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?

В магазине мороженого возрастает спрос на три вкуса. В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы – на 20%.Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте процент продаж мороженого, произведенного каждым отдельным мороженым в прошлом году.

Банан – 3%, тыква – 7%, а каменистая дорога – 2%

Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек. Кешью весит 3 г, фисташки – 4 г, миндаль – 5 г. Если сумка весит 3.7 кг, узнайте, сколько орехов каждого вида в мешке.

Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля. Для начала выясните, сколько орехов каждого типа было в пакете.

100 миндальных орехов, 200 кешью, 600 фисташек

Глоссарий

дополненная матрица

матрица коэффициентов, примыкающая к столбцу констант, разделенному вертикальной линией в скобках матрицы

матрица коэффициентов

матрица, содержащая только коэффициенты из системы уравнений

Исключение по Гауссу

с использованием элементарных операций со строками для получения матрицы в форме строка-эшелон

главная диагональ

записи из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы

рядная форма

после выполнения строковых операций матричная форма, содержащая единицы по главной диагонали и нули в каждом пробеле ниже диагонали

эквивалент ряда

две матрицы A

и

B

эквивалентны строкам, если один может быть получен из другого путем выполнения базовых операций со строками

строковые операции

добавление одной строки к другой строке, умножение строки на константу, перестановка строк и т. Д. С целью получения формы “строка-эшелон”

---

Эта работа находится под лицензией Creative Commons Attribution 4.0 Международная лицензия.

Вы также можете бесплатно скачать по адресу http://cnx.org/contents/[email protected]

Атрибуция:

3 Методы решения систем уравнений

Три метода, наиболее часто используемые для решения систем уравнений, – это подстановка, исключение и расширенные матрицы. Замена и исключение – это простые методы, с помощью которых можно эффективно решить большинство систем двух уравнений за несколько простых шагов. Метод расширенных матриц требует большего количества шагов, но его применение распространяется на большее количество систем.

Замена

Замена – это метод решения систем уравнений путем удаления всех переменных, кроме одной, в одном из уравнений, а затем решения этого уравнения. Это достигается путем выделения другой переменной в уравнении и последующей подстановки значений этих переменных в другое уравнение. Например, чтобы решить систему уравнений x + y = 4, 2x – 3y = 3, выделите переменную x в первом уравнении, чтобы получить x = 4 – y, затем подставьте это значение y во второе уравнение, чтобы получить 2 (4 – у) – 3у = 3.Это уравнение упрощается до -5y = -5 или y = 1. Подставьте это значение во второе уравнение, чтобы найти значение x: x + 1 = 4 или x = 3.

Исключение

Исключение – еще один способ решения системы уравнений, переписав одно из уравнений в терминах только одной переменной. Метод исключения достигает этого путем сложения или вычитания уравнений друг из друга, чтобы сократить одну из переменных. Например, сложение уравнений x + 2y = 3 и 2x – 2y = 3 дает новое уравнение 3x = 6 (обратите внимание, что члены y сокращены).Затем система решается с использованием тех же методов, что и для замены. Если невозможно сократить переменные в уравнениях, необходимо будет умножить все уравнение на коэффициент, чтобы коэффициенты совпали.

Расширенная матрица

Расширенные матрицы также могут использоваться для решения систем уравнений. Расширенная матрица состоит из строк для каждого уравнения, столбцов для каждой переменной и расширенного столбца, который содержит постоянный член с другой стороны уравнения.Например, расширенная матрица для системы уравнений 2x + y = 4, 2x – y = 0 имеет вид [[2 1], [2 -1] … [4, 0]].

Определение решения

На следующем этапе используются элементарные операции со строками, такие как умножение или деление строки на константу, отличную от нуля, и добавление или вычитание строк. Цель этих операций – преобразовать матрицу в форму строки-эшелона, в которой первая ненулевая запись в каждой строке равна 1, записи выше и ниже этой записи – все нули, а первая ненулевая запись для каждого row всегда находится справа от всех таких записей в строках над ней.Строчно-эшелонированная форма для указанной выше матрицы – [[1 0], [0 1] … [1, 2]]. Значение первой переменной задается первой строкой (1x + 0y = 1 или x = 1). Значение второй переменной задается второй строкой (0x + 1y = 2 или y = 2).