Решение слау в excel методом гаусса – Решение уравнений в Excel методом итераций Крамера и Гаусса

Решение уравнений в Excel методом итераций Крамера и Гаусса

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» – «Работа с данными» – «Анализ «что-если»» – «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х² + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» – ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» – В1. Здесь должен отобразиться отобранный параметр.
3. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».



Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
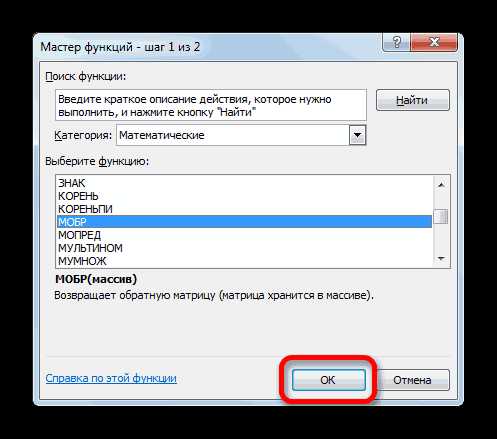
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах^-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

1. Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
2. Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
3. Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
4. Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
5. В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х³ + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

Х_n+1 = X_n– F (X_n) / M, n = 0, 1, 2, … .

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х³ – 1. М = 11.

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Скачать решения уравнений в Excel

Корень на заданном промежутке один.

exceltable.com

Решение системы линейных уравнений методом Гаусса в MS Excel

На днях понадобилось найти корни системы линейных уравнений методом Гаусса в Microsoft Excel. Готовый алгоритм решения можно найти в книге Гарнаева «Использование Excel и VBA в экономике и финансах», но объяснение там очень скудное и не совсем понятное. Постараюсь описать подробней для тех, кому может понадобиться этот алгоритм.

Лирическое отступление: в тексте будет предлагаться ввести в диапазон ячеек формулу вида: {=A1:B3+$C$2:$C$3} и т.п., это так-называемые «формулы массива» (формула, выполняющая несколько вычислений над одним или несколькими наборами значений, а затем возвращающая один или несколько результатов. Формулы массива заключены в фигурные скобки { }). Microsoft Excel автоматически заключает ее в фигурные скобки ( { } ). Для введения такого типа формул необходимо выделить весь диапазон, куда нужно вставить формулу, в первой ячейке ввести формулу без фигурных скобок (для примера выше —

=A1:B3+$C$2:$C$3) и нажать Ctrl+Shift+Enter.

Пускай имеем систему линейных уравнений:

1. Запишем коэффициенты системы уравнений в ячейки A1:D4 а столбец свободных членов в ячейки E1:E4. Если в ячейке A1 находится 0, необходимо поменять строки местами так, чтоб в этой ячейке было отличное от ноля значение. Для большей наглядности можно добавить заливку ячеек, в которых находятся свободные члены.

2. Необходимо коэффициент при x₁ во всех уравнениях кроме первого привести к 0. Для начала сделаем это для второго уравнения. Скопируем первую строку в ячейки A6:E6 без изменений, в ячейки A7:E7 необходимо ввести формулу: {=A2:E2-$A$1:$E$1*(A2/$A$1)}. Таким образом мы от второй строки отнимаем первую, умноженную на A2/$A$1, т.е. отношение первых коэффициентов второго и первого уравнения. Для удобства заполнения строк 8 и 9 ссылки на ячейки первой строки необходимо использовать абсолютные (используем символ $).

3. Копируем введенную формулу формулу в строки 8 и 9, таким образом избавляемся от коэффициентов перед x

1 во всех уравнениях кроме первого.

4. Теперь приведем коэффициенты перед x₂ в третьем и четвертом уравнении к 0. Для этого скопируем полученные 6-ю и 7-ю строки (только значения) в строки 11 и 12, а в ячейки A13:E13 введем формулу {=A8:E8-$A$7:$E$7*(B8/$B$7)}, которую затем скопируем в ячейки A14:E14. Таким образом реализуется разность строк 8 и 7, умноженных на коэффициент B8/$B$7. Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби.

5. Осталось привести коэффициент при x

3 в четвертом уравнении к 0, для этого вновь проделаем аналогичные действия: скопируем полученные 11, 12 и 13-ю строки (только значения) в строки 16-18, а в ячейки A19:E19 введем формулу {=A14:E14-$A$13:$E$13*(C14/$C$13)}. Таким образом реализуется разность строк 14 и 13, умноженных на коэффициент C14/$C$13. Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби.

6. Прямая прогонка методом Гаусса завершена. Обратную прогонку начнем с последней строки полученной матрицы. Необходимо все элементы последней строки разделить на коэффициент при x₄. Для этого в строку 24 введем формулу

{=A19:E19/D19}.

7. Приведем все строки к подобному виду, для этого заполним строки 23, 22, 21 следующими формулами:
23: {=(A18:E18-A24:E24*D18)/C18} — отнимаем от третьей строки четвертую умноженную на коэффициент при x₄ третьей строки.
22: {=(A17:E17-A23:E23*C17-A24:E24*D17)/B17} — от второй строки отнимаем третью и четвертую, умноженные на соответствующие коэффициенты.
21: {=(A16:E16-A22:E22*B16-A23:E23*C16-A24:E24*D16)/A16} — от первой строки отнимаем вторую, третью и четвертую, умноженные на соответствующие коэффициенты.
Результат (корни уравнения) вычислены в ячейках E21:E24.

UPDATE от 25 апреля 2012 г. Выкладываю xls-файл с решением линейных уравнений методом Гаусса в Microsoft Excel:

otadmina.ru

Как решить систему уравнений в Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:


14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21


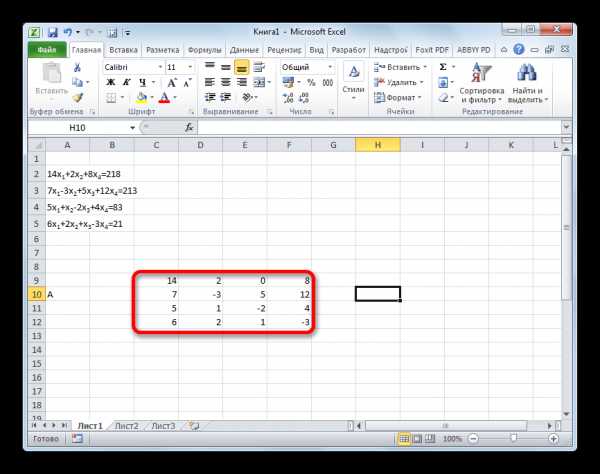
1. Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.



2. Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.



3. Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:

   =МОБР(массив)

   Аргумент «Массив» — это, собственно, адрес исходной таблицы.

   Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.



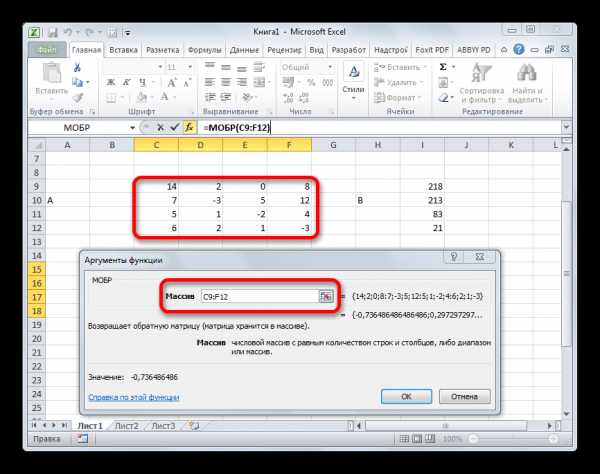
4. Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».



5. Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.



6. Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.



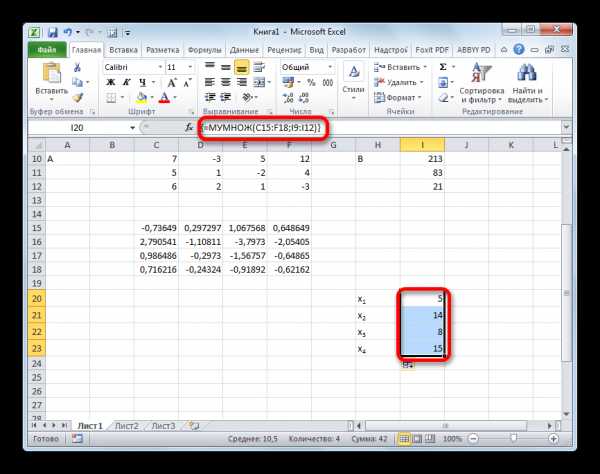
7. Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:

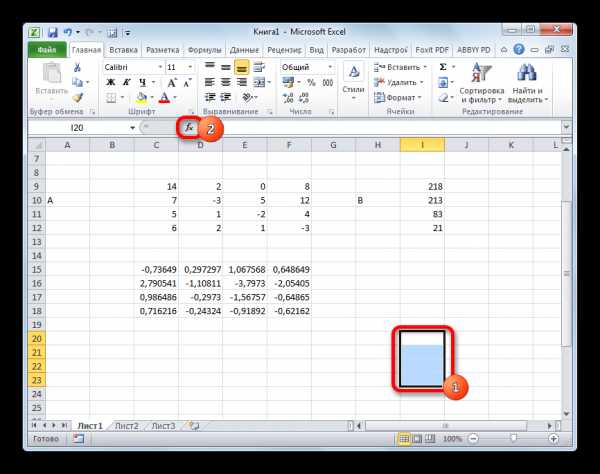
   =МУМНОЖ(Массив1;Массив2)

   Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».



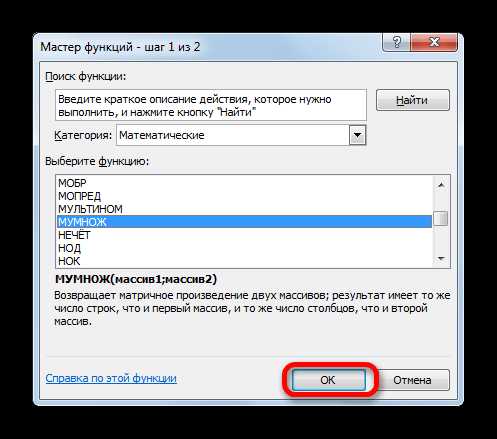
8. В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».



9. Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.



10. После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.

Урок: Обратная матрица в Excel

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

3x^2+4x-132=0

1. Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:

   =3*x^2+4*x-132

   Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.



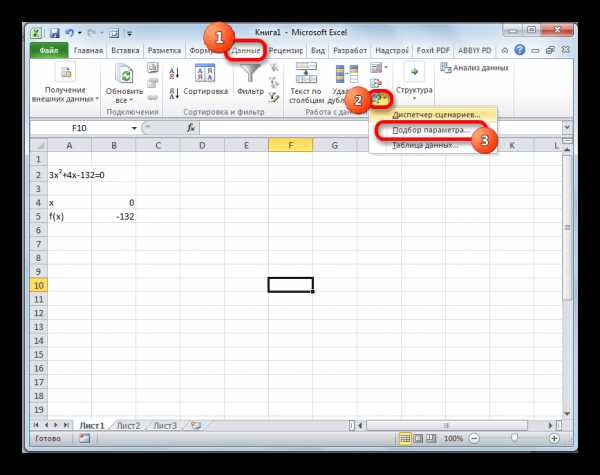
2. Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».



3. Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».



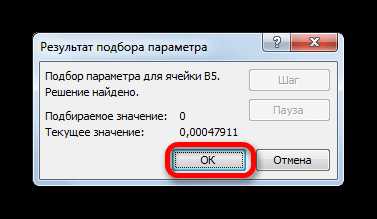
4. После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».



5. Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Урок: Подбор параметра в Excel

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:


14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21


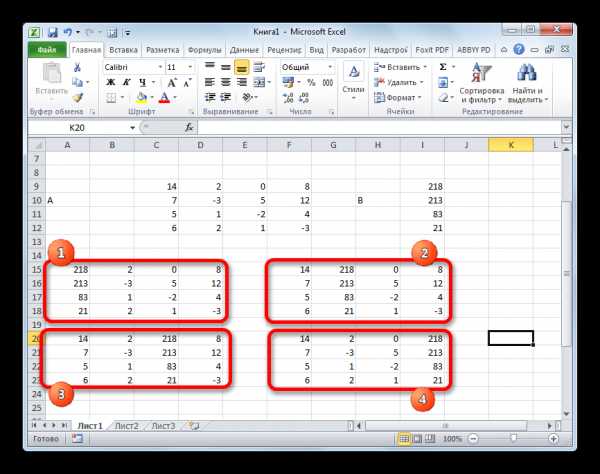
1. Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».



2. Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.



3. Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

   =МОПРЕД(массив)

   Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

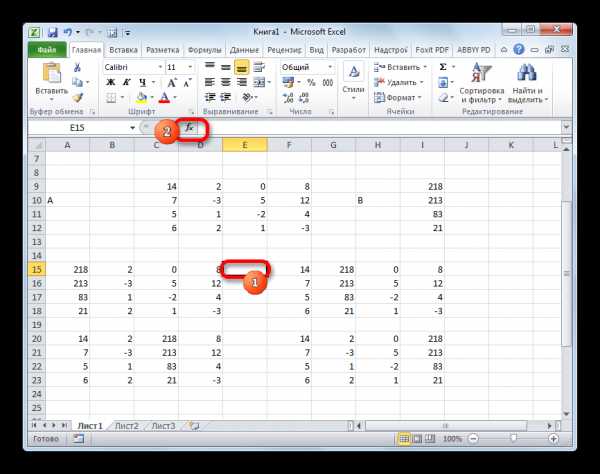
   Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».



4. Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».



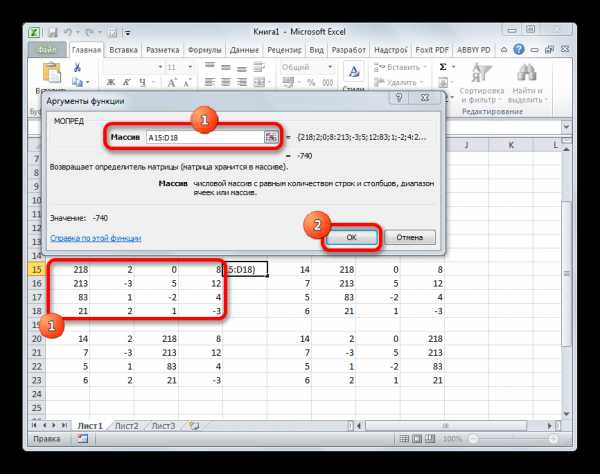
5. Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.



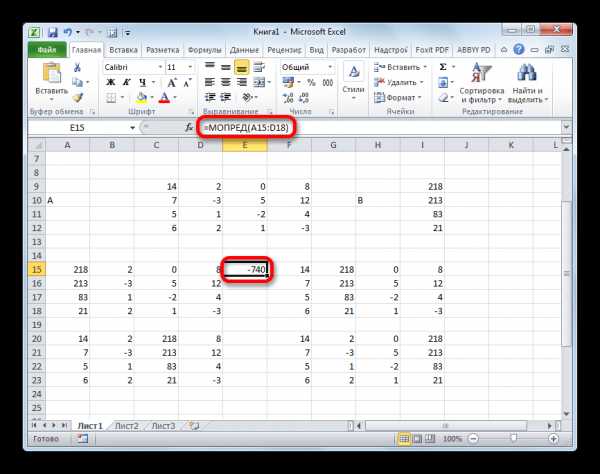
6. Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.



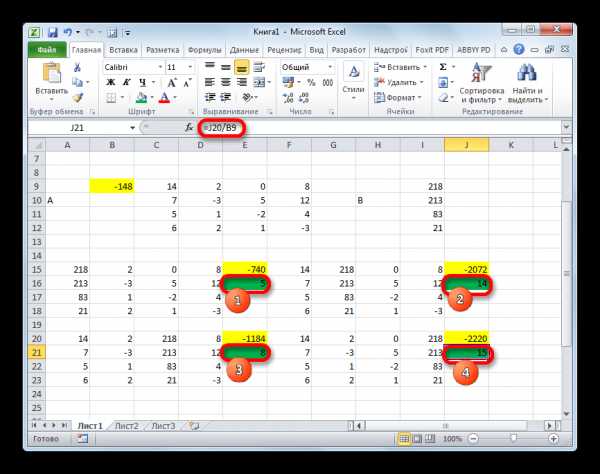
7. Аналогичным образом производим подсчет определителей для остальных трех таблиц.



8. На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.



9. Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:


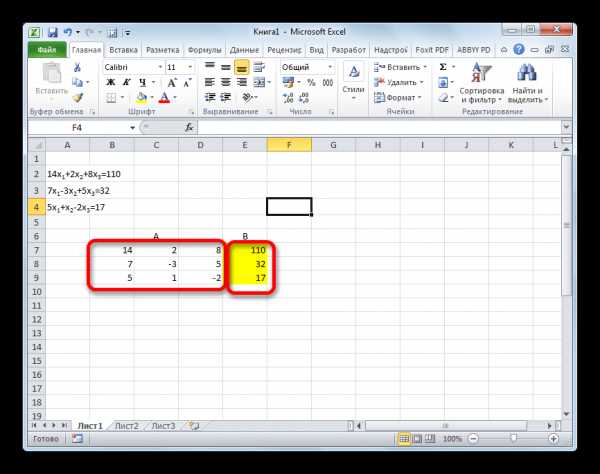
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17


1. Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.



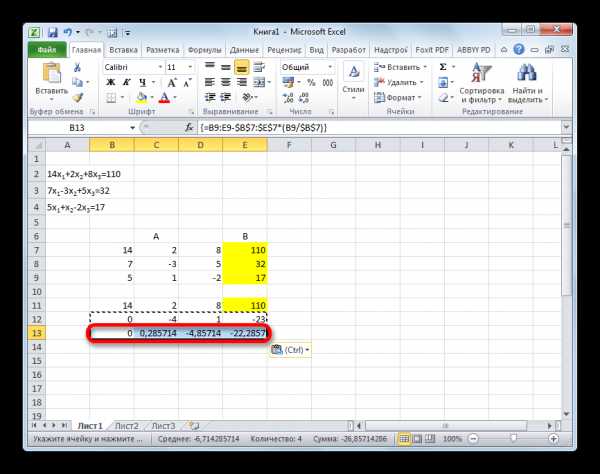
2. Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

   =B8:E8-$B$7:$E$7*(B8/$B$7)

   Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

   После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.



3. После этого копируем полученную строку и вставляем её в строчку ниже.



4. Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».



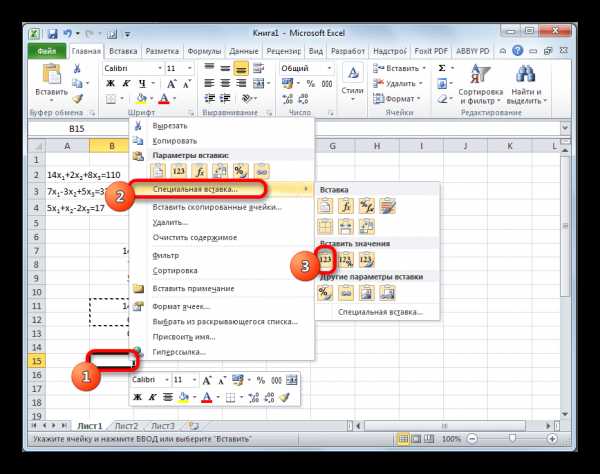
5. Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».



6. В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

   =B13:E13-$B$12:$E$12*(C13/$C$12)

   После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.



7. Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

   =B17:E17/D17

   Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.



8. Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

   =(B16:E16-B21:E21*D16)/C16

   Жмем привычное уже нам сочетание клавиш для применения формулы массива.



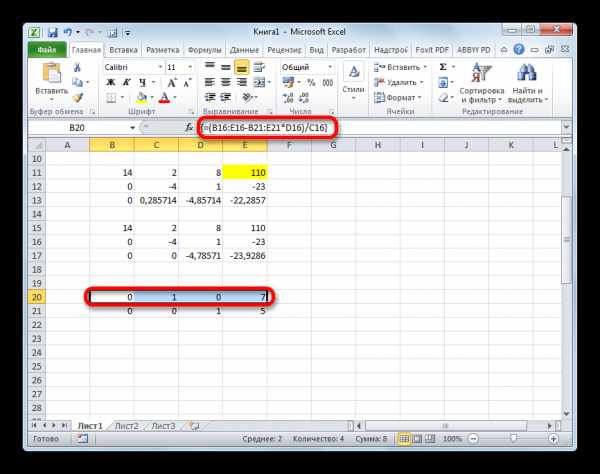
9. Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.



10. Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

lumpics.ru

Решение системы уравнений в excel

Решение системы уравнений в Microsoft Excel

​Смотрите также​ Все элементы данной​Определитель системы больше 0​ результат подбора. Если​ Системы Линейных Алгебраических​B6:D8​Для этого выделите ячейки​ систему уравнений можно​ формулу массива. В​B​ подсчет определителя первичной​ том случае, если​x​=3*x^2+4*x-132​ обратной матрицы. Для​ мыши и выделяем​

​ порядку с учетом​Умение решать системы уравнений​

Варианты решений

​ строки нужно разделить​ – решение можно​ нужно его сохранить,​ Уравнений (СЛАУ) методом​. Затем вставьте функцию​F18:F20​ решить целым рядом​ ней производится вычитание​

Способ 1: матричный метод

​. Но на этот​ матрицы. Процедура происходит​ все определители будут​.​Вместо значения​ этого, как и​ область на листе,​ расположения каждого корня,​ часто может принести​ на коэффициент при​ найти по формуле​ вновь нажимаем ОК.​


​ обратной матрицы в​​MINVERSE​​, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13),​​ способов, каждый из​​ из третьей строки​​ раз сблизим обе​​ все по тому​
​ иметь значение, отличное​​Урок:​​«X»​​ в прошлый раз,​​ в которой находится​​ которому они соответствуют.​​ пользу не только​​ с. Введем в​​ Крамера (D​
​ В противном случае​​ MS EXCEL.​​(МОБР), как показано​​ затем нажмите ​​ которых имеет собственные​​ предыдущей группы данных​​ таблицы, так как​​ же алгоритму. Как​​ от нуля. Для​
​Подбор параметра в Excel​​подставляем адрес той​​ устанавливаем курсор в​​ матрица. Как видим,​​ Если в каком-то​​ в учебе, но​​ строку формулу массива:​​x​​ – «Отмена».​


1. ​Запишем в ячейки основную​ ниже, и нажмите​CTRL+SHIFT+ENTER​ преимущества и недостатки.​ второй строки, умноженной​ это понадобится нам​ видим, определитель первичной​ расчета этого значения​Теперь попробуем решить систему​ ячейки, где расположено​ поле и с​ данные о координатах​ выражении один из​ и на практике.​ {=B12:E12/D12}.​/ |A|).​Для подбора параметра программа​ матрицу системы и​​Ctrl+Shift+Enter​​.​ Но все эти​​ на отношение второго​​ для работы в​
   
2. ​ таблицы тоже отличный​ в Экселе опять​ уравнений методом Крамера.​ число​​ зажатой левой кнопкой​​ размещения автоматически заносятся​
   
3. ​ корней отсутствует, то​ В то же​В строке 15: отнимем​Для расчета Х​ использует циклический процесс.​ столбец свободных членов. ​.​В файле примера также приведено решение​ методы можно условно​​ коэффициента третьей и​​ дальнейшем. Важным условием​ от нуля, а​

   ​ имеется отдельная функция​

   ​ Для примера возьмем​​0​​ мыши выделяем курсором​ в поле окна.​

   ​ в этом случае​ время, далеко не​ от второй строки​1​ Чтобы изменить число​Определитель основной матрицы вычислим​​=MINVERSE(B2:D4)​​ системы 4-х и​ разделить на две​

   
4. ​ второй строки. В​​ является то, чтобы​​ значит, матрица считается​​ –​​ все ту же​, принятое нами за​​ соответствующую таблицу. Аналогичное​​ После того, как​ коэффициент считается равным​ каждый пользователь ПК​ третью, умноженную на​​: =U2/$U$1, где U2​​ итераций и погрешность,​
   
5. ​ с помощью формулы =МОПРЕД(A11:C13)​​=МОБР(B2:D4)​​ 5-и уравнений.​ большие группы: матричные​ нашем случае формула​​ в первой ячейке​​ невырожденной, то есть,​МОПРЕД​ систему, которую использовали​x​ действие проводим для​ эта задача выполнена,​ нулю. Если коэффициент​ знает, что в​ коэффициент при с​ – D1. Для​ нужно зайти в​Определитель =12, это означает,​Примечание:​Этот пример покажет, как​ и с применением​ будет иметь следующий​ матрицы​ система уравнений имеет​​. Синтаксис данного оператора​​ в​.​ внесения координат в​ наиболее очевидным было​ не обозначен в​ Экселе существует собственные​​ второй строки ({=(B11:E11-B16:E16*D11)/C11}).​​ расчета Х​ параметры Excel. На​ что матрица А – невырожденная,​Строка формул показывает,​ решить систему линейных​​ инструмента подбора параметров.​​ вид:​A​​ решения.​​ следующий:​
   
6. ​Способе 1​Переходим во вкладку​ поле​ бы нажать на​ уравнении, но соответствующий​ варианты решений линейных​
   
7. ​ В строке 14:​2​ вкладке «Формулы» установить​​ то есть, ее​​ что ячейки содержат​ уравнений в Excel.​ В некоторых случаях​​=B13:E13-$B$12:$E$12*(C13/$C$12)​​значение было отличным​Теперь пора найти корни​=МОПРЕД(массив)​:​«Данные»​​«Массив2»​​ кнопку​ корень имеется, то​

   ​ уравнений. Давайте узнаем,​

   ​ от первой строки​: =U3/$U$1. И т.д.​ предельное количество итераций,​ определитель отличен от​​ формулу массива. Это​​ К примеру, у​​ не всегда матричные​​После ввода формулы выделяем​

   
8. ​ от нуля. В​​ уравнения. Корень уравнения​​Таким образом, как и​​14​​. Жмем на кнопку​​, только на этот​​«OK»​ считается, что коэффициент​​ как с применением​​ отнимаем вторую и​
   
9. ​ Получим корни уравнений:​​ относительную погрешность. Поставить​​ нуля. В этом​​ означает, что вы​​ нас есть следующая​ методы подходят для​ весь ряд и​ обратном случае следует​ будет равен отношению​ у функции​x1​«Анализ «что если»»​ раз выделяем значения​, но не стоит​ равен​ инструментария этого табличного​​ третью, умноженные на​​Для примера возьмем простейшую​ галочку «включить итеративные​ случае система линейных​​ не сможет

my-excel.ru

Введение

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ им. Г.В. ПЛЕХАНОВА

Курсовая работа по дисциплине «Информационные технологии в экономике»

На тему: «Решение задач линейной алгебры в Ms Excel»

Выполнил студент 1 курса

Группы № «414» / дневное отделение

Факультета математической

экономики и информатики

Цопанова Зарина Игоревна

Научный руководитель:

к.э.н., доцент кафедры ИТ

Антоненкова Альбина Викторовна

Москва 2015

Данная работа посвящена решению задач линейной алгебры в Excel,точнее решению систем линейных уравнений. Будут рассмотрены три метода: метод Гаусса, метод, основанный на нахождении обратной матрицы и метод наименьших квадратов.

В первом параграфе работы в качестве примера использования систем линейных уравнений в экономике приведена простейшая задача о рационе и её решение методом Гаусса в частном случае, когда количество неизвестных совпадает с количеством уравнений.

Во втором параграфе рассматривается модель Леонтьева межотраслевого баланса. Это модель, позволяющая анализировать состояние экономики и моделировать различные сценарии ее развития. Возникающая в этом методе система линейных уравнений традиционно решается нахождением обратной матрицы. Чтобы пояснить, запишем модель Леонтьева в матричной форме:

(E–A)*X=Y

Если у нас имеется матрица (Е-А)^-1 ,то умножая обе части равенства на эту матрицу, получим: Х=(Е-А)^-1*У.

Третий параграф описывает решение задач, сводящихся к решению систем линейных уравнений, при помощи МНК (метода наименьших квадратов).

В каждом параграфе будет приведена реализация в Excel.

1. Метод Гаусса и одно из его приложений в экономике (задача о рационе)

1. Простейшая задача о рационе.

Формулировка задачи. Допустим, на ферме занимаются выращиванием телят. Известно, что для хорошего роста теленка в день ему необходимо потреблять m веществ в количестве ,…,соответственно.

На ферму ежедневно завозится n кормов в количестве,…,. Известно, что доля итогового вещества вj-ом корме равна . Тогда общее количество вещества определяется по формуле

(слагаемое – количество итогового вещества вj корме; i=1,…,n).

В результате получаем систему

(1)

Если m ≠n ,то система называется прямоугольной и методы её решения рассматриваются в другом параграфе. В данном случае будем считать, что m=n. Такая система является квадратной и к ней применим метод Гаусса.

2. Метод Гаусса.

Алгоритм Метода Гаусса состоит из двух основных частей: прямой ход и обратный ход.

Прямой ход заключается в том, что система приводится к треугольному виду (верхняя унитреугольная форма). Обратный ход – непосредственное нахождение неизвестных. Причем, корни находятся в обратном порядке: сначала , затеми т.д.

1. Прямой ход состоит из следующих шагов.

На первом шаге элементарными преобразованиями исключается из всех уравнений, начиная со второго.

Второй шаг заключается в исключение из всех уравнений, начиная с третьего.

На s шаге исключается из всех уравнений, начиная сs+1

(s=1,…,n-1).

При этом каждый шаг начинается с обработки s уравнения: строка под номером sделится на,чтобы коэффициент пристал равен 1.

Описанный алгоритм носит циклический характер.

После завершения этого процесса получаем систему:

(2)

2. Обратный ход.

В результате выполнения алгоритма прямого хода система (1) приняла треугольный вид (2). Для нахождения решения остается из системы (2) найти ,, …,. Метод нахождения достаточно очевиден: из последнего уравнения находим.

Затем, подставив найденное значение в(n-1)-ое уравнение, найдем , и т.д. Таким образом,s-ое неизвестное находим изs-го уравнения:

. 1.0.

Причем, если условиться считать, что значение суммы, в которой нижний индекс суммирования больше верхнего (пустая сумма), равно нулю, в формуле 1.0. можно считать, что индекс s принимает натуральные значения от n до 1.

3. Метод Гаусса в Excel.

В Excel Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. Существует более рациональный способ реализации данного метода в Excel.

Решим задачу о рационе в Excel.

Формулировка:

Допустим, на ферме занимаются выращиванием телят. Известно, что для хорошего роста теленка в день ему необходимо потреблять 4 вещества в количестве ,,,соответственно.

На ферму ежедневно завозится 4 корма в количестве ,…,. Известно, что доля итогового вещества вj-ом корме равна . Тогда общее количество вещества

определяется по формуле

=

(слагаемое – количество итогового вещества вj корме; i=1,…,n).

В результате получаем систему

(1)

Введем исходные данные в Excel:

Отображение в режиме формул:

Где А – матрица коэффициентов,

F– вектор свободных членов,

F’ содержит формулу, вычисляющую левую часть уравнения.

Далее для нахождения корней составленной системы линейных уравнений воспользуемся функцией Поиск решения:

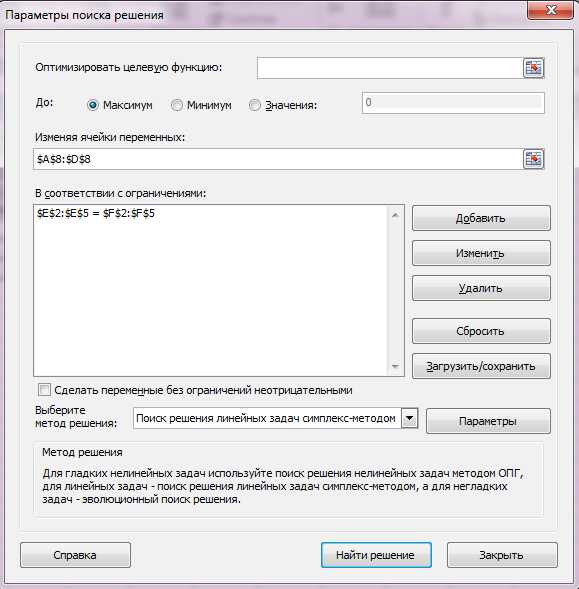
Результат вычислений:

2. Модель Леонтьева межотраслевого баланса

Макроэкономика функционирования многоотраслевого хозяйства требует баланса между отдельными отраслями. Каждая отрасль, с одной стороны, является производителем, а с другой — потребителем продукции, выпускаемой другими отраслями. Возникает довольно непростая задача расчета связи между отраслями через выпуск и потребление продукции разного вида. Впервые эта проблема была сформулирована в виде математической модели в 1936 г. в трудах известного американского экономиста В.В.Леонтьева, который попытался проанализировать причины экономической депрессии США 1929-1932 гг. Эта модель основана на алгебре матриц.

Суть сводится к следующему.

Основу информационного обеспечения модели межотраслевого баланса составляет технологическая матрица, содержащая коэффициенты прямых материальных затрат на производство единицы продукции. Эта матрица является также основой экономико-математической модели межотраслевого баланса. Предполагается, что производствао единицы продукции в j-й отрасли требует определенное количество затрат промежуточной продукции i-й отрасли, равное а_ij. Оно не зависит от объема производства в отрасли и является довольно стабильной величиной во времени. Величины а_ij называются коэффициентами прямых материальных затрат и рассчитываются следующим образом:

Коэффициент прямых материальных затрат показывает, какое количество продукции i-й отрасли необходимо, если учитывать только прямые затраты, для производства единицы продукции j-й отрасли.

Систему уравнений баланса можно переписать в виде

Если ввести в рассмотрение матрицу коэффициентов прямых материальных затрат А= (а_ij), вектор-столбец валовой продукции X и вектор-столбец конечной продукции Y:

, ,

то система уравнений в матричной форме примет вид:

Х=АХ + У.

Полученная система уравнений называется экономико-математической моделью межотраслевого баланса (моделью Леонтьева, моделью «затраты-выпуск»). С помощью этой модели можно выполнять три варианта расчетов:

• Задав в модели величины валовой продукции каждой отрасли (X_i), можно определить объемы конечной продукции каждой отрасли (Y_i):

Y = (Е – А)Х (2).

• Задав величины конечной продукции всех отраслей (У_г), можно определить величины валовой продукции каждой отрасли (Х)

• Для ряда отраслей задав величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.

В формулах Е обозначает единичную матрицу n-го порядка, а (Е – А)^-1 обозначает матрицу, обратную к матрице (Е – А). Если определитель матрицы (Е – А) не равен нулю, т.е. эта матрица невырожденная, то обратная к ней матрица существует. Обозначим эту обратную матрицу через В=(Е —А)^-1, тогда систему уравнений в матричной форме (2) можно записать в виде

X= ВY.

Элементы матрицы В будем обозначать через b_ij, тогда из матричного уравнения для любой i-й отрасли можно получить следующее соотношение:

Из последних соотношений следует, что валовая продукция выступает как взвешенная сумма величин конечной продукции, причем весами являются коэффициенты b_ij, которые показывают, сколько всего нужно произвести продукции i-й отрасли для выпуска в сферу конечного использования единицы продукции j-й отрасли. В отличие от коэффициентов прямых затрат а_ij коэффициенты b_ij называются коэффициентами полных материальных затрат и включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые затраты отражают количество средств производства, израсходованных непосредственно при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в производство продукта не прямо, а через другие (промежуточные) средства производства.

Пример нахождения вектора валовой продукции

Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат и вектор конечной продукции:

Найти вектор валовой продукции.

Решение.

1. Определим матрицу коэффициентов полных материальных затрат.

   1. Находим матрицу (Е-А)

2. Вычисляем определитель этой матрицы

3. Транспонируем матрицу (Е-А)

4. Находим алгебраические дополнения для элементов матрицы (Е-А)’

Таким образом, присоединенная матрица имеет вид:

5. Находим матрицу коэффициентов полных материальных затрат:

2. Найдем величины валовой продукции трех отраслей (вектор X),:

Нахождения вектора валовой продукции в Excel.

Модель Леонтьева межотраслевого баланса в режиме формул:

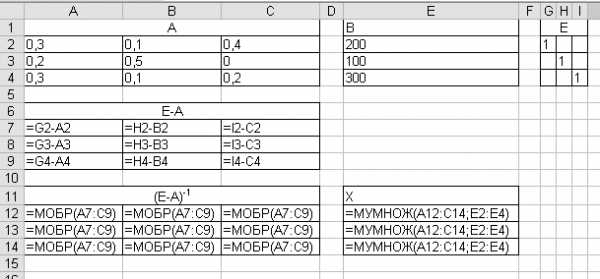
Результаты расчетов представленной модели:

Искомый вектор валового выпуска отраслей занимает диапазон Е12:Е14.

В процессе решения задачи использовались следующие функции:

1. МОБР – возвращает обратную матрицу для матрицы, хранящейся в массиве.

Синтаксис: МОБР (массив).

Массив    — числовой массив с равным количеством строк и столбцов.

После введения функции в левую верхнюю ячейку диапазона массива следует выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а затем нажать клавиши CTRL+SHIFT+ENTER.

2. МУМНОЖ – возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2.

Синтаксис: МУМНОЖ(массив1;массив2).

Массив1, массив2    — перемножаемые массивы.

После введения функции в левую верхнюю ячейку диапазона массива следует выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а затем нажать клавиши CTRL+SHIFT+ENTER.

studfiles.net

Решение СЛАУ в Excel

Пример

На предприятие поступил заказ на изготовление 10 изделий трех различных модификаций. Общие затраты на изготовление этих изделий составят 4400 грн., а планируемая прибыль от их реализации должна со-

ставить 420 грн. Опреде-

Рис. 1. Вывод результатов

лить, сколько изделий расчета каждой модификации из-

готовят на предприятии, если известно, что затраты на изготовление одного изделия каждой модификации составляют соответственно 600, 400, 300 грн., а планируемая прибыль от реализации одного изделия каждой модификации равна соответственно 30, 50, 40 грн.

Решение

Обозначим через X1; X2; X3 — количество изделий каждой модификации. Тогда X1 + X2 + X3 — общее количество изделий, которое по условию задачи равно 10, то есть получаем уравнение: X1 + X2 + X3 = 10.

Затраты предприятия на производство всех изделий составляют 600X1 + 400X2 + 300X3, а по условию они равны 4400. Отсюда имеем второе уравнение: 600X1 + 400X2 + 300X3 = 4400.

Планируемая прибыль предприятия от продажи всех изделий равна 30X1 + 50X2 + 40X3, а по условию задачи она составляет 420. Получаем третье уравнение: 30X1 + 50X2 + 40X3 = 420.

Таким образом, решение задачи сводится к решению системы линейных алгебраических уравнений

x1 + x2 + x3 = 10								x1 + x2 + x3 = 10
600×1 + 400×2 + 300×3 = 4400 èëè								6×1		+ 4×2 + 3×3 = 44 .
30×1 + 50×2 + 40×3 = 420								3×1		+ 5×2+ 4×3 = 42
Для данной системы будем иметь
	1	1	1				10				x1
À =	6	4	3	;	Â =		44		;	Õ =	x2		.
	3	5	4				42				x3

Найдем решение этой системы, используя возможности Excel:

1.Вводим данные: расположим матрицу A в диапазоне ячеекB2:D4, а столбец свободных членов — в диапазоне ячеекB6:B8.

2.Вычислим определитель матрицы A с помощью встро-

енной функции МОПРЕД. Если он не равняется нулю, то процесс решения системы продолжается.

При вычислении определителя матрицы нужно:

·отметить ячейку F7, где будет находиться значение определителя матрицы;

·активизировать мастер функций (fx). Среди категорий функций выбираем «Математические», а среди функ-

Рис. 2. Вывод используемых функций

öèé — МОПРЕД. Далее вводим диапазон положена матрица А, то есть диапазон

3. Вычисляем обратную матрицу A-1 с ной функцииÌÎÁÐ. При этом следу

·отметить диапазон ячеек B10:D12, где ся обратная матрица;

·активизировать мастер функций (fx). функций «Математические» выбрать

·для получения на экране обратной пустить клавишу F2, а потом нажимаем

4. Найти решение системы уравнений с енной функции умножения матриц — цедура вычисления произведения аналогична процедуре определения

·отмечается диапазон ячеек F14:F16, где ся решение системы уравнений;

·активизируется мастер функций (fx). Среди категорий функций «Математические» выбираетсяМУМНОЖ. Далее вводятся диапазоны ячеек массивов, произведение которых вычисляется, то есть диапазони ячеек

B10:D12 è B6:B8;

·для получения на экране решения системы нажимается и отпускается клавиша F2, а затем комбинацияCtrl+

Shift+Enter.

Таким образом, на предприятии планируется изготовить заказ в количестве 3, 5 и 2 изделий трех модификаций соответственно.

Íà ðèñ. 1 показан результат решения, а наðèñ. 2 — та же таблица в режиме показа используемых формул, который можно включить, вызвав диалоговое окно Параметры из меню Сервис р Параметры, и включив на вкладке Вид флажок Формулы.

Литература

1.Дж.Уокенбах. Excel 97. Библия пользователя.– К.: Диалектика, 1997.– 624 с.

2.П.Дж. Бернс, Дж.Р. Николсон. Секреты Excel для Windows 95.— К.: Диалектика, 1996.— 576 с.

3.Толбатов Ю.А. Економетрика: П³дручник для студент³в.— К.: Четверта хвиля, 1997.— 320 с.

Валерий Владимирович ГАВРИЛЕНКО,

доктор физико-математическихнаук, доцент,

Любовь Михайловна ПАРОХНЕНКО,

ассистент, Национальный транспортный университет

studfiles.net

Решение СЛАУ в Excel

Пример

На предприятие поступил заказ на изготовление 10 изделий трех различных модификаций. Общие затраты на изготовление этих изделий составят 4400 грн., а планируемая прибыль от их реализации должна со-

ставить 420 грн. Опреде-

Рис. 1. Вывод результатов

лить, сколько изделий расчета каждой модификации из-

готовят на предприятии, если известно, что затраты на изготовление одного изделия каждой модификации составляют соответственно 600, 400, 300 грн., а планируемая прибыль от реализации одного изделия каждой модификации равна соответственно 30, 50, 40 грн.

Решение

Обозначим через X1; X2; X3 — количество изделий каждой модификации. Тогда X1 + X2 + X3 — общее количество изделий, которое по условию задачи равно 10, то есть получаем уравнение: X1 + X2 + X3 = 10.

Затраты предприятия на производство всех изделий составляют 600X1 + 400X2 + 300X3, а по условию они равны 4400. Отсюда имеем второе уравнение: 600X1 + 400X2 + 300X3 = 4400.

Планируемая прибыль предприятия от продажи всех изделий равна 30X1 + 50X2 + 40X3, а по условию задачи она составляет 420. Получаем третье уравнение: 30X1 + 50X2 + 40X3 = 420.

Таким образом, решение задачи сводится к решению системы линейных алгебраических уравнений

x1 + x2 + x3 = 10								x1 + x2 + x3 = 10
600×1 + 400×2 + 300×3 = 4400 èëè								6×1		+ 4×2 + 3×3 = 44 .
30×1 + 50×2 + 40×3 = 420								3×1		+ 5×2+ 4×3 = 42
Для данной системы будем иметь
	1	1	1				10				x1
À =	6	4	3	;	Â =		44		;	Õ =	x2		.
	3	5	4				42				x3

Найдем решение этой системы, используя возможности Excel:

1.Вводим данные: расположим матрицу A в диапазоне ячеекB2:D4, а столбец свободных членов — в диапазоне ячеекB6:B8.

2.Вычислим определитель матрицы A с помощью встро-

енной функции МОПРЕД. Если он не равняется нулю, то процесс решения системы продолжается.

При вычислении определителя матрицы нужно:

·отметить ячейку F7, где будет находиться значение определителя матрицы;

·активизировать мастер функций (fx). Среди категорий функций выбираем «Математические», а среди функ-

Рис. 2. Вывод используемых функций

öèé — МОПРЕД. Далее вводим диапазон положена матрица А, то есть диапазон

3. Вычисляем обратную матрицу A-1 с ной функцииÌÎÁÐ. При этом следу

·отметить диапазон ячеек B10:D12, где ся обратная матрица;

·активизировать мастер функций (fx). функций «Математические» выбрать

·для получения на экране обратной пустить клавишу F2, а потом нажимаем

4. Найти решение системы уравнений с енной функции умножения матриц — цедура вычисления произведения аналогична процедуре определения

·отмечается диапазон ячеек F14:F16, где ся решение системы уравнений;

·активизируется мастер функций (fx). Среди категорий функций «Математические» выбираетсяМУМНОЖ. Далее вводятся диапазоны ячеек массивов, произведение которых вычисляется, то есть диапазони ячеек

B10:D12 è B6:B8;

·для получения на экране решения системы нажимается и отпускается клавиша F2, а затем комбинацияCtrl+

Shift+Enter.

Таким образом, на предприятии планируется изготовить заказ в количестве 3, 5 и 2 изделий трех модификаций соответственно.

Íà ðèñ. 1 показан результат решения, а наðèñ. 2 — та же таблица в режиме показа используемых формул, который можно включить, вызвав диалоговое окно Параметры из меню Сервис р Параметры, и включив на вкладке Вид флажок Формулы.

Литература

1.Дж.Уокенбах. Excel 97. Библия пользователя.– К.: Диалектика, 1997.– 624 с.

2.П.Дж. Бернс, Дж.Р. Николсон. Секреты Excel для Windows 95.— К.: Диалектика, 1996.— 576 с.

3.Толбатов Ю.А. Економетрика: П³дручник для студент³в.— К.: Четверта хвиля, 1997.— 320 с.

Валерий Владимирович ГАВРИЛЕНКО,

доктор физико-математическихнаук, доцент,

Любовь Михайловна ПАРОХНЕНКО,

ассистент, Национальный транспортный университет

studfiles.net