Системы линейных однородных уравнений онлайн
Системы линейных однородных уравнений – имеет вид ∑akixi = 0. где m > n или m n.Однородная система линейных уравнений всегда совместна, так как rangA = rangB. Она заведомо имеет решение, состоящее из нулей, которое называется тривиальным.
Назначение сервиса. Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция. Выберите размерность матрицы:
количество переменных:
2345678
и количество строк
23456
Свойства систем линейных однородных уравнений
Для того чтобы система имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше числа неизвестных.
Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.
Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.
Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из (
Алгоритм решения систем линейных однородных уравнений
- Находим ранг матрицы.
- Выделяем базисный минор. Выделяем зависимые (базисные) и свободные неизвестные.
- Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора, так как они являются следствиями остальных (по теореме о базисном миноре).

- Члены уравнений, содержащие свободные неизвестные, перенесем в правую часть. В результате получим систему из r уравнений с r неизвестными, эквивалентную данной, определитель которой отличен от нуля.
- Решаем полученную систему методом исключения неизвестных. Находим соотношения, выражающие зависимые переменные через свободные.
- Если ранг матрицы не равен количеству переменных, то находим фундаментальное решение системы.
- В случае rang = n имеем тривиальное решение.
Пример. Найти базис системы векторов (а1, а2,…,аm), ранг и выразить векторы по базе. Если а1=(0,0,1,-1), а2=(1,1,2,0), а3=(1,1,1,1), а4=(3,2,1,4), а5=(2,1,0,3).
Выпишем основную матрицу системы:
| 0 | 0 | 1 | -1 |
| 1 | 1 | 2 | 0 |
| 1 | 1 | 1 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 1 | 0 | 3 |
| x1 | x2 | x3 | x4 |
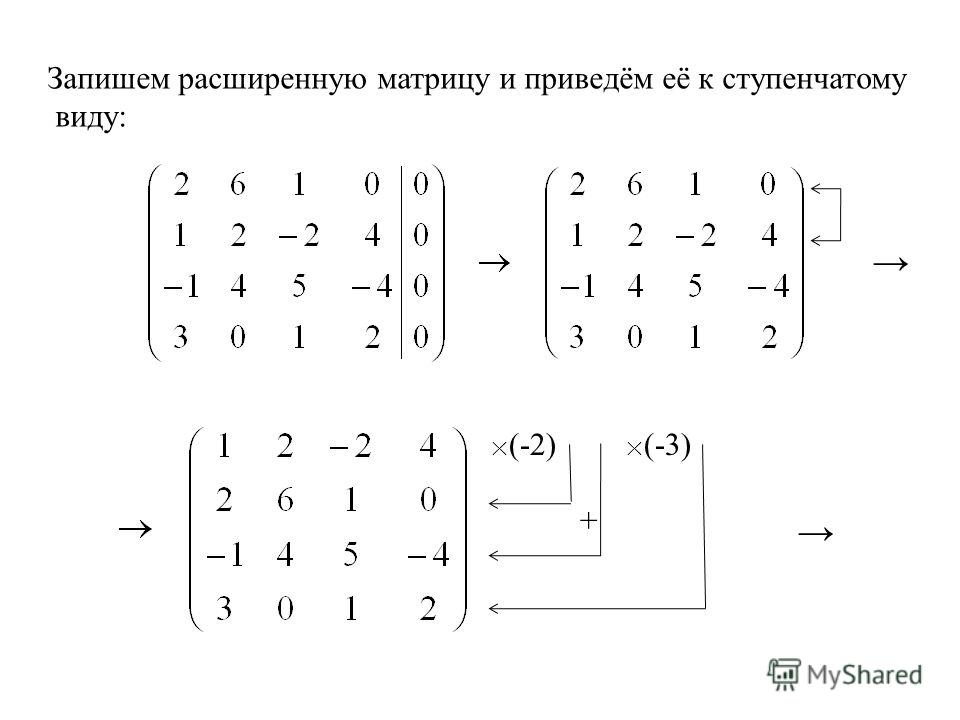
Приведем матрицу к треугольному виду.
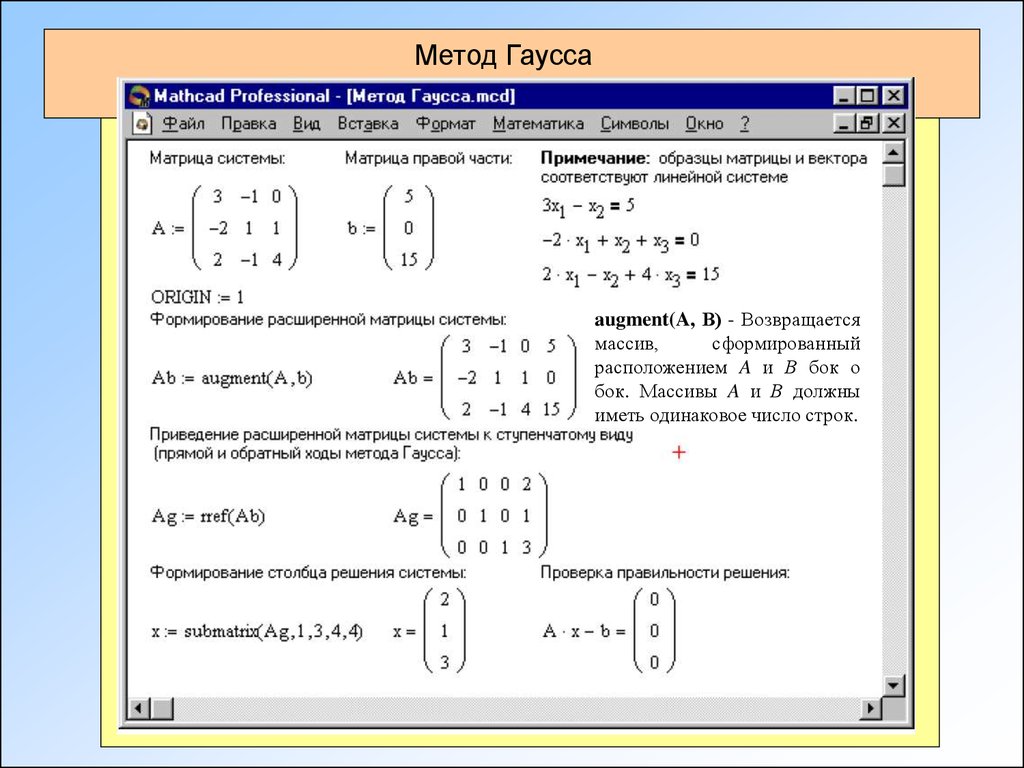 Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 1 | 1 | 1 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 1 | 0 | 3 |
Умножим 3-ую строку на (-3). Добавим 4-ую строку к 3-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 1 | 0 | 3 |
Умножим 4-ую строку на (-2). Умножим 5-ую строку на (3). Добавим 5-ую строку к 4-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
Умножим 3-ую строку на (-1).
 Добавим 4-ую строку к 3-ой:
Добавим 4-ую строку к 3-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
Добавим 2-ую строку к 1-ой:
| 0 | 0 | 0 | 0 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.

| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
Найдем ранг матрицы.
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
| x1 | x2 | x3 | x4 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 3.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 0 | -1 | -1 |
| 0 | -1 | -2 | -1 |
| 2 | 1 | 0 | -3 |
| x1 | x2 | x3 | x4 |
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
– x2 – 2x3 = – x4
2x1 + x2 = – 3x4
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x1,x2,x3 через свободные x4, то есть нашли общее решение:
x3 = x4
x2 = – x4
x1 = – x4
Калькулятор нормального распределения (статистика)
Калькулятор нормального распределения (статистика) Введите среднее (среднее), стандартное отклонение, точки отсечки, и этот калькулятор нормального распределения рассчитает площадь (=вероятность) под кривой нормального распределения.
- Страхование
Страховая компания получает в среднем два требования в неделю от определенного завода. Предполагая, что распределение Пуассона может моделировать количество требований, найдите вероятность, которую оно получит. три заявки в данную неделю, более четырех заявок в заданные - Нормальное распределение GPA
Средний средний балл равен 2,78 со стандартным отклонением 4,5. Какие студенты в нижней части 20% имеют какой средний балл? - Время сборки
Время сборки игрушки подчиняется нормальному распределению со средним значением 75 минут и стандартным отклонением 9 минут. Компания закрывается в 17:00 каждый день. Если человек начнет сборку в 16:00, какова вероятность того, что он закончит до ком - Срок службы
Срок службы лампочки является случайной величиной с нормальным распределением x = 300 часов, σ = 35 часов. а) Какова вероятность того, что случайно выбранная лампочка проработает более 320 часов? б) На какое значение L часов может ля - Ожидаемый срок службы
Ожидаемый срок службы батарей имеет нормальное распределение со средним значением 350 минут и стандартным отклонением 10 минут.
- Сравнительная характеристика
Стандартизированный тест был проведен для тысяч учащихся со средним баллом 85 и стандартным отклонением 8. Случайной выборке из 50 учащихся был проведен тот же тест, который показал средний результат. оценка 83,20. Имеются ли доказательства того, что в этой группе - Статистическое обследование
Напишите ВЕРНО ИЛИ НЕВЕРНО для каждого вопроса: 1 Стандартное отклонение измеряет центральное положение. 2. Наиболее частое наблюдение в наборе данных известно как мода. 3 Наиболее пассивным методом сбора данных является наблюдение. 4 Время доступа к вторичным данным составляет ш - Принимает решения
Решите расчетным путем, сколько кандидатов из общего числа 1000 кандидатов на должность генерального директора соответствуют требованиям приемлемости для желаемой производительности этой должности высшего руководства с вероятностью не менее 67% – при условии, конечно, что - SD – среднее
Среднее значение равно 10, а стандартное отклонение равно 3,5. Если набор данных содержит 40 значений данных, сколько примерно значений данных попадет в диапазон от 6,5 до 13,5?
Если набор данных содержит 40 значений данных, сколько примерно значений данных попадет в диапазон от 6,5 до 13,5? - Забег на 10 км
Время финиша Джоан в более смелом забеге на 10 км по валуну было на 1,77 стандартного отклонения быстрее, чем у женщин в ее возрастной группе. В ее возрастной группе участвовало 415 женщин. Предполагая нормальное распределение, сколько женщин бежало быстрее, чем Джоан? - Экзамен – нормальное распределение
Пять тысяч студентов сдают экзамен со средним значением 59 и отклонением 8. Сколько студентов наберет меньше 75 баллов?
more math problems »
- decimals
- fractions
- triangle ΔABC
- percentage %
- permille ‰
- prime factors
- complex numbers
- LCM
- GCD
- LCD
- combinatorics
- equations
- статистика
- … все математические калькуляторы
Калькулятор нормального распределения – Калькулятор нормального распределения онлайн
Калькулятор нормального распределения помогает вычислить кумулятивную вероятность того, что значение будет ниже или выше заданной точки данных. Нормальное распределение также известно как распределение Гаусса. Это наиболее значимое непрерывное распределение вероятностей.
Нормальное распределение также известно как распределение Гаусса. Это наиболее значимое непрерывное распределение вероятностей.
Что такое калькулятор нормального распределения?
Калькулятор нормального распределения — это онлайн-инструмент, который определяет вероятность того, что значение будет выше или ниже заданной точки данных x. Колоколообразная кривая вероятности используется для изображения нормального распределения. Чтобы использовать Калькулятор нормального распределения введите значения в соответствующие поля ввода.
Калькулятор нормального распределения
ПРИМЕЧАНИЕ. Пожалуйста, вводите значения не более трех цифр.
Как пользоваться калькулятором нормального распределения?
Выполните следующие шаги, чтобы найти вероятность того, что значение будет выше или ниже заданной точки данных, используя калькулятор нормального распределения.
- Шаг 1: Перейдите к онлайн-калькулятору нормального распределения Cuemath.

- Шаг 2: Введите среднее значение, стандартное отклонение и точку данных в поля ввода.
- Шаг 3: Нажмите кнопку “Рассчитать” , чтобы найти вероятность.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор нормального распределения?
Есть два параметра, которые необходимы при расчете нормального распределения. Это среднее значение и стандартное отклонение. Нормальное распределение симметрично относительно среднего. Приведенные ниже шаги используются для расчета площади под кривой нормального распределения, чтобы установить вероятность того, что значение будет выше или ниже случайной величины x.
- Шаг 1: Сначала мы вычисляем Z-показатель. Это определяется как Z = (x – u)/sd. Здесь u — среднее значение, а sd — стандартное отклонение данных.
- Шаг 2: Теперь мы используем таблицу нормального распределения для определения значения φ (Z).
 Это будет представлять P(X < x). Это связано с тем, что таблица нормального распределения представляет площадь под кривой нормального распределения слева от показателя Z.
Это будет представлять P(X < x). Это связано с тем, что таблица нормального распределения представляет площадь под кривой нормального распределения слева от показателя Z. - Шаг 3: Чтобы определить P (X > x), мы вычитаем значение P(X < x) из 1,
Вероятность того, что значение меньше x, определяется как
P (X < x) = φ (Z) = φ ((x - u)/sd)
P (X > x) = 1 – P(X < x)
P (X > x) = 1 – φ (Z) = 1 – φ ((x – u)/sd)
Хочу находить сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры на калькуляторе нормального распределения
Пример 1:
Найти P(X < 5) и P(X > 5), когда нам дано среднее значение = 4 и стандартное отклонение = 2 нормального распределения. Проверьте это с помощью калькулятора нормального распределения.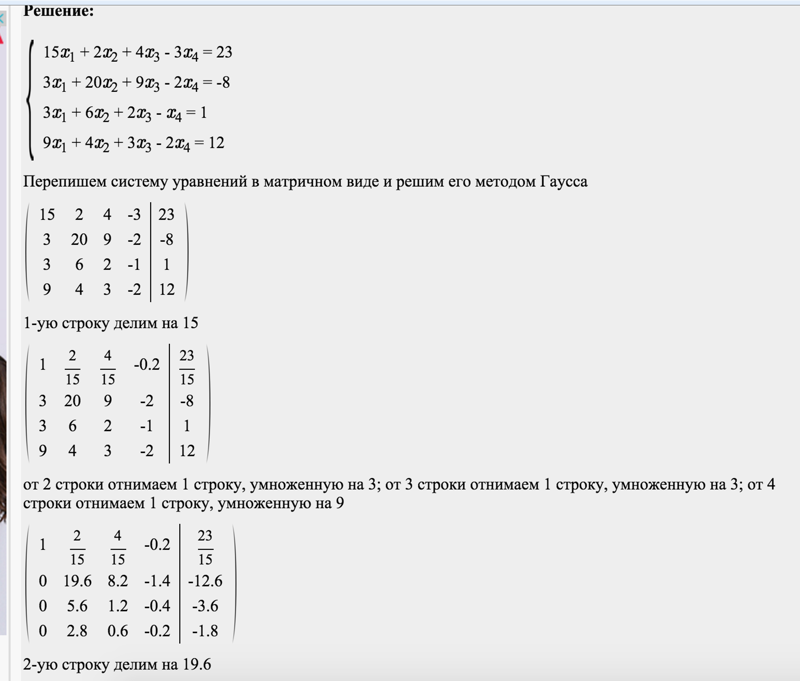


 Если набор данных содержит 40 значений данных, сколько примерно значений данных попадет в диапазон от 6,5 до 13,5?
Если набор данных содержит 40 значений данных, сколько примерно значений данных попадет в диапазон от 6,5 до 13,5?
 Это будет представлять P(X < x). Это связано с тем, что таблица нормального распределения представляет площадь под кривой нормального распределения слева от показателя Z.
Это будет представлять P(X < x). Это связано с тем, что таблица нормального распределения представляет площадь под кривой нормального распределения слева от показателя Z.